Effect of 3d/4p Mixing on 1s2p Resonant Inelastic X-ray Scattering: Electronic Structure of oxo-bridged Iron Dimers

Abstract

1s2p resonant inelastic x-ray scattering (1s2p RIXS) has proven successful in the determination of the differential orbital covalency (DOC, the amount of metal vs. ligand character in each d molecular orbital) of highly covalent centrosymmetric iron environments including heme models and enzymes. However, many reactive intermediates have non-centrosymmetric environments, e.g. the presence of strong metal-oxo bonds, which results in the mixing of metal 4p character into the 3d orbitals. This leads to significant intensity enhancement in the metal K-pre-edge and as shown here, the associated 1s2p RIXS features, which impact their insight into electronic structure. Binuclear oxo bridged high spin Fe(III) complexes are used to determine the effects of 4p mixing on 1s2p RIXS spectra. In addition to developing the analysis of 4p mixing on K-edge XAS and 1s2p RIXS data, this study explains the selective nature of the 4p mixing that also enhances the analysis of L-edge XAS intensity in terms of DOC. These 1s2p RIXS biferric model studies enable new structural insight from related data on peroxo bridged biferric enzyme intermediates. The dimeric nature of the oxo bridged Fe(III) complexes further results in ligand-to-ligand interactions between the Fe(III) sites and angle dependent features just above the pre-edge that reflect the superexchange pathway of the oxo bridge. Finally, we present a methodology that enables DOC to be obtained when L-edge XAS is inaccessible and only 1s2p RIXS experiments can be performed as in many metalloenzyme intermediates in solution.

Graphical Abstract

Introduction

The chemical and physical properties of the active sites in many proteins and enzymes are often determined by first-row transition metal ions. Spectroscopic tools to enhance the understanding of the metal 3d orbitals and their covalent ligand interactions are therefore of high importance. X-ray spectroscopy involves creating a core-hole and thus offers an element specific method for obtaining detailed insight into the electronic structure.¹ This is a particular advantage in highly covalent environments such as heme metallo-enzymes, where the metal signal can be obscured by the strong heme background in other spectroscopic methods. Soft X-ray absorption spectroscopy (XAS) in particular transition metal L_2,3-edge XAS, which studies the metal 2p → 3d transitions, has proven to be invaluable in determining detailed electronic structure information including the ligand-to-metal (LMCT) and metal-to-ligand (MLCT) charge transfer character (i.e. donor and acceptor bonding) for each metal 3d orbital (i.e. the differential orbital covalency, DOC).^2-4 As soft X-rays usually require high vacuum conditions partially due to the e⁻ detection over photon detection and low penetration depth, L-edge XAS is often not suitable for metallo-proteins and enzymes. Hard X-ray 1s2p resonant inelastic X-ray scattering (1s2p RIXS) measurements have a high penetration depth and do not require an UHV sample environment. This RIXS experiment involves resonantly exciting a 1s electron into unoccupied 3d orbitals, followed by a photon emitted by the decay of a 2p electron to fill the 1s core hole.⁵ Thus both the photon-in and photon-out energies are appropriate for metallo-enzymes in solution. The resulting 1s2p RIXS final states have the same configurations as the L-edge XAS final states, but with different selection rules than in direct L-edge XAS.⁶ In a previous study on cytochrome c, 1s2p RIXS only data were used to determine the DOC of the ferrous and ferric protein sites starting from well described heme model complexes.⁷ Characteristic features in the 1s2p RIXS planes were identified that reflect the main influences of the electronic structure changes associated with going from the heme model complex with two axial imidazole ligands to the heme protein with axial methionine and histidine ligands. ⁷

The intensity and shape of the K-pre-edge is largely dominated by the local ligation around the transition metal ion. In a complex with close to inversion symmetry the 1s → 3d pre-edge transitions are electric quadrupole allowed and relatively weak. In the absence of an inversion center, metal 4p character can mix into the 3d orbitals and contribute electric dipole allowed intensity in the K-pre-edge. Since this is approximately 100 times stronger than 1s → 3d transitions, only a few percent of 4p mixing can perturb and dominate the pre-edge spectral shape.⁸ 1s2p RIXS planes are constructed by moving the incident energy through the pre-edge region for fixed emission energies or the other way around. By integrating along the energy transfer direction (i.e. the vertical axis in the RIXS plane that is the energy difference between the photon in and the photon out), the full K-edge XAS is obtained. Therefore, 1s2p RIXS planes will also be affected by a loss of inversion. Importantly, due to the 2-dimensional nature of the RIXS planes, this electric dipole contribution to the pre-edge region can also provide information on the electronic structure that complements the insight available from direct 2p → 3d L-edge XAS.

Mixing of 4p character into the 3d orbitals can occur in two ways. One is a direct interaction due to the non-centrosymmetric components of the ligand field, which corresponds to a direct matrix element between the metal 3d and 4p orbitals.⁹ In this ligand field theory method, the amount of 4p character mixed into the 3d orbitals is independent of the ligand-metal covalent overlaps and has been used without the explicit inclusion of LMCT in the Hamiltonian.^10-13 The alternative and more efficient mechanism of p/d mixing involves their covalent interactions with the ligands. This requires the explicit inclusion of the ligand orbitals in the Hamiltonian resulting in a 3 × 3 matrix:

$$\begin{array}{cccc}\hfill \hfill & \hfill \mid Fe4p\rangle \hfill & \hfill \mid L2p\rangle \hfill & \hfill \mid Fe3d\rangle \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \langle Fe4p\mid \hfill & \hfill {\Delta }^{4p}\hfill & \hfill T^{4p}\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \langle L2p\mid \hfill & \hfill T^{4p}\hfill & \hfill 0\hfill & \hfill T\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \langle Fe3d\mid \hfill & \hfill 0\hfill & \hfill T\hfill & \hfill \Delta \hfill \end{array}$$ (1)

where the metal 3d (at an energy Δ) mixes with the ligand p orbitals through their overlap T, and the same ligand orbital further overlaps the metal 4p orbital, T^4p (at an energy Δ^4p).¹⁴ In this study, the LMCT p/d mixing method is included as a direct result of the covalent bonds (additional details are given in the Supporting Information).

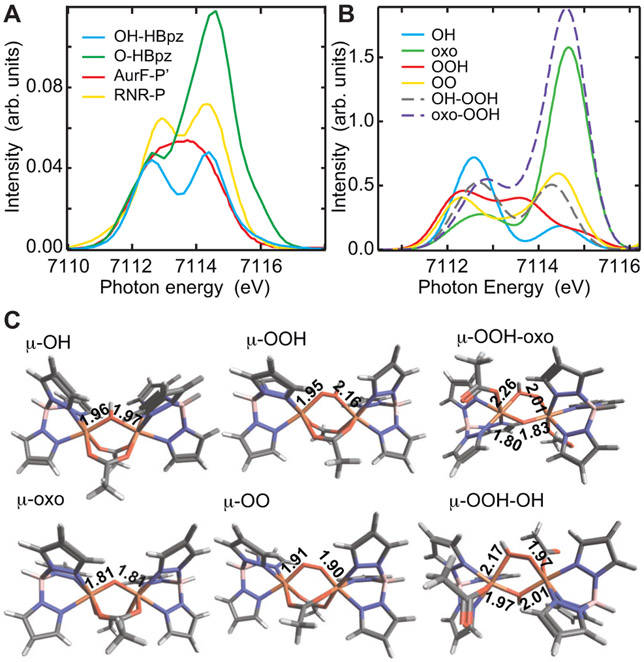
Many key biological active sites in particular the high valent Fe(IV)=O heme and nonheme enzyme intermediates and their model complexes^15,16 have no inversion center at the Fe site leading to intense K-pre-edge XAS features. This is also the case for the biferric peroxo and high-valent biferryl intermediates found in nonheme diiron enzymes and their model complexes.^17-19 1s2p RIXS offers a unique opportunity to study these complexes due to its element selectivity and sensitivity to DOC. In this study, we determine the effects of 3d/4p mixing on the spectral shape of 1s2p RIXS 2D maps of binuclear high-spin ferric Fe(III) complexes having approximate O_h and C_4v local symmetry. We have chosen high-spin Fe(III) systems as these are well understood from L-edge XAS² and provide a good starting point to understand the 4p mixing effects of an Fe(III)-oxo bond. In addition, they have key structural features anticipated to be present in biferric peroxo enzyme intermediates.²⁰ Three Fe-dimer complexes were studied: The hydroxo bridged Fe₂-OH-(HBpz₃)₂(μ-ac)₂ complex (hbpz₃ = tri-1-pyrazolylborate, μ-ac = carboxylate bridge)²¹ has a quasi-octahedral local Fe environment and serves as a centrosymmetric reference (see Figure 1 A). Deprotonation of the hydroxo bridge to form a biferric oxo-bridge (with the same ligand environment, Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, Figure 1 B), leads to short Fe-O bond lengths (1.96 to 1.79 Å in μ-OH and μ-oxo, respectively). This eliminates the approximate inversion symmetry at the Fe reducing the local symmetry to approximately C_4v. Both complexes have an Fe-O-Fe angle of ~124°. A second oxo-bridged biferric complex is included in this study, where the ligand system is changed to hedta, and the Fe-O-Fe bond angle increases to 165° (Figure 1 C), but keeps the same Fe-oxo bond lengths, the high-spin configuration and approximate local C_4v symmetry.

Figure 1:

Crystal structures of the three model compounds Fe₂-OH-(HBpz₃)₂(μ-ac)₂ (A), Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (B) and Fe₂-oxo-hedta₂ (C).

In this study, the L-edge, K-edge XAS spectra and 1s2p RIXS 2D maps of all three complexes are analyzed to extract the DOC using a valence bond configuration interaction (VBCI) mulitplet model to fit L-edge XAS and RIXS data.^2,6,7 The 2p core-hole in the L-edge XAS and 1s2p RIXS final states leads to strong 2p spin-orbit coupling and 2p-3d Coulomb repulsion that influence the relative intensities and shapes of the L₃- and L₂-edge and the 1s2p RIXS maps and must be included in the multiplet analysis to quantitatively estimate covalency (i.e. DOC). Advantages (and disadvantages) of the strong electric dipole intensity contributions from 4p mixing to the RIXS planes are determined by comparing cuts through the 1s2p RIXS map to L-edge and K-edge XAS data. For many biological systems, L-edge XAS cannot be measured and only 1s2p RIXS would be available. Therefore the determination of the covalent ligand-metal bonding in terms of DOC from 1s2p RIXS planes alone is further developed. This study also provides new insight into the molecular orbital origin of the 4p mixing in Fe=O systems and explains the dominant 3d(z²)/4p(z) intensity contribution found experimentally. The DOC allows access to the covalent mixing in the oxo-dπ and oxo-dσ orbitals, which are the frontier molecular orbitals (FMOs) in metal-oxo systems that play a key role in many reactions.

To fully analyze the data, we take two complementary approaches. One where we use the VBCI multiplet model to fit the experimental data and extract bonding information in terms of DOC from experiment. This is then compared to Mulliken populations from DFT calculations enabling the correlation of the experimental RIXS data to the DFT calculations. This complementary approach also provides insight into dimer specific covalent mixing through inter-oxo bridged ligand-ligand interactions and angle dependent inter Fe transitions reflecting oxo superexchange pathways

Using the advanced insight from the analysis of the full 1s2p RIXS maps of the hydroxo- and oxo-bridged model complexes as references, we also gain new insight into the geometric structures of several peroxo bridged biferric enzyme intermediates, in particular when an oxo bridge is also present that would greatly impact reactivity.

Experimental and Computational Methods

Sample Preparation:

Crystalline samples of Fe₂-OH-(HBpz₃)₂(μ-ac)₂, Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, and Fe₂-oxo-hedta₂ were prepared following standard procedures.^21-24

Experimental Methods:

In this study, two experimental methods have been employed: soft X-ray L-edge XAS and 1s2p RIXS. These experiments have been performed at the Stanford Synchrotron Radiation Lightsource (SSRL) at beam lines 10-1 (L-edge XAS) and 6-2 (1s2p RIXS).²⁵ Experimental details on both methods are given in the Supporting Material. All data sets (L-edge XAS, 1s2p RIXS) have been measured at least twice to ensure reproducible and reliable data. Special attention has been paid to avoid photo damage by moving over the sample and illuminating each sample spot for only a short amount of time.

All 1s2p RIXS planes are normalized to unity at the edge-jump allowing for a direct comparison with K-edge XAS results. The pre-edge in a 1s2p RIXS experiment includes the tail of the intense 1s → 4p transitions at approximately 15 eV above the pre-edge. This leads to an increase of the pre-edge background and complicates the direct comparison of L-edge data with constant incident energy (CIE, i.e. vertical) cuts through the RIXS plane. In order to estimate the RIXS pre-edge intensity from the tail of the rising-edge, the full RIXS planes were fit to extract the true pre-edge region as described previously.^7,26

Charge Transfer Multiplet Simulations:

To simulate both L-edge and RIXS X-ray spectra, charge transfer multiplet calculations were performed.^27-30 The calculations were performed in the C_4v crystal field symmetry for all three complexes. Covalent mixing of ligand character into unoccupied 3d orbitals was modeled using the valence bond configuration interaction (VBCI) approach. Ligand-to-metal charge transfer (LMCT) is introduced via a $d^{n+1}\underset{¯}{L}$ ($\underset{¯}{L}$ = ligand hole) configuration that is mixed into the dⁿ configuration in the ground state. LMCT charge transfer channels were included through the overlap parameters T(B₁), T(A₁), T(E), and T(B₂) with the corresponding ligand-to-metal charge transfer energy Δ. 4p mixing was included by the introduction of an additional ligand-to-metal(4p) charge transfer (LM_4pCT) configuration. Here, the LM_4pCT channels were included via T(A₁) (4p_z/3d_z²) and T(E) (4p_x,y/3d_xz,yz) as allowed in C_4v symmetry at an energy Δ^4p. Details including a description of the model and the calculation of absolute absorption intensities normalized to the edge jump are given in the Supporting Material. The metal-ligand covalency for each of the symmetry blocks (i.e. the DOC) was calculated using the projection method.² Here, each 3d hole has 100% metal character. Upon ligand-to-metal covalent mixing, the metal character decreases (and ligand character in the 3d orbitals increases).

Initial VBCI fits to the L-edge XAS spectra were obtained using a trust region reflective non-linear least squares fitting approach from a series of 100 sets of start parameters that were randomly generated. From these, the best parameter set was determined by their refinement of simultaneously fitting to both the L-edge XAS and 1s2p RIXS data (see Supporting Information for more details).

Density Functional Theory Calculations:

All calculations were carried out using the ORCA quantum chemistry program, version 4.0.0.2.³¹ For all calculations, the non-optimized crystal structures of the three complexes^21-23 were used. The B3LYP functional³² was employed with standard polarized triple-zeta basis set def2-TZVPP³³ and auxiliary basis set def2/J,³⁴ and the more flexible CP(PPP) basis set³⁵ on the central di-iron ions. A dense integration grid (grid4), and tight convergence criteria were enforced.

For TD-DFT derived K pre-edge XAS spectra,^36-40 the application of scalar relativistic corrections (ZORA)^41,42 did not lead to a better description and has thus been omitted, as found previously.³⁸ For all XAS calculations, electric dipole, electric quadrupole and magnetic dipole contributions are included. Calculated K pre-edge spectra were visualized using the ORCA_MAPSPC module with a Gaussian broadening of 1.0 eV. For transitions that are electric-dipole allowed, the electric-quadrupole and magnetic dipole contributions become origin dependent.^43-45 To account for this, the origin adjusted method (ABSQ) using a minimization procedure that guarantees the fastest convergence of the multipole expansion was used, which gave similar results as the origin independent method (ABSOI)^43,46 in the energy range of interest. A constant energy shift of 151.5 eV was applied to the calculated spectra. Mulliken population analyses⁴⁷ were performed using the QMForge Suite.⁴⁸

Results and Analysis

Three sets of data were obtained for the three complexes: Fe L-edge and K-edge XAS, and 1s2p RIXS. In this section, the L-edge XAS data are presented together with their charge transfer multiplet simulations and the resulting DOC. This is then compared to the results of DFT calculations. The K-edge is presented both from K-edge XAS and from high-resolution constant emission energy (CEE) cuts in the pre-edge and the extended pre-edge region of the RIXS plane and analyzed using TD-DFT calculations. The constant incident energy (CIE) cuts are then presented, connected to the L-edge XAS and analyzed with the multiplet model. Finally, given a well defined relevant model complex we show that the 1s2p RIXS plane alone can be used to define the DOC of an intermediate in solution.

L-edge XAS and DOC

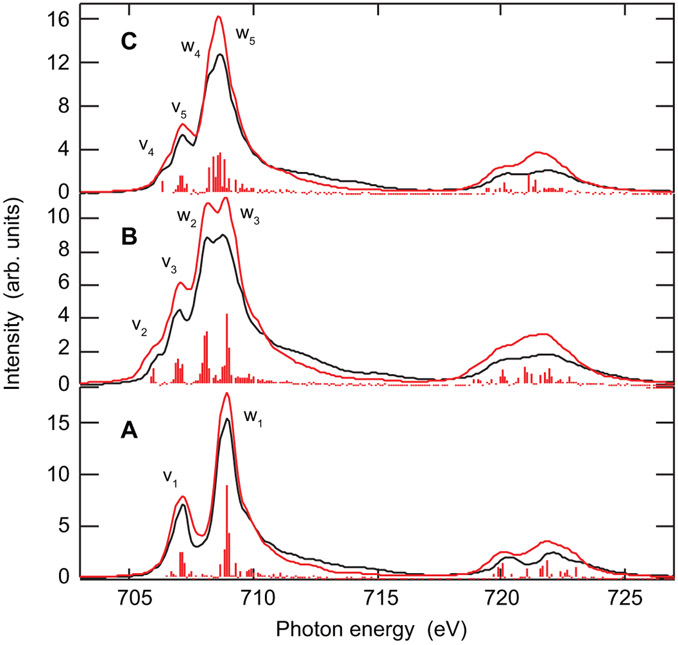
Soft X-ray L-edge XAS directly probes the unoccupied Fe 3d orbitals via electric dipole allowed 2p → 3d transitions and therefore experimentally quantitatives the covalency (by the decrease in d character and therefore intensity due to bonding). L-edge XAS for Fe₂-OH-(HBpz₃)₂(μ-ac)₂, Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, and Fe₂-oxo-hedta₂ are shown in Figure 2 A-C (black), respectively.

Figure 2:

Experimental L-edge XAS together with their charge transfer multiplet simulations of Fe₂-OH-(HBpz₃)₂(μ-ac)₂(A), Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (B), and Fe₂-oxo-hedta₂ (C). Experimental spectra are shown in black, while simulations are shown in red.

The Fe₂-OH-(HBpz₃)₂(μ-ac)₂ L-edge XAS spectrum (Figure 2A) is very similar to those of typical high spin O_h Fe(III) complexes.² For high spin ferric L₃-edges, the low energy intensity at 707.1 eV (v₁) originates predominantly from transitions into dπ orbitals (t_2g-like) with a small amount of dσ (e_g-like) character, while the intensity around 708.9 eV (w₁) contains similar dπ and dσ contributions to the intensity (mixed by the 3d-2p exchange).⁴⁹

Upon going from an OH to an oxo bridge (Figure 2 A to B and C), the L-edge XAS spectra change reflecting the change in electronic structure due to the shortened Fe-oxo bonds (by ~0.2 Å).^21-23 The shortened Fe-O(bridge) bond length in the oxo dimer reduces the local geometric structure from quasi O_h to C_4v. As a result, the low and high energy peaks broaden due to the energy splitting of the t₂ π (into b₂ (d_xy) and e (d_xz,yz)) and e σ (into b₁ (d_x²–y²) and a₁ (d_z²)) degeneracies.

The Fe₂-OH-(HBpz₃)₂(μ-ac)₂ peak at 707.2 eV (v₁) incident energy splits into two well separated features at 706.1 and 707.0 eV for Fe₂-oxo-(HBpz₃)₂(μ-ac)₂(v₂ and v₃), and 706.3 and 707.2 eV for Fe₂-oxo-hedta₂(v₄ and v₅). The main peak at 708.9 eV (w₁) for Fe₂-OH-(HBpz₃)₂(μ-ac)₂ splits into two well separated peaks at 708.1 and 707.7 eV for Fe₂-oxo-(HBpz₃)₂(μ-ac)₂(w₂ and w₃), and into a main peak at 708.7 eV and a shoulder at ~708.2 eV for Fe₂-oxo-hedta₂(w₄ and w₅). Due to the shorter Fe-O(bridge) bond length, the z² level shifts to higher energies, while the xy level should be at lowest energy. Quantitatively, the precise energy of these splittings are strongly influenced by the pd and dd e⁻-e⁻ Coulomb repulsion and exchange.^50,51

The absolute integrated intensity of a normalized and background subtracted Fe L-edge XAS spectrum reflects the total metal 3d character of the unoccupied valence orbitals.^52,53 For the three biferric complexes, the integrated intensities are: 47 ± 3 units (Fe₂-OH-(HBpz₃)₂(μ-ac)₂), 41 ± 8 units (Fe₂-oxo-(HBpz₃)₂(μ-ac)₂) and 45 ± 7 units (Fe₂-oxo-hedta₂). They represent similar metal 3d characters within error, with the trends of an increased covalent mixing (i.e. decreased intensity, therefore lower metal d character) upon deprotonation of the Fe-OH bridge (with the same (HBpz₃)₂(μ-ac)₂ ligand environment) and a decreased covalency (increased metal d character) upon exchanging the non-oxo ligand environment (HBpz₃(μ-ac)₂ to hedta₂).

While the total intensity is given by the ground state, the spectral shape is determined by the final states that are reached via the 2p → 3d electric dipole transitions.⁵³ To interpret the experimental spectra, simulations using charge transfer multiplet calculations are necessary that take the 3d/2p-core-hole interaction properly into account.⁵⁰ Figure 2A-C (red curves) shows the best fits of Fe₂-OH-(HBpz₃)₂(μ-ac)₂, Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, and Fe₂-oxo-hedta₂ L-edge spectra, respectively, using multiplet calculations with valence bond configuration interaction (VBCI) included. Details on the parameters used are given in the Supporting Information. Note that these best fits result from the simultaneous analysis of the L-edge XAS (Figure 2) and 1s2p RIXS data (vide infra). All spectral features and trends are well described including the additional ligand field broadening and splittings for the oxo bridged complexes.

For all three complexes, a high spin ground state is found consistent with experiment. By using the projection method on the ground state configurations, the metal 3d character for each individual 3d orbital, i.e. the differential orbital covalency (DOC), was determined.² The resulting values from the total d character from the L-edge XAS total intensity and from DFT Mulliken population analyses are given in Table 1.

Table 1:

Summary of L-edge Integrated Intensities, DOC Simulation Results, and Molecular Orbital Calculations. Note that the value for Fe(e) is per orbital and the e set carries twice this amount.

		L-edge + 1s2p RIXS covalency (%)					DFT covalency (%)
	intensity	Fe(b2)	Fe(e)	Fe(b1)	Fe(a1)	total	Fe(b2)	Fe(e)	Fe(b1)	Fe(a1)	total
Fe2-OH-(HBpz3)2(μ-ac)2	47 ± 3	88	88	74	74	413	84	88	74	74	408
Fe2-oxo-(HBpz3)2(μ-ac)2	41 ± 8	89	80	76	67	392	86	79	78	68	390
Fe2-oxo-hedta2	45 ± 7	91	84	77	69	405	88	81	76	68	394

The VBCI derived DOCs agree with the values found from DFT and with the total experimental intensity in showing an increased covalency (i.e. decreased metal d character) in going from Fe₂-OH-(HBpz₃)₂(μ-ac)₂ to Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (413 to 392%), as well as a decreased covalency (increased metal d character) by changing the Fe₂-oxo ligation from (HBpz₃)₂(μ-ac)₂ to hedta₂ (392 to 405%). Upon lowering the local symmetry from an OH to an oxo bridge, the orbitals having direct overlap with the bridging oxygen (local z-direction) are affected the most. The e (d(xz/yz) (dπ)) metal character decreases from 88 to 80% per orbital and the a₁ (d(z²) (dσ)) metal character decreases from 74 to 67%. In going to the hedta₂ Fe₂-oxo dimer, the largest changes are observed in the dπ orbitals (89→91% for b₂ and 80→84% for e). Both, experiment and DFT calculations reflect these changes.

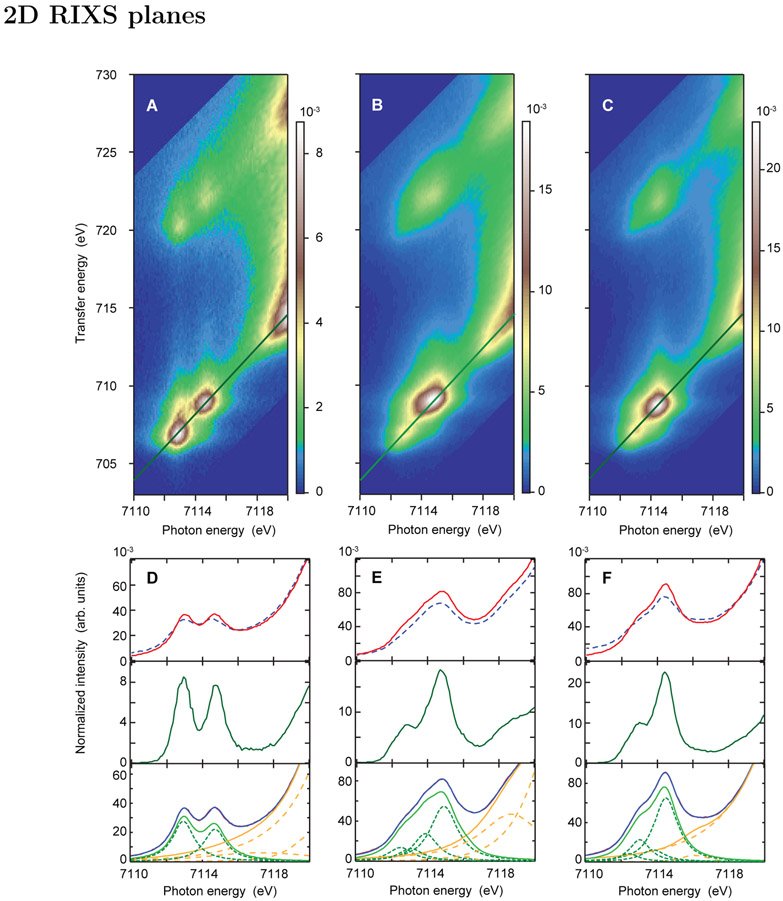
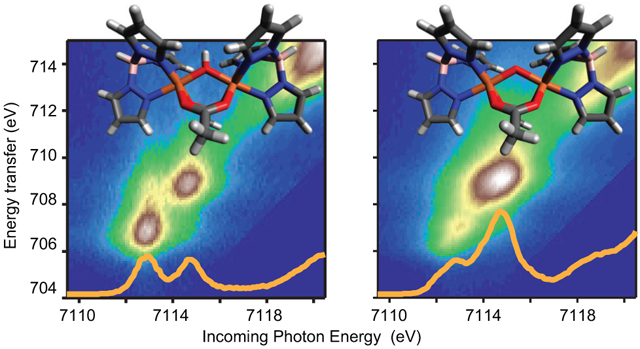
In the 1s2p RIXS process, a 1s electron is excited into unoccupied 3d orbitals with potential 4p character mixed in via electric quadrupole and electric dipole transition moments, respectively. This absorption process probes the unoccupied density of states with the corresponding incident energy being plotted along the horizontal axis in the 2D maps (Figure 3). In the electric dipole 2p → 1s emission process, plotted as the transfer energy (difference between the energy of the photon in and the photon out, vertical axis) in the 1s2p RIXS planes, the occupied density of states is probed through the Coulomb and exchange interaction of the 2p core-hole with the 3d electrons. Figure 3 shows the 1s2p RIXS planes normalized to the edge-jump of Fe₂-OH-(HBpz₃)₂(μ-ac)₂ (A), Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (B), and Fe₂-oxo-hedta₂ (C). The maximum of the color scale is set to the maximum intensity in the individual pre-edge region. All three complexes show pre-edge intensities between ~7112-7116 eV clearly separated from the rising edge (visible at >7119 eV) in the 2D presentation.

Figure 3:

Experimental 1s2p RIXS planes of (A) Fe₂-OH-(HBpz₃)₂(μ-ac)₂, (B) Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, and (C) Fe₂-oxo-hedta₂. All spectra are normalized to the edge jump and plotted such that the maximum intensity is in the pre-edge region. (D)-(F) show the corresponding K-edge spectra from the integrated RIXS plane (red solid) and the direct K-edge XAS measurement (blue dashed, top), together with the CEE cut (green solid, middle). The direct K-edge data are adapted from Ref. 8. The bottom figures show the fits to the K-edge derived from the integrated RIXS planes. The resulting background subtracted pre-edge fit is shown in light green solid.

For S=5/2 high spin systems in quasi O_h environments, two main transitions to the intermediate state (1s → 3d) are expected into the t_2g and e_g orbitals,⁸ while for the oxo-bridged systems in C_4v symmetry four transitions are expected due to the additional C_4v ligand field splitting (t_2g (O_h) splits into b₂, e, and e_g (O_h) into b₁, a₁). As expected, the Fe₂-OH-(HBpz₃)₂(μ-ac)₂ RIXS map shows two separated pre-edge peaks with similar intensities at 7112.9 and 7114.6 eV. In going to the oxo-bridged complexes, the pre-edge intensity pattern changes. In both oxo bridged high spin ferric complexes, one dominant feature at ~7114.8 eV (Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, Figure 3B) and 7114.4 eV (Fe₂-oxo-hedta₂, Figure 3C) is visible together with a low intensity feature at lower energies. The high intensity of the ~7114.8 and ~7114.4 eV peaks emphasizes the relevance of the additional electric dipole intensity due to the 4p character mixed in the 3d orbitals.

A more detailed analysis is done by cuts through the 2D 1s2p RIXS plane: Diagonal cuts through the RIXS plane along the constant emission energy (CEE) give K-edge like spectra with higher resolution than conventional K-edge XAS due to the long-lived 2p core-hole final state^54,55 These will be analyzed in the next section (K-Edge and CEE Spectra). Vertical cuts along the transfer energy direction at constant initial energy (CIE) reach final states that are identical to those reached in direct L-edge XAS but with different selection rules.⁶ This allows a direct comparison of 1s2p RIXS and L-edge XAS and will be presented in a later section (L-edge-like CIE cuts).

K-Edge and CEE Spectra

The Pre-Edge Region

K-pre-edge XAS involves 1s → 3d transitions into unoccupied valence orbitals. These spectra are shown in Figure 3 (D-F) as derived from the integrated RIXS map (red solid, top) and the direct K-edge XAS measurement (blue dashed, top). The 1s2p RIXS derived K-edge aligns well with the direct K-edge XAS measurement taken from Ref 8, including absolute intensities. The K-pre-edge spectrum of the approximately O_h complex, Fe₂-OH-(HBpz₃)₂(μ-ac)₂, resolves two peaks at ~7113 and ~7114.5 eV, consistent with other high spin d⁵ studies.⁸ Upon lowering the local symmetry to C_4v in the μ-oxo bridged complexes (Figure 3E and F), the pre-edge intensity doubles due to additional mixing of 4p character in the 3d orbitals. The increased intensity is most pronounced in the higher energy region of the K-pre-edge at ~7114.5 eV.

These observations become more prominent in the CEE cuts as shown in Figure 3D-F (green solid, middle). In high spin S=5/2 Fe(III) K-pre-edges the multiplet effects simplify to a one electron orbital description.⁸ Therefore, two main transitions are expected in O_h symmetry and four transitions in C_4v due to the additional orbital splittings. As anticipated, the Fe₂-OH-(HBpz₃)₂(μ-ac)₂ spectrum contains two CEE peaks, while four peaks are necessary to fit the CEE cuts of Fe₂-oxo-hedta₂ and Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (see Figure 3 D-F bottom).

The full K-edges i.e. integrated 1s2p RIXS planes, were fit with two (OH-bridged) and four peaks (oxo-bridged) in the pre-edge region together with a proper background. Note that relative intensities in the CEE cuts do not necessarily represent the correct intensity ratios due to off diagonal intensity contributions in the 1s2p RIXS planes. The fits to the three complexes are shown in Figure 3D-F (bottom) and Figure S2 together with a description of the procedure to fit the data. For Fe₂-OH-(HBpz₃)₂(μ-ac)₂, the low energy peak at 7112.9 eV accounts for 55% of the total pre-edge intensity, or 5.9 out of 10.7 total units of intensity normalized to the edge jump (Table 2).

Table 2:

Results of a multiple peak fit to the K pre-edge of the three complexes. The energy position is given in eV, while the intensity is given in absolute units.

	total intensity	peak i				peak ii
		energy		intensity		energy		intensity
Fe2-OH-(HBpz3)2(μ-ac)2	10.7	7112.9		5.9		7114.7		4.8
	total intensity	peak 1		peak 2		peak 3		peak 4
		energy	int.	energy	int.	energy	int.	energy	int.
Fe2-oxo-(HBpz3)2(μ-ac)2	24.9	7112.5	2.8	7113.0	2.7	7114.2	6.0	7115.0	13.4
Fe2-oxo-hedta2	22.7	7112.4	1.6	7113.0	4.1	7113.8	2.8	7114.5	14.2

In Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ and Fe₂-oxo-hedta₂, the local symmetry lowers to C_4v due to the short Fe-O bridge bond, and 4p character is mixed into the 3d orbitals.^{8,10-12,56,57} In C_4v symmetry, the 4p(z) orbital is allowed to mix with the 3d(z²) (a₁) and the 4p(x, y) orbitals are allowed to mix with the 3d(xz, yz) (e). The mixing of 4p character into the 3d orbitals results in a 1s → 4p electric dipole contribution to the pre-edge. As a consequence, the total pre-edge intensities of the Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ and Fe₂-oxo-hedta₂ spectra increase by around a factor of two relative to the Fe₂-OH-(HBpz₃)₂(μ-ac)₂ pre-edge intensity. In more detail, the spectral shapes of both μ-oxo-bridged complexes are now dominated by an intense feature at higher energies, which is better resolved in the CEE cuts. The four peaks fit to the data (Figure 3(bottom)) reveals that the highest energy peak at ~7115 eV gains considerable intensity, while the two lower energy peaks (peaks 1 and 2 in Table 2, the b₂ and e components in C_4v), which correlate to the first peak for the quasi octahedral Fe₂-OH-(HBpz₃)₂(μ-ac)₂ complex, do not gain intensity. Therefore, only a₁ mixing occurs, even though dπ/p_x,y (e) mixing is allowed by group theory.

Estimating the amount of 4p character mixed into the 3d pre-edge of the experimental spectrum was achieved by subtracting the estimated quadrupole contribution taken from the Fe₂-OH-(HBpz₃)₂(μ-ac)₂ K-edge data.⁸ The total intensities for Fe₂-oxo-hedta₂ and Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ are 22.7 and 24.9 units, respectively, while the Fe₂-OH-(HBpz₃)₂(μ-ac)₂ total intensity is 10.7 units. From the L-edge results in Table 1, Fe₂-oxo-hedta₂ has 0.98 of the metal d character of Fe₂-OH-(HBpz₃)₂(μ-ac)₂ (i.e. 2% more covalent), while Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ has 0.95 of the metal d character (i.e. 5% more covalent). Assuming that the K-pre-edge spectrum of Fe₂-OH-(HBpz₃)₂(μ-ac)₂ consists purely of electric quadrupole transitions, the expected quadrupole intensities of Fe₂-oxo-hedta₂ and Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ are ~10.5 and ~10.2 units, respectively. This gives ~12.2 and ~14.7 units of intensity for the electric dipole contribution to the Fe₂-oxo-hedta₂ and Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ spectra, respectively. From these values, the percentage of 4p mixing into the 3d orbitals can be estimated. Following Westre et al.⁸ this pre-edge extracted intensity correlates to 6% and 7% 4p mixing into the 3d orbitals for Fe₂-oxo-hedta₂ and Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, respectively.

From a Mulliken analysis of the DFT results for the two μ-oxo complexes, the amount of 4p character that is mixed into the 3d orbitals is given in Table 3. The total amount of 4p character is less than what is found experimentally, but similar to the experiment, there is only a limited amount of 4p character in the xz/yz orbitals, while more is present in the z² orbital for both μ-oxo complexes. Note that a small amount of 4p character is also found in Fe₂-OH-(HBpz₃)₂(μ-ac)₂ due to the lower than O_h symmetry of the actual Fe(III) site, which leads to an increased intensity at 7114.8 eV in the experimental spectrum and a deviation from the nominal 3/2 ratio of the t_2g/e_g intensities (Table 2). However, the effect is small (<0.7 % (see Ref. 8)) and does not significantly alter the estimate of 4p character mixed into the 3d orbitals in the oxo-bridged complexes.

Table 3:

Amount of 4p character mixed into the unoccupied 3d orbitals from a Mulliken analysis of the DFT single point calculations. The small values that are found in orbitals with x and y character originate from a deviation of the C_4v symmetry.

	Amount of 4p character [%]
	xy	xz/yz	x2 – y2	z2
Fe2-OH-(HBpz3)2(μ-ac)2	0.3	0.2	0.3	0.5
Fe2-oxo-(HBpz3)2(μ-ac)2	0.3	0.8	0.3	2.0
Fe2-oxo-hedta2	0.2	1.7	1.0	3.8

While the VBCI multiplet analysis is required for fitting the L-edge XAS spectrum, the K pre-edge can be correlated to TD-DFT calculations. Figure 4A shows the comparison of the experimental K-edges with the TD-DFT derived spectra. The top panel shows the TD-DFT spectra of Fe₂-OH-(HBpz₃)₂(μ-ac)₂ (red), Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (blue) and Fe₂-oxo-hedta₂ (green), which are compared to the experimental CEE cuts (middle panel) and the K-pre-edge spectra (bottom panel). The three TD-DFT spectra exhibit comparable intensities in the lower energy peak at around 7113 eV. At higher energies (~7115 eV) the two oxo-bridged complexes gain significant intensity with the main peak of Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (blue) being 0.5 eV higher in energy than Fe₂-oxo-hedta₂ (green), consistent with the experimental results. Each calculated spectrum consists of three contributions: electric dipole, magnetic dipole, and electric quadrupole contributions. The TD-DFT calculations do not do particularly well with respect to the quadrupole distribution, but nicely reproduce the large intensity increase observed in the oxo bridged dimers due to the dipole contribution. The individual contributions for the three complexes are shown in Figure 4B-D. For Fe₂-OH-(HBpz₃)₂(μ-ac)₂ (B), the spectrum is dominated by the quadrupole contribution (blue) as expected for a high spin ferric complex with quasi O_h local symmetry. The calculated spectra for both oxo-bridged complexes Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (C) and Fe₂-oxo-hedta₂ (D) exhibit a strong electric dipole intensity contribution (green) only at the higher energy side of the spectra, consistent with experiment. The intense electric dipole transition at ~7115 eV derives from excitations into the z² orbital. As observed experimentally above, there is no significant electric dipole intensity contribution from excitations into the d(xz/yz) orbitals, which are also allowed to mix with 4p_x,y by group theory.

Figure 4:

A: Comparison of the TD-DFT derived K pre-edge results (top) with the CEE cuts (middle) and the experimental K pre-edge (bottom) for Fe₂-OH-(HBpz₃)₂(μ-ac)₂ (red), Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (blue) and Fe₂-oxo-hedta₂ (green). The individual contributions from the electric dipole and quadrupole (green and blue, respectively) together with the magnetic dipole (orange) are shown in B-D for the three complexes. The sum of all three contributions is shown in red.

Extended Pre-Edge Region

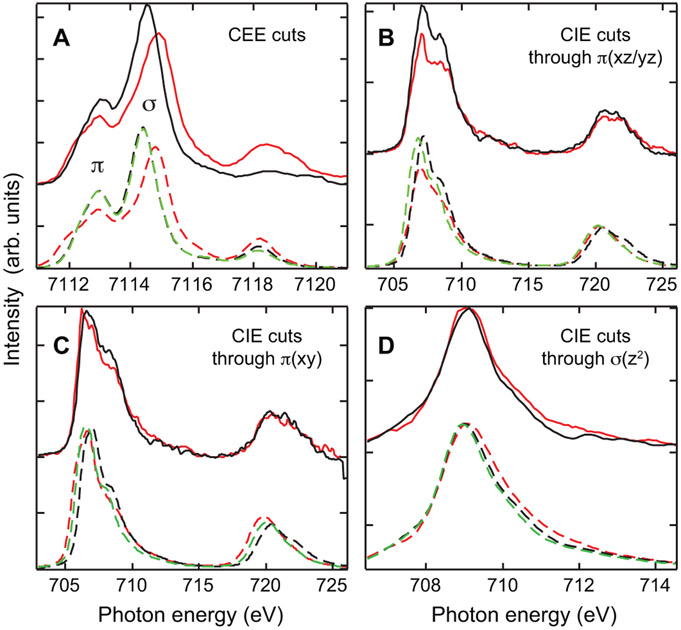
In the experimental K-edge XAS spectra at 3-4 eV above the pre-edge features, additional intensity is present at around 7118.5 eV in the Fe(III)-oxo dimers. In Figure 5(A-C) this is shown for the background subtracted 1s2p RIXS integrated pre-edges (blue) as well as for the CEE cuts (red). A blowup of the extended energy region as well as the non-background subtracted spectra are shown in the Supporting Information. For Fe₂-OH-(HBpz₃)₂(μ-ac)₂(A), there is no detectable intensity at around 7118.5 eV, while intensity in this region is clearly visible for Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (B) and also present but weaker for Fe₂-oxo-hedta₂ (C).

Figure 5:

Background subtracted K-edge (blue) and CEE cuts (red) for (A) Fe₂-OH-(HBpz₃)₂(μ-ac)₂, (B) Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, and (C) Fe₂-oxo-hedta₂. The corresponding TD-DFT calculations (K-edge with 1 eV braodening) are shown in D-F and VBCI simulations in G-I. The dashed vertical lines represent the energy separation of the pre-edge (left of line) and extended pre-edge (right of line).

Previously, intensity in this energy region has been observed for a number of complexes including ferric- and ferrous-hexacyanide⁶ and Fe(III)-oxalate. However, in these complexes, this additional feature arises from Fe 4p mixing into the unoccupied ligand π* orbitals with t_1u symmetry (in O_h).⁶ Complexes without unoccupied ligand π* orbitals relatively close in energy to the d manifold such as ferric- and ferrous-(tacn₂)ⁱ do not show a feature in this energy range.⁶ Due to the donating nature of the ligands, this mechanism is also not active for the Fe-oxo/OH complexes in this study.

In periodic materials, intensity has been observed from core transitions into non-local states through Fe⁽¹⁾(4p)-O(2p)-Fe⁽²⁾(3d) mixing.^10,11,58-61 A 1s electron is excited into the 4p character on Fe⁽¹⁾ that is mixed into the 3d orbitals of the (non-excited) Fe⁽²⁾ via an intermediate O 2p orbital (Figure 6 A,B). The resulting intensity appears a few eV higher in energy than the pre-edge, as the electronic relaxation associated with the 1s core-hole creation on Fe⁽¹⁾ acts on the d valence orbitals of Fe⁽¹⁾ but not on the Fe⁽²⁾ d orbitals. The core-hole on Fe⁽¹⁾ shifts its 4p down in energy, which allows an increased mixing with the Fe⁽²⁾(3d) orbitals. This mixing is sensitive to the Fe-O bond length and in particular Fe-O-Fe angle. For the lower energy 3d (π) orbitals on Fe⁽²⁾, optimal mixing is expected in a 90 degree Fe-O-Fe arrangement due to the Fe⁽¹⁾(4p_z)-O(2p_z) σ/π mixing (Figure 6A), which is more effective than the Fe⁽¹⁾(4p_x)-O(2p_x) π/π mixing that is required for a 180 degree Fe-O-Fe arrangement (Figure 6B). For the Fe⁽²⁾ 3d(z²) delocalized transitions, a high intensity feature in the extended pre-edge region is expected for a linear Fe-O-Fe arrangement. However, this dσ transition is at higher energy (~10 Dq) and obscured by the rising edge intensity.

Figure 6:

Non-local Fe 4p - O 2p - Fe 3d sketch of the orbital interaction for a Fe-O-Fe arrangement of 90° (A) and 180° (B). Local LMCT mechanism (C): Energy separation of the LMCT satellite for the final state multi-electron configurations taking charge transfer and Coulomb repulsion energies into account (left) and adding the LMCT mixing (right), which further splits the energy levels. Its intensity gets enhanced through 4p character mixed into the 3d orbitals.

This predicted behavior is reproduced in the TD-DFT calculations of the K-pre-edge (Figure 5D-F). The first higher energy feature at ~7118 eV originates from an Fe¹(1s) transition into the Fe⁽¹⁾(4p)-O(2p)-Fe⁽²⁾(3d(xz/yz)) orbitals. This peak is very weak in Fe₂-OH-(HBpz₃)₂(μ-ac)₂, has more intensity in Fe₂-oxo-hedta₂ and is strongest for Fe₂-oxo-(HBpz₃)₂(μ-ac)₂. While the calculated intensity is higher than the experimentally observed intensity and the energy separation from the pre-edge is lower (3.7 and 4.2 (exp) vs 2.6 and 3.3 eV (TD-DFT) for Fe₂-oxo-(HBpz₃)₂(μ-ac)₂and Fe₂-oxo-hedta₂, respectively), the expected angular dependence of the intensity (Figure 6A and B) is reproduced with Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (Fe-O-Fe ∢ ~123) being more intense than Fe₂-oxo-hedta₂(∢ ~165). The Fe¹(1s) to Fe⁽¹⁾(4p)-O(2p)-Fe⁽²⁾(3d(z²)) final state configurations are also calculated to be present at ~1.5-2.5 eV higher in energy relative to the Fe² dπ delocalized excitations and also show the expected opposite angular dependence. Core excitation into the 4s orbitals mixed with 4p⁶² appear ~3 eV higher in energy and are buried under the rising edge intensity.

The presence of additional peaks in the extended pre-edge region of the non-centrosymmetric μ-oxo complexes (at ~7118 eV) is also consistent with the predictions of VBCI simulations for these complexes (Figure 5(G-I)). These features are LMCT satellites that are associated with the main pre-edge features. In the multi-electron configuration description, the 3d⁶ $\underset{¯}{L}$ configuration is separated in energy from the 3d⁵ configuration by the charge transfer energy Δ and the LMCT mixing strength, where $\underset{¯}{L}$ denotes a ligand hole. In the presence of a 1s core-hole, this energy difference gets corrected by the Coulomb repulsion energy Δ + U_dd – U_sd, where U_dd describes the 3d-3d and U_sd the 1s-3d Coulomb repulsion. This is shown in the level diagram in Figure 6 C. Its transition energy appears ~3-4 eV above the main pre-edge peak, in the energy region of the additional features in the experimental spectra (Figure 5(A-C) at ~7118 eV). The LMCT satellite intensity also gets enhanced through mixing of Fe 4p character into the ligand, which can further mix with the Fe 3d orbitals in the absence of an inversion center. Its intensity therefore depends on Δ and the LMCT mixing strength, however, it is less pronounced than what is experimentally observed.

Thus, the higher energy features that are observed in the CEE cuts and (less pronounced) in the K-pre-edge of these non-centrosymmetric Fe(III) dimer complexes, have two contributions: the dominant delocalized transition to the neighboring Fe with a strong Fe-O-Fe angle dependence and the weaker LMCT satellite. While both mechanisms lead to a single excitation feature, the experimental feature in the expanded pre-edge region of the CEE cuts is broad and with some structure (~1.7 eV, see Figure 5(A-C), and expanded in Supporting Information). The experimental data therefore point to contributions from both intensity mechanisms for the higher energy features. Note that the LMCT satellites only have observable intensity in non-centrosymmetric complexes and the non-local transitions only occur in bridged dimers with a highly covalent bridging ligand.

The presence of the LMCT satellite intensity through 4p mixing also has implications for the 1s3d and 2p3d Coulomb and exchange interaction, U_1s3d and U_2p3d, respectively. Experimentally in 1s2p RIXS, the additional intensity in the extended pre-edge region is found on the diagonal through the main peak (Figure 3). In the charge transfer multiplet simulations, this requires U_1s3d = U_2p3d + 1 eV, i.e. more local screening of the 2p core hole. While a difference between U_1s3d and U_2p3d has only a minor effect on the K-pre-edge region, it has a strong effect on the LMCT satellite region (see Supporting Material). Thus 3d/4p mixing in non-centrosymmetric sites gives LMCT satellite intensity, enabling 1s2p RIXS to be unique in sensitivity to the relative values of U_1s3d and U_2p3d.

L-edge-like CIE cuts

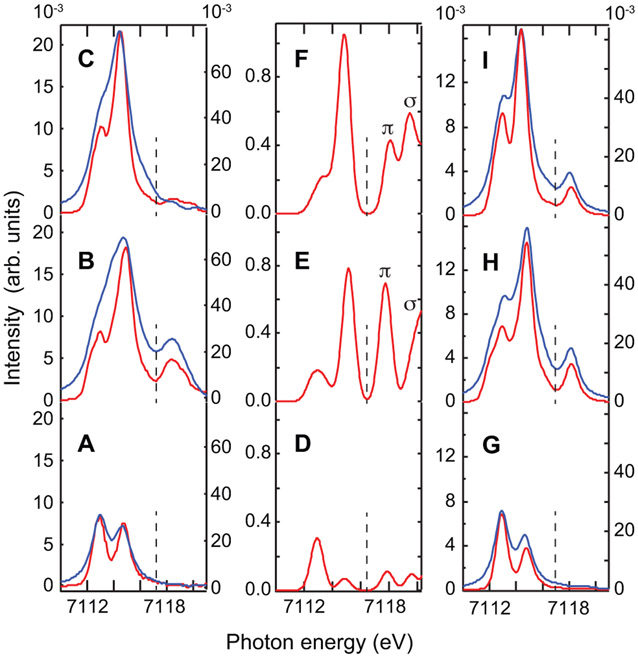
The advantage of recording 1s2p RIXS maps compared to K-edge XAS spectra, is their two-dimensionality. As discussed above, a CEE (diagonal) cut gives a high resolution K-edge XAS-like spectrum, while a CIE (vertical) cut gives an L-edge-like spectrum.^5-7,63 This has advantages over the direct L-edge XAS in that, by appropriately choosing the incident energy, a transition from the 1s orbital into a selected dπ or dσ orbital can specifically enhance L-edge final states containing this dπ or dσ contribution. The dπ and dσ character in direct L-edge XAS is complicated by multiplet effects from the strong 2p3d Coulomb interaction. Alternatively, the direct interpretation of π and σ character from each CIE cut can be complicated by intensity bleeding effects from peaks at higher incoming and transfer energy due to the large lifetime broadening in the incoming photon energy axis. Figure 7 shows selected CIE cuts for all three complexes (red and green for the OH-bridged complex, and orange, red, green, blue for the oxo-bridged complexes through selected contributions to the K-pre-edge) and compares these to their direct L-edge XAS spectra (shown in blue). Only the L₃-edge-like region is shown for clarity. The full spectra are given in the Supporting Material.

Figure 7:

Blow-up of the L₃ region of the 1s2p RIXS planes together with the CIE cuts at selected energies (vertical lines in RIXS planes) compared to the direct L-edge XAS spectrum: (A) Fe₂-OH-(HBpz₃)₂(μ-ac)₂, (B) Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, and (C) Fe₂-oxo-hedta₂.

For Fe₂-OH-(HBpz₃)₂(μ-ac)₂(Figure 7 A), the CIE cut through the dπ region (red curve) leads to an L-edge-like spectrum with a peak at the same energy as the low energy peak of the direct L-edge spectrum (blue). Similarly, the dσ CIE cut (green curve) gives an L-edge-like spectrum with a peak corresponding to the main peak of the direct L-edge XAS. Both cuts also show intensity at higher and lower energies, respectively. These point to a small amount of σ character in the lower energy L-edge peak, and π character in the higher energy L-edge peak, similar to what has been found previously from theoretical simulations of L-edge XAS character in O_h high spin Fe^III complexes.⁴⁹ Due to the width of the RIXS feature in the incoming photon energy direction, however, some intensity bleeds into the σ region (for the dπ CIE) and the π region (for the dσ CIE).

For the two oxo-bridged dimer complexes, four CIE cuts at peak energies found from the K-edge and CEE cut fits, are shown together with the direct L-edge XAS. In the oxo-dimer Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ complex (B), the two lower energy CIE cuts (orange and red) show an enhanced splitting in line with a low energy shoulder in the direct L-edge XAS (blue). This indicates the C_4v splitting of the dπ orbitals. Also the two higher energy CIE cuts at 7113.7 (light green) and 7114.8 eV (dark green) at the 1s → 3d(x² – y²) and 1s → 3d(z²) transition energies, respectively, show a splitting of 0.4 eV. This splitting is also visible in the direct L-edge XAS spectrum, where two intense peaks with an energy separation of 0.6 eV are observed. The 3d(z²) intensity is electric dipole resonance enhanced (from the 4p_z mixed into the 3d_z²) and appears on the higher energy side of the L-edge XAS spectrum.

For Fe₂-oxo-hedta₂, a CIE cut through the lower energy side of the low energy 1s2p RIXS feature (orange) has its maximum aligned with a weak low energy shoulder in the direct L-edge XAS spectrum (blue) at 706.4 eV. The CIE cut across the maximum of the dπ feature (red) has its maximum aligned with the maximum of the low energy feature of the direct L-edge XAS spectrum. The L-edge XAS low energy feature therefore contains a large amount of dπ character and the small shoulder in the L-edge dπ region originates from a splitting of the dπ orbitals again due to the C_4v symmetry. Additional intensity is also present in the higher energy part of the CIE cut, which mostly originates from a bleed-over from the intensity of the strong feature in the 1s2p RIXS plane at higher energy. The two cuts through the dσ region (light and dark green) lead to two L-edge-like spectra separated by approximately 0.3 eV with the higher energy cut (dark green) through the 4p dipole intensity enhanced region appearing at the higher energy side of the L-edge spectrum. Since the 4p mixing is into the d(z²) orbital, we can identify the high energy side of the L-edge XAS spectrum as originating mostly from the 2p → 3d(z²) transition.

The 1s2p RIXS VBCI simulations with the parameters used to derive the DOC in Table 1 successfully reproduce the experimental observations, including all energy splittings and relative intensities as shown in Figure 8. Thus these charge transfer multiplet calculations are capable of properly simulating the electronic structures of non-centrosymmetric complexes from direct L-edge XAS and 1s2p RIXS spectra. The 2D nature of the 1s2p RIXS maps with the ability to compare individual cuts (CIE and CEE) for different data sets, provides an enhanced sensitivity of the VBCI fits relative to fits only to the L-edge XAS. This is despite strong electric dipole transition contributions from 3d/4p mixing that does not significantly contribute to the direct L-edge XAS (see also the Supporting Information). Therefore, combining both methods give the most accurate solution space for the parameters used in the VBCI analysis and thus the DOCs in Table 1.

Figure 8:

VBCI simulations of the 1s2p RIXS planes: Blow-up of the Kα₁ (L₃) region together with the CIE at selected energies (vertical lines in RIXS map) compared to the direct L-edge XAS simulations: (A) Fe₂-OH-(HBpz₃)₂(μ-ac)₂, (B) Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, and (C) Fe₂-oxo-hedta₂.

DOC from 1s2p RIXS alone

In the analysis above, the combination of L-edge XAS and 1s2p RIXS data have been used together to simulate spectra and to obtain DOCs. A goal of the present study is to use 1s2p RIXS for systems where L-edge XAS is not accessible (as in a metallo-enzyme intermediate in solution) to obtain DOC of the associated Frontier Molecular Orbitals involved in reactivity. Further, this needs to be accomplished for non-centrosymmetric systems as many of the key intermediates are Fe^IV=O heme enzymes. We therefore constructed an approach to extract DOC from data where only the 1s2p RIXS plane is available for the intermediate, but when both L-edge XAS and 1s2p RIXS are available on a related model complex. Here, we treat the Fe₂-oxo-hedta₂ complex as the "intermediate" where only RIXS data are available and Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ as the well defined related model complex. For this, we searched for key spectral features in the 2D RIXS maps that allow a step-wise progression between the RIXS planes from Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ to Fe₂-oxo-hedta₂. Figure 9 shows a collection of experimental 1s2p RIXS cuts (solid curves) together with the corresponding simulations (dashed curves) for Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (red) and Fe₂-oxo-hedta₂ (black). Four characteristic changes are observed in going from the reference Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ to Fe₂-oxo-hedta₂: (i) The change in the overall spectral shape of the CEE cuts in the pre-edge region (7111-7117 eV, Figure 9A). The energy splitting between the σ and π regions decreases, together with an increased π energy splitting. (ii) The CIE cut through the dπ(xy/zy) feature of the RIXS plane at 7113.0 eV incident energy (Figure 9A) shows an increase in intensity (Figure 9B) due to a decreased π(xz/yz) LMCT mixing. (iii) 1s → 3d excitation into the xy orbital appears on the low energy side of the dπ peak at 7112.2 eV in Figure 9A. CIE cuts at this energy show a similar intensity for both Fe-oxo complexes. (Figure 9C) (iv) The CEE pre-edges of the Fe₂-oxo dimer complexes at 7114.8 and 7114.4 eV in Figure 9A are dominated by electric dipole transitions due to 4p_z(a₁) character mixed in the 3d(z²) orbitals. The CIE cuts through these energies (Figure 9D) show a narrower L₃-edge-like peak for Fe₂-oxo-hedta₂.

Figure 9:

Characteristic spectral changes when going from Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ to Fe₂-oxo-hedta₂. A: Comparison of the CEE cuts. B: CIE cuts through the π(xz/yz) feature at 7113 eV. C: CIE cuts through the lower energy feature of π character (xy) at 7112.2 eV D: CIE cuts through the main intensity dipole region (3d(z²) symmetry) normalized to one and shifted such that the spectra are energy aligned at half intensity. - Color scale: Red solid - experimental Fe₂-oxo-(HBpz₃)₂(μ-ac)₂; black solid - experimental Fe₂-oxo-hedta₂; dashed red - simulated Fe₂-oxo-(HBpz₃)₂(μ-ac)₂; dashed black - simulated Fe₂-oxo-hedta₂; dashed green - simulated Fe₂-oxo-hedta₂ with RIXS only.

Based only on these observed spectral changes starting from the well-defined Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ complex (from L-edge XAS and 1s2p RIXS), the 1s2p RIXS only Fe₂-oxo-hedta₂ plane could be simulated (green dashed line in Figure 9). The corresponding DOC values are given in Table 4 bottom row, together with the L-edge + RIXS derived values for Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ and Fe₂-oxo-hedta₂ taken from Table 1 (in italic). As also found from the full data set simulations in Table 1, RIXS only simulations find Fe₂-oxo-hedta₂ less covalent than Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, with larger increases in d(xz/yz) π and d(z²) σ character. Thus a large number of characteristic quantitative differences (relative to a well defined model) are available to properly simulate the 1s2p RIXS plane in the absence of an L-edge XAS spectrum, despite the strong spectral distortion associated with the electric dipole intensity contributions from 3d/4p mixing in non-centrosymmetric complexes.

Table 4:

DOC values derived from the full data set (L-edge + 1s2p RIXS) for Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ and Fe₂-oxo-hedta₂, as well as for using the Fe₂-oxo-hedta₂ 1s2p RIXS plane alone. Note that the first two rows are a repetition from Table 1 for simplicity. Note that the value for Fe(e) is per orbital and the e set carries twice the amount.

		DOC metal character (%)
		Fe(b2)	Fe(e)	Fe(b1)	Fe(a1)	total
Fe2-oxo-(HBpz3)2(μ-ac)2	(L-edge+RIXS)	89	80	77	67	392
Fe2-oxo-hedta2	(L-edge+RIXS)	91	84	77	69	405
Fe2-oxo-hedta2	(RIXS only)	90	85	79	71	410

Discussion

For systems containing local inversion symmetry, only electric quadrupole allowed 1s → 3d transitions occur, allowing the direct extraction of the DOC from 1s2p RIXS with the advantage of accessing L-edge XAS forbidden final states.⁶ Upon loss of inversion symmetry, 4p character can mix into the 3d orbitals, giving an electric dipole allowed 1s → 4p intensity contribution to the K-pre-edge region and therefore significantly enhancing their intensity.^{8,10-12,56,57}

In going from Fe₂-OH-(HBpz₃)₂(μ-ac)₂ to Fe₂-oxo-(HBpz₃)₂(μ-ac)₂, the Fe-O bridge bond length shortens leading to a loss of local inversion symmetry to C_4v enabling 4p mixing into specific 3d orbitals, and a splitting of the π and σ orbitals that is visible in the L-edge XAS, 1s2p RIXS and CEE spectra (Figures 2 and 3). Simultaneous L-edge XAS and 1s2p RIXS multiplet simulations that now include the 4p mixing were developed and used to determine the DOC (Table 1). For Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ they give increased oxo covalent mixing into the dπ and dσ orbitals, which are the frontier molecular orbitals (FMOs) in metal-oxo systems, that activate reactivity perpendicular to and along the Fe=O bond, respectively.

While both the d(z²) and the d(xz/yz) orbitals have high covalencies in the oxo bridged complexes and are allowed to mix with the 4p orbitals (a₁ (p(z)/d(z²)) and e (p(x, y)/d(xz, yz))), only 4p(z) mixing into the 3d(z²) orbital is experimentally found to be significant based experiment and TD-DFT calculations. As shown in Ref 10, p mixing into d orbitals originates from their simultaneous overlap with the same ligand valence orbital. This selective 3d(z²)/4p(z) mixing in oxo bridged Fe dimers can therefore be explained by a simple orbital overlap picture. Figure 10 shows a sketch of the orbitals involved in e (left) and a₁ (right) mixing via interaction with a p ligand valence orbital. The e overlap is of π character and this directionality limits the mixing between the oxo 2p(x/y) and the metal 4p(x/y) orbitals. The a₁ overlap is of σ character, leading to strong oxo 2p_z and Fe 4p(z) overlap and a dominant contribution of the 3d(z²)-4p(z) mixing to the spectral shape, i.e. the observed enhanced intensity of only the a₁ channel.

Figure 10:

Sketch of the orbitals involved in e (left) and a₁ (right) 3d/4p mixing via ligand mixing for the ligand 2p - metal 3d (bottom) and ligand 2p - metal 4p orbitals (top).

The two dimensionality of the 1s2p RIXS maps generally allows excitations of selected K-pre-edge intermediate states and, via vertical CIE cuts, projections of specific final states in the direct L-edge XAS spectrum that are identified through the specific symmetry of the allowed 3d/4p mixing. The enhanced intensity of only the a₁ channel described above additionally enables the selective determination of d_z² character in the L-edge XAS spectra of Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ and Fe₂-oxo-hedta₂ through the strong enhancement of a₁ states in the L-edge-like CIE cuts.

Correlation of the two oxo-bridged complexes through the results of the DOC from VBCI simulations of the RIXS data and Mulliken analyses of the associated DFT calculations, provides further insight into the differences in their electronic structure. In quantitatively comparing the HB(pz)₃(μ-ac)₂ to the hedta₂ ligand systems the total covalency of the Fe-O-Fe in the latter is lower both in experiment and DFT calculations, particularly for the dπ orbitals. Interestingly, both the oxo and total ligand contribution in the ferric unoccupied d orbitals have decreased. As the Fe-O-Fe bond lengths are the same, this decrease in the covalency of the hedta ligated complex can have two possible origins: i) the increase in Fe-O-Fe angle from 125 to 164.9 degrees, or ii) the difference in the ligand systems. Both possibilities are tested in the Supporting Information. Variation in the Fe-O-Fe angle with fixed hedta ligand has no effect. Calculations on hypothetical Fe^III-oxo monomers with the same ligations show that the hedta is a better donor than the (HBpz₃)(μ-ac) ligation. In Fe^III-oxo monomers this is compensated by the oxo donation leading to equivalent d character in both. In the oxo bridged dimers the oxo donation is shared between the two Fe^III leading to less oxo donation per Fe and in the (HBpz₃)₂(μ-ac)₂ complex increased ligand donation to compensate. However, in the Fe₂-oxo-hedta₂ complex the larger negative charge on each ligand limits its ability to donate and an increased net Fe character is observed both in RIXS data and calculations. In contrast to a lack of Fe-O-Fe angle effect on the covalency of the oxo bond, there is an effect on the extended pre-edge region where the experimental intensity decreases with increasing angle. This delocalized transition is unique to the dimers and reflects the oxo 2p superexchange pathway between the two Fe centers. However, in contrast to the 3d/4p single site mixing responsible for the dipole intensity of the pre-edge transition that involves the oxo 2p_z orbital, the delocalized transition intensity requires an oxo 2p_x,y mechanism (for the 90° angle) as it involves mixing into the low energy dπ of the adjacent Fe.

By going from a complex with a known structure and using the insight from the spectral features in the 2D 1s2p RIXS data to an unknown complex, as we did by going from Fe₂-OH-(HBpz₃)₂(μ-ac)₂ to Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ and to Fe₂-oxo-hedta₂, a clear assignment of spectral changes in different energy regions and hence elucidating the orbital contributions to these regions becomes possible. These RIXS correlations enable specific assignments of features in their corresponding CEE cuts (also called high energy resolution fluorescence detection (HERFD) spectra). These alone can then be used to assist in assigning HERFD spectra of related complexes. This approach provides insight into the structures of biferric peroxo intermediates P’ in 4-aminobenzoate N-oxygenase (AurF) and P in ribonucleotidereductase (RNR), for which HERFD spectra were recently published by Cutsail et al.⁶² Here, we use the assignments of the 2D 1s2p RIXS planes of the two pyrazolyl borate complexes Fe₂-OH-(HBpz₃)₂(μ-ac)₂ and Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ to interpret their HERFD spectral features. We then go from these structures with two μ-1,3-carboxylate bridges and a μ-hydroxo or μ-oxo, respectively, to structures with two μ-1,3-carboxylates and a μ-1,2-peroxo or a μ-1,2-hydroperoxo bridge.

Figure 11 A shows the HERFD data for the model complexes Fe₂-OH-(HBpz₃)₂(μ-ac)₂ (blue) and Fe₂-oxo-(HBpz₃)₂(μ-ac)₂(green) (i.e. CEE cuts from Figure 3), and the biferric enzyme intermediates P’ of AurF (red)⁶² and P in RNR (Ecβ-W48F/D84E) (yellow). ⁶² Relative to the μ-hydroxo bridged complex (blue), the intensity in the spectrum of P in RNR (yellow) increases, but not as much as for the μ-oxo bridged model complex (green). The P’ in AurF spectrum (red) shows only a slightly higher total intensity than Fe₂-OH-(HBpz₃)₂(μ-ac)₂ with the additional intensity found at ~7113.5 eV leading to a broad peak with little structure.

Figure 11:

A: Experimental HERFD data for Fe₂-OH-(HBpz₃)₂(μ-ac)₂ (blue), Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ (green), AurF-P’ (red) and RNR-P (yellow). The AurF-P’ and RNR-P data are adapted from Ref. 62. B: TD-DFT calculations of Fe₂-X-(HB(pz)₃)₂(μ-ac)₂ with X = oxo (solid green), hydroxo (solid blue), peroxo (solid yellow), hydroperoxo (solid red), as well as of Fe₂-X-Y-(HB(pz)₃)₂(ac)₂ with X = hydroperoxo and Y = hydroxo (dashed grey) and oxo (dashed purple), and monodentate carboxylates. C: Their corresponding DFT optimized structures.

For additional insight, we obtained optimized structures for Fe₂-OH-(HBpz₃)₂(μ-ac)₂ and Fe₂-oxo-(HBpz₃)₂(μ-ac)₂ that agree with crystallography (Figure 11 C, left), used these as references for the hypothetical complexes Fe₂-hydroperoxo-(HBpz₃)₂(μ-ac)₂ and Fe₂-peroxo-(HBpz₃)₂(μ-ac)₂ (middle), where the P complex in RNR has been shown to be a cis-μ-1,2-peroxo by resonance Raman⁶⁴ and the P’ in AurF a cis-μ-1,2-hydroperoxo from NRVS,²⁰vand calculated their TD-DFT spectra (Figure 11 B). The theoretical spectra reasonably correlate to the experimental spectra for the related biferric enzyme peroxo intermediates.

The calculated μ-peroxo complex has Fe-O distances of 1.91Å, which are shorter than the Fe-O bond length of μ-hydroxo (1.96Å) but longer than in μ-oxo (1.81Å). Consistent with these bond length trends, the observed moderate increase in the 3d(z²) intensity at ~7114.6 eV in the experimental RNR-P spectrum is therefore due to 4p(z) mixing for both Fe relative to the μ-hydroxo model complex, but much less than in the μ-oxo bridged model complex, as it is also observed in their calculated TD-DFT spectra. These results are consistent with resonance Raman results.

In going to P’ in AurF the HERFD intensity is lower than in RNR-P. This is consistent with NRVS data on P’ in AurF. In our DFT optimized structure of the μ-hydroperoxo complexe, the Fe-O distance for the non-protonated oxygen of the peroxo is the same as in the μ-hydroxo (1.95Å) while the Fe-OH distance for the protonated oxo is significantly longer (2.16Å). This leads to a ligand field (LF) splitting of the z² peaks for each Fe with the transition to the Fe with the protonated oxygen being at lower energy, but gaining intensity through additional 4p(z) mixing. Based on the additional intensity in the HERFD spectrum of P’ in AurF at ~7113.5 eV, this LF prediction is observed in the experimental spectrum, and confirmed in the TD-DFT calculated spectrum where the d(z²) from the two Fe^III splits in energy producing the new feature at ~7113.5 eV. Recent resonance Raman data on P’ in CmlI, an intermediate equivalent to P’ in AurF, have suggested that there may also be a μ-oxo bridge present in this intermediate.⁶⁵ This would have a strong impact on its reaction coordinate as an oxo bridge would stabilize the biferric site against the single electron transfer computationally derived from P’ in AurF. The HERFD data in Figure 11 A for P’ in AurF refute the presence of an additional μ-oxo bridge and are alternatively consistent with a μ-hydroxo bridge in addition to the μ-1,2-hydroperoxo. Inclusion of an additional μ-oxo (dashed purple in Figure 11 B) into the μ-1,2-hydroperoxo structure leads to an intensity increase at 7114.8 eV that is not observed experimentally. Inclusion of an additional μ-hydroxo (dashed grey) leads to a two feature spectrum without the additional intensity at ~7113.5 eV.

While the above analysis of the 1s2p RIXS planes and L-edge XAS spectra of structurally aligned models allowed for a clear interpretation of the HERFD data for the corresponding peroxo intermediates, the availability of full 1s2p RIXS planes on these would have been preferred as we would have then been able to extract the DOC and therefore obtain insight into the FMOs. While for P in RNR the two Fe sites are close to equivalent, this is not the case for P’ in AurF due to protonation of the peroxo. This leads to the two peaks corresponding to the z² transitions on each Fe in the HERFD spectra. This splitting would allow tuning into the z² of each Fe ion by individual vertical (i.e. CIE) cuts through the RIXS plane to enhance the L-edge-like spectrum and hence the ligand field information that is associated with each Fe.

Conclusion

The 1s2p RIXS intensity of non-centrosymmetric metal systems is strongly affected by electric dipole character resulting from metal 4p mixing into the 3d orbitals. This mixing reflects the frontier molecular orbitals that are key to reactivity in metal-oxo intermediates. This strongly affects the CEE cuts and results in the 3d/4p selective enhancement of specific L-edge final states in the CIE cuts.

A methodology is developed to include the p/d mixing via covalent overlap with the ligand in the multiplet analysis of 1s2p RIXS planes and to extract DOC information from enzyme intermediates in solution, providing 1s2p RIXS data are available on relevant models. In the present study bridged biferric model RIXS data were extended to obtain structural insight into biferric non-heme peroxo enzyme intermediates and in ongoing studies will be applied on Fe(IV)=O intermediates as their oxo-Fe(IV) bond strongly affects their spectral shape in regions important to π and σ FMO contributions to reactivity.