Did We Get Sensorimotor Adaptation Wrong? Implicit Adaptation as Direct Policy Updating Rather than Forward-Model-Based Learning

The human motor system can rapidly adapt its motor output in response to errors. The prevailing theory of this process posits that the motor system adapts an internal forward model that predicts the consequences of outgoing motor commands and uses this forward model to plan future movements. However, despite clear evidence that adaptive forward models exist and are used to help track the state of the body, there is no definitive evidence that such models are used in movement planning.

Abstract

The human motor system can rapidly adapt its motor output in response to errors. The prevailing theory of this process posits that the motor system adapts an internal forward model that predicts the consequences of outgoing motor commands and uses this forward model to plan future movements. However, despite clear evidence that adaptive forward models exist and are used to help track the state of the body, there is no definitive evidence that such models are used in movement planning. An alternative to the forward-model-based theory of adaptation is that movements are generated based on a learned policy that is adjusted over time by movement errors directly (“direct policy learning”). This learning mechanism could act in parallel with, but independent of, any updates to a predictive forward model. Forward-model-based learning and direct policy learning generate very similar predictions about behavior in conventional adaptation paradigms. However, across three experiments with human participants (N = 47, 26 female), we show that these mechanisms can be dissociated based on the properties of implicit adaptation under mirror-reversed visual feedback. Although mirror reversal is an extreme perturbation, it still elicits implicit adaptation; however, this adaptation acts to amplify rather than to reduce errors. We show that the pattern of this adaptation over time and across targets is consistent with direct policy learning but not forward-model-based learning. Our findings suggest that the forward-model-based theory of adaptation needs to be re-examined and that direct policy learning provides a more plausible explanation of implicit adaptation.

SIGNIFICANCE STATEMENT The ability of our brain to adapt movements in response to error is one of the most widely studied phenomena in motor learning. Yet, we still do not know the process by which errors eventually result in adaptation. It is known that the brain maintains and updates an internal forward model, which predicts the consequences of motor commands, and the prevailing theory of motor adaptation posits that this updated forward model is responsible for trial-by-trial adaptive changes. Here, we question this view and show instead that adaptation is better explained by a simpler process whereby motor output is directly adjusted by task errors. Our findings cast doubt on long-held beliefs about adaptation.

Introduction

When we make errors in our movements, the motor system automatically adapts its output in the next movement to reduce the error (Shadmehr et al., 2010; Krakauer et al., 2019). This capacity, referred to as “adaptation,” has been demonstrated across a wide variety of behaviors including eye movements (Kojima et al., 2004; Wong and Shelhamer, 2011), reaching movements (Shadmehr and Mussa-Ivaldi, 1994; Krakauer et al., 2000, 2005; Smith et al., 2006; Hadjiosif and Smith, 2015), locomotion (Malone et al., 2011; Jayaram et al., 2012), and speech (Parrell et al., 2017).

A popular theory of adaptation is that it is driven by updating of an internal forward model (Fig. 1A)—a network within the brain that predicts the consequences of outgoing motor commands (Bhushan and Shadmehr, 1999; Flanagan et al., 2003; Bastian, 2006; Krakauer and Shadmehr, 2006; Shadmehr et al., 2010; Krakauer and Mazzoni, 2011; Haith and Krakauer, 2013). There is strong behavioral (Miall et al., 2007; Synofzik et al., 2008; Wagner and Smith, 2008; Izawa and Shadmehr, 2011; Bhanpuri et al., 2013) and neurophysiological (Ebner and Pasalar, 2008) evidence for the existence of forward models in the cerebellum and that these forward models are updated when the consequences of our motor commands are altered by external perturbations (Ebner and Pasalar, 2008; Synofzik et al., 2008; Izawa and Shadmehr, 2011; McNamee and Wolpert, 2019). However, such changes to a forward model do not inherently prescribe how motor output should change in the future; they simply allow the motor system to anticipate altered consequences of a given motor command. It is certainly possible, in principle, for a forward model to be used to plan future motor output, but there is no definitive evidence to date to suggest that this is the case. Nevertheless, a broad consensus has emerged that forward-model-based learning of this kind explains how our movements are adapted when we experience movement errors (Jordan and Rumelhart, 1992; Miall and Wolpert, 1996; Wolpert and Kawato, 1998; Haruno et al., 2001; Flanagan et al., 2003; Bastian, 2006; Shadmehr et al., 2010; Haith and Krakauer, 2013).

Figure 1.

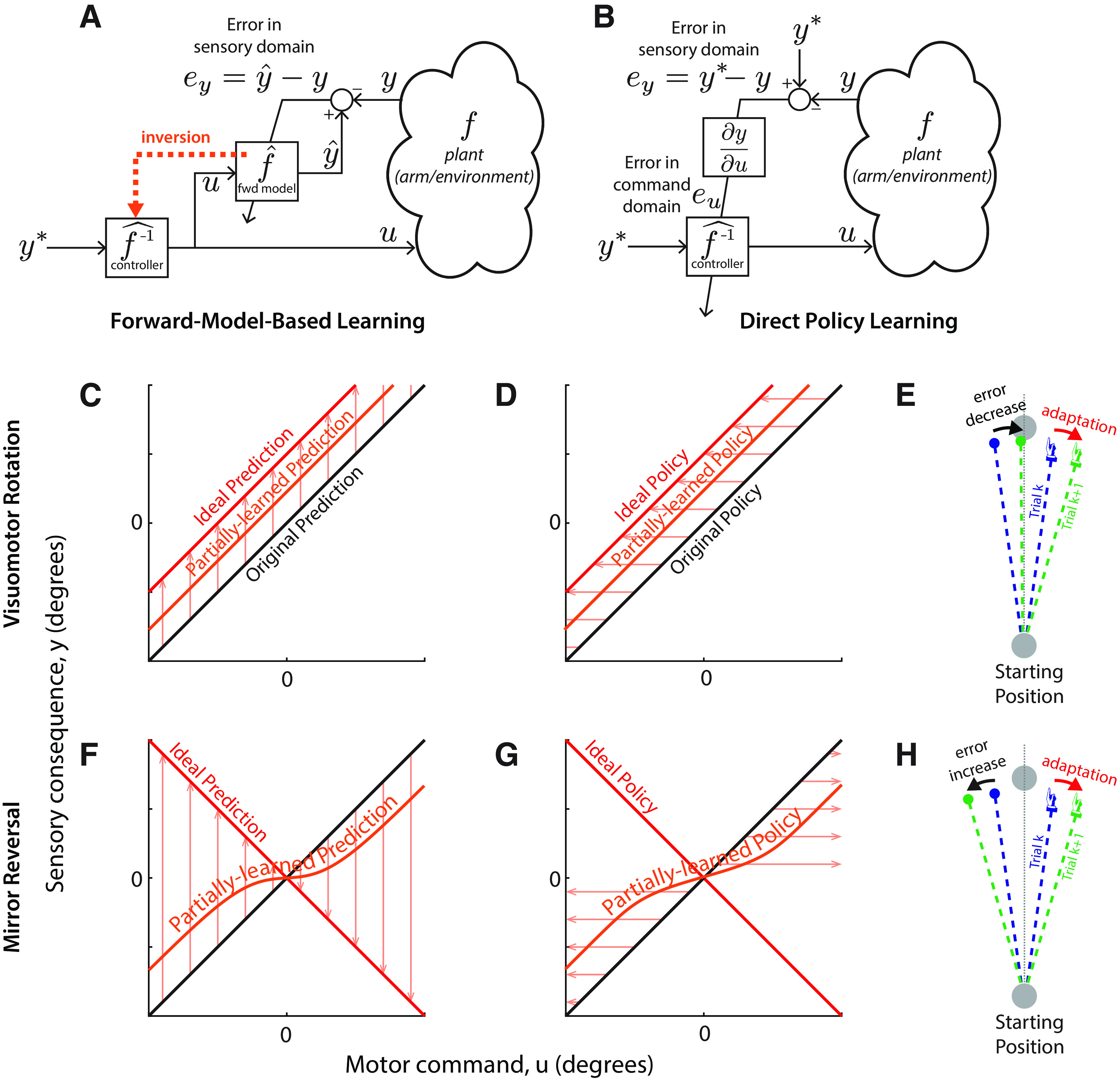
Forward-model-based learning and direct policy learning under visuomotor rotation and mirror reversal. A, Forward-model-based learning relies on updating an internal forward model that predicts the sensory consequences (y) of motor commands (u). In the case of simple cursor perturbations, we take u to be the direction the hand moves (motor command) and y to be the direction the cursor will move (sensory outcome). When the predicted sensory outcome (ŷ) differs from the observed one (y), the resulting error can be used to update the forward model without further assumptions. Given the desired sensory outcome, y*, the updated forward model can then be inverted to yield the appropriate motor command. B, In direct policy learning, sensory errors are used directly to update the policy (also often called an “inverse model”). Here, the policy is a function mapping movement goals (y*), represented in terms of desired sensory outcomes, to appropriate motor commands (u). Sensory errors must be translated to the motor domain, but this mapping depends on knowledge of the plant f (in mathematical terms, knowledge of the sensitivity derivative ∂f/∂u). In practice, direct policy learning must use an assumed mapping (Abdelghani and Tweed, 2010). C, D, Performance of forward-model-based learning (C) and direct policy learning (D) under visuomotor rotation. For forward-model-based learning, the arrows indicate the direction updates to the forward model; for direct policy updates, the arrows indicate the direction of changes to the control policy. In this example, y = u at baseline (black line), and direct policy updating therefore assumes that e_y = e_u. The red line represents the perturbed mapping (a visuomotor rotation by an angle θ, y = u + θ) and thus the ideal forward model prediction; the orange line represents a partially learned prediction. Under both models, adaptive changes are appropriate for the shifted visuomotor map: the forward model adjusts to predict the shifted sensory outcomes of efferent motor commands, whereas direct policy updates drive motor output in a direction that reduces error. E, Response of direct policy learning to errors resulting from a visuomotor rotation. In response to a leftward error, motor output is shifted rightward, reducing error in the next trial. F, G, forward-model-based learning (F) and direct policy learning (G) under mirror reversal. Here, 0 denotes the mirroring axis. Under the mirror reversal, y = –u, and therefore the relationship between task errors and motor errors is inverted: e_y = –e_u. If the sensitivity derivative used for direct policy learning is not updated accordingly, policy updates will occur in the wrong direction, driving motor output further and further away from that necessary to counter the mirror reversal. By contrast, there is no such difficulty associated with learning an updated forward model under the mirror reversal and therefore forward-model-based learning can occur without any issue. H, Response of direct policy learning to errors resulting from a mirror reversal. In response to a leftward error, motor output is shifted rightward, exactly as in E. Under the mirror reversal, however, this shift leads to an increase in error on the next trial.

An alternative theory of adaptation is that the motor system maintains a policy that prescribes what motor commands to generate to attain different goals, and that it uses movement errors to directly adjust this policy over time (Fig. 1B). For example, if a target is missed to the right, the policy can simply be adjusted to generate more leftward output in the future (Fig. 1E), without ever needing to rely on an adaptive forward model. This much more straightforward process, which we refer to as “direct policy learning,” has been proposed in the past as a potential mechanism of motor adaptation (Wolpert et al., 2001; Abdelghani et al., 2008), but has mostly been overlooked in favor of forward-model-based explanations. Both theories, however, generate more or less identical predictions about behavior in conventional adaptation paradigms such as visuomotor rotations or force fields, and, on current evidence, it seems impossible to distinguish between them.

A potential way to dissociate between these theories of adaptation is by imposing a more extreme perturbation: a mirror reversal of visual feedback. Mirror reversal is a much more drastic perturbation than those that are usually thought to engage implicit adaptation (e.g., visuomotor rotations), and it has been argued that it is learned through a completely different process than visuomotor rotations (Telgen et al., 2014). Nevertheless, despite the dominant influence of other learning processes, there is clear evidence that implicit adaptation still occurs under a mirror reversal (Lillicrap et al., 2013; Wilterson and Taylor, 2019), albeit that implicit adaptation in this case seems to drive learning in the wrong direction, acting to increase rather than decrease errors from one trial to the next.

We show that, in theory, this inappropriate adaptation under mirror reversal could be consistent with either forward-model-based learning or direct policy learning, but for very different reasons, leading to different patterns of failure. By closely examining the fine structure of learning under an imposed mirror reversal and comparing this to predictions of a computational model, we find that behavior is consistent only with direct policy learning and not forward-model-based learning.

Materials and Methods

Participants and ethics statement

A total of 51 individuals were recruited for the study. Four participants were excluded before analysis: three because they did not complete the study because of time constraints, and one because of inability to follow instructions. This resulted in 47 participants (mean ± SD age: 23.3 ± 5.2 years; 20 identifying as male, 26 identifying as female, 1 identifying as nonbinary): 12 participants in experiments 1, 1a, and 3; and 11 participants in experiment 2. Sample size was determined based on similar behavioral studies. Participants used their dominant arm for the task; four participants self-reported as left-handed and another was ambidextrous and used their right arm for the task. For left-handed participants, all data were flipped about the mirroring axis before further analysis. All participants had no known neurologic disorders and provided informed consent before participating. Study procedures were approved by the Johns Hopkins University School of Medicine Institutional Review Board.

Task details

Participants sat on a chair in front of a table, with their dominant arm resting on an air sled, which enabled planar movement with minimal friction against the glass surface of the table. Targets (diameter: 10 mm) and a hand-controlled cursor (diameter: 5 mm) were presented in the plane of movement with the help of a mirrored display. Hand position was tracked at 130 Hz using a Flock of Birds magnetic tracking device (Ascension Technologies).

Participants performed shooting movements through targets positioned 12 cm away from a central, starting position [experiments 1 and 1a: 4 different targets arranged along the cardinal directions (see Fig. 3B); experiment 2: 16 different targets, 2 horizontal ones (0° and 180° directions), 7 around the 90° direction in 2.5° increments (82.5°, 85°, 87.5°, 90°, 92.5°, 95°, 97.5°), and similarly 7 around the 270° direction (see Fig. 4B); experiment 3: 12 different targets evenly spaced across the circle (every 30°, beginning at 0°; see Fig. 6A)]. When the cursor reached 12 cm away from the starting position (equal to the target distance), its color would change and it would freeze for 0.5 s to indicate how close the participant came to going through the target; afterward, the participant was instructed to return to the starting position. During the return movement, we replaced cursor feedback with a circle, centered on the start location, whose diameter indicated the distance, but not the exact location, of the (hidden) cursor to avoid any learning during the return movement. To facilitate return movements, an air jet positioned above the start position blew a narrow stream of air downward that participants could feel on their hand.

Figure 3.

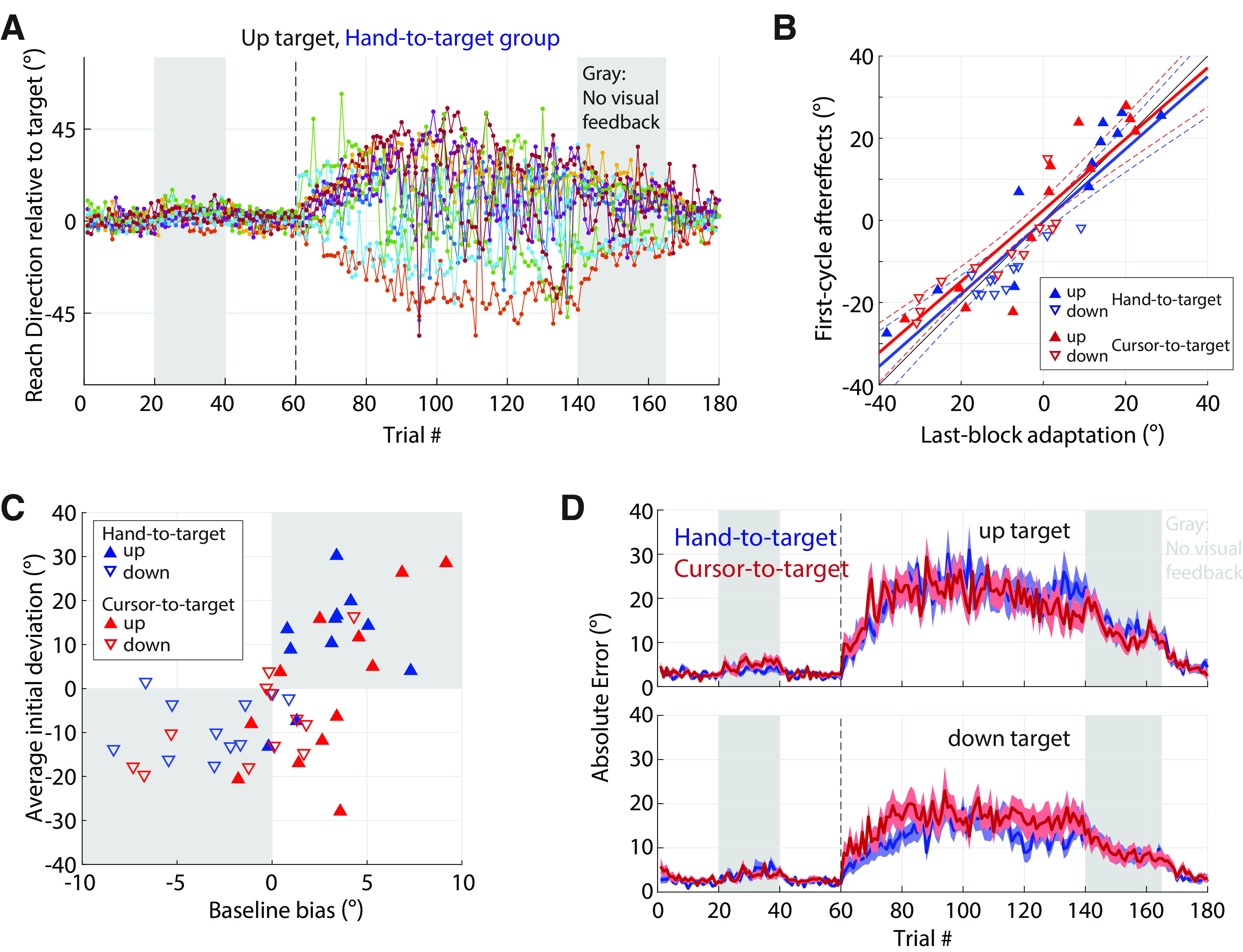
Instability of implicit adaptation under a mirror reversal. A, Errors in hand direction for the 90° (up) target in experiment 1. Each curve shows data from one participant. The mirror reversal was imposed during trials 61–140. Gray regions indicate trials during which visual feedback was withheld. The data show participants' reach directions immediately beginning to drift away from the ideal direction. Removal of visual feedback (gray region) led to clear and persistent aftereffects. B, The magnitude of aftereffects in experiments 1 and 1a matched the level of drift during late exposure to the mirror reversal. Plotted is the amount of aftereffects (first trial after visual feedback removal, trial 141) against the corresponding level of late drift (last 20 trials of preceding block). Upward-pointing triangles, Up target; downward-pointing triangles, down target; blue, hand-to-target group (experiment 1); red, cursor-to-target group (experiment 1a). Solid lines, Linear fits; colored dashed lines, the corresponding 95% confidence intervals; black thin solid line, the unity line. C, The direction of maladaptive/adaptive changes during mirror reversal training is predicted by directional biases measured during baseline. Biases measured during the second experiment block (trials 21–40) without visual feedback show a strong correspondence with the initial maladaptive changes measured during the first training block (trials 61–80). The shaded area indicates points where the direction of baseline biases and initial maladaptive changes are congruent. D, Absolute errors for the up (top) and down (bottom) targets in for the hand-to-target group (experiment 1, blue) and cursor-to-target group (experiment 1a, red). Shading indicates SEM.

Figure 4.

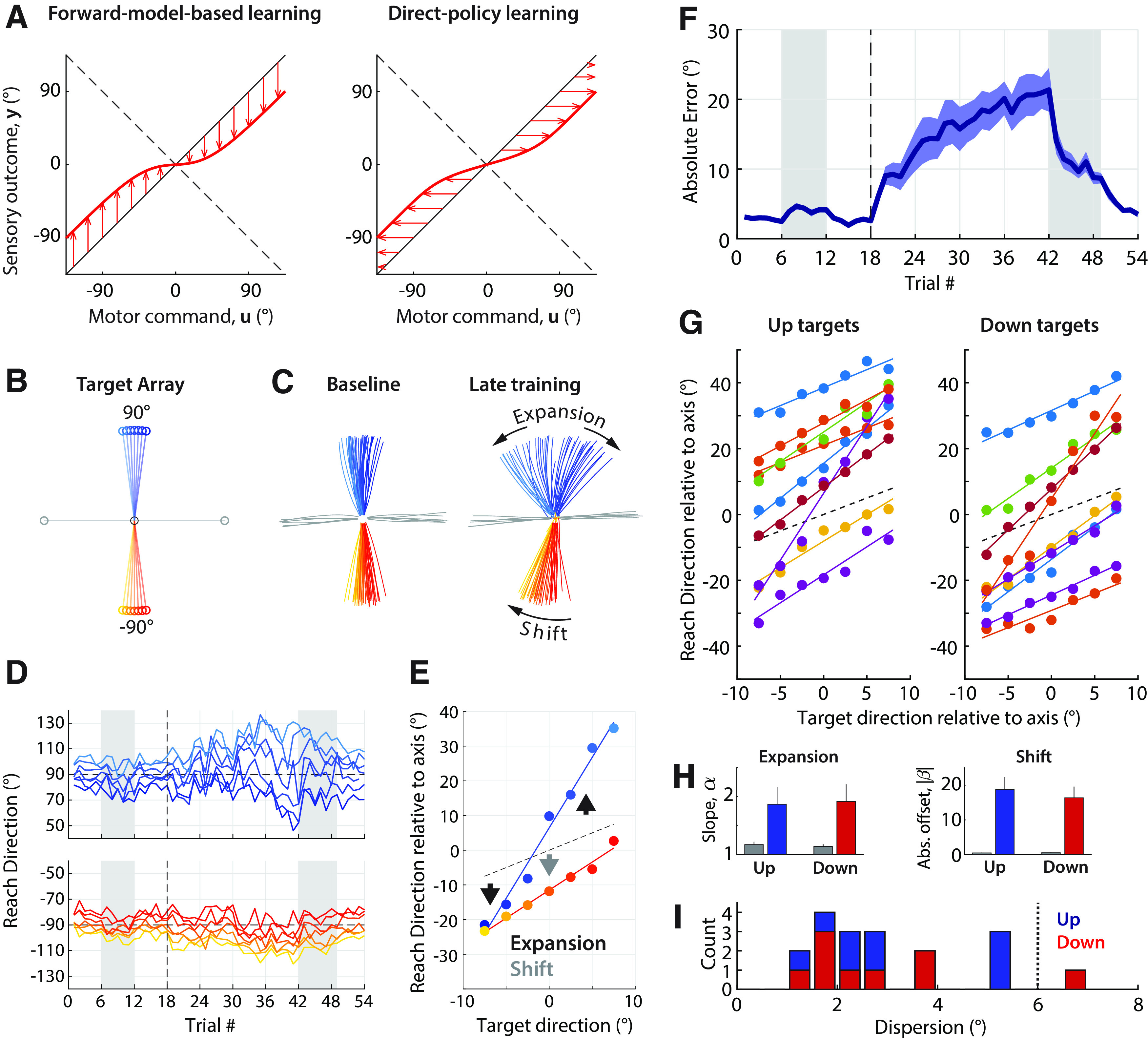
Instability of learning for a narrow range of targets. A, Left, Illustration of unstable learning predicted by forward-model-based learning. Learning occurs in the appropriate direction (arrows point toward the dashed line representing the new mapping) but a combination of saturation and broad generalization could give rise to a forward model that closely resembles the inverse of a policy arrived at by unstable direct policy learning (Right). B, Target array used in experiment 2. Targets are shown connected to the starting position (black) for clarity. C, Trajectories from an example participant during baseline (left) and the last training block (right). D, Trial-to-trial adaptive changes for the same participant (blue shades, up targets; red shades, down targets). E, Relationship between target and reach direction during late learning (filled circles) for the participant in B. The dashed line indicates the unity line, which would be close to baseline behavior. The up targets predominantly show expansion, whereas the down targets predominantly show a shift. F, Absolute error as a function of trial averaged across all participants. Shading indicates SEM. G, Relationship between target and reach direction during late learning for all participants, indicating a strong linear relationship. H, Estimated expansion and shift from baseline (gray) to asymptote adaptation, based on the linear relationship between target and reach direction. Left, slope, increase of which (>1) indicates expansion; right, offset (absolute), which indicates a shift. I, Histogram of dispersion of differences in reach direction across neighboring targets for up (blue) and down (red) targets, indicating the extent of nonlinearity of the relationship between target location and motor output.

Figure 6.

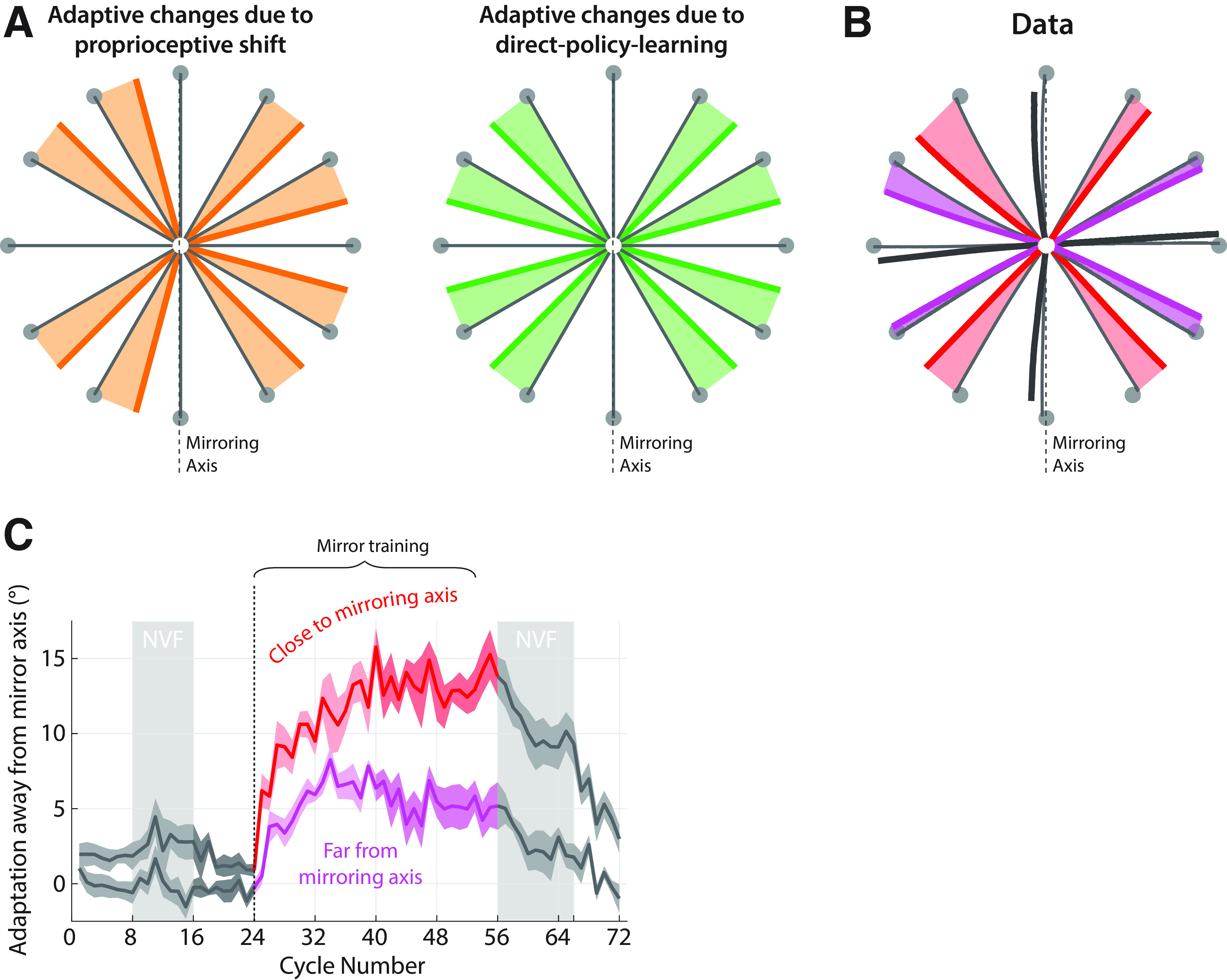
Adaptive changes to a mirror reversal when reaching to off-axis targets are consistent with direct policy learning, not forward-model-based learning or proprioceptive shifts. A, Expected pattern of changes in reach direction based on proprioceptive shift of the starting position (thick orange lines) versus direct policy learning adaptive changes (thick green lines). If the observed adaptive changes were because of a leftward shift in the perceived location of the hand at the start of each movement (Sober and Sabes, 2003), this would lead to systematic shift of all movements toward the rightward target. By contrast, drifts because of errant direct policy learning would always be directed away from the mirroring axis. Shading covers the area between baseline and adapted trajectories to highlight the predicted direction of changes. B, Average reaching trajectories in experiment 3 during baseline (thin black lines) and asymptote training (last two blocks; thick lines). Red, Off-axis targets close to the mirroring axis; magenta, off-axis targets far from the mirroring axis; gray, targets on the mirroring axis or perpendicular to it. Arrows show the direction of adaptive changes as a result of training. Shading highlights these changes in a similar way as in A. C, Trial-to-trial adaptation away from the mirroring axis for targets close to and far from the mirroring axis (red and magenta, respectively, as in A; darker shades illustrate the last block of training). Baseline adaptation levels are highlighted in dark gray; shading represents SEM. NVF, No visual feedback.

During the experiment, velocity was monitored by the experimenter. To ensure that participants were moving at a brisk speed, participants were encouraged to adjust their movement speed if they were being excessively slow or fast.

For all experiments, participants were informed of the nature of the mirror reversal right before the block in which it was first imposed. In experiments 1, 2, and 3, participants were instructed to keep aiming their hand through the target (hand-to-target groups)—even if that meant the cursor could deviate from the target. In experiment 1a, participants were instructed to try to get the cursor through the target (cursor-to-target group).

All experiments consisted of nine blocks, between which short rest breaks were given. The number of trials in each block depended on the experiment (experiments 1 and 1a: 20 trials to each of the 4 targets; experiment 2: 6 trials to each of the 16 targets; experiment 3: 8 trials to each of the 12 targets). Depending on the block, one of three different types of visual feedback was used for the out movements: veridical online cursor feedback (blocks 1 and 3), online cursor feedback inverted about the y-axis (mirror reversal, blocks 4–7), and no visual feedback (blocks 2 and 8), whereby cursor feedback was withheld to assess any baseline biases (in block 2) or aftereffects of adaptation (in block 8). Block 9 began without visual feedback then transitioned to veridical visual feedback. In experiments 1 and 1a, this transition happened after five cycles. For experiment 3 and three participants in experiment 2, because of an implementational error this transition occurred in the middle of a cycle (after 20 trials), rather than after a complete cycle. However, this did not significantly affect the results since data from these trials were not part of our main analysis. For the remaining participants in experiment 2, this was corrected so that the transition occurred after 16 trials (one cycle).

Data analysis

Analysis was performed using MATLAB (MathWorks). Position data were smoothed by filtering through a third-order Savitzky–Golay filter with a window size of nine samples (69 ms). The main outcome variable extracted from the data was the reaching angle relative to the target direction, measured at target distance (12 cm).

For experiments 1 and 1a, we focused on adaptation for the two targets on the mirroring axis. For these targets, the direction of the (mal-adaptive) drift was inconsistent across participants. Therefore, to aggregate data across participants, we used absolute error as the primary measure of adaptive changes.

For experiment 2, we focused on the adaptive changes for the two sets of targets about the up/down directions. As in experiment 1, we quantified learning in terms of the absolute error. However, to more precisely characterize the nature of adaptive changes we also fit a linear relationship between target direction and hand movement output. This yielded two parameters for each direction (upward/downward) for each participant: a slope and an offset. We refer to increases in the slope as “expansion,” and changes in the offset as a “shift.”

For experiment 3, we focused on adaptation for the eight targets not in cardinal directions. These targets were 30° or 60° away from the mirroring axis and used signed error as the primary measure of adaptive changes, flipping the sign as appropriate so that a positive error always indicated adaptive changes away from the mirroring axis.

Data inclusion criteria.

We analyzed trials along the horizontal targets to monitor adherence to the aiming instructions for experiments 1, 2, and 3. For example, if the participants were aiming their hand through the target despite cursor errors as was the instruction in experiment 1, the off-axis targets would show a cursor error of ∼180°, whereas if they were not following the instruction the cursor error would be closer to 0°. This resulted in a bimodal distribution of reach directions along the horizontal targets, making it easy to detect trials in which participants failed to follow this instruction (Extended Data Fig. 3-1). We classified horizontal trials as out of line with instructions if the reach direction was closer to the opposing target (i.e., hand direction error >90°). Errors of this kind were rather rare (average on participants included in analysis: 2.4%), with the exception of four participants (one in experiment 1, two in experiment 2, and one in experiment 3) who had such errors on >10% of horizontal-target trials during mirror adaptation. We excluded these four participants from our final analysis. A supplementary analysis including these participants is provided in Extended Data Figs. 3-2, 4-1, and 6-1, showing that they behaved in a way similar to the rest of the population, and thus retaining their data would not have altered our conclusions.

In addition, one participant in experiment 2 was excluded because of erratic reaching behavior, which was in line with neither forward-model-based nor direct policy update-based learning but likely reflected large trunk postural adjustments during the experiment. This participant's data are shown and discussed in Extended Data Fig. 4-2.

Finally, for trials to targets other than the horizontal ones, in all experiments, we excluded as outliers trials for which the absolute error was >75°; these trials constituted a very small fraction of the total (0.46%).

Statistics.

Within each group, we compared adaptation during baseline with adaptation during late learning using paired two-tailed t tests. To investigate the effect of instruction (experiment 1 vs 1a), we used a 2 × 2 ANOVA with group (hand-to-target group vs cursor-to-target group) and time (baseline vs late learning) as factors, whereas we used a similar 2 × 2 ANOVA to investigate the relationship between aftereffects and late adaptation with group (hand-to-target vs cursor-to-target group) and time (last training block vs first aftereffects cycle) as factors.

Simulating direct policy update and forward-model-based learning

Forward-model-based learning.

We assume that the forward model, $\widehat{f}$, which approximates the relationship, $f$, between motor commands, $u$ and their sensory outcome, $y=f\left(u\right)$, is constructed as a linear sum of nonlinear basis functions:

$$\widehat{y}=\widehat{f}\left(u\right)=\sum _i{w}_i{g}_i\left(u\right).$$

Here, individual basis functions $g_i$ are combined according to weights $w_i$ which can change during adaptation to build an improved approximation to the perturbed sensorimotor map.

In our simulations, we modeled adaptation of the forward model by assuming the motor system is using gradient descent to minimize a function, C, of the error, such as the following:

$$C=\frac{1}{2}{\left(y-y^{\mathrm{*}}\right)}^2,$$

where y* is the desired sensory output. Assuming that the motor system tries to select a motor command that would yield the desired sensory outcome y* by inverting the forward model at $\widehat{y}$, (which the motor system assumes to be correct), we can substitute $(\widehat{y}=y^{*})$, which makes the learning rule that minimizes C equal to the following:

$$\frac{\partial C}{\partial w_i}=-\left(y-\widehat{y}\right)\frac{\partial \widehat{y}}{\partial w_i},$$

or

$$\frac{\partial C}{\partial w_{\mathrm{i}}}=-\left(y-\widehat{y}\right)g_i\left(u\right).$$

Thus, the learning update is given by the sensory prediction error, $y-\widehat{y}$, multiplied by $g_i\left(u\right)$ and a learning rate, $\eta$.

Direct policy update-based learning.

The control policy (inverse model) $\widehat{f^{-1}}$ outputs the motor commands $u$ to bring about a desired sensory change, $y^{*}$, approximating the inverse of $f$, as follows:

$$u=\widehat{f^{-1}}\left(y^{\mathrm{*}}\right)=\sum _i{v}_i{k}_i\left(y^{\mathrm{*}}\right).$$

With the goal of minimizing error, as in Equation 2, the learning rule that minimizes C becomes the following:

$$\frac{\partial C}{\partial v_i}=-\left(y-y^{\mathrm{*}}\right)\frac{\partial y}{\partial v_i}=-\left(y-y^{\mathrm{*}}\right)\frac{\partial y}{\partial u}\frac{\partial u}{\partial v_i}=-\left(y-\widehat{y}\right)\frac{\partial y}{\partial u}\frac{\partial u}{\partial v_i}.$$

Here, $\frac{\partial y}{\partial u}$ transforms the sensory error into a motor error and is sometimes referred to as a sensitivity derivative (Abdelghani et al., 2008; Abdelghani and Tweed, 2010). Equation 6 can also be rewritten as follows:

$$\frac{\partial C}{\partial v_i}=-\left(y-\widehat{y}\right)\frac{\partial y}{\partial u}{k}_i\left(y\right).$$

Thus, as in forward model learning, the direct policy update-based learning update will be countering the sensory prediction error, $y-\widehat{y}$, times $k_i\left(y\right)$ and a learning rate $\eta$; however, this will also need to be multiplied by the sensitivity derivative $\frac{\partial y}{\partial u}$. Without a means to learn the sensitivity derivative, the motor system can only rely on simple rules about the sign and magnitude of the sensitivity derivative (i.e., here, $\frac{\partial y}{\partial u}$ is a constant).

To simulate forward-model-based and direct policy learning, we modeled the learning basis functions as Gaussian kernels, as follows:

$$g_i\left(u\right)=e^{-\frac{{\left(u-u_i\right)}^2}{2{\sigma }_u^2}},\hspace{1em}{k}_i\left(y\right)=e^{-\frac{{\left(y-y_i\right)}^2}{2{\sigma }_y^2}}.$$

The centers of each basis function, $u_i$ and $y_i$ above, were uniformly distributed around the mirroring axis with a spacing of 0.05°. The widths of these kernels, ${\sigma }_u$ and ${\sigma }_y$, were left as open parameters.

To model saturation in learning, we saturated the basis function weights using the following sigmoidal function:

$$w_{\mathrm{s}\mathrm{a}\mathrm{t}}=L\frac{1-e^{-w}}{1+e^{-w}}.$$

The asymptotic limit of adaptative changes in motor output, $u_{\mathrm{o}\mathrm{u}\mathrm{t},\mathrm{a}\mathrm{s}\mathrm{y}\mathrm{m}\mathrm{p}\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{e}}$, linearly scales with $L$, as follows:

$$u_{\mathrm{o}\mathrm{u}\mathrm{t},\mathrm{a}\mathrm{s}\mathrm{y}\mathrm{m}\mathrm{p}\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{e}}=\frac{L\sigma \sqrt{2\pi }}{\Delta },$$

where $\sigma$ is the width of the corresponding basis function ($g$ or $k$, correspondingly) and $\Delta$ is the spacing between consecutive basis functions (0.05° in our simulations).

For forward-model-based learning, we used a sensory prediction error to drive learning $\left(y-\widehat{y}\right)$; for direct policy update-based learning, we used a task error $(y-y^{*})$. Note that using the task error for the direct policy update simulations is, here, also equivalent to using sensory prediction error: since participants aim their hand directly at the intended target, the task error they experience relative to the aimed direction (the target itself) is equivalent to the sensory prediction error about that direction.

To select an action in each trial, under forward-model-based learning, we selected the action that the forward model predicted would lead to the desired outcome. In cases where multiple motor commands were predicted to lead to the same expected sensory outcome, we chose the motor command closest to the origin.

To identify possible model parameters, we systematically examined behavior for a range of values for the $\sigma$ and $\eta$ parameters [specifically, for forward-model-based learning: $\sigma \in \left[4°,14°\right]$ in 0.5° increments (15° and 20° simulations), and $\eta \in \left[1\text{,}14\right]\times {10}^{-4}$ (for 15° asymptote simulations) or $\eta \in \left[1\text{,}32\right]\times {10}^{-4}$ (for 20° asymptote simulations) in $0.5\times {10}^{-4}$ increments; for 25° simulations, two parts of the parameter space: σ ∈ [2°, 12°] in 0.5° increments with η ∈ [1,48] × 10⁻⁴ in 10⁻⁴ increments and σ ∈ [2°, 5°] in 0.5° increments with η ∈ [49,399] × 10⁻⁴ in 2 × 10⁻⁴ increments; for direct policy learning: $\sigma \in \left[5°,14°\right]$ in 0.5° increments; and $\eta \in \left[0.5\text{,}12\right]\times {10}^{-4}$ in $0.5\times {10}^{-4}$ increments (same for all three asymptote values)]. For each pair of parameters ($\sigma$, $\eta$) and for each of the two models, we ran 100 simulations, each with a different random target order. Specifically, we randomized the order of the seven targets within each cycle, for a total of 24 cycles (168 trials), to match the number of training cycles in experiment 2. We also included motor noise in our simulations by adding zero-mean Gaussian noise to the outgoing motor commands, with an SD of 3.2° based on baseline data. As in our analysis of experiment 2, we used the last two “blocks” (last 12 cycles) as a measure of asymptotic adaptation.

To classify which simulations led to expansion, we set a criterion that the resulting slopes of the target–output relationship should be >1.25. To estimate values for ($\sigma$, $\eta$) that are compatible with the learning and generalization characteristics of visuomotor adaptation, we simulated the adaptation of both types of models to single-target adaptation to a 22.5° visual clamp (Morehead et al., 2017). We evaluated the width of the resulting generalization function, taking as compatible parameters the ones that led to a full-width at half-maximum between 40° and 80°, and speed of learning, taking as compatible parameters the ones that led to between 6 and 18 trials to reach 80% of asymptotic adaptation.

Results

Mirror reversal elicits implicit adaptation that amplifies errors across trials

We first performed an experiment (experiment 1) to better characterize the properties of implicit learning under a mirror reversal and verify that it indeed bears the expected hallmarks of implicit adaptation. In experiment 1, 12 participants made planar 12 cm reaching movements to “shoot” through one of four different targets (Fig. 2A,B), two positioned on the mirroring axis (on-axis targets) and two perpendicular to it (off-axis targets). Based on prior studies (Lillicrap et al., 2013; Wilterson and Taylor, 2019), we expected that implicit adaptation would tend to amplify small initial errors over time.

Figure 2.

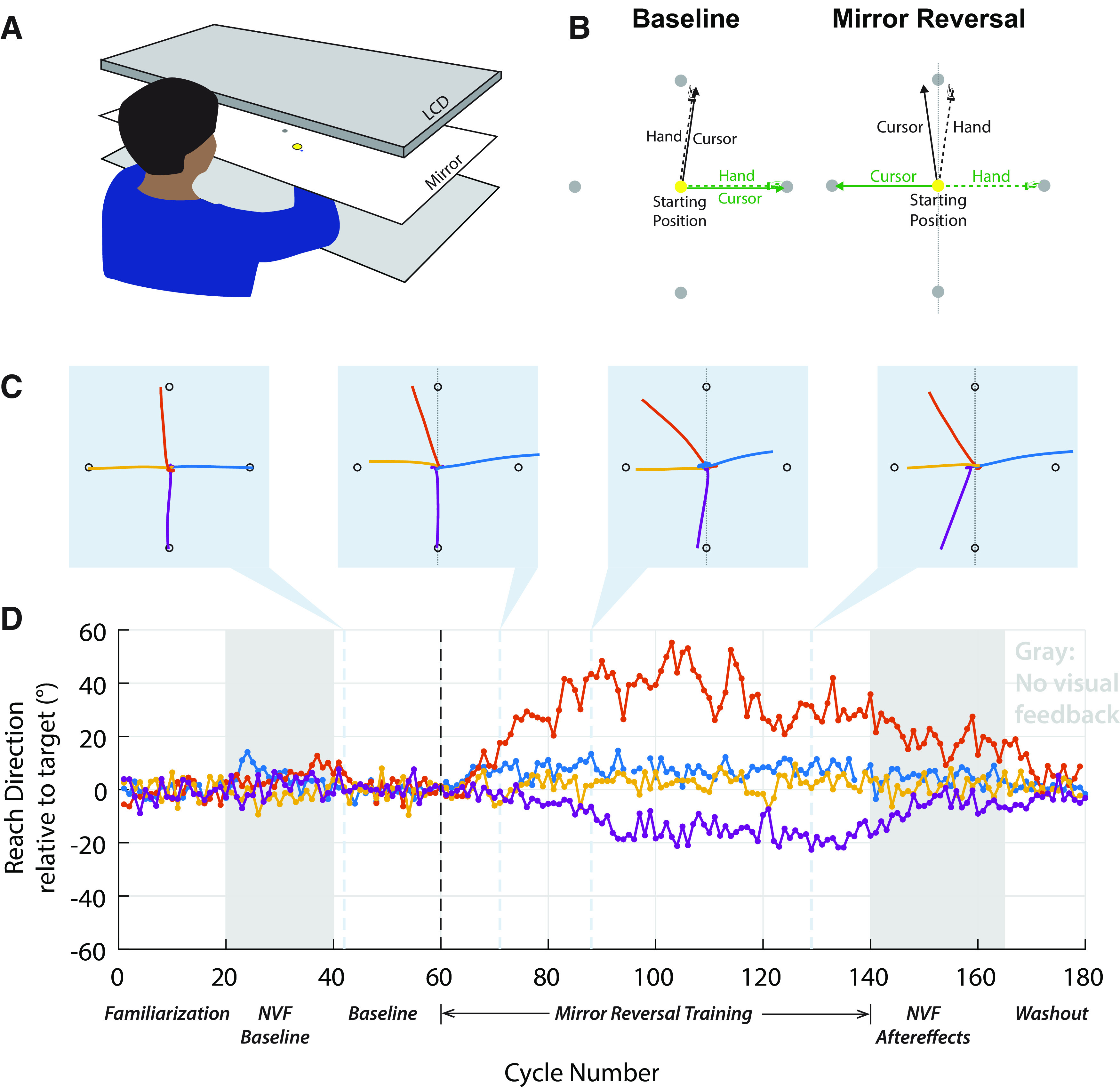
Experiment 1 design and example participant. A, Participants made reaching movements on a tabletop. Vision of the hand was occluded and an LCD screen projected a blue cursor that appeared at the level of the table through a mirror. B, Participants made center-out shooting movements from a central starting position (yellow circle) through different targets (gray circles). During baseline (left), the cursor followed hand position; during mirror reversal training (right), cursor feedback was reflected about the y-axis (vertical dashed line). C, Example hand trajectories from (left to right) baseline, early, middle, and late learning, for one participant. D, Reach direction relative to the target for all target directions. There is a clear drift away from the two targets along the mirroring axis (orange and purple), which persists after visual feedback is removed after trial 140 (gray). For clarity, trials to horizontal targets in which the participant moved toward the opposing target are omitted from this plot (three trials in blue curve). NVF stands for No Visual Feedback (NVF trials are indicated by the gray background).

We began with three blocks of unperturbed movements to familiarize participants with the task and to assess baseline behavior. This was followed by the training phase where we introduced a mirror reversal about the y-axis. To isolate implicit adaptation to the mirror reversal, we instructed participants to aim their hand directly through the target, rather than try to guide the mirrored cursor through the target, although the cursor might miss it. This approach has been demonstrated to successfully isolate implicit components of adaptation (Morehead et al., 2015; Kim et al., 2018). All participants but one were successful in following this instruction, as evidenced by their performance at off-axis targets, where they overwhelmingly aimed their hand toward the target (in 98.1 ± 0.5% of off-axis trials, mean ± SEM; Extended Data Fig. 3-1). The unsuccessful participant was removed from further analysis because of their frequent off-axis errors (13.8% of off-axis target trials).

Figure 2, C and D, shows the behavior of an example participant at different points during the experiment. After the mirror reversal was introduced (cycles 61–140), there was little, if any, change in the direction of reaching movements to off-axis targets (Fig. 2C,D, yellow and blue). For reaching movements to on-axis targets (Fig. 2C,D, orange and purple), however, small initial deviations tended to be amplified from trial to trial, rather than corrected, as illustrated in Figure 2D. This unstable adaptation is consistent with the adaptation in an inappropriate direction reported previously under a mirror reversal (Lillicrap et al., 2013; Wilterson and Taylor, 2019). The deviations in reach direction that we observed tended to saturate at ∼20–30° away from the axis, which is consistent with the limited capacity of the implicit adaptation system identified in visuomotor rotation studies (Bond and Taylor, 2015; Morehead et al., 2017; Kim et al., 2018).

Behavior of this example participant was similar to that observed across the population as a whole (Fig. 3A), with small deviations becoming amplified over time, resulting in a drift away from the mirroring axis (Fig. 3A, 0°). The direction of this drift varied across participants, being directed either clockwise or counterclockwise (negative or positive values, respectively, on the same panel). However, the absolute directional error for reaches to the two on-axis targets increased significantly from baseline to late adaptation [2.5 ± 0.2° in baseline vs 17.8 ± 1.3° in the last two mirror training blocks (sixth and seventh); t₍₁₀₎ = 11.3, p < 10⁻⁶, Cohen's d = 3.41; Fig. 3D, blue]. A post hoc analysis showed that the direction of the initial deviations and subsequent drift generally followed directional biases of baseline hand movements in almost every case (for 10 of 11 participants for the “up,” 90° target; and 8 of 11 participants for the “down,” 270° target; Fig. 3C). Although participants generally showed a monotonic drift that was either consistently clockwise or counterclockwise relative to the target, a small number of participants (2 of 11 at the up target and 1 of 11 at the down target) reversed the direction of their drift between the first and fourth training block, as illustrated in Figure 3A.

Figure 3-1

Distribution of hand reach directions for the horizontal targets in experiments 1 and 1a. In experiment 1 (hand-to-target group), reaches on the 180° direction suggest the participant erroneously aimed the cursor, rather than the hand, to the target. Correspondingly, in experiment 1a (cursor-to-target group), reaches on the 0° direction suggest the participant erroneously aimed the hand, rather than the cursor, to the target (or may in general signify a failure to implement the strategy of aiming in the opposite direction). Note that the scale is logarithmic to illustrate these relatively rare error events. Download Figure 3-1, EPS file ^{(1.2MB, eps)} .

Figure 3-2

Results from participants excluded because of frequent horizontal-target errors (experiment 1). In experiment 1, the one excluded participant (black curves) showed behavior in line with the included data (faded curves; compare Fig. 3A). There were no participants excluded in experiment 1a. Download Figure 3-2, EPS file ^{(3MB, eps)} .

In the eighth (penultimate) block, we assessed the presence and stability of aftereffects by removing visual feedback and reminding participants before the block to keep aiming their hand through the target. The example participant in Figure 2 (gray, trials 141–165) exhibited strong, slowly decaying aftereffects during this block. This pattern was consistent across the whole group of participants, which showed strong aftereffects during the no-visual-feedback block [absolute reaching angle on the first postlearning cycle: 16.2 ± 0.9° vs 4.1 ± 0.4° for the no-visual-feedback baseline (block 2), t₍₁₀₎=14.5, p < 10⁻⁷, Cohen's d = 4.37]. Furthermore, these aftereffects closely matched the amount of drift during the last exposure block (last 20 adaptation trials) as shown in blue in Figure 3B (linear fit between subject-averaged reaching angles during the last exposure block and the first aftereffect cycle: slope = 0.88 [95% confidence interval (CI), 0.66–1.10; R² = 0.90, p < 10⁻⁵]). These aftereffects persisted throughout the no-visual-feedback block, decaying slowly, and were only completely extinguished once veridical feedback was restored, as shown in Figure 3A. This gradual decay of aftereffects is a key signature of implicit adaptation (Galea et al., 2011; Kitago et al., 2013) and confirms that the change in behavior during the exposure blocks was attributable to implicit adaptation.

In summary, this experiment showed that implicit adaptation occurred under mirror reversal, displaying key signatures of implicit adaptation such as persistent, slowly decaying aftereffects when the perturbation was removed, as well as ceiling values in line with those seen under other visuomotor perturbations. Importantly, this adaptation did not act to reduce performance errors but instead initially amplified small errors, driving reaching movements away from the mirroring axis. This finding is consistent with previous reports (Lillicrap et al., 2013; Wilterson and Taylor, 2019), but these results clearly show that this phenomenon relates to implicit rather than explicit learning.

Allowing participants to use strategy did not prevent error amplification to targets on the mirroring axis

To assess the possible effect of explicit reaiming strategies on unstable learning under mirror reversal, we ran a second group of participants (experiment 1a) that experienced an identical training schedule with one major difference: on briefing participants about the nature of the upcoming mirror perturbation after the third block, we instructed them to do their best to bring the cursor through the target (unlike the first group in experiment 1, in which participants were instructed to bring their hand through the target). We refer to this group as the cursor-to-target group, in contrast to the first group, which we refer to as the hand-to-target group. Similar to the hand-to-target group, the cursor-to-target group showed an increase in errors for the on-axis targets, as shown in Figure 3D (2.7 ± 0.2° in baseline vs 18.0 ± 2.1° in the last two blocks of adaptation; t₍₁₁₎ = 7.71, p < 10⁻⁵, Cohen's d = 2.22). Despite the contrasting instructions, behavior was not significantly different between the two groups [two-way ANOVA for subject-averaged absolute errors, using time (baseline vs late learning) and group (cursor-to-target vs hand-to-target) as factors; there was a main effect of time (F_(1,45) = 142.28, p < 10⁻⁸, η² = 0.77), but no effect of group (F_(1,45) = 0.03, p = 0.86, η² = 2.9 × 10⁻⁴) or time × group interaction (F_(1,45) = 0.00, p = 1.00, η² = 0.0)].

Before the eighth block, participants were instructed to disengage any deliberate compensation strategies, and instead aim their hand through the target. Visual feedback was also removed for this block. Participants exhibited clear aftereffects [absolute reaching angle on the first postlearning cycle: 15.3 ± 1.8° vs 4.3 ± 0.4° for the no-visual-feedback baseline (block 2); t₍₁₁₎ = 6.30, p < 10⁻⁴, Cohen's d = 1.82], and the magnitude of the aftereffects matched the amount of late adaptation, as suggested by a linear relationship with a slope close to 1 [Fig. 3B, red; linear fit between last adaptation block and the first aftereffect cycle: slope = 0.87 (95% CI, 0.67–1.07), R² = 0.90, p < 10⁻⁵]. To systematically compare aftereffects in the two groups, we performed a two-way ANOVA for subject-averaged absolute errors, using time (last adaptation block vs first aftereffect cycle) and group (cursor-to-target vs hand-to-target) as factors; there was no main effect of time (F_(1,45) = 0.34, p = 0.57, η² = 0.0079), group (F_(1,45) = 0.11, p = 0.74, η² = 6.3 × 10⁻⁴), or any time × group interaction (F_(1,45) = 0.03, p = 0.87, η² = 0.0).

These aftereffects demonstrate that implicit adaptation occurred at the on-axis targets, and that this errant learning could not be countered by the explicit system during learning, although participants were allowed to adopt a strategy. This stands in contrast to the relative ease by which participants minimized error in the off-axis targets, as illustrated by smaller absolute errors (7.9 ± 1.5° in the last two adaptation blocks for the off-axis targets, compared with 18.0 ± 2.1° for the on-axis targets; t₍₁₁₎ = 4.54, p = 0.00084, Cohen's d = 1.31), suggesting that the effective use of explicit strategies was limited to the off-axis targets.

Failure of implicit adaptation under mirror reversal can be explained by both forward-model-based learning and direct policy updates

We considered, from a theoretical perspective, whether either of the two theories of adaptation—forward-model-based learning or direct policy learning—might be consistent with the observed instability of learning under a mirror reversal. We found that both theories can, in some circumstances, predict unstable adaptation consistent with the results of experiment 1.

Under direct policy learning, adaptation depends on translating an observed error in the sensory domain into an error in the motor domain, suitable for updating motor output (Fig. 1B). This process inherently relies on tacit assumptions about how motor output relates to sensory outcomes. In practice, it is not necessary for the translation from sensory to motor errors to be exact. It is sufficient that the update rule translating observed errors to changes in policy has the same sign as the sensitivity derivative of the task, which ensures that changes in motor output reduce sensory error (e.g., if you miss the target to the left, adjusting your motor output to the right in the next movement will reduce the error). Under a mirror reversal, however, the relationship between motor output and sensory outcome is flipped. Consequently, if you adjust your motor according to the baseline update rule (i.e., shift output to the left in response to a rightward error), you will increase, rather than decrease, error in the next trial (Fig. 1G,H). Unless the update rule appropriately reverses sign, direct policy learning will fail to adapt to a mirror reversal, increasing errors from trial to trial, consistent with the results of experiment 1. Although it may, in principle, be possible to learn to reverse the sign of the learning rule implicitly, this does not appear to be the case over the timescale of a typical adaptation experiment: while some studies show limited overall adaptation to mirror reversal over a single session (Abdelghani and Tweed, 2010; Lillicrap et al., 2013), recent work that isolated implicit adaptation, as we did in experiment 1, showed no learning of a mirror reversal even after multiple days (Wilterson and Taylor, 2019), suggesting that the limited learning observed earlier was because of explicit, rather than implicit, components of adaptation. Even if the update rule could be eventually learned, one would still see transient adaptation in the wrong direction until the update rule flips.

In contrast to direct policy learning, forward-model-based learning should, in principle, be able to compensate for a mirror reversal. Updating a forward model in response to an error does not rely on any assumptions about the relationship between motor output and sensory outcomes: if the cursor went further to the right than predicted, the forward model should just predict that the cursor will move further to the right in the future for that particular motor output (Fig. 1C,F). It ought to therefore be possible to successfully learn an appropriate forward model of any arbitrary perturbation, including a rotation or a mirror reversal. Indeed, the principle that a forward model can always be learned provides the basis for many approaches to learning control (Jordan and Rumelhart, 1992; Schaal and Atkeson, 2010).

Although forward-model-based learning should, in principle, be able to learn and compensate for a mirror reversal, in the context of iterative, trial-by-trial learning, however, the earliest updates during learning may in fact act to amplify errors, rather than to reduce them (Fig. 1F). Furthermore, the ability to adapt a forward model itself may be subject to limitations such as saturation (estimated to be ∼15–25°; Bond and Taylor, 2015; Morehead et al., 2017; Kim et al., 2018), which might prevent forward-model-based learning from ever successfully compensating for a mirror reversal. An additional limitation of forward-model-based learning is that, to learn to successfully compensate, it is not enough to simply update predictions about the consequences of the wrong (baseline) motor command for a given goal; participants must also at some point sample the correct motor command to learn that that it will generate the desired outcome. The failure to compensate for a mirror reversal in experiment 1 might thus have been because of the fact that the targets were isolated and participants never sampled the actions that would have successfully acquired the target.

Unstable learning cannot be explained by biased or limited-extent forward-model-based learning

As explained in the previous section, the behavior observed in experiment 1, and in prior studies, could be consistent with either forward-model-based learning or direct policy learning. We ran a second experiment, experiment 2, which addressed the shortcomings of experiment 1 by examining learning not at a single target but at a narrow array of targets centered on the mirroring axis. The pattern of behavior across these targets enabled us to dissociate between forward-model-based and direct policy learning as mechanisms of implicit adaptation. Importantly, as in experiment 1, participants were instructed to always bring their hand directly through the presented target. Targets were positioned between −7.5° and 7.5° about the 90° and 270° directions, in 2.5° increments (Fig. 4B). Potential limitations in adapting the forward model of ∼15–25° should not preclude accurate learning of the forward model within this narrow range of targets, since the largest adaptive change required is just 15°. Furthermore, distributing targets on either side of the mirroring axis ensured that participants would sample the solution for each possible target. Forward-model-based learning thus ought to be able to successfully adapt within this narrow range of targets, even given possible limited extent of learning. In contrast, we expected direct policy learning to lead to unstable performance.

Figure 4-1

Results from participants excluded because of frequent horizontal target errors (experiment 2). In experiment 2, the two excluded participants, indicated by the darker curves/points, show data in line with the main results (compare Fig. 4F–I). An additional participant excluded because of erratic behavior, likely because of a technical issue, is shown in Extended Data Figure 4-2. Download Figure 4-1, EPS file ^{(1.7MB, eps)} .

Figure 4-2

Data of participant excluded because of erratic behavior in experiment 2. A–C, Format is the same as in Figure 4C–E. Erratic behavior probably resulted from a large postural adjustment at the beginning of the sixth block (indicated by arrows), which would explain the abrupt changes and is in line with the participant mentioning that they had trouble reaching to the down target. Note that the result is in line with neither forward model-based learning (there is no reversal of the slope in C) nor direct policy update-based learning (the target–output relationship for the down target is not strongly linear). Download Figure 4-2, EPS file ^{(2.3MB, eps)} .

We found that, similar to experiment 1, participants' behavior was unstable for this set of targets, with absolute error increasing as training progressed (2.6 ± 0.1° during baseline vs 19.3 ± 2.6° during the last training block; t₍₈₎ = 6.38, p = 0.0002, Cohen's d = 2.13; Fig. 4F). Contrary to our expectations, we observed two distinct regimes of instability in participants' behavior: in some instances, trajectories diverged away from the mirroring axis (Fig. 4C–E, expansion) as we had expected. In other instances, however, trajectories to targets on both sides of the mirroring axis shifted approximately in parallel toward one direction or the other (Fig. 4C–E, shift). Some participants exhibited mixtures of these phenomena (i.e., a simultaneous shift and expansion), and patterns of behavior for upward and downward sets of targets for the same participant were also not necessarily the same.

Regardless of the specific pattern of divergence, we found that there was always a strong linear relationship between target and motor output (Fig. 4G; R² values for linear fit, all >0.87). Linear fits allowed us to quantify expansion as an increase in the slope of this relationship, and shift as an offset (Fig. 4H). Across all participants, we found both a significant slope increase (upward targets: 1.17 ± 0.05 in baseline vs 1.87 ± 0.30 in asymptote; t₍₈₎ = 2.59, p = 0.032, Cohen's d = 0.86; downward targets: 1.14 ± 0.04 in baseline vs 1.92 ± 0.30 in asymptote, t₍₈₎ = 2.66, p = 0.029, Cohen's d = 0.89) and increase in the absolute offset (up targets: 0.5 ± 0.1° in baseline vs 18.8 ± 3.5° in asymptote; t₍₈₎ = 5.08, p = 0.0010, Cohen's d = 1.69; down targets: 0.5 ± 0.1° in baseline vs 16.3 ± 3.2° in asymptote; t₍₈₎ = 4.85, p = 0.0013, Cohen's d =1.62) as illustrated in Figure 4H.

Although the instability of learning across even a narrow range of targets appears inconsistent with forward-model-based learning, we reasoned that it might be possible that interference (generalization) of learning either side of the mirroring axis might have impaired forward-model-based learning: clockwise learning at a target on one side of the axis might be offset by generalization of counterclockwise learning at a target on the opposite side. This interference might have prevented participants from ever being able to learn an accurate forward model or made them learn it only on one side of the mirroring axis.

To examine whether forward-model-based learning, hampered by issues associated with saturation and generalization, could credibly account for the behavior we observed in experiment 2, we simulated behavior in the protocol tested in experiment 2 using either forward-model-based or direct policy learning. Our simulations were based on standard state-space models of learning using a linear combination of Gaussian basis functions (Sanner and Slotine, 1991; Donchin et al., 2003; Shadmehr, 2004; Thoroughman and Taylor, 2005; Tanaka et al., 2009; Herzfeld et al., 2014). This is a well established framework for modeling trial-by-trial adaption and generalization, accounting for a variety of behavioral phenomena, particularly the ubiquitous Gaussian pattern of generalization observed behaviorally (Brayanov et al., 2012; McDougle et al., 2017; Zhou et al., 2017). We implemented saturation by limiting the weights associated with each basis function (see “Materials and Methods” for details). Our models each contained the following three free parameters: learning rate, η; basis function width, σ; and extent of saturation, u_asymptote.

Consistent with our participants' behavior, we observed both expansions and shifts in simulations of both models. The extent and likelihood of expanding or shifting depended on the exact sequence of targets experienced as well as on the model parameters (Fig. 5, examples). However, only the simulations based on direct policy learning predicted the preserved linear relationship we observed between target direction and reach direction (Fig. 5, compare D–F, J–L). Simulations assuming forward-model-based learning predicted nonlinear patterns of behavior with often abrupt differences in motor output for neighboring targets (Fig. 5D, right). Such abrupt transitions may occur when one target is outside the area where the forward model has learned to predict the mirror reversal, and the neighboring target is not.

Figure 5.

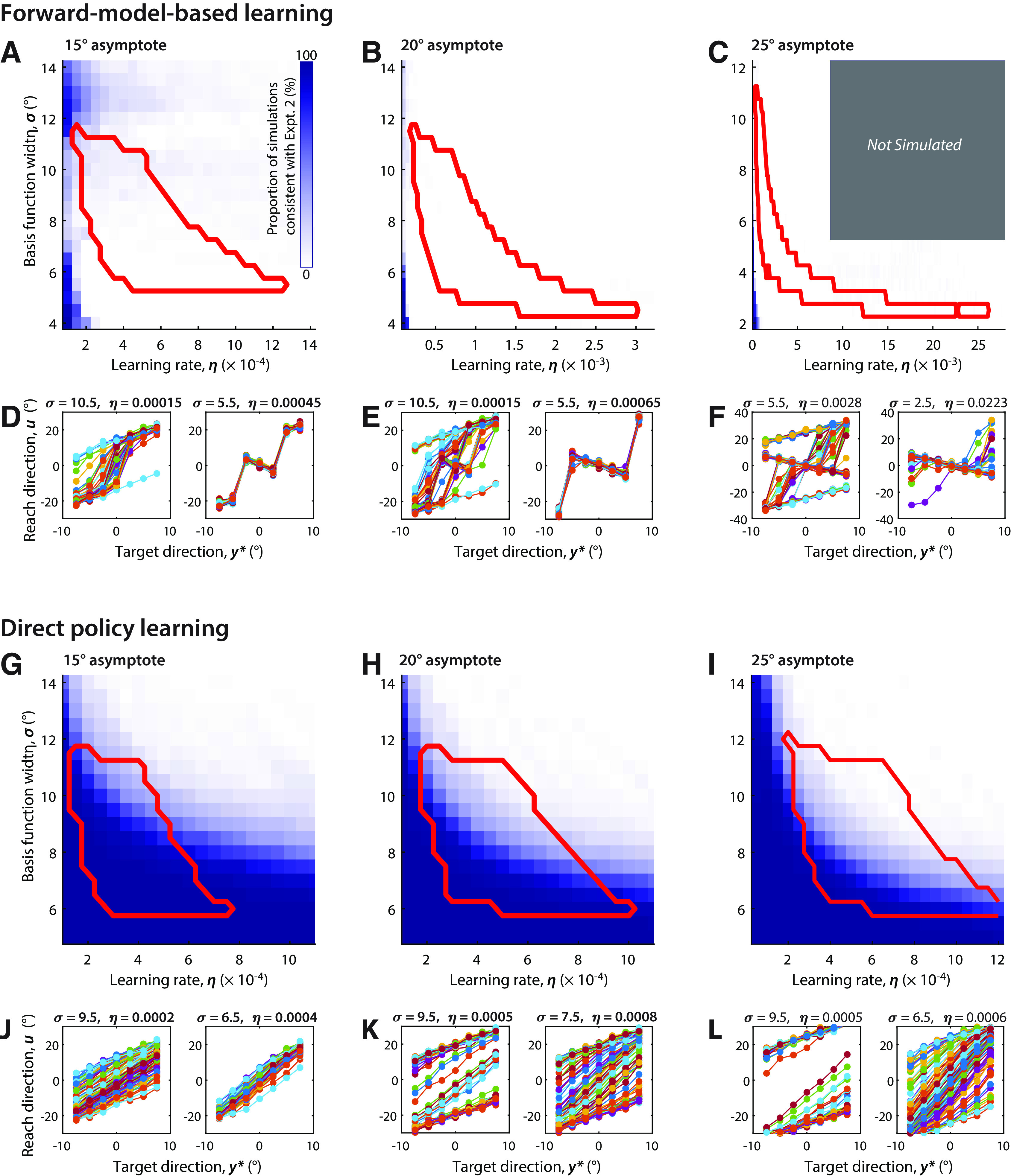
Simulations of forward-model-based learning and direct policy learning. A–J, Simulations of forward-model-based learning are inconsistent with the data and well characterized attributes of implicit adaptation. A–C, The extent to which simulations under different model parameters could qualitatively match the patterns of behavior observed in experiment 2, given an assumed asymptote of 15°, 20°, and 25° respectively. The color gradient indicates the proportion of pseudorandom simulations that resulted in both expansion (slope, >1.25) and smooth changes in reach direction across targets (dispersion of differences across targets, <6) given different values for basis function width and learning rate. The red border encloses parameter values consistent with known patterns of learning and generalization of visuomotor adaptation, based on the findings in the study by Morehead et al. (2017). The gray rectangle in C indicates (η, σ) pairs not simulated as they were well outside the red border. D–F, simulated steady-state relationships between target direction and reach direction (comparable to empirical data shown in Fig. 4G) for selected parameter values. For forward-model-based learning, there was no overlap between regions of parameter space for which simulated data were consistent with data in experiment 2 (regions shaded in blue), and regions of parameter space consistent with established properties of implicit adaptation (red-bordered region). G–L, same as A–F but for direct policy learning. G–I show that a wide range of model parameters for direct policy learning are qualitatively consistent with both empirical data in experiment 2 (regions shaded in blue) and with established properties of implicit adaptation (red-bordered regions).

To more systematically determine whether either class of model could account for our experimental data, we systematically varied the parameters of the simulated models (η, σ, and u_asymptote) over a wide range and assessed whether each model could qualitatively reproduce the main features of our data shown in Figure 4, G and H: expansion and linearity, characterized by a linear but increased slope of the relationship between target and asymptotic reach direction for that target. To assess whether simulation results reflected the linearity and smoothness of this relationship observed in the data, we characterized the simulated target/output relationships in terms of the dispersion (SD) of differences between neighboring targets, D. This metric captured the systematic nonlinearities in behavior predicted by forward-model-based learning better than simply computing squared residual error. Based on the distribution of the data (Fig. 4I), we required that the D value of the fitted model be <6, which was consistent with behavior in about 95% of the data. Furthermore, we assessed whether the model predictions for a particular set of parameters were consistent with well established properties of implicit adaptation, specifically the rate of adaptation, the maximum extent of adaptation, and generalization to neighboring directions when implicit adaptation is driven by a constant error under an error-clamp paradigm (Morehead et al., 2017).

For forward-model-based learning, there was no overlap between parameters that could qualitatively account for our data under mirror reversal and for parameters that could account for error-clamp behavior; simulation runs that predicted a linear expansion of motor output were very rare for an imposed asymptote of 15° (Fig. 5A), and essentially nonexistent for asymptotes of 20° (Fig. 5B) and 25° (Fig. 5C). These asymptote values were chosen based on the range of observed values for the limits of implicit adaptation to a visuomotor rotation (Bond and Taylor, 2015; Morehead et al., 2017; Kim et al., 2018). By contrast, there was broad overlap for the direct policy-learning model between parameters that accounted for our data and parameters that accounted for error-clamp behavior (Fig. 5G–I). We thus conclude that forward-model-based learning cannot account for our experimental observations, while they are naturally accounted for by the direct policy-updating model.

Implicit adaptation drove movement away from the mirroring axis for off-axis targets

A potential confound in our previous experiments is that some patterns of directional biases we observed could have been the result of a shift in the proprioceptive estimate of the starting position of the hand (Sober and Sabes, 2003), rather than reflecting patterns of implicit adaptation. For example, if the hand is perceived to be slightly to the left of its true starting position, this would lead to a clockwise bias at the up target and a counterclockwise bias at the down target, as illustrated in Figure 6A. We indeed observed such a bias for many of our subjects, as in the example given in Figure 2C. Other patterns of shifts might also be explicable in terms of misestimated initial limb posture (Sober and Sabes, 2003).

Figure 6-1

Results from participants excluded because of frequent horizontal target errors (experiment 3). In experiment 3, the one excluded participant (darker colors) also showed adaptation away from the mirroring axis. Data overlaid against results from included participants (compare Fig. 6B). Download Figure 6-1, EPS file ^{(1.5MB, eps)} .

To rule out this potential alternative explanation for the results of experiments 1 and 2, we ran a further experiment, experiment 3, in which we assessed behavior across a broader range of 12 equally spaced targets (Fig. 6A,B). We specifically focus on the off-axis targets, which allows us to assess whether shifts in the proprioceptive estimates about the origin can account for our data: if that is the case, targets on the left and right of the mirroring axis would move toward the same direction. Consequently, targets on one side of the mirroring axis would show adaptation away from the mirroring axis, and targets on the other side would show adaptation toward the mirroring axis (Fig. 6A). In contrast, under direct policy learning, these off-axis targets will show adaptation away from the mirroring axis on either side (Fig. 6A). Participants in experiment 3 completed 32 cycles of exposure to the mirror reversal with this set of targets, again under the instruction to always focus on bringing their hand to the center of the target.

We found that, for targets on the eight noncardinal directions, there was a clear change in reach direction away from the mirroring axis (targets 30° away from mirroring axis; Fig. 6B,C, red: 1.4 ± 0.4° vs 13.3 ± 1.2° for baseline vs asymptote adaptation, t₍₉₎ = 10.3, p = 0.000003, Cohen's d = 3.25; targets 60° away from mirroring axis; Fig. 6B,C, magenta: −0.4 ± 0.3° vs 5.3 ± 0.9°, t₍₉₎ = 6.59, p = 0.0001, Cohen's d = 2.08), and participants never became able to compensate for the perturbation. On both sides of the workspace, these changes were away from the mirroring axis, as shown in Figure 6B, and thus cannot be explained by a proprioceptive shift.

Adaptive changes tended to be greater for the more proximal targets (30° away from the mirroring axis) compared with the more distal targets (60° away from the mirroring axis; post hoc t test t₍₉₎ = 7.17, p = 0.00005, Cohen's d = 2.27). This is consistent with the well known observation that sensitivity to error tends to decrease for larger errors (Marko et al., 2012; Kim et al., 2018). Sensitivity to error at these targets might be further reduced because of the fact that the cursor lands even further from the aiming target itself, which is likely the point of fixation (de Brouwer et al., 2018). Furthermore, for targets almost orthogonal to the mirroring axis, it is not clear whether it remains reasonable to think about and quantify implicit adaptation in terms of a change in reach direction, rather than a change in gain.

Discussion

Our experiments sought to identify the process by which errors lead to adaptive changes in behavior. In particular, we sought to dissociate whether adaptation was based on forward-model-based learning or direct policy learning. Each of these mechanisms has previously been proposed to explain error-driven motor learning. Forward-model-based learning has become a widely accepted theory of adaptation. However, there has been no decisive evidence to support it over direct policy learning.

To dissociate these two theories, we focused on implicit adaptation under mirror reversal, a phenomenon that is rarely considered in discussions of implicit adaptation since the mirror paradigm is typically associated with other learning processes (Gutierrez-Garralda et al., 2013; Telgen et al., 2014; Yang et al., 2020). Data do nevertheless suggest that implicit adaptation occurs under mirror reversal (Lillicrap et al., 2013; Wilterson and Taylor, 2019). Our experiments confirmed this, but, importantly, they also clearly demonstrated that the implicit adaptation under mirror reversal is unstable: it tends to amplify errors over time rather than minimize them. This observation was also apparent in previous work (Abdelghani and Tweed, 2010; Lillicrap et al., 2013; Kasuga et al., 2015), though these experiments did not distinguish between implicit and explicit contributions to learning. Although theoretical considerations suggested that either forward-model-based or direct policy learning might account for this instability, fine-grained analysis of behavior in experiment 2 revealed that only direct policy learning could account for the patterns of implicit adaptation we observed under the mirror reversal.

It is important to emphasize that the goal of our experiments was not to study how participants learn to compensate for mirror reversal of visual feedback, which has already been extensively examined (Gritsenko and Kalaska, 2010; Lillicrap et al., 2013; Telgen et al., 2014; Wilterson and Taylor, 2019). Instead, we used a mirror reversal to probe the properties of implicit adaptation. Is the implicit adaptation seen in mirror reversal the same kind as that seen during visuomotor rotation? (Telgen et al., 2014; Yang et al., 2020). We think the answer is yes. Implicit adaptation seems to involuntarily adjust motor output in response to sensory prediction errors, and an experienced sensory prediction error itself carries no information about the kind of perturbation that gave rise to it. Positing the existence of distinct implicit adaptation systems for different types of perturbation would imply that the motor system can recognize the kind of perturbation that gave rise to the sensory prediction error. Furthermore, if the motor system were to use forward-model-based learning under a visuomotor rotation but switch to an alternative adaptation mechanism under a mirror reversal, this would introduce a paradox: the motor system switching away from a learning mechanism that could ultimately cope with mirror reversal (forward-model-based learning) in favor of one that never could. Thus, we believe that the implicit adaptation we observed under a mirror reversal is the same as is engaged under a visuomotor rotation.

It is nevertheless clear that people can learn to compensate for an imposed mirror reversal. It is well established, however, that compensation for a mirror reversal is not learned through the same implicit adaptation process that supports compensation for small rotations or displacements of visual feedback (Gutierrez-Garralda et al., 2013; Telgen et al., 2014; Wilterson and Taylor, 2019; Yang et al., 2020). Compensation for a mirror reversal requires higher preparation times (Telgen et al., 2014), does not generalize to online feedback corrections (Gritsenko and Kalaska, 2010; Telgen et al., 2014; unlike implicit adaptation), and does not result in aftereffects (Yang et al., 2020). Furthermore, a study of learning in patient populations has also suggested that the neural basis of these two forms of learning is different (Gutierrez-Garralda et al., 2013). Rather than adapting an existing policy, people likely learn to compensate for a mirror reversal by establishing a brand new policy (called “de novo learning”; Telgen et al., 2014; Yang et al., 2020). Our results suggest that the motor system must engage alternate learning processes to compensate for a mirror reversal largely because implicit adaptation fails in this case.

Do forward models play any role in motor learning?

Forward-model-based learning was originally proposed by Jordan and Rumelhart (1992) as a simple and effective solution to the distal error problem. The distal error problem encapsulates the major disadvantage of direct policy learning: that observed errors are in a different coordinate system than model updates; errors are observed in task coordinates but, to update the controller, it is necessary to know the error in the outgoing motor command. Observed errors must therefore be translated from task space to motor space before they can be used to update the controller. This translation requires precise knowledge of the relationship between motor commands and task outcomes (Wolpert et al., 2001), which is tantamount to knowing what actions to take in the first place. The key insight from the work of Jordan and Rumelhart (1992) was that translation of errors to the motor command space is not necessary when learning a forward model. Thus, a fruitful general strategy for learning a controller is to first focus on learning a forward model and then use this model to plan movements by inverting the forward model or to enable learning of the controller by guiding how observed errors are translated from task space to motor space.

The idea of forward-model-based learning introduced by Jordan and Rumelhart (1992) has had a lasting influence on thinking about human motor learning. Yet, the question of exactly how a learned forward model might influence action selection remains unanswered. One possibility is that the forward model could be used to simulate the outcomes of different motor commands and then select the one with the best outcome (Miall and Wolpert, 1996; Wolpert and Kawato, 1998; Haruno et al., 2001). This simulation argument, however, seems incompatible with the fact that implicit learning can be expressed at very short latencies (Fernandez-Ruiz et al., 2011; Haith et al., 2015; Huberdeau et al., 2019). Inversion could also be achieved by embedding the forward model in a recurrent loop (Porrill et al., 2004); however, the feasibility of this may be limited to simple cases as it relies on a restrictive set of assumptions (Haith and Vijayakumar, 2009). In any case, our results rule out this proposal, at least in the context of visuomotor adaptation of reaching movements.

Other theories suggest that a learned forward model might help to train a controller over longer timescales of learning. Flanagan et al. (2003) have suggested that a predictive forward model might be acquired before and influence the learning of a suitable controller, based on experiments that used grip force/load force coupling as the indicator of prediction. More recent work has, however, shown that early adjustments of grip force may be driven by uncertainty rather than by learning of a predictive forward model (Hadjiosif and Smith, 2015), calling these conclusions into question. Our current findings are nevertheless compatible with the idea that predictive forward models and adaptive policies are dissociable from one another and could learn over differing timescales.

One proposal as to how a learned forward model might influence later learning of a controller is that it might help to adjust the learning rule used to update a movement policy based on errors, a form of backpropagation (Karniel, 2002). The optimal learning rule relates to the sensitivity derivative between actions and outcomes, which could, in principle, be derived from an adaptive forward model. This did not appear to be occurring in our experiments; the learning rule did not appear to substantially change despite the fact that it should have flipped sign. However, it may be possible that the learning rule might ultimately flip to match the reversed sensitivity derivative under a mirror reversal (Abdelghani et al., 2008); we cannot rule out that a learned forward model might eventually play a role in this.

Other learning architectures

Other than direct policy learning, an alternative architecture for motor adaptation is the feedback error-learning model (Kawato, 1990; Kawato and Gomi, 1992; Albert and Shadmehr, 2016). The feedback error-learning hypothesis posits that motor commands used for online feedback corrections during movement act as a training signal for updating the controller in future movements. This scheme would also be unable to adapt under a mirror reversal, since the feedback controller would also fail to account for the flipped sensitivity derivative; feedback motor commands and, consequently, changes in feedforward motor commands would thus be in the opposite direction from what is needed. In our experiments, however, we used a task design in which feedback corrections were minimized (if they occurred at all), making feedback error learning a very unlikely explanation for the adaptive changes we observed.

Is there any role for a forward model in adaptation?

While we have argued that implicit adaptation does not result from the inversion of an updated forward model, it is important to clarify that we are not arguing against the existence of forward models. In addition to learning, Karniel (2002) delineates two other major roles for the forward model: “output predictor” and “forward dynamic model,” which both relate to real-time prediction. Our study does not question either of these two roles. In fact, there is substantial evidence, both behavioral and neurophysiological, that the brain uses an internal forward model to maintain an estimate of the state of the body (Miall et al., 2007; Ebner and Pasalar, 2008; Wagner and Smith, 2008; Bhanpuri et al., 2013; Herzfeld et al., 2018), and that these estimates can be updated in the presence of a perturbation (Synofzik et al., 2008; Cressman and Henriques, 2010; Izawa and Shadmehr, 2011). This state estimate is critical for maintaining stable control of the body using an existing policy in the presence of signaling delays.

Finally, forward models may also be indirectly important for learning even if they do not directly update motor commands. Implicit adaptation seems to be driven by sensory prediction error (Mazzoni and Krakauer, 2006; Taylor et al., 2014; Leow et al., 2018), which itself implies a sensory prediction,, which, presumably, arises as the output of a forward model. Therefore, although changes to the forward model do not directly influence action selection, they may provide the error with which the policy is updated.

Neural basis of implicit adaptation

A long-standing theory of the neural basis of adaptation suggests that internal models for motor control are encoded in the strengths of synaptic connections between cerebellar Purkinje cells and parallel fibers. When an error is experienced, strong discharges from climbing fibers (originating in the inferior olive) carry error information to the corresponding Purkinje cells. The resulting complex spike activity may in turn alter the strength of parallel-fiber connections in such a way as to update the internal model (Albus, 1971; Marr and Thach, 1991). Recent findings about the role of cerebellar Purkinje cells in adaptation in the oculomotor system shed more light on how such a mechanism might work (Herzfeld et al., 2018). Specifically, error-signaling complex spikes seem to result in changes to simple spike activity in Purkinje cells only along the dimension of the preferred error of the particular cell, with cells responsive to leftward errors only resulting in rightward shifts in motor output and vice versa. These findings are not necessarily incompatible with direct policy learning, as such hard-wired associations between error direction and correction direction could account for an inflexible learning rule.

Many prior attempts to understand the neural basis of adaptation have often appealed to the idea that adaptive forward models are integral to the implicit adaptation of behavior. Our findings challenge this idea and should have important implications for future attempts to understand the neural basis of implicit motor adaptation.