Abstract
BACKGROUND:
Current self-calibration and reconstruction methods for wave-encoded single-shot fast spin echo imaging (SSFSE) requires long computational time, especially when high accuracy is needed.
PURPOSE:
To develop and investigate the clinical feasibility of data-driven self-calibration and reconstruction of wave-encoded SSFSE imaging for computation time reduction and quality improvement.
STUDY TYPE:
Prospective controlled clinical trial.
SUBJECTS:
With Institutional Review Board approval, the proposed method was assessed on 29 consecutive adult patients (18 males, 11 females, 24–77 years).
FIELD STRENGTH/SEQUENCE:
A wave-encoded variable-density SSFSE sequence was developed for clinical 3.0T abdominal scans to enable 3.5x acceleration with full-Fourier acquisitions. Data-driven calibration of wave-encoding point-spread-functions (PSF) was developed using a trained deep neural network. Data-driven reconstruction was developed with another set of neural networks based on the calibrated wave-encoding PSF. Training of the calibration and reconstruction networks was performed on 15,783 2D wave-encoded SSFSE abdominal images.
ASSESSMENT:
Image quality of the proposed data-driven approach was compared independently and blindly with conventional approach using iterative self-calibration and reconstruction with parallel imaging and compressed sensing by three radiologists on a scale from −2 to 2 for noise, contrast, sharpness, artifacts, and confidence. Computation time of these two approaches was also compared.
STATISTICAL TESTS:
Wilcoxon signed-rank tests were used to compare image quality and two-tail t-tests were used to compare computation time with P values of under 0.05 considered as statistical significance.
RESULTS:
An average 2.1-fold speedup in computation was achieved using the proposed method. The proposed data-driven self-calibration and reconstruction approach significantly reduced the perceived noise level (mean scores 0.82, P<0.0001).
DATA CONCLUSION:
The proposed data-driven calibration and reconstruction achieved twice faster computation with reduced perceived noise, providing a fast and robust self-calibration and reconstruction for clinical abdominal SSFSE imaging.
Keywords: wave encoding, single-shot fast spin echo, data-driven, deep learning, parallel imaging and compressed sensing
INTRODUCTION
Spin echo (SE) MR sequences provide T2-weighted images are often used clinically. While conventional SE sequences provide high image quality, they are usually slow in acquisition. To accelerate the acquisition of T2-weighted images, single-shot (SS) and multi-shot fast spin echo (FSE) sequences have been developed1–3. In these sequences, multiple phase-encoding (PE) signals are acquired after each radio-frequency (RF) pulse. This approach reduces the scan time of T2-weighted imaging to less than a second per slice. However, in abdominal applications, conventional SSFSE (or HASTE) still requires more than 30 seconds to achieve full-abdomen coverage4–6. This duration is usually too long for single breath-holds, and may result in degraded image quality due to respiratory and cardiac motion or inconsistency between two separated breath-holds.
Various efforts have been made to accelerate SSFSE imaging. On the hardware side, multi-channel coils with increased number of channels up to 128 have been developed to improve parallel imaging performance and enable higher acceleration factors of up to 8-fold7. On the sequence development side, variable refocusing flip angles8, variable-density sampling6, and wave encoding9,10 have been developed to enable compressed sensing reconstruction and improve image sharpness. Among these techniques, wave-encoded SSFSE has been previously demonstrated to achieve improved sharpness and reduced scan time in comparison with standard SSFSE6.
Despite the improvement of image quality with wave-encoded SSFSE imaging, this imaging technique usually requires extra computation resources and leads to increased reconstruction time6. First, wave encoding uses sinusoidal waveforms during the readout. The actual waveform may differ from theoretical waveforms due to systematic imperfections such as gradient delays and eddy currents. Therefore, calibrating the waveform is usually required by either using a calibration scan or performing self-calibration of the point-spread function (PSF). Self-calibration techniques may require additional computation due to iterative optimizations11,13, which are both computationally expensive and time-consuming. Second, a parallel imaging and compressed sensing (PICS) reconstruction14–16 is used to reconstruct images from under-sampled wave-encoded k-spaces. This process may require up to 1000 iterations, leading to even longer computation time.
This long total computation time of self-calibration and reconstruction amounts to several minutes per series. This resulting delay to see images may impair clinical workflows, including prescription of subsequent images and detection and correction of issues, such as motion artifacts, incorrect scan prescription, or fat suppression failures. Therefore, acceleration of both self-calibration and reconstruction of wave-encoded SSFSE might lead to greater efficiencies.
Recently, data-driven deep-learning-based reconstruction has been developed and applied to various MRI applications to accelerate the speed of image reconstruction and improve image quality17–20. Specifically, for SSFSE, variational networks have been used to improve the signal-to-noise ratio and overall image quality of abdominal SSFSE imaging21–22.
The purpose of this work was to develop and investigate the clinical feasibility of using deep neural networks for data-driven self-calibration and reconstruction of wave-encoded SSFSE to improve the calibration and reconstruction speed and the image quality of abdominal wave-encoded SSFSE imaging.
MATERIALS AND METHODS
Data Acquisition with a Wave-Encoded SSFSE Sequence
A wave-encoded SSFSE sequence with variable refocusing flip angles and variable-density sampling was used to acquire under-sampled wave-encoded k-space. To achieve wave encoding, a sinusoidal wave-encoding gradient (Fig. 1a) was played out on the PE gradient axis during the readout of each frequency-encoding (FE, ) line. Detailed design of the sinusoidal waveform followed the reference6, with the area of the first and last sinusoidal lobes reduced by 50% and a maximum amplitude between 8.5 mT/m and 12.5 mT/m. This maximum amplitude was inversely proportional to the readout field-of-view to account for object signal spreading induced by wave encoding9. At the same time, a readout oversampling factor of 1.6 was used in all scans to capture all spreading signal.
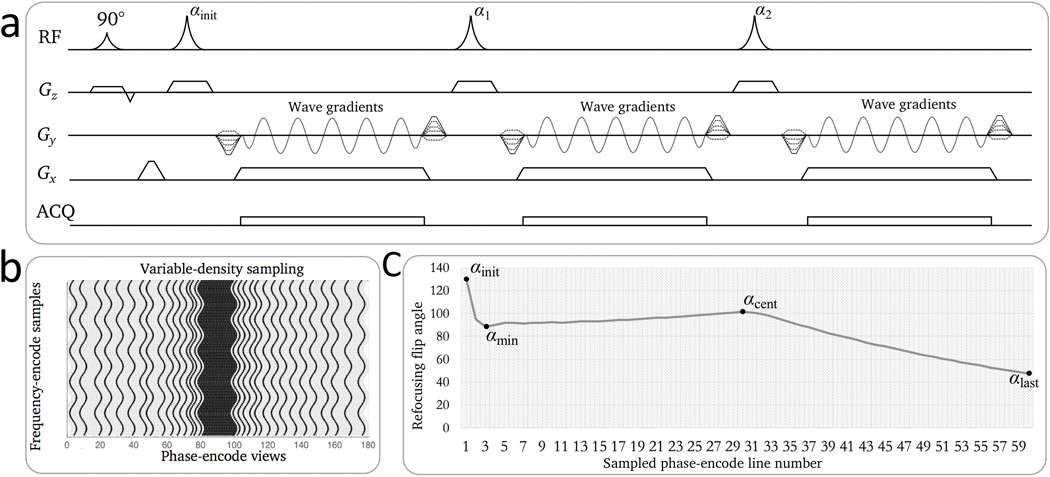
Figure 1.
Illustration of wave-encoded SSFSE imaging. a: Pulse sequence diagram of wave-encoded SSFSE with the first three echoes shown. Wave-encoding gradients were played during the readouts in the phase-encoding gradient axis. b: Illustration of a variable-density sampling pattern for self-calibrated wave encoding. Due to the modulation of wave-encoding gradients, wave-encoded trajectories are curved. c: Variable refocusing flip angles for wave-encoded SSFSE. The refocusing flip angles are controlled by four parameters: initial, minimum, center, and last flip angles.
Variable-density sampling and variable refocusing flip angle were used in the sequence to enable full-Fourier acquisitions6. The sampling pattern contains pseudo-random sampling PE locations and a central coil calibration region of around 20 PE views (Fig. 1b). Variable refocusing flip angle was also used in the sequence8 to minimize blurring from T2 delay. The variable refocusing flip angle echo train was mainly controlled by four determining flip angles: the initial flip angle αinit, the minimum flip angle αmin, the center flip angle αcent, and the last flip angle αlast (Fig. 1c). According to a previous study5, optimal refocusing flip angles for abdominal scans started with αinit of 130°, decreased to αmin of 90°, increased to αcent of 100°, and then decreased to αlast of 45°. As the spin-echo signal did not reach a stabilized state in the beginning of the echo train, the first four echoes were discarded.
PSF Calibration Using Data-Driven Estimation of Systematic Imperfections
Wave encoding usually requires waveform and PSF calibration due to systematic imperfections, such as gradient delays, eddy currents, and inaccurate isocenter locations. In practice, to correct this effect to the first order, a scaling factor defining the ratio between the actual and theoretical wave-encoding gradient amplitudes, a gradient delay time , and an isocenter location shift were introduced into the ideal waveform . This modified waveform is then used to correct the wave-encoding PSF6. With these parameters in consideration, the actual gradient is , and the actual wave-encoding PSF can be expressed as
| [1] |
where is the gyromagnetic ratio, sampling time (from the beginning of the readout) and spatial location define the two dimensions of the PSF with defined as the index along the frequency encoding direction and defined for phase encoding, and , and are three parameters for correcting PSF errors due to systematic imperfections. Previously, systematic-imperfection-related parameters were determined by maximizing the normalized gradient of reconstructed zero-padding images with an iterative Nelder-Mead simplex method23.
In this work, we replaced this iterative optimization process with a deep neural network. In our imaging systems, we observed a constant scaling factor of 0.995. Therefore, the scaling factor was kept constant in this study. In this case, the entire problem of determining systematic imperfection parameters can be described as
| [2] |
where is a trained neural network with three inputs: (1) the raw under-sampled, coil-combined, and wave-encoded k-space , (2) the theoretical maximum wave-encoding gradient amplitude , and (3) the theoretical isocenter location . Coil combination was performed by averaging the signal from all coil channels for fast computation. Both values of and are determined based on the scan prescription. and represent the calibrated time delay and the isocenter shift of the wave-encoding gradients. Trained network parameters are denoted as . There are 42,635,810 trainable parameters in in total.
The network architecture of contains three steps (Fig. 2a) similar to previous studies24. The first step converts complex numbers into real numbers by stacking the real and imaginary components together in the feature dimension. The second step contains 2D operations. This step uses 2D convolutional operations and 2D pooling operations to extract k-space-domain features of the input under-sampled wave-encoded k-space. The third step contains 2D to 1D operations that flatten the output of the second step into a one-dimensional vector and concatenate this vector with the input maximum wave-encoding gradient amplitude and the input theoretical isocenter location . After two fully-connected operations, the network outputs and , and these two parameters were used to generate the actual wave-encoding PSF according to Eq. 1.
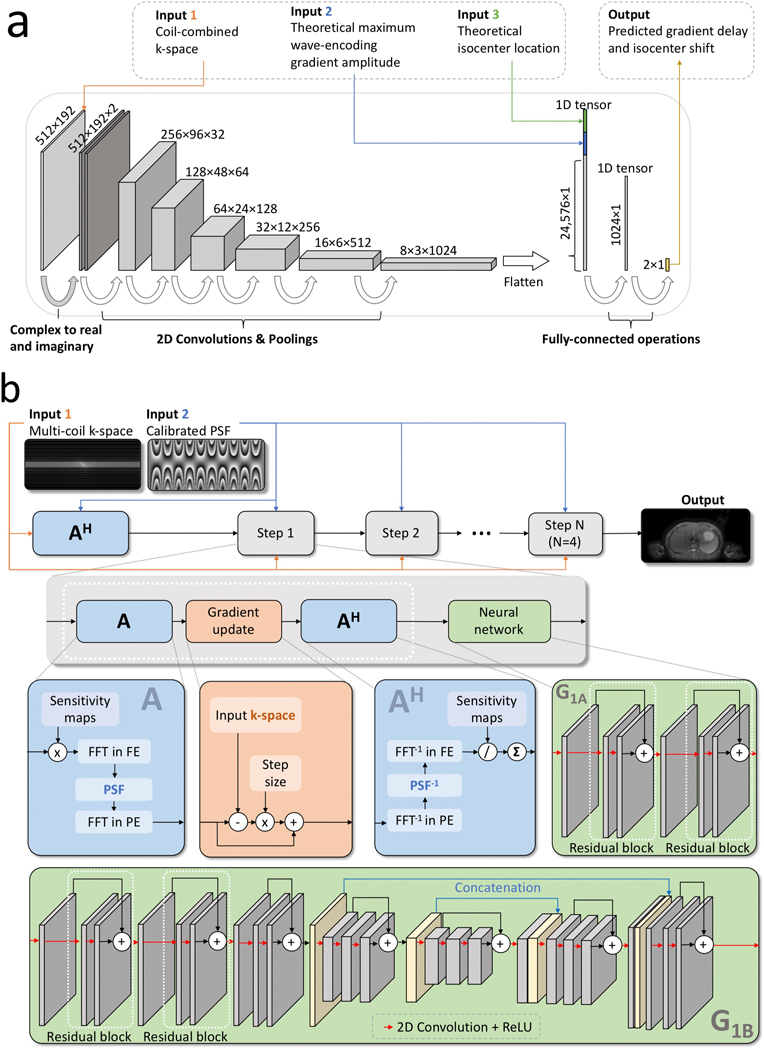
Figure 2.
a: Flow chart and network architecture of data-driven calibration of wave-encoded SSFSE. The input of this network includes the coil-combined k-space, the theoretical maximum wave-encoding gradient amplitude, and the theoretical isocenter location of the acquisition. This network architecture contains a complex to real and imaginary operation, six convolutional and pooling layers with ReLU activations, and two fully-connected layers. The final output includes the predicted gradient delay and the predicted shift between the actual and theoretical isocenters. b: Flow chart and network architecture for data-driven reconstruction of wave-encoded SSFSE. k-Spaces from multiple coil channels and the calibrated PSF generated with the data-driven self-calibration method were used as the input. After generating an initial image with AH, where A represents a chain of operations to generate images from multi-coil k-space, four steps of data-driven reconstruction blocks were used to perform gradient updates and neural network computations. Details about A, AH, gradient updates, and neural network architectures are shown in separate blocks. The neural network architecture in the last step (denoted as G1b) was different from first three steps (denoted as G1a).
Data-Driven Image Reconstruction Using Deep Neural Networks and Gradient Updates
With the calibrated wave-encoding PSF, a data-driven reconstruction using unrolled networks was used to recover the image. Each step of the data-driven reconstruction can be formulated as a gradient update and a proximal step with a learned regularization network operator with trained parameters . The entire step can be expressed as
| [3] |
where and refer to the output and input images of the step. is also the input of the step. refers to the step size of the gradient update17. In this study, four steps of iterations in Eq. 3 were used. The entire network is denoted as , with 1,247,044 trainable parameters. is the partially acquired wave-encoded k-space, and describes the wave-encoding model. As described previously, the wave-encoding model can be expressed as . In this model, is the k-space sampling operator, is the coil sensitivity operator, is the calibrated wave-encoding PSF, and and are the Fourier transform operators in PE and FE directions. In this study, was computed using the data-driven approach described in the previous section.
Two network architectures were designed and used for operators (Fig. 2b). First, a relatively small five-layer network was used for all but the last network operator ( in Fig. 2b). This network contains a 2D convolutional layer and two residual blocks. Residual blocks were chosen because it has been shown to have stable training for deep networks. Each residual block contains two 2D convolutional layers. Rectified linear unit (ReLU) activations and a kernel size of 3 by 3 were used after each convolutional layer. The last network operator contains the same five-layer network followed by a three-stage u-net25 ( in Fig. 2b) because u-net has been shown to yield state-of-the-art performance for image-to-image translation tasks. The u-net contains bypass concatenations between layers with same sizes as shown in Fig. 2b. This u-net also uses a kernel size of 3 by 3. Circular padding was used in all convolutional operations17.
Network Training and Model Deployment
To train the PSF-calibration network , conventional optimization-based self-calibration approach6 was used to generate ground truth labels of the gradient delay and the isocenter shift . Network parameters in were minimized through steps of stochastic gradient descent with an Adam optimizer26, a learning rate of 0.005, a batch size of 20, and loss.
To train the reconstruction networks in , conventional PICS reconstruction6 in the BART toolbox27 was used to generate ground truth labels of the image. Network parameters in were minimized through steps of stochastic gradient descent with an Adam optimizer, a learning rate of 0.005, a batch size of 4, and loss. Coil sensitivity maps were estimated directly using zero-padding reconstructions and SENSE14 models based on calibrated wave-encoding PSFs.
The networks and were trained separately on 15,783 2D wave-encoded SSFSE abdominal images on GE MR750 3T scanners collected with Institutional Review Board approval. After training of the networks was done, this data-driven pipeline can be clinically deployed and used to perform image reconstruction of wave-encoded SSFSE with constant and low computational cost.
The complete pipeline of the proposed method for deployment is demonstrated in Fig. 3 in comparison with the conventional PSF self-calibration and reconstruction workflow (in light gray). In the PSF calibration stage, we replaced the conventional iterative self-calibration with a neural network to output wave-encoding gradient delays and isocenter shifts. In the reconstruction stage, the conventional iterative PICS reconstruction was replaced with four iterations of gradient updates and proximal steps with neural networks to output reconstructed images. The entire calibration and reconstruction problem can be formulated as:
| [4] |
where is the desired image, generates the calibrated wave-PSF based on Eq. 1, and is the partially acquired wave-encoded k-space.
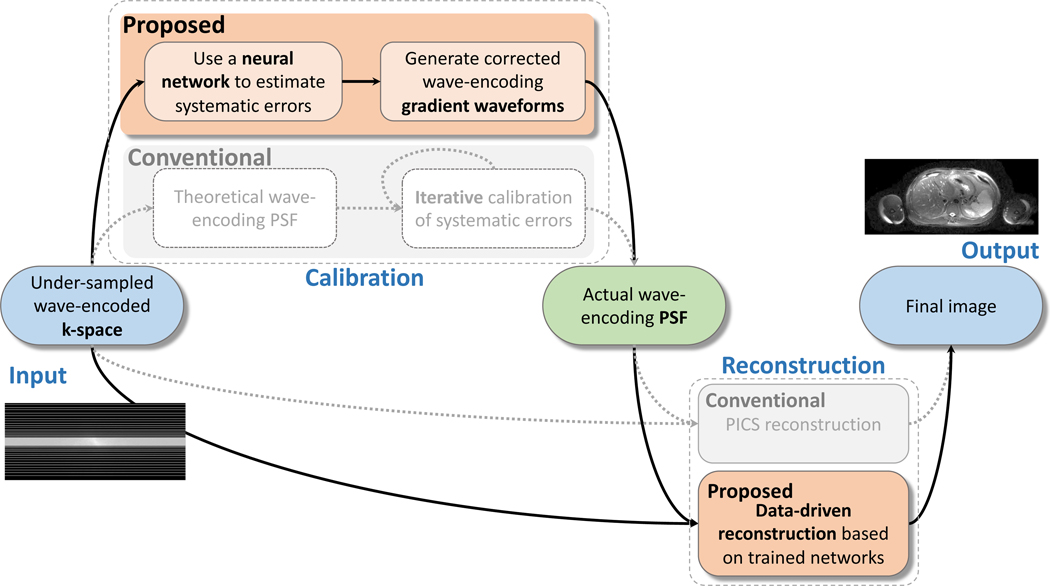
Figure 3.
Pipeline of the proposed data-driven self-calibration and reconstruction, in comparison with conventional self-calibration and PICS reconstruction (in light gray). In the first stage, under-sampled wave-encoded k-space was used to generate the actual wave-encoding PSF with a trained neural network. In the second stage, the under-sampled wave-encoded k-space and the calibrated wave-encoding PSF were used to generate the final images with the proposed data-driven reconstruction using gradient updates and trained neural networks.
Clinical Scanning
Clinical abdominal scanning was performed on 29 consecutive adult patients (18 males, 11 females, ranging from 24 to 77 years) on a 3T MRI scanner using a 32-channel torso coil and a 2D multi-slice wave-encoded SSFSE imaging sequence. The acquisition plane was axial and PE direction was anterior/posterior. Each subject was asked to breath hold during each acquisition period. Fat-suppression was incorporated with a spectral-spatial-selective pulse. Field of view was optimized to each patient’s anatomy (30–42 cm). Additional parameters are shown in Table 1. All images were reconstructed using (1) conventional PSF self-calibration and PICS reconstruction using a combination of C/C++ (the BART software package27) and Python with 50 iterations and an -wavelet regularization coefficient of 0.002, and (2) proposed data-driven self-calibration and reconstruction method implemented in Tensorflow.
Table 1.
Scan Parameter Summary
| Refocusing flip angles (initial/minimum/central/last) | 130°/90°/100°/45° |
| Slice thickness | 5 mm |
| Slice gap | 0 |
| Matrix | 320 × 180 |
| FOV | 300–420 mm × 240–336 mm |
| Number of slices | 35 – 64 |
| Echo time (TE) | 90.9 – 93.1 msec |
| Repetition time (TR) | 436.5 – 560.6 msec |
| Total scan time | 16.9 – 32.8 sec |
| Bandwidth | 488.2 Hz/pixel |
| Acceleration factor for variable density sampling | 3.5 |
| Sampling pattern | Variable-density sampling (51 acquired PE views) with an auto-calibration region (20 PE views) |
| Proportion of k-space coverage | 1 (full) |
Individual Assessments of Image Quality
Reconstructed clinical images were independently evaluated using a semi-quantitative grading system that rated noise, contrast, sharpness, general artifacts other than motion-related artifacts, and confidence of detecting liver lesions. The scores were predetermined on a scale from −2 to 2 (Table 2). Positive values favor the proposed data-driven method, and negative values favor the conventional self-calibration and PICS reconstruction. Three readers (S.S.V with twelve years of experience, V.R.S with five years of experience, and R.L.B with five years of experience in body MRI interpretation) independently scored each pair of the reconstructed images in a blinded, randomized order.
Table 2.
Scoring Criteria Utilized for Conventional Self-Calibration and Reconstruction vs. Proposed Data-Driven Self-Calibration and Reconstruction Evaluation
| Favors A | Favors B | ||||
|---|---|---|---|---|---|
| Score | −2 | −1 | 0 | 1 | 2 |
| Noise | A with decreased graininess with improved diagnostic capability | A with decreased graininess without diagnostic impact | Equivalent | B with decreased graininess without diagnostic impact | B with decreased graininess with improved diagnostic capability |
| Contrast | A with good contrast between liver/spleen AND renal cortex/medulla not seen in B | A with good contrast between liver/spleen OR renal cortex/medulla not seen in B | Equivalent | B with good contrast between liver/spleen OR renal cortex/medulla not seen in A | B with good contrast between liver/spleen AND renal cortex/medulla not seen in A |
| Sharpness | A with increased sharpness with improved diagnostic capability | A with increased sharpness without diagnostic impact | Equivalent | B with increased sharpness without diagnostic impact | B with increased sharpness with improved diagnostic capability |
| Artifacts (besides cardiac motion related nonuniformity) | A with decreased artifacts to the point of improved diagnostic capability | A with decreased artifacts without diagnostic impact | Equivalent | B with decreased artifacts without diagnostic impact | B with decreased artifacts to the point of improved diagnostic capability |
| Confidence of detecting liver lesions | A with improved confidence of detecting liver lesions in more than half of the images | A with improved confidence of detecting liver lesions in fewer than half of the images | Equivalent | B with improved confidence of detecting liver lesions in fewer than half of the images | B with improved confidence of detecting liver lesions in more than half of the images |
Wilcoxon signed-rank tests were used to test the null hypothesis that there was no significant difference between the conventional self-calibration and reconstruction approach and the proposed data-driven approach for each reader and their average scores. Inter-observer variability was assessed utilizing a Fleiss’ kappa statistic. The kappa coefficients were interpreted as almost perfect (0.8 − 1), substantial (0.6 − 0.8), moderate (0.4 − 0.6), fair (0.2 − 0.4), slight (0 − 0.2), and poor (<0). A two-tailed P value of under 0.05 was considered as statistical significance.
Evaluation of Online Computation Time
Online computation time was recorded for each patient scan using both conventional iterative self-calibration and PICS reconstruction method and the proposed data-driven calibration and reconstruction method under identical hardware settings with GPU-optimized computations (two Intel Xeon CPU E5–2670 v3 @ 2.30GHz CPUs with 24 cores each, 256 Gb RAM, and two NVIDIA TITAN X GPUs). The ratio of the average computation time between these two approaches was calculated. A t-test was performed to test the null hypothesis that there is no significant difference between the computation time of the conventional approach and the proposed approach. A two-tailed P value of under 0.05 was considered as statistical significance.
RESULTS
Clinical Scanning
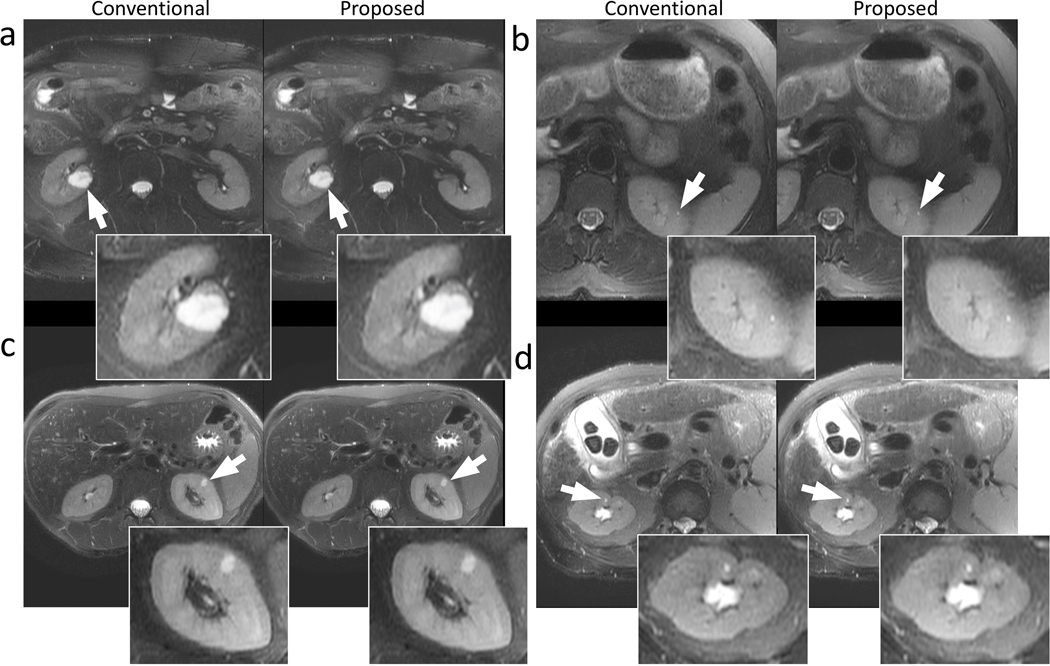
Representative images containing the liver are shown in Fig. 4. The proposed data-driven calibration and reconstruction approach achieved comparable structural delineation of the liver and the lesions (white arrows in Fig. 4) compared to the conventional approach using iterative calibration and PICS reconstruction. Improvements in perceived signal-to-noise ratio were observed in the proposed reconstruction, with reduced level of graininess (Fig. 4a and Fig. 4c). The proposed method and the conventional approach yielded similar image contrast. Significant artifacts were observed in neither approach.
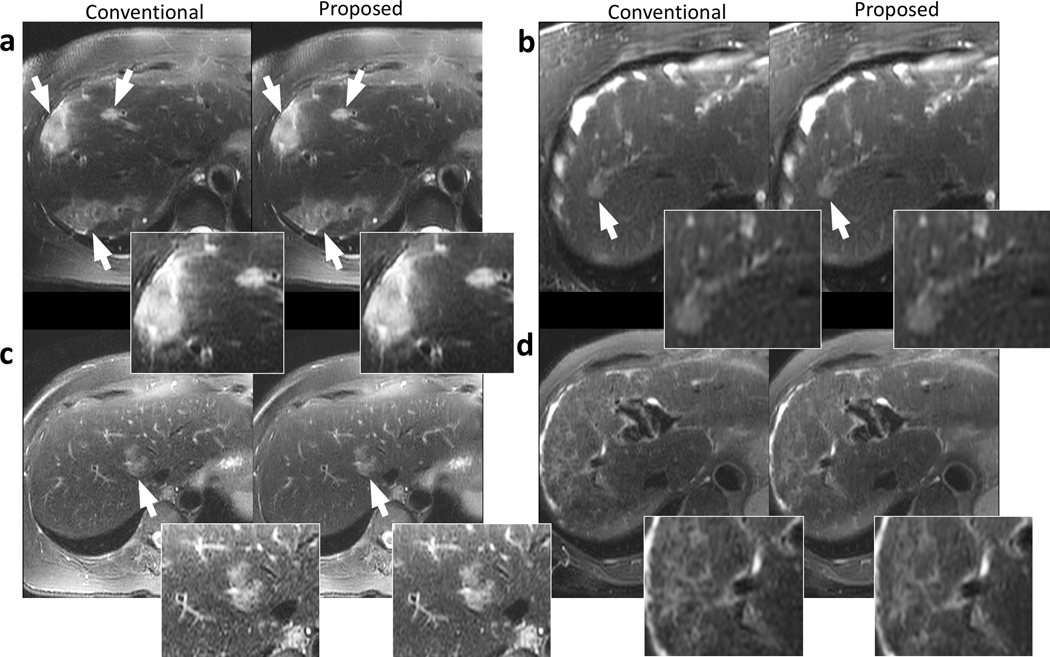
Figure 4.
Example images of the liver using conventional reconstruction (left) and the proposed data-driven reconstruction (right) on a 73-year-old female patient with focal liver lesions (a), a 67-year-old female patient with a focal liver lesion (b), a 52-year-old female patient with a focal liver lesion (c), and a 58-year-old female patient with cirrhosis (d). Regions with potential lesions are indicated by white arrows. The proposed method and the conventional reconstruction achieved comparable structural delineation of the lesions. Less perceived noise can be observed in (a) and (c) in the proposed reconstructions.
Representative images containing the kidneys are shown in Fig. 5. Comparable structural delineation and sharpness of the kidney were observed in all examples using both the proposed reconstruction and the conventional method. The proposed data-driven reconstruction was able to reconstruct very small lesions, as indicated by arrows in Fig. 5b and Fig. 5d. Less perceived noise can be observed in Fig. 5a, Fig. 5b, and Fig. 5d. Similar contrast between these two methods was achieved. No significant artifacts were observed in both methods.
Figure 5.
Example images of the kidneys using conventional reconstruction (left) and the proposed data-driven reconstruction (right) on a 39-year-old male patient (a), a 56-year-old female patient (b), a 48-year-old female patient (c), and a 58-year-old female patient (d). Kidney lesions are indicated by the white arrows. The proposed data-driven reconstruction achieved comparable delineation of large lesions in (a) and (c) as well as small lesions in (b) and (d). Less perceived noise can be observed in (a), (b), and (d) in the proposed reconstructions.
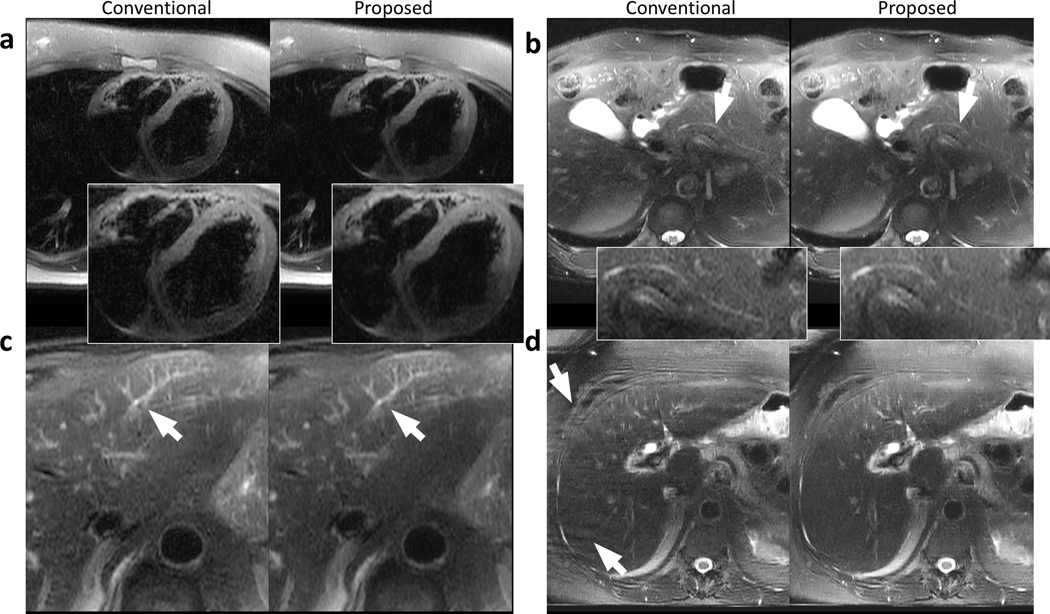
Representative images containing the heart (Fig. 6a), the pancreatic duct (Fig. 6b), and structures in the left lobe of the liver (Fig. 6c) are shown in Fig. 6. The proposed approach yielded comparable structural delineation of these regions and was able to reconstruct the detailed structures in Fig. 6b and Fig. 6c. Similar contrast was achieved in these regions (Fig. 6a-c). Reduced perceived noise can be observed in Fig. 6a and Fig. 6c.
Figure 6.
Example images containing other regions of interest or artifacts using the conventional reconstruction (left) and the proposed data-driven reconstruction (right) on a 25-year-old female patient (a), a 66-year-old male patient (b), a 73-year-old male patient (c), and a 64-year-old female patient (d). Comparable sharpness of the heart was achieved using the proposed method (a) with reduced perceived noise. The pancreatic duct was visible in both conventional and proposed reconstructions (b) with reduced perceived noise using the proposed method. Small structures in the liver can be reconstructed and share similar quality with both methods (c). The data-driven approach reduces the phase-wrapping artifacts occurred in the conventional reconstruction in (d).
Representative images showing the reduction of ghosting artifacts are demonstrated in Fig. 6d. Due to a tight prescribed field-of-view smaller than the patient’s size, phase wrapping happened during the breath-held period of the scan and resulted in ghosting artifacts. With the proposed data-driven reconstruction, these ghosting artifacts were reduced (as indicated by arrows in Fig. 6d).
Mean difference of the gradient delays between the data-driven approach and the conventional approach was 0.0497 msec. Mean difference of the isocenter shifts between the data-driven approach and the conventional approach was 0.1006 pixel.
Individual Assessments of Image Quality
The Fleiss’ kappa statistic for the proposed data-driven reconstruction vs. the conventional comparison indicated fair agreement among the readers in image sharpness (0.21) and confidence of detecting liver lesions (0.24), and slight agreement among the readers in perceived noise (0.13), general artifacts (0.09), and image contrast (0.04).
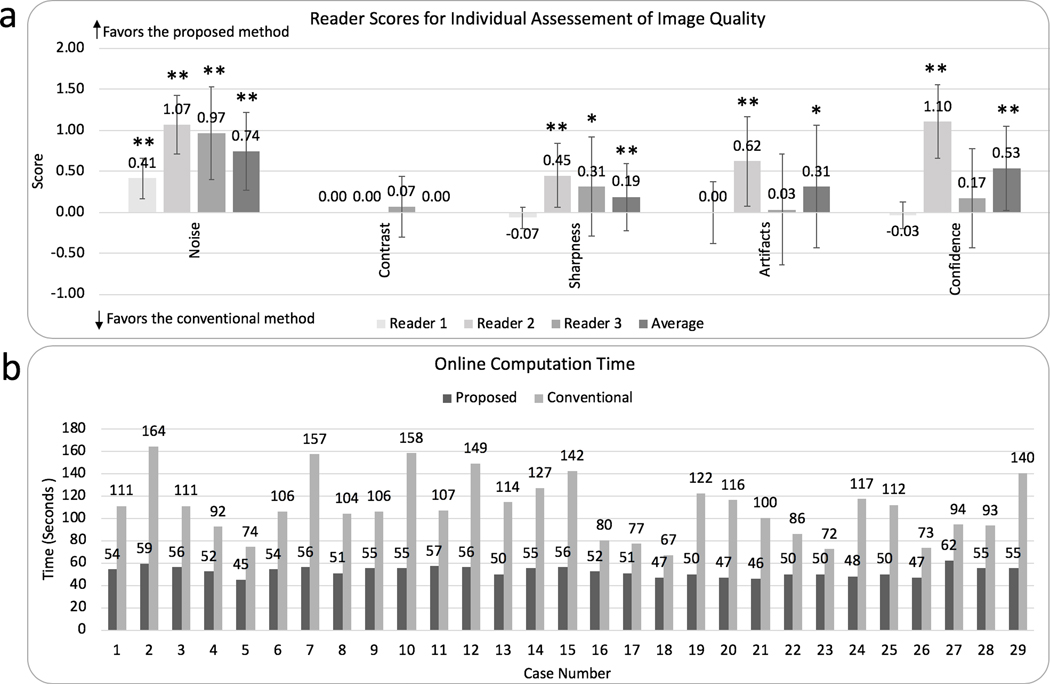
Results of individual assessments of image quality are shown in Fig. 7a. The proposed data-driven self-calibration and reconstruction approach showed significantly reduced perceived noise (overall mean score 0.82 with P<0.0001, mean score 0.41 with P=0.0005 for reader 1, mean score 1.07 with P<0.0001 for reader 2, and mean score 0.97 with P<0.0001 for reader 3) and no difference in image contrast (mean score 0 with P=1 for readers 1 and 2, mean score 0.07 with P=0.6 for reader 3).
Figure 7.
a: Results of overall image quality assessments for the conventional reconstruction and the proposed data-driven reconstruction from reader 1, reader 2, reader3, and their average scores (from left to right). Grading features include the perceived noise, contrast, sharpness, artifacts, and confidence of detecting liver lesions. Statistically different results with P < 0.05 were marked with (*). Statistically different results with P < 0.005 were marked with (**). Error bars are standard error of the mean. b: Comparison of the total online computation time for the proposed method (dark gray) and conventional reconstruction (light gray). An average reduction factor of 2.1 in computation time was achieved with the proposed method.
Non-inferior image sharpness, artifacts, and diagnosis confidence for the proposed data-driven approach were observed by all three readers (Fig. 7a). Non-inferior image quality means the proposed approach has significantly improved image quality with P<0.05 or non-significant difference in image quality (with P values no less than 0.05) when compared to the conventional approach. Reader 1 gave a mean score of −0.07 for image sharpness, 0 for artifacts, and −0.03 for confidence of detecting liver lesions, with P values of 0.5, 1, and 1, indicating no significant difference in sharpness, artifacts, and diagnosis confidence between the proposed method and the conventional approach. Reader 2 gave a mean score of 0.45 for image sharpness, 0.62 for artifacts, and 1.10 for confidence of detecting liver lesions, with P values of 0.007, 0.007, and <0.0001, indicating significantly improved sharpness, artifacts, and diagnosis confidence using the proposed data-driven approach. Reader 3 gave a mean score of 0.31 for image sharpness, 0.03 for artifacts, and 0.17 for confidence of detecting liver lesions, with P values of 0.02, 1, and 0.23, indicating significantly improved sharpness and no significant difference in artifacts and diagnosis confidence using the proposed data-driven approach. Pairwise comparison of the average scores from the readers demonstrated significance in improved image sharpness, reduced artifacts, and confidence of detecting liver lesions, with mean scores of 0.23, 0.22, and 0.41, and P values of 0.001, 0.04, and 0.0003.
Evaluation of Online Computation Time
An image reconstruction time decrease was consistently achieved in all 29 cases (Fig. 7b). The average online computation time of the proposed data-driven calibration and reconstruction to reconstruct the entire volume was 52.4 ± 4.2 seconds, while conventional calibration and reconstruction took 108.3 ± 27.2 seconds. Statistical analysis shows significant difference between the computation time of the proposed approach and the conventional approach (P < 0.0001). This comparison indicated an average reduction factor of 2.1 using the proposed data-driven reconstruction approach, corresponding to a 51.6% decrease in computation time.
DISCUSSION
This study developed a data-driven calibration and reconstruction method for reconstructing clinically-relevant images of wave-encoded SSFSE imaging. By replacing iterative wave-encoding PSF calibration and PICS reconstruction with trained neural network models, the proposed approach brought the reconstruction time closer to the acquisition duration, reducing the lags and queues in the clinical workflow. At the same time, the proposed approach achieved reduction in perceived noise while preserving the contrast and sharpness of the current iterative approach. This approach also demonstrated a potential in reducing ghosting artifacts caused by limited field-of-views.
Network architectures may affect the performance of the proposed method. In the self-calibration stage, the goal was to output two systematic imperfection parameters, i.e., the gradient delay and the isocenter shift between theoretical locations and actual locations. This type of output requires the neural network to reduce layer size as the layer goes deeper to extract features in the k-space domain. In the reconstruction stage, a five-layer neural network was used as a regularization function along with gradient updates. This relatively shallow design may also reduce the chance of overfitting and generating hallucinations in the early stage of the data-driven reconstruction. In the last step, a u-net was designed to improve the capacity of the network in reducing general artifacts and improving the signal-to-noise ratio. There are in total four iterations of gradient update blocks and neural network blocks. The number of iterations was empirically chosen according to a previous study28 to achieve a tradeoff between computational speed and reconstruction performance.
The calibration stage and the reconstruction stage can be trained together or separately. Training of the calibration network took 148.8 hours and training of the reconstruction network took 2331.3 hours on a single NVIDIA GTX 1080Ti GPU. Training these two stages separately improves the flexibility of model deployment, as these two stages can be upgraded independently in clinical systems. Separate training may also benefit the training speed, as there are fewer unknown weights to learn in each training step, compared with joint training of all networks. At the same time, it is more convenient to check the correctness of the imperfection outputs and terminate the training of either the calibration network or the reconstruction networks when these networks are trained separately. Inaccurate PSF mainly results in ghosting artifacts near the edges of the imaging target. Therefore, improvements of PSF accuracy will reduce the level of ghosting artifacts. In this study, ghosting artifacts due to PSF inaccuracy were hardly visible. Accuracy of the data-driven reconstruction model will affect most aspects of the final image, including sharpness, noise level, and ghosting artifacts. Therefore, the reconstruction model usually plays a more important role in the final image quality than the calibration model.
The proposed data-driven approach reduces the total online reconstruction time by performing straightforward computations using the trained networks. In conventional calibration of the wave-encoding PSF, we notice an instability in the number of required optimization steps before convergence. In this study, the conventional approach has been optimized for parallel computation among multiple slices. There are 48 CPU cores on our computation hardware; therefore, when the number of slices is greater than 48, the total computation time nearly doubles because a second round of computation is required for slices other than the first 48 slices. When the number of acquired slices is no larger than 48, we saw computation times of around 80 sec. When there were more than 48 slices, the computation time was around 150 sec using the conventional approach. This factor increases the instability of reconstruction time for the conventional approach. For the data-driven calibration approach, the number of computations is fixed after the models are trained, thus this approach has a relatively stable computation time. Similar behaviors can be observed in the reconstruction stage. For different number of slices (smaller or greater than 48), the computation time is relatively stable, as the reconstruction of multiple slices can be parallelized on the GPU. This time increases at a scale of 1–10 sec with increasing number of slices. The computation time of the proposed approach in different reduction factors is also stable, as this time is only related to the number of operations in the model.
The proposed data-driven approach reduced the perceived noise in reconstructed images by learning an optimal regularization among a large number of existing datasets. This observation is consistent with a previous study22. The improvement in perceived signal-to-noise ratio may be attributed to the diversity of the training dataset. Since our training dataset contains scans with different parameters, conditions, and thus different noise level, the trained model learns an average reconstruction of this large amount of reconstructions. Therefore, compared with conventional PICS reconstruction with a fixed regularization parameter, the resultant data-driven reconstruction achieves a more uniform perceived signal-to-noise ratio. Image-domain convolutions may also contribute to the reduction in noise level, as these operations tend to average the noise over image patches defined by the receptive field of neural networks.
The proposed approach is able to capture small structures and maintain comparable image sharpness and contrast with respect to the conventional iterative reconstruction. This capability can be attributed to the unrolled pipeline used in the proposed data-driven reconstruction. This pipeline contains four steps of gradient updates, which promote the data consistency between the reconstructed images and the acquired raw signal. Accurate calibration of the gradient delays and the isocenter shifts also enables good image sharpness and structural delineation comparable to the conventional reconstruction. The proposed approach reduced phase-wrapping artifacts, as most images in the training dataset contain no phase-wrapping artifact. Pre-selection of images for training may help improve the reconstruction performance. The removal of phase wrapping artifacts using deep neural networks also means potential loss of small lesions. In this case, gradient update blocks in the reconstruction model can help ensure good data-consistency with the partially acquired k-space. The diagnostic information provided by removing phase-wrapping artifacts needs to be further evaluated.
Gradient amplitude changes and gradient delays are typically caused by eddy currents in the gradient system of the scanner. Isocenter shifts are usually caused by gradient field inhomogeneity. Therefore, for difference scanners, these imperfections may be different, and the performance of the proposed method with extreme imperfections still needs to be evaluated. The scaling factor of maximum wave-encoding gradient was fixed in the calibration stage based on our observations that the scaling factor was stable among the scanners we have access to within a period of approximately a month. For a different constant gradient scaling factor, it is necessary to retrain the calibration network. When unstable or different scaling factors are observed on different scanners, it is also possible to include the scaling factor as an extra output parameter in the training and prediction stage while keeping the same architecture for other parts of the network. In this case, the output size of the calibration network contains three variables. The number of iterations and the regularization coefficient were also fixed in our study. This is based on previous studies on variable-density SSFSE imaging4–6. However, for applications in other regions of interest, these parameters may be different and need to be chosen empirically.
There are three limitations of the proposed method when applied in clinical scans. First, since the proposed approach is data-driven, sufficient amount of data is necessary. However, for certain applications, it may be difficult or time-consuming to acquire these datasets29–31. Second, the acquisition matrix size is fixed for the data-driven approach. Although there are potential solutions for reconstructing scans with varying matrix sizes17, this data-driven approach may not be as flexible in scan parameters and settings as the conventional approach. Third, although the proposed method enables 2.1-fold acceleration of the reconstruction of the entire volume of a patient and reduces the waiting time by 56 seconds in the clinical workflow, current reconstruction time is still longer than the acquisition time of SSFSE imaging.
There are several limitations to this study. First, no fully-sampled data or external validation standard was used to evaluate the accuracy of both the conventional and the proposed data-driven approaches. Acquiring fully-sampled data is not feasible due to T2 decay over the echo train. Second, quantitative assessment of signal-to-noise ratio and contrast-to-noise ratio was not performed in this study, as quantitative noise level is less straightforward to calculate for compressed-sensing-based reconstruction and infeasible to obtain in vivo with nonuniformly distributed noise over the image. Third, this study only focused on wave-encoded SSFSE applications in clinical abdominal scans with fat suppression and a reduction factor of 3.5. The feasibility of the proposed method for other reduction factors and in other applications still needs to be evaluated. Finally, the Fleiss’ kappa coefficients show slight agreement among readers in noise, image contrast, and image artifacts. The perceived noise level of conventional PICS reconstruction may vary among slices, causing large variance of perceived noise level in the assessment. This also affects the evaluation of image contrast. Artifacts were visible in both conventional reconstruction and data-driven reconstruction. However, these artifacts may appear in different slices between these two approaches. Therefore, high variance may happen in the assessment of image artifacts.
In conclusion, the proposed data-driven self-calibration and reconstruction of wave-encoded SSFSE achieves an average 2.1-fold acceleration of the online computation and reduced perceived noise while maintaining non-inferior image contrast, image sharpness, artifacts, and confidence of detecting liver lesions of standard reconstruction. Together with wave-encoded SSFSE acquisition, this imaging approach provides fast and robust T2-weighted imaging as well as a fast and efficient clinical workflow. As wave encoding is a hybrid non-Cartesian sampling technique, this study also provides insights for reconstructing general non-Cartesian k-spaces using data-driven deep-learning techniques.
Acknowledgments
Grant Support:
This work was supported by NIH/NIBIB R01 EB009690, R01 EB019241, R01 HL136965 01a1, and GE Healthcare.
Part of this work will be presented at the 27th Annual Meeting of ISMRM in Montreal, Canada.
REFERENCES
- 1.Semelka RC, Kelekis NL, Thomasson D, Brown MA, Laub GA. HASTE MR imaging: description of technique and preliminary results in the abdomen. J Magn Reson Imaging 1996; 6:698–699. [DOI] [PubMed] [Google Scholar]
- 2.Feinberg DA, Hale JD, Watts JC, Kaufman L, Mark A. Halving MR imaging time by conjugation: demonstration at 3.5 kG. Radiology 1986; 161:527–531. [DOI] [PubMed] [Google Scholar]
- 3.Mugler JP. Optimized three-dimensional fast-spin-echo MRI. J Magn Reson Imaging 2014; 39:745–767. [DOI] [PubMed] [Google Scholar]
- 4.Loening AM, Litwiller DV, Saranathan M, Vasanawala SS. Increased Speed and Image Quality for Pelvic Single-Shot Fast Spin-Echo Imaging with Variable Refocusing Flip Angles and Full-Fourier Acquisition. Radiology 2017; 282:561–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Loening AM, Saranathan M, Ruangwattanapaisarn N, Litwiller DV, Shimakawa A, Vasanawala SS. Increased speed and image quality in single-shot fast spin echo imaging via variable refocusing flip angles. J Magn Reson Imaging 2015; 42:1747–1758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen F, Taviani V, Tamir JI, Cheng JY, Zhang T, Song Q, Hargreaves BA, Pauly JM, Vasanawala SS. Self‐Calibrating Wave‐Encoded Variable‐Density Single‐Shot Fast Spin Echo Imaging. J Magn Reson Imaging 2018; 47(4):954–966. [DOI] [PubMed] [Google Scholar]
- 7.Hardy CJ, Giaquinto RO, Piel JE, Rohling AAS KW, Marinelli L, Blezek DJ, Fiveland EW, Darrow RD, Foo TK. 128‐channel body MRI with a flexible high‐density receiver‐coil array. J Magn Reson Imaging 2008; 28(5):1219–1225. [DOI] [PubMed] [Google Scholar]
- 8.Busse RF, Brau AC, Vu A, Michelich CR, Bayram E, Kijowski R, Reeder SB, Rowley HA. Effects of refocusing flip angle modulation and view ordering in 3D fast spin echo. Magn Reson Med 2008; 60:640–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K. Wave-CAIPI for highly accelerated 3d imaging. Magn Reson Med 2015; 73:2152–2162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gagoski BA, Bilgic B, Eichner C, Bhat H, Grant PE, Wald LL, Setsompop K.RARE/turbo spin echo imaging with Simultaneous Multislice Wave-CAIPI. Magn Reson Med 2015; 73:929–938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen F, Zhang T, Cheng JY, Shi X, Pauly JM, Vasanawala SS. Auto-calibrating motion-corrected wave-encoding for highly accelerated free-breathing abdominal MRI. Magn Reson Med 2017; 78(5):1757–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen F, Zhang T, Cheng JY, Taviani V, Hargreaves B, Pauly J, Vasanawala S, inventors; General Electric Co, Leland Stanford Junior University, assignee. System and method for performing wave-encoded magnetic resonance imaging of an object. United States patent application US 15/481,893. 2018. May 24. [Google Scholar]
- 13.Cauley SF, Setsompop K, Bilgic B, Bhat H, Gagoski B, Wald LL. Autocalibrated wave-CAIPI reconstruction; Joint optimization of k-space trajectory and parallel imaging reconstruction. Magn Reson Med 2017; 78(3):1093–1099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT: an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014; 71:990–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007; 58:1182–1195. [DOI] [PubMed] [Google Scholar]
- 16.Shi X, Ma X, Wu W, Huang F, Yuan C, Guo H. Parallel imaging and compressed sensing combined framework for accelerating high‐resolution diffusion tensor imaging using inter‐image correlation. Magn Reson Med 2015;73(5):1775–1785. [DOI] [PubMed] [Google Scholar]
- 17.Cheng JY, Chen F, Sandino C, Mardani M, Pauly JM, Vasanawala SS. Compressed Sensing: From Research to Clinical Practice with Data-Driven Learning. arXiv preprint arXiv:1903.07824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cheng JY, Chen F, Alley MT, Pauly JM, and Vasanawala SS. Highly Scalable Image Reconstruction using Deep Neural Networks with Bandpass Filtering. arXiv preprint arXiv:1805.03300. [Google Scholar]
- 19.Yang Y, Sun J, Li H, and Xu Z. ADMM-Net: A Deep Learning Approach for Compressive Sensing MRI. NIPS 2017; 10–18. [Google Scholar]
- 20.Adler J, Öktem O. Learned primal-dual reconstruction. IEEE transactions on medical imaging. 2018;37(6):1322–32. [DOI] [PubMed] [Google Scholar]
- 21.Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med 2018;79(6):3055–3071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen F, Taviani V, Malkiel I, Cheng JY, Tamir JI, Shaikh J, Chang ST, Hardy CJ, Pauly JM, Vasanawala SS. Variable-density single-shot fast spin-echo MRI with deep learning reconstruction by using variational networks. Radiology. 2018;289(2):366–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Olsson DM, Nelson LS. The nelder-mead simplex procedure for function minimization. Technometrics 1975; 17:45–51. [Google Scholar]
- 24.Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems 2012; 1097–1105. [Google Scholar]
- 25.Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention 2015; 234–241. [Google Scholar]
- 26.Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980. [Google Scholar]
- 27.Uecker M, Ong F, Tamir JI, Bahri D, Virtue P, Cheng JY, Zhang T, Lustig M. Berkeley advanced reconstruction toolbox. Proc. Intl. Soc. Mag. Reson. Med 2015; 23:2486. [Google Scholar]
- 28.Mardani M, Sun Q, Donoho D, Papyan V, Monajemi H, Vasanawala S, Pauly J. Neural proximal gradient descent for compressive imaging. In Advances in Neural Information Processing Systems 2018; 9573–9583. [Google Scholar]
- 29.Chen F, Cheng JY, Pauly JM, Vasanawala SS. Semi-Supervised Learning for Reconstructing Under-Sampled MR Scans. Proc. Intl Soc Mag Reson Med 2019; 27:4649. [Google Scholar]
- 30.Chen F, Shi X, Chen S, Johnson EM, Chen B, Ren G, Wei X, Wang S, Ying K. Accelerated model-based proton resonance frequency shift temperature mapping using echo-based GRAPPA reconstruction. Magnetic resonance imaging 2015;33(2):240–245. [DOI] [PubMed] [Google Scholar]
- 31.Hu Y, Levine EG, Tian Q, Moran CJ, Wang X, Taviani V, Vasanawala SS, McNab JA, Daniel BA, Hargreaves BL. Motion‐robust reconstruction of multishot diffusion‐weighted images without phase estimation through locally low‐rank regularization. Magn Reson Med 2019;81(2):1181–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]