Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Mar 24;125(12):3080–3091. doi: 10.1021/acs.jpcb.0c10839

Temperature-Responsive Peptide–Nucleotide Coacervates

Tiemei Lu 1, Karina K Nakashima 1, Evan Spruijt 1,*
PMCID: PMC8020381  PMID: 33757284

Abstract

graphic file with name jp0c10839_0008.jpg

Coacervates are a type of liquid–liquid phase separated (LLPS) droplets that can serve as models of membraneless organelles (MLOs) in living cells. Peptide–nucleotide coacervates have been widely used to mimic properties of ribonucleoprotein (RNP) granules, but the thermal stability and the role of base stacking is still poorly understood. Here, we report a systematic investigation of coacervates formed by five different nucleoside triphosphates (NTPs) with poly-l-lysine and poly-l-arginine as a function of temperature. All studied combinations exhibit an upper critical solution temperature (UCST), and a temperature-dependent critical salt concentration, originating from a significant nonelectrostatic contribution to the mixing free energy. Both the enthalpic and entropic parts of this nonelectrostatic interaction decrease in the order G/A/U/C/T, in accordance with nucleobase stacking free energies. Partitioning of two dyes proves that the local hydrophobicity inside the peptide–nucleotide coacervates is different for every nucleoside triphosphate. We derive a simple relation between the temperature and salt concentration at the critical point based on a mean-field model of phase separation. Finally, when different NTPs are mixed with one common oppositely charged peptide, hybrid coacervates were formed, characterized by a single intermediate UCST and critical salt concentration. NTPs with lower critical salt concentrations can remain condensed in mixed coacervates far beyond their original critical salt concentration. Our results show that NTP-based coacervates have a strong temperature sensitivity due to base stacking interactions and that mixing NTPs can significantly influence the stability of condensates and, by extension, their bioavailability.

Introduction

Cells contain a variety of membraneless organelles (MLOs), which are important in cellular organization and could be relevant for synthetic cells.1In vitro models of MLOs can provide a useful platform to gain a better understanding of the role of membraneless compartmentalization in living cells. Recently, researchers have shown intracellular liquid–liquid phase separation (LLPS) underlies the formation of many MLOs, such as the nucleolus, P-granules, and Cajal bodies.2,3

Coacervates are condensed droplets that are formed by LLPS.4 They have been used as in vitro models of MLOs owing to their similarities in composition and physicochemical properties. Coacervates are commonly divided into simple coacervates, which are formed from a single type of macromolecule, and complex coacervates, which are formed by complexation between two types of usually oppositely charged macromolecules.5 A variety of biological and nonbiological macromolecules have been used to form complex coacervates, including combinations of synthetic polyelectrolytes, polysaccharides, peptides (polypeptides and oligopeptides), proteins, RNA, single-stranded DNA (ssDNA), and nucleoside di- and triphosphates.6−11 From all these combinations, peptide–nucleotide coacervates have become an attractive model system with many physicochemical characteristics, such as density and viscosity, in common with ribonucleoprotein granules.12−15 Moreover, their properties make them interesting as protocell models,13,16 which can concentrate small-molecule solutes17 and nucleic acids,18 while their formation can be controlled by pH19,20 and enzymatic reactions.21 Other, similar complex coacervates have been found to support RNA22,23 and enzyme catalysis24 and protein self-assembly.25,26 However, the effect of temperature on the phase behavior of complex coacervates is still incompletely understood, even though temperature could play an important role in the formation of protocells and the synthesis and stability of biomolecules.27,28

Koga et al. were the first to introduce peptide–nucleotide (nucleoside mono-, di-, and triphosphates) coacervates as protocell models. They reported that ATP/PLys and CTP/PLys coacervates remain stable up to 90 °C.16 Williams and coauthors used a different type of polycation, poly(diallyldimethylammonium) chloride (PDDA) and confirmed that PDDA–nucleotide droplets are also stable up to at least 85 °C.29 However, others reported significant effects of temperature changes on the stability of different complex coacervates. Keating and co-workers have shown that poly-U RNA in the presence of spermine can undergo LLPS and that the mixture shows lower critical solution temperature (LCST) behavior: the oppositely charged molecules are soluble below a critical temperature (LCST) and only phase separate when heated to above the LCST.30,31 Complex coacervates formed by cationic elastin-like polypeptides and hyaluronic acid also display LCST behavior, where the transition temperature could be tuned by the charge ratio of the employed macromolecules.32,33

On the other hand, complex coacervates of protamine and multivalent anions, such as citrate and tripolyphosphate, were reported to have upper critical solution temperatures (UCST): the coacervates dissolved upon heating to 36 or 55 °C, respectively.34 Finally, de novo designed intrinsically disordered peptides bearing oppositely charged residues can display both UCST and LCST behavior, depending on their sequence.35,36 In short, it is not clear how temperature is expected to impact the formation of peptide–nucleotide complex coacervates. If aromatic stacking interactions play a role in the formation of peptide–nucleotide coacervates, increasing temperature could weaken the interactions and possibly dissolve the coacervates, analogous to the melting of DNA and RNA duplexes. Typically, DNA duplexes exhibits a melting temperature (Tm), which depends on numerous factors, the most important one being the sequence itself.37

Here, we investigated the temperature dependence of complex coacervates made of one of five nucleoside triphosphates (ATP, GTP, CTP, dTTP, UTP, collectively referred to as NTPs) or tripolyphosphate (TPP) together with an oppositely charged polypeptide (poly-l-lysine (PLys) or poly-l-arginine (PArg)) in a systematic way. We show that all the peptide–NTP coacervates are temperature-responsive and exhibit a UCST. The coacervates can be reversibly dissolved by heating and formed again by cooling. The critical temperature of coacervates made with the five different nucleoside triphosphates (NTPs) varies significantly, and the order coincides with their base stacking free energy. We derive a simple relation between the salt concentration and temperature at the critical point, which can be used to deduce the enthalpic and entropic contributions to the interaction free energy. We find that the combinations with higher base stacking free energy exhibited higher critical salt concentration and we rationalize our findings by demonstrating that the most stable coacervates are the most hydrophobic using partitioning of two moderately hydrophobic dyes. We also report on mixed coacervates that contained two or more different NTPs and show that these coacervates are characterized by a single critical salt concentration and temperature, between the values for coacervates made with a single type of NTP. Our results suggest that peptide–NTP coacervates can be used as artificial organelles to store and release all NTPs upon changes in temperature.

Materials and Methods

Materials

The materials used for coacervate formation include poly-l-lysine hydrobromide (PLys, 15–30 kDa), poly-l-arginine trifluoroacetic acid (PArg, sequence: CR20-NH2, 5.5 kDa, with a cysteine used for labeling, >95% purity, Caslo), adenosine 5′-triphosphate disodium salt hydrate (ATP), guanosine 5′-triphosphate disodium salt hydrate (GTP), cytidine 5′-triphosphate disodium salt (CTP), 2′-deoxythymidine 5′-triphosphate sodium salt (dTTP), uridine 5′-triphosphate trisodium salt hydrate (UTP), sodium tripolyphosphate (TPP), sodium chloride (NaCl), magnesium chloride hexahydrate (MgCl2·6H2O), and 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES). These were all purchased from Sigma-Aldrich unless otherwise specified. Relevant molecular structures can be found in the Supporting Information (Table S1).

For partitioning experiments, we used rhodamine B (RhoB) and 6-aminofluorescein (6-AF), which were both purchased from Sigma-Aldrich. The fluorescently labeled DNA oligonucleotides used for compositional analysis of mixed coacervates include poly-A15 (Cy5-A15), poly-C15 (Cy5-C15), poly-T15 (T15-Cy3Sp), and poly-G11(G5-Super-dG-G5-Cy3Sp). These were all purchased from Integrated DNA Technologies (IDT). In this paper, we have used a shorter poly-G11 than the other oligonucleotides, because long poly-G oligonucleotides are known to form G-quadruplex secondary structures. Super-G bases can be added to prevent G-quadruplex formation, while retaining the Watson–Crick base pairing ability.38 Because of the shorter length, poly-G partitioning coefficients cannot be compared in absolute sense with partitioning coefficients of the other oligonucleotides; we therefore always compare poly-G partitioning relative to its partitioning in noncomplementary coacervates.

For the modification of microscopy chambers, we used poly(vinyl alcohol) (PVA, 13–23 kDa, 87–89% hydrolyzed, Sigma-Aldrich) and μ-slides with 18 wells (No. 1.5, polymer coverslip, Ibidi GmbH). The Ibidi μ-slide chambers were modified by adding 30 μL of a 5 wt % PVA solution to each well, covering it with the lid and incubating the slide at room temperature for 24 h. The wells were washed with copious amounts of MQ water and ethanol, dried with compressed air and then placed in an oven at 60 °C overnight to reach complete dryness.

Stock Solutions and Coacervate Formation

All NTPs and TPP were dissolved in Milli-Q water (MQ, 18.2 MΩ cm) at concentrations of 50 and 100 mM, respectively. In addition, the following stock solutions were prepared in MQ for coacervate formation and partitioning: PLys (50 mg/mL, 0.24 M in monomer units), PArg (10 mg/mL, 0.037 M in monomer units), HEPES (500 mM, pH 7.4), MgCl2 (50 mM), NaCl (3 M), RhoB (1.5 mM), and 6-AF (20 mM, adjusted with 1 M NaOH to pH 7.0). The labeled DNA oligonucleotides poly-A15, poly-G11, poly-C15, and poly-T15 were dissolved in nuclease-free water at a concentration of 100 μM. All stock solutions were stored at −20 °C, except HEPES, MgCl2, NaCl, RhoB, and 6-AF, which were stored at 4 °C.

Typically, coacervates were prepared by first mixing NaCl, HEPES, MgCl2, MQ, and the desired type of NTP (or TPP) in a microcentrifuge tube (0.5 mL, Eppendorf) at the required concentration, followed by the addition of positively charged PLys or PArg from their respective stock solutions in a 1:1 molar (monomer basis) ratio to the NTPs. The total volume of the mixtures was 20 μL. The final concentration of NaCl in the mixture varied from 0 to 1.2 M and the final concentration of HEPES and MgCl2 are 50 and 5 mM, respectively. Mixing was done by gentle pipetting (three times).

Turbidity Measurement

We used turbidity titrations, complemented with microscopic analysis, to determine the optimal mixing ratio of NTPs and polypeptides, and the critical salt concentration of peptide–NTP and TPP/PArg coacervates. Turbidity was measured on a microplate reader (Tecan Spark M10), equipped with an automated microinjector (1 mL syringes with heating and stirrer option), as described elsewhere.39 Samples for turbidity measurements were directly prepared into 96-well plates (Greiner Bio-one, clear flat-bottom wells). In order to determine suitable measurement conditions for investigating the effect of temperature on the stability of peptide–NTP coacervates, we prepared coacervates of PLys (5 mM, monomer concentration) with varying concentrations of ATP. Figure S1 shows that the critical salt concentration of ATP/PLys increased sharply at low ATP concentrations, before increasing much more slowly beyond 3 mM ATP. We selected 5 mM as the fixed NTP concentration for all experiments, because the critical salt concentration was sufficiently high to be accurately determined, while the phase transition was still sharp.

To determine the critical salt concentration of these and other coacervates, we performed titrations of 100 μL ATP/PLys coacervate dispersion with NaCl (0.60 M) in 5 μL steps for dissolution, or titrations of a 50 μL solution above the critical salt concentration with MQ in 5 μL steps for condensation. The temperature was kept constant at 20 ± 0.5, 25 ± 0.5, 30 ± 0.5, and 40 ± 0.5 °C, respectively, and the plate was kept at this temperature for 10 min before starting the titration. After each injection step, the samples were mixed by shaking for 5 s, followed by equilibration for 2.5 min, and shaken for another 5 s before every readout. A total of 15–40 injections were made, and all measurements were made in triplicate. The absorbance at 600 nm was recorded as a measure of turbidity. The turbidity is reported as (100 – T%), where T% is the percentage of light that is transmitted:39

graphic file with name jp0c10839_m001.jpg

The critical salt concentration was determined by plotting the recorded turbidity (100 – T%) as a function of the added salt concentration (NaCl) and then extrapolating the first-order derivative at the inflection point to zero turbidity. Note that this critical salt concentration does not take into account the addition of other ions from sources. Their concentration is the same for all the combinations we tested, and then we verified that the counterions from the peptide and NTPs have a negligible effect on the extrapolation (Figure S2a). We also confirmed that the turbidity signal does not decrease to below 50% for a typical duration of a titration experiment (Figure S2b) and that the addition order, titration rate (the lowest value is 5 μL per step), settling time, and shaking time (minimal: 3s) all have no effect on the measured turbidity (Figure S2c–f).

The turbidity of the samples (Figure 1a, Figures S3, S4, and S11a,d) was recorded on a JASCO V-630 UV–vis spectrophotometer in a quartz microcuvette (Hellma, path length 10 mm, volume 400 μL). Like on the plate reader, the samples were equilibrated for 10 min before starting the measurement. For variable temperature measurements, the temperature was increased from 10 to 60 °C and back at a rate of 2.5 °C/min and the absorbance at 600 nm was recorded every 2 °C by holding the temperature for 10 s. With faster heating and cooling rates, the hysteresis became more pronounced (Figure S3b–d), while at lower rates, the turbidity dropped at low temperatures and the cycle could not be repeated starting from the same turbidity level, because a full cycle takes more than 3 h at rate of 0.5 °C/min (Figure S3a). Therefore, we used 2.5 °C/min as the optimal temperature ramp. For determining the critical salt concentration at constant temperature, samples with a starting volume of 300 μL were equilibrated for 10 min at 20 ± 0.3, 25 ± 0.3, 30 ± 0.3, 40 ± 0.3, 50 ± 0.3, and 60 ± 0.3 °C, respectively, and then the salt concentration was increased stepwise by addition of NaCl (0.60 M, kept in thermal shaker at the same temperature) in 5–20 μL per step. After addition, the sample was mixed 3× with a glass pipet and equilibrated for 2.5 min before readout.

Figure 1.

Figure 1

Open in a new tab

(a) Temperature-dependent decrease of turbidity between 10 and 60 °C of ATP/PLys coacervates prepared at different salt concentrations. (b)–(d) Bright-field microscope images of ATP/PLys coacervate droplets at a salt concentration of 0.22 M, showing the effect of their dissolution and formation triggered by varying the temperature: (b) droplets at the starting temperature of 10 °C, (c) when the temperature is increased to 60 °C at a rate of 2.5/°C droplets are completely dissolved and the solution is clear, and (d) when the temperature is decreased to 10 °C at the same rate droplets are visible again.

Wide-Field and Confocal Microscopy

Images were obtained by using a Leica Liachroic Sp8 confocal microscope, equipped with a EL6000 light source, DFC7000 GT camera, DMi8 CS motorized stage, LAS X SP8 controller software, and a HC PL APO CS2 20×/0.75 objective (air), or a Leica TCS Sp8X confocal microscope, equipped with HyDs and PMTs detectors and a pulsed white light laser and a HC PL APO CS2 40×/0.6 objective (air). Temperature ramp videos were recorded on a bright-field transmission optical inverted microscope (IX71, Olympus), equipped with a Linkam PE 100 Peltier stage using a heating/cooling rate of 2.5 °C/min. Images were recorded with a default frequency of 1 s/picture. Samples for the microscopy experiments were prepared in Eppendorf tubes. Normally, 10–30 μL of a freshly prepared coacervate dispersion was added directly to a modified μ-slide chamber for taking images or videos.

For partitioning experiments, small quantities (0.4 μL for 6-AF and RhoB, 0.2 μL for Cy3- and Cy5-labeled oligonucleotides) of the stock solutions of the dye molecules were added to the coacervates, mixed by gentle pipetting, and visualized by excitation at the indicated wavelengths. 6-AF was excited at 484 nm, RhoB at 573 nm, Cy3 (poly-G11, poly-T15) at 554 nm and Cy5 (poly-A15, poly-C15) at 649 nm. The partitioning coefficient (Kp) was determined from average fluorescence intensities as Kp = (Icoa – Ib)/(Id – Ib), where Icoa, Ib, and Id are the intensity inside of a coacervate, a blank solution, and the dilute phase surrounding the coacervate droplets, respectively.

HPLC Analysis of the Components of the Coacervate Droplets

For high-pressure liquid chromatography (HPLC) analysis, we used phosphate buffers prepared using mono- and dibasic potassium phosphate (KH2PO4 and K2HPO4, Sigma-Aldrich). For determination of the nucleoside base composition of mixed coacervates, we used a Shimadzu Nexera X2 HPLC system with an anion exchange column (Shim-pack WAX-1, 4.0 × 50 mm, 3 μm particle size), operated at 45 °C, UV–vis detector (SPD-20A), and LC-30AD liquid chromatograph and a Nexera X3 HPLC system with the same column as Nexera X2, UV–vis detector (SPD-40), and LC-40D liquid delivery pump.

Samples for HPLC, were prepared by centrifugation of a 1 mL coacervate dispersion for 30 min at 6000 rpm to separate the dilute phase (top) from the coacervate phase (bottom). The dilute phase was diluted a further 10× with MQ water before injection. The coacervate was dissolved by adding a known volume of NaCl (3 M) and MQ water, after which the total volume was determined by pipet and was finally diluted 100×. The pure samples (NTPs) were prepared by directly diluting their stock solutions to 100 μM. For HPLC measurement, the pump flow rate was 1 mL/min (X2) or 0.8 mL/min (X3), the injection volume was 2–10 μL, depending on the sample, eluents were 20 mM KH2PO4/K2HPO4 buffer A (pH 7.0) and 480 mM KH2PO4/K2HPO4 buffer B (pH 6.9), and the gradient program in total was 25 min (0–100% B in 15 min, 100% B for 4 min, 100–0% B in 2 min, 0% B for 4 min). The nucleotide bases were detected by absorbance at 254 nm.

Results and Discussion

Temperature-Responsive ATP/PLys Coacervates with Different Salt Concentrations

Peptide–NTP coacervates have been used as protocells and in vitro membraneless organelle mimics, but the influence of temperature on the stability and composition is still unclear. On the basis of the marked melting behavior of DNA and RNA duplexes caused in part by disruption of the base stacking interactions, we hypothesized that peptide–NTP coacervates would also “melt” upon increasing the temperature. In order to establish if temperature could lead to dissolution of peptide–NTP coacervates, we first prepared coacervates of ATP and PLys at different salt concentrations and monitored their turbidity upon changing the temperature. We cycled the temperature between 10 and 60 °C. As shown in Figure 1a, when the temperature was increased from 10 to 60 °C, the turbidity of the coacervates with salt concentrations from 0.18 to 0.26 M decreased significantly, dropping to close to zero above a characteristic transition temperature. These curves show a characteristic upper critical solution temperature (UCST) behavior, similar to that observed for complex coacervates of protamine and citrate.34 Increasing the temperature to 60 °C had little effect on samples with salt concentrations below 0.14 M, most likely because the transition temperature was higher than 60 °C under these conditions. Interestingly, the salt concentration in all samples displayed in Figure 1a is much lower than the critical salt concentration at room temperature, which is 0.30 M (measured at 22 °C by titration from low to high salt concentration).

There is a clear correlation between the transition temperature and the salt concentration: the transition temperature of the coacervates shifts to lower temperatures as the salt concentration gets closer to the critical salt concentration. In all cases, the temperature-induced transition is quite pronounced: for example, for a salt concentration of 0.22 M, the turbidity of mixture falls from almost 100% to nearly zero as the temperature is increased from 35 to 48 °C, which is a similar width to the melting curve of many short DNA and RNA duplexes.40 Additionally, when we cooled the mixture from 60 to 10 °C, the turbidity increased again to the original level with decreasing temperature (Figure S4).

We interpret the fall in turbidity as complete dissolution of the coacervate droplets and the subsequent rise as formation of coacervates by condensation. We verified that the coacervates were indeed dissolved and formed again using optical microscopy. The bright-field microscope images in Figure 1b–d show the sample of ATP/PLys with a salt concentration of 0.22 M at the starting temperature of 10 °C, at the final temperature after heating to 60 °C, and after cooling to 10 °C again. At 10 °C, both before heating and after cooling again, we observed clear coacervate droplets (Figure 1b,d), while at 60 °C, we observed no coacervate droplets (Figure 1c), which confirms that changes in temperature can be used to reversibly dissolve and form peptide–NTP coacervates. The dissolution and formation process also can be followed in time in Movie S1 and Movie S2. The videos show that as the temperature increases, the droplets dissolve slowly, decreasing in size first and then disappearing, while when the temperature is decreased, the droplets form rapidly and then grow larger as they cool further. These results highlight the reversibility of ATP/PLys coacervates.

UCST Behavior of Peptide–Nucleotide Coacervates

In order to better understand the effect of the interactions between the nucleotide bases on the UCST behavior of peptide–NTP coacervates, we repeated these experiments with coacervate droplets of GTP, CTP, TTP, and UTP, all mixed with PLys. All combinations could form coacervate droplets directly after mixing, as shown in the bright-field microscope images in Figure S5.

We found in Figure 1 that there was a direct correlation between the critical temperature and critical salt concentration of ATP/PLys coacervates. Therefore, we studied the turbidity of ATP/PLys, GTP/PLys, CTP/PLys, TTP/PLys and UTP/PLys coacervates during a salt titration at different temperatures in a plate reader (Figure S6, ATP/PLys as an example). The critical salt concentration was determined from the turbidity titrations and is shown in Figure 2a as a function of temperature. In other words, Figure 2a shows the UCST of different peptide–NTP coacervates as a function of salt concentration. For all NTPs, a decreased critical salt concentration could be observed with increasing temperature. However, the NTP-based coacervates exhibited significantly different critical salt concentrations at the same temperature (and different UCST at the same salt concentration). The critical salt concentration decreased in the order GTP/PLys (G) > ATP/PLys (A) > CTP/PLys (C) ≥ UTP/PLys (U) > TTP/PLys (T), in line with the relative stacking free energies of the nucleobases.41 In addition, the critical salt concentration increased more rapidly with decreasing temperature for ATP and GTP than for CTP, TTP, and UTP.

Figure 2.

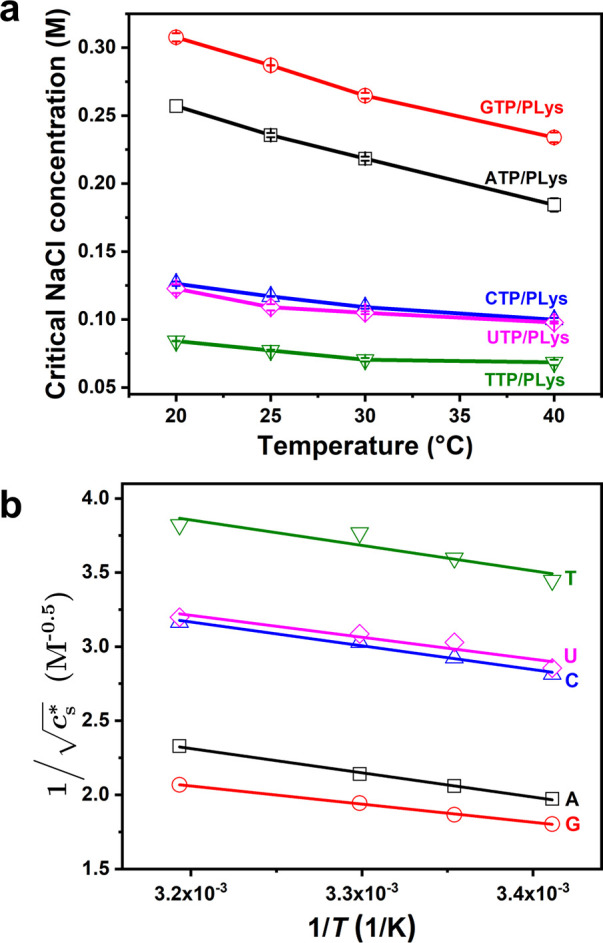
Figure 2

Open in a new tab

(a) Critical salt concentrationof different NTP-PLys coacervates as a function of temperature. (b) Linearization of (a), according to eq 4.

To rationalize the relation between critical salt concentration and temperature of complex coacervates, we start from a simplified mean-field Flory–Huggins model, which has been widely used to describe LLPS of peptides and proteins.42−44 According to this model, the mixing free energy density (f) of a peptide or disordered protein that undergoes phase separation can be written as

graphic file with name jp0c10839_m002.jpg 1

where ϕ is the volume fraction of a polymeric species and χ is the interaction parameter, which accounts for the interaction free energy between the polymer and the solvent and includes both enthalpic and entropic components.45 The complex coacervation of a pair of oppositely charged polyelectrolytes can be described with the same framework using an effective χ, which has been defined as follows46

graphic file with name jp0c10839_m003.jpg 2

where l is the lattice size, lB is the Bjerrum length, σ is the charge density, cs is the ionic strength, χr is a residual, nonelectrostatic part of the interaction parameter, and 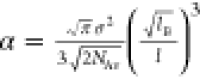Inline graphic is a constant.

The Flory–Huggins-type model with an effective electrostatic interaction, as outlined above, has its limitations. From the point of view of the interactions, it is assumed that the species involved in phase separation are symmetric in terms of length and charge density, and that no salt is added. Moreover, the derivation is valid for low charge densities and ignores correlation effects. Nevertheless, this model has been found to describe the experimental phase behavior, critical salt concentration (cs*), and interfacial tension of complex coacervates surprisingly well.47,48 It has been suggested that the reason it is able to describe coacervation is the fact that all contributions to the associative interaction are grouped under a single effective interaction parameter, which could mask some of the intrinsic shortcomings of Flory–Huggins theory.49 Other, more advanced models of complex coacervation have been developed in recent years.48 However, our goal is not to quantitatively predict the local polymer concentrations. Instead, we aim to find a simple analytical expression that captures the relation between cs and temperature, which the Flory–Huggins model allows for.

The residual (nonelectrostatic) component of the interaction parameter (χr) is often written as the sum of an entropic and enthalpic part:49

graphic file with name jp0c10839_m005.jpg 3

where A is the temperature-independent entropic part and B/T is the temperature-dependent enthalpic part. The Flory–Huggins model predicts the presence of a critical point when the spinodal curve exhibits a minimum or maximum (∂χs/∂ϕ = 0). This critical point (indentified by a critical value χc) can be reached by variation of any parameter that affects the interaction parameter χ, such as temperature or, in the case of complex coacervates, salt concentration. It is common for polymers with LCST behavior to have A > 0 and B < 0, such that χ increases to above the critical value χc upon heating, whereas UCST behavior commonly occurs if A > 0 and B > 0, and their sum is close to the critical value.

The critical point of complex coacervates is a function of temperature and salt concentration. By combining eqs 2 and 3 with the classical expression for the critical value χc of a polymer in solution, 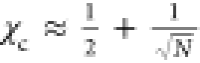Inline graphic, we find the following relation between the cs* and temperature:

graphic file with name jp0c10839_m007.jpg 4

In the case of peptide–NTP coacervates, there is a significant asymmetry in length between the two phases separating molecules. However, we can still use eq 4 by realizing that these complex coacervates have a defined critical value χc, which could be expressed in terms of an effective length Neff that is the same for all different NTPs.

According to eq 4, we expect a linear relationship between the inverse square root of the critical salt concentration, 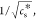Inline graphic which is proportional to the reciprocal Debye length (κ) and the inverse absolute temperature, 1/T, provided that the parameters combined in α do not show a significant dependence on temperature. α is defined in eq 2 as a combination of the charge density, the lattice size and the Bjerrum length. The latter can be written as lB = e2/4πϵrϵ0kT. Although the temperature is included in the definition of the Bjerrum length, the relative permittivity ϵr is to a good approximation inversely proportional to temperature for aqueous solutions.50 As a result, the Bjerrum length in water varies only 5% between 20 and 60 °C, the temperature range we are interested in. Therefore, we can assume that α is effectively independent of temperature, and the UCST behavior of complex coacervates is governed by the enthalpic component B of the nonelectrostatic interactions.

We investigated if eq 4 indeed captures the observed dependence of the cs* on temperature, by plotting 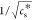Inline graphic as a function of 1/T. We note that by measuring the salt concentration at which a peptide–NTP mixture of a given concentration no longer phase separates, as we do, we do not measure the true critical point, which is located at the spinodal maximum, but an approximate value at a slightly lower concentration. However, at the NTP concentration we selected, the critical salt concentration varied only slightly with NTP concentration (Figure S1b) and is a reasonable approximation of the salt concentration at the critical point. Moreover, because we compare all NTP coacervates at the same concentration, a possible underestimation of the salt concentration at the critical point is the same for all coacervates.

As can be seen in Figure 2b, we find a linear relation for all NTPs. The fitted intercepts (A′) and slopes (−B′) are shown in Figure 3. A′ and B′ are related to entropic and enthalpic parts of the nonelectrostatic component of the interaction parameter, respectively, according to eq 4. We note that A′ contains additional terms related to the expression of χc, and that a large positive A′ implies a small entropic component A > 0. In contrast, a large negative B′ corresponds to a large enthalpic component B > 0. In order to verify that eq 4 holds over a wider range of temperatures, we repeated the measurements with a larger volume of ATP/PLys coacervates dispersion using a UV–vis spectrophotometer Figure S7 shows how the cs* of ATP/PLys decreases with increasing the temperature, revealing a linear relation between 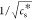Inline graphic and T–1 over the entire range of temperatures tested here.

Figure 3.

Figure 3

Open in a new tab

(a) Slopes (−B/α) and (b) intercepts (A′) of linear fits of the data in Figure 2b for different NTPs.

The slopes and intercepts shown in Figure 3 reveal why the peptide–NTP coacervates exhibit UCST behavior. For all NTPs, we found a negative slope (Figure 3a), suggesting B > 0, in agreement with typical UCST behavior. The positive value of B/α for these complex coacervates can be explained by a decreased solvation of charges with increasing temperature,51 which makes dissolving ion-paired complexes from the coacervate phase easier. The slopes in Figure 3a had similar values within experimental uncertainty, except for G, which had a slightly smaller slope. The intercept shown in Figure 3b was positive and found to increase systematically in the order G < A < U ≤ C < T.

According to eq 4, the intercept A′ increases as the entropic part of the nonelectrostatic interaction (A) decreases, assuming that N and α are the same for all NTPs (see above). The observed order is therefore in good agreement with the strength of base stacking interactions, which are the strongest for purine bases G and A.52−54 Base stacking interactions can stabilize peptide–NTP coacervates and these interactions are likely to be captured by the entropic part of the nonelectrostatic interaction (A), as the dominant contributor to base stacking interactions was found to be solvent entropy.55 Moreover, this effect is more pronounced for larger and more hydrophobic bases.56 As a consequence, peptide–NTP coacervates made from purine bases (G and A) are more stable than those made from pyrimidine bases (U, C, T) and their UCST is higher at the same salt concentration. Guanine has a slightly larger contact area than adenine, while the methyl group in thymine reduces the stacking efficiency compared to cytosine and uracil.

Our analysis suggests that other peptides or polymers should also form temperature-responsive coacervates with NTPs (or NDPs and NMPs), and a similar dependence of cs* on temperature is expected for these other peptide–nucleotide coacervates. To prove this is the case, we selected poly-l-arginine (PArg) as another peptide to form coacervates with ATP and GTP (Figure S8 and S9). The PArg we used is shorter than PLys, because longer PArg peptides have been found to form aggregates with ATP.13 We found that (ATP, GTP, or TPP)/PArg could form coacervates and that these coacervates exhibited a temperature dependence: the cs decreased with increasing temperature in a similar way as for PLys. After linearizing the plot according to eq 4 and fitting the data, we found that intercepts increased in the order G < A, in agreement with our results for PLys-based coacervates (G < A). The slope of ATP/PArg was higher than that of GTP/PArg, similar to our observations with PLys (Figure 3a), which may be explained by an increased hydrogen bonding character between the polycations and the guanine bases, compared to adenine, contributing to the nonelectrostatic part of the interaction parameter.

Finally, to show that the temperature responsiveness is mostly caused by the nucleotide bases, we selected tripolyphosphate (TPP), which has three phosphate groups, like NTPs, but lacks the ribose and base (Table S1). Unfortunately, TPP’s higher net charge and smaller molecular size means that it has a significantly higher charge density than all NTPs, resulting in the formation of aggregates with PLys (Figure S8a). With the PArg we selected, which is significantly shorter, we did observe coacervate formation (Figure S8b), although the critical salt concentration of these coacervates was relatively high, owing to the high charge density. We used these coacervates to check the temperature sensitivity of peptide–TPP coacervates without a nucleobase. As can be seen in Figure S9, the critical salt concentration of TPP/PArg coacervates shows a significantly weaker dependence on temperature than the NTPs, as expected when eliminating the possibility of base stacking. The fact that these coacervates still show a mild temperature dependence indicates that the other contributions to the interaction free energy (electrostatics, hydration) also have an enthalpic component.

In summary, the strong similarities in salt and temperature dependence of the PLys and PArg-based coacervates demonstrate that temperature responsiveness of peptide–NTP coacervates is mainly caused by the nucleotide bases, rather than the peptides.

Partitioning Reveals Different Local Polarities

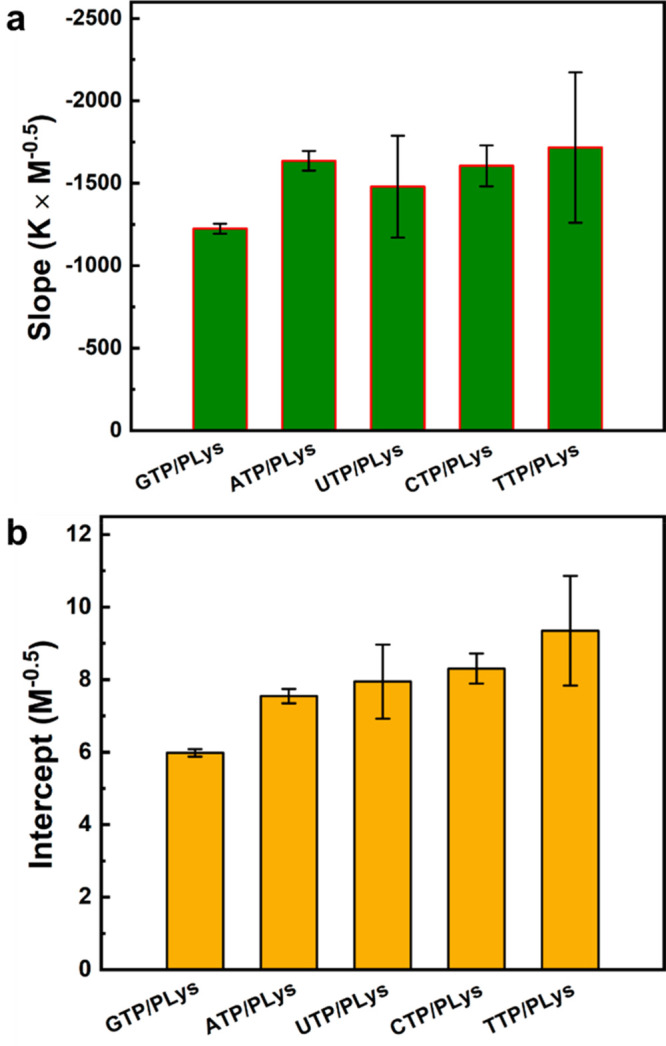
The observed order of the upper critical solution temperatures and entropic components (A) in coacervates made with different NTPs suggests that these coacervates have different interior polarities. Moreover, the interior polarity changes with temperature: as the temperature increases, the cs* of the coacervate droplets decreases, which indicates an increased water content in the coacervates.46 We therefore expected that the different peptide–NTP coacervates would take up guest molecules to a different extent.17 We chose moderately hydrophobic dyes, one zwitterionic rhodamine-B (RhoB), and one with a net negative charge at pH 7.4, 6-aminofluorescein (6-AF),57 and measured their partitioning in NTP/PLys and ATP/PArg coacervates.

Both of RhoB and 6-AF were concentrated in the coacervate droplets. Figure 4a shows a typical example fluorescence microscope image of RhoB and 6-AF in ATP/PLys coacervates. We calculated the partitioning coefficients (Kp) for all peptide–NTP coacervates and found significantly different partitioning coefficients for the different NTPs (Figure 4b), ranging from 6.1 to 68.4 for RhoB and 15.4 to 61.7 for 6-AF. ATP/PArg has the highest partitioning coefficient for both dyes, in agreement with the fact that ATP/PArg also has the highest cs* in comparison with NTP/PLys coacervates at same temperature (Figure S9). For the different PLys-based coacervates, the Kp of RhoB in GTP/PLys is higher than in ATP/PLys, followed by UTP/PLys, CTP/PLys, and TTP/PLys, which have almost the same partitioning coefficients. For 6-AF, the Kp decreased even more clearly in the order G > A > U > C > T. This is the same order as their cs and the same order as the entropic part of the interaction parameter and the base stacking free energy. These results show that the peptide–NTP coacervates have different polarity, and that partitioning provides a powerful method to probe this polarity.

Figure 4.

Figure 4

Open in a new tab

(a) Example of partitioning of RhoB and 6-AF guest molecules into ATP/PLys coacervate droplets visualized by confocal fluorescence microscopy. (b) Partitioning coefficients of two different hydrophobic guest molecules into the peptide–NTP coacervates.

Mixed NTPs Make Hybrid Peptide–Nucleotide Coacervates

We sought to use the newly found UCST behavior of peptide–NTP coacervates to create LLPS compartments from which NTP could be released upon increasing the temperature, for instance to fuel cell-free, in vitro transcription and translation (IVTT) reactions.58,59 During in vitro transcription-translation, polymerases and ribosomes consume all NTPs (ATP, GTP, CTP, and UTP), in a specific ratio.60 Thus, we were interested in storing a collection of NTPs in peptide–NTP coacervates. However, it is not clear if a mixed population of NTPs with a common peptide would lead to hybrid coacervates in which all NTPs are contained, or if they create separate or multiphase coacervates. Even if a hybrid coacervates are formed, it remains unclear how temperature will affect these coacervates, since different NTPs-based coacervates were found to exhibit a different UCST and cs*. We therefore investigated the formation of hybrid coacervates from mixed NTPs with a common peptide.

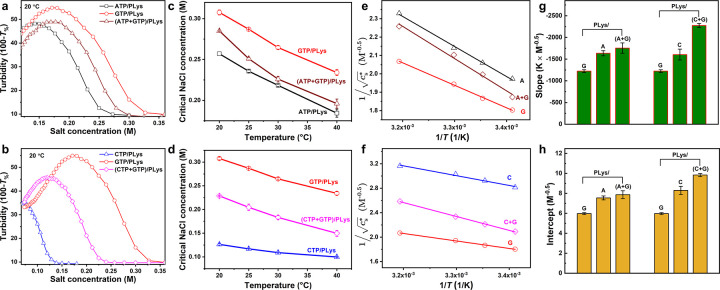
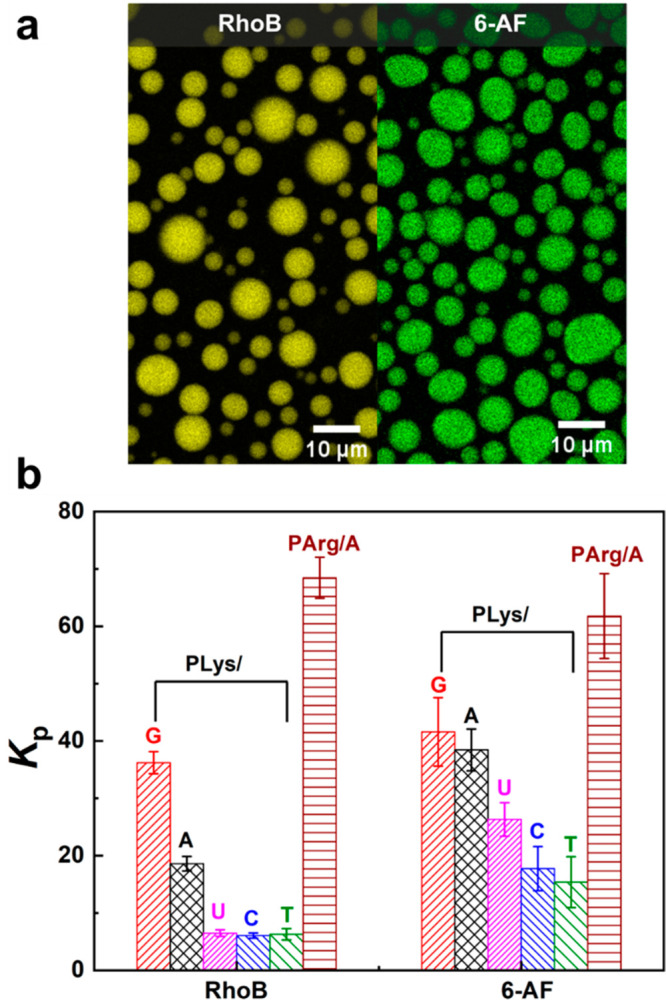
We prepared coacervates from all possible combinations of two NTPs together with PLys. All combinations could form coacervate droplets without signs of multiple coexisting phases (Figure S5), despite their distinct critical salt concentrations. This can be explained by the fact that the small NTPs have a non-negligible translational entropy, which means that multiphase droplets only appear when the difference in critical salt concentrations are much larger.46 We followed the same approach as described above to investigate the cs* of hybrid peptide–NTP coacervates as a function of temperature (Figure S10). In Figure 5, we show the results of two representative mixtures, one containing complementary NTPs (C+G) with PLys, and the other containing noncomplementary NTPs (A+G) with PLys. Both types of coacervates show a single cs, intermediate between the critical salt concentrations of the respective single NTP coacervates (Figure 5a,b). The cs* of both types of coacervates decreased with increasing temperature and could be fitted to eq 4 (Figure 5c,d). The single critical salt concentration suggests that the coacervates contain a mixture of both NTPs, and that the NTP with a lower critical salt concentration (A and C) could remain condensed in mixed coacervates (A+G or C+G) far beyond their original critical salt concentration.

Figure 5.

Figure 5

Open in a new tab

UCST behavior of mixed NTP coacervates. (a) Turbidity of ATP, GTP and their mixture with PLys as a function of salt concentration. (b) Turbidity of CTP, GTP, and their mixture with PLys as a function of salt concentration. (c) Temperature dependence of the critical salt concentration (cs*) of ATP, GTP, and their combination with PLys. (d) Temperature dependence of cs of CTP, GTP, and their combination with PLys. (e, f) Linearization of (c, d) according to eq 4. (g) Slopes (−B/α) and (h) intercepts (A′) of linear fits of the data in (e) and (f).

Results with single NTP coacervates showed that the stability of peptide–NTP coacervates decreases in the order G > A > C ≥ U > T, due to the fact that the nucleotide bases have different stacking free energies and create differently hydrophobic environments. In hybrid coacervates containing two different NTPs, such as CTP and GTP with PLys, the mean stacking free energy between bases in the coacervate is an average between C and G, and the local polarity is intermediate between CTP/PLys and GTP/PLys. In the same vein, if all the NTPs are mixed together, the cs* is between the extremes of G and T (Figure S11) and these coacervates can be dissolved and formed easily with a transition temperature around 48 °C (at 0.16 M salt). The transition is fully reversible and repeating the cycle yields a nearly identical transition temperature (Figure S11d).

We then analyzed the slopes and intercepts of (A+G) with PLys and (C+G) with PLys (Figure 5e–h) using the same method as for Figure 2. The fitting results revealed that in most cases both the slope and intercept of the coacervates obtained after combination of the NTPs were higher than those of the single NTP coacervates (Figure S12), except for the combination of GTP and TTP. This is most likely caused by the fact that the composition of the hybrid coacervates changes slightly upon increasing temperature: the less stable NTP (e.g., C in the case of C+G) will be released from the mixed coacervates slightly more easily than the more stable NTP, thereby leading to a marginally more hydrophobic coacervate environment. Interestingly, this effect does not lead to a pure G-based coacervate at sufficiently high temperatures, due to the release of all C from the mixed coacervates. Instead, all coacervate droplets had dissolved at significantly lower temperature and salt concentration than the single GTP/PLys coacervates.

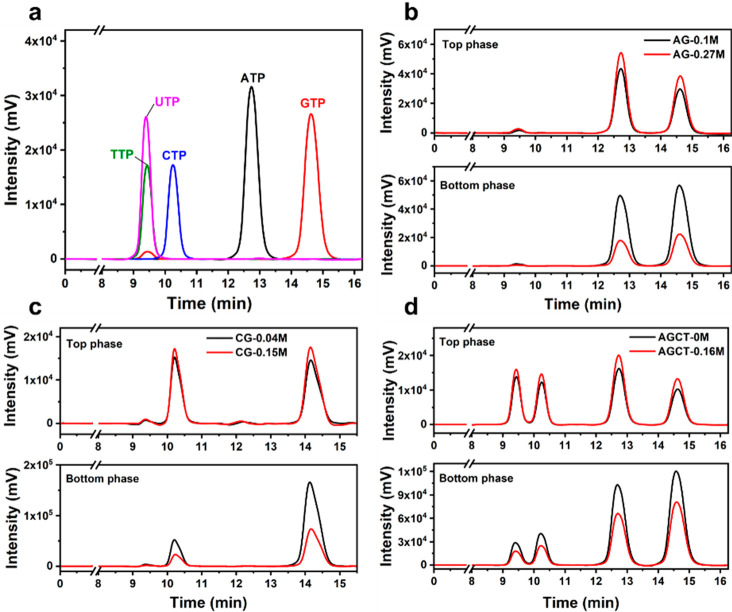
To prove that mixed coacervates contain all NTPs after phase separation with PLys, we investigated their composition with the aid of HPLC. We first determined the pure NTPs by HPLC, and Figure 6a shows that all NTPs are well separated, except for TTP and UTP, which eluted at the same time. We then analyzed the dilute (top) and coacervate (bottom) phase of samples with noncomplementary NTPs (A+G), complementary NTPs (C+G), and all NTPs mixed together (A+G+C+T and A+G+C+U), all combined with PLys. For all combinations we selected two different salt concentrations: one salt concentration below the lowest cs* of the NTPs and the other above the cs of one or two of them, but below the cs* of the mixture. To confirm that the dilute (top) phase was free of coacervate droplets, we measured the turbidity of (A+G)/PLys after centrifugation (Figure S13a). We found that the turbidity of the top phase was identical to a blank solution (without A, G, and PLys).

Figure 6.

Figure 6

Open in a new tab

HPLC analysis of (a) the pure NTPs and (b)–(d) the top phase and bottom phase of different coacervates combinations with two different salt concentration after centrifugation, respectively. Note: chromatograms in (a), (b), and (d) were recorded on X3, while chromatograms in (b) and Figure S13b were recorded on X2.

The HPLC results are shown in Figure 6b–d and Figure S13b. In all cases, we found all NTPs back in the coacervate phase, even if the mixture was prepared above the critical salt concentration of one of them. The results indicate that after mixing, the hybrid NTP coacervates exhibited a common cs* rather than two or four independent cs values, and that the coacervates had intermediate polarity and stability due to the averaging of base stacking energies. Figure 6b–d and Figure S13b also indicate that the ratio of T/U:C:A:G changes slightly upon changing salt concentration: the amount of the less stable NTP (mostly C and T) decreased more than the amount of the more stable NTP (G). We expect the same effect to occur when changing temperature, which could explain why the value of B/α (slopes) of mixed coacervates was higher than that of both single NTP coacervates.

Enhanced Partitioning of ssDNA Oligonucleotides in Mixed NTP Coacervates

Previous studies have shown that oligonucleotides can be sequestered in coacervates. The uptake was strongly enhanced if the coacervates already contained complementary oligonucleotides.30 In addition, coacervates formed with DNA duplexes were shown to exhibit a melting transition, suggesting that base pairing in complex coacervates is possible.61 We thus expect that our mixed NTP coacervates will be able to enhance the uptake of multiple oligonucleotides of different sequence. Here, we focused on coacervates containing two NTPs (ATP+GTP)/PLys and coacervates containing all NTPs (AGCT)/PLys. As for HPLC, two different salt concentrations were chosen for comparison. At low salt concentrations, all NTPs are able to form coacervates separately with PLys, while at high salt concentration (0.27 M for A+G and 0.16 M for A+G+C+T) only GTP or ATP and GTP can form single NTP coacervates with PLys, respectively.

We added four different labeled DNA oligonucleotides (poly-A15, poly-G11, poly-C15, and poly-T15) to the coacervate dispersions and quantified their partitioning by confocal fluorescence microscopy (Figure S14). All oligonucleotides could be concentrated in (ATP+GTP)/PLys and (AGCT)/PLys coacervate droplets (Kp > 58), as shown in Figure 7 and in agreement with previous findings.13,14,62 For (ATP+GTP)/PLys coacervates (Figure 7a), poly-C15 and poly-T15 exhibit significantly higher partitioning coefficients at 0.10 M salt than poly-A15 and poly-G11, despite the fact that A and G are the more hydrophobic bases, which display stronger base stacking interactions. This difference could be explained by a favorable base pairing interaction between the poly-C15 and GTP in the coacervates, as well as poly-T15 and ATP. In poly-U/spermine and poly-U/RRASLRRASL coacervate systems, poly-A15 partitioned more strongly than poly-N15.30,63 The absolute partitioning coefficients in refs (30) and (63) were much higher than the values we observed in Figure 7, but this is due to the fact that a single poly-U can form multiple base pairs with poly-A15. In our systems, GTP and ATP are single nucleotide bases, and their base pairing interaction with complementary oligonucleotides is quite weak. Nevertheless, the interaction is strong enough to induce a 2-fold higher partitioning, and it confirms that both ATP and GTP are in the coacervate droplets, as was previously established by HPLC.

Figure 7.

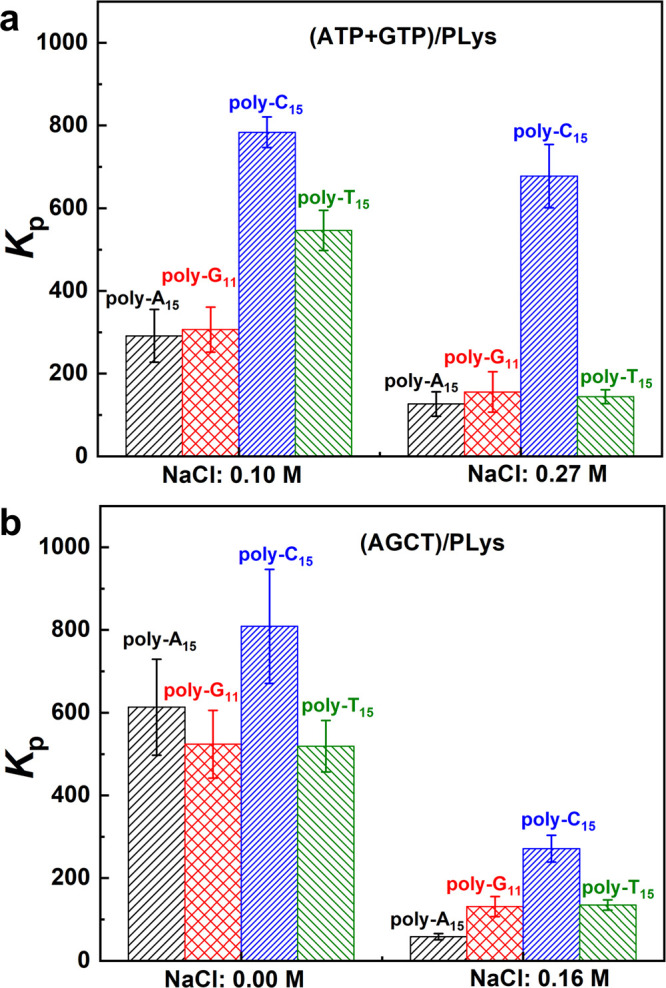
Figure 7

Open in a new tab

Partitioning coefficients of four different labeled DNA oligonucleotides into (a) (ATP+GTP)/PLys prepared at a NaCl concentration of 0.10 and 0.27 M and (b) (AGCT)/PLys coacervates prepared at a NaCl concentration of 0 and 0.16 M.

When the salt concentration was increased to 0.27 M, only poly-C15 had a significantly higher partitioning coefficient compared with the others. The partitioning of poly-T15 was reduced to the same level as poly-A15 and poly-G11, which suggests that the level of ATP in these coacervates has decreased compared to GTP. The ATP is probably not completely absent from the coacervates: the partitioning coefficient of poly-T15 was already lower than that of poly-C15 because of the weaker base pairing between T and A. Another possible reason for the low partitioning coefficient of poly-T15 is that as the salt concentration approached the cs* of (ATP+GTP)/PLys, the droplets became very small (Figure S14h), which made quantifying the partitioning difficult.

When the coacervates were made from a mixture of all four NTPs (AGCT), together with PLys (Figure 7b), the partitioning coefficients of poly-A15 and poly-G11 were significantly increased compared to the (ATP+GTP)/PLys coacervates, while the partitioning coefficients of poly-C15 and poly-T15 remained equally high. This confirms our earlier findings that the mixed coacervates contain all NTPs and that base pairing can enhance the uptake of all labeled oligonucleotides. When the salt concentration was increased to 0.16 M, the partitioning coefficient of all labeled oligonucleotides decreased. The partitioning of labeled poly-C15 remained the highest, as expected on the basis of the marginal increase in GTP content of the coacervates and the strength of the G-C base pairing. In summary, we find that partitioning coefficients can be used to identify if an NTP is present in the coacervate droplets at low salt concentration. However, for high salt concentration, especially close to cs*, there is no enhanced partitioning.

Conclusions

We studied the temperature responsiveness of peptide–nucleotide coacervates and found that all NTPs (A, G, C, T, U) can form coacervates when mixed with different cationic peptides (PLys or PArg) and that all of them exhibit UCST behavior. There is a direct relation between the critical salt concentration (cs*) and temperature, which follows from an analysis of the electrostatic and nonelectrostatic contributions to the Flory interaction parameter. cs decreases with increasing temperature for all single NTP coacervate droplets, but there is a significant difference between the NTPs. Their cs* values follow the order G > A > C ≥ U > T, coinciding with their base stacking free energies. Purine NTPs, which have the largest base stacking free energy, are the most stable and require the highest temperatures and salt concentrations to be dissolved. These coacervates also provide the most hydrophobic local environment, as found by hydrophobic dye partitioning experiments.

When several NTPs are mixed, hybrid, homogeneous coacervates can be formed, which exhibit a single well-defined cs* and temperature, intermediate between the values of the single peptide–NTP coacervates. HPLC analysis of the dilute and coacervate phases and partitioning experiments with labeled complementary oligonucleotides proves that the hybrid coacervates contain all NTPs, even after increasing the salt concentration to beyond the critical salt point of some of them. As a result, a mixture of NTPs can be stored together in membrane-free compartments beyond the cs of the weakest bases and released approximately simultaneously by increasing the temperature to above a single and well-defined critical salt point. This could prove useful in cell-free systems, where NTPs are required to feed gene expression and other reconstituted biomolecular processes.

Acknowledgments

This work was supported financially by The Netherlands Organization for Scientific Research (NWO) and a Scholarship from the China Scholarship Council (CSC). The authors thank Merlijn H. I. van Haren (Radboud University) for providing a Matlab routine to determine the critical salt concentration.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.0c10839.

  • Molecular structures, turbidity vs salt concentrations, turbidity increase/decrease plots, microscope images, UCST behavior, temperature dependence of cs*, partitioning images (PDF)

  • Dissolution process of ATP/PLys coacervate droplets (AVI)

  • Formation process of ATP/PLys coacervate droplets (AVI)

Author Contributions

T.L. and E.S. conceived the project and designed the experiments. T.L. carried out experiments and analyzed data. K.K.N. performed HPLC measurements. T.L. and E.S. wrote the manuscript. All authors have discussed the results and approved the final version of the manuscript.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Liquid−Liquid Phase Separation”.

Supplementary Material

jp0c10839_si_001.pdf (3.3MB, pdf)
jp0c10839_si_002.avi (10.5MB, avi)
jp0c10839_si_003.avi (7.5MB, avi)

References

  1. Crowe C. D.; Keating C. D. Liquid-liquid phase separation in artificial cells. Interface Focus 2018, 8 (5), 20180032. 10.1098/rsfs.2018.0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Banani S. F.; Lee H. O.; Hyman A. A.; Rosen M. K. Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 2017, 18 (5), 285–298. 10.1038/nrm.2017.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bracha D.; Walls M. T.; Brangwynne C. P. Probing and engineering liquid-phase organelles. Nat. Biotechnol. 2019, 37 (12), 1435–1445. 10.1038/s41587-019-0341-6. [DOI] [PubMed] [Google Scholar]
  4. Astoricchio E.; Alfano C.; Rajendran L.; Temussi P. A.; Pastore A. The Wide World of Coacervates: From the Sea to Neurodegeneration. Trends Biochem. Sci. 2020, 45 (8), 706–717. 10.1016/j.tibs.2020.04.006. [DOI] [PubMed] [Google Scholar]
  5. Perry S. L. Phase separation: Bridging polymer physics and biology. Curr. Opin. Colloid Interface Sci. 2019, 39, 86–97. 10.1016/j.cocis.2019.01.007. [DOI] [Google Scholar]
  6. Nakashima K. K.; Vibhute M. A.; Spruijt E. Biomolecular Chemistry in Liquid Phase Separated Compartments. Front Mol. Biosci 2019, 6, 21. 10.3389/fmolb.2019.00021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Dignon G. L.; Zheng W.; Kim Y. C.; Mittal J. Temperature-Controlled Liquid-Liquid Phase Separation of Disordered Proteins. ACS Cent. Sci. 2019, 5 (5), 821–830. 10.1021/acscentsci.9b00102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Dignon G. L.; Best R. B.; Mittal J. Biomolecular Phase Separation: From Molecular Driving Forces to Macroscopic Properties. Annu. Rev. Phys. Chem. 2020, 71, 53–75. 10.1146/annurev-physchem-071819-113553. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Jing H.; Bai Q.; Lin Y.; Chang H.; Yin D.; Liang D. Fission and Internal Fusion of Protocell with Membraneless “Organelles” Formed by Liquid-Liquid Phase Separation. Langmuir 2020, 36 (27), 8017–8026. 10.1021/acs.langmuir.0c01864. [DOI] [PubMed] [Google Scholar]
  10. Fanalista F.; Deshpande S.; Lau A.; Pawlik G.; Dekker C. FtsZ-Induced Shape Transformation of Coacervates. Advanced Biosystems 2018, 2 (9), 1800136. 10.1002/adbi.201800136. [DOI] [Google Scholar]
  11. Frankel E. A.; Bevilacqua P. C.; Keating C. D. Polyamine/Nucleotide Coacervates Provide Strong Compartmentalization of Mg(2)(+), Nucleotides, and RNA. Langmuir 2016, 32 (8), 2041–9. 10.1021/acs.langmuir.5b04462. [DOI] [PubMed] [Google Scholar]
  12. Mitrea D. M.; Chandra B.; Ferrolino M. C.; Gibbs E. B.; Tolbert M.; White M. R.; Kriwacki R. W. Methods for Physical Characterization of Phase-Separated Bodies and Membrane-less Organelles. J. Mol. Biol. 2018, 430 (23), 4773–4805. 10.1016/j.jmb.2018.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cakmak F. P.; Choi S.; Meyer M. O.; Bevilacqua P. C.; Keating C. D. Prebiotically-relevant low polyion multivalency can improve functionality of membraneless compartments. Nat. Commun. 2020, 11 (1), 5949. 10.1038/s41467-020-19775-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Jia T. Z.; Hentrich C.; Szostak J. W. Rapid RNA exchange in aqueous two-phase system and coacervate droplets. Origins Life Evol. Biospheres 2014, 44 (1), 1–12. 10.1007/s11084-014-9355-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yewdall N. A.; André A. A. M.; Lu T.; Spruijt E. Coacervates as models of membraneless organelles. Curr. Opin. Colloid Interface Sci. 2021, 52, 101416. 10.1016/j.cocis.2020.101416. [DOI] [Google Scholar]
  16. Koga S.; Williams D. S.; Perriman A. W.; Mann S. Peptide-nucleotide microdroplets as a step towards a membrane-free protocell model. Nat. Chem. 2011, 3 (9), 720–4. 10.1038/nchem.1110. [DOI] [PubMed] [Google Scholar]
  17. Tang T. Y. D.; Antognozzi M.; Vicary J. A.; Perriman A. W.; Mann S. Small-molecule uptake in membrane-free peptide/nucleotide protocells. Soft Matter 2013, 9 (31), 7647. 10.1039/c3sm50726b. [DOI] [Google Scholar]
  18. Shakya A.; King J. T. DNA Local-Flexibility-Dependent Assembly of Phase-Separated Liquid Droplets. Biophys. J. 2018, 115 (10), 1840–1847. 10.1016/j.bpj.2018.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Love C.; Steinkuhler J.; Gonzales D. T.; Yandrapalli N.; Robinson T.; Dimova R.; Tang T. D. Reversible pH-Responsive Coacervate Formation in Lipid Vesicles Activates Dormant Enzymatic Reactions. Angew. Chem., Int. Ed. 2020, 59 (15), 5950–5957. 10.1002/anie.201914893. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Last M. G. F.; Deshpande S.; Dekker C. pH-Controlled Coacervate-Membrane Interactions within Liposomes. ACS Nano 2020, 14 (4), 4487–4498. 10.1021/acsnano.9b10167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Nakashima K. K.; Baaij J. F.; Spruijt E. Reversible generation of coacervate droplets in an enzymatic network. Soft Matter 2018, 14 (3), 361–367. 10.1039/C7SM01897E. [DOI] [PubMed] [Google Scholar]
  22. Drobot B.; Iglesias-Artola J. M.; Le Vay K.; Mayr V.; Kar M.; Kreysing M.; Mutschler H.; Tang T. D. Compartmentalised RNA catalysis in membrane-free coacervate protocells. Nat. Commun. 2018, 9 (1), 3643. 10.1038/s41467-018-06072-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Poudyal R. R.; Guth-Metzler R. M.; Veenis A. J.; Frankel E. A.; Keating C. D.; Bevilacqua P. C. Template-directed RNA polymerization and enhanced ribozyme catalysis inside membraneless compartments formed by coacervates. Nat. Commun. 2019, 10 (1), 490. 10.1038/s41467-019-08353-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Altenburg W. J.; Yewdall N. A.; Vervoort D. F. M.; van Stevendaal M.; Mason A. F.; van Hest J. C. M. Programmed spatial organization of biomacromolecules into discrete, coacervate-based protocells. Nat. Commun. 2020, 11 (1), 6282. 10.1038/s41467-020-20124-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Te Brinke E.; Groen J.; Herrmann A.; Heus H. A.; Rivas G.; Spruijt E.; Huck W. T. S. Dissipative adaptation in driven self-assembly leading to self-dividing fibrils. Nat. Nanotechnol. 2018, 13 (9), 849–855. 10.1038/s41565-018-0192-1. [DOI] [PubMed] [Google Scholar]
  26. McCall P. M.; Srivastava S.; Perry S. L.; Kovar D. R.; Gardel M. L.; Tirrell M. V. Partitioning and Enhanced Self-Assembly of Actin in Polypeptide Coacervates. Biophys. J. 2018, 114 (7), 1636–1645. 10.1016/j.bpj.2018.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Dzieciol A. J.; Mann S. Designs for life: protocell models in the laboratory. Chem. Soc. Rev. 2012, 41 (1), 79–85. 10.1039/C1CS15211D. [DOI] [PubMed] [Google Scholar]
  28. Mast C. B.; Schink S.; Gerland U.; Braun D. Escalation of polymerization in a thermal gradient. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (20), 8030–8035. 10.1073/pnas.1303222110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Williams D. S.; Koga S.; Hak C. R. C.; Majrekar A.; Patil A. J.; Perriman A. W.; Mann S. Polymer/nucleotide droplets as bio-inspired functional micro-compartments. Soft Matter 2012, 8 (22), 6004. 10.1039/c2sm25184a. [DOI] [Google Scholar]
  30. Aumiller W. M. Jr.; Pir Cakmak F.; Davis B. W.; Keating C. D. RNA-Based Coacervates as a Model for Membraneless Organelles: Formation, Properties, and Interfacial Liposome Assembly. Langmuir 2016, 32 (39), 10042–10053. 10.1021/acs.langmuir.6b02499. [DOI] [PubMed] [Google Scholar]
  31. Poudyal R. R.; Pir Cakmak F.; Keating C. D.; Bevilacqua P. C. Physical Principles and Extant Biology Reveal Roles for RNA-Containing Membraneless Compartments in Origins of Life Chemistry. Biochemistry 2018, 57 (17), 2509–2519. 10.1021/acs.biochem.8b00081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Nuhn H.; Klok H.-A. Secondary Structure Formation and LCST Behavior of Short Elastin-Like Peptides. Biomacromolecules 2008, 9 (10), 2755–2763. 10.1021/bm800784y. [DOI] [PubMed] [Google Scholar]
  33. Tang J. D.; Caliari S. R.; Lampe K. J. Temperature-Dependent Complex Coacervation of Engineered Elastin-like Polypeptide and Hyaluronic Acid Polyelectrolytes. Biomacromolecules 2018, 19 (10), 3925–3935. 10.1021/acs.biomac.8b00837. [DOI] [PubMed] [Google Scholar]
  34. Kim H.; Jeon B. J.; Kim S.; Jho Y.; Hwang D. S. Upper Critical Solution Temperature (UCST) Behavior of Coacervate of Cationic Protamine and Multivalent Anions. Polymers (Basel, Switz.) 2019, 11 (4), 691. 10.3390/polym11040691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Quiroz F. G.; Chilkoti A. Sequence heuristics to encode phase behaviour in intrinsically disordered protein polymers. Nat. Mater. 2015, 14 (11), 1164–71. 10.1038/nmat4418. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Dzuricky M.; Rogers B. A.; Shahid A.; Cremer P. S.; Chilkoti A. De novo engineering of intracellular condensates using artificial disordered proteins. Nat. Chem. 2020, 12 (9), 814–825. 10.1038/s41557-020-0511-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Breslauer K. J.; Frank R.; Blocker H.; Marky L. A. Predicting DNA duplex stability from the base sequence. Proc. Natl. Acad. Sci. U. S. A. 1986, 83, 3746–3750. 10.1073/pnas.83.11.3746. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Kutyavin I. V.; Lokhov S. G.; Afonina I. A.; Dempcy R.; Gall A. A.; Gorn V. V.; Lukhtanov E.; Metcalf M.; Mills A.; Reed M. W.; Sanders S.; Shishkina I.; Vermeulen N. M. J. Reduced aggregation and improved specificity of G-rich oligodeoxyribonucleotides containing pyrazolo[3,4-d]pyrimidine guanine bases. Nucleic Acids Res. 2002, 30 (22), 4952–4959. 10.1093/nar/gkf631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nakashima K. K.; André A. A. M.; Spruijt E. Enzymatic control over coacervation. Methods Enzymol. 2021, 646, 353–389. 10.1016/bs.mie.2020.06.007. [DOI] [PubMed] [Google Scholar]
  40. Wienken C. J.; Baaske P.; Duhr S.; Braun D. Thermophoretic melting curves quantify the conformation and stability of RNA and DNA. Nucleic Acids Res. 2011, 39 (8), e52 10.1093/nar/gkr035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Brown R. F.; Andrews C. T.; Elcock A. H. Correction to Stacking Free Energies of All DNA and RNA Nucleoside Pairs and Dinucleoside-Monophosphates Computed Using Recently Revised AMBER Parameters and Compared with Experiment. J. Chem. Theory Comput. 2018, 14 (12), 6742–6743. 10.1021/acs.jctc.8b00594. [DOI] [PubMed] [Google Scholar]
  42. Brangwynne C. P.; Tompa P.; Pappu R. V. Polymer physics of intracellular phase transitions. Nat. Phys. 2015, 11 (11), 899–904. 10.1038/nphys3532. [DOI] [Google Scholar]
  43. Brady W. J.; Wills J. A.; Jost J. T.; Tucker J. A.; Van Bavel J. J. Emotion shapes the diffusion of moralized content in social networks. Proc. Natl. Acad. Sci. U. S. A. 2017, 114 (28), 7313–7318. 10.1073/pnas.1618923114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Martin E. W.; Holehouse A. S.; Peran I.; Farag M.; Incicco J. J.; Bremer A.; Grace C. R.; Soranno A.; Pappu R. V.; Mittag T. Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science 2020, 367 (6478), 694–699. 10.1126/science.aaw8653. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Freed K. F.; Bawendi M. G. Lattice theories of polymeric fluids. J. Phys. Chem. 1989, 93 (6), 2194–2203. 10.1021/j100343a006. [DOI] [Google Scholar]
  46. Lu T.; Spruijt E. Multiphase Complex Coacervate Droplets. J. Am. Chem. Soc. 2020, 142 (6), 2905–2914. 10.1021/jacs.9b11468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Spruijt E.; Westphal A. H.; Borst J. W.; Cohen Stuart M. A.; van der Gucht J. Binodal Compositions of Polyelectrolyte Complexes. Macromolecules 2010, 43 (15), 6476–6484. 10.1021/ma101031t. [DOI] [Google Scholar]
  48. Sing C. E.; Perry S. L. Recent progress in the science of complex coacervation. Soft Matter 2020, 16 (12), 2885–2914. 10.1039/D0SM00001A. [DOI] [PubMed] [Google Scholar]
  49. Rubinstein M.; Colby R. H.. Polymer Physics; Oxford University Press, 2003; pp 140–168. [Google Scholar]
  50. Malmberg C. G.; Maryott A. A. Dielectric Constant of Water from 0° to 100 °C. J. Res. Natl. Bur. Stand. 1956, 56 (1), 2641. [Google Scholar]
  51. Tielrooij K.-J.; Hunger J.; Buchner R.; Bonn M.; Bakker H. J. Influence of Concentration and Temperature on the Dynamics of Water in the Hydrophobic Hydration Shell of Tetramethylurea. J. Am. Chem. Soc. 2010, 132 (44), 15671–15678. 10.1021/ja106273w. [DOI] [PubMed] [Google Scholar]
  52. Brown R. F.; Andrews C. T.; Elcock A. H. Stacking Free Energies of All DNA and RNA Nucleoside Pairs and Dinucleoside-Monophosphates Computed Using Recently Revised AMBER Parameters and Compared with Experiment. J. Chem. Theory Comput. 2015, 11 (5), 2315–28. 10.1021/ct501170h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Mak C. H. Theoretical Model for Solvent-Induced Base Stacking Interactions in Solvent-Free DNA Simulations. J. Phys. Chem. B 2019, 123 (9), 1939–1949. 10.1021/acs.jpcb.8b10848. [DOI] [PubMed] [Google Scholar]
  54. Guckian K. M.; Schweitzer B. A.; Ren R. X.-F.; Sheils C. J.; Tahmassebi D. C.; Kool E. T. Factors Contributing to Aromatic Stacking in Water: Evaluation in the Context of DNA. J. Am. Chem. Soc. 2000, 122 (10), 2213–2222. 10.1021/ja9934854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Mak C. H. Unraveling Base Stacking Driving Forces in DNA. J. Phys. Chem. B 2016, 120 (26), 6010–20. 10.1021/acs.jpcb.6b01934. [DOI] [PubMed] [Google Scholar]
  56. Wheeler R. J.; Hyman A. A. Controlling compartmentalization by non-membrane-bound organelles. Philos. Trans. R. Soc. B 2018, 373. 10.1098/rstb.2017.0193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. McHedlov-Petrossyan N. O.; Cheipesh T. A.; Vodolazkaya N. A. Acid-base dissociation and tautomerism of two aminofluorescein dyes in solution. J. Mol. Liq. 2017, 225, 696–705. 10.1016/j.molliq.2016.10.121. [DOI] [Google Scholar]
  58. Deng N. N. Complex coacervates as artificial membraneless organelles and protocells. Biomicrofluidics 2020, 14 (5), 051301. 10.1063/5.0023678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Simon J. R.; Eghtesadi S. A.; Dzuricky M.; You L.; Chilkoti A. Engineered Ribonucleoprotein Granules Inhibit Translation in Protocells. Mol. Cell 2019, 75 (1), 66–75. 10.1016/j.molcel.2019.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Sokolova E.; Spruijt E.; Hansen M. M. K.; Dubuc E.; Groen J.; Chokkalingam V.; Piruska A.; Heus H. A.; Huck W. T. S. Enhanced transcription rates in membrane-free protocells formed by coacervation of cell lysate. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (29), 11692–11697. 10.1073/pnas.1222321110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Vieregg J. R.; Lueckheide M.; Marciel A. B.; Leon L.; Bologna A. J.; Rivera J. R.; Tirrell M. V. Oligonucleotide-Peptide Complexes: Phase Control by Hybridization. J. Am. Chem. Soc. 2018, 140 (5), 1632–1638. 10.1021/jacs.7b03567. [DOI] [PubMed] [Google Scholar]
  62. Beneyton T.; Love C.; Girault M.; Tang T. Y. D.; Baret J. C. High-Throughput Synthesis and Screening of Functional Coacervates Using Microfluidics. ChemSystemsChem. 2020, 2 (6), e2000022. 10.1002/syst.202000022. [DOI] [Google Scholar]
  63. Aumiller W. M. Jr.; Keating C. D. Phosphorylation-mediated RNA/peptide complex coacervation as a model for intracellular liquid organelles. Nat. Chem. 2016, 8 (2), 129–37. 10.1038/nchem.2414. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp0c10839_si_001.pdf (3.3MB, pdf)
jp0c10839_si_002.avi (10.5MB, avi)
jp0c10839_si_003.avi (7.5MB, avi)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES