Promises and Pitfalls of Latent Variable Approaches to Understanding Psychopathology: Reply to Burke and Johnston, Eid, Junghänel and colleagues, and Willoughby

Abstract

The commentaries by Burke and Johnston (this issue), Eid (this issue), Junghänel et al. (this issue), and Willoughby (this issue) on Burns et al. (this issue) provide useful context for comparing three latent variable modeling approaches to understanding psychopathology—the correlated first-order syndrome-specific factors model, the bifactor S – 1 model, and the symmetrical bifactor model. The correlated first-order syndrome-specific factors model has proven useful in constructing explanatory models of psychopathology. The bifactor S – 1 model is also useful for examining the latent structure of psychopathology, especially in contexts with clear theoretical predictions. Joint use of correlated first-order syndrome-specific model and bifactor S – 1 model provides leverage for explaining psychopathology, and both models can also guide individual clinical assessment. In this reply, we further clarify reasons why the symmetrical bifactor model should not be used to study the latent structure of psychopathology and also discuss a restricted bifactor S – 1 model that is equivalent to the first-order syndrome-specific factors model.

Latent variable models play an important role in understanding psychopathology. Beginning with early work in the mid-1960s to the present (Willoughby, this issue), the correlated first-order syndrome-specific factors model has been instrumental in explanations of psychopathology. This latent variable model has been used countless times to evaluate the internal validity of dimensions of psychopathology. Internal validity occurs with convergent and discriminant validity of symptoms and syndromes within and across methods, sources, occasions, and age groups.

It is a mistake, however, to consider a latent variable as a cause of covariation among symptoms in a syndrome (Preszler & Burns, 2019). Rather, latent variables are descriptive representations of common variance across sets of symptoms; additional research is required to establish causes and specify external correlates of a latent syndrome. Establishing causal linkages across levels of analyses (e.g., genetic, neural, environmental influences on latent symptom dimensions) is, however, a complex endeavor (Beauchaine & Hinshaw, in press). With this context in mind, we discuss the four commentaries to Burns et al. (this issue).

Commentaries

As Eid (this issue) elegantly describes, the correlated first-order syndrome-specific factors model (Figure 1A) and bifactor S – 1 model (Figure 1B) are both important in studies of psychopathology. First, the correlated first-order syndrome-specific factors model is essential for developing measures of psychopathology. Second, this model is essential for establishing convergent and discriminant validity of scores from such measures. Third, this model is used in many studies to determine external correlates of latent symptom dimensions. Thus, the correlated factors model has a clear role in descriptive and explanatory research on psychopathology.

Figure 1.

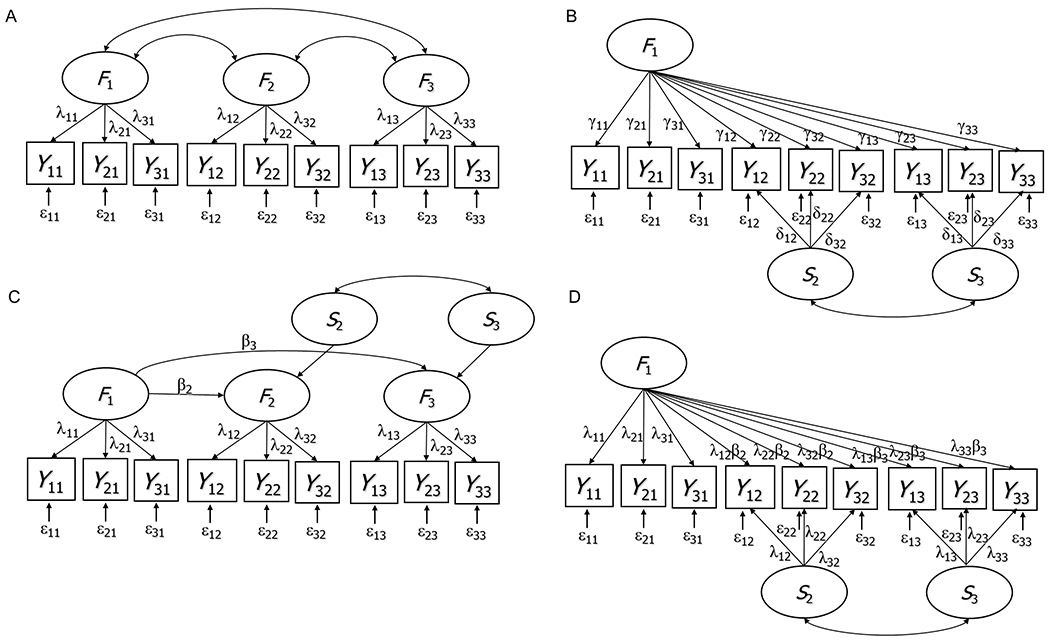
Confirmatory factor models for multi-facet data. Y_if: ith observed variable or symptom pertaining to facet (or syndrome) f. F_f: true score variable (latent factor) pertaining to facet f. S_f: specific (residual) factor pertaining to facet f. λ_if, γ_if, δ_if: factor loadings. β_f: latent regression slope coefficient. A: correlated first-order factors model. B: Standard bifactor S – 1 model. C: Reformulation of the correlated first-order factors model into a latent regression model. D: Reformulation of the latent regression model into a restricted bifactor S – 1 model. Models A, C, and D are equivalent. In Models B, C, and D, Facet 1 serves as reference. Note that in Model D, the reference factor loadings of the non-reference indicators are constrained to equal the product λ_if ∙ β_f.

After establishing validity of syndromes with the correlated factors model, the bifactor S – 1 model can be used for more theory-driven studies of the structure of psychopathology (Eid, this issue; Heinrich et al. 2018). Joint use of both models is not to determine the better model, but rather to provide a richer context for understanding specific predictions from the bifactor S – 1 model. As also mentioned by Eid (this issue), the first-order correlated factors model and a restricted version of the bifactor S – 1 model can be formulated as equivalent models (see our discussion below). Eid’s guidelines for use of both models should prove useful for research and clinical (individual assessment) activities.

Junghänel and colleagues (this issue) replicate our findings in the use of the bifactor S – 1 model with attention-deficit/hyperactivity disorder (ADHD)/oppositional defiant disorder (ODD) symptoms among children and adolescents with ADHD/ODD diagnoses. It was encouraging to see such consistent findings across the studies. Such similar results speak well for use of psychometrically sound models to advance knowledge of psychopathology.

Burke and Johnston (this issue) and Willoughby (this issue), however, raise important issues about the symmetrical bifactor model and bifactor S – 1 model. Our commentary addresses these issues through discussion of six overlapping questions.

(1) Does the bifactor S – 1 model result in overfitting in a manner similar to the symmetrical bifactor model? The symmetrical bifactor model frequently shows better model fit than the correlated first-order factors model and has therefore been seen as the “preferred” model. Burke and Johnston (this issue) note that superior fit of the symmetrical bifactor model may in fact reflect overfitting (estimating more, unnecessary parameters). They raise the important question of whether the bifactor S – 1 model is similarly prone to overfitting.

It is true that the standard version of the bifactor S – 1 model estimates more parameters than the correlated first-order factors model (more loading parameters). As shown in Figure 1, for example, for a design with three facets and three indicators (observed variables such as items or specific symptoms), the correlated first-order factors model (Figure 1A) estimates 3 × 3 = 9 standardized factor loadings (λ). For the same design, the bifactor S – 1 model (Figure 1B) estimates 3 × 3 = 9 reference factor loadings γ (all 9 variables load onto the reference factor) plus 2 × 3 = 6 specific factor loadings δ (only the indicators pertaining to the two non-reference facets have specific factor loadings). Therefore, the standard bifactor S – 1 model estimates more loading parameters and may show better fit to the correlated factors model for a given set of data.

For cases in which overfitting is a concern, an alternative restricted bifactor S – 1 model can be used (Figure 1C and 1D) that has the same number of parameters and is equivalent to the correlated first-order factors model. To define this restricted bifactor S – 1 model, the correlated first-order factors model is used as a starting point. Instead of estimating the three correlations between the first-order factors F_f as shown in Figure 1A, the non-reference factors (here: F₂ and F₃) are regressed on the reference factor (here: F₁) using linear regression analysis (Figure 1C). Residuals of these regressions represent specific factors S_f. Specific factors in the S – 1 approach thus have very clear meaning: They represent variance specific to Facet f that cannot be linearly predicted from the reference facet.

In this model, all specific factors are allowed to correlate. The example shown in Figure 1C is equivalent to the model in Figure 1A. The structural (latent variable) model in Figure 1C has the same number of parameters as the structural model in Figure 1A. Instead of estimating three latent correlations, we now estimate two regression slope coefficients (β_f) and one latent residual correlation between the two specific factors S₁ and S₂.

A mathematical reformulation of this latent regression model yields the equivalent restricted bifactor S – 1 model shown in Figure 1D.¹ In this model, indicators pertaining to the reference facet (f = 1) have the exact same loadings (λ) as in the correlated first-order factors model (Figure 1A). Thus, the general reference factor in the restricted bifactor S – 1 model is identical to the factor F₁ in the correlated first-order factors model. General reference factor loading parameters of the non-reference indicators are constrained to equal the products of the relevant λ and β parameters. The number of independent loading parameters in this model is 11 (9 independent λ and 2 independent β parameters). In addition, there is only 1 latent correlation (between S₁ and S₂) rather than 3 latent correlations as in the correlated first-order factors model (which estimates correlations between all three F_f factors). Therefore, the model in Figure 1D has the same total number of parameters as the correlated first-order factors model in Figure 1A.

For a given set of data, the restricted bifactor S – 1 model yields the exact same fit as the correlated first-order factors model and thus there is no overfitting relative to the correlated first-order factors model. A researcher can thus use the restricted bifactor S – 1 model if there is a concern with overfitting with the bifactor S – 1 model. The conceptual meaning of the general reference and specific factors in the restricted bifactor S – 1 model is the same as in the bifactor S – 1 model (Geiser, Eid, & Nussbeck, 2008).

Appendix A shows Mplus code, global fit indices, factor loadings, and factor variances/correlations for the four models with our data. Figure 1A, 1C, and 1D are shown to be equivalent models. These results also show the meaning of the general reference and specific factors is the same across the bifactor S – 1 and restricted bifactor S -1 models. ADHD-HI symptom loadings are the same across the four models as well.

(2) Does selection of a different general reference factor in the bifactor S – 1 model change findings? Burke and Johnston (this issue) also raise the important question of whether selection of a different reference facet changes the interpretation of results from the bifactor S – 1 approach. The answer is yes, (and this change is expected). To explain, we use an analogy to regression analysis with dummy-coded nominal independent variables. In the same way as interpretation of regression coefficients (intercepts and slopes) changes when a different reference group is selected in dummy coding, interpretation of reference and specific factors changes in the S – 1 approach when a different symptom group or facet is selected as reference. This can be seen most easily from Figures 1C and 1D, which depict the restricted bifactor S – 1 model. When a different first-order factor (e.g., F₂ instead of F₁) is selected as reference and the remaining factors are regressed on this factor, the meaning of the general reference factor changes to equal the meaning of the different first-order factor (e.g., F₂). It is therefore important to carefully consider a priori which facet should serve as reference. This choice should be based on theoretical grounds and/or ease of interpretation.

Note that when using the restricted bifactor S – 1 approach, overall model fit remains the same regardless of which facet (F₁, F₂, or F₃) is used as reference facet (Geiser et al., 2008). This is again analogous to dummy coding in regression analysis where the overall R² value is unaffected by the choice of the reference category in dummy coding.

(3) Why does the general factor in the symmetrical bifactor model change its meaning from a general to a specific factor when one specific factor collapses or when one or more indicators have specific factor loadings of zero? Willoughby (this issue) questioned one of our central arguments—that is, the meaning of the general factor in the symmetrical bifactor model changes from a general to a specific factor when one specific factor collapses or when one or more indicators have zero loadings on their specific factors. Specifically, Willoughby (this issue) commented that “Burns and colleagues (…) maintain that [in this case] the general factor should be interpreted as the HI factor. I do not understand how this can be true.” (p. xx). Willoughby argued that all 18 items still contribute to the general factor given that they all load onto this factor. We believe that this confusion is shared by many researchers. We therefore elaborate in more detail immediately below.

To understand why the general factor turns into a specific factor under the conditions described above (factor collapse or non-significant individual specific factor loadings), reconsider our discussion of the restricted bifactor S – 1 model. Figures 1C and 1D show that the restricted bifactor S – 1 model is a direct mathematical reformulation of the correlated first-order factors model (Figure 1A). As we explained above, the models in Figures 1A, 1C, and 1D are equivalent and will always fit equally well for a given data set (Appendix A).

Most researchers would agree that the factors in the correlated first-order factors model (Figure 1A) are facet-specific factors (e.g., HI, IN, and ODD factors). Reformulation of this model into an equivalent restricted bifactor S – 1 model (Figures 1C and 1D) shows us that the reference factor F₁ remains the exact same facet-specific factor (e.g., an HI factor), even though all items now load onto this reference factor as shown in Figure 1D. In other words, the fact that all items load onto a factor does not necessarily make this factor a general factor. The same issue occurs when a specific factor collapses empirically in the symmetrical bifactor model, leading to a reduction of this model to an S – 1 model and a change in the interpretation of the general factor to a facet-specific factor.² Table S2 shows the ADHD-HI symptom loadings remain the same across the four models (1A, 1B, 1C, and 1D).

(4) Can the bifactor S – 1 model be used to test additional hypotheses about the structure of ADHD and ODD symptoms? We describe one additional theoretical-driven hypothetical study to address this question. Other theoretical-driven studies are also possible; though space only allows one example.

ODD symptoms are considered to involve separate irritability and defiant factors (Burke & Johnston, this issue). To date, the correlated first-order syndrome-specific factors model and the symmetrical bifactor model have been used to evaluate the internal and external validity of the two ODD factors (Burke and Johnston, this issue). The bifactor S – 1 model could be used to further evaluate distinctiveness of the two ODD factors relative to the correlated factors model.

One possibility would be to use the ADHD-HI symptoms to define the general reference factor, with specific ODD irritability and ODD defiant residual factors. Given evidence that ADHD-HI symptoms confer considerable vulnerability to later development of ODD, whereas ADHD-IN symptoms do not (Beauchaine, Zisner, & Sauder, 2017), using the bifactor S – 1 model would allow for examination of true score variance in ODD irritability and ODD defiant factors independent of the general ADHD-HI reference factor as well as discriminant validity of the two ODD residual factors. A developmental psychopathology hypothesis could be that the amount of residual true score variance in the two ODD specific factors (after accounting for shared variance with the general ADHD-HI factor) increases with age. Finally, the model could determine if the two specific ODD residual factors have common and unique external correlates, independent of the general reference factor. Such a model would yield clear, psychometrically sound definitions of the two specific ODD residual factors.

(5) Are problems associated with the symmetrical bifactor model restricted to symptom ratings (item-level data)? Willoughby (this issue) suggest that problematic issues with the symmetrical bifactor model that we highlighted in Burns et al. (this issue) are only an issue for item-level data: “It is important to appreciate that the problems that Burns and colleagues raised with respect to B_Sym [the symmetrical bifactor model] were specific to questions that are focused on the structure of item-level data” (p. xx; emphasis in the original). We disagree as we believe this issue is much more general in nature. It appears to cause problems whenever researchers apply the symmetrical bifactor model to structurally different (as opposed to exchangeable) facets. Heinrich et al. (2018) showed that the same issues occurred in attempts to identify a general factor of depression. Studies of the p factor of psychopathology (e.g., Caspi et al. 2014) typically use scale-level data and are prone to the same issues that we highlighted for ADHD/ODD symptom ratings. For example, Caspi et al. (2014) examined three first-order factors (internalizing, externalizing, thought disorder) and reported a negative specific factor variance in their bifactor model. According to Caspi et al., this indicated that no specific factor could be identified for the thought disorder facet. Caspi et al. subsequently dropped the specific factor for thought disorder from their model. Thus, the general factor became a specific thought disorder factor. The same issues occurred in bifactor applications to summary scores of intelligence facets (Eid et al. 2018) as well as in multitrait-multimethod studies in which structurally different raters (e.g., mothers and teachers) serve as “facets” (Eid et al., 2008).

In summary, problems with the symmetrical bifactor model are not limited to item-level (symptom) data. Similar problems result any time the symmetrical bifactor model is used with structurally different facets or raters. Thus, it does not matter whether the manifest variables are individual symptoms or summary (interval-scale) scores on a symptom dimension such as in p studies—the statistical issues remain the same, and we thus discourage use of the symmetrical bifactor model not just for item-level (symptom) data, but more generally whenever researchers analyze structurally different facets or data from non-interchangeable raters.

(6) Can we obtain a general factor that represents a general propensity to psychopathology as originally intended by users of the symmetrical bifactor approach? Maybe one of the most important criticisms from Willoughby (this issue) concerns an original goal of researchers who apply bifactor models: to identify a general overarching factor that represents “general psychopathology.” As Willoughby correctly points out, such a general factor is not obtained in the S – 1 model unless this general factor is directly measured by a separate set of indicators as proposed by Eid (this issue). Therefore, as mentioned by Willoughby as well as Burke and Johnston (both in this issue), some questions addressed by the S – 1 approach differ from the answers sought with the symmetrical bifactor model.

Although we understand the desire to identify a general psychopathology dimension, we argue that the symmetrical bifactor approach does not hold this promise. This may be a sign that different ways of identifying a “general factor of psychopathology” should be developed and used, and/or that related questions should be asked in different ways. As we show in our original article and explain in more detail in this reply, the originally-intended general psychopathology factor is typically not obtained in empirical applications of the symmetrical bifactor model. As we demonstrate above, the symmetrical bifactor model reduces to an S – 1 model (with a specific factor defining the general factor) when one specific factor collapses or when one or more variables do not load significantly on their specific factors. As we show in Burns et al. (this issue), this happens in the majority of applications to ADHD symptom reports, and so the intended general factor is not actually found as also occurs in p studies (e.g., Caspi et al. 2014).³

Conclusions

Latent variable models remain quite useful—and perhaps essential—to our understanding of psychopathology. The correlated first-order syndrome-specific factors model has proved especially useful for development of measures of psychopathology. This model has also proved useful for identifying external correlates of latent symptom dimensions. These two uses—establishment of internal and external validity—are critical toward explaining rather than describing psychopathology. Individual clinical assessments benefit from this model as well.

Although the symmetrical bifactor model enjoys widespread appeal, this model should not be used to examine the latent structure of psychopathology. Use of this model requires randomly selected and thereby interchangeable facets, whereas symptom dimensions represent structurally different facets. Violation of this assumption usually yields inadmissible/anomalous solutions that often result in the general factor becoming facet- or even symptom-specific. In contrast, the bifactor S – 1 model is fully appropriate to use when examining the latent structure of psychopathology, especially when used with clear theoretical predictions, and in conjunction with the correlated first-order syndrome-specific factors model. Together, the correlated first-order syndrome-specific factors model and the bifactor S – 1 model hold considerable potential to advance our understanding of psychopathology.