Abstract
Since the 1940s, population projections have in most cases been produced using the deterministic cohort component method. However, in 2015, for the first time, in a major advance, the United Nations issued official probabilistic population projections for all countries based on Bayesian hierarchical models for total fertility and life expectancy. The estimates of these models and the resulting projections are conditional on the UN’s official estimates of past values. However, these past values are themselves uncertain, particularly for the majority of the world’s countries that do not have longstanding high-quality vital registration systems, when they rely on surveys and censuses with their own biases and measurement errors. This paper extends the UN model for projecting future total fertility rates to take account of uncertainty about past values. This is done by adding an additional level to the hierarchical model to represent the multiple data sources, in each case estimating their bias and measurement error variance. We assess the method by out-of-sample predictive validation. While the prediction intervals produced by the extant method (which does not account for this source of uncertainty) have somewhat less than nominal coverage, we find that our proposed method achieves closer to nominal coverage. The prediction intervals become wider for countries for which the estimates of past total fertility rates rely heavily on surveys rather than on vital registration data, especially in high fertility countries.
Keywords: Bayesian hierarchical model, Markov chain Monte Carlo, Measurement error, Population projection, Total fertility rate, Vital registration
1. Introduction.
Population projections or forecasts consist of forecasts of future population numbers and also of the components of population change, namely births, deaths and migration, broken down by age and sex, and possibly also by other categories such as race. They are used by governments at all levels (local, regional, state, national and international) for planning and policy decision-making, since knowing the future numbers of people is key to government policy-making. They are also used by the private sector for strategic decisions, and by researchers in the health and social sciences.
The most widely used population projections for many individual countries are produced by their national statistical agency, such as the U.S. Census Bureau in the United States (U.S. Census Bureau, 2017), as well as international organizations, including the UN Population Division or Eurostat. The United Nations publishes projections of population by age and sex, and mortality and fertility rates, as well as estimates of net migration for all countries by five-year age-groups in five-year periods to the year 2100, updated every two years in the UN’s World Population Prospects, whose most recent edition was published in 2017 (United Nations, 2017). The UN’s population projections are widely viewed as the gold-standard and regularly updated projections for all countries (Lutz and Samir, 2010).
Since the 1940s, population projections have in most cases been produced by a deterministic method called the cohort-component method (Cannan, 1895; Whelpton, 1928, 1936; Preston, Heuveline and Guillot, 2000). This is based on the demographic balancing equation, namely
where Population refers to the number at time t, and Births, Deaths, Immigration and Emigration refer to the numbers in the time interval from time t to time t + 1. The cohort-component method uses an age-structured version of this, of which a simple form is
where the subscript a refers to age, and net migration is equal to the number of immigrants minus the number of emigrants. For a full treatment of the method, see (Preston, Heuveline and Guillot, 2000).
This method is simple to implement, but it requires assumptions about future fertility, mortality and migration rates by age and sex. These have typically been produced subjectively by experts, either in-house experts working at the agency producing the projections, or a panel of outside experts assembled by the agency. Uncertainty has commonly been communicated by scenarios; for example the UN traditionally published High, Medium and Low variants, in which the total fertility rates (TFR, definition could be found in Section 2.1) for all countries and all future periods were increased or decreased by half a child per woman. This deterministic approach has been criticized on the grounds that it has no probabilistic basis, and that it can give implausible results over multiple projection periods (Keyfitz, 1981; Stoto, 1983; Lee and Tuljapurkar, 1994); for a review and summary of this literature see the National Research Council report on the topic (Lee and Bulatao, 2000).
Many methods for probabilistic forecasting of future fertility rates have been proposed, including those of (Lee, 1993), (Alders, Keilman and Cruijsen, 2007), (Alho et al., 2006), (Alho, Jensen and Lassila, 2008) and (Booth, Pennec and Hyndman, 2009), in each case either for individual countries or groups of countries, typically in the developed world. However, these methods cannot be easily applied to the UN’s task of producing forecasts for all countries. No fewer than 20 major methods, with 162 variants altogether, were identified and evaluated by (Bohk-Ewald, Li and Myrskylä, 2018), although not all of these were probabilistic. They found that only three probabilistic methods outperformed the simplest method of assuming that future fertility rates would be the same in the future as in the past, namely those of (Myrskylä, Goldstein and Cheng, 2013), (Schmertmann et al., 2014) and (Ševčíková et al., 2016). The latter method is based on the probabilistic methods for projecting the total fertility rate used by the UN.
In 2015, the UN adopted a different method for their official population projections for all countries (United Nations, 2015a). This method was probabilistic and statistically-based, replacing the previous deterministic method, thus responding to the critiques. The UN used Bayesian hierarchical models to produce probabilistic projections of the total fertility rate (Alkema et al., 2011; Raftery, Alkema and Gerland, 2014; Fosdick and Raftery, 2014; Ševčíková, Alkema and Raftery, 2011), and life expectancy (Raftery et al., 2013; Raftery, Lalic and Gerland, 2014), and then simulated trajectories from the resulting predictive distributions, and translated each trajectory into age-specific fertility and mortality rates. These in turn were input into the cohort-component method to yield many possible future population trajectories of all countries (Ševčíková et al., 2016; Ševčíková and Raftery, 2016).
This method indicated that world population was likely to be higher than had previously been thought, reaching 11.2 billion (95% prediction interval 9.5 to 13.2 billion) in 2100, from 7.4 billion now (Gerland et al., 2014; United Nations, 2017). The main reason for this is that fertility in high-fertility countries, many of them in Sub-Saharan Africa, has been declining more slowly than experts had expected, and the statistical approach took this into account more fully than the expert-based assumptions.
The method discussed above takes UN estimates of past and present TFR as the source of data, which is also the standard in other studies, such as (Murray et al., 2018). Although the new UN method takes account of uncertainty more systematically than previous methods, there are still sources of uncertainty that it does not account for. The Bayesian hierarchical model used by the UN is conditional on estimates of present and past population, as well as fertility and mortality rates. In countries with long-established high quality vital registration systems, and hence accurate counts of births and deaths, this is not a large source of uncertainty; this is the case for 80 of the world’s 201 countries, which have at least 30 years of Vital Registration Records according to the World Fertility Database 2015 Version (United Nations, 2015b).
However, the remaining 120 or so countries do not have longstanding high quality vital registration systems, and their fertility and mortality rates are typically estimated from surveys that can be subject to poor coverage in time and space, biases and measurement error. For example, the Demographic and Health Surveys (DHS) are one of the most important and reliable sources of data on fertility rates in countries without good long-term vital registration data (National Population Commission, 2009), but they have suffered from large underestimates of TFR in some countries in Sub-Saharan Africa (Schoumaker, 2010, 2011, 2014; Pullum et al., 2013).
Thus the estimated present and past vital rates and population numbers for these countries are not exact, and the uncertainty about them is not accounted for in the projections. This may lead uncertainty in the projections to be underestimated (Abel et al., 2016). Demographers have developed methods for correcting estimates of TFR for specific forms of bias, such as recall errors, developing indirect estimation methods for this purpose (Brass, 1964, 2015). Bias and uncertainty of past and present estimates were modeled by (Alkema et al., 2012), using multiple data quality indicators, such as the source of the data, the estimation method (e.g. direct or indirect), and recall time for retrospective birth history surveys. But these methods do not account for the uncertainty in total fertility rate projections, and consequently population projections, that is due to uncertainty about past and present values.
In this paper we extend the UN probabilistic projection method to account for uncertainty about past and present total fertility rates, which may be the most important remaining unaccounted source of uncertainty. This is made possible by the recent publication of a new dataset by the UN Population Division that contains not just estimates of past and present fertility rates for all countries, but also the data from the primary data sources on which the estimates are based, including censuses, vital registration systems, partial and sample vital systems, international surveys such as the DHS and the Multiple Indicator Cluster Surveys, or MICS (UNICEF, 2016), and national, regional and local surveys (United Nations, 2015b). We do this by developing a new Bayesian hierarchical model that extends the UN model to account for bias and measurement error in the different information sources.
The article is organized as follows. The data and proposed methodology are described in Section 2. In Section 3 we report the method’s performance using out-of-sample predictive validation. We then provide more detail in Section 4, which is a case study of how the method works for Nigeria, which is one of the most important countries for uncertainty about future world population, because it is the most populous country in Africa, has high fertility, and does not have a long-established high-quality vital registration system. We conclude with a discussion in Section 5.
2. Method.
2.1. Notation.
We restrict our attention to estimation of the TFR of each country. The TFR is a period measure. It is defined as the number of children a woman would bear if she survived to the end of the reproductive interval and at each age she experienced the age-specific fertility rates prevalent in the period to which it refers. It is defined in units of children per woman.
We use the symbol y to denote TFR estimates from different data sources and the symbol f to denote the true (unobserved) TFR. Although the UN Population Division’s estimates of past TFR values do contain error, we assume that they are unbiased, in the sense that the errors do not tend to be systematically in one direction or the other; for discussion of this assumption see (Alkema et al., 2012). These official UN estimates of past TFR values will be denoted by u. All of these parameters will be indexed by country c and time t. Data from different sources y are also indexed by their source, denoted by s. Here, by source we mean the type of data involved, for the given country. For example, one source would be the direct estimates of TFR from the Census, for Nigeria. The bias and measurement error variance of these estimates are denoted by δ and ρ2, respectively. The quantities of interest are the unknown past, present and future TFR, f. We estimate past TFR for the time period [t0, t1], while prediction will be for the period [t1, t2]. In practice in this article, t0 = 1950, t1 = 2015 and t2 = 2100.
The three-phase Bayesian hierarchical model of (Alkema et al., 2011) will be used to model the total fertility rates. For describing the Bayesian hierarchical model, the vector of five country-specific parameters controlling the evolution of total fertility rates of country c is denoted by θc, and the vector of global parameters is denoted by ψ. In constructing the probabilistic projections of TFR for all countries, we are also interested in the country-specific parameters θc.
2.2. Data.
We use the World Fertility Data 2015 (United Nations, 2015b) from the UN Population Division for 201 countries in the world. This database is publicly available and includes estimates of TFR from surveys, censuses and sample or partial vital registration data for countries without high-quality vital registration systems. It includes data available as of November 2015 and covers the time period from 1950 to 2015. These data were used to produce the estimates of past TFR in the United Nations World Population Prospects (WPP) 2015 Revision. These estimates were in turn part of the basis for the UN’s 2015 population projections for all countries.
We use TFR estimates from national and international surveys, indirect estimates and vital registration for all 201 countries to estimate the bias and variance of different data sources. We take the estimates in the WPP 2015 revision as a baseline, assuming that they are unbiased (but not that they are without error). This assumption, also used by (Alkema et al., 2012), is made because the analysts producing past estimates were often aware of sources of bias in datasets and tried to correct for them. While this assumption is not perfect, it seems reasonable to argue that WPP provides the least biased set of estimates available.
To estimate TFR from multiple sources, it is necessary to make some assumption about a baseline unbiased (although not error-free) estimate, and we have used the official UN estimate. An alternative would be to choose one of the individual information sources as unbiased; a possible candidate would be the direct estimates from the DHS surveys. However, these estimates (and estimates from any one source) are not without flaws, and some of them were of poor quality, as discussed by (Alkema et al., 2012) and others. Another possibility would be to use an average of the available estimates, but similar comments apply. The UN analysts used all the available data sources, while being aware of problems with them, and adjusted or downweighted them accordingly in developing their own estimates. The information used by the UN analysts is currently often available only implicitly, through the official UN estimates they produced, and so these estimates seem likely to be of higher quality than the individual estimates.
In the 2015 revision of the WPP, the UN estimated the five-year average TFR, uc,t, for country c in time period (t, t + 5), for each five-year period from 1950 to 2015. The outcome in each five-year period (t, t + 5) is an estimate of the average TFR between July 1 of year t and July 1 of year t + 5, and so is centered at January 1 of year t + 3. This paper constructs trajectories and estimations in five-year intervals, and project TFR up to year 2100 probabilistically according to these estimated trajectories of the past.
2.3. Model.
Three Phase Bayesian Hierarchical Model.
Our methodology builds on that of (Alkema et al. (2011) Page Number 818–824, Raftery, Alkema and Gerland (2014) Page Number 64–65) for fertility transition phase and post-fertility transition phase respectively, and was implemented by (Ševčíková, Alkema and Raftery, 2011). This divides the evolution of TFR in a country into three phases: pre-fertility transition, transition and post-transition, as illustrated in Figure 1.
Fig 1.
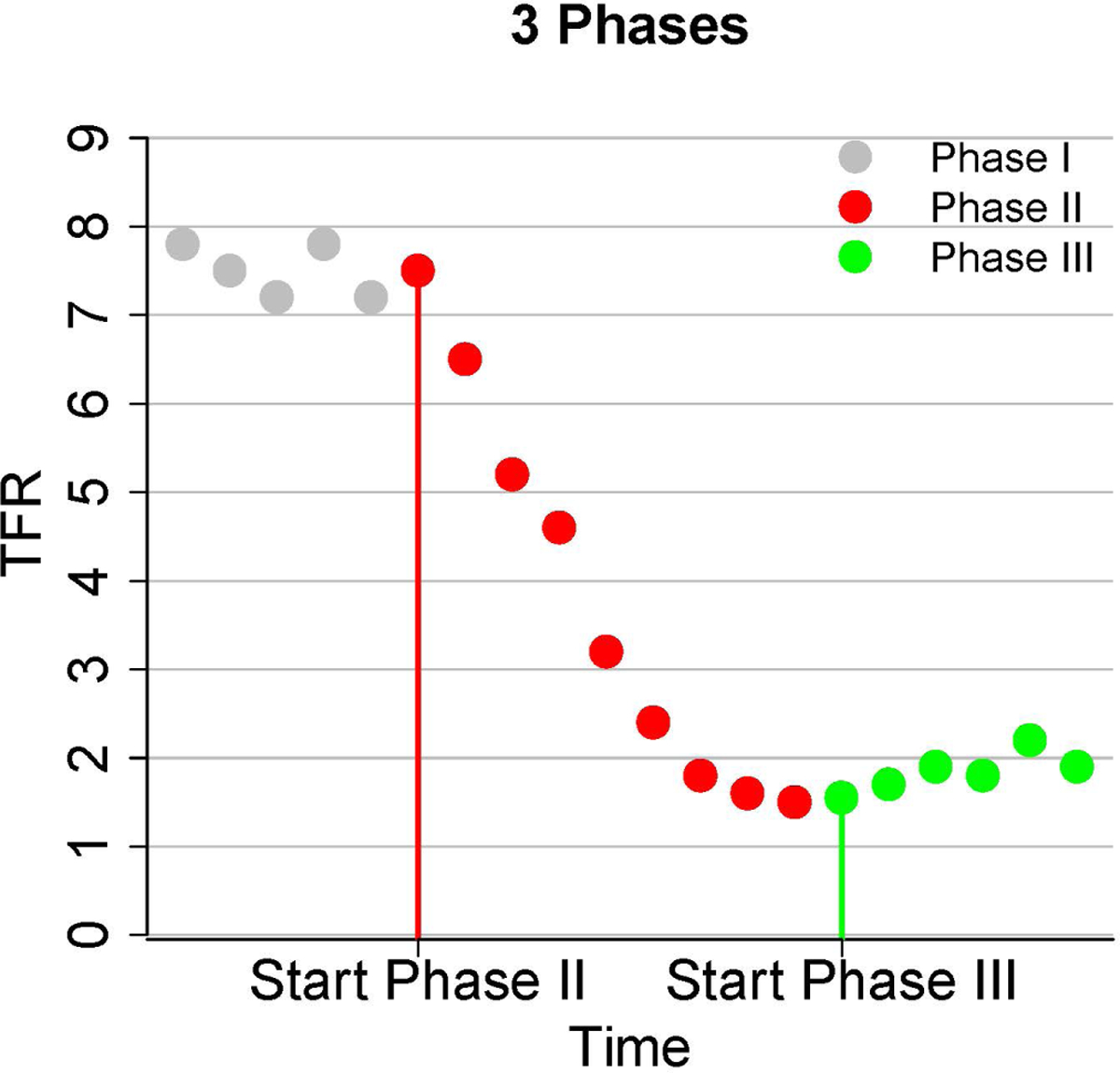
Illustration of the three phases in the typical evolution of fertility in a country: pre-transition high fertility (Phase I; grey), transition from high to low fertility — (Phase II; red), and post-transition fertility fluctuations and recovery (Phase III; green).
During the fertility transition or decline phase (Phase II), the total fertility rate is modeled as a random walk with negative drift, namely
| (2.1) |
where g(·|θc) is the expected five-year decrement in the TFR over the next period, modeled by a double logistic function governed by the country-specific parameter vector θc = (Δc1, Δc2, Δc3, Δc4, dc), and εc,t is random noise around the expected decrement. The double logistic curve we are using is given by
During the post-transition phase (Phase III), the total fertility rate is modeled by a Bayesian Hierarchical Autoregressive Model as:
| (2.2) |
where μc is the long-term mean of the TFR for country c, and εc,t is the random noise similar to that in phase II.
Since all or almost all countries have already started the fertility transition, modeling the TFR during the pre-fertility transition Phase I was not necessary for projection purposes in previous work. However, for constructing probabilistic estimation of past TFR from 1950 to 2015, we do need to model the Phase I data. They are modeled by a random walk model from year 1950 to the start of fertility transition as:
| (2.3) |
The country-specific parameters in all three phases, (θc, μc), follow a world distribution, which is governed by world parameters ψ, and these in turn have a prior distribution. The start and end of the fertility transition (phase II) are defined based on the UN estimates uc,t, by rules given in (Alkema et al., 2011).
Model of Imperfect Data.
The TFR estimates from different data sources yc,t,s are modeled based on the unobserved true value fc,t. Building on (Alkema et al., 2012), we distinguish between the bias and measurement error variance in our model. The estimated TFR values are modeled by a conditional normal distribution as:
| (2.4) |
| (2.5) |
| (2.6) |
The bias and measurement error standard deviations, δc,s and ρc,s, are estimated using data quality indicators, denoted by xc,s. The estimation process is described in the following sections.
Complete Model Layout.
We combine the three-phase Bayesian hierarchical model and imperfect data model into a four-level Bayesian hierarchical model with an additional level for the data sources. Estimation and prediction is then equivalent to obtaining the posterior distribution of the unknown TFR values fc,t in the estimation period [t0, t1] and the prediction period [t1, t2], based on the observed TFR estimates from different data sources.
The observed estimates of TFR can be measured for any time between t0 and t1. However, we seek estimates of the average over five-year periods. We approximate the true TFR at any time by assuming that the TFR evolves linearly between the centers of any two successive five-year intervals. This is a reasonable assumption because most demographic quantities, including the TFR, typically evolve fairly smoothly over time. Specifically, for any t ∈ [tℓ, tℓ + 5], where tℓ and tℓ + 5 are the centers of two successive five-year periods, we assume that
| (2.7) |
Thus, the overall model is specified as follows:
Thus we model the observed TFR estimates in Level 1, conditional on the true total fertility rates. These are in turn modeled by the extant three-phase BHM in Level 2, conditional on the country-specific parameters. The country-specific parameters are then modeled conditionally on the global parameters in Level 3, which have a prior distribution specified by hyperparameters (Level 4).
Here, g denotes the double logistic function, and h and π denote the conditional and unconditional distributions of the parameters of interest, respectively. The parameter vector θc, with five elements, controls the shape of the double logistic curve, and the hyper parameter ψ, with ten elements, specifies the mean and variance of the conditional normal distribution of some transformation of θc. The detailed functional form of the prior distribution π(·) and the conditional distribution h(·|ψ) can be found in the Supplementary Material, and are the same as specified by (Alkema et al., 2011).
Inference is based on the joint posterior distribution of (fc,t, θc). The model is summarized graphically in Figure 2.
Fig 2.
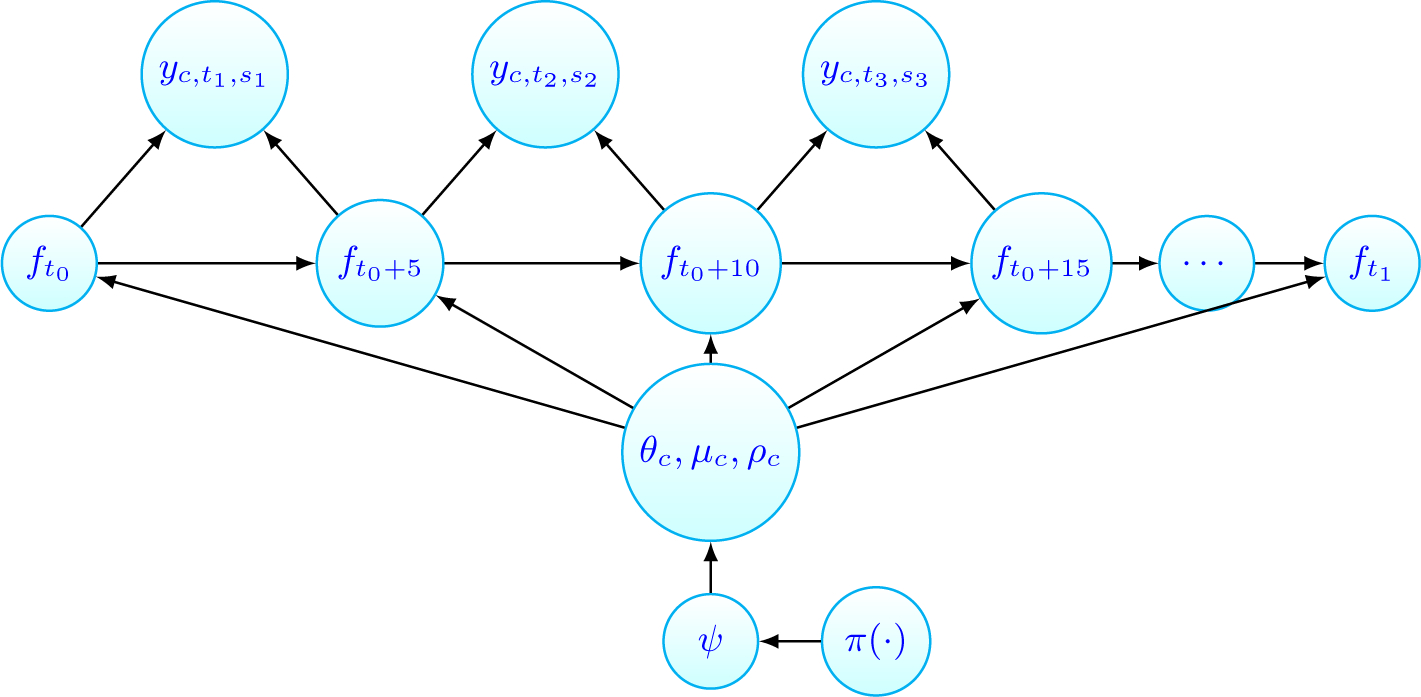
Model Specification: yc,t,s are the observed TFR, fc,t are the unknown TFR values, θc are the country-specific parameters and ψ are the global parameters. Detailed explanation of these parameters can be found in this section previously and the complete specification can be found also in the supplementary materials Section 1. Here, t1, t2, t3 are representative of some arbitrary time points between [t0, t0 + 5], [t0 + 5, t0 + 10], [t0 + 10, t0 + 15] respectively.
2.4. Estimation.
Estimation of Bias and Measurement Error Variance.
The bias δc,s, and measurement error variance, , of the observed TFR estimates are estimated in a first stage, as input to the Bayesian hierarchical model, building on the method of (Alkema et al., 2012).
We first estimate the bias of TFR. As we discussed in Section 2.3, the UN estimates will be treated as unbiased but not error-free, providing a baseline reference. Then, for each observation yc,t,s, we have
Thus we can use the difference between the observed TFR values and the UN estimates, (yc,t,s−uc,t), as samples for our estimation of the bias and measurement error variance of each source. The parameters β are estimated by linear regression on data quality indicators xc,s, as in equation (2.5). The estimated biases are then equal to the fitted values .
In this study, we used two data quality indicators: data source, and estimating method. Other potential data quality indicators were available, but we found that using them would not have improved the performance of the method.
We estimate the source-specific measurement error variance of the TFR estimates by regression on the data quality covariates xc,s of the plug-in estimate , where zc,t,s is defined as the estimation error of the observed TFR estimates yc,t,s, which is the difference between the TFR estimates yc,t,s and the true TFR fc,t, namely (yc,t,s − fc,t). Since the true TFR is unknown, the unobserved true values fc,t are replaced by the UN estimates of TFR (uc,t) (taken to be unbiased), which means that in practice, zc,t,s is replaced by .
Estimation of the Complete Model:.
Given the estimated bias and measurement error variance , we estimate the Bayesian hierarchical model for TFR using a purpose-built Markov Chain Monte Carlo (MCMC) algorithm coded in R. The roughly 3,600 parameters and unknown TFR values are updated one at a time, using Gibbs steps, Metropolis-Hastings steps or slice sampling (Neal, 2003) for each parameter as appropriate. We monitored convergence by inspecting trace plots and using standard convergence diagnostics (Gelman and Rubin, 1992; Raftery and Lewis, 1996).
We thinned enough for the thinned sample to be roughly independent. In practice, for the final results we ran 3 chains, each of length 12,000 iterations with a burn-in of 2,000, and we thinned the resulting chains by 10, to obtain a final, approximately independent sample of size 3,000 from the posterior distribution. More information about the convergence diagnostics used is provided in the Supplementary Information.
2.5. Prediction of Future TFR.
Unlike the projection process developed by (Alkema et al., 2011) and used by the UN, we have probabilistic rather than point TFR estimates of past rates over the time period [t0, t1]. Thus, instead of just sampling from the posterior trajectories of country-specific parameters obtained from estimation process, we also generate posterior trajectories of past TFR values.
We proceed by repeating the following process many times. We first select a joint sample of model parameters and past and present TFR for all countries from the posterior distribution. Then, given the sampled model parameters and past and present TFR values, we simulate a trajectory of future TFR values, from 2015 to 2100 using the model specified by (2.1) and (2.2). This yields a sample from the joint posterior predictive distribution of future TFR in all countries and time periods considered, taking account of uncertainty about past values.
Our method also differs slightly from the extant method in the way how the end of the fertility transition. at which the model shifts from that for Phase II to that for Phase III, is determined. The current UN method uses deterministic rules based on the UN estimates (Alkema et al., 2011), and does not account for uncertainty about when the fertility transition ended. In our method, we retain the deterministic rules, but apply them separately to each sampled trajectory of past TFR values. Thus our method takes account of uncertainty about when the fertility transition ended in a particular country, and hence which phase the country is in at the end of the estimation period.
3. Validation.
We assess the predictive performance of our model using out-of-sample predictive validation, used for probabilistic forecasts, for example, by (Raftery et al., 2005). We include all countries and regions in our validation exercise.
3.1. Study Design.
The data we have cover the period from 1950 to 2015. We split this into the estimation period, [t0 = 1950, t1 = 2005], and the prediction period, [t1 = 2005, t2 = 2015]. The inputs to our method consist of all TFR estimates from different sources referring to the estimation period.
For the UN estimates used as a reference, we take the values published in the WPP 2008 revision (United Nations, 2008). The UN estimates of the past have been refined since then as more data have become available, but we deliberately do not take advantage of this in our estimation. This makes our validation exercise more analogous to the real prediction task at hand, for which we are using UN estimates in the WPP 2015 revision of past TFR values up to 2015 to predict values past 2015. It can be expected that these estimates of TFR values up to 2015 will become more accurate in the future as data accumulate, but we are not able to take advantage of this at the present time.
We are making probabilistic projections, and so we evaluate not only the point predictions, but also the predictive intervals. Our aim is to account for an important source of uncertainty ignored by the present state of the art method, so the accuracy of the prediction intervals may be even more important than that of the point predictions. If our method is working well, we would expect the current state of the art intervals to have less than nominal coverage, and our method to give coverage closer to nominal. To evaluate our method, we compare our probabilistic projections with those produced by the UN in WPP 2015.
Our out-of-sample validation experiment proceeds as follows.
Choose the subset of the original data set with TFR observed before year 2005 as the training data . We remove those observations before 2005 for those estimates in studies that provide series of estimates ending after 2005. For example, if a study lasts for 20 years and ends in 2008, yielding TFR observations for 1988 to 2008, we remove all observations from this study even though some of the estimates are for years before 2005. This is because these data would typically not have been available in 2005.
Estimate bias and measurement error variance for all the data points with the UN estimates, uc,t from the WPP 2008 revision as the reference. The reason that we use the 2008 revision as the reference instead of the 2015 revision is that UN is estimating historical TFR based only on current data available at the time of the revision. Thus if we were to use WPP 2015 as the reference, we would be using what is effectively future information in the out of sample validation.
Draw a sample from the joint posterior distribution of model parameters and past TFR values for 1950 to 2005, using MCMC.
For each sampled trajectory including the unobserved past TFR values and the model parameters, determine the TFR phase of country c for each time period for this trajectory, and make probabilistic projections for the projection period [2005, 2015].
3.2. Out of Sample Validation Results.
We produce results for all 201 countries using our method. For comparison, we also produce results using the method of (Alkema et al., 2011), which underlies the current UN methodology and does not take account of uncertainty about past TFR values.
We summarize the results in Table 1. This is based on the predictive intervals for each of the 201 countries and for both of the periods [2005, 2010] and [2010, 2015], so that each entry in Table 1 is an average over 201 × 2 = 402 values. For each TFR value to be predicted, we take the predictive median as the point estimate, and we compute the quantile-based 80% and 95% prediction intervals. The table shows the mean absolute error (MAE) of the point estimates (the smaller the better), and the coverage of the prediction intervals (the closer to the nominal value the better). If we split by periods and proportion of left-out UN estimates that fall above or below their 80% and 95% projection intervals, the performance of the new method is summarized in Table 2. (Note that the out of sample performance is different from that in (Alkema et al., 2011) because of the different forecasting horizons and the updated versions of the WPP data set used here for validation.)
Table 1.
Mean Absolute Error and Coverage of Out of Sample TFR Point and Interval Predictions for Original Method (Alkema et al., 2011), and Proposed Method.
| Original Method | Proposed Method | |
|---|---|---|
| Mean Absolute Error | 0.250 | 0.242 |
| Coverage of 80% interval | 64.0% | 77.8% |
| Coverage of 95% interval | 80.1% | 92.1% |
Table 2.
Proportion of Left-Out UN Estimates that Fall Above or Below their 80% and 95% Projection Intervals Split by Period.
| 95% PI | 80% PI | |||||
| Below | Coverage | Above | Below | Coverage | Above | |
| 2005–2010 | 1.0% | 91.7% | 7.3% | 1.0% | 78.1% | 20.9% |
| 2010–2015 | 0.0% | 92.7% | 7.3% | 4.7% | 77.5% | 17.8% |
The proposed method improves the point predictions over the current method, as measured by the MAE, by about 3%. It improves the coverage of the prediction intervals much more substantially. Under the current method, the coverage of the prediction intervals is somewhat below the nominal level, suggesting that some of the uncertainty is being missed. Under the proposed method, the coverage of the prediction intervals is much closer to the nominal level, suggesting that the new method is capturing most of the missed uncertainty by taking account of uncertainty in past TFR values.
The overall coverage rate of the method of (Alkema et al., 2011) is worse than that reported in the original paper mainly because of the change of the historical data between WPP versions. For example, in WPP 2008, the estimate of TFR for Nigeria in 2000–2005 was 5.67, but that value changed to 6.05 in WPP version 2015; the latter is presumably more accurate because it is based on additional information available in 2015 but not in 2008. The model of (Alkema et al., 2011) performed extremely well for forecasting the UN estimates of the same version (WPP 2008), but not as well for forecasting the updated estimate of TFR in 2000–2005 that was made on the basis of data available in 2015.
For illustration, results of the out-of-sample validation exercise are shown in Figure 3 for Argentina, Botswana, Nigeria and the United States. Of these, only the United States has had a high-quality vital registration system for the entire period, while Argentina has a vital registration that was of lower quality in the early years, and the other two countries have no comprehensive vital registration systems, relying instead on censuses and periodic surveys.
Fig 3.
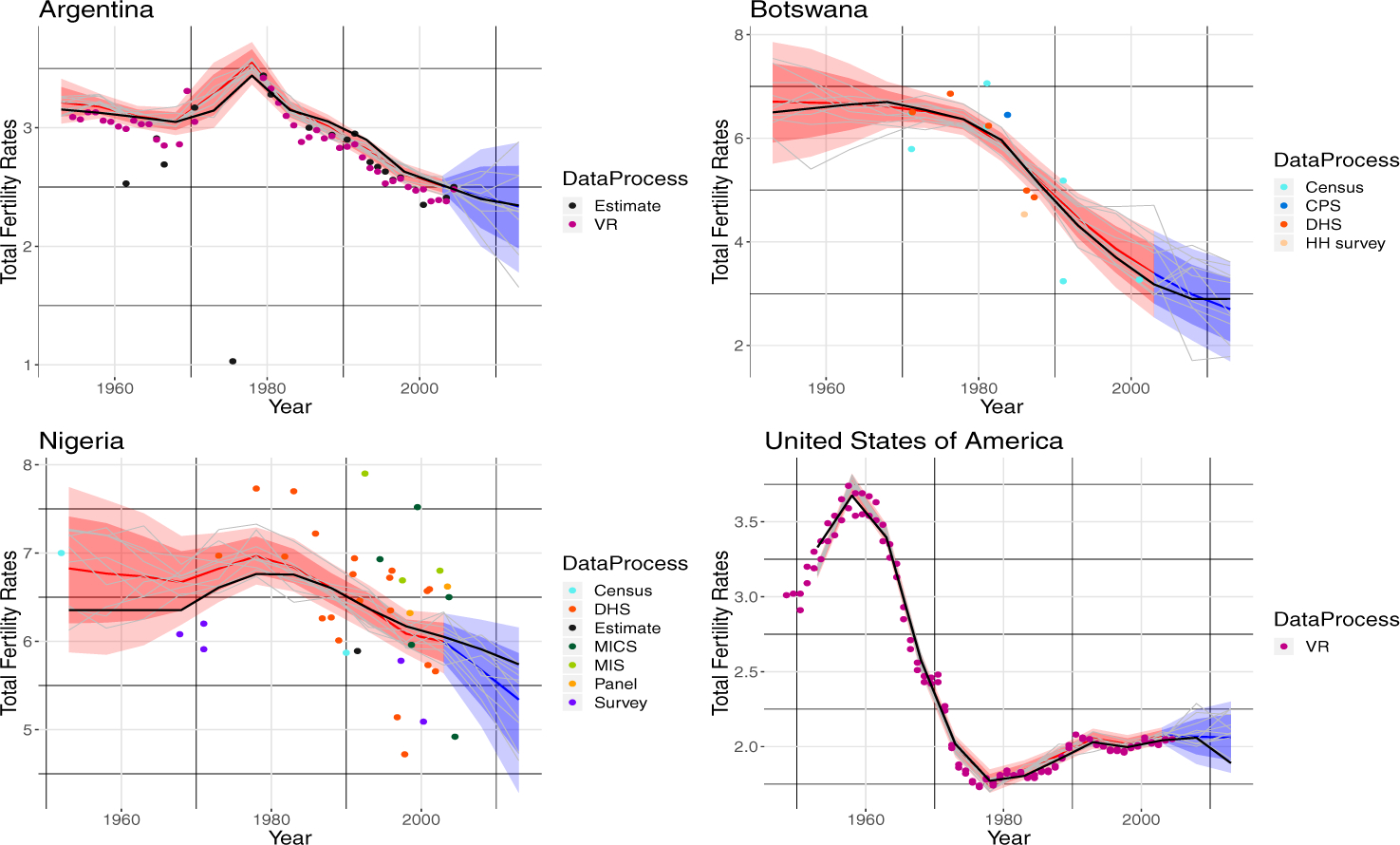
Out of Sample Validation Results for Argentina, Botswana, Nigeria and the United States. Estimates of past TFR values for [1950, 2005] are shown by dots, with different sources corresponding to different colors, as described in the side captions. The UN estimates are shown in black. The posterior distributions of past values for [1950, 2005] are shown in orange, with the posterior median as the solid line, the posterior 80% interval as the dark shaded region, and the posterior 95% intervals as the light shaded region. The corresponding posterior predictive distributions for [2005, 2015] based on data up to 2005, are shown in blue.
The posterior intervals of past TFR values are very narrow for the United States, reflecting the high quality vital registration data available for the entire period, while for Argentina they are somewhat wider. For both Botswana and Nigeria the intervals are far wider, reflecting the much lower quality of the available data. For the earlier years, from the 1950s to the 1970s, the intervals for Botswana and Nigeria are especially wide, reflecting the sparsity of the data for these decades. The predictive distributions cover the observations in all cases, although in some cases they lie towards the edge of the intervals, as expected if the intervals are well calibrated.
Additional out of sample validation results for comparing our method with that of (Alkema et al., 2011) are available in the Supplementary Information. We find that the coverage rate remained close to the nominal levels for other out of sample forecasting periods.
3.3. Robustness Across WPP Versions.
To illustrate the extent to which the new method is consistent across all WPP versions, we consider the same validation study as in Section 3.1, but evaluating our forecasts with reference to different WPP versions instead of only WPP 2015 in Section 3.1.
In order to compare with the WPP 2008 revision and the 2010 revision, we could not do validation on the 2010–2015 period. Thus, we train the model with the WPP 2008 Revision, and for the new method, we use only data before 2005. Then we make forecasts of TFR for 2005–2010 with the model trained, and measure the coverage rate of the forecast of TFR for 2005–2010 using the data from the WPP 2008, 2010, 2012, 2015 and 2017 revisions. The results are summarized in Table 3.
Table 3.
Coverage rate of 80% and 95% of prediction intervals based on model trained with data before 2005 and WPP 2008 Revision.
| WPP Version | Testing Period | Original Method | Proposed Method | ||
|---|---|---|---|---|---|
| 95% PI | 80% PI | 95% PI | 80% PI | ||
| WPP 2008 | 2005–2010 | 98.5% | 92.9% | 98.5% | 88.0% |
| WPP 2010 | 2005–2010 | 89.8% | 73.0% | 97.4% | 83.3% |
| WPP 2012 | 2005–2010 | 79.9% | 62.9% | 95.4% | 79.1% |
| WPP 2015 | 2005–2010 | 78.6% | 61.3% | 92.1% | 77.7% |
| WPP 2017 | 2005–2010 | 78.4% | 62.4% | 92.4%, | 78.1% |
The later the version of WPP, the more information the TFR estimates are based on, and so the more accurate they should be. Therefore, we are more interested in the coverage rate based on later revisions (especially the 2015 and 2017 revisions) than the earlier revisions. We found that our intervals overcovered the estimates from the earlier revisions, but had coverage close to nominal for the more accurate 2012 and later revisions, while the original method had coverage substantially below nominal for the later revisions.
4. Case Study: TFR Estimation and Projection For Nigeria.
We illustrate the method by producing probabilistic forecasts of the TFR of Nigeria from 2015 to 2100, using data available up to 2015. As we have discussed, the method first estimates the bias and measurement error variance of the different data sources. It then estimates the uncertainty about past TFR values, and takes this uncertainty into account when making probabilistic projections.
4.1. Estimation of Bias and Measurement Error Variance of Different Data Sources.
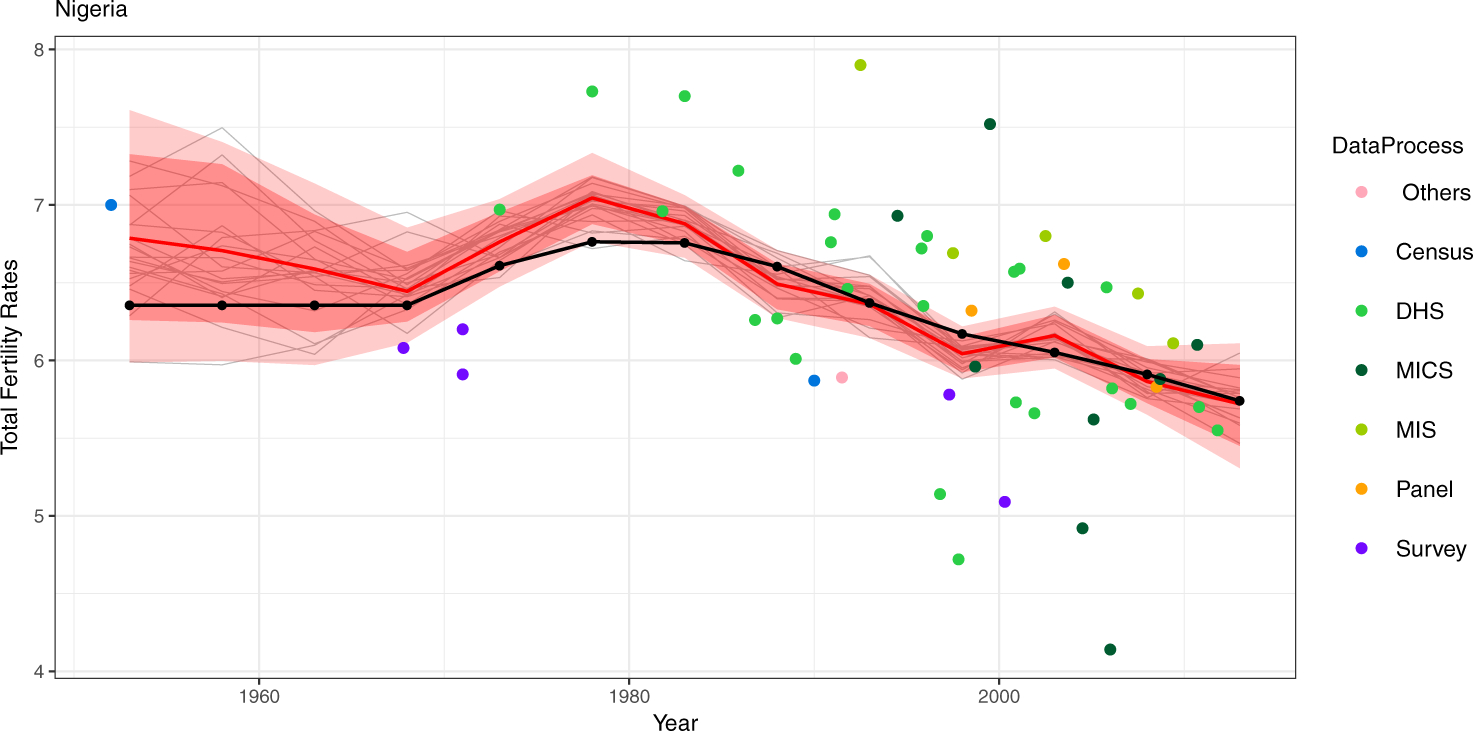
From 1950 to 2015, according to the UN’s WPP 2015 revision, the TFR in Nigeria reached its peak around 1980 at about 6.7 children per woman. It then declined slowly, reaching about 5.7 in 2015. However, the data on which these estimates are based are surprisingly noisy, as can be seen in Figure 4.
Fig 4.
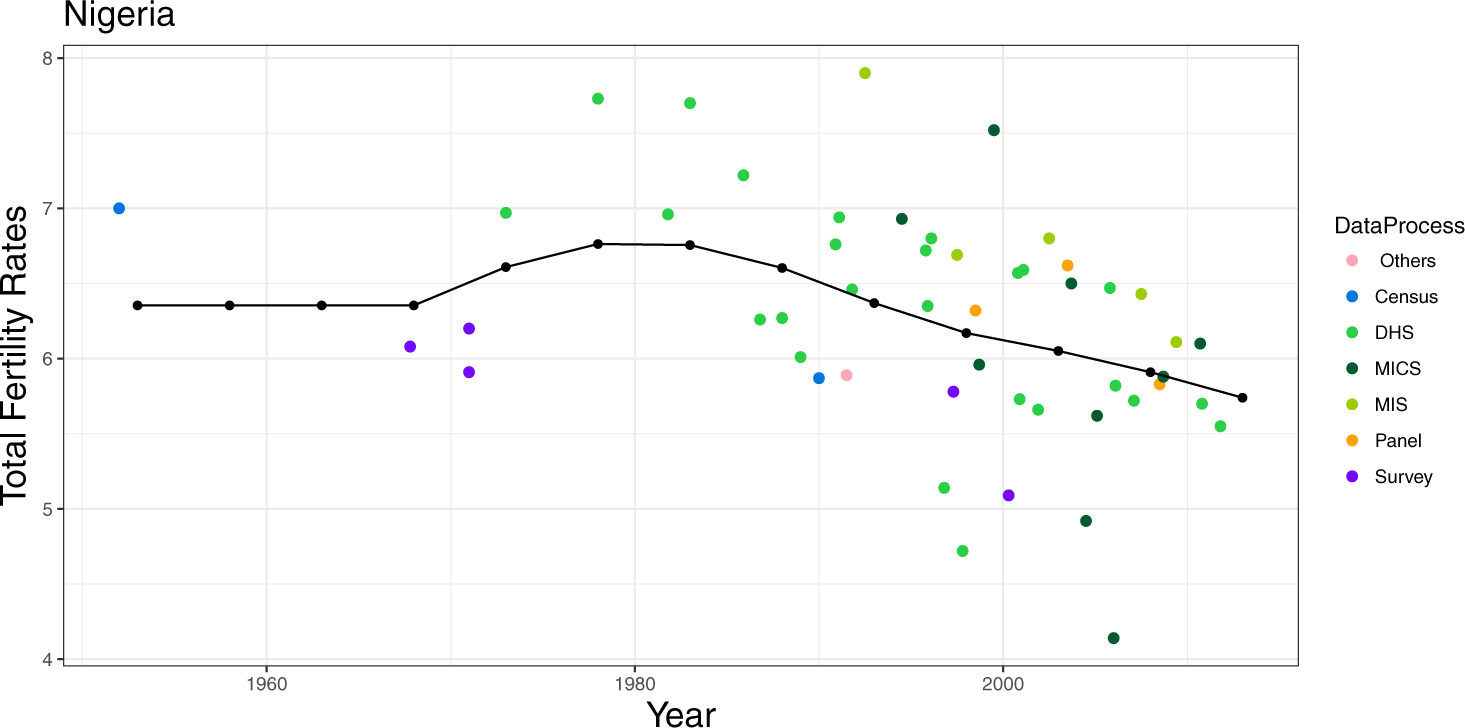
Nigeria TFR Estimates, 1950–2015.
These data come from several sources, including national censuses, which are comprehensive but are sparse in time and have issues of coverage. The other sources are mostly surveys, including the internationally organized Demographic and Health Surveys (DHS), the Multiple Indicator Cluster Surveys (MICS) run by UNICEF, and the Malaria Indicators Survey, or MIS, also run by DHS. There are also several occasional national cross-sectional and panel surveys. Some of the surveys, notably DHS and MICS, collect birth histories, which allow one survey to generate estimates for several past years, in some cases using indirect methods.
The black line represents the UN estimate of Nigeria’s TFR in 1950 to 2015 from WPP 2015. We could also see the changes in the UN estimates of Nigeria’s past TFR, from WPP 2008 to WPP 2017. We show those changes in Table 4.
Table 4.
WPP estimates of Nigeria’s TFR from version 2008 to 2017. The most recent TFR estimates are changing significantly. For example, in WPP 2008, the TFR for 2005–2010 is estimated as 5.32, but in later versions, the TFR is estimated as 5.91, which is about 0.6 more children per woman. The values for 2000–2005 and 2005–2010, on which we focus, are bolded for emphasis.
| year | WPP 2008 | WPP 2010 | WPP 2012 | WPP 2015 | WPP 2017 |
|---|---|---|---|---|---|
| 1950–1955 | 6.55 | 6.35 | 6.35 | 6.35 | 6.35 |
| 1955–1960 | 6.55 | 6.35 | 6.35 | 6.35 | 6.35 |
| 1960–1965 | 6.55 | 6.35 | 6.35 | 6.35 | 6.35 |
| 1965–1970 | 6.55 | 6.35 | 6.35 | 6.35 | 6.35 |
| 1970–1975 | 6.72 | 6.61 | 6.61 | 6.61 | 6.61 |
| 1975–1980 | 6.89 | 6.76 | 6.76 | 6.76 | 6.76 |
| 1980–1985 | 6.93 | 6.76 | 6.76 | 6.76 | 6.76 |
| 1985–1990 | 6.76 | 6.56 | 6.60 | 6.60 | 6.60 |
| 1990–1995 | 6.44 | 6.23 | 6.37 | 6.37 | 6.37 |
| 1995–2000 | 6.05 | 5.99 | 6.17 | 6.17 | 6.17 |
| 2000–2005 | 5.67 | 5.79 | 6.05 | 6.05 | 6.05 |
| 2005–2010 | 5.32 | 5.61 | 6.00 | 5.91 | 5.91 |
| 2010–2015 | NA | NA | 6.00 | 5.74 | 5.74 |
We first estimate the bias and measurement error variance of the different data sources using the approach outlined in Section 2.3. From each observed TFR estimate yc,t,s we subtract the corresponding UN TFR estimate to obtain an estimate of the bias for that source, country and time, namely zc,t,s = yc,t,s − uc,t. As data quality covariates, xc,s, we use the source of the data and whether the estimate is direct or indirect. We then estimate the bias δc,s for country c and data source s as the fitted value from a regression of the zc,t,s on the data quality covariates xc,s, as in (Alkema et al., 2012).
The UN TFR estimates are for five-year periods, and we treat them as referring to the middle of the period. Thus, for example, we treat estimates for 2010–2015 as referring to the beginning of 2013. An observed TFR estimate can refer to any year between 1950 and 2015, and we use the convex combination of the two UN estimates closest to the time to which it refers as the corresponding UN estimate, uc,t.
Similarly, after we get the fitted value of the bias estimates , we obtain the measurement error standard deviation estimates by regressing on the same data quality covariates. The fitted biases and measurement error standard deviations are summarized in Table 5.
Table 5.
Estimates of Bias and Measurement Error Variance for All Combinations of Source and Estimate Types, for Nigeria. Survey-NR are different Nigeria nationwide surveys and Survey represents other survey estimates. Under estimate type, D represents direct estimates, C cohort estimates and I indirect analysis. Here μ(δ) and σ(δ) are the sample bias and measurement error standard deviations; when a hat is added they represent the estimates from the models. Estimated root mean squared errors are summarized in the column RMSE . The number of observations for each combination is shown in the column n.
| Source | Estimate Type | μ(δ) | σ(δ) | RMSE | n | |||
|---|---|---|---|---|---|---|---|---|
| 1 | DHS | D | 0.04 | 0.48 | 0.11 | 0.38 | 0.40 | 28 |
| 2 | DHS | C | −0.26 | 0.51 | −0.48 | 0.46 | 0.66 | 10 |
| 3 | Census | D | 0.00 | 0.91 | −0.43 | 0.50 | 0.66 | 2 |
| 4 | Census | C | −1.46 | 0.43 | −1.02 | 0.58 | 1.17 | 2 |
| 5 | MICS | D | −1.10 | 1.03 | −0.33 | 0.81 | 0.87 | 2 |
| 6 | MICS | C | −0.79 | 0.18 | −0.92 | 0.89 | 1.28 | 2 |
| 7 | MICS | I | 0.29 | 1.64 | 0.20 | 1.35 | 1.36 | 15 |
| 8 | MIS | D | 0.70 | 0.48 | 0.22 | 0.56 | 0.60 | 5 |
| 9 | MIS | I | 0.68 | 1.37 | 0.75 | 1.09 | 1.32 | 30 |
| 10 | Survey | D | −0.50 | 0.58 | −0.47 | 0.42 | 0.63 | 4 |
| 11 | Survey | C | −1.18 | 0.95 | −1.06 | 0.49 | 1.17 | 8 |
| 12 | Survey | I | 0.14 | 0.98 | 0.06 | 0.95 | 0.95 | 15 |
| 13 | Survey-NR | D | −0.40 | 0.18 | −0.60 | 0.21 | 0.64 | 3 |
| 14 | Survey-NR | C | −1.48 | 0.18 | −1.18 | 0.29 | 1.22 | 2 |
We can see from Table 5 that the direct estimates from the DHS are the highest quality estimates as measured by estimated root mean squared error (equal to ). Direct estimates generally have smaller variances than indirect estimates. Figure 5 plots the fitted biases and measurement error standard deviations against the observed ones; the model fit seems reasonably good.
Fig 5.
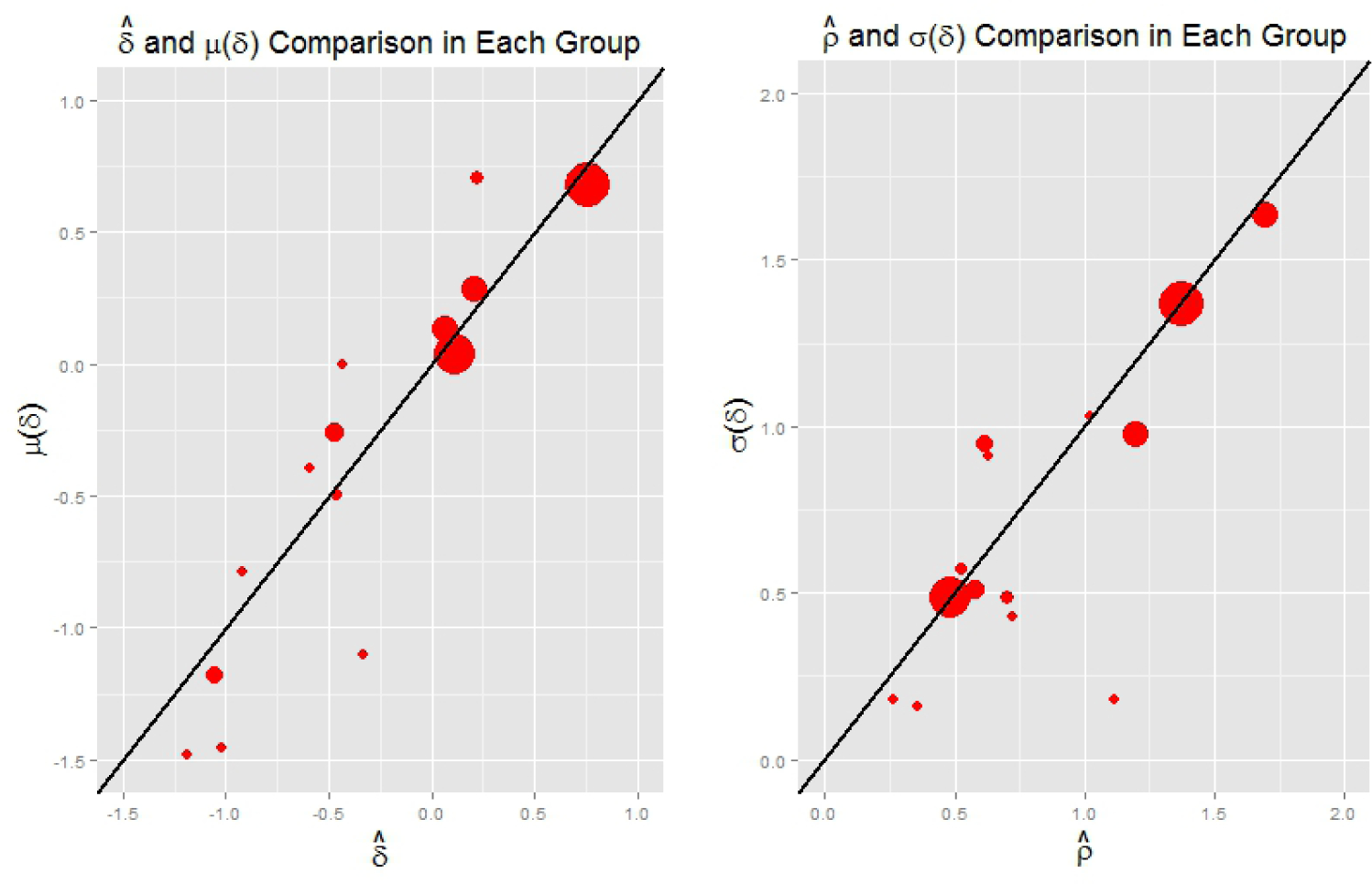
Bias and Variance Estimates for Nigeria: Fitted against Observed. The size of the dots represents the number of observations. Most large dots are along the diagonal line.
4.2. Estimation of Past and Projection of Future TFR.
The fertility transition, or Phase II, started in 1980 in Nigeria, according to the definition of (Alkema et al., 2011). We initialize the MCMC algorithm with a warm start, simulating the starting values for the global parameters ψ and the country-level parameters θc from their posterior distribution from the model that does not take account of uncertainty about past TFR values (Alkema et al., 2011; Raftery, Alkema and Gerland, 2014). The true past fertility rates are initialized as the UN estimates.
The results are shown in Figure 6. These are based on data up to 2015, and can be compared with Figure 3(c), which is based on data up to 2005. The posterior distribution for the 2000–2005 period is tighter, because more data relevant to this period were available in 2015 than in 2005. The posterior distibution widens slightly for the past period, 2010–2015, again reflecting the relative paucity of data relevant to this period by 2015. We expect that this posterior distribution will tighten as more data relevant to 2010–2015 become available in the future.
Fig 6.
Past and Present TFR Estimates for Nigeria. Colored dots are observed TFR, red shaded areas are 95% estimation intervals and the black line is the UN TFR estimates (from WPP 2015)
We make projections in two steps. In the first step, we sample one trajectory from the MCMC results obtained in Section 4.2. Then given the sampled trajectory, the phase of the most recent year is determined by this trajectory, and then future TFR is sampled according to the country-specific parameters of this trajectory. The resulting projection is summarized in Figure 7.
Fig 7.
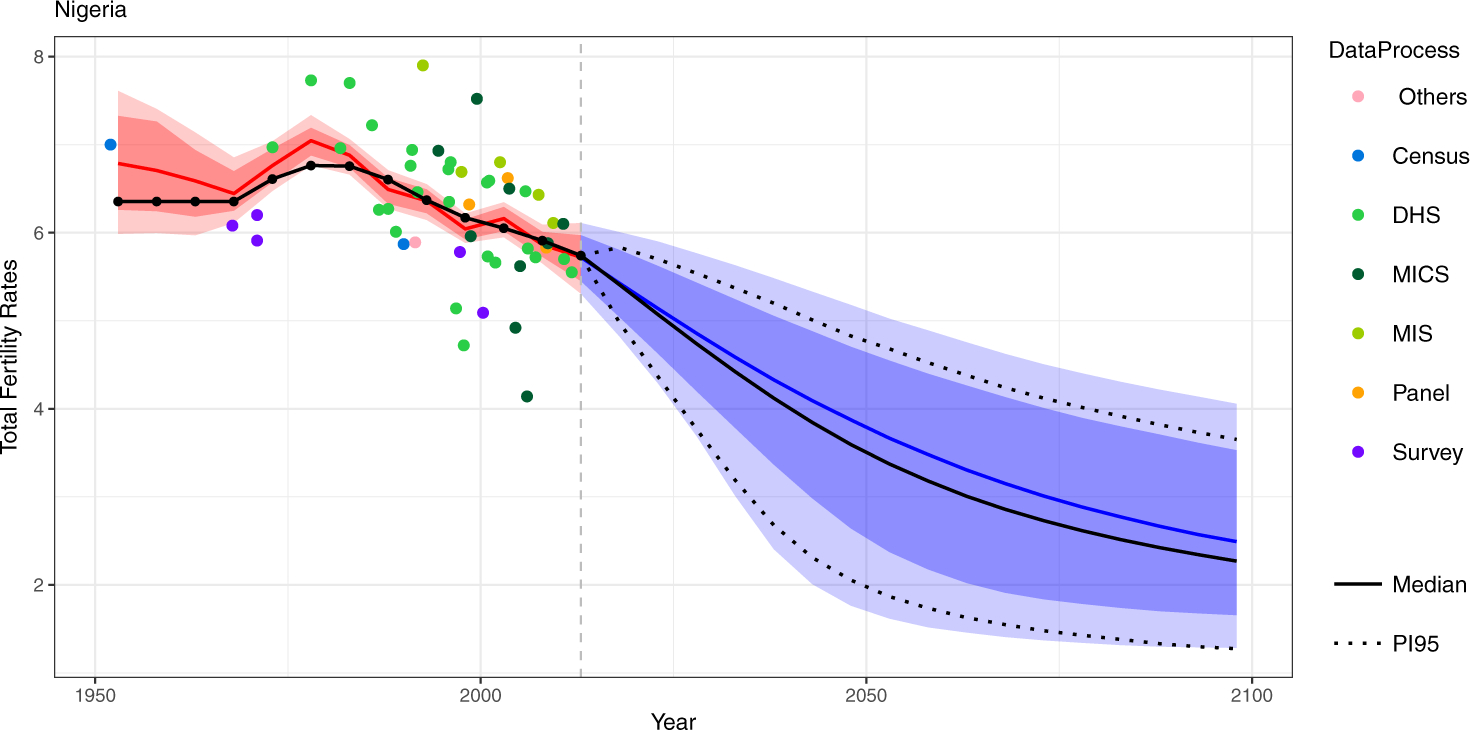
TFR projections for Nigeria. The red shaded areas are the estimated TFR with 95% estimation intervals, and the blue shaded areas are the projected TFR with 95% prediction interval, where the present is taken to be 2015, marked by a dashed vertical line. The black line and the black dotted lines represent the UN WPP 2015 median and 95% predictions.
The projections of future TFR from 2015 to 2100, taking account of uncertainty about the past, are shown in Figure 7. The black solid and dotted curves show the UN’s 2015 probabilistic projection (not taking account of uncertainty about the past), while the blue line and shaded region show the projection from our method. Both project that Nigeria’s TFR will likely decline, with a great deal of uncertainty about how fast this will happen. Our proposed method yields a similar predictive median to the current UN method, but somewhat wider prediction intervals. As we saw in the out-of-sample validation study, these wider intervals do incorporate an important additional source of uncertainty, and, on average, take the intervals from undercovering the truth to some extent to the nominal coverage.
4.3. Model Validation: Simulation Study.
We now run a simulation study with input data on past TFRs chosen to resemble the Nigerian data, to see how accurately the proposed method captures past TFR values. Assuming we have trained the MCMC process beforehand and have got the estimates of past TFR estimates for Nigeria as we showed in previous sections. Then for each simulation, we sampled one TFR trajectory from the posterior distribution of these samples, and we assume the sampled trajectory to be the true (unobserved) TFR. Then we randomly generated TFR estimates from the normal distribution in Level 1 of the model, by assuming the bias of data points are the previous estimated bias (), and measurement error variances are the previous estimated variances (). We then treated sampled data points as the input data for the estimation process. We still treated the UN estimates as unbiased, as before.
We repeated the simulation process 1000 times, with 10,000 trajectories of fertility rates drawn in each simulation. The estimation results of one simulation are shown in Figure 8.
Fig 8.
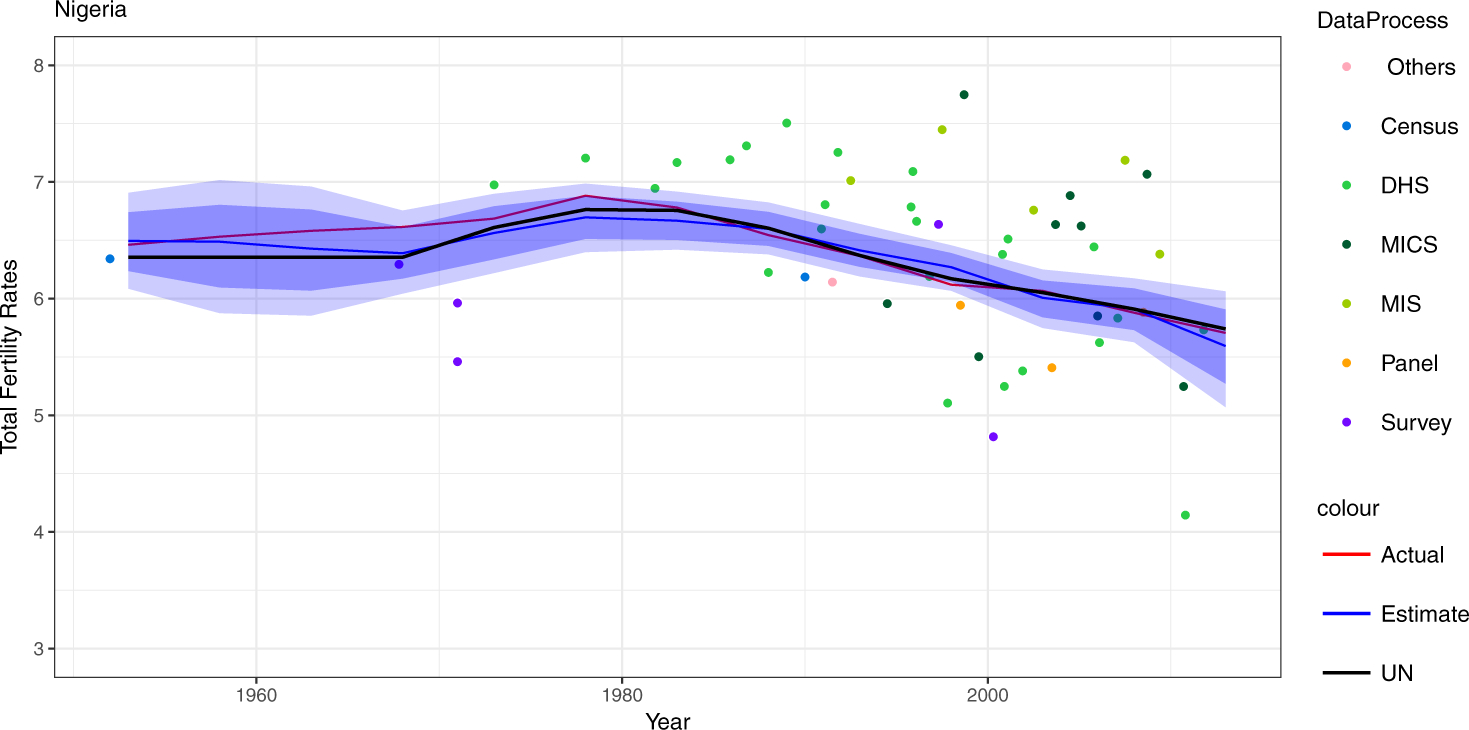
Past and Present TFR Estimates for Nigeria. Colored dots are simulated observations. The red curve is the assumed true TFR, which is assumed unobserved and the black line is the UN estimate. Shaded areas are 95% estimation intervals based on the simulated observations.
If we take the posterior median as the point estimate, the mean absolute error (MAE) for all 13 time periods is 0.157. We could also break it down by the 13 time periods, and the results are shown in Table 6.
Table 6.
Simulation Coverage and Mean Absolute Errors for 13 Estimation Periods.
| 80% Interval Coverage | 95% Interval Coverage | Mean Absolute Error | |
|---|---|---|---|
| fNigeria,1953 | 0.865 | 0.917 | 0.259 |
| fNigeria,1958 | 0.888 | 0.976 | 0.263 |
| fNigeria,1963 | 0.895 | 0.982 | 0.222 |
| fNigeria,1968 | 0.794 | 0.914 | 0.177 |
| fNigeria,1973 | 0.847 | 0.967 | 0.139 |
| fNigeria,1978 | 0.718 | 0.898 | 0.152 |
| fNigeria,1983 | 0.797 | 0.933 | 0.118 |
| fNigeria,1988 | 0.926 | 0.979 | 0.103 |
| fNigeria,1993 | 0.936 | 0.980 | 0.097 |
| fNigeria,1998 | 0.952 | 0.981 | 0.116 |
| fNigeria,2003 | 0.848 | 0.940 | 0.090 |
| fNigeria,2008 | 0.893 | 0.963 | 0.103 |
| fNigeria,2013 | 0.805 | 0.935 | 0.198 |
The overall coverage rate of the 80% interval was 85.9%, and the overall coverage rate of the 95% interval was 95.1%. The overall coverage rate was close to the nominal rate. Thus the model gave accurate point and intervals estimates of past values in the simulation study.
5. Discussion.
We have developed a new method for projecting the total fertility rate probabilistically for all countries that extends the UN method to take account of uncertainty about past TFR values. In a validation experiment, we found that the existing UN method leads to prediction intervals whose coverage is somewhat lower than nominal, while for our new method the coverage is close to nominal. For the countries with the highest quality data on past rates, mostly in Europe and North America, our method gives results that are similar to the current method.
However, for countries with lower quality data where TFR estimates have been estimated based on surveys for at least part of the past 60 years, our method gives intervals that are noticeably wider than the current ones.
These results call for improvements in the mechanisms and practice of data collection in those countries, which today have to rely on surveys in the absence of reliable vital registration. This is also one of the underlying aims of the Sustainable Development Goals agenda (Assembly, 2015).
The long-term implications of these results could be far reaching. The countries with the most uncertainty about past TFR values are also largely those with the highest current fertility levels and the greatest uncertainty about future levels, many of which are in Sub-Saharan Africa. Not surprisingly, therefore, our method indicates that these are also the countries for which the understatement of uncertainty was greatest. Thus our TFR results could lead to a considerable increase in uncertainty for long-term population projections in these countries, especially as the effects of differences in TFR compound over generations. The population of Sub-Saharan Africa is currently around 1 billion, and current projections are that it will increase to between 3.4 and 4.8 billion in 2100 with 80% probability (Gerland et al., 2014; United Nations, 2017). This interval will be wider still once uncertainty about past TFR has been factored in, with even larger implications for future population levels in Africa, and hence for the world as a whole.
The method proposed in this paper is in two stages. In the first stage we estimate the bias and measurement error variance of the different data sources by country using a classical analysis of variance method. In the second stage we estimate a Bayesian hierarchical model taking the point estimates from the first stage as input. In principle it would be possible to unify these two stages by including the estimation of the bias and variance of the different sources in the Bayesian hierarchical model. However, this would complicate the model considerably, making it harder to specify, code, debug and interpret, and it seems unlikely that it would change the results appreciably. It is also possible that the assumption that bias and measurement error variance is time invariant is not always true for all countries and regions and different sources of data, but considering these would also complicate the model. We feel that our modeling decisions strike a reasonable balance between complexity and performance. This is supported by the good assessment of predictive uncertainty provided by our method.
To use these projections of total fertility in population projections, one must convert them to age-specific fertility rates. The UN currently does this using the methodology described by (Ševčíková et al., 2016). Each simulated future TFR value is converted to a corresponding age-specific fertility pattern, which is used with age-specific mortality and volume of net migration in the cohort-component projection method to project the corresponding future population by age and sex. A subtle point is that this takes account of uncertainty about future total fertility, but not about future age-specific fertility given total fertility, i.e. about the number but not the timing of future births. Because the age pattern of births is relatively concentrated regardless of their number, this is a much smaller source of uncertainty than uncertainty about the number of births (Ediev, 2013). Nevertheless, it should be addressed in future research.
Our method does not explicitly use available information on survey design and design-based errors for DHS, MICS and other data sources, or possible measurement error in the vital registration data. Instead we estimate overall error as part of the method, including these specific contributors to error, thus bypassing these questions. We found that our overall estimated standard errors were considerably larger than the design-based estimates of standard errors for DHS (for example four to five times larger for Nigeria), providing some support for the idea that the measurement error variance assessed by our method includes the sources of error assessed by the design-based approach. This also suggests that using the design-based estimates of standard errors alone would estimate overall uncertainty.
We have produced results for all the world’s countries with populations over 100,000 as of 2015, except for one: China, the most populous country. We did not include China in our analysis because the estimates for its TFR suffer from a unique form of bias, which would require a different kind of analysis. This is due to the One Child Policy, introduced in 1979. As a result of this policy, many Chinese families did not report births to the authorities, with the hope of being able to circumvent the policy and have additional children. This underreporting was particularly severe in the late 1990s, and (Goodkind, 2004) has argued that this was because the 1991 Decree pushed the responsibility of implementing family planning rules, especially the one-child policy, to local governments, giving them a greater incentive to underreport the number of births.
There have been many efforts to correct for this underreporting. For example, (Yi, 1996; Retherford et al., 2005; Cai, 2008) and (Merli and Raftery, 2000) attempted to correct estimates of TFR in 2000. The clearest evidence of this underreporting comes from primary school enrollments several years later, which were typically substantially larger than the reported number of births during this period. (Zhai and Chen, 2007) used these enrollment data to correct the TFR estimates for the late 1990s. The UN has also been using enrollment data to correct the available estimates. Our method would not be sufficient to give good estimates of China’s TFR in the period of severe underreporting. Instead, for China it would be desirable to extend our method to include enrollment data, taking account of uncertainty in the enrollment data in the model. A simpler approach would be to include enrollment-corrected survey and census estimates as inputs to our method, but we felt that a more comprehensive approach was desirable given the great demographic importance of China and the unique data issues it presents, and so we omitted China from the present analysis.
This is a topic for a separate, tailored paper, targeted at a demographic audience. Scientists at the UN Population Division have been developing such a method and are currently preparing a paper to describe it (Wheldon, 2019).
Our method was developed to incorporate uncertainty about past fertility into projections of future fertility by the method of (Alkema et al., 2011), which is used by the UN. It focuses on uncertainty in the TFR rather than age-specific fertility rates, because for many countries without longstanding high-quality vital registration systems (the majority), estimates of past age-specific fertility rates are often not very good, while estimates of TFR are more solidly based. The same basic conceptual approach could be combined with other probabilistic fertility forecasting methods. In particular, (Bohk-Ewald, Li and Myrskylä, 2018) identified two other probabilistic fertility forecasting methods that also outperform the simple persistence, or “freeze rates”, approach, namely those of (Myrskylä, Goldstein and Cheng, 2013) and (Schmertmann et al., 2014). These methods require good estimates of past age-specific fertility rates, not just total fertility, and are tailored for countries that do have well-established high-quality vital registration systems. Thus to be combined with these projection methods, our approach to assessing uncertainty about past total fertility would need to be extended to age-specfic fertility rates.
We plan to develop an R package to implement this method and make it publicly available, building on and extending the existing bayesTFR R package that is used by the UN for their projections (Ševčíková, Alkema and Raftery, 2011).
Supplementary Material
Acknowledgements.
This work was supported by NICHD grants R01 HD054511 and R01 HD070936. Raftery’s research was also partly supported by the Center for Advanced Study in the Behavioral Sciences (CASBS) at Stanford University. This work was carried out in cooperation with the United Nations Population Division, and in particular we thank Kirill Andreev, Ann Biddlecom, Vladimíra Kantorová, Stephen Kisambira and other colleagues from the Population Division for preparing and making available the UN World Fertility Data, an invaluable resource for researchers. We also thank Hana Ševčíkova for methodological support, and Patrick Gerland and Laina Mercer for helpful comments.
References.
- Myrskylä M, Goldstein JR and Cheng YA (2013). New cohort fertility forecasts for the developed world: Rises, falls, and reversals. Population and Development Review 39 31–56. [Google Scholar]
- Abel GJ, Barakat B, Samir KC and Lutz W (2016). Meeting the Sustainable Development Goals leads to lower world population growth. Proceedings of the National Academy of Sciences 113 14294–14299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alders M, Keilman N and Cruijsen H (2007). Assumptions for Long-term Stochastic Population Forecasts in 18 European Countries. European Journal of Population/Revue Européenne de Demographie 23 33–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alho JM, Jensen SEH and Lassila J (2008). Uncertain Demographics and Fiscal Sustainability. Cambridge University Press, Cambridge, U.K. [Google Scholar]
- Alho J, Alders M, Cruijsen H, Keilman N, Nikander T and Pham DQ (2006). New Forecast: Population Decline Postponed in Europe. Statistical Journal of the United Nations Economic Commission for Europe 23 1–10. [Google Scholar]
- Alkema L, Raftery AE, Gerland P, Clark SJ, Pelletier F, Buettner T and Heilig GK (2011). Probabilistic Projections of the Total Fertility Rate for All Countries. Demography 48 815–839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alkema L, Raftery AE, Gerland P, Clark SJ and Pelletier F (2012). Estimating Trends in the Total Fertility Rate with Uncertainty Using Imperfect Data: Examples from West Africa. Demographic Research 26 331–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assembly G (2015). sustainable Development goals. SDGs), Transforming our world: the 2030. [Google Scholar]
- Bohk-Ewald C, LI P and Myrskylä M (2018). Forecast accuracy hardly improves with method complexity when completing cohort fertility. Proceedings of the National Academy of Sciences 115 9187–9192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Booth H, Pennec S and Hyndman RJ (2009). Stochastic Population Forecasting Using Functional Data Methods: The Case of France. In Annual Meeting of the International Union for the Scientific Study of Population, Marrakech, Morocco. [Google Scholar]
- Brass W (1964). Uses of Census or Survey Data for the Estimation of Vital Rates. United Nations, New York. [Google Scholar]
- Brass W (2015). Demography of Tropical Africa. Princeton University Press, Princeton, N.J. [Google Scholar]
- Cai Y (2008). An Assessment of China’s Fertility Level Using the Variable-r Method. Demography 45 271–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannan E (1895). The Probability of Cessation of Growth of Population in England and Wales During the Next Century. Economic Journal 5 506–515. [Google Scholar]
- Ediev D (2013). Comparative importance of the fertility model, the total fertility, the mean age and the standard deviation of age at childbearing in population projections. Paper presented to the International Population Conference, Busan, Korea. https://www.iussp.org/en/event/17/programme/paper/3054. [Google Scholar]
- Fosdick BK and Raftery AE (2014). Regional Probabilistic Fertility Forecasting by Modeling Between-Country Correlations. Demographic Research 30 1011–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A and Rubin DB (1992). Inference from iterative simulation using multiple sequences. Statistical Science 457–472. [Google Scholar]
- Gerland P, Raftery AE, Ševčíková H, Li N, Gu D, Spoorenberg T, ALKEMA L, Fosdick BK, Chunn JL, Lalic N, Bay G, Buettner T, Heilig GK and Wilmoth J (2014). World Population Stabilization Unlikely This Century. Science 346 234–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodkind DM (2004). China’s Missing Children: the 2000 Census Underreporting Surprise. Population Studies 58 281–295. [DOI] [PubMed] [Google Scholar]
- Keyfitz N (1981). The Limits of Population Forecasting. Population and Development Review 7 579–593. [Google Scholar]
- Lee RD (1993). Modeling and Forecasting the Time Series of US Fertility: Age Distribution, Range, and Ultimate Level. International Journal of Forecasting 9 187–202. [DOI] [PubMed] [Google Scholar]
- Lee RD and Bulatao RA (2000). Beyond Six Billion: Forecasting the World’s Population. National Academies Press. [Google Scholar]
- Lee RD and Tuljapurkar S (1994). Stochastic Population Forecasts for the United States: Beyond High, Medium, and Low. Journal of the American Statistical Association 89 1175–1189. [PubMed] [Google Scholar]
- Lutz W and Samir KC (2010). Dimensions of Global Population Projections: What do we Know about Future Population Trends and Structures? Philosophical Transactions of the Royal Society B 365 2779–2791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merli MG and Raftery AE (2000). Are Births Underreported in Rural China? Manipulation of Statistical Records in Response to China’s Population Policies. Demography 37 109–126. [PubMed] [Google Scholar]
- Murray CJ, Callender CS, Kulikoff XR, Srinivasan V, Abate D, Abate KH, Abay SM, Abbasi N, Abbastabar H, Abdela J et al. (2018). Population and fertility by age and sex for 195 countries and territories, 1950–2017: a systematic analysis for the Global Burden of Disease Study 2017. The Lancet 392 1995–2051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Population Commission, F. R. O. N. (2009). Nigeria Demographic and Health Survey 2008.
- United Nations (2008). World Population Prospects: The 2008 Revision. United Nations, New York. [Google Scholar]
- United Nations (2015a). World Population Prospects: The 2015 Revision. United Nations, New York. [Google Scholar]
- United Nations (2015b). World Fertility Data. http://www.un.org/en/development/desa/population/publications/dataset/fertility/wfd2015.shtml.
- United Nations (2017). World Population Prospects: The 2017 Revision. United Nations, New York. [Google Scholar]
- Neal RM (2003). Slice Sampling. Annals of Statistics 31 705–741. [Google Scholar]
- Preston SH, Heuveline P and Guillot M (2000). Demography: Measuring and Modeling Population Processes. Blackwell, Malden, Mass. [Google Scholar]
- Pullum TW, Schoumaker B, Becker S and Bradley SE (2013). An Assessment of DHS Estimates of Fertility and Under-five Mortality. In International Population Conference of the International Union for the Scientific Study of Population (IUSSP), Session 132: Data Quality in Demographic Surveys, August 28. [Google Scholar]
- Raftery AE, Alkema L and Gerland P (2014). Bayesian Population Projections for the United Nations. Statistical Science 29 58–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raftery AE, Lalic N and Gerland P (2014). Joint Probabilistic Projection of Female and Male Life Expectancy. Demographic Research 30 795–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raftery AE and Lewis SM (1996). Implementing MCMC. In Practical Markov Chain Monte Carlo (Gilks W, Spiegelhalter DJ and Richardson S, eds.) 115–130. Chapman and Hall, London. [Google Scholar]
- Raftery AE, Gneiting T, Balabdaoui F and Polakowski M (2005). Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Monthly Weather Review 133 1155–1174. [Google Scholar]
- Raftery AE, Chunn JL, Gerland P and Ševčíková H (2013). Bayesian Probabilistic Projections of Life Expectancy for all Countries. Demography 50 777–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Retherford RD, Choe MK, Chen J, Xiru L and Hongyan C (2005). How Far Has Fertility in China Really Declined? Population and Development Review 31 57–84. [Google Scholar]
- Schmertmann C, Zagheni E, Goldstein JR and Myrskylä M (2014). Bayesian forecasting of cohort fertility. Journal of the American Statistical Association 109 500–513. [Google Scholar]
- Schoumaker B (2010). Reconstructing Fertility Trends in Sub-Saharan Africa by Combining Multiple Surveys Affected by Data Quality Problems. In Proceedings of the 2010 Annual Meeting of the Population Association of America. [Google Scholar]
- Schoumaker B (2011). Omissions of Births in DHS Birth Histories in Sub-Saharan Africa: Measurement and Determinants. In Proceedings of the 2011 Annual Meeting of the Population Association of America 31. [Google Scholar]
- Schoumaker B (2014). Quality and Consistency of DHS Fertility Estimates, 1990 to 2012. ICF International Rockville. [Google Scholar]
- Stoto MA (1983). The Accuracy of Population Projections. Journal of the American Statistical Association 78 13–20. [DOI] [PubMed] [Google Scholar]
- Unicef (2016). UNICEF Annual Report 2015.
- U. S. Census Bureau, D. P (2017). Annual Estimates of the Resident Population: April 1, 2010 to July 1, 2017.
- Ševčíková H, Alkema L and Raftery AE (2011). bayesTFR: An R Package for Probabilistic Projections of the Total Fertility Rate. Journal of Statistical Software 43 1–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ševčíková H and Raftery AE (2016). bayesPop: Probabilistic Population Projections. Journal of Statistical Software 75 1–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ševčíková H, Li N, Kantorová V, GERLAND P and RAFTERY AE (2016). Age-Specific Mortality and Fertility Rates for Probabilistic Population Projections. In Dynamic Demographic Analysis (Schoen R, ed.) 15, 285–310. Springer. [Google Scholar]
- Wheldon MC (2019). Personal communication.
- Whelpton PK (1928). Population of the United States, 1925–1975. American Journal of Sociology 31 253–270. [Google Scholar]
- Whelpton PK (1936). An Empirical Method for Calculating Future Population. Journal of the American Statistical Association 31 457–473. [Google Scholar]
- Yi Z (1996). Is Fertility in China in 1991–92 Far Below Replacement Level? Population Studies 50 27–34. [Google Scholar]
- Zhai Z and Chen W (2007). Research of China’s Total Fertility Rates in Late 1990s (in Chinese). Demographic Research (in Chinese) 31 19–31. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


