New insights into ice multiplication using remote-sensing observations of slightly supercooled mixed-phase clouds in the Arctic

Significance

During secondary ice events, ice particle number concentrations in mixed-phase clouds can increase by orders of magnitude with profound implications for the cloud evolution. However, characterization of secondary ice events in the natural environment has been a challenge for the community for decades. We show the long-term frequency of secondary ice events in Arctic supercooled clouds for temperatures warmer than −${\mathrm{10}}^{\hspace{0.17em}○}$C, made possible by applying a remote-sensing technique to 6 y of data. Secondary ice events are found to occur preferentially in the presence of drizzle droplets, compared with the better-known rime-splintering process, causing up to a 1,000-fold enhancement in ice number concentration. These results provide critical insights for model parameterizations and future laboratory experiments.

Abstract

Secondary ice production (SIP) can significantly enhance ice particle number concentrations in mixed-phase clouds, resulting in a substantial impact on ice mass flux and evolution of cold cloud systems. SIP is especially important at temperatures warmer than −${\mathrm{10}}^{\hspace{0.17em}○}$C, for which primary ice nucleation lacks a significant number of efficient ice nucleating particles. However, determining the climatological significance of SIP has proved difficult using existing observational methods. Here we quantify the long-term occurrence of secondary ice events and their multiplication factors in slightly supercooled clouds using a multisensor, remote-sensing technique applied to 6 y of ground-based radar measurements in the Arctic. Further, we assess the potential contribution of the underlying mechanisms of rime splintering and freezing fragmentation. Our results show that the occurrence frequency of secondary ice events averages to <10% over the entire period. Although infrequent, the events can have a significant impact in a local region when they do occur, with up to a 1,000-fold enhancement in ice number concentration. We show that freezing fragmentation, which appears to be enhanced by updrafts, is more efficient for SIP than the better-known rime-splintering process. Our field observations are consistent with laboratory findings while shedding light on the phenomenon and its contributing factors in a natural environment. This study provides critical insights needed to advance parameterization of SIP in numerical simulations and to design future laboratory experiments.

Mixed-phase clouds, where supercooled cloud droplets and ice particles coexist, are frequently observed in the Arctic (1). These clouds play a critical role in the hydrological cycle and radiative energy balance, and they have unignorable impacts on sea ice loss and warming in the Arctic (2, 3). Recent theoretical and modeling investigations suggest that the number concentration of ice particles in mixed-phase clouds has a significant influence on the evolution of the cloud microphysical properties (4). Improper representation of ice formation compromises simulation of Arctic mixed-phase clouds in climate and regional models, which can cause considerable errors in the simulated radiative budget (5). Extensive modeling and laboratory studies have been conducted in recent years to investigate ice formation by ice nucleation, especially for heterogeneous ice nucleation for which nucleation is catalyzed by ice-nucleating particles (6–9). The fundamental underlying mechanisms of heterogeneous ice nucleation are still not fully understood, and the parameterizations that are widely used in atmospheric models are generated by fitting the results from laboratory experiments for various types of ice-nucleating particles. However, observed ice number concentrations can be several orders of magnitude greater than in simulations, especially in supercooled clouds with the temperature warmer than −${\mathrm{10}}^{\hspace{0.17em}○}$C (hereafter, “slightly supercooled clouds”). In this temperature range, some biological aerosols originating from soil, plants, and the ocean are found to be efficient ice-nucleating particles that can trigger ice nucleation above −${\mathrm{10}}^{\hspace{0.17em}○}$C (10–13). However, these efficient ice-nucleating particles are rare, suggesting that secondary ice production (SIP) is important (14).

The best-known mechanism of SIP in slightly supercooled clouds is the rime-splintering process, also known as the Hallett–Mossop (HM) process. The HM process occurs preferentially for a temperature range of −${\mathrm{3}}^{\hspace{0.17em}○}$C $\sim$ −${\mathrm{8}}^{\hspace{0.17em}○}$C in which small ice splinters are generated during riming. The HM process has been demonstrated in the laboratory using a riming rod rotating in a small chamber filled with supercooled liquid droplets (15). SIP can also be caused by other mechanisms, such as collision fragmentation (16), freezing fragmentation (17, 18), and sublimation fragmentation (19). Details regarding the current understanding of those mechanisms can be found in recent review articles by Field et al. (20) and Korolev and Leisner (21). Among those mechanisms, the HM process is argued to be the most important mechanism for SIP in slightly supercooled clouds (20, 22). However, recent in situ measurements show that substantial numbers of needles and columns (signs of splintering) are observed in mixed-phase clouds without the presence of rimers (i.e., fast falling ice particles). Instead, the presence of large cloud droplets suggests that those observed SIP events are likely due to freezing fragmentation rather than the HM process (23). Pitter and Pruppacher (24) also found in a laboratory wind tunnel study that a noticeable fraction of freezing drizzle drops developed pronounced knobs or spikes, with the spikes breaking off in many cases. The theory of freezing fragmentation is further supported by recent laboratory experiments in which SIP was observed during freezing of a levitated droplet (17, 18). However, conditions for the occurrence of SIP are still poorly known and which SIP mechanism is dominant in mixed-phase clouds is far from clear.

Although laboratory experiments can demonstrate the existence of SIP under certain controlled conditions, the idealized mechanisms used for the studies (e.g., rotating rod or a levitated droplet in a calm environment) are not directly translatable to characterizing SIP processes in atmospheric clouds. Therefore, parameterizations of SIP in models using laboratory data are of debatable accuracy (25) because we still do not understand SIP mechanisms at a fundamental level. Aircraft in situ measurements of ice particles and ice-nucleating particles can help to identify the occurrence of SIP in atmospheric clouds; however, statistical studies using such measurements are severely restricted by the small sampling volumes and limited coverage of aircraft flights (23, 26).

Remote-sensing techniques provide an alternative way to observe atmospheric clouds, offering larger sampling volumes and longer periods compared with in situ measurements. These features are beneficial for observing processes that are transient and/or infrequent, as may be true for SIP. The occurrence of a SIP event in mixed-phase clouds is indicated by the presence of a large concentration of small ice particles, especially at warmer temperatures where these concentrations are unlikely to be due solely to primary ice nucleation. A common foundation of existing radar-based remote-sensing techniques for identification of SIP events includes the detection of small, nonspherical ice particles using polarimetric variables, such as differential reflectivity (${\mathrm{Z}}_{DR}$) (the ratio of the power returned from horizontally versus vertically transmitted and received pulses) and linear depolarization ratio (LDR) (the ratio of cross-polarized versus copolarized power returned with respect to the polarization of transmitted pulses) (27, 28). Close to the time of SIP initiation, radar methods and in situ measurements are challenged alike, as distinguishing small spherical ice particles from cloud droplets is extremely difficult (4). As newly formed small ice particles prefer growing into needle-like ice crystals within the HM temperature zone (between −${\mathrm{3}}^{\hspace{0.17em}○}$C and −${\mathrm{8}}^{\hspace{0.17em}○}$C), they can then alter the value of ${\mathrm{Z}}_{DR}$ and LDR compared with spherical hydrometers, which makes detection of SIP events possible using remote-sensing techniques. Most previous remote-sensing studies of SIP focus on specific cases, for which the thermodynamic properties of the subject mixed-phase clouds are carefully chosen such that the detection of nonspherical ice particles is a readily apparent signal of a SIP event in a small dataset (29, 30).

In this study, we obtain a statistical understanding of SIP events. A remote-sensing technique is used to identify SIP events occurring within 6 y (March 2013 to May 2019) of ground-based observations of slightly supercooled liquid clouds. As detailed later, the technique determines the presence of SIP events using joint thresholds of radar LDR and spectral reflectivity and, moreover, quantifies the enhancement of needle-like particle concentrations (i.e., multiplication) based on the spectral reflectivity with respect to a base threshold. We link the occurrence of SIP to the presence of rimers and drizzle, and we estimate the enhancement in ice number concentration with respect to rimer velocity and drizzle size. We show that SIP events can significantly impact ice number concentrations locally when they occur, and we are able to assess the relative importance of two SIP mechanisms, finding that freezing fragmentation is more productive at SIP than the rime splintering normally regarded as the leading process for SIP.

Results

Occurrence of Secondary Ice Events.

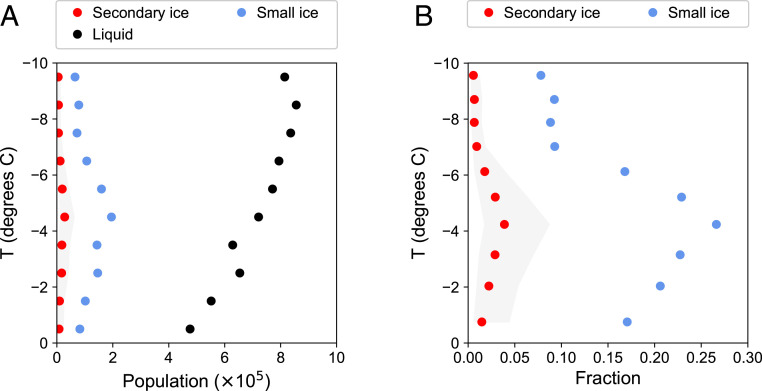
We first investigate the occurrence of secondary ice events within each radar range gate, which is a cylindrical sampling volume of about 380 ${\mathrm{m}}^3$, measuring 4 m in diameter and 30 m in height. Fig. 1A shows the population of three radar range-gate classes: those that contain liquid cloud droplets and two subsets that additionally contain either small ice particles (only) or secondary ice particles. The population of each class is binned in ${\mathrm{1}}^{\hspace{0.17em}○}$C intervals. Results show that the population of range gates containing liquid droplets increases from 5$\times {\mathrm{10}}^5$ at −${\mathrm{1}}^{\hspace{0.17em}○}$C to more than 8$\times {\mathrm{10}}^5$ below −${\mathrm{6}}^{\hspace{0.17em}○}$C, while the population of the small ice class is approximately four to five times smaller than its cloud droplet superset. The population of range gates containing secondary ice particles is one order of magnitude smaller than its cloud droplet superset, suggesting that secondary ice events are uncommon in slightly supercooled clouds. The population of range gates containing small ice particles and those with secondary ice particles both peak around −${\mathrm{5}}^{\hspace{0.17em}○}$C. This is the well-known temperature region for which the Hallett–Mossop process is most efficient. This is also the temperature region most favorable for the growth of ice needles and columns, to which radar linear depolarization ratio is sensitive. The ratio of the range-gate population containing secondary ice particles to its cloud droplet superset shows the relative frequency of secondary ice events in slightly supercooled liquid clouds. Here we divide all range gates containing cloud droplets into 10 subgroups with equal population according to temperature. Results show that the occurrence of secondary ice events ranges from 1% to 10% depending on the reflectivity threshold used, with a maximum at around −4.${\mathrm{5}}^{\hspace{0.17em}○}$C (Fig. 1B). This shows the frequency of occurrence of secondary ice events in natural, slightly supercooled clouds, based on a robust, long-term statistical dataset.

Fig. 1.

(A) Population of radar range gates in a slightly supercooled cloud for the following conditions: black, range gate contains cloud droplets; blue, range gate contains small ice particles (and cloud droplets); and red, range gate contains secondary ice particles (and cloud droplets). Small ice particles exist if LDR is at least −16 dB, while secondary ice particles exist if, additionally, the spectral reflectivity is at least −21 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$ (Materials and Methods). Confidence of the existence of secondary ice particles increases with greater reflectivity. The red points represent the spectral reflectivity threshold of −16 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$, while the lower and upper boundaries of the gray shading represent the spectral reflectivity thresholds of −21 and −11 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$. (B) Fraction of range gates containing small ice particles (blue) and secondary ice particles (red) relative to the number of range gates containing cloud droplets (black dots in A). The set of all range gates containing cloud droplets is divided into 10 subsets of equal population, ordered by temperature.

It is important to note several sources of uncertainty impacting our determination of the occurrence of secondary ice events. First, near the crossover boundary between the small ice and secondary ice reflectivity regimes, a certain amount of “noise” from the small ice subset unavoidably infiltrates and contaminates the secondary ice subset, resulting in an overestimate of weak (i.e., low number) multiplication events. Choosing a larger reflectivity threshold value would lead to fewer identified secondary ice events with the advantage of greater confidence. In Fig. 1, the edges of the gray uncertainty envelope are determined by applying thresholds of −11 and −21 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$. We use the same scheme to depict uncertainty in Figs. 2 and 3. Second, newly formed secondary ice particles are not instantaneously asymmetrical or large enough to be detected by LDR, resulting in an underestimation of secondary ice events. Third, as distance increases from the source region, dilution and transport might decrease the concentration of secondary ice particles such that their reflectivity falls below the detection threshold. Finally, the observed occurrence of secondary ice events necessarily involves a scale dependency. Results in Fig. 1B are based on range gates with a volume of about 380 ${\mathrm{m}}^3$. Increasing that sampling volume by aggregating multiple gates, or even by using a whole cloud entity, would increase the opportunity to observe secondary ice particles within it and, thus, increase the apparent occurrence of secondary ice events. Therefore, the definition of sampling volume should be considered carefully when our results of the occurrence of secondary ice events are compared with other studies or parameterized in models.

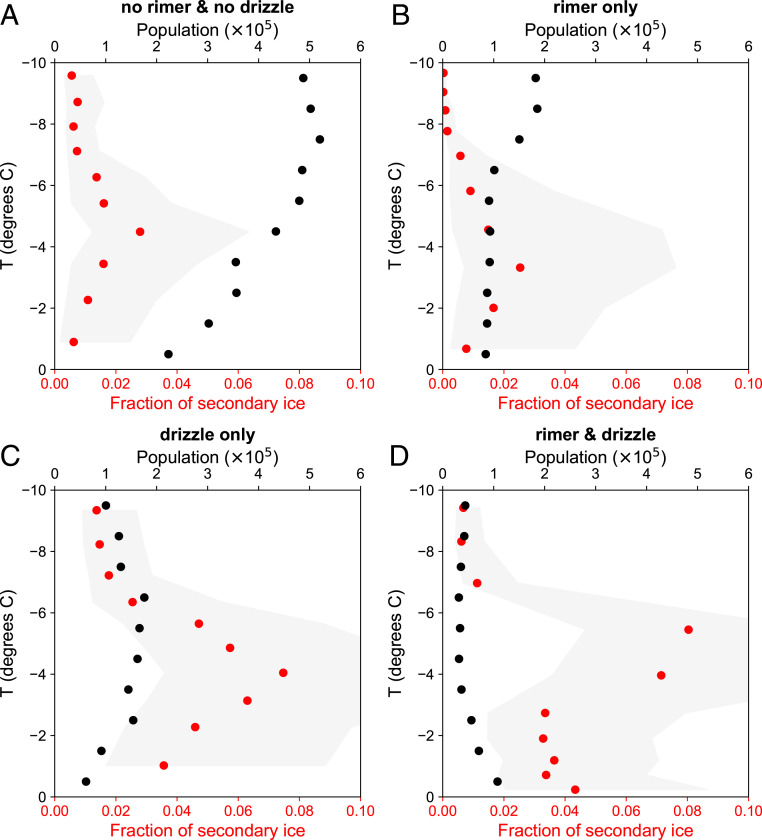
Fig. 2.

Population of range gates containing cloud droplets (black dots; top axis) binned into $1^{○}$ intervals, and fraction of secondary ice events relative to the number of range gates containing cloud droplets (red dots; bottom axis) binned into 10 subsets with equal population. A–D show four subclasses: (A) neighborhoods without rimer or drizzle, (B) those with rimer only, (C) those with drizzle only, and (D) those with both rimer and drizzle. As in Fig. 1, the edges of the gray shading depict secondary ice events with reflectivity threshold of −21 and −11 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$, while the red dots correspond to events of −16 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$.

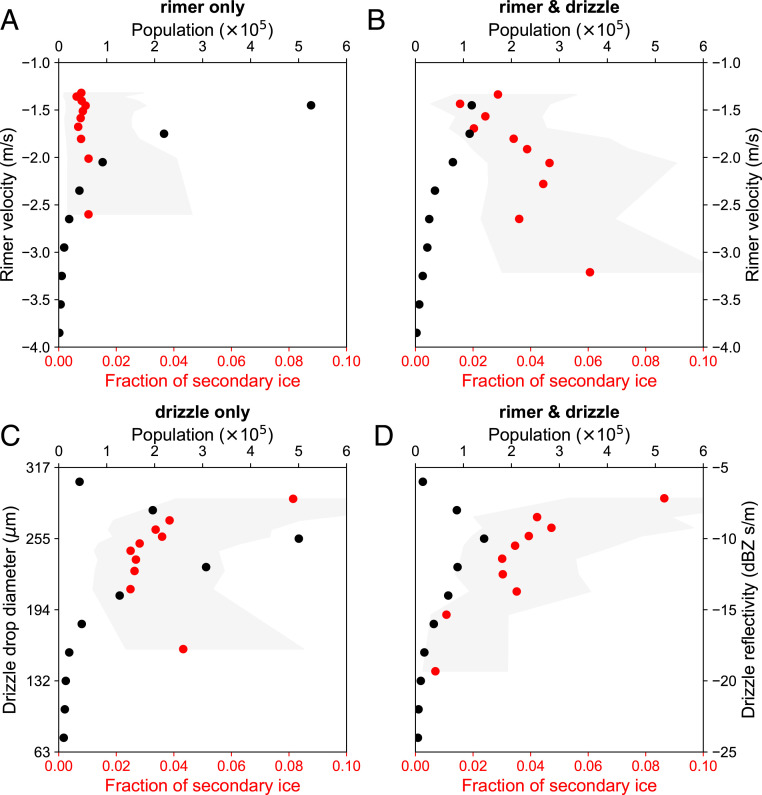
Fig. 3.

The influence of neighborhoods’ rimer velocity and drizzle drop diameter on the fraction of secondary ice events vs. rimer velocity (A and B) and drizzle size (C and D). Drizzle drop diameter is associated with drizzle spectral reflectivity (right y axis in D). A and B are binned by rimer velocity every 0.3 m$\cdot {\mathrm{s}}^{-1}$, and C and D are binned by drizzle spectral reflectivity every 2 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$.

Effects of Drizzle and Rimer on Secondary Ice Production.

Laboratory experiments have shown convincing evidence for the formation of secondary ice particles due to rime splintering (15) and freezing fragmentation (17, 18), which are believed to be the two most important mechanisms for SIP in mixed-phase clouds (20). Those experimental results find that SIP is related to the speed of small moving rods (a rimer proxy) for the rime splintering and drizzle size for the freezing fragmentation. Sullivan et al. (25) parameterized the secondary ice process based on laboratory experiments and used the parameterization in a numerical model to explore the thermodynamic conditions conducive to the occurrence of SIP. However, little is known about the conditions leading to the occurrence of SIP in real clouds. Here, we investigate the relationship between the SIP observed in a radar sampling volume and rimer and/or drizzle observed in its surrounding local neighborhood, defined as all gates within a 2-min window and a vertical extent of 200 m (detailed in Materials and Methods). The rimer and drizzle quantification methodology is presented in detail at the end of this paper. We focus on the following two questions: 1) How often do secondary ice events occur in conjunction with the presence of rimer and/or drizzle? 2) Is rimer velocity or drizzle drop size related to the occurrence of secondary ice events?

Each range gate containing slightly supercooled liquid water is categorized according to one of four subclasses based on the properties of its local neighborhood: The neighborhood contains neither rimer nor drizzle, contains rimer only, contains drizzle only, or contains both rimer and drizzle. Analysis indicates that the total number of range gates per cloud thickness has a decreasing trend with an increase in liquid cloud thickness for each subclass (SI Appendix, Fig. S1). For each of these four subclasses, a histogram of class occurrence versus temperature is shown by the black dots in Fig. 2. Results show that the class without rimer or drizzle has the largest population compared with the other classes. This class is defined as the background class, as secondary ice events cannot be attributed to the presence of rimer or drizzle. In the background class, the secondary ice particles might still have originated through rime splintering or freezing fragmentation, but with their precursors (rimer and/or drizzle) outside the local neighborhood region, or they may result from other mechanisms altogether.

The fractions of secondary ice events versus temperature in each class are shown in Fig. 2. The fraction is calculated as the ratio of the number of range gates containing secondary ice particles to the total number of gates, in temperature bins of equal sample population. Note that the fractions of secondary ice events have a distinctive peak around −${\mathrm{5}}^{\hspace{0.17em}○}$C for all classes. This feature might imply that −5 °C is the preferential temperature region for secondary ice production, such as by the Hallett–Mossop process. But it might also be linked to the use of high LDR values to identify small ice particles. Because −5 °C is the most favorable growth temperature regime for needle particles, our method likely has maximum sensitivity to SIP at this temperature range and may underestimate SIP away from it. We note that this issue is not unique to our method as the same limitation affects analyses of in situ aircraft observations. It should be mentioned that secondary ice particles that form at a higher altitude, colder temperature region grow relatively slowly in diameter (31). When they reach the −3 to −8 °C temperature region, it is possible they cannot be detected because they had insufficient time to grow into a needle, particularly when the supercooled liquid layers are often thin (SI Appendix, Fig. S2).

Results show that the fraction of secondary ice events in the rimer-only class is similar to that of the background, while the fraction in the drizzle-only class is two to three times larger, suggesting that drizzle is a more important factor in SIP than rimer. The class with coexisting rimer and drizzle has a slightly higher peak compared with the drizzle-only class, suggesting that the presence of rimer within drizzling conditions may further enhance the occurrence of secondary ice events. Compared with the drizzle-only class, the uncertainty envelope is shifted toward greater secondary ice fractions. This shift is important because, as we examine in further detail below, infrequent but highly productive ice multiplication events become significant (i.e., those surpassing a very high reflectivity threshold). Note that this class, as well as the rimer-only class, does not show an enhancement in the fraction of secondary ice events at the coldest temperatures (below −${\mathrm{7}}^{\hspace{0.17em}○}$C), which is interesting and worthy of future investigation.

We now investigate the influence of rimer velocity and drizzle drop size on the occurrence of secondary ice events, as present-day understanding of both relies substantially on laboratory experiments and neither one is well understood for natural conditions. This study examines rimers with fall speed between 1.2 and 4.0 m/s and drizzle drops with fall speed between 10 and 90 cm/s (i.e., those having diameters between 60 and 245 $\mathrm{\mu }$m; SI Appendix, Table S1). Quantification of rimer velocity and drizzle size is detailed in Materials and Methods. In Fig. 3A, results show that for the rimer-only class, the fraction of secondary ice events is generally insensitive to the rimer velocity, except that the right boundary (corresponding to the spectral reflectivity threshold of −11 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$) slightly increases with the rimer fall velocity, suggesting an increase in low-yield (i.e., low-number multiplication) events. For the drizzle-only class (Fig. 3C), the fraction of secondary ice events is larger than that of the rimer-only class, which is consistent with Fig. 2. Additionally, the fraction is more sensitive to drizzle size compared to rimer velocity. For the rimer-and-drizzle class, the fraction of secondary ice events increases faster with rimer velocity compared with the rimer-only class (Fig. 3B), while the behavior is similar for drizzle size compared with the drizzle-only class (Fig. 3D). These results suggest that larger drizzle drops or faster rimer particles in the presence of drizzle are more conducive to SIP, which is consistent with laboratory experiments (15, 17, 18). Our results semiquantitatively show the effect of rimer and drizzle on SIP in natural clouds.

Enhancement of Ice Number Concentration.

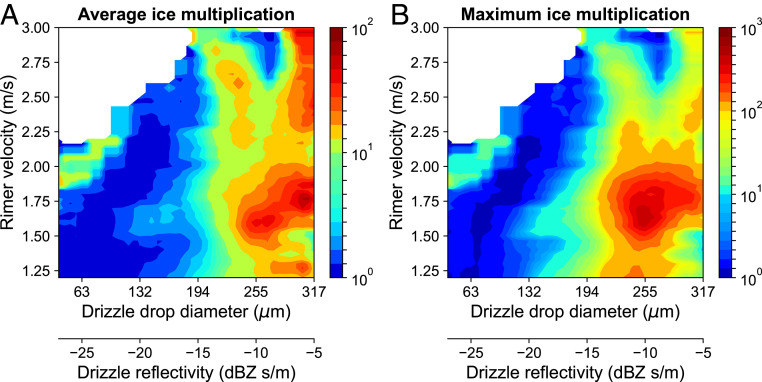
We now investigate the joint effects of rimer velocity and drizzle drop size on number concentration of secondary ice particles. To quantify these effects, we use ice multiplication number, defined as the ratio between the detectable ice number concentration due to SIP and the background ice number concentration (detailed in Materials and Methods). Results show that ice multiplication number is more sensitive to drizzle drop size compared with rimer velocity (Fig. 4). The average ice multiplication number for larger drizzle sizes shows a bimodality with rimer velocity, with a first peak around 1.7 m$\cdot {\mathrm{s}}^{-1}$, a valley around 2.1 m$\cdot {\mathrm{s}}^{-1}$, and a second broader peak extending beyond 3.0 m$\cdot {\mathrm{s}}^{-1}$ (Fig. 4A). Note that a similar bimodality with rimer velocity has been observed in laboratory experiments by Hallett and Mossop (15). The average ice multiplication number can be up to 100 for larger drizzle sizes, while the maximum ice multiplication number (Fig. 4B) can be close to 1,000 when the rimer velocity is close to 1.6 m$\cdot {\mathrm{s}}^{-1}$ and the drizzle drop diameter is about 255 $\mathrm{\mu }$m (associated with drizzle spectral reflectivity of −10 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$). These results demonstrate that SIP can lead to three orders of magnitude enhancement in ice number concentration, but that such occurrences are infrequent.

Fig. 4.

Ice multiplication as a function of rimer velocity and drizzle drop diameter. The color bars in A and B represent the average and maximum ice multiplication numbers over the full dataset, respectively, which are both unitless quantities. Drizzle drop diameter is associated with drizzle spectral reflectivity (second x axis). Note the different scales for the color bars.

Impact of Secondary Ice Production within a Local Region.

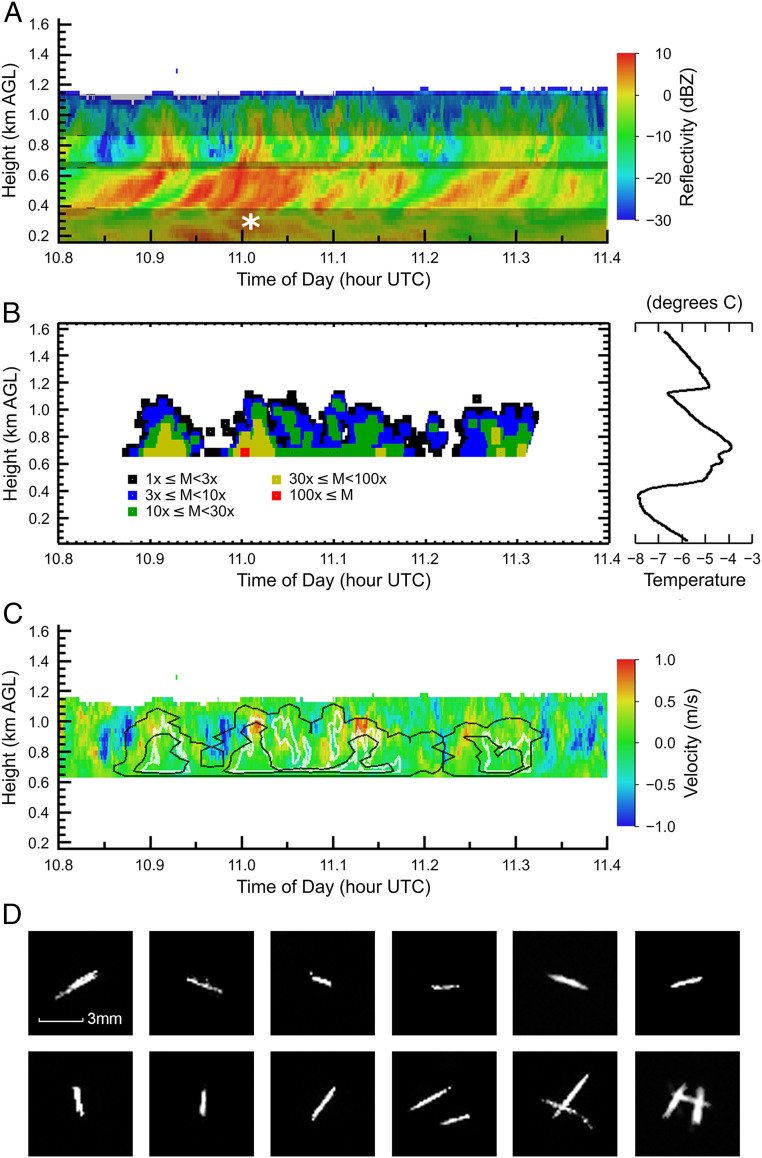
Although the occurrence of secondary ice events is below 10% in slightly supercooled clouds (Figs. 1–3), we will show that secondary ice events might be clustered in a short period and have a significant impact on ice number concentration and precipitation within a local region. An example is shown in Fig. 5, which was observed at the Utqiaġvik Atmospheric Radiation Measurement (ARM) site on 11 May 2019 at around 11 Coordinated Universal Time (UTC). A radiosonde launched just after 11 UTC (marked with a white asterisk) identified three liquid layers (>98% relative humidity), shown by the gray shading overlaying the time–height plot of radar reflectivity in Fig. 5A. It is important to note that our retrievals exclusively use the radar’s high-sensitivity “chirp” mode, which has a minimum operational range of 690 m. Therefore, secondary ice events can only be seen in the top liquid layer (between 850 and 1,150 m). However, to provide full spatial context, Fig. 5A includes observations down to the minimum available short-pulse range of 160 m. Fig. 5B shows the identified secondary ice events in the upper liquid layer as well as their ice multiplication numbers in five ranges. It can be seen that the secondary ice events between 10.9 and 11.3 UTC are clustered. In fact, the average occurrence of the secondary ice events during this period is 33%, much higher than the 6-y statistical average (up to 10%). In addition, the occurrence of secondary ice events can be significantly higher in a local neighborhood region, with a maximum value of 78% at around 11.28 UTC (179 events of 230 range gates in that neighborhood region). Ice multiplication number is smaller close to the top of the liquid layer and larger close to its base. This trend might be due to more efficient production of secondary ice particles in the lower part of the liquid layer or from the depositional growth of secondary ice particles from freshly generated small spherical particles (low reflectivity and low LDR) into larger nonspherical shapes that can be detected (high reflectivity and high LDR), or both. We note that the liquid layer exists entirely within the preferential temperature zone for the depositional growth of needles. Fig. 5C shows the vertical air motion, retrieved by removal of the particle sedimentation velocity from the mean Doppler velocity. This is accomplished by subtracting the time series of mean Doppler velocity from its average for each range gate during the time period from 10.8 to 11.4 UTC. It is interesting to note that updraft air velocity has a strong spatial correlation with both the large ice multiplication number zones and the zones of reflectivity maxima. Our results suggest a connection between SIP and dynamics, which is worth further investigation. Surface observations show a burst of snow precipitation during this period. Most of the precipitation particles are needles, consistent with key assumptions of our methodology, with a few in a simple aggregated form. Some needles recorded by the multiangle snowflake camera (MASC) at the surface are shown in Fig. 5D, and a video of all MASC ice particle observations can be seen in Movie S1. Furthermore, analysis of the 7-mo period of MASC images recorded during our study shows a strong correlation between the number of needles observed by the MASC and the magnitude of ice multiplication events determined by our method (SI Appendix, Fig. S3), supporting our methodology.

Fig. 5.

Secondary ice events observed at the Utqiaġvik ARM site on 11 May 2019 around 11 UTC. (A) Time–height radar reflectivity (dBZ) between 10.8 and 11.4 UTC. The white asterisk marks the time when a radiosonde was launched. Three liquid layers identified by the radiosonde profile are shown by the gray-shaded regions. (B) Secondary ice events and their ice multiplication numbers (M, a unitless quantity) in five ranges retrieved for the upper liquid layer. B, Right shows the temperature profile from the sounding. (C) Retrieved air vertical velocity (m/s). The black line shows the 1× (outer) and 10× (inner) contours of ice multiplication, and the white line shows a high-reflectivity (−3 dBZ) contour (compare to A). (D) Examples of precipitated particles observed at the surface by the multiangle snowflake camera.

Conclusion

Long-term statistics are demonstrated in the atmosphere for the occurrence of secondary ice events in slightly supercooled clouds (${\mathrm{0}}^{\hspace{0.17em}○}$C to −${\mathrm{10}}^{\hspace{0.17em}○}$C) and their connection with rime splintering and freezing fragmentation. The findings are based on 6 y of Arctic ground-based remote-sensing observations at Utqiaġvik, Alaska. These results are made possible by the development of a remote-sensing retrieval method described in Materials and Methods that identifies the occurrence of secondary ice events, their multiplication number, the amount of precursor rimer and drizzle present, and, respectively, their fall velocity and drizzle size. The methodology is based on polarimetric data from the Doppler spectra of a zenith-pointing cloud radar combined with measurements from balloon soundings, for characterization of the thermodynamic profiles and identification of supercooled liquid layers.

Results show that the overall occurrence of secondary ice events for the entire dataset is less than 10%, recognizing that the percentage has a scale dependency on the sampling volume. The fraction is even lower for higher-reflectivity thresholds, suggesting that secondary ice events are not common in slightly supercooled clouds at Utqiaġvik. However, although uncommon, once an event occurs it can have a significant impact on ice number concentration and precipitation in a local region. A case study shows that secondary ice events were spatiotemporally clustered, with a maximum density reaching 78% occurrence in a local neighborhood region. The high ice multiplication zones are clearly correlated with the columns of updraft air motion, suggesting that dynamics play a role in SIP.

We characterize the relative importance of the rime-splintering and freezing fragmentation mechanisms to SIP by linking the detected secondary ice events to the existence of rimer and drizzle within their local neighborhood regions. Results show that the occurrence of secondary ice events is higher when only drizzle exists compared to when only rimer exists, and the event occurrence is highest when both rimer and drizzle exist. Rimer velocity does not affect the secondary ice event occurrence for the rimer-only cases, but it does have a large effect when rimer and drizzle coexist. Increase in drizzle drop size consistently correlates with an increase in the occurrence of secondary ice events. Ice multiplication number is also more sensitive to drizzle drop size than rimer velocity. Our results suggest that freezing fragmentation is a more productive and efficient way to generate secondary ice particles in slightly supercooled clouds compared with rime splintering.

Previous studies on this topic have been based either on laboratory experiments or on episodic aircraft observations. While laboratory studies provide insights, observations in the atmosphere have been limited in scope owing to the difficulty in building statistics from short-term aircraft flights. This study investigates secondary ice processes in slightly supercooled clouds using long-term observations. Results in this study shed light on two fundamental unsolved questions related to SIP: 1) the conditions under which SIP occurs and 2) the extent to which ice number concentration is enhanced during SIP events. Our technique can be readily applied to different sites with a suitably long-term observational record. Knowing that freezing fragmentation is likely more significant to SIP than rime splintering for these cloud conditions may be of immediate benefit to the modeling community and provide important guidance to future research efforts for laboratory experiments and in situ measurements.

Materials and Methods

The US Department of Energy (DOE) operates a number of sophisticated ground-based atmospheric remote-sensing observatories in climatologically important locations worldwide through its ARM user facility. One of the longest continuously running sites has collected data at Utqiaġvik (formerly Barrow) on the North Slope of Alaska for over two decades. In this study, we analyze 6 y of data from March 2013 to May 2019 obtained at Utqiaġvik by the Ka-band zenith-pointing profiling radar (KAZR) in conjunction with in situ atmospheric state variables measured by radiosondes launched on average twice daily. Due to the high temporal resolution of the KAZR (one profile every 3.7 s), radar observations may be restricted to those occurring within close proximity of a radiosonde, in both time and distance, and still maintain a very large dataset. Thus, a radiosonde measurement provides a reasonably accurate determination of the vertical boundaries of and temperature within mixed-phase cloud around the radar observations for feature analysis.

Dual-polarized radar Doppler spectra are a rich source of information from which we can identify and quantify the presence of secondary ice particles and their precursors. Radar Doppler spectra resolve returned echo power into discrete bins according to the fall velocity of the target particles. From these spectra, we can infer the simultaneous presence of multiple hydrometeor classes within an observation volume—the properties of rimers, secondary ice particles, and drizzle drops can be quantified based on their contribution to their respective characteristic Doppler velocity ranges. Furthermore, the KAZR measures the electromagnetic polarization for each velocity bin, which depends on particle shape, allowing determination of particle aspect ratio for further discrimination of the particle classes.

Specifically, the radar Doppler spectra used for this study are limited to those occurring within 15 min and 4 lateral km of a balloon sounding, where relative humidity is above 98% and temperature is between 0 and −${\mathrm{10}}^{\hspace{0.17em}○}$C (SI Appendix, Fig. S4A). We define these temperature and relative humidity conditions to be slightly supercooled liquid in this study. A vertically continuous sounding observation meeting these criteria is assumed to have the lateral spatiotemporal extent stated above. The length of each KAZR range gate is 30 m. Each range gate within a slightly supercooled liquid layer contributes its properties to the overall SIP statistics; in some of our analyses, these properties are evaluated in conjunction with those of the surrounding range gates within 2 min duration and 200 m vertical extent to capture potential causal links (SI Appendix, Fig. S4B). Here, these two cases are referred to, respectively, as the central range gate and local neighborhood. In total, we have analyzed over 9 million range gates, most of which are in shallow supercooled liquid layers having thickness less than 360 m (SI Appendix, Fig. S2).

As stated previously, three types of hydrometers—secondary ice particles, rimers, and drizzle drops—are identified based on their unique Doppler spectra fingerprints, as shown in SI Appendix, Fig. S4C. Specifically, a decision tree as shown in SI Appendix, Fig. S5 is used for the identification process. Doppler spectra are first preprocessed as follows: A first-order removal of the contribution of vertical air motion to spectral velocity is performed by shifting each spectrum in velocity such that its upward edge velocity is 28 cm/s (32). The value of 28 cm/s accounts for the typical effect of spectral broadening due to turbulence. Next, the bin velocities of each Doppler spectrum are compensated for the effect of air density on terminal fall speed by multiplication with a scale factor (33). We define rimer to be radar echos with a downward modal spectral velocity between 1.2 and 4 m$\cdot {\mathrm{s}}^{-1}$, although occurrences approaching 3.0 m$\cdot {\mathrm{s}}^{-1}$ are rare. The faster-falling limit is used to eliminate any potential particles irrelevant to our study, such as large rain drops. The slower-falling limit of 1.2 m$\cdot {\mathrm{s}}^{-1}$ provides 30 cm$\cdot {\mathrm{s}}^{-1}$ of separation from the slower-falling particle classes (described next), which constitutes six Doppler spectrum velocity bins given the KAZR’s 4.66-cm/s velocity resolution. The modal velocity of its Doppler spectrum is assigned to be the range gate’s rimer velocity. For all range gates belonging to a local neighborhood, the mean value of these rimer velocities represents the neighborhood’s rimer velocity. Drizzle is defined to be radar echos with a downward velocity between 10 and 90 cm$\cdot {\mathrm{s}}^{-1}$, LDR less than −23 dB, and constrained by the following Z-V relationship: $|\left(-27.0-Z_{driz}\right)/18.0-V_{driz}|$ < 0.1. In practice, occurrences in our dataset faster than 60 cm$\cdot {\mathrm{s}}^{-1}$ are uncommon. The relationship is determined empirically from ARM drizzle observations in the maritime Eastern North Atlantic (ENA) and Utqiaġvik from warm (>${\mathrm{0}}^{\hspace{0.17em}○}$C) near-cloud-base, subcloud conditions during light drizzle (34–36). The velocity range implies coverage of drop sizes from roughly 60 to 245 $\mathrm{\mu }$m in diameter (37). This approach provides a rough estimate of the dominant reflectivity-weighted drizzle drop size, but does not attempt to determine the full drizzle drop size distribution. Furthermore, the maximum reflectivity in this drizzle velocity range (10 to 90 cm$\cdot {\mathrm{s}}^{-1}$) is required to be at least 15.0 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$ greater than that between 130 and 115 cm$\cdot {\mathrm{s}}^{-1}$, where this latter velocity band forms a barrier to prevent potential “crosstalk” from rimer echos. Here, reflectivity is used as a proxy for drizzle size. The corresponding terminal velocity can be associated with a drizzle drop size, following Beard (37), as shown in SI Appendix, Table S1. The mean value of the drizzle reflectivities within a local neighborhood is used to represent the neighborhood’s drizzle size. We define small ice to be radar echos with a downward velocity between 10 and 90 cm$\cdot {\mathrm{s}}^{-1}$ and have an LDR greater than −16 dB. Studies have shown needle and columnar ice habits to be associated with LDR around this value (38, 39). Furthermore, we define secondary ice to be the subset of small ice having a reflectivity of at least −21 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$. Five examples of actual Doppler spectra from our dataset containing different combinations of these particle classes are shown in SI Appendix, Fig. S6.

We now justify the reflectivity criterion to identify secondary ice particles, as it is the foundation for studying the secondary ice events. By definition, secondary ice events increase the local concentration of small ice particles above the background level. This can be observed by radar through an increase in reflectivity. However, a particle size increase will also increase reflectivity (and, in general, fall velocity). To illustrate that the number (not the size) effect on reflectivity dominates here, we separate our dataset into two subsets both within −5 $\pm \hspace{0.17em}{\mathrm{1}}^{\hspace{0.17em}○}$C: one containing rimer, as defined above, and one without. Note that slightly supercooled cloud within this temperature range is the optimal condition for the production of secondary ice particles through the HM process. The contrast between cases with and without rimers can inform the criteria of reflectivity and LDR to be used to separate “background” small ice and secondary ice. SI Appendix, Fig. S7 shows occurrence contour plots of only the slowly falling particles (10 to 90 cm$\cdot {\mathrm{s}}^{-1}$) from these two subsets. When rimer is absent, the peak population for nonspherical small ice particles (LDR $\ge$ −16 dB) has a spectral reflectivity centered around −30 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$; when rimer is present, nonspherical small ice particles dominate at spectral reflectivities larger than −21 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$. Because we constrain the particle size by considering only a narrow, slowly falling range of the Doppler spectrum, the enhancement of reflectivity in the subset with rimer must be due to increased number concentration, not size, which we infer to be SIP. SI Appendix, Fig. S7 also shows two additional thresholds of spectral reflectivity at −16 and −11 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$ that correspond to, respectively, 5 and 10 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$ above the −21 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$ threshold that are used to derive uncertainty estimates in the main text.

We have thus far established a threshold for the detection of a secondary ice event based on reflectivity of a specific subset of Doppler spectra bins. Furthermore, we have demonstrated that this spectral reflectivity enhancement is primarily driven by ice particle number concentration rather than size (SI Appendix, Fig. S7). Thus, we can now translate the amount by which this reflectivity exceeds the detection threshold (−21 dBZ$\cdot$s$\cdot {\mathrm{m}}^{-1}$) into a quantitative estimate of the enhancement in ice number concentration due to SIP (called ice multiplication number). An increase of 3 dBZ in spectral reflectivity means a doubling in number (ice multiplication number of 2); likewise, a 10-dBZ increase indicates an order of magnitude increase in number (ice multiplication number of 10). Evaluation of our method in terms of the number enhancement or multiplication that we associate with SIP requires a robust statistical approach. We obtained such an evaluation using all 7 mo of data from the MASC that overlapped with our analysis period. We applied digital image analysis to all 800,000 camera images to obtain a count of needles occurring in each image. We then computed the maximum needle count from the MASC images within $\pm$25 min of each sounding profile and plotted it against the maximum reflectivity of secondary ice identified by our method. Results in SI Appendix, Fig. S3 show a clear correlation between maximum reflectivity of small ice in the supercooled liquid layers and the surface-observed needle concentrations, supporting our methodology identifying secondary ice events.

Note that we not only investigate Doppler spectra in the central range gate but also link the central range gate to its nearby neighborhood. There are several reasons for doing this. First, newly formed secondary ice particles are usually small and quasi-spherical, making them difficult to distinguish from liquid drops even for in situ measurements (20), not to mention remote sensing. Secondary ice particles need time to grow asymmetrically and large enough to be detected by remote-sensing observations. When we identify the existence of secondary ice particles in one radar range gate, those secondary ice particles, almost by necessity, originated from a region nearby. Second, drizzle and small ice (including secondary ice) occupy the same velocity range within the radar Doppler spectrum (as shown in SI Appendix, Fig. S4C), preventing their reliable detection and measurement in the same range gate. This velocity–range overlap requires us to analyze groups of neighboring range gates to measure the statistical coexistence of drizzle and secondary ice particles. The presence of rimers or drizzle, inferred from the Doppler spectra (SI Appendix, Fig. S4D), is used to study SIP at the process level. For example, a secondary ice event is likely caused by the rime splintering or freezing fragmentation if a rimer or drizzle is nearby. Therefore, linking the secondary ice particles observed in the central range gate to their precursors (rimer and drizzle) in the nearby neighborhood enables investigating the potential mechanisms of the secondary ice events.

Data Availability

KAZR radar Doppler spectra, radiosonde, and MASC data (DOIs: 10.5439/1095603, 10.5439/1095604, 10.5439/1021460) are available from the ARM Data Discovery website (https://www.archive.arm.gov/discovery/). Data needed to evaluate the conclusions are available on the GitHub website at https://github.com/eluke/secondary-ice.