The structure of the native cardiac thin filament at systolic Ca²⁺ levels

Significance

Heartbeats rely on cyclical interactions between myosin thick and actin thin filaments orchestrated by rising and falling Ca²⁺. During systole, Ca²⁺ binds to the thin filament and allows its interaction with the thick filament to produce force required for contraction. The structure of the thin filament at physiological Ca²⁺ levels is unknown, which limits our understanding of the thin filament regulation by Ca²⁺. Here, we directly observe thin filament structural states along individual filaments at systolic Ca²⁺ levels to show that the thin filament is activated stochastically with short-range cooperativity evident only on one strand of the thin filament. We suggest how cardiac muscle can be regulated by a narrow range of Ca²⁺ levels upon transition from diastole to systole.

Abstract

Every heartbeat relies on cyclical interactions between myosin thick and actin thin filaments orchestrated by rising and falling Ca²⁺ levels. Thin filaments are comprised of two actin strands, each harboring equally separated troponin complexes, which bind Ca²⁺ to move tropomyosin cables away from the myosin binding sites and, thus, activate systolic contraction. Recently, structures of thin filaments obtained at low (pCa ∼9) or high (pCa ∼3) Ca²⁺ levels revealed the transition between the Ca²⁺-free and Ca²⁺-bound states. However, in working cardiac muscle, Ca²⁺ levels fluctuate at intermediate values between pCa ∼6 and pCa ∼7. The structure of the thin filament at physiological Ca²⁺ levels is unknown. We used cryoelectron microscopy and statistical analysis to reveal the structure of the cardiac thin filament at systolic pCa = 5.8. We show that the two strands of the thin filament consist of a mixture of regulatory units, which are composed of Ca²⁺-free, Ca²⁺-bound, or mixed (e.g., Ca²⁺ free on one side and Ca²⁺ bound on the other side) troponin complexes. We traced troponin complex conformations along and across individual thin filaments to directly determine the structural composition of the cardiac native thin filament at systolic Ca²⁺ levels. We demonstrate that the two thin filament strands are activated stochastically with short-range cooperativity evident only on one of the two strands. Our findings suggest a mechanism by which cardiac muscle is regulated by narrow range Ca²⁺ fluctuations.

Striated muscle contraction and relaxation is governed by rising and falling Ca²⁺ levels that control actomyosin interactions—the force generating interaction between the thick (myosin) and thin (actin) filaments (1–4). Thin filaments (TFs) are comprised of F-actin, the troponin complex (Tn), and tropomyosin (Tm). Tn itself is a multiprotein complex comprised of the TnI (e.g., inhibitory) subunit, the TnC (e.g., Ca²⁺ binding) subunit, and TnT—the subunit which links the Tn complex to the Tm cable. During muscle activation, conformational changes within Tn caused by Ca²⁺ binding to its TnC subunit allosterically relieve the Tm-induced actomyosin inhibition (4–6). Kinetics, biochemical, and structural studies led to the steric blocking model of muscle regulation, which holds that at low Ca²⁺ (relaxing) conditions, Tm blocks myosin binding sites on the actin surface, whereas at high Ca²⁺ (activating) conditions, Tm moves away from the myosin binding sites (5, 7). Early electron microscopy (EM) studies of negatively stained TFs identified three structural states for Tm, termed “blocked,” “closed,” and “myosin” (“open”), which corresponded to relaxed, activated, and myosin-bound conditions, respectively (8). Later, structural analysis of frozen hydrated cardiac TFs (9) updated the positioning of the Tm on the surface of the TF and showed that at either relaxing or activating conditions, Tm was not constrained in one structural state but rather was distributed among the three structural positions on the surface of the TF. In all aforementioned studies, a helical approach to three-dimensional (3D) reconstruction was applied to the TFs since the actin filament, which comprises the backbone of the TF, is a helical structure (10). On the other hand, the periodicity of the TF regulatory units (RUs) comprised of one Tm and one Tn complex bound to seven actin protomers along the actin filament is not consistent with the symmetry of the actin helix. For that reason, the helical approach to 3D reconstruction of the TF generates helically averaged Tm densities while eliminating any information on the structure of the Tn complex. Despite those shortcomings, the helical approach to frozen hydrated TFs accurately predicted the range of Tm swing upon activation of the TF and showed a rocking movement of the Tn on the surface of the TF (9). The revolutionary work by Yamada et al. (6) utilized a nonhelical algorithm for reconstruction of the cardiac TF and for the first time ever showed structural transition of the TF RUs from Ca²⁺ free to the Ca²⁺-bound state. While this important study enormously advanced our understanding of the TF regulation, the use of recombinant proteins expressed in a heterologous system without the naturally occurring posttranslational modifications found in the mammalian heart left some questions regarding how accurately the structures represented native cardiac TFs. Furthermore, the structures were obtained in a nonphysiological either Ca²⁺-free (pCa ∼9) (subdiastolic) or excessive (pCa ∼3) suprasystolic Ca²⁺ levels. However, in the working heart, the intracellular Ca²⁺ concentration fluctuates within a range of 0.1 (pCa ∼7) to 1.0 µM (pCa ∼6) during the cardiac cycle (11). Therefore, to understand the mechanism(s) of the TF activation, it was imperative to perform structural studies at physiological Ca²⁺ levels.

Here, we used native cardiac TFs to carry out cryogenic EM (cryo-EM) structural studies at systolic (pCa = 5.8) Ca²⁺ levels. The cryo-EM structures and the use of statistical tools in analysis of individual frozen hydrated native cardiac TFs allowed us to develop a model for the structural state of the cardiac TF at systolic Ca²⁺ levels. We demonstrate that the cardiac TF has a network of weakly correlated structural states and operates as a stochastic Ca²⁺-controlled machine.

Results

Comparison of Reconstituted and Native TF Structures at Low (pCa = 8) and Saturating (pCa = 4) Levels.

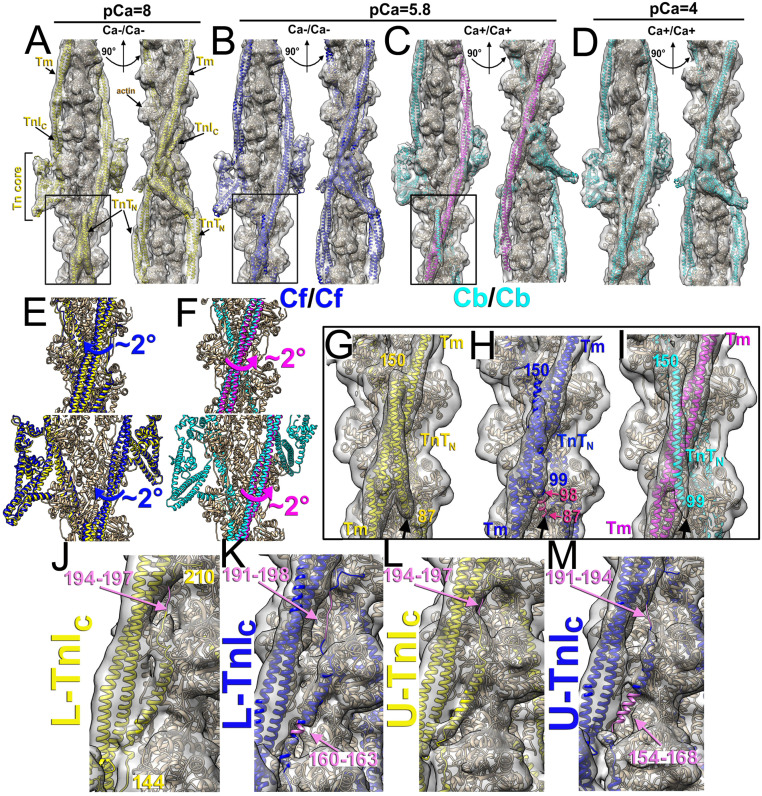
The first structure of the cardiac TF complex was obtained using reconstituted TFs with an approximate 21-fold excess of Tm and Tn over its stoichiometry in the native TF (6). We therefore sought to determine whether the structure of the native cardiac TF is comparable to the structure of the reconstituted TF. We verified the integrity of the porcine native cardiac TFs used for cryo-EM by looking at its composition (SI Appendix, Fig. S1A) and response to Ca²⁺ levels (SI Appendix, Fig. S1B). The 93.5% inhibition of the TFs at pCa = 8 (SI Appendix, Fig. S1B) confirmed the integrity of the TFs. Since protein kinase A (PKA) biphosphorylation of cTnI serines 23 and 24 has been shown to reduce TF Ca²⁺ sensitivity (12), we determined the basal level of phosphorylation of these residues in our TFs (SI Appendix, Fig. S2A). We found only monophosphorylated cTnI species, which accounted for ∼51% of all cTnI units (SI Appendix, Fig. S2 B and C). The absence of biphosphorylated cTnI units suggested that our TFs did not possess reduced Ca²⁺ sensitivity. Since the original studies were obtained in the nominal absence (pCa ∼9) or excessive (pCa ∼3) levels of Ca²⁺, we followed the same strategy and used a single particle approach to reconstruct native cardiac TFs at either pCa = 8 (Fig. 1A and SI Appendix, Fig. S3) or pCa = 4 (Fig. 1B and SI Appendix, Fig. S4). Reconstruction of native TFs was more challenging than that for reconstituted TF (6) due to dissociation of the native TF components that was not suppressed by excess Tm and Tn added to the sample. Because of the intrinsic heterogeneity of the sample, we achieved a modest 7.4 Å and 8 Å resolution (using Fourier shell correlation [FSC] criterion of 0.143) for Ca²⁺-bound and Ca²⁺-free structures, respectively (SI Appendix, Fig. S5). Using local resolution measurements in RELION software package (13), we determined the resolution within the actin region to be ∼6 Å dropping to ∼10 to 11 Å in the Tn region (SI Appendix, Fig. S5 A and B, colored maps). The resolution within the Tn complex was not significantly lower than the resolution obtained for the reconstituted TF in that region (9 to 11 Å as shown in (6) SI Appendix, Fig. S3 A and B), and we therefore were able to compare the structures of the reconstituted and native TFs. Only minor structural perturbations were required to dock the atomic model of the Ca²⁺-free TF (Protein Data Bank [PDB] 6KN7) into our pCa = 8 density map (SI Appendix, Fig. S5H), while the Ca²⁺-bound TF atomic model (PDB 6KN8) fit our pCa = 4 density map without any perturbations. The resultant models with their corresponding maps (Fig. 1) show that at ∼11 Å resolution, the structure of the native TF is in good agreement with the previously published structure of the reconstituted complex (6) for both Ca²⁺-free (Fig. 1A) and Ca²⁺-bound (Fig. 1B) states. Consistently, the two Tn complexes on opposite sides of the TF (denoted as U-Tn and L-Tn for upper and lower Tns, respectively) are nonequivalent. U-Tn and L-Tn differ in the Tn core conformation and the distance to the junction region (Fig. 1A, black arrow) that is stabilized by a segment of the N-terminal domain of TnT (TnT_N) (Fig. 1A, blue arrow). We confirm that at pCa = 8, the α-helical density of the TnT_N domain is longer (Fig. 1A, blue arrow, residues 87 to 150) than that at pCa = 4 (Fig. 1B, residues 100 to 150) and that the TnT_N domain makes an interaction with actin only at low Ca²⁺ (Fig. 1A, magenta arrow). We also confirm that at pCa = 8, the C-terminal part of TnI (TnI_C) comprised of residues 137 to 210 forms an extended, partially α-helical density that interacts with up to three adjacent actins along the F-actin strand (Fig. 1A, red arrows), while this density is not present at pCa = 4 (Fig. 1B). Therefore, our data are consistent with the previously reported structural differences between completely Ca²⁺-free (pCa ∼9) and saturated with Ca²⁺ (pCa ∼3) TFs (6). Importantly, a good agreement with the previously published work validates our reconstruction algorithm.

Fig. 1.

The structure of the cardiac native TF at low (pCa = 8) and high (pCa = 4) Ca²⁺ levels. (A) The model of the Ca²⁺-free TF at pCa = 8 (Cf/Cf^{pCa = 8}) shown as colored ribbons fitted into the cryo-EM density map (gray transparent surface). A total of 12 actin subunits (tan) are shown with a pair of Tm cables (yellow) and a pair of Tn complexes composed of TnC N- and C-lobes (green), TnI (red) spanning up from the Tn core over three actin subunits (red arrows), and TnT (blue) with its N terminus (blue arrow) extended to the Tm junction region (black arrow) to make a contact with actin (magenta arrow). The two Tn complexes are not equivalent and are therefore marked as upper (U-Tn) and lower (L-Tn). (B) The model of the Ca²⁺-bound at pCa = 4 (Cb/Cb^{pCa = 4}) TF has the same color codes as in A, except Tm cables are purple. In contrast to A, the TnI_C is not locked (6) on the surface of the TF, and TnT_N does not make a contact with actin.

The Structural States of Native Cardiac TF at Systolic (pCa = 5.8) Ca²⁺ Level Revealed by Cryo-EM.

The Ca²⁺ level in a working cardiac muscle never reaches extremely low (pCa > 8) or extremely high (pCa < 4) levels (11) that are often used in structural experiments (5, 6, 9). Hence, it was important to examine whether the structural states observed at pCa = 8 and 4 (Fig. 1 A and B) also exist at physiological Ca²⁺ levels. Since Ca²⁺-activated steady-state tension reaches ∼50% of the maximum at pCa = 5.8, we aimed to elucidate the structure of the native cardiac TF at this physiological Ca²⁺ level. The activation level of TFs used for cryo-EM at pCa = 5.8 was ∼47% (SI Appendix, Fig. S1B). This activation level suggests that at pCa = 5.8, the ratio of activated and inhibited RUs, comprised of a tandem of Tn complexes and associated Tm cables, should be ∼1:1. From here, we will term the Ca²⁺-free TF state as “Cf” and the Ca²⁺-bound TF state as “Cb.” This split may be achieved by three mechanisms: 1) TFs may be comprised of an equal mixture of homogeneous Tn tandems (e.g., U-Tn and L-Tn are in the same Cf or Cb state), 2) TFs may consist of a mixture of heterogeneous Tn tandems (e.g., one Tn is in Cf state, while the other in Cb state), and 3) TFs may be comprised of a mixture of homogeneous and heterogeneous Tn tandems. To evaluate the structural state of the TF at pCa = 5.8, we sorted out TF segments into four classes using available atomic models of the Ca²⁺-free (PDB 6KN7) and Ca²⁺-bound (PDB 6KN8) TF (SI Appendix, Fig. S6). The first class had segments having both Tn complexes in the Ca²⁺-free state (termed here as Cf/Cf). In the second class, segments had both Tn complexes in the Ca²⁺-bound state (Cb/Cb). The third class had the U-Tn in the Ca²⁺-free state, while the L-Tn was in the Ca²⁺-bound state (Cf/Cb). Finally, the fourth class had the U-Tn in Ca²⁺-bound states and the L-Tn in Ca²⁺-free states (Cb/Cf). Excluding the partially occupied TFs (SI Appendix, Fig. S6E), we found that ∼15% of segments were assigned to the Cf/Cf state and ∼24% of segments were in the Cb/Cb class, while the majority of TF segments (∼61%) were equally split between the Cf/Cb and Cb/Cf structural classes.

The resolution of the obtained structures at pCa = 5.8 was in the range of 7.8 to 8.3 Å according to the FSC criterion of 0.143 (SI Appendix, Fig. S5 C–G). Using local resolution measurements in RELION (13), we determined the resolution within the actin region to be ∼6 Å, dropping to ∼10 to 11 Å in the Tn region (SI Appendix, Fig. S5 C–G, colored maps). The resolution within the Tn complex was not significantly lower than the resolution obtained for the reconstituted TF in that region (9 to 11 Å as shown in (6) SI Appendix, Fig. S3 A and B). Taking in account the heterogeneous nature of the TFs at pCa = 5.8, we believe that this resolution is a significant achievement in elucidating the structure of the native TF. Since the Tn region was the point of interest, we filtered all the structures obtained for pCa = 8, pCa = 4, and pCa = 5.8 to 11 Å resolution so that those could be compared despite some variations in the Tn region resolution.

We next compared the Cf/Cf (Fig. 2B) and Cb/Cb (Fig. 2C) structures obtained at physiological pCa = 5.8 (Cf/Cf^{pCa = 5.8} and Cb/Cb^{pCa = 5.8}, respectively) with the corresponding structures obtained at pCa = 8 (Fig. 2A) and pCa = 4 (Fig. 2D). Comparison of the Tm position revealed that in the Cf/Cf^{pCa = 5.8} structure, the two Tm cables were in the same azimuthal positions on both strands of the TF. However, both Tm were shifted azimuthally by ∼2° from their fully inhibited position in the Cf/Cf^{pCa = 8} structure toward more activated state (Fig. 2E, blue arrows). Consequently, the TnT_N bound to the Tm was azimuthally shifted together with the Tm cable on both strands. This TnT_N relocation presumably disrupted the contact between TnT_N and actin (compare Fig. 2G and Fig. 2H, black arrow) formed by the 87 to 98 N-terminal residues of TnT since the density corresponding to those residues was missing in the map (Fig. 2H, pink arrows). Interestingly, in the Cb/Cb^{pCa = 5.8} set (Fig. 2C), the Tm cables of the two TF strands were in slightly different azimuthal positions. Tm associated with the L-Tn was not significantly altered from its position in the fully activated state in the Cb/Cb^{pCa = 4} structure (Fig. 2C, cyan), while its counterpart on the U-Tn side (Fig. 2C, magenta) was azimuthally shifted by ∼2° toward the inhibited structural state (Fig. 2F, magenta arrows). A comparison of Tn core structures revealed only minor differences between Ca²⁺-free Tn complexes at pCa = 8 and pCa = 5.8. The structures of Ca²⁺-bound Tn complexes at pCa = 5.8 and pCa = 4 were very similar as well. The minor differences that we observed could not be deemed significant due to medium resolution within the Tn region (SI Appendix, Fig. S5 A–D).

Fig. 2.

Comparison of TF structures obtained at pCa = 8, pCa = 5.8, and pCa = 4 in which L- and U-Tn complexes are in the same Ca²⁺ state. (A–D) Atomic models (ribbons) and corresponding maps (gray transparent surfaces) are shown for Cf/Cf^{pCa = 8}, Cf/Cf^{pCa = 5.8}, Cb/Cb^{pCa = 5.8}, and Cb/Cb^{pCa = 4} in two views related by 90° rotation around the actin helical axis. The Cf/Cf^{pCa = 8} model has the Tn complex and Tm in yellow; the Cf/Cf^{pCa = 5.8} model has Tn and Tm in blue; the Cb/Cb^{pCa = 5.8} model is shown with Tn in cyan, U-Tn Tm in magenta, and L-Tn Tm in cyan; and the Cb/Cb^{pCa = 4} model has both Tn and Tm in cyan. (E) Comparison of the Tm positioning between Cf/Cf^{pCa = 8} and Cf/Cf^{pCa = 5.8} shows an ∼2° rotation of the Tm cable (blue arrow) above and below the Tn complex. (F) Tm associated with U-Tn in the Cb/Cb^{pCa = 5.8} structure is azimuthally rotated by ∼2° from its position in the Cb/Cb^{pCa = 4} structure (magenta arrow) above and below the Tn complex. (G–I) Details of the TnT_N region from structures in A–C (black frames) show that in contrast to the Cf/Cf^{pCa = 8} structure (G), the Cf/Cf^{pCa = 5.8} map (H) lacks density (black arrows) that corresponds to residues 87 to 98 (pink numbers and arrows). In the Cb/Cb^{pCa = 5.8} structure (I), TnT_N does not make interactions with actin (black arrow). (J–M) Detailed view of the TnI_C region for the L-Tn (J and K) and U-Tn (L and M) for the Cf/Cf^{pCa = 8} (J and I) and Cf/Cf^{pCa = 5.8} (K and M) models. Residues that correspond to missing densities in the cryo-EM maps, are denoted in plum.

At pCa = 8, TnI_C binds to actin/Tm and contributes to the inhibition of actomyosin interactions, while at pCa = 4, it dissociates from the filament, enabling its TnI switch region to bind the TnC subunit (6). We found that the TnI_C density in the low Cf/Cf^{pCa = 8} (Fig. 2 J and L) and systolic Cf/Cf^{pCa = 5.8} maps (Fig. 2 K and M) was different. In the Cf/Cf^{pCa = 8} structure, the TnI_C density corresponding to either L-Tn or U-Tn was well preserved (Fig. 2 J and L, respectively) with just a few disordered residues in the upper loop region (Fig. 2 J and L, plum arrows). In the Cf/Cf^{pCa = 5.8} structure, the U-Tn TnI_C density was significantly weaker than that in the Cf/Cf^{pCa = 8}, suggesting that a large portion of TnI_C represented by residues 154 to 168 and 191 to 194 (Fig. 2M, plum ribbons) was disordered and hence, not tightly bound to its actin/Tm interface. Interestingly, the L-Tn TnI_C density was better preserved (Fig. 2K).

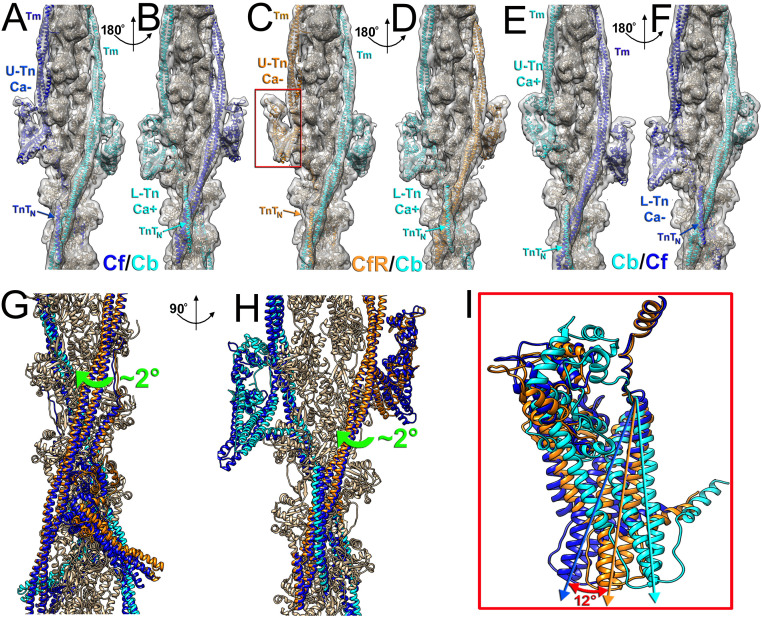
Finally, we compared the structures of RUs comprised of heterogeneous Tn tandems (e.g., Cf/Cb^{pCa = 5.8} and Cb/Cf^{pCa = 5.8}) with the homogeneous structures (e.g., Cf/Cf^{pCa = 5.8} and Cb/Cb^{pCa = 5.8}) (Fig. 3). The overall reconstruction for the Cf/Cb^{pCa = 5.8} structure was missing a significant portion of its Tn-I/Tn-T (IT) arm tip (SI Appendix, Fig. S6I, blue arrow), suggesting conformational variability in the orientation of the U-Tn unit. Subsequent analysis (SI Appendix, Fig. S6J) revealed two classes possessing the U-Tn core in different orientations. In the first class, the U-Tn core and associated Tm cable (Fig. 3 A and B, blue) were in the same conformation as found in the Cf/Cf^{pCa = 5.8} structure (Fig. 2B). In the second class, the Ca-free U-Tn (Fig. 3 C and D, orange) had its Tn core rotated halfway toward the Ca²⁺-bound state (Fig. 3I, red arrow) while possessing the TnC cleft closed. At the same time, the position of the associated Tm was different from that in the Cf/Cf^{pCa = 5.8} structure and possessed a noticeable rotation of ∼2° toward an even more activated position (Fig. 3 G and H, green arrow). Therefore, the Tm cable within that RU (Fig. 3 C and D, orange) was 4° away from its position in the Cf/Cf^{pCa = 8} structure. No alterations were found in the positioning of Ca²⁺-bound L-Tn and its associated Tm cable (Fig. 3 C and D, cyan) when compared with the Cb/Cb^{pCa = 5.8} structure (Fig. 2C). Finally, the upper and lower strands of the Cb/Cf^{pCa = 5.8} structure (Fig. 3 E and F) were, respectively, very similar to the upper strand of Cb/Cb^{pCa = 5.8} structure and the lower strand of the Cf/Cf^{pCa = 5.8} structure.

Fig. 3.

Comparison of TF structures obtained at pCa = 5.8 in which adjacent Tn complexes across the strand are in different Ca²⁺-bound states. (A and B) Two views of the Cf/Cb^{pCa = 5.8} structural model related by 180° azimuthal rotation have blue U-Tn and Tm on the Ca²⁺-free strand and cyan L-Tn and Tm on the Ca²⁺-bound strand. (C and D) Two views of the CfR/Cb^{pCa = 5.8} structural model related by 180° azimuthal rotation have orange U-Tn and Tm on the Ca²⁺-free strand and cyan L-Tn and Tn on the Ca²⁺-bound strand. U-Tn has altered conformation with its IT arm located in between the Ca²⁺-free and Ca²⁺-bound positions (I, red arrow). The Tm cable on the Ca²⁺-free strand of the CfR/Cb^{pCa = 5.8} structure is rotated by 2° toward Ca²⁺-bound state (G and H, green arrows). (E and F) Two views of the Cb/Cf^{pCa = 5.8} model related by 180° azimuthal rotation have cyan U-Tn and Tm on the Ca²⁺-bound strand and blue L-Tn and Tm on the Ca²⁺-free strand. Atomic models are ribbons, while actual density maps are gray transparent surfaces.

Comparison of the Activation States of the Native Cardiac TF at Low (pCa = 8), Systolic (pCa = 5.8), and Saturating (pCa = 4) Ca²⁺ Levels.

To elucidate the regulation of the native TFs at physiological Ca²⁺ levels, we analyzed how the positioning of Tm in all of the described homogeneous (Fig. 2) and heterogeneous (Fig. 3) structural modes of the cardiac TF would affect actomyosin interactions. To determine the activation state of the TF, we tested for the existence of steric clashes between the Tm cable and a myosin head (14) for every actin on the upper and the lower strand (SI Appendix, Fig. S7). The summary of this analysis is shown in Fig. 4. As expected, all six actins in the Cf/Cf^{pCa = 8} structure were inhibited (Fig. 4A, red numbers). In the Cb/Cb^{pCa = 4} structure, however, not all actins were available for actomyosin interactions (6)—actin number one was inhibited due to partial occupancy of its actomyosin site by the Tm junction and associated TnT_N, while the actin number four actomyosin site was covered by the Tn core (Fig. 4B, red numbers). To quantitate the activation level of the TF, we set the activation level to 0% for structures where all six actins on each strand were inhibited (e.g., Cf/Cf^{pCa = 8}) (Fig. 4A, A = 0%) and set it to 100% when four actins were available for actomyosin interactions on both strands (e.g., Cb/Cb^{pCa = 4}) (Fig. 4B, A = 100%). Above, we showed that the position of Tm in both Cf/Cf^{pCa = 5.8} and Cb/Cb^{pCa = 5.8} structures was different from that in the Cf/Cf^{pCa = 8} and Cb/Cb^{pCa = 4} structures, respectively (Fig. 2 E and F, respectively). Nonetheless, our structural analysis (SI Appendix, Fig. S7 C and C′) showed that all actins in the Cf/Cf^{pCa = 5.8} structure were still inhibited. Similarly, despite a 2° movement of Tm in the upper strand, all four actins on both strands of the Cb/Cb^{pCa = 5.8} structure were activated (SI Appendix, Fig. S7 E and E′). Therefore, the activation levels for Cf/Cf^{pCa = 5.8} and Cb/Cb^{pCa = 5.8} were set to 0 and 100%, respectively. Analysis of the mixed structures (e.g., Cf/Cb^{pCa = 5.8} and Cb/Cf^{pCa = 5.8}) required individual analysis of each strand (Fig. 4 F–K). As expected, Cf/Cb^{pCa = 5.8} has one strand 100% activated (Fig. 4F, green numbers), while the other one possesses an activation level of 0% (Fig. 4G, red numbers), yielding an overall activation level of 50%. CfR/Cb^{pCa = 5.8} had its Ca²⁺-free strand only partially inhibited, since actin number two was not inhibited (SI Appendix, Fig. S7D′) and therefore possessing an activation level of 25% (Fig. 4I). The position of Tm in the Ca²⁺-bound strand was not different from that in the Cb/Cb^{pCa = 4} structure and therefore yielded a 100% activation level (Fig. 4H). Overall, the activation level for CRf/Cb^{pCa = 5.8} was set to 62.5%. The Ca²⁺-bound strand of the Cb/Cf^{pCa = 5.8} structure was 100% activated (Fig. 4K), while the Ca²⁺-free strand was 100% inhibited (Fig. 4J), yielding an overall activation level of 50%. Finally, we determined the overall activation level of the TF at pCa = 5.8 by multiplying the activation levels of individual structural modes (Fig. 4A[%]) by the frequencies of those modes (Fig. 4F[%]), which yielded 56.25%. Notably, the activation level for the TF at pCa = 5.8 determined using solely structural tools is in good agreement with the observed activation level of native cardiac TFs at pCa = 5.8 (SI Appendix, Fig. S1B). It is also consistent with the steady-state tension of ∼50% of the maximum in cardiac sarcomeres observed at pCa = 5.8.

Fig. 4.

Comparison of the activation levels of the native cardiac TF at low (pCa = 8), intermediate (pCa = 5.8), and high (pCa = 4) Ca²⁺ levels. Six actin subunits that comprise half the regulatory unit on one of the two strands are marked in numbers; actins that are available for actomyosin interactions are in green, while inhibited actins are in red. The activation level is set to 0% if all six actins on both strands are inhibited (A and C), while if four actins on each strand are activated, the level is set to 100% (B, D, and E). For the mixed structures (F–K), the activation level is calculated for each strand and averaged to yield the overall activation level shown below the black bar. The overall activation level of the TF at pCa = 5.8 (table) is calculated as a sum of values obtained by multiplying the activation levels of individual structural modes A (percent) found at pCa = 5.8 (C–K) by their frequencies F (percent). The color codes for Tn and Tm molecules are the same as in Figs. 2 and 3.

The Structural State of the Cardiac TF at Physiological Systolic Ca²⁺ Level (pCa = 5.8).

One of the most important questions related to our understanding of TF function is how the structural states of individual homogeneous (Fig. 2) and heterogeneous (Fig. 3) RUs are distributed within the TF at systolic Ca²⁺ levels. We selected individual TF segments harboring 4 to 10 clearly visible, adjacent Tn pairs without gaps on any strand (SI Appendix, Fig. S8A), and those segments were cut into individual nonoverlapping consecutive boxes used to determine their structural state by comparison with the earlier determined structures (Figs. 2 and 3 and SI Appendix, Fig. S8D). χ² analysis of pairs of adjacent Tn states on the upper strand was not significantly different from a random distribution (P = 0.26). Similarly, χ² analysis of pairs of adjacent RU states on the lower strand was also not significantly different from a random distribution (P = 0.78). This suggests that Ca²⁺ binds randomly to Tn complexes on either of the two strands.

The probability ratios matrix (SI Appendix, Fig. S8J) shows a more extensive set of interrelationships among nearby RUs than could be deduced from simpler models that were subjected to χ² analyses. The matrix shows that the correlation between the Tn/Tm structural states along and across the TF is very close to a random distribution. There are two exceptions: the CfR (Ca²⁺-free rotated) state (Fig. 3 C and I) has higher chances to be flanked by the Cf and the Cb states along the upper strand (SI Appendix, Fig. S8F, green arrows), while there is a weak correlation between the Cb and Cf states across the strand (SI Appendix, Fig. S8F, yellow arrows). These weak couplings that were identified are summarized in Fig. 5. In this arrangement, the terminal Cf/Cf^{pCa = 5.8} pair toward either the minus or plus end breaks any further possible weak correlations. How does the statistical analysis correlate with the structural data? First of all, the shift of the Tm cable on both strands in the Cf/Cf^{pCa = 5.8} state from its position in the Cf/Cf^{pCa = 8} structure strongly suggests that the Tm position is somewhat sensitive to the state of the adjacent units. Therefore, randomly mixed Ca²⁺-free and Ca²⁺-bound Tn complexes on both strands cause the 2° shift of Tm toward the more activated state (Fig. 2E, blue arrows). While this shift does not change the activation state of RUs (Fig. 4C), it has significant consequences for the Cf/Cf^{pCa = 5.8} RUs. The bridge of density between TnT_N and actin breaks (Fig. 2H, black arrow). At the same time, the interface between TnI_C and actin/Tm is disturbed, and therefore, part of the TnI_C is disordered (Fig. 2 K and M). The weakened interaction of TnI_C with actin/Tm may make the TnI regulatory helix (residues 149 to 160) readily available for binding to the TnC cleft upon Ca²⁺-induced activation in order to stabilize the activated state of the RU (6). In this case, coexistence of activated and inhibited RUs next to each other may make the Ca²⁺-free RUs more susceptible for Ca²⁺ binding and maybe less resistant to activation by the active cross-bridges. Second, the localization of the CfR state between the Cf and Cb states has important consequences for our understanding of TF dynamics. The CfR state has a unique conformation—the TnC cleft is closed, and therefore, CfR is a Ca²⁺-free Tn complex. At the same time, its Tn core is halfway rotated toward the Ca²⁺-bound position. Statistical analysis of states along the TF places the CfR state between the Ca²⁺-free and Ca²⁺-bound units. This means that the Tn core and the Tm cable can be significantly shifted from the Ca²⁺-free conformations without binding Ca²⁺ and predicts internal mobility within the TF, which may be important for the TF activation by the active cross-bridges at falling Ca²⁺ levels. Third, statistical analysis shows that the two strands are noticeably different in terms of short-range cooperativity—the lower strand does not possess any correlated pairs. We do not have direct structural data to explain this observation, but it is likely that the explanation resides in the nonequivalence of the two Tn complexes in terms of the distance to which the TnT linker region (residues 151 to 198) is stretched—the distance between the U-TnT residues 150 and 199 (82 Å) is significantly larger than that for the L-Tn complex (48 Å). Overall, our data show that the native cardiac TF at systolic Ca²⁺ levels has close to a random distribution of Ca²⁺-free and Ca²⁺-bound Tn complexes with, at most, short-range cooperativity along the upper strand.

Fig. 5.

Statistical predictions of structural state distribution within the cardiac native TF at the systolic Ca²⁺ level (pCa = 5.8). Deviations from the random distribution of structural states along and across the TF strands (red numbers) tabulated in SI Appendix, Fig. S8F were used to plot preferable composition of RUs within the TF. The nonrandom chances for the two structural states along (green arrows) or across the strand (yellow arrows) to be neighbors are shown as red percentiles. The randomly defined neighboring state is marked with a red R.

Discussion

The recent groundbreaking experimental approach to 3D reconstruction of TFs without imposition of the actin’s helical symmetry showed the mechanism of Ca²⁺-induced activation of the TF (6) but also raised questions about the validity of the previously obtained positions of the Tm cable on the surface of the TF when actin helicity was used (9). The helically obtained c-blocked, c-closed, and c-open structural states of the frozen hydrated cardiac TF (9) can be explained by the Tm path observed in the nonhelical structures of the Ca²⁺-free and Ca²⁺-bound TFs (6) (SI Appendix, Fig. S9). A more important question regarding the previously published TF structures (6) was whether the structure of the reconstituted complex represents the structure of the native TF which carries posttranslational modifications (SI Appendix, Fig. S2). Our data (Fig. 1) strongly suggest that the structure of the native and reconstituted TFs at reported resolution are very similar. This finding paves the way of using reconstituted complexes to elucidate the structural consequences of cardiomyopathy-linked mutations using Tn components recombinantly expressed in Escherichia coli. Finally, despite the fundamental importance of the transitions observed by Yamada et al. between the inhibited and activated structural states (6), the structures were obtained at a nonphysiological extremely low (pCa ∼9) or high (pCa ∼3) Ca²⁺ level. While those conditions allowed obtaining structurally homogeneous TFs, which indeed yielded a better overall resolution of their structures, they left open the question about the TF structure at physiological levels of Ca²⁺, that is, Ca²⁺-free and Ca²⁺-bound RUs are intermixed together. Here, we structurally and statistically analyzed TFs at systolic pCa = 5.8. While the expected heterogeneity reduced the apparent resolution of the complex (SI Appendix, Fig. S5), the approach nevertheless revealed the coexistence of the previously reported structures within individual native TFs.

An important question is how well one can distinguish between structural states of the TF at a modest 10 to 11 Å resolution in the Tn region (SI Appendix, Fig. S5 A–G)? The structural states revealed at the systolic Ca²⁺ levels that we report here (Figs. 2 and 3) are significantly different even at 15 Å resolution (SI Appendix, Fig. S10). Therefore, the reported differences between the structural modes of the native cardiac TF at systolic Ca²⁺ levels are profound and do not rely solely on the spatial frequency bands close to the resolution limits of the experimental maps.

Our structural and statistical analyses provide valuable insights into the two forms of cooperative interactions that have been proposed to play a role in Ca²⁺ activation of the cardiac TF. The use of pCa = 5.8 is not only physiologically relevant for systole, but it also provides a mixture of RU states within individual TFs that allows us to examine relationships between and among states of nearby RUs. Of the many forms of cooperativity that have been proposed within the sarcomere (15), the first type of cooperativity that we can examine is between adjacent RUs on the same strand of Tm. This is the “head-to-tail” cooperativity because of near-neighbor, end-to-end interactions between adjacent Tm molecules when Tm polymerizes on F-actin, an interaction that is stabilized by the N terminus of TnT to form a five-helix coiled coil bundle that can transmit structural changes in one regulatory unit to the next (16–19). While χ² analyses suggest random distributions of adjacent pairs of Tn states along each Tm strand, the probability ratio matrices (SI Appendix, Fig. S8F) provide evidence for weak coupling between adjacent RUs (Fig. 5). This apparent coupling along the Tm strand is most evident for the CfR state of Tn on the upper strand (Fig. 5). The relatively weak coupling reported here is consistent with the observation that the length of the functional RU in Ca²⁺-activated cardiac muscle is less than seven actin monomers (20), that is, the spread of Ca²⁺ activation along the cardiac TF is no longer than the length of the structural RU. This is comparable to the size of the functional RU estimated in skeletal muscle TFs in the absence of Ca²⁺ (∼7 actin monomers) (21) and is smaller than that observed in skeletal muscle TFs in the presence of Ca²⁺ (10 to 12 actin monomers) (21–23). When comparing our results obtained from individual TF with the previous ensemble measurements, it is important to consider that previous measurements were done in presence of myosin bound to the TF that are expected to augment the observed cooperativity (15, 24) and compliance of TF. Also, the bound myosin could influence the apparent cooperativity obtained from those assays that involved Ca²⁺-activated force measurements (25). In the absence of these factors (myosin binding and force), our structural and statistical analyses provide resolution in measurement of the cooperativity within the cardiac TF due solely to activation by Ca²⁺ that was not available in previous studies.

A second type of cooperativity is between the two strands of Tm, a possibility that was suggested by the structural model of Manning et al. (25). This aspect of their model, confirmed by Yamada et al. (6) and by our structural studies shown here (Fig. 1), suggests that TnT, because of the size of the N-terminal extension, must reach across the TF to connect the core domain of Tn bound on one strand of Tm to the binding site for the N-terminal extension at a “head-to-tail” junction between two Tms on the opposite strand. Examination of the probability ratio matrices (SI Appendix, Fig. S8F) shows that in most instances, there is a stochastic, albeit slightly biased, relationship between a structural state on the upper strand of Tm and structural states on the lower strand. This suggests that there is no strong (i.e., deterministic) coupling between the upper and lower strands. An interesting, apparent exception to the above involves the CfR state that is found only on the upper Tm strand. The CfR state is relatively rare (∼18% of RUs on the upper strand and therefore ∼9% overall). According to the probability ratio matrix, the CfR state is most likely to be found between a Cf state toward the minus end of the TF and a Cb state toward the plus end on the upper strand and across from a Cb state on the lower strand (Fig. 5). This suggests that multiple weak couplings on the same and opposite Tm strands discussed above may combine into a stronger coupling that distorts the structure of a RU into the CfR state. It is possible that this is simply the result of random distributions of Cf and Cb states on the upper and lower strands, which would be expected to yield 8.6 to 9.7% CfR states based on the specific combination of Cf and Cb states emphasized in the probability ratio matrices. Functionally, it is possible that this combination of states allows the CfR state to act as a circuit breaker for the spread of activation. What is not yet clear, with regard to the limited cooperative spread of activation, is why it appears to be stronger on the upper strand. The answer may have to do with the distance between the N-terminal end of the IT arm to the resolved portion of TnT’s N terminus on Tm, with that distance being shorter for the lower Tn. Further experiments will be required to specifically test this hypothesis.

Overall, this analysis indicates that Ca²⁺ activation of the cardiac TF is a highly stochastic process, with only weak coupling between RUs. This strongly suggests that the cardiac TF is tuned to respond linearly to the rising or falling Ca²⁺ concentration within the physiologically relevant Ca²⁺ levels (from pCa ∼7 to pCa ∼6) as stochastic binding of Ca²⁺ to Tn activates RUs randomly throughout the filament. Such a random spread would give equal chances for myosin heads to find actin-binding sites irrespective to their position within the thick filament. Several studies have suggested that both Ca²⁺ and cross-bridges are necessary for cardiac TF activation (20, 26, 27). These data beg the question of what effect active cross-bridges would have on the observed structures and the distribution of RU states along TFs. Full activation of the cardiac TF under near-isometric conditions requires <20% of myosin heads bound to TFs (28, 29), consistent with the 10 to 20% attached fraction measured in separate experiments (30, 31). During the cardiac cycle, the fraction of attached motors is expected to decrease during the ejection phase relative to the isovolumic phase due to sarcomere shortening (32). Out of those interacting cross-bridges, only a negligibly small fraction is bound in rigor at any time during active contraction (33, 34). While actively cycling cross-bridges may influence cTnC structure and TF activation (20, 26), it is the rigor cross-bridges that have the greatest effect on the TF cooperativity (27, 35–37). We therefore suggest that the impact of cross-bridges during systole on the structural state of the TF would be relatively limited, although this needs to be examined experimentally.

The capability of myosin heads to bind to the TF within the C-zone is tweaked by muscle regulatory proteins such as cardiac myosin binding protein-C (cMyBP-C) (38). The N-terminal domains of cMyBP-C have been shown to modulate the activation state of the TF (39, 40) and hence may affect the distribution of activated and inhibited RUs within the C-zone. It is therefore feasible that cMyBP-C plays a role in modulating the cooperativity between the TF RUs either directly through its ability to activate the TF or via its ability to affect the activation state of the thick filament. It is also plausible that the familial cardiomyopathy-linked mutations in either thin or thick filament proteins alter cooperativity along and across the TF strands, which leads to pathological alterations in the heart muscle.

Overall, our data provide a backbone structure of the TF, which lacks TnI biphosphorylation and is not altered by the presence of rigor bound cross-bridges at systolic Ca²⁺ levels. Therefore, our structure is an important starting point to look into the TF regulation by biphosphorylation of TnI implied in the inotropic response of the heart to beta-agonists, effects of rigor myosin-bound cross-bridges, and effects of muscle regulatory proteins beyond Tn (e.g., cMyBP-C).

Materials and Methods

Proteins and Buffers.

Native porcine cardiac TFs were prepared as described in ref. 40. A-buffer was used for cryo-EM experiments: 50 mM potassium acetate, 10 mM 3-(N-morpholino)propanesulfonic acid (MOPS), 3 mM MgCl₂, and either 0.1 mM CaCl₂ (pCa = 4), 1.5 mM Ca²⁺, and 2.0 mM (ethylene glycol-bis(β-aminoethyl ether)-N,N,N′,N′-tetraacetic acid (EGTA) (pCa = 5.8) or 2 mM EGTA (pCa = 8). The pH was adjusted to 7.0 after all of the components were mixed.

Cryo-EM.

A total of 1.8 µL of [1 μM] native TFs in A-buffer in activating high Ca²⁺ (pCa = 4), physiological sub- activating (pCa = 5.8), or Ca²⁺-free (pCa = 8) conditions were applied to the center of the glow discharged lacey carbon grid so that they form a small droplet in the center of the grid. The small droplet was immediately blotted with Whatman Grade 1 Filter Paper for 3 to 5 s and vitrified in a Vitrobot Mark IV (FEI, Inc.). The summary for imaging conditions and image reconstruction is provided in SI Appendix, Table S1. Image analysis was performed using RELION (13) and SPIDER (41) packages, while modeling was done using University of California San Francisco (UCSF) Chimera (42) and PHENIX (43) software suits. Experimental details are provided in SI Appendix, SI Materials and Methods.

Statistical Analyses.

We selected 118 individual TF segments harboring 4 to 10 well-visible Tn pairs without gaps on any strand. Experimental details are provided in SI Appendix, SI Materials and Methods. These individual TF segments were cut into individual nonoverlapping consecutive boxes (n = 1,096) that were used to determine their structural state by cross-correlation comparison with the earlier determined structures (SI Appendix, Fig. S8D) using the SPIDER (41) package. The result of the sorting was tabulated into a database (SI Appendix, Fig. S8E). The database was used to calculate the expected distribution of pairs of states, based on random distribution of each state, along the same strand and across the opposite strand of TF (SI Appendix, Fig. S8F). Details are provided in SI Appendix, SI Materials and Methods.

Data Availability

The atomic models have been deposited in PDB (www.rcsb.org) with accession codes 7KO4 (Cf/Cf), 7KO5 (Cb/Cb), 7KO7 (Cf/Cb), 7KON (CfR/Cb), and 7KOR (Cb/Cf). The corresponding cryo-EM maps were deposited in the Electron Microscopy Data Bank (https://www.ebi.ac.uk/pdbe/emdb) with accession codes EMD-22964, EMD-22965, EMD-22966, EMD-22978, and EMD-22981, respectively.