Amount and time exert independent influences on intertemporal choice

Intertemporal choices involve tradeoffs between the value of rewards and the delay before those rewards are experienced. Canonical intertemporal choice models such as hyperbolic discounting assume that reward amount and time until delivery are integrated within each option prior to comparison^1,2. An alternative view posits that intertemporal choice reflects attribute-wise processes in which amount and time attributes are compared separately^3–6. Here, we use multi-attribute drift diffusion modeling (DDM) to show that attribute-wise comparison represents the choice process better than option-wise comparison for intertemporal choice in a young adult population. We find that, while accumulation rates for amount and time information are uncorrelated, the difference between those rates predicts individual differences in patience. Moreover, patient individuals incorporate amount earlier than time into the decision process. Using eye-tracking, we link these modeling results to attention, showing that patience results from a rapid, attribute-wise process that prioritizes amount over time information. Thus, we find converging evidence that distinct evaluation processes for amount and time determine intertemporal financial choices. Because intertemporal decisions in the lab have been linked to failures of patience from insufficient saving to addiction^7–13, understanding individual differences in the choice process is important for developing more effective interventions.

Substantial research shows that intertemporal choices between smaller, sooner (SS) and larger, later (LL) monetary rewards can be characterized by a hyperbolic discounting function in which rewards lose value very rapidly over short delays and then more slowly over longer periods of time^1,2. A single hyperbolic discount rate (k) describes choices, such that a higher k indicates steeper discounting of future rewards and thus more impatient choices, whereas a lower k indicates more patient choices. Such hyperbolic option-wise models have been generally accepted for several reasons: the discount rate often relates to other measures of individual differences^7–9,11, hyperbolic models account for preference reversals as rewards become more proximal in time², and value functions derived from hyperbolic models match well to neural data^14–19. Yet, it is also known that directing attention toward one attribute (e.g., time) can alter decisions, perhaps by encouraging attribute-wise processing^20–23. Recent research into heuristic and sequential sampling models has suggested that such an attribute-wise process may better fit choice behavior^3–6, although there remains debate about whether the form of these previous models accounts for all factors²⁴.

The current experiments examine whether amount and time make independent contributions to individual differences in intertemporal choice in young adults. To support this conclusion, three conditions must be met. First, intertemporal choices should be better modeled by a combination of uncorrelated parameters for amount and time than by either of those parameters in isolation. If this condition holds, two individuals could exhibit the same intertemporal patience (i.e., the same apparent k value) through different combinations of decision weights on amount and time. Second, a model that combines amount and time parameters in an attribute-wise manner (i.e., comparing amounts to amounts and times to times) should be better matched to choice behavior than a similar option-wise model that integrates amount and time information to determine the value of each option. Third, amount and time should have distinct influences on the attentional process during choice, measured independently of choice behavior; if such attentional effects are observed, they would provide an important lever for shifting the process of choice. Our experiments provide evidence that meets all three of these conditions.

We investigated the dynamic process of intertemporal choice using multi-attribute drift diffusion modeling (DDM)^24–27. This approach builds on prior work indicating that intertemporal choice – like other forms of value-guided decision making – involves a dynamic accumulation of evidence before reaching a decision threshold^5,25. Expanding on other studies, our multi-attribute model introduces a separation of amount and time information in multiple parts of the decision process. Drift diffusion models split up the decision process into fundamental components that shape both choices and response times; each component provides a potential source for inter-individual variation in choice patience (see Supplementary figure 1 for more information on the structure of the DDM)²⁶. A necessary component to account for differences in patience is variation in attribute-specific drift slopes for amount compared to time. The drift slope reflects the weight placed on an attribute during the evidence accumulation process. On a given trial, the total evidence accumulation (i.e., trial drift rate) depends on the trial-specific value differences between the two options as modulated by the subject- and attribute-specific drift slope. Because drift slopes play a dominant role in evidence accumulation, they will necessarily have a large part in driving choice and thus explaining individual differences. A steeper drift slope for amount compared to time would promote more patient choices while a steeper drift slope for time would promote more impatient choices. Nevertheless, another possible contributing mechanism is attribute latency, or the temporal advantage that results if one attribute is processed earlier than another. Faster latency for one attribute would initially bias choice toward the better value on that attribute before the other attribute starts influencing value accumulation²⁷. Finally, decision bounds represent response caution, which can manifest as a tradeoff in speed vs. accuracy²⁸. Differences in boundaries could contribute to individual differences in choice with lower bounds relating to faster, less cautious, and noisier responses, although bounds do not directly bias choice in one direction.

We adopted a multi-stage procedure for data collection, analysis, and replication (see Supplementary figure 2 for approach and Supplementary figures 3–5 for manipulation checks). Our task (Figure 1) offered participants incentive-compatible choices between smaller rewards delivered that day and larger rewards delivered up to a year later. In our primary sample, options were presented vertically with amount information at the top of the screen and time information at the bottom. In our replication sample, options were presented horizontally with amount and time information location (left or right) switching halfway through the experiment. In both samples, the locations of the SS and LL options were randomized across trials. While participants performed the task, we sampled their gaze position at high temporal resolution using eye-tracking, so that we could obtain real-time assessments of information processing in advance of each decision^29–34. We examined not only the relative gaze bias between the SS and LL options, which has been linked to overall patience in intertemporal choice³⁵, but also the pattern of eye movements between elements in the display, which can reveal variation in decision heuristics across individuals^36,37. We used choices and response times from the task to fit the drift diffusion models and data from the eye tracker during choice periods to characterize gaze patterns. Successful analyses in the primary sample determined which analyses were conducted in the replication sample – and all analyses are reported in this paper, regardless of replication success.

Figure 1.

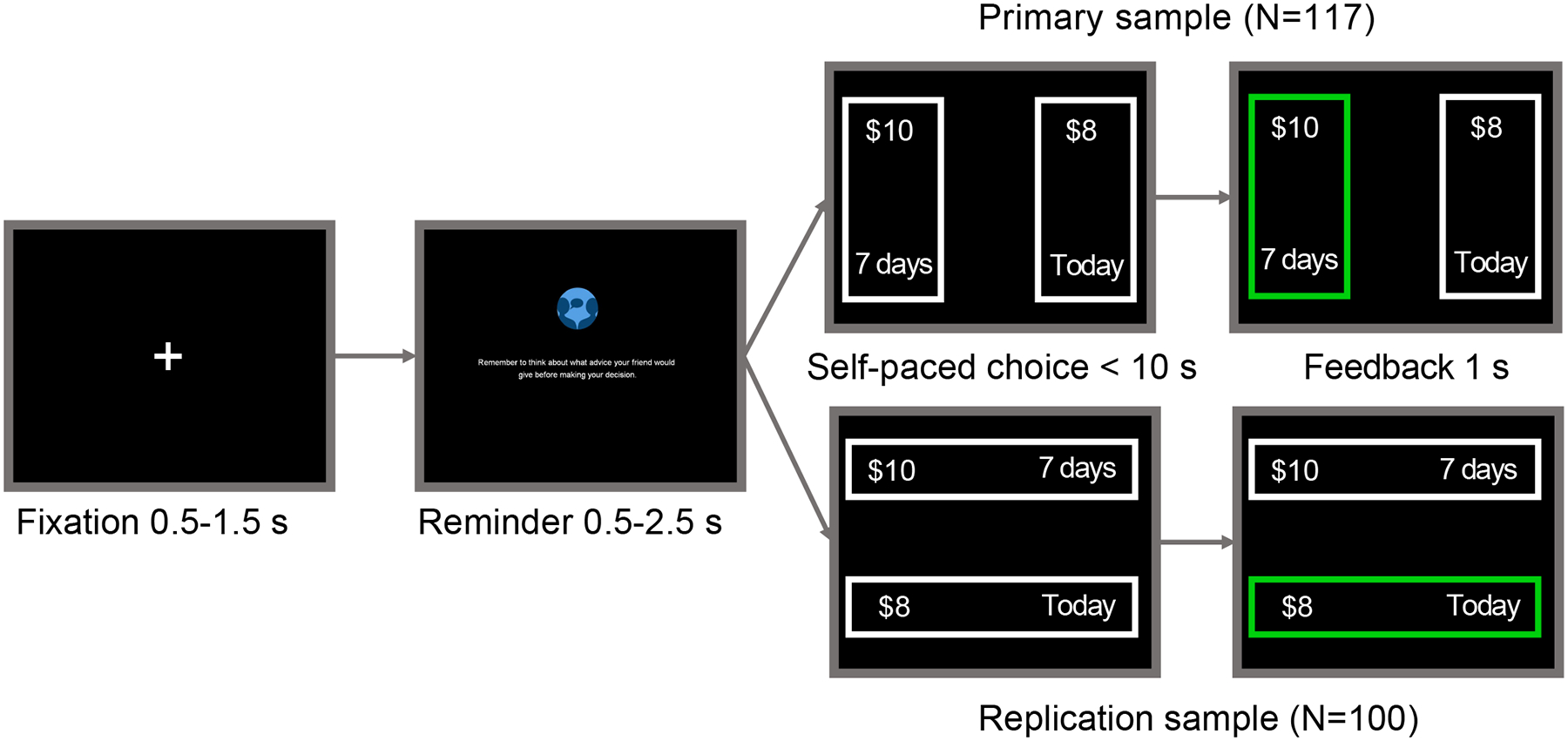
Intertemporal choice task. On every trial, participants saw a fixation cross followed by a reminder to follow the task instructions. Next, they viewed and made a choice between a LL and SS option and received 1s of feedback highlighting the choice made. The positions of the LL and SS options were randomized across trials. The orientation of amount and time information in the primary sample was rotated in the replication sample.

We tested two drift diffusion models that differed in how and when amount and time information contributed to the decision process. The attribute-wise model [Equation (3)] assumes that people make direct comparisons between amounts and direct comparisons between times, whereas the option-wise model [Equation (2)] assumes that people integrate time and amount for each option before comparing options. We compared model fits using Bayesian information criterion (BIC); because both models fit the same number of parameters, here the BIC is a transformation of the negative log likelihood. Nearly all participants were better fit by an attribute-wise model (Two-sided exact binomial tests: primary sample 107/117, p < 0.001, 95% CI = 0.85 – 0.96; replication sample 99/100, p < 0.001, 95% CI = 0.95 − 1.0), and analyses reported in the following sections use parameters from that model (see Supplementary Figures 6 and 7 for option-wise results). Moreover, the difference in fit was significantly correlated with discount rate (Figure 2) as tested by a two-tailed Pearson’s product-moment correlation: primary sample t(103) = 12.66, p < 0.001, r = 0.78, 95% CI = 0.69 – 0.85; replication sample t(77) = 5.56, p < 0.001, r = 0.54, 95% CI = 0.36 – 0.68), such that more patient individuals’ choices were much better fit by an attribute-wise model, while very impatient individuals’ choices tended to be more similarly fit by both models.

Figure 2.

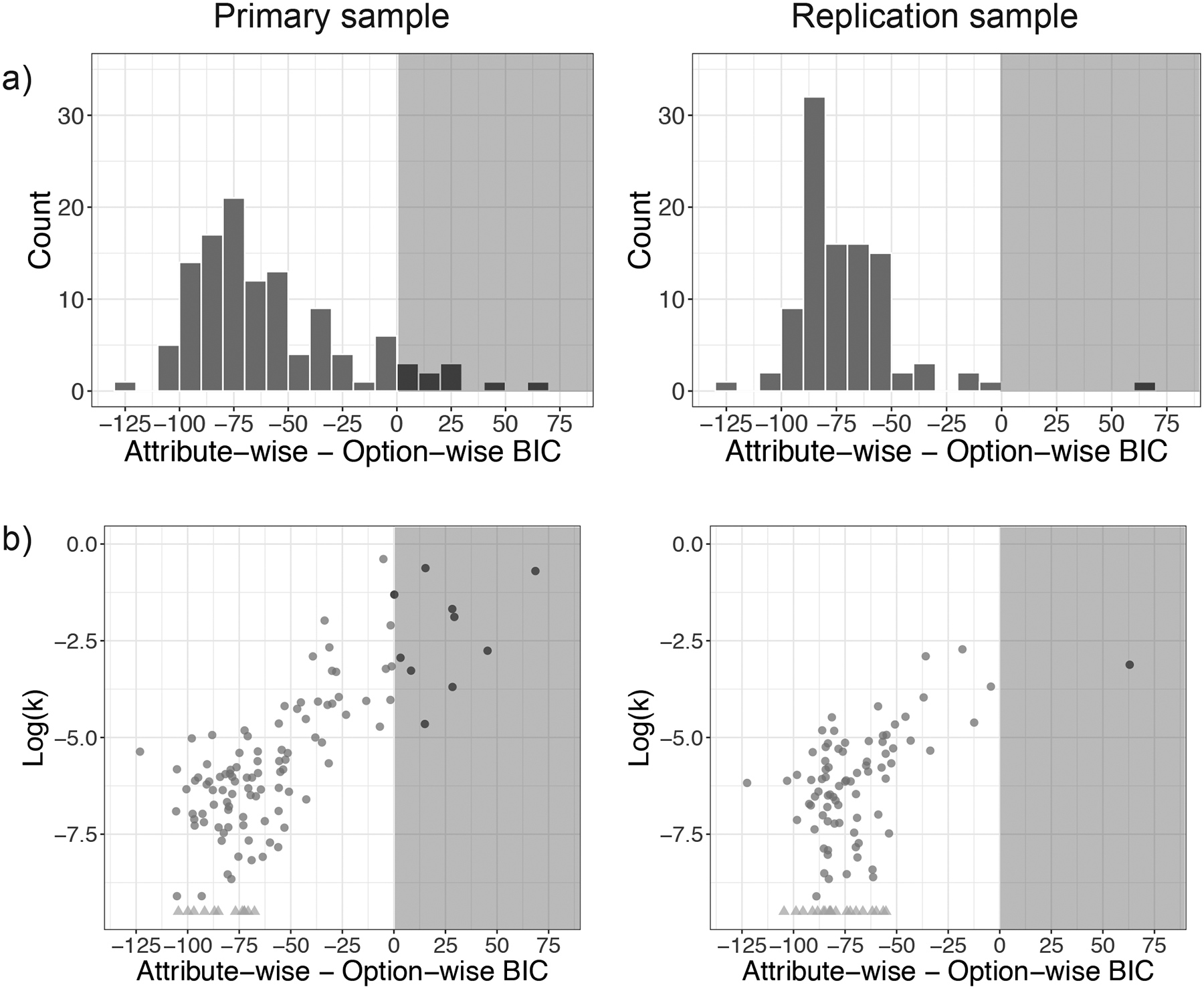
Attribute-wise vs. option-wise DDM model comparison using Bayesian Information Criterion (BIC). Shown are data from all participants (primary sample N = 117, replication sample N = 100); note that participants that could not be fit to a single discount rate (primary sample N = 12, replication sample N = 21) were excluded from subsequent statistical testing. a) A histogram of the difference in BIC for each participant across models showing that overall the attribute-wise model fit better. Two-sided exact binomial tests comparing model performance: primary sample: 107/117, p < 0.001 95% CI = 0.85 – 0.96; replication sample 99/100, p < 0.001, 95% CI = 0.95 − 1.0. b) The difference in BIC has a positive correlation with individual discount rate, log(k). Two-sided Pearson’s product-moment correlations primary sample: t(103) = 12.66, p < 0.001, r = 0.78, 95% CI = 0.69 – 0.85; replication sample: t(77) = 5.56, p < 0.001, r = 0.54, 95% CI = 0.36 – 0.68. Participants with all patient choices are displayed in light gray triangles at −9.5 on the y-axis for illustrative purposes. Gray shading indicates values better fit by the option-wise model, whereas no shading indicates values better fit by the attribute-wise model (lower BIC values indicate better fit). Because both models contain the same number of parameters this is a transformation of the difference in negative log likelihood.

Because intertemporal choices involve trade-offs between two attributes – amount and time – those attributes influence choice in opposite directions; that is, an increased decision weight on time will potentiate SS choices, while an increased decision weight on amount will lead to LL choices. Within the DDM, an increased weight on one attribute would be evident in a steeper drift slope compared to the other attribute. For every participant, we used a multi-attribute DDM (see Methods) to estimate the unique drift slopes associated with amount information and with time information. We found that these two drift slopes were uncorrelated across participants (Figure 3a; Two-sided Pearson’s product-moment correlations: primary sample t(115) = 0.24, p = 0.81, r = 0.02, 95% CI = −0.16 – 0.20; replication sample t(98) = 0.74, p = 0.46, r = 0.07, 95% CI = −0.12 – 0.27) indicating that amount and time make distinct contributions to the process of intertemporal choice.

Figure 3.

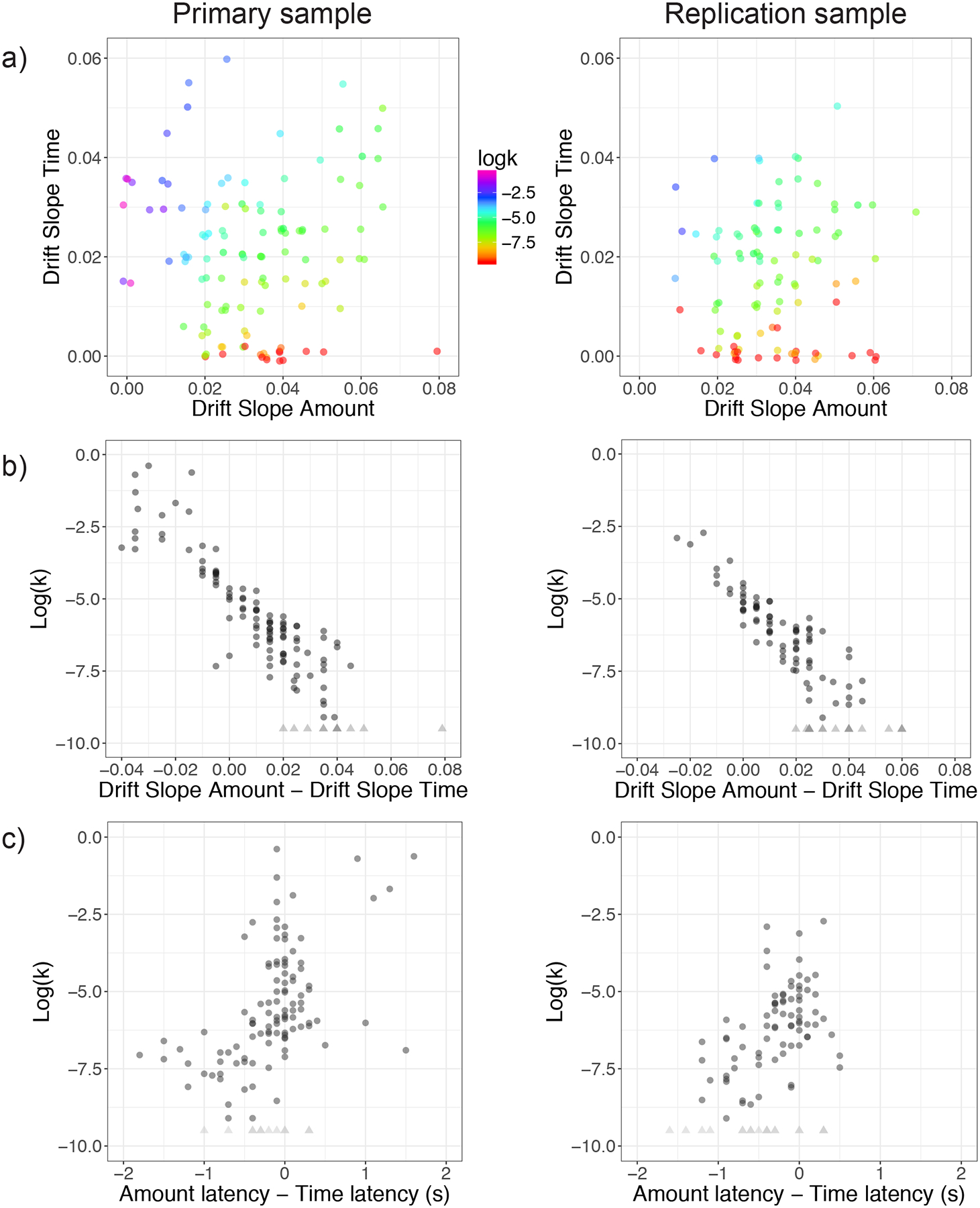
Patience reflects the difference in drift slopes and latencies for amount and time. Primary sample N = 117, replication sample N = 100, participants not able to be fit to a single discount rate were excluded from analyses involving the discount rate (primary sample N = 12, replication sample N = 21). a) The drift slopes for amount (x-axes) and for time (y-axes) were uncorrelated across participants: Two-sided Pearson’s product-moment correlations: t(115) = 0.24, p = 0.81, r = 0.02, 95% CI = −0.16 – 0.20; replication sample: t(98) = 0.74, p = 0.46, r = 0.07, 95% CI = −0.12 – 0.27. Values are jittered (.001 horizontal and vertical jitter) to reduce over-plotting. The color-map indicates the log(k) value for each participant; note that participants with similar levels of patience had different combinations of drift slopes for the two attributes. b) The difference in drift slopes was related to patience, in both samples: Two-sided Pearson’s product-moment correlations primary sample, t(103) = −19.14, p < 0.001, r = −0.88, 95% CI = −0.92 – −0.83; replication sample t(77) = −16.22, p < 0.001, r = −0.88, 95% CI = −0.92 – −0.82. c) The relative attribute latency for amount and time also relates to patience: Two-sided Pearson’s product-moment correlations primary sample: t(103) = 6.21, p < 0.001, r = 0.52, 95% CI = 0.37 – 0.65; replication sample: t(77) = 4.86, p < 0.001, r = 0.48, 95% CI = 0.29 – 0.64. Participants with all patient choices are displayed in light gray triangles at −9.5 on the y-axis for illustration and were excluded from statistics.

As a manipulation check of the fit of the drift slopes, we examined the relationship between the difference in drift slopes for amount and time and individual differences in intertemporal choice as measured by the discount rate (Figure 3b). As expected, more patient individuals accumulated amount information at a faster rate than time information, whereas more impatient individuals accumulated time information at a faster rate than amount information (Two-sided Pearson’s product-moment correlations: primary sample t(103) = −19.14, p < 0.001, r = −0.88, 95% CI = −0.92 – −0.83; replication sample (t(77) = −16.22, p < 0.001, r = −0.88, 95% CI = −0.92 – −0.82). This result confirms that the model correctly distributes weight between the amount and time parameters to predict choice. Together, these results demonstrate that patience results from the combination of two uncorrelated factors—time and amount—rather than from a single factor or a slower overall drift slope (i.e., the sum of the axes on Figure 3a). Preferences in intertemporal choice are proportional to the difference between these drift slopes but the drift slopes themselves are not correlated with each other.

While the previous section shows that attribute-specific differences in drift slope are closely connected to intertemporal choice, differences in attribute latency could amplify (or moderate) those effects. We found that the latency for amount information was shorter than that for time information overall (Two-sided Welch’s paired t-test: primary sample, mean difference of 160 ms, t(116) = −3.24, p = .0015, Cohen’s d = −0.30, 95% CI = −0.56 – −0.04; replication sample, mean difference of 325 ms, t(99) = −7.17, p < 0.001, Cohen’s d = −0.72, 95% CI = −1.00 – −0.43), and that the difference between attribute latencies for amount and time was positively correlated with k values (Figure 3c, Two-sided Pearson’s product-moment correlations: primary sample t(103) = 6.21, p < 0.001, r = 0.52, 95% CI = 0.37 – 0.65; replication sample t(77) = 4.86, p < 0.001, r = 0.48, 95% CI = 0.29 – 0.64). That is, people who are more patient begin accumulating amount information more quickly, while those who are less patient begin accumulating time information more quickly.

Within the DDM, the decision boundary provides a measure of how much evidence is required before making a choice – and thus expanded bounds could be plausibly linked to patient intertemporal choices. However, there were no correlations between decision bounds and discount rate in either sample (Two-sided Pearson’s product-moment correlations: primary sample t(103) = −0.85, p = 0.40, r = −0.08, 95% CI = −0.27 – 0.11; replication sample t(77) = 0.18, p = 0.85, r = 0.02, 95% CI = −0.20 – 0.24). We found a positive correlation between discount rate and response time such that impatient participants actually took longer to make choices than more patient participants (primary sample t(103) = 3.49, p < 0.001, r = 0.33, 95% CI = 0.14 – 0.49; replication sample t(77) = 4.16, p < 0.001, r = 0.43, 95% CI = 0.23 – 0.59, Supplementary Figure 8). Together, these data suggest that there is no systematic relationship between patience in the intertemporal domain and the amount of evidence or speed required to make a decision; instead, individual differences in attribute-specific latency and drift slopes account for which individuals exhibit intertemporal patience.

If amount and time are uncorrelated contributors to intertemporal choice, there should be observable attentional biases toward one attribute or the other that relate to variation in drift slope. We tested this hypothesis by examining whether differences in drift slope showed a relationship with our Attribute Index, which quantifies relative looking time at amount versus time information (Figure 4a). There was a significant positive correlation between difference in drift slope and relative gaze in both the primary sample (two-sided Pearson’s product-moment correlation: t(103) = 6.35, p < 0.001, r = 0.53, 95% CI = 0.38 – 0.66) and the replication sample (t(83) = 6.05, p < 0.001, r = 0.55, 95% CI = 0.39 – 0.69). That is, individuals direct more attention toward the attribute for which they show a higher drift slope. This could be due either to attention driving the information gathering process or to underlying preferences driving attention; the challenge in separating these explanations is considered below. We also tested whether the location of the first fixation was related to individual differences in attribute latency for amount and time and found a significant correlation in our primary sample (two-sided Kendall’s rank correlation tau: z(103) =−3.40, p < 0.001, tau = −0.23, 95% CIs = −0.35 – −0.12) and in our replication sample (z(83) = −2.16, p = 0.031, tau = −0.16, 95% CIs = −0.30 – −0.03) such that those who had a faster amount latency were more likely to fixate first on amount information (Supplementary figure 9).

Figure 4.

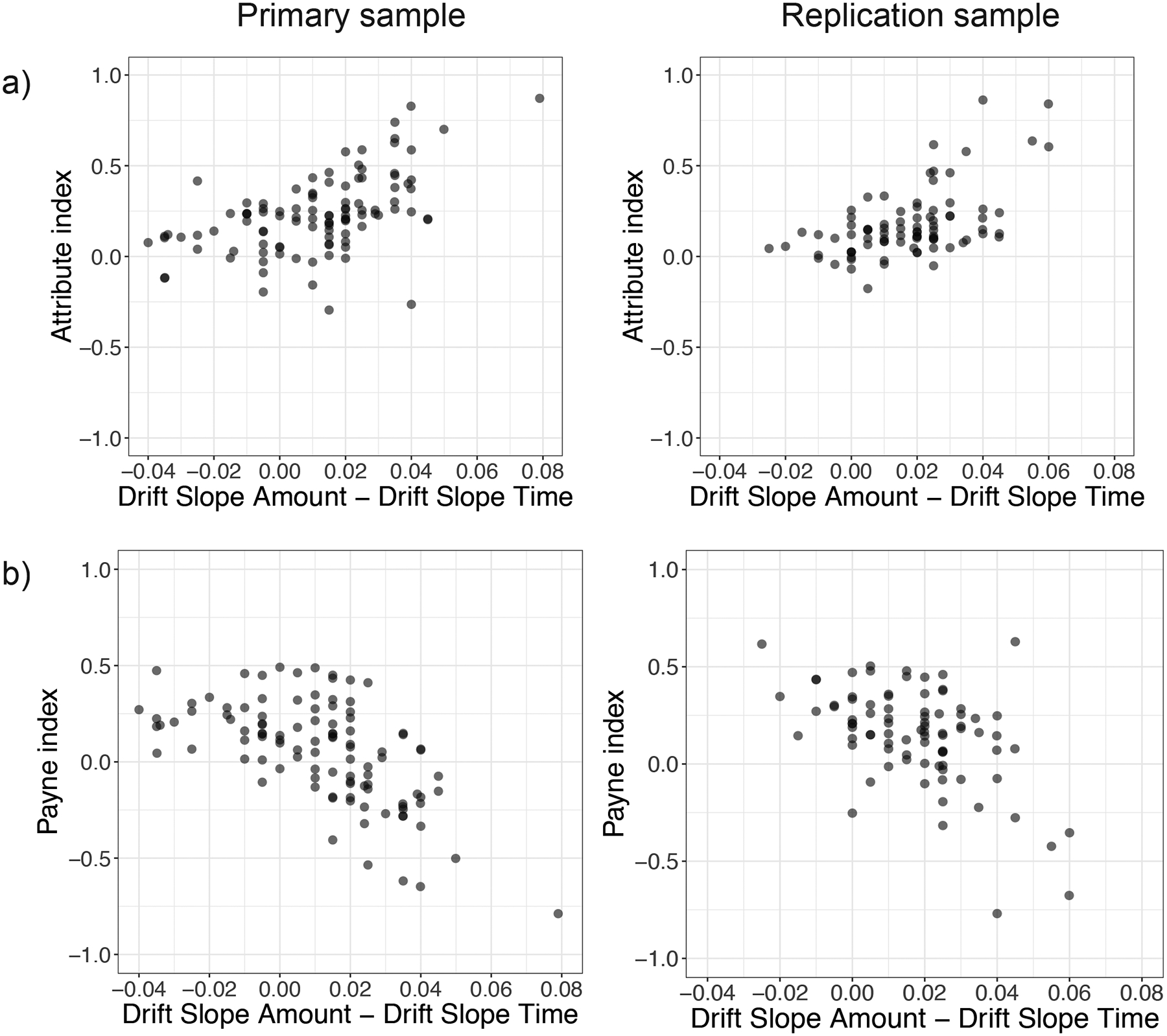
Differences in drift slope between amount and time attributes are reflected in measures of attention. Primary sample N = 105, replication sample N = 85 which includes all participants with sufficient eye-tracking data. a) The Attribute Index measures relative looking at amounts (index>0) versus times (index<0). Across participants, a bias toward looking at amounts was associated with a greater drift slope for amount information: two-sided Pearson’s product-moment correlation primary sample: t(103) = 6.35, p < 0.001, r = 0.53, 95% CI = 0.38 – 0.66; replication sample: t(83) = 6.05, p < 0.001, r = 0.55, 95% CI = 0.39 – 0.69. b) The Payne Index measures the relative likelihood of gaze transitions within options (index>0) or between attributes (index<0). Participants who tended to make more attribute-wise transitions also showed a greater drift slope for amount information; two-sided Pearson’s product-moment correlation primary sample: t(103) = −7.60, p < 0.001, r = −0.60, 95% CI = −0.71 – −0.46; replication sample: t(83) = −5.51, p < 0.001, r = −0.52, 95% CI = −0.66 – −0.34.

While the results from the previous sections show attribute-specific biases in decision making, they do not in themselves provide evidence that participants directly compare attribute values when making decisions. To obtain that evidence, we identified all gaze transitions in our eye-tracking data and then measured the relative proportions of attribute-based transitions (e.g., SS time to LL time) and option-based transitions (e.g., SS time to SS amount). The difference in transition probabilities is quantified by the Payne Index³⁸, for which positive values reflect more option-based gaze transitions. We observed a strong negative correlation between the Payne Index and the difference in attribute drift slopes: individuals with a higher drift slope for amount were indeed more likely to engage in attribute-wise comparisons, while those with a higher drift slope for time used more option-wise comparison (Figure 4b two-sided Pearson’s product-moment correlations: primary sample t(103) = −7.60, p < 0.001, r = −0.60, 95% CI = −0.71 – −0.46; replication sample t(83) = −5.51, p < 0.001, r = −0.52, 95% CI = −0.66 – −0.34). Moreover, those with higher Payne Index values tended to look more at amounts than times (t(103) = −7.80, p < 0.001, r = −0.61, 95% CI = −0.72 – −0.47; replication sample t(83) = −11.04, p < 0.001, r = −0.77, 95% CI = −0.85 – −0.67 Supplementary Figure 10). We also examined the relationship between eye tracking indices and the discount rate (Supplementary figure 11). Together, these results indicate that people who make more patient choices tend to directly compare the amounts offered (and largely ignore temporal information), whereas those who are less patient tend to integrate amount and time within an option before comparing the two options.

Collectively, our results support the conclusion that intertemporal choices result from the combination of two distinct processes – one evaluating amount information and the other evaluating time information – that combine to shape an individual’s choice patience. This conclusion follows from converging evidence drawn from choice behavior, multi-attribute drift diffusion modeling, and metrics of attention obtained using eye-tracking (Supplementary tables 1 and 2 summarize these results). Moreover, markers of the choice process (e.g., patterns of gaze transitions, latency of attribute integration) were predictive of subject-specific individual differences in patience (see Supplementary figure 12 for trial by trial differences in the choice process). These markers contribute to an improved understanding of the mechanisms of intertemporal choice, which in turn could inform policy and interventions that ameliorate negative real-world outcomes^{7–12,39–43}.

Three features of our results are particularly relevant for understanding intertemporal choice. First, we show that the processing of amount information and time information have uncorrelated contributions to the choice process. While our design cannot confirm complete statistical independence, the observed lack of correlation between drift slopes for amount and time stands in contrast to other models that assume a limited capacity constraint on attention such that weights on amount and time trade-off within the decision process (i.e., sum to a constant)^5,44. Moreover, prior work suggests that although attention can constrain processes of evidence accumulation in decision making, this bias is partial rather than absolute³⁰. We note, however, that modeling approaches like ours could miss idiosyncratic violations of independence, as could be the case if a subject adopts different choice heuristics on different trials that are mixed across trials in an overall model. Future work should extend these analysis procedures to identify potential decision heuristics, including attentionally constrained trade-offs in processing, that may be manifest in some contexts.

Second, because the pattern of gaze transitions provides an index of overt attention^30,45–49, we could link parameters extracted from diffusion models to observable online behavior during the period of choice. This connects biases observed in the models (e.g., a steeper drift slope for amount information) to potential heuristics observed in eye movements (e.g., attribute-wise transitions between amounts).

Third, our large sample size and replication strategy allowed us to make strong claims about inter-individual variability in patience. We showed, for example, that the overall biases toward amount information in drift slope and latency are modulated by participants’ preferences, with more patient individuals showing more bias toward amount information. While our study focused on young adults, expanding this understanding of inter-individual variability in the mechanisms of intertemporal choice will be particularly important for studies of groups characterized by excessively impatient choices (e.g. people with addiction⁹).

Our modeling results revealed a strong bias toward an attribute-wise comparison process, rather than an integration of attributes within a choice option. Importantly, our eye tracking data indicated that this bias was not universal; there is not one best-fitting approach, but rather both attribute-wise and option-wise strategies may be employed in different contexts, with substantial individual variability. This result builds upon the similar finding (using mouse-tracking methods) from Reeck and colleagues³⁷; we extend their results by showing that the attribute-wise model fits best for those at the most patient end of the spectrum whereas the option-wise model fits better for those who are less patient. Moreover, Wulff et al. (2017) have suggested that specifics of the modeling can influence the dominance of attribute-wise vs. option-wise models. Indeed, while the relationship between modeling and eye tracking is as expected, many of our participants show a small positive (option-wise) bias in their eye tracking. More research is needed to confirm the underlying psychological mechanism, particularly for participants with no extreme measurable eye tracking bias who likely look at all information on the screen. Further experiments could extend a display to include more options as has been done in risky decision-making^50,51 to explore whether clearer patterns of information gathering develop. Therefore, while the attribute-wise computational model fits better overall, individuals may still differ in the mechanisms by which they make these choices, given the clear individual differences both in choice behavior and in processes of information acquisition.

High-patience individuals showed a striking – and potentially counterintuitive – pattern of behavior. Rather than exhibiting a slow and analytic comparison process that integrated all available information, they tended to employ a heuristic strategy of directly comparing amounts and choosing the larger. In contrast, low-patience individuals showed a more balanced process of examining both amounts and times, as evident in gaze tracking and model parameters. This combination of results – with patient decisions arising from heuristics, and impatient decisions arising from a more analytic comparison process – seems counter to rational choice models. However, it echoes previous findings in other choice domains that point to the use of heuristics as a characteristic feature of effective decision making^52–55. Interventions to promote patience by encouraging analytic integration of outcome attributes might not be effective, accordingly. Instead, patient decisions might be nudged through interventions that encourage comparison of amounts, rather than times to delivery, which could be considered a “cost” or “penalty”^22,56,57. Attentional manipulations may be particularly effective for decisions involving relatively short periods of time until reward delivery; in such cases, attention toward the time component increases the number of smaller, sooner choices^21–23. While our study cannot disentangle whether attentional bias itself drives choice or whether some underlying preference drives both attentional biases and choices, research showing a positive feedback loop between attention and preference (i.e., the gaze cascade effect) suggests that even externally directing attention can influence choice⁵⁸. Future interventions could provide strong tests of the directionality of our effects by attempting to force the “patient” attentional patterns we observed.

Our results do not obviate conclusions derived from simpler models that assess individual differences in behavior. The commonly used hyperbolic model assumes a relatively steeper discount curve for immediately available rewards, while the beta-delta model explains temporal variability in discount rates through separate parameters for relatively immediate and for relatively distal rewards^2,15,59,60. Each of these approaches explains dynamic inconsistencies in behavior (e.g., preference reversals with the passage of time) while also being measurable through simple survey or laboratory experiments¹⁴. We emphasize that for diagnostic tests in the field or in clinical settings, such simpler measures that are restricted to choice behavior will often be preferable to the more complex models used in our analyses⁶¹. We use modeling and eye tracking to better understand the attentional processes underlying the mechanisms of intertemporal choice – and where those mechanisms might be incompletely specified by behavioral models (e.g., the limitations of option-wise integration, as assumed by both hyperbolic and beta-delta models). The resulting insights into mechanism could in turn generate new hypotheses for future research and provide markers that could be studied in other populations.

Because both this study and others^27,62 have found that attributes processed more rapidly have an overall advantage in choice, interventions intended to encourage patient choices could draw attention to amount information before time information (e.g., via sequential presentation or a manipulation of stimulus salience)^63–67. Similarly, to facilitate attribute-wise transitions during the process of choice, amounts could be placed closer to each other and further from time information to encourage attribute-wise processing, or information could be revealed in a step-wise manner that promotes attribute comparison^37,68–74. For example, Reeck et al. (2017) were able to shift strategies toward attribute-wise (or option-wise patterns) by changing the speed of revealing key information based on the transition pattern used and thus reduce (or increase) discount rates³⁷. Future work should investigate what factors predict whether an individual can flexibly shift decision strategies (e.g., the pattern of information acquisition) across contexts. Also important for interventions will be extensions to impatience in other domains such as primary food rewards, health outcomes, and even environmental consequences^39,41–43.

Our sample included relatively few people at the extreme end of impatience, which limits our ability to extend our claims to all populations (e.g., individuals with pathologically impatient choices, as in addiction). We hypothesize, however, that a different heuristic, attribute-wise approach may also be utilized in extremely impatient people who compare options according to their time-to-delivery attribute instead of their amounts. If that result were observed, there would be a quadratic relationship between response time and patience. Some evidence in our data supports this hypothesis; in our larger primary sample, which has more extremely impatient individuals, this relationship is best fit by a quadratic curve (Supplementary Figure 8). However, this conclusion must be tempered because our replication sample does not have a sufficient number of extremely impatient individuals to confirm this finding. Future experiments could test the shape of this relationship with varying stimuli and across a larger sample with people with more diverse socioeconomic backgrounds and in populations known to be at the more extreme end of impatience. Such an approach could show that extreme discounters fall along the continuum of information-gathering patterns we observed or could find that those individuals employ an entirely different pattern altogether.

Another limitation of our study is that we allowed some stimulus information to vary (SS amount and LL delay) while keeping other information constant across trials. While one might hypothesize that participants would attend primarily to information that varies across trials, our eye-tracking results show that participants still used all information on the screen and made very few diagonal transitions between the cells with variable information. This suggests that attention was not driven by novelty or salience but instead by the information carried by each attribute, similar to prior research^37,75. Future experiments could manipulate additional features of the display, in order to evaluate whether reported moderators of choice behavior (e.g., the magnitude of the later reward) have concomitant effects on the patterns of attention. Dai & Busemeyer (2014) found that an attribute-wise model could account for variations in stimuli such as the magnitude effect, although that conclusion about choice behavior has not yet been accompanied by process-tracing data⁵. Furthermore, it would be interesting to test how the frequency of attractive LL or SS options for a given individual’s discount rate affects their attentional strategies and response times⁷⁶.

Temporal discounting has a profound influence on overall well-being and life outcomes – and interventions to encourage intertemporal patience could have a significant impact in many life domains. Both behavioral work and neural findings have suggested that working memory may be involved in choosing delayed options, and that training this skill may improve choice^77–80. In addition, time perception, positive episodic prospection, and concreteness of future events can influence intertemporal patience^81–85. Finally, framing choices using default options, directing attention to options or attributes or tradeoffs can shift choices^{4,8,20,22,37,86}. Our results are consistent with this last category, in that we show that factors that shape attention also influence selective parameters of the choice process – leading to more patient or impatient choices. These results could direct new interventions (e.g., modulations of attention that lead to heuristic choices) to help individuals focus more on the benefits of future rewards rather than the cost of waiting for these rewards. Through a better understanding of the underlying mechanisms of intertemporal choice, interventions that work for financial decision making could potentially be extended to improve choices across many contexts.

METHODS

Participants:

Primary Sample.

We recruited 117 subjects (mean age=21.3 years, SD=2.3 years; 75 female). Before data collection, we established a target sample size of 100 participants. No statistical methods were used to pre-determine sample sizes, but our sample sizes are larger than those reported in previous publications^32,35,87. Because of a data collection error with a second unrelated task completed by the same participants, we collected additional participants who completed both tasks – leading to a final sample of 117 for this experiment. Of these participants, 12 were excluded from eye tracking analyses because of poor-quality or insufficient data (subjects were excluded if in 50% or more of the eye tracking data for one or both eyes could not be identified or if their calibration was poor.) All participants were recruited from the Durham, NC and Duke University communities and provided informed consent under a protocol approved by the Institutional Review Board of Duke University.

Participants:

Replication Sample.

We recruited 100 subjects (mean age=21.5 years, SD=2.0 years; 68 female); 15 of whom were excluded from eye tracking analyses because of poor-quality or insufficient data. All recruitment, consent, and instructional procedures were identical to those of our Primary Sample.

Procedure.

Following informed consent, participants read a brochure about financial decision making; that brochure described either a traditional information-based strategy or a social cognition strategy. Conditions were randomly assigned to subject numbers before participants signed up for the experiment. Data collection and analysis were not performed blind to the conditions of the experiments. Note that because initial analyses revealed that the strategies did not evoke differences in ITC behavior that replicated across experiments, we hereafter combine across them in all reported analyses. Participants then completed two independent economic decision-making tasks – an intertemporal choice task (reported here) and an unrelated shopping task – in randomized order. After both tasks, subjects provided open-ended feedback about the strategies they used during decision making and completed the Abbreviated Barratt Impulsivity Scale (ABIS) as a general measure of individual differences in impulsivity⁸⁸. Because the ABIS did not correlate with intertemporal choice across samples, we do not further report on its relationship to other variables. See Supplementary Figure 2 for a detailed description of our analysis and replication workflow.

Tasks.

Participants completed 141 intertemporal choices. The SS choice was always available that day and varied between $0.50-$10 in increments of $.50, while the LL choice was always $10 but delivered between 1–365 days later (1, 7, 15, 30, 90, 180, and 365 days). All possible combinations of immediate amounts and later delays were used. In the Primary experiment (Figure 1, top row), the choice options were displayed on the left and right sides of the screen, with amount on top and time on bottom. In the Replication experiment (Figure 1, bottom row), the choice options were displayed at the top and bottom of the screen; with left-right position of time and amount information counterbalanced across the first and second halves of the experiment in blocks. The left-right (Primary) or top-bottom (Replication) order of the SS and LL options was randomized across trials.

Participants indicated their chosen option via keyboard button press. The task was self-paced with a 10s maximum response time; most choices were much faster (primary sample: mean RT=2.21s, SD=.70; replication sample: mean RT= 2.14s, SD=.64). Our maximum response time was well above the average response time; it was implemented to minimize extended lapses of attention and to keep participants focused on the task. At the end of the experiment, each participant received a base payment of $6 (cash) for their participation, and 1 trial was resolved for additional payment in an Amazon gift certificate that was delivered via email at the date on that trial. We used this payment method to minimize transaction costs and risk of delivery for future rewards^20,89,90; that is, subjects could be confident that they would receive the chosen reward on the promised date, with no additional time or effort commitment on their part.

Eye tracking.

Tasks were presented on a Tobii T60 eye tracker, which uses an unobtrusive camera system to sample gaze position at 60hz while allowing free head motion by the participant. We established areas of interest (AOIs) around the four pieces of information present on each display; each AOI was 350 by 350 pixels within the 1280 by 1024 total resolution of the screen. Before ROI analyses (gaze indices), we preprocessed the gaze position data using a clustering algorithm that identified drifts in calibration and then shifted the centers of mass of fixation clusters into the appropriate AOIs.

Analysis:

Modeling intertemporal value.

For each subject, we used maximum likelihood estimation to identify their temporal discounting coefficient (k) within a hyperbolic function (Equation 1).

$$SV=\frac{A}{1+kT}$$ Equation 1:

In this equation, SV is the subjective value of an option for an individual, A is its amount (in dollars), T is the time until its delivery (in days), and k is the discount rate. In addition, because k-values are non-normally distributed, we use a natural log transformation of k for analysis^19,23,75. Participants with uniformly patient choices or almost all patient choices with a few highly inconsistent choices (Primary Sample, N = 12; Replication Sample, N = 19) could not be fit by this function and were excluded from statistical analysis; on figures, their data is shown in lighter gray triangles to facilitate comparison with the other participants. Two additional participants in the replication sample had highly inconsistent choices that could not be fit to a single discount rate; those participants are excluded both from statistical analysis and from figures plotting the discount rate. Once k was identified for a given subject, we used its value to estimate the subjective value of the LL options on each trial, assuming a linear utility function for money over the range of values used; note that the subjective value for each SS option is equivalent to its nominal value. We chose the hyperbolic model for baseline comparison to our multi-attribute DDM as it has been shown to best fit with neural data and is widely used in relevant literature^18,19,91.

Multi-attribute DDM models:

To examine individual differences in the processing of amount and time information, we fit two multi-attribute DDM models for each participant, one based on attribute-wise comparison and the other on option-wise comparison.

DDMs assume that people stochastically accumulate evidence toward one choice option or the other until a relative value signal (RVS) reaches a decision boundary, triggering the execution of the choice^92,93. Our computational implementation of the DDM involved the following steps. First, we model the decision as a choice between two options (i.e., left or right in the primary sample, top or bottom in the replication sample) that differ in two attributes: amount and time. We assume that the relative value signal (RVS) is unbiased and starts at 0, equidistant from the decision boundaries for the two options; this assumption is appropriate because of our randomization of options to left/right or top/down locations (see Supplementary figure 13). Second, we estimate separate attribute latency values for amount ($t_A^{*}$) and for time ($t_T^{*}$). These values reflect the interval after the onset of the stimulus when no information is accumulating related to that attribute; both attribute latency values include perceptual and motor processing^94,95, while differences between latency values reflect a temporal advantage of one attribute over the other. The RVS accumulates in 10 ms time steps according to the amounts and times of each option weighted by separate drift slopes for time and amount attributes (δ_A or δ_T). All terms in the model are proportional to a stochastic error signal (ϵ_t) that is defined by a Gaussian distribution centered at 0 with standard deviation σ = 0.1.

In our option-wise model, equation (2), amount and time for each option are integrated in an option-wise manner similar to typical hyperbolic models. Prior to the attribute latency for a given attribute, the average over the experiment is used in place of the actual amounts or times on that trial as a scaling factor. We kept amount and time in their original scales to preserve the relative relationship between them.

$$RV{S}_t=RV{S}_{t-1}+\frac{{\delta }_A\cdot A_{\mathit{\text{left}}}}{1+{\delta }_T\cdot T_{\mathit{\text{left}}}}-\frac{{\delta }_A\cdot A_{\mathit{\text{right}}}}{1+{\delta }_T\cdot T_{\mathit{\text{right}}}}+{ϵ}_t$$ Equation 2:

Where:

$$A_{\mathit{\text{left}}},A_{\mathit{\text{right}}}=\overline{A}\text{ if }t<t_A^{*};$$

$$T_{\mathit{\text{left}}},T_{\mathit{\text{right}}}=\overline{T}\text{ if }t<t_T^{*}.$$

In comparison, in our attribute-wise model, equation (3), following an attribute-specific latency period, each attribute begins contributing to the RVS according to the difference in values. We normalized amount and time values to each be within the range [−1,1]; this allows their relative drift slopes to be directly comparable.

$$RV{S}_t=RV{S}_{t-1}+{\delta }_A^{\prime }\left(A_{\mathit{\text{left}}}-A_{\mathit{\text{right}}}\right)+{\delta }_T^{\prime }\left(T_{\mathit{\text{left}}}-T_{\mathit{\text{right}}}\right)+{ϵ}_t$$ Equation 3:

Where:

$$A_{\mathit{\text{left}}}-A_{\mathit{\text{right}}}=0\text{ if }t<t_A^{*\prime };$$

$$T_{\mathit{\text{left}}}-T_{\mathit{\text{right}}}=0\text{ if }t<t_T^{*\prime }.$$

We estimated the parameters of this model for each participant, independently, from their response time and choice data. To improve the stability of our estimation process, we excluded the 2.5% slowest and 2.5% fastest response times for each subject. We simulated each participant’s data 1000 times to identify the combination of parameters that best generated their choices and response time distribution (using 8 RT bins for each subject). The two models take different forms, but both fit the same five parameters – amount latency, time latency, amount drift slope, time drift slope, and decision boundary – while holding noise and bias constant. This similarity means that model fits can be directly compared on a subject-by-subject basis.

We used the Bayesian Information Criterion (BIC) to compare model fits. The equation for the criterion is BIC = −2 × log likelihood + d × log(N) where N is the number of trials completed and d is the number of parameters fit. Lower scores indicate better fit. See Supplementary Figures 14 and 15 for average model-predicted and actual choice and response time for each individual.

For all models we used a grid-search procedure with an initial common coarse grid for all subjects, followed by a finer grid search around each individual’s best fitting parameters (see Supplementary methods for parameter ranges). Linear spacing was appropriate for all DDM parameters, save for drift slope in the option-wise model (which used a log spacing to as log-normalization was needed to obtain a normal distribution for the time drift slope). We did not include negative drift slopes because they do not make theoretical sense in our paradigm; that is, subjects did not prefer to receive smaller amounts of money at later times, as would be needed to generate a negative slope. We note that there are a variety of methods to solve DDMs that seek to account for a variety of psychological processes such as inconsistencies in choice, but we chose a grid search to minimize assumptions about the attentional process^93,96,97.

Indices of looking behavior.

We derived three measures of gaze behavior from our eye tracking data. All measures were scaled to a −1 to 1 range. The Attribute Index, equation (4) describes the proportion of time a participant looked at the amount AOIs (compared to the total time looking at AOIs); positive values indicate more time spent looking at amounts, negative indicate more time spent looking at time AOIs.

$$\frac{\mathit{\text{Gaze points in Amount ROIs}}-\mathit{\text{Gaze points in Time ROIs}}}{\mathit{\text{Gaze points in Amount ROIs}}+\mathit{\text{Gaze points in Time ROIs}}}$$ Equation 4:

The Option Index, equation (5) measures the proportion of time a participant looked at SS AOIs (again compared to the total looking time); positive values indicate looking at SS options, negative at LL³⁵.

$$\frac{\mathit{\text{Gaze points in Immediate option ROIs}}-\mathit{\text{Gaze points in Delayed option ROIs}}}{\mathit{\text{Gaze points in Immediate option ROIs}}+\mathit{\text{Gaze points in Delayed option ROIs}}}$$ Equation 5:

Finally, the Payne Index³⁸, equation (6), quantifies whether transitions in gaze tend to be within options (e.g., from the SS amount to the SS time; positive Payne Index) or within attributes (e.g., from the SS amount to the LL amount; negative Payne Index).

$$\frac{\mathit{\text{Option}}-\mathit{\text{wise transitions}}-\mathit{\text{Attribute}}-\mathit{\text{wise transitions}}}{\mathit{\text{Option}}-\mathit{\text{wise transitions}}+\mathit{\text{Attribute}}-\mathit{\text{wise transitions}}}$$ Equation 6:

Statistics:

All statistics are stated in the text and figure captions. Binomial tests are compared to a hypothesized probability of 0.5. Normality was not directly tested because of our large sample sizes, but unless otherwise noted, data was assumed to be normally distributed and individual data points are provided in the figure scatterplots.

Programming environments:

MATLAB was used to calculate discount rates, run drift diffusion models, preprocess eye tracking data, and create eye tracking indices⁹⁸. R was used to make plots and calculate statistics^99,100.