Automatic breast tissue segmentation in MRIs with morphology snake and deep denoiser training via extended Stein’s unbiased risk estimator

Abstract

Accurate segmentation of the breast tissue is a significant challenge in the analysis of breast MR images, especially analysis of breast images with low contrast. Most of the existing methods for breast segmentation are semi-automatic and limited in their ability to achieve accurate results. This is because of difficulties in removing landmarks from noisy magnetic resonance images (MRI). Especially, when tumour is imaged for scanning, how to isolate the tumour region from chest will directly affect the accuracy for tumour to be detected. Due to low intensity levels and the close connection between breast and chest portion in MRIs, this study proposes an innovative, fully automatic and fast segmentation approach which combines histogram with inverse Gaussian gradient for morphology snakes, along with extended Stein’s unbiased risk estimator (eSURE) applied for unsupervised learning of deep neural network Gaussian denoisers, aimed at accurate identification of landmarks such as chest and breast.

Introduction

Currently breast cancer is listed as the second most common cause of deaths for women [1]. Over 1.3 million women worldwide that undergo tumour screening are diagnosed with breast cancer each year, making it one of the most common forms of cancer. To reduce the mortality rate from breast cancer, early diagnosis and treatments are essential [2]. Breast (MRI) is an established clinical imaging modality for high-risk screening, diagnosis, preoperative staging, and neoadjuvant therapy response evaluation. The most common clinical indication was diagnostic evaluation (40.3%), followed by screening (31.7%) [3].

MRIs enable to identify and mitigate breast diseases by generating a series of 3D images that a radiologist uses to manually detect the diseased part and identify problems [4, 5]. The manual process is time consuming because of the high number of images [6–9]. Hence, automatic computer-algorithm based image analysis has become essential for performing computer-aided detection and diagnosis, which aim to provide prompt output and help radiologist to accurately locate the diseased area.

The segmentation in medical images is a complex process because of shape variation in the noisy and inhomogeneous image domain. The type, size and location of the organs and particular structures are important information in medical images. Vast surveys using diversified image processing algorithms are available [10–12] for breast tumor segmentation.

Accurate recognition and segmentation of target regions determines the success of computer detection and diagnosis. According to the degree of radiologist's participation in the process of identifying lesion regions by a computer, it can be divided into fully automatic recognition (such as automatic recognition based on the overall three-dimensional morphology or statistical significance), and semi-automatic recognition (such as threshold segmentation, region growth or fuzzy C clustering, etc.), along with interactive recognition (manually select the area of interest and then cut the edge). Compared with semi-automatic recognition of region of interest, full-automatic recognition has the characteristics of fast speed and wide applicability; compared with interactive recognition of lesion images, full-automatic recognition has the characteristics of simple structure and less manual operation, which lays the foundation for the widespread application of computer-aided diagnosis (CAD), but the accuracy of automatic target identification needs to be further improved [13, 14].

Segmentation techniques such as threshoulding, edge detection and pixel based classification depend on pixel intensity. Intensity along may not be sufficient to segment breast MRIs. Quality of these medical images to be segmented are often affected by noise, low contrast, blurry edges, intensity overlapping and motion artifacts. These approaches are often combined with other segmentation methods to provide solution. Active contours have played a fabulous role to obtain the object boundaries due to its evolution property of contraction and expansion. Those models enable to obtain sub-pixel accuracy of object boundaries as well as smooth and closed contour as segmentation result [15]. Active contour models are an energy-minimizing curve, does not require any a prior knowledge or any training set about images to be analysed. It is to minimize the energy function that drives the deforming contour towards the object boundary under the influence of internal and external forces. Internal forces are defined within the curve itself that discourage smoothness and tautness of the contours, whereas the external forces arise from the image data that pull the contours toward features of interest, such as edges. These forces ensure that the active contour is confined to object boundaries or any other feature in the image. Traditional active contour models can be categorized into two types: a parametric active contour model and a geometric active contour model (ACM).

Parametric contour model is a greedy-based model, such as traditional active contour or a snake. Parametric active contours synthesize parametric curves within the domain of an image and aid them to move towards edges of the image object of interest. Some typical improved models have been reviewed by [16], including but not being limited to Traditional snake [17], Distance potential force [18], Gradient vector flow (GVF) snake [19], Vector field convolution (VFC) snake [20].

Geometry active contour model is implemented using a level set function which allows multiple object segmentation. Level set method, introduced by Osher and Sethian [21], offers highly robust and accurate methods for tracking interfaces moving under complex motions. The basic idea of the level set model is to represent image contours by the zero level set of a higher dimensional function, and the motion of the contour is formulated based on the evolution of the level set function. It has been demonstrated that level set models are a useful tool for modeling time-varying objects with practical and theoretical advantages over conventional surface models [22]. The level set model does not work well on images with noise. This often leads to either a complete breakdown or delayed termination of the curve evolution process. The stability and convergence of the level set method are influenced by the speed function and parameters of the level set.

Further geometric contour model can be classified based on the stopping criterion. If edge function is used to stop the evolution of the contour, then it is referred as edge-based contour model, sensitive to noise and illumination variation. In 2001, Chan and Vese proposed region based stopping function [23]. Distinct from the first kind of models, region-based models make use of statistical information in global or local regions to drive contour curve to obtain desirable target boundaries. In this model, the image is considered to be piecewise constant function and binary segmentation is performed using external force estimated via statistical parameters of the regions. This model encounters problem for medical images such as X-ray and MRI having intensity inhomogeneity and noisy image domain. Various models have been proposed to improve the Chan–Vese model. Dolz et al. provides a framework for a region-based contouring technique in clinical practice [24], they advise further investigation into more accurate atlas selection methods to improve the clinical usability. Liu et al. [25] defined a local region-based Chan–Vese (LRCV) model by considering the local characteristics of an image as the initial contour with the application of Gaussian filtering for smoothing evolution process. Pratondo et al. [26] constructed a active contour framework that integrated machine learning with region-based active contour models for tumour detection from MRI images, and so on.

Owing to the emergence of deep learning learning technique that has been seen rapid development in the past decade, new active contour models based on deep learning have been developed and shown promising results compared to existing solutions. Different from unsupervised active contour that no training datasets are required, the new model integrates priors and constraints into the active contour process via the deep learning strategies, to achieve continuous boundaries, smooth edges, and sharp corners, etc. Xu et al. [26] presented a method for automated detection and segmentation of breast cancer nuclei, which uses a convolutional neural network to initialize active contour model with adaptive ellipse fitting. Chen et al. [27] desined new active contour models based on deep learning by proposing a new loss function, which incorporates area and size information and integrates this into a dense deep learning model, aimed at the segmentation of cardiac MRI scans with clearly defined boundaries. Guo et al. [28] exploited single network architecture to define an external constraint force of active contour models, and to generate a pixel label map containing spatial regional information (foreground and background) as well as layered boundary information. A unique property of the designed force is that both its strength and direction are adaptive to its position and relative distance to the object boundary. it allows to place the initial contour far away from the liver boundary and potentially enable to control the evolution of the contour in order to preserve the topology of the liver.

Apart from robust of the active contour algorithm, image noise will affect the accuracy of active contour for image segmentation. Collecting high-quality noiseless images is a challenging task in image processing and computer vision. The two main limitations in image accuracy are categorized as blur and noise. Blur is intrinsic to image acquisition systems, as digital images have a finite number of samples and must satisfy the Shannon–Nyquist sampling conditions [29]. The second main image perturbation is noise. Noise is an inherent property of medical imaging, and it generally tends to reduce the image resolution and contrast, thereby reducing the diagnostic value of this imaging modality, degrade the performance and usefulness of quantitative MRI diagnostics, when conducting voxel-based tissue classification, extracting organ shape or tissue boundaries, estimating physiological parameters.

Magnetic resonance imaging is used to extract images of soft tissues of human body. It is used to analyze the human organs without the need for surgery. Generally MRI images contain a significant amount of noise caused by operator performance, equipment and the environment, such as impulse, Gaussian, and speckle, which leads to serious inaccuracies MRI and seems to be efficient in providing information regarding the location of tumors and even the volume. The noise present in the MRI image can be removed by using various de-noising techniques whichever is best suited depending upon the image acquired and then can be processed by any of the segmentation methods. Numerous research works have been conducted in detection and elimination of noise in medical images. Image denoising via machine learning techniques has played an important role in the various application areas of medical imaging such as pre-processing (noise removal from Ultrasound (US) Images, segmentation (MRI of Brain Tumor, lungs infection using X-ray), Computer Aided Diagnosis (CAD) for breast cancer, Fetus development and many more) [30–33]. These techniques learn a set of bases from the denoised images aimed at creating a dictionary to sparsely represent image patches as a linear combination of dictionary atoms [34]. There has been an attentiveness in using multi-resolution wavelet filters in a variety of medical imaging applications [35, 36].

More recently, deep learning received considerable attention, emerging as a machine learning approach in delivering robust MR image processing. Bermudez et al. proposed an autoencoder with skip connections for T1-weighted (T1w) imaging of the brain [37].The developed network, trained with 528 T1w images, significantly improved the image quality based on PSNR analysis. DnCNN is also widely used for denoising of brain MR images [38, 39]. Denoising using DL is used not only for the improvement of image quality but also for reducing scan time. In addition, In [40] an adaptive filter with edge preserving property for Rician noise in MRI images is proposed. In [41], for Gaussian and impulse noise detection in tomography images, a discriminative bilateral filtering for is proposed. In [42] an adaptive median filter for removal of impulse noise in X-ray images and speckle noise in ultrasound images is proposed. In [43] medical images which are used for detecting cancer in different parts of human body are considered and different types of noise effecting such images are reviewed.

The main objective of this study is to segment the breast region of interest (BROI) from breast MRIs with low contrast, which is carried out with a framework consisting of three major steps. Firstly, an approximated image, removing the noise while preserving the main structures, is found in the feature space of the original image via deep denoiser training via extended Stein’s unbiased risk estimator (eSURE). Secondly, we use Adaptive histogram equalization for image contrast enhancement, which is as a preprocessing strategy with an aim to find the edge that can be used as a reference to partition between breast and chest in MRI images. Thirdly, inverse Gaussian gradient for morphology snakes is designed. In this step, we adopt adjust sigmoid for image enhancement, and perform inverse gradient to keep the edge of chest, before morphological geodesic active contour can be applied. The motivation is to separate the imaged breast segmentation from background region via threshold easily, in the meanwhile, to accurately isolate the chest region from MRIs. The proposed method is validated in two types of MRI images: breast MRI 3.0 T and breast MRI 1.5 T with tumour and non-tumour images using the 1160 breast images from 10 female subjects and 1740 breast images from 15 female subjects, respectively. These breast images are extracted from breast MRIs with and without tumours. The pixel-based quantitative analysis showed excellent segmentation.

The paper is organized as follows. In Sect. 2, we introduce the mathematical framework based on the level sets and morphology based active contour. In Sect. 3, we introduce the extended Stein’s unbiased risk estimator and the numerical algorithm of deep denoiser training via extended Stein’s unbiased risk estimator. In Sect. 4, we validate our model by some experiments on medical images. In Sect. 5, we end the paper by a brief conclusion.

Methodology

The general workflow breast segmentation at the region of interest (BROI) as illustrated in Fig. 1. Each step is successively explained in the following sections. Breast segmentation is carried out with a framework consisting of three major steps. Firstly, we adopt eSURE denoising method to remove noised MRI images, in comparison with threshold based method, for noise type analysis and denosing performance comparison. Secondly, adaptive histogram equalization for image contrast enhancement, which is as a preprocessing strategy with an aim to find the edge that can be used as a reference to partation between breast and chest in MRI images. The second step carries inverse Gaussian gradient for morphology snakes. In this step, the two different portions in relation to breast and chest are processed and analysed differently according to the different properties of their own. For Imaged chest, we try the method called adjust sigmoid for image enhancement, and perform inverse gradient to keep the edge of chest; therefore, morphological geodesic active contour can be applied to accurately isolate the chest region from MRIs. While in the breast segmentation, we aim to find the upper and lower edge of breast, with an aim to separate the imaged breast segmentation from background region via threshold easily [44].

Fig. 1.

Illustration of the general workflow regarding breast segmentation at the region of interest (BROI)

Preprocessing

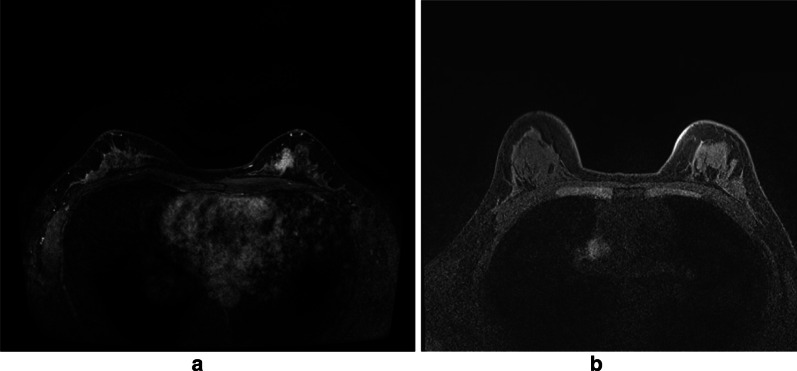
The original breast MRIs are T1-weighted nonfat-suppressed MRI images, in which fat appears as the brightest and air (background) as the darkest signal. Fibroglandular tissue, tumors, and the chest wall appear as moderate signals with similar signal intensity [12]. The figure below shows a contrast enhanced image after the injection of contrast agent. Figure 2a, b is breast MRI 3.0 T (1.5 T) with (without) tumour. In this case, a part of the fibroglandular tissue with (without) tumour tissue are connected to the chest wall and there is no fat along the anterior side of the chest wall. The contrast in those regions are not be sufficiently enhanced in addition to the partly enhanced tumour tissues.

Fig. 2.

A contrast enhanced image after the injection of contrast agent. a and b is breast MRI 3.0 T (1.5 T) with (without) tumour

Adaptive histogram equalization (AHE) is used to improve contrast in images. Different from ordinary histogram equalization, AHE allows to compute several histograms, with each corresponding to a distinct section of the image. Calculated histograms can be used to redistribute the intensity values of the image. It is therefore suitable for improving the local contrast and enhancing the definitions of edges in each region of MR image. In order to find the edge between breast and chest wall, it requires the increased contrast in details over these small areas. This problem can be solved if we use a transformation function that is derived from the neighborhood of every pixel in the image. This is what AHE do.

Deep denoiser training via extended Stein’s unbiased risk estimator (SURE)

As an important part of preprocssing to denoise an MRI image, we make it a single subsection in the methodology part to highlight the deep learning based denoising strategy. Due to the bright noise pixels existing around the edge of breast region, when performing segmentation, these noise pixels actually lead to false edges of breast, which either encloses the true edges or excludes the true edges. Therefore, it is challenging to achieve breast segmentation.

SURE based deep denoiser training

Typically, Gaussian contaminated signal (or image) is modeled as a linear equation: y = x + n, where x ∈ R^N is an unknown signal, y ∈ R^N is a known measurement, n ∈ R^N is an i.i.d. Gaussian noise such that n ∼ N (0, σ² I), and I is an identity matrix, We denote n ∼ N (0, σ² I) as n ∼ N_0,σ2.

Given a deep estimator h_θ(y) of x, the deep SURE has the following form:

$$\eta ({\text{h}}_{\theta }(y))=\frac{1}{M}\sum _{j=1}^M\{||{\text{y}}^{(j)}{\text{- h}}_{\theta }{\text{(y}}^{\text{(}j)}{\text{)||}}^{\text{2}}-N{\sigma }^2+\frac{2{\sigma }^2}{\epsilon }{({\tilde{n}}^{{}_{(j)}})}^t(h_{\theta }(y^{(j)}+\epsilon {\tilde{n}}^{(j)})-h_{\theta }(y^{(j)}))\}$$ 1

where θ is the set of DNN denoiser parameters, M is the size of mini-batch, is a small fixed positive constant, and $\tilde{\text{n}}(j)$ is a single realization from standard normal distribution for each training data j [45].

Extended SURE

The original SURE in (1) works well with a single noise realization per image, but it can not take advantage of having multiple noise realizations per image. Thus, an extend SURE denoising is proposed to be able to handle pairs of noisy images per ground truth image. The extended SURE (eSURE) can be formulated in the following way [45]:

Let $y_1\sim \mathrm{N}(\text{x,}{\sigma }_{y1}^2\mathrm{I}),z\sim \mathrm{N}(0,{\sigma }_z^2\mathrm{I})$, and $y_2\underset{\_}{\underset{\_}{\mathrm{\Delta }}}(y_1+z)\sim N(x,({\sigma }_{y1}^2+{\sigma }_z^2)\mathrm{I}).$ Then, the random variable $\gamma (h_{\theta }(y_2),y_1)$ is an unbiased estimator of mean squre error(MSE):

$$\gamma (h_{\theta }(y_2),y_1)=\frac{1}{N}||y_1-h_{\theta }(y_2){||}^2-{\sigma }_{y1}^2+\frac{2{\sigma }_{y1}^2}{N}\sum _{i=1}^N\frac{\partial h_i(y_2)}{\partial {(y_2)}_i}$$ 2

where y₁ and z are independent or uncorrelated and

$${\mathrm{E}}_{y_2}\{\frac{1}{N}||x-h_{\theta }(y_2){||}^2\}={\mathrm{E}}_{y_2}\{\gamma (h_{\theta }(y_2),y_1)\}$$

When we apply the eSURE framework to a pair of uncorrelated Gaussian noisy images (y ∼ N (x, ${\sigma }_y^2$) and z ∼ N (x, ${\sigma }_z^2$). In that case, the divergence term vanishes leaving us the following expression:

$${\mathrm{E}}_{z,y}\{\gamma (h_{\theta }(y),z)\}={\mathrm{E}}_{z,y}\{{\frac{||z-h_{\theta }(y)||}{N}}^2\}-{\sigma }_z^2$$

Inverse Gaussian gradient for morphological geodesic active contour

Morphological geodesic active contour

Morphological geodesic active contour is also called Morphology Snakes. This operation consists of the morphological operations and geodesic active contour. Active contour based segmentation methods are being used in medical image processing research for years now. Geodesic active contour (GAC) is one of the most popular contour evolution methods [13, 14]. GAC tries to separate foreground (object) and background with the help of image intensity and gradient. GAC solves a partial differential equation (PDE) to evolve the curve towards the object boundary [46–48].

The fundamental objective of GAC model was to track a closed surface $\mathrm{\Gamma }(\text{u)}$ for which $\mathrm{\Gamma }(u):[0:\infty ]\to R^N$ as it evolved in data space. Such an interface was represented as a closed curve $\text{C}(u)$ in 2D or a set of points on the boundaries of the region of interest Ω. Initially introduced by Osher and Sethian [15], the level set (geodesic) method performed well at capturing dynamic interfaces and shapes. The basic idea of this method was that the contour could be embedded as the zero level set of a high-dimensional function $\varphi (x,y,t)$ known as a zero level set function (LSF). Assuming a dynamic parametric contour $\text{C}(p,t):[0,1]\times [0,\infty )\to R^2$ with a spatial parameter $\text{p}\in [0,1][0,1]$ and t was a temporal variable $\text{t}\in [0,\infty )$, then the target contour was described as the zero level set function $C(p,t)=\{(x,y)u(x,y,t)=0\}$.

Embedding level set function u which was described by the continuous Lipschitz function with signed distance d from (x, y) to the initial curve C0. Such a Lipschitz function implied that the existence of a bounded first derivative. The distance was given a positive sign outside the initial boundary $({\text{R}}^2\mathrm{\Omega })$, a negative sign inside the boundary (Ω \∂Ω) and zero on the boundary (∂Ω). The curve evolution equation of GAC can be represented in implicit form as $\frac{\partial \text{u}}{\partial t}=g(I)|\mathrm{\nabla }u|(\nu +div(\frac{\mathrm{\nabla }u}{|\mathrm{\nabla }u|}))+\mathrm{\nabla }g(I)\mathrm{\nabla }u$, where, ν is the balloon force parameter describing the evolve direction of the active contour curve. For ν > 0, the GAC will evolve in the inward direction, or in opposite direction when ν < 0. We use $\text{di}v(\frac{\mathrm{\nabla }u}{|\mathrm{\nabla }u|})$ to indicate the curvature of the curve C. For I is one slice of the breast MRI sequential images, the edge indicator function g may be used to control the curve evolution and stop the curve from evolving when it arrives at an object’s boundaries. Such a function is defined to be $g(I)=1/\sqrt{1+\alpha |\mathrm{\nabla }G\ast I|}$, where $\ast$ is the convolution operator and G is a Gaussian kernel with standard deviation σ.With this definition, $|\mathrm{\nabla }\text{G|}\ast \text{I}\to 0$ and $\text{g}(I)\to 1$ in homogenous regions without fine texture. In contrast, $|\mathrm{\nabla }\text{G|}\ast \text{I}\to 255$ and $\text{g}(I)\to 0$ at edge regions.

The GAC contour evolution equation comprises of three forces: (a) Balloon force, (b) Smoothing force and (c) Attraction force. However, solving PDEs involves computationally expensive numerical algorithms. In this paper morphological operators are used to solve the PDE of GAC as proposed in [16, 17]. Let the contour at nth iteration is represented by ${\text{u}}^{\text{n}}(x)$. The balloon force $(\text{g}(I)|\mathrm{\nabla }u|\nu )$ can be solved using a threshold $\theta$, binary erosion (E_h) and dilation (D_h) operations for (n + 1)th iteration as

$$u^{n+\frac{1}{3}}(x)=,\stackrel{}{}\left\{\begin{array}{c}(D_h{u}^n(x)),\stackrel{}{}if\stackrel{}{}g(I)(x)>\theta \stackrel{}{}and\stackrel{}{}\nu >0,\\ ({\text{E}}_h{u}^n(x)),\stackrel{}{}if\stackrel{}{}g(I)(x)>\theta \stackrel{}{}and\stackrel{}{}\nu <0,\\ u^n(x),\stackrel{}{}otherwise\\ \end{array}\right)$$

The attraction force (∇g(I)∇u) can be solved very easily from intuition. The main purpose of attraction force is to attract the curve C towards the edges. Mathematically we can discretize this force as

$$u^{n+\frac{2}{3}}(x)=,\stackrel{}{}\left\{\begin{array}{c}1,\stackrel{}{}if\stackrel{}{}\mathrm{\nabla }{u}^{n+\frac{1}{3}}\mathrm{\nabla }g(I)(x)>0,\\ 0,\stackrel{}{}\stackrel{}{}if\stackrel{}{}\mathrm{\nabla }{u}^{n+\frac{1}{3}}\mathrm{\nabla }g(I)(x)<0,\\ u^{n+\frac{1}{3}}(x),\stackrel{}{}otherwise\\ \end{array}\right)$$

In order to solve the smoothing term $(g(I)|\mathrm{\nabla }u|div(\frac{\nu u}{|\mathrm{\nabla }u|}))$ Alvarez et al. [49, 50] defined two morphological operators, sup-inf (SIh) and inf–sup (ISh). In binary images, both SIh and ISh operators look for small straight lines (3 pixels long) in four possible spacial directions. If no straight line is found, the pixel is made inactive and active respectively. The difference between SIh and ISh is that, the first one operates on active pixels (i.e. pixels having values 1) and the second one operates on inactive pixels (i.e. pixels having values 0). It can be proved that, the mean curvature $\text{(div}(\mathrm{\nabla }u/|\mathrm{\nabla }u|))$ can be obtained using the composition of these operators (SI_h◦IS_h). So, the smoothing force with smoothing constant $\mu$ can be written as

$$u^{n+1}(x)=,\stackrel{}{}\left\{\begin{array}{c}({(S{I}_h\circ I{S}_h)}^u{u}^{n+\frac{2}{3}})(x),\stackrel{}{}if\stackrel{}{}g(I)(x)>0,\\ u^{n+\frac{2}{3}}(x),\stackrel{}{}\stackrel{}{}otherwise\\ \end{array}\right)$$

This morphological geodesic active contour is applied which is a composition of the three forces (balloon force, attraction force followed by smoothing force) to each of the slices of the CT volume.

Localization of chest from breast MRIs

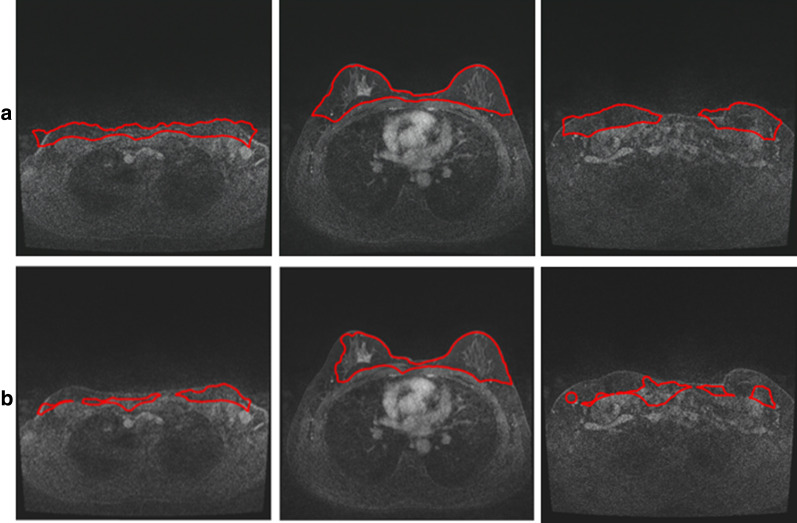
In order to localize the breast and chest regions of interests, a suitable edge in relation to the two regions from the axial 2D slice needs to be determined in terms of its geometry of breast MRIs. Firstly, we look for the edge of breast region of interest, then we derive how to use this edge to calculate the edge of chest region. Breast images is approximately symmetric and there are two breasts on the right and left hand of the MR image. In order to find the edge pixels, we search the middle line and then a middle region can be determined.

Part of the edge of the breast region is assumed to be involved in the middle region along y axis. Before the edge region is located, the MR image stack is first processed by a morphological binary erosion operation with a disk type structuring element of radius 3 pixel. The main purpose of this operation is to remove all the undesirable small regions present in the MRI slices. The middle region of MRI stack is calculated along its veritcal directions (y axis) of the axial 2D slice, within the distance of ± 20 pixels to its middle line. The main edge of the breast region of interest is the first bottom line along x axis, as shown in Fig. 3.

Fig. 3.

The middle region of MRI is calculated along its veritcal directions (y axis) of the axial 2D slice, within the distance of ± 20 pixels to its middle line

The bottom edge of chest therefore, is N–middle_pix-5, which is viewed as a 5 pixel distance from the lowest edge of the middle region of breast (y = middle_pix), aimed at removal of the edge of breast. The number of N is the total number of pixels along its y direction of MRIs. We view this as an ending point for downward direction of chest. Therefore, we get the boxed chest image region as follows, where The enclosed area (body_cc) with curve is the mophological active contour of chest, as shown in Fig. 3.

Then compare the intensity of the pixel with its neighbor line of the pixel along the y direction. This procedure is repeated for each other line, throughout the whole image, and replace the weaker pixel intensity with the previous line of the pixel intensity, if the previous line shows stronger intensity pixels. This aims to add one more pixels at the each important edge of the chest, breast, and tumour when they are changed from light to dark so as not to wrongly remove edge pixels when conducting gradient transform. Our aim is to find the edge with color change from bright to dark that includes the edge we wish to detect.

Localization of breast MRIs

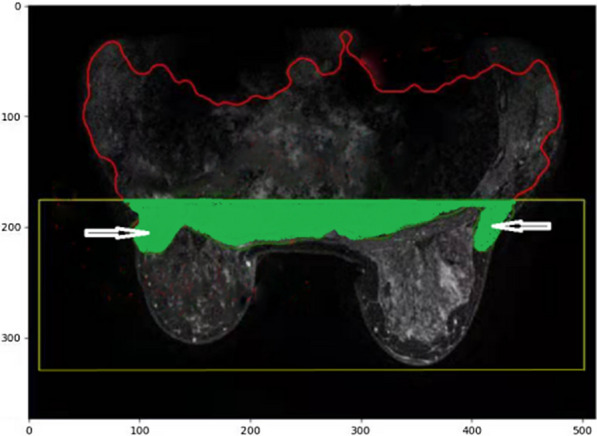
In order to define top and bottom boundaries of breast segmentation, we use such an expression as 4/5*(N–middle_pix), which is the approximate distance between the chest and the bottom edge of breast in the middle region with an aim to pick up all the breast tissue that has been classified as chest tissues. It is illustrated as the figure below. The green colored part is the region cutted from the chest region of interest, where the white arrows indicate the misclassified breast tissue to chest tissue. In order to redo the breast segmentation accurately, we involve this as part of the breast region of interest and calculate the breast segmentation. The y posiition is calculated by 4/5*(N–middle_pix) as a starting line of upward direction from breast region.

After find the top edge of breast region, we need to determine the lowest edge of breast. Considering the noise around breast edge, we take 0.1 as a threshold, which means the pixel with intensity value larger than 0.1 will be added together along the horizontal line, if the accumulated intensity along the horisantal line is larger than 10, the bottom of horizontal line with additional 5 pixel gap will be viewed as the bottom edge of breast, an ending point of for downward direction of breast. The 5 pixel gap aims to involve, for example, the imaged nipple related pixels. In the mealwhile, the accurate bottom edge will also reduce the effect of noise which may wrongly detected as the edge of breast when conduct morphological active contour, as shown in Fig. 4.

Fig. 4.

It is illustrated how to achieve the boxed chest image region, in which the enclosed area with curve is the morphological active contour of chest

As illustrated in Fig. 5, the yellow line means 10 pixel gap from the initial calculated bottom line, as this will introduce some noise and make a wrongly drawing breast shape due to much noise around the edge of breast, so finally, we use 5 pixel of extra gap instead to be the final bottom line of the breast region for active contour to be conducted.

Fig. 5.

Illustration of noise around breast edge leads to wrongly determined edge of breast

In order to find the threshold of breast image intensity range, we first to find the intensity value of noise outside of breast. In the following figure, below the bottom boundary of breast, there are some noise around, which results in wrong boundary decision when using mophological active contour as illustrated by white arrow. We gradually add random noise of different intensities to the images.To release the noise effect, we find the maximum value of the noise intensity. We decide the intensity threshold of breast region is maximum noise intensity plus extra 12 according to our test and revise till find the ideal results.

Then we extract the breast tissue image by threshould the image in the boxed region. Before it, we use binary openning to remove possible noise and binary close to smooth the edge of breast tissue. We draw the boundary of breast using morphological active contour (Fig. 6).

Fig. 6.

The yellow line means 10 pixel gap from the innital calculated bottom line, and the green line is achieved via the use of 5 pixel of extra gap that is the final bottom line of the breast region for active contour to be conducted

The stack is thresholded at this decided value in the boxed region which retains the lower intensity air filled regions (including surrounding air) in the MR image stack. A morphological binary erosion operation has been done with a disk type structuring element of radius 1 pixel on the thresholded MRI stack I. The main purpose of this operation is to remove all the undesirable small regions present in the MRI slices. Binary openning is involved to remove possible noise and binary close to smooth the edge of breast tissue. The boundary of breast using morphological active contour is finally performed.

MRI measurements

In this paper, we validate our algorithms using two type of MRIs using 1.5 T MRIs and 3.0 T MRIs.

1.5 T related potocol: DCE-MRI was acquired by using the fat-suppressed 3D-FLASH with one pre-contrast and four post-contrast frames, with TR/TE = 4.50/1.82 ms, flip angle = 12 degrees, number of signal average = 1, matrix size = 512 × 512, FOV = 32 cm, and slice thickness = 1.5 mm. The imaging resolution (voxel size) was 0.6 × 0.6 × 1.5 mm.

3 T related protocol: The MRI scan was acquired using the volume imaging for breast assessment (VIBRANT) sequence in the axial view to cover both breasts, with repetition time (TR) = 5 ms; echo time (TE) = 2 ms; flip angle (FA) = 10°; slice thickness = 1.2 mm; field of view (FOV) = 34 × 34 cm2; matrix size = 416 ×  416.

Experiment results

The following figures are the resultant experiments that are achieved via the proposed approaches. There are 15 cases of female subjects with 12 × 160 = 1820 layers of MRIs that have been tested for validation. The measurement uses MRI machine of 1.5 T. As illustrated in Fig. 7, we achieve the segmentation of breast before and after the deep denoising via eSURE, with application of transmitting learning of nature images. Before denoising, as illustrated in Fig. 7a, orange colored arrow indicates the contours with slightly away from its original position. Green arrow shows small variation of contours around the edge between the two breast. Figure 7b shows the contours detected after the first level of Gaussian noise is added. The signal to noise ratio is 46.44. One the top of Fig. 7b, shows increased errors in the detected edges of breast compared with resultant contours on the original images, highlighted by the colored arrows. After denoising, as shown on the bottom of Fig. 7b, the detected contours have been much close to the real edge of breast, compared with contours delineated in Fig. 7a and the top of Fig. b. The signal to noise ratio has been improved to 47.75. Figure c shows the contours detected after the fourth level of Gaussian noise is added. The resultant contours on the top of Fig. c, is becoming worse than the detected contours with first level noise, due to the added signal to noise ratio. However, after denoising, the resultant contours with errors have been partly corrected, but still shows less corrections than resultant contours delineated on the first level of denoising images, as the bottom of Fig. b. The noise ratio of Fig. 7c is changed from 38.96 to 41.59.

Fig. 7.

Below the bottom boundary of breast, there are some noise around, which results in wrong boundary decision when using morphological active contour as illustrated by white arrow

To some extent, there exists slightly false classification of breast tissues when conducting segmentation on denoised images. It is found when performing division of the image intensity by 3 to achieve weakened image intensities on MRIs, the image contours show improved performance, as illustrated in Fig. 8. Figure 8a illustrates the original MRIs that will be segmented. Figure 8b are the background truth delineated by one of experienced doctors. Figure 8c–e are contours calculated based on denoising images on level 1 and level 4 noisey MRIs, and intensity weakened images, respectively. The contours shown in Fig. 8e locate well on the edge of breast, whereas Fig. 8c, d display some errors when locate the contours after denoising on the level 1 and level 4 images.

Fig. 8.

Contour detection on (a) original images; Before and after eSURE denoising on the top and bottom images respectively with the first level noise (b) and the fourth level noise (c)

However, in most situation, denoising on level 1 MRIs performs well in achieve active contour images. In Fig. 9, a comparison between the contours achieved after eSure denoising on level 1 noisy images Fig. 9a and intensity weakened images Fig. 9b. Though there exists small errors in achieving contours on the breast region of interest after denoising, the whole shape of breast is obviously to be drawn. For comparison, the intensity weakened images could not get the correct classification of the breast when conducting the proposed segmentation approach.

Fig. 9.

Illustration of the original MR images in (a), background truth in (b), contour detection in denoising images with level 1 noise (c) and level 4 noise (d), along with the intensity weakened images (e)

The statistical analysis is conducted for the validation of segmentation results in relation to deep denoising method. The resultant statistical data are listed in the following tables. Table 1 is signal to noise ratio in 12 female cases before and after denoising on level 1 noisy images and level 4 noisy images. The deep denoising method allows to improve the signal to noise ratio from 46 on level 1 noisy images to 48 or so on level 4 images, and from 38 to 41 around on level 4 noisy images. The denoising method enables to improve signal to noise ratio well in level 4 noisy images compared with level 1 noisy images.

Table 1.

Illustration of signal to noise ratio in 12 female cases before and after denosing on level 1 noisy images and level 4 noisy images

	001	002	003	004	005	006	007	008	009	010	011	012
Noise Lev1	46.21	46.43	46.43	46.43	46.43	46.43	46.43	46.43	46.42	46.43	46.42	46.43
Denoi. Lev1	47.83	47.74	47.84	46.48	48.22	47.75	47.85	47.72	47.87	48.12	48.00	48.40
Noise Lev4	38.91	38.95	38.95	38.95	38.96	38.95	38.95	38.95	38.95	38.95	38.95	38.95
Denoi. Lev4	41.69	41.59	41.66	40.99	41.79	41.53	41.62	41.74	41.59	41.68	41.68	41.91

Table 2 lists the statistical analysis of breast image segmentation using proposed morphology snake strategies, according to the segmentation on original images (Original), on the denosed MR images with level 1 (Denoised_1) and level 4 noise (Denoised_4), along with the intensity weakened images (Weaken). The statistical analysis is conducted according to dice rate (DSI), accuracy, recall rate and specificity. For the proposed segmentation conducted on original images, the highest value of DSI is 0.91, and lowest value is 0.33. Intensity weakened images allows achieving increased values in the lowest and the highest value of DSI, which are 0.45 and 0.94, respectively, due to the weakened noise intensity. But their averaged values keep the same. For the recall rate, though the lowest value of original images is lower than weakened intensity images, their highest value and averaged value keep the same. Compared with original images, MR images with weakened intensity result in the improved performance in accuracy and specificity, with an increased averaged value of 1% and 2%, and the highest and lowest value show an increased value between 3 and 4% as well.

Table 2.

List of the statistical analysis of breast image segmentation using proposed strategies, according to the segmentation on original images (Original), and the intensity weakened images (Weaken)

Indicators patient	Original				Weaken
	DSI	Accuracy	Recall	Specificity	DSI	Accuracy	Recall	Specificity
1	0.91	0.98	0.95	0.97	0.94	0.99	0.95	0.98
2	0.33	0.98	0.31	0.98	0.45	0.98	0.45	0.98
6	0.91	0.97	0.98	0.98	0.90	0.98	0.97	0.98
15	0.82	0.98	0.97	0.97	0.87	0.98	0.96	0.98
18	0.78	0.97	0.97	0.97	0.81	0.97	0.95	0.98
19	0.83	0.96	0.95	0.98	0.82	0.98	0.94	0.98
21	0.90	0.98	0.94	0.99	0.90	0.97	0.92	0.99
23	0.86	0.98	0.95	0.98	0.90	0.99	0.95	0.99
24	0.87	0.96	0.97	0.96	0.87	0.96	0.97	0.96
26	0.86	0.98	0.93	0.99	0.83	0.98	0.90	0.99
27	0.83	0.99	0.98	0.97	0.81	0.97	0.97	0.97
29	0.73	0.97	0.96	0.97	0.73	0.97	0.97	0.97
30	0.84	0.98	0.93	0.98	0.83	0.98	0.94	0.98
Average	0.81	0.97	0.91	0.98	0.82	0.98	0.91	0.98

Bold numbers mean the maximum and minimum values of the corresponding items to be calculated and compared

Table 3 lists the statistical analysis of breast image segmentation using proposed morphology snake strategies, according to the segmentation on the denoised MR images with level 1 (Denoised_1) and level 4 noise (Denoised_4). For the proposed segmentation conducted on level 4 noisy images, the highest value of DSI is 0.92, and lowest value is 0.74, with averaged value of 0.85, higher than the other three types of images. Recall rate is 0.98, 0.88 and 0.94 for the highest, lowest, and averaged value, respectively, the best performance on the four types of images. The averaged value of accuracy at the two denoised levels of MR images shows the same score of 0.98 or high. The specificity is similar among the four types of images. The images with level 1 and level 4 noise shows essentially the same performance.

Table 3.

List of the statistical analysis of breast image segmentation using proposed strategies, according to the denoised MR images with level 1 (Denoised_1) and level 4 noise (Denoised_4)

Indicators patient	Denoised_1				Denoised_4
	DSI	Accuracy	Recall	Specificity	DSI	Accuracy	Recall	Specificity
1	0.90	0.97	0.93	0.97	0.92	0.98	0.94	0.96
2	0.73	0.98	0.84	0.98	0.74	0.98	0.88	0.98
6	0.91	0.98	0.98	0.98	0.91	0.98	0.98	0.98
15	0.85	0.98	0.96	0.98	0.82	0.98	0.93	0.98
18	0.85	0.98	0.96	0.98	0.83	0.97	0.95	0.98
19	0.85	0.96	0.93	0.99	0.84	0.98	0.94	0.99
21	0.92	0.99	0.93	0.99	0.92	0.99	0.92	0.99
23	0.87	0.98	0.94	0.98	0.88	0.98	0.94	0.98
24	0.89	0.97	0.97	0.97	0.88	0.97	0.97	0.97
26	0.87	0.99	0.92	0.99	0.87	0.99	0.90	0.99
27	0.85	0.98	0.97	0.98	0.85	0.98	0.97	0.98
29	0.75	0.97	0.96	0.97	0.75	0.97	0.94	0.97
30	0.85	0.98	0.92	0.99	0.85	0.99	0.91	0.99
Average	0.85	0.98	0.94	0.98	0.85	0.98	0.94	0.98

Bold numbers mean the maximum and minimum values of the corresponding items to be calculated and compared

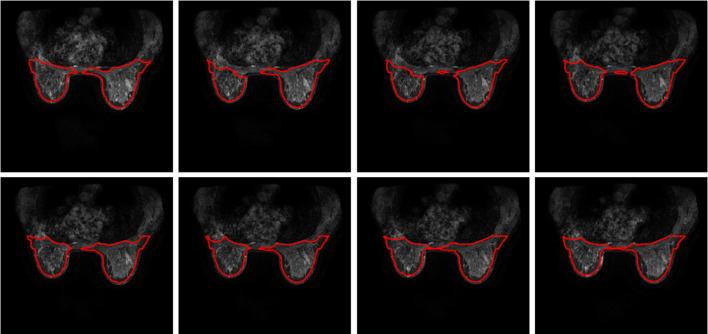
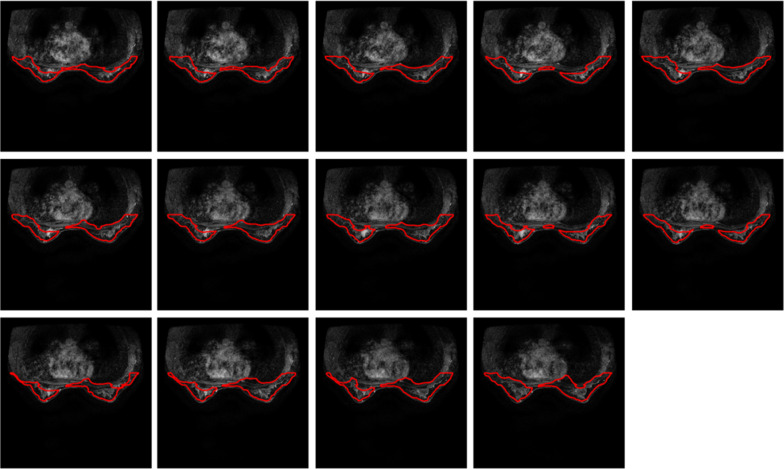
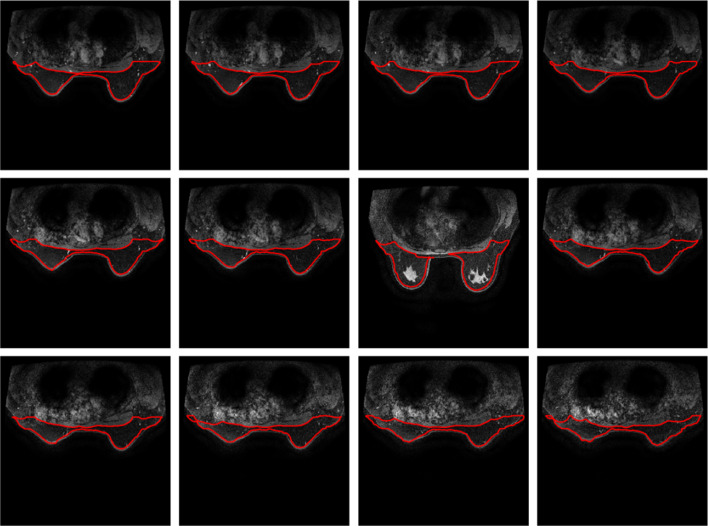
The proposed method is also applied in 11 female subjects measured using MRI machine of 3.0 T. These breast images are extracted from breast MRIs with tumour inside. The resultant segmentations are illustrated in Figs. 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21.

Fig. 10.

Illustration of a comparison between the contours achieved after eSure denoising on level 1 noisy images in (a) and intensity weakened images in (b)

Fig. 11.

Breast segmentation with tumours. Case 1

Fig. 12.

Breast segmentation with tumours. Case 2

Fig. 13.

Breast segmentation with tumours. Case 3

Fig. 14.

Breast segmentation with tumours. Case 4

Fig. 15.

Breast segmentation with tumours. Case 5

Fig. 16.

Breast segmentation with tumours. Case 6

Fig. 17.

Breast segmentation with tumours. Case 7

Fig. 18.

Breast segmentation with tumours. Case 8

Fig. 19.

Breast segmentation with tumours. Case 9

Fig. 20.

Breast segmentation with tumours. Case 10

Fig. 21.

Breast segmentation with tumours. Case 11

From the above figures, case 3 and case 5 show slight changes in the outlines of breast with part of edge cross tumour pixels, due to weak contrast in the breast images. All the remaining cases of stacked breast images are drawn with good visualized shapes and enclosed tumours inside. It is a challenge for the level sets algorithm in location of image edge with low contrast, as presentation in methodology section. The edge process and analysis is fully automatic without application of any prior knowledge. The approach allows to achieve tumour detection in the region of interest in relation to breast with slightly increases size related to the region of interest.

Also we compare the results with other algorithms that have performed well in recent years. We selected DICE, recall (RE), specificity (Sp) and accuracy (acc) for a more comprehensive comparison,the result in Table 4.

Table 4.

Quantitative comparison of performance of breast segmentation using the proposed method with the recently developed other approaches

	RE	Sp	DICE	acc
Gallego et al. (2012) [51]	0.89	–	0.88	–
Albert et al. (2014)	–	0.98	0.85	–
Aida et al. (2017) [52]	0.94	0.98	0.96	0.97
Doran et al. 2017[53]	–	–	0.90	–
Our	0.94	0.98	0.85	0.98

A breast MRI image includes not only various tissues, but also subcutaneous fat, as shown in the red area, which is the fat portion of this image. However, for the binary marker, the doctor removed the fat portion, when they manually drawing the breast region. While, in the actual analysis, this portion tends to be retained, as a result, the score of DICE rate looks not as high as the other algorithms, which is a different understanding in the determination of breast regions of interest. As show in Fig. 22.

Fig. 22.

Effect of fat on breast segmentation

Conclusion

Current breast MRI segmentation is not sufficiently accurate due to difficulties in removing landmarks from noisy magnetic resonance images (MRI) with similar intensity levels and the close connection to BROI. To achieve accurate detection of BROI, the proposed hybrid methodology integrates adaptive histogram equalization, inversed morphology snake, along with eSURE deep denoising for breast segmentation. It is found that the denoising MR images with slightly added noise show improved performance in breast segmentation. The algorithm paves the way for automated tissue diagnosis. One of the advantages of the proposed segmentation is also to incorporate deep transfer learning with nature images in noise removing. Due to some important parameters that have been transferred from nature image to the learn of medical images, the classification accuracy of the breast ROI has been much increased.

As high dimensional MRI data may be sparse, after the image intensity to be weakened, morphology snake can stop at the gradient of image edge, with reduced affection of noisy pixels that lead to misclassified breast edges. This is to consider that some noisy pixels on denoised images still exist. If the image intensity is reduced, there will be a reduction in noisy pixel intensity, which allow the morphology snake to be shrinkaged to its correct edges of breast.

For the future work, it is expected to find a parameter to determine which image should be denoised, and which image can use the intensity weakened operation instead to find the breast edges to be better located.

In this paper, the proposed algorithm frameworks have been tested on 12 cased of breast MRIs of 1.5 T and 11 different cases that comprised of different shapes with tumour patterns using MRIs of 3.0 T. We list different classification performance on original and denoised images via 1.5 T MRI machines and display all the stack of breast MRI via with tumours achieved using 3.0 T MRI machines. It is observed that the proposed algorithm enables to perform segmentation of the breast effectively and automatically on breast MRIs. The presented model can act as a preliminary step that further assists in the diagnosis of breast cancer.