Accrual of functional redundancy along the lifespan and its effects on cognition

Abstract

Despite the necessity to understand how the brain endures the initial stages of age-associated cognitive decline, no brain mechanism has been quantitatively specified to date. The brain may withstand the effects of cognitive aging through redundancy, a design feature in engineered and biological systems, which entails the presence of substitute elements to protect it against failure. Here, we investigated the relationship between functional network redundancy and age over the human lifespan and their interaction with cognition, analyzing resting-state functional MRI images and cognitive measures from 579 subjects. Network-wide redundancy was significantly associated with age, showing a stronger link with age than other major topological measures, presenting a pattern of accumulation followed by old-age decline. Critically, redundancy significantly mediated the association between age and executive function, with lower anti-correlation between age and cognition in subjects with high redundancy. The results suggest that functional redundancy accrues throughout the lifespan, mitigating the effects of age on cognition.

1. Introduction

Redundancy, defined as the existence of alternate elements within a system that ensure functionality in case of failure (Glassman, 1987; Patterson et al., 1988; Tononi et al., 1999), has been suggested to operate as a neuroprotective mechanism that is deployed in the early stages of neurodegenerative diseases such as Parkinson’s disease (PD) and Alzheimer’s disease (AD) (Arkadir et al., 2014a; Postuma and Montplaisir, 2009). As a design principle, redundancy has been studied extensively in both engineering and biological systems. The field of reliability engineering has utilized system redundancy in construction and preservation of a wide range of complex machines, structures, communication systems and computers (Billinton and Allan, 1992; Kapur and Lamberson, 1977). Similarly, redundancy has been studied extensively in systems biology (Navlakha et al., 2014), in genetics in particular (Nowak et al., 1997), where redundant designs allow for information retrieval during repair processes (Ayala et al., 1980; Stent, 1971).

It has long been postulated that redundancy may allow the human brain to cope with perturbation and progressive alterations introduced by aging and age-associated diseases. Early examples include the conjecture that recovery of function as observed in adults with hydrocephalus is modulated by redundant brain mass (Smith and Sugar, 1975). Redundancy has also been suggested to mitigate the early effects of neurodegeneration (Arkadir et al., 2014a; Postuma and Montplaisir, 2009). Specifically, it may ensure functionality in the preclinical and prodromal phases of PD and AD, where neurodegeneration is believed to have commenced, yet healthy function is for the most part retained (Dayan and Browner, 2017; Postuma and Berg, 2016). Thus, a brain network with redundancy allows the brain to retain functionality when some of its pathways are compromised by neurodegeneration (Fig. 1A).

Fig. 1.

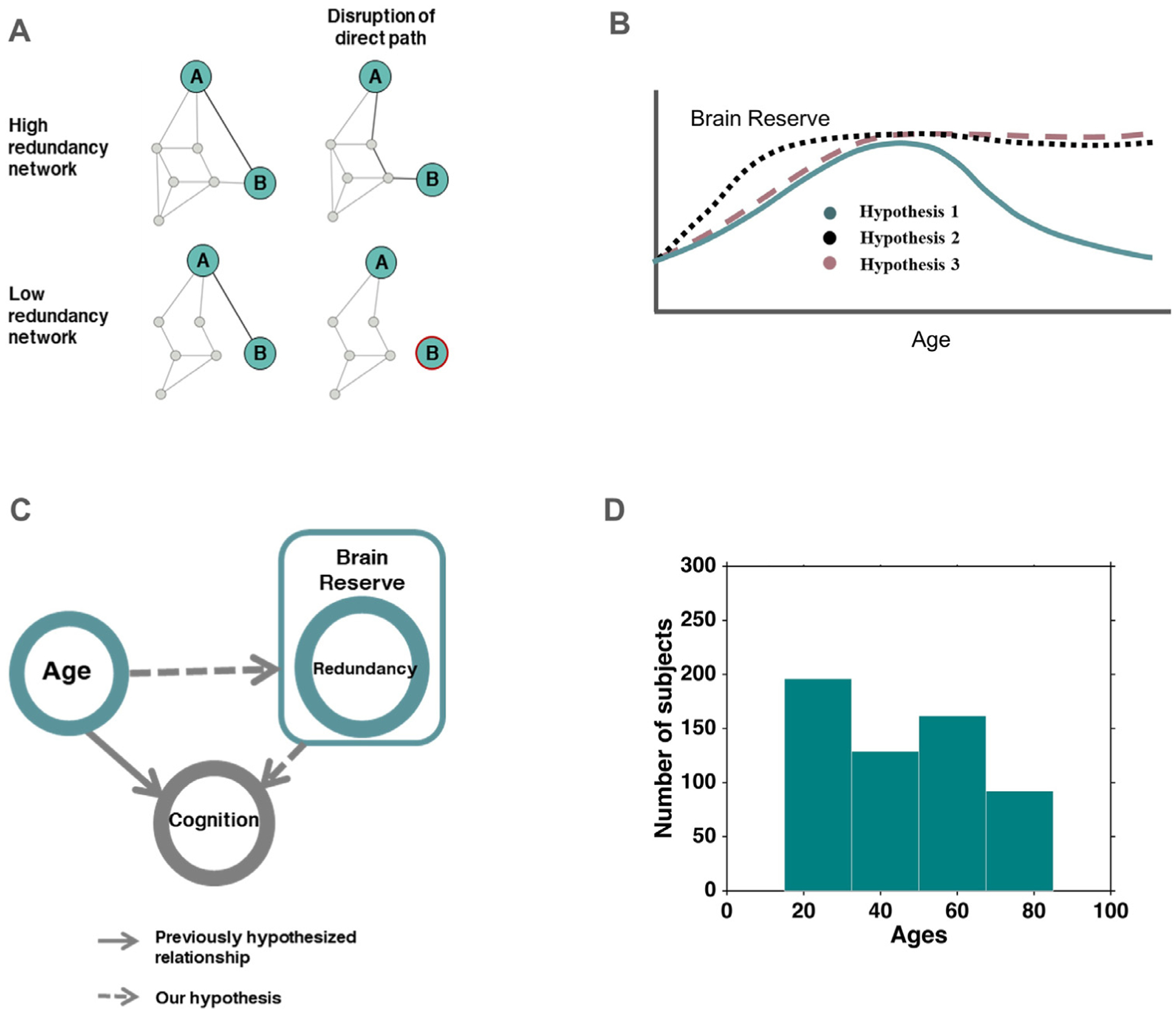
Definitions, hypotheses and study setup, A: Illustration of high and low redundancy networks under disruption, B: Different trajectories of hypothesized variation of functional network redundancy over the human lifespan, Hypothesis 1 follows the pattern of accumulation and later-age decline, Hypothesis 2 suggests early development followed by slow decline, Hypothesis 3 takes the course of accrual similar to 1, but does not lead to old-age decline, C: Schematic showing the hypothesized framework for age-cognition-redundancy relationship. We hypothesize that the established association between age and cognition (indicated by arrow), will be mediated by redundancy (dashed arrows) operating as a mechanism of reserve in this context, D: Age distribution of the participants in the study.

Although redundancy is believed to play a major role in the early phases of neurodegeneration, very little is known empirically about this putative mechanism. In particular, as a compensatory mechanism, it remains unknown if redundancy is a neural resource that accumulates over time. As a neural substrate critical to endure network disruption, redundancy is possibly related to the brain’s reserve capacity to withstand damage. In this context, redundancy could potentially be a form of reserve (Cabeza et al., 2018; Montine et al., 2019) i.e. a neural resource that accrues over time allowing the brain to withstand perturbation. As such, redundancy may follow the previously proposed dynamics of brain reserve over the lifespan (Fig. 1B, Hypothesis 1) which exhibit a pattern of accumulation followed by old-age decline. Redundancy may also exhibit a pattern of childhood/adolescent development followed by slow decline (Fig. 1B, Hypothesis 2) such as the changes seen in grey matter/white matter volume (Bartrés-Faz and Arenaza-Urquijo, 2011; Hedman et al., 2012). Finally, another plausible trajectory for redundancy over the lifespan (Fig. 1B, Hypothesis 3) could include a gradual accumulation of redundancy in development and adulthood with no subsequent decline. We further reason that redundancy, constituting a reserve mechanism, may allow some individuals to mitigate age-associated reduction in cognitive performance (Deary et al., 2009; Murman, 2015) (Fig. 1C). Hence, a remaining inquiry is whether redundancy affects the relationship between age and cognition (Fig. 1C), a question which has not been studied to date. Finally, the specificity of the association between age and redundancy in comparison with other major network topological properties is unknown, despite previous work on brain reorganization in aging (Cabeza et al., 2018; Dolcos et al., 2002; Sala-Llonch et al., 2015; Stern, 2009) and adaptive brain aging (Park and Reuter-Lorenz, 2009).

In the current study, we set out to uncover the role of redundancy over the human lifespan using a publicly available data set (Nooner et al., 2012). We used resting state functional MRI rather than task-based data, reasoning that task performance may strongly interact with the recruitment of redundant connections in functional networks. The resting-state functional images were used to construct connectivity matrices for each subject. A graph-based approach was applied to reconstruct networks and quantify redundancy for every subject, where redundancy was defined as the number of walks between all node pairs (De Vico Fallani et al., 2011) (see Methods). Edge redundancy calculated in this manner (i.e. presence of multiple paths between pairs of nodes) is a central property thought to contribute to the robustness of many biological systems, for example cellular and protein networks (Aittokallio and Schwikowski, 2006; Brady et al., 2009). Measures of redundancy similar to ours, based on total pathway counts, have been widely used in systems biology (Papin et al., 2002; Price et al., 2002; Stelling et al., 2002). Here, the interrelation between redundancy in functional brain networks and age was analyzed along with its possible effect on cognition.

2. Methods

2.1. Participants and data acquisition

The study used data from the publicly available Nathan Kline Institute Rockland Sample (NKI-RS) (Nooner et al., 2012). Subjects aged (6–14) were excluded from the study due to difficulty in the application of adult templates for registration (Fonov et al., 2011). The NKI-RS sample used in this study was composed of N = 590 unique subjects (male = 212, female = 378, aged 15–85 years; for age distribution see Fig. 1D) who were part of the study’s Discovery sub-study. The NKI-Rockland study is a community sample, and as such it included minimally restrictive exclusion criteria. However, subjects previously diagnosed with major neuropsychiatric conditions such as Dementia and Attention Deficit Disorder (ADD) were excluded from our cohort. This study was approved by the local Institutional Review Board and informed consent was received from all participating individuals (Nooner et al., 2012). Demographic characteristics for the participants are provided in Supplementary Table 1.

As part of a comprehensive protocol, subjects underwent resting-state functional MRI scans with a Siemens TrioTM 3T MRI scanner, using an echo-planar imaging (EPI) sequence with TR/TE = 1400/30 ms, voxel size = 2 mm isotropic, (FA) = 65°, FOV = 224 × 224 mm 2, number of slices = 64, scan length = 10 min. Additionally, T1-weighted images were acquired using a magnetization-prepared rapid gradient echo (MPRAGE) sequence and were used for spatial normalization and group-level analysis. Subjects were instructed to keep their eyes open and stay awake during the scan.

Subjects also underwent additional cognitive assessments including the Delis–Kaplan Executive Function System (DKEFS) test battery during their visit. They also completed other standard tests and questionnaires detailed online (http://fcon_1000.projects.nitrc.org/indi/enhanced/assessments.html). The DKEFS evaluation provides assessment of various executive functions including problem solving, fluent productivity, flexibility of thinking and verbal inhibition.

2.2. Data preprocessing

Resting-state functional images were analyzed using the MATLAB Conn pipeline (conn18b) for volume-based analysis (Whitfield-Gabrieli and Nieto-Castanon, 2012). Structural images were segmented to define grey matter, white matter and cerebrospinal fluid (CSF) masks. Functional pre-processing included motion correction (realignment and unwarping), registration to structural images, spatial normalization and outlier detection (subject motion threshold = 0.9 mm and global signal threshold of Z = 5). Spurious, non-neuronal noise from white-matter and CSF masks as well as 6 motion realignment parameters and their first order derivatives were used as nuisance regressors. Motion artifacts were detected using an ART-based scrubbing method (Power et al., 2012) and outlier volumes were discarded. 7 subjects had more than 50% volumes removed due to excessive motion during denoising and were excluded from the subsequent analysis. Neither number of retained frames nor mean motion for our cohort of participants (remaining after scrubbing) showed significant associations with age (p-values = 0.30 and 0.96 respectively).

Functional time-series were obtained based on a functionally defined atlas with 300 regions-of-interest (ROIs), encompassing cortex, subcortex and cerebellum (Seitzman et al., 2020). Quality assessment resulted in removal of 4 sessions due to undefined entries in the connectivity matrix, found to arise from failure of the imaging volume to encompass all relevant structures. This step resulted in correlation matrices for a total of 579 subjects (male = 204, female = 375). Connectivity matrices were binarized prior to redundancy computation using proportional thresholding (Achard and Bullmore, 2007), for each threshold value preserving a fixed fraction of edges per subject, ranging from 2.5% to 25% of all node pairs. When computing other graph metrics, anti-correlations in the functional connectivity matrices were set to zero to avoid negative edges (Fornito et al., 2013).

2.3. Redundancy and other graph metrics

Connectivity matrices were used to compute redundancy along with degree (Telesford et al., 2010), clustering coefficient (Saramäki et al., 2006), system segregation (Sporns, 2013), and global efficiency (Rubinov and Sporns, 2010) – four major measures considered central to understanding network dynamics and topology. Degree and density distributions have consequences for network resilience and development (Rubinov and Sporns, 2010). Clustering coefficient, a measure of the tendency of nodes to cluster together, was included here as one may plausibly expect clustering to increase the number of redundant paths in the network. System segregation (Chan et al., 2014) is another topological property that has been shown to co-vary as a function of age and was used here to quantify the degree of integration and segregation exhibited in functional networks (Sporns, 2013). Taken together, degree, clustering coefficient and system segregation allowed us to assess the specificity of the association of redundancy with age. Global efficiency, a network measure of communication efficiency, was used to assess if increases in redundancy are associated with inefficient network communication. Redundancy was also correlated with degree, clustering coefficient and segregation to gain further insight into its relationship with basic connectivity measures.

Redundancy:

The total number of direct and indirect paths up to a maximum length (L_max = 4) between two nodes was calculated at each network density resulting in the Path array P (300 × 300 × L_max) (Rossini, 2000). The redundancy matrix R encodes the number of paths of any length (up to L_max, the maximum path length of the walk) between each pair of nodes i and j:

$$R\left(i,j\right)=\sum _l^{L_{max}}P\left(i,j,l\right)$$

The redundancy matrix R was used for analyzing single network and nodal characteristics.

Connectivity matrices were binarized over a range of network densities retaining 2.5–25% of all connections and converted to unweighted graphs (with nodes representing ROIs), prior to computing redundancy. Since finding all possible paths between two nodes in a graph is an NP-complete problem (Leistritz et al., 2013), the total number of paths up to a total length L_max between two nodes was computed to obtain the Path array P (n × n × L_max), where n is the total number of nodes in the graph.

Scalar redundancy, R_s, computed as the total number of paths up to a length L_max, between any pair of nodes, was used for whole-brain analysis and comparisons.

$$R_s=\sum _i^n\sum _j^n\sum _l^{L_{max}}P\left(i,j,l\right)$$

Degree:

The weighted degree (“nodal strength”) of a node i is the sum of all its edge weights: $k_i=\sum _j^n{d}_{i,j}$ where d_i,j is the edge weight between nodes i and j.

Clustering coefficient:

The clustering coefficient quantifies the connectivity that exists between neighbors of a given node as a proportion of the maximum connectivity possible (Rubinov and Sporns, 2010), given by $C_i=\frac{2}{k_i\left(k_i-1\right)}\sum _{j,k}{\left(d_{i,j}{d}_{j,k}{d}_{k,i}\right)}^{1/3}$ where k_i is the (weighted) degree of node i. Higher clustering in brain networks suggests higher degree of segregation, previously identified in diseases like Alzheimer’s (Sanz-Arigita et al., 2010).

System segregation:

System segregation denotes the relative strength of within-network connections, in comparison to between-network connections i.e. $S=\frac{z_w-z_b}{z_w}$ where z_w denotes within-network connectivity and z_b corresponds to between-network connectivity. Higher network segregation suggests the presence of optimal network structures underlying, among other functions, successful cognition (Cohen and D’Esposito, 2016).

Global efficiency:

Global efficiency is a metric of information flow defined as the inverse of the shortest path length i.e. $E_{\mathit{\text{global}}}=\frac{1}{n\left(n-1\right)}\sum _{i,j,j\ne i}\frac{1}{L_{i,j}}$, where L_i,j is the length of shortest path between nodes i and j, and n is total number of nodes in the graph. Shortest path length L_i,j is computed as smallest weighted path length irrespective of number of intermediate edges (weighted distance between nodes i and j is computed as 1/ d_i,j where d_i,j is the edge-weight between nodes i and j) (Rubinov and Sporns, 2010). In functional brain networks, higher global efficiency is interpreted as indicating better integration, and lower global efficiency is associated with disrupted information flow (Nakamura et al., 2009; Pandit et al., 2013).

2.4. Experimental design and statistical analysis

2.4.1. Examining age association and topological differences

To model the variation of redundancy with age, redundancy was fitted with polynomials (degree 2 and 3) using the fitlm function in MATLAB to perform robust regression. Since our a priori hypotheses assume a non-linear shape for redundancy across the lifespan (Fig. 1B), a non-linear polynomial, rather than a linear model, was used. We then tested if the observed association between age and redundancy was unique, or if other major topological network properties capture the same association with age. To accomplish this, three other network topological properties i.e. weighted degree (strength), clustering coefficient and system segregation were also computed (as defined above) and compared with redundancy.

The dynamics observed for these network metrics were also fitted with the same model, and the quality of these fits was compared using each model’s Adjusted R². The 3rd order polynomial fit for redundancy had the form ax³ + bx² + cx + d with polynomial coefficients: a = −3.25 × 10⁻⁶, b = 1.29 × 10⁻⁴, c = 0.02 and d = −0.76. For model selection, redundancy and other metrics were also fitted using 2nd order polynomials, and these 2nd and 3rd order models were compared using the Akaike Information Criterion or AIC (Akaike, 1974). AIC determines how well observed samples support the model, taking both the sum-of-squares error and model parameters into account. Model fits were also compared using the likelihood ratio test.

We also performed stratified 5-fold cross-validation to test the generalizability of the 3rd order model. For this purpose, subjects were placed in age bins of 10 years each for age stratification (b₁ = 15–24, b₂ = 25–34 etc.) and age-stratified cross-validation was performed using a 70–30% split for training and testing.

Since the underlying distribution of redundancy was unknown, a non-parametric method was also used to test the quality of the redundancy fit. A randomization procedure was used (Rubinov and Sporns, 2010), wherein random graphs were constructed by rewiring the connections in our original redundancy matrices, while preserving the size, degree-distribution and density of the graphs. For each redundancy matrix (N = 579), a randomized redundancy matrix was obtained using this procedure, resulting in a null distribution of 579 randomized scalar redundancies. These randomized redundancies were similarly fit with a 3rd order polynomial, and this process was repeated over M = 10,000 random permutations. This resulted in a null distribution of model fits, quantified with Adjusted R² values. This distribution was used to calculate the probability of obtaining a random fit which exceeds the one found with the original redundancy values.

Previous studies on the role played by redundancy in small-world and scale-free networks have highlighted differences in the resilience of these networks (Quattrociocchi et al., 2014). In this context, we also compared functional network redundancy to that derived from a Watts–Strogatz small-world network (Watts and Strogatz, 1998), Barabási–Albert (Barabási et al., 2002) scale-free network and random Erdős–Rényi network (Erdős, 1960), retaining the overall network degree. The Barabási–Albert network was generated using sample_fitness_pl in the R igraph package with power law exponent 2.2. The Watts–Strogatz small-world network was generated using MATLAB’s WattsStrogatz function with rewiring probability 0.15.

Age-associated differences in brain function are not uniform across the brain. For example, age-related localized hyperactivity has been consistently reported in the pre-frontal cortex (Turner and Spreng, 2012), while a host of studies have observed increased and decreased activity and connectivity in the default-mode, attention and motor networks (Betzel et al., 2014; Tomasi and Volkow, 2010). These studies motivated us to test if the association of age and redundancy was localized to cognitive networks or extended to other sensory and motor networks.

2.4.2. Cognitive evaluations and mediation

Next, the question of whether redundancy mediated the association between age and cognition was tested with a mediation analysis performed using the R mediation package (Tingley et al., 2014). The proposed model tested the association between age (independent variable) and cognition (dependent variable), with redundancy acting as the mediator (denoted as age-cognition-redundancy mediation) and gender as a covariate. A similar mediation analysis was performed to test degree, clustering coefficients and system segregation as potential mediators between age and cognition.

Cognitive performance was measured using a subset of the DKEFS test, including the color-word interference, trail-making, verbal fluency and design fluency tests. These test results were available for a subset of subjects whose functional processing was completed successfully (N = 538 subjects; male = 202, female = 336), hence these subjects were used in the analysis involving cognitive assessments.

Within these tests, achieved scores were derived using previously described methodology (Karr et al., 2018). As the four-test battery results in 9 measures, we sought to minimize the number of multiple comparisons in subsequent analyses. When assessing the differential effect of redundancy on the age-cognition relationship, we thus contrasted performance in two cognitive measures having varying associations with age: one having the largest and another with the smallest (but still significant) effect size, when testing for the association with age. Combining these two constraints, the 9 measures were sorted according to the effect sizes of their associations with age, and only the tests with significant associations with age, having the largest and smallest effect sizes (i.e., while being significant at p < 0.05) were retained. Since we were interested in examining the mediating role of redundancy on the association between age and executive function, considering the test with the strongest negative association with age would exclude potential inferences regarding cognitive abilities which do not deteriorate as strongly. Analyzing two cognitive tests in the way we did, allowed us to compare the effect of redundancy on two executive functions showing significant, but differing associations with age.

Color–word interference (inhibition/switching time-to-completion; denoted CW score) and verbal-fluency (category-switching; denoted VF score) showed the largest and smallest effect sizes (yet being above the significance threshold) in their association with age. CW score measures inhibitory control in addition to being a function of cognitive flexibility (Lippa and Davis, 2010), hence showing an evident negative association with age while VF relies on verbal production of words with a more moderate age-association. These two measures were standardized to z-scores and used in the subsequent analysis. To quantify the uncertainty estimates, we ran 1000 simulations for each model using a bootstrapping method included in the R mediation package (Marselle et al., 2016). The presence of direct and indirect effect in the age-cognition-redundancy mediation was tested by the estimated Direct Effect and Mediation Effect respectively. To dissect this relationship further, this mediation model was repeated with whole-brain redundancy replaced by single cognitive network redundancy, and thus the contribution of each network was analyzed.

2.4.3. Associating global efficiency with redundancy

An important concern about accumulation of redundancy with age is whether the alternate edges existing in redundant functional networks come at the cost of loss of efficient network communication. As a common metric of network communication efficiency, we used global efficiency – a measure of the averaged inverse shortest path length in networks. This metric is interpreted as quantifying the efficiency of information flow (Latora and Marchiori, 2001). Intuitively, more redundant paths can possibly be expected to arise from loss of direct paths resulting in loss of efficiency. Another possibility is that redundant paths accumulate over age irrespective of the existence (or length) of direct paths. To test these alternative possibilities, a two-line test (Simonsohn, 2018) was used to detect the break point (T) between the upward and downward trends in the variation of redundancy across age. Then, the association between redundancy and efficiency was examined for the ages below and above T separately.

2.4.4. Statistical analysis

Since ordinary least squares regression provides a robust estimate of parameters and confidence intervals for large datasets irrespective of distributions (Li et al., 2012), two-way associations (for example, age – cognitive measure) were tested through a linear regression model fit. Effect sizes of each association (Cohen’s f²) were reported along with standardized β. This procedure was also used for testing the significance of two-way associations in the age-cognition-redundancy mediation. To account for multiple comparisons, (i.e., during analysis of each network’s mediation role), the Benjamini and Hochberg procedure was used to reduce the false discovery rate (FDR) (Benjamini and Hochberg, 1995). Given the lack of monotonicity of effect size estimates in mediation models (Wen and Fan, 2015) only standardized β estimates for the direct and indirect effects are presented for each mediation.

For redundancy analysis at the single network level, network communities identified by Seitzman et al. (2020) were used, which divided the set of 300 ROIs into mutually exclusive communities namely auditory, visual, somato-motor dorsal and ventral, salience, rewards, default mode, cingulo-opercular, medio-temporal, fronto-parietal, parieto-medial and dorsal and ventral attention networks. Within-network redundancy of a network was calculated by averaging the R matrix over the connections between its own nodes, while its between-network redundancy was computed by averaging over outside-network edges (edges connecting nodes of this network with the rest of the brain). Nodes with a significant age-association were identified by fitting a 3rd degree polynomial on each node’s redundancy variation with age, and testing the significance of each fit after correcting for multiple comparisons (Benjamini and Hochberg FDR corrected at 0.05 threshold).

3. Results

3.1. Age – redundancy association over the human lifespan

We first sought to delineate the association between redundancy and age. To this end, a 3rd order polynomial was fit to redundancy values observed across the lifespan (N = 579). Redundancy showed a strong fit to age with the 3rd order polynomial (Adjusted R² = 0.246, Cohen’s f² = 0.332 (Fig. 2A)) after adjusting for gender. More specifically, the number of redundant edges correlated positively with age over the earlier decades of the lifespan, with this association subsequently reversing over the last two decades. Fitting polynomials to associate weighted degree (strength), clustering coefficient and system segregation with age (Fig. 2B) resulted in substantially lower fits (Adjusted R² = 0.049, 0.034 and 0.010 respectively) compared to redundancy. We then repeated the analysis by fitting 2nd order polynomials to redundancy, clustering-coefficient, degree and system segregation. The observed fits were very similar to those obtained using 3rd order polynomials (with Adjusted R² = 0.22, 0.043, 0.033 and 0.010, respectively), confirming that the superior fit obtained for redundancy and age was not a model artifact. Model comparison, achieved by computing AIC (Akaike, 1974) for the 2rd and 3rd order models, yielded lower AIC for the latter model. The likelihood ratio test also rejected the null hypothesis that the 2nd order fit was better than the 3rd order fit (p = 0.92). These results suggest that the observed samples support the 3rd order model better, taking model parameters into account. To rule out overfitting and assess the generalizability of these results we also performed age-stratified 5-fold cross-validation, repeating the fitting procedure over 5 age-stratified folds, with a 70–30% training-testing split (Supplementary Table 2). Testing error, observed in the analysis, did not exhibit a significant deviation from the training error, which indicates good generalizability for the model.

Fig. 2.

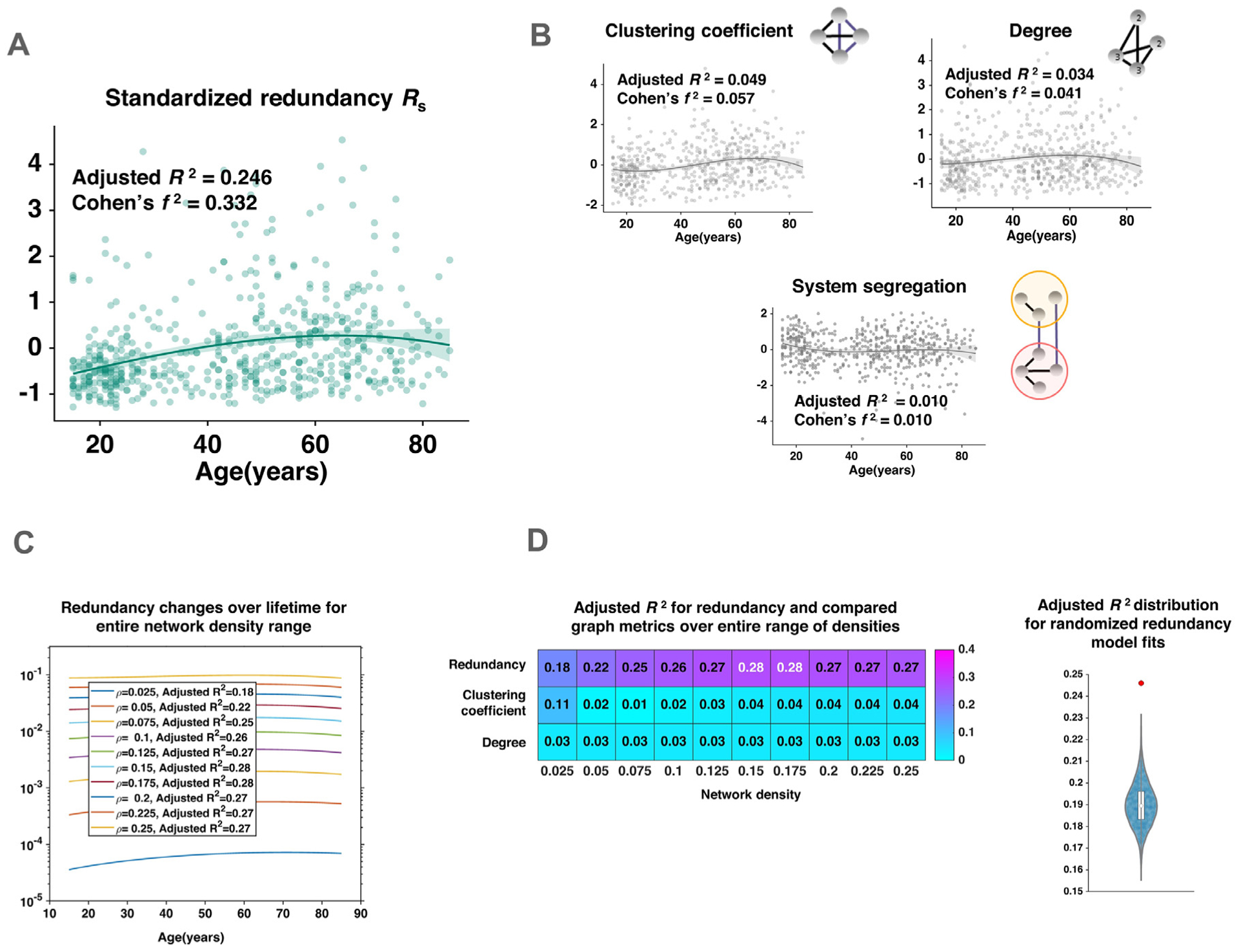
Association of whole brain redundancy with age over the human lifespan. A: A 3rd-order polynomial was fit to redundancy; points represent redundancy of individual subjects, line shows polynomial fit with 95% confidence interval (shaded), redundant edges accumulated over the earlier years of age and declined over the last decades, B: Variation of standardized clustering coefficient, degree and system segregation with age over the lifespan; lines show polynomial fit with 95% confidence interval (shaded), polynomial fits to clustering coefficient, degree and segregation show much lower Adjusted R², C: Effect of different network densities on the association of redundancy and age, with network density denoted as ρ, D: (left) Comparison of Adjusted R² for polynomial fit of redundancy in comparison with those of clustering-coefficient and degree, (right) Distribution of redundancy fits obtained from randomized null graphs, along with the original model fit shown in red.

Similar results were obtained when associating age with degree and clustering coefficient on unweighted graphs, where the same range of network densities (2.5–25%) was used as described before. Since averaged degree is overridden by proportional thresholding in single-subject graphs, an absolute threshold of 0 was used for calculating binarized average degree instead (Fig. 2D and Supplementary Fig. 1). As system segregation is a weighted metric, it was excluded from the unweighted comparison.

The non-parametric randomization procedure performed to check the quality of the redundancy fit revealed that the original model fit was significantly better than the null distribution of model fits (p < 10⁻⁴; Fig. 2D). The non-parametric model-fitting procedure thus confirmed that the significant age-redundancy association was independent of any assumptions made on the distribution of the redundancy metric.

Redundancy showed a similar association over the entire range of network densities considered here, hence the results were invariant to density change (Fig. 2C). Since the results showed little variation between weighted and unweighted metrics over all network densities, we discuss findings using redundancy, weighted degree and clustering coefficient at a single network density (ρ = 0.075, retaining 7.5% of connections), for brevity. Redundancy presented a markedly different association with age than the three metrics (i.e. weighted degree, clustering coefficient and system segregation), despite correlating significantly with these measures (β = 0.53, 0.51 and −0.17; p-values < 0.01). We did not find redundancy to correlate significantly with other centrality measures, such as mean betweenness-centrality (Supplementary results and Supplementary Fig. 2).

We also compared functional network redundancy to that derived from a Watts–Strogatz small-world network, Barabási–Albert preferential attachment (“scale-free”) network and an Erdős–Rényi network, retaining the overall network mean degree (Supplementary Fig. 3). The functional brain network exhibited higher redundancy than the small-world and random networks, while being comparable with the scale-free network.

3.2. Association of single-network redundancy with age

The results reported above focused on the association of whole-brain redundancy with age. We next computed redundancy in single functional networks, assessing the degree to which it associated with age. Functional networks used in this analysis were identified previously and included in the parcellation used in the current study (Seitzman et al., 2020) (Supplementary Fig. 4). This analysis revealed that the somato-motor (dorsal and lateral), attention (dorsal and ventral) and visual networks’ redundancy showed the most significant association with age (Fig. 3A). In several of the networks more than half of the network nodes showed a significant relationship with age in both within-network redundancy (edges within the same functional network) and between-network redundancy (edges that connect a functional network with the rest of the brain). These networks included the somato-motor dorsal (85% of nodes) and ventral networks (81.8%), and dorsal attention network (81.2%). On the other hand, in other networks more than 50% of nodes showed a significant relationship between age and redundancy in between-network edges only. This pattern was observed in the parieto-medial (60%), visual (54.5%) and fronto-parietal (58.8%) networks. The association between redundancy and age in these networks exhibited the pattern previously observed for whole-brain redundancy (Fig. 3B). Within-network redundancy was significantly higher than between-network redundancy (p < 0.01) for each network (Fig. 3C). Finally, previous findings of lateral differences in aging patterns (Dolcos et al., 2002) prompted us to test whether the same differences in laterality could be observed in redundancy. We found that the networks exhibited no significant differences between left and right hemispheres in the number of nodes showing a significant association with age (Fig. 3D).

Fig. 3.

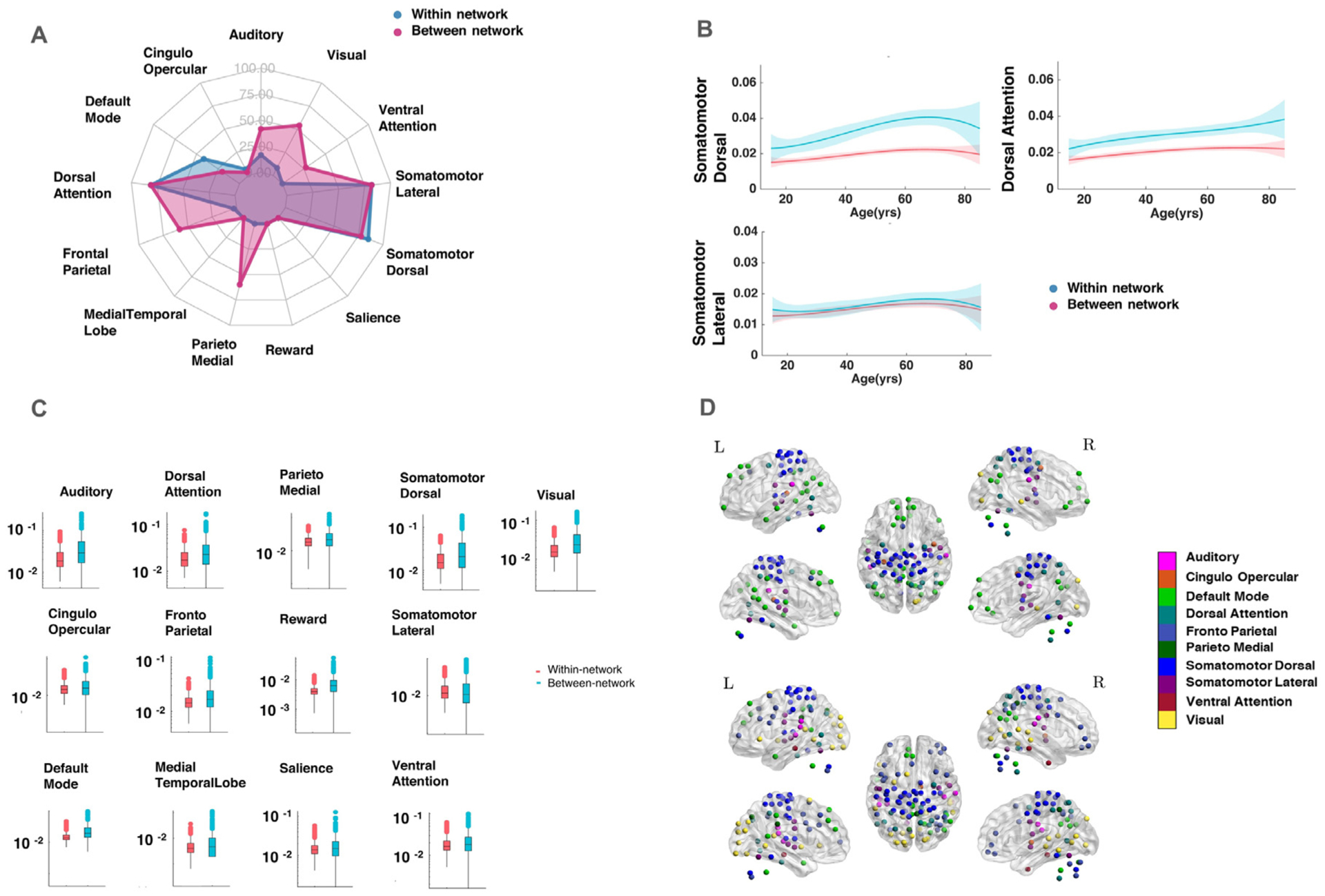
Relationship of single-network redundancy with age, A: Networks showing significant association between redundancy and age in within-network (blue) and between-network (red) connections, somato-motor (dorsal and lateral), attention (dorsal) and visual networks exhibited the most widespread association with age (% of nodes showing significant association), B: Profile of networks showing significant association with age for both within and between-network connections, C: Box and whisker plot showing within-network and between-network redundancy for each network; y-axis is shown on logarithmic scale, D: ROIs belonging to each network showing significant association with age in (top) within-network connections and (bottom) between-network connections; colors represent community membership.

3.3. Age – executive function association is mitigated by redundancy

We next examined whether redundancy mediates the association between age and cognition. More specifically, mediation models were considered, testing if redundancy mediated the association between age and executive function, measured by the color-word interference (CW) and verbal-fluency (VF) tests. These two tests showed the largest and smallest significant negative association with age (ranked across effect sizes), among 9 total tests available in the dataset (Fig. 4A and B).

Fig. 4.

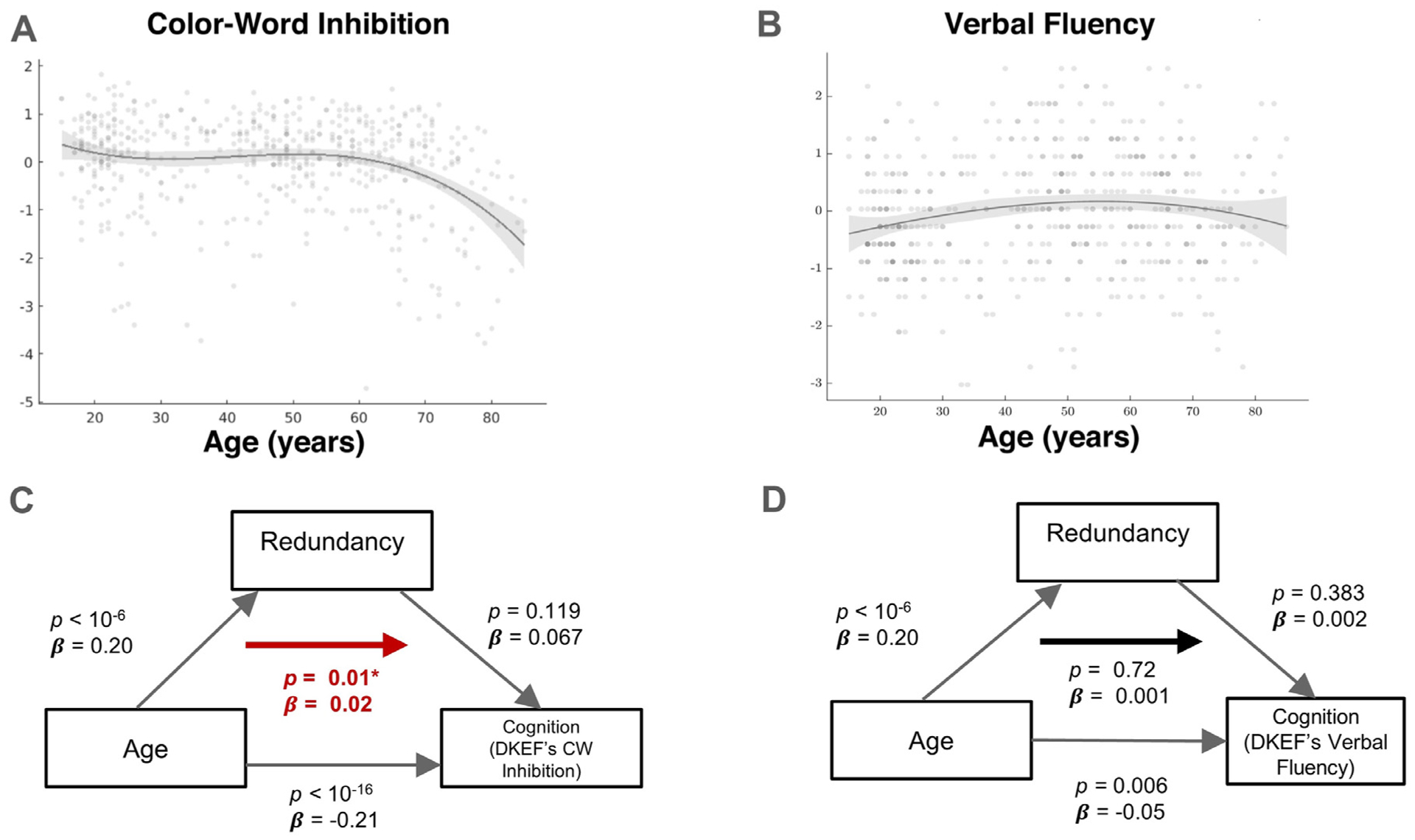
Effect of redundancy on the association between age and executive function. A: Lower standardized CW score was associated with older age (p < 10⁻¹⁶), B: Lower standardized VF score was also associated with older age (p = 0.008), C: Mediation of the age-CW association by redundancy; strength of associations is indicated by arrows while the bold arrow shows the significance of the overall mediation, D: Mediation of age-VF association by redundancy; strength of associations is indicated by arrows while the significance of the overall mediation is shown by the bold arrow.

Both the direct (age on performance) and indirect effects (age on performance through redundancy) for the CW test were significant. More specifically, performance on the CW test was negatively associated with age (β = −0.21, p < 10⁻¹⁶; Cohen’s f2 = 0.086), whereas redundancy positively mediated this association (β = 0.02, p = 0.01; Fig. 4C), after adjustment for gender. Redundancy was not significantly associated with CW (β = 0.067, p = 0.119; Cohen’s f2 = 0.01) or VF performance (β = 0.002, p = 0.38; Cohen’s f2 = 0.0002). Note that significant indirect effects in contemporary mediation models can be detected when one of the direct paths is not significant (Hayes, 2018). In contrast, no significant mediation effect was found with regards to the association between age and VF performance. For this test, the direct effect was found significant (β = −0.05, p = 0.006; Cohen’s f2 = 0.013), indicating a significant deterioration of verbal fluency with age. However, the Mediation effect was observed to be non-significant (β = 0.001, p = 0.723; Fig. 4D). Thus, higher redundancy was associated with less pronounced association between inhibition and age, while no such effect was evident for verbal fluency (Fig. 4C).

The mediating role of redundancy in the association between age and inhibition was specific to this topological network property. No significant mediating effect was found for clustering coefficient, degree or segregation when the same analysis was repeated using these graph measures (overall mediation β = 0.0004, p = 0.35; β = 3.9 × 10⁻⁴, p = 0.058 and p = 0.46; β = 1.3 × 10⁻⁴ respectively).

Finally, to gain further insight into the role of different cognitive networks in each mediation, we refitted each mediation model focusing on the contribution of single cognitive networks (namely the dorsal and ventral attention, default-mode, parieto-medial, fronto-parietal, medial-temporal lobe cingulo-opercular networks). For the age-CW relationship, this mediating effect was led by the dorsal and ventral attention, parieto-medial and cingulo-opercular networks, with the dorsal attention network showing the strongest effect (Supplementary Fig. 5)

3.4. Does higher redundancy come at the expense of less efficiency?

Global efficiency showed a small, but significant association with age (β = 0.088; p = 0.03; Fig. 5B). Redundancy, on the other hand, was not associated significantly with global efficiency (β = 0.063; p = 0.424). Further, using a break-point of T = 57 years, detected using the two-line test (Fig. 5C), redundancy and global efficiency were not significantly associated in neither subjects who were 57 years or younger (β = 0.049; p = 0.33) nor in subjects who were older than 57 (β = 0.066; p = 0.37).

Fig. 5.

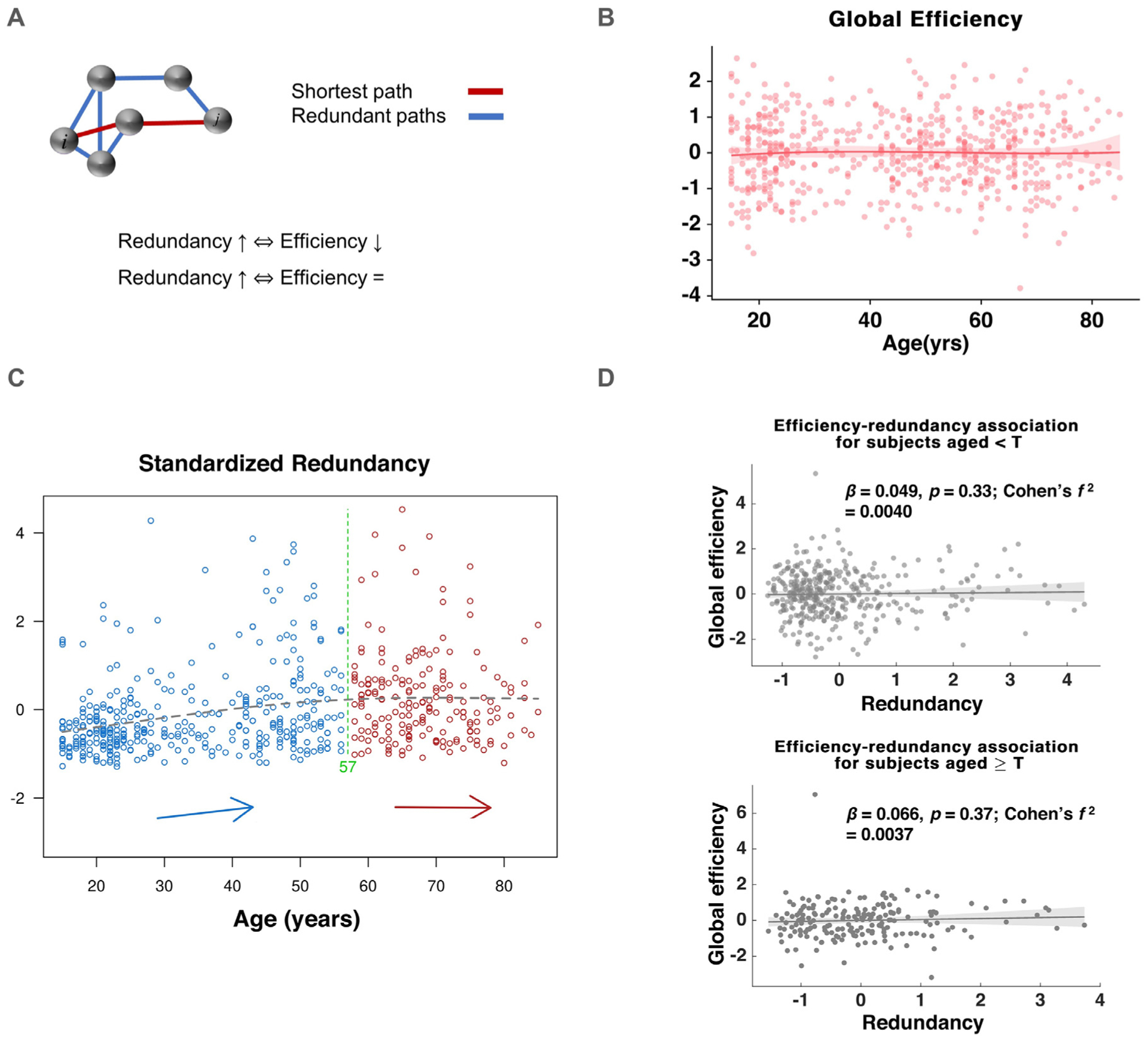
Relationship of redundancy and communication efficiency. A: Visual illustration of global efficiency-redundancy trade-off and different variants of the hypothesized relationship between global efficiency, redundancy and age, B: Global efficiency variation with age, C: Partitioning the sample according to subjects’ age-redundancy association using the two-line test revealed a break-point of age = 57 years, D: Association between redundancy and global efficiency for subjects above and below the break-point age of 57 years.

4. Discussion

Redundancy as a measure of duplicate components within a system has been employed in a versatile range of applications and contexts, including in engineering, computer science, genetics and systems biology (Ayala et al., 1980; Patterson et al., 1988). Similar to other artificial and biological systems, the human brain relies on coordinated and intricate interactions of multiple sub-systems, and may thus plausibly rely on redundancy to ensure functionality in case of failure. Previous studies have indeed posited a neuroprotective role for anatomical and physiological redundancy in neurodegeneration (Arkadir et al., 2014b; Rossini, 2000). However, whether or not redundancy accrues over the lifespan, acting as a mechanism of reserve, has not be investigated to date. Here, we demonstrate that whole-brain redundancy shows a significant association with age, presenting a pattern of accumulation followed by later-age flattening or slow decline, resembling the hypothetical trajectory of reserve mechanisms. This pattern was unique to redundancy and was not evident in other prominent topological network properties. Further, it was found that whole-brain redundancy mediated the negative association between age and inhibitory executive function. Finally, redundancy was found to accrue over age with no concurrent effect on global efficiency, providing evidence that higher redundancy does not occur at the expense of loss of efficient network communication.

Functional redundancy provides a measure of recruitment of alternate, indirect pathways between brain regions, which may support functional adaptations to reduce the cognitive impact of aging. The gradual accrual of redundancy is consistent with the buildup of neural resources during childhood and adulthood (Stern, 2006). Whole-brain functional redundancy showed a strong resemblance to the previously hypothesized trajectory of brain reserve i.e. accumulation of neural resources that mitigates the effects of age-associated neural decline (Barulli and Stern, 2013). It was previously posited that factors affecting neural resources and cognitive demands change (Cabeza et al., 2018) as a result of a combination of reserve, maintenance and compensation mechanisms, resulting in a pattern of accumulation, which reverses during the later phases of life. Although the different factors playing a role in the accrual of redundancy are not clear, it is likely attributable to previously identified contributors to reserve capacity such as genetics (Lee, 2003; Soldan et al., 2015) and environmental and lifestyle factors such as education and occupational achievement (Cabeza et al., 2018).

The definition of redundancy used in our work (De Vico Fallani et al., 2011) quantifies indirect functional connectivity between network nodes, which suggests the existence of alternate modes of functional communication between brain regions. This form of indirect functional communication might come into play under conditions of network disruption and perturbation such as aging, traumatic injury or pathological dysfunction. Many recent studies have computed measures of connectivity and topology relying on indirect paths between nodes (Kambeitz et al., 2016; Tewarie et al., 2015; Zhu et al., 2019). Hence, the use of indirect paths is not new or unique to redundancy, with these measures providing useful insight into functional networks not accessible through other means. Further, our comparison of redundancy in functional networks with that of other topologies showed that the former networks possess higher redundancy than small-world and random networks, which is in agreement with previous work suggesting a combination of small-world and scale-free topology in functional networks (van den Heuvel et al., 2008).

Comparison of the age-association of redundancy with that observed for clustering coefficient, average weighted degree (i.e., node strength) and system segregation reveals that other major topological network properties show substantially lower fit with age when compared with redundancy. Moreover, the shape of the fitted curves for the association of age with degree, clustering coefficient and system segregation was markedly different than the one observed for redundancy. Whole-brain network degree was not significantly associated with age. This finding augments previous studies that found evidence of heterogenous, localized decrease or increase of functional connectivity and nodal degree with age (Betzel et al., 2014; Liu et al., 2012; Wang et al., 2012), possibly resulting in no consistent pattern for whole-brain network connectivity. Clustering coefficient was found to show a moderately-low positive relationship with age, as previously reported (Shah et al., 2018), but it did not exhibit a strong 3rd order polynomial fit resembling the dynamics of accumulation followed by decline as observed for redundancy. The degree of system segregation, exhibited in the functional networks tested here, also showed substantially lower fit to age, despite this measure being moderately associated with redundancy. While previous work on network segregation found an association between segregation and cognitive function (Kong et al., 2020), the system segregation metric was not found to significantly mediate the relationship between age and cognition in our study. These differences may originate from various methodological differences (for example, the examination of different cognitive domains and age groups), which render the comparisons between the studies challenging.

Redundancy changes across the lifespan extend previously reported findings on network reorganization in aging (for a review, see Sala-Llonch et al., 2015). The examination of the association between redundancy and age in single networks revealed significant differences primarily in the somato-motor, attention and visual networks. Within-network redundancy was generally significantly higher than between-network redundancy, pointing to utilization of alternate modes of communication in functionally-associated regions, and less so in the context of integrative, between-network interactions, in agreement with age-related changes in inter-modular connections found previously (Meunier et al., 2009). Redundancy did not exhibit lateralized differences associated with age, which are manifest in other network metrics (Cabeza, 2002). Previous functional connectivity studies have found similar age-associated changes in somato-motor (Betzel et al., 2014; Song et al., 2014) and attention networks (Tomasi and Volkow, 2010; Zhang et al., 2014), while other studies (Jones et al., 2011; Onoda et al., 2012) found connectivity changes in the salience and default-mode networks not found in the current analysis. More generally, age-related changes within and between large-scale functional networks observed here are in line with adaptive aging models such as the scaffolding theory of aging and cognition (STAC) (Park and Reuter-Lorenz, 2009; Reuter-Lorenz and Park, 2014), where compensatory recruitment of additional circuitry to counter cognitive aging is posited. In contrast, we did not find evidence for significant laterality effects in the association of redundancy and age, as one may expect to find given dedifferentiation models such as HAROLD (Dolcos et al., 2002) and PASA (Davis et al., 2008). This lack of laterality effects observed here, may reflect our reliance on task-free as opposed to task-based measures of brain function and remains to be further explored in future research.

The two executive function tests analyzed here, the color-word interference and verbal fluency tests, showed significant inverse relationship with age, in agreement with similar findings of age-related worsening in these two tests (Clark et al., 2009; Uttl and Graf, 1997). Our results demonstrate that redundancy significantly mediated the association between age and performance in the color-word interference test, which was the test that showed the strongest association with age. Similar results were not observed with respect to the verbal fluency test, where performance was more moderately associated with age. These results demonstrate the utility of redundancy in accounting for differences among cognitive measures in the degree to which they are affected by age. Combined, these results suggest that the alternate means of communication resulting from higher redundancy can mediate cognitive functions that exhibit strong association with age, while no evidence of such mediating role was found in at least one cognitive function, which was more moderately associated with age. Our finding of redundancy mediating inhibitory control is supported by previous findings of inhibitory control linked with better network integration and resilience (Newman, 2002; Spielberg et al., 2015). Similar to our findings, other topological properties such as modularity and global efficiency were previously shown to correlate with age (Iordan et al., 2018). However, most of these topological properties were modeled as age-associated variables that worsen with age. Our mediation model provides a novel framework for understanding the relationship between age and cognition, with redundancy demonstrated as a quantitative measure that can effectively mitigate the age-cognition relationship. A further inspection of the mediating role played by specific functional networks revealed significant contribution of attention networks similar to previously found changes in attention networks to support executive function (Andrews-Hanna et al., 2007; Spielberg et al., 2015; Wang et al., 2012). Other networks that contributed to the mediating role of redundancy included the cingulo-opercular and default-mode networks. Age-association in these networks was previously connected with decline in executive function and processing speed (Onoda et al., 2012; Zhang et al., 2014).

Global network efficiency showed a small but marginally significant association with age. The weak association with age adds to an assortment of mixed previous findings, with some studies showing no global efficiency changes (Iordan et al., 2018) and others suggesting a gradual age-associated loss (Achard and Bullmore, 2007). Further, our results demonstrate no interaction between redundancy and communication efficiency, neither in the entire sample, nor when the sample was divided into two age groups (Ages ≤ 57 and > 57) in a data driven manner. Efficiency is a measure closely linked with communication via shortest-paths (Crucitti et al., 2003), a strategy characterized as fast and direct, but vulnerable to bottlenecks and edge failures (Tombu et al., 2011; Yan et al., 2005). Evidence from functional MRI studies has also led researchers to study a host of routing strategies beyond shortest-path communication (Avena-Koenigsberger et al., 2019) subject to competing constraints of global as well as local efficiency, cost and resilience. Hence, the accrual of alternate means of information transfer through ages 15–57 may be intended to preserve network function through close-to-optimal communication channels when shortest pathways are disrupted later on. Thus, redundancy likely constitutes a continuous supplementary mechanism – not necessarily invoked in response to network disruption – that serves to provide secondary channels of information flow which develop throughout one’s adult life.

5. Limitations

Several limitations should be noted. First, we acknowledge that any study investigating changes over the lifespan should ideally follow the same cohort of subjects longitudinally to minimize confounds. However, studying large cohorts of subjects over a lifespan is practically impossible. Second, although subjects with major neurological disorders including dementia were excluded from the study, there is evidence of amyloid and tau accumulation in mild-cognitive impairment (MCI) as well as in healthy aging (Mitchell et al., 2002), which may correlate with, or even drive age-related functional changes. The NKI-Rockland sample does not include CSF or Positron Emission Tomography (PET) based measures of amyloid and tau depositions, and we could therefore not evaluate if these have contributed to the reported results. Future work focusing on the interaction of redundancy with amyloid and tau depositions could be very insightful. Third, despite the instructions to stay awake during the resting-state scans, subjects’ ability to adhere to these instructions may co-vary with age. Thus, wakefulness monitoring should be considered in future work. Fourth, the binarized version of redundancy used in the study can be improved if adapted to a weighted version in future work, although that is unlikely to change any of our findings considerably since our analysis was repeated over a large range of network densities. Finally, while the reported findings strongly position redundancy as a robust and specific measure of brain aging, we acknowledge the challenges in interpreting correlation-based measures in graph-based analysis of brain connectivity (Power et al., 2013). Future work highlighting the relationship between structural and functional measures of redundancy could significantly contribute to our understanding of redundancy in the aging human brain.

To conclude, we report that redundancy (both as a whole-brain property and within single cognitive, sensory and motor networks) is significantly associated with age, manifesting a pattern of accrual which flattens or reverses during old age. This pattern was unique to redundancy when compared with other major topological properties. In addition, we found that whole-brain redundancy mediated the association between age and inhibitory control, alleviating the impact of aging on performance for subjects with high functional redundancy. Finally, we report that the association between age and redundancy was not accompanied by concurrent loss of communication efficiency. The robust and specific association between age and redundancy and its mitigating role with respect to the inverse relationship between age and executive function position this topological design principle as a resource used by the brain to restrict and minimize the effect of aging. As such we conclude that redundancy is a mechanism of brain reserve.

Abbreviations:

MRI

Magnetic Resonance Imaging

AD

Alzheimer’s disease

R_s

Redundancy matrix R and scalar redundancy

DKEFS

Delis–Kaplan Executive Function System

CW

Color–Word interference

VF

Verbal Fluency