An efficient and accurate method for robust inter‐dataset brain extraction and comparisons with 9 other methods

Abstract

Brain extraction is an important first step in many magnetic resonance neuroimaging studies. Due to variability in brain morphology and in the appearance of the brain due to differences in scanner acquisition parameters, the development of a generally applicable brain extraction algorithm has proven challenging. Learning‐based brain extraction algorithms in particular perform well when the target and training images are sufficiently similar, but often perform worse when this condition is not met. In this study, we propose a new patch‐based multi‐atlas segmentation method for brain extraction which is specifically developed for accurate and robust processing across datasets. Using a diverse collection of labeled images from 5 different datasets, extensive comparisons were made with 9 other commonly used brain extraction methods, both before and after applying error correction (a machine learning method for automatically correcting segmentation errors) to each method. The proposed method performed equal to or better than the other methods in each of two segmentation scenarios: a challenging inter‐dataset segmentation scenario in which no dataset‐specific atlases were used (mean Dice coefficient 98.57%, volumetric correlation 0.994 across datasets following error correction), and an intra‐dataset segmentation scenario in which only dataset‐specific atlases were used (mean Dice coefficient 99.02%, volumetric correlation 0.998 across datasets following error correction). Furthermore, combined with error correction, the proposed method runs in less than one‐tenth of the time required by the other top‐performing methods in the challenging inter‐dataset comparisons. Validation on an independent multi‐centre dataset also confirmed the excellent performance of the proposed method.

1. INTRODUCTION

Brain extraction, also known as skull‐stripping, is an important first step in almost all brain magnetic resonance (MR) image analysis pipelines. It consists of the removal of all tissues external to the brain, such as skull, dura, and eyes, without removing any part of the brain itself. Because brain extraction is performed early in the processing pipeline, high accuracy is crucial to avoid propagating errors into subsequent processing steps, such as tissue segmentation, registration, and cortical surface reconstruction and analysis. For example, a failure to sufficiently remove nonbrain tissue can result in over‐estimation of cortical thickness (van der Kouwe, Benner, Salat, & Fischl, 2008), or add errors to regional volume and atrophy estimates (Battaglini, Smith, Brogi, & De Stefano, 2008). On the other hand, over‐segmentation results in a permanent loss of information that cannot be recovered in subsequent processing steps. Suboptimal outcomes of automatic brain extraction often require manual adjustment to ensure that the brain mask is suitable for further processing. However, particularly in large population studies, manual intervention is undesirable and possibly infeasible, as it is extremely time‐consuming process (manually correcting poor initial segmentations can require up to 8 hr per image [Puccio, Pooley, Pellman, Taverna, & Craddock, 2016]), and sensitive to both inter‐ and intra‐rater variability.

To address these concerns, numerous fully automatic brain extraction methods have been developed. These methods can be roughly categorized into nonlearning‐ and learning‐based approaches. Nonlearning based methods do not require training data. Instead, the algorithms are driven with various heuristics. For example, the Brain Extraction Toolbox (BET) (Smith, 2002) uses a deformable model that iteratively evolves to fit the brain surface by locally adaptive forces, whereas 3dSkullStrip (3DSS) from the AFNI toolkit (Cox, 1996) modifies BET to avoid segmentation of the eyes and ventricles and reduce leakage into the skull. The Hybrid Watershed Algorithm (HWA) (Ségonne et al., 2004), part of the FreeSurfer package (Fischl, 2012), combines a watershed segmentation with a corrective deformable model under geometric constraints, and the Brain Surface Extractor (BSE) (Shattuck & Leahy, 2002) algorithm employs a series of processing steps such as image denoising, edge detection, and morphological operations.

Learning‐based methods, on the other hand, use a template or set of atlases to drive the segmentation a target image (for clarity, we use the term “atlas” to refer to an image with its corresponding reference labeling). ROBEX (Iglesias, Liu, Thompson, & Tu, 2011), for instance, combines a discriminative random forest classifier (to detect voxels along the brain boundary) with a generative point distribution model (to ensure that the result is plausible), whereas SPECTRE (Carass et al., 2011) and ANTs (Avants et al., 2011) use prior‐based tissue classification, the results of which are further modified using mathematical morphological operations to produce the final brain mask. Other learning‐based methods work by augmenting or combining other brain extraction methods. For example, optiBET (Lutkenhoff et al., 2014) refines an initial BET brain mask using nonlinear registration to a labeled template, whereas LABEL (Shi et al., 2012) and the work of Souza et al. (2017) combine, using machine learning classifiers, the brain masks given by other methods.

A common class of learning‐based methods is that of multi‐atlas segmentation. In these methods, labels from multiple atlases are propagated to the target image and then combined to form a consensus solution. For example, Brain MAPS (Leung et al., 2011) combines linear registration with spline‐based nonlinear registration algorithm (Rueckert et al., 1999) to register a subset of similar atlases to a target image, and then fuses the registered labels using shape‐based averaging (Rohlfing & Maurer, 2007) to form a consensus segmentation. Pincram (Heckemann et al., 2015) uses a registration‐based iterative refinement approach to propagate labels from the atlases to a target image. Instead of propagating labels via nonlinear registration, BEaST (Eskildsen et al., 2012) requires only a coarse linear registration between images, which translates into better runtime performance. Label propagation is then accomplished using a multi‐resolution patch‐based approach (Coupé et al., 2011; Rousseau, Habas, & Studholme, 2011) where the label of each voxel in a target image is determined by comparing its surrounding neighborhood with nearby patches drawn from a subset of similar atlases. Other similar methods include that of Huang et al. (2014), which is distinguished by its use of a locally linear representation‐based classification (Wang et al., 2010) for patch‐based segmentation, and that of Roy, Butman, and Pham (2017), which combines multi‐contrast patch‐based segmentation with nonlinear registration for more robust performance in the presence of brain pathologies.

Most brain extraction methods are designed to work on T1‐weighted (T1w) images. This is largely due to the popularity of the T1w modality, as it produces images with excellent tissue contrast. Even in the case that images from other modalities are to be segmented, brain extraction can be performed on the same individual's T1w image, and then accurately propagated by linear registration. Nonetheless, the development of a generic, robust, and accurate brain extraction method remains a difficult task because of the significant variations in image characteristics that occur due to differences in scanner manufacturer, acquisition sequence, and scanner strength. In addition, neuroimaging studies are performed on individuals of all ages, with and without tissue altered by various pathologies. Consequently, nonlearning based methods for brain extraction algorithms often need to be adapted specifically for a certain type of study, or, in the best case, need to be fine‐tuned (Fennema‐Notestine et al., 2006; Shattuck, Prasad, Mirza, Narr, & Toga, 2009). Learning‐based methods generally perform better than nonlearning based methods, offering very high performance when the atlases are sufficiently similar to the target images, but show substantially lower performance when this condition is not met. This can be overcome by either manually correcting poor segmentations, or by generating a new set of dataset‐specific atlases. Both options are impractical, and indeed infeasible for modern large‐scale multi‐centre datasets consisting of hundreds or thousands of images from many different sources. Recognizing these considerations, other authors have focused on developing learning‐based methods that are more easily customizable to the study of interest, for example by reducing the number of dataset‐specific atlases needed to obtain accurate segmentations (Doshi, Erus, Ou, Gaonkar, & Davatzikos, 2013; Serag et al., 2016). However, these methods still require dataset‐specific atlases, which may still be impractical.

Regardless of the choice of segmentation algorithm, some error is unavoidable. Wang et al. (2011), proposed a novel generic method to improve the performance of automated segmentation by correcting systematic errors (i.e., errors that occur from subject to subject) using a machine learning classifier to learn spatial, intensity, and contextual patterns of segmentation errors in automated segmentation. Error correction has been shown to boost performance in a wide variety of automated segmentation tasks (Wang, Ngo, Hessl, Hagerman, & Rivera, 2016; Wang & Yushkevich, 2013; Zandifar, Fonov, Coupé, Pruessner, & Collins, 2017). However, like the learning‐based methods described above, it is generally assumed that dataset‐specific atlases are available. One exception is the work of Wang et al. (2016), which assessed the usefulness of error correction applied to FreeSurfer segmentations of the cerebellum and brainstem, when trained using atlases differing from the target images with respect to the type of head coil used during scan acquisition and the level of brain atrophy. However, the efficacy of error correction under still more challenging circumstances, that is, when the training subjects differ from the target images more drastically (e.g., with respect to the age of the subjects, the scanner acquisition protocol, and the scanner strength) has not been evaluated, particularly for brain extraction algorithms.

The primary goal of this article is twofold. First, we outline and validate a new brain extraction method that is specifically designed for robust and accurate processing across datasets, that is, without requiring additional and potentially costly dataset‐specific atlases. Like BEaST, our proposed method incorporates a patch‐based label fusion technique within a multi‐resolution framework. We present several modifications to this algorithm that increase its performance, including the use of a more robust patch‐based label fusion scheme based on discriminative sparse representation (Huang & Aviyente, 2006; Tong, Wolz, Coupé, Hajnal, & Rueckert, 2013), and the application of a modified error correction algorithm. Second, we compare the proposed method with 9 other commonly used brain extraction methods, both with and without error correction, in two extensive scenarios. The first is a challenging inter‐dataset segmentation scenario, in which no dataset‐specific atlases are used. The second is a simpler intra‐dataset segmentation scenario, in which only dataset‐specific atlases are used. For evaluation, we use a diverse collection of labeled images from 5 distinct datasets, covering subjects of all ages (from children to the elderly), with varying atrophy, and acquired from varying scanning machines with different acquisition protocols and scanner strengths. We additionally validate our proposed method on a secondary multi‐centre publicly available dataset (Souza et al., 2017).

2. MATERIALS AND METHODS

2.1. Image data

We used T1w MR images of the human brain acquired from a variety of datasets, which are briefly described below.

(1) The Alzheimer's Disease Neuroimaging Initiative (ADNI) (Mueller et al., 2005) dataset used in this study contains images of 30 elderly adults (mean age 74.9 ± 7.0 years). Images of 10 subjects from each of the following three subgroups were included: cognitively normal subjects, subjects with mild cognitive impairment, and subjects with Alzheimer's disease. These data were acquired on 1.5 T General Electric (GE), Philips, and Siemens scanners using a magnetization‐prepared rapid acquisition gradient‐echo (MP‐RAGE) sequence. Semi‐automatically generated brain masks are available as part of the publicly available BEaST atlas set. Specifically, these brain masks were originally made by manually correcting initial segmentations produced by fitting a spherical mesh to the publicly available automatic segmentations produced by Brain MAPS (Leung et al., 2011) (see Eskildsen et al. [2012] for details).

(2) The International Consortium for Brain Mapping (ICBM) (Mazziotta et al., 2001) dataset used in this study contains images of 10 healthy young adults (mean age 23.8 ± 4.0 years) acquired on a Philips 1.5 T Gyroscan scanner using a spoiled gradient‐echo sequence. Semi‐automatically generated brain masks are available as part of the publicly available BEaST atlas set. Specifically, these brain masks were originally made by manually correcting initial segmentations produced by applying BET (Smith, 2002) to fused‐modality images (see Eskildsen et al. [2012] for details).

(3) The Neurofeedback Skull‐stripped (NFBS) repository (Puccio et al., 2016) dataset used in this study contains images of 20 adults (mean age 33.2 ± 4.9 years) acquired on a Siemens 3 T Magnetom TIM Trio Scanner using an MP‐RAGE sequence. The publicly available brain masks were previously semi‐automatically constructed in accordance with a brain mask definition similar to that of Eskildsen et al. (2012).

(4) The National Institute of Health Pediatric Database (NIHPD) (Evans, 2006) dataset used in this study contains images of 10 healthy children (mean age 12.0 ± 4.0 years) acquired on either Siemens or GE 1.5 T scanners, using a spoiled gradient‐echo sequence. Semi‐automatically generated brain masks are available as part of the publicly available BEaST atlas set. These masks were originally made in the same way as the ICBM masks.

(5) The Open Access Series of Imaging Studies (OASIS) (Marcus et al., 2007) dataset used in this study contains images of 20 healthy young adults (mean age 23.4 ± 4.0 years) acquired on a Siemens 1.5 T Vision scanner using an MP‐RAGE sequence. Manually generated multi‐label volumes, provided by Neuromorphometrics, Inc. (Somerville, MA, under academic subscription, available at http://neuromorphometrics.com), were merged into a single binary volume which includes cerebral and cerebellar white and gray matter, and excludes all nonbrain tissue in addition to some ventricular and sulcal cerebrospinal fluid (CSF).

2.2. Preprocessing

The following preprocessing steps are applied to all the images described above:

(1) Spatial normalization is achieved by affine (12 parameter) registration to the stereotaxic MNI‐ICBM152 template (Fonov et al., 2011) using the in‐house script bestlinreg.pl, based on the open source MINC toolkit, which optimizes a normalized mutual information (NMI) similarity measure in a multi‐resolution fashion. Nearest‐neighbor interpolation was used when applying the estimated transformation to the label images to preserve their binary nature. The resulting images had a size of 193 × 229 × 193 with an isotropic voxel size of 1 mm³.

(2) Image nonuniformity is corrected using the N3 (Sled, Zijdenbos, & Evans, 1998) method (nu_correct in the MINC toolkit). Instead of correcting for nonuniformity in native space, we observed better results when applying N3 on spatially normalized images, using the MNI‐ICBM152 template brain mask. As recommended in other studies (Boyes et al., 2008), we used a smaller ‐distance parameter (an estimate of the distance over which the nonuniformity field varies) of 50 mm for images acquired on 3 T scanners, and a larger parameter of 200 mm for images acquired on 1.5 T scanners.

(3) Intensity normalization is performed on the spatially normalized and nonuniformity corrected images by linearly scaling the intensities to the range 0–100 using 0.1–99.9% of the voxels in the intensity histogram within the MNI‐ICBM152 template brain mask.

2.3. Definition of brain mask

Our definition of the brain is largely the same as that of Eskildsen et al. (2012), however the brain masks in this study are constructed in a different way (see Section 2.4). Nonbrain tissue is defined as skin, skull, eyes, dura mater, external blood vessels, and nerves (e.g., optic chiasm, carotid arteries, and the superior and transverse sinus). Brain tissue is defined as all cerebral and cerebellar white and gray matter, in addition to the brainstem, pons, penduncles, and CSF in the ventricles and in deep sulci.

2.4. Construction of reference brain masks

The labeled brain masks acquired from the datasets described above contain some differences which, without modification, would make comparisons across different datasets difficult and possibly biased. For example, the brain mask closely follows the boundary of the cortex in the ICBM and NIHPD datasets, but includes more subarachnoid CSF in the ADNI (particularly in brains with a large degree of atrophy), OASIS, and the NFBS datasets. In addition, some internal and sulcal CSF is excluded in the OASIS masks. Since a primary focus of this study is to assess the efficacy of brain extraction algorithms when using atlases consisting of labeled images from different datasets, it is crucial that the brain masks are consistent across the datasets.

To improve the anatomical consistency of the masks across datasets without spending an inordinate amount of time, we used a semi‐automated method to modify the original brain masks. In the first step, manual thresholding was applied to remove excessive CSF from the pre‐processed original brain masks, yielding combined white/gray matter masks. For this step, denoised (Manjón, Coupé, Martí‐Bonmatí, Collins, & Robles, 2010) versions of the images were used to obtain smoother thresholded masks. Second, to recover ventricular and sulcal CSF from the white/gray matter masks, we adapted a procedure recommended by Heckemann et al. (2015) by blurring with a Gaussian kernel (8 mm standard deviation [SD]), thresholding at 0.5, erosion with a box kernel (3 mm width) in two iterations, and merging with the original white/gray matter mask. Finally, the masks were examined and manually corrected, where necessary, to suit the definition of the brain mask described in Section 2.3. Examples of the final brain masks resulting from this process are shown in Figure 1.

Figure 1.

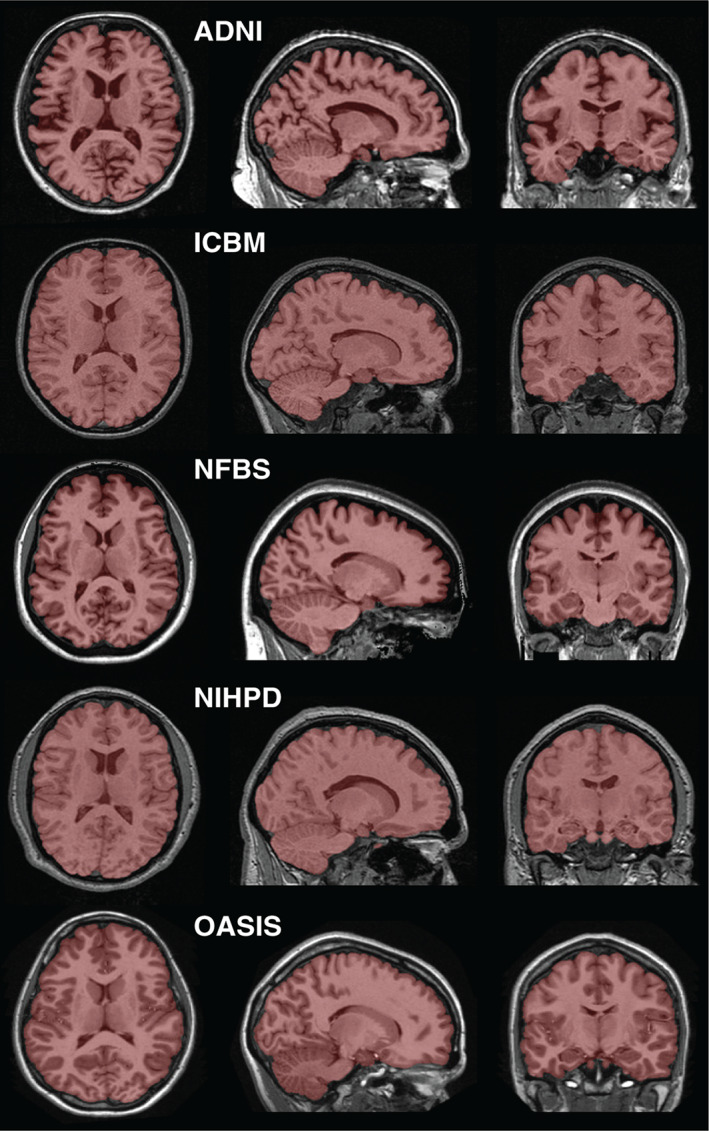
Example reference labels. One labeled image is displayed from each of the 5 datasets used in this study [Color figure can be viewed at wileyonlinelibrary.com]

2.5. Proposed method for robust brain extraction

As described earlier, our proposed method modifies the BEaST method with the goal of improving not only the accuracy of the segmentation but also the robustness to differences between the target image and the available atlases. We summarize our proposed method, emphasizing the differences with respect to the BEaST method, as follows.

2.5.1. Preprocessing

The target image is affinely aligned with the atlases, corrected for nonuniformity, and intensity normalized using the preprocessing pipeline described in Section 2.2.

2.5.2. Atlas selection

Following preprocessing, the N closest atlases to the target image are selected based on the sum of squared distances (SSD) between each atlas and the target image. In our preliminary experiments, other similarity metrics (such as normalized mutual information and global cross‐correlation) were considered, but were not found to improve results. In BEaST, N possibly different atlases are selected at each successively finer resolution by calculating the SSD within an increasingly narrow initialization mask. In our preliminary experiments, we found that this tended to result in the selection of some visually dissimilar atlases, and slightly worse results. In this study, we therefore select the N atlases only once, at the native resolution, calculating the SSD within a brain margin mask; these same atlases are then used for every level of the multi‐resolution segmentation (Section 2.5.4). The margin mask is obtained by subtracting the intersection of the atlas masks from the union of the atlas masks.

2.5.3. Patch‐based label fusion

In BEaST, classical patch‐based label fusion (Coupé et al., 2011) is used to automatically segment the preprocessed target image using the N selected atlases. For a given target voxel in the target image, the surrounding patch is first extracted (denoted by p) and then re‐shaped into a column vector. Then, a cubic search volume is defined around the target voxel, and all patches within the search volume are extracted from each of the selected atlases. The resulting patch library is generally very large. Therefore, one can use patch preselection (Coupé et al., 2011) to prune the library before the computationally expensive weight estimation step. Patch preselection can be done very efficiently using the structural similarity (ss) index (Wang, Bovik, Sheikh, & Simoncelli, 2004) between the target patch p and each patch p _j in the patch library:

$${\mathit{ss}}_{\mathrm{j}}=\frac{2{\mathit{\mu \mu }}_{\mathrm{j}}}{{\mu }^2+{\mu }_{\mathrm{j}}^2}\times \frac{2{\mathit{\sigma \sigma }}_{\mathrm{j}}}{{\sigma }^2+{\sigma }_{\mathrm{j}}^2}$$ (1)

where μ and σ denote the mean and SD, respectively, of target patch p, and μ _j and σ _j denote the same for library patch p _j. Patches p _j in the patch library with ss _j < γ can be discarded, where γ is a pre‐defined patch preselection threshold. Since the computation of ss between two patches requires only the value of their mean and SDs, preselection can be accelerated using pre‐computed maps of local means and SDs to avoid repeated calculations. Supposing there are n patches in the pruned patch library, the preselected patches are re‐shaped into column vectors and grouped into a matrix L = [p ₁, p ₂ …, p _n].

In classical patch‐based label fusion, a label probability is assigned to the target voxel based on the similarity of its surrounding patch p to all the patches in the patch library L. The label probability v can be estimated as:

$$v=\frac{{\sum }_{j=1}^n{w}_{\mathrm{j}}{l}_{\mathrm{j}}}{{\sum }_{j=1}^n{w}_{\mathrm{j}}}$$ (2)

where l _j is the label for the central voxel of patch p _j in the library. Note that because the segmentation problem is here binary, the probability v is always between 0 and 1. The weight w _j assigned to label l _j depends on the intensity similarity between p and p _j, the jth patch in the patch library:

$$w_{\mathrm{j}}=\exp \left(-{‖p-p_{\mathrm{j}}‖}_2^2/h\right)$$ (3)

where h is the smoothing parameter, which is locally adapted in proportion to the minimal distance between p and the library patches as

$$h=\beta \underset{j}{\text{argmin}}{‖p-p_{\mathrm{j}}‖}_2^2+\mathrm{\varepsilon }$$ (4)

where β is a free parameter and ɛ is a small constant to ensure numerical stability.

Whereas classical patch‐based label fusion has been shown to be highly accurate in many cases, there are nonetheless several limitations that hinder its performance in certain tasks. First, the weighting function in Equation 3 is based on a simple intensity similarity, which assumes that not only the overall brightness but also the tissue contrast between images is sufficiently similar. When the target image and the atlases come from different sources, that is, different scanners and/or acquisition protocols, it is unlikely that this assumption is satisfied, even after intensity normalization. Second, given the weight formulation in Equation 3, even dissimilar patches will be assigned a nonzero weight, limiting segmentation accuracy.

To address both limitations, we estimate the weights using a sparse representation framework (Huang & Aviyente, 2006; Tong et al., 2013). In the sparse representation method, rather than assigning weights to the library patches independently based on patch‐wise intensity similarity, the problem is re‐framed in terms of reconstruction, and all the weights are simultaneously estimated by a sparse representation problem:

$$w=\underset{a\ge 0}{\text{argmin}}\frac{1}{2}{‖p-\mathit{aL}‖}_2^2+\lambda {‖a‖}_1$$ (5)

where L is the patch library matrix. The l ₁ penalty, weighted by the free parameter λ, encourages sparse solutions (e.g., only a few patches in the library are assigned a nonzero weight). In our study, Equation 5 was optimized using the SPAMS toolbox (Mairal, Bach, & Ponce, 2014). As noted in other studies using sparse representation (Huang & Aviyente, 2006; Mairal et al., 2014; Tong et al., 2013), to get a meaningful estimate of the weights, it is important to normalize both the target patch p and the patches in the patch library. To this end, we normalize each patch to zero mean and unit l ₂ norm. By normalizing in this way, the weight estimation in Equation (5) is more robust to differences in overall brightness and contrast.

Finally, we use a multi‐point label estimation such that label estimates for whole patches are estimated (Rousseau et al., 2011) rather than for the central pixel of each patch. This is advantageous because each voxel benefits from multiple label estimates from neighboring points (depending on the spatial distribution of voxels that are flagged for processing, see Section 2.5.4). We use simple averaging to fuse these multiple estimates.

2.5.4. Multi‐resolution implementation

In order to increase accuracy and to drastically reduce processing time, the patch‐based label fusion is embedded in a multi‐resolution framework as done in BEaST. In brief, the multi‐resolution framework enables propagation of the segmentation across scales using the segmentations at coarser scales to initialize the segmentation at the subsequent finer scale. First, all atlases are isotropically downsampled using trilinear interpolation to the lowest resolution, and patch‐based label fusion is carried out. The whole estimated probability map is then isotropically upsampled to the next finer resolution using trilinear interpolation, and voxels for which the estimated probability is less than a pre‐defined constant α are set to 0. Similarly, voxels for which the estimated probability is greater than (1 − α) are set to 1. The remaining voxels are then flagged for processing with patch‐based label fusion (in the BEaST paper, this set of flagged voxels is called the initialization mask). This procedure is repeated until the final resolution is met, and the final binary label is obtained by thresholding the final estimated probability map at 0.5.

2.5.5. Parameters

The proposed method has a number of parameters to select. For a fair comparison to BEaST, the same patch preselection threshold γ and multi‐resolution configuration (i.e., downsampling factors and multi‐resolution propagation parameter α) as used in the latest version of the software (1.12.00) are also used in this study. However, as our modified method solves a computationally expensive sparse representation problem to calculate patch weights, we use slightly smaller search volumes at the 2 and 1 mm resolutions to reduce processing time. Also as in BEaST, we select up to N = 20 atlases for segmenting each target image. If fewer than 20 atlases are available, then all available atlases are used. The remaining parameters were empirically chosen. A summary of the parameter settings used in this study are presented in Table 1.

Table 1.

Multi‐scale parameters used for proposed method at each resolution level

	Voxel size	Patch size	Search volume	γ	λ	α
Level 1	4 mm3	3 × 3 × 3	5 × 5 × 5	0.95	0.15	0.2
Level 2	2 mm3	3 × 3 × 3	7 × 7 × 7	0.95	0.15	0.2
Level 3	1 mm3	5 × 5 × 5	11 × 11 × 11	0.95	0.15	–

γ = Patch preselection threshold; α = multi‐resolution propagation parameter; λ = l ₁ term penalty for sparse patch‐based label fusion. Patch sizes and search volumes are reported in voxel units.

2.6. Compared methods

In this section, we briefly describe the methods for brain extraction that have been chosen for comparison.

2.6.1. ANTs

Brain extraction using ANTs combines template priors, high‐performance nonlinear image registration (Avants, Tustison, Song, et al., 2011), and tissue classification (Avants, Tustison, Wu, Cook, & Gee, 2011) with topological refinements based on morphological operations. We used the MNI‐ICBM152 template and corresponding brain mask prior (Fonov et al., 2011). The default parameters were used for all steps with the exception of the similarity measure used for the nonlinear image registration. We changed the measure from local cross‐correlation to mutual information, which resulted in considerably better performance.

2.6.2. BEaST

As described in Section 2.5, the latest version at the time of writing (1.12.00) from the MINC toolkit (http://bic-mni.github.io) with the default parameters was used.

2.6.3. BET

The BET (Smith, 2002) from the FMRIB Software Library (FSL) (Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012) uses a deformable model that iteratively evolves to fit the brain surface by local intensity‐based adaptive forces and smoothness criteria. We used the latest version of FSL at the time of writing (5.0) with the default parameters.

2.6.4. Brain MAPS

Brain MAPS (Leung et al., 2011) is a multi‐atlas segmentation approach based on the multi‐atlas segmentation framework. In the original article, the definition of the brain mask excludes all CSF. To ensure that all CSF is removed, the method described in the original article includes an automated thresholding step, followed by a dilation step to ensure that any accidentally removed brain tissue is recovered. Because our definition of the brain mask includes internal and some sulcal CSF, we implemented the method as closely as possible, but omitting the thresholding and dilation steps. In brief, our implemented method consists of the following steps.

Atlas selection

As suggested in the original article, the closest N = 19 atlases to the target image are selected using the cross‐correlation measure. If fewer than 19 atlases are available, then all the available atlases are used for label propagation.

Label propagation

The selected atlases are registered to the target image using linear followed by nonlinear registration. The nonlinear registration is based on a multi‐resolution free‐form deformation (Rueckert et al., 1999), based on a normalized mutual information similarity measure, with three isotropic control point spacings of 16, 8, and 4 mm. The corresponding reference label images are re‐sampled to the target image using the results of the registrations. For both linear and nonlinear registration, we used the NiftyReg package (https://sourceforge.net/projects/niftyreg), which implements fast multi‐threaded variants of the registration algorithms used in the original Brain MAPS paper. Apart from the control point spacings, the default parameters for the registration algorithms were used.

Label fusion

The multiple re‐sampled label images are fused into a consensus segmentation using shape‐based averaging (SBA) (Rohlfing & Maurer, 2007). However, the authors also evaluated two other label fusion techniques: simultaneous truth and performance level estimation (STAPLE) (Warfield, Zou, & Wells, 2004) and majority vote (MV). In this study, we also evaluate all three label fusion techniques.

2.6.5. Optimized BET

Optimized BET (optiBET; Lutkenhoff et al., 2014) augments BET by refining an initial (BET‐derived) mask using nonlinear registration to a labeled template. We used the default parameters. The brain masks produced by optiBET exclude some ventricular CSF, which is inconsistent with the definition of the brain mask used in this study. Therefore, we postprocess all optiBET brain masks using hole‐filling.

2.6.6. Pincram

Pincram is unique among the compared methods in that it was also specifically developed for robust cross‐dataset segmentation. Pincram (Heckemann et al., 2015) is an augmented multi‐atlas segmentation method in which a progressively more accurate segmentation is estimated by applying increasingly more accurate registration techniques (6‐parameter linear, affine, and nonlinear). At each step, a consensus segmentation is generated by thresholding the mean of the registered labels (the thresholds at each step are configurable parameters). At the subsequent step, the search for the brain boundary is constrained to the neighborhood of this consensus segmentation. Note that, by default, Pincram uses all available atlases in the first refinement step. Pincram is freely available (http://soundray.org/pincram). The latest version at the time of writing (0.2.7) was used.

2.6.7. ROBEX

ROBEX (Iglesias et al., 2011) combines a random forest classifier (Breiman, 2001) to detect the brain boundary, with a generative point distribution model to enforce smoothness and plausibility of the resulting segmentation. ROBEX is freely available (http://www.nitrc.org/projects/robex), and has no parameters to tune. The latest version at the time of writing (1.2) was used.

2.7. Error correction

Error correction (Wang et al., 2011) uses a voxel‐wise classifier to automatically detect and correct systematic errors produced by a “host” segmentation method. In brief, error correction requires a set of atlases to which the particular host segmentation method has been applied. A classifier is then trained to discriminate between voxels correctly or incorrectly labeled by the host method on the basis of voxel‐specific feature sets. When segmenting a new target image, the host segmentation method is first applied, and then each voxel is examined by the classifier. In the context of binary segmentation, if the classifier determines that a voxel was mislabeled, then its label is flipped.

The features used to describe each voxel include spatial, appearance, and contextual information. Since all images considered in this study undergo a pre‐processing step in which they are linearly spatially aligned, the spatial features for each voxel consists of its (x, y, z) position in MNI‐ICBM152 space. The appearance feature for each voxel is directly derived by extracting a patch from the image centered on the same voxel, and the contextual feature is similarly derived by extracting a patch from the initial segmentation produced by the host segmentation method. Furthermore, joint spatial‐appearance and joint spatial‐contextual features are included by multiplying each spatial feature with each of the appearance and contextual features.

As discussed in Section 2.5.3, using raw intensity patches may lead to poor results if the atlases differ from the target image with respect to overall brightness and contrast. In the original work on error correction, the authors suggest to normalize each appearance feature using the mean of the working region of interest (obtained by dilating the initial segmentation produced by the host method) from which the appearance feature is drawn. We instead normalized each appearance feature to zero mean and unit l ₂ norm, which we found resulted in improved performance for cases in which the atlases differed significantly from the target image. Also in our implementation, we use a fast multi‐threaded implementation (http://scikit-learn.org/stable) of the random forests classifier (Breiman, 2001), rather than the AdaBoost classifier (Freund & Schapire, 1995) used in the publicly available error correction tool (Wang & Yushkevich, 2013). The parameters for error correction (patch size, dilation radius, and sampling rate for training) were set to values suggested by the original authors (Wang et al., 2011) in their experiments on error correction applied to the BET method (patch size of 5 × 5 × 5 voxels, dilation radius of 1 voxel, and sampling rate of 1%).

2.8. Performance measures

The similarity between the automatically segmented labels image and the reference label images were quantified using the following 5 metrics.

Dice coefficient

The Dice coefficient measures the extent of spatial overlap between two binary images. The Dice coefficient is defined as 100% × 2|A ∩ R|/(|A| + |R|) where A is an automatically segmented label image, R is the reference label image, ∩ is the intersection, and |·| counts the number of nonzero elements. We here express the Dice coefficient as a percentage, with 100% indicating perfect overlap.

Sensitivity and specificity

Sensitivity and specificity measures provide information that complements overlap measures (such as the Dice coefficient) by separately assessing the ability of the algorithm to correctly classify either foreground (sensitivity) or background (specificity) voxels. The sensitivity is defined as 100% × TP/(TP + FN) where TP is the number of true positives and FP is the number of false positives. The specificity is defined as 100% × TN/(TN + FP) where TN is the number of true negatives and FP is the number of false positives. These measures are also reported as percentages, and values closer to 100% are better.

Normalized volume difference

As overlap measures do not provide information about volumetric differences between the label pairs, we also consider the normalized volume difference (NVD), defined as 200% × abs((A| − |R|)/(|A| + |R|)) where abs(·) is the absolute value function. The NVD is reported as a percentage. Values closer to 0% are better.

Volumetric correlation

Finally, we also calculate the Pearson correlation coefficient r between the volumes of the reference and automatic segmentations.

2.9. Error visualization

To visualize errors, we generated mean false‐positive and mean false‐negative images as suggested by Shattuck et al. (2009). False‐negative and false‐positive images for each subject were nonlinearly deformed and then averaged in MNI‐ICBM152 stereotaxic space, and the resulting images were summed in the direction perpendicular to the sagittal plane for visualization.

3. EXPERIMENTS AND RESULTS

We consider two distinct scenarios in our experiments: an inter‐dataset segmentation scenario and an intra‐dataset segmentation scenario. In the inter‐dataset segmentation scenario, no dataset‐specific atlases were used, either for the multi‐atlas segmentation methods or for training the corrective classifier. Each dataset was processed using a set of atlases consisting of all the labeled images from the other respective datasets. In the intra‐dataset segmentation scenario, only dataset‐specific atlases were used. Each dataset was processed using a 5‐fold cross‐validation strategy. As mentioned in Section 2.7, to train a corrective classifier on a set of atlases, the host segmentation method must be applied to each atlas first. For the multi‐atlas segmentation methods, this was achieved using a leave‐one‐out strategy among the set of atlases.

3.1. Multi‐resolution label fusion and error correction: Improving efficiency

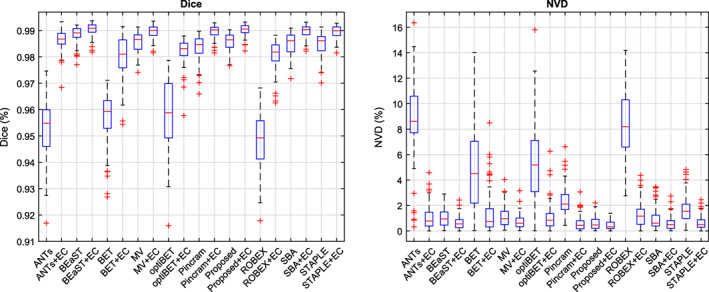
Unlike classical patch‐based segmentation, the sparse representation method for patch‐based label fusion requires solving a more complex optimization problem (Equation 5) for each target patch and is therefore much more computationally demanding. The processing time required for the proposed method, like BEaST, can be substantially reduced by forgoing patch‐based label fusion at the higher resolutions, but the resulting segmentations are correspondingly coarse. While computationally efficient intensity‐based algorithms, such as graph‐cuts (Tong et al., 2015) or expectation–maximization models (Ledig et al., 2012) can be used to recover high‐resolution detail, it has been recently suggested that error correction can also be used for this purpose (Wang, Prasanna, & Syeda‐Mahmood, 2017). We therefore assessed the impact of error correction on the proposed method when terminating the multi‐scale patch‐based label fusion at various resolutions (Table 1) in both the inter‐ and intra‐dataset experiments. Distributions of Dice coefficients and NVD values, over all 90 images from the 5 datasets, are shown in Figure 2.

Figure 2.

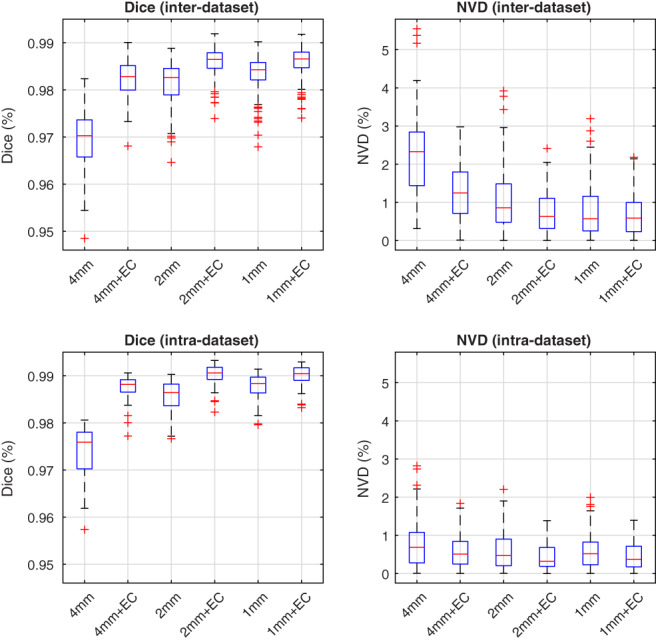
Effect of early termination on the multi‐scale patch‐based label fusion. Distributions of Dice coefficients and NVD values are shown both before and after error correction (EC), in the inter‐ and intra‐dataset segmentation experiments. Centre lines: median, boxes: interquartile range, whiskers: truncated range, “+”: outliers [Color figure can be viewed at wileyonlinelibrary.com]

Although there remain significant performance gaps between the full multi‐resolution patch‐based label fusion and the early terminated versions before applying error correction, the differences between methods greatly diminished after applying error correction. After error correction, the performance of the full multi‐resolution version (operating at 4, 2, and 1 mm resolutions) was comparable with version terminated after the 2 mm resolution. On the other hand, terminating the patch‐based label fusion after the lowest resolution (4 mm) resulted in degraded performance, persisting even after applying error correction. We therefore chose to forgo patch‐based label fusion at the highest resolution level, which resulted in a substantial reduction in processing time from roughly 22 min per subject to 1.5 min per subject (Section 3.3). This accelerated method, used in the comparison experiments below, is hereafter referred to as the “proposed method” for brevity.

3.2. Comparison of methods

All 10 methods were compared in both the inter‐ and intra‐dataset segmentation scenarios. In both segmentation scenarios, each method was applied to segment each of the 5 datasets, and error correction was applied to each of the 10 methods. These comparisons of brain extraction methods are among the most comprehensive in the literature, requiring a total of 5,760 brain extractions. While this number seems large, it is the result of applying each multi‐atlas segmentation method to both the test images and the training images for each combination of testing/training images, as required for training the corrective classifier (note that, for non‐multi‐atlas segmentation methods which do not require explicitly provided training data, each image needs to be segmented only once).

3.2.1. Inter‐dataset segmentation scenario

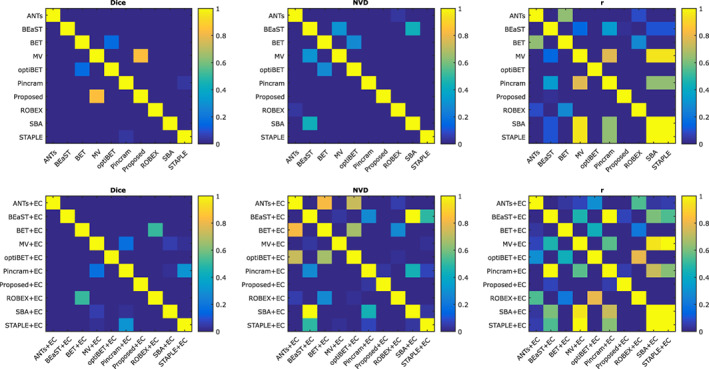
Distributions of Dice coefficients and NVD values for each segmentation method, both before and after error correction, are shown in Figure 3. Table 2 summarizes the performance of each method, over all 90 images from the 5 datasets, with respect to all 5 performance measures outlined in Section 2.8. Wilcoxon signed‐rank tests were used to test for significant differences between all pairs of methods both before and after applying error correction. Fisher r‐to‐z transforms were used to similarly test for significant differences with respect to volumetric correlation. Detailed results of the significance tests between methods are shown in Figure 4. All p values were corrected for multiple comparisons using false discovery rate (FDR).

Figure 3.

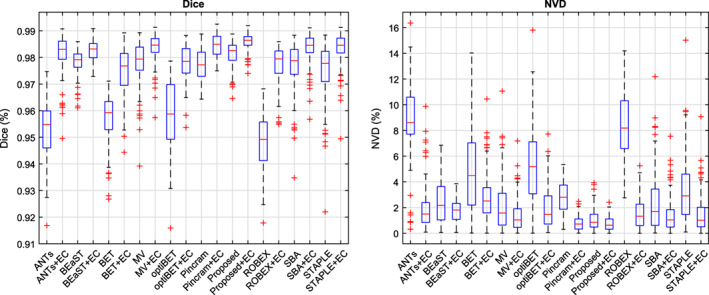
Distributions of Dice coefficients and normalized volume difference (NVD) values for each method, both before and after error correction (EC), in the inter‐dataset segmentation scenario. Centre lines: median, boxes: interquartile range, whiskers: truncated range, “+”: outliers [Color figure can be viewed at wileyonlinelibrary.com]

Table 2.

Summary of 5 performance measures for each method in the inter‐dataset segmentation scenario, both before and after error correction (EC)

	Dice	Sens.	Spec.	NVD	r
ANTs	95.30 (1.12)	99.58 (0.85)	97.43 (0.70)	8.74 (2.97)	.9064
ANTs + EC	98.14 (0.75)	98.42 (1.73)	99.42 (0.29)	2.00 (1.85)	.9426
BEaST	97.80 (0.50)	98.69 (0.94)	99.16 (0.38)	2.46 (1.63)	.9592
BEaST + EC	98.26 (0.37)	98.38 (1.08)	99.50 (0.24)	1.73 (0.88)	.9718
BET	95.69 (0.91)	97.62 (2.19)	98.22 (0.70)	4.72 (3.01)	.9224
BET + EC	97.48 (0.95)	97.17 (2.38)	99.39 (0.40)	2.94 (1.96)	.9478
MV	97.76 (0.88)	98.71 (0.64)	99.14 (0.49)	2.22 (2.17)	.9588
MV + EC	98.35 (0.59)	98.85 (0.56)	99.42 (0.32)	1.42 (1.33)	.9807
optiBET	95.87 (1.24)	97.97 (1.48)	98.28 (0.89)	5.38 (3.17)	.8037
optiBET + EC	97.80 (0.64)	98.08 (1.19)	99.33 (0.38)	1.92 (1.60)	.9562
Pincram	97.76 (0.65)	96.41 (1.18)	99.78 (0.10)	2.81 (1.26)	.9871
Pincram + EC	98.45 (0.45)	98.29 (0.76)	99.62 (0.13)	0.80 (0.57)	.9932
Proposed	98.12 (0.49)	98.28 (0.53)	99.45 (0.24)	1.08 (0.84)	.9897
Proposed + EC	98.57 (0.34)	98.60 (0.52)	99.61 (0.14)	0.74 (0.52)	.9938
ROBEX	94.84 (1.06)	98.97 (0.89)	97.33 (0.61)	8.33 (2.58)	.9467
ROBEX + EC	97.74 (0.70)	98.26 (1.10)	99.24 (0.29)	1.60 (1.30)	.9759
SBA	97.63 (0.98)	98.67 (0.67)	99.08 (0.56)	2.43 (2.45)	.9471
SBA + EC	98.33 (0.62)	98.84 (0.57)	99.41 (0.34)	1.48 (1.43)	.9781
STAPLE	97.48 (1.14)	99.19 (0.47)	98.84 (0.61)	3.47 (2.72)	.9476
STAPLE + EC	98.32 (0.66)	98.93 (0.54)	99.38 (0.36)	1.54 (1.54)	.9777

For the Dice coefficient, sensitivity (Sens.), specificity (Spec.), and normalized volume difference (NVD), each table cell reports the mean and SD (in parentheses). The two top‐performing methods for each performance measure are emboldened. Note that both “Proposed” and “Proposed + EC” refer to the accelerated version of the method described in Section 3.1.

Figure 4.

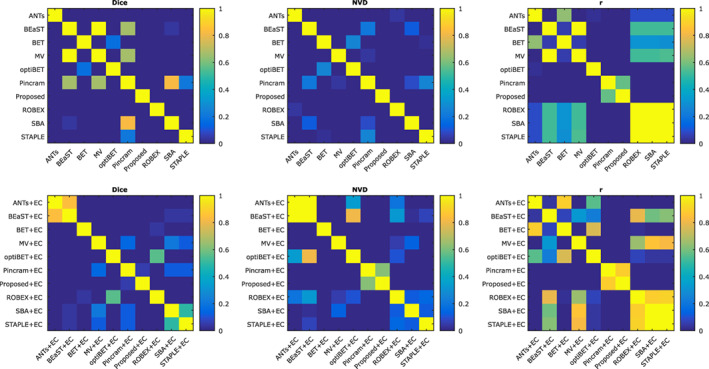
Significance of differences between methods, both before and after error correction, in the inter‐dataset segmentation scenario. FDR corrected p values (Wilcoxon signed‐rank tests) are reported [Color figure can be viewed at wileyonlinelibrary.com]

As shown in Figure 3 and Table 2, error correction increased the performance of all methods with respect to mean Dice coefficient, mean NVD, and volumetric correlation with the reference labels. We therefore restrict our discussion to comparing the error‐corrected methods (“+ EC”). While Proposed + EC performed better than Pincram + EC in terms of mean Dice coefficient, mean NVD, and volumetric correlation, the differences were not statistically significant (p > .05). However, while both Proposed + EC and Pincram + EC produced segmentations with similar specificity (p = .18), Proposed + EC produced segmentations with higher sensitivity (p < 1 × 10⁻⁷), better avoiding false negatives. Compared to all other methods, Proposed + EC also produced generally tighter distributions marked by lower SDs.

Among the remaining methods, MV + EC performed second best, followed by BEaST + EC. Compared to Proposed + EC, MV + EC produced more drastic outliers (Figure 3) and a lower mean Dice coefficient (98.35%, p < 1 × 10⁻⁹ compared to Proposed + EC), corresponding to a 14.2% difference in the mean number of misclassified voxels. BEaST + EC produced segmentations with lower overlap (mean Dice coefficient = 98.26%, p < 1 × 10⁻⁹ compared to Proposed + EC), corresponding to a 20.6% difference in the mean number of misclassified voxels (or an average of roughly 12,000 more misclassified voxels per segmentation) compared to Proposed + EC, in addition to comparatively poor volumetric agreement with reference labels (NVD = 1.73%, r = .9718). Among the non‐multi‐atlas segmentation methods (ANTs, BET, optiBET, and ROBEX), ANTs + EC performed best in terms of mean Dice coefficient, but performed relatively poorly on volumetric performance measures. ROBEX + EC achieved the best volumetric performance measures when compared to the other non‐multi‐atlas segmentation methods. Following error correction, the three Brain MAPS methods were the most sensitive methods, best avoiding false negative errors, whereas Pincram and the proposed method were the most specific, best avoiding false positive errors.

To visualize the spatial distribution of errors, mean error images both before and after error correction are shown in Figure 5. ANTs, BET, optiBET, and ROBEX show general under‐segmentation, whereas BET and optiBET show specific over‐segmentation in the frontal lobe. BET showed several failures which manifested as large segments of additional tissue inferior to the brain. While the error patterns of the multi‐atlas segmentation methods are considerably more uniform and show less overall segmentation error, Pincram better avoided false positive errors, at the cost of increased false negative errors. In contrast, BEaST and Brain MAPS with each of the three label fusion techniques had a slight tendency toward under‐segmentation, particularly along the boundary of the cortex. In individual cases, this usually manifested as the erroneous inclusion of dura in the segmentations, which can pose problems for subsequent surface‐based processing tasks. Compared to the other multi‐atlas segmentation methods, the proposed method produced segmentations with a more balanced ratio of false negatives to false positives. As shown in Figure 5, error correction successfully improved the performance of each method by reducing overall error and by better balancing the ratio of false negatives to false positives (see in particular the non‐multi‐atlas segmentation methods ANTs, BET, optiBET, and ROBEX).

Figure 5.

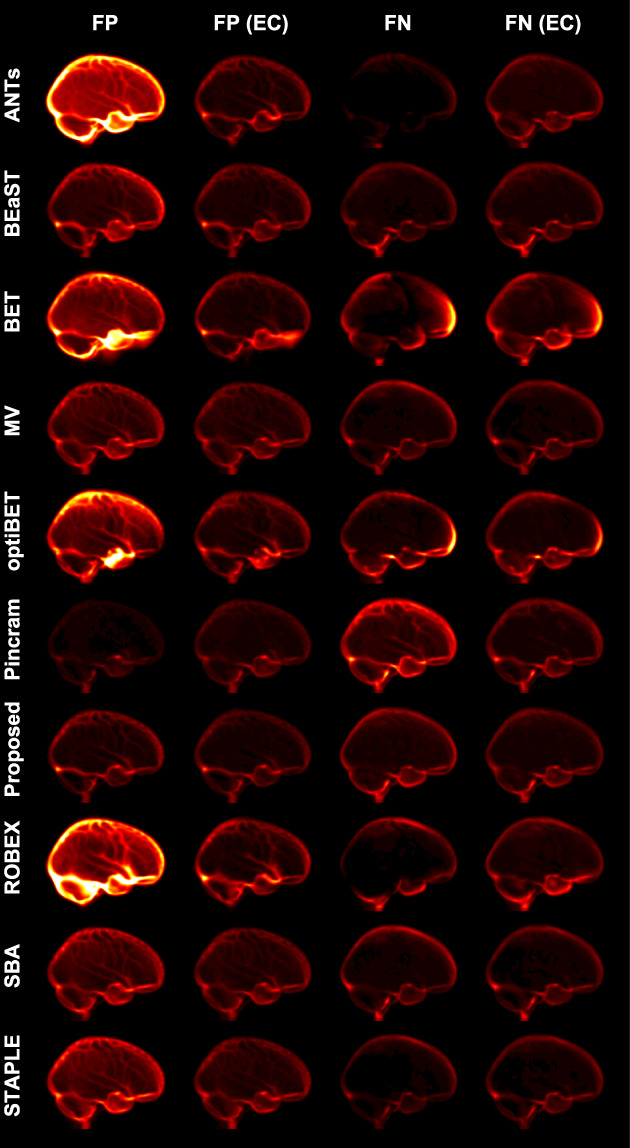
Mean false‐negative (FN) and mean false‐positive (FP) images for each method in the inter‐dataset segmentation scenario, both before and after error correction (EC). All error images are displayed with the same color scale [Color figure can be viewed at wileyonlinelibrary.com]

3.2.2. Intra‐dataset segmentation scenario

Distributions of Dice coefficients and NVD values for each segmentation method, both before and after error correction, are shown in Figure 6. Table 3 summarizes the performance of each method, over all 90 images from the 5 datasets, with respect to all 5 performance measures outlined in Section 2.8. Wilcoxon signed‐rank tests were used to test for significant differences between all pairs of methods both before and after applying error correction. Fisher r‐to‐z transforms were used to similarly test for significant differences with respect to volumetric correlation. Detailed results of the significance tests between methods are shown in Figure 7. All p values were corrected for multiple comparisons using false discovery rate (FDR).

Figure 6.

Distributions of Dice coefficients and normalized volume difference (NVD) values for each method, both before and after error correction (EC), in the intra‐dataset segmentation scenario. Centre lines: median, boxes: interquartile range, whiskers: truncated range, “+”: outliers [Color figure can be viewed at wileyonlinelibrary.com]

Table 3.

Summary of 5 performance measures for each method in the intra‐dataset segmentation scenario, both before and after error correction (EC)

	Dice	Sens.	Spec.	NVD	r
ANTs	95.30 (1.12)	99.58 (0.85)	97.43 (0.70)	8.74 (2.97)	.9064
ANTs + EC	98.61 (0.38)	98.90 (0.65)	99.55 (0.18)	1.04 (0.89)	.9889
BEaST	98.84 (0.30)	99.25 (0.47)	99.57 (0.16)	1.04 (0.70)	.9942
BEaST + EC	99.04 (0.24)	99.14 (0.43)	99.71 (0.12)	0.64 (0.50)	.9956
BET	95.69 (0.91)	97.62 (2.19)	98.22 (0.70)	4.72 (3.01)	.9224
BET + EC	98.00 (0.77)	97.67 (1.60)	99.55 (0.16)	1.35 (1.61)	.9772
MV	98.56 (0.36)	99.00 (0.52)	99.48 (0.21)	1.12 (0.83)	.9905
MV + EC	98.97 (0.23)	99.14 (0.46)	99.67 (0.15)	0.73 (0.57)	.9940
optiBET	95.87 (1.24)	97.97 (1.48)	98.28 (0.89)	5.38 (3.17)	.8037
optiBET + EC	98.22 (0.45)	98.27 (0.95)	99.51 (0.17)	1.06 (1.01)	.9835
Pincram	98.36 (0.45)	97.24 (0.95)	99.87 (0.07)	2.30 (1.11)	.9917
Pincram + EC	98.96 (0.23)	98.92 (0.50)	99.73 (0.10)	0.57 (0.54)	.9953
Proposed	98.57 (0.32)	98.75 (0.39)	99.57 (0.12)	0.59 (0.49)	.9972
Proposed + EC	99.02 (0.20)	99.09 (0.35)	99.72 (0.08)	0.45 (0.36)	.9976
ROBEX	94.84 (1.06)	98.97 (0.89)	97.33 (0.61)	8.33 (2.58)	.9467
ROBEX + EC	98.09 (0.49)	98.56 (0.89)	99.35 (0.19)	1.31 (1.03)	.9856
SBA	98.50 (0.40)	98.81 (0.51)	99.51 (0.21)	0.97 (0.86)	.9899
SBA + EC	98.98 (0.23)	99.04 (0.43)	99.70 (0.14)	0.62 (0.55)	.9945
STAPLE	98.45 (0.44)	99.28 (0.35)	99.35 (0.24)	1.71 (1.10)	.9899
STAPLE + EC	98.96 (0.23)	99.04 (0.44)	99.70 (0.14)	0.67 (0.53)	.9942

For the Dice coefficient, sensitivity (Sens.), specificity (Spec.), and normalized volume difference (NVD), each table cell reports the mean and SD (in parentheses). The two top‐performing methods for each performance measure are emboldened. Note that both “Proposed” and “Proposed + EC” refer to the accelerated version of the method described in Section 3.1.

Figure 7.

Significance of differences between methods, both before and after error correction, in the intra‐dataset segmentation scenario. FDR corrected p values (Wilcoxon signed‐rank tests) are reported [Color figure can be viewed at wileyonlinelibrary.com]

After applying error correction to each method, all multi‐atlas segmentation methods produced very good overlap (mean Dice coefficient ≥ 98.96%) and volumetric agreement (mean NVD ≤ 0.67%, r ≥ .9942) with the reference labels. BEaST + EC performed best in terms of overlap (mean Dice coefficient = 99.04%), presenting a very small but nonetheless statistically significant improvement (p < 1 × 10⁻³) compared to Proposed + EC (mean Dice coefficient = 99.02%), which performed second best. In terms of mean NVD, Proposed + EC performed best (mean NVD = 0.45%), a statistically significant improvement (p = .03) over the second best method, Pincram + EC (mean NVD = 0.57%). With respect to volumetric correlation, Proposed + EC again perform best (r = .9976), but was not found to be statistically significantly different (p = .07) from BEaST + EC (r = .9956), the second best method. Among the non‐multi‐atlas segmentation methods, ANTs + EC performed best in terms of mean Dice coefficient, mean NVD, and volumetric correlation.

To visualize the spatial distribution of errors in the intra‐dataset segmentation scenario, mean error images both before and after error correction are shown in Figure 8. The error patterns in the intra‐dataset segmentation scenario are very similar to those in the inter‐dataset segmentation scenario, although the magnitude of error has decreased for the multi‐atlas segmentation methods both before and after error correction, and for the non‐multi‐atlas segmentation methods following error correction due to the availability of dataset‐specific atlases for training the corrective classifiers.

Figure 8.

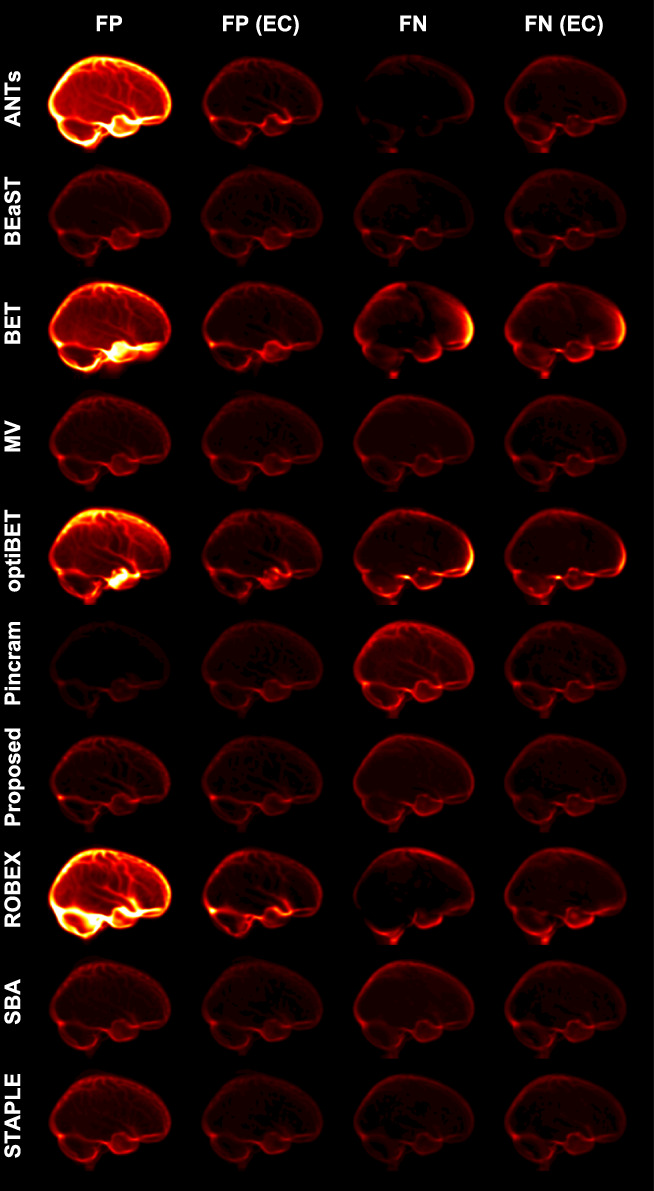
Mean false‐negative (FN) and mean false‐positive (FP) images for each method in the intra‐dataset segmentation scenario, both before and after error correction (EC). All error images are displayed with the same color scale [Color figure can be viewed at wileyonlinelibrary.com]

3.3. Processing time

Table 4 summarizes the mean and SD of the time required to process the same three randomly selected subjects (applied to inter‐dataset segmentation) for each method and processing step. All experiments were performed on the same workstation equipped with two Dual Intel Xeon E5‐2680 v2 (10‐core, 2.80 GHz) processors. We report processing times for the full multi‐resolution version of the proposed method as well as the accelerated method used in our comparison experiments. Of the overall top‐performing methods, BEaST was the most efficient, followed by the proposed method. Brain MAPS (the choice of label fusion technique, that is, MV, SBA, or STAPLE, had a negligible impact on processing time relative to the time required for registration) and Pincram were much slower than both the patch‐based methods, despite both taking advantage of multiple CPU cores.

Table 4.

Mean and SD (in parentheses) processing time, in min, required for various methods and processing steps used in the experiments carried out in this study

	Processing time (min)
Pre‐processing (Section 2.2)	2.92 (0.25)
Error correction	4.07 (0.40)
Error correction (accelerated)	0.41 (0.01)
ANTs	6.13 (0.29)
BEaST	1.11 (0.02)
BET	0.10 (0.01)
Brain MAPS	16.94 (1.05)
optiBET	19.33 (2.08)
Pincram	24.12 (0.05)
Proposed (full‐resolution)	21.77 (1.44)
Proposed (accelerated)	1.48 (0.06)
ROBEX	2.66 (0.10)

Error correction required approximately 4 min per subject, however it can be accelerated considerably by restricting the region of interest in which it is applied. For example, when restricting the region of interest to a narrow boundary (obtained by subtracting the erosion from the dilation of the initial label estimate, using a square structuring element with side length 5 mm) around the initial label estimate, error correction can be performed in less than 30 s. However, we opted against the accelerated variant in favor of a fairer comparison of methods, as the worse performing methods tended to make more drastic errors which were typically not contained in a narrow boundary region of interest. For example, in the inter‐dataset comparisons, while an average of 96.6% of the errors made by the proposed method occurred within the estimated narrow boundaries, this number is reduced to only 85.0% when using BET, which tended to incorrectly include large segments of nonbrain tissue inferior to the cortex (Figures 5 and 8). Combined with the accelerated boundary‐confined error correction described above, the proposed method can run in less than 2 min, or roughly an order of magnitude faster than the other top‐performing methods in the inter‐dataset comparisons (Pincram and MV).

3.4. Independent validation

We additionally validated the proposed method using a set of 12 publicly available labeled images available from Souza et al. (2017). The brain masks were manually generated from scratch, and the dataset consists of two images (one male and one female) from each of three different vendors (GE, Philips, and Siemens) acquired at two different field strengths (1.5 and 3 T). As done in Souza et al. we performed a 2‐fold cross‐validation using, in each fold of 6 images, a single sample from each vendor/field strength combination. Also for a fair comparison, while the preprocessing routine described in Section 2.2 is required before applying the proposed method, we calculated the performance measures in native space using segmentations obtained by applying the inverse of the affine transformation estimated during the preprocessing routine.

The performance of the proposed method, both before and after applying error correction, is shown in Table 5. We also include in Table 5 the results of several other methods on the same dataset as reported by Souza et al. The proposed method, both before and after applying error correction, performed best in terms of mean Dice coefficient. In addition, the proposed method was able to segment each image in roughly 40 s (the processing time was less than as reported in Table 4 because fewer atlases were available), and also produced tighter distributions marked by lower SDs. We note that the next two top‐performing methods (STAPLE and “Silver standard”) are both consensus methods which require the output of each of the other brain extraction methods listed in Table 5 (excluding the proposed method), and therefore require long processing times. Specifically, the “Silver standard” method combines the output of the different segmentation methods into a consensus solution using a machine learning classifier, whereas the STAPLE method forms a consensus solution using an expectation–maximization algorithm detailed in Warfield et al. (2004).

Table 5.

Validation of the proposed method on a secondary dataset (Souza et al., 2017)

	Dice	Sensitivity	Specificity
ANTs	95.93 (0.87)	94.51 (1.58)	99.71 (0.11)
BEaST	95.77 (1.23)	93.84 (2.57)	99.76 (0.13)
BET	95.22 (0.94)	98.26 (1.61)	99.13 (0.23)
BSE	90.49 (7.03)	91.44 (5.32)	98.65 (2.27)
HWA	91.66 (1.11)	99.93 (0.12)	97.83 (0.82)
MBWSS	95.57 (1.46)	92.78 (2.67)	99.85 (0.04)
optiBET	95.43 (0.71)	96.13 (0.95)	99.36 (0.31)
Proposed	97.35 (0.44)	97.72 (0.81)	99.64 (0.16)
Proposed + EC	97.58 (0.38)	98.11 (0.80)	99.65 (0.14)
ROBEX	95.61 (0.72)	98.42 (0.70)	99.13 (0.28)
STAPLE	96.80 (0.74)	98.98 (0.60)	99.38 (0.22)
Silver standard	97.14 (0.51)	96.83 (0.68)	99.71 (0.11)

The performances of other methods as reported in the original study are shown. The two top‐performing methods for each performance measure are emboldened. Note that both “Proposed” and “Proposed + EC” refer to the accelerated version of the method described in Section 3.1.

4. DISCUSSION

The quality of MR images segmented, the segmentation protocol itself, and the reliability of manual labelings can all affect reported segmentation accuracy (Collins & Pruessner, 2010), making it difficult to compare the results obtained in this study to the results obtained in other studies. One strength of the present study is that a wide variety of brain extraction methods were compared in the same experimental settings using the same reference labels, permitting a meaningful comparison between methods. These experiments are among the most extensive in the current literature, involving a comparison of 10 methods both with and without error correction, and required a total of 5,760 brain extractions. A possible limitation of this study is that the default parameters were used for the 9 additional methods under comparison, possibly biasing the results. For the proposed method, we chose parameters similar to those used by default in BEaST, which also may not be optimized (particularly for inter‐dataset segmentation scenarios). Each of the methods under comparison (with the exception of ROBEX) contain a number of configurable parameters which likely could have been fine‐tuned to obtain better results. Therefore, our results do not necessarily reflect the best possible performance of each method. However, errors due to suboptimal default parameters were, to an extent, remedied by applying error correction to each method. Indeed, one of the development goals for the error correction method was to adapt algorithms, without explicit modification of the algorithm itself, to improve performance on segmentation tasks when applied to data different from that used to train or optimize the algorithm (Wang et al., 2011).

This study is the first large‐scale evaluation of error correction when applied in a challenging inter‐dataset segmentation scenario (i.e., in which no dataset‐specific atlases are used). Our results indicate that the use of error correction is indeed beneficial and even crucial for good performance in this challenging case: error correction improved the performance of each brain extraction method under consideration in terms of mean Dice coefficient, mean normalized volume difference, and volumetric correlation. In both the inter‐ and intra‐dataset segmentation scenarios, ANTs, BET, optiBET, and ROBEX benefited most from error correction, whereas the multi‐atlas segmentation methods benefited less. This is expected because error correction performs best when the differences between the output of a given algorithm and the reference labels are systematic and therefore learnable by the corrective classifier. While the multi‐atlas segmentation methods attempt to propagate consistently defined labels between images, BET and ROBEX instead are driven by various heuristics without explicitly referencing a specific anatomical definition, whereas optiBET and ANTs propagate labels from a pre‐defined template to the target image. In other words, the segmentations produced by the multi‐atlas segmentation methods can be expected to match the definition of the brain mask used in this study, while this is not necessarily the case for latter methods.

We demonstrated in Section 3.1 that the runtime performance of the proposed method can be substantially improved, without any degradation in performance, by combining error correction with coarse segmentations produced by lower resolution patch‐based label fusion. Consequently, our accelerated proposed method requires only about 1.5 min to segment an image, or roughly an order of magnitude less compared to the other top‐performing methods (Pincram and Brain MAPS with MV label fusion) in challenging inter‐dataset applications. We note that it would be trivial to also improve the runtime performance of BEaST in the same way, but this would be unnecessary since BEaST is already very efficient, requiring only about 1 min to segment an image on our workstation (Table 4). It may also be possible to accelerate methods based on nonlinear registration in a similar way (e.g., using a sparser distribution of control points for nonlinear registration), but both Brain MAPS and Pincram additionally require the estimation of a rigid and/or affine transformation between each selected atlas and the target image, which would remain a computational bottleneck.

Like the method presented in this study, Pincram was developed with robustness to the choice of atlases as a primary development goal. Indeed, following error correction, both Pincram and the proposed method were the top performers in the inter‐dataset segmentation scenario. In part, the robustness of Pincram is due to the choice of normalized mutual information (NMI) as the similarity measure which drives image registration. NMI has been shown to robust to differences in contrast and overall brightness between images (Pluim, Maintz, & Viergever, 2003), and is therefore a similarity measure especially suitable for challenging inter‐dataset segmentation scenarios. On the other hand, the proposed method showed increased robustness in more challenging scenarios due to a more appropriate patch‐based label fusion which benefits from sparse representation, instance‐wise feature normalization, and multi‐point label estimation. However, we note that the images used in this study were acquired using either MP‐RAGE or spoiled gradient sequences, which produce images with somewhat similar contrasts. It would therefore be useful, in future work, to assess the performance of the proposed method using images from a wider variety of acquisition sequences, such as conventional or fast spin echo sequences. We suspect that in cases where the atlases and target images differ more drastically, the proposed method may still benefit further from improvements directed at the patch preselection method (since the ss index used in this study is partially sensitive to both brightness and contrast). However, these changes were not necessary for achieving top performance in our comparative experiments, and may add to the processing time of our method.

In terms of overlap with the reference labels, the differences between top‐performing methods were small (<1% in terms of mean Dice coefficient) following error correction. This is expected because residual errors were found predominantly along the boundary of the cortex (Figures 5 and 8), which accounts for only a small fraction of the total brain volume. We emphasize that therefore even small differences in mean Dice coefficient can be significant. For example, in the inter‐dataset comparisons, and following the application of error correction to each method, the difference between the proposed method (mean Dice coefficient = 98.57%) and BEaST (mean Dice coefficient = 98.26%) corresponded to a 20.6% reduction in the mean number of misclassified voxels (or roughly 12,000 fewer misclassified voxels per brain), further translating into more than a twofold reduction in normalized volume difference.

Given the combination of a very low processing time (roughly 1.5 min per subject using 20 preselected atlases) and the best overall performance in both the inter‐ and intra‐dataset segmentation comparisons, the proposed method is a good choice for a generic brain extraction algorithm. Among non‐multi‐atlas segmentation methods, BET and ROBEX demonstrated good runtime performance, whereas optiBET and ANTs were slower but performed slightly better in terms of mean overlap. We note, however, that each of these latter methods performed worse compared to the multi‐atlas segmentation methods. Nonetheless, these methods, particularly when combined with error correction, may still be sufficient for subsequent processing tasks that do not require highly accurate segmentations (e.g., bias correction or image registration).

By providing a new method and thorough comparisons of commonly used brain extraction methods, our contributions should help provide the means to guide users toward robust and accurate processing in the absence of dataset‐specific atlases, translating into substantial practical advantages. The proposed method will be made freely available online (http://nist.mni.mcgill.ca/) including the atlases (pending permission to re‐distribute the data) and a pre‐trained corrective classifier.

Novosad P, Collins DL, Alzheimer's Disease Neuroimaging Initiative. An efficient and accurate method for robust inter‐dataset brain extraction and comparisons with 9 other methods. Hum Brain Mapp. 2018;39:4241–4257. 10.1002/hbm.24243