Global motion detection and censoring in high‐density diffuse optical tomography

Abstract

Motion‐induced artifacts can significantly corrupt optical neuroimaging, as in most neuroimaging modalities. For high‐density diffuse optical tomography (HD‐DOT) with hundreds to thousands of source‐detector pair measurements, motion detection methods are underdeveloped relative to both functional magnetic resonance imaging (fMRI) and standard functional near‐infrared spectroscopy (fNIRS). This limitation restricts the application of HD‐DOT in many challenging imaging situations and subject populations (e.g., bedside monitoring and children). Here, we evaluated a new motion detection method for multi‐channel optical imaging systems that leverages spatial patterns across measurement channels. Specifically, we introduced a global variance of temporal derivatives (GVTD) metric as a motion detection index. We showed that GVTD strongly correlates with external measures of motion and has high sensitivity and specificity to instructed motion—with an area under the receiver operator characteristic curve of 0.88, calculated based on five different types of instructed motion. Additionally, we showed that applying GVTD‐based motion censoring on both hearing words task and resting state HD‐DOT data with natural head motion results in an improved spatial similarity to fMRI mapping. We then compared the GVTD similarity scores with several commonly used motion correction methods described in the fNIRS literature, including correlation‐based signal improvement (CBSI), temporal derivative distribution repair (TDDR), wavelet filtering, and targeted principal component analysis (tPCA). We find that GVTD motion censoring on HD‐DOT data outperforms other methods and results in spatial maps more similar to those of matched fMRI data.

Motion‐induced artifacts can significantly corrupt optical neuroimaging, as in most neuroimaging modalities. For high‐density diffuse optical tomography (HD‐DOT) with hundreds to thousands of source‐detector pair measurements, motion detection methods are underdeveloped relative to both functional magnetic resonance imaging (fMRI) and standard functional near‐infrared spectroscopy (fNIRS). Here, we evaluated a new motion detection method for multi‐channel optical imaging systems that leverages spatial patterns across channels. Specifically, we introduced a global variance of temporal derivatives (GVTD) metric as a motion detection index and showed that it strongly correlates with external measures of motion.

1. INTRODUCTION

High‐density diffuse optical tomography (HD‐DOT) has tremendous potential to be a surrogate for functional magnetic resonance imaging (fMRI) (Eggebrecht et al., 2014; Hassanpour, Eggebrecht, Culver, & Peelle, 2015; Ferradal et al., 2016; White et al., 2009; Sherafati et al., 2018; Hassanpour, 2015; Burke et al., 2019; Sherafati et al., 2020). However, methods for dealing with detection and suppression of motion artifacts in HD‐DOT data are relatively underdeveloped, which limits its application to many important clinical populations. While fMRI has become a gold standard for cognitive neuroimaging, it is contraindicated in subjects with metal implants and cannot be used in many clinical settings, and studies seeking more naturalistic imaging environments. In contrast, functional near‐infrared spectroscopy (fNIRS)‐based methods are portable, suitable for naturalistic imaging, and not contraindicated in subjects with electronic or metal implants (Dashtestani et al., 2018; Dashtestani et al., 2019; Farzam et al., 2017; Fishell et al., 2016; Fishell et al., 2020; Fishell, Burns‐Yocum, Bergonzi, Eggebrecht, & Culver, 2019; Franceschini & Boas, 2004; Khaksari et al., 2019; Liao et al., 2012; Lloyd‐Fox, Blasi, & Elwell, 2010; Morishita et al., 2016; Saliba, Bortfeld, Levitin, & Oghalai, 2016; Salsabilian et al., 2019; Salsabilian et al., 2020). Sparse fNIRS imaging arrays yield poor resolution and low image quality. HD‐DOT provides improved image resolution and depth profiling, particularly when used with anatomical head models (Eggebrecht et al., 2012; Ferradal et al., 2014; Wu, Eggebrecht, Ferradal, Culver, & Dehghani, 2014). However, as in both fMRI and fNIRS, detection, classification, and removal of motion‐induced artifacts remains a challenge for HD‐DOT.

Multiple fMRI studies have documented the spurious effects of motion artifacts in blood oxygen level‐dependent (BOLD) fMRI despite the use of common motion suppression methods (Fair et al., 2013; Power, Barnes, Snyder, Schlaggar, & Petersen, 2012; Power, Plitt, Kundu, Bandettini, & Martin, 2017; Satterthwaite et al., 2012; Siegel et al., 2017; Van Dijk, Sabuncu, & Buckner, 2012). Motion‐induced changes in T2*‐weighed fMRI signals are shared across brain voxels, hence generate spatially structured artifacts. Such artifacts alter functional connectivity by decreasing long‐distance correlations and increasing short‐distance correlations (Power et al., 2012; Power et al., 2017; Satterthwaite et al., 2012; Van Dijk et al., 2012). However, two simple data quality indices, frame‐wise displacement (FD) and root mean squared (RMS) signal change over sequential frames (DVARS), are commonly used in fMRI data processing pipelines to identify and exclude data segments (motion censoring or scrubbing) from behaviorally relevant fMRI measures (Power et al., 2012; Satterthwaite et al., 2013; Yan et al., 2013).

In HD‐DOT, similar to fMRI, the effects of head motion are global across the field of view (FOV) and impact a majority of measurements or voxels. In fMRI, head movements shift the position of the brain in space and modulate the BOLD signal (Friston et al., 1995; Friston, Williams, Howard, Frackowiak, & Turner, 1996). In HD‐DOT, head motion induces a torque on the fibers in the optical imaging array that, in turn, modulates the location, angle (Figure 1b center), or both location and angle (Figure 1b right) of optode‐scalp coupling. Thus, motion induces artifacts in the optical signals that can appear as brief transient spikes or baseline shifts. These artifacts propagate from measurement space to voxel space in the image reconstruction process and corrupt the neuroimaging results.

FIGURE 1.

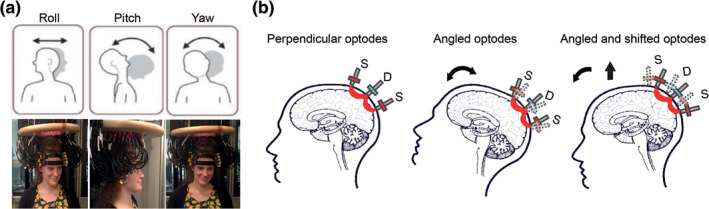
Effects of head motion on HD‐DOT optode coupling. (a) Research participant wearing an HD‐DOT imaging cap. Head rotation may occur about three axes (roll, pitch, and yaw). (b) Schematic illustration of how head motion can affect optode couplings. The far‐left figure shows the ideal perpendicular angle between the source‐detector optodes and the head. The middle figure shows the angled optodes as a result of nodding up and back to the center. The far‐right figure shows the angled and shifted optodes as a result of nodding up and body movement

Numerous strategies for managing motion‐induced artifact have been described in the fNIRS literature. However, a consensus on how best to correct for motion artifacts has not emerged (Brigadoi et al., 2014; Cooper et al., 2012; Di Lorenzo et al., 2019). Extant motion correction methods in fNIRS mainly involve two steps: first, motion detection, and second, signal correction (Aghayee et al., 2017; Chiarelli, Maclin, Fabiani, & Gratton, 2015; Cui, Bray, & Reiss, 2010; Fishburn, Ludlum, Vaidya, & Medvedev, 2019; Jahani, Setarehdan, Boas, & Yücel, 2018; Molavi & Dumont, 2012; Scholkmann, Spichtig, Muehlemann, & Wolf, 2010). The fNIRS literature has largely focused on correcting motion artifacts on individual source‐detector pair measurements and much less attention has been placed on multi‐channel or full‐array assessments. Moreover, most fNIRS studies have not assessed the efficacy of the denoising methods through comparison against fMRI.

We address these limitations by conducting a comprehensive evaluation of motion artifact removal methods for HD‐DOT data by including independent measures of motion (accelerometry) and comparisons against gold standard matched fMRI data sets. We introduce a novel index of motion, the global variance of the temporal derivatives (GVTD) for multi‐channel optical devices, inspired by the DVARS in fMRI (Smyser et al., 2010). For each time point, GVTD, similar to DVARS, is computed as the RMS of the temporal derivatives across time‐courses. In fMRI, DVARS is calculated based on the voxels time‐courses, and in optical imaging, it can be calculated based on either measurements or voxels time‐courses. In HD‐DOT, the equivalent of the framewise displacement (FD) cannot be defined, since there is no access to the absolute x, y, z coordinates of the image, and thus, we use an external motion sensor as the direct measurement for translational and rotational movements.

We first evaluate the efficacy of GVTD by calculating its correlation with directly transduced measures of motion using an accelerometer. We then optimize the parameters of GVTD and compare its application to voxel time‐courses versus measurement time‐courses using an artifact‐to‐background ratio (ABR) as a metric of quality. Finally, we investigate the efficiency of the GVTD‐based motion detection and censoring on HD‐DOT task and resting state images by comparisons with fMRI gold standards and to other fNIRS motion removal methods.

2. METHODS

2.1. Novel motion detection methods

2.1.1. The global variance of the temporal derivatives

Global variance of the temporal derivatives (GVTD) indexes global instantaneous change in the optical time‐courses. For each time point, GVTD is computed as the RMS of the temporal derivatives across a set of measurements or voxels (Equation (1)). The simple analytic formula for GVTD is

$$\mathit{g}=\left[\begin{array}{c}{g}_1\\ ⋮\\ g_M\end{array}\right],g_i=\sqrt{\frac{1}{N}\sum _{j=1}^N{\left(y_{\mathit{ji}}-y_{\mathit{ji}-1}\right)}^2},g_i\in {ℝ}_{>0},$$ (1)

where g is the GVTD vector, y_ji ε ℝ is either the optical density change or molar HbO₂ or HbR change at spatial coordinate j. i indexes the time points, N is the number of coordinates, and M is the number of time points.

2.1.2. Independent measurement of head motion

A motion sensor (3‐space™ USB/RS232; Yost Labs, Portsmouth, Ohio) was attached to the top strap of the HD‐DOT cap in a subset of the data acquired with instructed motion (more details in §2.6). This sensor includes a triaxial inertial measurement unit (IMU), which uses a gyroscope, an accelerometer, and a compass sensor (Figure S1). Onboard electronics compute and report in real‐time, the quaternion‐based orientation relative to an absolute reference. We synchronized the outputs of the motion sensor with our HD‐DOT data acquisition system using audio pulses at the start and end of data streams. The motion sensor data were down‐sampled from 200 to 1 Hz to match the final sampling rate of the HD‐DOT data. Then, the motion sensor and HD‐DOT signals were aligned by delaying the earlier signal based on the cross‐correlation delay time with maximum correlation value.

2.1.3. Angular rotation

The angular rotation (Φ) time‐course was defined as the norm of the temporal derivatives of the head orientation in terms of Euler angles (α roll, β pitch, and γ yaw), measured by the motion sensor. This index was defined in a manner similar to that of GVTD to facilitate comparisons between GVTD and motion sensor outputs (Equation (2)).

$$\mathbf{\Phi }=\left[\begin{array}{c}{\varphi }_1\\ ⋮\\ {\varphi }_M\end{array}\right],{\varphi }_i=\sqrt{{\left({\alpha }_i-{\alpha }_{i-1}\right)}^2+{\left({\beta }_i-{\beta }_{i-1}\right)}^2+{\left({\gamma }_i-{\gamma }_{i-1}\right)}^2},{\varphi }_i\in {ℝ}_{>0}$$ (2)

In this notation, i indexes the time points, and M is the number of time points.

2.1.4. Artifact‐to‐background ratio

To quantify the magnitude of the motion artifacts, we defined the artifact‐to‐background (ABR [ρ]), where ABR is the mean GVTD of all the time points above the noise threshold (defined in §3.3), divided by the mean GVTD of all the time points below the noise threshold (Equation (3)).

$$\mathrm{\rho }=\left(n/m\right)\sum _i\left(g_i|g_i>g_{\mathit{\text{thresh}}}\right)/\sum _i\left(g_i|g_i<g_{\mathit{\text{thresh}}}\right)$$ (3)

In this formula, g_i is the GVTD value at time index i, g_thresh is the threshold value, n is the number of time points below the threshold, and m is the number of time points above the threshold.

2.2. Motion removal methods

2.2.1. Motion censoring using GVTD

Motion censoring (scrubbing) excludes the time points or data blocks exceeding the GVTD noise threshold from further analysis of resting state and task data (Sherafati et al., 2017; Sherafati et al., 2018). Details concerning the noise threshold criterion are explained in §3.3. This proposed HD‐DOT censoring strategy follows a similar practice that resulted in statistical improvements in resting state as well as task fMRI data (Birn, Cox, & Bandettini, 2004; Power et al., 2012; Siegel et al., 2014; Smyser et al., 2010).

2.2.2. Correlation‐based signal improvement

Correlation‐based signal improvement (CBSI) motion correction is based on the assumption that oxygenated and deoxygenated hemoglobin signals are negatively correlated under all circumstances. In the presence of motion artifacts, the correlation between these two signals becomes more positive. CBSI corrects the oxyhemoglobin concentrations by subtracting the scaled deoxyhemoglobin to match the variance of the oxygenated signal. This process removes the positive correlation content between the two signals, taking into account their different amplitudes. Then, the corrected deoxyhemoglobin is calculated by multiplying the corrected oxyhemoglobin by the inverse of the same scaling factor between the original signals (Cui et al., 2010). In this paper, we performed this motion correction method after spectroscopy on the down‐sampled 1 Hz data (Figure S2).

2.2.3. Targeted principal component analysis

Principal component analysis (PCA) projects an arbitrary set of signals onto orthogonal principal components. Then, the principal components with the least variance are excluded, and the signal is reconstructed from the remaining components. Targeted PCA (tPCA) applies PCA to temporal epochs of the data that are identified to contain motion artifacts. tPCA reduces the risk of eliminating the physiological content in the motion‐free epochs of the signal (Yucel et al., 2014a). Hence, this method is followed by a prior step of motion detection in the temporal domain. Conventionally, this motion detection is performed by setting a threshold on signal amplitudes or the windowed signal amplitude changes. In this paper, we used the HOMER2 functions hmrMotionArtifactByChannel to detect noisy time points, and hmrMotionCorrectPCA to perform PCA, and set the parameters of this algorithm in the similar range as in the original study (Yucel et al., 2014a); tMotion = 0.5, tMask = 2, STDEVthresh = 20, AMPthresh = 0.5, nSV = 0.97 (Tables S1 and S2, Figure S2).

2.2.4. Wavelet filtering

Wavelet‐based motion correction is based on discrete wavelet transformation of single‐channel measurements. This method assumes that the distribution of the wavelet coefficients of a motion‐free signal should follow a Gaussian distribution. Therefore, motion artifacts are detected based on the deviations from the Gaussian distribution. By setting an outlier detection threshold, the coefficients associated with motion artifacts are excluded, and the clean signal is reconstructed based on the remaining wavelet coefficients (Molavi & Dumont, 2012). We used the HOMER2 hmrMotionCorrectWavelet function, setting the interquartile parameter as 1.5, as suggested in the original paper (Molavi & Dumont, 2012) (Tables S1 and S2, Figure S2).

2.2.5. Kurtosis‐based wavelet filtering

The kurtosis‐based wavelet filtering (kbWF) method optimizes the use of the wavelet filtering motion correction by setting the threshold based on the kurtosis of the coefficient distributions (Chiarelli et al., 2015). The hmrMotionCorrectKurtosisWavelet function was used with the kurtosis threshold parameter set to 3.3, as recommended in the original paper (Chiarelli et al., 2015) (Tables S1 and S2, Figure S2).

2.2.6. Hybrid (spline + Savitzky Golay)

The spline and Savitzky–Golay hybrid method is a three‐step algorithm that aims to identify and correct different types of motion artifacts (Jahani et al., 2018). First, single‐channel measurements are passed through a Sobel filter to identify time points exceeding a threshold of 1.5 times the interquartile interval of the signal gradient. Second, this method performs a spline interpolation on those epochs containing motion to remove the baseline shifts and slow spikes. Steps 1 and 2 were introduced in a previous fNIRS motion removal method, commonly known as the motion artifact removal algorithm (MARA) (Scholkmann et al., 2010). After this step, the hybrid method then applies a Savitsky‐Golay smoothing filter to remove the remaining fast spikes. We used the HOMER2 hmrMotionCorrectSplineSG function defined in the original paper with its default parameters and setting p = .99 and FrameSize_sec = 1.5 (Jahani et al., 2018) (Tables S1 and S2, Figure S2).

2.2.7. Temporal derivative distribution repair

Temporal derivative distribution repair (TDDR) also is a three‐step algorithm that aims to automatically identify and correct motion artifacts at the single‐channel level. First, by computing the temporal derivative of the signal, TDDR initializes the vector of observation weights. Second, it iteratively estimates the robust observation weights by applying the resulting robust weights to the centered temporal derivative to produce the corrected derivative. Finally, it integrates the corrected temporal derivative to yield the corrected signal (Fishburn et al., 2019). We used the HOMER2 function hmrMotionCorrectTDDR proposed in the original paper with its default parameters (Fishburn et al., 2019) (Tables S1 and S2, Figure S2).

2.3. Data sets and their objective

Data set 1: For validation, we collected an fMRI data set in which adult subjects (n = 8) were scanned in both resting state and during a hearing words (HW) task. This data set served as ground truth. Data set 2: As a positive control, in this HD‐DOT data set, healthy adults (n = 12) performed instructed motion while performing the same HW task performed during fMRI. Data set 3: In this HD‐DOT data set, adult subjects (n = 13) performed the same HW task without instructed motion. Data set 4: In this HD‐DOT data set, healthy adults (n = 8) were scanned while awake in a task‐free (resting) state. Data set 5: In this HD‐DOT data set, healthy term infants (n = 11) were imaged in the resting state (awake or asleep). This is a previously published data set (Ferradal et al., 2016). Demographic information and the objective of using each data set are reported in Table 1

TABLE 1.

Demographic information

Data set	Number of subjects	Sex (f/m)	Age mean (STD)	Condition	Modality	Objective
1: Adults	8	6/2	62.37 y (6.3)	Rest and HW	fMRI	Gold standard
2: Adults	12	8/4	25.41 y (2.06)	HW	HD‐DOT	Instructed motion, motion sensor
3: Adults	13	10/3	42.92 y (19.75)	HW	HD‐DOT	Natural motion method comparison
4: Adults	8	5/3	30.25 y (11.18)	Rest	HD‐DOT	Natural motion method comparison, ABR test
5: Infants	11	6/5	1.1 d (0.4)	Rest	HD‐DOT	Validation for ABR test

Abbreviations: ABR, artifact‐to‐background ratio; d, day; HW, hearing words; y, year.

All aspects of these studies were approved by the Human Research Protection Office of the Washington University School of Medicine. All adult participants in the previous and new data sets were right‐handed, native English speakers, and reported no history of neurological or psychiatric disorders. Adults were recruited from the Washington University campus and the surrounding community (IRB 201101896, IRB 201609028). All full‐term infants were recruited from the Newborn Nursery at Barnes‐Jewish Hospital in St Louis, Missouri, within the first 48 hr of life (IRB 201101813). All subjects (or their guardians) gave informed consent and were compensated for their participation in accordance with institutional and national guidelines.

2.4. HD‐DOT systems, image reconstruction, and spectroscopy

All adult HD‐DOT data sets (Data sets 2, 3, and 4) were collected using a previously described continuous‐wave HD‐DOT system comprising 96 sources (LEDs, at both 750 and 850 nm) and 92 detectors (coupled to avalanche photodiodes, APDs) (Eggebrecht et al., 2014). Acquisition in infants was performed at the bedside using a previously reported portable continuous‐wave HD‐DOT system with an optode array consisting of 32 sources (LEDs, at both 750 and 850 nm) and 34 detectors (Ferradal et al., 2016). The setup time for both systems was approximately 5–15 min for combing the HD‐DOT optode array embedded in a cap design through the hair to ensure the maximum optode scalp coupling using a real‐time software for light level readouts. More detailed descriptions of the imaging systems and the setup process are given in the corresponding references. Light modeling was computed using the standard MNI atlas‐based absorption model; details can be found in (Ferradal et al., 2014). Volumetric movies of relative changes in absorption at 750 and 850 nm were reconstructed after inverting the sensitivity matrix using Tikhonov regularization and spatially variant regularization (Eggebrecht et al., 2014). Relative changes in hemoglobin concentration were obtained via a spectral decomposition of the absorption data, as previously described (Eggebrecht et al., 2014; Ferradal et al., 2016).

2.5. Functional MRI system and imaging

All Functional MRI (fMRI) data were collected on a research‐dedicated Siemens 3.0 T Magnetom Prisma system (Siemens Medical Solutions, Erlangen, Germany) with an iPAT compatible 20‐channel head coil. Blood Oxygenation Level Dependent (BOLD) sensitized fMRI data with TR = 1,230 ms, TE = 33 ms, voxel resolution = 2.4 mm³, FA = 63°, with a multiband factor of four for both resting state functional connectivity MRI (3 runs each 10 min) and HW task BOLD (1 run, 3.5 min) were acquired for all subjects in Data set 1.

2.6. Paradigms

Hearing words: Subjects were seated for HD‐DOT or supine for fMRI and instructed to fixate on a white crosshair against a gray background while listening to words. The HW task was administered as block design. Each trial consisted of 15 s of hearing words followed by 15 s of silence. Each run included multiple trials, n = 10 for Data set 2, and n = 6 for Data sets 1 and 3. The total number of acquired runs per session was 7 (Data set 2) or 1 (Data sets 1 and 3).

Instructed motion: The instructed motion was performed by subjects during the HW task (Data set 2), with 15% of the trials including instructed motion. Participants viewed a screen with a crosshair and were instructed to perform a specific motion type when the crosshair color changed. Movements were performed for about 2 s every 3–5 s over a 15s word presentation section. Subjects were monitored in real‐time using a digital camera to ensure that they were engaged in the assigned tasks. Specific motions included (a) head turn to the left and back to center (roll, Figure 1a left), (b) head nod up and back to center (pitch, Figure 1a center), (c) shifting body position, (d) taking deep breaths, and (e) raising eyebrows. Head twist (yaw, Figure 1a right) motion was avoided to prevent cap displacement.

Resting state: Resting state data in adults (Data sets 1 and 4) were collected over 10 min runs while subjects were seated for HD‐DOT or supine for fMRI and visually fixating on a white crosshair against a gray background. Subjects were asked to stay awake and still during data acquisition. The number of runs per session was 3 (Data set 1) or 1 (Data sets 4). Resting state HD‐DOT in infants was acquired at the bedside (Data set 5) within the first 24–48 hours of life during natural (un‐medicated) sleep or quiet rest (Ferradal et al., 2016).

2.7. HD‐DOT preprocessing

All HD‐DOT data were processed using the NeuroDOT toolbox following the flowchart in Figure S2 (Eggebrecht et al., 2014; Eggebrecht & Culver, 2019; Eggebrecht & Culver, n.d.). HD‐DOT light measurement data were converted to log‐ratio (using the temporal mean of a given source‐detector pair measurement as the relative baseline for that measurement). Noisy measurements were empirically defined as those with greater than 7.5% temporal standard deviation in the least noisy (lowest mean GVTD) 60 s of each run (Eggebrecht et al., 2012) and were excluded from further processing. Then the data were high‐pass filtered (0.02 Hz cutoff for task‐based data sets, 0.009 Hz for resting state data sets) to remove low‐frequency drift. To serve as an estimate of the global superficial signal, we computed the average of all remaining first nearest neighbor measurements (13 mm source‐detector pair separation in the adult system and 10 mm source‐detector pair separation in the infant system). This global signal estimate was regressed from all measurements (Gregg et al., 2010). After that, all adult task‐based data were low‐pass filtered to 0.5 Hz cutoff to remove the cardiac oscillations (Brigadoi et al., 2014; Cui et al., 2010; Fishell et al., 2019; Jahani et al., 2018). All resting state data were low‐pass filtered to 0.08 Hz to remove the cardiac oscillations and to narrow the signal to the spontaneous, low‐frequency fluctuations of the signal following the previous recommendations for functional connectivity analysis in both adults and infants (Eggebrecht et al., 2014; Ferradal et al., 2016; Biswal, Zerrin Yetkin, Haughton, & Hyde, 1995; Smyser, Snyder, & Neil, 2011). Task data provides two advantages over resting state. First, the task design can impart high‐amplitude and high‐frequency dynamics beyond what would normally be found in resting state. Second, the block averaging of the tasks provides an approach to lower the noise and physiological clutter in the data. While resting state uses the common infra‐slow band (0.009–0.08 Hz) of the vast majority of the functional connectivity MRI literature (Eggebrecht et al., 2014; Ferradal et al., 2016; Biswal et al., 1995; Smyser et al., 2011), the task pre‐processing uses a higher filter band (0.02 to 0.5 Hz) to avoid the 1/f noise (Brigadoi et al., 2014; Cui et al., 2010; Fishell et al., 2019; Jahani et al., 2018). Following this band‐pass filtering, the time‐courses were then down‐sampled from 10 to 1 Hz and then used for image reconstruction. The efficacy of GVTD was evaluated at four stages of the HD‐DOT processing pipeline, as indicated in Figure S2 (green boxes) on 10 Hz sampled data. All other motion correction methods except CBSI were also performed on the 10 Hz sampled optical density signals (immediately after the log‐ratio step) (Figure S2).

2.8. fMRI preprocessing

fMRI preprocessing was performed using in‐house 4dfp tools (Snyder, 2019): (a) correction for systematic slice‐dependent time shifts; (b) elimination of odd‐even slice intensity differences due to interleaved acquisition; (c) rigid‐body realignment for head motion within and across runs; (d) normalization of signal intensity to a mode value of 1,000. Signal intensity normalization enables identification of artifact by evaluation of the temporal signal derivative. Atlas transformation was computed by the composition of affine transforms derived by a sequence of coregistration of the fMRI volumes via the T2‐weighted and MP‐RAGE structural scans. Head motion correction and atlas transformation were applied in a single resampling step that generated volumetric time series in (3 mm³) atlas space. Data underwent spatial smoothing (6 mm full width at half maximum in each cardinal direction) and temporal band‐pass filtering (0.02–0.5 Hz for the HW task and 0.009–0.08 for resting state). Nuisance regressors included six rigid body values derived from head motion correction, white matter, and CSF signals and the mean whole‐brain signal. Motion artifacts were reduced in resting state data through DVARS‐based motion scrubbing using session‐specific thresholding expressible as $g_{\mathit{\text{thresh}}}=\tilde{\kappa }+2.5{\sigma }_L$ (Equation (5)) (White 3rd et al., 2019). The fraction of censored frames was 21 ± 12%.

2.9. Statistical analysis

2.9.1. HW task response mapping in Data sets 1, 2, and 3

Another objective of acquiring HW task data was to evaluate GVTD as an index of HD‐DOT data quality (Data set 2). To this end, 70 trials of HW (15 s of HW (On), 15 s of silence (Off)) were acquired in each session; 10 trials included instructed motion; the remaining 60 trials (ordinary trials) did not. The reconstructed voxel‐wise data represent the changes in the hemoglobin concentrations (Δ Hb O₂ or ΔHbR) in units of μmol/L (Bluestone, Abdoulaev, Schmitz, Barbour, & Hielscher, 2001). The quantitative response magnitude was then calculated with a standard general linear model (GLM). The design matrix was constructed by convolving the experimental design with a canonical hemodynamic response function (HRF) using a two‐gamma function fitted to the in vivo HD‐DOT data, as described in (Hassanpour et al., 2014). Extracted hemodynamic response estimations for each subject were then combined in a simple group‐level fixed effects analysis (Friston, Holmes, & Worsley, 1999). Fixed effect analysis was adopted as we expect the variance in our data set to be most strongly driven by scan‐to‐scan variability rather than from subject‐to‐subject differences.

2.9.2. Seed‐based correlation analysis of functional connectivity in Data sets 1 and 4

Seed regions were 5 mm radius spheres centered on coordinates used in our previous study (Eggebrecht et al., 2014). Five seeds representing the auditory (AUD.), visual (VIS.), somatomotor (MOT.), dorsal attention network (DAN), and frontoparietal cortex (FPC) networks were selected within the HD‐DOT FOV. Correlation maps were generated by calculating the Pearson correlation between the time‐series of each seed region with all other voxels in the FOV. Correlation maps in individuals were Fisher's z‐transformed and averaged across subjects.

2.9.3. Similarity metric

To summarize the quality of each HD‐DOT image into a quantitative reduced metric that does not lose the spatial structure information, we computed a Similarity score for each HD‐DOT image with the corresponding image in the fMRI data set. The Similarity metric is calculated as the voxel‐wise Pearson correlation between the non‐thresholded HD‐DOT and the corresponding fMRI images by only including voxels in the HD‐DOT FOV (Figures 6, 7, and 8). HD‐DOT FOV is defined as the voxels with greater than 1% of the maximum sensitivity after inverting and smoothing (details explained in the supplementary materials of [Eggebrecht et al., 2014]).

FIGURE 6.

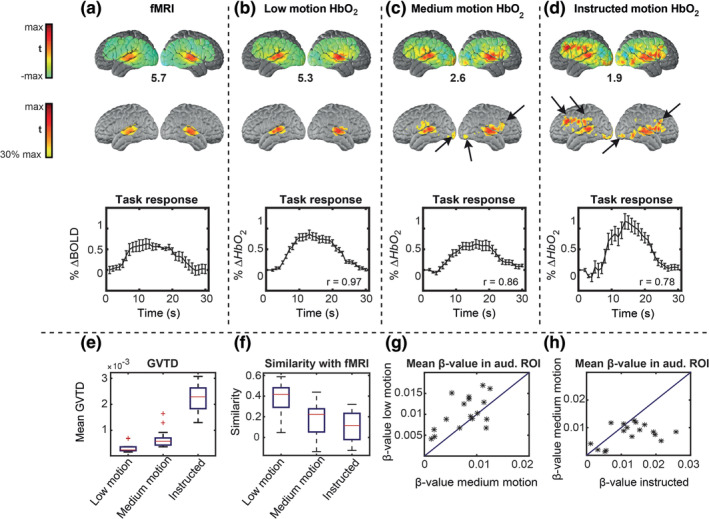
HW task t‐statistic evoked responses. Voxel‐wise maps are shown in the first and second rows; the percent signal changes are averaged over a region of interest (ROI) and shown in the third row. Error bars on the time‐courses indicate standard error of the mean across sessions. (a) Reference data set. (b) Low motion data. (c) Medium motion data. (d) Instructed motion data. Black arrows indicate false‐positive responses, designated since they occur outside auditory ROI defined based on the reference fMRI data set. The maximum t‐value of each group is shown below the maps. (e) Mean GVTD values across all trials in low motion, medium motion, and instructed motion data. (f) Mean similarity of the maps in each condition with the reference data set; similarity defined as the voxel‐voxel Pearson correlation. (g) Scatter plot of responses in low versus medium motion ordinary trials; GVTD indexed stronger responses in low motion trials in 15 of 17 sessions. (d) Scatter plot of medium motion versus instructed motion trials; note the higher spurious response magnitudes for the instructed motion

FIGURE 7.

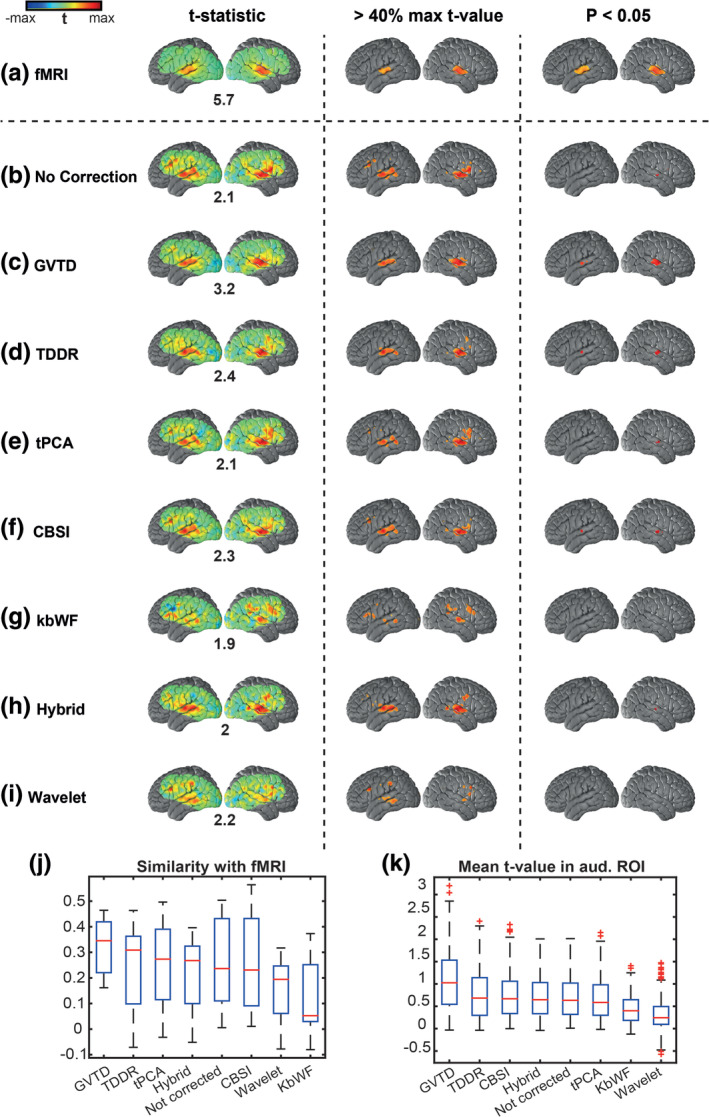
Comparison between different motion removal methods on HW task HD‐DOT data in Data set 3 based on the gold standard fMRI map from Data set 1. Three columns represent the same t‐statistic map for each row with: 1. no threshold, 2. thresholded at 40% of the maximum t‐value of each method (mapped as an alternative visualization), and 3. thresholded based on the p < .05 statistical significance. The maximum t‐value of each group is shown below the maps in column one. (a) fMRI maps based on reference Data set 1. HW map for Data set 3 with (b) no motion correction, (c) GVTD‐based motion censoring, (d) TDDR, (e) tPCA, (f) CBSI, (g) kbWF, (h) hybrid, and (i) wavelet motion correction methods. (j) The similarity between the non‐thresholded t‐statistic maps is calculated based on the voxel‐wise Pearson correlation with fMRI t‐statistic map. (k) The mean t‐value is calculated in the auditory ROI based on the fMRI HW map thresholded at p < .05 shown in panel (a) column 3

FIGURE 8.

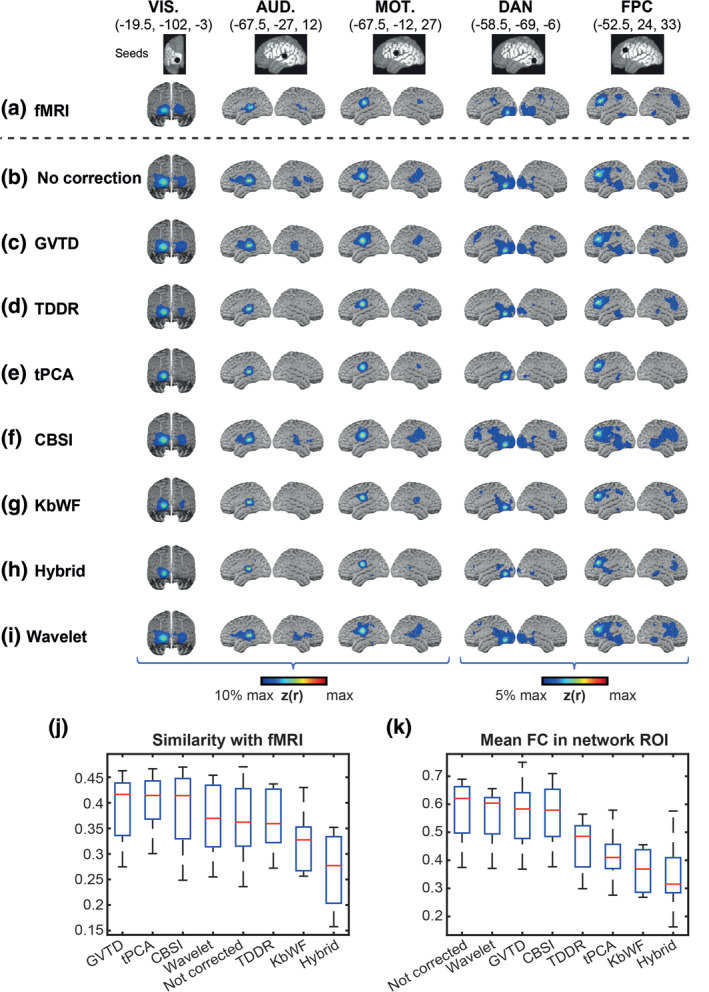
Comparison between different motion removal methods on resting state HD‐DOT data in Data set 4 and gold standard fMRI data. Five columns represent the seed maps for visual (VIS.), auditory (AUD.), somatomotor (MOT.), dorsal attention (DAN), and frontoparietal (FPC) networks. (a) fMRI maps based on reference Data set 1. HD‐DOT maps for Data set 4 with (b) no motion correction, (c) GVTD‐based motion censoring, (d) TDDR, (e) tPCA, (f) CBSI, (g) kbWF, (h) hybrid, and (i) wavelet motion correction methods. Spatial similarity (j) was computed as the Fisher's z‐transformed spatial correlation between the HD‐DOT and fMRI FC maps, evaluated over the HD‐DOT FOV (white area illustrated in the top row). (k) ROI‐based FC was evaluated as the mean Fisher's z‐transformed correlation with the seed in the colored regions shown in panel (a). These regions were determined by thresholding the group‐level fMRI FC maps at 10% for lower‐level networks (VIS., AUD., and MOT.) and 5% for higher‐level networks (DAN and FPC) of maximum z(r) value

2.9.4. Receiver operator characteristic curve

To evaluate the sensitivity and specificity of different motion detection indices, we evaluated the experimental receiver operator characteristic (ROC) curves for binary classification of clean and noisy time points by sweeping the detection threshold. We defined ground truth for motion as the time points during which the subjects performed instructed movements. The ROC curves were then created by plotting the true positive rate (sensitivity) against the false positive rate (1 minus specificity) at various threshold settings for each motion index.

3. RESULTS

3.1. Effect of motion artifacts on HD‐DOT data

We investigated the effects of various types of movements on HD‐DOT data using the instructed motion. During the HW task, subjects performed five different types of instructed motion, including large movements (head rotation) and small movements (raising eyebrows) (§2.6). One way to track the effect of motion is to spatially display the measurement pair channels (Figure 2b). For example, for all the second nearest neighbor (nn2) pairs, we can mark sources and detectors with very high standard deviations over time during instances of instructed roll rotation (red circles) and eyebrow motion (blue circles) (Figure 2b). Alternatively, one can analyze a source‐detector pair measurement (pair highlighted by large circles in Figure 2b) by comparing its time‐course during runs without instructed motion (“ordinary”), or with different levels of instructed motion, that is, low eyebrow motion or gross roll rotation (Figure 2c). The difference in signal quality between the clean and corrupted responses are evident after block averaging (Figure 2d).

FIGURE 2.

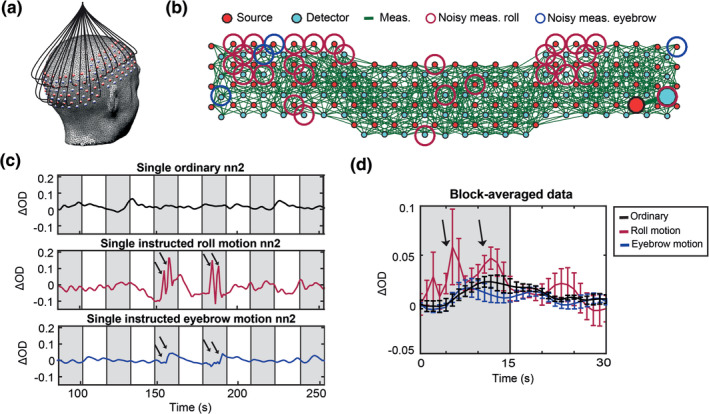
(a) Adult HD‐DOT cap structure illustrating a subset of optical fibers. (b) Green lines indicate source‐detector pairs that have standard deviation of less than 7.5%. Source or detector locations identified as noisy for the roll (large red circles) and the eyebrow (large blue circles) movements, respectively. (c) Changes in the light levels of a representative source‐detector pair during HW runs that were ordinary (black), instructed roll motion (red), and instructed eyebrow motion (blue). Arrows indicate motion. Gray shading indicates auditory stimulus presentation. (d) Block averages of ordinary (black), instructed roll motion (red), and instructed eyebrow motion (blue) runs. Error bars represent standard error of the mean across trials

We assessed the effects of different motion artifacts on the measurements by calculating the number of measurements with excessive noise for each type of motion artifact across all subjects. The HD‐DOT array contains n = 1,500 total measurements per wavelength with nn1 ~ 13 mm, nn2 ~ 30 mm, nn3 ~ 39 mm, and nn4 ~ 47 mm separations, respectively. All five motion types affected multiple source‐detector channels distributed across the FOV; specifically, 51 ± 8% of the channels for gross body movement and 39 ± 4% for small eyebrow movement (Table 2). Based on these observations, we concluded that each type of motion generates global effects. Therefore, we adopted the GVTD as a global index of motion, taking into account optical signals over the full FOV.

TABLE 2.

Percent of the noisy measurements (nn1 through nn4) across five different instructed motion artifacts in Data set 2. Noisy measurements were empirically defined as ones having a temporal standard deviation of 7.5% or greater.

Type of motion	Roll	Pitch	Deep breaths	Body motion	Eyebrow motion
% Noisy measurements	49 ± 9%	47 ± 4%	41 ± 5%	51 ± 8%	39 ± 4%

3.2. GVTD and its correlation with the head angular rotation

The global effect of motion artifacts in HD‐DOT can be visualized as a matrix where each row is a measurement signal, and the columns index time (Figure 3a). This type of visualization is similar to fMRI gray plots (Power et al., 2012; Power et al., 2013; Power et al., 2014). Inspection of Figure 3a reinforces the notion that the effects of head motion in HD‐DOT are global. GVTD time‐course is computed in four steps. First, starting from the matrix of selected 850 nm nn1 optical density changes (Figure 3a), the matrix of the backward differentiation of the selected time‐courses is calculated (Figure 3b). Then, from the matrix of the squares of backward differences (Figure 3c), GVTD is defined as the square root of the mean across the selected measurement array (Figure 3d). This sequence of steps progressively increases the sensitivity and specificity of the measure to motion (Figure 3a–d).

FIGURE 3.

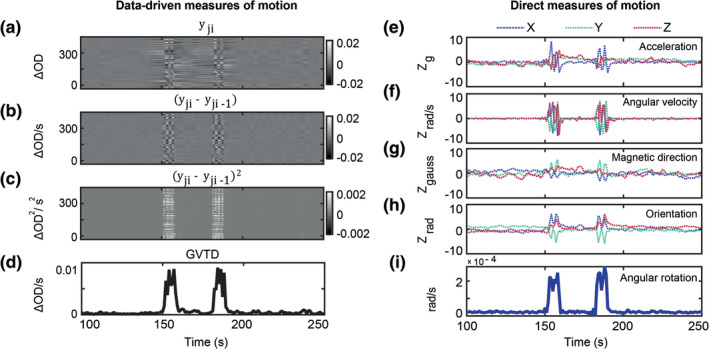
(a) All 850 nm nn1 measurements (n = 322) for a run containing instructed roll motion, represented as a matrix of measurements by time. (b) Temporal derivative of the data shown in (a); note intensified contrast between instructed motion versus neighboring time points. (c) Squared values (by element) of the matrix shown in (b). (d) GVTD time‐course is calculated as the RMS of the squared values shown in (c). (e–h) Standardized (Z‐scored) time‐courses captured during instructed head motion in one subject. Colored traces correspond to x‐, y‐, and z‐axes of the (e) accelerometer, (f) gyroscope, (g) compass, and (h) head orientation. (i) Angular rotation is calculated as the norm of the temporally differentiated x, y, and z time‐courses shown in (h)

To evaluate the sensitivity of GVTD to motion, we concurrently recorded accelerometry as an independent measure in a subset of our instructed motion data set (Figure 3e–h). The graded quantitative motion capture of the accelerometer provided insight into the sensitivity and specificity of GVTD to motion. To facilitate comparisons between the accelerometer and GVTD, the angular rotation was calculated based on the final head orientation time‐course (§2.1.3, Figure 3i).

We evaluated the efficacy of GVTD and angular rotation for motion detection through different scenarios. First, we compared these two motion indices for a gross and a small artifact and found that GVTD shows a higher amplitude spike than the angular rotation in the case of small artifacts such as eyebrow motion (Figure 4a,b). To quantify these comparisons, we first calculated the Pearson correlation between GVTD and angular rotation (Φ) for all runs containing instructed motion. The correlations were averaged over the six subjects that had concurrent HD‐DOT and motion sensor data for all runs in the session (Figure 4c). These correlations were greatest in cases of head rotations (r = 0.86 ± 0.06 for roll and pitch) and lowest for eyebrow motion (r = 0.46 ± 0.2). This difference most likely reflects the transducer characteristics of the motion sensor and the fact that it is not sensitive to the small muscle movements when attached to the top of the HD‐DOT cap.

FIGURE 4.

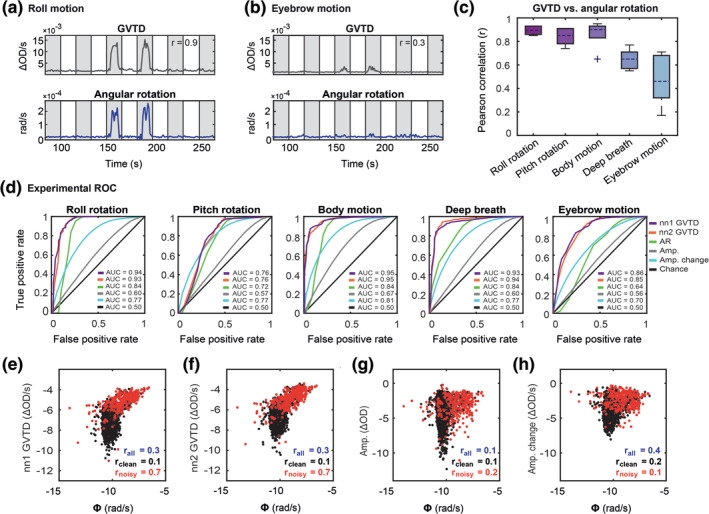
GVTD and angular rotation for an example HW run containing instructed (a) roll and (b) eyebrow motion artifacts. Gray shaded regions indicate auditory stimulation. The Pearson correlations between each pair is noted on the GVTD plots. (c) Pearson correlation between GVTD and angular rotation averaged over the six subjects with instructed motion runs. Note a high Pearson correlation of GVTD with roll, pitch, and body motion. (d) Experimental ROC plots for GVTD based on nn1 and nn2 measurements and angular rotation and the mean of the ROCs for signal amplitudes (Amp.) and windowed amplitude changes (Amp. change) for five types of instructed motion. Log–log scatter plots of 850 nm (e) nn1 GVTD, (f) nn2 GVTD, (g) nn1 signal amplitudes, (h) nn1 windowed amplitude changes versus angular rotation are shown for all runs with instructed motion. The correlation between the GVTD (either nn1 or nn2) and the motion sensor is higher than both amplitudes and the windowed amplitude changes. The cutoff between black and red dots is based on the instructed motion time points

To evaluate the sensitivity of the GVTD to motion, we leveraged the ground truth built into our instructed motion paradigm. Experimental ROC curves for GVTD (based on both nn1 with SD distance ~13 mm and nn2 with source‐detector distance of ~30 mm) and angular rotation were created for binary classification of clean and noisy time points by sweeping the detection threshold (§2.9.4, Figure 4d). We defined ground truth for motion as the time points during which the subjects performed instructed movements. We also plotted these ROC curves for two common temporal motion detection methods in fNIRS, that is, absolute single‐channel signal amplitudes and windowed amplitude changes for all motion types and all 850 nm nn1 measurements (Figure S3) and compared the mean of these ROC curves against GVTD and angular rotation (Figure 4d). In all motion types, GVTD (for either nn1 or nn2 measurements) showed better or similar performance area under the curve (AUC) compared to angular rotation, absolute signal amplitudes, and windowed amplitude changes (Table 3).

TABLE 3.

The area under the curve (AUC) of the experimental receiver operator characteristic (ROC) of GVTD and angular rotation (based on the motion sensor outputs), and the mean of the ROC of the absolute signal amplitudes and windowed amplitude changes based on the instructed motion as ground truth, in Data set 2.

Motion index	GVTD (either nn1 or nn2)	Angular rotation	Signal amplitude	Windowed amplitude change
AUC	0.88 ± 0.08	0.77 ± 0.08	0.6 ± 0.04	0.76 ± 0.04

We used the instructed motion protocol to examine the relation between GVTD and angular rotation for all runs with instructed motion (Figure 4e). Low versus high motion time points (black vs. red in Figure 4e) were determined based on the ground truth of the instructed motion protocol (high motion as defined as time points when the subject performed instructed motion). When the motion was low (black dots) GVTD and angular rotation were not correlated (r = 0.05 ± 0.05), but when the motion was high (red dots), GVTD and angular rotation were highly correlated (r = 0.8 ± 0.1). The same log–log scatter plots for absolute signal amplitudes (Figure 4f) and the windowed amplitude changes (Figure 4g), show much lower correlations with the angular rotation (0.2 and 0.1, respectively) compared to GVTD using either nn1 or nn2 measurements (0.7).

In summary, these results show that GVTD can be used as an alternative or in conjunction with motion sensors in detecting noisy time points of data. For the rest of this paper, 850 nm nn1 measurements were used with a source‐detector distance of 13 mm for the adult and 10 mm for the infant HD‐DOT systems for GVTD calculations.

3.3. Motion detection strategy using GVTD

To censor data using the GVTD time‐course, we developed an outlier detection strategy that separates good data from motion artifacts.

We assume that the detected signal, y(t), is a linear combination of the true physiological signal, S(t), and noise, ε(t):

$$y\left(t\right)=S\left(t\right)+\epsilon \left(t\right)$$ (4)

We followed the fMRI approaches for DVARS and FD and developed a data distribution driven strategy for finding motion criterion. In fMRI, S(t) is approximately normally distributed (Laumann et al., 2017). Accordingly, the DVARS distribution is right‐skewed (Afyouni & Nichols, 2018). Therefore, we investigated the skew of the GVTD distribution as a potential index of head motion artifact in HD‐DOT. We evaluated the GVTD distribution for HD‐DOT data from a still Styrofoam phantom, a low motion trial, and a high motion trial. The phantom GVTD histogram peaked at a relatively small value (mode = 4 × 10⁻⁵) and exhibited a small rightward skew (Figure S4a). In the low motion human data, GVTD values had a higher mode and proportionately smaller skew (Figure S4b). In data with instructed motion (high motion), the GVTD distribution is strongly skewed to the right (Figure S4c). These results suggest that the skew provides a basis for censoring HD‐DOT data.

Thus, we defined a noise threshold (g_thresh) based on the GVTD distribution mode ($\tilde{\kappa })$ plus a constant (c) times the standard deviation computed on the left (low) side of the mode (σ_L). The right tail of the GVTD distribution corresponds to motion artifacts (Equation (5)). Thus,

$$g_{\mathit{\text{thresh}}}=\tilde{\kappa }+c{\sigma }_L,$$ (5)

where $\tilde{\kappa }$ is the histogram mode and σ_L is computed as ${\sigma }_L=\sqrt{\left(1/n_L\right)\sum _{g_i<\tilde{\kappa }}{\left(g_i-\tilde{\kappa }\right)}^2}$, where n_L is the number of GVTD time points less than $\tilde{\kappa }$. The value of c controls the tradeoff between the exclusion of artifact versus data loss. Source code calculating the GVTD time‐course and GVTD threshold can be accessed at https://github.com/sherafatia/GVTD.

3.4. Determining the best stage for performing GVTD‐based motion detection and censoring

GVTD is a generic measure that can be applied to any data in the form of channels (or voxels) by time. Therefore, we needed to determine where in the processing pipeline, GVTD should be performed. We evaluated four potential locations (green boxes in Figure S2). To evaluate GVTD's ability to separate noise from the signal, we defined an ABR as the mean of the GVTD values above a noise threshold over the mean of the GVTD values below the threshold (Equation (3)). Specifically, GVTD was calculated for (a) source‐detector pair log‐mean optical densities (after log‐mean; unit = optical density change per second [∆OD/s]), (b) after temporal filtering before superficial signal regression (SSR) (after filtering no SSR; unit = ∆OD/s), (c) after both temporal filtering and SSR (after filtering with SSR; unit = ∆OD/s), and (d) on reconstructed image voxels (after reconstruction; unit = ∆HbO₂/s). These results were compared based on their ABR means on two different data sets with a natural motion to determine the most effective GVTD strategy. GVTD time‐courses, GVTD histograms, and their associated gray plots calculated at these four stages are plotted for an example resting state data from Data set 4 (Figure 5a–c). The ABR index (Equation (3)) was calculated using the motion threshold defined as g_thresh = $\tilde{\kappa }+4{\sigma }_L$ (Equation (5)). Results showed that ABR was consistently highest after both filtering and SSR but before image reconstruction in both Data sets 4 and 5 (Figure 5d).

FIGURE 5.

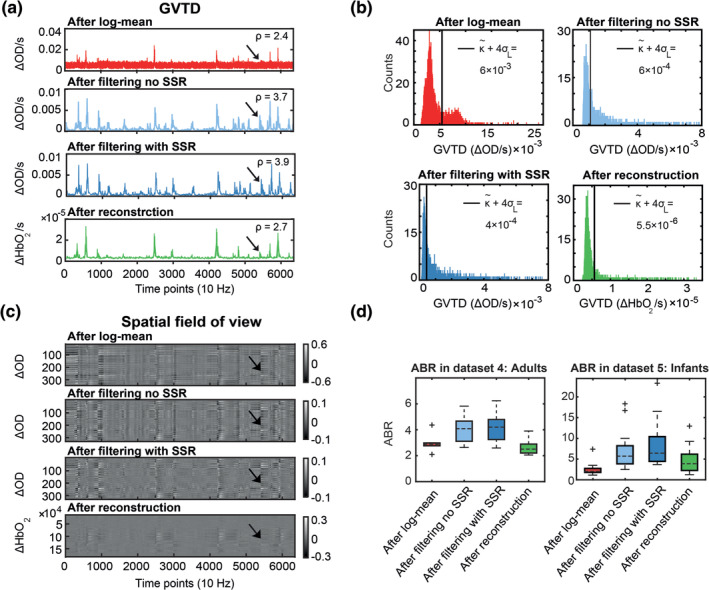
Determination of optimal GVTD stage in the processing pipeline based on the artifact‐to‐background ratio (ABR [ρ]; Equation (3)) of the 850 nm first nearest neighbor measurements. (a) GVTD computed after log‐mean, after filtering and without SSR, after filtering and with SSR, and after reconstruction. (b) Histograms of the GVTD values for the four time‐courses; black lines indicate the noise threshold ($\tilde{\kappa }+$ 4σ_L). (c) Four gray plots associated with the four GVTD time‐courses shown in (a). Black arrows indicate a small motion artifact. Note the greatest contrast between the motion artifact and the baseline after filtering (third time‐course). (d) ABR values calculated for all four processing stages for all subjects in Data sets 4 and 5. GVTD after filtering (light and dark blue) was maximal in all cases and the highest after filtering with SSR (dark blue)

3.5. Indexing data quality with GVTD in task HD‐DOT data by comparison against fMRI

Data set 2 was used to evaluate the ability of GVTD to index the HD‐DOT data quality. HD‐DOT responses to hearing words were compared to the group‐mean fMRI response to the same task, which was independently acquired in a separate experiment and treated as a gold standard. We rank‐ordered ordinary HD‐DOT trials (trials without instructed motion) for each subject according to their mean GVTD value; for each subject, the 10 lowest and 10 highest GVTD ordinary trials were defined as low motion and medium motion, respectively. The instructed motion trials were defined as high motion. Responses were extracted from a fixed region of interest (ROI) defined as p < .05 in the fMRI data set (Figure 7a, third column map), expressed as percent signal change (Figure 6a, third row). The Pearson correlation between the HD‐DOT and fMRI time‐courses were computed for each of the three HD‐DOT conditions (Figure 6b–d). This correlation progressively decreased from 0.97 for low motion to 0.86 for medium motion, to 0.78 for instructed motion. Medium motion responses were comparable to fMRI, but with a smaller peak value and higher mean squared error (0.08). Trials that GVTD identified as low motion (Figure 6b) generated the cleanest maps with the lowest mean squared error (0.06). Additional results derived from the HW response analysis show a progressively lower similarity of the HW responses with fMRI results in association with greater GVTD values (Figure 6e,f). The relationship between low motion and medium motion data within each session shows that the GLM‐derived beta‐values are systematically greater in low motion as opposed to medium motion (true in 15 of 17 sessions) (Figure 6g). The responses are comparably compromised by spontaneous motion in medium motion trials (as indexed by greater GVTD) and spuriously higher in instructed motion trials with the highest GVTD scores (Figure 6h).

A cautionary point regarding GLM‐derived beta values is raised by the instructed motion trials, which generated the highest mean squared error (0.12) as well as the greatest HbO₂ response modulations, hence, the greatest GLM‐derived beta values (Figure 6h). These response time‐courses were the least similar to those obtained by fMRI and were accompanied by voxel‐wise activations outside of the auditory cortex. Thus, the apparently strong HD‐DOT responses in the instructed motion condition are attributable to motion artifacts, as detected by GVTD (Figure 6e). We conclude that the results shown in Figure 6 demonstrate that GVTD effectively indexes HD‐DOT data quality.

We replicated these results with the HbR contrasts in Figure S5. For the rest of the paper, we presented the results only using one chromophore (HbO₂) as we did not expect to see any significant changes in the performance of the denoising methods across chromophores.

3.6. Comparison between motion removal methods applied to HW task HD‐DOT data

To compare the performance of different motion removal methods on HD‐DOT data, we used Data set 3, acquired in older subjects (n = 13; 42 ± 19.75 years old) performing the hearing words task (no instructed motion). Data set 3 included a wide range of motion contamination levels. The details of the various motion removal methods used in this analysis are explained in §2.2. Responses were evaluated in terms of statistical significance at the voxel and ROI levels as well as voxel‐wise similarity with fMRI (§2.9.1 and §2.9.3).

Without motion removal, the group‐level t‐statistic map contained several spurious activations that are not present in the fMRI results (Figure 7b). Moreover, the expected superior temporal cortex response did not achieve statistical significance at p < .05. In this analysis, the GVTD threshold was computed as g_thresh = $\tilde{\kappa }+3{\sigma }_L$ (Equation (5)). Exemplary low motion and high motion runs are illustrated in Figure S6. This threshold excluded all blocks in 6 subjects, leaving 7 subjects contributing to the final result illustrated in Figure 7c. Results obtained with TDDR, tPCA, CBSI, kbWF, hybrid (spline + Savitzky Golay), and wavelet filtering are illustrated in Figure 7d–i. GVTD censoring, TDDR, and CBSI methods recovered bilateral superior temporal cortex activations in thresholded t‐statistic maps (p < .05). tPCA and hybrid methods also recovered a unilateral right hemisphere activation. However, no statistically significant (p < .05) response was obtained with other methods (wavelet and kbWF).

We quantified the performance of the results shown in Figure 7b–i using two metrics: (a) Similarity score, defined as the voxel‐wise Pearson correlation between the non‐thresholded maps and the fMRI gold standard map (§2.9.3), and (b) mean t‐value in the auditory ROI defined as the voxels with p < .05 in the fMRI t‐map (Figure 7a, third column). The spatial similarity to fMRI was greatest for the GVTD‐censored map, followed by TDDR, tPCA, hybrid, not‐corrected, CBSI, wavelet, and kbWF maps (Figure 7j). The mean ROI t‐value was greatest for the GVTD‐censored maps, followed by TDDR, CBSI, hybrid, not corrected, tPCA, kbWF, and wavelet corrections (Figure 7k).

3.7. Comparison between motion removal methods applied to resting state HD‐DOT data

We compared the performance of different HD‐DOT motion removal methods in application to resting state HD‐DOT data using Data set 4 (n = 8 adults, 30.25 ±11.18 years old). Seed‐based functional connectivity (FC) was computed using the five seed ROIs (§2.9.2, Figure 8 top row). In parallel with §3.6, we quantified the performance of each correction method using two metrics: (a) Similarity score, defined as the spatial similarity between the HD‐DOT and fMRI FC maps (§2.9.3); and (b) mean FC in functionally connected ROIs identified based on the fMRI data. The spatial similarity was computed as the spatial Pearson correlation between non‐thresholded mean Fisher's z‐transformed maps, evaluated over the HD‐DOT FOV (white area illustrated in the top row of Figure 9). Mean FC was evaluated in the colored ROIs illustrated in Figure 8a. Thus, this measure reflected simple homotopic FC in primary cortical areas as well as ipsilateral FC in the higher‐order networks (DAN and FPC). The GVTD threshold was computed as g_thresh = $\tilde{\kappa }+10{\sigma }_L$ (Equation (5)). This lenient threshold minimized data loss. On the basis of preliminary testing, GVTD censoring was extended to retain only epochs of duration at least 30 s.

The results obtained by the various correction methods are shown in Figure 8c–i. The most extensive HD‐DOT FC maps were obtained in uncorrected data (Figure 8b). However, these maps were not spatially most similar to the fMRI gold standard data set. Rather, GVTD censoring (Figure 8c) yielded HD‐DOT FC maps most similar to fMRI (Figure 8j). Of all motion removal methods, GVTD had the highest similarity to fMRI, followed by tPCA, CBSI, wavelet, not corrected, TDDR, KbWF, and hybrid. For mean FC in each network ROI (defined based on fMRI data), the scores were: not corrected, wavelet, and then GVTD, followed by CBSI, TDDR, tPCA, kbWF, and hybrid, respectively (Figure 8k). As in the HW task responses, strong FC in the evaluation of network ROIs does not necessarily indicate good data quality, especially when accompanied by spurious effects outside of the network identified on the basis of fMRI (e.g., as seen in the no correction, wavelet, and CBSI maps). On the other hand, some methods may overcorrect, leading to falsely weak correlations (TDDR, tPCA, kbWF, and hybrid methods).

4. DISCUSSION

4.1. A general summary of the novel strategies and findings

We developed a novel motion detection method suitable for high‐density optical imaging arrays, inspired by the DVARS in fMRI (Smyser et al., 2010). Specifically, we defined the global measure of variance of the temporal derivatives across measurement channels (GVTD) and developed a method for denoising structured artifacts in HD‐DOT. We found that GVTD successfully indexes motion artifacts in HD‐DOT and has higher sensitivity and specificity (evaluated using AUC of the ROC curve against the ground truth of instructed motion) for motion detection compared to an accelerometer motion sensor and to single‐channel motion detection methods commonly used in fNIRS (absolute signal amplitudes and windowed amplitude changes).

While there are a number of papers evaluating motion removal methods for standard fNIRS (Chiarelli et al., 2015; Cui et al., 2010; Fishburn et al., 2019; Izzetoglu, Devaraj, Bunce, & Onaral, 2005; Jahani et al., 2018; Metz et al., 2015; Molavi & Dumont, 2012; Scholkmann et al., 2010; Yucel et al., 2014a; Yucel et al., 2014b; Zhang et al., 2005), the literature on motion removal strategies for HD‐DOT is limited. Previous studies lack some combination of HD‐DOT data sets and comparisons to gold standard data (fMRI) for image quality validations, and most are restricted to single‐channel motion detection. In this paper, we introduce a novel global approach and evaluate the efficacy of multiple motion removal methods in HD‐DOT by comparison against matched fMRI data sets.

We show that the mean GVTD score is correlated with the similarity of the HD‐DOT task images to those of fMRI. Thus, the mean GVTD score can be used to classify data sets as either clean or noisy (Figure 6). We also show that applying GVTD censoring to both task and resting state HD‐DOT data sets outperforms other fNIRS‐based motion correction methods and makes HD‐DOT maps more similar to those of fMRI (Figures 7 and 8). Together, HD‐DOT imaging arrays and anatomical atlasing combined with GVTD motion censoring, all aid in making HD‐DOT data more comparable to fMRI and furthers the use of HD‐DOT as a surrogate to fMRI.

4.2. Optimizing the implementation of GVTD in the HD‐DOT processing pipeline

We optimized the use of GVTD motion detection in HD‐DOT by testing it at different steps of the processing pipeline using the artifact‐to‐background ratio (ABR). In fMRI, DVARS has only been evaluated before and after filtering (Power et al., 2013). In contrast, in HD‐DOT, we can consider GVTD in either measurement space or image space (after image reconstruction). Our results show that the ABR was the highest in measurement space prior to image reconstruction and after filtering the high‐frequency content of the data. It was also statistically better when performed after SSR, a common fNIRS and DOT processing step (Figure 5d). Therefore, based on our ABR analysis, we recommend performing GVTD after filtering the measurements, but prior to image reconstruction.

An important decision with GVTD is to determine the censoring threshold. Since the baseline GVTD value was different across people, similar to findings with DVARS in fMRI (White 3rd et al., 2019), we evaluated a noise detection strategy based on the GVTD distribution (histogram) specific to each subject. The differences in the baseline GVTD distribution is possibly due to variable physiological signal levels as well as respiratory patterns, heart rate, facial muscle activity, restlessness, tremor, and so forth (Power et al., 2012; Power et al., 2013). Therefore, we developed an outlier detection strategy individualized for each subject's data that semi‐automates the noise threshold determination and takes into account subject differences. Specifically, we set the threshold using the GVTD distribution mode ($\tilde{\mathit{\kappa }})$ plus a constant (c) determined based on the left side (lower side) of the mode of the GVTD distribution. For practical implementation, we recommend that the threshold be greater than the standard deviation of the baseline signal.

4.3. Evaluation and validation of denoising through comparisons to fMRI

Most fNIRS studies measure the efficiency of motion removal techniques based on the recovery of a synthetic HRF (Brigadoi et al., 2014; Cooper et al., 2012; Di Lorenzo et al., 2019; Jahani et al., 2018), or in the case of real data, based on the variance across subjects or data sets (Di Lorenzo et al., 2019). However, as fMRI is the current gold standard, the strongest validation of image quality advancements in HD‐DOT is through direct comparisons to fMRI (Eggebrecht et al., 2014; Ferradal et al., 2014; Eggebrecht et al., 2012). We follow this approach herein to evaluate the efficacy of motion removal methods in HD‐DOT using a control fMRI data set with identical paradigms. Although cross‐modality comparisons are the strongest at the single‐subject level or with identical subjects at the group level, identifying atlas‐based group‐level cortical ROIs is a common practice in the fMRI literature for localizing the cognitive task responses and resting state networks (Barch et al., 2013; Caspers, Eickhoff, Zilles, & Amunts, 2013; Glasser et al., 2016; Gratton et al., 2018; Power et al., 2011). In general, it is more difficult to find cross‐modality agreement in non‐matched groups (our case) than a matched control group or single‐subject level. Therefore, we expect that the similarity scores reported in this paper to only improve by having a subject‐matched control fMRI group.

The comparisons in this study are based on the reasonable assumption that the functional maps for a basic auditory activation (superior and middle temporal gyri ROIs) and dominant resting state networks would be approximately similar across healthy adult Data sets 1, 3, and 4. However, we think that subject‐matched comparisons both at the subject level and group level would be informative to explore in another study.

Using the fMRI‐based ROIs for both hearing words task and resting state functional connectivity enables identifying false negatives, false positives, and localization errors (Figures 7 and 8), all of which would be difficult to determine without a target image. The advantages over in silico simulations are that both the HD‐DOT and fMRI data contain real image features, including the spatial extent, signal magnitude, distribution of spatial frequencies, and time‐courses. Further, the noise structure has real‐world complexity. In contrast, in silico studies that would permit manipulation of many parameters, while out of the scope of the current work, would be informative and should be the focus of future studies.

Using the fMRI comparisons, we rank‐ordered several motion removal methods in both task and resting state data. The general pattern observed was that motion censoring using GVTD worked best, with near contenders being CBSI, TDDR, and following those, tPCA in both task and rest data. TDDR and tPCA both suppressed the mean t‐value in the auditory ROI and FC in the evaluation ROIs, which may indicate overcorrection, that is, removal of the true signal. Wavelet filtering ranked higher in resting state data both in terms of similarity with fMRI and mean FC in the resting state networks. This is in distinction to its lower performance in the task data.

4.4. On different performances of motion correction methods in fNIRS literature

A striking aspect of the fNIRS literature is the variable performance of motion correction methods across different studies (Brigadoi et al., 2014; Chiarelli et al., 2015; Cooper et al., 2012; Di Lorenzo et al., 2019;Fishburn et al., 2019; Jahani et al., 2018). One possible reason for the variability between the studies could be the different levels of motion present in each study. This variability has also been evaluated in a recent fNIRS study (Di Lorenzo et al., 2019). To address this topic, we performed a supplementary analysis of the low motion, medium motion, and high motion HW task data in Data set 2 (Figure 6). We evaluated the performance of different motion correction methods on different levels of motion artifacts in these three categories (Figures S7 and S8).

This analysis shows that, in the low motion group, all methods can preserve bilateral auditory cortex HW responses. In the medium and instructed motion groups, GVTD, TDDR, CBSI, and tPCA again outperformed other methods by recovering either a unilateral or bilateral HW activation with no obvious false positives in the p < .05 thresholded maps (Figure S7). Note that, in the high motion data (instructed motion group), none of the motion correction techniques fully recovered bilateral auditory responses (present in fMRI). However, GVTD was able to distinguish between clean versus motion‐corrupted data (Figure 6). We hypothesize that GVTD can provide a means of rank‐ordering data based on quantitative motion estimation (as suggested in Figure 6), something that is normally done subjectively prior to applying motion correction methods. Thus, GVTD may also be useful in denoising sparse fNIRS data. This notion could be tested by evaluating the efficacy of GVTD in sparse fNIRS arrays or by subsampling the HD‐DOT imaging array.

GVTD focuses on motion detection, followed by simple censoring. GVTD could be used as an alternative to either absolute signal amplitudes or windowed amplitude changes included in the HOMER2 code package (Huppert et al., 2009). Further, GVTD could be used in conjunction with motion correction methods such as spline interpolation (MARA) (Scholkmann et al., 2010), Kalman filtering (Izzetoglu, Chitrapu, Bunce, & Onaral, 2010; Zhang et al., 2005), PCA (Zhang et al., 2005), tPCA (Yucel et al., 2014a), hybrid methods (Jahani et al., 2018), or any method that depends on motion detection in the temporal domain. However, we note that, in the results presented here, GVTD‐based censoring alone provided better image quality than any of the alternative motion correction procedures.

4.5. Strengths and limitations of the GVTD‐based motion censoring

When tested in HD‐DOT, the most promising results were obtained using GVTD‐based motion censoring. A likely reason for GVTD efficacy is that it leverages the effect of small artifacts across many measurements. The simplicity of GVTD censoring guarantees that the signal is neither over‐smoothed nor overcorrected.

As described here, GVTD is used as a binary classifier to censor the time points marked as noisy. However, it also could work with a non‐binary weight associated with the time points based on their GVTD value to soften the impact of threshold choice. For example, time points with GVTD values closer to the GVTD distribution mode could be assigned higher weights than ones further from the mode (Tanenbaum, Snyder, Brier, & Ances, 2015).

Another important challenge in scrubbing data is the tradeoff between losing signal versus removing noise (Raut, Mitra, Snyder, & Raichle, 2019). For motion criterion, one can ensure that sufficient data remains after censoring by tuning c (Equation (5)). Another approach would be to use GVTD to determine the useable data yielded from a run and then adjust the data collection to either collect more data within the session or add sessions to the study. These active data quality approaches are currently being pioneered in fMRI with runtime assessment of motion (Dosenbach et al., 2017; Fair et al., 2019; Greene et al., 2018).

4.6. Summarizing the consensus regarding the top‐performing denoising strategies in the fNIRS literature

Among the fNIRS‐based methods that worked best for HD‐DOT, besides GVTD, CBSI performed well in both task and resting state data. CBSI does not require tuning of parameters but has been less recommended in the literature (Fishburn et al., 2019; Jahani et al., 2018) as it relies on the assumption of a negative correlation between HbO₂ and HbR. Therefore, it is limited to populations in which a normal correlation between HbO₂ and HbR can be assumed (Cui et al., 2010).

The TDDR method performed well in the task HD‐DOT data and fairly well in the resting state analysis. TDDR, like CBSI, does not require tuning of parameters. However, one disadvantage of TDDR is that it relies on the derivative of single measurements and, thus, is less sensitive to small motion artifacts such as eyebrow motion. Moreover, TDDR only performs an efficient motion correction on the low‐frequency content of the data, because the higher frequencies inflate the variance of the temporal derivative distribution and create bias in the distribution of estimates (Fishburn et al., 2019).

Targeted PCA also yielded HD‐DOT maps similar to those in fMRI but with decreased response magnitudes in both task and resting state data. tPCA removes a fixed proportion of variance through the removal of the principal components with the least variance; hence, as observed here and in other studies, it is prone to overcorrection (Fishburn et al., 2019; Yucel et al., 2014a).

Wavelet filtering, despite a poor performance in task data, showed good performance in resting state HD‐DOT data. However, this method is computationally expensive. On average, for both HW and rest HD‐DOT runs, wavelet filtering ran 10 times slower than other motion removal methods. The kbWF method, while faster than the full wavelet approach, did not perform well in either task or rest HD‐DOT data.

5. CONCLUSION

We developed GVTD, a novel motion detection metric, and optimized its use in the HD‐DOT pre‐processing pipeline. GVTD can be used alone or in combination with other motion correction methods to increase the quality of data obtained with multi‐channel optical imaging systems. We evaluated GVTD using several independent HD‐DOT data sets, including an instructed motion protocol, accelerometer motion measures, and a matched fMRI data set serving as ground truth. Although GVTD‐based censoring removes data, the obtained HD‐DOT maps were most similar to those of fMRI, and it outperformed alternative motion correction methods previously described in the fNIRS literature.

CONFLICT OF INTERESTS

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supporting information

Figure S1 The motion sensor (3‐space™ USB/RS232; Yost Labs) was attached to the top strap of the HD‐DOT device for concurrent recording of the head motion and optical data in Data set 2.

Figure S2 Processing of HD‐DOT data. Dashed pink and blue boxes show the pre‐ and post‐processing steps, respectively. GVTD was evaluated (§3.4) at four stages in the pipeline indicated by 3 green boxes (after filtering with SSR and after filtering no SSR are shown in one box). The best separation between baseline signal and motion artifacts was also obtained for GVTD calculated after filtering (thicker outlined green box).

Figure S3 The experimental ROC curves are drawn for (a) the absolute signal amplitudes of 850 nm nn1 measurements and (b) the windowed amplitude changes of the signals shown in (a). The yellow curves show the mean of all ROC curves for each plot. The goal of this figure is to show that regardless of the type of motion, both maximum and mean of the area under the curve (AUC) of the ROC curves in each figure is still lower than or equal to the AUC of GVTD shown in Figure 4.

Figure S4 Histograms of the GVTD values for (a) a Styrofoam phantom, (b) a low motion run, and (c) an high motion run in one subject. Note the constant x‐axis limits; values above that limit fall into the last bin. Note mode (red arrow), left standard deviation, σ_L, and noise threshold computed according to Equation 5. Pink and green shadings indicate GVTD values that do or do not exceed the noise threshold, respectively.

Figure S5 Same HW task t‐statistic evoked responses as Figure 6 are replicated with HbR contrasts. (a) Reference data set. (b) Low motion data. (c) Medium motion data. (d) Instructed motion data. Black arrows indicate false‐positive responses, designated since they occur outside the auditory ROI defined based on the reference fMRI data set. The maximum t‐value of each group is shown below the maps. (e) Mean GVTD values across all trials in low motion, medium motion, and instructed motion data. (f) Mean similarity of the maps in each condition with the reference data set, similarity defined as the voxel‐wise Pearson correlation. (g) Scatter plot of the responses in low vs. medium motion ordinary trials; GVTD indexed stronger responses in low motion trials in 15 of 17 sessions. (d) Scatter plot of medium motion vs. instructed motion trials; note the higher spurious response magnitudes for the instructed motion.

Figure S6 GVTD censoring process for the hearing words (HW) task. The four‐step process (explained in Figure 3a–d) for calculating the GVTD time‐courses (a) for a low motion subject, and (b) a high motion subject in Data set 3. Dashed lines indicate the onsets of the blocks of the HW runs (6 runs each 30 s). The red line shows the GVTD threshold of ${\mathrm{g}}_{\text{thresh}}=\text{mode}+3{\sigma }_L$. Blocks with time points exceeding the GVTD threshold are excluded from the analysis (4, 5, 6 for the low motion subject, and all blocks for the high motion subject). Dark blue arrows indicate some examples of the high contrast in both the gray plots and the spikes of the GVTD time‐courses for instances of motion artifacts.

Figure S7 HW task t‐statistic maps. Voxel‐wise maps are shown for (a) reference fMRI data set, (b) low motion data, (c) medium motion data, and (d) instructed motion data for the three motion level categories determined with mean GVTD scores. Rows represent maps corrected with TDDR, tPCA, CBSI, kbWF, hybrid, and wavelet filtering methods.

Figure S8 Same maps described in Figure S7 visualized with P < .05 threshold. Voxel‐wise maps are shown for (a) reference fMRI data set, (b) low motion data, (c) medium motion data, and (d) instructed motion data for the three motion level categories determined with mean GVTD scores. Rows represent maps corrected with TDDR, tPCA, CBSI, kbWF, hybrid, and wavelet filtering methods.

Table S1 List of the parameters for motion correction in task data.

Table S2: List of the parameters for motion correction in resting state data.

Sherafati A, Snyder AZ, Eggebrecht AT, et al. Global motion detection and censoring in high‐density diffuse optical tomography. Hum Brain Mapp. 2020;41:4093–4112. 10.1002/hbm.25111

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.