SUMMARY
The need to test anticancer drugs in multiple indications has been addressed by basket trials, which are Phase I or II clinical trials involving multiple tumor subtypes and a single master protocol. Basket trials typically involve few patients per type, making it challenging to rigorously compare responses across types. We describe the use of permutation testing to test for differences among subgroups using empirical null distributions and the Benjamini-Hochberg procedure to control for false discovery. We apply the approach retrospectively to tumor-volume changes and progression-free survival in published basket trials for neratinib, larotrectinib, pembrolizumab, and imatinib and uncover examples of therapeutic benefit missed by conventional binomial testing. For example, we identify an overlooked opportunity for use of neratinib in lung cancers carrying ERBB2 Exon 20 mutations. Permutation testing can be used to design basket trials but is more conservatively introduced alongside established approaches to enrollment such as Simon’s two-stage design.
Graphical Abstract
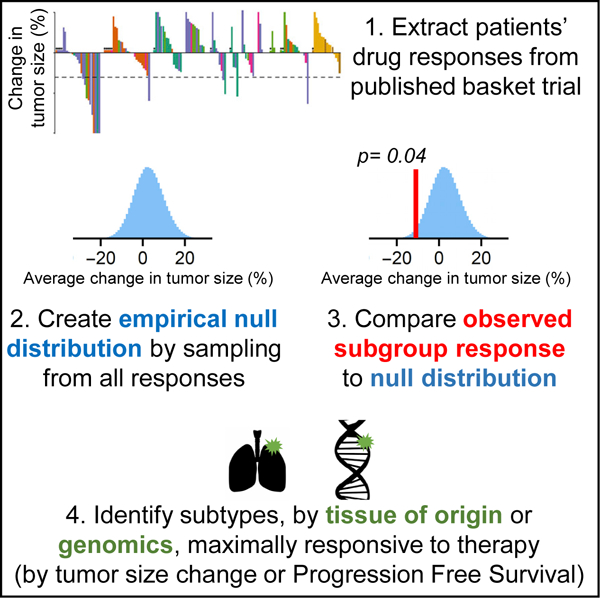
In Brief
Basket clinical trials simultaneously test a single drug in multiple tumor subtypes, but statistical challenges limit the comparison of responses across subtypes. We describe a rigorous approach to permutation testing using empirical null distributions that can identify previously overlooked opportunities for use of targeted therapy in genetically defined cancer subtypes.
INTRODUCTION
In a traditional clinical trial for a cancer therapy, a potential therapeutic agent is tested in patients defined by specific inclusion and exclusion criteria that usually involves tissue of origin and disease stage. Widespread development of molecularly targeted therapies has driven interest in simultaneously evaluating multiple patient populations having different tumor “types.” In a basket trial, “tumor type” can refer to tissue of origin or to tumors distinguishable by histopathology, but with targeted drugs, tumors can alternatively be classified by genetic biomarkers (mutations, amplifications, or gene fusions) implicated in drug response. “Master-protocol” trial designs test several therapeutic hypotheses at the same time via multiple parallel substudies (“baskets”) under a single clinical protocol (and its associated ethical and regulatory reviews) (Park et al., 2019).
The use of master protocols facilitates evaluation of drugs in multiple subtypes while involving fewer patients and using fewer resources than performing multiple traditional trials of the same set of hypotheses. Additionally, because master protocols can rigorously assess drug benefit in small numbers of patients, they are well-suited to studying rare types of cancer (Hirakawa et al., 2018; Park et al., 2019; Renfro and Mandrekar, 2018). For example, the NCI-MATCH Phase II precision medicine trial (ClinicalTrials.gov, number NCT02465060) currently underway is comparing ~40 treatment arms and multiple genetic biomarkers using a master protocol (Mullard, 2015). Basket trials are particularly helpful when: (1) expanding from an initially successful indication to one or more additional tumor types, (2) searching for a responsive setting in which to perform pivotal trials, (3) studying the predictive value of a biomarker in, multiple cancer types (Redig and Jänne, 2015; Tao et al., 2018; Woodcock and LaVange, 2017), and (4) evaluating rare tumors and/or tumors with rare molecular subgroups (for example, the study of vemurafenib in BRAFV600 Erdheim-Chester disease and Langerhans cell histiocytosis; NCT01524978, Diamond et al., 2018).
Two recently completed trials demonstrate the potential for basket trials to identify tissue-agonistic biomarkers. When the TRK inhibitor larotrectinib was tested in a diverse set of 12 solid-tumor types (NCT02122913, NCT02637687, and NCT02576431) (Drilon et al., 2018), the presence of a TRK-fusion gene, irrespective of tumor tissue of origin, was found to identify tumors responsive to larotrectinib. Similarly, in 12 tumor types, mismatch repair (MMR) deficiency was found to be predictive of responsiveness to the PD-1 immune checkpoint inhibitor pembrolizumab (NCT01876511) (Le et al., 2017). In most cases, however, both biomarker status and tissue of origin have an influence on drug activity; for example, BRAF inhibitors (such as vemurafenib) are much less effective in BRAF-mutant colorectal carcinomas than in BRAF-mutant melanomas (Hyman et al., 2015; Korphaisarn and Kopetz, 2016; Subbiah et al., 2020). For any single gene, the type of mutation (i.e., inhibitory, truncating, or activating) can also affect response (Tao et al., 2018). Depending on the way subtypes are defined, a basket trial can be used to assess the impact of one or more of these variables. In a basket trial, as in a conventional trial, the clinical hypothesis being tested is specific to a particular drug and disease since drugs with the same nominal targets can elicit different responses, even when used in the same cancer type (Hafner et al., 2019). Direct comparison of drugs in the same class is not a common use of basket trials, which would generally be underpowered as compared with conventional noninferiority or superiority trials.
The ongoing SUMMIT trial, which is studied in detail in the current paper, is testing the activity of the ERBB kinase inhibitor neratinib in 21 types of cancer having 42 different mutations in the ERBB2 and ERBB3 receptor tyrosine kinases (HER2 and HER3, respectively) (Hyman et al., 2018). Neratinib is an irreversible pan-ERBB (pan-HER) inhibitor approved in 2017 for a relatively narrow indication: patients with early-stage HER2-positive breast cancer who had postsurgical adjuvant therapy using the ERBB2 inhibitor trastuzumab (Singh et al., 2018). Mutation or overexpression of ERBB receptors is implicated in a range of human cancers, but ERBB biology is complex, and preclinical models provide conflicting data on the potential efficacy of ERBB inhibition in human disease. The multicenter SUMMIT basket trial seeks to resolve this issue by testing neratinib in a wide range of tumor types and genotypes.
In common with a majority of Phase II clinical trials, SUMMIT has no comparator control arm, and instead makes use of a Simon two-stage optimal design (Simon, 1989). In this approach a trial has two stages: stage 1 tests a drug in few patients (commonly ~7) per tumor type, and stage 2 expands the number of patients to be tested (commonly to ~ 25) specifically for tumor types that showed promise in stage 1. Drug response is measured using a radiological assessment of tumor volume according to RECIST (response evaluation criteria in solid tumors) (Eisenhauer et al., 2009) followed by dichotomous scoring. Patients whose tumors shrink by ≥30% are scored as responders and the others as nonresponders; the fraction of responders represents the overall response rate (ORR). A binomial test is then used to evaluate the ORR statistically. Using a prespecified value of ORR for a lack of efficacy (the null hypothesis, typically set at ORR ≤ 10%), the ORR expected under the alternative hypothesis (typically ORR ≥30%), and the desired rates of type I and type II error (≤ 5% and ≤ 20%, respectively, corresponding to ≥80% power), the Simon design uses a binomial distribution to calculate the minimum number of patients who must respond in each subgroup for the null hypothesis to be rejected; this calculation is performed separately for each subgroup. If the number of responses in the first stage of a basket is consistent with the null hypothesis, then the treatment is considered futile and corresponding trial arm is terminated. Otherwise the arm expands in a second stage involving additional patients with the goal of testing the alternative hypothesis (e.g., 30% ORR); parameters of the trial design determine the number of patients enrolled in the second stage and the number of responses needed for a therapy to be considered efficacious. The Simon design thereby seeks to detect strong responses in the first phase while minimizing futility–the number of patients subjected to ineffective treatments–and then expands potentially positive subgroups for a larger and more rigorous test in the second phase. In the case of the SUMMIT trial, up to seven patients were initially enrolled per subgroup in stage 1 and response was evaluated radiologically. Enrollment in each basket was expanded in stage 2, typically to include 25 patients in total, only if at least one stage 1 patient exhibited an objective overall response.
Because all basket trials described to date use ORR, in which the assessment of response is dichotomous, the magnitude of tumor-volume changes, and changes in other measures of drug response such as the rate of tumor progression, are not considered. The Simon design, as well as supporting Bayesian and frequentist interim analyses developed to help determine whether to close enrollment in any subgroups (Cunanan et al., 2017a, 2017b; Drilon et al., 2018; Hyman et al., 2015; LeBlanc et al., 2009; Simon et al., 2016), also assesses efficacy independently for each subgroup thereby answering the question, “Which cancer subtypes surpass a prespecified threshold for response?” Note that subtype in this case can refer either to the tumor tissue of origin or to a genomic feature such as type of mutation.
In this paper, we propose a complementary approach in which tumors are compared across subtypes in a basket trial by using permutation testing to evaluate two related null hypotheses: no difference in efficacy by tumor type or no difference in efficacy by class of mutation. These hypotheses are directly relevant to basket trials that may ultimately lead to Phase III trials, which test therapies for multiple tumor types defined by genetic features. Moreover, the formulation of hypothesis testing with respect to difference has the substantial benefit that all patients enrolled in a trial contribute to the null distribution, and that continuous response variables rather than dichotomous scores can be evaluated (in the current work, magnitude of change in tumor volume and duration of Progression-Free Survival or PFS).
For any specific subgroup, null distributions having an appropriate number of patients are generated by subsampling the all-patient distribution. When response rates are low, as in SUMMIT, the no-difference null hypothesis is similar to a null hypothesis of low or no activity and can be used to test whether any group has significantly superior responses. When response rates are high, as with larotrectinib, the no-difference hypothesis tests for both inferior and superior responses. In the case of SUMMIT, lung cancers fail Simon criteria but significantly exceed the no-difference null with respect to volume changes and PFS. In contrast, breast cancers in SUMMIT exhibit a high ORR, but are no different from average with respect to PFS. These data suggest an alternative approach for interpreting basket trials with the potential to better discover therapeutic opportunities for subsequent testing in Phase III trials. While these applications of permutation testing represent post hoc analysis of published trials, the approach can be used for analyzing ongoing basket trials and potentially adapted for making real-time enrollment decisions.
RESULTS
Analysis of SUMMIT Trial Reveals Overlooked Therapeutic Opportunity for Neratinib in Lung Cancers Carrying ERBB2 Exon 20 Mutations
Results for the first 141 patients in the SUMMIT basket trial were recently reported (Hyman et al., 2018). Multiple genetic markers were assessed, including 31 unique ERBB2 and 11 unique ERBB3 mutations. Clinical response was measured by radiological assessment of tumor-volume changes and by progression-free survival (PFS), the time from enrollment until death or radiological evidence of tumor progression. FDA guidance recommends the use of ORR as measured by RECIST criteria (Eisenhauer et al., 2009) in master-protocol trials (U.S. Food and Drug Administration, 2018) largely because ORR is an accepted surrogate endpoint for accelerated drug approval (Pazdur, 2008). Although the SUMMIT trial uses ORR, the authors report changes in tumor volume as a continuous variable. In common with previous basket trials (Cunanan et al., 2017b) SUMMIT (Hyman et al., 2018) recorded PFS data, but it was not analyzed formally or compared with ORR; this reflects the perceived challenge of evaluating 21 tumor types using data from only 141 patients. Another commonly expressed concern is that PFS duration may not be comparable for cancers having different rates of progression. However, it is also controversial whether tumor-volume changes are predictive of overall survival (OS), the “gold standard” (Buyse et al., 2000; El-Maraghi and Eisenhauer, 2008; Fleming and DeMets, 1996; Kaiser, 2013). For example, in a retrospective analysis of non-small-cell lung cancer, PFS was correlated with OS (Blumenthal et al., 2015), but ORR was not. The use of PFS in breast cancer trials is also supported by a variety of other data (Adunlin et al., 2015). Thus, although it is standard practice to rely on ORR rather than PFS in basket trials, we hypothesized that the use of both of types of information might provide new therapeutic insights (see Discussion). There is no established method for thresholding PFS data into dichotomous responder and nonresponder classes. Thus, it is not possible to use a binomial test. Instead we used permutation testing by repeated Monte Carlo resampling of the distribution of continuous volume changes and PFS from all patients as a means to construct null distributions for each subgroup. We tested the null hypothesis: following exposure to neratinib, there was no difference in volume change or PFS for a subgroup (as defined by tumor type or genotype) relative to all patients.
When neratinib-treated patients in SUMMIT were classified by tissue of origin (Figure 1A) and compared with an appropriately resampled no-difference null distribution, breast cancers exhibited significantly greater volume reduction than any other tumor type (a 45% difference in average volume change from all nonbreast tumors; p < 10−6). This agrees with the conclusion by Hyman et al. that breast cancers are the most neratinibresponsive of all tumor types tested based on ORR (Hyman et al., 2018). Because breast cancers dominate volume-change data, we constructed a second set of null distributions for volume changes that included only nonbreast (NB) tumors (see STAR Methods).
Figure 1. Analysis of Neratinib Response by Tumor Tissue of Origin.
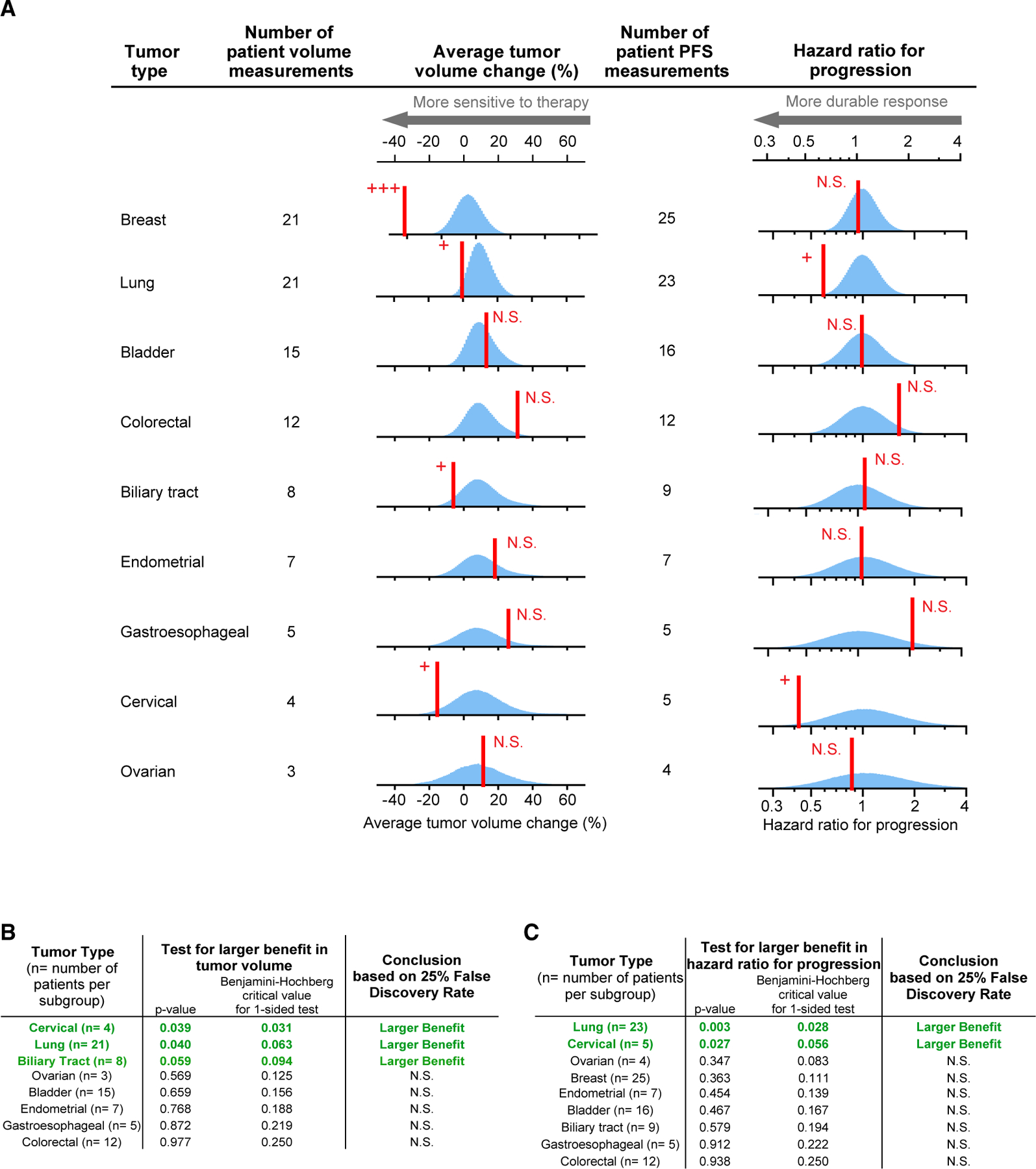
(A) Red line, observed response; blue histogram, responses simulated according to the null hypotheses of no difference in response between tumors types. As explained in the main text, breast-tumor-volume changes are compared with null distributions drawn by Monte Carlo resampling from all tumors; for this reason, the null distribution for breast-tumor volume changes has a different mean. For all other tumor volume changes, the null distributions are drawn from all nonbreast tumors due to breast tumors being a strong outlier (p < 10−6; see STAR Methods).
(B and C) “Hazard ratio for progression” null distributions are drawn from all tumors. (B) Observed responses that significantly exceed the null hypothesis, according to Benjamini-Hochberg procedure (to control the false discovery rate during multiple hypothesis testing), are indicated with +; N.S. denotes not significant; +++ denotes p < 10−6 (B and C). (C) Observed responses that significantly exceed the null hypothesis for hazard ratio for progression, according to Benjamini-Hochberg procedure (to control the false discovery rate during multiple hypothesis testing), are indicated with +; N.S. denotes not significant; +++ denotes p < 10-6.
When NB distributions were resampled and compared with tumor-specific volume-change data, lung, cervical, and biliary cancers were found to significantly exceed the no difference by type null hypothesis (p = 0.04, 0.04, and 0.06, significant according to Benjamini-Hochberg procedure; Figure 1B). Whereas cervical and biliary cancers passed the criteria for the first stage of a Simon two-stage design, lung cancer failed at the second stage (Table 1). Thus, evaluation of continuous volume-change data identified a statistically significant volume change in lung cancers that was found to be negative by dichotomous scoring and by a binomial test used in a traditional two-stage design. This discordance arises because half of lung cancers shrank on therapy but only one shrank enough to surpass a threshold of >30% tumor-volume change and was therefore classified as a response by RECIST. The permutation test and Simon criteria therefore provide different insights into the drug responsiveness of this small patient population.
Table 1.
Conclusions from Analysis of Neratinib in ERBB-Mutant Tumors in Context of Trial Status
| Status in Simon Optimal 2-Stage Design |
Responses Significantly Different from Other Tumorsa? |
||||
|---|---|---|---|---|---|
| Tumor Type | Number of Patients | Stage 1 | Stage 2 | Volume | PFS |
| Ovarian | 4 | ongoing | – | – | – |
| Gastroesophageal | 5 | ongoing | – | – | – |
| Colorectal | 12 | failed | – | – | – |
| Bladder | 16 | failed | – | – | – |
| Endometrial | 7 | failed | – | – | – |
| Biliary | 9 | passed | ongoing | superior | – |
| Cervical | 5 | passed | ongoing | superior | superior |
| Lung | 26 | passed | failed | superior | superior |
| Breast | 25 | passed | passed | superior | – |
Dash denotes no significant difference by Benjamini-Hochberg procedure.
Analysis of Progression-Free Survival
Comparison of response duration among different types of tumors is potentially complicated by differences in tumor kinetics. While slow growth is not in and of itself a measure of “sensitivity” to therapy, the durability of response as measured by PFS is clinically important, is commonly used as an endpoint in conventional cancer trials, and can provide complementary insight to volume changes. We therefore applied permutation testing to PFS. The null distribution was drawn from all tumor types (n = 141) because no tumor type was so responsive as to dominate the distribution (STAR Methods). Significantly smaller hazard ratios, which are indicative of longer PFS, were identified by a no-difference test in cervical cancers (p = 0.03; median PFS, 20 months) and lung cancers (p = 0.003; median PFS, 5.4 months) but–strikingly–not in breast cancers (p = 0.36; median PFS, 3.5 months, Figure 1C). Only five neratinib-treated cervical cancers are present in the SUMMIT dataset, and the empirical null distribution was consequently broad (Figure 1A). Nonetheless, the observed responses were sufficiently strong and durable to achieve statistical significance, (Cervical tumors also met the criteria to begin stage 2, and so additional patients are currently accruing [Table 1]). Whereas lung cancers exceed no-difference tests for both volume changes and hazard ratios based on PFS data, breast cancers differ from the overall population by volume change alone. Lung cancers therefore appear to represent a therapeutic opportunity for neratinib missed by dichotomous assessment of response.
Our approach identifies differences in PFS that are statistically significant, but interpreting whether this is clinically meaningful requires attention to absolute duration in context of the kinetics of that specific tumor type. In this case, as noted by Hyman, a therapeutic response exceeding 12 months in non-small-cell lung cancer is clinically meaningful (Hyman et al., 2018). Moreover, in the case of neratinib-treated lung and cervical cancers, significant differences from the null distribution were observed for both volume-change and PFS data, increasing confidence in the conclusion that the drug may be active in these tumor types (see also Discussion).
Analysis of Genetic Biomarkers
Differences in neratinib sensitivity have been observed in cell lines with different mutations in ERBB receptors (Nagano et al., 2018), but the impact of such differences on therapeutic response has not been reported for patients. When a basket trial is structured as many subtrials each involving tumors having different tissues of origin (as in SUMMIT), the evaluation of response rate (and cohort expansion in the case of a two-stage trial) is exclusively based on the tissue of origin and not genotype. However, such trials generate the necessary data for post hoc analysis of the influence of genotype. SUMMIT enrolled patients on the basis of qualifying mutations in ERBB2 or ERBB3, which were classified as “hotspot” if they occurred in recurrently mutated regions of either gene or “nonhotspot” if they lay in other, rarely mutated regions (Hyman et al., 2018). When we applied permutation testing to ERBB genotypes and neratinib responses we found that tumors with ERBB2 hotspot mutations exceeded the no-difference null model as judged by changes in tumor volume and also PFS (Figure 2A) (p = 0.03 for volume changes and p = 0.0005 for PFS; Figures 2B and 2C), which agrees with Hyman’s conclusion that ERBB2 hotspot tumors are responsive to therapy. When ERBB2 hotspot mutations were further divided into functional classes (e.g., S310; Exon 20 insertions; V777; L755; and a class of “other hotspot mutations”), Exon 20 insertions significantly exceeded the no-difference null for PFS (p = 0.01), which could be attributed almost exclusively to lung tumors (Hyman et al., 2018). (Six lung tumors were among the seven most durable responses observed for all cancer types having Exon 20 insertions.) No other significant signals were detected among subgroups when scoring for classes of ERBB2 mutation (Table S1).
Figure 2. Analysis of Neratinib Response by General Mutation Class.
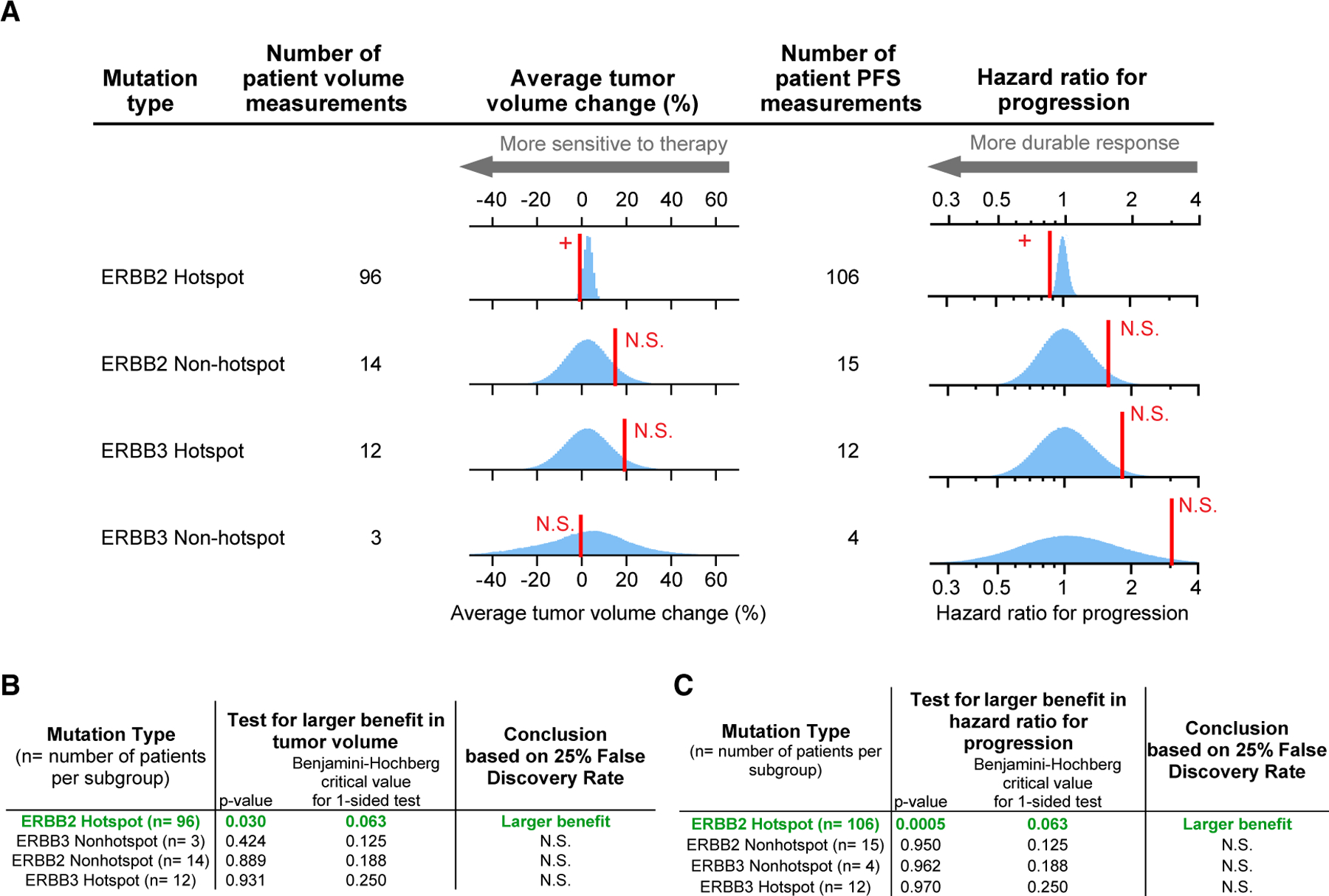
(A) Red line, observed response; blue histogram, responses simulated according to the null hypotheses of no difference in response between tumors types.
(B) Observed responses that significantly exceed the null hypothesis, according to Benjamini-Hochberg procedure (to control the false discovery rate during multiple hypothesis testing), are indicated with +; N.S. denotes not significant. (C) Observed responses that significantly exceed the null hypothesis for hazard ratio for progression, according to Benjamini-Hochberg procedure (to control the false discovery rate during multiple hypothesis testing), are indicated with +; N.S. denotes not significant. See also Table S1.
ERBB2 mutations are substantially less common in lung cancer than ERBB1 (EGFR) mutations, having been identified in about 3% of patients with non-small-cell lung cancer; however, 90% of these mutations lie in Exon 20 (Arcila et al., 2012). Exon 20 in ERBB1 and ERBB2 encodes residues in the middle of the tyrosine kinase domain and recurrent mutations in this region have been associated with intrinsic resistance to clinically approved EGFR inhibitors and correlate with a poor patient prognosis (Robichaux et al., 2018; Vyse and Huang, 2019). The demonstration that neratinib is potentially active clinically in lung cancers with Exon 20 mutant ERBB2 is therefore of clinical significance.
Permutation Testing Provides Statistical Support for the Use of Imatinib in Select Cancer Types
As a second application of our approach we examined the Phase II, open-label Imatinib Target Exploration Consortium Study B2225, which tested imatinib in 186 patients having 40 different malignancies. (In this trial only 145 out of 186 patients who were enrolled had evaluable responses and also fell into subtypes with a sample size greater than 2; thus, only 145 responses were used for the analysis presented here) (Heinrich et al., 2008). Objective responses were observed in six types of malignancy, of which five were described as “notable” by Heinrich et al. but not subjected to formal statistical analysis. By testing against a no-difference null we found that three malignancies had a significantly higher ORR to imatinib than all other tumors tested (dermatofibrosarcoma protuberans, myeloproliferative disorders, and hypereosinophilic syndrome; Table 2). These malignancies were represented by 6 to 13 patient measurements each, out of 186 total patients, confirming that statistically significant drug activity can be detected in small subgroups. Imatinib was approved for use in dermatofibrosarcoma protuberans by the FDA in 2006, partly based on earlier data from the Imatinib Target Exploration Consortium Study B2225 ((McArthur et al., 2005) and, following a Phase II study published in 2010 (NCT00122473), it was incorporated into the National Comprehensive Cancer Network’s treatment guidelines for this malignancy (Navarrete-Dechent et al., 2019). The use of imatinib in hypereosinophilic syndrome is supported by case studies (Gleich et al., 2002; Pardanani and Tefferi, 2004), and our analysis provides additional support from a Phase II basket trial for this use (Heinrich et al., 2008).
Table 2.
Analysis of Imatinib Tumor-Volume Responses by Tumor Type
| Test for Larger Benefit in Tumor Volume |
|||
|---|---|---|---|
| Tumor Type (n = number of patients per subgroup) | pValue | Benjamini-Hochberg Critical Value for 2-Sided Test | Conclusion Based on 25% False Discovery Rate |
| Dermatofibrosarcoma protuberans (n = 11)a | < 0.001 | 0.015 | larger benefit |
| Myeloproliferative disorders (n = 6)a | 0.008 | 0.029 | larger benefit |
| Hypereosinophilic syndrome (n = 13)a | 0.012 | 0.044 | larger benefit |
| Aggressive fibromatosis (n = 17) | 0.798 | 0.059 | N.S. |
| Synovial sarcoma (n = 15) | 0.934 | 0.074 | N.S. |
| Myelofibrosis (n = 6) | 1.000 | 0.088 | N.S. |
| Multiple myeloma (n = 6) | 1.000 | 0.103 | N.S. |
| Intraocular melanoma (n = 3) | 1.000 | 0.118 | N.S. |
| Malignant melanoma (n = 4) | 1.000 | 0.132 | N.S. |
| Mesothelioma (n = 3) | 1.000 | 0.147 | N.S. |
| Adenoid cystic carcinoma (n = 11) | 1.000 | 0.162 | N.S. |
| Desmoplastic small round cell tumor (n = 5) | 1.000 | 0.176 | N.S. |
| Chordoma (n = 4) | 1.000 | 0.191 | N.S. |
| Ewing’s sarcoma (n = 3) | 1.000 | 0.206 | N.S. |
| Chondrosarcoma (n = 6) | 1.000 | 0.221 | N.S. |
| Liposarcoma (n = 11) | 1.000 | 0.235 | N.S. |
| Leiomyosarcoma (n = 9) | 1.000 | 0.250 | N.S. |
Significant by Benjamini-Hochberg procedure.
Permutation Testing Provides Statistical Support for Tumor-Agnostic Use of Larotrectinib and Pembrolizumab in Biomarker Positive Populations
Basket trials of the immune checkpoint inhibitor pembrolizumab (Le et al., 2017) and kinase inhibitor larotrectinib (Drilon et al., 2018; Lassen et al., 2018) contrast with the trials of neratinib and imatinib described above because response rates were high: both drugs were found to be effective in tumors from multiple tissues positive for a particular genetic biomarker. In the case of a basket trial of pembrolizumab (NCT01876511) involving 86 patients and 12 tumor types, tumors with mismatch repair (MMR)-deficiency were found to be highly responsive to PD-1 blockade regardless of tissue of origin (Le et al., 2017). Similarly, high rates of larotrectinib response were observed among 122 patients having 15 different types of tumors expressing TRK-fusion proteins (NCT02122913, NCT02637687, and NCT02576431) (Drilon et al., 2018; Lassen et al., 2018). When we compared data from each of these trials with a no-difference null hypothesis, testing in for both superiority and inferiority, no significant differences were observed for any tumor type represented by three or more patients. (This corresponded to eight tumor types for larotrectinib and seven types for pembrolizumab.) The sole exception was infantile fibrosarcomas, which were more responsive to larotrectinib than other TRK-fusion tumors (Figures 3A, 3B, 4A, and 4B). Our reanalysis therefore supports tumor-type agnostic approval of pembrolizumab for MMR-deficient cancers and larotrectinib for cancers carrying TRK fusions.
Figure 3. Analysis of Larotrectinib by Tumor Tissue of Origin Finds Consistent Activity in Multiple Tumor Types, and Even Greater Activity in Infantile Fibrosarcoma.
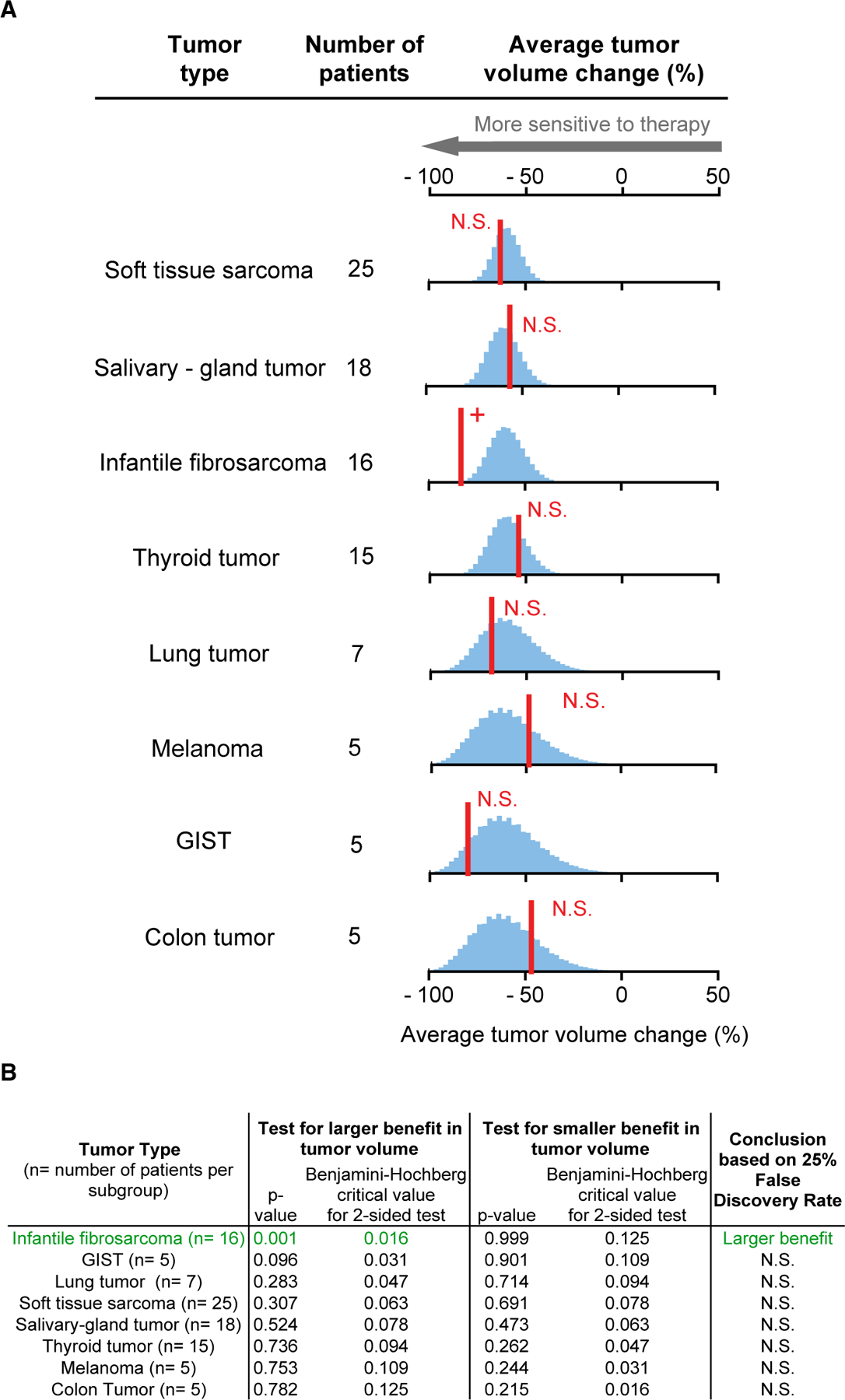
(A) Red line, observed average response; blue histogram, responses simulated according to the null hypothesis of no difference in response between tumors types.
(B) Observed responses that significantly exceed the null hypothesis, according to Benjamini-Hochberg procedure (to control the false discovery rate during multiple hypothesis testing), are indicated with +; N.S. denotes not significant. See also Table S2.
Figure 4. Analysis of Pembrolizumab by Tumor Tissue of Origin Finds Consistent Activity in Multiple Tumor Types.
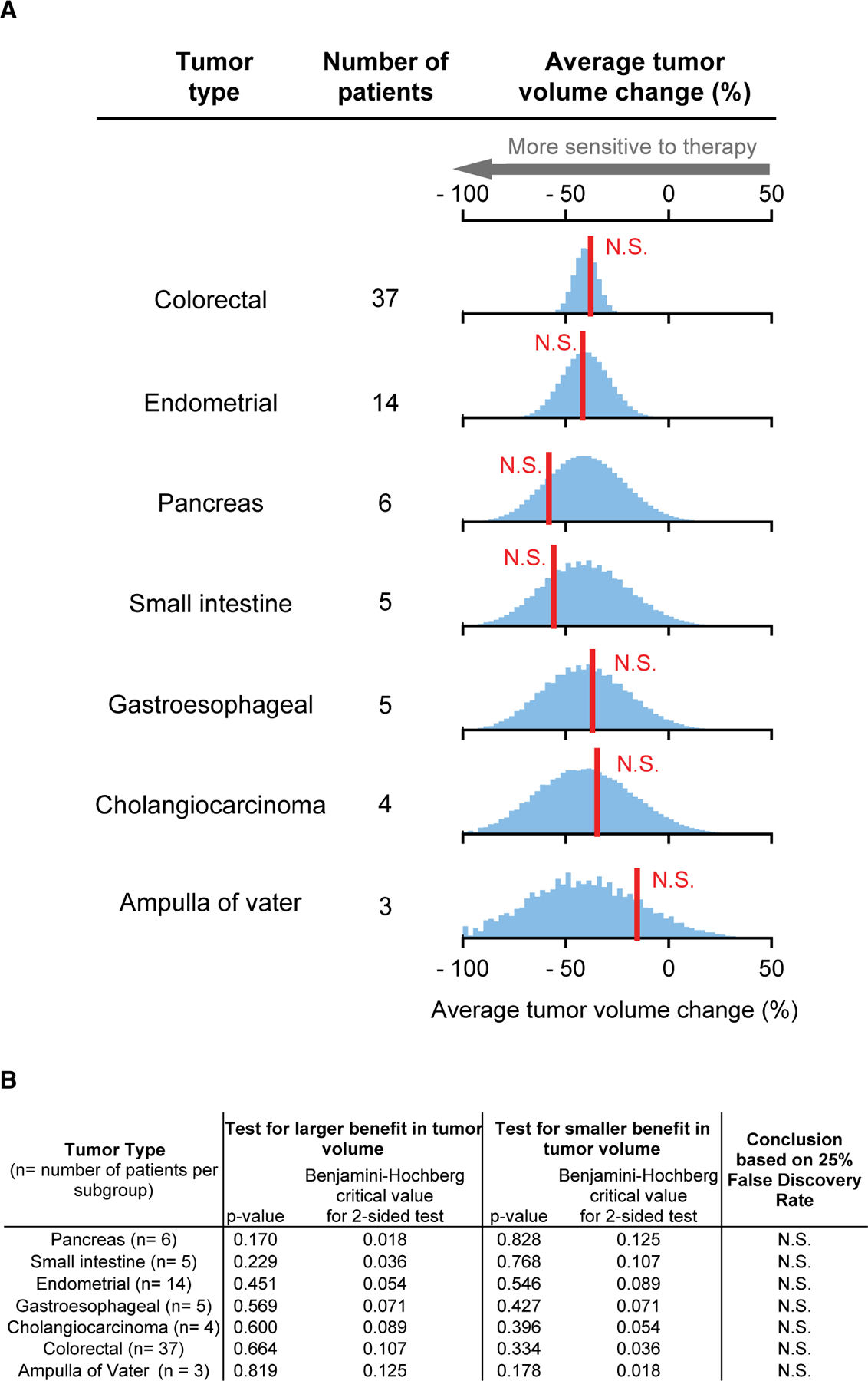
(A) Red line, observed average response; blue histogram, responses simulated according to the null hypothesis of no difference in response between tumors types.
(B) Observed responses that significantly exceed the null hypothesis, according to Benjamini-Hochberg procedure (to control the false discovery rate during multiple hypothesis testing), are indicated with +; N.S. denotes not significant. See also Figure S1.
More recent trials of pembrolizumab in noncolorectal cancers in KEYNOTE-158 (NCT02628067) (Marabelle et al., 2020) and in colorectal cancer in KEYNOTE-164 (NCT02460198) (Le et al., 2020) found that patients in both trials exhibited similar distributions of tumor-volume changes (Figure S1). Unfortunately, volume-change data for KEYNOTE-158 were not reported for specific tumor types, so we cannot test whether differences exist. One of the two published larotrectinib trials reported drug responses by NTRK paralog and fusion partner (Drilon et al., 2018; Lassen et al., 2018) and reanalysis of this trial (n = 55) revealed no difference by NTRK-fusion type (Table S2). However, patient-level response and mutation data were not reported in larger, subsequent trials of larotrectinib or pembroluzimab making reanalysis of mutation-specific differences impossible with published data. Permutation testing could be applied by trial sponsors, however, or mandated by regulatory agencies to determine whether a refinement in the current tumor-agnostic approval is warranted.
Comparison of Type 1 and Type 2 Errors of Permutation Tests and Binomial Tests in Basket Trials
As described above, when some but not all tumor subtypes respond to therapy, responsive subtypes can be identified by permutation tests that evaluate a “no difference by tumor type” null based on continuous measures of responses or a prespecified “low efficacy” null for each tumor type using dichotomous measures of response–typically ORR–and binominal testing (as in the Simon two-stage design). To compare rates of type I error (a false positive corresponding to misclassification of a nonresponsive tumor type as responsive) and type II error (a false negative, corresponding to misclassification of a responsive tumor type as nonresponsive) between these approaches, we simulated basket trials in which a proportion of tumor subtypes responded to therapy to differing degrees (see STAR Methods).
As expected, by permutation testing on continuous volume-change data, the false-positive rate (type 1 error) declined as the treatment effect increased (i.e., the decrease in tumor volume was greater). In small cohorts typical of the first stage of a two-stage trial (n = 7 patients per tumor type), permutation tests had substantially smaller false-positive rates than binomial tests (Figure 5). Two-stage trial designs balance the two aims of detecting positive signals in small patient populations and minimizing the number of patients exposed to a potentially futile treatment. In the Simon two-stage design, stage 1 is intentionally permissive with a high false-positive rate (stage 2 is more stringent). In contrast, permutation tests had a smaller false-positive rate in stage 1, and positive findings were associated with greater confidence. This came at the expense of a lower true-positive rate (also known as power, or 1 minus the type II error rate), making permutation tests more stringent than binomial tests in stage 1. Power could in principle be increased in the permutation test, at the cost of greater Type 1 error, but we did not explore this in simulation.
Figure 5. Comparison of False-Positive and True-Positive Rates of Permutation Tests and Binomial Tests in Basket Trials for Different Numbers of Responsive Subgroups.
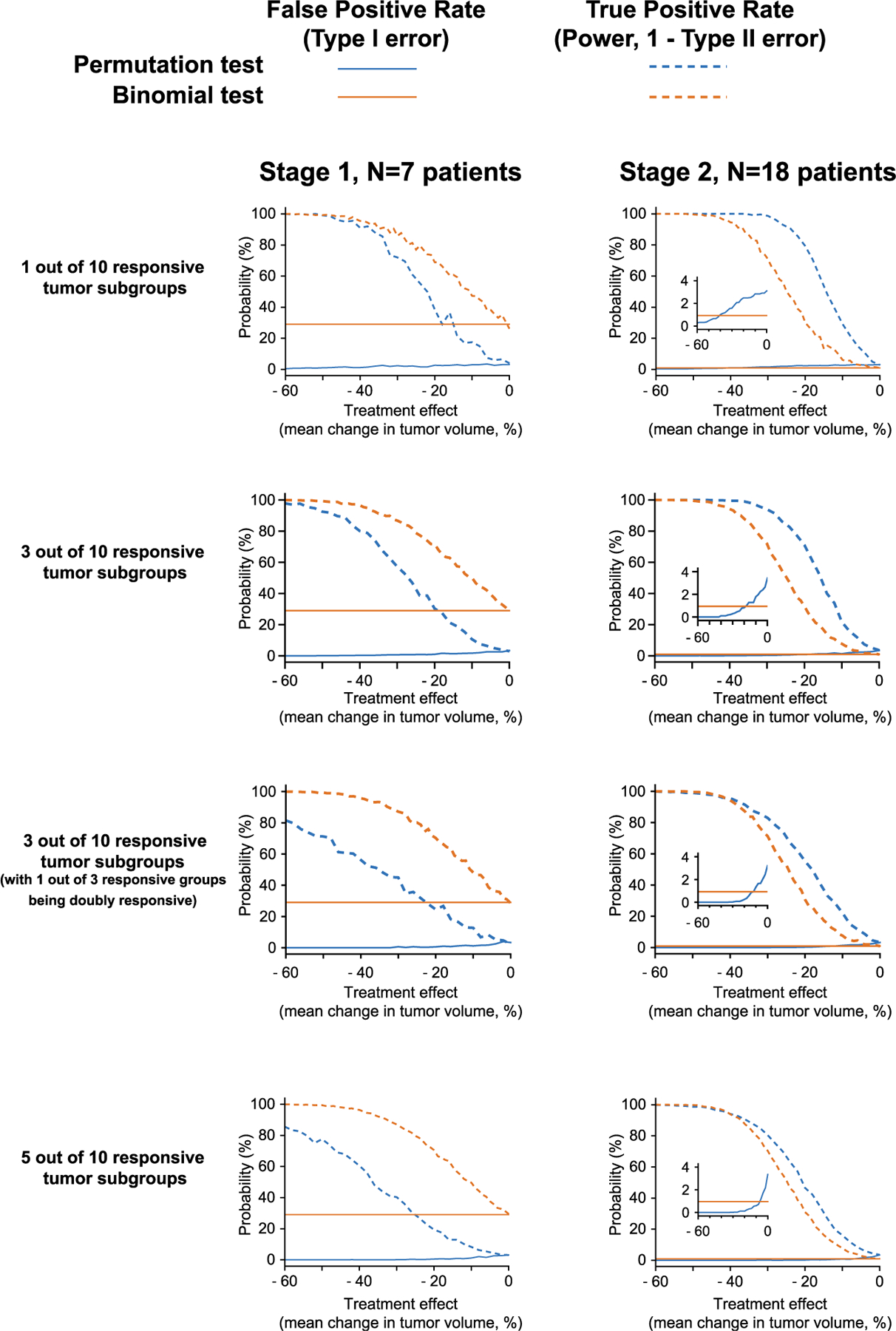
Basket trials were simulated in which 1 out of 10, 3 out of 10, and 5 of 10 tumor types respond to therapy. False-positive and true-positive rates (also known as type 1 error rate and power, respectively) for detecting one of the responsive subgroups were compared between: (blue) permutation tests, comparing all tumor types to find those significantly more responsive than average, and (orange) binomial tests of objective response rate, such as are used in two-stage trial designs (see STAR Methods). Note that the third row depicts the characteristics for detecting either one of the two responsive groups, in the presence of one other group that is doubly responsive. Simulations were repeated across a range of treatment effect sizes (difference in mean volume change between responsive and nonresponsive tumors) for 7 patients per tumor type (typical of the first stage of a two-stage trial), and 18 patients per tumor type (typical of the second stage). Inset: zoom on the type 1 error rate (<4%). See also Figure S2.
In larger cohorts typical of stage 2 (n = 25 patients per tumor type), permutation tests had greater true-positive rate than a binomial test for all effect sizes. Permutation testing also had a smaller false-positive rate for treatment effects stronger than 20% difference in tumor volume. These findings remained qualitatively the same irrespective of the number of responsive subgroups chosen for the simulation. (Figure 5 shows simulations for 1 out of 10 responsive subgroups, 3 out of 10 responsive subgroups, 3 of 10 responsive subgroups in which one of these subgroups is doubly responsive, and 5 out of 10 responsive subgroups.) We also found that significant signals could be reliably detected (with 80% power) using permutation tests when only 3 patients exhibit objective responses in either stage of the Simon design (Figure S2), demonstrating the utility of this approach in detecting signals in small numbers of patients. The superior performance of permutation testing in these simulations is in agreement with recent theoretical analysis (Arfè et al., 2020). Historically, an important advantage of binomial tests was that they could be computed rapidly and exactly using simple algorithms and slow computers. Permutation testing with resampling (necessary when n is too large for an exact enumeration) is more computationally intensive; this was an issue in 1980s when basket trials were first proposed but is no longer relevant.
DISCUSSION
A primary motivation for performing a basket trial is to determine which of several tumor types or genotypes are sufficiently responsive to an investigational therapy to warrant further study in a Phase III pivotal trial. Because Phase II trials rarely involve a no-treatment control population, contemporary designs for basket trials use a prespecified cutoff to evaluate whether or not a drug is effective. Currently this involves a dichotomous assessment of tumor-volume changes to determine if the ORR exceeds a threshold set by a binomial test. In this paper we demonstrate an alternative approach involving a permutation test in which both continuous volume changes and survival data (PFS) are formally compared against empirical null distributions that are constructed using data from all patients in the trial. Responses in subgroups are then compared with the null distribution to test the hypothesis of no difference in efficacy by subtype (most commonly tumor tissue of origin or mutation class or genotype) as a means to identify subtypes that are most responsive.
Constructing subtype-specific null distributions involves repeated Monte Carlo resampling of an all-patient distribution, drawing the same number of samples as the number of patients in the subtype. The resulting null distributions appropriately anticipate the greater variability observed in small cohorts, thereby adjusting the threshold for identifying a statistically significant increase or decrease in response based on a prespecified false-positive (type 1) error rate. For example, the SUMMIT trial reported PFS data for five cervical cancer patients. In this case, the null distribution was calculated by repeatedly sampling five response durations from the set of duration data for all patients, generating a relatively wide subtype-specific null distribution. Despite this, the observed hazard ratio in cervical cancers was significantly smaller than the no-difference null distribution (p = 0.03) implying an above-average response. Conclusions drawn from testing for no difference in continuous volume change can differ from binomial testing based on ORR. For example, lung cancers exposed to neratinib exceed the no-difference null with respect to both volume changes (p = 0.04; sampling from all nonbreast tumors) and PFS (p = 0.003, sampling from all tumors) even though lung cancers failed the second stage of a Simon design. In contrast, breast cancers exhibited highly significant changes in tumor volume by both Simon and no-difference criteria but failed the no-difference test with respect to PFS. We therefore propose that neratinib be studied further in ERBB-mutant lung tumors and that early evidence be sought in expansion cohorts to ascertain whether neratinib can in fact provide a clinically meaningful survival benefit in breast cancer patients.
Basket trials of larotrectinib in TRK-fusion-positive cancers and pembrolizumab in MMR-deficient cancers are characterized by high response rates (Drilon et al., 2018; Lassen et al., 2018; Le et al., 2017). By permutation testing, no subgroup was identified in either trial as being significantly less responsive than the average of all tumors. Thus, a formal no-difference test supports the recent tumor-agnostic FDA approvals of larotrectinib and pembrolizumab for cancers with specific genetic features. Infantile fibrosarcomas stood out in our reanalysis as being more responsive to larotrectinib than other TRK-fusion tumors, but unfortunately recent publications of larger trials of larotrectinib (and pembrolizumab) lack the patient-level data needed to look more broadly at subtype-specific differences in drug response.
Comparison of Subgroups in Basket Trials
The continuing growth of genomic and biomarker-driven oncology enables refined subdivision of patient populations whether in a basket trial or by stratifying patients in conventional Phase II and Phase III studies (Hyman et al., 2018). The promise of such subdivision is better precision in oncology, but the risk is smaller subsamples and reduced statistical significance; thus, new approaches to analyzing tumor subtypes are required. Our reformulation of null hypotheses, generation of null distributions by permutation, and derivation of empiric p values for comparing responses across subgroups in basket trials has the potential to better identify therapeutic opportunities for targeted drugs. The approach is grounded less in novel statistical theory (permutation tests are well established) than in the accumulation of empirical evidence from completed basket trials. Nonetheless, among all tests that control the type I error rate at a fixed α level, the permutation test has been proven mathematically to be the procedure that maximizes finite-sample power for a late-stage study conditional on early-stage data (Arfè et al., 2020). Simulation shows that permutation testing is even applicable to small patient populations and makes it possible to obtain appropriately scaled null distributions and derive empirical p values for drug response as measured by both volume change and PFS. The methodology is expected to be of value other Phase II studies that lack control arms and involve multiple patient subgroups each of which is generally thought to be too small for formal comparison (Hyman et al., 2018).
Despite the clear importance for precision medicine of reliably comparing drug response across subgroups, this is not conventionally done; FDA guidance specifically discourages it, probably because of the dangers of false discovery (Pazdur, 2008; U.S. Food and Drug Administration, 2018). The specific concern is that, in trials with a large number of arms, testing all arms against each other involves a potentially uncontrolled multihypothesis test. However, in the procedure described here, all null distributions are sampled from the same all-patient distribution, and the Benjamini-Hochberg procedure is used to appropriately correct significance thresholds used to test individual hypotheses. In some cases, one tumor subtype can dominate responses for the entire trial, obscuring smaller but potentially significant differences in other subtypes. In SUMMIT this was true of volume changes in neratinib-treated breast cancers (p<10−6 relative to the no-difference null). To enable detection of next-most-different volume responses, we created an additional null distribution in which breast cancers were removed from the all-patient distribution. We performed this procedure only for a single outlier subgroup because repeated adjustment of the null distribution heightens the risk of false discovery, as described above (Bishop and Thompson, 2016) (see STAR Methods).
A second potential concern arises when comparing the magnitude of volume changes across subgroups; because tumors respond differently to therapy, the magnitude of volume changes and the frequency of confounding factors, such pseudoprogression (an increase in the size of a primary tumor for reasons other than disease progression, such as immune infiltration, followed by tumor regression), (Ma et al., 2019) also differ. However, in scoring ORR in the Simon design, a very similar issue arises; the same threshold for volume change is used to establish a meaningful response in all subgroups. Thus the need for a common interpretation of subgroups is not specific to our methodology and arises with all other methods (e.g., Bayesian or frequentist) of assessing drug efficacy (Berry, 2015). It is also noteworthy that the 30% reduction in volume conventionally used to threshold ORR subdivides a unimodal distribution of tumor-volume changes. The need for a threshold is often justified based on the technical complexities of tumor-volume assessment (Sharma et al., 2012); a 30% difference is generally judged as greater than measurement noise, but the introduction of threshold is nonetheless arbitrary.
A third potential concern involves our use of PFS data to compare subgroups. Historically, a key limitation on the use of PFS data in basket trials is that there exists no agreed upon threshold in duration that can define a meaningful (or “objective”) response. (In contrast, tumor-volume changes are commonly thresholded to determine ORR.) In the absence of a PFS threshold and a dichotomous score, the binomial test in the Simon two-stage design cannot be used. Permutation testing using an all-patient null distribution overcomes this issue. A biological concern in comparing PFS data across tumor types derives from the observation that different cancers naturally progress at different rates (Friberg and Mattson, 1997). However, rates of progression for solid tumors in the SUMMIT trial were similar to each other; tumors that did not shrink on therapy progressed rapidly irrespective of tumor type (85% of nonshrinking tumors progressed in ≤ 3 months). Moreover, it is well established that overall survival, the gold standard for measuring response to anticancer drugs, correlates more strongly with duration of PFS than with tumor-volume changes (Fleming and DeMets, 1996; Kaiser, 2013; Seymour et al., 2010; Zabor et al., 2016). Significant reductions in tumor volume do not necessarily predict durable PFS, and durable PFS can be achieved with modest changes in tumor volume. Thus, past experience and theoretical considerations suggest that PFS and tumor volume can both provide valuable data in a permutation testing framework for most tumor types. We nonetheless note that the strength of correlation between PFS or tumor-volume changes and overall survival differs across cancer types, and ultimately the decision regarding whether to include one or both of these data types is likely to be influenced by clinical experience in a specific disease and treatment setting (Davis et al., 2012). If an effect is only apparent in PFS but not size change, one should carefully consider whether the particular tumor type is naturally slow growing. The ideal situation arises when reductions in tumor volume and increases in PFS are concordant and both significant, as observed for neratinib in ERBB-mutant lung and cervical cancers.
Limitations of This Study
The current study involves only retrospective analysis of published trials. A key limitation in such an approach is that it is contingent on the availability of patient-level outcome data across tumor subtypes. Unfortunately, such information is not currently required for the publication of basket trials and is often missing in favor of summary statistics. There is no ethical reason for failing to report these data, and their omission introduces a substantial barrier to gaining new insight from a completed trial. Going forward, we believe that new basket trials should use permutation testing to compare response between tumor types and genetic features, whenever this method is compatible with the trial design. An appropriately conservative approach might be to apply an established Simon or Bayesian-Simon design for enrollment decisions and use permutation testing for analysis. Using permutation testing for real-time enrollment decisions is also feasible but requires an exploration of how differences in accrual rates across subgroups would impact power and false-positive rates; examination of how external, historical control arms could contribute to null distributions for such analysis; and a comparison of permutation methods to Bayesian adaptive approaches. Such analysis would be best performed when a trial is first designed.
STAR★METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Prof. Peter Sorger (peter_sorger@hms.harvard.edu, cc: sorgeradmin@hms.harvard.edu).
Materials Availability
This study did not generate new unique reagents.
Data and Code Availability
Basket trial data analyzed in this study is available at https://github.com/labsyspharm/palmer-plana-2020.
The original code reported in this study is available at https://github.com/labsyspharm/palmer-plana-2020.
The scripts used to generate the figures reported in this paper are available at https://github.com/labsyspharm/palmer-plana-2020.
Any additional information required to reproduce this work is available from the Lead Contact.
METHOD DETAILS
To test the null hypothesis that patient subgroups are equally responsive to a therapy, outcome data as reported in a basket trial (comprising either change in tumor volume, or duration of PFS) were pooled for all patients who received the drug, regardless of tumor type. We derive a null distribution for each subgroup by permutation of responses among tumor subgroups. We have elected to consider both PFS and tumor volume for all of analysis when both types of response data were available. However, we note that a meaningful correlation between PFS or tumor volume changes and overall survival has not been demonstrated in all cancer types, and ultimately the decision of whether to include both of these data types into post-hoc analysis should be informed by clinical experience in a specific disease and treatment setting (Davis et al., 2012).
Exact permutation tests compute all possible combinations of categorical variables, but this is computationally intractable for continuous variables (e.g. there are 1023 ways to choose 25 samples from 100 patients). We therefore used Monte Carlo permutation tests, in which a large but non-exhaustive set of permutations is randomly generated. Monte Carlo permutation yields type 1 error rates (false positive rate) equal to those of an exact permutation test for probabilities P >> 1/N where N is the number of random permutations; we used N=107 and therefore can accurately report P values as small as 0.0001 (106 simulations were performed for the neratinib PFS analysis due to the computational time required to calculate hazard ratio, and since neratinib PFS analyses produced no P values smaller than 10–4, sufficient precision was provided by 106 simulations). Monte Carlo permutation of trial outcomes involves randomly drawing from a pool of all patient responses, with the number of samples drawn equal to the number of patients found in the cohort being tested (e.g. 26 patients for lung and 5 patients for cervical cancer). A response metric (volume change or PFS) for the sampled set is then calculated and the procedure repeated N=107 times to compose a reliable null distribution for the cohort. For the analysis of changes in tumor volume, the response metric was the average volume change for a cohort; for the analysis of PFS, the response metric was the hazard ratio (computed using the Cox proportional hazards model) of the Kaplan-Meier survival function for a subset of patients as compared to the survival function for all patients. An empiric P value was then determined by the location of the observed response metric (which was the test statistic) on that null distribution. In common with an exact permutation test, the rate of type I error is the significance level. The Benjamini-Hochberg procedure (Benjamini and Hochberg, 1995) was used to control the False Discovery Rate (FDR) associated with multiple hypothesis testing (multiple hypothesis correction is generally absent from analyses of basket trials). Consistent with practice in genomics, we used an FDR of 25%, which we observed by simulations to yield a false positive (type I error) rate ≈ 3% (see Results); this is smaller than the 10% false positive rate commonly chosen for Simon two-stage designs.
In the case of the SUMMIT trial permutation testing was separately applied to reported tumor volume changes and to durations of PFS; in the case of the larotrectinib and pembrolizumab trials (Drilon et al., 2018; Lassen et al., 2018; Le et al., 2017) it was applied only to tumor volume changes (PFS outcomes by tumor type are not available). For imatinib, permutation tests were applied to objective response rates (Heinrich et al., 2008). For the SUMMIT trial, volume (but not PFS) changes in breast tumors were far stronger than for any other tumor type: none of 107 simulations of the null hypothesis matched the observed average tumor volume change of breast tumors (we report this as P < 10−6). The magnitude of difference between breast tumors and all tumors (45% difference in average volume change) is so large that the inclusion of breast tumors in the null distribution makes it impossible to detect any difference among other tumor types. Because breast tumors represent an outlier with regard to volume changes in response to neratinib treatment, we considered it inappropriate to include breast tumor volume changes in the between-tumor comparison of all other tumor types. We therefore constructed a “no breast tumor” (NB) null distribution using volume data for all non-breast cancers (n=116). This reformulation of the null distribution was applied only for this case of a P<10−6 outlier, and we advocate for a similarly stringent approach to any future application that may remove subtypes from the null distribution. We did not encounter any other tumor subtype in any basket trial for which reformulation of the null distribution was appropriate
Responses in any one tumor type could not be meaningfully inferior to the poor response across all patients to neratinib (median volume change ≈ 0%; median PFS ≈ 2 months; objective response rate 12%). We therefore tested only for superiority of each tumor type or mutation class relative to all types; the same was true of imatinib (objective response rate 13% over all patients), and basket trials in general use one-sided tests for efficacy. In the cases of larotrectinib and pembrolizumab, overall response rates were high, and we tested for both superiority and inferiority relative to the average of all tumors in those trials.
Finally, basket trials were simulated in which only some tumor types respond to therapy, in order to compare type I and type II error rates between permutation tests (comparing efficacy across tumor types) and binomial tests (evaluating objective response rate in individual tumor types, according to a Simon two-stage trial design). A ‘non-responsive’ distribution of tumor volume changes was empirically defined based on the observed volume changes in non-responsive tumor types in the SUMMIT trial: volume changes were drawn from a normal distribution with mean response μ = +20%, and standard deviation σ = ±30%; these parameters resulted in fewer than 5% of tumors exhibiting volume change ≤ −30%, defined as ‘objective response’ for these simulations. Basket trials were simulated in which ten tumor types were studied, of which seven types were ‘non-responsive’ (μ = 20%, σ = ±30%), and three types were ‘responsive’ (μ = α + 20%, σ = ±30%; where α is the ‘treatment effect’, the average difference in volume change compared to non-responsive tumors). 1000 basket trials were simulated for each value of ‘treatment effect’ between −60% and 0%, first with 7 patients per tumor type, and next with 18 patients per tumor type, matching the intended number of patients in Stages One and Two of the two-stage design of the SUMMIT trial. Each simulated trial’s results were analyzed by both permutation testing, and by the binomial test used in the Two-Stage design (pass requires ≥ 1 objective response at stage 1, and ≥ 4 objective responses at stage 2). Type 1 error rates were calculated as the fraction of truly non-responsive tumor types that were misclassified as responsive, and type 2 error rates were calculated as the fraction of truly responsive tumor types that were misclassified as non-responsive.
QUANTIFICATION AND STATISTICAL ANALYSIS
All analysis was performed using Wolfram Mathematica Version 12.1.0.0. Details of the statistical analysis performed, exact values of n and what they represent, definitions of the summary statistics used, definitions of significance, and participant inclusion and exclusion criteria can be found in the Method Details, Figure captions, and Results sections of the manuscript.
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited Data | ||
| Basket trial data files analyzed in article: “Comparing the efficacy of cancer therapies between subgroups in basket trials” | This manuscript | https://github.com/labsyspharm/palmer-plana-2020. |
| Software and Algorithms | ||
| Mathematica code for article: “Comparing the efficacy of cancer therapies between subgroups in basket trials” | This manuscript | https://github.com/labsyspharm/palmer-plana-2020. |
Highlights.
Basket clinical trials test a drug in multiple subtypes but rarely compare subtypes
A rigorous approach to such comparison would advance precision medicine
Permutation testing with empirical null distributions allow subtypes to be compared
In a published trial we identify ERBB2-mutant lung cancers responsive to neratinib
ACKNOWLEDGMENTS
We thank L. Trippa and B. Alexander for helpful discussions and comments on this manuscript. This work was supported by NIH grants P50-GM107618 and U54-CA225088 (to P.K.S.). D.P. is supported by NIGMS grant T32-GM007753.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information can be found online at https://doi.org/10.1016/j.cels.2020.09.003.
DECLARATION OF INTERESTS
P.K.S. is a member of the SAB or Board of Directors of Glencoe Software, Applied Biomath, and RareCyte Inc. and has equity in these companies; P.K.S. is also a member of the SAB of NanoString. P.K.S. declares that none of these relationships are directly or indirectly related to the content of this manuscript. The other authors declares no competing interests.
REFERENCES
- Adunlin G, Cyrus JWW, and Dranitsaris G (2015). Correlation between progression-free survival and overall survival in metastatic breast cancer patients receiving anthracyclines, taxanes, or targeted therapies: a trial-level meta-analysis. Breast Cancer Res. Treat 154, 591–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arcila ME, Chaft JE, Nafa K, Roy-Chowdhuri S, Lau C, Zaidinski M, Paik PK, Zakowski MF, Kris MG, and Ladanyi M (2012). Prevalence, clinicopathologic associations, and molecular spectrum of ERBB2 (HER2) tyrosine kinase mutations in lung adenocarcinomas. Clin. Cancer Res 18, 4910–4918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arfè A, Alexander B, and Trippa L (2020). Optimality of testing procedures for survival data in the nonproportional hazards setting. Biometrics 10.1111/biom.13315. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, and Hochberg Y (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57, 289–300. [Google Scholar]
- Berry DA (2015). The brave new world of clinical cancer research: adaptive biomarker-driven trials integrating clinical practice with clinical research. Mol. Oncol 9, 951–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop DVM, and Thompson PA (2016). Problems in using p-curve analysis and text-mining to detect rate of p-hacking and evidential value. PeerJ 4, e1715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blumenthal GM, Karuri SW, Zhang H, Zhang L, Khozin S, Kazandjian D, Tang S, Sridhara R, Keegan P, and Pazdur R (2015). Overall response rate, progression-free survival, and overall survival with targeted and standard therapies in advanced non-small-cell lung cancer: US food and drug administration trial-level and patient-level analyses. J. Clin. Oncol 33, 1008–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buyse M, Thirion P, Carlson RW, Burzykowski T, Molenberghs G, and Piedbois P (2000). Relation between tumour response to first-line chemotherapy and survival in advanced colorectal cancer: a meta-analysis. Meta-analysis group in Cancer. Lancet 356, 373–378. [DOI] [PubMed] [Google Scholar]
- Cunanan KM, Gonen M, Shen R, Hyman DM, Riely GJ, Begg CB, and Iasonos A (2017b). Basket trials in oncology: a trade-off between complexity and efficiency. J. Clin. Oncol 35, 271–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunanan KM, Iasonos A, Shen R, Begg CB, and Gönen M (2017a). An efficient basket trial design. Stat. Med 36, 1568–1579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis S, Tappenden P, and Cantrell A (2012). A review of studies examining the relationship between progression-free survival and overall survival in advanced or metastatic cancer, National Institute for Health and Care Excellence (NICE) https://pubmed.ncbi.nlm.nih.gov/28481488/. [PubMed] [Google Scholar]
- Diamond EL, Subbiah V, Lockhart AC, Blay JY, Puzanov I, Chau I, Raje NS, Wolf J, Erinjeri JP, Torrisi J, et al. (2018). Vemurafenib for BRAF V600–mutant Erdheim-Chester disease and Langerhans cell histiocytosis: analysis of data From the histology-independent, Phase 2, open-label VEBASKET study. JAMA Oncol 4, 384–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drilon A, Laetsch TW, Kummar S, DuBois SG, Lassen UN, Demetri GD, Nathenson M, Doebele RC, Farago AF, Pappo AS, et al. (2018). Efficacy of Larotrectinib in TRK fusion-positive cancers in adults and children. N. Engl. J. Med 378, 731–739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenhauer EA, Therasse P, Bogaerts J, Schwartz LH, Sargent D, Ford R, Dancey J, Arbuck S, Gwyther S, Mooney M, et al. (2009). New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1). Eur. J. Cancer 45, 228–247. [DOI] [PubMed] [Google Scholar]
- El-Maraghi RH, and Eisenhauer EA (2008). Review of phase II trial designs used in studies of molecular targeted agents: outcomes and predictors of success in phase III. J. Clin. Oncol 26, 1346–1354. [DOI] [PubMed] [Google Scholar]
- Fleming TR, and DeMets DL (1996). Surrogate end points in clinical trials: are we being misled? Ann. Intern. Med 125, 605–613. [DOI] [PubMed] [Google Scholar]
- Friberg S, and Mattson S (1997). On the growth rates of human malignant tumors: implications for medical decision making. J. Surg. Oncol 65, 284–297. [DOI] [PubMed] [Google Scholar]
- Gleich GJ, Leiferman KM, Pardanani A, Tefferi A, and Butterfield JH (2002). Treatment of hypereosinophilic syndrome with imatinib mesilate. Lancet 359, 1577–1578. [DOI] [PubMed] [Google Scholar]
- Hafner M, Mills CE, Subramanian K, Chen C, Chung M, Boswell SA,Everley RA, Liu C, Walmsley CS, Juric D, and Sorger PK (2019). Multiomics profiling establishes the polypharmacology of FDA-approved CDK4/6 inhibitors and the potential for differential clinical activity. Cell Chem. Biol 26, 1067–1080.e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinrich MC, Joensuu H, Demetri GD, Corless CL, Apperley J, Fletcher JA, Soulieres D, Dirnhofer S, Harlow A, Town A, et al. (2008). Phase II, open-label study evaluating the activity of imatinib in treating life-threatening malignancies known to be associated with imatinib-sensitive tyrosine kinases. Clin. Cancer Res 14, 2717–2725. [DOI] [PubMed] [Google Scholar]
- Hirakawa A, Asano J, Sato H, and Teramukai S (2018). Master protocol trials in oncology: review and new trial designs. Contemp. Clin. Trials Commun 12, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyman DM, Piha-Paul SA, Won H, Rodon J, Saura C, Shapiro GI, Juric D, Quinn DI, Moreno V, Doger B, et al. (2018). HER kinase inhibition in patients with HER2- and HER3-mutant cancers. Nature 554, 189–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyman DM, Puzanov I, Subbiah V, Faris JE, Chau I, Blay JY, Wolf J, Raje NS, Diamond EL, Hollebecque A, et al. (2015). Vemurafenib in multiple nonmelanoma cancers with BRAF V600 mutations. N. Engl. J. Med 373, 726–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser LD (2013). Tumor burden modeling versus progression-free survival for phase II decision making. Clin. Cancer Res 19, 314–319. [DOI] [PubMed] [Google Scholar]
- Korphaisarn K, and Kopetz S (2016). BRAF-directed therapy in metastatic colorectal cancer. Cancer J 22, 175–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lassen UN, Albert CM, Kummar S, van Tilburg CM, Dubois SG, Geoerger B, Mascarenhas L, Federman N, Schilder RJ, Doz F, et al. (2018). Larotrectinib efficacy and safety in TRK fusion cancer: an expanded clinical dataset showing consistency in an age and tumor agnostic approach. Ann. Oncol 29 (8), viii133–viii148. [Google Scholar]
- Le DT, Durham JN, Smith KN, Wang H, Bartlett BR, Aulakh LK, Lu S, Kemberling H, Wilt C, Luber BS, et al. (2017). Mismatch repair deficiency predicts response of solid tumors to PD-1 blockade. Science 357, 409–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le DT, Kim TW, Van Cutsem E, Geva R, Jäger D, Hara H, Burge M, O’Neil B, Kavan P, Yoshino T, et al. (2020). Phase II open-label study of pembrolizumab in treatment-refractory, microsatellite instability–high/mismatch repair–deficient metastatic colorectal cancer: KEYNOTE-164. J. Clin. Oncol 38, 11–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeBlanc M, Rankin C, and Crowley J (2009). Multiple histology phase II trials. Clin. Cancer Res 15, 4256–4262. [DOI] [PubMed] [Google Scholar]
- Ma Y, Wang Q, Dong Q, Zhan L, and Zhang J (2019). How to differentiate pseudoprogression from true progression in cancer patients treated with immunotherapy. Am. J. Cancer Res 9, 1546–1553. [PMC free article] [PubMed] [Google Scholar]
- Marabelle A, Le DT, Ascierto PA, Di Giacomo AM, De Jesus-Acosta A, Delord JP, Geva R, Gottfried M, Penel N, Hansen AR, et al. (2020). Efficacy of pembrolizumab in patients with noncolorectal high microsatellite instability/mismatch repair–deficient cancer: results From the Phase II KEYNOTE-158 study. J. Clin. Oncol 38, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArthur GA, Demetri GD, van Oosterom A, Heinrich MC, Debiec-Rychter M, Corless CL, Nikolova Z, Dimitrijevic S, and Fletcher JA (2005). Molecular and clinical analysis of locally advanced dermatofibrosarcoma protuberans treated with imatinib: imatinib target exploration consortium study B2225. J. Clin. Oncol 23, 866–873. [DOI] [PubMed] [Google Scholar]
- Mullard A (2015). NCI-MATCH trial pushes cancer umbrella trial paradigm. Nat. Rev. Drug Discov 14, 513–515. [DOI] [PubMed] [Google Scholar]
- Nagano M, Kohsaka S, Ueno T, Kojima S, Saka K, Iwase H, Kawazu M, and Mano H (2018). High-throughput functional evaluation of variants of unknown significance in ERBB2. Clin. Cancer Res 24, 5112–5122. [DOI] [PubMed] [Google Scholar]
- Navarrete-Dechent C, Mori S, Barker CA, Dickson MA, and Nehal KS (2019). Imatinib treatment for locally advanced or metastatic dermatofibrosarcoma protuberans: a systematic review. JAMA Dermatol 155, 361–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardanani A, and Tefferi A (2004). Imatinib therapy for hypereosinophilic syndrome and eosinophilia-associated myeloproliferative disorders. Leuk. Res 28, S47–S52. [DOI] [PubMed] [Google Scholar]
- Park JJH, Siden E, Zoratti MJ, Dron L, Harari O, Singer J, Lester RT, Thorlund K, and Mills EJ (2019). Systematic review of basket trials, umbrella trials, and platform trials: a landscape analysis of master protocols. Trials 20, 572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pazdur R (2008). Endpoints for assessing drug activity in clinical trials. Oncologist 13, 19–21. [DOI] [PubMed] [Google Scholar]
- Redig AJ, and Jänne PA (2015). Basket trials and the evolution of clinical trial design in an era of genomic medicine. J. Clin. Oncol 33, 975–977. [DOI] [PubMed] [Google Scholar]
- Renfro LA, and Mandrekar SJ (2018). Definitions and statistical properties of master protocols for personalized medicine in oncology. J. Biopharm. Stat 28, 217–228. [DOI] [PubMed] [Google Scholar]
- Robichaux JP, Elamin YY, Tan Z, Carter BW, Zhang S, Liu S, Li S, Chen T, Poteete A, Estrada-Bernal A, et al. (2018). Mechanisms and clinical activity of an EGFR and HER2 exon 20-selective kinase inhibitor in non-small cell lung cancer. Nat. Med 24, 638–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seymour L, Ivy SP, Sargent D, Spriggs D, Baker L, Rubinstein L, Ratain MJ, Le Blanc M, Stewart D, Crowley J, et al. (2010). The design of phase II clinical trials testing cancer therapeutics: consensus recommendations from the clinical trial design task force of the National Cancer Institute investigational drug steering committee. Clin. Cancer Res 16, 1764–1769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma MR, Maitland ML, and Ratain MJ (2012). Why RECIST works and why it should stay–reply to counterpoint. Cancer Res 72, 5158. [DOI] [PubMed] [Google Scholar]
- Simon R (1989). Optimal two-stage designs for phase II clinical trials. Control. Clin. Trials 10, 1–10. [DOI] [PubMed] [Google Scholar]
- Simon R, Geyer S, Subramanian J, and Roychowdhury S (2016). The Bayesian basket design for genomic variant-driven phase II trials. Semin. Oncol 43, 13–18. [DOI] [PubMed] [Google Scholar]
- Singh H, Walker AJ, Amiri-Kordestani L, Cheng J, Tang S, Balcazar P, Barnett-Ringgold K, Palmby TR, Cao X, Zheng N, et al. (2018). U.S. food and drug administration approval: neratinib for the extended adjuvant treatment of early-stage HER2-positive breast cancer. Clin. Cancer Res 24, 3486–3491. [DOI] [PubMed] [Google Scholar]
- Subbiah V, Puzanov I, Blay JY, Chau I, Lockhart AC, Raje NS, Wolf J, Baselga J, Meric-Bernstam F, Roszik J, et al. (2020). Pan-cancer efficacy of vemurafenib in BRAF V600 -mutant non-melanoma cancers. Cancer Discov 10, 657–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao JJ, Schram AM, and Hyman DM (2018). Basket studies: redefining clinical trials in the era of genome-driven oncology. Annu. Rev. Med 69, 319–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- U.S. Food and Drug Administration (2018). Master protocols: efficient clinical trial design strategies to expedite development of oncology drugs and biologics guidance for industry https://www.fda.gov/regulatory-information/search-fda-guidance-documents/master-protocols-efficient-clinical-trial-design-strategies-expedite-development-oncology-drugs-and.
- Vyse S, and Huang PH (2019). Targeting EGFR exon 20 insertion mutations in non-small cell lung cancer. Signal Transduct. Target. Ther 4, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodcock J, and LaVange LM (2017). Master protocols to study multiple therapies, multiple diseases, or both. N. Engl. J. Med 377, 62–70. [DOI] [PubMed] [Google Scholar]
- Zabor EC, Heller G, Schwartz LH, and Chapman PB (2016). Correlating surrogate endpoints with overall survival at the individual patient level in BRAFV600E-mutated metastatic melanoma patients treated with vemurafenib. Clin. Cancer Res 22, 1341–1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Basket trial data analyzed in this study is available at https://github.com/labsyspharm/palmer-plana-2020.
The original code reported in this study is available at https://github.com/labsyspharm/palmer-plana-2020.
The scripts used to generate the figures reported in this paper are available at https://github.com/labsyspharm/palmer-plana-2020.
Any additional information required to reproduce this work is available from the Lead Contact.


