Social network analysis of the genealogy of strawberry: retracing the wild roots of heirloom and modern cultivars

Abstract

The widely recounted story of the origin of cultivated strawberry (Fragaria × ananassa) oversimplifies the complex interspecific hybrid ancestry of the highly admixed populations from which heirloom and modern cultivars have emerged. To develop deeper insights into the three-century-long domestication history of strawberry, we reconstructed the genealogy as deeply as possible—pedigree records were assembled for 8,851 individuals, including 2,656 cultivars developed since 1775. The parents of individuals with unverified or missing pedigree records were accurately identified by applying an exclusion analysis to array-genotyped single-nucleotide polymorphisms. We identified 187 wild octoploid and 1,171 F. × ananassa founders in the genealogy, from the earliest hybrids to modern cultivars. The pedigree networks for cultivated strawberry are exceedingly complex labyrinths of ancestral interconnections formed by diverse hybrid ancestry, directional selection, migration, admixture, bottlenecks, overlapping generations, and recurrent hybridization with common ancestors that have unequally contributed allelic diversity to heirloom and modern cultivars. Fifteen to 333 ancestors were predicted to have transmitted 90% of the alleles found in country-, region-, and continent-specific populations. Using parent–offspring edges in the global pedigree network, we found that selection cycle lengths over the past 200 years of breeding have been extraordinarily long (16.0-16.9 years/generation), but decreased to a present-day range of 6.0-10.0 years/generation. Our analyses uncovered conspicuous differences in the ancestry and structure of North American and European populations, and shed light on forces that have shaped phenotypic diversity in F. × ananassa.

Introduction

The strawberries found in markets around the world today are produced by cultivated strawberry (Fragaria × ananassa (Weston) Duchesne ex Rozier), a species domesticated over the past 300 years (Darrow 1966). F. × ananassa is technically not a species but an admixed population of interspecific hybrid lineages between cross-compatible wild allo-octoploid (2n = 8x = 56) species with shared evolutionary histories (Duchesne 1766; Darrow 1966; Liston et al. 2014). The earliest F. × ananassa cultivars originated as spontaneous hybrids between F. chiloensis and F. virginiana in Brittany, the Garden of Versailles, and other Western European gardens in the early 1700s, shortly after the migration of F. chiloensis from Chile to France in 1714 (Duchesne 1766; Bunyard 1917; Darrow 1966; Pitrat and Faury 2003). Their serendipitous origin was discovered by the French Botanist Antoine Nicolas Duchesne (1747-1827) and famously described in a treatise on strawberries that biologists suspect included one of the first renditions of a phylogenetic tree (Duchesne 1766). Even though those studies predated both the advent of genetics and the discovery of ploidy differences in the genus, the phylogenies were remarkably close to hypotheses that emerged more than 150 years later (Darrow 1966; Staudt 1989, 2003; Dillenberger et al. 2018). The early interspecific hybrids were observed to be more phenotypically variable than and horticulturally superior to their wild octoploid parents, factors that drove the domestication of F. × ananassa. The increase in phenotypic variability can be directly linked to an increase in nucleotide diversity and heterozygosity, and presumably to the introduction of complementary favorable alleles that were not found in either parent. Hardigan et al. (2020, 2021) showed that hybrids between F. chiloensis and F. virginiana have nearly double the genome-wide heterozygosity of their parents. With the mysterious origin of the spontaneous interspecific hybrids solved (Duchesne 1766), breeding and cultivation shifted to F. × ananassa, which supplanted the cultivation of the wild relatives and forever changed strawberry production and consumption worldwide (Fletcher 1917; Darrow 1966; Wilhelm and Sagen 1974; Finn et al. 2013).

The romanticized and widely recounted story of the origin of cultivated strawberry, while compelling, oversimplifies the complexity of the wild ancestry and 300-year history of domestication, for which we have an incomplete understanding (Clausen 1915; Fletcher 1917; Darrow 1966; Wilhelm and Sagen 1974; Sjulin and Dale 1987; Bringhurst et al. 1990; Dale and Sjulin 1990; Johnson 1990; Sjulin 2006; Hancock et al. 2008; Horvath et al. 2011; Sánchez-Sevilla et al. 2015). One of our motives for reconstructing the genealogy of cultivated strawberry was to shed light on the origin and diversity of the wild founders and the breeding history. The only pedigree-informed studies of the breeding history of cultivated strawberry focused on an analysis of the ancestry of 134 North American cultivars developed between 1960 and 1985 (Sjulin and Dale 1987; Dale and Sjulin 1990). They identified 53 founders in the pedigrees of those cultivars, estimated that 20 founders contributed approximately 85% of the allelic diversity, and concluded that North American cultivars had originated from a genetically narrow population (Sjulin and Dale 1987; Dale and Sjulin 1990).

Others have reached similar conclusions (Hancock and Luby 1995; Graham et al. 1996; Hancock et al. 2001; Hummer 2008), and the notion that cultivated strawberry “displays limited genetic variability” has persisted (Gaston et al. 2020). Gaston et al. (2020) were possibly alluding to the absence of morphological diversity on par with that found in tomato (Solanum lycopersicum L.). Nevertheless, the genetic narrowness hypothesis has not been supported by genome-wide analyses of DNA variants, which have shown that F. chiloensis, F. virginiana, and F. × ananassa harbor massive nucleotide diversity and that a preponderance of the alleles transmitted by the wild octoploid founders have survived domestication and been preserved in the global F. × ananassa population (Hardigan et al. 2020, 2021). Hardigan et al. (2021) proposed an alternative to the “limited genetic variability” hypothesis (Gaston et al. 2020), arguing that genetic variation has not been reduced by directional selection or population bottlenecks in certain populations. One of the consequences predicted by this hypothesis is the persistence of a high frequency of unfavorable alleles in domesticated populations.

The domestication of cultivated strawberry has followed a path different from that of other horticulturally important species, many of which were domesticated over millennia and traced to early civilizations, e.g., apple (Malus domestica), olive (Olea europaea subsp. europaea), and wine grape (Vitis vinifera subsp. vinifera) (Purugganan and Fuller 2009; Myles et al. 2011; Meyer et al. 2012; Meyer and Purugganan 2013; Cornille et al. 2014; Larson et al. 2014; Diez et al. 2015; Duan et al. 2017). Although the octoploid progenitors were cultivated before the emergence of F. × ananassa, the full extent of their cultivation is unclear and neither appears to have been intensely domesticated; e.g., Hardigan et al. (2021) did not observe changes in the genetic structure between land races and wild ecotypes of F. chiloensis, a species cultivated in Chile for at least 1,000 years (Finn et al. 2013). With less than 300 years of breeding, pedigrees for thousands of F. × ananassa individuals have been recorded, albeit in disparate sources. To delve more deeply into the domestication history of cultivated strawberry, we assembled pedigree records from hundreds of sources and reconstructed the genealogy as deeply as possible.

One of our initial motives for reconstructing the genealogy of cultivated strawberry was to identify historically important and genetically prominent ancestors of domesticated populations, in large part to guide the selection of individuals for whole-genome shotgun sequencing and DNA variant discovery, inform the development of single-nucleotide polymorphism (SNP) genotyping platforms populated with octoploid genome-anchored subgenome-specific assays, and identify individuals for inclusion in genome-wide studies of biodiversity and population structure (Hardigan et al. 2020, 2021). The genetic relationships and genetic contributions (GCs) of ancestors uncovered in the genealogy (identity-by-descent) study described here guided the selection of individuals for downstream genomic studies that shed light on genetic variation and the genetic structure of domesticated populations worldwide (Hardigan et al. 2020, 2021).

Our other early motive for reconstructing the genealogy of strawberry was to support the curation and stewardship of a historically and commercially important germplasm collection preserved at the University of California, Davis (UCD), with accessions tracing to the early origins of the strawberry breeding program at the University of California, Berkeley (UCB), in the 1920s (Bringhurst et al. 1990). We sought to develop a complete picture of genetic relationships among living and extinct individuals in the California and worldwide populations, in part to assess how extinct individuals relate to living individuals preserved in public germplasm collections. Because 80% or more of the individuals we documented in the genealogy appear to be extinct, they could only be connected to living individuals through their pedigrees. One of the ways we explored ancestral interconnections between extinct and living individuals was through multivariate analyses of a combined pedigree–genomic relationship matrix estimated from genotyped and ungenotyped individuals (Legarra et al. 2009).

The holdings and history of the UCD Strawberry Germplasm Collection were shrouded in mystery when our study was initiated in 2015. The only individuals in the collection with pedigree records were publicly released and patented cultivars. The immediate challenge we faced in reconstructing the genealogy was the absence of pedigree records for 96% of the 1,287 accessions preserved in the collection, which is hereafter identified as the “California” population. To solve this problem, authenticate pedigrees, and fully reconstruct the genealogy of the California population, we applied an exclusion analysis in combination with high-density SNP genotyping (Chakraborty et al. 1974; Elston 1986; Goldgar and Thompson 1988; Pena and Chakraborty 1994; Vandeputte 2012; Vandeputte and Haffray 2014). Here, we demonstrate the exceptional accuracy of diploid paternity (exclusion) analysis methods when applied to individuals in an allo-octoploid organism genotyped with subgenome-specific SNPs on high-density (35-K, 50- K, or 850-K) arrays (Bassil et al. 2015; Verma et al. 2017; Hardigan et al. 2020). Several thousand SNP markers common to the three arrays were integrated to develop a SNP profile database for the parentage (exclusion) analyses described here. SNPs on the 50-K and 850-K arrays are uniformly distributed across the octoploid genome and informative in octoploid populations worldwide (Hardigan et al. 2020, 2021). The 50-K SNP array harbors 1 SNP/16,200 bp, whereas the 850-K array harbors 1 SNP/953 bp, telomere-to-telomere across the 0.81-Gb octoploid genome.

The genealogies (pedigree networks) of domesticated plants, especially those with long-lived individuals, overlapping generations, and extensive migration and admixture, can be challenging to visualize and comprehend (Mäkinen et al. 2005; Trager et al. 2007; Voorrips et al. 2012; Shaw et al. 2014; Fradgley et al. 2019; Muranty et al. 2020). We used Helium (Shaw et al. 2014) to visualize smaller targeted pedigrees; however, the strawberry pedigree networks we constructed and investigated were too large and mathematically complex to be effectively visualized and analyzed with Helium and other traditional hierarchical pedigree visualization approaches. Hierarchical methods often produce comprehensible insights and graphs when applied to pedigrees of individuals or small groups but yield exceedingly complex, labyrinthine graphs that are difficult to interpret when the genealogy contains a large number of individuals and lineages. We turned to social network analysis (SNA) (Barabási et al. 2011; Barabási 2016; Contandriopoulos et al. 2018) to explore alternative approaches to search for patterns and extract information from the complex genealogy of strawberry.

The pedigree networks of plants and animals share many of the features of social networks with nodes (individuals) connected to one another through edges (parent–offspring (PO) relationships) (Barabási et al. 2011; Barabási 2016; Contandriopoulos et al. 2018). We used SNA methods, in combination with classic population genetic methods, to analyze the genealogy and develop deeper insights into the domestication history of strawberry (Lacy 1989, 1995; Barabási et al. 2011; Barabási 2016; Contandriopoulos et al. 2018). SNA approaches have been applied in diverse fields of study but have apparently not been applied to the problem of analyzing and characterizing pedigree networks (Moreno 1953; Scott 1988; Edwards 1992; Wasserman and Faust 1994; Kominakis 2001). With SNA, narrative data (birth certificates and pedigree records) are translated into relational data (PO and other genetic relationships) and summary statistics (betweenness centrality and out-degree) and visualized as sociograms (pedigree networks) (Barabási et al. 2011; Barabási 2016; Contandriopoulos et al. 2018). Here, we report insights gained from genealogical studies of domesticated strawberry populations worldwide. Our studies shed light on the complex wild ancestry of F. × ananassa, the diversity of founders of domesticated populations of cultivated strawberry that have emerged over the past 300 years, and genetic relationships among extinct and extant ancestors in demographically unique domesticated populations tracing to the earliest ancestors and interspecific hybrids (Darrow 1966).

Materials and methods

Pedigree record assembly, documentation, and annotation

We located and assembled pedigree records for strawberry accessions from more than 807 documents, databases, and other sources, including (1) US Patent and Trademark Office Plant Patents (https://www.uspto.gov/); (2) Germplasm Resource and Information Network (GRIN) passport data for accessions preserved in the USDA National Plant Germplasm System (NPGS; https://www.ars-grin.gov/); (3) the original unpublished UCD laboratory notebooks and other documents of Royce S. Bringhurst archived in a special collection at the Merrill-Cazier Library, Utah State University, Logan, Utah (Bringhurst 1918-2016; USU_COLL_MSS_515; http://archiveswest.orbiscascade.org/ark:/80444/xv47241/); (4) the original unpublished UCB laboratory notebooks of Harold E. Thomas loaned by Phillip Stewart (Driscoll’s, Watsonville, California); (5) an obsolete electronic database discovered and recovered at UCD; (6) an electronic pedigree database for public cultivars developed by Thomas Sjulin, a former strawberry breeder at Driscoll’s, Watsonville, California; (7) scientific, technical bulletins, and popular press articles; and (8) garden catalogs (Supplementary Files S1–S3).

The pedigree records and other input data were manually curated and deduplicated. The database was constructed in a standard trio format (offspring, mother, and father) with supporting passport data, which included (1) alphanumeric identification numbers; (2) common names or aliases; (3) accession types (e.g., cultivars, breeding materials, or wild ecotypes); (4) birth years (years of origin); (5) geographic origin; (6) inventor (breeder or institution) names; (7) taxonomic classifications; and (8) DNA-authenticated pedigrees for genotyped UCD accessions, as described below (Supplementary File S1). Because a parent could be a male in one cross and a female in another, and parent sexes were frequently unknown or inconsistently recorded in pedigree records, the “mother” (parent 1) and “father” (parent 2) designations were arbitrary and unimportant to our study.

Germplasm accession numbers in the pedigree database included “plant introduction” (PI) numbers for USDA accessions, UCD identification numbers for UCD accessions, and assorted other identification numbers. UCD accession numbers were written in a 10-digit machine-readable and searchable format to convey birth year and unique numbers; e.g., the UCD ID “65C065P001” identifies a single individual (P001) in full-sib family C065 born in 1965 that was identified in historic records as “65.65-1” (Bringhurst 1918-2016; Bringhurst and Voth 1980). The latter is the “Bringhurst” notation found in the historic pedigree records for UCD accessions and US Plant Patents. The decimals and dashes in the original notation created problems with data curation, analysis, and sorting. To solve this, the original “Bringhurst” accession numbers (e.g., 65.65-1) were converted into the 10-digit machine-readable accession numbers (e.g., 65C065P001) reported in our pedigree database, where “C” identifies a cultivated strawberry accession. Common names (aliases) of cultivars and accessions (if available) were concatenated with underscores to create machine-readable and sortable names, e.g., the name for the F. × ananassa cultivar “Madame Moutot” was stored as “Madame_Moutot.” Cultivars sharing names were made unique by appending an underscore and their year. Throughout the pedigree database, unknown individuals were created as necessary and identified with unique alphanumeric identification numbers starting with the prefix “Unknown,” followed by an underscore, a species acronym when known or NA when unknown, an underscore, and consecutive numbers, e.g., “Unknown_FC_071” identifies unknown F. chiloensis founder 71. The species acronyms applied in our database were FA for F. × ananassa, FC for F. chiloensis, FV for F. virginiana, FW for F. vesca (woodland strawberry), FI for F. iinumae, FN for F. nipponica, FG for F. viridis (green strawberry), FM for F. moschata, and FX for other wild species or interspecific hybrids, e.g., F. × vescana.

Plant material and SNP profile database

To develop a SNP profile database for DNA forensic and population genetic analyses (see below), we recalled and reanalyzed SNP marker genotypes for 1,495 individuals, including 1,235 UCD and 260 USDA accessions (asexually propagated individuals) previously genotyped by Hardigan et al. (2018) with the iStraw35 SNP array (Bassil et al. 2015; Verma et al. 2017). SNP marker genotypes were automatically called with the Affymetrix Axiom Analysis Suite (v1.1.1.66, Affymetrix, Santa Clara, CA). DNA samples with > 6% missing data were dropped from our analyses. We used the quality metrics output by the Affymetrix Axiom Analysis Suite and custom R scripts and the R package SNPRelate (Zheng et al. 2012) to identify and select codominant SNP markers with genotypic clustering confidence scores $(1-p_C)\ge 0.01$, where p_C is the posterior probability that the SNP genotype for an individual was assigned to the correct genotypic cluster (Affymetrix Inc. 2015). This yielded 14,650 high-confidence codominant SNP markers for paternity–maternity analyses. While SNP markers are codominant by definition, a certain percentage of the SNP markers assayed in a population produce genotypic clusters lacking one of the homozygous genotypic clusters. These so-called no minor homozygote SNP markers were excluded from our analyses.

For a second DNA forensic analysis, 1,561 UCD individuals were genotyped with 50-K or 850-K SNP arrays (Hardigan et al. 2020). This study population included 560 hybrid offspring from crosses among 27 elite UCD parents, the F. × ananassa cultivar “Puget Reliance,” and the F. chiloensis subsp. lucida ecotypes “Del Norte” and “Oso Flaco.” Hardigan et al. (2020) included 16,554 SNP markers from the iStraw35 and iStraw90 SNP arrays on the 850-K SNP array. To build a SNP profile database for the second paternity–maternity analysis, we identified 2,615 SNP markers that were common to the three arrays and produced well-separated codominant genotypic clusters with high confidence scores ($p_C>0.99)$ and < 6% missing data (Bassil et al. 2015; Verma et al. 2017; Hardigan et al. 2020).

We subdivided the global population (entire pedigree) into “California” and “Cosmopolitan” populations, in addition to continent-, region-, or country-specific populations, for different statistical analyses. These subdivisions are documented in the pedigree database (Supplementary File S1). The California population included 100% of the UCD individuals (n = 3,540) from the global population, in addition to 262 non-California individuals that were ascendants of UCD individuals. The Cosmopolitan population included 100% of the non-California (non-UCD) individuals (n = 5,193), in addition to 160 California individuals that were ascendants of non-California individuals. We subdivided individuals in the US population (excluding UCD individuals) into Midwestern, Northeastern, Southern, and Western US populations. The Western US population included only those UCD individuals that were ascendants in the pedigrees of Western US individuals. The country-specific subdivisions were Australia, China, Japan, South Korea, Belgium, Czechoslovakia, Denmark, England, Finland, France, Germany, Israel, Italy, the Netherlands, Norway, Poland, Russia, Scotland, Spain, Sweden, and Canada.

DNA forensic analyses

We applied standard DNA forensic approaches for diploid organisms to the problem of identifying parents and authenticating pedigrees in allo-octoploid strawberry (Chakraborty et al. 1974; Elston 1986; Jones and Ardren 2003; Telfer et al. 2015; Muranty et al. 2020). Genotypic transgression ratios were estimated for all possible duos and trios of individuals in two study populations (described above) from genotypes of multiple SNP marker loci. For PO duos of individuals in the SNP profile database for a population, the genotypic transgression score for the ith SNP marker was estimated by

$$S_i=f(A{A}_{O_i})·f(B{B}_{P_i})+f(B{B}_{O_i})·f(A{A}_{P_i})$$ (1)

where $i=1,2,\dots ,m$, m = number of SNP marker loci genotyped in each pair of probative DNA samples, $f(-{-}_{O_i})$ is the frequency of a homozygous genotype (coded AA and BB) in the candidate offspring individual, and $f(-{-}_{P_i})$ is the frequency of a homozygous genotype in the candidate parent individual (similarly coded AA and BB) for the ith SNP marker locus. This equation was applied to a single pair of candidate individuals at a time and was thus constrained to equal 0 or 1; hence, S_i = 0 when homozygous genotypes were identical for a pair of individuals and S_i = 1 when homozygous genotypes were different for a pair of individuals. Duo transgression ratios (DTRs) were estimated for every pair of individuals in the population by summing S_i estimates from equation (1) over m marker loci:

$$\mathit{DTR}=\frac{1}{m}\sum _{i=1}^m{S}_i$$ (2)

For trios of individuals in the SNP profile database for a population, the genotypic transgression score for the ith SNP marker was estimated by

$$\begin{array}{cc}{T}_i=\hfill & f(A{B}_{O_i})·f(A{A}_{P{1}_i})·f(A{A}_{P{2}_i})\hfill \\ \hfill & + f(A{B}_{O_i})·f(B{B}_{P{1}_i})·f(B{B}_{P{2}_i})\hfill \end{array}$$ (3)

where $f(A{B}_{O_i})$ is the frequency of a heterozygous genotype (coded AB) in the candidate offspring individual, $f(-{-}_{P{1}_i})$ is the frequency of either homozygous genotype (AA or BB) in candidate parent 1 (P1), and $f(-{-}_{P{2}_i})$ is the frequency of either homozygous genotype in candidate parent 2 (P2) for the ith SNP marker locus. Trio transgression ratios (TTRs) were estimated for every parent–parent–offspring (PPO) trio of individuals in the population by summing T_i estimates from equation (3) over m marker loci:

$$\mathit{TTR}=\frac{1}{m}\sum _{i=1}^m{T}_i+S{1}_i+S{2}_i-S{1}_i·S{2}_i$$ (4)

where m is the number of SNP marker loci genotyped for a trio of individuals, $S{1}_i$ is the score estimated from equation (1) for candidate parent 1, and $S{2}_i$ is the score estimated from equation (1) for candidate parent 2. To avoid double-counting transgressions, TTR estimates were corrected by subtracting $S{1}_i$ × $S{2}_i$.

DTR and TTR statistics were estimated from equations (2) and (4) using custom R code that we developed and provided as supplemental material (Supplementary File S7). DTR estimates for PO duos and TTR estimates for PPO trios were compared to empirically estimate statistical thresholds to exclude parents. With a perfect dataset (one with zero genotyping errors), TTR = 0 when both parents in a trio are correctly identified. When estimated from a real-world dataset (one with genotyping errors), $\mathit{TTR}\ne 0$ even when both parents in the trio are correctly identified. However, TTR estimates for correctly identified parents are typically exceedingly small and approach zero when genotyping errors are small and DNA profiles are informative (Jones and Ardren 2003; Vandeputte 2012; Vandeputte and Haffray 2014). The probability of a type I (false-positive) error depends on the genetic relatedness of individuals in the DNA profile database and the number, informativeness, and genotyping error rates of the DNA markers (Jones and Ardren 2003; Vandeputte and Haffray 2014). A false-positive error occurs when an individual that is not a parent is declared to be a parent (included), whereas a false-negative error occurs when an individual that is a parent is excluded (declared to not be a parent).

DTR and TTR thresholds for excluding parents were empirically estimated by bootstrapping (Efron 1980; Simon and Bruce 1991; Manly 2006; Berry et al. 2014). We drew 50,000 bootstrap samples from a population of 1,002 individuals with known pedigrees by replacing one or both parents in the known PPO trio with a randomly selected individual (nonparent) from the population. We built empirical (bootstrap) DTR and TTR distributions from the 50,000 estimates and ascertained the statistical thresholds needed to accurately identify (include) parents, exclude nonparents, and minimize false-positive errors. The bootstrap-estimated DTR threshold of $\mathit{DTR}\le 0.0016$ yielded a false-positive probability of zero and a false-negative probability of 5%, whereas the bootstrap-estimated TTR threshold of $\mathit{TTR}\le 0.01$ yielded false-positive and false-negative probabilities of zero. These thresholds were estimated by summing transgression scores summed over 14,650 SNP marker loci. To increase the computational speed and efficiency, DTR statistics were estimated for every PO combination, whereas TTR statistics were only estimated for PPO combinations where the DTR estimates for both parents were less than the empirical threshold (DTR < 0.0016). This was done because the number of PPO combinations was prohibitively large (close to one billion) and most PPO combinations could be unequivocally excluded using DTR estimates.

Social network analyses

The pedigree networks for global, California, and Cosmopolitan populations were analyzed and visualized as directed social networks using the R package igraph (version 1.2.2; Csardi and Nepusz 2006), where every edge in the graph connects a parent node to an offspring node and information flows unidirectionally from parents to offspring (Wasserman and Faust 1994). The pedigree networks or sociograms were visualized using the open-source software Gephi (version 0.9.2; Bastian et al. 2009; https://gephi.org/). We estimated the number of edges (d = degree) and in-degree (d_i), out-degree (d_o), and betweenness-centrality (B) statistics for every individual in a sociogram (Wasserman and Faust 1994). d_i estimates the number of known parents, where d_i = 0 when neither parent is known (for founders), 1 when one parent is known, and 2 when both parents are known. d_o estimates the number of descendants of an individual. A “geodesic” is the shortest path between two nodes in the network and estimates the number of generations in the pedigree of an individual (Hayes 2000). D is the longest geodesic in the network and estimates the largest number of generations for a descendant in the pedigree or the maximum depth of the pedigree (Hayes 2000). B estimates the connectivity of an individual to other individuals in a network (the number of geodesics connecting a node to other nodes), essentially the flow of information (alleles) and information “bottlenecks” (Freeman 1977; Wasserman and Faust 1994; Yu et al. 2007; Pavlopoulos et al. 2011). B was estimated by

$$B(n_i)=\sum _{j<k}\frac{g_{jk}(n_i)}{g_{jk}}$$ (5)

where n_i is the ith node (individual); i, j, and k are different nodes; $g_{jk}$ is the number of geodesics occurring between nodes j and k; and $g_{jk}(n_i)$ is the number of geodesics that pass through the ith node (Freeman 1977; Wasserman and Faust 1994; Brandes 2001; Csardi and Nepusz 2006). B = 0 when d_i or d_o equals zero.

Standard SNA metrics and terminology were used to classify individuals and describe their importance in the genealogy, which are analogous to applications in diverse fields of study (Gursoy et al. 2008; Koschützki and Schreiber 2008; Morselli 2010; Kim and Song 2013; Nerghes et al. 2015). Using B and d_o estimates, ancestors were classified as globally central (d_o > ${\overline{d}}_o$$\wedge$B > $\overline{B}$), locally central (d_o > ${\overline{d}}_o$$\wedge$B < $\overline{B}$), broker (d_o < ${\overline{d}}_o$$\wedge$B > $\overline{B}$), or marginal (d_o < ${\overline{d}}_o$$\wedge$B < $\overline{B}$).

Selection cycle length calculations

The pedigree network for every cultivar was extracted from the global pedigree network and included the cultivar (the youngest terminal node) and every ascendant (founder and non-founder) of the cultivar. Selection cycle lengths (S = years/generation) were estimated for every cultivar by tracing every possible path (back in time) in the pedigree network from the cultivar to founders and by calculating birth year differences for every PO edge (y_i) in the path, where y_i is the number of years separating the ith PO edge. The mean selection cycle length was estimated by $\overline{S}=\sum _i{y}_i/n_e$, where y_i is the birth year difference for the ith PO edge, n_e is the number of PO edges, and $i=1,2,\dots ,n_e$. To understand how selection cycle length changed over time, we considered all 14,275 unique PO edges available in the pedigree, among which 9,486 had birth years known for both the parent and the offspring. For each edge, we computed its midpoint as the average birth year between the parent and the offspring and its size, i.e., the selection cycle length (S), as the difference in birth years between the parent and the offspring.

Estimation of coancestry and pedigree–genomic relationship matrices

The kinship or coancestry matrix (A) was estimated for the entire pedigree (n = 8,851 individuals) using the create.pedigree and kin functions in the R package synbreed (version 0.12-12; Wimmer et al. 2012), where the ith diagonal element of A is the coefficient of coancestry of individual i with itself ($C_{ii})$ and the ijth off-diagonal element of A is the coefficient of coancestry between individuals i and j (C_ij) (Lynch and Walsh 1998). The genomic relationship matrix (G) was estimated for 1,495 individuals genotyped with 14,650 SNP markers selected to have minor allele frequencies (MAFs) $\ge 0.05$ and $\le 10\%$ missing data. G was estimated as described by VanRaden (2008) using the function A.mat in the R package rrBLUP (version 4.6.1; Endelman 2011). Missing genotypes were imputed using the mean genotype for each SNP marker.

We estimated the combined pedigree–genomic relationship matrix (H) for the entire pedigree (n = 8,851 individuals) as described by Legarra et al. (2009). The A matrix was partitioned into four sub-matrices ($A_{11},A_{12},A_{21},\mathit{and}{A}_{22}$), where the subscript 1 indexes ungenotyped and 2 indexes genotyped individuals. G and A₂₂ had the same dimensions but different scales. To construct the scaled G matrix (Christensen 2012; Christensen et al. 2012; Gao et al. 2012), the mean of off-diagonal elements of G ($\overline{oG}$) were scaled to match $\overline{o{A}_{22}}$ and the mean of diagonal elements of G ($\overline{dG}$) were scaled to match $\overline{d{A}_{22}}$:

$$\begin{array}{c}\overline{dG}\beta +\alpha =\overline{d{A}_{22}}\hfill \end{array}$$

and

$$\begin{array}{c}\overline{oG}\beta +\alpha =\overline{o{A}_{22}}\hfill \end{array}$$

with scalar solutions

$$\begin{array}{c}\alpha =\overline{o{A}_{22}}-\overline{oG}\beta \hfill \end{array}$$

and

$$\begin{array}{c}\beta =\frac{\overline{d{A}_{22}}-\overline{o{A}_{22}}}{\overline{dG}-\overline{oG}}\hfill \end{array}$$

The H matrix was estimated using the scaled G matrix ($\tilde{G}=G\beta +\alpha$) as described by Legarra et al. (2009):

$$H=\left[\begin{array}{cc}{A}_{11}+A_{12}{A}_{22}^{-1}(\tilde{G}-A_{22})A_{22}^{-1}{A}_{21}& A_{12}{A}_{22}^{-1}\tilde{G}\\ \tilde{G}{A}_{22}^{-1}{A}_{21}& \tilde{G}\end{array}\right]$$ (6)

The open-source R code we developed to estimate H has been deposited in a FigShare database (Supplementary File S6).

To study genetic relationships among extinct and extant individuals, we estimated separate H matrices for the California and Cosmopolitan populations, and applied principal component analysis (PCA) to the unscaled H matrices. Principal components were estimated by spectral decomposition of H using the eigen function from base R (version 4.0.0), which yielded eigenvalues, eigenvectors, and component scores. Scores for the first two principal components were then plotted using the R package ggplot2 (Wickham 2016).

Genetic contributions of founders and ancestors

Coancestry or kinship (A) matrices were estimated for individuals within continent-, region-, and country-specific focal populations using the create.pedigree and kin functions in the R package synbreed (version 0.12-9; Wimmer et al. 2012). Focal populations consisted of cultivars and their ascendants (ancestors). Founders are ancestors with unknown parents, which were assumed to be unrelated (Lacy 1989, 1995; Hartl and Clark 2007), whereas non-founders are ancestors with known parents. Terminal nodes in a pedigree network (sociogram) are either founders or the youngest descendants. The mean kinship (MK) between the ith founder and cultivars in a focal population was estimated by

$$M{K}_i=\sum _j{C}_{ij}$$

where C_ij = the kinship coefficient between the ith founder and jth cultivar in a focal population, $i=1,2,\dots ,n,\hspace{0.17em}j=1,2,\dots ,k$, n = the number of founders in the focal population, and k = the number of cultivars in the focal population (Lacy 1989, 1995; Lynch and Walsh 1998; Hartl and Clark 2007). The proportional GC of the ith founder to a focal population was estimated by $P_i=M{K}_i/\sum _{i}M{K}_i$. The number of founder equivalents (F_e) was estimated by $F_e=1/\sum _{i}M{K}_i$, where $i\in \{{\text{founder}}_1,{\text{founder}}_2,\dots ,{\text{founder}}_n\}$ (Lacy 1989, 1995). Founder equivalents “are the number of equally contributing founders that would be expected to produce the same genetic diversity as in the population under study” (Lacy 1989).

The GCs of ancestors (founders and non-founders) to a focal population were estimated by constructing a directed distance matrix (D) with dimensions identical to A (n × n) such that parents appeared in the matrix before offspring (alleles flow from parents to offspring, but not vice versa). We used the directed distance (the number of PO edges between two accessions) to modify A so that coancestry coefficients were only estimated between ancestors and direct path cultivars. The directed distance matrix D was estimated using the distances function in the R package igraph (version 1.2.5; Csardi and Nepusz 2006), where nonzero distances in the D matrix were set equal to one. Coancestry coefficients for ascendants with no direct path to a cultivar were set equal to zero by taking the Hadamard product to generate the corrected coancestry matrix $A^{\star }=A\odot D$, where element C_ii = the coancestry coefficient for individual i with itself (Hartl and Clark 2007). To estimate GC for each ancestor, we applied an iterative approach that entailed (1) computing D, A, and $A^{\star }=A\odot D$ from the current pedigree; (2) estimating MK_i for each ancestor; (3) ranking MK_i estimates from largest to smallest; (4) setting GC_i = MK_i for the ancestor with the largest MK_i estimate; (5) deleting the ancestor with the largest MK_i estimate and rebuilding the pedigree; and (6) repeating the previous steps until GCs (GC_i) had been estimated for each ancestor. The proportional GC of the ith ancestor to a focal population was estimated by $P_i=G{C}_i/\sum _{i}G{C}_i$.

Data availability

Supplementary File S1 contains the pedigree database with parents and offspring in a standard trio format (offspring, mother, and father) with the following passport data: (1) alphanumeric identification number; (2) common names or aliases; (3) accession types (e.g., cultivars, breeding materials, or wild ecotypes); (4) birth years (years of origin); (5) geographic origins; (6) inventor (breeder or institution) names; (7) taxonomic classifications; and (8) DNA-authenticated pedigrees for genotyped UCD accessions. Supplementary File S2 contains pedigrees in the Helium format with parents and offspring identified by common names or aliases (Shaw et al. 2014; https://github.com/cardinalb/helium-docs/wiki). Supplementary File S3 is a complete bibliography of the databases and documents we referenced to build the pedigree database. Supplementary Files S4 and S5 contain betweenness-centrality (B), in-degree (d_i), and out-degree (d_o) statistics, structural role assignments, giant or halo component assignments, and coancestry-based estimates of the GCs of founders and ancestors to cultivars in the California and Cosmopolitan populations, respectively. Supplementary File S6 contains R code developed to estimate H from A and G as described by Legarra et al. (2009). The example input files from Legarra et al. (2009) for computing the H matrix are included. Supplementary File S7 contains R code developed for exclusion (paternity–maternity) analyses. Supplementary Table S1 details the most prominent ecotype founders and their coancestry-based estimates of GC to the California and Cosmopolitan populations.

Supplementary material is available at figshare DOI: https://doi.org/10.25387/g3.6007715.

Results and discussion

Genealogy of cultivated strawberry

We reconstructed the genealogy of cultivated strawberry as deeply as possible from wild founders to modern cultivars (Figure 1; Supplementary File S1). To build the database, pedigree records for 8,851 individuals were assembled from more than 800 documents, including scientific and popular press articles, laboratory notebooks, garden catalogs, cultivar releases, plant patent databases, and germplasm repository databases (Figure 1; see Supplementary File S3 for a complete bibliography). The database holds pedigree records and passport data for 2,656 F. × ananassa cultivars, of which approximately 310 were private sector cultivars with pedigree records in public patent databases (Supplementary File S1). The parents of the private sector cultivars, however, were nearly always identified by cryptic alphanumeric codes, and thus could not be integrated into the “giant component” of the sociogram (pedigree network) (Figure 1).

Figure 1.

Global pedigree network for cultivated strawberry. Sociogram depicting ancestral interconnections among 8,851 accessions, including 8,424 F. × ananassa individuals originating as early as 1775, of which 2,656 are cultivars. The genealogy includes F. chiloensis and F. virginiana founders tracing to 1624 or later. Nodes and edges for 267 wild species founders are shown in blue, whereas nodes and edges for 1,171 F. × ananassa founders are shown in red. Founders are individuals with unknown parents. Nodes and edges for descendants (non-founders) are shown in light gray. The outer ring (halo of nodes and edges) are orphans or individuals in short dead-end pedigrees disconnected from the principal pedigree network or the so-called giant component.

The global population was subdivided into “Cosmopolitan” and “California” populations to delve more deeply into their unique breeding histories (Hardigan et al. 2021; Figures 1 and 2). This split was informed by demography and geography, insights gained from genome-wide analyses of nucleotide diversity and population structure (Hardigan et al. 2020, 2021), and earlier studies of genetic diversity (Sjulin and Dale 1987; Horvath et al. 2011; Sánchez-Sevilla et al. 2015; Hardigan et al. 2018). The Cosmopolitan population included 100% of the non-California (non-UCD) individuals (n = 5,193) from the global population, in addition to 160 California individuals identified as ascendants of non-California individuals. The non-California cultivar “Cascade” (PI551759), for example, is a descendant of a cross between the California cultivar “Shasta” (PI551663) and non-California cultivar “Northwest” (PI551499) (https://www.ars.usda.gov/); hence, “Shasta” was included in both the Cosmopolitan and California populations. Similarly, the California population included 100% of the UCD individuals (n = 3,540) from the global population, in addition to 262 non-California individuals that were identified as ascendants of UCD individuals. We nearly completely reconstructed the genealogy of the California population; however, as described below, pedigree records were missing for nearly every individual in the California population but were accurately ascertained using computer and DNA forensic approaches.

Figure 2.

Genealogy for California and Cosmopolitan populations of cultivated strawberry. (A) Sociogram depicting ancestral interconnections among 3,802 individuals in the “California” population. This population included 3,452 F. × ananassa individuals developed at the (UCD, from 1924 to 2012, in addition to 151 non-UCD F. × ananassa ascendants that originated between 1775 and 1924. Node and edge colors depict the year of origin of the individual in the pedigree network from oldest (red) to youngest (blue) with a continuous progression from warm to cool colors as a function of time (year of origin). Nodes and edges for individuals with unknown years of origin are shown in gray. (B) Sociogram depicting ancestral interconnections among 5,354 individuals in the “Cosmopolitan” population. This population included 5,106 F. × ananassa individuals developed across the globe between 1775 and 2018 and excluded UCD individuals other than UCD ancestors in the pedigrees of non-UCD individuals. Node and edge colors depict the continent where individuals in the pedigree network originated: Australia (orange), Asia (red), North America (blue), and Europe (green). Nodes and edges for individuals of unknown origin are shown in gray. (A and B) For both sociograms, node diameters are proportional to the betweenness centrality (B) metrics for individuals (nodes). Orphans and short dead-end pedigrees that were disconnected from the principal pedigree network (“giant component”) are not shown. (C) PCA of the pedigree–genomic relationship matrix (H) for the California population. The H matrix ($8,851\times 8,851$) was estimated from the coancestry matrix (A) for 8,851 individuals and the genomic relationship matrix (G) for 1,495 individuals genotyped with a 35-K SNP array. The PCA plot shows PC1 and PC2 coordinates for 3,802 individuals in the California population color-coded by year of origin. (D) PCA of the H matrix for the Cosmopolitan population. The PCA plot shows PC1 and PC2 coordinates for 5,354 individuals in the Cosmopolitan population color-coded by country, region, or continent of origin.

DNA forensic approaches for parent identification and pedigree authentication in octoploid strawberry

When this study was initiated in early 2015, 1,235 F. × ananassa germplasm accessions (asexually propagated individuals) were preserved in the UCD Strawberry Germplasm Collection. The collection included 68 UCD cultivars with known pedigrees; however, pedigree records for the other 1,184 UCD individuals were unavailable. Using computer forensic approaches, pedigree records for 1,002 of these individuals were recovered from an obsolete electronic database. Because the authenticity and accuracy of those records were uncertain, every individual was genotyped with the iStraw35 SNP array to build a SNP profile database for parent identification by exclusion analysis (Jones and Ardren 2003; Vandeputte 2012; Vandeputte and Haffray 2014; Bassil et al. 2015; Verma et al. 2017). SNP marker genotypes were automatically called using the Affymetrix Axiom Suite, then manually curated to identify and extract subgenome-specific SNP markers with well-separated codominant genotypic clusters and MAFs > 0. We selected 14,650 SNP markers for the parentage analyses described here. Genotyping errors were negligible (0.06-0.37%), and genotype-matching percentages for array-genotyped SNPs ranged from 99.63 to 99.95% among biological and technical replicates. On the basis of these genotyping error rates, we predicted that parents could be accurately identified and false-positive errors could be virtually eliminated by applying stringent empirically estimated statistical thresholds.

To estimate DTR and TTR thresholds for excluding parents with negligible false-positive errors, 50,000 bootstrap samples were drawn with replacement among 1,002 individuals with known pedigrees by substituting one or both of the known parents in a PPO trio with a randomly selected individual from the population. This yielded empirical distributions of DTR and TTR estimates from which false-positive and false-negative errors were estimated. The bootstrap-estimated DTR threshold of 0.0016 yielded a false-positive probability of zero and a false-negative probability of 5% when estimated by summing genotypic transgression scores (S_i) over 14,650 SNP marker loci among individuals with known parentage (Figure 3A). Using this DTR threshold, there was a 0 in 50,000 chance of reaching an incorrect conclusion (failing to exclude an individual that is not a parent). The false negatives (known parents that were excluded as parents) had DTR estimates slightly greater than the 0.0016 threshold.

Figure 3.

Lower tails of duo and trio transgression ratio distributions. DTRs and TTRs were estimated from the genotypes of 14,650 SNP markers among 1,235 individuals in the California population of strawberry. DTR and TTR thresholds for parent exclusion were empirically estimated by bootstrapping. Vertical dashed lines demarcate the bootstrap-estimated thresholds (DTR < 0.0016 and TTR < 0.01) applied in parent exclusion analyses. (A) Distribution of 2,708 DTR estimates in the lower tail (0.00 to 0.01) of the 0.00 to 1.00 distribution (DTR estimates > 0.01 are not shown). There were 761,995 possible PO duos (DTR estimates) among 1,235 individuals in the California population. (B) Distribution of 2,815 TTR estimates in the lower tail (0.00 to 0.03) of the 0.00 to 1.00 distribution (TTR estimates > 0.03 are not shown). There were 941,063,825 possible TTR estimates for trios among 1,235 individuals in the California population.

The bootstrap-estimated TTR threshold of 0.01 yielded zero false positives and zero false negatives when estimated by summing trio transgression scores (T_i) over 14,650 SNP marker loci for individuals with known parentage (Figure 3B). Using this TTR threshold, we found that there was a 0 in 50,000 chance of reaching an incorrect conclusion when eliminating a parent in a trio (replacing one or both of the known parents with a random individual from the population). There were zero known true trios in our study that exceeded the 0.01 TTR threshold (100% of the TTR estimates for trios with correctly identified parents were in the $0.0007<\mathit{TTR}<0.008$ range; Figure 3B).

We estimated DTRs for all possible PO duos (761,995) (Figure 3A). TTRs were only estimated for only those PPO trios where both parents had DTR estimates below the empirically estimated DTR significance threshold (Figure 3B). This eliminated the need to compute TTR statistics for individuals that could be unequivocally excluded as parents ($\mathit{DTR}\ge 0.0016$; Figure 3), greatly increased computational efficiency, and was necessary because the number of PPO (TTR) permutations in our reference population was astronomically large (approximately one billion). For trio analyses, we included the possibility that offspring could arise by self-pollination, which yielded $n\times (n-1)=1,235\times 1,234=1,523,990$ possible trios. Although this possibility does not arise in human or animal parent identification problems (Jones and Ardren 2003; Vandeputte 2012), offspring can arise from self-pollination in cultivated strawberry and other self-compatible plants. The number of possible trios arising from crosses between two parents in the reference population was $(n\times [n-1])+(n\times [n-1]\times [n-2])/2=941,063,825$. We are only showing the lower tails of the DTR and TTR distributions (Figure 3) because the upper tails (0.01 to 1.00 for DTR and 0.03 to 1.00 for TTR) dwarfed their respective distributions, visually obscured the lower tails (0.00 to 0.01 for DTR and 0.00 to 0.03 for TTR), and included hundreds of thousands or millions of estimates for PO or PPO combinations that exceeded the statistical thresholds and could be unequivocally excluded as parents (Figure 3).

Trio exclusion analysis accurately identified the parents of 1,044 UCD individuals (TTR < 0.01; Figure 3B). When the SNP profile for only one parent was present in the database (134 out of 1,235 individuals), duo exclusion analysis had to be applied and accurately identified 95% of the known parents with zero false positives (Figure 3A). We could not unequivocally identify 5% of the parents using duo exclusion analysis because those parents had DTR estimates exceeding the 0.0016 threshold. DTR estimates for these false-negative PO combinations, however, were only slightly greater than the threshold. When the DNA profile for only one parent exists in the DNA profile database, the probability of a false negative slightly increases and the power to unequivocally identify that parent slightly decreases (Vandeputte 2012; Vandeputte and Haffray 2014). The difference in statistical power between the duo and trio methods stems from differences in the informativeness of the underlying genotypic combinations (Elston 1986; Goldgar and Thompson 1988). For a diploid or allo-polyploid organism, two out of nine possible genotypic combinations are informative for duo exclusion analysis, whereas 12 out of 27 possible genotypic combinations are informative for trio exclusion analysis (Vandeputte 2012; Vandeputte and Haffray 2014). Moreover, trio exclusion analysis includes two highly informative (statistically powerful) combinations where the candidate offspring are heterozygous (AB) and both parents are homozygous for the same allele (either AA or BB). Our study unequivocally showed that parents can be identified with exceptional accuracy and zero false positives when high-quality genotypic data are available for both parents.

Our computer forensic search did not recover pedigree records for 220 individuals in the California (UCD) population; however, we suspected that their parents might be present in the SNP profile database. Using duo and trio exclusion analyses, we identified both parents for 214 of these individuals and one parent each for the other six individuals. Hence, using a combination of computer and DNA forensic approaches, 2,222 out of 2,470 possible parents of 1,235 individuals (90.0%) in the California population were identified and documented in the pedigree database (Supplementary File S1; Figure 2). The parents declared in pedigree records (if known), identified by DNA forensic methods (if conclusive), or both are documented in the pedigree database (Supplementary File S1). Despite their historic and economic importance, the pedigrees of individuals preserved in the UCD Strawberry Germplasm Collection (“California” population) had not been previously documented. Besides reconstructing the genealogy of the California population, previously undocumented pedigrees of extinct and extant individuals were discovered in the laboratory notebooks of Harold E. Thomas, Royce S. Bringhurst, and others (Bringhurst 1918-2016; Bringhurst et al. 1990; Johnson 1990), and integrated into the pedigree database (Supplementary File S1).

To further validate the accuracy of DNA forensic approaches for parent identification in strawberry, we applied an exclusion analysis to a population of 560 hybrid individuals developed from crosses among 30 UCD individuals (parents). The pedigrees of the parents and hybrids were known. The parents and hybrids (n = 590) and 1,561 additional UCD individuals were genotyped with 50-K or 850-K SNP arrays (Hardigan et al. 2020). The 50-K array was developed with SNP markers from the 850-K array (Hardigan et al. 2020), which included a subset of 16,554 legacy SNP markers from the iStraw35 and iStraw90 arrays (Bassil et al. 2015; Verma et al. 2017). We developed an integrated SNP profile database using 2,615 SNP markers common to the three arrays. Using PPO trios, we discovered that the SNP profile for one of the parents (11C151P008) was a mismatch, whereas the SNP profiles of the other 29 parents perfectly matched their pedigree records. We discovered that the parent stated for 11C151P008 was correct, but that the DNA sample and associated SNP marker profile were incorrect. Hence, the DNA sample mismatch was traced by trio exclusion analysis to a single easily corrected laboratory error. This analysis empirically demonstrated the utility of exclusion analysis for authenticating pedigrees and curating germplasm collections, and showed that parents can be accurately identified with substantially smaller numbers of DNA markers than those applied in our initial study.

These results highlight the power and accuracy of diploid Mendelian exclusion analysis methods for pedigree authentication (paternity and maternity analyses), intellectual property protection, and quality control monitoring of germplasm and nursery stock collections in octoploid strawberry using subgenome-specific DNA markers. The application of these approaches was straightforward because of the simplicity and accuracy of subgenome-specific genotyping approaches in octoploid strawberry populations (Hardigan et al. 2020). The development and robustness of SNP genotyping platforms has facilitated the application of standard diploid genetic theory and methods in octoploid strawberry, including the exclusion analysis methods applied in the present study (Jones and Ardren 2003; Vandeputte 2012; Vandeputte and Haffray 2014; Figure 3). The power and accuracy of these methods were rigorously tested and affirmed in a court of law where DNA forensic evidence was pivotal in proving the theft of University of California intellectual property (strawberry germplasm) by the defendants in a 2017 case in US District Court for the Northern District of California captioned The Regents of the University of California v California Berry Cultivars, LLC, Shaw, and Larson (Chivvis 2017). The DNA forensic approaches and evidence applied in that case are documented in a publicly available expert report identified by case number 3:16-cv-02477 (https://ecf.cand.uscourts.gov/cgi-bin/login.pl).

Social network analyses uncover distinctive differences in the domestication history of California and cosmopolitan populations

We estimated that 80-90% of the individuals in the California and Cosmopolitan pedigree networks were extinct (Figure 2). Using SNP array-genotyped individuals preserved in public germplasm collections as anchor points, we searched for evidence that the allelic diversity transmitted by extinct founders had been “lost.” This is a difficult question to answer with certainty; however, the findings reported here, combined with the findings of Hardigan et al. (2021), suggest that genetic diversity has been exceptionally well preserved in domesticated populations. Using SNA and PCAs of H, we did not observe structural features in sociograms or PCA plots that were indicative of the loss of novel ancestral genetic diversity (Figure 2). The kinship or numerator relationship matrix (A) was estimated for the entire pedigree of genotyped and ungenotyped individuals (VanRaden 2008; Legarra et al. 2009). For the present study, 1,495 historically important and geographically diverse UCD and USDA F. × ananassa individuals were genotyped with high-density SNP arrays (Bassil et al. 2015; Verma et al. 2017; Hardigan et al. 2020). The genomic relationship matrix (G) was estimated for the genotyped individuals and combined with the A matrix to estimate the H matrix for the entire pedigree (Legarra et al. 2009). The global H matrix was partitioned as needed for subsequent analyses (Figure 2).

PCAs of the H matrices yielded two-dimensional visualizations of genetic relationships that were remarkably similar in shape and structure to sociograms for the California and Cosmopolitan populations (Figure 2). We observed distinctive differences in the shapes and structures of the sociograms and PCA plots between the populations (Figure 2). The pattern in the Cosmopolitan population was a characteristic of pervasive admixture among individuals across geographies (Figure 2, B and D). We observed a strong chronological trend in the California population (Figure 2, A and C) but not in Cosmopolitan population (Figure 2, B and D). We observed a mid-twentieth-century bottleneck in the California population (the sharp interior angle in the V-shaped structure of the PCA plot), in addition to a bottleneck pinpointed to approximately 1987-1993 when the California population became closed. We discovered that 48 founders contributed 100% of the allelic diversity to the California population from 1987 onward (Figure 2, A and C; Supplementary File S1). Hardigan et al. (2021) showed that even though nucleotide diversity had been progressively reduced by bottlenecks and selection, a significant nucleotide diversity has persisted in the California population but was found to be unevenly distributed across the genome.

The wild roots of cultivated strawberry

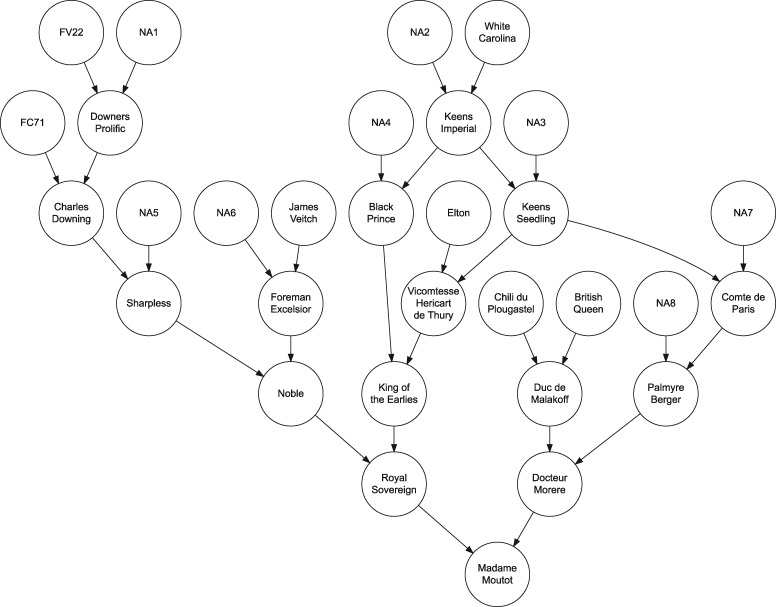
Our genealogy search did not uncover pedigree records for F. × ananassa cultivars developed between 1714 and 1775, the 61-year period following the initial migration of F. chiloensis ecotypes from Chile to Europe (Duchesne 1766; Darrow 1966). The scarcity of pedigree records from the eighteenth century was anticipated because the interspecific hybrid origin of F. × ananassa was not discovered until the mid-1700s (Duchesne 1766). “Madame Moutot” was the only cultivar in the database with ancestry that could be directly traced to one of the putative original wild octoploid progenitors of the earliest F. × ananassa hybrids that emerged in France in the early 1700s (Figure 4). Although the genealogy primarily covers the past 200 years of domestication and breeding (Supplementary File S1), ascendants in the pedigree of the cultivar “Madame Moutot” (circa 1906) traced to “Chili de Plougastel” (Figure 4), a putative clone of one of the original F. chiloensis subsp. chiloensis plants imported from Chile to France by the explorer Amédée-François Frézier (Gloede 1865; Carriére 1879; Bunyard 1917; Darrow 1966; Pitrat and Faury 2003). These plants were carried aboard the French frigate “St. Joseph,” delivered by Frézier to Brest, France (Bunyard 1917), and shared with Antoine Laurent de Jussieu, a botanist at the Jardin des plantes de Paris. According to de Lambertye (1864), the Frézier clone was widely disseminated and cultivated in Plougastel near Brest and interplanted with F. virginiana (Duchesne 1766; Bunyard 1917; Pitrat and Faury 2003). Hence, some of the earliest spontaneous hybrids between F. chiloensis and F. virginiana undoubtedly arose in the strawberry fields of Brittany in the early 1700s (de Lambertye 1864; Darrow 1966; Pitrat and Faury 2003). The French naturalist Bernard de Jussieu, the brother of Antoine Laurent de Jussieu and a mentor of Antoine Duchesne—“the father of the modern strawberry”—brought clones of the original Frézier F. chiloensis plants to the Jardins du Château de Versailles (Gardens of Versailles) where Duchesne (1766) unraveled the interspecific hybrid origin of F. × ananassa (Darrow 1966; Williams 2001). The next earliest F. chiloensis founders appear to be a California ecotype identified in German breeding records from the mid-1800s and an anonymous ecotype in the pedigree of the French cultivar “La Constante” from 1855 (Supplementary Files S1 and S2; Gloede 1865; Merrick 1870; Darrow 1937, 1966; Wilhelm and Sagen 1974).

Figure 4.

Pedigree for the heirloom cultivar “Madame Moutot” (circa 1906). Arrows indicate the flow of genes from parents to offspring. FV22 is an unknown F. virginiana ecotype, FC71 is an unknown F. chiloensis ecotype, and “Chili du Plougastel” is purportedly one of the original F. chiloensis individuals imported by Amédée-François Frézier from Chile to France in 1714. Unknown parents of individuals in the pedigree are identified by NA1, NA2,…, NA7. Terminal individuals in the pedigree are founders (individuals with unknown parents). The oldest F. × ananassa cultivar in the pedigree is “White Carolina” (PI551681), which originated sometime before 1775.

The origins and identities of the earliest F. virginiana founders of F. × ananassa remain a mystery because their migrations from North America to Europe in the early 1600s and subsequent intracontinental migrations were not well documented (Supplementary File S1; Duchesne 1766; de Lambertye 1864; Darrow 1937). The oldest F. virginiana individuals identified in historic documents and pedigree records were “Large Early Scarlet” (1624), “Old Scarlet” (1625), and “Hudson Bay” (1780), all extinct (Supplementary File S1). We identified 30 anonymous F. virginiana and 76 anonymous F. chiloensis founders in the pedigree records. These individuals were assigned unique alphanumerical aliases to facilitate the reconstruction of the genealogy; e.g., FV22 is the alias for an anonymous F. virginiana founder and FC71 is the alias for an anonymous F. chiloensis founder in the pedigree of “Madame Moutot” (Figure 4; Supplementary File S1).

The complex hybrid ancestry of cultivated strawberry

Once the interspecific hybrid origin of F. × ananassa became widely known (Duchesne 1766), domestication began in earnest with extensive intra- and interspecific hybridization, artificial selection, and intra- and intercontinental migration (Merrick 1870; Fletcher 1917; Darrow 1937). These forces shaped the genetic structure of the F. × ananassa populations that emerged in Europe and North America, and ultimately migrated around the globe (Fletcher 1917; Darrow 1966; Sjulin and Dale 1987; Johnson 1990; Sjulin 2006; Horvath et al. 2011; Sánchez-Sevilla et al. 2015; Hardigan et al. 2018, 2021). Over the next 250 years, horticulturalists and plant breeders repeatedly tapped into the wild reservoir of genetic diversity, especially wild octoploid taxa native to North America (Figure 1; Table 1). There are numerous narrative accounts of what transpired, especially in Europe, North America, and California (Clausen 1915; Darrow 1937, 1966; Sjulin and Dale 1987; Bringhurst et al. 1990; Dale and Sjulin 1990; Johnson 1990; Hancock et al. 2001; Sjulin 2006; Hancock et al. 2010; Horvath et al. 2011; Sánchez-Sevilla et al. 2015; Hancock et al. 2018), but none have painted a holistic picture of the complicated wild ancestry and dynamic forces that shaped genetic diversity in F. × ananassa.

Table 1.

Number of primary and secondary gene pool founders in the global genealogy of cultivated strawberry

Species	Ploidy	Giant	Halo	Complete
Primary gene pool
F. chiloensis	2n = 8x = 56	79	33	112
F. virginiana	2n = 8x = 56	41	24	65
F. × ananassa	2n = 8x = 56	656	515	1,171
Unknown octoploid Fragaria	2n = 8x = 56	9	1	10
Primary gene pool total		785	573	1,358
Secondary gene pool
F. iinumae	2n = 2x = 14	1	2	3
F. nilgerrensis	2n = 2x = 14	2	0	2
F. nipponica	2n = 2x = 14	0	2	2
F. nubicola	2n = 2x = 14	2	0	2
F. orientalis	2n = 2x = 14	3	1	4
F. viridis	2n = 2x = 14	4	2	6
F. vesca	2n = 2x = 14	20	24	44
F. moschata	2n = 6x = 42	6	0	6
F. × vescana	2n = 10x = 70	1	0	1
P. glandulosa	2n = 2x = 14	3	0	3
P. anserina	2n = 4x = 28	1	0	1
P. palustris	2n = 6x = 42	1	4	5
Unknown Potentilla	NA	0	1	1
Secondary gene pool total		44	36	80

Founders are individuals with unknown parents. The sociogram for the global genealogy consisted of “giant” and “halo” components. The giant component consisted of the highly interconnected mass of individuals in the sociogram (pedigree network), whereas the halo component consisted of orphans and other isolated individuals in small dead-end pedigrees that were disconnected from the giant component.

We identified 1,438 founders in the genealogy of cultivated strawberry (Figure 1; Table 1; Supplementary Files S1, S4, and S5). Here and elsewhere, “founders” are individuals with unknown parents, whereas “ancestors” are ascendants that may or may not be founders (Lacy 1989, 1995). The terminal nodes in the pedigree networks are either founders or the youngest descendants in a pedigree (Figures 1 and 2). Of the 1,438 founders, 267 were wild species and 1,171 were F. × ananassa individuals (Figure 1; Table 1). Because the F. × ananassa founders are either interspecific hybrids or descendants of interspecific hybrids, the number of wild species founders could exceed 268. One of the challenges we had with estimating the number of wild species founders was the anonymity of ecotypes that were used as parents before breeders began carefully documenting pedigrees (Supplementary File S1). We could not rule out that some of the anonymous wild species founders in the pedigree records might have been clones of the same individuals, which means that the estimated number of wild species founders reported here could be inflated.

As interspecific hybridization with wild founders became less important and intraspecific (F. × ananassa) hybridization became more important in strawberry breeding, the proportional GC of wild founders to the gene pool of cultivated strawberry decreased (Figure 5; Supplementary Files S4 and S5). This seems paradoxical because 100% of the alleles found in F. × ananassa were inherited from wild founders, but increasingly flowed through F. × ananassa descendants over time—wild octoploids numerically only constituted 14% of the founders we identified (Table 1). Several trends emerged from our analyses of genetic relationships and founder contributions. First, inbreeding has steadily increased over time as a consequence of population bottlenecks and directional selection (Figure 5B). Second, the California population was significantly more inbred than the Cosmopolitan population (Figure 5B). These results were consistent with the findings of Hardigan et al. (2021) from genome-wide analyses of DNA variants and population structure. They found selective sweeps on several chromosomes in the California population, which was shown to be unique and bottlenecked. Finally, the relative number of founder equivalents (Lacy 1989, 1995) has decreased over time, consistent with the increase in inbreeding over time (Figure 5, A and B).

Figure 5.

Relative founder equivalents, inbreeding coefficients, and wild founder genetic contributions over time. (A) Relative founder equivalent ($F_e/n$) estimates for California and Cosmopolitan cultivars over time, where F_e = founder equivalents and n = number of founders. The California population included 69 cultivars developed at the UCD, since the inception of the breeding program in 1924. The birth year (year of origin) was known for all of the UCD cultivars. The Cosmopolitan population included 2,140 cultivars with known birth years. (B) Wright’s coefficient of inbreeding (F) for individuals in the California and Cosmopolitan populations over time. F was estimated from the relationship matrix (A). (C) Estimates of the GCs of wild species founders to allelic diversity in the California and Cosmopolitan populations.

Primary and secondary gene pool founders of cultivated strawberry

The primary gene pool of cultivated strawberry is comprised of eight cross-compatible, interfertile octoploid taxa: F. chiloensis subsp. chiloensis, F. chiloensis subsp. lucida, F. chiloensis subsp. pacifica, F. chiloensis subsp. sandwicensis, F. virginiana subsp. virginiana, F. virginiana subsp. glauca, F. virginiana subsp. grayana, and F. virginiana subsp. platypetala (Staudt 1989; Hummer et al. 2011), seven of which were found in pedigree records (Figure 1; Table 1; Supplementary File S1). The only primary gene pool taxon not found in the pedigree records was F. virginiana subsp. grayana. We identified 112 F. chiloensis, 65 F. virginiana, and 1,171 F. × ananassa founders, which constituted 95% of the founders and were estimated to have contributed $\ge 99\%$ of the allelic diversity to global, California, and Cosmopolitan F. × ananassa populations (Figure 6; Table 1; Supplementary Files S4 and S5). Even though wild species from the secondary gene pool constituted 6% of the founders and 30% of the wild species founders identified in pedigree records, they were estimated to have contributed $<0.1\%$ of the allelic diversity in the global F. × ananassa population (Table 1; Supplementary Files S4 and S5).

Figure 6.

Genetic contributions of ancestors to cultivars. (A) The GCs of ancestors to the allelic diversity among k cultivars within a focal population were estimated from the mean coancestry between the ith ancestor and the k cultivars within the focal population. The GCs of the ancestors were ordered from largest to smallest to calculate the cumulative GCs of ancestors to cultivars in a focal population. (B) The proportion of ancestors needed to account for p% of the allelic diversity among cultivars within a focal population was estimated by dividing the cumulative GC by k.

While the assignment of F. chiloensis and F. virginiana subspecies to the primary gene pool was unequivocal and uncontroversial, the assignment of non-octoploid Fragaria and Potentilla species to secondary or tertiary gene pools, as per the definitions of Harlan and de Wet (1971), was tenuous because evidence for the inheritance of alleles from exotic donors (diploid, tetraploid, or hexaploid Fragaria and Potentialla) among inter-ploidy hybrid offspring with cultivated strawberry was not always clear from genealogical and breeding records. We lumped the non-octoploid Fragaria and Potentilla into the secondary gene pool solely because they were recorded as ancestors of F. × ananassa individuals (Table 1), which implied that interspecific, intergeneric, and inter-ploidy hybrid descendants inherited alleles transmitted by secondary gene pool donors. However, the genetic proof was not always clear or available. One or more of the species assigned to the secondary gene pool might belong in the tertiary gene pool (Harlan and de Wet 1971), a distinction of negligible practical importance.

The secondary gene pool founders in the genealogy were nearly always parents of orphans or other isolated individuals in short dead-end pedigrees that have not materially contributed allelic diversity to important cultivated strawberry populations or cultivars. The exotic founders have included decaploid ($2n=10x=70$) F. × vescana and pentaploid ($2n=5x=35$) F. × bringhurstii individuals (Bringhurst and Senanayake 1966; Bauer 1994; Sangiacomo and Sullivan 1994; Hummer et al. 2011). Although cited as important genetic resources for strawberry breeding (Darrow 1966; Hummer 2008), the secondary gene pool species have had a limited utility because of the range of biological challenges one encounters when attempting to introgress alleles from exotic donors through interspecific, intergeneric, and inter-ploidy hybrids, e.g., reproductive and recombination barriers, ploidy differences, meiotic abnormalities, and hybrid sterility (Bringhurst and Senanayake 1966; Bringhurst and Gill 1970; Harlan and de Wet 1971; Evans 1977; Bauer 1994; Sangiacomo and Sullivan 1994).

Genetic variation in the secondary gene pool has not been needed to drive genetic gains or solve problems in strawberry breeding. As highlighted earlier, Hardigan et al. (2021) showed that genetic diversity is massive in the primary gene pool and has not been eroded by domestication and breeding on a global scale, even though it has been significantly reduced and restructured in certain populations, e.g., the California population. The profound changes and restructuring in the California population over time, as previously noted, were clearly evident in the sociograms and PCAs of the pedigree–genomic relationship matrices (Figures 1 and 2). Because the California population has been the source of numerous historically and commercially important cultivars, we hypothesize that intense selection and population bottlenecks have purged a high frequency of unfavorable alleles compared to many other populations, thereby yielding an elite population with lower genetic diversity than the highly admixed Cosmopolitan population (Figures 1 and 2; Hardigan et al. 2021).

Prominent and historically important ancestors of cultivated strawberry

We used coancestry, betweenness-centrality (B), and out-degree (d_o) statistics to estimate the GC of founders and non-founders to genetic variation within a population and identify the most prominent and important ancestors in the genealogy of cultivated strawberry (Freeman 1977; Scott 1988; Lacy 1989, 1995; Figure 6; Table 2; Supplementary Files S4 and S5). The estimation of GC from the coancestry matrix (A) differed between founders and ancestors (founders and non-founders). For founders, GC was estimated by the mean coancestry or MK between each founder and cultivars within a focal population (Supplementary Files S4 and S5). For ancestors, GC was iteratively estimated by MK between each ancestor and cultivars within a focal population, starting with the ancestor with the largest MK estimated from A, deleting that ancestor, re-estimating the coancestry matrix ($A^{*}$), selecting the ancestor with the largest MK estimated from the pruned coancestry matrix ($A^{*}$), deleting that ancestor, re-estimating the coancestry matrix, and repeating until every ancestor had been dropped. We compiled GC, B, and d_o estimates for every founder and non-founder in the pedigree database (Supplementary Files S4 and S5).

Table 2.

The twenty-most prominent and historically important ancestors of cultivars

California				Cosmopolitan
Ancestor	GC (%)	B	${\mathbf{d}}_{\mathbf{o}}$	Ancestor	GC (%)	B	${\mathbf{d}}_{\mathbf{o}}$
Tufts	12.2	52,013.9	80	Howard 17	4.4	47,942.5	99
Lassen	7.1	56,157.0	42	Fairfax	1.9	13,090.4	91
Cal 177.21	6.4	36,728.6	49	Hovey	1.8	12,390.6	19
Douglas	5.7	72,781.8	32	Tufts	1.4	16,579.3	12
71C098P605	3.6	16,434.8	13	Crescent	1.3	16,803.7	59
Nich Ohmer	3.0	2,977.0	124	Aberdeen	1.2	7,908.6	35
Camino Real	2.6	17,797.1	23	Sharpless	1.2	11,727.0	51
Howard 17	2.5	52,231.1	16	Blakemore	1.2	13,265.9	49
Sequoia	2.4	40,254.5	38	Wilson	1.0	4,012.6	51
Diamante	2.3	31,032.9	27	Royal Sovereign	0.9	19,373.0	23
Irvine	2.0	11,938.8	12	Harunoka	0.9	6,193.6	24
Palomar	1.9	27,644.3	22	Douglas	0.8	22,433.6	23
Albion	1.8	22,016.6	11	Gorella	0.7	12,053.2	41
42C008P016	1.8	12,687.4	26	Hoffman	0.7	5,738.0	17
Parker	1.5	2,924.8	10	Marshall	0.7	0.0	58
65C065P601	1.5	19,867.1	13	Holiday	0.6	6,157.4	39
Seascape	1.5	8,637.0	12	Senga Sengana	0.6	3,258.0	58
San Andreas	1.3	35,857.9	22	Bubach	0.6	0.0	56
Aiko	1.2	8,141.0	5	Reiko	0.6	2,766.0	19
Oso Grande	1.1	48,118.7	20	Cumberland Triumph	0.5	10,544.7	12

GC statistics are tabulated for the twenty-most important ancestors of cultivars in the California and Cosmopolitan populations. The proportional GC of the ith ancestor to cultivars within a population was estimated by $P_i=G{C}_i/\sum _{i}G{C}_i$, where GC_i is the GC of ith ancestor to cultivars in the focal population. B is the betweenness-centrality estimate of the ancestor in the focal population. B = 0 for founders and B > 0 for non-founders. Out-degree (d_o) is the number of descendants of the ancestor in the focal population.

We identified four F. chiloensis, five F. virginiana, and 40 F. × ananassa founders in the genealogy of the California population (Supplementary File S4). Cumulative GC estimates for the California population were 1.8% for F. chiloensis, 12.7% for F. virginiana, and 85.5% for F. × ananassa founders. Four of the nine wild octoploid founders of the California population were founders of the historic Ettersburg population that supplied genetic diversity for private and public sector breeding programs in California (Clausen 1915; Wilhelm and Sagen 1974; Bringhurst et al. 1990; Sjulin 2006). The wild octoploid founders with the largest GCs were three F. virginiana ecotypes: “New Jersey Scarlet” (8.3%), “Hudson Bay” (2.7%), and “Wasatch” (1.3%) (Supplementary Table S1). Wasatch is the F. virginiana subsp. glauca donor of the PERPETUAL FLOWERING mutation that Bringhurst et al. (1980) transferred into F. × ananassa (Bringhurst et al. 1989). The Wasatch ecotype appears in the genetic background of every day-neutral cultivar developed at the UCD. Similarly, we identified 26 F. chiloensis, 24 F. virginiana, and 490 F. × ananassa founders in the genealogy of the Cosmopolitan population (Supplementary File S5). Cumulative GC estimates for the Cosmopolitan population were 4.6% for F. chiloensis, 14.1% for F. virginiana, 79.9% for F. × ananassa, and 1.4% for other founders. Similar to what we found for the California population, the wild octoploid founders with the largest GCs were “New Jersey Scarlet” (8.3%) and “Hudson Bay” (3.5%) (Fletcher 1917; Darrow 1937). The next largest GC was made by FC_071 (1.9%), an F. chiloensis ecotype of unknown origin found in the pedigrees of Madame Moutot, Sharpless, Royal Sovereign, and other influential early cultivars (Supplementary Table S1; Figure 4).

A significant fraction of the alleles found in F. × ananassa populations have flowed through a comparatively small number of common ancestors, each of which have contributed unequally to standing genetic variation (Figure 6; Table 2; Supplementary Files S4 and S5). The most important ancestors are described as “stars” in the lexicon of SNA, and are either locally or globally central (Moreno 1953; Scott 1988; Wasserman and Faust 1994). Globally central individuals reside in the upper-right quadrant of the $B\times d_o$ distribution (d_o > ${\overline{d}}_o$$\wedge$B > $\overline{B}$), where $\overline{B}$ is the mean of B and ${\overline{d}}_o$ is the mean of d_o—8.7-8.9% of the ancestors that were classified as globally central (Figure 7; Moreno 1953; Scott 1988; Wasserman and Faust 1994). Locally central individuals reside in the upper-left quadrant of the $B\times d_o$ distribution (d_o > ${\overline{d}}_o$$\wedge$B < $\overline{B}$)—11.8-12.1% of the ancestors were classified as locally central (Figure 7; Moreno 1953; Scott 1988; Wasserman and Faust 1994). “Tufts,” “Lassen,” “Nich Ohmer,” “Howard 17,” and “Fairfax” were among the biggest stars, along with several other iconic, mostly heirloom cultivars, and all were either locally or globally central (Table 2). Stars are “gatekeepers” that have numerous descendants (the largest d_o estimates), transmitted a disproportionate fraction of the alleles found in a population (have the largest GC estimates), have the largest number of interconnections (largest B estimates) in the pedigree, and are visible in sociograms as nodes with radiating pinwheel-shaped patterns of lines (Figure 2; Table 2; Supplementary Files S4 and S5). Several of the latter are visible in the sociograms we developed for the California and Cosmopolitan populations. Stars have the largest nodes (B estimates) in the sociograms (Figure 2).

Figure 7.

Structural roles and betweenness centrality (B) and out-degree (d_o) statistics for individuals in cultivated strawberry sociograms. (A) B and d_o estimates for individuals in the California population. (B) B and d_o estimates for individuals in the Cosmopolitan population. (A) and (B) The red dashed lines delineate globally central (upper right; d_o > ${\overline{d}}_o$$\wedge$B > $\overline{B}$), locally central (upper left; d_o > ${\overline{d}}_o$$\wedge$B < $\overline{B}$), broker (lower right; d_o < ${\overline{d}}_o$$\wedge$B > $\overline{B}$), and marginal (lower left; d_o < ${\overline{d}}_o$$\wedge$B < $\overline{B}$) quadrants, where $\overline{B}$ = the mean of B estimates and $\overline{d_o}$ = the mean of d_o estimates. $\overline{B}$ = 755.6 and ${\overline{d}}_o$ = 1.8 for the California population, whereas $\overline{B}$ = 315.2 and ${\overline{d}}_o$ = 1.5 for the Cosmopolitan population. B and d_o estimate densities are plotted along the x- and y-axes.

We estimated and compiled GC statistics for every ancestor in the California and Cosmopolitan populations (Supplementary Files S4 and S5). The twenty-most prominent and historically important ancestors of the California and Cosmopolitan populations are shown in Table 2. They include several iconic and well-known heirloom and modern cultivars, e.g., “Tioga,” “Douglas,” and “Royal Sovereign” (Fletcher 1917; Darrow 1937, 1966; Wilhelm and Sagen 1974; Sjulin and Dale 1987; Bringhurst et al. 1990), in addition to “unreleased” germplasm accessions preserved in the UCD Strawberry Germplasm Collection, e.g., 65C065P601 (aka 65.65-1). The latter is the oldest living descendant of the aforementioned F. virginiana subsp. glauca “Wasatch” ecotype collected by Royce S. Bringhurst from the Wasatch Mountains, Little Cottonwood Canyon, Utah (Bringhurst and Voth 1980, Bringhurst et al. 1989, Ahmadi et al. 1990). The “Wasatch” ecotype is a founder of every day-neutral cultivar in the California population and many day-neutral cultivars in the Cosmopolitan population with alleles flowing through 65C065P601 and the UCD cultivar “Selva” (Bringhurst et al. 1989; Supplementary Files S4 and S5).

GC statistics were ordered from largest to smallest ($G{C}_1\ge G{C}_2\ge \dots \ge G{C}_n$) and progressively summed to calculate the cumulative GCs of ancestors and the number of ancestors needed to explain p% of the genetic variation (n_p) in a focal population, where p ranges from 0 to 100% (Figure 6). The parameter n₁₀₀ estimates the number of ancestors needed to account for 100% of the genetic variation among k cultivars in a focal population (each focal population was comprised of cultivars, ascendants, and descendants). n₁₀₀ estimates were 153 for the California population and 3,240 for the Cosmopolitan population. The latter number was significantly larger than the number for the California population because the Cosmopolitan population includes pedigrees for 2,499 cultivars developed worldwide, whereas the California population includes pedigrees for 69 UCD cultivars only (Supplementary File S1). Within European countries, n₁₀₀ ranged from 25 for Belgium to 342 for England (Figure 6A). Within the United States, n₁₀₀ ranged from a minimum of 367 for the southern region to a maximum of 444 for western and northeastern regions.

Predictably, n_p increased at a decreasing rate as the number of GC-ranked ancestors increased (Figure 6). Cumulative GC estimates increased as nonlinear diminishing-return functions of the number of ancestors (Table 2; Supplementary Files S4 and S5). The slopes were initially steep because a fairly small number of ancestors accounted for a large fraction of the genetic variation within a particular focal population. Across continents, regions, and countries, eight to 112 ancestors accounted for 50% of the allelic variation within focal populations (Figure 6; Table 2). The differences in n_p estimates were partly a function of the number of cultivars (k) within each focal population. When n_p was expressed as a function of k, we found that the proportion of ancestors needed to explain p% of the allelic variation in a focal population was strikingly similar across continents, regions, and countries, e.g., the Western US population, which had the largest n₁₀₀ estimate (Figure 6A), fell squarely in the middle when expressed as a function of k (Figure 6B).

Breeding speed and pedigree-informed predictive breeding in cultivated strawberry

SNAs of the pedigree networks shed light on the speed of breeding and changes in the speed of breeding over the past 200 years in strawberry (Figures 8 and 9). We retraced the ancestry of every cultivar through nodes and edges in the sociograms (Figures 1 and 2). The year of origin was known for 71% of the individuals. These edges yielded robust estimates of the mean selection cycle length in years ($\overline{S}$ = mean number of years/generation). $\overline{S}$ was calculated from thousands of directed acyclic graphs, which are unidirectional paths traced from cultivars back through descendants to founders (Thulasiraman and Swamy 1992). Collectively, cultivars in the California population (n = 69) visited 27,058 PO edges, whereas cultivars in the Cosmopolitan population (n = 1,982) visited 155,487 PO edges. The selection cycle length means ($\overline{S}$) and distributions over the past 200 years were strikingly similar across continents, regions, and countries—$\overline{S}$ was 16.9 years/generation for the California population and 16.0 years/generation for the Cosmopolitan population (Figure 8). These extraordinarily long selection cycle lengths are more typical of a long-lived woody perennial than of a fast cycling annual (van Nocker and Gardiner 2014; Jighly et al. 2019); however, the speed of breeding has steadily increased over time (Figure 8). By 2000, $\overline{S}$ had decreased to six years/generation in the California population and 10 years/generation in the Cosmopolitan population (Figure 9).

Figure 8.

Selection cycle length distributions by geography. Selection cycle length means ($\overline{S}$ = mean number of years/generation) were estimated for k cultivars within continent-, region-, and country-specific focal populations of cultivated strawberry (k is shown in parentheses for each geographic group). $\overline{S}$ was estimated from edge lengths (years/edge) for all possible paths (directed graphs with alleles flowing from parents to offspring, but not vice versa) in pedigrees connecting cultivars to founders, where the length of an edge = the birth year difference between parent and offspring. $\overline{S}$ probability densities are shown for cultivars developed in different countries, regions, or continents. Only estimates in the zero to 30 year/generation range are shown because estimates exceeding 30 years/generation were extremely rare.

Figure 9.

Breeding speed over time. Selection cycle lengths (S = years/generation) were estimated for 3,693 independent PO edges in the pedigree networks for the California and Cosmopolitan populations. S estimates were limited to parents and offspring with known birth years. Selection cycle lengths are plotted against the midpoint (m) between parent and offspring birth years for California (black points) and Cosmopolitan (gray points) populations. The plotted lines are exponential decay functions fitted by nonlinear regression of S on m. The function for the California population was $y=35.06·e^{-0.0090·(x-1790.5)}$ (Nagelkerke pseudo-R² = 0.25; p < 0.001). The function for the Cosmopolitan population was $y=76.69·e^{-0.0079·(x-1736.5)}$ (Nagelkerke pseudo-R² = 0.08; p < 0.001).

The genealogy does not account for lineages underlying what must have been millions of hybrid progeny screened in breeding programs worldwide; e.g., Johnson (1990) alone reported screening 600,000 progeny over 34 years (1956-1990) at Driscoll’s (Watsonville, California). Cultivars are, nevertheless, an accurate barometer of global breeding activity and the only outward-facing barometer of progress in strawberry breeding. When translated across the past 200 years of breeding, our selection cycle length estimates imply that the 2,656 cultivars in the genealogy of cultivated strawberry have emerged from the mathematical equivalent of only 12.9 cycles of selection (200 years $÷$ 15.5 years per generation). Even though offspring from 250 years of crosses have undoubtedly been screened worldwide since 1770, 15.5 years has elapsed on average between parents and offspring throughout the history of strawberry breeding (Figures 8 and 9). Because genetic gains are affected by selection cycle lengths, and faster generation times normally translate into greater genetic gains and an increase in the number of recombination events per unit of time (Bernardo 2002; Ceccarelli 2015; Bernardo 2017; Jighly et al. 2019; Bernardo 2020), our analyses suggest that genetic gains can be broadly increased in strawberry by shortening selection cycle lengths. Genome-informed breeding and speed breeding are both geared towards that goal and have the potential to shorten selection cycle lengths and increase genetic gains (van Nocker and Gardiner 2014; Whitaker et al. 2020).

We reconstructed the genealogy of strawberry to inform the curation of a historically important germplasm collection, forensically identify the parents of individuals without pedigree records, authenticate the parents of individuals with pedigree records, shed light on the domestication history of strawberry, and retrospectively examine where we have been and how we got there. The reconstruction was greatly facilitated by the availability of outstanding SNP genotyping platforms (Hardigan et al. 2020), the development of an extensive DNA profile database to complement the pedigree database (Hardigan et al. 2021), and the application of robust and highly accurate diploid exclusion analysis methods for parent identification and pedigree authentication. We provided an open-source R code to support future parentage analyses in agricultural species.

Our backward-facing genealogy study, in retrospect, yielded unexpected insights about the complex hybrid ancestry and breeding history of cultivated strawberry that should inspire future generations and guide where we should go from here. Our critical examination of historical selection cycle lengths was meant to be provocative and perhaps inspire the implementation of strategies for increasing breeding speed and accelerating the improvement of strawberry. We suspect that improvements can be achieved, at least in part, through changes in breeding schemes and the application of pedigree-informed predictive breeding methods. The open-source pedigree database we compiled should find broad utility in predictive breeding schemes (Henderson 1975; Habier et al. 2013) and can be easily expanded and modified for specific breeding problems, other populations, and future analyses. Because of the depth and completeness of the pedigree records commonly available in strawberry, pedigree best linear unbiased prediction (pedigree-BLUP) has the potential to increase genetic gains and enhance selection decisions, especially when combined with genomic prediction (Henderson 1975; Habier et al. 2013). The pedigree database we assembled will facilitate the application of pedigree-BLUP and identity-by-descent prediction of alleles and haplotypes (Powell et al. 2010), in addition to providing a solid foundation for expanding the genealogy over time.