Abstract
With the advances in high-throughput sequencing technologies, it is not difficult to extract tens of thousands of single-nucleotide polymorphisms (SNPs) across many individuals in a fast and cheap way, making it possible to perform genome-wide association studies (GWAS) of quantitative traits in outbred forest trees. It is very valuable to apply traditional breeding experiments in GWAS for identifying genome variants associated with ecologically and economically important traits in Populus. Here, we reported a GWAS of tree height measured at multiple time points from a randomized complete block design (RCBD), which was established with clones from an F1 hybrid population of Populus deltoides and Populus simonii. A total of 22,670 SNPs across 172 clones in the RCBD were obtained with restriction site-associated DNA sequencing (RADseq) technology. The multivariate mixed linear model was applied by incorporating the pedigree relationship matrix of individuals to test the association of each SNP to the tree heights over 8 time points. Consequently, 41 SNPs were identified significantly associated with the tree height under the P-value threshold determined by Bonferroni correction at the significant level of 0.01. These SNPs were distributed on all but two chromosomes (Chr02 and Chr18) and explained the phenotypic variance ranged from 0.26% to 2.64%, amounting to 63.68% in total. Comparison with previous mapping studies for poplar height as well as the candidate genes of these detected SNPs were also investigated. We therefore showed that the application of multivariate linear mixed model to the longitudinal phenotypic data from the traditional breeding experimental design facilitated to identify far more genome-wide variants for tree height in poplar. The significant SNPs identified in this study would enhance understanding of molecular mechanism for growth traits and would accelerate marker-assisted breeding programs in Populus.
Keywords: genome-wide association study, randomized complete block design, mixed linear model, single-nucleotide polymorphism, Populus
Introduction
The genus Populus (Salicaceae) is a deciduous and dioecious tree taxon, comprising aspens, poplars, and cottonwoods, widely distributed in the Northern Hemisphere. Because of its unique biological characteristics, such as rapid growth rate, small genome size, facile asexual reproduction, and easy transgenesis, the genus has been selected as a model system in forest trees (Bradshaw et al. 2000). In the past three decades, poplar breeders focused on dissecting genetic architectures underlying growth traits targeted for producing new cultivars to meet the intensive need for wood-based products including timber, paper, and pulp or for bioenergy to mitigate carbon emissions (Taylor 2002). To investigate the genetic mechanism of ecologically and economically important traits, both molecular marker and phenotype data across a genetic mapping population are prerequisite to establish a statistical model for analyzing the marker-trait relationship. One of the approaches for this task is to identify quantitative trait loci (QTLs) on genome based on genetic linkage maps constructed with a set of markers generated from a full-sib family, like a backcross (BC) and F2 population in inbred lines or an F1 hybrid population in outbred species (Lander and Botstein 1989; Zeng 1994; Tong et al. 2012; Liu et al. 2017). Another approach is so-called genome-wide association study (GWAS), which allows to detect markers closely linked to QTLs with a large number of single-nucleotide polymorphisms (SNPs) in natural populations or multiple families (Gonzalez-Martinez et al. 2007; Li et al. 2014; Zhao et al. 2019).
In the 1990s, Bradshaw and Stettler (1995) first conducted QTL analysis of 2-year stem growth traits in an F2 hybrid population of Populus trichocarpa and Populus deltoides. Later on, Wu (1998) performed QTL mapping for 3-year growth traits in the same F2 population. Maybe due to the sparse linkage map or insufficient number of individuals used in the analyses, the two early studies were not able to detect more than two QTLs for the tree height. Recently, Monclus et al. (2012) identified about 7 QTLs on average controlling tree height and circumference measured in the first and the second year in an F1 hybrid population of P. deltoides × P. trichocarpa. More recently, Du et al. (2016) detected 3 and 6 QTLs for tree height and diameter at breast height, respectively, using a large number of progeny in an F1 population derived by crossing the female ‘YX01’ (P. alba × P. glandulosa) and the male ‘LM50’ (P. tomentosa). These previous studies applied the traditional molecular markers such as RAPD, RFLP, AFLP and SSR, probably limiting the power of detecting QTLs due to their low throughput (Tong et al. 2016). With advances in the next-generation sequencing (NGS) technologies, thousands of SNPs can be obtained across many individuals in a fast and low-cost way for QTL mapping. Recently, Tong and colleague performed a series of studies on extracting a large number of SNPs with restriction site-associated DNA sequencing (RADseq) technology, constructing genetic linkage maps, and mapping QTLs in an F1 hybrid population of P. deltoides and P. simonii (Mousavi et al. 2016; Tong et al. 2016; Liu et al. 2017; Yao et al. 2020). Meanwhile, GWAS emerged as a powerful method for identifying SNPs associated with the growth traits in poplar. Liu et al. (2018) conducted GWAS with 156,362 SNPs to identify significant SNP effects on the dynamic growth of tree diameter and height in a full-sib family of P. deltoides and P. euramericana.
In various GWAS, linear mixed models (LMMs) have been widely used with multiple available software packages such as TASSEL (Bradbury et al. 2007), EMMA (Kang et al. 2008), and GCTA (Yang et al. 2011). Because algorithms for fitting LMMs involve nonlinear optimization problem and have high computational cost (Zhou and Stephens 2014), these software packages have their own limitations in estimating genetic parameters (Zhang et al. 2009). It is because of this reason that two-stage approaches were applied to reduce the computational burden especially in plant GWAS, where replicated plants within blocks and plots are often used in traditional experimental designs (Xue et al. 2017). In some scenarios, the first stage was to obtain the best linear unbiased estimate (BLUE) or prediction (BLUP) for each line from a linear model with environmental effects but without any marker effects, whereas in the second stage the BLUE or BLUP was used as a dependent variable to perform GWAS with a reduced LMM (Zhang et al. 2009; Lipka et al. 2013; Xue et al. 2017; Vanous et al. 2018). Although most GWAS were conducted under a univariate framework, the use of multivariate linear mixed model (mvLMM) for GWAS is increasingly important because it is powerful to detect genetic variants that affect multiple traits or different growth stages (Zhou and Stephens 2014; Liu et al. 2018; Carlson et al. 2019). Like the two-stage approaches, different reduced strategies were also applied in multivariate GWAS such as using ratios between two phenotypes (Gieger et al. 2008) and the principal components of multiple traits (Aschard et al. 2014; Rice et al. 2020) to perform a univariate association analysis. However, from the statistical perspective, the direct use of mvLMM by incorporating various environmental effects undoubtedly enhances the power of GWAS not only over the univariate analysis but also over the reduced approaches (Galesloot et al. 2014; Zhou and Stephens 2014; Onogi 2019).
In this study, we reported a multivariate GWAS of tree height with longitudinal data from a randomized complete block design (RCBD). The design was established with clones from the F1 hybrid progeny of P. deltoides and P. simonii as described above. Each clone has several cuttings planted in different blocks, which have the same genome as a single seedling tree in the F1 population. In the previous studies (Mousavi et al. 2016; Tong et al. 2016), we performed RAD sequencing of many individuals in the hybrid population. By mapping RADseq data of each clone to the reference genome of P. trichocarpa (Tuskan et al. 2006), we obtained 22,667 SNPs across 172 clones. With the SNP genotype data at these SNPs for each individual, we applied mvLMM to perform GWAS of tree height measured over multiple time points using the R package EMMREML (https://cran.r-project.org/web/packages/EMMREML, accessed January 6, 2021). To compare with the multivariate method, we also conducted a univariate GWAS of the tree height at each single time point using a two-stage approach with the software TASSEL (Bradbury et al. 2007). The result showed that the multivariate method showed a superior ability over the univariate approach in detecting the association of SNPs with the tree height. Moreover, we could identify far more significant SNPs associated with the tree height than the previous QTL mapping studies in Populus. In addition, we also investigated the candidate genes of the significant SNPs, which were related to plant hormones, to the growth and development of tree tissues, and to response to stresses, or involved in photosynthesis.
Materials and methods
Plant materials and measurement of growth traits
An RCBD was established for testing the clones from an F1 hybrid population, which was derived by crossing P. deltoides and P. simonii in the springs from 2009 to 2011. The two parents have substantial differences in growth and adaptability and their hybrids display significant segregation traits in morphology and physiology (Mousavi et al. 2016; Tong et al. 2016). In the spring of 2017, a total of 234 clones were chosen to plant with 3 blocks, 6 cuttings for each clone per plot within a block, and a 50 × 60 cm spacing on Xiashu Forest Farm of Nanjing Forestry University, Jurong County, Jiangsu Province, China. During the growth season, each tree was measured in cm using a telescoping height measuring pole for height at 8 different times, that is, on June 8 (T1), June 23 (T2), July 6 (T3), July 16 (T4), July 27 (T5), August 14 (T6), September 2 (T7), and October 14 (T8), 2017. We preliminarily performed correlation analysis and multivariate analysis of variance for these phenotypic data with SAS 9.3 software (SAS Institute, Cary, USA).
SNP genotyping
In our previous studies, we performed RADseq of hundreds of individuals in the Populus F1 hybrid population (Mousavi et al. 2016; Tong et al. 2016). Of the clones used in the RCBD, 172 clones and their two parents were sequenced previously and the RADseq data were already deposited at the SRA database in NCBI with accession numbers in Supplementary Table S1. These RADseq data were filtered to obtain high-quality (HQ) reads data using the NGS QC toolkit with default parameters (Patel and Jain 2012). We used the HQ reads data to call SNP genotypes for each clone with the reference genome of P. trichocarpa. The whole calling procedures were almost the same as described in our previous studies such as Mousavi et al. (2016) and Yao et al. (2020) except for the utilization of different reference sequence. In brief, the paired-end (PE) reads of each clone were first aligned to the reference sequence with the software BWA (v0.7.17) to generate a SAM formatted file (Li and Durbin 2009). The SAM file was converted into BAM formatted file which was further sorted and indexed with SAMtools (v1.9) (Li et al. 2009). Then, the sorted BAM file was used to generate a BCF file and further to a VCF file using the software BCFtools (v1.9) (Li et al. 2009). Finally, we filtered the VCF file to obtain SNP genotypes for each clone such that a heterozygous allele has a read coverage depth (DP) of at least 3 and the quality of each SNP genotype is greater than 30.
After obtaining SNP genotypes of each clone, we further filtered the genotype data across the 172 clones by considering the missing genotype rate and the segregation ratio at each SNP site. We kept those SNPs that were not seriously deviated from the Mendelian segregation ratios (P > 0.01), which possibly include the ratios of 1:1, 1:2:1, and 1:1:1:1 due to the complicated genetic structure of the F1 hybrid population in outbred forest species (Maliepaard et al. 1997; Tong et al. 2010). Meanwhile, if there were more than 5% missing genotypes at an SNP site, it was removed from the data set.
Statistical model for association analysis
The mvLMM was applied to find an SNP association to the tree height as follows:
| (1) |
where is the height of the kth tree of the jth clone in the ith block at the tth time point, is the overall mean of tree height, is the effect of the ith block, is the genotype effect of the jth clone at the tested SNP site, is the polygene background effect of the jth clone (Yu et al. 2006), and is the residual effect. It is assumed that and are fixed effects each with the sum-to-zero constraint, whereas and are the random effects with and . In matrix form, model (1) can be expressed as:
| (2) |
where is the matrix of tree heights of individuals at the time points; is a known design matrix of fixed effects, including overall mean, block effects, and individual genotype effects at the tested SNP site; is the matrix of fixed-effect coefficients; is the matrix of random additive genetic effects with , where is the number of clones and Vec denotes the matrix vectorization function (Searle et al. 2006, pp. 458),is the additive relationship matrix for the clones and is the additive genetic covariance matrix for the time points ;is thecoefficient matrix corresponding to the matrix;is the random residual matrix with . Hence, the covariance matrix of Vec(Y) can be expressed as:
| (3) |
Since the clones in the RCBD were from a full-sib family and their parents were unrelated and not inbred, the coefficient of additive genetic covariance between any two different clones is 0.5 in theory (Loiselle et al. 1995; Lynch and Walsh 1998), leading to thematrix with ones on the diagonal and 0.5 elsewhere.
We used the R package EMMREML to calculate the REML estimates of and and then the BLUE of (https://cran.r-project.org/web/packages/EMMREML, accessed January 6, 2021). To test the effects of SNP genotypes, an statistics was used under the null hypothesis M Vec (B) = 0for a full-rank matrix, as:
| (4) |
withnumerator degrees of freedom anddenominator degrees of freedom (Kang et al. 2008). The P-value for testing each SNP was adjusted based on Bonferroni-correction and the genome-wide false discovery rate (FDR) was set to be 0.01. As the method described in Xu (2003), the percent of phenotypic variance explained by a significant SNP was calculated as:
| (5) |
where and are the residual sums of squares under the null and full hypothesis models, respectively.
To compare the multivariate GWAS approach to the univariate method, we performed GWAS of the tree height at each time point separately with two-stage approach using the software TASSEL (Bradbury et al. 2007). First, the best linear unbiased estimates (BLUEs) of the clone effects were obtained with the reduced linear model from model (1) by omitting the SNP genotype effects and fixing time point t as follows:
| (6) |
Second, the BLUEs at a fixed time point were used for the association analysis using TASSEL with parameters set as “-mlmVarCompEst P3D -mlmCompressionLevel None.”
Additionally, to obtain the heritability of the tree height at each time point, we used model (6) to first estimate the genetic and residual variance components with EMMREML and then to calculate the heritability as:
| (7) |
Investigation of candidate genes
The upstream and downstream genes of the significant SNPs were investigated for candidate genes affecting the tree height. If a gene harbored an SNP that had a linkage disequilibrium (LD) value () above a threshold with a neighboring significant SNP, then this gene was considered as a candidate gene for further investigation. The LD threshold was determined by performing LD decay analysis with all the SNPs using the software PopLDdecay (Zhang et al. 2019). After that, the coding sequences of the candidate genes around each significant SNP were extracted from the gene annotation of P. trichocarpa at Phytozome (v4.1; https://genome.jgi.doe.gov). These genes were annotated afresh by first performing blast searches with their coding sequences against the non-redundant protein database (Altschul et al. 1990; Pruitt et al. 2007) and then mapping the hits to GO terms with Blast2GO (https://www.blast2go.com). The result of these gene annotations was saved in a text file, in which we searched the keywords related to the tree growth and development as well as response to stresses. Furthermore, these candidate genes were used to perform GO enrichment analysis with Blast2GO for finding which GO terms are over-represented for the growth of tree height.
Data availability
The RADseq data of the 172 clones have been deposited in the SRA database at the National Center for Biotechnology Information (NCBI) with accession numbers presented in Supplementary Table S1. The phenotypic and genotypic data generated for GWAS in this study can be found in Supplementary Tables S2 and S6, respectively. All of the supplemental materials (Supplementary Tables S1–S13 and Supplementary Figures S1 and S2) for this study are available at figshare DOI: 10.25387/g3.13017866.
Results
Phenotype and genotype data
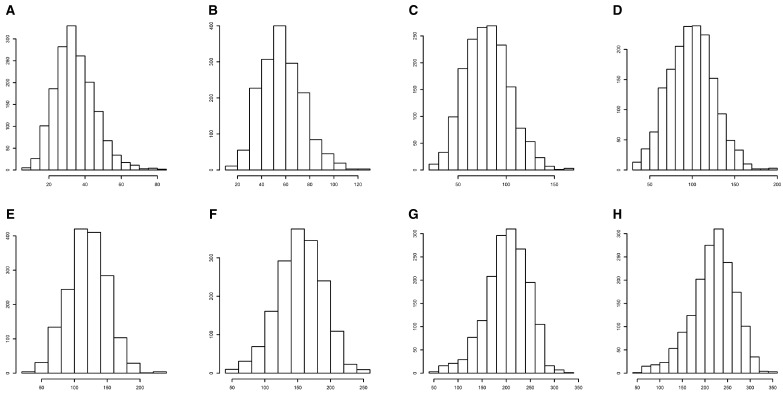
We successfully obtained tree height and SNP genotype data of 172 clones and a total of 1664 individual trees (Supplementary Table S2). The tree heights were measured at 8 different times during the growth season in 2017. Histograms showed that the tree height basically followed a normal distribution at each time point (Figure 1). The average and standard deviation of the tree height were consistently increased across the growth season, but the coefficient of variation (CV) was decreased from about 32% to 22% (Supplementary Table S3). We also found that the CV of the tree height increment between successive time points varied smoothly in a range of 29.60–37.16% over the first six time intervals. However, the CV of the increment abruptly rose to 63.83% at the last time interval (September 2 to October 14, 2017). It is mainly due to the fact that the mean of the increment was the smallest and the standard deviation was relatively high for the last time interval (Supplementary Table S3). Meanwhile, the heritabilities at each time point did not change much with a range of 0.54–0.55 during the vigorous growth season (June to July), but then dropped to 0.47 in the late growth season (August to October; Supplementary Table S3). Correlation analysis of the phenotypic data showed that the tree height was significantly correlated between any two time points, with a coefficient of over 0.94 (P < 0.01) between adjacent time points and a minimum coefficient value of 0.541 between the first and the last measure time points (Supplementary Table S4). Furthermore, we also calculated the genetic correlation coefficients of the tree heights at different time points from the genetic covariance matrix estimated with model (1) by ignoring SNP effects. The result showed that the genetic correlation coefficients were consistently higher than the phenotypic correlation coefficients and that the genetic coefficients between adjacent time points were all greater than 0.960 (Supplementary Table S4). Moreover, multivariate analysis of variance for the longitudinal data showed that the effects of tree height were significantly different among the blocks, the clones, and the interactions of blocks and clones (Supplementary Table S5). These primary statistical analyses showed that the tree height over multiple time points in the RCBD variated largely and was worth further exploring the molecular mechanism.
Figure 1.
Histograms of tree height measured in the randomized complete block design at eight different time points: (A) June 8, (B) June 23, (C) July 6, (D) July 16, (E) July 27, (F) August 14, (G) September 2, and (H) October 14 in 2017.
A total of 22,670 SNPs across the 172 clones (Supplementary Table S6) were obtained by mapping their RADseq data separately to the reference genome of P. trichocarpa (v4.1; https://genome.jgi.doe.gov). Each clone had an average of 16.89 million RADseq reads and 4.61 Gb data with a mean genome coverage depth of 9.6X (Supplementary Table S1). After a stringent quality control with NGS QC toolkit, an average amount of 4.45 Gb HQ reads data per clone was remained for calling SNP genotypes. Since the clones were from the F1 hybrid population in Populus, as expected, the majority of SNPs were segregated in the ratio of 1:1 (P > 0.01) with a minority in 1:2:1 and 1:1:1:1 (Table 1). Each SNP genotype was satisfied such requirements that the allele of a heterozygous genotype had a coverage depth of at least three reads and the coverage depth for the allele of a homozygous genotype was at least 5. In addition, the quality of each genotype had a Phred score of at least 30. The missing genotype rate at each SNP was controlled to be not greater than 5%.
Table 1.
Summary of SNPs obtained across clones in the randomized complete block design
| Segregation type | Ratio | Genotype | Number |
|---|---|---|---|
| aa×ab | 1:1 | aa, ab | 8,968 |
| aa×bc | 1:1 | ab, ac | 23 |
| ab×aa | 1:1 | aa, ab | 13,512 |
| ab×cc | 1:1 | ac, bc | 48 |
| ab×ab | 1:2:1 | aa, ab, bb | 105 |
| ab×ac | 1:1:1:1 | aa, ab, ac, bc | 14 |
| Total | 22,670 |
Significant SNPs associated with tree height
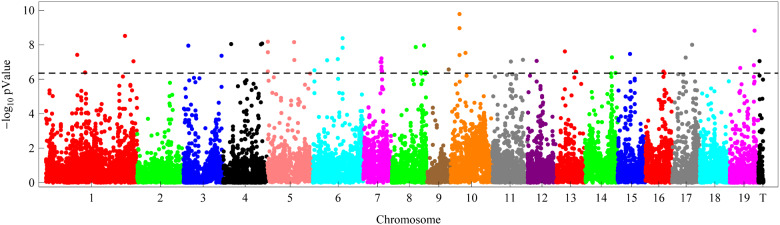
We applied the mvLMM to perform the GWAS for the tree height with the 22,670 HQ SNPs distributed on the 19 chromosomes and several scaffolds in Populus. The P-value threshold for significant SNPs was set to 4.41E–7 (-log10(P-value) = 6.36) based on the Bonferroni correction at the 0.01 significant level. If a small region (<1000 bp) harbored several significant SNPs, the most significant was chosen to represent that region. As a result, 41 SNPs were found to be significantly associated with the tree height. Figure 2 shows the Manhattan plot of the SNP position against the corresponding negative base 10 logarithm of P-value. It can be seen that these significant SNPs were distributed on all but 2 (Chr02 and Chr18) chromosomes with one SNP on scaffold 45. The physical distance between adjacent significant SNPs was greater than 123 kb, the minimum distance found between the second and the third significant SNPs on chromosome 5 (Table 2).
Figure 2.
Manhattan plot of genome-wide association analysis of tree height in the randomized complete block experiment. The horizontal line indicates the genome-wide significant threshold of 6.36, a base 10 logarithm of P-value based on the Bonferroni correction at the 0.01 significant level.
Table 2.
Summary of the significant SNPs associated with the tree height on chromosomes and scaffolds
| SNP ID | Chromosome | Position | Segregation type | -log10( P -value) | R 2 (%) |
|---|---|---|---|---|---|
| DSC01H1* | Chr01 | 17015054 | ab×aa | 7.42 | 1.17 |
| DSC01H2 | Chr01 | 21306230 | aa×ab | 6.40 | 1.70 |
| DSC01H3* | Chr01 | 43104197 | aa×ab | 8.52 | 2.43 |
| DSC01H4 | Chr01 | 47744299 | aa×ab | 7.04 | 1.47 |
| DSC03H1 | Chr03 | 2674990 | ab×aa | 7.95 | 1.02 |
| DSC03H2 | Chr03 | 20842084 | aa×ab | 7.37 | 2.34 |
| DSC04H1* | Chr04 | 4423234 | aa×ab | 8.04 | 1.84 |
| DSC04H2 | Chr04 | 20708892 | aa×ab | 8.02 | 1.59 |
| DSC04H3 | Chr04 | 21344054 | ab×aa | 8.07 | 2.39 |
| DSC05H1* | Chr05 | 336929 | aa×ab | 8.18 | 0.26 |
| DSC05H2* | Chr05 | 14685227 | aa×ab | 8.15 | 1.84 |
| DSC05H3* | Chr05 | 14808652 | ab×aa | 7.12 | 1.99 |
| DSC06H1 | Chr06 | 810179 | aa×ab | 6.52 | 1.35 |
| DSC06H2 | Chr06 | 7733888 | aa×ab | 7.10 | 1.19 |
| DSC06H3* | Chr06 | 13575979 | ab×aa | 7.17 | 1.58 |
| DSC06H4* | Chr06 | 16203991 | aa×ab | 8.38 | 1.13 |
| DSC07H1 | Chr07 | 9357528 | ab×aa | 7.00 | 1.60 |
| DSC07H2 | Chr07 | 9920573 | aa×ab | 7.21 | 2.38 |
| DSC07H3* | Chr07 | 10256748 | aa×ab | 6.45 | 0.64 |
| DSC08H1 | Chr08 | 13071948 | ab×aa | 7.87 | 1.54 |
| DSC08H2 | Chr08 | 15844780 | ab×aa | 6.42 | 1.47 |
| DSC08H3 | Chr08 | 17642966 | aa×ab | 7.96 | 2.05 |
| DSC08H4 | Chr08 | 18644603 | ab×aa | 6.40 | 1.22 |
| DSC09H1* | Chr09 | 11900120 | ab×aa | 6.57 | 1.48 |
| DSC10H1* | Chr10 | 4825843 | aa×ab | 9.79 | 1.96 |
| DSC10H2* | Chr10 | 8084409 | ab×aa | 7.53 | 0.58 |
| DSC11H1 | Chr11 | 10094625 | aa×ab | 7.03 | 0.46 |
| DSC11H2 | Chr11 | 16687705 | aa×ab | 7.13 | 1.97 |
| DSC12H1 | Chr12 | 4890486 | ab×aa | 7.07 | 1.33 |
| DSC13H1* | Chr13 | 4732990 | ab×aa | 7.62 | 1.99 |
| DSC13H2 | Chr13 | 10764896 | aa×ab | 6.44 | 1.72 |
| DSC14H1* | Chr14 | 14722576 | aa×ab | 7.27 | 1.22 |
| DSC14H2 | Chr14 | 16676502 | aa×ab | 6.36 | 1.99 |
| DSC15H1 | Chr15 | 6813100 | ab×aa | 7.47 | 1.37 |
| DSC16H1* | Chr16 | 9864836 | ab×aa | 6.45 | 1.11 |
| DSC17H1 | Chr17 | 7378390 | ab×aa | 7.26 | 1.09 |
| DSC17H2 | Chr17 | 10908093 | ab×aa | 8.00 | 2.01 |
| DSC19H1 | Chr19 | 5741825 | aa×ab | 6.66 | 1.65 |
| DSC19H2 | Chr19 | 13202165 | ab×aa | 6.81 | 0.99 |
| DSC19H3 | Chr19 | 13578941 | ab×aa | 8.82 | 2.64 |
| DST45H1 | scaffold_45 | 28115 | ab×aa | 7.06 | 1.93 |
Consistent significant SNPs in position with QTLs of tree height in Populus identified in previous studies.
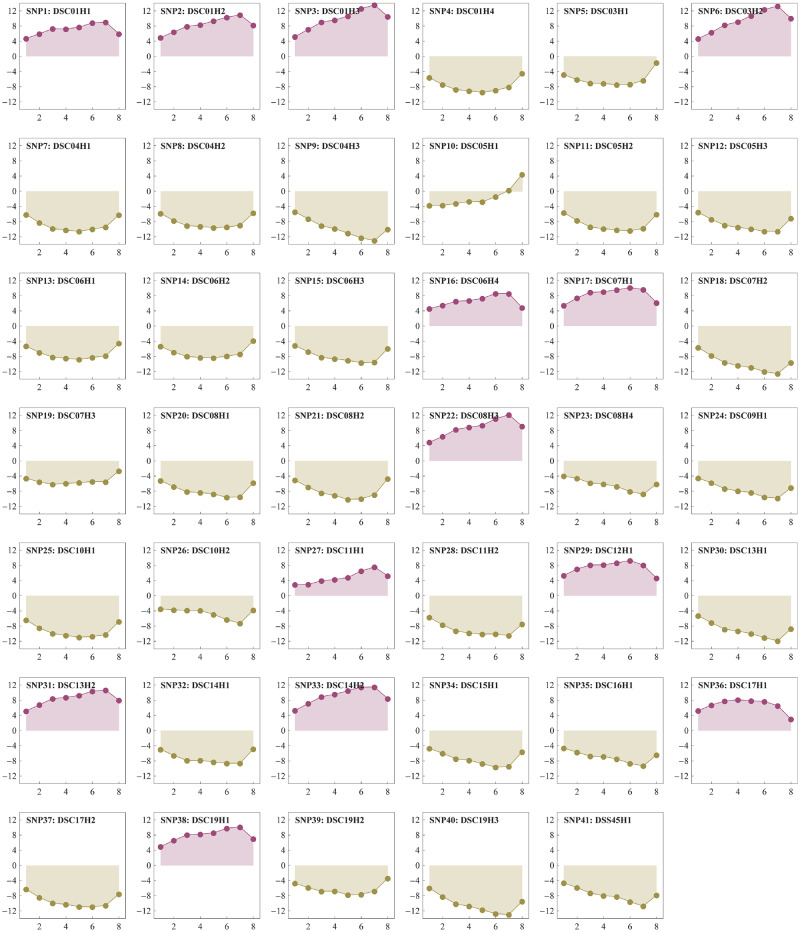
Table 2 summarizes the significant SNPs on their IDs, positions, segregation types, P-values, and ratios of explaining the phenotypic variance (R2). The SNP IDs were named after the two parents of the clones currently used in this study, the chromosome and scaffold name, and the order within a chromosome, where D stands for P. deltoides, S for P. simonii, C for chromosome, and T for scaffold (e.g., DSC05H2 indicates the second significant SNP affecting the tree height on chromosome 5). We found that all the SNPs segregated in the ratio of 1:1 with 21 segregating in the type of aa×ab and 20 in ab×aa. The percent of phenotypic variance (R2) explained by the SNPs ranged from 0.26% to 2.64%, amounting to 63.68% in total. Moreover, the effect of each SNP at each time point was also estimated, which was defined as the difference between the homozygous (aa) and heterozygous (ab) effects (Zeng 1994). Figure 3 presents the connected scatter plot of each SNP effects. It can be seen that the SNPs were largely divided into two categories: one possessed positive effects and the other had negative effects over multiple time points.
Figure 3.
Scatter plots of SNP effects over the eight time points. Positive effect plots are labeled with purple and negative effect plots with light yellow.
We found 15 significant SNPs were consistent in position with most QTLs identified in the previous studies for mapping tree height in Populus (Monclus et al. 2012; Du et al. 2016; Liu et al. 2017). Supplementary Table S7 lists those SNPs that were consistent with one or more QTLs detected in the three recent studies, excluding the two early studies due to no position information available in the physical map for the QTLs (Bradshaw and Stettler 1995; Wu 1998). It can be seen that most QTLs detected in the three previous studies either were located not far from or their confidence intervals contained a significant SNP. The physical distance between the consistent SNP and QTL was less than 5.0 Mb for most pairs with a few greater than 5.0 Mb but less than 15.0 Mb. Interestingly, we found that these consistent SNPs have stronger association signals than the others. It is obvious to see that 5 of the consistent SNPs have the first and the third to sixth lowest P-values (Table 2). Moreover, we performed the Kruskal–Wallis rank-sum test (Hollander and Wolfe 1973) to test the difference of the minus logarithm P-values between the 15 consistent SNPs and the others. The test result showed that the consistent SNP group had the minus logarithm P-values significantly higher than the other group with a P-value of 0.0482.
In comparison with the univariate approach, we also performed the association analysis for each single tree height with the software TASSEL. The result showed that there were 6 SNPs significantly associated with the tree height measured at the first time point (T1), which were distributed on chromosomes 4, 10, 17, and 19 (Supplementary Figure S1). However, no significant SNPs were found for the tree height at time points T2–T8.
Exploration of candidate genes
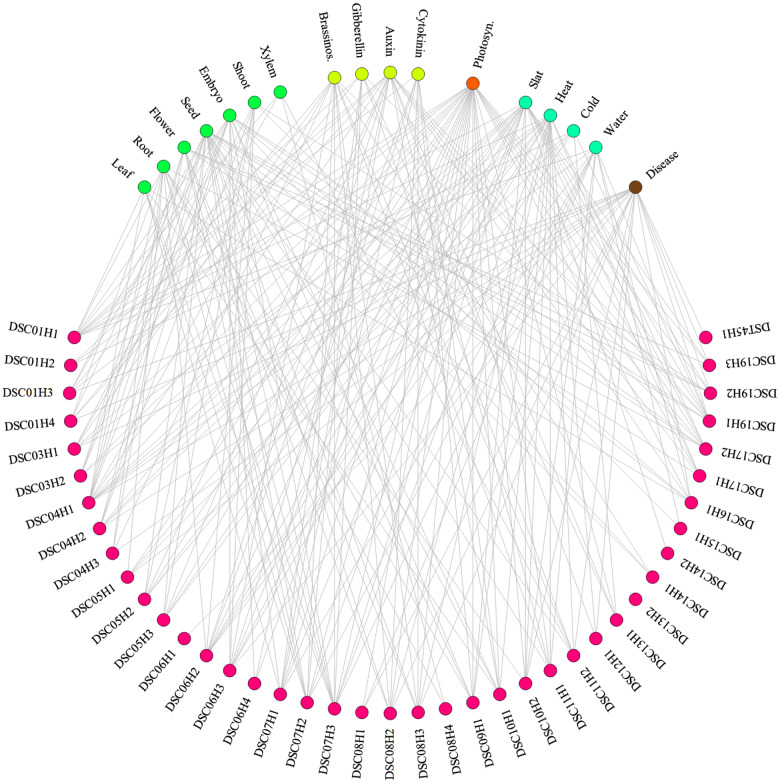
To explored candidate genes of the significant SNPs, we extracted 100 coding genes surrounding each SNP in the genome annotation database of P. trichocarpa at Phytozome (v4.1; https://genome.jgi.doe.gov). To obtain enough annotation information, the coding sequences were first blasted against the non-redundant (nr) protein database (Pruitt et al. 2007) and then the blast hits were mapped to Gene Ontology (GO; http://geneontology.org) terms. With the newly annotation result, we searched keywords related to tree growth and development, such as “brassinosteroid,” “gibberellin,” “leaf,” “xylem,” “photosynthesis,” “salt,” and “disease.” Consequently, 248 genes nearby the significant SNPs corresponded to at least one of the 17 keywords; all but one SNP (DSC13H2) had at least one candidate genes related to these words (Supplementary Table S8; Figure 4). It can be seen that there were 13, 8, 17, and 8 SNPs that had candidate genes involved in brassinosteroids, gibberellins, auxins, and cytokinins, respectively. These hormones were confirmed to have direct effects on plant height (Dubouzet et al. 2013). Furthermore, 7 SNPs possessed candidate genes related to leaf growth and development, 12 to root, 10 to flower, 21 to seed, 14 to embryo, 8 to shoot, and 4 to xylem. For responses to stress, 20 SNPs owned candidate genes for salt stress, 19 for heat stress, 6 for cold stress, and 12 for water deprivation or activity. It was surprising that up to 30 SNPs were identified with candidate genes related to photosynthesis, which plays an important role in the tree growth and development (Wang et al. 2017). In addition, 20 SNPs were found to be associated with candidate genes for disease resistance. Particularly, for the 15 significant SNPs consistent with the previous identified QTLs (Supplementary Table S7), we observed that all but one SNP (DSC05H1) had candidate genes that response to hormones or involve hormone activities, that all but two (DSC10H2 and DSC13H1) directly affected the growth and development of different tissues such as leaf, root, seed, and xylem, that all but three (DSC10H1, DSC10H2, and DSC14H1) were related to response to stresses or resistance to diseases, and that all but four (DSC05H1, DSC07H3, DSC10H2, and DSC14H1) were involved in photosynthesis.
Figure 4.
Significant SNPs with potential candidate genes related to biological functions and processes. All but one SNP (DS13H2) possessed candidate genes related to the tree growth and development of leaf, root, flower, seed, embryo, shoot, and xylem, to stress responses of salt, heat, cold, and water deprivation, and to disease resistance, or involved in brassinosteroid, gibberellin, auxin, cytokinin, and photosynthesis.
To further understand the function of the 248 candidate genes described above, we conducted the GO enrichment analysis using all the 34,698 genes in the annotation database of P. trichocarpa (v4.1) as a reference set. As a result, 289 GO terms were significantly enriched with the FDR value <0.05, of which 223 belonged to the category of biological process, 40 to molecular function, and 26 to cellular component (Supplementary Table S9). Interestingly, almost all the searched words except “disease” were contained in at least one significant GO terms in the category of biological process (Table 3). For the four hormones, these GO terms included “response to brassinosteroid” (GO:0009741), “response to gibberellin” (GO:0009739), “response to auxin” (GO:0009733), and “response to cytokinin” (GO:0009735). For the tree tissues, the significantly enriched GO terms contained the developments of leaf (GO:0048366), root (GO:0048364), flower (GO:0009908), seed (GO:0048316), embryo (GO:0009790), shoot (GO:0048367), and xylem (GO:0010089). For the responses to stress, the similar GO terms consisted of responses to salt stress (GO:0009651), to heat (GO:0009408), to cold (GO:0009409), and to water deprivation (GO:0009414). Also, we found that the most enriched GO terms in Table 3 was “photosynthesis” (GO:0015979) with the smallest FDR value of 7.48E-24. Although no significant GO terms were found to be related to disease, there existed several significantly enriched descriptions related to disease resistance when we used annotations resulted from the blast hits in the enrichment analysis with Blast2Go (Supplementary Table S10). The reason that no significant GO terms were related to disease in this study may be due to the fact that there are only 2 GO terms (GO:0009614, GO:0106093) related to disease in the current GO database (http://geneontology.org).
Table 3.
Some significantly enriched GO terms related to plant hormones, to the development of tree tissues, and to response to stresses, or involved in photosynthesis
| GO ID | GO Name | FDR | P -value | Nr test | Nr reference | Non Annot test | Non Annot reference |
|---|---|---|---|---|---|---|---|
| GO:0009741 | Response to brassinosteroid | 1.1E–8 | 9.86E–11 | 9 | 42 | 239 | 34408 |
| GO:0009742 | Brassinosteroid mediated signaling pathway | 4.91E–5 | 7.06E–7 | 6 | 38 | 242 | 34412 |
| GO:0016131 | Brassinosteroid metabolic process | 0.0121 | 3.28E–4 | 4 | 42 | 244 | 34408 |
| GO:0009739 | Response to gibberellin | 1.28E–4 | 1.94E–6 | 6 | 46 | 242 | 34404 |
| GO:0009733 | Response to auxin | 2.69E–15 | 1.22E–17 | 22 | 229 | 226 | 34221 |
| GO:0009734 | Auxin-activated signaling pathway | 6.84E–9 | 5.95E–11 | 12 | 106 | 236 | 34344 |
| GO:0009735 | Response to cytokinin | 8.76E–7 | 9.15E–9 | 7 | 31 | 241 | 34419 |
| GO:0009736 | Cytokinin-activated signaling pathway | 1.76E–6 | 1.98E–8 | 6 | 19 | 242 | 34431 |
| GO:0009690 | Cytokinin metabolic process | 0.0039 | 8.86E–5 | 4 | 29 | 244 | 34421 |
| GO:0048366 | Leaf development | 0.021 | 6.15E–4 | 5 | 90 | 243 | 34360 |
| GO:0009965 | Leaf morphogenesis | 0.037 | 0.0011 | 3 | 26 | 245 | 34424 |
| GO:0048364 | Root development | 6.87E–4 | 1.24E–5 | 7 | 100 | 241 | 34350 |
| GO:0022622 | Root system development | 6.87E–4 | 1.24E–5 | 7 | 100 | 241 | 34350 |
| GO:0009908 | Flower development | 0.0129 | 3.54E–4 | 7 | 175 | 241 | 34275 |
| GO:0048316 | Seed development | 4.45E–10 | 3.41E–12 | 16 | 195 | 232 | 34255 |
| GO:0090351 | Seedling development | 0.0064 | 1.55E–4 | 4 | 34 | 244 | 34416 |
| GO:0009845 | Seed germination | 0.0468 | 0.0015 | 3 | 29 | 245 | 34421 |
| GO:0009790 | Embryo development | 3.18E–5 | 4.09E–7 | 9 | 120 | 239 | 34330 |
| GO:0048367 | Shoot system development | 1.81E–9 | 1.55E–11 | 18 | 295 | 230 | 34155 |
| GO:0010016 | Shoot system morphogenesis | 2.15E–6 | 2.44E–8 | 8 | 58 | 240 | 34392 |
| GO:0010089 | Xylem development | 0.009 | 2.28E–4 | 3 | 14 | 245 | 34436 |
| GO:0010087 | Phloem or xylem histogenesis | 0.0121 | 3.28E–4 | 4 | 42 | 244 | 34408 |
| GO:0015979 | Photosynthesis | 7.48E–24 | 7.81E–27 | 29 | 213 | 219 | 34237 |
| GO:0009651 | Response to salt stress | 1.99E–22 | 3.46E–25 | 24 | 130 | 224 | 34320 |
| GO:0009408 | Response to heat | 1.78E–13 | 1.01E–15 | 16 | 110 | 232 | 34340 |
| GO:0009409 | Response to cold | 0.0172 | 4.8E–4 | 5 | 85 | 243 | 34365 |
| GO:0009414 | Response to water deprivation | 1.01E–6 | 1.08E–8 | 9 | 76 | 239 | 34374 |
We also performed GO enrichment analyses to investigate the difference of candidate gene functions between the significant SNP group with positive effects and the group with negative effects (Figure 3). There were 71 and 177 candidate genes for the positive- and negative-effect groups, respectively. Two GO enrichment analyses were conducted with the 71 and 177 candidate genes as test sets separately and all the 34,698 genes as the reference set. The results showed that 95 GO terms were significantly enriched for the positive group and 220 for the negative group (Supplementary Tables S11 and S12). We observed that there were 73 GO terms enriched in both groups, such as “response to hormone,” “photosynthesis,” and “post-embryonic development.” However, there were 22 unique GO terms enriched in the positive group and up to 147 in the negative group. In the positive group, the unique enriched GO terms included “auxin-activated signaling pathway,” “stigma development,” “flower development,” and the others (Supplementary Table S11), whereas in the negative group those unique GO terms included “response to brassinosteroid,” “shoot system development,” “xylem development,” etc. (Supplementary Table S12). Although the candidate genes were involved in many GO terms, these unique GO terms could be used to link the two groups of significant SNPs.
Discussion
Application of traditional experimental design for GWAS
The RCBD is one of the most widely used experimental designs in traditional forest breeding program for estimating genetic parameters (Wright 1976; Williams et al. 2002). However, this kind of test experiments was rarely directly used with mvLMM to identify the associations between molecular markers and phenotypic traits, such as GWAS and QTL mapping, possibly due to the lack of suitable software. In this study, we first used mvLMM to perform GWAS of tree height with longitudinal measurements from the traditional RCBD in Populus. The poplar hybrid F1 clones were planted repeatedly not only among blocks but also within plots in the RCBD. One advantage of these repeated clones is to allow us to obtain repeated phenotypic data for a genotype that originated from a seed. Theoretically, the repeated data can control spatial effects in field and reduce the systematic errors, thus improving the accuracy and power in GWAS. Another advantage is that each genotype can be preserved almost forever especially in forest trees because the repeated plants provide redundancy for the same genotype in the case of natural damages caused by insect, disease or wind. On the contrary, in most previous GWAS or QTL mapping studies in Populus (Bradshaw and Stettler 1995; Monclus et al. 2012; Du et al. 2016; Liu et al. 2018), phenotypic traits were measured from single plants with different genotypes in natural populations or a full-sib family such as the traditional BC and F2 populations in inbred lines and the F1 hybrid population in outbred species. In these populations, each tree corresponds to a unique genotype so that either the number of genotypes could gradually reduce over times or distortion measurements could be produced on some genotypes owing to the natural damages. Such reduction in genotype number or existence of distortion measurements would greatly affect the genetic parameter estimation and thus discount the power of GWAS or QTL mapping. Overall, the RCBD established with poplar clones in this study provided a unique population for effectively studying the molecular mechanism underlying important traits in Populus.
Implementation of GWAS with longitudinal measurements from the RCBD
We successfully applied mvLMM to the GWAS of tree height with longitudinal measurements from the RCBD in this study. Because of the unique population structure and the multiple phenotypic measurements, we cannot directly apply current available GWAS software to simultaneously estimate the genetic variance components of tree heights at the 8 time points. Generally, the software such as EMMA (Kang et al. 2008), EMMAX (Kang et al. 2010), and GEMMA (Zhou and Stephens 2012) are usually applied in animal and human GWAS by incorporating the minor allele effect of a bi-allelic SNP into LMM, in which only one column with elements of 0, 1, and 2 for SNP genotype effects is added in the design matrix of fixed effects. However, there were triallelic SNPs in our SNP data set (Table 1), which segregated in 1:1 (aa×bc and ab×cc), 1:2:1 (ab×bb), or 1:1:1:1 (ab×ac). Apparently, these SNPs cannot be applied into the GWAS software only for biallelic SNPs. To solve this problem, we used SNP genotype effects of each SNP in the LMM (1) with the restriction of the sum of expected genotype effects equal to zero. Next, the function emmremlMultivariate in the R package EMMREML was used to calculate the estimates of the genetic and residual matrices of variances. This function is flexible for the design matrix of the fixed effects and focuses on dealing with multivariate phenotypic traits, but it cannot flexibly provide statistics for testing SNPs if their genotype effects correspond to more than two columns in the design matrix. We resolved the hypothesis testing problem by converting the multivariate LMM (1) into univariate LMM through matrix vectorization (Searle et al. 2006) (pp. 458) and then conducting the hypothesis test using formula (3) as constructed in Kang et al. (Kang et al. 2008).
The issue of additive genetic relationship matrix
One of the crucial parts in the LMMs is the additive genetic relationship matrix which reflects population structure and directly affects the estimate of background genetic variance. The relationship matrix is the kinship matrix multiplied by 2 (Lynch and Walsh 1998; Bae et al. 2016), which can be inferred by pedigree- or marker-based methods (Thornton and McPeek 2007; VanRaden 2008; Yang et al. 2010). Although various marker-based methods for inferring a kinship matrix with a large number of SNPs have been proposed, they showed small differences in correcting population structure (Nievergelt et al. 2007) and some of them had the limitation that the estimated kinship matrix may not be guaranteed to be positive semidefinite, which could distort the genetic parameter estimations (Kang et al. 2008). Moreover, these marker-based methods were typically based on the markers each segregating in three genotypes, that is, the homozygote, heterozygote, and other homozygote. The genotype effects were usually assumed to be a scale of 1, 0, and -1 with frequencies of , , and , respectively. The variance of the genotype effects can be derived as a scale of and it was used to generate the relationship matrix (VanRaden 2008). However, in this study, the majority of SNPs are segregated only in two genotypes expressed as aa and ab with frequencies of and (Table 1), which is attributed to the two highly heterozygous parents of the F1 hybrid population (Mousavi et al. 2016; Tong et al. 2016). Apparently, the variance of the two genotype effects is totally different from that of the three genotype effects. Therefore, the relationship matrix cannot be properly calculated from our SNP data with currently available software such as TASSEL and EMMA. Nevertheless, we noted that our samples were all from a full-sib family of two unrelated parents in Populus. In theory, the coefficient of kinship (or coancestry) is expected to be 0.25 for full-sibs assuming random mating (Loiselle et al. 1995; Lynch and Walsh 1998). This led to the relationship matrix with elements of ones on the diagonal and 0.5 elsewhere, which was applied as a pedigree-method in this study.
P-value threshold and the number of significant SNPs
The LMM is one of the most popular approaches in GWAS, but it tests one SNP at a time so as unable to simultaneously identify many loci that underlie the objective trait. For this reason, it is critical to determine the P-value threshold for significant SNPs by performing multiple testing. The most commonly used methods for multiple hypothesis testing include the Bonferroni correction and Benjamini–Hochberg (BH) procedure (Benjamini and Hochberg 1995). The Bonferroni correction is considered to be more conservative and certainly to result in less significant SNPs than the BH method. Both methods limit the false positive rate, but they very likely inflate the false-negative rate. We used the Bonferroni correction to determine the P-value threshold under a lower common significant level of 0.01, leading to 41 significant SNPs detected for the tree height. This means that the expected number of false-positive SNPs was less than one, but the number of negative false SNPs was uncertain. Such a medium number of extremely significant SNPs each explaining a small fraction of the phenotypic variance (0.26%–2.64%) is in accord with the infinitesimal model, assuming that a quantitative trait is typically controlled by an infinite number of genes each with a tiny effect (Fisher 1919; Bulmer 1971). Considering those cases of up to 100 significant SNPs found for a complex trait, such as in animal and crop GWAS (Ober et al. 2012; Bali et al. 2018), it is very likely that there exist a lot of undetected SNPs that have much smaller effects and explain the rest portion of the phenotypic variance in this study. However, we virtually identified far many more loci associated with tree height than QTLs detected in the previous QTL mapping studies in Populus (Bradshaw and Stettler 1995; Wu 1998; Monclus et al. 2012; Du et al. 2016; Liu et al. 2017). This could be attributed to the application of the traditional RCBD and the use of longitudinal phenotypic measurements in the LMM, enhancing the power of detecting association of SNPs to the tree height.
Alternative approach for finding candidate genes
We used the nearby genes for each significant SNP to investigate candidate genes that could be related to the tree height under study. The genes nearby each SNP spanned a physical region with a mean length of 2.03 Mb and a standard deviation of 1.17 Mb. This approach could be called the proximate strategy, which has been frequently used for finding candidate genes in GWAS or QTL studies (Monclus et al. 2012; Geng et al. 2015; Su et al. 2017; Vanous et al. 2018). Alternatively, LD analysis can be used to search candidate genes with procedures as described by (Slaten et al. 2020). As a comparison, we also tried this method to find candidate genes that are in LD with the significant SNP. First, LD threshold was determined by performing LD decay analysis with all the SNPs using the software package PopLDdecay (Zhang et al. 2019). The resut showed that LD decayed rapidly to about corresponding to a physical distance of ∼650 bp (Supplementary Figure S2), which was consistent with the reports in the literature that LD decayed at a short distance of 100-1500 bp in outcrossing species and that the threshold of can be used at which LD stops to exist. Next, we used this threshold to find the candidate genes of a significant SNP on the condition that between an SNP within a gene and this significant SNP. As a result, a total of 94 candidate genes were found for 31 significant SNPs, most (73.40%) of which were in low LD () with their corresponding significant SNPs (Supplementary Table S13). Unfortunately, few of these candidate genes had meaningful descriptions about the growth and development of tree height. This undesirable result could be explained by the fact that many genes around a significant SNP did not contain any SNPs due to the less number of SNPs available in this study as compared to the number of genes on the reference genome (22,670 versus 34,699), so that they had no chance to be chosen as candidate genes through LD analysis. Therefore, it was an appropriate way to use the proximate strategy for studying candidate genes of the significant SNPs in this study.
Conclusion
The combined use of the traditional RCBD along longitudinal measurements could greatly improve the power of GWAS, leading to identifying far more significant SNPs associated with tree height than QTLs detected in previous studies in Populus. The detected SNPs were distributed on all but 2 chromosomes and explained a large portion of the phenotypic variance. Most of these SNPs possessed potential candidate genes that were significantly related to the growth and development of different tissues, to stress responses, and to disease resistance, or involved in several plant hormones. The result would enhance understanding of molecular mechanism for growth traits and would accelerate marker-assisted breeding programs in such species.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 31870654 and 31270706) awarded to CT and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Conflicts of interest: None declared.
Literature cited
- Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ.. 1990. Basic local alignment search tool. J Mol Biol. 215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- Aschard H, Vilhjalmsson BJ, Greliche N, Morange P-E, Tregouet D-A, et al. 2014. Maximizing the power of principal-component analysis of correlated phenotypes in genome-wide association studies. Am J Hum Genet. 94:662–676. doi: 10.1016/j.ajhg.2014.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bae H, Monti S, Montano M, Steinberg MH, Perls TT, et al. 2016. Learning Bayesian networks from correlated data. Sci Rep. 6:25156. doi: 10.1038/srep25156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bali S, Robinson BR, Sathuvalli V, Bamberg J, Goyer A.. 2018. Single nucleotide polymorphism (SNP) markers associated with high folate content in wild potato species. PLoS One. 13:e0193415. doi: 10.1371/journal.pone.0193415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y.. 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc. 57:289–300. doi: 10.1111/j.2517-6161.1995.tb02031.x. [DOI] [Google Scholar]
- Bradbury PJ, Zhang Z, Kroon DE, Casstevens TM, Ramdoss Y, et al. 2007. TASSEL: software for association mapping of complex traits in diverse samples. Bioinformatics. 23:2633–2635. doi: 10.1093/bioinformatics/btm308. [DOI] [PubMed] [Google Scholar]
- Bradshaw HD, Ceulemans R, Davis J, Stettler R.. 2000. Emerging model systems in plant biology: poplar (Populus) as a model forest tree. J Plant Growth Regul. 19:306–313. doi: 10.1007/s003440000030. [DOI] [Google Scholar]
- Bradshaw HD, Stettler RF.. 1995. Molecular genetics of growth and development in Populus. IV. Mapping QTLs with large effects on growth, form, and phenology traits in a forest tree. Genetics. 139:963–973. doi: 10.2307/2446076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulmer MG. 1971. The effect of selection on genetic variability. Am Naturalist. 105:201–211. doi: 10.1086/282718. [DOI] [Google Scholar]
- Carlson MO, Montilla-Bascon G, Hoekenga OA, Tinker NA, Poland J, et al. 2019. Multivariate genome-wide association analyses reveal the genetic basis of seed fatty acid composition in oat (Avena sativa L.). G3 (Bethesda). 9:2963–2975. doi: 10.1534/g3.119.400228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Q, Gong C, Wang Q, Zhou D, Yang H, et al. 2016. Genetic architecture of growth traits in Populus revealed by integrated quantitative trait locus (QTL) analysis and association studies. New Phytol. 209:1067–1082. doi: 10.1111/nph.13695. [DOI] [PubMed] [Google Scholar]
- Dubouzet JG, Strabala TJ, Wagner A.. 2013. Potential transgenic routes to increase tree biomass. Plant Sci. 212:72–101. doi: 10.1016/j.plantsci.2013.08.006. [DOI] [PubMed] [Google Scholar]
- Fisher RA. 1919. The correlations between relatives on the supposition of Mendelian inheritance. Philos Trans R Soc Edinb. 52:399–433. [Google Scholar]
- Galesloot TE, van Steen K, Kiemeney L, Janss LL, Vermeulen SH.. 2014. A comparison of multivariate genome-wide association methods. PLoS One. 9:e95923. doi: 10.1371/journal.pone.0095923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geng X, Sha J, Liu S, Bao L, Zhang J, et al. 2015. A genome-wide association study in catfish reveals the presence of functional hubs of related genes within QTLs for columnaris disease resistance. BMC Genomics. 16:196. doi: 10.1186/s12864-015-1409-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gieger C, Geistlinger L, Altmaier E, de Angelis MH, Kronenberg F, et al. 2008. Genetics meets metabolomics: a genome-wide association study of metabolite profiles in human serum. Plos Genet. 4:e1000282. doi: 10.1371/journal.pgen.1000282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez-Martinez SC, Wheeler NC, Ersoz E, Nelson CD, Neale DB.. 2007. Association genetics in Pinus taeda L. I. wood property traits. Genetics. 175:399–409. doi: 10.1534/genetics.106.061127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollander M, Wolfe DA.. 1973. Nonparametric Statistical Methods. New York: John Wiley & Sons. [Google Scholar]
- Kang HM, Sul JH, Service SK, Zaitlen NA, Kong SY, et al. 2010. Variance component model to account for sample structure in genome-wide association studies. Nat Genet. 42:348–354. doi: 10.1038/ng.548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HM, Zaitlen NA, Wade CM, Kirby A, Heckerman D, et al. 2008. Efficient control of population structure in model organism association mapping. Genetics. 178:1709–1723. doi: 10.1534/genetics.107.080101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Botstein D.. 1989. Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics. 121:185–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F, Chen B, Xu K, Wu J, Song W, et al. 2014. Genome-wide association study dissects the genetic architecture of seed weight and seed quality in rapeseed (Brassica napus L.). DNA Res. 21:355–367. doi: 10.1093/dnares/dsu002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Durbin R.. 2009. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics. 25:1754–1760. doi: 10.1093/bioinformatics/btp324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, 1000 Genome Project Data Processing Subgroup, et al. 2009. The sequence alignment/map format and SAMtools. Bioinformatics. 25:2078–2079. doi: 10.1093/bioinformatics/btp352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipka AE, Gore MA, Magallanes-Lundback M, Mesberg A, Lin HN, et al. 2013. Genome-wide association study and pathway-level analysis of tocochromanol levels in maize grain. G3 (Bethesda). 3:1287–1299. doi: 10.1534/g3.113.006148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu F, Tong C, Tao S, Wu J, Chen Y, et al. 2017. MVQTLCIM: composite interval mapping of multivariate traits in a hybrid F1 population of outbred species. BMC Bioinformatics. 18:515. doi: 10.1186/s12859-017-1908-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Ye M, Zhu S, Jiang L, Sang M, et al. 2018. Two-stage identification of SNP effects on dynamic poplar growth. Plant J. 93:286–296. doi: 10.1111/tpj.13777. [DOI] [PubMed] [Google Scholar]
- Loiselle BA, Sork VL, Nason J, Graham C.. 1995. Spatial genetic structure of a tropical understory shrub, Psychotria officinalis (Rubiaceae). Am J Bot. 82:1420–1425. doi: 10.1002/j.1537-2197.1995.tb12679.x. [DOI] [Google Scholar]
- Lynch M, Walsh B.. 1998. Genetics and Analysis of Quantitative Traits. Sunderland, MA: Sinauer Associates, Inc. [Google Scholar]
- Maliepaard C, Jansen J, Van Ooijen JW.. 1997. Linkage analysis in a full-sib family of an outbreeding plant species: overview and consequences for applications. Genet Res. 70:237–250. doi: 10.1017/s0016672397003005. [DOI] [Google Scholar]
- Monclus R, Leple JC, Bastien C, Bert PF, Villar M, et al. 2012. Integrating genome annotation and QTL position to identify candidate genes for productivity, architecture and water-use efficiency in Populus spp. BMC Plant Biol. 12:173. doi: 10.1186/1471-2229-12-173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mousavi M, Tong C, Liu F, Tao S, Wu J, et al. 2016. De novo SNP discovery and genetic linkage mapping in poplar using restriction site associated DNA and whole-genome sequencing technologies. BMC Genomics. 17:656. doi: 10.1186/s12864-016-3003-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nievergelt CM, Libiger O, Schork NJ.. 2007. Generalized analysis of molecular variance. PLoS Genet. 3:e51.doi: 10.1371/journal.pgen.0030051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ober U, Ayroles JF, Stone EA, Richards S, Zhu D, et al. 2012. Using whole-genome sequence data to predict quantitative trait phenotypes in Drosophila melanogaster. PLoS Genet. 8:e1002685. doi: 10.1371/journal.pgen.1002685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onogi A. 2019. Comparison of F-tests for univariate and multivariate mixed-effect models in genome-wide association mapping. Front Genet. 10:30. doi: 10.3389/fgene.2019.00030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel RK, Jain M.. 2012. NGS QC Toolkit: a toolkit for quality control of next generation sequencing data. PLoS One. 7:e30619.doi: 10.1371/journal.pone.0030619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruitt KD, Tatusova T, Maglott DR.. 2007. NCBI reference sequences (RefSeq): a curated non-redundant sequence database of genomes, transcripts and proteins. Nucleic Acids Res. 35:D61–D65. doi: 10.1093/nar/gkl842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice BR, Fernandes SB, Lipka AE.. 2020. Multi-trait genome-wide association studies reveal loci associated with maize inflorescence and leaf architecture. Plant Cell Physiol. 61:1427–1437. doi: 10.1093/pcp/pcaa039. [DOI] [PubMed] [Google Scholar]
- Searle SR, Casella G, McCulloch CE.. 2006. Variance Components. New York: John Wiley & Sons, Inc. [Google Scholar]
- Slaten ML, Yobi A, Bagaza C, Chan YO, Shrestha V, et al. 2020. mGWAS uncovers Gln-Glucosinolate seed-specific interaction and its role in metabolic homeostasis. Plant Physiol. 183:483–500. doi: 10.1104/pp.20.00039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su C, Wang W, Gong S, Zuo J, Li S, et al. 2017. High density linkage map construction and mapping of yield trait QTLs in maize (Zea mays) using the genotyping-by-sequencing (GBS) technology. Front Plant Sci. 8: 706. doi: 10.3389/fpls.2017.00706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor G. 2002. Populus: Arabidopsis for forestry. Do we need a model tree? Ann Bot. 90:681–689. doi:doi: 10.1093/aob/mcf255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton T, McPeek MS.. 2007. Case-control association testing with related individuals: a more powerful quasi-likelihood score test. Am J Hum Genet. 81:321–337. doi: 10.1086/519497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong CF, Li HG, Wang Y, Li XR, Ou JJ, et al. 2016. Construction of high-density linkage maps of Populus deltoides × P. simonii using restriction-site associated DNA sequencing. PLoS One. 11:e0150692. doi: 10.1371/journal.pone.0150692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong CF, Zhang B, Li HG, Shi JS.. 2012. Model selection for quantitative trait loci mapping in a full-sib family. Genet Mol Biol. 35:622–631. doi: 10.1590/S1415-47572012005000044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong CF, Zhang B, Shi JS.. 2010. A hidden Markov model approach to multilocus linkage analysis in a full-sib family. Tree Genet Genomes. 6:651–662. doi: 10.1007/s11295-010-0281-2. [DOI] [Google Scholar]
- Tuskan GA, Difazio S, Jansson S, Bohlmann J, Grigoriev I, et al. 2006. The genome of black cottonwood, Populus trichocarpa (Torr. & Gray). Science. 313:1596–1604. doi: 10.1126/science.1128691. [DOI] [PubMed] [Google Scholar]
- Vanous A, Gardner C, Blanco M, Martin-Schwarze A, Lipka AE, et al. 2018. Association mapping of flowering and height traits in germplasm enhancement of maize doubled haploid (GEM-DH) lines. Plant Genome. 11:170083–170014. doi: 10.3835/plantgenome2017.09.0083. [DOI] [PubMed] [Google Scholar]
- VanRaden PM. 2008. Efficient methods to compute genomic predictions. J Dairy Sci. 91:4414–4423. doi: 10.3168/jds.2007-0980. [DOI] [PubMed] [Google Scholar]
- Wang L, Wang B, Du Q, Chen J, Tian J, et al. 2017. Allelic variation in PtoPsbW associated with photosynthesis, growth, and wood properties in Populus tomentosa. Mol Genet Genomics. 292:77–91. doi: 10.1007/s00438-016-1257-1. [DOI] [PubMed] [Google Scholar]
- Williams ER, Matheson AC, Harwood CE.. 2002. Experimental Design and Ananlysis for Tree Improvement. Collingwood, Australia: CSIRO Publishing. [Google Scholar]
- Wright JW. 1976. Introduction to Forest Genetics. New York, NY: Academic Press. [Google Scholar]
- Wu RL. 1998. Genetic mapping of QTLs affecting tree growth and architecture in Populus: implication for ideotype breeding. Theor Appl Genet. 96:447–457. doi: 10.1007/s001220050761. [DOI] [PubMed] [Google Scholar]
- Xu R. 2003. Measuring explained variation in linear mixed effects models. Statist Med. 22:3527–3541. doi: 10.1002/sim.1572. [DOI] [PubMed] [Google Scholar]
- Xue S, Ogut F, Miller Z, Verma J, Bradbury PJ, et al. 2017. Comparison of one-stage and two-stage genome-wide association studies. bioRxiv. doi: 10.1101/099291. [DOI] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, et al. 2010. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 42:565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Lee SH, Goddard ME, Visscher PM.. 2011. GCTA: a tool for genome-wide complex trait analysis. Am J Hum Genet. 88:76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao D, Wu H, Chen Y, Yang W, Gao H, et al. 2020. gmRAD: an integrated SNP calling pipeline for genetic mapping with RADseq across a hybrid population. Brief Bioinformatics. 21:329–337. doi: 10.1093/bib/bby114. [DOI] [PubMed] [Google Scholar]
- Yu JM, Pressoir G, Briggs WH, Bi IV, Yamasaki M, et al. 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat Genet. 38:203–208. doi: 10.1038/ng1702. [DOI] [PubMed] [Google Scholar]
- Zeng Z-B. 1994. Precision mapping of quantitative trait loci. Genetics. 136:1457–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C, Dong S-S, Xu J-Y, He W-M, Yang T-L.. 2019. PopLDdecay: a fast and effective tool for linkage disequilibrium decay analysis based on variant call format files. Bioinformatics. 35:1786–1788. doi: 10.1093/bioinformatics/bty875. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Buckler ES, Casstevens TM, Bradbury PJ.. 2009. Software engineering the mixed model for genome-wide association studies on large samples. Brief Bioinformatics. 10:664–675. doi: 10.1093/bib/bbp050. [DOI] [PubMed] [Google Scholar]
- Zhao Y, Wang H, Bo C, Dai W, Zhang X, et al. 2019. Genome-wide association study of maize plant architecture using F1 populations. Plant Mol Biol. 99:1–15. doi: 10.1007/s11103-018-0797-7. [DOI] [PubMed] [Google Scholar]
- Zhou X, Stephens M.. 2012. Genome-wide efficient mixed-model analysis for association studies. Nat Genet. 44:821–824. doi: 10.1038/ng.2310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X, Stephens M.. 2014. Efficient multivariate linear mixed model algorithms for genome-wide association studies. Nat Methods. 11:407–409. doi: 10.1038/nmeth.2848. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The RADseq data of the 172 clones have been deposited in the SRA database at the National Center for Biotechnology Information (NCBI) with accession numbers presented in Supplementary Table S1. The phenotypic and genotypic data generated for GWAS in this study can be found in Supplementary Tables S2 and S6, respectively. All of the supplemental materials (Supplementary Tables S1–S13 and Supplementary Figures S1 and S2) for this study are available at figshare DOI: 10.25387/g3.13017866.