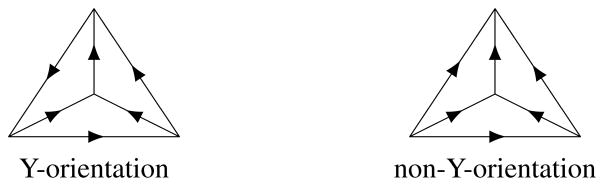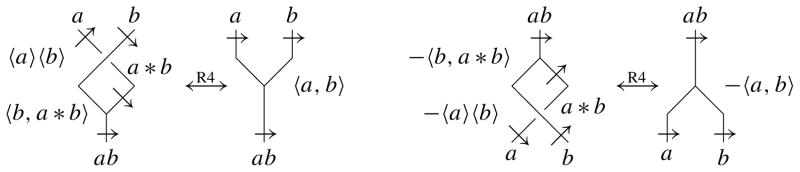HOMOLOGY FOR QUANDLES WITH PARTIAL GROUP OPERATIONS

Abstract

A quandle is a set that has a binary operation satisfying three conditions corresponding to the Reidemeister moves. Homology theories of quandles have been developed in a way similar to group homology, and have been applied to knots and knotted surfaces. In this paper, a homology theory is defined that unifies group and quandle homology theories. A quandle that is a union of groups with the operation restricting to conjugation on each group component is called a multiple conjugation quandle (MCQ, defined rigorously within). In this definition, compatibilities between the group and quandle operations are imposed which are motivated by considerations on colorings of handlebody-links. The homology theory defined here for MCQs takes into consideration both group and quandle operations, as well as their compatibility. The first homology group is characterized, and the notion of extensions by 2-cocycles is provided. Degenerate subcomplexes are defined in relation to simplicial decompositions of prismatic (products of simplices) complexes and group inverses. Cocycle invariants are also defined for handlebody-links.

1. Introduction

In this paper, a homology theory is proposed that contains aspects of both group and quandle homology theories, for algebraic structures that have both operations and certain compatibility conditions between them.

The notion of a quandle [Joyce 1982; Matveev 1982] was introduced in knot theory as a generalization of the fundamental group. Briefly, a quandle is a set with a binary operation that is idempotent and self-distributive, and a bijective corresponding right action. The axioms correspond to the Reidemeister moves, and quandles have been used extensively to construct knot invariants. They have been considered in various other contexts, for example as symmetries of geometric objects [Takasaki 1943], and with different names, such as distributive groupoids [Matveev 1982] and automorphic sets [Brieskorn 1988]. A typical example is a group conjugation a * b = b⁻¹ab which is an expression of the Wirtinger relation for the fundamental group of the knot complement. The same structure but without idempotency is called a rack, and is used in the study of framed links [Fenn and Rourke 1992].

In [Fenn et al. 1995] a chain complex was introduced for racks. The resulting homology theory was modified in [Carter et al. 2003] by defining a quotient complex that reflected the quandle idempotence axiom. The motivation for this homology was to construct the quandle cocycle invariants for links and surface-links. Since then a variety of applications have been found. The quandle cocycle invariants were generalized to handlebody-links in [Ishii and Iwakiri 2012]. When a set has multiple quandle operations that are parametrized by a group, the structure is called a G-family of quandles; this notion, with its associated homology theory, was introduced in [Ishii et al. 2013] and it too was motivated from handlebody-knots. This homology theory is called IIJO. In particular, cocycle invariants were introduced that distinguished mirror images of some handlebody-knots. These G-families were further generalized to an algebraic system called a multiple conjugation quandle (MCQ) in [Ishii 2015b] for colorings of handlebody-knots. An MCQ has a quandle operation and partial group operations, all linked by compatibility conditions.

This paper proposes to unify the group and quandle homology theories for MCQs. The definition of an MCQ is recalled in Section 2 as a generalization of a G-family of quandles. A homology theory is defined (in Section 3) that simultaneously encompasses the group and quandle homologies of the interrelated structures. As in the case of [Carter et al. 2003], some subcomplexes are defined in order to compensate for the topological motivation of the theory. The first homology group is characterized, and the notion of extensions by 2-cocycles is provided in Section 4.

The homology theory for MCQs is well suited for handlebody-links such that each toroidal component has its core circle oriented, as defined in Section 5. When considering colorings for unoriented handlebody-links, we also need to take into consideration issues about the inverse elements in the group (Section 6). Prismatic sets (products of simplices) are decomposed into subsimplices that are higher-dimensional duals of graph moves; Section 7 defines a subcomplex that compensates for these subdivisions. In Sections 8 and 9, we relate this homology theory with group and quandle homology theories. Finally, in Section 10, we discuss approaches to finding new 2-cocycles of our homology theory.

2. Multiple conjugation quandles

First, recall a quandle [Joyce 1982; Matveev 1982] is a nonempty set X with a binary operation *: X × X → X satisfying the following axioms:

1. For any a ∈ X, we have a * a = a.

2. For any a ∈ X, the map S_a: X → X defined by S_a(x) = x * a is a bijection.

3. For any a, b, c ∈ X, we have (a * b) * c = (a * c) * (b * c).

Definition 1 [Ishii 2015b]

A multiple conjugation quandle (MCQ) X is the disjoint union of groups G_λ, where λ is an element of an index set Λ, with a binary operation *: X × X → X satisfying the following axioms:

1. For any a, b ∈ G_λ, we have a * b = b⁻¹ab.

2. For any x ∈ X and a, b ∈ G_λ, we have x * e_λ = x and x * (ab) = (x * a) * b, where e_λ is the identity element of G_λ.

3. For any x, y, z ∈ X, we have (x * y) * z = (x * z) * (y * z).

4. For any x ∈ X and a, b ∈ G_λ, we have (ab) * x = (a * x)(b * x) in some group G_μ.

We call the group G_λ a component of the MCQ. An MCQ is a type of quandle that can be decomposed as a union of groups, and the quandle operation in each component is given by conjugation. Moreover, there are compatibilities, (2) and (4), between the group and quandle operations.

Note that the quandle axiom a * a = a follows immediately since the operation in any component is given by conjugation. The second quandle axiom also follows, since for the map S_a: X → X defined by S_a(x) = x * a, the inverse map is given by S_a⁻¹. The second axiom of MCQs implies that the map ϕ: G_λ → Aut_Qnd X defined by ϕ(a) = S_a is a group homomorphism, where Aut_Qnd X is the set of quandle automorphisms of X and is the group with the multiplication defined by S_a S_b: = S_b ∘ S_a. The last axiom (4) may be replaced by the following:

• (4′)For any x ∈ X and λ ∈ Λ, there is a unique element μ ∈ Λ such that S_x(G_λ) = G_μ and that S_x: G_λ → G_μ is a group isomorphism.

The axiom (4) immediately follows from (4′). Conversely, (4′) follows from (4): the condition (4) contains the condition that for any a, b ∈ G_λ and x ∈ X, there exists a unique μ ∈ Λ such that a * x, b * x ∈ G_μ. Hence we have S_x(G_λ) ⊂ G_μ, which implies that S_x: G_λ → G_μ is a well-defined group homomorphism by the condition (ab) * x = (a * x)(b * x). The homomorphism S_x: G_λ → G_μ is a group isomorphism, since S_x⁻¹: G_μ → G_λ gives its inverse.

A multiple conjugation quandle can be obtained from a G-family of quandles as follows.

Example 2

Let G be a group with identity element e, let (M, {*^g}_{g ∈ G}) be a G-family of quandles [Ishii et al. 2013]; i.e., a nonempty set M with a family of binary operations *^g: M × M → M (g ∈ G) satisfying

$$\begin{array}{ll}\hfill x{\ast }^{g}x=x,x{\ast }^{gh}y& =(x{\ast }^{g}y){\ast }^{h}y,x{\ast }^{e}y=x,\hfill \\ \hfill (x{\ast }^{g}y){\ast }^{h}z& =(x{\ast }^{h}z){\ast }^{h^{-1}gh}(y{\ast }^{h}z)\hfill \end{array}$$

for x, y, z ∈ M and g, h ∈ G. Then ∐_{x ∈ M}{x} × G is a multiple conjugation quandle with

$$(x,g)\ast (y,h)=(x{\ast }^{h}y,h^{-1}gh),(x,g)(x,h)=(x,gh).$$

The following are specific examples of G-families of quandles.

1. Let M be a group, and G be a subgroup of Aut M. Then for x, y ∈ M and g ∈ G, x * y = (xy⁻¹)^g y gives a G-family of quandles. Here x^g denotes g acting on x. The fact that this is a G-family was pointed out in [Przytycki 2011]; however, that any specific automorphism g yields a quandle was earlier observed in [Joyce 1982; Matveev 1982]. When M is abelian and an element g ∈ G is fixed, the resulting quandle is called an Alexander quandle.

2. Let (X, *) be a quandle. We denote $S_b^n(a)$ by a *ⁿ b. Put Z: = ℤ or ℤ/mℤ, where m: = min{i > 0 | x *ⁱ y = x for any x, y ∈ X}. Then (X, {*ⁿ}_{n ∈ Z}) is a Z-family of quandles.

For a multiple conjugation quandle X = ∐_{λ ∈ Λ} G_λ, an X-set is a nonempty set Y with a map *: Y × X → Y satisfying the following axioms, where we use the same symbol * as the binary operation of X.

• For any y ∈ Y and a, b ∈ G_λ, we have y * e_λ = y and y * (ab) = (y * a) * b, where e_λ is the identity of G_λ.

• For any y ∈ Y and a, b ∈ X, we have (y * a) * b = (y * b) * (a * b).

Any multiple conjugation quandle X itself is an X-set with its binary operation. Any singleton set {y₀} is also an X-set with the map * defined by y₀ * x = y₀ for x ∈ X, which is called a trivial X-set. The index set Λ is an X-set with the map * defined by λ * x = μ when S_x(G_λ) = G_μ for λ, μ ∈ Λ and x ∈ X.

3. Homology theory

In this section, we define a chain complex for MCQs that contains aspects of both group and quandle homology theories. A subcomplex is also defined that corresponds to a Reidemeister move for handlebody-links.

Let X = ∐_{λ ∈ Λ} G_λ be a multiple conjugation quandle, and let Y be an X-set. In what follows, we denote a sequence of elements of X by a bold symbol such as a, and denote by |a| the length of a sequence a. For example, (a), 〈a〉, (y; a; b) respectively denote

$$(a_1,\dots ,a_{\mid \mathit{a}\mid }),\langle a_1,\dots ,a_{\mid \mathit{a}\mid }\rangle ,(y;a_1,\dots ,a_{\mid \mathit{a}\mid };b_1,\dots ,b_{\mid \mathit{b}\mid }).$$

Let P_n(X)_Y be the free abelian group generated by the elements

$$(y;a_{1,1},\dots ,a_{1,n_1};\dots ;a_{k,1},\dots ,a_{k,n_k})\in \underset{n_1+\cdots +n_k=n}{\cup }Y\times \prod _{i=1}^k\underset{\lambda \in \mathrm{\Lambda }}{\cup }{G}_{\mathrm{\lambda }}^{n_i}$$

if n ≥ 0, and let P_n(X)_Y = 0 otherwise. The elements of P_n(X)_Y are called prismatic chains and P_n(X)_Y is called the prismatic chain group. Note that for each j, the elements a_j,1, …, a_{j,n_j} belong to one of the G_λ. For example, P₃(X)_Y is generated by the elements (y; a; b; c), (y; a; e, f), (y; d, e; c) and (y; d, e, f) (where a, b, c ∈ X, d, e, f ∈ G_λ, y ∈ Y). Here a, b, c may or may not belong to the same G_μ (μ ∈ Λ), but d, e, f belong to the same G_λ. All may belong to the same G_λ.

We represent (y; a₁; …; a_k) using the noncommutative multiplication form

$$\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle {\mathit{a}}_k\rangle .$$

We define 〈y〉〈a₁〉 ··· 〈a_k〉 * b: = 〈y * b〉〈a₁ * b〉 ··· 〈a_k * b〉, where 〈a * b〉 denotes 〈a₁ * b, …, a_|a| * b〉. We set |〈y〉〈a₁〉 ··· 〈a_k〉|: = |a₁| + ··· + |a_k|.

We define a boundary homomorphism ∂_n: P_n(X)_Y → P_n−1(X)_Y by

$$\partial \left(\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle {\mathit{a}}_k\rangle \right)=\sum _{i=1}^k{(-1)}^{\mid \langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle {\mathit{a}}_{i-1}\rangle \mid }\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \partial \langle {\mathit{a}}_i\rangle \cdots \langle {\mathit{a}}_k\rangle ,$$

where

$$\partial \langle a_1,\dots ,a_m\rangle =\ast a_1\langle a_2,\dots ,a_m\rangle +\sum _{i=1}^{m-1}{(-1)}^i\langle a_1,\dots ,a_i{a}_{i+1},\dots ,a_m\rangle +{(-1)}^m\langle a_1,\dots ,a_{m-1}\rangle .$$

The resulting terms ∂(〈a〉) = *a〈 〉 − 〈 〉 for m = 1 in the above expression mean that the formal symbol 〈 〉 is deleted. For n = 0, we define ∂〈y〉 = 0.

Example 3

The boundary maps in two and three dimensions are computed as follows.

$$\begin{array}{ll}\hfill {\partial }_2(\langle y\rangle \langle a\rangle \langle b\rangle )& =\langle y\ast a\rangle \langle b\rangle -\langle y\rangle \langle b\rangle -\langle y\ast b\rangle \langle a\ast b\rangle +\langle y\rangle \langle a\rangle ,\hfill \\ \hfill {\partial }_2(\langle y\rangle \langle a,b\rangle )& =\langle y\ast a\rangle \langle b\rangle -\langle y\rangle \langle ab\rangle +\langle y\rangle \langle a\rangle ,\hfill \\ \hfill {\partial }_3(\langle y\rangle \langle a\rangle \langle b\rangle \langle c\rangle )& =\langle y\ast a\rangle \langle b\rangle \langle c\rangle -\langle y\rangle \langle b\rangle \langle c\rangle -\langle y\ast b\rangle \langle a\ast b\rangle \langle c\rangle +\langle y\rangle \langle a\rangle \langle c\rangle +\langle y\ast c\rangle \langle a\ast c\rangle \langle b\ast c\rangle -\langle y\rangle \langle a\rangle \langle b\rangle ,\hfill \\ \hfill {\partial }_3(\langle y\rangle \langle a\rangle \langle b,c\rangle )& =\langle y\ast a\rangle \langle b,c\rangle -\langle y\rangle \langle b,c\rangle -\langle y\ast b\rangle \langle a\ast b\rangle \langle c\rangle +\langle y\rangle \langle a\rangle \langle bc\rangle -\langle y\rangle \langle a\rangle \langle b\rangle ,\hfill \\ \hfill {\partial }_3(\langle y\rangle \langle a,b\rangle \langle c\rangle )& =\langle y\ast a\rangle \langle b\rangle \langle c\rangle -\langle y\rangle \langle ab\rangle \langle c\rangle +\langle y\rangle \langle a\rangle \langle c\rangle +\langle y\ast c\rangle \langle a\ast c,b\ast c\rangle -\langle y\rangle \langle a,b\rangle ,\hfill \\ \hfill {\partial }_3(\langle y\rangle \langle a,b,c\rangle )& =\langle y\ast a\rangle \langle b,c\rangle -\langle y\rangle \langle ab,c\rangle +\langle y\rangle \langle a,bc\rangle -\langle y\rangle \langle a,b\rangle .\hfill \end{array}$$

Proposition 4

P_*(X)_Y = (P_n(X)_Y, ∂_n) is a chain complex.

Proof

The Leibniz rule

$$\partial (\sigma \tau )=(\partial \sigma )\tau +{(-1)}^{\mid \sigma \mid }\sigma (\partial \tau )$$

is a restatement of the definition when k = 2. In fact, the general definition follows from this by induction. Also ∂(σ * a) = (∂σ) * a, and ∂ ∘ ∂ = 0 follows from these two facts.

We will later define a degeneracy subcomplex that is analogous (albeit more complicated) to the subcomplex of degeneracies for quandle homology. Before its definition, we give a description of simplicial decompositions of products of simplices for motivation. We identify an n-simplex Δⁿ with the set

$$\{(x_1,x_2,\dots ,x_n)\in {[0,1]}^n:0\le x_1\le x_2\le \cdots \le x_n\le 1\},$$

called the right n-simplex. Then the n-cube [0, 1]ⁿ can be decomposed into n! sets each of which is congruent to this right n-simplex that has n edges of length 1, and has (n − k + 1) edges of length $\sqrt{k}$ for k = 1, …, n. More specifically, for x⃗ ∈ [0, 1]ⁿ consider the permutation σ ∈ Σ_n such that 0 ≤ x_σ(1) ≤ x_σ(2) ≤ ··· ≤ x_σ(n) ≤ 1. If the coordinates of x⃗ are all distinct, then there is a unique such σ and an n-simplex ${\mathrm{\Delta }}_{\sigma }^n$ congruent to the right n-simplex such that x⃗ lies in the interior of ${\mathrm{\Delta }}_{\sigma }^n$. Otherwise x⃗ lies in the boundary of more than one such simplex. Now consider the product of right simplices

$${\mathrm{\Delta }}^s\times {\mathrm{\Delta }}^t=\left\{(\overrightarrow{x},\overrightarrow{y})\in {[0,1]}^{s+t}|\begin{array}{l}0\le x_1\le x_2\le \cdots \le x_s\le 1\hfill \\ 0\le y_1\le y_2\le \cdots \le y_t\le 1\hfill \end{array}\right\},$$

where the notation (x⃗, y⃗) represents (x₁, …, x_s, y₁, …, y_t). This can be decomposed as a union of simplices of the form given above. For

$$\overrightarrow{z}=(\overrightarrow{x},\overrightarrow{y})\in {\mathrm{\Delta }}^s\times {\mathrm{\Delta }}^t\subset {[0,1]}^n,$$

where n = s + t, there is an associated simplex ${\mathrm{\Delta }}_{\sigma }^n$ that contains the point (x⃗, y⃗). Suppose all coordinates of z⃗ are distinct, and let σ ∈ Σ_n be a permutation such that 0 < z_σ(1) < ··· < z_σ(n). Then the subset {i₁, i₂, …, i_s} ⊂ {1, 2, …, s + t} with i₁ < i₂ < ··· < i_s is determined from the positions of coordinates of x⃗, so that z_{i_k} = x_k for k = 1, …, s. Thus a given subset {i₁, i₂, …, i_s} ⊂ {1, 2, …, s + t} where i₁ < i₂ < ··· < i_s determines an n-simplex in the decomposition of Δ^s × Δ^t. We proceed to the definition of the degeneracy subcomplex.

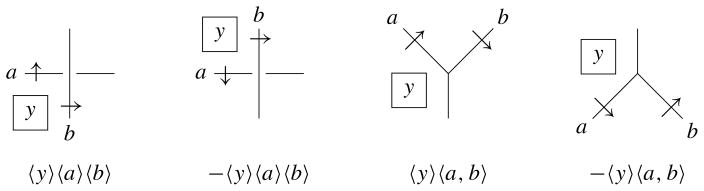
For an expression of the form 〈a〉〈b〉 in a chain in P_n(X)_Y, where 〈a〉 = 〈a₁, …, a_s〉 and 〈b〉 = 〈b₁, …, b_t〉 satisfy a_i, b_j ∈ G_λ for all i = 1, …, s and j = 1, …, t, let the notation 〈〈a〉〈b〉〉_{i₁,…,i_s} represent ${(-1)}^{{\sum }_{k=1}^s(i_k-k)}\langle c_1,\dots ,c_{s+t}\rangle$, where 1 ≤ i₁ < ··· < i_k < ··· < i_s ≤ s + t, and

$$c_i=\{\begin{array}{ll}{a}_k\ast (b_1\cdots b_{i-k})\hfill & \text{if}i=i_k,\hfill \\ b_{i-k}\hfill & \text{if}{i}_k<i<i_{k+1}.\hfill \end{array}$$

If i = k in the first case, then we regard (b₁ ··· b_{i − k}) to be empty. For example, 〈〈a〉〈b〉〉₁ = 〈a, b〉, 〈〈a〉〈b〉〉₂ = −〈b, a * b〉, and 〈〈a, b〉〈c〉〉_1,3 = −〈a, c, b * c〉. We also define the notation 〈〈a〉〈b〉〉 by

$$\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle :=\sum _{1\le i_1<\cdots <i_s\le s+t}{\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_s}.$$

Define D_n(X)_Y to be the subgroup of P_n(X)_Y generated by the elements of the form

$$\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle \mathit{a}\rangle \langle \mathit{b}\rangle \cdots \langle {\mathit{a}}_k\rangle -\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle \cdots \langle {\mathit{a}}_k\rangle ,$$

where we implicitly assume the linearity of the notations 〈〈a〉〈b〉〉_{i₁,…,i_s} and 〈〈a〉〈b〉〉, that is,

$$\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle \cdots \langle {\mathit{a}}_k\rangle =\sum _{1\le i_1<\cdots <i_{\mid \mathit{a}\mid }\le \mid \langle \mathit{a}\rangle \langle \mathit{b}\rangle \mid }\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots {\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_{\mid a\mid }}\cdots \langle {\mathit{a}}_k\rangle .$$

The chain group D_n(X)_Y is called the group of decomposition degeneracies. We will see that D_*(X)_Y = (D_n(X)_Y, ∂_n) is a subcomplex of P_*(X)_Y in Section 7.

We remark that the elements of the form

$$\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle a\rangle \langle a\rangle \cdots \langle {\mathit{a}}_k\rangle$$

belong to D_n(X)_Y.

For example, D₂(X)_Y is generated by the elements of the form

$$\langle y\rangle \langle a\rangle \langle b\rangle -\langle y\rangle \langle a,b\rangle +\langle y\rangle \langle b,a\ast b\rangle ,$$

and D₃(X)_Y is generated by the elements of the form

$$\begin{array}{l}\langle y\rangle \langle a\rangle \langle b\rangle \langle x\rangle -\langle y\rangle \langle a,b\rangle \langle x\rangle +\langle y\rangle \langle b,a\ast b\rangle \langle x\rangle ,\\ \langle y\rangle \langle x\rangle \langle b\rangle \langle c\rangle -\langle y\rangle \langle x\rangle \langle b,c\rangle +\langle y\rangle \langle x\rangle \langle c,b\ast c\rangle ,\\ \langle y\rangle \langle a,b\rangle \langle c\rangle -\langle y\rangle \langle a,b,c\rangle +\langle y\rangle \langle a,c,b\ast c\rangle -\langle y\rangle \langle c,a\ast c,b\ast c\rangle ,\\ \langle y\rangle \langle a\rangle \langle b,c\rangle -\langle y\rangle \langle a,b,c\rangle +\langle y\rangle \langle b,a\ast b,c\rangle -\langle y\rangle \langle b,c,a\ast (bc)\rangle \end{array}$$

for a, b, c ∈ G_λ, x ∈ X.

Definition 5

The quotient complex of P_*(X)_Y modulo decomposition degeneracies D_*(X)_Y is denoted by C_*(X)_Y = (C_n(X)_Y, ∂_n), where C_n(X)_Y = P_n(X)_Y/D_n(X)_Y. For an abelian group A, define the cochain complex C^*(X; A)_Y = Hom(C_*(X)_Y, A). Denote by H_n(X)_Y the n-th homology group of C_*(X)_Y.

4. Algebraic aspects of the homology

In this section we study algebraic aspects of the homology theory we defined. Specifically, we characterize the first homology group, and show that a 2-cocycle defines an extension. For simplicity we consider the case Y = {y₀} is a singleton, and we suppress the symbols 〈y₀〉 whenever possible.

Let X be a multiple conjugation quandle, and Y = {y₀} be a singleton. Then P₀(X)_Y is infinite cyclic, generated by 〈y₀〉, and ∂₁(〈y₀〉〈a〉) = 〈y₀ * a〉 − 〈y₀〉 for a ∈ X. Hence H₀(X)_Y = ℤ. If X is a multiple conjugation quandle consisting of a single group, H₁(X)_Y ≅ X^ab, since P₁(X)_Y is the free abelian group generated by the elements 〈y₀〉〈a〉 (a ∈ X), and

$$\begin{array}{ll}\hfill {\partial }_2(\langle y_0\rangle \langle a,b\rangle )& =\langle y_0\rangle \langle b\rangle -\langle y_0\rangle \langle ab\rangle +\langle y_0\rangle \langle a\rangle ,\hfill \\ \hfill {\partial }_2(\langle y_0\rangle \langle a\rangle \langle b\rangle )& =-\langle y_0\rangle \langle a\ast b\rangle +\langle y_0\rangle \langle a\rangle ={\partial }_2(\langle y_0\rangle \langle a,b\rangle )-{\partial }_2(\langle y_0\rangle \langle b,b^{-1}ab\rangle ).\hfill \end{array}$$

Proposition 6

Let X = ∐_{λ ∈ Λ} G_λ be a multiple conjugation quandle, let Y = {y₀} be a singleton, and A an abelian group. A map ϕ: P₂(X)_Y → A is a 2-cocycle of C^*(X)_Y if and only if X × A = ∐_{λ ∈ Λ}(G_λ × A) with

$$\begin{array}{ll}\hfill (a,s)\ast (b,t)& :=\left(a\ast b,s+\varphi (\langle a\rangle \langle b\rangle )\right)\mathit{for}(a,s),(b,t)\in X\times A,\hfill \\ \hfill (a,s)(b,t)& :=\left(ab,s+t+\varphi (\langle a,b\rangle )\right)\mathit{for}(a,s),(b,t)\in G_{\mathrm{\lambda }}\times A\hfill \end{array}$$

is a multiple conjugation quandle, where ϕ(〈y₀〉〈a〉〈b〉) and ϕ(〈y₀〉〈a, b〉) are respectively denoted by ϕ(〈a〉〈b〉) and ϕ(〈a, b〉) for short. Further, (e_λ, −ϕ(〈e_λ, e_λ〉)) is the identity of the group G_λ × A, and (a⁻¹, −s −ϕ(〈a, a⁻¹〉) −ϕ(〈e_λ, e_λ〉)) is the inverse of (a, s) ∈ G_λ × A.

Proof

We show correspondences between cocycle conditions and MCQ conditions for the extension.

(1) The correspondence between the cocycle condition ϕ(∂₃(〈a, b, c〉)) = 0 and the associativity of a group.

For (a, s), (b, t), (c, u) ∈ G_λ × A, ϕ(〈a, b〉) + ϕ(〈ab, c〉) = ϕ(〈b, c〉) + ϕ(〈a, bc〉) if and only if ((a, s)(b, t))(c, u) = (a, s)((b, t)(c, u)), since

$$\begin{array}{ll}\left((a,s)(b,t)\right)(c,u)\hfill & =\left(\mathit{abc},s+t+u+\varphi (\langle a,b\rangle )+\varphi (\langle ab,c\rangle )\right),\hfill \\ (a,s)\left((b,t)(c,u)\right)\hfill & =\left(\mathit{abc},s+t+u+\varphi (\langle b,c\rangle )+\varphi (\langle a,bc\rangle )\right).\hfill \end{array}$$

We note that ϕ(〈a, b〉) + ϕ(〈ab, c〉) = ϕ(〈b, c〉) + ϕ(〈a, bc〉), or equivalently ((a, s)(b, t))(c, u) = (a, s)((b, t)(c, u)) implies that ϕ(〈a, e_λ〉) = ϕ(〈e_λ, c〉) and that ϕ(〈b⁻¹, b〉) = ϕ(〈b, b⁻¹〉). These equalities respectively imply

$$(a,s)=(a,s)\left(e_{\mathrm{\lambda }},-\varphi (\langle e_{\mathrm{\lambda }},e_{\mathrm{\lambda }}\rangle )\right)=(e_{\mathrm{\lambda }},-\varphi (\langle e_{\mathrm{\lambda }},e_{\mathrm{\lambda }}\rangle ))(a,s)$$

and

$$\begin{array}{l}\left(e_{\mathrm{\lambda }},-\varphi (\langle e_{\mathrm{\lambda }},e_{\mathrm{\lambda }}\rangle )\right)=(a,s)\left(a^{-1},-s-\varphi (\langle a,a^{-1}\rangle )-\varphi (\langle e_{\mathrm{\lambda }},e_{\mathrm{\lambda }}\rangle )\right)\\ =\left(a^{-1},-s-\varphi (\langle a,a^{-1}\rangle )-\varphi (\langle e_{\mathrm{\lambda }},e_{\mathrm{\lambda }}\rangle )\right)(a,s).\end{array}$$

It follows that (e_λ,−ϕ(〈e_λ, e_λ〉)) is the identity of the group G_λ × A, and that (a⁻¹,−s −ϕ(〈a, a⁻¹〉)−ϕ(〈e_λ, e_λ〉)) is the inverse of (a, s) ∈ G_λ × A.

(2) The correspondence between the degeneracy of ϕ on D₂(X)_Y and the first axiom of MCQs.

For (a, s), (b, t) ∈ G_λ× A, ϕ(〈a〉〈b〉)+ϕ(〈b, a *b〉) = ϕ(〈a, b〉) if and only if (b, t)((a, s) * (b, t)) = (a, s)(b, t), since

$$\begin{array}{ll}\hfill (b,t)\left((a,s)\ast (b,t)\right)& =\left(b(a\ast b),s+t+\varphi (\langle a\rangle \langle b\rangle )+\varphi (\langle b,a\ast b\rangle )\right),\hfill \\ \hfill (a,s)(b,t)& =\left(ab,s+t+\varphi (\langle a,b\rangle )\right).\hfill \end{array}$$

(3) The correspondence between the cocycle condition ϕ(∂₃(〈x〉〈a, b〉)) = 0 and the second axiom of MCQs.

For (x, r) ∈ X × A and (a, s), (b, t) ∈ G_λ × A,

$$\varphi (\langle x\rangle \langle ab\rangle )=\varphi (\langle x\rangle \langle a\rangle )+\varphi (\langle x\ast a\rangle \langle b\rangle )$$

if and only if (x, r) * ((a, s)(b, t)) = ((x, r) * (a, s))* (b, t), since

$$\begin{array}{ll}\hfill (x,r)\ast \left((a,s)(b,t)\right)& =\left(x\ast (ab),r+\varphi (\langle x\rangle \langle ab\rangle )\right),\hfill \\ \hfill \left((x,r)\ast (a,s)\right)\ast (b,t)& =\left((x\ast a)\ast b,r+\varphi (\langle x\rangle \langle a\rangle )+\varphi (\langle x\ast a\rangle \langle b\rangle )\right).\hfill \end{array}$$

Note ϕ(〈x〉〈ab〉)=ϕ(〈x〉 〈a〉)+ϕ(〈x*a〉〈b〉), or equivalently (x, r)*((a, s)(b, t))= ((x, r) * (a, s)) * (b, t), implies that ϕ(〈x〉〈e_λ〉) = 0. Then we have

$$(a,s)\ast \left(e_{\mathrm{\lambda }},-\varphi (\langle e_{\mathrm{\lambda }},e_{\mathrm{\lambda }}\rangle )\right)=(a,s).$$

(4) The correspondence between the cocycle condition ϕ(∂₃(〈a〉 〈b〉 〈c〉)) = 0 and the third axiom of MCQs.

For (a, s), (b, t), (c, u) ∈ X × A,

$$\varphi (\langle a\rangle \langle b\rangle )+\varphi (\langle a\ast b\rangle \langle c\rangle )=\varphi (\langle a\rangle \langle c\rangle )+\varphi (\langle a\ast c\rangle \langle b\ast c\rangle )$$

if and only if ((a, s) * (b, t))* (c, u) = ((a, s) * (c, u))* ((b, t) * (c, u)), since

$$\begin{array}{ll}\hfill \left((a,s)\ast (b,t)\ast (c,u)\right)& =\left((a\ast b)\ast c,s+\varphi (\langle a\rangle \langle b\rangle )+\varphi (\langle a\ast b\rangle \langle c\rangle )\right),\hfill \\ \hfill \left((a,s)\ast (c,u)\right)\ast \left((b,t)\ast (c,u)\right)& =\left((a\ast c)\ast (b\ast c),s+\varphi (\langle a\rangle \langle c\rangle )+\varphi (\langle a\ast c\rangle \langle b\ast c\rangle )\right).\hfill \end{array}$$

(5) The correspondence between the cocycle condition ϕ(∂₃(〈a, b〉〈x〉)) = 0 and the last axiom of MCQs.

For (x, r) ∈ X × A and (a, s), (b, t) ∈ G_λ × A,

$$\varphi (\langle a,b\rangle )+\varphi (\langle ab\rangle \langle x\rangle )=\varphi (\langle a\rangle \langle x\rangle )+\varphi (\langle b\rangle \langle x\rangle )+\varphi (\langle a\ast x,b\ast x\rangle )$$

if and only if ((a, s)(b, t)) * (x, r) = ((a, s) * (x, r))((b, t) * (x, r)), since

$$\begin{array}{ll}\hfill \left((a,s)(b,t)\right)\ast (x,r)& =\left((ab)\ast x,s+t+\varphi (\langle a,b\rangle )+\varphi (\langle ab\rangle \langle x\rangle )\right),\hfill \\ \hfill \left((a,s)\ast (x,r)\right)\left((b,t)\ast (x,r)\right)& =\left((a\ast x)(b\ast x),s+t+\varphi (\langle a\rangle \langle x\rangle )+\varphi (\langle b\rangle \langle x\rangle )+\varphi (\langle a\ast x,b\ast x\rangle )\right).\hfill \end{array}$$

Therefore ϕ is a 2-cocycle if and only if X×A is a multiple conjugation quandle.

5. Quandle cocycle invariants for handlebody-links

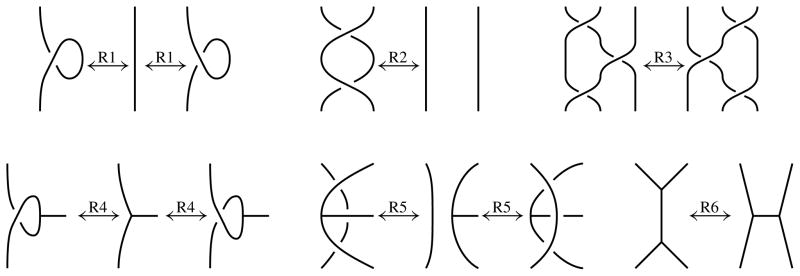
The definition of a multiple conjugation quandle is motivated from handlebody-links and their colorings [Ishii 2015b]. A handlebody-link is a disjoint union of handlebodies embedded in the 3-sphere S³. A handlebody-knot is a one component handlebody-link. Two handlebody-links are equivalent if there is an orientation-preserving self-homeomorphism of S³ which sends one to the other. A diagram of a handlebody-link is a diagram of a spatial trivalent graph whose regular neighborhood is the handlebody-link, where a spatial trivalent graph is a finite trivalent graph embedded in S³. In this paper, a trivalent graph may contain circle components. Two handlebody-links are equivalent if and only if their diagrams are related by a finite sequence of R1–R6 moves depicted in Figure 1 [Ishii 2008].

Figure 1.

Reidemeister moves for handlebody-links.

An S¹-orientation of a handlebody-link is an orientation of all genus 1 components of the handlebody-link, where an orientation of a solid torus is an orientation of its core S¹. Two S¹-oriented handlebody-links are equivalent if there is an orientation-preserving self-homeomorphism of S³ which sends one to the other preserving the S¹-orientation. A Y-orientation of a spatial trivalent graph is an orientation of the graph without sources and sinks with respect to the orientation (see Figure 2). We note that the term Y-orientation is a symbolic convention, and has no relation to an X-set Y. A diagram of an S¹-oriented handlebody-link is a diagram of a Y-oriented spatial trivalent graph whose regular neighborhood is the S¹-oriented handlebody-link where the S¹-orientation is induced from the Y-orientation by forgetting the orientations except on circle components of the Y-oriented spatial trivalent graph. Y-oriented R1–R6 moves are R1–R6 moves between two diagrams with Y-orientations which are identical except in the disk where the move applied. Two S¹-oriented handlebody-links are equivalent if and only if their diagrams are related by a finite sequence of Y-oriented R1–R6 moves [Ishii 2015a]. Note that in Figure 1 (R6), if all end points are oriented downward, then either choice of the two possible orientations of the middle edge makes the diagram Y-oriented locally. Thus reversing an orientation of this edge can be regarded as applying Y-oriented R6 moves twice. This is the case whenever both orientations of an edge give Y-orientations.

Figure 2.

Y-orientation.

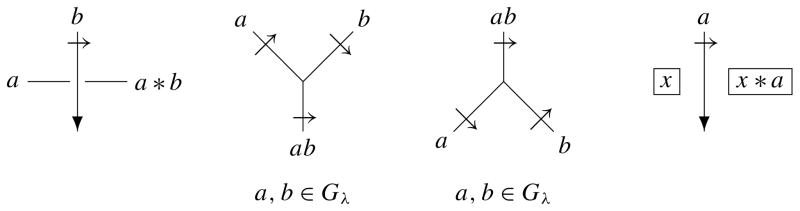
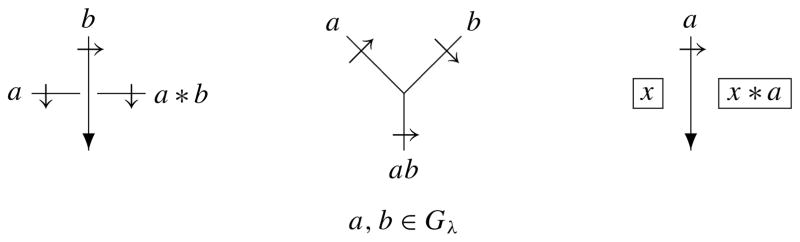
Let X = ∐_λ∈Λ G_λ be a multiple conjugation quandle, and let Y be an X-set. Let D be a diagram of an S¹-oriented handlebody-link H. We denote by 𝒜(D) the set of arcs of D, where an arc is a piece of a curve each of whose endpoints is an undercrossing or a vertex. We denote by ℛ(D) the set of complementary regions of D. In this paper, an orientation of an arc is represented by the normal orientation obtained by rotating the usual orientation counterclockwise by π/2 on the diagram. An X-coloring C of a diagram D is an assignment of an element of X to each arc α ∈ 𝒜(D) satisfying the conditions depicted in the left three diagrams in Figure 3 at each crossing and each vertex of D. An X_Y -coloring C of D is an extension of an X-coloring of D which assigns an element of Y to each region R ∈ ℛ(D) satisfying the condition depicted in the rightmost diagram in Figure 3 at each arc. We denote by Col_X (D) (resp. Col_X (D)_Y) the set of X-colorings (resp. X_Y -colorings) of D. Then we have the following proposition.

Figure 3.

Rules of a coloring.

Proposition 7 [Ishii 2015a]

Let X = ∐_λ∈Λ G_λ be a multiple conjugation quandle, and let Y be an X-set. Let D be a diagram of an S¹-oriented handlebody-link H. Let D′ be a diagram obtained by applying one of the Y-oriented R1–R6 moves to the diagram D once. For an X-coloring (resp. X_Y -coloring) C of D, there is a unique X-coloring (resp. X_Y -coloring) C′ of D′ which coincides with C except near a point where the move applied.

For an X_Y -coloring C of a diagram D of an S¹-oriented handlebody-link, we define the local chains w(ξ;C) ∈ C₂(X)_Y at each crossing ξ and each vertex ξ of D as depicted in Figure 4. We define a chain W(D;C) ∈ C₂(X)_Y by

Figure 4.

Local chains represented by crossings and vertices.

$$W(D;C)=\sum _{\xi }w(\xi ;C),$$

where ξ runs over all crossings and vertices of D. This is similar to the definitions found in [Carter et al. 2001] for links and surface-links, and in [Ishii and Iwakiri 2012] for handlebody-links.

Lemma 8

The chain W(D;C) is a 2-cycle of C_*(X)_Y. Further, for cohomologous 2-cocycles θ, θ′ of C^*(X; A)_Y, we have

$$\theta \left(W(D;C)\right)={\theta }^{\prime }\left(W(D;C)\right).$$

Proof

It is sufficient to show that W(D;C) is a 2-cycle of C_*(X)_Y. We denote by 𝒮𝒜(D) the set of semiarcs of D, where a semiarc is a piece of a curve each of whose endpoints is a crossing or a vertex. We denote by 𝒮𝒜(D; ξ) the set of semiarcs incident to ξ, where ξ is a crossing or a vertex of D.

For a semiarc α, there is a unique region R_α facing α such that the normal orientation of α points from the region R_α to the opposite region with respect to α. For a semiarc α incident to a crossing or a vertex ξ, we define

$$\epsilon (\alpha ;\xi ):=\{\begin{array}{ll}\hfill 1& \text{if}\text{the}\text{orientation}\text{of}\alpha \text{points}\text{to}\xi ,\hfill \\ \hfill -1& \text{otherwise.}\hfill \end{array}$$

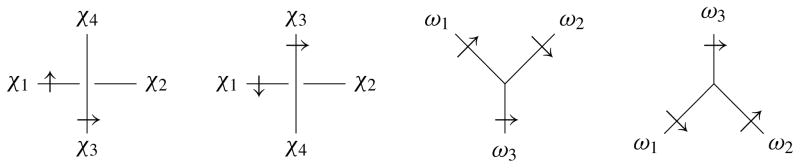
Let χ₁, …, χ₄ and ω₁, ω₂, ω₃ be the semiarcs incident to a crossing χ and a vertex ω as depicted in Figure 5. From

Figure 5.

Semiarcs near crossings and vertices.

$$\begin{array}{ll}{\partial }_2\left(w(\chi ;C)\right)\hfill & =\sum _{\alpha \in \mathcal{S}\mathcal{A}(D;\chi )}\epsilon (\alpha ;\chi )\langle C(R_{\alpha })\rangle \langle C(\alpha )\rangle ,\hfill \\ {\partial }_2\left(w(\omega ;C)\right)\hfill & =\sum _{\alpha \in \mathcal{S}\mathcal{A}(D;\omega )}\epsilon (\alpha ;\omega )\langle C(R_{\alpha })\rangle \langle C(\alpha )\rangle ,\hfill \end{array}$$

it follows that

$${\partial }_2\left(W(D;C)\right)=\sum _{\chi }{\partial }_2\left(w(\chi ;C)\right)+\sum _{\omega }{\partial }_2\left(w(\omega ;C)\right)=0,$$

where χ and ω, respectively, run over all crossings and vertices of D.

Lemma 9

Let D be a diagram of an S¹-oriented handlebody-link H. Let D′ be a diagram obtained by applying one of the Y-oriented R1–R6 moves to the diagram D once. Let C be an X_Y -coloring of D, let C′ be the unique X_Y -coloring of D′ such that C and C′ coincide except near a point where the move applied. Then we have [W(D;C)] = [W(D′;C′)] in H₂(X)_Y.

Proof

We have the invariance under the Y-oriented R1 and R4 moves, since the difference between [W(D;C)] and [W(D′;C′)] is an element of D₂(X)_Y. The invariance under the Y-oriented R2 move follows from the signs of the crossings which appear in the move. We have the invariance under the Y-oriented R3, R5, and R6 moves, since the difference between [W(D;C)] and [W(D′;C′)] is an image of ∂₃. See Figure 6 for Y-oriented R6 moves, where all arcs are directed from top to bottom.

Figure 6.

Chains for Y-oriented R6 moves.

For a 2-cocycle θ of C^*(X; A)_Y, we define

$$\begin{array}{ll}\hfill \mathcal{H}(D)& :=\{[W(D;C)]\in H_2{(X)}_Y\mid C\in {\text{Col}}_X{(D)}_Y\},\hfill \\ \hfill {\mathrm{\Phi }}_{\theta }(D)& :=\{\theta (W(D,C))\in A\mid C\in {\text{Col}}_X{(D)}_Y\}\hfill \end{array}$$

as multisets. By Lemmas 8 and 9, we have the following theorem.

Theorem 10

Let D be a diagram of an S¹-oriented handlebody-link H. Then ℋ(D) and Φ_θ (D) are invariants of H.

For an S¹-oriented handlebody-link H, let H^* be the mirror image of H, and −H be the S¹-oriented handlebody-link obtained from H by reversing its S¹-orientation. Then we also have

$$\mathcal{H}(-H^{\ast })=-\mathcal{H}(H),{\mathrm{\Phi }}_{\theta }(-H^{\ast })=-{\mathrm{\Phi }}_{\theta }(H),$$

where −S = {−a | a ∈ S} for a multiset S. It is desirable to further study these invariants and applications to handlebody-links.

6. For unoriented handlebody-links

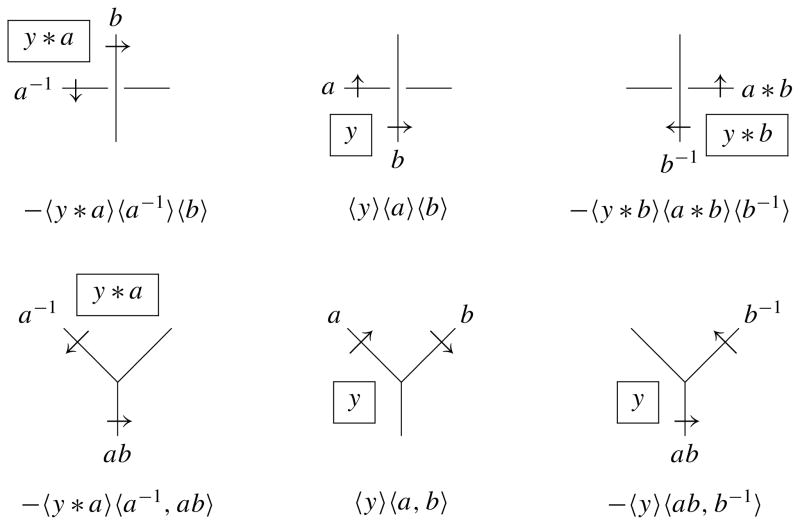
Let X =∐_λ∈Λ G_λ be a multiple conjugation quandle, and let Y be an X-set. Let D be a diagram of an (unoriented) handlebody-link H. An (X, ↑)-color C_α of an arc α ∈ 𝒜(D) is a map C_α from the set of orientations of the arc α to X such that C_α(−o) = C_α(o)⁻¹, where −o is the inverse of an orientation o. An (X, ↑)-color C_α is represented by a pair of an orientation o of α and an element C_α(o) ∈ X on the diagram D. Two pairs (o, a) and (−o, a⁻¹) represent the same (X, ↑)-color (see Figure 7).

Figure 7.

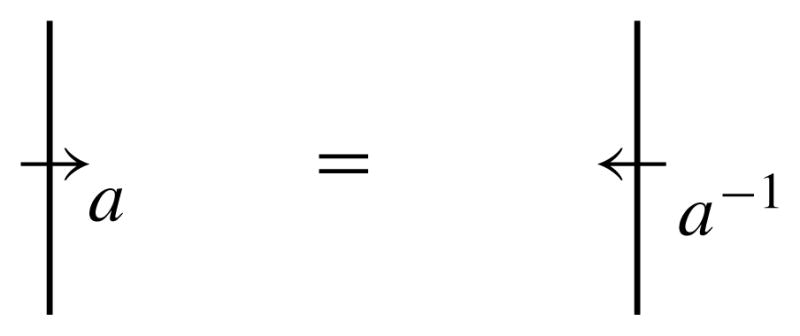
(X, ↑)-color.

An (X, ↑)-coloring C of a diagram D is an assignment of an (X, ↑)-color C_α to each arc α ∈ 𝒜(D) satisfying the conditions depicted in the left two diagrams in Figure 8 at each crossing and each vertex of D. An (X, ↑)_Y -coloring C of D is an extension of an (X, ↑)-coloring of D which assigns an element of Y to each region R ∈ ℛ(D) satisfying the condition depicted in the rightmost diagram in Figure 8 at each arc. We denote by Col_(X,↑)(D) (resp. Col_(X,↑)(D)_Y the set of (X, ↑)-colorings (resp. (X, ↑)_Y -colorings) of D. The well-definedness of an (X, ↑)-coloring (resp. (X, ↑)_Y -coloring) follows from

Figure 8.

Rules of an unoriented coloring.

$$\begin{array}{lll}{(a^{-1})}^{-1}=a,\hfill & a^{-1}\ast b={(a\ast b)}^{-1},\hfill & (a\ast b)\ast b^{-1}=a,\hfill \\ b{(ab)}^{-1}=a^{-1},\hfill & {(ab)}^{-1}a=b^{-1}.\hfill & \hfill \end{array}$$

The first three equalities are the defining conditions of a good involution considered in [Kamada 2007; Kamada and Oshiro 2010]. They used the notion of a good involution precisely to allow for appropriate changes of orientations. Following their arguments, we can show the following proposition in the same way as Proposition 7.

Proposition 11

Let X =∐_λ∈Λ G_λ be a multiple conjugation quandle, and let Y be an X-set. Let D be a diagram of a handlebody-link H. Let D′ be a diagram obtained by applying one of the R1–R6 moves to the diagram D once. For an (X, ↑)-coloring (resp. (X, ↑)_Y -coloring) C of D, there is a unique (X, ↑)-coloring (resp. (X, ↑)_Y -coloring) C′ of D′ which coincides with C except near a point where the move applied.

Let $D_n^{\uparrow }{(X)}_Y$ be the subgroup of P_n(X)_Y generated by the elements of the form

$$\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle \mathit{a}\rangle \cdots \langle {\mathit{a}}_k\rangle +\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots {\langle \mathit{a}\rangle }_i^{-1}\cdots \langle {\mathit{a}}_k\rangle ,$$

where ${\langle a_1,\dots ,a_m\rangle }_i^{-1}$ denotes

$$\{\begin{array}{ll}\ast a_1\langle a_1^{-1},a_1{a}_2,a_3,\dots ,a_m\rangle \hfill & \text{if}i=1,\hfill \\ \langle a_1,\dots ,a_{i-2},a_{i-1}{a}_i,a_i^{-1},a_i{a}_{i+1},a_{i+2},\dots ,a_m\rangle \hfill & \text{if}i\ne 1,m,\hfill \\ \langle a_1,\dots ,a_{m-2},a_{m-1}{a}_m,a_m^{-1}\rangle \hfill & \text{if}i=m.\hfill \end{array}$$

The chain group $D_n^{\uparrow }{(X)}_Y$ will be called the group of orientation degeneracies. For example, $D_1^{\uparrow }{(X)}_Y$ is generated by the elements of the form

$$\langle y\rangle \langle a\rangle +\langle y\ast a\rangle \langle a^{-1}\rangle ,$$

and $D_2^{\uparrow }{(X)}_Y$ is generated by the elements of the form

$$\begin{array}{ll}\langle y\rangle \langle a\rangle \langle b\rangle +\langle y\ast a\rangle \langle a^{-1}\rangle \langle b\rangle ,\hfill & \langle y\rangle \langle a\rangle \langle b\rangle +\langle y\ast b\rangle \langle a\ast b\rangle \langle b^{-1}\rangle ,\hfill \\ \langle y\rangle \langle a,b\rangle +\langle y\ast a\rangle \langle a^{-1},ab\rangle ,\hfill & \langle y\rangle \langle a,b\rangle +\langle y\rangle \langle ab,b^{-1}\rangle .\hfill \end{array}$$

We remark that the elements of the form

$$\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle a_1,\dots ,a_m\rangle \cdots \langle {\mathit{a}}_k\rangle -{(-1)}^{m(m+1)/2}\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \ast (a_1\cdots a_m)\langle a_m^{-1},\dots ,a_1^{-1}\rangle \cdots \langle {\mathit{a}}_k\rangle$$

belong to $D_n^{\uparrow }{(X)}_Y$. Furthermore, we can prove that the elements of the form

$$\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \langle a_1,\dots ,a_m\rangle \cdots \langle {\mathit{a}}_k\rangle -{(-1)}^{i(i+1)/2}\langle y\rangle \langle {\mathit{a}}_1\rangle \cdots \ast (a_1\cdots a_i)\langle a_i^{-1},\dots ,a_1^{-1},a_1\cdots a_{i+1},a_{i+2},\dots ,a_m\rangle \cdots \langle {\mathit{a}}_k\rangle$$

belong to $D_n^{\uparrow }{(X)}_Y$ by induction.

Lemma 12

$D_{\ast }^{\uparrow }{(X)}_Y=(D_n^{\uparrow }{(X)}_Y,{\partial }_n)$ is a subcomplex of P_*(X)_Y.

Proof

We have ${\partial }_n(D_n^{\uparrow }{(X)}_Y)\subset D_{n-1}^{\uparrow }{(X)}_Y$, since

$$\begin{array}{l}\partial (\langle a_1,\dots ,a_m\rangle +\ast a_1\langle a_1^{-1},a_1{a}_2,a_3,\dots ,a_m\rangle )\\ =\langle a_1,a_2{a}_3,a_4,\dots ,a_m\rangle +\ast a_1\langle a_1^{-1},a_1{a}_2{a}_3,a_4,\dots ,a_m\rangle \\ +\sum _{i=3}^{m-1}{(-1)}^i\left(\langle a_1,\dots ,a_i{a}_{i+1},a_{i+2},\dots ,a_m\rangle +\ast a_1\langle a_1^{-1},a_1{a}_2,a_2,\dots ,a_i{a}_{i+1},a_{i+2},\dots ,a_m\rangle \right)\\ +{(-1)}^m(\langle a_1,\dots ,a_{m-1}\rangle +\ast a_1\langle a_1^{-1},a_1{a}_2,a_3,\dots ,a_{m-1}\rangle )\end{array}$$

and

$$\begin{array}{l}\partial (\langle a_1,\dots ,a_m\rangle +\langle a_1,\dots ,a_{i-1}{a}_i,a_i^{-1},a_i{a}_{i+1},a_{i+2},\dots ,a_m\rangle )\\ =\ast a_1\langle a_2,\dots ,a_m\rangle +\ast a_1\langle a_2,\dots ,a_{i-1}{a}_i,a_i^{-1},a_i{a}_{i+1},a_{i+2},\dots ,a_m\rangle \\ +\sum _{j=1}^{i-2}{(-1)}^j\left(\langle a_1,\dots ,a_j{a}_{j+1},a_{j+2},\dots ,a_m\rangle +\langle a_1,\dots ,a_j{a}_{j+1},a_{j+2},\dots ,a_{i-1}{a}_i,a_i^{-1},a_i{a}_{i+1},a_{i+2},\dots ,a_m\rangle \right)\\ +\sum _{j=i+1}^{m-1}{(-1)}^j\left(\langle a_1,\dots ,a_j{a}_{j+1},a_{j+2},\dots ,a_m\rangle +\langle a_1,\dots ,a_{i-1}{a}_i,a_i^{-1},a_i{a}_{i+1},a_{i+2},\dots ,a_j{a}_{j+1},\dots ,a_m\rangle \right)\\ +{(-1)}^m(\langle a_1,\dots ,a_{m-1}\rangle +\langle a_1,\dots ,a_{i-1}{a}_i,a_i^{-1},a_i{a}_{i+1},a_{i+2},\dots ,a_{m-1}\rangle ).\end{array}$$

Thus $D_{\ast }^{\uparrow }{(X)}_Y$ is a subcomplex of P_*(X)_Y.

Definition 13

We set $C_n^{\uparrow }{(X)}_Y=P_n{(X)}_Y/(D_n{(X)}_Y+D_n^{\uparrow }{(X)}_Y)$. The quotient complex ( $C_n^{\uparrow }{(X)}_Y$, ∂_n) is denoted by $C_{\ast }^{\uparrow }{(X)}_Y$. For an abelian group A, we define the cochain complex $C_{\uparrow }^{\ast }{(X;A)}_Y=\text{Hom}(C_{\ast }^{\uparrow }{(X)}_Y,A)$. We denote by $H_n^{\uparrow }{(X)}_Y$ the n-th homology group of $C_{\ast }^{\uparrow }{(X)}_Y$.

For an (X, ↑)_Y -coloring C of a diagram D for a handlebody-link, we define the local chains w(ξ;C) at each crossing ξ and each vertex ξ of D as depicted in Figure 4. The local chain is well-defined, since

$$\begin{array}{ll}\hfill -\langle y\ast a\rangle \langle a^{-1}\rangle \langle b\rangle & =\langle y\rangle \langle a\rangle \langle b\rangle =-\langle y\ast b\rangle \langle a\ast b\rangle \langle b^{-1}\rangle ,\hfill \\ \hfill -\langle y\ast a\rangle \langle a^{-1},ab\rangle & =\langle y\rangle \langle a,b\rangle =-\langle y\rangle \langle ab,b^{-1}\rangle \hfill \end{array}$$

in $C_2^{\uparrow }{(X)}_Y$ (see Figure 9). Then we can define the chain $W(D;C)\in C_2^{\uparrow }{(X)}_Y$ in the same way as W(D;C) ∈ C₂(X)_Y, and obtain invariants ℋ(H), Φ_θ (H) for an (unoriented) handlebody-link H.

Figure 9.

Well-definedness of local chains for unoriented handle-body-links.

7. Simplicial decomposition

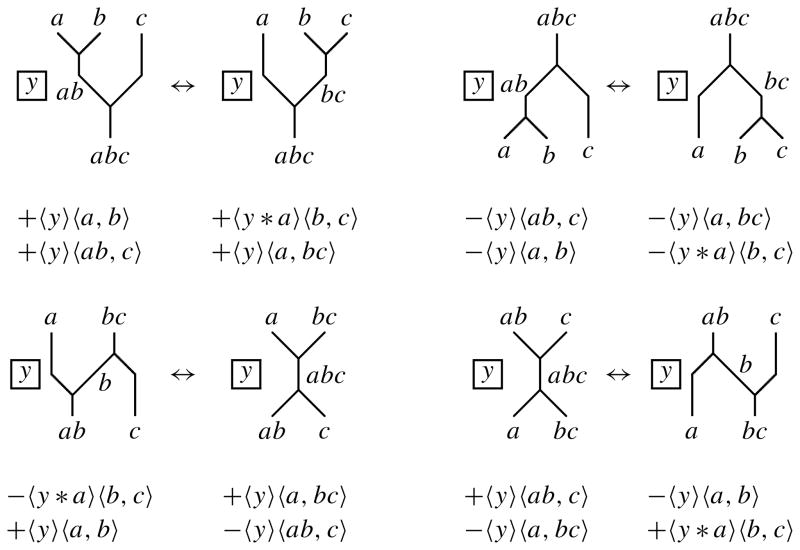
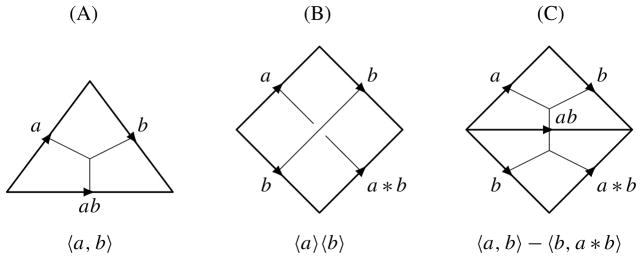
The goal of this section is to prove Lemma 15 stating that D_*(X)_Y is a subcomplex. The formula of D₂(X)_Y, when 〈y〉 is omitted, is written as

$$\langle a\rangle \langle b\rangle -\langle a,b\rangle +\langle b,a\ast b\rangle ,$$

and its geometric interpretation is depicted in Figure 10. In (A), a colored triangle representing 〈a, b〉 is depicted, as well as its dual graph with a trivalent vertex. The colorings of such a graph were discussed in Section 5. A colored square representing 〈a〉 〈b〉 is depicted in (B), with the dual graph that corresponds to a crossing. In (C), a triangulation of the square is depicted, and after triangulation it represents 〈a, b〉 – 〈b, a * b〉. Thus the triangulation corresponds to the above formula. This decomposition is found in [Carter et al. 2003].

Figure 10.

Dividing a square into triangles.

At the same time, this equation corresponds to Y-oriented R4 moves in Figure 1 as follows. In Figure 11, colored diagrams of Y-oriented R4 moves are depicted. In the left diagram, the left-hand side represents the chain 〈a〉 〈b〉+ 〈b, a * b〉 and the right-hand side represents 〈a, b〉. In the right diagram, the left-hand side represents the chain −〈a〉 〈b〉 – 〈b, a * b〉 and the right-hand side represents –〈a, b〉. Thus the above equality is needed for colored diagrams to define equivalent chains in the quotient complex. A geometric interpretation of the last expression of D₃(X)_Y omitting 〈y〉,

Figure 11.

Colors for Y-oriented R4 moves.

$$\langle a\rangle \langle b,c\rangle -\langle a,b,c\rangle +\langle b,a\ast b,c\rangle -\langle b,c,a\ast (bc)\rangle$$

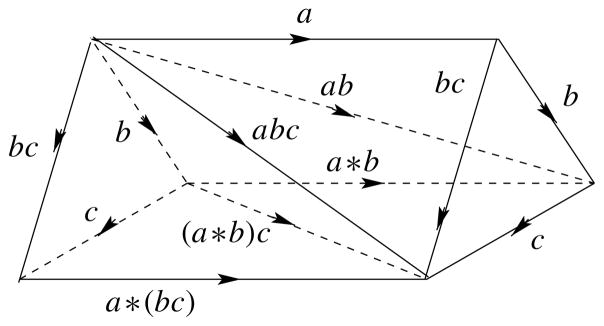
is found in Figure 12. The symbol 〈a〉 is represented by the horizontal 1-simplex, 〈b, c〉 is represented by the right triangular face, and 〈a〉 〈b, c〉 is represented by a prism. The term 〈a, b, c〉 corresponds to the right top tetrahedron in the prism. The expressions of the form 〈〈a〉 〈b, c〉〉_i provides a triangulation of a product of simplices. Each term corresponds to

Figure 12.

Decomposition of a prism into tetrahedra.

$$\begin{array}{ll}\hfill \langle a,b,c\rangle & ={\langle \langle a\rangle \langle b,c\rangle \rangle }_1,\hfill \\ \hfill \langle b,a\ast b,c\rangle & =-{\langle \langle a\rangle \langle b,c\rangle \rangle }_2,\hfill \\ \hfill \langle b,c,a\ast (bc)\rangle & ={\langle \langle a\rangle \langle b,c\rangle \rangle }_3.\hfill \end{array}$$

Below we use the notation

$$\begin{array}{ll}\hfill {\partial }_{(0)}\langle x_1,\dots ,x_m\rangle & =\ast x_1\langle x_2,\dots ,x_m\rangle ,\hfill \\ \hfill {\partial }_{(i)}\langle x_1,\dots ,x_m\rangle & ={(-1)}^i\langle x_1,\dots ,x_i{x}_{i+1},\dots ,x_m\rangle ,\hfill \\ \hfill {\partial }_{(m)}\langle x_1,\dots ,x_m\rangle & ={(-1)}^m\langle x_1,\dots ,x_{m-1}\rangle .\hfill \end{array}$$

Then the boundaries of 〈〈a〉 〈b, c〉〉_i are computed as

$${\langle \langle a\rangle ,\langle b,c\rangle \rangle }_i\stackrel{\partial }{\mapsto }{\partial }_{(0)}{\langle \langle a\rangle \langle b,c\rangle \rangle }_i+{\partial }_{(1)}{\langle \langle a\rangle \langle b,c\rangle \rangle }_i+{\partial }_{(2)}{\langle \langle a\rangle \langle b,c\rangle \rangle }_i+{\partial }_{(3)}{\langle \langle a\rangle \langle b,c\rangle \rangle }_i$$

and the right-hand sides for i = 1, 2, 3 are computed as follows:

$$\begin{array}{l}{\langle \langle a\rangle \langle b,c\rangle \rangle }_1\stackrel{\partial }{\mapsto }\ast a\langle b,c\rangle -\langle ab,c\rangle +\langle a,bc\rangle -\langle a,b\rangle \\ ={\langle ({\partial }_{(0)}\langle a\rangle )\langle b,c\rangle \rangle }_1+{\partial }_{(1)}{\langle \langle a\rangle \langle b,c\rangle \rangle }_1-{\langle \langle a\rangle {\partial }_{(1)}\langle b,c\rangle \rangle }_1-{\langle \langle a\rangle {\partial }_{(2)}\langle b,c\rangle \rangle }_1,\\ {\langle \langle a\rangle \langle b,c\rangle \rangle }_2\stackrel{\partial }{\mapsto }-\ast b\langle a\ast b,c\rangle +\langle b(a\ast b),c\rangle -\langle b,(a\ast b)c\rangle +\langle b,a\ast b\rangle \\ =-{\langle \langle a\rangle {\partial }_{(0)}\langle b,c\rangle \rangle }_1-{\partial }_{(1)}{\langle \langle a\rangle \langle b,c\rangle \rangle }_1-{\partial }_{(2)}{\langle \langle a\rangle \langle b,c\rangle \rangle }_3-{\langle \langle a\rangle {\partial }_{(2)}\langle b,c\rangle \rangle }_2,\\ {\langle \langle a\rangle \langle b,c\rangle \rangle }_3\stackrel{\partial }{\mapsto }\ast b\langle c,a\ast (bc)\rangle -\langle bc,a\ast (bc)\rangle +\langle b,c(a\ast (bc))\rangle -\langle b,c\rangle \\ =-{\langle \langle a\rangle {\partial }_{(0)}\langle b,c\rangle \rangle }_2-{\langle \langle a\rangle {\partial }_{(1)}\langle b,c\rangle \rangle }_2+{\partial }_{(2)}{\langle \langle a\rangle \langle b,c\rangle \rangle }_3+{\langle ({\partial }_{(1)}\langle a\rangle )\langle b,c\rangle \rangle }_1,\end{array}$$

where 〈(∂_(i)〈a〉) 〈b, c〉〉₁ is regarded as (∂_(i) 〈a〉)〈b, c〉. The canceling terms of the form ∂_(i) 〈〈a〉 〈b, c〉〉_j in the above boundaries correspond to internal triangles in Figure 12 that are shared by a pair of tetrahedra. Other terms are of the form 〈∂_(i) 〈a〉 〈b, c〉〉_j or 〈〈a〉∂_(i) 〈b, c〉〉_j, and they are outer triangles that constitute the boundary of the prism. The expression 〈∂_(i) 〈a〉 〈b, c〉〉_j represents the two triangles on the right and the left in Figure 12, since this represents

$$(\text{boundary}\text{of}\text{the}\text{interval}\text{represented}\text{by}\langle a\rangle )\times (\text{the}\text{triangle}\text{represented}\text{by}\langle b,c\rangle ).$$

Thus the outer boundary follows the pattern of Leibniz rule.

In terms of the coloring invariant of graphs, as in the case of the preceding relation for the Y-oriented R4 move, this relation corresponds to an equivalence of colored 2-complexes called foams, which are higher-dimensional analogues of the move depicted in Figure 11. See [Carter and Ishii 2012] for more on colored foams.

Lemma 14

For 〈a〉 = 〈a₁,…, a_s〉 and 〈b〉 = 〈b₁, …, b_t 〉 where a_i, b_j ∈ G_λ, we have

$$\partial \langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle =\langle (\partial \langle \mathit{a}\rangle )\langle \mathit{b}\rangle \rangle +{(-1)}^{\mid \mathit{a}\mid }\langle \langle \mathit{a}\rangle \langle \partial (\mathit{b})\rangle \rangle ,$$

where 〈〈·〉 〈 ·〉〉 is linearly extended.

Proof

By definition, we have

$$\partial \langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle =\sum _{i=0}^{s+t}{\partial }_{(i)}\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle =\sum _{i=0}^{s+t}\sum _{1\le i_1<\cdots <i_s\le s+t}{\partial }_{(i)}{\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_s}.$$

Direct computations show that

$$\begin{array}{l}{\partial }_{(0)}{\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_s}\\ =\{\begin{array}{ll}{\langle ({\partial }_{(0)}\langle \mathit{a}\rangle )\langle \mathit{b}\rangle \rangle }_{i_2-1,\dots ,i_s-1}\hfill & \text{if}(i_1=1),\hfill \\ {(-1)}^s{\langle \langle \mathit{a}\rangle ({\partial }_{(0)}\langle \mathit{b}\rangle )\rangle }_{i_1-1,\dots ,i_s-1}\hfill & \text{if}(i_1>1),\hfill \end{array}\\ {\partial }_{(i)}{\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_s}\\ =\{\begin{array}{ll}{\langle ({\partial }_{(k)}\langle \mathit{a}\rangle )\langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_k,i_{k+2}-1,\dots ,i_s-1}\hfill & \text{if}(i_k=i<i+1=i_{k+1}),\hfill \\ -{\partial }_{(i)}{\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_{k-1},i_k+1,i_{k+1},\dots i_s}\hfill & \text{if}(i_k=i<i+1<i_{k+1}),\hfill \\ -{\partial }_{(i)}{\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_k,i_{k+1}-1,i_{k+2},\dots ,i_s}\hfill & \text{if}(i_k<i<i+1=i_{k+1}),\hfill \\ {(-1)}^s{\langle \langle \mathit{a}\rangle ({\partial }_{(i-k)}\langle \mathit{b}\rangle )\rangle }_{i_1,\dots ,i_k,i_{k+1}-1,\dots ,i_s-1}\hfill & \text{if}(i_k<i<i+1<i_{k+1}),\hfill \end{array}\\ {\partial }_{(s+t)}{\langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_s}\\ =\{\begin{array}{ll}{\langle ({\partial }_{(s)}\langle \mathit{a}\rangle )\langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_{s-1}}\hfill & \text{if}(i_s=s+t),\hfill \\ {(-1)}^s{\langle \langle \mathit{a}\rangle ({\partial }_{(t)}\langle \mathit{b}\rangle )\rangle }_{i_1,\dots ,i_s}\hfill & \text{if}(i_s<s+t).\hfill \end{array}\end{array}$$

The terms of the form − ∂_(i) 〈〈a〉 〈b〉〉_{i₁,…,i_k–1,i_k+1,i_k+1,…,i_s} (i_k = i < i +1 < i_k+1) and −∂_(i) 〈〈a〉 〈b〉〉_{i₁,…,i_k,i_k+1–1,i_k+2,…,i_s} (i_k < i < i +1 = i_k+1) cancel in pairs. The other terms are organized as

$$\begin{array}{l}\sum _{\begin{array}{c}1\le i_1<\cdots \\ <i_{s-1}\le s+t-1\end{array}}\sum _{i=0}^s{\langle ({\partial }_{(i)}\langle \mathit{a}\rangle )\langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_{s-1}}+\sum _{\begin{array}{c}1\le i_1<\cdots \\ <i_s\le s+t-1\end{array}}\sum _{i=0}^t{(-1)}^s{\langle \langle \mathit{a}\rangle ({\partial }_{(i)}\langle \mathit{b}\rangle )\rangle }_{i_1,\dots ,i_s}\\ =\sum _{\begin{array}{c}1\le i_1<\cdots \\ <i_{s-1}\le s+t-1\end{array}}{\langle (\partial \langle \mathit{a}\rangle )\langle \mathit{b}\rangle \rangle }_{i_1,\dots ,i_{s-1}}+\sum _{\begin{array}{c}1\le i_1<\cdots \\ <i_s\le s+t-1\end{array}}{(-1)}^s{\langle \langle \mathit{a}\rangle (\partial \langle \mathit{b}\rangle )\rangle }_{i_1,\dots ,i_s}\\ =\langle (\partial \langle \mathit{a}\rangle )\langle \mathit{b}\rangle \rangle +{(-1)}^s\langle \langle \mathit{a}\rangle (a\langle \mathit{b}\rangle )\rangle ,\end{array}$$

where 〈·〉_{i₁,…,i_s} is linearly extended.

Since the Leibniz rule holds (by the preceding Lemma 14), we have the following.

Lemma 15

D_*(X)_Y = (D_n(X)_Y, ∂_n) is a subcomplex of P_*(X)_Y.

8. Chain map for simplicial decomposition

In this section we examine relations between group and MCQ homology theories.

8.1. Simplicial decomposition (general case)

We observe an associativity of the notation 〈〈a〉 〈b〉〉 defined in Section 3, and extend the notation to multi-tuples. For an expression of the form 〈a〉 〈b〉 〈c〉 in a chain in P_*(X)_Y, where $\mathit{a},\mathit{b},\mathit{c}\in {\cup }_{m\in \mathbb{N}}{G}_{\mathrm{\lambda }}^m$, it is easy to see that we have the following.

Lemma 16

$$\langle \langle \langle \mathit{a}\rangle \langle \mathit{b}\rangle \rangle \langle \mathit{c}\rangle \rangle =\langle \langle \mathit{a}\rangle \langle \langle \mathit{b}\rangle \langle \mathit{c}\rangle \rangle \rangle .$$

By Lemma 16, we can define 〈〈a〉 〈b〉 〈c〉〉 by 〈〈〈a〉 〈b〉〉 〈c〉〉 = 〈〈a〉 〈〈b〉 〈c〉〉〉. Moreover, for an expression of the form 〈a₁〉 ··· 〈a_k〉 in a chain in P_*(X)_Y, where ${\mathit{a}}_1,\dots ,{\mathit{a}}_k\in {\cup }_{m\in \mathbb{N}}{G}_{\mathrm{\lambda }}^m$, we can define 〈〈a₁〉 ··· 〈a_k〉〉 inductively. By Lemma 14, this notation is compatible with the boundary homomorphism ∂ in the following sense.

Lemma 17

$$\partial \langle \langle {\mathit{a}}_1\rangle \cdots \langle {\mathit{a}}_k\rangle \rangle =\langle \partial (\langle {\mathit{a}}_1\rangle \cdots \langle {\mathit{a}}_k\rangle )\rangle .$$

We give a direct formula (instead of induction) for the notation 〈〈a₁〉 ··· 〈a_k〉〉 later in Section 8.3.

8.2. Chain map (from MCQ to group)

Let X = ∐_λ∈Λ G_λ be a multiple conjugation quandle, and let Y be an X-set. Let $P_n^G{(X)}_Y$ be the subgroup of P_n(X)_Y generated by the elements of the form 〈y〉 〈a〉. Let $D_n^G{(X)}_Y$ and $D_n^{G,\uparrow }{(X)}_Y$ be respectively $P_n^G{(X)}_Y\cap D_n{(X)}_Y$ and $P_n^G{(X)}_Y\cap D_n^{\uparrow }{(X)}_Y$, which are the subgroups of $P_n^G{(X)}_Y$. Note that $D_n^G{(X)}_Y=P_n^G{(X)}_Y\cap D_n{(X)}_Y$ is the trivial group. We put

$$\begin{array}{ll}\hfill C_n^G{(X)}_Y& :=P_n^G{(X)}_Y/D_n^G{(X)}_Y=P_n^G{(X)}_Y,\hfill \\ \hfill C_n^{G,\uparrow }{(X)}_Y& :=P_n^G{(X)}_Y/(D_n^G{(X)}_Y+D_n^{G,\uparrow }{(X)}_Y)=P_n^G{(X)}_Y/D_n^{G,\uparrow }{(X)}_Y.\hfill \end{array}$$

Then $C_{\ast }^G{(X)}_Y=(C_n^G{(X)}_Y,{\partial }_n)$ and $C_{\ast }^{G,\uparrow }{(X)}_Y=(C_n^{G,\uparrow }{(X)}_Y,{\partial }_n)$ are chain complexes. If X is a group (regarded as X =∐_λ∈Λ G_λ with Λ a singleton) and Y is a singleton, $C_{\ast }^G{(X)}_Y$ is essentially the same as the chain complex of the usual group homology. For an abelian group A, we define the cochain complexes

$$C_G^{\ast }{(X;A)}_Y=\text{Hom}(C_{\ast }^G{(X)}_Y,A)\text{and}{C}_{G,\uparrow }^{\ast }{(X;A)}_Y=\text{Hom}(C_{\ast }^{G,\uparrow }{(X)}_Y,A).$$

When X is a multiple conjugation quandle consisting of a single group, define homomorphisms $\mathrm{\Delta }:P_{\ast }{(X)}_Y\to P_{\ast }^G{(X)}_Y$ by

$$\mathrm{\Delta }(\langle {\mathit{a}}_1\rangle \cdots \langle {\mathit{a}}_m\rangle ):=\langle \langle {\mathit{a}}_1\rangle \cdots \langle {\mathit{a}}_m\rangle \rangle .$$

Then by Lemma 17 and from these definitions, we have the following.

Proposition 18

The homomorphisms $\mathrm{\Delta }:P_{\ast }{(X)}_Y\to P_{\ast }^G{(X)}_Y$ give rise to a chain homomorphism. Furthermore, Δ induces the chain homomorphisms $\mathrm{\Delta }:C_{\ast }{(X)}_Y\to C_{\ast }^G{(X)}_Y$ and $\mathrm{\Delta }:C_{\ast }^{\uparrow }{(X)}_Y\to C_{\ast }^{G,\uparrow }{(X)}_Y$.

When n = 0, 1, the induced homomorphisms $\mathrm{\Delta }:C_n{(X)}_Y\to C_n^G{(X)}_Y$ and $\mathrm{\Delta }:C_n^{\uparrow }{(X)}_Y\to C_n^{G,\uparrow }{(X)}_Y$ are identities. Furthermore $H_n{(X)}_Y\cong H_n^G{(X)}_Y$ and $H_n^{\uparrow }{(X)}_Y\cong H_n^{G,\uparrow }{(X)}_Y$ for n = 0, 1. We note that the chain homomorphisms Δ are defined only for an MCQ consisting of a single group. In this case, we also have the cochain homomorphisms $\mathrm{\Delta }:C_G^{\ast }{(X;A)}_Y\to C^{\ast }{(X;A)}_Y$ and $\mathrm{\Delta }:C_{G,\uparrow }^{\ast }{(X;A)}_Y\to C_{\uparrow }^{\ast }{(X;A)}_Y$ for an abelian group A. Hence, for a given cocycle of group homology theory, we can obtain that of our theory through Δ. This approach will be discussed in Section 10.

Remark 19

We point out here that for a group X = ℤ₃ and a trivial X-set Y, there is a group 2-cocycle η that satisfies the conditions in $C_{G,\uparrow }^2{(X)}_Y$ (coming from $D_n^{G,\uparrow }{(X)}_Y$),

$$\eta \langle a,b\rangle +\eta \langle a^{-1},ab\rangle =0\text{and}\eta \langle a,b\rangle +\eta \langle ab,b^{-1}\rangle =0.$$

Specifically, let η : ℤ₃ ×ℤ₃→ℤ₃ denote the function that has values η(1, 1) = 1, η(2, 2) = 2 and η(g, h) = 0 otherwise. It is a direct calculation that the condition above is satisfied. Furthermore, to see that η is a cocycle, consider the generating cocycle over G = ℤ_p where p is a prime that is defined by

$${\eta }_0(x,y)=(1/p)(\overline{x}+\overline{y}-\overline{x+y})(modp),$$

where x̄ is an integer 0 ≤ x̄ < p such that x̄ = x (mod p). It is known that η₀ is a generating 2-cocycle for $H_G^2({\mathbb{Z}}_p;{\mathbb{Z}}_p)$ for prime p. For p = 3, let ζ be a 1-chain defined by ζ(0) = 0 and ζ(1)+ζ(2) = 2. Then one can easily compute that η = η₀ +δζ. Hence there is a 2-cocycle $\eta \in C_{G,\uparrow }^2{(X)}_Y$ of our theory that is cohomologous to the standard group 2-cocycle η₀.

8.3. Simplicial decomposition (direct formula)

We give a direct formula (instead of induction) for the notation 〈〈a₁〉 ··· 〈a_k〉〉. To the term 〈〈a〉 〈b〉〉_{i₁,…,i_s}, we associate a vector v = (v₁, …, v_n) ∈ {1, 2}ⁿ by defining v_i = 1 if i = i_j for some j, and otherwise v_i = 2, where n = s +t. In the term

$$c_i=\{\begin{array}{ll}{a}_k\ast (b_1\cdots b_{i-k})\hfill & \text{if}i=i_k,\hfill \\ b_{i-k}\hfill & \text{if}{i}_k<i<i_{k+1},\hfill \end{array}$$

the first entry with a_k in it corresponds to v_i = 1 and the second with b_i–k to v_i = 2. We note that the term a_k came from the first part 〈a〉 in 〈〈a〉 〈b〉〉_{i₁,…,i_s} so that v_i = 1 is assigned, and the term b_i–k belongs to the second part 〈b〉 receiving v_i = 2.

Example 20

For the term 〈a〉 〈b, c〉 discussed for Figure 12, the terms 〈a, b, c〉, –〈b, a * b, c〉, and 〈b, c, a * (bc)〉 correspond to the vectors (1, 2, 2), (2, 1, 2), and (2, 2, 1), respectively. Note that (2, 1, 2) is obtained from (1, 2, 2) by a transposition of the first two entries, and this is reflected in Figure 12 by the fact that the tetrahedra represented by these vectors share a triangular internal face. We indicate by an edge between two vectors when one is obtained from the other by a transposition of consecutive entries. In this case we draw the graph:

$$(1,2,2)—(2,1,2)—(2,2,1).$$

For 〈a, b〉 〈c, d〉, the terms 〈〈a〉 〈b〉〉_{i₁,…,i_s} are listed as 〈a, b, c, d〉, –〈a, c, b*c, d〉, 〈c, a*c, b*c, d〉, 〈a, c, d, b*(cd)〉, –〈c, a*c, d, b*(cd)〉, 〈c, d, a*(cd), b*(cd)〉, and these correspond to vectors

$$(1,1,2,2),(1,2,1,2),(2,1,1,2),(1,2,2,1),(2,1,2,1),(2,2,1,1),$$

respectively. They are connected by edges as

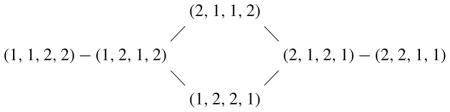
indicating which simplices share internal faces. Note that from a vector v = (v₁, …, v_n) ∈ {1, 2}ⁿ the subscripts i₁, …, i_s in 〈〈a〉 〈b〉〉_{i₁,…,i_s} are recovered by the condition v_{i _j} = 1.

For an expression of the form 〈a₁〉 ··· 〈a_k〉 in a chain in P_*(X)_Y, where

$${\mathit{a}}_1,\dots ,{\mathit{a}}_k\in \underset{m\in \mathbb{N}}{\cup }{G}_{\mathrm{\lambda }}^m,$$

we put n = |a₁| + ··· + |a_k| and consider vectors v = (v₁, …, v_n) ∈ {1, …, k}ⁿ, and denote by ${\#}_j^i\mathit{v}$ the number of j’s in v₁, …, v_i. Then for a given v define i( j, 1) < ··· < i( j, n_j) by the condition that v_i(j,1) =···=v_{i(j,n_j)} = j.

With these notations in hand, we temporarily define 〈〈a₁〉 ··· 〈a_k〉〉′ by

$$\sum _{\begin{array}{c}\mathit{v}\in {\{1,\dots ,k\}}^n\\ {\#}_j^n\mathit{v}=n_j(j=1,\dots ,k)\end{array}}{(-1)}^{{\sum }_{j=1}^{k-1}{\sum }_{t=1}^{n_j}(i(j,t)-t-{\sum }_{s=1}^{j-1}{n}_s)}\langle c_1,\dots ,c_n\rangle$$

for 〈a₁〉 ··· 〈a_k〉 = 〈a_1,1, …, a_1,n₁〉 ··· 〈a_k,1, …, a_{k,n_k}〉, where

$$c_i=a_{v_i,{\#}_{v_i}^i\mathit{v}}\ast \prod _{s=v_i+1}^k\prod _{t=1}^{{\#}_s^i\mathit{v}}{a}_{s,t}.$$

Then we have 〈〈a₁〉 ··· 〈a_k〉〉′ = 〈〈a₁〉 ··· 〈a_k〉〉, from the fact that simplices of both sides are in one-to-one correspondence with vectors v = (v₁, …, v_n) ∈ {1, …, k}ⁿ, and the signs correspond to the number of transpositions, modulo 2, of a given vector v from the vector (1, …, 1, 2, …, 2, …, k, …, k).

Example 21

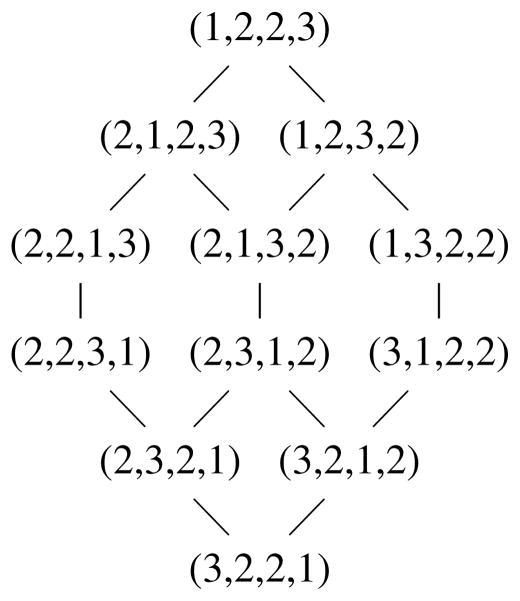
The terms of 〈〈a〉 〈b, c〉 〈d〉〉 consist of

$$\begin{array}{lll}\langle a,b,c,d\rangle ,\hfill & \langle b,a\ast b,c,d\rangle ,\hfill & \langle a,b,d,c\ast d\rangle ,\hfill \\ \langle b,c,a\ast (bc),d\rangle ,\hfill & \langle b,a\ast b,d,c\ast d\rangle ,\hfill & \langle a,d,b\ast d,c\ast d\rangle ,\hfill \\ \langle b,c,d,a\ast (\mathit{bcd})\rangle ,\hfill & \langle b,d,a\ast (bd),c\ast d\rangle ,\hfill & \langle d,a\ast d,b\ast d,c\ast d\rangle ,\hfill \\ \langle b,d,c\ast d,a\ast (\mathit{bcd})\rangle ,\hfill & \langle d,b\ast d,a\ast (bd),c\ast d\rangle ,\hfill & \langle d,b\ast d,c\ast d,a\ast (\mathit{bcd})\rangle ,\hfill \end{array}$$

which, respectively, correspond to the vectors

$$\begin{array}{lll}(1,2,2,3),\hfill & (2,1,2,3),\hfill & (1,2,3,2),\hfill \\ (2,2,1,3),\hfill & (2,1,3,2),\hfill & (1,3,2,2),\hfill \\ (2,2,3,1),\hfill & (2,3,1,2),\hfill & (3,1,2,2),\hfill \\ (2,3,2,1),\hfill & (3,2,1,2),\hfill & (3,2,2,1).\hfill \end{array}$$

The graph representing shared faces is depicted in Figure 13.

Figure 13.

Boundaries of 〈a〉 〈b, c〉 〈d〉.

9. Relationship between MCQ and IIJO

Let X = ∐_λ∈Λ G_λ be a multiple conjugation quandle, and let Y be an X-set. Let $P_n^{\text{IIJO}}{(X)}_Y$ be the subgroups of P_n(X)_Y generated by the elements of the form 〈y〉 〈a₁〉 ··· 〈a_n〉. Then $P_{\ast }^{\text{IIJO}}{(X)}_Y=(P_n^{\text{IIJO}}{(X)}_Y,{\partial }_n)$ is a subcomplex of P_*(X)_Y. Let $D_n^{\text{IIJO}}{(X)}_Y$ be the subgroup of $P_n^{\text{IIJO}}{(X)}_Y$ generated by the elements of the forms

$$\langle y\rangle \langle a_1\rangle \cdots \langle b_1\rangle \langle b_2\rangle \cdots \langle a_n\rangle ,\langle y\rangle \langle a_1\rangle \cdots \partial \langle b_1,b_2\rangle \cdots \langle a_n\rangle$$

for a₁, …, a_n ∈ X and b₁, b₂ ∈ G_λ. We note that the former elements relate to the invariance under the R1 and R4 move, and that the latter elements relate to the invariance under the R5 move and reversing orientation.

Lemma 22

$D_{\ast }^{\mathit{IIJO}}{(X)}_Y=(D_n^{\mathit{IIJO}}{(X)}_Y,{\partial }_n)$ is a subcomplex of $P_{\ast }^{\mathit{IIJO}}{(X)}_Y$.

Proof

This follows from

$$\partial (\langle b_1\rangle \langle b_2\rangle )=\partial \langle b_1,b_2\rangle -\partial \langle b_2,b_1\ast b_2\rangle ,\partial (\partial \langle b_1,b_2\rangle )=0$$

for b₁, b₂ ∈ G_λ.

We put

$$C_n^{\text{IIJO}}{(X)}_Y=P_n^{\text{IIJO}}{(X)}_Y/D_n^{\text{IIJO}}{(X)}_Y.$$

Then $C_{\ast }^{\text{IIJO}}{(X)}_Y=(C_n^{\text{IIJO}}{(X)}_Y,{\partial }_n)$ is a chain complex. If X is obtained from a G-family of quandles as in Example 2, $C_{\ast }^{\text{IIJO}}{(X)}_Y$ is the chain complex defined in [Ishii et al. 2013]. For an abelian group A, we define the cochain complexes

$$C_{\text{IIJO}}^{\ast }{(X;A)}_Y=\text{Hom}(C_{\ast }^{\text{IIJO}}{(X)}_Y,A).$$

We note that a natural projection ${\text{pr}}_{\ast }:P_{\ast }{(X)}_Y\to P_{\ast }^{\text{IIJO}}{(X)}_Y$ does not induce a chain homomorphism ${\text{pr}}_{\ast }:C_{\ast }{(X)}_Y\to C_{\ast }^{\text{IIJO}}{(X)}_Y$, since IIJO homology theory is invariant under the invariance for reversing orientations. (See Table 1.) It is seen, however, that this map induces the chain homomorphism ${\text{pr}}_{\ast }:C_{\ast }^{\uparrow }{(X)}_Y\to C_{\ast }^{\text{IIJO}}{(X)}_Y$ and the cochain homomorphism ${\text{pr}}^{\ast }:C_{\text{IIJO}}^{\ast }{(X;A)}_Y\to C_{\uparrow }^{\ast }{(X;A)}_Y$ for an abelian group A. Hence, for a given cocycle of IIJO homology theory (with some modification for a multiple conjugation quandle as above), we can obtain that of our theory through pr^*. This implies that our invariant is a generalization of the IIJO quandle cocycle invariant.

Table 1.

Comparison between IIJO theory and MCQ theory

IIJO	2-boundary	degenerate $D_2^{\text{IIJO}}{(X)}_Y$	cancelled by sign	zero by definition
moves	R3	R4(⇝ R1), R5(⇝ ori.)	R2	R6

MCQ	2-boundary	degenerate D2(X)Y	degenerate $D_2^{\uparrow }{(X)}_Y$	cancelled by sign
moves	R3, R5, R6	R4(⇝ R1)	orientation	R2

10. Towards finding 2-cocycles

We discuss approaches to finding 2-cocycles that are not induced from the IIJO (co)homology theory. Let G be a group, M a right G-module, and A an abelian group. The module M and the set X = M×G (= ∐_x∈M{x}×G) can be considered as a G-family of quandles and a multiple conjugation quandle as in Example 2, respectively.

We take an X-set Y as a singleton {y₀} and suppress the notation 〈y₀〉. For a 2-cocycle ψ ∈ P²(X; A)_Y, we denote ψ(〈(x, g)〉 〈(y, h)〉) by ϕ((x, g), (y, h)), and ψ(〈(x, g), (x, h)〉) by η_x(g, h). Then the 2-cocycle conditions are written as

1. η_x (g, h)+η_x (gh, k) = η_x (h, k)+η_x (g, hk),

2. ϕ((x, g), (y, k))+ϕ((x, h), (y, k))−ϕ((x, gh), (y, k)) = η_x (g, h)−η_x*^ky(g * k, h * k),

3. ϕ((x, g), (y, h))+ϕ((x *^h y, g * h), (y, k)) = ϕ((x, g), (y, hk)),

4. ϕ((x, g), (y, h))+ϕ((x *^h y, g * h), (z, k)) = ϕ((x, g), (z, k))+ϕ((x *^k z, g * k), (y *^k z, h * k)),

   where x, y, z ∈ M and g, h, k ∈ G. Furthermore, for a 2-cochain ψ ∈ P²(X; A)_Y, the condition that ψ is a 2-cochain in C²(X; A)_Y is written as

5. ϕ((x, g), (x, h)) = η_x (g, h) − η_x (h, g * h),

   where x ∈ M and g, h ∈ G.

Towards constructing MCQ 2-cocycles that are not from the IIJO homology, first we note that if ϕ above is an IIJO 2-cocycle, then ϕ satisfies the conditions (3),(4), and the condition that the LHS of (2) vanishes. By considering ψ′ = ψ − ϕ, we obtain an MCQ 2-cocycle ψ′ that consists only of terms of η_x for x ∈ M. Thus we first consider such a case in Example 23 below. In this case, we can take an approach described in Section 8 for finding MCQ cocycles from group cocycles.

Example 23

For a 2-cochain ψ ∈ P²(X; A)_Y with the assumption

• (0)ψ(〈(x, g)〉 〈(y, h)〉) (= ϕ((x, g), (y, h))) = 0,

  we discuss what conditions are needed for the 2-cochain ψ being a 2-cocycle in P²(X; A)_Y. When we use the notation η_x (g, h) for ψ(〈 (x, g), (x, h) 〉), the 2-cocycle conditions are written as

• (1)η_x (g, h)+η_x (gh, k) = η_x (h, k)+η_x (g, hk),
• (2′)η_x (g, h)−η_x*^ky(g * k, h * k) = 0,

  where x, y ∈ M and g, h, k ∈ G. We note that the condition (0) implies (3) and (4). Furthermore, for a 2-cochain ψ ∈ P²(X; A)_Y with the assumption (0), the condition that ψ is a 2-cochain in C₂(X; A)_Y are written as

• (5′)η_x (g, h)−η_x (h, g * h) = 0,

  where x ∈ M and g, h ∈ G. Hence if ψ satisfies (0),(1), (2′) and (5′), then ψ is a 2-cocycle in C²(X; A)_Y and defines an invariant for handlebody-knots.

If y = x, then (2′) implies η_x (g *k, h *k) = η_x (g, h), called the right invariance of η_x. If x = 0, then (2′) with right invariance implies η_y·(1−k) ≡ η₀, which is another necessary condition for the condition (2′). Hence if any element in M can be represented by the form y · (1 − k) for some y ∈ M and k ∈ G, then we have η_x ≡ η₀ for any x ∈ M. In this case, we can check that the 2-cocycle ψ in C²(X; A)_Y comes from the dual of the composition of the chain homomorphisms

$$C_{\ast }{(X)}_Y\stackrel{{\text{pr}}_2}{\to }{C}_{\ast }{(G)}_Y\stackrel{\mathrm{\Delta }}{\to }{C}_{\ast }^G{(G)}_Y,$$

where a chain homomorphism pr₂ is induced from a natural projection into the second factor and the chain homomorphism Δ was defined in Section 8.2. In this case, ψ assigned at a crossing is decomposed into a pair of weights η corresponding to trivalent vertices as depicted in Figure 10 (B) and (C). Hence the resulting invariant is equivalent to the invariant of the trivalent graph obtained by replacing all crossings with vertices, that is, embedded in the 2-sphere without crossing. Such an embedded graph is equivalent to a circle with small bubbles, and has trivial invariant value (W(D;C) = 0 for any coloring C). Thus, in this case, ψ defines a trivial invariant for handlebody-knots by the group 2-cocycle η₀, whose cohomology class may not be zero in $H_G^2{(G;A)}_Y$.

If the condition that any element in M can be represented by the form y · (1−k) for some y ∈ M and k ∈ G is not satisfied, then ψ satisfying (0), (1), (2′) and (5′) may give rise to a nontrivial invariant for handlebody-links.

Example 24

In contrast to Example 23, next we consider the case when ϕ is not an IIJO 2-cocycle, so that the LHS of (2) does not vanish for ϕ.

For any G-invariant A-bilinear map f: M²→ A, Theorem 5.2 of [Nosaka 2013] claimed that the map ϕ_f: X²→ A defined by

$${\varphi }_f((x,g),(y,h)):=f(x-y,y·(1-h^{-1}))$$

satisfies the conditions (3) and (4) above. For the G-invariant A-bilinear map f, if we can find maps η_x such that the conditions (1) and (2) are also satisfied, then we obtain a 2-cocycle, which may be new. We remark here that ϕ_f itself can be modified as in [Nosaka 2013, Corollary 4.7] (by using an additive homomorphism form G to some commutative ring) so that the conditions (1) and (2) are also satisfied under the assumption η_x ≡ 0 for any x ∈ M.

The condition (1) merely says that η_x is a usual group 2-cocycle for any x ∈ M. The condition (2) is equivalent to

• (2″)f (x − y, y · (1−k⁻¹)) = η_x (g, h) − η_{x*^k y}(g * k, h * k)

  from the definition of f. If y = x, then (2″) implies that η_x is right invariant in the sense that η_x (g * k, h * k) = η_x (g, h) as above. If y = 0, then (2″) with the right invariance implies η_x·k ≡ η_x, called the orbit dependence of η_x. Thus we obtain these two necessary conditions for the condition (2″).

We examine the following specific examples. For a prime number p, let G denote SL(2, ℤ_p) that acts on M =(ℤ_p)² from the right. For A=ℤ_p, the map f: M²→A defined by $f(x,y):=det\left(\begin{array}{c}x\\ y\end{array}\right)$ is a G-invariant A-bilinear map, where x, y ∈ M are row vectors on which G acts on the right, and det denotes the determinant. This setting is motivated from [Nosaka 2013, Proposition 4.5].

First, we consider the case where p = 2. Define m: M → A by

$$m(x):=\{\begin{array}{ll}0\hfill & \text{if}x=0,\hfill \\ 1\hfill & \text{if}x\ne 0.\hfill \end{array}$$

Then we can check that

$${\varphi }_f\left((x,g),(y,h)\right)=-m(x)+m(x{\ast }^{h}y)$$

for any x, y ∈ M and g, h ∈G. Take η_x (g, h) to be m(x) for any x ∈ M and g, h ∈G. Then we can show that the 2-cochain ψ, defined by ϕ_f and η_x, is a 2-coboundary as follows. Define a 1-cochain m̃ ∈ P¹(X; A) by m̃ (〈(x, g)〉):= m(x). Then the 2-coboundary δm̃ ∈ P²(X; A) is written as

$$\begin{array}{ll}\hfill (\delta \stackrel{\sim }{m})(\langle (x,g)\rangle \langle (y,h)\rangle )& =-m(x)+m(x{\ast }^{h}y),\hfill \\ \hfill (\delta \stackrel{\sim }{m})(\langle (x,g),(x,h)\rangle )& =m(x),\hfill \end{array}$$

where x, y ∈ M and g, h ∈ G. This implies that ψ = δm̃.

Second, we consider the case where p > 2. If x = (0, 0) and $k=\left(\begin{array}{rr}\hfill -1& \hfill 0\\ \hfill 0& \hfill -1\end{array}\right)$, the condition (2″) implies η_2y(g, h)=η₀(g, h) for any y ∈ M and g, h ∈ G. Since p is odd, we have that η_x ≡η₀ for any x ∈ M. If we substitute y =(1, 0) and $k=\left(\begin{array}{rr}\hfill 1& \hfill -1\\ \hfill 0& \hfill 1\end{array}\right)$ for (2″), then LHS is 1 and RHS is 0, which turns out to be a contradiction. Hence there is no choice of η_x such that the conditions (1) and (2″) are satisfied.

Although our attempts have not resulted in new nontrivial 2-cocycles, it appears useful to record our approaches and facts we have found, for future endeavors towards constructing new cocycles using these approaches. Further studies are desirable on this homology theory, as it unifies group and quandle homology theories for a structure of multiple conjugation quandles, which have ample interesting examples and applications to handlebody-links.