QM/MM Study of the Catalytic Reaction of Myrosinase; Importance of Assigning Proper Protonation States of Active-Site Residues

Abstract

Myrosinase from Sinapis alba hydrolyzes glycosidic bonds of β-d-S-glucosides. The enzyme shows an enhanced activity in the presence of l-ascorbic acid. In this work, we employed combined quantum mechanical and molecular mechanical (QM/MM) calculations and molecular dynamics simulations to study the catalytic reaction of wild-type myrosinase and its E464A, Q187A, and Q187E mutants. Test calculations show that a proper QM region to study the myrosinase reaction must contain the whole substrate, models of Gln-187, Glu-409, Gln-39, His-141, Asn-186, Tyr-330, Glu-464, Arg-259, and a water molecule. Furthermore, to make the deglycosylation step possible, Arg-259 must be charged, Glu-464 must be protonated on OE2, and His-141 must be protonated on the NE2 atom. The results indicate that assigning proper protonation states of the residues is more important than the size of the model QM system. Our model reproduces the anomeric retaining characteristic of myrosinase and also reproduces the experimental fact that ascorbate increases the rate of the reaction. A water molecule in the active site, positioned by Gln-187, helps the aglycon moiety of the substrate to stabilize the buildup of negative charge during the glycosylation reaction and this in turn makes the moiety a better leaving group. The water molecule also lowers the glycosylation barrier by ∼9 kcal/mol. The results indicate that the Q187E and E464A mutants but not the Q187A mutant can perform the glycosylation step. However, the energy profiles for the deglycosylation step of the mutants are not similar to that of the wild-type enzyme. The Glu-464 residue lowers the barriers of the glycosylation and deglycosylation steps. The ascorbate ion can act as a general base in the reaction of the wild-type enzyme only if the Glu-464 and His-141 residues are properly protonated.

1. Introduction

Glucosinolates are anionic β-d-S-glucosides (Scheme 1), consisting of a glucose ring and a sulfur-containing aglycon moiety. The glucosides are found prominently in the Brassicaceae plant family.¹ These plants also produce thioglucoside glucohydrolase (myrosinase; EC 3.2.1.147). Glucosinolates and myrosinase are stored especially in the plant seeds. Mixing of the enzyme and glucosinolates induces glucosinolate hydrolysis and generates products with a strong and characteristic smell and taste, well-known from mustard, horseradish, and cabbage, which are believed to have a role in the plant’s defense system.² Furthermore, some of the hydrolase products produced during the ingestion of glucosinolate-rich foods may cause liver and thyroid diseases.³

Scheme 1. Reaction Catalyzed by Myrosinase.

The anomeric carbon is marked with a star. R = allyl in sinigrin.

The amino acid sequence of myrosinase is very similar to those of several O-glycosidases.² Myrosinase and O-glycosidases catalyze similar reactions. The glycosidases hydrolyze glycosidic bonds in polysaccharides. For example, β-galactosidase from Bacillus circulans sp. alkalophilus and Escherichia coli hydrolyzes the glycosidic linkage of lactose⁴⁻⁶ (cf. Scheme 2 for the reaction mechanism). There are many O-glycosidases, whereas myrosinase is the only known S-glycosidase. O-glycosidases are divided into two families, depending on whether their reaction products involve an overall retention or inversion of the configuration of the anomeric carbon.⁷⁻¹⁰ In both cases, two carboxylic residues (glutamate or aspartate) participate directly in the reaction. On the one hand, in the inverting enzymes, the two carboxylic residues are separated by 9–10 Å, and the reaction occurs via a single-displacement mechanism, wherein one of the carboxylic residues functions as a general acid and the other as a general base (Scheme 2a). On the other hand, the two carboxylic residues in the retaining glycosidases are separated by ∼5 Å and perform a double displacement at the anomeric center. In the first step (glycosylation), the carboxyl residue that acts as a general acid protonates the glycosidic oxygen, and the other catalytic residue performs a nucleophilic attack at the anomeric carbon, simultaneously. This leads to the formation of a glycosyl–enzyme intermediate with an inverted anomeric configuration. In the second step (deglycosylation), the carboxylic residue that acted as the general acid in the glycosylation step activates a water molecule to attack the anomeric center (thus, the residue acts as a general acid in the glycosylation and a general base in the deglycosylation steps; cf. Scheme 2b).¹¹⁻¹⁴

Scheme 2. Reaction Mechanisms for (a) an Inverting and (b) a Retaining β-O-Glycosidase¹⁵.

On the one hand, a residue alignment analysis suggested that only one of the two carboxylic residues in the active sites of O-glycosidases is present in the Sinapis alba plant myrosinase.¹⁶ On the other hand, aphid myrosinase has two catalytic glutamic acid residues similar to β-glucosidases.¹⁷ In this work, we study the catalytic reaction of the plant enzyme, so in the following, myrosinase refers to the enzyme from Sinapis alba. The preserved glutamate residue in myrosinase (Glu-409) is equivalent to the nucleophilic carboxylic residue of O-glycosidases, whereas the second glutamate residue (general acid/base) is replaced by a glutamine in myrosinase (Gln-187).¹⁸⁻²¹

The active site of myrosinase is very similar to that of the retaining O-glycosidases. Gln-187 of myrosinase is located at the same position as the acid/base residue of the related O-glycosidases (∼5 Å from the nucleophilic oxygen), and the enzyme retains the anomeric configuration of its substrate^2,22 (cf. Scheme 3). Without an acid/base residue, the hydrolysis of glucosinolates by myrosinase would become harder. The catalytic activity of the enzyme can be explained by the excellent leaving-group properties of the aglycon moiety of the substrate.^2,16 It was suggested that the role of Gln-187 in myrosinase is the precise positioning of a water molecule (W1 in our terminology; see Section 3.1) rather than to provide a general base assistance.²

Scheme 3. Catalytic Reaction of Myrosinase.

Proposed by Burmeister et al.¹⁶

A few covalent glycosyl–enzyme intermediate complexes have been trapped and crystallized using substrates that are fluorinated at the C-2 position of the glucose ring (cf. Scheme 3 for the numbering of carbon atoms in a glucose ring) and carry an aglycon with a good leaving-group ability.^2,16,23 In such structures, the fluorinated sugar ring is bound to the nucleophilic residue (Glu-409) via an α-glycosidic linkage. This confirms the role of Glu-409 as the catalytic nucleophile in the myrosinase catalytic machinery.

Close to the active site of myrosinase, there is a hydrophobic pocket that is formed by the Ile-257, Tyr-330, Phe-331, Phe-371, and Phe-473 residues. It has been suggested that the aglycon part of the substrate binds in the hydrophobic pocket and that the sulfate moiety is bound by Arg-194 and Arg-259 (these residues are strictly conserved among myrosinase and absent in the related β-glycosidases).^2,16

Myrosinase shows enhanced activity in the presence of l-ascorbic acid, ranging from 1.8- to 400-fold, depending on the substrate sources of myrosinase.²⁴⁻²⁸ Likewise, the reactivation of the 2-F-glucosyl inhibited enzyme shows a 14-fold enhancement in the presence of 1 mM ascorbate.¹⁶ Ettlinger et al.²⁴ suggested that ascorbate plays the catalytic acid/base role for myrosinase. In a crystallographic study, Burmeister et al.¹⁶ showed that ascorbate and an intact substrate cannot bind together in the active site. However, ascorbate binds once the aglycon of the substrate has diffused away after the nucleophilic attack of Glu-409 to the anomeric center. They showed that, in the presence of a 2-fluoroglucosyl group in the active site, a hydrogen bond is formed between the O6 hydroxyl group of the glucose ring and the O6′ hydroxyl group of ascorbate (the positions of carbon atoms in a glucose ring and of oxygen atoms of ascorbic acid are shown in Scheme 3) and that ascorbate is placed in an ideal position to act as a catalytic base and to activate a water molecule, substituting for the general acid/base residue in the catalytic action of O-glycosidases.

A few theoretical calculations have been reported on the glycosylation and deglycosylation processes for β-glucosidases.²⁹⁻³² However, to the best of our knowledge, there is no reported theoretical work on the reaction mechanism of myrosinase. In this work, we use combined quantum mechanical and molecular mechanical (QM/MM) methods to elucidate and clarify the chemical events involved in the hydrolysis reaction of sinigrin by myrosinase (Scheme 1). In addition, we study the role of l-ascorbate in the catalytic reaction and compare the energetics of the reaction of an unassisted enzyme with an l-ascorbate-assisted one. We also investigate the role of Glu-464 and Gln-187, by performing in silico mutations. In particular, we perform a large amount of test calculations to find a proper QM system that can successfully perform the glycosylation and deglycosylation steps.

2. Methods

2.1. The Protein

There are more than a dozen reported crystal structures for myrosinase from Sinapis alba.^2,16,33,34 In this work, we use two of the structures (1E6S and 1E73 Protein Data Bank (PDB) Identifications (IDs)).¹⁶ The former involves an inhibitor (d-gluconhydroximo-1,5-lactam (DGHL); cf. Chart S1 in the Supporting Information) that binds simultaneously with a sulfate ion and mimics the enzyme–substrate complex. The latter harbors 2-deoxy-2-fluoro-α-d-glucopyranose (G2F; cf. Chart S2 in the Supporting Information) and an l-ascorbate ion in its active site and mimics the reactant state of the deglycosylation reaction (i.e., the state after the second double arrow in Scheme 3). These are also the two structures with the highest resolution reported for the myrosinase from Sinapis alba (1.35 and 1.50 Å for 1E6S and 1E73, respectively).¹⁶ The former PDB file was used in the substrate docking and the QM/MM calculations, whereas the latter was used in the molecular dynamics (MD) simulations. There are two residues from the N-terminal of the protein that are not visible in the crystal structure (Asp-1 and Glu-2). No attempts were made to model these missing residues.

From the 1E6S structure, all heteromolecules were removed, except the Zn ion. These include sulfate ions from the buffer, N-acetyl-d-glucosamine, α-l-fucose, α- and β-d-mannose, β-d-xylopyranose, (2S,3S,4R,5R)-6-(hydroxyamino)-2-(hydroxymethyl)-2,3,4,5-tetrahydropyridine-3,4,5-triol, glycerol, d-gluconhydroximo-1,5-lactam, and propane-1,2,3-triol. These molecules bind on the surface of the enzyme, far from the active site. The Zn ion is on the edge of the enzyme (∼20 Å from the active site) and is coordinated to His-56 and Asp-70. The ion is a connector between two monomers of the dimeric protein and is also coordinated to His-56′ and Asp-70′ from another monomer.² However, since the monomers are not closely connected, we decided to study only one of them and, therefore, completed the His-56′ and Asp-70′ empty coordination sites of the Zn ion with two water molecules, giving a tetrahedrally coordinated Zn site. There are 21 residues with two alternative conformations in the crystal structures (Leu-20, Ile-30, Ser-62, Glu-88, Ser-101, Ile-118, Ser-126, Asp-169, Ser-213, Ser-220, Ser-271, Glu-305, Ser-309, Ser-338, Val-342, Ser-344, Ile-360, Ser-363, Tyr-366, Val-449, and Asn-462). The conformations with the higher occupation numbers were kept, and conformations with the lower occupation numbers were removed. However, for Ser-309, Val-342, and Ser-344, the two conformations have the same occupancy. To choose the best alternative conformations of Ser-309, Val-342, and Ser-344, we performed eight sets of MD simulations differing in the conformation (A or B) of these residues in the crystal structures. Details of the simulations are described in the next subsection. Information about which alternative is more stable can be obtained by studying the root-mean-square deviation (RMSD) values of various atoms from the positions observed in the crystal structure. A similar method has been used to determine preferred protonation states of the active-site glutamates of glyoxalase I,^35,36 His residues in three proteins,³⁷ and for homocitrate and its nearby residues in nitrogenase.³⁸ The MD simulations showed almost the same RMSDs for the A and B conformations of Ser-309 and Val-342 but a much lower average RMSD for the B conformation of Ser-344 (0.17 vs 0.63 Å). Thus, we used the A conformations of Ser-309 and Val-342 and the B conformation for Ser-344. Conformations of these residues in each simulation and the calculated mass-weighted RMSD values are summarized in Table S1 in the Supporting Information. All crystal water molecules were kept, but those with a low occupancy (HOH-1051, -1157, and -1767) or with short contacts to each other or to other residues were removed (HOH-1008, -1019, -1022, -1114, -1311, and -1574).

The setup of the 1E73 PDB structure was similar to that of 1E6S, except that we kept the G2F and ascorbate hetero groups and that the removed waters from this structure were HOH-2025, -2274, and -2299, all with 50% occupancy.

Protonation states of all protein residues were determined by a study of the hydrogen-bond pattern, the solvent accessibility, and the possible formation of ionic pairs. They were also checked by PROPKA calculations.³⁹⁻⁴¹ All Glu, Arg, and Lys residues were assumed to be charged. Asp-143 was assumed protonated (it is buried inside the protein with no positively charged residue close to it), but all the other Asp residues were negatively charged. Cys-73 and Cys-171 were assumed to be protonated, whereas the other six Cys residues form disulfide bridges. A thorough manual investigation of all His residues gave the following protonation assignment: His-56, -141, and -436 were assumed to be protonated on the ND1 atom, His-66, -122, -229, -247, and -270 were presumed to be protonated on both the ND1 and NE2 atoms (and therefore positively charged), whereas the remaining four His residues (His-228, -234, -347, and -365) were modeled with a proton on the NE2 atom. A QM/MM model based on these protonation states can perform the glycosylation reaction but fails in the deglycosylation reaction. We will show that, to have a successful deglycosylation reaction, Glu-464 must be protonated on OE2 and His-141 must be protonated on NE2 instead of ND1 (cf. Section 3.1).

2.2. MD Simulations

All MD simulations were performed using the graphics processing unit (GPU)-accelerated pmemd code⁴²⁻⁴⁴ of AMBER 18.⁴⁵ The protein was modeled by the Amber ff14SB⁴⁶ force field, and ligands were described with the general Amber force field (GAFF).⁴⁷ Heteromolecules were optimized at the B3LYP/6-31G(d)⁴⁸⁻⁵² level of theory, and electrostatic potentials were calculated at the Hartree–Fock/6-31G(d) level of theory with points sampled according to the Merz–Kollman scheme.⁵³ These were calculated by the Gaussian 16 program package.⁵⁴ Atomic charges were then fitted to these potentials using the restrained electrostatic potential (RESP) procedure,⁵⁵ as implemented in the antechamber program,⁵⁵ which also assigned GAFF atom types to the molecules.

The metal site at the edge of the protein (Zn(H₂O)₂(His-56)(Asp-70)) was treated by a nonbonded model with restraints between the metal and the ligands.⁵⁶ RESP charges were employed,⁵⁵ calculated in the same way as for the ligands. The distances, force constants, and RESP charges were obtained from the optimized model in Figure S1 in the Supporting Information. The calculations were performed at the TPSS/def2-SV(P) level of theory,^57,58 using the Turbomole software (version 7.1)⁵⁹ and sped up by expanding the Coulomb interactions in an auxiliary basis set; the resolution-of-identity approximation^60,61 and empirical dispersion corrections were included with the DFT-D3 approach⁶² and Becke–Johnson damping,⁶³ as implemented in Turbomole. The force constants were calculated by the method of Seminario.^64,65 The calculated distances, force constants, and charges are given in Tables S2 and S3 in the Supporting Information.

The setup of the MD simulations is similar to that in our recent works.^35,36 First, the prepared protein was immersed in a periodic truncated octahedral box of TIP3P water molecules,⁶⁶ extending at least 10 Å from the solute using the tleap program in the Amber suite.⁴⁵ This made a final system containing ∼44 700 atoms. Next, the system was subjected to 1000 cycles of minimization, restraining the heavy atoms toward the starting crystal structure with a force constant of 100 kcal/mol/Ų. Then, two 20 ns equilibrations (one with constant volume and one with constant pressure) were performed with the same restraints, but the force constant was 50 kcal/mol/Ų. After that, the system was equilibrated for 1 ns without any restraints. Finally, the production simulations were performed for 200 ns, and the coordinates were sampled every 10 ps.

RMSDs were calculated with the AMBER cpptraj module,⁶⁷ analyzing trajectories with saved coordinates in the production simulations, and using the crystal structure as the reference. Reported values are averages over these 20 000 sets of coordinates. Further details of the MD simulations are collected in the Supporting Information.

2.3. Docking

To study the glycosylation and the deglycosylation reactions, we docked sinigrin and l-ascorbate into the enzyme’s active site, respectively. First, all water molecules of the prepared protein (cf. Section 2.1) were removed. Then, we protonated the protein and assigned Amber ff14SB⁴⁶ charges to the atoms using the tleap module of the Amber program⁴⁵ (and the RESP charges of sinigrin, the reaction products, and other heterogroups). After that, we removed all nonpolar hydrogen atoms (adding their charge to the neighboring carbon atoms). This was done automatically by a local software.⁶⁸ All bonds of the ligands were rotatable during the docking process, except those that were either terminal or in the rings. Preparation for docking was done using MGLTools.⁶⁹ Finally, the docking was performed using the AutoDock Vina program suite.⁷⁰ The final output files from AutoDock Vina were converted to the PDB format by Open Babel.⁷¹ We employed the default exhaustiveness of the global search (exhaustiveness = 8). The binding sites were boxes with dimensions of 14 × 24 × 16 and 18 × 18 × 18 ų for sinigrin and ascorbate, respectively. During the docking process, there was no flexible residue in the protein. Further details of docking and the selection of the best binding modes are given in the Supporting Information.

2.4. QM/MM Calculations

After docking the substrate into the 1E6S structure, the protein–ligand complex was solvated in a periodic truncated octahedral box of TIP3P⁶⁶ water molecules, extending at least 20 Å from the solute. After solvation, first only the hydrogen atoms and then both the hydrogen atoms and added water molecules were subjected to 1000 cycles of minimizations with the heavy atoms of the protein restrained. This was followed by a 10 ps constant-volume equilibration with the same restraints. Finally, the system was equilibrated by a 1 ns constant-volume simulation and a 1 ns simulated annealing at constant pressure with the restraints (the force constant for the restraints in all steps was 1000 kcal/mol/Ų). Bond lengths to hydrogen atoms were constrained by the SHAKE algorithm⁷² in the equilibrations (but not in the minimizations). The constant volume and pressure conditions and the cutoff radius were the same as in the MD simulations and are described in the Supporting Information. After the final equilibration, the octahedral system was truncated to a spherical one with a radius of 40 Å from the geometric center of the protein.

We also performed calculations for four mutants of myrosinase (E464A, Q187A, and Q187E; in the latter case, the glutamate was either protonated or deprotonated). The mutations were built manually, by changing the residue names and deleting atoms or changing atom names. Then, we ran the tleap module as for the wild-type protein. The mutated proteins were also relaxed before the QM/MM calculations, as was described in the previous paragraph.

After the relaxation of the wild-type and mutated systems, QM/MM calculations were performed with the ComQum software.^73,74 In this approach,^75,76 the protein and solvent are split into three subsystems (systems 1–3). System 1 (the QM region) was treated by QM methods. System 2 consisted of all residues or water molecules within 6 Å of any atom in system 1. In some calculations (called protein-fixed), system 2 was kept fixed at the original (crystallographic) coordinates. Such calculations were run to ensure that the surroundings reside in the same local minimum in all calculations, making the energies stable, although all outer-sphere reorganization is ignored. In other calculations (called protein-free), all residues and solvent molecules in system 2 were allowed to relax by a full MM minimization in each cycle of the QM optimization. Finally, system 3 contained the remaining part of the protein and the solvent. It was kept fixed at the original coordinates (equilibrated crystal structure).

In the QM calculations, system 1 was represented by a wave function, whereas all the other atoms were represented by an array of partial point charges, one for each atom, taken from MM libraries. Thereby, the polarization of the QM system by the surroundings is included in a self-consistent manner. When there is a bond between systems 1 and 2 (a junction), the hydrogen link-atom approach was employed. In this approach, the QM system was capped with hydrogen atoms (hydrogen link atoms, HL), the positions of which are linearly related to the corresponding carbon atoms (carbon link atoms, CL) in the full system.^73,77 All atoms were included in the point-charge model, except the CL atoms.⁷⁸ The point charges do not necessarily sum up to an integer, because the Amber force field does not employ charge groups.⁷⁹ The total QM/MM energy in ComQum is calculated as^73,74

1

where E_QM1+ptch23^HL is the QM energy of system 1, truncated by HL atoms, and embedded in the set of point charges representing systems 2 and 3 (but excluding the self-energy of the point charges). E_MM1,q1=0 is the MM energy of the QM system, still truncated by HL atoms, but without any electrostatic interactions. Finally, E_MM123,q1=0^CL is the classical energy of all atoms in systems 1−3 with CL atoms and with the charges of the QM system set to zero (to avoid double counting of the electrostatic interactions). By using this approach, which is similar to the one used in the Oniom method,⁸⁰ errors caused by the truncation of the quantum system should partly cancel out. Thus, ComQum employs a subtractive scheme with electrostatic embedding and van der Waals link-atom corrections.⁸¹

The QM/MM geometry optimizations were performed using the Turbomole software⁵⁹ at the TPSS-D3/def2-SV(P) level of theory.^{57,58,60−63} The MM calculations were performed with the Amber software,⁷⁹ using the Amber ff14SB⁴⁶ and GAFF⁴⁷ force fields for the protein and ligands, respectively. Water molecules were described by the TIP3P model.⁶⁶

All first-order stationary states (reactants, intermediates, and products) were fully optimized without any restraints. To go from one stationary point to another, we scanned distances step by step, applying H–O, O–C, or H–S restraints with a force constant of 1 au and changing the corresponding target value in steps of 0.2 Å (0.1 Å around the maximum of the energy profiles). The transition states were approximated as the highest point on the potential energy surface along the reaction coordinates.

2.5. Big-QM Calculations

Previous studies have shown that QM/MM energies strongly depend on the size of the studied QM system.^78,82 Therefore, we developed the big-QM approach to obtain converged QM/MM energies.^83,84 This method corrects the main error sources of QM/MM methods by choosing a very big QM system and moving junctions away from the reaction center.⁸³ In this work, our big-QM systems consisted of all chemically reasonable groups (i.e., keeping functional groups as well as conjugated and aromatic systems intact) with at least one atom within 4.5 Å of any atom in the QM3 system (the QM3 system is defined in Section 3.1). Moreover, all junctions were moved at least three residues away from the QM3 system. These gave ∼1000 atoms in the big-QM system and ∼29 000 atoms in the MM system from the surrounding protein, modeled by point charges in the calculations. A typical big-QM system is shown in Figure S3 in the Supporting Information.

Single-point big-QM energy calculations were performed on this system at the TPSS-D3/def2-SV(P) level of theory,^{57,58,60−63} as is described in Section 2.4, but they employed also the multipole-accelerated resolution-of-identity J approach (marij keyword).⁸⁵ The calculations were run with the parallel version of Turbomole.⁸⁶ To the big-QM energies, we added the DFT-D3 dispersion correction and a standard MM correction (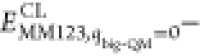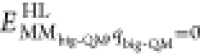; cf. Equation 1), yielding a standard QM/MM energy but with the big-QM system as the QM region.

These overall big-QM energies (E_big-QM^SV(P)) were improved by extrapolating them to the larger def2-TZVPD basis set, which also includes diffuse functions.^87,88 This was performed by single-point calculations on the normal QM regions (cf. Section 3.1) at the TPSS-D3/def2-TZVPD level of theory. Then the big-QM energies were extrapolated to the def2-TZVPD basis set by

2

where E_big-QM^TZVPD is the extrapolated big-QM energy, E_big-QM is the normal big-QM energy at the def2-SV(P) level of theory, and, E_QM1+ptch23^HL,TZVPD and E_QM1+ptch23 are the QM energy of the normal QM region (QM3), truncated by HL atoms and embedded in the set of the point charges, calculated at the TPSS-D3/def2-TZVPD and TPSS-D3/def2-SV(P) levels of theory, respectively.

2.6. QTCP Calculations

The QM/MM thermodynamic cycle perturbation (QTCP) approach is a method to calculate free energies between two states, A and B, with a high-level QM/MM method, using free-energy perturbation (FEP) with sampling at only the MM level.⁸⁹⁻⁹¹ It employs the thermodynamic cycle in Scheme 4, showing that the QM/MM free-energy difference between A and B can be obtained from three calculations: an FEP from A to B at the MM level and two FEP calculations in the method space from MM to QM/MM, one each for the A and B states.

3

Scheme 4. Thermodynamic Cycle Employed in the QTCP Calculations.

The QTCP calculations were performed as has been described before.^91,92 First, each state of interest was optimized by QM/MM, keeping systems 2 and 3 fixed. Then, the protein was further solvated in an octahedral box of TIP3P water molecules, extending at least 6 Šfrom the QM/MM system. For the A state, all hydrogen atoms and water molecules except water molecules in the QM system were subjected to a 1000-step minimization, restraining all heavy atoms from the starting structure with a force constant of 1000 kcal/mol/Ų. Then the whole system was subjected to another 1000-step minimization, keeping the atoms in the QM part fixed and restraining all heavy atoms with a force constant of 100 kcal/mol/Ų. Then, two 20 ps MD simulations were run with the heavy atoms still restrained. The first was run with a constant volume; the second was run with a constant pressure. Next, a constant-pressure MD simulation equilibrated the size of the periodic box for 100 ps, and only the heavy atoms in the QM system were restrained to the QM/MM structure. The final structure of this simulation was used as the starting structure for the B state. Finally, an equilibration of 200 ps and a production of 400 ps were run with a constant volume for each state. During the production run, 200 snapshots were collected every 2 ps.

On the basis of these 200 snapshots, three sets of FEPs were performed as is shown in Scheme 4. First, FEPs were performed at the MM level in the forward and reverse directions along the reaction coordinate by changing the charges and coordinates of the QM system to those of the QM/MM ones.⁹² Charges were first modified in nine steps, keeping the coordinates at those of the A state. Then, the coordinates were modified in 21 steps to those of the B state, with the charges in the product state (normally only five steps are used for the coordinate perturbation, but in this case, 21 steps were needed to obtain a reasonable uncertainty of the free energies, ∼0.5 kcal/mol). Finally, MM → QM/MM FEPs were performed for both the reactant and product states, keeping the QM systems fixed, as has been described before.^90,91 All FEP calculations were performed with the local software, calcqtcp. Further details of the QTCP calculations can be found in http://signe.teokem.lu.se/~ulf/Methods/qtcp.html.

3. Results and Discussion

3.1. The Active-Site Model

A proper model of the active site of myrosinase should be able to perform both the glycosylation and deglycosylation reactions, and it should be big enough and include all important atomic movements. Furthermore, the protonation states of the active-site residues in the model must be correctly assigned. To select a proper active-site model, we tested the three different QM regions (QM1, QM2, and QM3) shown in Figure 1. QM1 is our minimal system and consists of the entire substrate, as well as models of Gln-187 and Glu-409, the most important residues in the catalytic machinery of myrosinase. QM2 contains all atoms and groups of QM1 and models of Gln-39, His-141, Asn-186, Tyr-330, and Glu-464. Finally, QM3 contains all atoms and groups of QM2, as well as Arg-259 and 0–2 water molecules (discussed below). The amino acids were included up to their α-carbons. There are 60, 119, and 138 atoms in QM1, QM2, and QM3, respectively. The total charges of the QM systems are included in Table S5 in the Supporting Information.

Figure 1.

QM systems used in the QM/MM calculations. (a) QM1, (b) QM2, (c) QM3+W1+W2, (d) QM3+W1, and (e) the modified QM3+W1 system. Hydrogen bonds between the NE2 atom of His-141 and the hydrogen of O3 of the glucose moiety, the carboxylate group of Glu-464 and the hydrogen of O6 of the glucose moiety, and the hydrogen of OE2 of Glu-464 and O6 of the glucose moiety are shown with dashed blue lines and circled in green in c, d, and e, respectively.

We calculated QM/MM reaction energies for the first reaction step in Scheme 3 (nucleophilic attack of Glu-409 by its carboxylic group to the anomeric carbon of sinigrin (Ca), the glycosylation step) and summarized the resulting profiles in Figure 2. As is shown in the figure, the reaction is not possible with the QM1 system: It is uphill by 22.7 kcal/mol when the protein surroundings in system 2 is fixed and returns to the starting point after releasing any bond constraints. In other words, QM1 is too small and rigid to catalyze the reaction. On the other hand, the reaction was successful for the larger QM2 and QM3 systems. However, the barrier of QM2 is higher than that of QM3 (19.9 vs 14.3 kcal/mol). Moreover, the resulting intermediate of QM2 is more unstable than that of QM3 (the reaction energies are 4.3 and 2.9 kcal/mol, respectively). Thus, we can conclude that QM1 is too small to study the myrosinase reaction. The glycosylation step is successful with the QM2 and QM3 systems, and the latter has a lower barrier and reaction energy.

Figure 2.

QM/MM energetics of the glycosylation reaction with (a) QM1, (b) QM2, (c) QM3, (d) QM3+W1, and (e) QM3+W1+W2 with system 2 fixed or allowed to relax. To provide a fair comparison between the calculations, all energy axes have the same scale.

We calculated also the QM/MM energy profiles for the first reaction step in all QM systems when the surrounding protein in system 2 was free to relax (protein-free calculations), and the reaction profiles are also shown in Figure 2 (green profiles). It can be seen that the energy profiles of QM3 have the smallest difference between the protein-fixed and free calculations. The small difference between the protein-fixed and protein-free energy profiles indicates that all important movements are included in the QM system and that there is no risk of ending up in spurious local minima. Thus, we can conclude that QM3 is a proper QM system to study the catalytic reaction of myrosinase and that it is important to include the flexibility of Arg-259 in the QM/MM calculations.

As explained in the Introduction, the catalytic acid/base residue of O-glycosidases is replaced by Gln-187 in myrosinase, and it was suggested that the role of this glutamine residue is to provide a proper position for a water molecule to take part in the deglycosylation step of the reaction.¹⁶ To the best of our knowledge, this has never been studied using computational methods. Therefore, we calculated the first reaction step with either one or two water molecules added to the QM3 system. The first water molecule (W1) was placed close to Gln-187, and the second one (W2) was inserted in the vicinity of Glu-464 and the S1 atom of the substrate (the atom names and the added water molecules are shown in Figure 1c). Energy profiles for the nucleophilic attack obtained in the presence of the water molecules are shown in Figure 2d,e. On the one hand, it can be seen that including W1 in the QM3 system lowers the energy barrier significantly (from 14.3 to 5.7 kcal/mol). Moreover, the reaction energy goes from slightly endothermic to slightly exothermic (from 2.9 to −1.4 kcal/mol; compare the red profiles in Figure 2c,d). On the other hand, including the W2 molecule into the QM3+W1 system changes neither the barrier nor the reaction energy significantly (the barrier remains at 5.7 kcal/mol, and the reaction energy becomes −1.8 kcal/mol; compare the red profiles in Figure 2d,e). Furthermore, the protein-fixed and protein-free energy profiles with water molecules in QM3 show even lower differences. In summary, including W1 into the QM3 system is important to obtain a lower barrier, but adding W2 to the QM3+W1 system does not have any significant effects on the reaction barrier and reaction energy. Therefore, in the following, we report results obtained with QM3+W1 and system 2 fixed.

From Figure 2, it can be seen that the energy difference between the protein-fixed and free profiles is still rather large for the selected QM3+W1 system (up to 4.4 kcal/mol). Therefore, we employed the QTCP (which relaxes the surroundings by MD simulations and calculates free energies) and Big-QM (which calculates the energy of the closest surroundings by explicit QM calculations) approaches to obtain more reliable energies.

In the optimized structure of the QM3+W1 system (cf. Figure 1d), the water molecule is positioned next to the C1 atom of the glucose moiety of sinigrin, donating a hydrogen bond to OE1 of Gln-187 (the Ow–OE1 distance is 2.53 Å), whereas the Ow–NE2 distance is 4.28 Å. These are in a reasonable agreement with the reported distances in a glycosyl-enzyme crystal structure (the reported distances are 2.79 and 3.27 Å, respectively).¹⁶ This suggests that W1 is correctly positioned in the QM/MM optimized structure.

The lower barrier of the glycosylation step with the QM3+W1 system compared to the QM3 system can be related to the hydrogen bonds that W1 forms with the H1 and S1 atoms of the substrate and OE1 of Gln-187 (these hydrogen bonds are absent in QM3 without the water molecule). As can be seen in Figure 1d, the Ow–H1, Ha–S1, and Hb–OE1 distances are 1.91, 2.29, and 1.57 Å, respectively. This hydrogen-bond network helps the aglycon moiety of the substrate to carry a more negative charge at the reactant state, making it a better leaving group (the aglycon moiety of sinigrin carries a charge of −2 after leaving the substrate). The calculated charges on the aglycon moiety of the reactant state with the QM3 and QM3+W1 systems are −0.95 and −1.62, respectively (calculated for the QM region of the optimized QM/MM structures using the RESP method at the TPSS-D3/def2-SV(P) level of theory).^{57,58,60−63}

Up to this point, the QM3+W1 system has passed the test for the glycosylation step. However, a proper QM system must also be able to catalyze the deglycosylation step. After the glycosylation step, the aglycon moiety of sinigrin leaves the active site, and an l-ascorbate ion binds to the enzyme. Figure 3 shows optimized structures of the first intermediate of the reaction of the wild-type enzyme, when the aglycon moiety is still in the active site (IM1-WT; Figure 3a), when the aglycon moiety has left the active site (IM1-WT–agl; Figure 3b), and when ascorbate is bound to the active site after leaving the aglycon moiety (IM1-WT–agl+asc; Figure 3c). In the latter, an l-ascorbate molecule was docked into the IM1-WT–agl structure. Details of the ascorbate docking are described in the Supporting Information. In the deglycosylation step of the reaction, a hydroxide group should connect to the Ca atom of the glucose moiety, releasing Glu-409. It has been suggested that this OH group comes from the water molecule, positioned by Gln-187 (W1).¹⁶ From the ascorbate-bound enzyme, there are three possible reactions, namely, Hb to OE1 of Gln-187, Ha to O3′ of l-ascorbate, and Ow to Ca (the possible reactions are shown in Scheme 5).

Figure 3.

Optimized structures of the intermediates formed after the glycosylation reaction in the wild-type enzyme (a) when the aglycon moiety is still in the active site (IM1-WT), (b) when the aglycon moiety has left the active site (IM1-WT–agl), and (c) when ascorbate is bound to the active site after the aglycon moiety has left (IM1-WT–agl+asc). The α-face of the anomeric carbon is occupied by Glu-409, and W1 can only attack the β-face of this carbon.

Scheme 5. Schematic View of the IM1-WT–agl+asc Intermediate.

Reactions found to be possible and impossible (they return to the starting point after releasing any bond constraints) are shown with arrows in green and red, respectively. The solid and dashed arrows represent the reactions with the Arg-259 in the QM3+W1 system charged and neutralized, respectively.

On the one hand, the results show that the water molecule cannot pass any of its protons in the IM1-WT–agl+asc state (the first two reactions are not possible). On the other hand, the Ow nucleophilic attack produces the structure shown in Figure 4 (IM2-WT; note that in IM1-WT–agl+asc, the product of the glycosylation step and then the reactant of the deglycosylation step, Glu-409 is connected to Ca, whereas in IM2-WT, a water molecule is connected to Ca replacing Glu-409; compare the structures in Figure 3c and Figure 4). The IM2-WT intermediate has an extra proton on the glucose moiety. In the proposed mechanism shown in Scheme 3, a proton from the attacking water molecule is abstracted by ascorbate, concurrently by the attack of Ow to Ca. Our results showed that ascorbate cannot abstract the extra proton in IM2-WT (the water molecule connected to Ca with an extra proton is circled in green in Figure 4). In other words, in the QM3+W1 system, ascorbate is not basic enough to abstract the extra proton from the protonated glucose. Thus, our calculations are not in line with the proposed mechanism in Scheme 3. This implies that there is a problem in our model that causes the discrepancy.

Figure 4.

IM2-WT structure that resulted from the attack of W1 to the anomeric carbon of the substrate in IM1-WT–agl+asc. The water molecule connected to Ca with an extra proton is circled with green.

The failure of the QM3+W1 system in moving the extra proton from the glucose moiety to ascorbate is probably related to either its size or to the protonation states of the residues in the QM system. To solve this problem, we followed three paths: (i) the QM system is not big enough to include all chemically reasonable groups, (ii) protonation states of groups that make ascorbate more basic might be wrongly assigned, and (iii) protonation states of groups that make the protonated glucose in IM2-WT more acidic might be wrongly assigned. First, we tried a larger QM system by adding the side chains of Ile-257 and Phe-331 to the QM3+W1 system. The philosophy of adding these groups was that the ascorbate ion needs to move backward after abstracting the extra proton of the glucose moiety, and these groups are located directly behind ascorbate and can give more freedom in movement for the ascorbate ion (the larger QM4 system is shown in Figure S5 in the Supporting Information). However, the larger QM system did not solve the problem of the low basicity of ascorbate.

For the second path, we found that residues with at least one atom within 5 Å of the ascorbate ion are Phe-473, Phe-331, Ile-356, and Arg-259. The first three are with hydrophobic side chains and cannot help ascorbate to abstract a proton, whereas Arg-259 is already included in the QM system. On the one hand, arginine has a positively charged side chain and cannot abstract a proton. On the other hand, a neutralized arginine may help the ascorbate ion to abstract the extra proton of glucose in IM2-WT.

Therefore, we neutralized Arg-259 in the QM3+W1 system (removing a proton from its NH2 atom, parametrizing the neutralized Arg, and re-equilibrating the structure) and redid the reactions shown in Scheme 5. The results showed that the Hb to Gln-187 transfer is still not possible. However, the Ha to ascorbate transfer is feasible and directly produces the reaction product (Ow connects to Ca concurrently; the optimized structure of this state is shown in Figure S6 in the Supporting Information). The Ow to Ca reaction is also possible and produces a positively charged glucose (the IM2-WT state). However, in this QM system, ascorbate can abstract the extra proton of the glucose moiety in IM2-WT, and the reaction product is produced.

There are two problems with the QM system in which Arg-259 is neutralized: First, arginine is a highly basic amino acid (pK_a = 12.0), so its neutralization is unlikely. Second, the QM system with the neutralized Arg-259 fails to perform the glycosylation step (the Glu-409 to Ca nucleophilic attack is unsuccessful in this QM system). This failure shows the importance of a positively charged residue in the active site of myrosinase (the positive charge is necessary to stabilize part of the developing negative charge on the aglycon moiety, induced by the nucleophilic attack of Glu-409 on Ca in the glycosylation step). The calculated charges on the aglycon moiety of the reactant state with the charged and neutralized Arg-259 in the QM3+W1 system are −1.62 and −0.94, respectively. Interestingly, it has been suggested that the aglycon part of the substrate binds in the hydrophobic pocket and that the sulfate moiety of the substrate is bound by Arg-194 and Arg-259, which are strictly conserved among myrosinase and absent in the related β-glycosidases.^2,16 This implies that Arg-259 is necessary for the catalytic machinery of myrosinase, because the enzyme does not have a catalytic acid/base residue (like those of O-glycosidases) to protonate the leaving group at the glycosylation step, and the positively charged Arg-259 stabilizes part of the negative charge on the leaving group at the glycosylation step. Therefore, we went through the third path, looking for a residue that makes the protonated glucose more acidic.

A visual inspection around the glucose moiety identifies Glu-409, Glu-464, and His-141 as residues that can have more than one protonation state. On the one hand, the former is the nucleophile in the glycosylation step and therefore must be charged (otherwise it would be a weaker nucleophile and could not easily attack to Ca of sinigrin). On the other hand, Glu-464 does not directly participate in the catalytic reaction but makes a hydrogen bond with the −CH₂OH group of the glucose moiety (cf. Figure 1d). Likewise, His-141 does not take a direct part in the catalytic reaction but accepts a hydrogen bond from O3 of the glucose moiety to its NE2 atom (this hydrogen bond is indicated in Figure 1c). The carboxylate group of Glu-464 can have three different protonation states, specifically, fully deprotonated, protonated on OE1, and protonated on OE2 (the OE1 and OE2 oxygen atoms of Glu-464 are indicated in Figure 1). Similarly, His-141 can have three different protonation states, namely, protonated on ND1, protonated on NE2, and protonated on both ND1 and NE2 atoms (the ND1 and NE2 atoms of His-141 are indicated in Figure 1c).

The three protonation states of Glu-464 and the three of His-141 give us nine different protonation states overall. To find the correct protonation states of these two residues we performed nine sets of MD simulations, differing in the protonation states of Glu-464 and His-141. For the simulations, we used the 1E73 PDB structure of myrosinase,¹⁶ because it harbors a G2F molecule and an l-ascorbate ion in the active site, which resemble the glucose moiety and ascorbate in the IM1-agl+asc structure.

After performing the MD simulations, we calculated mass-weighted RMSD values for the studied residue and all residues with at least one atom within 3.0 Å of the studied residue as well. The first RMSD shows whether the studied residue stays close to the crystal position or not, whereas the second one indicates whether any of the neighboring residues move to release any unfavorable interaction. The calculated RMSDs are summarized in Table 1. On the one hand, as can be seen in the fifth column, the RMSDs of Glu-464 are lower when it is protonated on OE2 than for the other protonation states (the average is 0.25 Å for simulations 7–9, whereas it is 1.12 Å for simulations 4–6 and 0.61 Å for simulations 1–3). On the other hand, the RMSDs of the nearby residues of Glu-464 are almost equal in all protonation states (∼0.7 Å; cf. the last column of Table 1). When Glu-464 is deprotonated, it accepts a hydrogen bond from O6 of the glucose moiety; when it is protonated on OE1, it donates a hydrogen bond to O4 of glucose, whereas when it is protonated on OE2, it donates a hydrogen bond to O6 of glucose (seen in the QM/MM optimized structures in Figures 1d,e and S7). These results suggest that Glu-464 is protonated on OE2 and donates a hydrogen bond to O6 of the glucose moiety.

Table 1. Mass-Weighted RMSD Values (in Å) of Glu-464, His-141, and Their Nearby Residues^a.

			RMSD
	protonated atom(s)		residue alone		nearby residues
simulation number	His-141	Glu-464	His-141	Glu-464	His-141	Glu-464
1	ND1	none	1.18	0.58	0.71	0.65
2	NE2	none	0.40	0.64	0.74	0.59
3	ND1 and NE2	none	0.90	0.62	0.92	0.72
4	ND1	OE1	0.35	1.12	0.93	0.89
5	NE2	OE1	0.42	1.12	0.77	0.60
6	ND1 and NE2	OE1	0.65	1.13	0.97	0.77
7	ND1	OE2	0.30	0.22	0.78	0.72
8	NE2	OE2	0.44	0.27	0.85	0.66
9	ND1 and NE2	OE2	0.54	0.26	0.96	0.71
average	Glu-464	none		0.61		0.65
		OE1		1.12		0.75
		OE2		0.25		0.70
	His-141	ND1	0.61		0.81
		NE2	0.42		0.79
		ND1 and NE2	0.70		0.95

^aThe RMSDs are calculated for the heavy atoms only. The reference for the RMSDs is the crystal structure.

The calculated RMSD values of His-141 are summarized in the fourth column of Table 1. The last three numbers in the column are the average RMSDs of this residue in the simulations. It can be seen that the average RMSDs of this residue are 0.61, 0.42, and 0.70 Å when it is protonated on ND1 (simulations 1, 4, and 7), protonated on NE2 (simulations 2, 5, and 8), and protonated on both ND1 and NE2 (simulations 3, 6, and 9), respectively. The average RMSD of nearby residues of His-141 is also lower when it is protonated on NE2 (cf. the last three numbers in the sixth column of Table 1). This implies that His-141 is probably protonated on NE2.

To obtain further support for the MD results (that Glu-464 is protonated on OE2 and His-141 is protonated on NE2), we compared QM/MM energies of the QM3+W1 system for the IM1-WT–agl+asc state with Glu-464 protonated on OE1 or OE2 and His-141 protonated on ND1 or NE2 (four QM/MM calculations; cf. Table 2). As can be seen in the table, systems with His-141 protonated on NE2 are ∼20 kcal/mol more stable than the systems with His-141 protonated on ND1. Moreover, structures with Glu-464 protonated on OE2 are ∼8 kcal/mol more stable than those with a proton on OE1 (cf. Table 2). Therefore, in the following we discuss results based on the QM3+W1 system in which Arg-259 is charged, Glu-464 is protonated on OE2, and His-141 is protonated on NE2. We call it the modified QM3+W1 system, and its structure is shown in Figure 1e).

Table 2. QM/MM Energy Differences (kcal/mol) between the Various Protonation States of Glu-464 and His-141 using the QM3+W1 System in the IM1-WT–agl+asc State.

protonated atom(s)
His-141	Glu-464	QM/MM energy difference
NE2	OE2	0.0
ND1	OE2	20.8
NE2	OE1	7.6
ND1	OE1	28.3

Then we redid the deglycosylation step of the reaction and scanned the reactions shown by arrows in Scheme 5. With this new QM system, Ow attacks Ca of the glucose moiety and passes one of its protons to the ascorbate ion, leaving β-glucose and a protonated ascorbate (l-ascorbic acid), in line with the proposed reaction mechanism by experimentalists.¹⁶ The modified QM3+W1 system gives a proper acidity of the protonated glucose moiety to pass its extra proton to ascorbate. In addition, it successfully catalyzes the glycosylation step, unlike the system with the neutralized Arg-259.

3.2. Reaction Steps

In the following, we study the glycosylation and deglycosylation reactions shown in Scheme 3 for wild-type myrosinase and its E464A, Q187A, Q187E, and Q187Eh mutants (the latter is a variant of Q187E in which the mutated glutamate is protonated on the carboxylate group). There are two alternative paths for the deglycosylation reaction, one assisted with l-ascorbate and the other without such assistance. Both paths were studied in atomic detail, and we examine on equal footing all possible reactions from the reactant and intermediate states.

Reported energies in the following are E_tot energies, which are obtained according to E_tot = E_big-QM^TZVPD + ΔG_QTCP – E_QM/MM. The exceptions are the dashed profiles in Figure 5 that are obtained using QM-cluster calculations for the second reaction step shown in Scheme 3 (cf. the first paragraph of Section 3.2.2) and the deglycosylation step of the E464A mutant, which is based on big-QM energies.

Figure 5.

Comparison of the glycosylation (left-hand side) and deglycosylation (right-hand side; assisted by ascorbate) reaction profiles between wild-type myrosinase and the mutants. The dashed lines represent reaction energies for the second reaction step shown by the second double arrow in Scheme 3 (leaving aglycon and binding ascorbate to the active site; the IM1 + ascorbate → IM1–agl+asc + aglycon reaction). Energy components of these profiles are collected in Table S7 in the Supporting Information.

3.2.1. The Glycosylation Reaction

Starting from the reactant state of the wild-type enzyme (Re-WT), there are four possible reactions (nucleophilic attack of Glu-409 and W1 on Ca and transfer of Ha and Hb from W1 to S1 and OE1 of Gln-187; these are shown by arrows in Scheme 6a). Our calculations indicated that the latter two reactions are not possible (they are uphill, and no stable products were found). In other words, the water molecule is more basic than the substrate and Gln-187. On the other hand, both nucleophilic attacks are possible. However, the barrier of the Glu-409 to Ca reaction is much lower than the barrier of W1 to Ca (9.6 vs ∼60 kcal/mol).

Scheme 6. Schematic Views of the Reactant States of the Wild-type and Mutated Proteins, Together with Tested Reactions.

Reactions found to be possible, not possible (they return to the starting point after releasing any bond constraints), and with high barriers are shown with arrows in green, red, and blue, respectively. Optimized structures of Re-WT and the mutated proteins are shown in Figure 1e and Figure S8 in the Supporting Information, respectively.

We also studied the catalytic reaction for the mutants. We start the discussion with the reactions from the reactant state of the E464A mutant (Re-E464A). The Glu-464 residue is far from the reaction center and does not directly participate in the catalytic reaction. However, it forms a hydrogen bond between the protonated carboxylate group and the −CH₂OH group of the glucose moiety of the substrate, with a −CH₂HO···HOE2− distance of 1.54 Å. This hydrogen bond is shown with a dashed blue line and is circled in green in Figure 1e. The same reactions as those of the wild-type enzyme (Scheme 6a) are possible also for the E464A mutant. Like the wild-type enzyme, the W1 to Ca nucleophilic attack has a very high barrier (∼50 kcal/mol), but that of the nucleophilic attack of Glu-409 on Ca is uphill by 9.6 kcal/mol (cf. Figure 5).

To study the importance of the Gln-187 residue in the catalytic reaction of myrosinase, we investigated all reasonable reactions from the reactant state also with the three Q187A, Q187E, and Q187Eh mutants. The reactant states of the mutated protein are shown in Scheme 6 and Figure S8 in the Supporting Information. In the reactant state of the Q187A mutant (Re-Q187A; Scheme 6b), Gln-187 is replaced by an alanine. Alanine is a hydrophobic amino acid and cannot make any hydrogen bonds with the substrate or activate the water molecule in the catalytic reaction. Our results showed that the Glu-409 to Ca reaction is not possible in this mutant. There are also other possible reactions from this mutant (Ha to S1 and W1 to Ca; cf. Scheme 6b). The results showed that both reactions are prohibitively uphill (by ∼32 and ∼70 kcal/mol, respectively). In summary, the Q187A mutant cannot catalyze any successful glycosylation reaction.

However, in the Q187E mutant, Gln-187 is replaced by a more polar and basic glutamate residue. There are four possible reactions from the reactant state of the Q187E mutant (Re-Q187E), specifically, nucleophilic attacks of Glu-409 and W1 to Ca, and transfers of Ha to S1 and Hb to Glu-187 (these are shown by arrows in Scheme 6c). Like the wild-type enzyme and the E464A and Q187A mutants, the Ha to S1 and Hb to Glu-187 reactions are unsuccessful. However, the nucleophilic attack of Glu-409 to Ca is possible (the barrier and reaction energy are 17.8 and 2.2 kcal/mol), but the nucleophilic attack of W1 has a very high barrier (∼75 kcal/mol).

The Q187Eh mutant is the same as Q187E, but the mutated glutamate residue is assumed to be protonated (Re-Q187Eh; cf. Scheme 6d and Figure S8d for the structure). The protonated glutamate resembles the catalytic acid/base group in O-glycosidases. From the reactant state of this mutant, there are five possible reactions, specifically, Ow to Ca, Ha to S1, Hb to OE2 of Glu-187, Glu-409 to Ca, and Hq (the hydrogen atom connected to OE1 of Glu-187) to S1 (these are shown by arrows in Scheme 6d). In this case, the direct nucleophilic attack of W1 to Ca has a high barrier (∼60 kcal/mol), and the Ha and Hb atoms cannot leave the water molecule (reactions shown by red arrows in Scheme 6d), as in the previous mutants. Moreover, S1 cannot abstract Hq from the protonated Glu-187. However, the nucleophilic attack of Glu-409 to Ca produces IM1′-Q187Eh (cf. Scheme 7a for the schematic structure), crossing a barrier of 5.5 kcal/mol. From the IM1′-Q187Eh intermediate, Hq can be transferred to S1. This produces IM1-Q187Eh, in which S1 is protonated by Hq, the Ca–S1 bond is cleaved, and Glu-409 forms a covalent bond to the glucose moiety (cf. Scheme 7b for the structure). Thus, there is a possible path from Re-Q187Eh to IM1-Q187Eh with an overall barrier of 10.7 kcal/mol (the energy profiles of the first reaction step from the wild-type and mutated enzymes are compared in the left-hand side of Figure 5).

Scheme 7. Schematic Views of the (a) IM1′-Q187Eh and (b) IM1-Q187Eh Intermediates.

Optimized structures of these states are shown in Figure S9 in the Supporting Information.

In summary, the W1 to Ca nucleophilic attack cannot be the first step in the myrosinase reaction (it always has a higher barrier than the Glu-409 to Ca nucleophilic attack). Moreover, the W1 water molecule cannot act as the general acid in the catalytic reaction (it can pass a proton to the S1 atom neither in the wild-type enzyme nor in the mutants). The Q187A mutant disables the enzyme, whereas the glycosylation reaction step is possible in the wild-type enzyme and the Q187E, Q187Eh, and E464A mutants. This emphasizes the necessity of a polar amino acid at the 187 position of myrosinase for the glycosylation reaction.

After the nucleophilic attack of Glu-409 on the anomeric carbon of sinigrin, Glu-409 becomes covalently bonded to the Ca of the glucose ring, the Ca–S1 bond is cleaved, and the aglycon moiety of the substrate leaves the glucose ring, producing the first intermediate of the reaction. Such a connection has been observed in crystal structures of myrosinase with a glucose ring fluorinated at the C-2 position^2,16,23 and in the glycosylation step of other enzymes in the same family.^14,31,93,94

The glycosylation step in the E464A mutant is ∼5 kcal/mol more endothermic than that of the wild-type enzyme (compare the blue and green profiles on the left-hand side of Figure 5). This shows that Glu-464 is an important residue in the glycosylation step and is important to drive the reaction in the forward direction (the E464A mutant reaction is uphill by 9.6 kcal/mol).

The Q187Eh mutant has a similar barrier to that of the wild-type enzyme (compare the purple profile with the green one on the left-hand side of Figure 5). This shows that the protonation of the S1 atom of the substrate (Glu-187 passes Hq to S1 in the first reaction step of the Q187Eh mutant) does not help in the glycosylation reaction. It has been suggested that the aglycon moiety of sinigrin is such a good leaving group that myrosinase does not need an acid/base catalyst for its activity.¹⁶ Our results confirm this: The Ca–S1 bond is cleaved after the first reaction (nucleophilic attack of Glu-409 to Ca), independent of whether the S1 atom has accepted a proton or not (the first step is possible in the wild-type enzyme, the Q187E and E464A mutants without accepting a proton, and also in the Q187Eh mutant after accepting a proton by S1). This reveals that no catalytic acid is needed for the myrosinase reaction, in contrast to O-glycosidases, which hydrolyze substrates with poor leaving groups.

As can be seen in Figure 5, the Q187E mutant has a higher barrier than those of the wild-type enzyme and the other mutants for the glycosylation step. The difference between this mutant and the others is that there are two negatively charged glutamate residues in the vicinity of sinigrin (Glu-409 and Glu-187). The extra charged glutamate residue (Glu-187) in the Q187E mutant reduces the negative charge on the aglycon moiety of sinigrin (the calculated charge of the aglycon moiety in the reactant states of the wild-type enzyme, Q187Eh, and Q187E mutants are −0.91, −1.17, and −0.76, respectively; the former is different from the charge reported in Section 3.1 because the QM systems are different). Since the aglycon moiety must leave the glucose moiety with two negative charges in the glycosylation reaction; this lower negative charge (−0.76) raises the barrier of the reaction to 17.8 kcal/mol in the Q187E mutant. Moreover, the MD simulations show that Glu-187 has a high RMSD value in this mutant, which indicates that this residue is incompatible with the active site (cf. Table 3).

Table 3. Mass-Weighted RMSD Values of the Heavy Atoms of the Backbones (BB) and Side Chains (SC) of the Active-Site Residues and the Whole Protein (in Å)^a.

	Gln-39		His-141		Asn-186		Gln-187b		Arg-259		Tyr-330		Glu-409		Glu-464c		Protein
	BB	SC	BB	SC	BB	SC	BB	SC	BB	SC	BB	SC	BB	SC	BB	SC	BB	SC
WT	0.05	0.21	0.17	0.23	0.06	0.21	0.06	0.15	0.07	0.45	0.06	0.20	0.07	0.31	0.05	0.21	1.04	1.82
E464A	0.05	0.19	0.17	0.22	0.06	0.21	0.06	0.17	0.07	0.32	0.06	0.20	0.08	0.28	0.05	0.18	1.02	1.78
Q187A	0.05	0.21	0.18	0.28	0.05	0.12	0.07	0.18	0.08	0.41	0.06	0.20	0.08	0.39	0.05	0.23	1.06	1.80
Q187E	0.05	0.19	0.14	0.15	0.08	0.10	0.06	0.96	0.08	0.37	0.06	0.20	0.08	0.34	0.05	0.23	1.05	1.83
Q187Eh	0.05	0.20	0.18	0.25	0.06	0.18	0.06	0.16	0.08	0.46	0.06	0.20	0.07	0.35	0.05	0.20	1.09	1.86

^aThe reference for the RMSD calculations was the 1E73 crystal structure.

^bThis residue is mutated to alanine and to charged and neutralized glutamate in the Q187A, Q187E, and Q187Eh mutants, respectively.

^cThis residue is mutated to alanine in the E464A mutant.

3.2.2. The Deglycosylation Reaction

In this section, we study the last reaction step, shown by the third double arrow in Scheme 3, for the wild-type enzyme and the E464A, Q187E, and Q187Eh mutants (the Q187A mutant was omitted because it failed to catalyze the glycosylation step). Moreover, since the aglycon moiety departs with a proton abstracted from Glu-187 in the Q187Eh mutant, both the Q187E and Q187Eh mutants reach to the same intermediate structure, that is, with Glu-187 deprotonated (IM1-Q187E and IM1-Q187Eh). We study the deglycosylation reaction step both with and without the assistance of ascorbate.

To connect the glycosylation and deglycosylation reaction profiles we need to have an estimate of the reaction energy shown by the second double arrow in Scheme 3 (the dissociation of aglycon and the binding of ascorbate to the active site; IM1 + ascorbate → IM1–agl+asc + aglycon). To calculate the energy of this reaction, we used QM-cluster calculations. We extracted the structures of the enzyme states (IM1 and IM1–agl+asc) from the QM/MM calculations and then optimized them without the point charge medium of the MM system, fixing the carbon atoms connected to the H-junction atoms in the crystallographic positions. However, structures of the ligands (aglycon and ascorbate) were optimized without any fixed atoms. Then, we performed frequency calculations for all states and estimated zero-point and thermal corrections to the Gibbs free energies using a normal-mode harmonic-oscillator ideal-gas approximation. To these, we added solvation energies, which were calculated with a continuum COSMO solvation model,^95,96 and single-point electronic energies in vacuum. The dielectric constant for the enzyme states and the ligands were 4 and 80, respectively. A similar method was used by Brás et al. to calculate the dissociation energy of a ligand in β-galactosidase.³² The optimization and frequency calculations were performed at the TPSS-D3/def2-SV(P) level of theory, whereas the single-point energy and COSMO calculations were performed at the def2-TZVPD level. The calculations show that the second reaction step is almost thermoneutral (0.7, 1.1, 0.9, and 0.0 kcal/mol for the wild-type enzyme and the E464A, Q187E, and Q187Eh mutants, respectively). The profiles of the second reaction step are represented by dashed lines in the middle part of Figure 5.

As is shown in Scheme 5 and discussed in Section 3.1, there are three possible reactions from the IM1-WT-agl+asc intermediate (Ow to Ca, Ha to ascorbate, and Hb to Gln-187). Among these, only the Ow to Ca reaction is possible, with a barrier and reaction energy of 3.3 and −4.9 kcal/mol, respectively (cf. the green profile in the right-hand side of Figure 5). The reaction directly produces the final product of the myrosinase reaction. The optimized structure of the product state (Pr-WT; cf. Figure 6a) shows that the enzyme retains the stereochemistry of the anomeric center, in line with experiments.²² To invert the conformation of the anomeric center, the water molecule must attack the α-face of the anomeric carbon. But this face is occupied by Glu-409 in the IM1 structure making an α-glycosidic bond (the OE1 atom of this residue is covalently bonded to Ca; cf. Scheme 5). Besides, W1 is positioned somewhere above Ca by Gln-187, which can attack the β-face only, and this retains the conformation of the anomeric center (cf. Figure 3c).

Figure 6.

Structures resulting from the attack of W1 on the anomeric carbon of (a) the wild-type enzyme and the (b) E464A and (c) Q187E/Eh mutants.

The same reactions are possible also for the IM1 state of the E464A mutant (IM1-E464A–agl+asc; cf. Figure S10a in the Supporting Information; the Hb to ascorbate and Ha to Gln-187 reactions are not possible). However, the barrier and reaction energy of the Ow to Ca reaction (8.6 and 4.1 kcal/mol, respectively) are higher than those of the wild-type enzyme (compare the blue and green profiles on the right-hand side of Figure 5). The extra proton on the glucose moiety is abstracted by the ascorbate ion (cf. Figure 6b). This was unexpected because, in this mutant, the Glu-464 is replaced by alanine, and the results in Section 3.1 showed that protonation of Glu-464 was necessary to increase the acidity of glucose to pass the extra proton. This indicates that the protonation of His-141 on NE2 and a neutral side chain of residue 464 (either a protonated glutamate in the wild-type enzyme or alanine in the E464A mutant) give enough acidity to the glucose moiety to abstract the extra proton. However, the E464A mutation elevates the deglycosylation barrier.

The optimized structure of the IM1-Q187E/Eh–agl+asc intermediate is shown in Figure S10b in the Supporting Information. We tested the three reactions in Scheme 5 also for this intermediate. The calculations showed that the Ha to ascorbate and Hb to Glu-187 reactions are not possible for this mutant (like the wild-type enzyme and the E464A mutant). However, the Ow to Ca nucleophilic attack has a low barrier (3.9 kcal/mol, cf. the red and purple profiles in the right-hand side of Figure 5) and is very exothermic (−9.5 kcal/mol). Unlike the product state of the wild-type enzyme and the E464A mutant, the extra proton of the water molecule is abstracted by Glu-187 instead of ascorbate (compare the structures in Figure 6c with the others). This shows that Glu-187 is a stronger base than ascorbate in the Q187E/Eh mutants. These mutants have a similar barrier to that of the wild-type enzyme for the deglycosylation step (3.9 vs 3.3 kcal/mol for the Q187E/Eh mutant and the wild-type enzyme, respectively).

We also tested an alternative path for the deglycosylation reaction from the IM1 structures. The leaving aglycon has two negative charges in the IM1-WT structure (cf. Figure 3a). Therefore, the sulfur anion could be a proper base to activate a water molecule for the reverse attack in the deglycosylation step. We studied the ability of the sulfide anion to activate the W1 water molecule, scanning the Ha to S1 distance in the IM1 structures of the wild-type myrosinase and the E464A and Q187E mutants. However, in none of the systems, the sulfide anion can activate the water molecule (Ha returns on Ow after releasing any distance constraints). In summary, the S1 atom of the aglycon moiety is not basic enough to activate W1 for a reverse attack.

To better understand the effects of the mutations on the catalytic reaction of myrosinase, we performed MD simulations for the wild-type and mutated enzymes. The simulations were performed starting from the 1E73 crystal structure that mimics the IM1-agl+asc intermediate. Table 3 summarizes the mass-weighted RMSDs of the heavy atoms of the backbone and side chains of the active-site residues and the whole protein. It can be seen that the backbones of the active-site amino acids in the wild-type and mutated enzymes are almost rigid and are not changed during the 200 ns simulations (the RMSDs of the backbone are between 0.05 and 0.18 Å). This shows that the mutations do not change the secondary and tertiary structures of the protein. The same applies to the side-chain RMSDs, except that of Glu-187 in the Q187E mutant (0.96 Å; this value is shown in boldface in Table 3). This implies the incongruence of this mutated residue inside the protein (the Q187E mutant has the largest barrier in the glycosylation reaction; cf. Figure 5). Thus, the RMSD values in Table 3 show that the other mutants do not significantly influence the dynamics of the active site. Therefore, they can perform the myrosinase reaction if they have electronic effects similar to those of the wild-type enzyme (the Q187A mutant disables the enzyme because alanine is much less polar than the native glutamine residue).

We performed the deglycosylation reaction also without ascorbate and compared the calculated profiles with the ascorbate-assisted ones in Figure 7. It can be seen that ascorbate decreases reaction barriers by 6–49 kcal/mol and thus increases the reaction rate. Furthermore, without such assistance, the wild-type enzyme and the E464A mutant cannot abstract the extra proton from the glucose moiety of the product. The optimized structures of the resulting products of the ascorbate-unassisted reaction are shown in Figure S11 in the Supporting Information.

Figure 7.

Comparison of the deglycosylation reaction profiles between the wild-type myrosinase and the E464A and Q187E/Eh mutants (a) with and (b) without assistance of ascorbate. To provide a fair comparison between the calculations, all energy axes have the same scale.

Myrosinase from Sinapis alba grains shows a 400-fold acceleration of the reaction rate upon addition of ascorbate, using sinigrin as the substrate.²⁴ This rate enhancement would give a barrier difference of less than 4 kcal/mol, still appreciably lower than the barrier difference in Figure 7, 7.7 kcal/mol. This overestimation could be related to the fact that the absolute unbinding energies of the aglycon moiety are not included in Figure 7b because it is hard to calculate accurate absolute unbinding energies. Including such energies in the figure may decrease the overestimation.

4. Conclusion

We have employed QM/MM calculations and MD simulations to study the catalytic reaction of myrosinase. Preliminary calculations indicated that a proper QM region to study the myrosinase reaction must contain the whole substrate, models of Gln-187, Glu-409, Gln-39, His-141, Asn-186, Tyr-330, Glu-464, Arg-259, and a water molecule close to Gln-187. It has been suggested that Gln-187 positions a water molecule for the deglycosylation reaction.¹⁶ However, our calculations show that the water molecule plays an important role also in the glycosylation step. It helps the aglycon moiety of sinigrin to tolerate a more negative charge, forming a favorable hydrogen-bond network with S1 of the substrate and OE1 of Gln-187. Thereby, the water molecule lowers the glycosylation barrier by ∼9 kcal/mol (compare the profiles in Figure 2c,d).

Our initial QM3+W1 system (shown in Figure 1d) successfully performed the glycosylation reaction, but it failed for the deglycosylation reaction (ascorbate could not abstract the extra proton from the glucose moiety in IM2-WT). Our results showed that this is not related to the size of the QM3+W1 system because a larger QM system (cf. Figure S5 for the structure) also failed in abstracting the extra proton.

Neutralizing Arg-259 in the QM3+W1 system made ascorbate basic enough to abstract the extra proton on the glucose moiety. However, this causes the QM system to fail in performing the glycosylation step. This failure shows the importance of a positively charged residue in the active site of myrosinase, which is necessary to stabilize part of the developing negative charge on the aglycon moiety in the glycosylation step (myrosinase does not have a catalytic acid/base residue like those of O-glycosidases to protonate the leaving group at the glycosylation step, and Arg-259 stabilizes part of the negative charge on the leaving group at the glycosylation step). Moreover, having a neutralized Arg-259 is unlikely owing to its large pK_a value. Interestingly, it has been suggested that the aglycon part of the substrate binds in the hydrophobic pocket and that the sulfate moiety is bound by Arg-194 and Arg-259, which are strictly conserved among myrosinase and absent in the related β-glycosidases.^2,16 This confirms the necessity of positively charged residues in the active site of myrosinase.

However, protonating Glu-464 on OE2 and His-141 on NE2 makes the glucose moiety acidic enough to pass the extra proton to the ascorbate ion, and it can still catalyze the glycosylation step. These protonation states were also stable in the MD simulations, which illustrate the use of MD simulations to assign correct protonation states of protein residues, before QM/MM calculations. This shows the necessity of choosing a proper model to study enzymatic reactions and that the size of the model system is less important than to assign proper protonation states of the active-site residues for myrosinase.

Our study of the first reaction step revealed that the water molecule (W1) can be neither the nucleophile nor the general acid in the glycosylation step (cf. Section 3.2.1). Moreover, the Q187A mutant cannot perform the glycosylation reaction. However, the glycosylation reaction step is possible in the wild-type enzyme and the Q187E, Q187Eh, and E464A mutants. This shows that residue 187 needs to have a polar side chain to make the glycosylation step possible. The E464A mutant has the highest reaction energy for the glycosylation step (cf. the left-hand side of Figure 5), which indicates that Glu-464 makes the glycosylation reaction less endothermic (by ∼5 kcal/mol). The Q187Eh mutant has a similar glycosylation barrier to that of the wild-type enzyme, and it also protonates S1, in contrast to the wild-type enzyme. This reveals that the aglycon moiety is such a good leaving group that no catalytic acid is needed for the myrosinase reaction, in line with the proposal of Burmeister et al.¹⁶ However, the charged Glu-187 residue in the Q187E mutant induces less negative charge on the aglycon moiety of the substrate, which strongly increases the glycosylation barrier (by ∼8 kcal/mol; compare the red profile with the others in the left-hand side of Figure 5). The charged Glu-187 also gives the highest RMSD compared to the other mutants (cf. Table 3), indicating some incompatibility with the active site.

Our calculations reproduce the anomeric retaining characteristic of myrosinase and indicate that the glycosylation reaction is the rate-determining step of the reaction. The barrier of the deglycosylation reaction in the E464A mutant is higher than that of the wild-type enzyme (cf. the profile on the right-hand side of Figure 5), and this confirms the importance of the Glu-464 residue in lowering the barrier of the deglycosylation step (it lowers the barrier and reaction energy by 5.3 and 9.0 kcal/mol, respectively). However, the extra proton on the glucose moiety is abstracted by the ascorbate ion (cf. Figure 6a), which shows that the protonation of His-141 on NE2 and a neutral residue 464 (either a protonated glutamate or an alanine) gives a proper acidity to the glucose moiety.

In summary, our calculations show that the ascorbate ion can act as the general base in the reaction of the wild-type enzyme if the Glu-464 and His-141 residues are properly protonated (Glu-464 protonated on OE2 and His-141 on NE2). The deglycosylation reaction has a lower barrier in the wild-type enzyme than in the mutants. In the deglycosylation step of the Q187E/Eh mutants, the Glu-187 residue acts as the general base and abstracts the extra proton instead of ascorbate in the wild-type enzyme (cf. Figure 6c).

We have also performed the deglycosylation step without the assistance of ascorbate. Comparing the energy profiles in Figure 7a,b shows that the reaction barriers are higher without ascorbate assistance. These results also are in agreement with experiments that show a lower reaction rate for myrosinase reaction without ascorbate in the medium.^{16,24−28,97}

Our calculated overall barrier for the reaction of the wild-type enzyme is 9.6 kcal/mol (cf. the green profile in Figure 5). This is in a reasonable agreement with an experiment that shows a k_cat of 119 s^–1 for the hydrolysis of sinigrin by myrosinase from Sinapis alba.⁹⁸ This value corresponds to ∼14 kcal/mol using the k_cat = 6.2 × 10¹² s^–1 exp(−ΔE/RT) formula at 300 K. The difference between the calculated and the experimental barriers can be related to different experimental and theoretical conditions.

Comparing MD simulations of the wild-type enzyme and the mutants shows that the mutations do not change the structure of the active-site residues (cf. Table 3), except that the RMSD of Glu-187 in the Q187E mutant is large (0.96 Å). Therefore, the mutants can perform the myrosinase reaction if they give rise to similar electronic effects as those in the wild-type enzyme. Among the mutants, only Q187Eh gives a similar barrier as that of the wild-type enzyme for the glycosylation step (cf. Figure 5). However, none of the mutants have a similar behavior as the wild-type enzyme for the subsequent steps.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c01121.

• Schematic views of DGHL and G2F; the model used to calculate charges for the MM force field; conformations and RMSD values of Ser-309, Val-342, and Ser-344 in the MD simulations; MM charges, force constants, and the Zn–ligand distances; further details of the MD simulations; configuration files, details, and results of the docking calculations; optimized structure of the reactant state for the QM4 system; resulting structure from transferring Ha to ascorbate when Arg-259 is neutralized; the optimized structure of the reactant state of the wild-type enzyme in the QM3+W1 system, when His-141 is protonated on NE2, and also Glu-464 is protonated on OE1; optimized structures of the Re-E464A, Re-Q187A, Re-Q187E, and Re-Q187Eh enzymes, optimized structures of the IM1′-Q187Eh, IM1-Q187Eh, IM1-E464A–agl+asc, and IM1-Q187E/Eh–agl+asc intermediates; structures resulting from the attack of W1 on the anomeric carbon of the wild-type, E464A, and Q187E/Eh enzymes without ascorbate assistance; energy components of E_tot for the reaction paths of wild-type myrosinase and its mutants; a three-plot variant of Figure 7; potential-energy profiles with QM and MM contributions; Cartesian coordinates of optimized QM regions (PDF)

The authors declare no competing financial interest.