Effects of pH on an IDP conformational Ensemble Explored by Molecular Dynamics Simulation

Abstract

The conformational ensemble of intrinsically disordered proteins, such as α-synuclein, are responsible for their function and malfunction. Misfolding of α-synuclein can lead to neurodegenerative diseases, and the ability to study their conformations and those of other intrinsically disordered proteins under varying physiological conditions can be crucial to understanding and preventing pathologies. In contrast to well-folded peptides, a consensus feature of IDPs is their low hydropathy and high charge, which makes their conformations sensitive to pH perturbation. We examine a prominent member of this subset of IDPs, α-synuclein, using a divide-and-conquer scheme that provides enhanced sampling of IDP structural ensembles. We constructed conformational ensembles of α-synuclein under neutral (pH ~ 7) and low (pH ~ 3) pH conditions and compared our results with available information obtained from experimental smFRET, SAXS (small-angle X-ray scattering), and NMR studies. Specifically, α-synuclein has been found to in a more compact state at low pH conditions and the structural changes observed are consistent with those from experiments. We also characterize the conformational and dynamic differences between these ensembles and discussed the implication on promoting pathogenic fibril formation. We find that under low pH conditions, neutralization of negatively charged residues leads to compaction of the C-terminal portion of α-synuclein while internal reorganization allows α-synuclein to maintain its overall end-to-end distance under both pH conditions. We also observe different levels of intra-protein interaction between three domains of α-synuclein at varying pH and a shift towards more hydrophilic interactions with decreasing pH.

I. Introduction

A common theme of structural biology is the connection of structure to the mechanism of biological function, and indeed in nature, most structures of proteins infer their functions [1]. A plethora of work in recent years, however, has delved into the existence and characterization of an entire class of proteins that evade conventional structural biology techniques such as crystallography, NMR, and cryo-EM. These proteins are either completely disordered called intrinsically disordered proteins (IDPs), or contain large disordered segments referred to as intrinsically disordered regions (IDRs) [2–7]. About 10% of eukaryotic proteins are suspected to be fully disordered, and 40% contain a disordered loop region of at least 50 amino acids (IDRs) [8]. Over-represented among IDPs and IDRs are proteins with regulatory functions, such as protein kinases and nuclear hormone receptors [9]. It is still unclear what is common function(s) of these IDPs and IDRs. Still, researchers assume that the outsized role of IDPs and IDRs in a host of vital cellular functions underscores the importance of understanding their underlying mechanisms. For some IDPs, their disordered nature could provide generic polymer properties important to the biopolymer, such as a linker connecting functional domains or a space-filling polymer material that is capable of phase separation for regulation [10, 11]. What is clear is that IDPs display a large degree of variation of their conformational ensembles and the ensembles are sensitive to their environments. Compared to well-folded soluble proteins containing a stable hydrophobic core and a hydrophilic exterior, the high charge and low hydrophobicity of IDPs make them more susceptible to reconfiguration due to environmental factors that affect the polar-hydrophobic “balance”, such as pH, salt concentration, and presence of amphiphilic molecules such as membrane phospholipids and micelles. Under low pH conditions, amino acid residues with ionizable sites of lower pKa values, such as aspartic and glutamic acid, are protonated reducing electrostatic interaction within the protein. Several IDPs have been shown to varying compactness under changing pH conditions [12] sometimes leading to the formation of local secondary structures, such as alpha-helices and beta-strands. A comprehensive understanding of IDP structural ensemble change modulated by pH change can be essential to fully understand not only their natural function but also the mechanisms underlying malfunction and disease states. These stimuli-responding biopolymers may also inspire researchers further design of functional biomimetics [13, 14]. Synthetic IDPs have already been explored for such applications, e.g., potential treatments for diseases such as Parkinson’s disease [15].

One of the most well studied IDP, α-synuclein, is a 140 amino acid-long protein which is upregulated in some presynaptic terminals in the brain [16]. α-synuclein is believed to be involved in vesicle trafficking and has been observed in a primarily helical form at the membrane surface, interacting more specifically with phospholipid and phospholipid-containing portions of membrane and membrane rafts [17]. While α-synuclein may form extended helical structures in lipophilic environments, it is largely unstructured in solution [18]. As with many IDPs, α-synuclein’s conformational freedom is what elude researcher from pinning down its exact function. However, α-synuclein may sometimes ‘misfold’, or take on a pathogenic configuration causing neurodegenerative diseases [19]. In patients with Parkinson’s disease (PD), for example, monomers of this protein aggregate at the hydrophobic non-beta amyloid region (NAC, residues 61–95) to form beta-amyloid plaques (termed Lewy bodies) in the perinuclear region and at the cellular periphery [20], leading to severe impairment of cognitive functioning or even death [19]. Studies have shown enhanced aggregation of α-synuclein in solution at low pH conditions [21], and understanding how these ensembles differ may provide hints about the mechanisms underlying plaque development in PD patients. It is of interest that we characterize alpha-synuclein in all of its accessible states at different pH conditions to understand what drives the aggregative properties of each ensemble. As previously discussed, the structural ensemble explored by an IDP is largely dependent on the environment [22, 23], and α-synuclein is no exception. The charge decoration of α-synuclein essentially creates three electrostatically diverse regions within the protein. The N-terminal region (residues 1–60) contains a relatively even proportion of charges, the middle ‘NAC’ region (residues 61–95) is largely hydrophobic with few charged residues, and the C-terminal portion (residues 96–140) consists largely of negatively charged amino acids. Each of these regions are expected to respond differently to factors such as pH and salt concentration. Since α-synuclein aggregates more quickly at low pH, it is important to understand how the conformational ensembles, as well as intra- and inter-protein interactions differ with changing pH. Neurodegenerative Lewy bodies are not simply the result of α-synuclein aggregating with itself but often include other disordered component proteins such as tau and Aβ-protein [24]. Examining intra-protein interactions of the synuclein monomer allows us to make inferences about inter-protein interactions involved in the heterogeneous complexes that characterize these plaques.

Because such proteins do not have a well-defined native structure, many experimental and computational strategies have difficulties when applied to IDPs straightforwardly. IDPs exhibit many low-energy conformations resulting in extremely diverse structural ensembles [9]. Only a few global properties of IDPs are routinely determined experimentally, and often they do not adequately describe, at the molecular level, the full range of structures that IDPs may explore. For example, small-angle neutron scattering (SANS) is commonly used to study the shape of these proteins [25], by inferring properties such as radius of gyration and hydrodynamic radius from neutron scattering profiles. Förster Resonance Energy Transfer (FRET) is used to determine when residues are in close proximity, revealing details about conformational changes IDPs may undergo [26]. A typical unbiased all-atom simulation of an entire large protein, including those that display intrinsic disorder, will primarily sample a single basin of the free energy landscape within computationally-accessible timescales. For a structured protein confined to a free energy landscape with a single global minimum, this does not impact sampling of a realistic conformational ensemble, especially when the native structure (ground state) is given. However, for an IDP rapidly sampling a rugged free energy landscape with many shallow basins (metastable states), this is insufficient and ineffective in terms of sampling the conformations that would be expected to be observed in practical situations.

Instead, we adopt a computational method that is specifically designed to take advantage of the weakly-interacting nature of IDPs [27]. We approach the problem of constructing a structural ensemble of IDPs from a divide-and-conquer approach, which we term PATCH, a recursive acronym standing for Patch Approach Through Connecting Hamiltonian. As we demonstrated below, these computationally-constructed ensembles reproduced key statistical properties obtained by experimental studies. Specifically, we use the simulation-based PATCH method to construct ensembles of α-synuclein under two different pH conditions which we refer to as asyn3 and asyn7, respectively. Our simulation results on pH-induced conformational changes compare well with the corresponding FRET results. Specifically, the low pH ensemble (asyn3) shows a compacted C-terminal region as compared with the neutral pH ensemble (asyn7) while maintaining approximately the same end-to-end distance, a result also seen in FRET data. Additionally, global properties, such as radius of gyration (RG) of our PATCH ensembles support the conclusion of a more compact protein at lower pH conditions and closely matches values obtained using SEC-SAXS (size exclusion chromatography-small-angle X-ray scattering) experiments [28]. We show that charge neutralization is responsible for compaction at low pH and use contact analysis methods to identify dynamically and/or structurally related domains within α-synuclein. Charge neutralization at low pH results in an increase in hydrophobicity, which has been shown to be positively correlated with the formation of pathogenic α–synuclein fibrils [29]. We investigated how contacts between the N-terminal, NAC, and C-terminal regions differ between neutral and low pH ensembles and characterize the chemical nature (hydrophobicity/hydrophilicity) of interactions between these regions.

II. Methods and systems

Many traditional protein modeling programs have been developed and have been quite successful in modeling structured proteins such as Rosetta [30], TRADeS [31], and MODELLER [32] and many others [33]. Fundamentally, these packages compute interactions based on either a bioinformatics approach [34], a biophysical approach [35], or a combination of the two. Many of these bioinformatics approaches depend on homology [36] and threading [37] techniques that largely rely upon the presence of previously discovered structured domains, which is not useful for IDPs. The biophysical approaches often employ ab-initio methods which depend on detailed all-atom and/or coarse-grained simulations, and accurately sampling sufficient conformational space requires huge amounts of computational resources and time, especially in the case of IDPs where many free-energy minima must be sampled to fully characterize the dynamics [38]. Time and resources scale exponentially with sequence length, which limits the effectiveness of these approaches to small proteins containing only a couple dozen amino acids [39]. Historically, the force fields used to describe all-atom dynamics are tuned for natively folded proteins leading to artifacts, such as over-compaction and left-handed helix formation, in disordered proteins [40]. Some have attempted to address these issues, such as the CHARMM36m force field [41] used in this work, but discrepancies with experimental results continue to be an issue when simulating IDPs. In order to adequately characterize the structural landscape of IDPs, new approaches are needed that are capable of describing their diverse conformational ensembles. It is becoming increasingly evident that computational techniques, in combination with experimental data, are greatly valuable in this area [42]. Indeed, a myriad of general methods have been developed to improve the sampling of protein energy landscapes, including simulated annealing, landscape paving, replica exchange, umbrella sampling, and simulations with experimentally-determined constraints [43]. Below, we describe and implementation of the novel PATCH method of modeling IDP ensembles.

A. IDP Sampling method overview

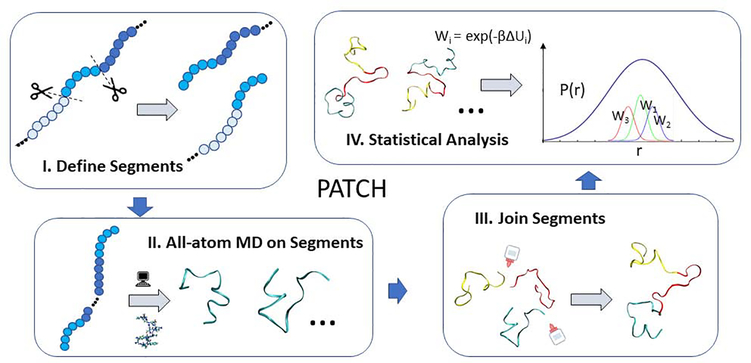
Unbiased long-time all-atom simulation does not easily capture the diversity that is characteristic of IDP conformational ensembles, especially for the system sizes beyond ~100 residues. As shown in Figure 1, the PATCH method of sampling conformations we used in the work is comprised of four steps. In Step I, we divide long peptides in to segments with overlapping regions. We then run all-atom simulations of the independent segments separately, during which only intra-segment interactions are considered, as the segments are simulated independently and do not interact in Step II. Once individual segments have been sampled, in a manner conceptually reminiscent of Monte Carlo simulation [44] of chain growth model, we rejoin the segments with matching local secondary structure. This can produce a large number of physically reasonable conformations in Step III with bonded interaction between neighboring segments approximated. Finally, we assign a statistical weight (a postori perturbation scheme) to the configurations generated, to correct for the loss of the long-ranged inter-segment interactions in Step IV.

Figure 1.

An overview of sampling method used to study α-synuclein. Panel I illustrates the cutting of a protein into shorter segments. Panel II represents the use of molecular dynamics simulations to produce a diverse ensemble of conformers fora given segment. Panel III depicts the combining of conformers to produce full IDP structures. Panel IV depicts the weighting process used to obtain the final ensemble statistics.

The rationale of statistical physics underlying this method is that total energy of the system composed of N segments can be described as a sum of three groups

$$\text{H}={\sum }_{j=1}^N{H}_{j,j}+{\sum }_{j=1}^{N-1}{H}_{j,j+1}+\sum {\sum }_{|i-j|>1}{H}_{i,j}.$$

where i and j represent segment indices. Here, we have three types of interactions: a) short-range, intra-segment interactions H_i,j (Type I), b) medium-range bonded interaction interactions H_i,j+1 between bonded atoms in neighboring segments (Type II), and c) long-range inter-segment interactions H_i,j occurring between non-bonded atoms from different segments (Type III). We employ different methods to account for each type of interaction. For intra-segment interaction H_i,j, all-atom MD simulation directly samples the conformations with appropriate statistics. Beyond the internal interactions of each segment, we use two correcting perturbation schemes to account for appropriate inter-segment interactions. One scheme is an a priori scheme, i.e., how we join different segments to form the conformation of the whole protein is affected by H_i,j+1. The other is an a postori scheme by which we weighted different joined conformations by the statistical weight of inter-segment interactions H_i,j.

For type III interaction we did not include inter-segment interaction from sequential neighboring segments. The reason for this is not dissimilar to the reasoning behind 1–4 interaction scaling to avoid double counting [45]. These ‘mid-range’ interactions are already partially accounted for during the selective joining step of the PATCH algorithm, since clashing between a segment and its sequential neighboring segment(s) would lead to prohibitively high energies, and subsequently such joined configurations being discarded. Additionally, we have also tested the same calculations including this neighboring segment interaction and found the results to have a similar R_g) in our setup. While in theory, one could devise a more elegant scaling scheme to obtain a more precise interaction energy, our simple approximation is practical and efficient, and our results have been corroborated by experimental measurements.

B. Modeling a-synuclein

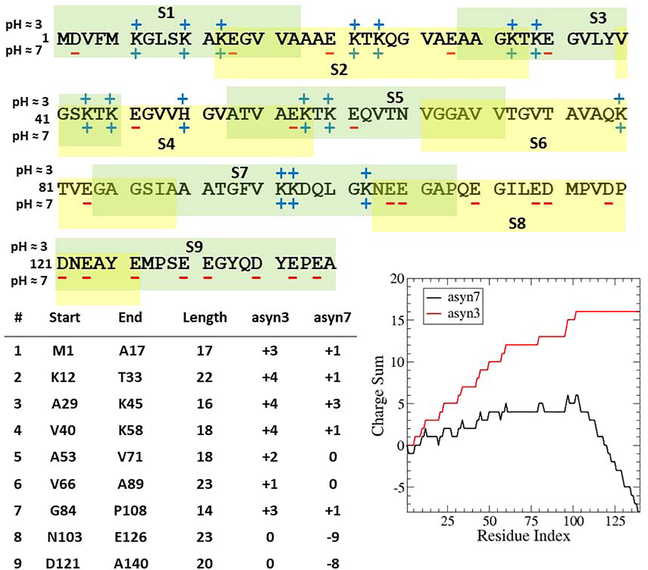
Like most IDPs, α-synuclein has an abundance of residues which are charged at pH 7, however, under low pH conditions many of these negatively charged residues are neutralized. This is shown in Figure 2 (bottom-right panel) as a running sum of charges under both approximate pH conditions of 7 (black) and 3 (red). The overall charge of the two systems is significantly different, with asyn7 having a net charge of −8 and asyn3 at +16. Here, it is apparent that the N-terminal end (residues 1 – 60) contains a relatively even mix of negatively and positively charged residues in asyn7, with slightly more positive residues than negative (8 and 11, respectively). The hydrophobic middle region (residues E61 - V95), termed the non-amyloid beta component (NAC), contains only two charged residues (K80 and E83). The C-terminal region (residues 96 – 140) possesses an abundance of negatively charged residues, with 15 negatively charged residues and only 3 positively charged. In fact, the last 38 residues contain 14 negative charges and zero positive.

Figure 2.

(top panel) Sequence of human α-synuclein with charged residues labeled for asyn3 and asyn7. Individual segments are denoted by shaded boxes with overlapping regions shown by overlapping frames. The charge state of each amino acid at pH 3 is shown above the sequence and charge state of pH 7 is shown below. (lower left) A list of charge properties for each segment.

(lower right) A running sum of the charge of α-synuclein at pH 7 (black) and pH 3 (red), where the total charge can be read at the C-terminus as −8 e and +16 e, respectively.

We obtain the relevant protein sequence from the UniProt database [46] and then divide it into segments of roughly 20 amino acids in length, including five to six overlapping residues on either end between segments, such that every segment shares five to six residues with its nearest neighbor or neighbors. In this case, six-residue overlaps were generally employed with one exception between segments 2 and 3 which have an overlap of five residues due to missing parameters in the force field which complicated the inclusion of charged glutamic acid bound to the acetyl end cap. Both the length of the overlapping boundary regions and the length of the segments themselves must be determined with care. A too-thick boundary will make the joining step difficult and the method more costly, whereas a too-thin one could lead to artificial torsion angles between segments in the reconstructed protein. In choosing the lengths and definition of the segments themselves, it is important to neither divide two highly-interactive regions nor to create segments so short that the assumption of segment independence is compromised; however, creating segments that are too long will incur a computational penalty due to the increasing number of degrees of freedom. In the case of α-synuclein, we had the benefit of data from previously performed network analysis studies [47], however, this type of information will not be readily available for most IDPs. It can be useful to employ secondary structure prediction algorithms when defining segments; care can be taken not to disrupt any regions predicted to have a typical secondary structure feature such as α-helical or β-strand character. In this regard, it is to our benefit that IDPs are generally lacking in strong long-range interactions, as was shown to be the case with α-synuclein. In this case, Sethi et al. [47] employed a network analysis model on more than 10 microseconds of simulation data and showed that α-synuclein can be divided into 9 segments in which residues frequently interact while interactions between residues of different segments are rarely observed. Therefore, in step I of the PATCH method, the protein was divided at the boundaries of those modular regions (see Table 1 for the exact segment definitions).

After segment definition, initial configurations for all-atom simulations are generated using Random Coil Generator (RCG) [48] to produce random backbone conformations with only coils and loops (no helices or beta-sheets) for both asyn7 and asyn3. Scwrl4 [49] is then used to place the sidechains on the protein backbone. Protonation states are chosen to reflect pKa values of alpha-synuclein measured using NMR [50]. pKa values, and thus, protonation states, are determined by chemical environment, which is transient in IDPs. As a result, glutamic acid and aspartic acid are always assigned a charge of −1 for asyn7 and 0 for asyn3 while lysine maintains a +1 charge in all cases, asparagine is not present in the peptide, and the lone histidine residue (H50) has a charge of +1 in both cases. Once a random starting structure for the full protein is created, the structure is split into independent segments of about twenty amino acids in length. Each segment contains the last five to six residues of the previous segment, and the first five to six residues of the next segment, a crucial step for reconstructing the entire protein later. All segments and their charge states are represented for both asyn7 and asyn3 in Figure 2.

C. Obtaining conformational ensembles at high and low pH

With our initial segment conformers generated, we performed configurational sampling of α-synuclein at approximate pH values of 3 and 7 in solution. The CHARMM36m force field was selected for parameters of protein molecules, because this version of the CHARMM force field contains CMAP corrections to improve accuracy of dihedral angles in IDPs. Conformers were placed in a rectangular PBC box solvated with TIP3P explicit water atoms and a concentration of 150mM KCL. Each of the 9 resulting segments was minimized three times using the NPT protocol. The first minimization constrained the entire protein, allowing solvent molecules to reorient around the protein. The second minimization constrained the protein backbone, allowing the sidechains to reorient. The final minimization included no constraints. The system was then heated to 298K followed by an equilibration run performed for 50 ns. Radius of gyration, N-C distance, and H-bonding were all examined for convergence to confirm proper equilibration of each system. Each system was equilibrated using the Berendsen thermostat [51] and barostat [52]. A long-time production run of 100 ns was then performed for each segment with a time step of 2 fs using the Nosé-Hoover thermostat [53] and Parrinello-Rahman barostat [54].

Once the simulations of segments are complete, structure files are extracted from the trajectories every picosecond. Statistical analysis of backbone torsion angels is performed on the overlapping residues of each segment. The optimal joint positions between two segments are ranked by how well the ψ and φ values match (evaluated by peak position of Ramachandran plots). This selection procedure ensures no two segments are joined at an “unnatural” angle. Once the preference of residues at which to join each segment were selected and the individual conformations were extracted from the trajectories, a conformer from each segment is chosen and joined to produce the entire protein (Figure 1, panel III). We first attempt to join two segments, randomly cycling through the available conformations for each segment until a structure which resulted in no steric clashes. If a resulting structure was found in close contact with heavy atoms of non-neighboring residues of the peptide (heavy atoms closer than 4.2 Å), we backtrack and attempt to join a different conformation of the current segment to the growing peptide.

The joining procedure performs RMS fitting of the backbone atoms, aligning the backbone residues of the join-residue to achieve proper orientation, sets the omega torsion angle to 180 degrees in order to avoid cis-peptide bond formation, and creates a new bond between segments while eliminating “leftover” atoms of overlapping residues. If the available conformations are exhausted with no successful join partners found, the next residue in the list of best overlapping residues is used to repeat the process. This process is iterated until all segments of the protein are re-joined to create a unique protein conformation. This resultant structure is saved in PDB format and the processes starts again. We seek to exclude cis-bonds as these are only rarely seen in proline residues in nature, and we want to ensure only natural left-handed peptides are created. Each final structure is checked for chirality errors and the presence of cis-peptide bonds.

Although we assume that the segments are primarily independent (non-interacting), it is nonetheless true that there may be some long-range interactions that we have lost in the reconstruction procedure. To correct for this, we employ a weighting technique which allows the recovery of these interactions in the final ensemble (Figure 1, panel IV). Each configuration is weighted according to the Boltzmann factor and an energy function which only takes into consideration inter-segment long-range interactions (Coulombic and Lennard-Jones terms). To accomplish this, each conformer is minimized for 10,000 steps using a Generalized Born implicit solvation method (GBSA) [55]. Implicit solvent methods can efficiently average over solvent configurations and provide meaningful interaction free energies between different segments [56]. After this minimization, the inter-segment energies are found by first calculating the energy of the entire protein and then subtracting energy contributions from intra-segment interactions. A weight factor is determined for each conformer and this value is used to determine the contribution of each conformation to the overall statistics of the ensemble.

III. Results and Discussion

Following the PATCH procedure, a total of 1734 conformations for asyn7 and 1894 conformations for asyn3 were obtained for further analysis. Note that since not every join attempt results in a successful conformation, the final number of conformations are not artificially held to be the same for asyn3 and asyn7. Below, we examine pH induced global changes measured by distances between residues in subsection A, and then local, secondary structure changes in subsection B. Subsection C provides a contact-based description of asyn7 and asyn3, and subsection D takes a closer look at the types of interactions characteristic of each ensemble. Since the resulting IDP conformational ensemble contains a diverse set of partially unfolded structures and, unlike RMSD fitting for folded structures, a structural alignment is not informative, we provide representative snapshots of the ensemble in Supplementary Information (SI) Figure S1. Besides the ensemble average presented for each property, we also display the results of block analysis in SI Figures S1–S4, where we divide the data for two subsets to test statistical robustness of the results. For asyn7, both subsets 1 and 2 contain 867 conformations and for asyn3, both subsets contain 947 conformations. The level of the convergence between the two subsets illustrates the robustness of the results we presented.

A. pH induced global conformational changes

Once ayn3 and asyn7 ensembles were obtained we assessed their structural differences by observing their radius of gyration and residue-residue distance values. Gyradius is a global property typically used to describe the size of a protein. We display the probability distribution of radii of gyration for these two systems in Figure 3 (left panel). As seen in Figure 3, when comparing the radius of gyration values for the weighted ensembles, the asyn7 ensemble had an average 4.09nm (peak at 3.75 nm), whereas, in the case of asyn3, the average value is 3.68 (peak at 3.6 nm). This compaction is consistent with trends seen in SAXS experiments, which are denoted in Figure 3 by vertical lines. The black dashed line represents the experimental gyradius value of 3.59 nm at pH 7.4 calculated by Araki et. al [28] using SEC-SAXS. The dotted-dashed lines show SAXS-based gyradius values calculated by Uversky et. al at physiological pH (black) and pH 3 (red), 4.0 nm and 3.0 nm, respectively [57]. While radius of gyration can be informative about the general level of compaction of a system, it is only one value, and taken alone is not enough to accurately characterize the full structural ensemble of an IDP. Besides gyradius information, we also provide an internal scaling profile (ISP) in Figure 3 (right panel), which is essentially a distance measurement used as a measure of compactness to characterize IDP global conformations [58]. The ISP shows that for residue pairs within 15 amino acids in sequence (short-range interactions), asyn3 shows slightly larger distances, while pairs more than 15 residues apart in sequence are closer together for asyn3 than for asyn7. This supports the conclusion that α-synuclein is more globally compact at lower pH.

Figure 3.

(A) The probability distribution of gyradius for asyn7 (black) and asyn3 (red). The black dashed line represents the experimental gyradius value at physiological pH calculated by Araki et. al [28] using SEC-SAXS. The dotted-dashed lines show SAXS-based gyradius values calculated by Fink et. al at physiological pH (black) and pH ~ 3 (red). (B) The internal scaling profile is shown for asyn7 (black) and asyn3 (red).

Previously, traditional all-atom MD simulations have been used to calculate the radius of gyration of alpha-synuclein. In this study, Sethi et. al run as set of 100 100ns long simulations of alpha-synuclein using the OPLS forcefield and the SPC-E water model. The average radius of gyration after equilibration was found to be 2.1 nm with values falling in the range of 1.6 to 3.0 nm, which indicates a more compact structure relative to our results and recent experimental values. Similar results have been obtained from simulations using the CHARM 27 forcefield [59]. This difference demonstrates the limitations of earlier, and even current [60], force fields in studying intrinsically disordered proteins. More recent studies have been performed utilizing protein force fields and water models modified to more closely reproduce experimental values of IDPs [61]. Benchmarks run by Robustelli et. al tested multiple force fields with modified parameters intended to increase accuracy for IDPs, including one based on the AMBER99SB force field and TIP4P water model which produced a mean R_g of 3.7nm, and another using a combination of the CHARMM force field along with a chain-growth model which reported an average R_g of 4.0nm [60].

To further validate the ensembles obtained with the PATCH method, we compare our results with smFRET studies performed by Rhoades et al. [26]. The FRET efficiency distributions for asyn7 and asyn3 were examined, specifically, one FRET probe at residue E130 and a second probe at residue S9, T33, T54, T72, or T92. High FRET efficiency corresponds to a short distance between probes and vice versa. Quantitative conversion between FRET electron transfer efficiency and physical distance between residues is not always plausible due to several factors including probe’s chemistry and geometry and the resolution of microscopy experiments. Further, limitation on capturing protein dynamics experimentally and adequate sampling of computationally derived ensemble makes a direct comparison between FRET experiments and simulation challenging. However, comparisons can be made to identify corresponding trends in the data. In Figure 4, we show the inverse distance distributions calculated by the PATCH method at neutral pH and pH ~ 3 and find our ensembles are qualitatively consistent with the FRET trends observed by Trexler et. al (see Figure 2 of reference [26]). We see very little difference between the end-to-end distance (the distance and FRET efficiency of residues S9 and E130) dependent on pH. In contrast, there is a significant shortening of the C-terminal end for asyn3, as seen in the corresponding lower distances and higher FRET efficiencies between residues E130 and T92, E130 and T72, and E130 and T54.

Figure 4.

Inverse of residue pair distances (selected residues to E130 at C-terminus) obtained from simulation. They are selected for a direct comparison with available experimental data and arranged in the same order used in FRET efficiency (Figure 2 of ref. [26]). The distributions of 1/r are shown with pH ~ 7 represented by a black line and pH ~ 3 represented by a red line.

The C-terminal shortening observed in the FRET/distance comparison is the result of this heavily negatively charged region becoming neutralized upon protonation at low pH. Electrostatic repulsion from glutamic and aspartic acid residues is eliminated allowing nearby residues to interact more freely. This point is illustrated in Figure 5, which, examines the distances between six charged residue pairs with decreasing sequence distance for each pH condition. Figure 5a shows a significant difference with asyn3 exhibiting distances an average of 40 Å less than asyn7 between residues E104 and E139. This trend is observed further in subsequent panels until sequence distance is reduced to just a few amino acids. The N-terminal region contains a relatively well-balanced combination of negatively and positively charged residues at pH 7, and one might speculate that protonation of negatively charged side chains in this region reduces the influence of attractive electrostatic interactions by leaving a net negative charge in the region, resulting in a compensatory elongation of the N-terminus. After plotting distance values of residue pairs of decreasing distance as before, we found this was not observed to be the case (Figure S5); both distance data from PATCH ensembles and FRET data from the N-terminal region show no significant difference, including no compensatory elongation, in the N-terminus (Figure S6).

Figure 5.

Distance distributions of six charged residue pairs for asyn7 (black) and asyn3 (red). Panel A has the largest sequence distance between residues, which decreases with each panel.

B. pH induced local conformational changes

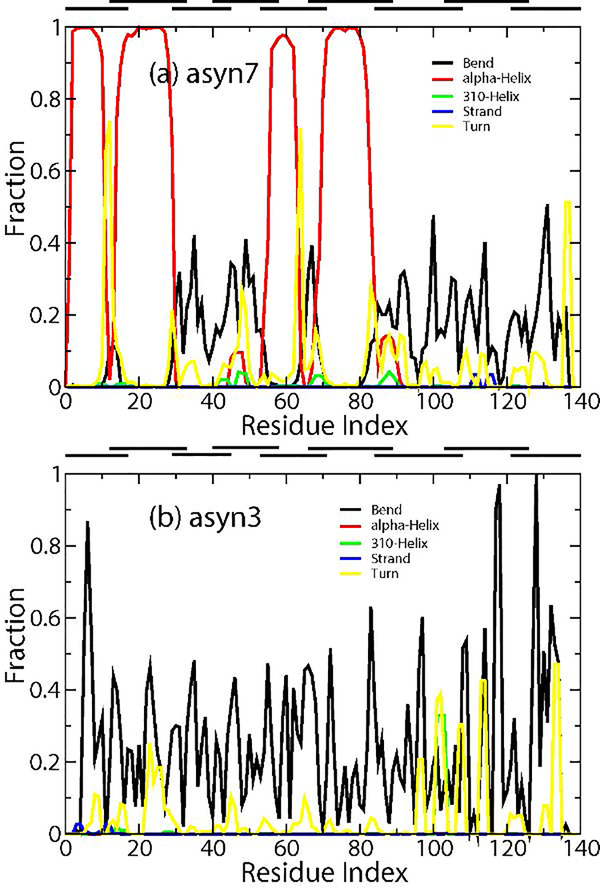
While IDPs generally lack structure, many do explore transient (very short-lived and small) structures such as α-helices and β-strands. For some IDPs, environmental conditions, such as pH, can trigger ordering and disordering of local structures [22, 23]. The propensities of asyn7 and asyn3 to form secondary structures are shown in Figure 6, excluding the unstructured coils that are the primary component of IDPs. Some of the predominant components of each are turns and bends, representative of the disorder of the peptide. However, one particularly interesting result is the near constant presence of four short α-helical segments (approximately residues 2–11, 14–29, 55–64, and 70–83) in asyn7; such features are absent in asyn3. There are two prevalent beta-turns, one separating the first and second helices, and another between the third and fourth helices, which cause a sharp angle disrupting what may otherwise be two larger helices. in asyn7 Secondary structure predictors, such as JPRED [62], consistently predict the N-terminal portion of α-synuclein to be α-helical, however experiments find that these helices may exist only in lipophilic environments or transiently in monomeric α-synuclein at physiological pH. Eliezer et al. performed NMR experiments and observed five transient helices within the first 100 residues [63], while Kim et al. found only a single transient helix between residues 10 and 30 in a lipid-free environment [64]. The only exception was reported in the presence of other factors such as a heavy concentration of lipophilic molecules [65, 66].

Figure 6.

Secondary structure composition of asyn7 ensemble (A) and asyn3 ensemble (B). Multiple types of coils and turns indicative of disorder are excluded for clarity. Y-axis represents the fraction of conformers where a structure is present.

Upon further inspection of Figure 6a, it is notable that each helix is expressed within the bounds of individual segments, although not always positioned in the center of the segment. Segments 1 and 2 both contain α-helices separated by a turn or bend at the segment boundary, whereas JPRED predicts a single helix spanning these two segments and part of segment 3. The same is true for segments 5 and 6; they are both mostly helical in a region predicted to be one long helix. JPRED also predicts the presence of a shorter α-helix from residues 46 to 56 which is present in about 10% of conformers. Figure 6b shows the only secondary structure present in the asyn3 ensemble are short transient 3₁₀ helices at the N-terminal end and a more prevalent short 3₁₀ helix in segment 7. Each segment which contains an α-helix in asyn7 has a relative increase in net charge in asyn3, with three of four segments gaining multiple protons. These changes appear to be sufficient to remove the helix-forming tendencies within their respective peptides. It is also plausible that the membrane-bound state of α-synuclein promotes the formation of predicted α-helices through disruption of intra-protein interactions or formation of lipid-protein interactions.

Studies on aggregation of α-synuclein fibrils report β-sheet formation of monomers at the NAC region with monomers showing evidence of transient β-pin structures near the beginning of the C-terminal domain or, less frequently, towards the end of the N-terminal domain [67, 68]. The PATCH ensembles agree somewhat, as asyn7 shows a small percentage of β-hairpin tendency with two short β-strands at residues 112 and 116 only while asyn3 displays β-hairpin tendencies with β-strands at residues 2–7 and 10–15 of the N-terminus and a lesser propensity represented at the C-terminal domain by residues 100–102 and 104–106 (Figure 6b).

C. pH induced structural changes viewed from contact analysis

IDPs among other semi-structured biopolymers present unique challenges to structure characterization since they contain an ensemble of ambiguous and transient structures, whereas a typical protein can be described by a well-defined set of Cartesian coordinates. Rather than attempting to pin down a single structure expressed by its Cartesian coordinates, residue-residue contacts can be a more appropriate degree of freedom for describing the structural features of partially folded and unfolded structures [69, 70]. Statistical analysis of residue-residue contacts can be more suitable than that of Cartesians when they are used to describe conformational change. Contact DOFs have been used to examine protein dynamics in a variety of cases, from folding, conformational switch, to allostery [71–73]. Contact interaction and contact DOFs can be used to describe the conformations of other structured or semi-structured biopolymers such as chromosomes [74] and polysaccharides [75]. Although IDPs do not have well-defined 3D structured domains, they may still contain consistent structure features identifiable using statistical analysis of contacts.

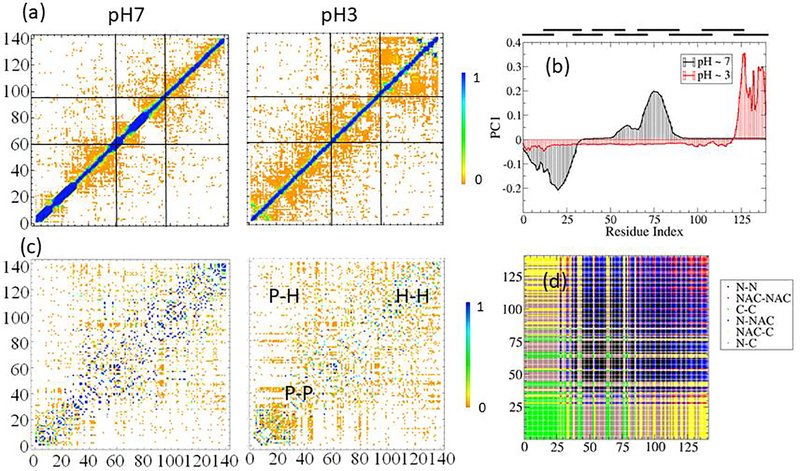
Using a simple binary definition of a contact formation between residues i and j, u_ij = Θ(R^C−R_ij), where Heaviside function Θ() renders u = 1 when contact is formed and 0 otherwise. Here R_ij is the shortest distance between any heavy atoms (non-hydrogen) of the two residues and R^C corresponds to a distance cutoff. In this case, R^C = 4.5Å. Further, we define an ensemble average contact frequency, U_ij = 〈u_ij〉. The average is appropriate ensemble average which weighted by inter-segment contacts as we have defined in the Method Section. The mean contact maps U_ij are shown in Figure 7a for the asyn7 (left panel) and asyn3 (right panel) systems. One key observation is that asyn3 forms more residue-residue contacts in general relative to asyn7, which indicates α-synuclein is more packed at low pH condition than the high pH condition. This greater degree of interaction for asyn3 is especially prominent when comparing the C-terminal regions due to the neutralization of negative charges. The black lines at the top of Figure 7a delineate the three regions of the protein: N-terminus, NAC, and C-terminus. The formation of stable helices restricts the residues involved from interacting with other parts of the protein, exaggerating the fact that asyn3 has more interactions between all regions.

Figure 7.

Results of contact analyses. (A) Weighted contact maps representing the persistent contacts at each pH condition are shown, with asyn7 on the left and asyn3 on the right. (B) The graph depicts the first principal component resulting from mean implicit principal component analysis (mi-PCA), with neutral pH represented by a black line and low pH with a red line. (C) Residues are re-ranked according to their hydrophobicity and contacts are plotted onto this hydrophobicity space. Index 1 represents the least hydrophobic (most hydrophilic) residue and index 140 represents the most hydrophobic (least hydrophilic) residue. All rankings are based on the physiological pH condition. (C, left) Hydrophobicity-ranked contact map for asyn7. (C, right) Hydrophobicity-ranked contact map for asyn3. (D) Residues are shown re-ranked by hydrophobicity with contacts between differing regions (N-terminus, NAC, C-terminus) represented by different colors.

Several types of contact analyses can be applied to study protein structures and often as a result, they define protein domains, from network analysis [47] to principal component analysis of contacts such as I-PCA [74]. Specifically, network analysis can group residues based on properties of the protein structural network. In the case of α-synuclein, long-time all-atom MD simulations of the whole asyn7 system were carried out and the results of a network analysis are used in this work as the basis of the definitions of the 9 segments, as we recapitulated in the method section [47]. Alternatively, I-PCA (and its variant form, MI-PCA) is also based on contact matrices and can reveal the consensus structure of a semi-structured ensemble of biopolymers; I-PCA has been commonly used to analyze chromosome contact interaction data [76]. Such methods have been useful for identifying spatially correlated regions of chromosomes, so-called compartments, regions which tend to pack together and are either gene rich (A-compartment) or gene poor (B-compartment). Application of I-PCA to folded protein can lead to domain identification for well folded proteins [74]. It is interesting to apply I-PCA to IDPs to see whether there are any features that can be located.

The results of I-PCA are described using the eigenvectors plotted as functions of residue index [74]. Distinct structural domain boundaries can be associated with the locations of the curve intercepting with x-axis. Often a high peak (or vice versa, a deep valley) indicates a strong and concerted contact formation and thus a structural domain. In terms of IDPs, such peaks and valleys may indicate strongly packed regions of the protein. The input information is of MI-PCA is the mean contact matrix (Figure 7a) and the top eigenvector is shown as the result of the analysis for both systems (Figure 7b). In asyn3, we see largely two domains. The first domain is roughly represented by segments 1 through 8, after which a sign of the top eigenvector curve changes which indicates a domain boundary. The second domain has a strong peak at the C-terminus spanning segment 9. For asyn7, the structure ensemble again largely contains two domains, the first domain spanning from segments 1 and 2, and the second spanning segments 3 to 9 with a peak in segment 6. Taking a closer look at asyn7 in Figure 7b, both peaks are bimodal and align with the four helices observed in Figure 6 (left panel). Figure 7 captures the vast structural difference of this region due to pH changes and subsequent charge differences. The results indicate that for asyn3, the C-terminus is largely collapsed whereas for the asyn7, a more packed N-terminal region is shown. This conclusion is consistent with both the distance calculation-based results of the previous subsection and with the underlying electrostatic driving force due to the change of protonation status at different pH values.

D. Physical interaction of pH induced conformational changes

For conventional soluble proteins of moderate size, folding into a stable and specific conformation relies on a strong hydrophobic core. A typical folded protein has largely hydrophilic outside and hydrophobic interior whereas an integral membrane protein has an “inside-out” design. In contrast, IDPs lack these features and often are highly charged and hydrophilic [38]. Interestingly, a change of pH affects the protonation status of the ionizable sites and thus may affect the hydrophobic-hydrophilic balance and one speculates it may be the driving forces for α-synuclein conformation changes induced by pH change. It is thus useful to examine what is the dominant contact interaction for the IDP structure ensemble from the viewpoint of physical interaction. Thus, in this subsection, we focus on the nature of the contacts by hydrophobic vs polar (hydrophilic) residues.

To achieve this, we rearrange and display the conventional contact strength information (contact map) which is based on residue index to a new index that is based on hydrophobicity. The transformed plot can explicitly indicate how the strength of hydrophobic vs hydrophilic residues affects the IDP ensemble. Such plots have been called ‘saddle’ plots and are frequently used in chromosome structural analysis where A/B compartments (representing euchromatin and heterochromatin, respectively) drive the phase separation of the copolymer resulting in stronger AA and BB contacts and weaker AB contacts [76]. Similarly, protein structural formation has been viewed as phase separation of hydrophobic vs polar residues. Specifically, the mean contact matrices displayed in Figure 7(a) are rearranged as follows. The axis of a typical contact map is according to the residue index, whereas in the new plot, the hydrophobicity score of the residue can be used for this purpose. Thus, for asyn7, the most hydrophilic residue is ranked as 1 and the most hydrophobic is ranked as 140. For scoring, we chose the conventional Kyte-Doolittle hydrophobicity scoring method [77]. Since this score is purely a function of 20 types of residue identity, we must employ a scoring function capable of breaking symmetry caused by multiple amino acid residues of the same type showing up in the sequence. Thus, for our hydrophobicity ranking to be meaningful, we consider not only the target residue position, but those neighboring residues which compose the local chemical environment. In our quantification, we weight each residue and its adjacent residues according to a weight 0.95^|i−j| if |i − j| ≤ 5 and 0 otherwise. Several weighting schemes were tested and this ad hoc scheme captures a decaying influence of neighbors up to a few residues ensuring the reported value is neither too local, defined almost entirely by a single amino acid, or too broad, giving very similar values to a large region of the map.

Using a mean contact map of the IDP ensemble as input, we project the average contact information onto this hydrophobicity-hydrophilicity (H-P) indexed space. Note that hydrophobicity values of the Kyte-Doolittle scale were determined for residues at a pH near 7 and there is no independent scale for low pH conditions, thus, the same index for both plots in Figure 7c are based on hydrophobic rankings at pH = 7. Even though many residues will become more or less hydrophobic under low pH conditions, keeping the indices consistent allows us to see how the contacts change. In the lower-left corner are the hydrophilic residue contacts (PP) while those in the upper-right corner show contacts between hydrophobic residues (HH). Intuitively, only contact interaction between the same classes of residues (hydrophobic-hydrophobic and polar-polar) residues are prominent, giving the matrix a ‘saddle’-like shape for well-folded proteins that fold around a hydrophobic core. This feature is notably absent here, and we speculate the absence is the case for a class of IDPs. The resulting matrix in Figure 7c shows that, for asyn3, we have a relatively even distribution of forces with a slight emphasis on hydrophobic interactions. The neutralization of negatively charged aspartic acid and glutamic acid residues in asyn3 leads to a decrease in the prevalence of polar interactions and an increase in polar-hydrophobic interactions relative to asyn7. The increased hydrophobicity of the C-terminus due to protonation of aspartic and glutamic acid residues along with the compaction due to removal of repulsive negative charges leads to more interactions with the hydrophobic NAC region.

As a reference to better understand the connection between the three regions (N, NAC, and C) of contacts made and the contact map displayed on the hydrophobicity index, we rearrange the six regions (intra-N, intra-NAC, intra-C, N-NAC, NAC-C, and N-C) of the original contact map and display ranked by hydrophobicity in Figure 7d. Interactions between the most polar pairs of residues (lower left) are comprised of residues within the C-terminal region, which contains heavily polar and charged residues, followed by interactions by residues within the N-terminal region with the most hydrophobic driven interactions occurring within the NAC region. At neutral pH, the NAC region is by far the most hydrophobic region and tends to be self-interacting, however, at low pH, the increased hydrophobicity of the C-terminus allows more interactions between the NAC domain and C-terminus. The reduced self-interaction of NAC may free up this region to interact with the N and C termini regions of the alpha-synuclein monomer, but also with other alpha-synuclein molecules and even with other proteins, such as tau and Aβ-protein found in Lewy bodies. This change in interaction strength may play a role in increased rates of pathogenic aggregation observed at low pH by experiments.

IV. Concluding remarks

To fully understand IDPs/IDRs, it is essential to characterize not just an average structure or ground state structure, but a well-populated ensemble of configurations. Furthermore, IDP conformations by nature are often sensitive to environmental conditions such as pH. Here, we use a novel approach to obtain a diverse sampling of the conformational landscape of α-synuclein at two pH conditions. Using the divide-and-conquer PATCH approach, we have constructed pH-dependent ensembles which have local and global structural features consistent with the corresponding experimental characterizations of α-synuclein. Drastic local and global structural differences between asyn3 and asyn7 were reported and the neutralization of negative charges in the C-terminal region is responsible for the significant compaction seen at low pH conditions. The structural finding here may have implications on the pathogenic aggregation of α-synuclein. Particularly, reduced self-interaction of the NAC region as well as increased interaction between the NAC and C-terminal domains due to increased hydrophobicity and elimination of adjacent negative charges may create new opportunities for inter-protein interactions resulting in aggregation. The computational method used can be a useful method to sample the conformations of other natural IDPs and to design synthetic IDPs for desired pH sensing properties.

• a novel divide-and-conquer computational method to sample IDP at different pH conditions

• predicted conformational changes upon pH perturbation are shown to be consistent with experiments

• under low pH conditions, neutralization of negatively charged residues leads to compaction of the C-terminal portion of α-synuclein

• internal reorganization allows α-synuclein to maintain its overall end-to-end distance under both pH conditions.