Unsupervised random forests

Abstract

sidClustering is a new random forests unsupervised machine learning algorithm. The first step in sidClustering involves what is called sidification of the features: staggering the features to have mutually exclusive ranges (called the staggered interaction data [SID] main features) and then forming all pairwise interactions (called the SID interaction features). Then a multivariate random forest (able to handle both continuous and categorical variables) is used to predict the SID main features. We establish uniqueness of sidification and show how multivariate impurity splitting is able to identify clusters. The proposed sidClustering method is adept at finding clusters arising from categorical and continuous variables and retains all the important advantages of random forests. The method is illustrated using simulated and real data as well as two in depth case studies, one from a large multi-institutional study of esophageal cancer, and the other involving hospital charges for cardiovascular patients.

1 |. INTRODUCTION

Machine learning is generally divided into two branches: supervised and unsupervised learning. In supervised machine learning, the response is known and the intent is to train a model to predict its value, while in unsupervised learning the target variable needs to be determined from a set of known features. One of the most famous examples of this type of algorithm is k-means clustering [14] but a major drawback of this method is its lack of feature selection which becomes increasingly important as the dimensionality of the problem increases. Another challenging aspect is when the data exhibit a mix of both numerical as well as categorical feature variables (referred to as mixed data). Such data is very common in modern big data settings such as in medical and health care problems. However many unsupervised methods are better suited for data containing only continuous variables. This includes methods dependent on densities [12], those that rely on connectivity-based approaches [10] and methods that rely on distance metrics such as k-nearest neighbor approaches [16]. Even mixture model methods, which are widely used tools for unsupervised clustering, are not always appropriate. This is because when the data are of a mixed type, standard distributions used for mixture modeling may not be valid [15].

In this paper, we introduce a new random forests based method for unsupervised learning. The benefit of using random forests [1] is that we can take advantage of its many excellent properties to deal with the challenges of unsupervised learning. For example, dealing with mixed data is naturally addressed under the random forests framework, as the process of growing and splitting a tree naturally accommodates both continuous and categorical data. Also random forests is scalable to big data, due to trees being trained independently, thus allowing for parallelization of the algorithm. Furthermore, it is robust to outliers due to the well-known robustness property of trees. Feature selection has been shown to be an imperative part of high-dimensional clustering [6, 11], otherwise the noise features can greatly influence the clustering result away from the desired result. Our approach will be able to circumvent this issue by taking advantage of random forests ability to weed out uninformative variables.

Algorithm 1.

sidClustering

1: procedure sidClustering(${\left({\mathbf{X}}_i\right)}_{i=1}^n$, δ)

2:  Sidify the original variables using Algorithm 2

3:  Use SID interaction features to predict SID main features using MVRF

4:  Extract the random forest distance from the trained multivariate forest

5:  Calculate Euclidean distance on the matrix of distances

6:  Cluster the observations based on distance of Step 5 utilizing HC or PAM

7: end procedure

One strategy of unsupervised algorithms involves reworking the problem into a supervised classification problem [5, 13]. Breiman’s unsupervised method [2] is one widely known random forests method which uses this strategy. The idea is to generate an artificial dataset that goes into the model alongside the original data. A random classification forest (RF-C) is trained on the combined data (original + artificial) and the proximity matrix is extracted from the resulting forest. Then standard clustering techniques can be utilized on the proximity matrix such as hierarchical clustering [7] or partitioning about medoids [18] to determine clusters (for convenience we refer to these techniques as hierarchcial clustering [HC] and partitioning about medoids [PAM], respectively).

Although Breiman’s clustering method has been demonstrated to work well, it is highly dependent on the distribution chosen for the artificial data class. Therefore, we introduce a new random forests based method for unsupervised learning which we call sidClustering. The new sidClustering method is based on two new concepts: (1) sidification of the data; (2) multivariate random forests (MVRF) [22] applied to the sidified data to develop distance between points via the multivariate relationship between features and their two-way interactions. Section 2 formally describes the sidClustering method and details how sidification works. We show uniqueness of the sidification mapping and provide justification for how multivariate splitting using sidified interactions yields good clustering properties. Section 3 provides two real world data examples illustrating the algorithm. Section 3.1 describes a case study involving esophageal cancer patients while Section 3.2 presents a case study of hospital costs for cardiovascular patients. Section 4 uses benchmark experiments to compare sidClustering to Breiman clustering and other competitive procedures using both simulations and real datasets and shows superiority of the proposed method in many cases. Section 5 discusses our primary findings.

2 |. SIDCLUSTERING

Throughout we use X = (X₁, …, X_d)^T to represent the d-dimensional feature and ${\mathcal{L}}_n={\left({\mathbf{X}}_i\right)}_{i=1}^n$ to denote the i.i.d. learning data. Algorithm 1 presents a formal description of the sidClustering algorithm. Line 2 creates the enhanced feature space from the sidification of the data. We call this new data, staggered interaction data (SID). Line 3 fits a MVRF using the SID main features as response values and the SID interaction features as the predictors. The distance matrix between points obtained from the multivariate regression are extracted in Line 4 and then converted to Euclidean distance in Line 5. Clusters are then obtained in Line 6 by applying either HC or PAM using the Euclidean distance based on the random forest distance matrix obtained in Line 4.

The key idea behind sidClustering is to turn the unsupervised problem into a multivariate regression problem. The multivariate outcomes are denoted by Y = (Y₁, …, Y_d)^T and are called the SID main effects. The Y is obtained by shifting the original X features by making them strictly positive and staggering them so their ranges are mutually exclusive (we think of this process as “staggering”). Translating the range of the original features in this way is permissible due to the invariance of trees under monotonic transformations [3]. For example, suppose X_j and X_k are coordinates of X which are continuous. Then the SID main effects obtained from X_j and X_k are coordinates Y_j and Y_k of Y defined by

$$Y_j={\delta }_j+X_j,Y_k={\delta }_k+X_k,$$

where δ_j, δ_k > 0 are real values suitably chosen so that Y_j, Y_k are positive and the range of Y_j and Y_k do not overlap. Section 2 provides a detailed description of sidification, here we are discussing things more informally in order to motivate the key ideas behind our approach. The features used in the multivariate regression are denoted by Z and are called the SID interaction features. The SID interaction features are obtained by forming all pairwise interactions of the SID main effects, Y. Going back to our example above, the SID interaction corresponding to features X_j and X_k is some coordinate of Z denoted by X_j ★ X_k and defined to be the product of Y_j and Y_k

$$X_j★X_k=Y_j\times Y_k=({\delta }_j+X_j)({\delta }_k+X_k).$$

As will be shown, the staggering of Y_j and Y_k so that their ranges do not overlap will ensure identification between the SID interactions Z (which are the features in the multivariate regression) and the SID main effects Y (which are the outcomes in the multivariate regression).

The rationale for using sidified data for our multivariate regression tree approach is as follows. Because Y is directly related to X, informative X features will be cut by their SID interactions Z because this bring about a decrease in impurity in Y (and hence X). This then allows cluster separation, because if coordinates of X are informative for clusters, then they will vary over the space in a systematic manner. As long as the SID interaction features Z are uniquely determined by the original features X, cuts along Z will be able to find the regions where the X informative features vary by cluster, thereby not only reducing impurity, but also separating the clusters which are dependent on those features.

Obviously uniqueness between X, Y, and Z plays a crucial role in making sidClustering work. The identification of sidification will be established shortly, but first we provide an example to help motivate the basic idea. For our illustration we simulate data from a V-shaped distribution that creates two clusters that intersect at the origin (X₁, X₂)^T = (0, 0)^T and diverge as X₁ becomes positive. Table 1 describes the simulation. Notice that d = 10 because the simulation contains noise variables; however while the data lies in d = 10 dimensions, the V-shape cluster sits within the lower dimensional space of the first two coordinates. For simplicity we therefore focus only on (X₁, X₂)^T and ignore the other coordinates for our discussion.

TABLE 1.

V-shaped cluster simulation

Variable	Simulated by
X1 (signal variable)	~Uniform(0, 1)
X2 (signal variable)	First 250, = X1 + Normal(0, 0.2)
	Last 250, = −X1 + Normal(0, 0.2)
X3, …, X10 (noise variables)	~Uniform(0, 1)

The top left panel of Figure 1 displays the data for the first two dimensions from the simulation. Data values are colored black and red to indicate cluster membership: observe how points lie along a V-shape. The top right panel plots X = (X₁, X₂)^T against the SID interaction feature Z = X₁ ★ X₂. In the bottom coplot, SID main effects Y = (Y₁, Y₂)^T are plotted against Z. We can use this coplot to understand how a multivariate regression tree might behave using Y for the outcome and Z as the feature. Looking at the coplot notice how there are promising cuts along Z that can not only reduce impurity of the responses (Y₁, Y₂)^T but also lead to effective separation between the true clusters. For example, low values of Z (region A) yield small Y₁ values and large Y₂ values, whereas large values of Z (region F) yield large Y₁ values and large Y₂ values, and the two groups are perfectly separated in cluster membership. Due to the large difference in response values in regions A and F, a split on Z separating these values would lead to a large drop in impurity, and thus a multivariate regression tree would seek to split these regions. The same holds true for regions B, C, D, and E. On the other hand, consider what would happen if the same tree used the original data (X₁, X₂)^T for the multivariate outcome. The coplot from the top panel illustrates this scenario. The problem is that (X₁, X₂)^T varies far less than (Y₁, Y₂)^T as Z changes. For example, regions C, D, E, which correspond to data near the origin, have similar X₁ and X₂ values. Thus a split on Z between these regions would be less effective in reducing impurity and the multivariate tree would be less likely to separate region C from D and E. This does not happen when (Y₁, Y₂)^T is used because Y₁ and Y₂ do not overlap due to staggering and thus (Y₁, Y₂)^T changes more rapidly with Z. This also explains why we use (Y₁, Y₂)^T and not (X₁, X₂)^T for the outcomes in the multivariate regression, even though these two values are directly related (compare the left top panel to the left bottom panel to see the effect of staggering).

FIGURE 1.

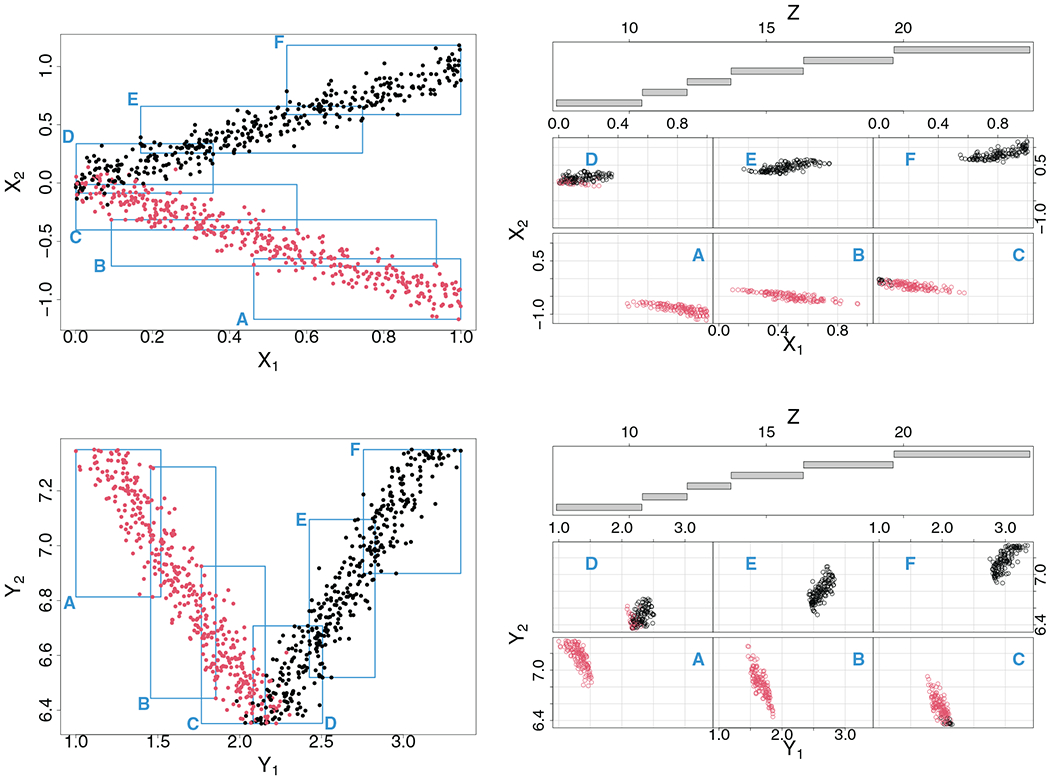
V-shaped two cluster simulation illustrating the basic concept behind sidification and sidClustering. Data are displayed as points on the figures and are colored black and red to indicate cluster membership (observe how points lie along a V-shape). Top right panel shows coplot of original features (X₁, X₂)^T against SID interaction Z = X₁ ★ X₂. Regions labeled A–E in the coplot are identified by rectangles in the left scatter plot. In the bottom panel, the coplot is displayed in terms of the SID main effects (Y₁, Y₂)

We also would like to explain why we use SID interactions Z for the features in the multivariate regression. Basically, interactions are a way to create meaningful synthetic features so that the unsupervised problem can be converted to a multivariate regression problem. However for this to work, it is crucial for identification to hold between Z and X. This is an important property which does not hold for just any type of interaction: for example standard interactions constructed from X do not have this property. Figure 2 illustrates this point. The figure shows the difference between an algebraic interaction and a SID interaction for the V-shaped data. Arrows map (X₁, X₂)^T points to their interaction value (displayed on the second horizontal axis). Arrows in the right-hand figure display mapping to the algebraic interaction X₁ × X₂. As X₁ gets closer to zero, there is more symmetry in the values for X₁ and X₂ which leads to nearly identical X₁ × X₂ values. This is apparent by the bunching up of arrows (both black and red) for these points. Thus there is a lack of uniqueness between X₁ × X₂ and (X₁, X₂)^T. In contrast, the left-hand figure displays the mapping to the sidified interaction Z = X₁ ★ X₂. Notice that arrows are no longer bunched up and are mapped to unique values. Thus SID interactions Z are uniquely mapped to the original features (X₁, X₂)^T. This uniqueness is due to the staggering used for (Y₁, Y₂)^T because recall that the Z interaction, Z = X₁ ★ X₂, equals the algebraic interaction of the Y values, Z = Y₁ ★ Y₂, and because of staggering (Y₁, Y₂)^T does not suffer from the symmetry seen with (X₁, X₂)^T which is what causes the breakdown in identification.

FIGURE 2.

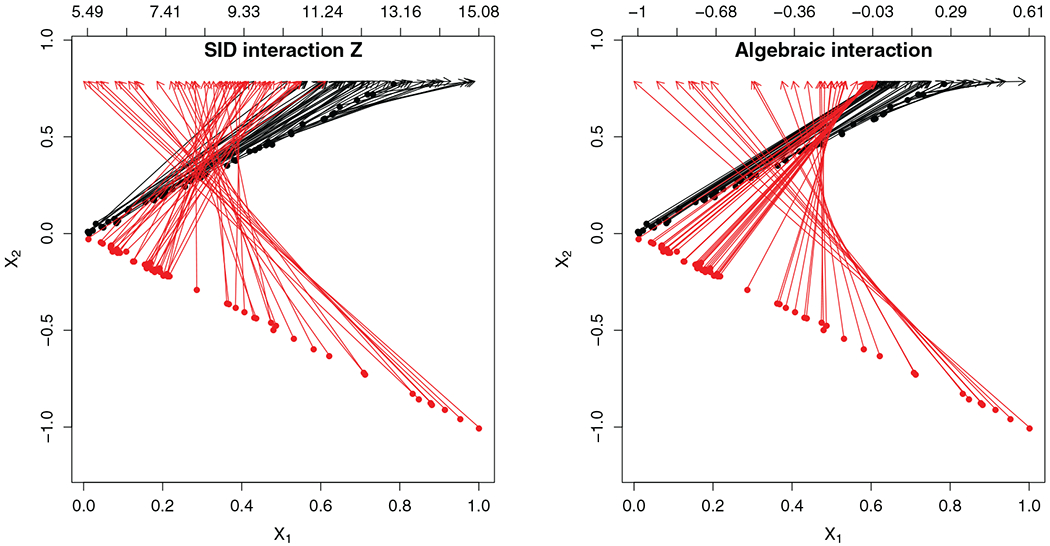
V-shaped two cluster simulation illustrating uniqueness of sidification. Arrows map (X₁, X₂) points to their interaction value displayed on the second horizontal axis. Left-hand figure shows mapping to the sidified Z interaction. Right-hand figure is the map to the usual algebraic product X₁ × X₂. Observe the bunching up of arrows indicating lack of uniqueness

The remainder of this section is devoted to providing further details for the sidClustering algorithm as well as presenting supporting theory. We start in Section 2 by describing sidification in detail. A parameter required by sidification is δ > 0 which specifies the size of the translation used in staggering. As will be shown in Section 2.3 (Theorem 3) δ can be set to an arbitrary positive number (we use δ = 1) under a simple data preprocessing step. Multivariate regression trees which are used in Line 3 of the algorithm are discussed in Section 2.2. There we describe the relationship between impurity and multivariate splitting. Finally, Section 2.4 discusses the random forest distance metric used in Line 4. This is a new forest distance metric and calculated in a different way than traditional random forest proximity.

2.1 |. Sidification

Formally, sidification is a two-step map from the feature space $\mathcal{X}$ for the original features X to the artificially created SID space for (Y, Z), which we denote by $\mathcal{Y}\times \mathcal{Z}$. In the first step, called staggering, the SID main space is obtained by shifting the original features X by making them strictly positive and staggering them so their ranges are mutually exclusive, yielding Y. We denote this map by $\mathcal{Y}=\varphi \left(\mathcal{X}\right)$. In the second step, SID interaction features Z are obtained by forming all pairwise interactions of the SID main effects, Y. We denote this second step as the map $\mathcal{Z}=\psi \left(\mathcal{Y}\right)$. Thus sidification is the map:

$$\mathbf{X}\in \mathcal{x}\to (\mathbf{Y},\mathbf{Z})\in \mathcal{y}\times \mathcal{z}=\left\{(\varphi (\mathbf{X}),\psi (\varphi (\mathbf{X})):\mathbf{X}\in \mathcal{x}\right\}.$$

In practice, sidification is applied to the learning data ${\mathcal{L}}_n={\left({\mathbf{X}}_i\right)}_{i=1}^n$. To distinguish abstract sidification from sidification used in practice, we will use a subscript of n. In practice, sidification maps the learning space to the sidified space as follows:

$$\begin{gathered} {\mathcal{L}}_n\to {\mathcal{L}}_n^S=\left\{({\varphi }_n({\mathbf{X}}_i),{\psi }_n({\varphi }_n({\mathbf{X}}_i))):i=1,\dots ,n\right\} \\ =\left\{({\mathbf{Y}}_1,{\mathbf{Z}}_1),\dots ,({\mathbf{Y}}_1,{\mathbf{Z}}_n)\right\}. \end{gathered}$$

Algorithm 2 provides a formal description of this procedure. Lines 2 and 3 translate continuous features to be positive with the same maximum value and then reorders them by their range. Theorem 3 will show this improves separation of distance between certain types of clusters. Lines 4–8 are the staggering process which results in the main SID features ${\left({\mathbf{Y}}_i\right)}_{i=1}^n$ (see Line 9). Lines 10–16 form pairwise interactions of main SID features resulting in the SID interaction features ${\left({\mathbf{Z}}_i\right)}_{i=1}^n$ described in Line 17. The algorithm returns the sidified data ${\mathcal{L}}_n^S={({\mathbf{Y}}_i,{\mathbf{Z}}_i)}_{i=1}^n$ in Line 19.

2.1.1 |. Uniqueness of sidification

Because sidClustering is designed to uncover clustering in the original features, it is clear that sidified data must preserve the structure of the original data in order for the procedure to work. In particular to be successful, we require a 1:1 relationship between the SID main features, ${\left({\mathbf{Y}}_i\right)}_{i=1}^n$, the SID interaction features, ${\left({\mathbf{Z}}_i\right)}_{i=1}^n$, and the original features, ${\left({\mathbf{X}}_i\right)}_{i=1}^n$.

To satisfy uniqueness, we assume that coordinates of X are either finitely discrete or that they are continuous with a nondegenerate density. For notational convenience we assume the coordinates of X have been arranged so that discrete features appear first. If 0 ≤ p ≤ d denotes the number of discrete features, then the remaining d − p features are assumed to be continuous (if p = d then there are no continuous features). We make the following assumptions:

• A1. If X_j is a discrete feature, then X_j has a discrete density function with respect to counting measure and its space ${\mathcal{X}}_{\left(j\right)}$ satisfies $\mid {\mathcal{X}}_{\left(j\right)}\mid <\infty$.

• A2. The joint density for the continuous features has a d − p dimensional support with respect to Lebesgue measure on ${\mathbb{R}}^{d-p}$.

Under these mild assumptions, the following uniqueness property of sidification holds (see the Appendix for a proof).

Theorem 1. Let (Y_i, Z_i) be the sidified main and interaction features corresponding to X_i for i = 1, …, n. Then with probability one, Z_i = Z_i′, if and only if X_i = X_i′ if and only if Y_i = Y_i′.

2.2 |. Multivariate regression trees: relationship of impurity to clusters

Earlier we used the V-shaped clustering problem to motivate sidClustering by illustrating how impurity and clustering were related (recall Figure 1). This relationship between impurity and clustering holds in general and is formalized by the next result. To simplify matters, we will assume d = 2 and that both coordinates of Y are continuous. Let Y = (Y₁, Y₂)^T and ${\mathbf{Y}}^{\ast }=(Y_1^{\ast },Y_2^{\ast })$ be two distinct points to be separated. Let ${\mathcal{Y}}_n$ denote the SID main space which is assumed to be a two-dimensional rectangle, ${\mathcal{Y}}_n=[a_1,a_2]\times [b_1,b_2]$. The following result describes how splits defined in the SID interaction space ${\mathcal{Z}}_n$ are able to separate points in the main effect space ${\mathcal{Y}}_n$ while preserving clusters (see the Appendix for a proof).

Algorithm 2.

Sidification

1: procedure Sidification(${\left({\mathbf{X}}_i\right)}_{i=1}^n$, δ = 1

2:  Translate each continuous feature so that they are positive and all have the same maximum value (note that the minimum value can differ over variables)

3:  Order the variables in terms of their range with variables with largest range appearing first. This applies only to continuous variables (factors are placed randomly at the end)

4:  Convert any categorical variable with more than two categories to a set of zero-one dummy variables with one for each category

5:  Add δ to the first variable

6:  for number of input variables, excluding the first do

7:   Add δ plus the maximum of the previous input variable to the current variable

8:  end for

9:  ${\left({\mathbf{X}}_i\right)}_{i=1}^n$ have now been staggered to ${\left({\mathbf{Y}}_i\right)}_{i=1}^n={\left({\varphi }_n\right({\mathbf{X}}_i\left)\right)}_{i=1}^n$ the main SID features

10:  for all pairs of main SID features (from Line 9) do

11:   if a pair consists of two dummy variables then

12:    Interaction is a four level factor for each dummy variable combination

13:   else

14:    Create interaction variable by multiplying them

15:   end if

16:  end for

17:  This yields ${\left({\mathbf{Z}}_i\right)}_{i=1}^n={\left({\psi }_n\right({\varphi }_n\left({\mathbf{X}}_i\right))}_{i=1}^n$ the SID interaction features

18: end procedure

19: return ${\mathcal{L}}_n^S={({\mathbf{Y}}_i,{\mathbf{Z}}_i)}_{i=1}^n={\left({\varphi }_n\right({\mathbf{X}}_i),{\psi }_n({\varphi }_n\left({\mathbf{X}}_i\right)\left)\right)}_{i=1}^n$ the sidified data

Theorem 2. Without loss of generality, let $Y_1<Y_1^{\ast }$.

Case I: $Y_2\le Y_2^{\ast }$. Then every value along the vector $\mathbf{Y}{\overrightarrow{\mathbf{Y}}}^{\ast }$ from Y to Y* can be separated by a single SID interaction split with values along $\mathbf{Y}{\overrightarrow{\mathbf{Y}}}^{\ast }$ assigned to Y if they are to the left of the split-point and to Y* if they are to the right of the split-point.

Case II: $Y_2>Y_2^{\ast }$ and $Y_1{Y}_2<Y_1^{\ast },Y_2^{\ast }$. Then Y and Y* can be separated using two SID interaction splits with values along $\mathbf{Y}{\overrightarrow{\mathbf{Y}}}^{\ast }$ to the left of the first split assigned to Y and values to the right of the second split assigned to Y*.

We return to Figure 1 to help explain Theorem 2. Case I applies to points Y = (Y₁, Y₂)^T in region C and points ${\mathbf{Y}}^{\ast }={(Y_1^{\ast },Y_2^{\ast })}^T$ in region E. This is because $Y_1<Y_1^{\ast }$ and $Y_2<Y_2^{\ast }$ for most points in these two regions. Theorem 2 asserts that for any two points satisfying Case I, there exists a split on Z that separates the two points as well as any data lying along their vector $\mathbf{Y}{\overrightarrow{\mathbf{Y}}}^{\ast }$. For example any value of Z in region D would be an example of such a split. Because $\mathbf{Y}{\overrightarrow{\mathbf{Y}}}^{\ast }$ passes through D, all data in D along this vector will be assigned either to the cluster for C (left split on Z) or the cluster for E (right split on Z). Applying this principle to all Y and Y* in C and E, we can conclude that since the multivariate tree will seek to split C and E (as it will lead to a large impurity drop), it will split C and E within D using a single split on Z. This will assign C and E to different nodes of the tree with most values within D likely assigned to the node with E.

Case II applies to points in regions C and D. This is because there are Y = (Y₁, Y₂)^T in C and ${\mathbf{Y}}^{\ast }=(Y_1^{\ast },Y_2^{\ast })$ in D such that $Y_1<Y_1^{\ast }$ and $Y_2>Y_2^{\ast }$. Also, $Z=Y_1{Y}_2<Z^{\ast }=Y_1^{\ast }{Y}_2^{\ast }$ for any two points in C and D. Theorem 2 asserts that for points satisfying Case II, two splits on Z are needed. One split will separate data primarily using the Y₁ response. The second split will separate primarily on Y₂. Notice that this makes sense as it would help separate the black points in C and the red points D, which are the difficult cases to classify.

2.3 |. Ordering coordinates and selecting δ

A third and final case arises for Theorem 2 when the two coordinates have the following configurations: $Y_1<Y_1^{\ast }$, $Y_2>Y_2^{\ast }$ and $Y_1{Y}_2\ge Y_1^{\ast }{Y}_2^{\ast }$. This is a more difficult scenario but can be mitigated by the simple remedy of ordering the coordinates so that the first coordinate always has a much larger range; thus helping to reduce this scenario. This helps explain why we use the ordering step in Line 3 of the sidification algorithm (Algorithm 2). Ordering also has an another important consequence for sidClustering. By reordering the original features in descending order of range, this maximizes the range of the resulting SID interaction, thus further improving separation of distance for the two cases considered in Theorem 2.

The next result describes how ordering increases the range of SID interactions. However as the result shows, this requires setting δ > 0 to a suitable value. Because this may not always be easy to do, a simple method for preprocessing the data is provided which makes the choice of δ irrelevant. This preprocessing step is implemented in Line 2 of Algorithm 2. See the Appendix for a proof of the following.

Theorem 3. For a suitably large enough δ > 0, sorting the SID main effects in descending order of range of the original features maximizes the range of SID interaction features. Thus the range of X_k ★ X_l is larger when X_k is placed before X_l in the design matrix if the range of X_k is larger than X_l. Because selecting δ may be difficult to do in practice, the following preprocessing step can be used which allows any value of δ > 0 to be used: prior to sidifying the data, first translate each continuous feature so that they are positive and all have the same maximum value. Then if variables are sorted by their range, the conclusion above holds for the resulting sidified data for any δ > 0. For concreteness the value δ = 1 is used in all examples throughout the paper.

2.4 |. New forest distance

Finally we discuss the new forest distance metric used in Line 4 of Algorithm 1. Like proximity, the goal of the new distance is to measure dissimilarity between observations, however unlike proximity it does not use terminal node membership for assessing closeness of data points. Instead, it uses a measurement of distance based on the tree topology to provide a more sensitive measurement. The issue with proximity is that if two observations split far down the tree versus close to the root node, both scenarios are counted as having a proximity of zero, even though the first scenario involves data points closer in the sense of the tree topology.

Let T_b denote the bth tree in a forest. The forest distance is applied to SID interaction features Z. For each pair of observed data points Z_i and Z_j, define S(Z_i, Z_j, T_b) to equal the minimum number of splits on the path from the terminal node containing Z_i to the terminal node containing Z_j in T_b such that the path includes at least one common ancestor node of Z_i and Z_j. Similarly, define R(Z_i, Z_j, T_b) as the minimum number of splits on the path from the terminal node containing Z_i to the terminal node containing Z_j in T_b such that the path includes the root node. We define the forest distance between Z_i and Z_j as:

$$\begin{gathered} D({\mathbf{Z}}_i,{\mathbf{Z}}_j)=\frac{1}{\mathrm{ntree}}\sum _{b=1}^{\mathrm{ntree}}D({\mathbf{Z}}_i,{\mathbf{Z}}_j,T_b) \\ =\frac{1}{\mathrm{ntree}}\sum _{b=1}^{\mathrm{ntree}}\frac{S({\mathbf{Z}}_i,{\mathbf{Z}}_j,T_b)}{R({\mathbf{Z}}_i,{\mathbf{Z}}_j,T_b)}. \end{gathered}$$

As an example, observe when two observations share the same terminal node, we have D(Z_i, Z_j, T_b) = 0 since the numerator is a measure of zero splits. Also, in the case where two observations diverge at the first split, S(Z_i, Z_j, T_b) = R(Z_i, Z_j, T_b), and the tree distance equals one.

2.5 |. Motivating examples comparing sidClustering to Breiman clustering

We end this section by providing two detailed examples that illustrate the difference in splitting between Breiman clustering, the current clustering method used by random forests, and sidClustering. These examples neatly explain why sidClustering is superior.

Algorithm 3 presents a formal description of the Breiman clustering method. The algorithm requires the following parameters: ntree (number of trees trained in the forest), nodesize (terminal node size), and mtry (number of random features used to split a tree node). As discussed earlier, the idea is to generate an artificial dataset with an artificial class label and then train a random classification forest on the combined data. Clustering is performed using the proximity matrix extracted from the resulting forest. As was mentioned, a concern with Breiman’s clustering method is its sensitivity to the method used to generate the artificial data. Shi and Horvath [21] refine Breiman’s clustering method to address this. They considered two different modes for generating the artificial class data which we will use as comparative procedures:

SH mode 1: Randomly draw from each set of observed features to form new features.

SH mode 2: Fit a uniform distribution for each of the features and draw from it. The uniform distribution is constrained to lie between the minimum and maximum value of a given feature.

Algorithm 3.

Breiman Clustering

1: Develop second artificial set of data

2: Label original observations class 1 and newly devised ones class 2

3: Set the class label Ci as the response i = 1, …, N where N = 2n

4: procedure RF-C(${({\mathbf{X}}_i,C_i)}_{i=1}^N$, ntree, nodesize, mtry)

5:  for ntree do

6:   Select N values with replacement from (Xi, Ci), i = 1, .., N

7:   for all nodes do

8:    while observations in node > nodesize & impurity present do

9:     Randomly select mtry features for splitting

10:      Split tree node decreasing impurity most

11:    end while

12:   end for

13:  end for

14: end procedure

15: Utilizing HC or PAM, cluster the data using the proximity matrix for the original observations

2.5.1 |. V-shaped cluster simulation

For our first example, we return to our previous V-shaped cluster simulation. Figure 3(A) displays the results of running a single multivariate regression tree on the sidified data (results are displayed for the first two coordinates). Observe how the tree is able to accurately separate the two clusters. This is confirmed by the confusion matrix displayed in table (D). The latter was obtained by running sidClustering using 1000 multivariate regression trees. Clusters were obtained using PAM.

FIGURE 3.

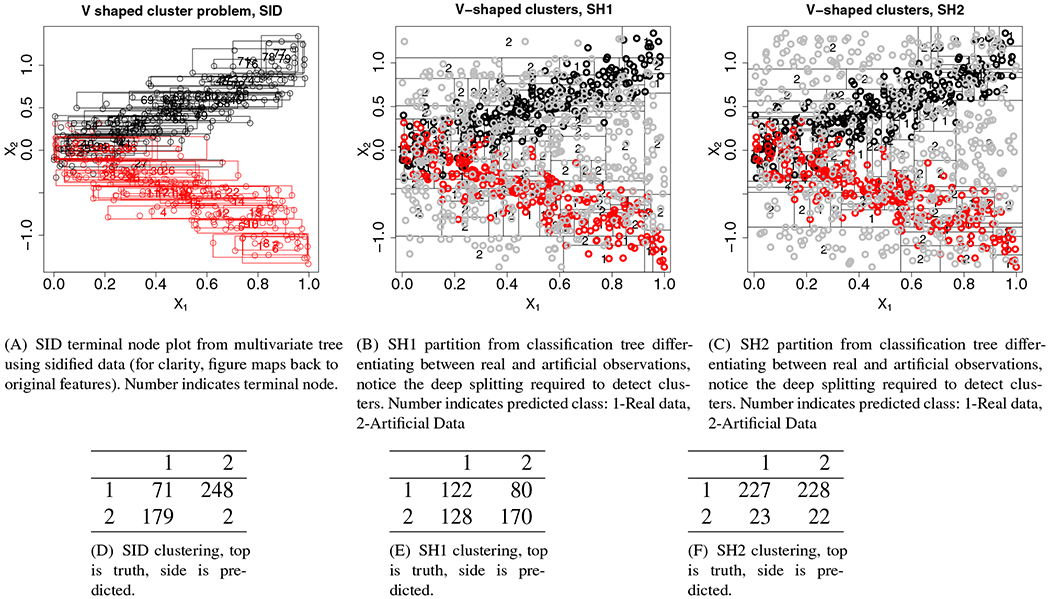
Splitting by three methods on V-shaped cluster problem. (●) Cluster 1; () Cluster 2; () SH artificial data

Comparing sidClustering to Breiman clustering, panels (B), (C) display the partition resulting from a single classification tree using artificial data obtained using Shi-Horvath Modes 1 and 2 (denoted by SH1 and SH2). The goal in Breiman clustering is for the tree to separate the artificial data (gray points) from the true classes (black and red points). However even with a very deep tree (large number of cells), the tree is not able to properly discern differences between the two clusters. This is most apparent as we move toward the origin, which is where clustering is the most difficult. This poor performance is confirmed by tables (E) and (F). The two tables display the confusion matrices obtained by running 1000 trees using Breiman clustering for SH1 and SH2 data with PAM applied to the proximity matrix. The tables clearly demonstrate poor performance.

2.5.2 |. Four-bivariate normal clusters

Table 2 presents our second example and changes the problem in two major ways. First, we now have two-way symmetry between the clusters, and second we have increased the number of clusters from 2 to 4. Again, we see that both SH methods require heavy splitting to detect the clusters (subpanels (C) and (D) of Figure 4). This unfortunately works diametrically to the idea of random forest proximity. Random forest proximity measures the average number of times two observations share a terminal node and if each tree requires deep splitting to discern clusters then it is likely that the average proximity between any two given points will be close to zero. This is illustrated in tables (F) and (G) by the tendency of both methods to put the vast majority of points in the same cluster (in other words, SH is only detecting one cluster). In comparison, the partitions for SID are able to carve out the space such that the clusters are grouped together (subpanel (B) of Figure 4), and this in conjunction with random forest distance, allows for observations in different terminal nodes to still have an informative measure (table (E)). Notice from the coplot in Figure 4 (subpanel [H]) how there are promising cuts along the SID interaction feature x₁ ★ x₂ that can reduce impurity of the SID variables (x₁, x₂) while also separating the four clusters.

TABLE 2.

Four-bivariate normal simulation

Variable	Simulated by
X1, X2 (signal variables)	~First 500, Bivariate Normal $\left(\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 4\hfill \end{array}\right],\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 4\hfill \end{array}\right]\right)$
	Next 500, Bivariate Normal $\left(\left[\begin{array}{c}\hfill 4\hfill \\ \hfill 0\hfill \end{array}\right],\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 4\hfill \end{array}\right]\right)$
	Next 500, Bivariate Normal $\left(\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -4\hfill \end{array}\right],\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 4\hfill \end{array}\right]\right)$
	Final 500, Bivariate Normal $\left(\left[\begin{array}{c}\hfill -4\hfill \\ \hfill 0\hfill \end{array}\right],\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 4\hfill \end{array}\right]\right)$
X3, …, X20 (noise variables)	~Normal(0, 1)

FIGURE 4.

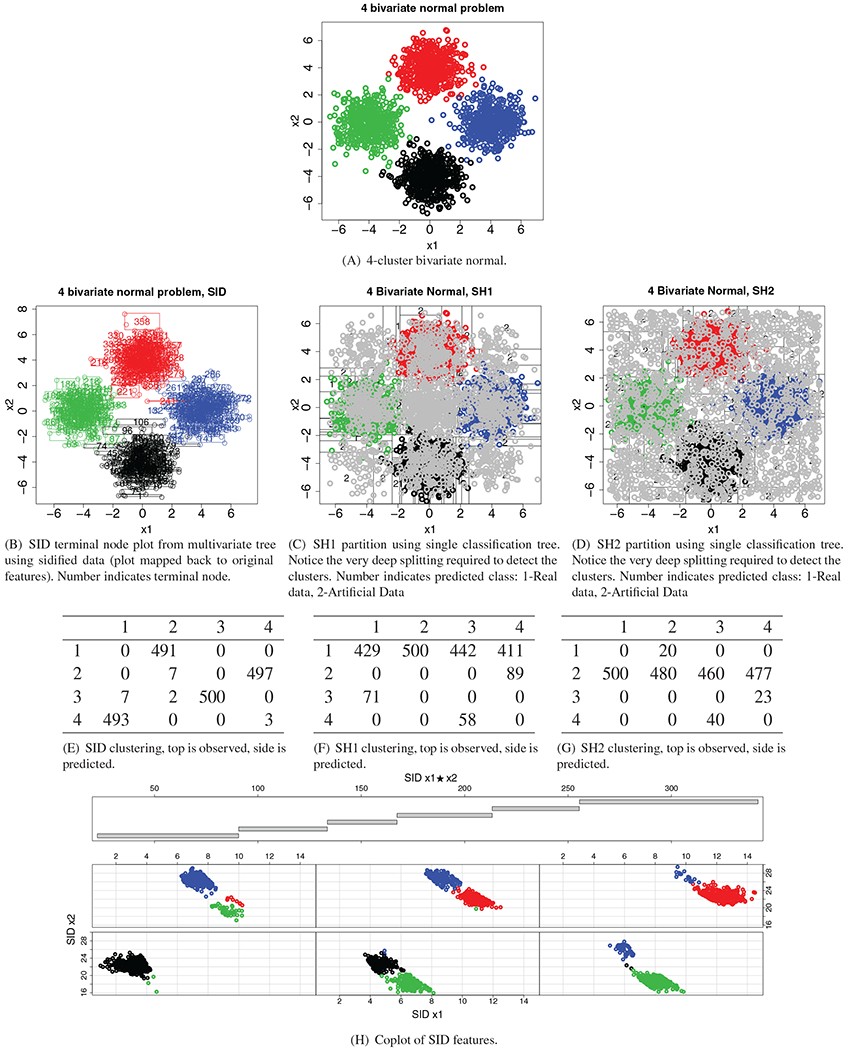
Splitting by three methods on 4-bivariate normal cluster problem. () Cluster 1; () Cluster 2; () Cluster 3; (●) Cluster 4; () SH artificial data

3 |. REAL WORLD EXAMPLES

In this section, we provide two illustrations of sidClustering to real world data. In both cases, sidClustering was implemented using the randomForestSRC R-package [8]. Because feature selection was necessary to reduce dimensionality in the two problems, and in order to control run time performance, we utilized a feature selection algorithm. We used Shi–Hovarth’s method as a first pass through, which is relatively computationally cheap, and used variable importance [9] from the classification forest to select the most informative variables. sidClustering was then run using the filtered variables.

3.1 |. Identifying patient differences across multiple institutions

The World Wide Esophageal Cancer Collaboration (WECC) was a large multi-institutional effort to accrue data from esophageal cancer patients. The goals were to: (1) better understand clinical and pathologic prognostic implications for the disease; (2) better facilitate pretreatment prognostication; and (3) improve clinical decision-making [19]. In total, 22,654 patients were accrued at 33 different institutions from 6 different continents. Of these patients, 13,993 were adenocarcinoma, which will be the focus of our analysis.

Patients were represented across the spectrum of common therapies. This included esophagectomy alone, the primary treatment for esophageal cancer patients, esophagectomy and adjuvant therapy, neoadjuvant therapy with esophagectomy and neoadjuvant and adjuvant therapy with esophagectomy. Additionally patients receiving endoscopy only, chemoradiotherapy only, palliative care and no therapy were also accrued. Patient cancer variables included clinical level characteristics (cTNM), pathological level characteristics (pTNM), and characteristics for patients with neoadjuvant therapy (ypTNM). Other cancer characteristics included histologic grade, length of tumor, number of regional resected nodes, and location and distance of cancer. Patient level information included demographics (age, gender, race), patient characteristics (BMI, weight loss, ECOG), and comorbidities (example: diabetes, heart related diseases, other cancers, kidney). In total, there were d = 38 variables comprising dichotomous, categorical, and continuous variables.

The endpoint used for the primary WECC analysis was all-cause mortality defined from first management decision for a patient. Here we consider a different goal and remove the outcome and apply sidClustering to the unsupervised data in order to study and quantify differences in patient makeup across institutions. We regard this as the first step in assessing quality of hospital care. Quantifying patient characteristics helps to identify possible systematic differences between hospitals. This is important, since if systematic bias exists, then quality of care cannot be assessed by direct comparison of outcomes, and advanced techniques (such as causal inference) would have to be applied to obtain correct inference.

Hierarchical clustering (HC) was applied to the distance matrix obtained from running sidClustering to the data. Number of clusters was set to 20. The results are displayed in Figure 5. Features appear along rows of the heatmap, while columns are patients which have been sorted by institution with institutions grouped by proximity according to clusters.

FIGURE 5.

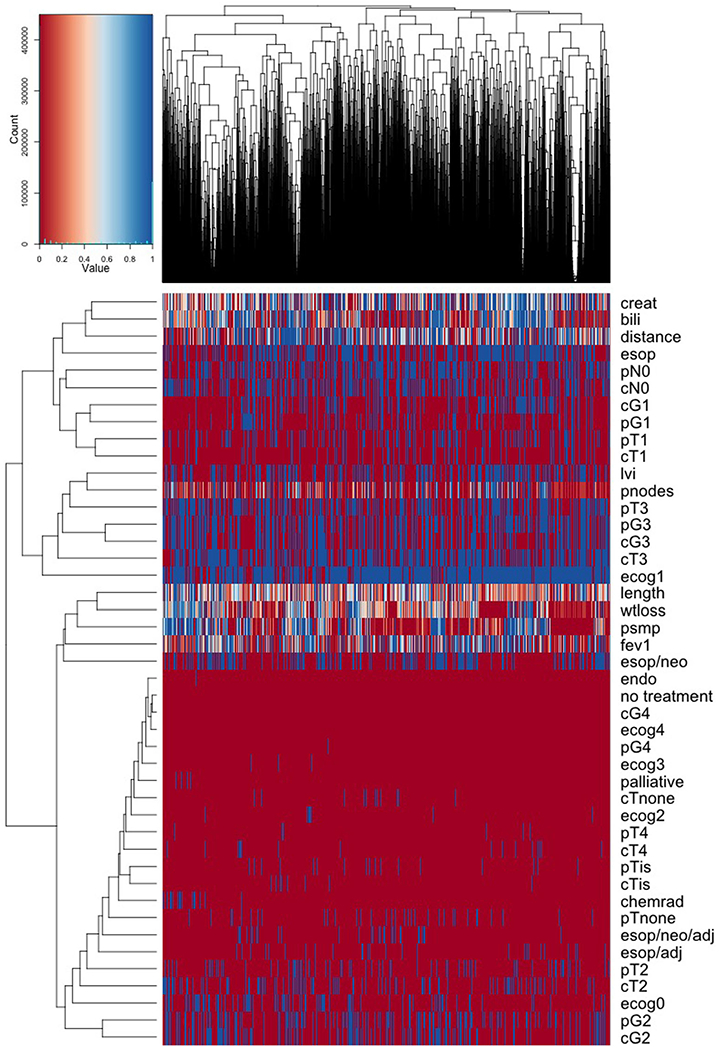
Heatmap from sidClustering analysis of WECC esophageal cancer data where data have been sorted by institution (columns of the heatmap). Rows display patient and cancer characteristics for identifying patient differences across institutions

Figure 5 reveals no general systematic differences between institutions. Most differences that do exist appear largely related to patient therapy assignment. For example, prevalence of palliative care and chemoradiotherapy is generally low (red values) across all institutions excepting a few small patches near the left hand side (blue values). Upon investigating, we found that these two therapies (which are generally rare) were predominately found in one hospital. Another noticeable pattern we found relates to the variable psmp, defined as number of lymph nodes resected by lymphadenectomy. Fewer nodes are generally associated with improved survival. We observe a pattern of low values for this variable (red regions to the right of heatmap and some also in the middle). This pattern is mirrored by low values of bilirubin, low values of weight loss, and to a lesser extent, higher pT2 prevalence (the variable “pT” measures tumor invasiveness). Low bilirubin can be considered a sign of health and a patient with stable weight is also a positive indicator. Also pT2 is a less invasive cancer than pT3, which is the predominant pT classification. This pattern suggests therefore a small subset of hospitals with a slightly healthier patient cohort. Indeed, upon careful inspection of the data this does match with what we found—although we certainly would not have been able to discern such a subtle difference without the results of the unsupervised analysis.

3.2 |. Hospital charges

Cost data for cardiovascular patients was collected at a large US hospital. Values recorded included cost, margin, and profit characteristics of each encounter along with data on the type of procedure, location of residence of the patient, and referral source of the patient. This data (sample size n = 5741, d = 37 attributes) was run through sidClustering with hierarchical clustering (HC) used for the distance matrix. The intention was to determine if there existed clusters in the data for which the financial attributes were unique versus the rest of the population. Figure 6 depicts the most influential variables across clusters that had the most differentiating effect between clusters.

FIGURE 6.

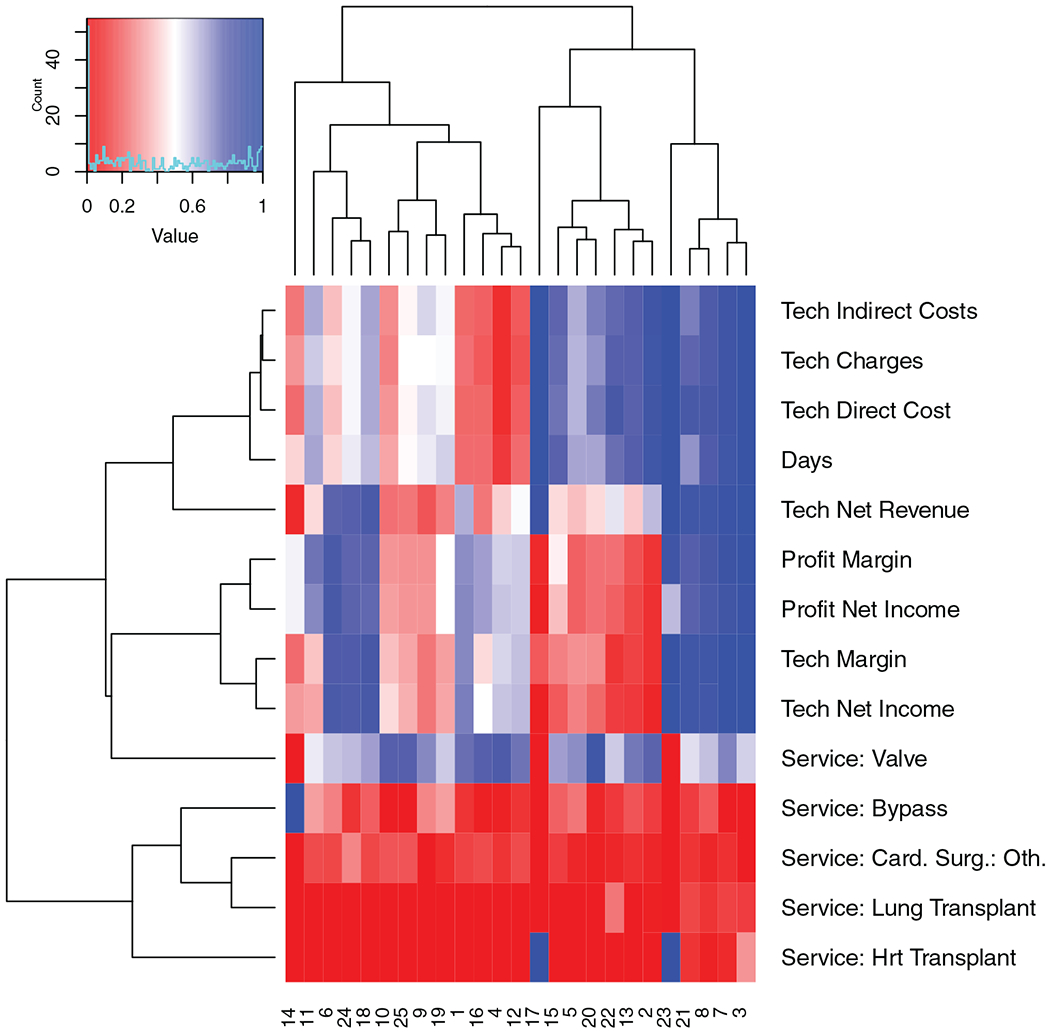
Heatmap from sidClustering analysis of hospital costs data. Rows display encounter characteristics for identifying different clusters of encounters

There were several clusters of note that were revealed by the analysis. One example was the pair of clusters, numbers 17 and 23. These represent a high proportion of heart transplants but they vary vastly in regards to profit margin despite being very similar in regards to many of the plotted metrics. Looking further it can be observed that the tech margin (amount made in tech charges or revenue, minus tech costs to the hospital) varied just as largely suggesting that this is the component that drew down the profit of the encounter since the overall profit margin is the sum of the margins from all sources including tech. Technician services include labs, tests, equipment use and other procedures not provided by doctors or nurses. This may suggest that adjustments to charges may be required for a particular subset of patients to adjust for tech costs that are outpacing their corresponding charges and bringing overall profit down despite the comparable revenue levels being collected. Opposite adjustments may be applied to the high profit group for higher equability. Another interesting cluster is number 14 which contains many of the bypass procedures and we can see that overall their profit margins are very middle of the range but the tech margin drags it down which indicates that the other components are what bring it back to a median profit margin. Lastly, it was very interesting to see how valves as a service was distributed across many difference clusters as opposed to the other services that tended to concentrate. This suggests high levels of heterogeneity in this service type which is further confirmed by the plot. For example, if we look at days at hospital, we can see this includes the full range of encounter lengths from very short to very long.

4 |. BENCHMARK EXPERIMENTS

In this section we used benchmark experiments to compare sidClustering to Breiman clustering using Shi–Hovarth’s two generation modes (SH1 and SH2). Performance was also compared to the Cluster Forest (CF) method of Yan et al. [23] and to Gaussian Mixture Models (GMM) described in [17]. Both simulated and real world data were used in the experiments. sidClustering was applied with and without the feature selection algorithm. The procedure using variable selection is referred to as SID varselect. As before, all random forest calculations including sidClustering were implemented using the randomForestSRC R-package [8]. For all competing methods default settings are utilized including ntree = 1000 and nodesize = 5. For sidClustering and Shi–Horvath, both HC and PAM were used for clustering the distance and proximity matrices.

4.1 |. Performance measures

Performance of methods was assessed using measures based on Gini and entropy, which are related to mutual information proposed by Romano et al. [20]. These measures function as weighted averages of impurity in the predicted clusters. Weights are determined by cluster size which then takes into count the possibility of gaming the measure by forming small clusters. Smaller clusters have a higher chance of being pure by random chance but their contribution to the score is reduced to compensate. The idea is that we want clusters that are both as large and pure as possible in order to obtain the best possible score. The entropy and Gini measures of performance are as follows:

$$\begin{gathered} {\rho }_{\mathrm{E}}=\sum _{i=1}^k\frac{n_i}{n}\sum _{j=1}^k-\frac{L_{ij}}{n_i}{\log }_2\left(\frac{L_{ij}}{n_i}\right), \\ {\rho }_{\mathrm{G}}=\sum _{i=1}^k\frac{n_i}{n}\sum _{j=1}^{k_t}\frac{L_{ij}}{n_i}\left(1-\frac{L_{ij}}{n_i}\right), \end{gathered}$$

where:

n = total number of cases;

n_i = number of cases in cluster i;

k_t = number of clusters targeted by clustering algorithm;

k = true number of clusters;

L_ij = number of cases when predicted cluster label is j when true label is i.

Both measures can be normalized to a range of 0–1 by dividing by the maximum value which occurs under uniform guessing. A lower score indicates better overall clustering. Also, squaring the normalized measure retains the 0–1 range and adds a middle point of comparison where a score of 0.5 corresponds with 50% correct clustering. It should also be noted that these are measures of purity which are robust to label switching since our goal is to determine ability to cluster similar observations.

When testing these two measures we noticed that they ranked procedures similarly. We chose therefore to use the entropy measure for evaluating performance due to the involvement of Gini splitting by random forests which may marginally, but unfairly, favor the methods based on random forests.

4.2 |. Synthetic experiments

Tables 3 and 4 describe simulations utilized in our experiments. The number of noise variables is represented by d, which is set to d = 17 and d = 100 in order to reflect low- and high-dimensional settings. The simulations drew inspiration from the examples of Shi and Horvath [21]. In addition to these simulations we also ran the V-shaped cluster and 4-bivariate normal simulation (Table 2) described earlier. All simulations were run 100 times independently.

TABLE 3.

Eight-cluster simulation

Variable	Simulated by
X1	~Binomial(m = 1, p = 0.5)
X2	~Binomial(m = 1, p = 0.5)
X3	First 1000 ~ Uniform(0, 1), second 1000 ~ Uniform(1.1, 2.1)
X4, …, Xd	Noise variables ~ Uniform(0, 1)
Cluster	X1	X2	X3
1	1	1	≥1.1
2	1	1	≤1.0
3	0	1	≥1.1
4	0	1	≤1.0
5	1	0	≥1.1
6	1	0	≤1.0
7	0	0	≥1.1
8	0	0	≤1.0

TABLE 4.

Twelve-cluster simulation

Variable	Simulated by
X1	~Binomial(m = 1, p = 0.5)
X2	~Binomial(m = 1, p = 0.5)
X3	First 1000 ~ Uniform(0, 1), second 1000 ~ Uniform(1.1, 2.1)
X4, …, Xd	Noise variables ~ Uniform(0, 1)
Cluster	X1	X2	X3
1	1	1	≥1.1
2	1	1	≤1.0
3	0	1	≥1.1
4	0	1	≤1.0
5	1	0	≥1.1
6	1	0	≤1.0
7	0	0	≥1.1
8	0	0	≤1.0
9	0	2	≥1.1
10	0	2	≤1.0
11	1	2	≥1.1
12	1	2	≤1.0

Figure 7 displays the results from the experiment. We can see that in nearly all simulations, sidClustering outperforms the other methods by a large margin. Furthermore, in some cases the performance was nearly equal to a supervised forest (red values) calculated using the true class labels (which should be our limit of performance since this is the case where the target is known). We notice that the clustering algorithm used on the proximity matrix seems to be important for SH1 and SH2, while for sidClustering, performance does not vary very much if we switch between HC or PAM. We suspect the geometry of the clusters hinders the ability of SH1 and SH2. Since in the simulations the informative features are mostly categorical and the only continuous one has very little space between the clusters, it made it very difficult for either method to flood the empty space with the artificial class.

FIGURE 7.

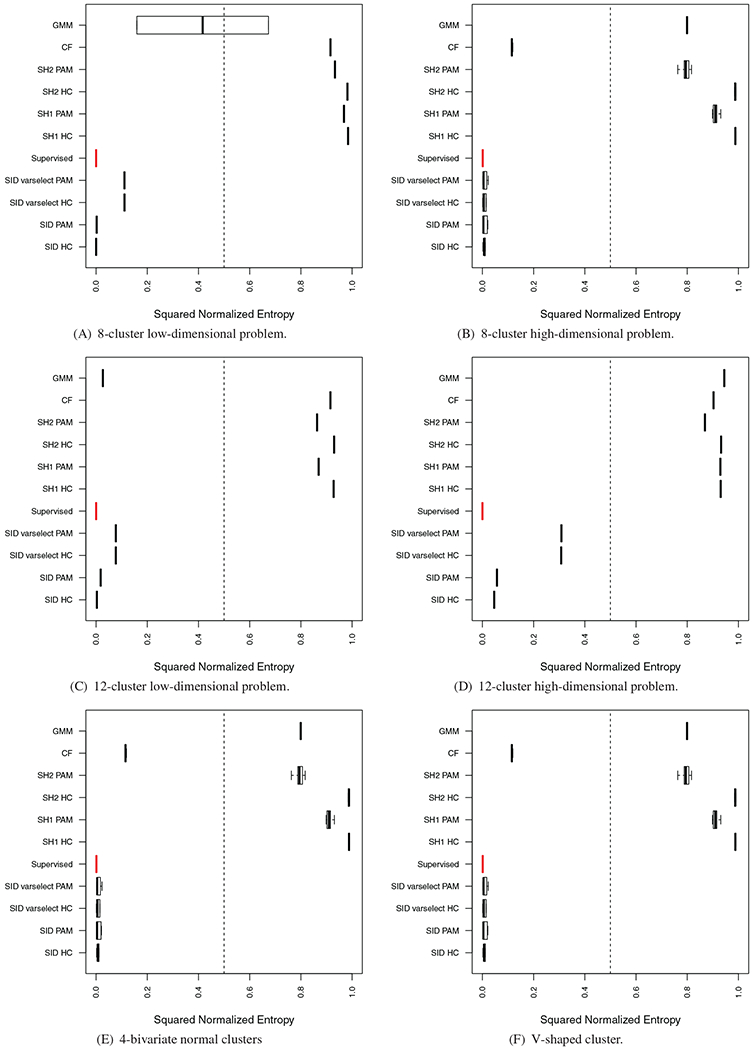
Results on simulated datasets. Red boxplot signifies supervised random forest performance. (Section 4.1 discusses normalized entropy)

4.3 |. Real data experiments

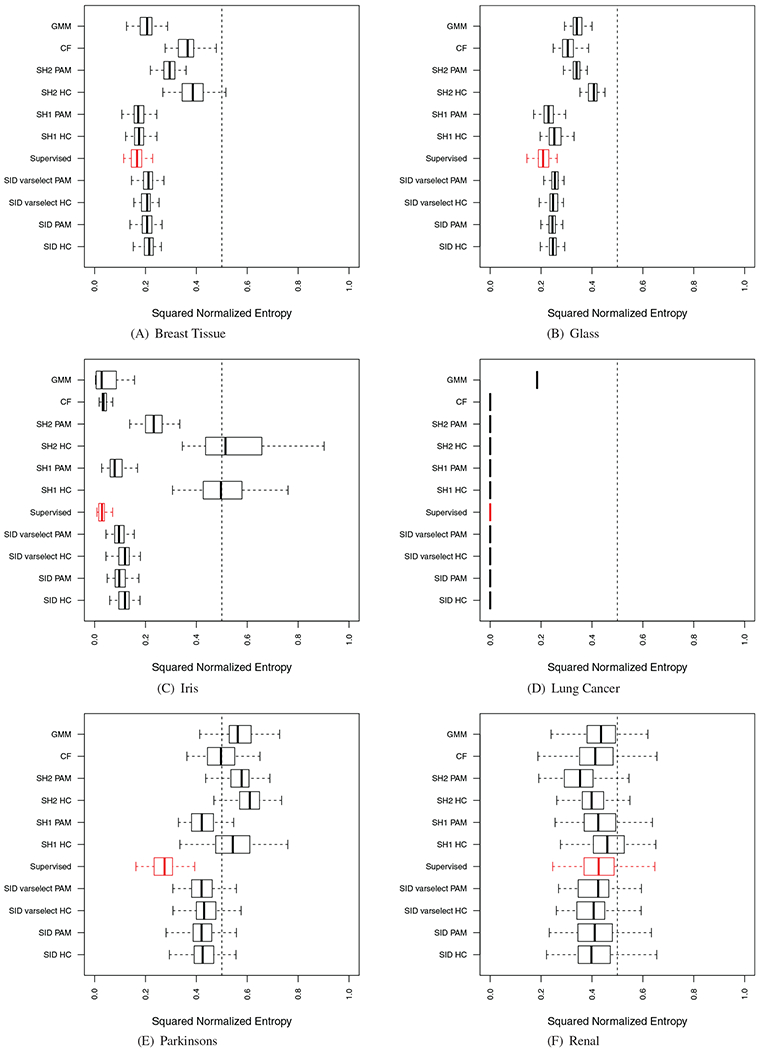
Performance of sidClustering was also tested on a collection of real datasets (Table 5): some have purely continuous or categorical features or mixed, the number of true classes varies, as well as sample size. For each simulation, the entire procedure was run 100 times using stratified subsampling (40% rate) in order to assess variability of performance. Stratified subsampling was used because we wanted to ensure that all clusters were represented in each run, otherwise k could potentially vary between runs. Some of these results are displayed in Figure 8, the remaining can be found in Figure A1 of the Appendix. As in the synthetic experiments, a supervised random forest was run using the true class labels to provide a benchmark performance value (depicted using red values). Performance was calculated by comparing the predicted out-of-bag (OOB) class labels to the truth.

TABLE 5.

Data experiments

Data	Continuous features	Categorical features	k	n
Biomechanical	7	0	2	310
Breast tissue	9	0	6	106
Esophagus	0	9	5	2343
Glass	9	0	7	214
Heart	10	3	2	270
Iowa housing—categorical	2	12	4	2930
Iowa housing—continuous	8	2	2	1470
Iris	4	0	3	150
Lung cancer	26	0	3	27
Parkinson	22	0	2	195
Pima	8	0	2	768
Renal	16	9	2	87
Robot	90	0	5	164
Soybean	8	13	4	47
SPECT	0	22	2	267
WDBC	30	0	2	569
Wine	13	0	3	178
VO2	13	26	2	2231

FIGURE 8.

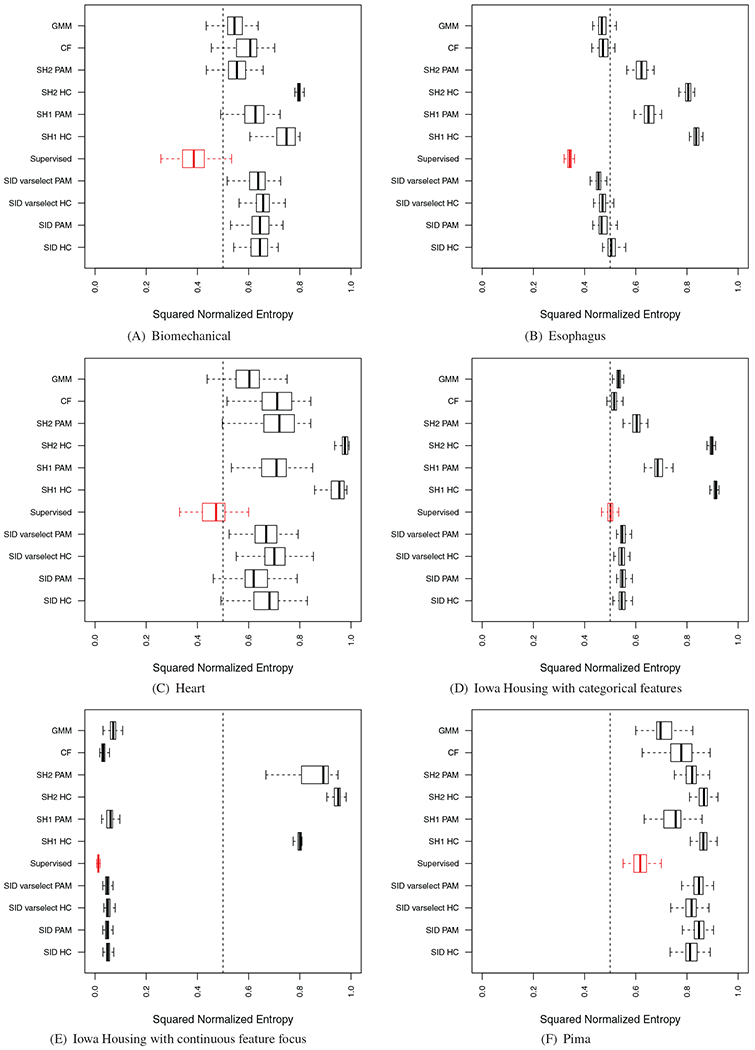
Results on real world data. Red boxplot signifies supervised random forest performance. (Section 4.1 discusses normalized enotrpy)

Table 6 summarizes overall performance of methods. We also make the following comments:

1. For SH1 and SH2, the type of clustering algorithm used on the proximity matrix was again found to greatly affect performance in most cases, while sidClustering was for most cases generally robust to this.

2. There is only one sidClustering mode, therefore there is no possibility of choosing the incorrect mode, while if one chooses the incorrect mode between SH1 and SH2, performance could be greatly hindered. This issue is further compounded by the fact that in practice the truth is not known therefore there is no way of knowing which is correct. Also, although in many cases SH1 does outperform SH2, there are two cases, Renal and Iowa housing (categorical), where SH2 rendered better performance.

3. The sidClustering variable selection algorithm performed very well. Performance was also very good in the previous synthetic experiments. This shows it is possible to use the dimension reduction to improve computational cost while at the same time retaining clustering performance. This is especially true for the two high-dimensional cases where the original data contained over 100 features which produced over 4000 total SID features.

TABLE 6.

Summary of performance on real data experiments: ✓ indicates top performing (within 1 SE) method in at least half of the datasets

Dataset type	SID HC	SID PAM	SID varselect HC	SID varselect PAM	SH1 HC	SH1 PAM	SH2 HC	SH2 PAM	CF	GMM
Continuous features only		✓		✓		✓			✓
Categorical features only	✓	✓	✓	✓						✓
Mixed features	✓	✓	✓	✓				✓	✓	✓
2-class	✓	✓	✓	✓		✓			✓	✓
>2 class	✓	✓	✓	✓		✓			✓

5 |. DISCUSSION

sidClustering is a random forests based clustering algorithm that greatly eases on the requirements for the original Brieman clustering approach. No artificial set of observations needs to be generated. In most data where performance was compared, sidClustering outperformed either one, or both, of Shi–Hovarth’s modes. In the cases where sidClustering did not outperform both there usually was a wide margin in the performance between the two Shi–Hovarth modes. This means that if the incorrect mode were to be chosen then performance can potentially be greatly hindered. As complexity of the data increases, it becomes more difficult to determine the correct mode.

Another point worth noting is the constraints imposed on the artificial data used by Breiman clustering. Here the number of observations in this class has to be roughly the same as the original data. The problem is that if we unbalance the combined data, then this potentially becomes a class imbalanced problem. This would hinder any machine learning algorithm’s ability to differentiate the two classes. This constraint precludes one from taking the most direct solution to artificial data creation, which would be to replicate each of the points a few times plus a small amount of error to create the second class. Then the resulting artificial class would perfectly cover the first and truly force the random forest to fit a model that distinguishes the two classes. It would be similar to what is done in data smearing [4] for increasing predictive performance of random forests. Unfortunately, each time one replicates a point in the original class, this diminishes the ratio between the original class and the artificially generated class, thus increasing the potential of inducing a class imbalanced problem.

Looking at GMM and CF, we notice there are a number of high performing situations but they seem to falter in certain places. For example, GMM seems to have issues with more than two clusters or purely continuous features. This could stem from the increased number of conformations clusters could take in this case and increase the difficult of selecting borders between clusters. The more complex these boundaries can be, the more difficulty GMM seems to have. In the case of CF, we have somewhat the opposite with regard to complexity of the data: CF performs well in cases with purely continuous features, this may be because the algorithm is tree based and therefore able to select very precise boundaries. However CF falters in purely categorical cases, possibly due to sparsely filled space which makes selection of the boundary more tricky. This is an advantage of SID which performs will with both continuous and categorical features.

In future work, we will include the implementation of semisupervision in the clustering in order to emphasize what features should be most driving clusters. Also, we believe that it is possible to use this method to determine the number of clusters that should be created. And lastly, since random forests was used to develop the groups, then random forests should be able to also impart the identity of the group’s members; therefore, we intend to develop a rule generator for this purpose.

Biographies

AUTHOR BIOGRAPHIES

Alejandro Mantero received his PhD in biostatistics from University of Miami, he received his Masters and Bachelors of Arts in Economics, and Bachelors of Science in Physics, from University of Miami (UM). He was been working in unsupervised machine learning both with respect to clustering and its uses in defining distances between observations for use in imputation of high-dimensional data.

Hemant Ishwaran is a professor of biostatistics at the University of Miami. He received his PhD in statistics from Yale University in 1993, an MSc in applied statistics from Oxford University in 1988, and a BSc in mathematical statistics from the University of Toronto in 1987. Dr. Ishwaran has an h-index of 41 since 2015 (last 5 years) and has published articles on a broad range of topics in statistics. He works in the area of boosting, ensemble learning, trees and random forests and is the developer of the popular random survival forests R-package.

APPENDIX A. PROOFS

Proof of Theorem 1. First suppose that p > 1 so that X contains at least two discrete features. We can assume without loss of generality that the discrete features X₁, …, X_p are all dichotomous. Because if they were not, then Line 4 of Algorithm 2 would convert them to a finite set of q > p dichotomous values (and notice q remains finitely bounded as n → ∞ because of the finite discrete Assumption A1).

X1	=	{0, 1}	$\stackrel{{\varphi }^D}{\to }$	Y(1)	=	{1, 2}	=	2 − (1 − X1)
X2	=	{0, 1}	$\stackrel{{\varphi }^D}{\to }$	Y(2)	=	{3, 4}	=	4 − (1 − X2)
X3	=	{0, 1}	$\stackrel{{\varphi }^D}{\to }$	Y(3)	=	{5, 6}	=	6 − (1 − X3)
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
Xj	=	{0, 1}	$\stackrel{{\varphi }^D}{\to }$	Y(j)	=	{2j − 1, 2j}	=	2j − (1 − Xj)
⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮	⋮
Xp	=	{0, 1}	$\stackrel{{\varphi }^D}{\to }$	Y(p)	=	{2p − 1, 2p}	=	2p − (1 − Xp).

We will first look at identification for the discrete features. Now because we are working with finite sample spaces (of cardinality two without loss of generality), we can dispense with the distinction between the theoretical and actual sidification map and simply work with the theoretical map. For notational convenience, we use a superscript D to indicate we are subsetting to discrete features. The following is the theoretical staggering map ${\varphi }^D:{\mathcal{X}}^D\to {\mathcal{Y}}^D$, where we assume as in Algorithm 2 that δ = 1: We now show that an arbitrary ${\mathit{Z}}^D\in \left(\psi \right(\varphi \left({\mathcal{X}}^D\right))$ cannot be produced using two different ${\mathbf{X}}^D\in {\mathcal{X}}^D$. Because the SID interaction feature Z^D is comprised of all possible pairwise interactions of Y^D (Lines 10–16 of Algorithm 2),

$${\mathbf{Z}}^D={(Y^{(1)}{Y}^{(2)},\dots ,Y^{(1)}{Y}^{(p)},Y^{(2)}{Y}^{(3)},\dots ,Y^{(2)}{Y}^{(p)},\dots ,Y^{(p-1)}{Y}^{(p)})}^T.$$

Observe that each of the coordinates of Z^D is of the form

$$Y^{(j)}{Y}^{(k)}=(2j-1+X_j)(2k-1+X_k)$$

which is a factor with one of the following four unique categories (Line 12 of Algorithm 2),

$$\left\{(2j-1)(2k-1),(2j)(2k-1),(2j-1)(2k),(2j)(2k)\right\}.$$

Thus, each coordinate of Z^D uniquely determines the values for two coordinates X_j and X_k, and since Z^D contains all possible pairs of coordinates, it follows that Z^D can only correspond to one specific X^D. Finally, it is clear that Y^D can only correspond to one X^D value.

Thus, we have shown that when X contains at least two discrete coordinates, ${\mathbf{Z}}_i^D={\mathbf{Z}}_{i^{\prime }}^D$ if and only if ${\mathbf{X}}_i^D={\mathbf{X}}_{i^{\prime }}^D$ if and only if ${\mathbf{Y}}_i^D={\mathbf{Y}}_{i^{\prime }}^D$.

Consider next the case when X contains at least one discrete and one continuous coordinate. Suppose that coordinates j and k of X are discrete and continuous, respectively. By Line 14 of Algorithm 2, the interaction between a continuous and binary feature is obtained by multiplying their staggered values. Thus, we must show for two data cases i ≠ i′

$$Y_{ij}{Y}_{ik}=Y_{i\text{'}j}{Y}_{i;k}$$ (A1)

if and only if

$${(X_{ij},X_{ik})}^T={(X_{i\text{'}j},X_{i\text{'}k})}^T$$

if and only if

$${(Y_{ij},Y_{ik})}^T={(Y_{i\text{'}j},Y_{i\text{'}k})}^T.$$

The staggered discrete coordinate j is

$$Y_{ij}=2j-1+X_{ij},Y_{i\text{'}j}=2j-1+X_{i\text{'}j},$$

while the staggered continuous coordinate k is

$$Y_{ik}={\delta }_{kn}+X_{ik},Y_{i\text{'}k}={\delta }_{kn}+X_{i\text{'}k},$$

where δ_kn > 0 denotes the value used to stagger X_k. It is clear there is a 1:1 map between staggered values and the original features. Therefore, we focus on proving the first if and only if. Observe that (A1) holds if and only if

$$(2j-1+X_{ij})({\delta }_{kn}+X_{ik})=(2j-1+X_{i\text{'}j})({\delta }_{kn}+X_{i\text{'}k}).$$

Canceling and collecting terms, we obtain

$$(2j-1)(X_{ik}-X_{i\text{'}k})+{\delta }_{kn}(X_{ij}-X_{i\text{'}j})=X_{i\text{'}j}{X}_{i\text{'}k}-X_{ij}{X}_{ik}.$$

Recall that X_j ∈ {0, 1} is binary. If X_ij = X_i′j, then

$$(2j-1)(X_{ik}-X_{i\text{'}k})=X_{ij}(X_{i\text{'}k}-X_{ik}),$$

which implies X_ik = X_i′k regardless if X_ij = 0 or X_ij = 1. On the other hand, suppose that X_ij ≠ X_i′j. If X_ij = 1 and X_i′j = 0, we obtain

$$2j{X}_{ik}=(2j-1)X_{i\text{'}k}-{\delta }_{kn},$$

which occurs with probability zero by Assumption A2 because X_k is continuous and X_ik and X_i′k are independent. A similar conclusion holds if X_ij = 0 and X_i′j = 1.

The final case is when X contains at least two coordinates that are continuous. Suppose that j and k are coordinates that are continuous. Then their SID interaction is obtained by multiplying their SID main effects similar to (A1). In this case, (A1) holds if and only if

$$({\delta }_{jn}+X_{ij})({\delta }_{kn}+X_{ik})=({\delta }_{jn}+X_{i\text{'}j})({\delta }_{kn}+X_{i\text{'}k}).$$

Under Assumption A2, (X_j, X_k) has a nondegenerate density. Using this and independence, deduce that the above event occurs with probability zero unless X_ij = X_i′j and X_ik = X_i′k.

Proof of Theorem 2. Let Z = Y₁Y₂ and $Z^{\ast }=Y_1^{\ast }{Y}_2^{\ast }$. Define

$$\alpha (\theta )=\theta Y_1+(1-\theta )Y_1^{*},\beta (\theta )=\theta Y_2+(1-\theta )Y_2^{*},0\le \theta \le 1.$$

By convexity, $Y\left(\theta \right)={\left(\alpha \right(\theta ),\beta (\theta \left)\right)}^T\in {\mathcal{Y}}_n$. Therefore Y(θ) is a properly defined SID main effect and Z(θ) = α(θ)β(θ) is a properly defined SID interaction value. Notice also that every point along the vector $\mathbf{Y}{\overrightarrow{\mathbf{Y}}}^{\ast }$ between Y and Y* can be written as

$$\mathbf{Y}+(1-\theta )({\mathbf{Y}}^{\ast }-\mathbf{Y})=\theta \mathbf{Y}+(1-\theta ){\mathbf{Y}}^{\ast }=\mathbf{Y}(\theta )$$

for some 0 < θ < 1. Therefore the SID interaction value for a point Y(θ) along $\mathbf{Y}{\overrightarrow{\mathbf{Y}}}^{\ast }$ is Z(θ).

We consider Case I first. By assumption we have $Y_1<Y_1^{\ast }$ and $Y_2\le Y_2^{\ast }$. Therefore

$$Y_1<\alpha (\theta )<Y_1^{*},Y_2\le \beta (\theta )\le Y_2^{*},0<\theta <1.$$

By uniqueness Z ≠ Z*. Therefore because all values are non-negative due to sidification,

$$Z=Y_1{Y}_2<Z(\theta )=\alpha (\theta )\beta (\theta )<Z^{*}=Y_1^{*}{Y}_2^{*},0<\theta <1.$$

Therefore, we can use the split-point Z(θ) to assign cases to Y if their SID interactions values are less than or equal to Z(θ) or to Y* if their SID interactions values are greater than Z(θ). Furthermore, because Z(θ*) is the SID interaction value for a point Y(θ*) along the vector $\mathbf{Y}{\overrightarrow{\mathbf{Y}}}^{\ast }$, this shows that assignment of points along $\mathbf{Y}{\overrightarrow{\mathbf{Y}}}^{\ast }$ depend on whether Z(θ*) ≤ Z(θ) or Z(θ*) > Z(θ).

Now for Case II, we have $Y_1<Y_1^{\ast }$ and $Y_2<Y_2^{\ast }$. Also by assumption, Z < Z*. Therefore since Z(θ) → Z for θ → 1 and Z(θ) → Z* for θ → 0, we can find values $0<\widehat{\theta }$, ${\widehat{\theta }}^{\ast }<1$ such that

$$Z=Y_1{Y}_2<Z(\widehat{\theta })<Z({\widehat{\theta }}^{*})<Z^{*}=Y_1^{*}{Y}_2^{*}.$$

Therefore assign all values to the left of $Z\left(\widehat{\theta }\right)$ to Y and all values to the right of $Z\left({\widehat{\theta }}^{\ast }\right)$ to Y*.

Proof of Theorem 3. It suffices to consider features X₁ ∈ [a, b] and X₂ ∈ [c, d] (the same argument can then be applied to the remaining finite number of features). We can assume without loss of generality that R = b − a > r = d − c and the ranges of our features have a lower bound of at least zero and a strictly positive upper bound due to the sidification algorithm which translates all features to this space. Therefore, assume without loss of generality

$$b,d>0\mathrm{and}a,c\ge 0b-a=R>0\mathrm{and}d-c=r>0.$$

We can now define the SID main features:

$$Y_1\in [a+\delta ,b+\delta ],Y_2\in [c+\delta +b+\delta ,d+\delta +b+\delta ].$$

We denote Z^DES as the SID interaction feature formed when the ranges are descending in order:

$$Z^{DES}\in [(a+\delta )(c+b+2\delta ),(b+\delta )(d+b+2\delta )].$$

The range of the SID interaction feature is

$$\begin{gathered} \mathrm{range}(Z^{DES})=(b+\delta )(d+b+2\delta )-(a+\delta )(c+b+2\delta ) \\ =bd+b^2+2b\delta -ac-ab-2a\delta +\delta (d+b+2\delta -c-b-2\delta ) \\ =b^2-ac+b(d-a)+2\delta (b-a)+\delta (d-c). \end{gathered}$$

Now we reverse the order of the ranges to obtain the suboptimal ordering effect:

$$X_1\in [c,d],X_2\in [a,b].$$

The resulting SID main effects are:

$$Y_1\in [c+\delta ,d+\delta ],Y_2\in [a+\delta +d+\delta ,b+\delta +d+\delta ].$$

We denote Z^ASC as the SID interaction feature when the ranges are suboptimally ordered ascendingly:

$$Z^{ASC}\in [(c+\delta )(a+d+2\delta ),(d+\delta )(b+d+2\delta )].$$

Its range equals,

$$\begin{gathered} \mathrm{range}(Z^{ASC})=(d+\delta )(b+d+2\delta )-(c+\delta )(a+d+2\delta ) \\ =db+d^2+2d\delta -ca-cd-2c\delta +\delta (b+d+2\delta -a-d-2\delta ) \\ =d^2-ca+d(b-c)+2\delta (d-c)+\delta (b-a). \end{gathered}$$

Now taking the difference between the ranges of the two SID interaction features, we have

$$\begin{gathered} \mathrm{range}(Z^{DES})-\mathrm{range}(Z^{ASC}) \\ =b^2-ac+b(d-a)+2\delta (b-a)+\delta (d-c)-(d^2-ca+d(b-c)+2\delta (d-c)+\delta (b-a)) \\ =b^2-ba-d^2+dc+\delta (b-a)-\delta (d-c) \\ =bR-dr+\delta (R-r). \end{gathered}$$ (A2)

The proof is completed if we can show (A2) is strictly positive. If b ≥ d, then

$$\begin{gathered} bR-dr+\delta (R-r)=d\left(\frac{b}{d}R-r\right)+\delta (R-r) \\ \ge d(R-r)+\delta (R-r)=(d+\delta )(R-r) \end{gathered}$$

which is greater than zero for any δ > 0 since d > 0 and R > r by assumption. On the other hand, if d > b, then (A2) is strictly positive if and only if

$$\delta >\frac{dr-bR}{R-r}.$$ (A3)

Such a δ can always be found since the denominator is nonzero ensuring that the bound is finite.

In fact, it is only the case d > b when δ must be selected carefully, since (A2) is strictly positive for any δ > 0 when d ≤ b. Therefore we are free to choose any δ > 0 if we eliminate the latter case. This can be readily achieved as follows. Prior to reordering the data, translate each continuous feature so that all feature values are positive and all have the same maximum value. Even though the minimum value may differ over variables their maximum value is the same which forces d = b and removes the case d > b.

FIGURE A1.

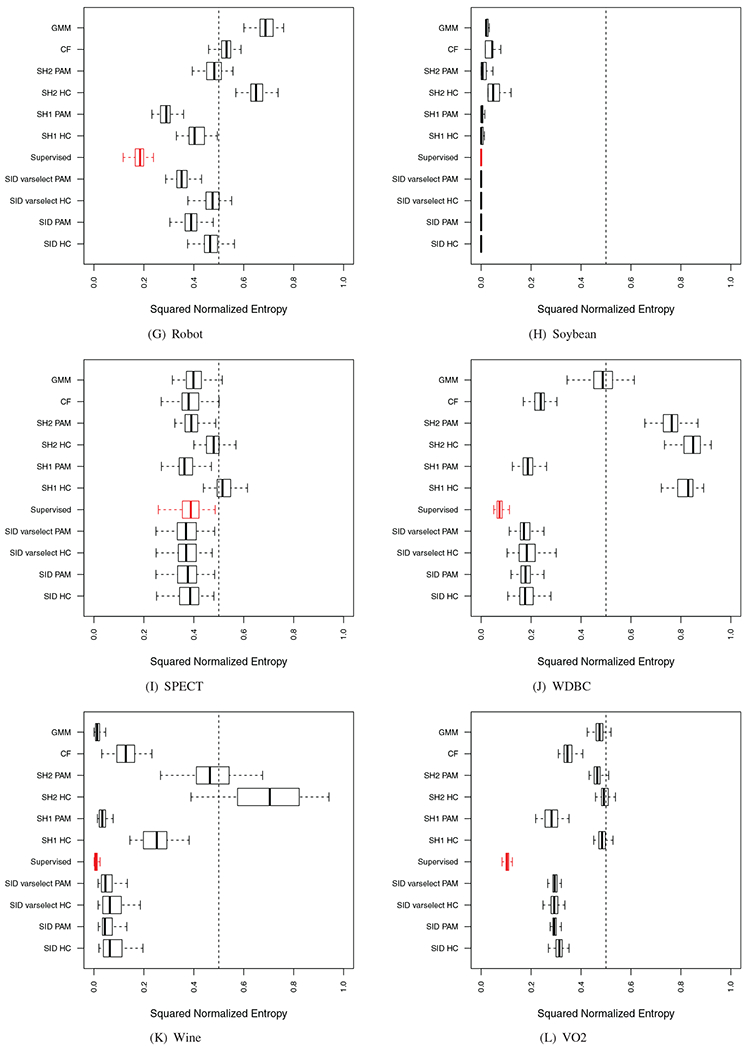
Results on real world data. Red boxplot signifies supervised random forest performance. (Section 4.1 discusses normalized enotrpy)

APPENDIX B. PERFORMANCE ON REAL DATA

Performance of sidClustering on a collection of datasets. For each dataset, the true class label was removed and sidClustering applied. The entire procedure was run 100 times using stratified subsampling (40% rate). Comparison procedures include Breiman clustering [2] under Shi–Hovarth’s [21] two generation modes (SH1 and SH2) and cluster forest (CF) [23]. A supervised random forest was run using the true class labels to provide a benchmark performance value (depicted using red values). Performance was calculated by comparing the predicted OOB class labels to the truth.