Social Space Diffusion: Applications of a Latent Space Model to Diffusion with Uncertain Ties

Abstract

Social networks represent two different facets of social life: (1) stable paths for diffusion, or the spread of something through a connected population, and (2) random draws from an underlying social space, which indicate the relative positions of the people in the network to one another. The dual nature of networks creates a challenge – if the observed network ties are a single random draw, is it realistic to expect that diffusion only follows the observed network ties? This study takes a first step towards integrating these two perspectives by introducing a social space diffusion model. In the model, network ties indicate positions in social space, and diffusion occurs proportionally to distance in social space. Practically, the simulation occurs in two parts. First, positions are estimated using a statistical model (in this example, a latent space model). Then, second, the predicted probabilities of a tie from that model – representing the distances in social space – or a series of networks drawn from those probabilities – representing routine churn in the network – are used as weights in a weighted averaging framework. Using longitudinal data from high school friendship networks, I explore the properties of the model. I show that the model produces smoothed diffusion results, which predict attitudes in future waves 10% better than a diffusion model using the observed network, and up to 5% better than diffusion models using alternative, non-model-based smoothing approaches.

Introduction

Social networks have historically been used for two different purposes. First, social networks represent the paths that contagions – like innovations such as the use of a new medicine (Coleman, Katz, and Menzel 1966), information such as job opportunities (Granovetter 1973, 1995), diseases such as HIV (Morris et al. 2009), or even a medical condition such as obesity (Christakis and Fowler 2007; but see Lyons 2011) – take to spread through a population. Second, social networks represent the relative positions of people to one another – for example, status (Rossman, Esparza, and Bonacich 2010), hierarchy (Martin 2002), popularity (Moody et al. 2011), informal peer group membership (Newman 2006), role structures (White, Boorman, and Breiger 1976), or levels of intergroup contact (Smith, McPherson, and Smith-Lovin 2014). Under the former framework, network ties indicate stable conduits for social influence or information; under the latter, network ties are simply a random draw from an underlying social space.

The dual nature of networks as stable connections and as random draws from social space creates a challenge – if the observed network ties are a single random draw, is it realistic to expect that diffusion, or the spread of something through a connected group of people, only follows the observed network ties? Under experimental conditions, where online network ties are created by the researcher (e.g., Centola 2011), it is reasonable to assume that diffusion can only follow the given network ties. A growing literature on measurement error in networks (Eagle and Proeschold-Bell 2015; Paik and Sanchagrin 2013), however, suggests that in observed networks, the specific ties that are observed depend heavily on how the data were collected. As such, in real networks, the absence of a tie may not be meaningful, and it may not be reasonable to assume that there is no direct information transmission when no tie is observed.

To address this challenge, I introduce a new class of network diffusion models, social space diffusion models. In a social space diffusion model, ties represent a random draw from an underlying social space, and the spread of a contagion between two people occurs proportionally to distance in social space, rather than strictly following the presence or absence of a tie. To estimate distances in social space, I use a latent space model (Handcock, Raftery, and Tantrum 2007; Hoff, Raftery, and Handcock 2002), and then I simulate diffusion over those distances using the weighted averaging model elaborated by Friedkin and colleagues (Friedkin 1998; Friedkin and Johnsen 2011). Although I focus on the weighted averaging model for analytical tractability, this method, with appropriate modifications, could be extended to other diffusion models, such as threshold models (Centola and Macy 2007; Granovetter 1978; Watts 2002) or voter models (Durrett et al. 2012; Holme and Newman 2006). Similarly, while I focus on predicted probabilities derived from a latent space model, this method could be extended to use predicted probabilities from any model for a network, making this a general approach for predicting diffusion in networks that have been observed incompletely or with error.

The remainder of the paper proceeds as follows. I begin by outlining the theoretical contribution of this method. Specifically, this approach seeks to integrate two potentially contradictory views of networks – stable connections, and random draws, which I will refer to as the “connectionist” and “positionist” viewpoints, respectively (Borgatti and Foster 2003).ⁱ The difference between these viewpoints hinges on their assumptions of how quickly the network changes relative to the speed of the influence and information traveling over it. I describe existing diffusion models in terms of the connectionist and positionist ideal types, and then describe how the social space diffusion approach integrates these two perspectives.

Next, I show how the social space diffusion approach performs in practice. To illustrate, I use longitudinal data from a study of middle- and high-school students’ friendship networks. The illustration takes two parts. First, I explore the properties of the model using a single network. A key characteristic of the model is that it smooths the diffusion predictions by shrinking the network towards full connectedness and reciprocity. I show that this leads to diffusion estimates that reduce the effects of isolation on diffusion predictions. Second, I use all of the longitudinal data to compare the predictions from the social space diffusion model across several attitudinal scales to predictions from the raw, unsmoothed network as well as several other non-model-based approaches. The social space diffusion approach produces estimates that predict the next survey wave’s attitude values with lower mean squared errors across several attitude scales. In addition, the social space diffusion approach produces estimates with a margin of error, unlike other approaches that do not explicitly model the uncertainty in network ties. I conclude with a discussion of the benefits of this approach, as well as drawbacks and potential areas for further extensions.

Background: diffusion models on changing networks

The two approaches to networks, networks as stable connections that carry information and influence, and networks as fluid indicators of relative positions, can be considered in terms of the simplifying assumptions made by researchers modeling the changes in the network over time. Most important of these is the choice to hold either the network or the diffusing bit constant, based on which one is changing faster. In the discussion that follows, I limit my focus to models whose aim is simulating diffusion over a network. I do not consider models whose primary aim is estimating diffusion from observed data, such as stochastic actor-based models (Snijders 2017; Snijders, van de Bunt, and Steglich 2010) or the heterogeneous diffusion model (Greve, Strang, and Tuma 1995).

When the network changes relatively slowly compared to the thing that is spreading through the network, holding the network constant and studying the movement of a bit through the network can be a reasonable approximation. Modeling bits spreading through a static network is sometimes called a social influence process or dynamics on the network.ⁱⁱ For example, in studies of attitude diffusion, Friedkin and colleagues (2011) generally assume that the network is unchanging while people influence each other. The network may change, but it is changing slowly enough that it can be approximated by a static network. Holding the network constant treats the network ties as stable conduits for a diffusing piece of information to travel across.

By contrast, when the network changes relatively quickly compared to the thing that is spreading, studying changes in the network, instead of changes in the thing spreading through the network, becomes a better approximation. For example, in the Schelling model of racial segregation in housing (1971, 1978), race does not change over each person’s life, but people can change their neighbors. The Schelling model focuses on the change in network ties – meaning neighbors in this case – and assumes that the thing spreading through the network, race, is not moving between people at all. Models that examine the change in network and hold spreading bits constant are referred to as homophily processes or as models of dynamics of networks. Holding the diffusing bit stable treats network ties as fluid indicators of how much people who share a particular attribute interact, or as the relative social position of the people holding one attribute to people holding the other.

A set of hybrid models exist, for when the network changes at roughly the same time scale as the thing spreading through it and neither the network nor the thing spreading through it can be held stable as an approximation. Voter models (Durrett et al. 2012; Holme and Newman 2006) and the constructural model (Carley 1991), for example, consider changes in the network and changes of the attitudes of people in the network simultaneously; at every time step, a person has the option of changing his or her mind, or changing who he or she is connected to. Studies where the network changes and the diffusing bit coevolve simultaneously are designed to model selection and influence processes and may be referred to as dynamics of and on the network.

Each of these approximations treats changes in the network as meaningful variation, rather than stochastic. A long line of research, however, suggests that measuring networks introduces a considerable amount of stochastic variation.ⁱⁱⁱ In a series of studies in the 1970s and 1980s, Killworth and Bernard found that network ties elicited in surveys bear little similarity to the ties that might have been inferred from observing respondents’ behavior (Bernard and Killworth 1977; Bernard, Killworth, and Sailer 1979, 1982; Killworth and Bernard 1976, 1979). More recently, Paik and Sanchagrin (2013), for example, showed that significant differences in core discussion networks could be traced back to differences in which interviewer contacted the respondent. Eagle and Proeschold-Bell (2015) similarly showed that surveys administered by web and by phone produced differently sized core discussion networks. Additionally, Eagle and Proeschold-Bell found evidence for interviewer effects, as Paik and Sanchagrin found, and panel conditioning, meaning that if a person had taken the survey before, he or she would report a smaller network on the next round of the survey, presumably to avoid answering as many follow-up questions.

In addition to systematic variation caused by how the network ties were elicited, network ties also show random, routine churn. Considering two surveys of adolescent friendships separated by three weeks, for example, Carins and Cairns (1994) found a 0.74 probability that a friendship would remain. Although friendship churn among adolescents appears to be associated with some changes in the underlying social structure of the school (e.g., Moody et al. 2011), much of the change is idiosyncratic, simply representing measurement error in the friendship ties.

Stochastic variation in the network ties introduces another possibility for diffusion models. Changes in network ties can be decomposed into two parts, systematic variation and random variation. The two types of variation may occur at different rates. The random variation, meaning the routine churn in network ties, may occur at roughly the same rate as the movement of the thing diffusing through the network, while the systematic variation may occur much more slowly. That is, the actual friendships that a researcher would observe may change on a day to day basis, but the underlying social structure, such as the peer groups, the students’ academic tracks, or the rates of interaction between sociodemographic groups may be much more stable. Under those circumstances, although the network’s stochastic changes happen at roughly the same rate as the spread of the thing diffusing through the network, the systematic structure of the network changes much more slowly than the spread of the diffusing thing.

In that case, an appropriate network diffusion model could hold the underlying social structure stable and model diffusion of something over that space, while accounting for the stochastic changes in a network. Thus a model would proceed by using the observed network to estimate the positions of the people in an underlying social space. The model could then estimate diffusion over various realizations of the social space, or could model diffusion over the social space directly. To develop such a model, I use the latent space model framework^iv (Handcock et al. 2007; Hoff et al. 2002), described in the following section.

Latent space models for networks

Latent space models were introduced by Hoff et al. (2002), and have since been expanded to include model-based clustering (Handcock et al. 2007) and dynamic networks (Sewell and Chen 2015). Latent space models are similar to a logistic regression predicting whether or not a tie will occur between each pair of people in the network. The models include a random effect – a position in the latent space – for every person. The latent positions are usually constrained to lie in a low-dimensional, Euclidean space to make the model easier to fit and to interpret. A tie is more likely between 2 people who are closer in the latent space.

More formally, for a network with n people, or vertices, let Y denote the n × n adjacency matrix, whose elements, y_i,j, are 1 if i is connected to j, and are 0 otherwise. The latent space model treats the connections, which I will also refer to as ties or edges, as conditionally independent given the vertices positions in an underlying latent space. That is,

$$\mathrm{Pr}\left(Y|X,\theta ,Z\right)=\prod _{i\ne j}\mathrm{Pr}\left(y_{ij}|x_{i,j},z_i,z_j,\theta \right)$$

Where X is the matrix of covariates on each pair of vertices with elements x_i,j, Z, is the matrix of latent positions and θ are a set of parameters. Both Z and θ are to be estimated from the data. The most common parameterization is a logistic regression framework where the latent positions are constrained to lie in a low-dimensional, Euclidean space. The model is then written as

$$\begin{gathered} {\eta }_{i,j}=\text{logit}\left(y_{i,j}=1|x_{i,j},z_i,z_j,\beta \right) \\ \hspace{0.5em}\hspace{0.5em}\hspace{0.17em}={\beta }^T{x}_{i,j}-\left|z_i-z_j\right| \end{gathered}$$

That is, the log-odds of a tie is proportional to the distance of two vertices in the latent space. Since the positions themselves are not identified, the |z_i − z_j| term is replaced with a single distance term, δ_i,j. Although any distance that satisfies the triangle inequality can be used (e.g., Hoff 2005, 2009), usually distances are modeled in a low-dimensional Euclidean space for parsimony and ease of interpretation.

People who are isolated, meaning they do not have any ties to others in the observed data, present a problem for latent space models, since the maximum likelihood estimate of the distance from an isolate to any other person in the network is infinite. To address this problem, most authors fit latent space models in a Bayesian framework (Handcock et al. 2007; Krivitsky and Handcock 2008; Sewell and Chen 2015). Giving the latent positions a minimally informative prior, centered at 0, shrinks the position of isolates towards the center of the latent space, which gives isolates a positive probability of being connected to others in the network. I also take a Bayesian approach to estimation, using the minimally informative priors and the MCMC algorithm outlined by Krivistky and Handcock (2008). I denote draws from the posterior distribution of the parameters as θ⁽¹⁾,…, θ^(K), and draws from the posterior predictive distribution as ${\tilde{Y}}^{\left(1\right)},\dots ,{\tilde{Y}}^{\left(K\right)}$.

Under the latent space framework, ties are modeled as random realizations of an underlying latent space. Thus changes in observed ties represent stochastic, rather than systematic, variation in the distances between the vertices. Viewing the distances as a type of social distance follows the positionist approach to social networks (Burt 1987), where stable social distances govern the process of tie formation and dissolution (McPherson 1983; McPherson, Smith-Lovin, and Cook 2001; Smith et al. 2014). While typical diffusion approaches, called connectionist approaches, treat the ties as stable conduits for information, a positionist approach treats ties as indications of the social position of each person relative to the other people in the network.

The connectionist and positionist approaches generally have been viewed as mutually incompatible. If a tie is a random draw from an underlying social space, then it cannot also be a stable conduit for information. Viewing ties as random realizations of an underlying social space provides several benefits for modeling diffusion, however. First, once fit, the model incorporates missing data gracefully. Since each of the predicted probabilities of a tie is conditionally independent given the distances, if one vertex is missing, it will not affect the path lengths that a diffusing bit must travel to get from one person to another.^v Second, the model predictions incorporate stochastic variation in the ties.^vi The stochastic variation can be incorporated in one of two ways: either by using the predicted probabilities of a tie or by using networks drawn from those probabilities (that is, the predictive distribution), to model diffusion. The following section introduces a simple diffusion model and describes these two approaches in the context of that model in greater detail.

The weighted averaging diffusion model

For this study, I use a weighted averaging diffusion model to illustrate how a latent space model could be used in conjunction with a diffusion model. With appropriate modifications, however, a latent space approach could be used with other diffusion models, such as the Watts threshold model (Watts 2002) or a complex contagion model (Centola and Macy 2007). The weighted averaging model developed independently in sociology (French 1956; Friedkin 1998; Friedkin and Johnsen 2011; Harary 1959) as a model for the diffusion of attitudes, and in statistics (Berger 1981; Chatterjee and Seneta 1977; DeGroot 1974) as a model for the formation of consensus. At its core, the model supposes that each person in a group starts with a particular attitude about a given topic, usually meaning that each person falls somewhere along the continuum from favorable to unfavorable for the topic. Then, under the model, each person updates his or her attitude by taking the average of his or her friends’ attitudes. If this updating is done repeatedly, the group will eventually reach a consensus on the topic, under certain conditions.

Formally, the model is written as A(t + 1) = WA(t), where A(t) is an n × 1 vector of people’s opinions at time t and W is an n × n matrix whose elements, w_i,j indicate the weight that person i gives to the opinion of person j. The weights are normalized such that the rows sum to 1, i.e., ${\sum }_{j=1}^n{w}_{i,j}=1$ for each i = 1,…, n. Typically, the weights are given by the row-normalized adjacency matrix. Denoting the adjacency matrix as Y, typically $w_{i,j}=\left(y_{i,j}\right)/\left({\sum }_{j=1}^n{w}_{i,j}\right)$.

The diagonal of the matrix, w_i,i, represents the weight that a person places on his or her own attitude. I follow Friedkin and Johnson (2011:40)’s construct framework to choose diagonal values. In it, for an arbitrary self-weight value α ∈ [0, 1], values of the diagonal are given by α and the off-diagonal elements are given by $\left(1-\alpha \right)\left(y_{i,j}/{\sum }_{i\ne j}{y}_{i,j}\right)$. Setting an arbitrary value for the diagonal allows comparisons between different models, while holding the percentage of social influence versus individual stability constant.

The row normalized weight matrix can be thought of as a transition matrix for a Markov chain. If the weight matrix does not change between iterations, the diffusion process at any time step can be written in terms of change from the initial position as A(t + 1) = W^tA(1), where A(1) denotes the initial attitudes for each person. After many iterations, meaning as t → ∞, the chain will stabilize into a stationary distribution, denoted W^∞. This final distribution, which I denote A(∞) =W^∞ A(1), represents the value of the consensus that the group reaches. If the transition matrix for the chain representing the entire network is irreducible and aperiodic,^vii then everyone in the group will reach a single consensus value, where each person’s contribution to the final consensus is given by their weight in the stationary distribution. If the transition matrix is not irreducible, as is the case for networks that have more than one strongly connected component, such as in the example to follow, there will be multiple consensus values, one for each strongly connected component in the network.

Incorporating the latent space model into the weighted averaging process

Using results from the latent space model, stochastic changes in the ties can be incorporated by changing the weight matrix W. W can either be changed to the predicted probability of a tie between each person i and j, or it can be changed to a simulated network drawn from the predictive distribution of the latent space model. Setting the elements of W as the predicted probability of a tie between each pair of people suggests that, at each iteration, a person takes the opinion of every other person in the network into account. People who are very distant still influence each other, but, because they are very distant, the probability of a tie between them is very low and they therefore give each other’s attitudes very little weight. Formally, to set the elements of W to predicted probabilities, I transform the draws from the posterior distribution, ${\eta }_{i,j}^{\left(1\right)},\dots ,{\eta }_{i,j}^{\left(K\right)}$ into predicted probabilities, which I denote $p_{i,j}^{\left(1\right)},\dots ,p_{i,j}^{\left(K\right)}$ using the inverse logit transformation:

$$p_{i,j}^{\left(k\right)}=\exp \left({\eta }_{i,j}^{\left(k\right)}\right)/\left(1+\exp \left({\eta }_{i,j}^{\left(k\right)}\right)\right)$$

for each i = 1,…,n, j = 1,…, n, and k = 1,…, K. I then create a weight matrix for each of the K draws from the posterior by setting the i^th, j^th cell of W^(k) to $p_{i,j}^{\left(k\right)}$ and dividing by the row sums to row-normalize W^(k). I simulate diffusion using the weighted averaging model, meaning A(t + 1)(k) = W^(k)A(t)^(k), where A(t)^(k) indicates the value of the attitudes at time t using the k^th draw from the posterior distribution. To simulate several iterations of the diffusion process, I hold the weight matrix for a given draw from the posterior distribution, W^(k), constant, giving A(t + 1)^(k) = (W^(k))^t A(1).^viii This process produces a distribution of attitude values for each person i at each iteration of the diffusion process t, for each draw from the posterior distribution k. Using the different draws from the posterior distribution incorporates the stochastic uncertainty about how close each person is in the underlying space.

Alternatively, setting the elements of W to a draw from the posterior predictive distribution of the model suggests that, at a single iteration, people are only influenced by people to whom they are directly connected, but that the connections are randomly generated. To incorporate stochastic uncertainty, the connections must change at each iteration of the model. Formally, I take an adjacency matrix drawn from the posterior predictive distribution, ${\tilde{Y}}^{\left(k\right)}$, and transform it into a weight matrix W^(k) using the same procedure as the observed adjacency matrix: setting the diagonal equal to 1 and dividing by the sum of the rows. I then use each weight matrix created from a draw from the posterior predictive distribution for one iteration of the diffusion model. That is,

$$\begin{gathered} A\left(2\right)=\left(W^{\left(1\right)}\right)A\left(1\right) \\ A\left(3\right)=\left(W^{\left(2\right)}{W}^{\left(1\right)}\right)A\left(1\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮ \\ A\left(K\right)=\left(W^{\left(K\right)}\cdots W^{\left(1\right)}\right)A\left(1\right) \end{gathered}$$

Thus at each iteration, a new adjacency matrix, representing a new network, is drawn from the posterior predictive distribution, and that draw is used to simulate one iteration of the diffusion process. Stochastic uncertainty about which ties are present is incorporated because at each iteration a different set of ties, drawn from the same set of underlying distances, is used to simulate the diffusion process.

Effectively, both of these methods shrink the diffusion results towards the results from the network predicted by the latent space model. The shrinkage can either happen at the point of the predicted probabilities, as in the first method, or at the point of the predicted networks, as in the second method. The methods also correspond to different assumptions about the diffusion process. The first method assumes that every person can observe every other person’s attitudes, and takes every other person in the network into account when changing his or her mind. In small groups of less than ten people, this assumption is almost certainly true, but it may be supported in larger groups, such as a school, as well. For example, Fujimoto and Valente (2012) suggest that students in a school mimic structurally equivalent others in the school, rather than people they are directly connected to.

By contrast, the second method extends the existing diffusion model more directly. Using the posterior predictive distribution, meaning the predicted networks drawn from the model predictions, implies that a person only considers his or her immediate network neighbors when he or she changes his or her mind. Unlike in the original weighted averaging model, however, the second method suggests that those ties are random draws from an underlying probability, and may vary from day to day, or from iteration to iteration. Thus the second model takes the uncertainty in the observed network ties into account by using a different, but similar, set of network ties at every iteration. The following section illustrates how this method is used in practice, using a friendship network from a school.

Data

Sample

To illustrate how this method works in practice, I consider friendship networks from a school in the PROmoting School-university-community Partnerships to Enhance Resilience (PROSPER) Peers study (Spoth et al. 2004, 2007). PROSPER Peers is a longitudinal study of adolescents in schools originally designed to test substance use interventions. Researchers identified 28 rural communities – 14 in Iowa, and 14 in Pennsylvania – and interviewed two cohorts of students at each of the schools in those communities. Each cohort was interviewed in the fall of 6^th grade, and then was re-interviewed in the spring each year from 6^th grade until 12^th grade, for a total of 8 waves of in-school interviews. Friendship networks were collected by asking students to name up to two best friends and five other close friends. The names were matched to a class roster to produce a directed friendship network within each grade, where student i is connected to student j (denoted i → j) if student i listed student j as a friend.

The empirical demonstration of this method has two parts. First, I explore properties of the model using a single school setting. The school setting that I use is the 6^th grade fall survey administration of a single school, which I call School 212. Second, I use the full dataset to consider how various approaches – the observed network, the social space diffusion method that I propose, and two alternative methods for smoothing the network – predict the attitude values of students at the next wave.

Attitude scales

I use four attitude and behavioral scales: attitudes towards substance use, expectations about substance use, school adjustment and bonding, and deviance. I focus on the first scale, attitudes towards substance use, to illustrate the properties of the model, and consider all four scales to test how effectively each approach predicts future values. The full text of each of the survey items that compose these scales are given in Table 1. Attitudes towards substance use captures how wrong students feel smoking is. Expectations about substance use captures students’ expectations about whether they will be accepted by their peers if they use substances. School adjustment and bonding captures how much students pay attention to, and feel they belong at school. Finally, the deviance scale is a score indicating how many deviant behaviors, such as illegal substance use, destroying property, or skipping school, the students have engaged in over the last 12 months. Taken together, these scales cover a range of potentially contagious attitudes and behaviors.

Table 1:

Text of attitude scales

Attitudes about substance use
How wrong is it for someone your age to smoke cigarettes?	1=Not at all wrong, 2=A little bit wrong, 3=Fairly wrong, 4=Very Wrong, 9=Missing
How wrong is it for someone your age to drink alcohol?	1=Not at all wrong, 2=A little bit wrong, 3=Fairly wrong, 4=Very Wrong, 9=Missing
How wrong is it for someone your age to use marijuana?	1=Not at all wrong, 2=A little bit wrong, 3=Fairly wrong, 4=Very Wrong, 9=Missing
Expectations about substance use
A/D: Teens who smoke have more friends	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Smoking cigarettes makes you look cool	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Smoking cigarettes lets you have more fun	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Teens who drink alcohol have more friends.	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Drinking alcohol is a good way of dealing with your problems.	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Drinking alcohol makes you look cool	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Drinking alcohol lets you have more fun	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Drinking helps you get along with more people	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Teens who use marijuana have more friends	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Smoking marijuana makes you look cool	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
A/D: Smoking marijuana lets you have more fun	1=None or almost none, 2=Less than half, 3=About half, 4=More than half, 5=All or almost all, 9=Missing
School adjustment and bonding attitudes
True? I like school a lot	1=Never true, 2=Seldom true, 3=Sometimes true, 4=Usually true, 5=Always true
True? I try hard at school	1=Never true, 2=Seldom true, 3=Sometimes true, 4=Usually true, 5=Always true
True? Grades are very important to me	1=Never true, 2=Seldom true, 3=Sometimes true, 4=Usually true, 5=Always true
True? School bores me	1=Never true, 2=Seldom true, 3=Sometimes true, 4=Usually true, 5=Always true
True? I don’t feel like I really belong at school	1=Never true, 2=Seldom true, 3=Sometimes true, 4=Usually true, 5=Always true
True? I feel very close to at least one of my teachers	1=Never true, 2=Seldom true, 3=Sometimes true, 4=Usually true, 5=Always true
True? I get along well with my teachers	1=Never true, 2=Seldom true, 3=Sometimes true, 4=Usually true, 5=Always true
True? I feel that teachers are picking on me	1=Never true, 2=Seldom true, 3=Sometimes true, 4=Usually true, 5=Always true
Deviance scale
In the past 12 months, how many times have you …
…Taken something worth less than $25 that didn’t belong to you.	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Taken something worth $25 or more that didn’t belong to you	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Beat up someone or physically fought with someone because they made you a	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Purposely damaged or destroyed property that did not belong to you	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Broken into or tried to break into a building just for fun or to look around	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Thrown objects such as rocks or bottles at people to hurt or scare them	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Been picked up by the police for breaking a law	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Run away from home	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Skipped school or classes without an excuse	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Carried a hidden weapon	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Avoided paying for things such as movies, rides, food, or computer services	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing
…Taken something from a store that you did not pay for	1=Never, 2=Once, 3=Twice, 4=Three or four times, 5=Five or more times, 9=Missing

Latent space model specification

For simplicity, in this example, I focus on a single model specification, a latent space model with a term for a 2-dimensional Euclidean latent space. In general, the latent space model smooths irregularities in the network, and the specification of the latent space model can be used to control the amount of smoothing. Higher dimensions apply less smoothing, while lower dimensions apply more smoothing.^ix Additionally, model specifications can include matching terms and latent clustering (Handcock et al. 2007) to account for potential in-group biases (Hewstone, Rubin, and Willis 2002) within either sociodemographic groups or informal peer groups. Choosing between model specifications can be accomplished with posterior predictive checks. That is, predicted networks can be generated from the fitted model, and characteristics of those networks such as the degree distribution or the number of isolates can be compared against the observed network. In the absence of prior notions about how much smoothing is necessary, the simplest model that reproduces the relevant characteristics of the network should be chosen.

I chose the 2-dimensional model for two reasons. First, the 2-dimensional latent space model is the simplest, most parsimonious model for the network, which helps clarify the model’s presentation. In addition, the 2-dimensional Euclidean latent space model can be readily visualized, allowing visual interpretation of the results as well. Second, I tried additional model specifications, using different numbers of dimensions, as well as matching terms for gender, SES, and latent peer groups. Posterior predictive checks showed that including the different terms did not change the diffusion results substantially over the simple, 2-dimensional Euclidean latent space model. As such, they have been excluded; future work may examine when additional terms in the model specification produce different diffusion outcomes. The following section shows the results from diffusion simulated using the 2-dimensional, Euclidean latent space model.

Alternative models

For comparison, I show how the social space differences compare to two other, simpler methods of predicting future observations using the network of friendships and attitude values in the previous survey wave. I call these approaches the class average approach, and the density smoothing approach.

Class average

Under the class average approach, I assume a person’s attitude at t + 1 is the weighted average of their own attitude value at t and the average of the others’ attitudes in the class at time t. Denoting person i’s attitude at t as a_i(t) and the average of the others’ attitudes at time t, $\left[{\sum }_{i\ne j}{a}_i\left(t\right)\right]/\left(n-1\right)$, as $\overline{a}\left(t\right)$, the class average approach assumes that $a_i\left(t+1\right)=\gamma \left(a_i\left(t\right)\right)+\left(1-\gamma \right)\left(\overline{a}\left(t\right)\right)$, where γ ∈ [0,1] is a tunable parameter. In Friedkin and Johnson (2011)’s construct framework introduced earlier, this approach is equivalent to setting w_i,j ∝ 1 for i ≠ j, and w_i,i = γ. I use this approach to show how the predictions from the network models compare to a simple averaging that is independent of the network.

Density smoothing

Under the density smoothing approach, I test how the social space diffusion approach that I suggest compares to a different, simpler smoothing approach. Instead of constructing the weight matrix using the predicted probabilities from a statistical model, I use the weighted average of the presence of a tie and the density of the network as the weight matrix, W. That is, I set $w_{i,j}\propto \delta \left(y_{i,j}\right)+\left(1-\delta \right)\left(\overline{y}\right)$, where δ ∈ [0, 1] is a tunable parameter, and $\overline{y}=\left({\sum }_{i\ne j}{y}_{i,j}\right)/\left(\begin{array}{l}n\\ 2\end{array}\right)$, or the density of the network. This simple smoothing approach allows low-weight connections across the network, but does not incorporate local structure in the form of triadic closure, reciprocity, or peer group structure.^x Therefore, the density smoothing approach serves as a useful point of comparison, to see how much of the improvement in the model can be attributed to simply adding noise, versus adding noise that respects the local structure of the network.

Results

Figure 1 illustrates the diffusion process in School 212 visually. Each column represents one of the diffusion processes: using the observed network, using the posterior predicted probabilities from the latent space model, and using the posterior predictive distribution, meaning the simulated networks, from the latent space model. Each row represents one iteration of the model – the first row represents the initial conditions, the second row represents the attitudes after the weighted averaging has been performed once, the third row represents the attitudes after the weighted averaging has been performed twice, and so on. The coloring of the vertices^xi represents each person’s attitude after each iteration of diffusion process. The initial attitudes are taken from the attitudes about substance use scale listed in Table 1. The response options for each item in the scale were coded as 1=Not at all wrong, 2=A little bit wrong, 3=Fairly wrong, 4=Very Wrong, and items were averaged to create the scale. Darker colors indicate that a student feels smoking cigarettes, drinking alcohol, and using marijuana is more wrong. To ease comparison, the vertices have the same position, their average location in the latent space from the fitted model, in each of the plots.

Figure 1:

Visualization of weighted averaging diffusion processes

Figure 1 shows the diffusion process for each of the three types of diffusion visually. In the left column, the diffusing bit, attitudes about substance use, spreads along unchanging, observed network ties. Most of the people in the network believe that substance use is very wrong (indicated by dark blue), and that attitude spreads to most of the people who believe smoking is not at all wrong (indicated by light yellow) after the weighted averaging is taken twice. Several people remain unchanged from their initial attitudes, however. These people do not send ties to others in the network, and therefore are not influenced by others in the weighted averaging diffusion model using the observed network after any number of iterations. Appendix Figure 2 shows the trajectory of each student’s predicted attitudes under each of the three types of diffusion.

The second column shows the weighted averaging process using the predicted probabilities of a tie between each person as a weight. Since each person is effectively connected with each other person, albeit often with very low weights, the network is completely connected in this case. Rather than drawing all of the ties, for clarity, I removed the ties, so that the distances between vertices would be more apparent. Using the predicted probabilities as weights causes the weighted averaging to converge almost entirely after two iterations. Since each person is connected to every other person, each person takes the attitudes of every other person into account during the weighted averaging process, leading to very rapid convergence on a single value for the diffusing attitude.

The third column shows the weighted averaging process using the draws from the predictive distribution. At each step, a new set of ties is drawn from the underlying distances in social space, and then a weighted averaging process is simulated once over that set of ties. This corresponds to an accurate model with unreliably measured ties. In each plot, the set of ties shown are the set of ties that will be used for that instance of the weighted averaging process. As the figure shows, after five iterations, the weighted averaging process has mostly converged on a single consensus value. Although a few people who started off believing that substance use was not at all wrong take one or two more iterations to reach the consensus value, all of the people ultimately reach the consensus value. Unlike in the model using the static, observed network, any people who are isolated do not necessarily stay isolated, meaning that they will ultimately contribute to the final consensus in the school. Their contribution is visible both as a slightly lower final value of the consensus attitude, and as a lack of isolates who hold the same attitudes as they did initially.

The illustration in Fig. 1 shows several key properties of the social space diffusion model, compared to using the observed network. Using the social space model smooths irregularities in the network, meaning that isolates are probabilistically reconnected to the network, and people are reconnected to their nearby peers. As a first consequence of this smoothed traffic pattern, estimates from the social space diffusion model stabilize at a consensus in fewer iterations than estimates using the observed network. The process using draws from the posterior predictive distribution of the latent space model fluctuates more, because the network changes between each iteration, but ultimately, the models change by approximately the same amount between each iteration. By contrast, the weighted averaging process using the predicted probabilities as weights converges much more quickly.^xii In the predicted probability model, since everyone is connected to everyone else, the weighted averaging process proceeds much more rapidly than when people can only take into account their immediate network neighbors. In both cases the models have mostly converged before 6 iterations have been performed. This convergence is illustrated in a figure in a supplemental appendix.

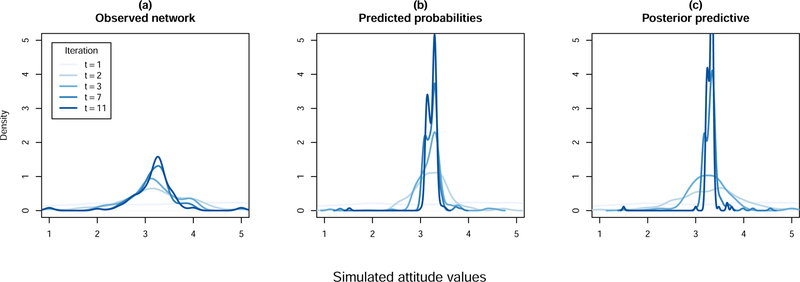
As a second consequence, the smoothed traffic pattern reduces the number of outliers in the diffusion predictions. This results in better behaved predictions, which converge to a single consensus value for all people in the network. By contrast, using the observed network results in convergence to a series of different consensus values for each weakly connected component.^xiii Figure 2 illustrates this by showing the distribution of attitude values at 1, 2, 3, 7, and 11 iterations for each of the models. To avoid confounding the convergence of the model with pre-existing homophily on an attitude, instead of using values from the attitudes towards substance use scale as in previous figures, for Fig. 2 I randomly assigned each person in the network a simulated attitude value of 1, 2, 3, 4, or 5, and then ran the diffusion process as before.

Figure 2:

Distribution of attitude values by simulated iteration

In each panel of Fig. 2, the distribution of attitude values begins as a flat, nearly uniform, distribution across the range from 1 to 5. In models (b) and (c), representing the diffusion processes simulated using the latent space model predictions, the distribution gradually becomes increasingly tightly centered at the mean, approximately 3.5. As in Fig. 1, the model using the predicted probabilities, (b), becomes more tightly centered at 3.5 in fewer steps than the model using draws from the posterior predictive distribution, (c). After 2 and 3 steps, the density at 3 is higher for (b) than for (c), and the difference between 7 and 11 steps is still perceptible for (c), while it is not for (b). Unlike the diffusion models simulated from using the latent space model predictions, however, the diffusion model simulated using the observed network, (a), does not converge to a single point as the number of iterations increases. Instead, the model using the observed network develops a distribution of attitudes centered around 3.5, but never achieves the tight distribution at 3.5 that models (b) or (c) do. Unlike in models (b) and (c), people who are disconnected from the network in model (a) never become connected, and therefore maintain their attitudes throughout the simulation. Furthermore, people who do not receive any friendship nominations do not influence anyone, and remain that way throughout the simulation. Model (a) treats the ties as fixed, stable quantities, suggesting that the lack of a tie is always meaningful. As such, model (a) never converges to a single consensus value, while models (b) and (c) do.

But which estimator is closer to the truth? Figure 3 shows how the estimates of diffusion of attitudes about smoking compare to the attitudes about smoking observed at the second wave of the survey.^xiv In Fig. 3, the initial attitude values, A(1), are given by students’ responses to attitudes towards substance use scale, as in Fig. 1 and 2. I simulated the diffusion process for five iterations using each of the methods, holding the diagonal weights, α, at 0.7, and after each iteration, I calculated the mean squared error (MSE) of the results of the diffusion simulation, and the students’ responses to the same questions at the second survey wave. That is, Fig. 3 shows the MSE of the diffusion results and the observed values of the diffusing attitude at the next survey administration. Lower values of the MSE indicate that the particular diffusion method is capturing the diffusion process more accurately.

Figure 3:

Mean square error of predictions, School 212

Figure 3 shows that diffusion simulated using the predicted probabilities of a tie as weights predicts future attitudes about smoking more accurately than diffusion simulated using either the observed network or the posterior predictive distribution. The MSE for the model using predicted probabilities is approximately 0.1, or 20%, lower than the MSE for the model using either the posterior predictive distribution or the observed network after 1 iteration of the model. Since simulations using the predicted probabilities of a tie allow each person in the network to incorporate information from every other person in the network, while the other two methods do not, Fig. 3 suggests that students incorporate information from the other students in the school more broadly, and not just from the people that they are connected to.

Over each iteration, the MSE from the simulation using the posterior predictive distribution declines, until at the 5^th iteration, the MSE from the simulation using the posterior predictive distribution and the posterior probabilities of a tie are approximately the same. After 1 iteration, the 95% credible intervals from the models simulated using the posterior predictive distribution and the posterior probabilities overlap only slightly, but by the 6^th iteration, the credible interval from the posterior probabilities overlaps the credible interval from the posterior predictive distribution entirely. By contrast, the MSE from the simulation using the observed network declines in the first iteration, and then remains stable in later iterations. This follows the results on the convergence of the different models. As Fig. 2 showed, the simulations using the predicted probabilities of a tie and the posterior predictive distribution, or the networks drawn from those probabilities, converge to approximately the same consensus value. The approaches differ primarily in the amount of time it takes to reach consensus; since the predicted probabilities average over all the people in the network at each iteration, the simulations using the predicted probabilities converge much faster. Figure 3 shows that the consensus value reached by the latent space diffusion model is closer^xv to the true attitude values measured in the second survey administration. The simulations using the predicted probabilities approach the consensus value within 1 or 2 steps, while the simulations using the simulated networks approach the consensus value within 4 or 5 steps. The observed network does not approach a single consensus value, and therefore predicts the final outcome less accurately.

To see whether this improvement holds across a larger sample, I consider how the MSE of the prediction from the latent space model compares to the MSE from the observed network across the entire set of PROSPER schools. Figure 4 shows the MSE values from the latent space model predictions, the observed model predictions, as well as predictions from two alternative smoothing approaches, the class averaging and density smoothing approaches. Each of these MSE values are shown for the 4 attitudinal and behavioral scales, and across each of the first 7 survey waves. To show how the results compared against different parameter values for each of the alternative smoothing approaches, I present results that hold the diagonal weighting value, α, at 3 levels, 0.5, 0.7, and 1, to focus on the primarily social influence range of the parameter, and I show predictions from the density smoothing approach with the density weighting parameter, δ, held at 3 different values, 0.2, 0.5, and 0.7, to show values spanning the parameter’s range. For simplicity, I focus on mean predictions, and disregard the within-school confidence intervals generated by the latent space model.^xvi I consider only the predicted probabilities approach, using the predicted probability derived by averaging over the whole posterior, and I only consider one iteration of the model in each case. The distributions shown in Fig. 4 denote the between-schools variation in average MSE.

Figure 4:

Mean squared error of next survey wave predictions

Focusing first on the MSE values over time, Fig. 4 shows a broad increase in MSE for each of the scales related to substance use and deviance over time. In attitudes towards substance use, MSE values climb from roughly 0.25 to 0.60 in the α = 0.5 panel (denoting 50% social influence), and to 0.90 in the α = 1 panel (denoting 100% social influence). Expectations towards substance use and deviance show similar increases, although the latter is less pronounced. School adjustment and bonding, by contrast, shows a slight decrease in MSE over time, indicating that the diffusion measures become slightly better at predicting school adjustment and bonding as students age. These differences are likely due to the lack of prevalence of substance use in early high school. As students begin to use drugs, the amount of variance in the scales increase, leading to worse predictions.

Focusing next on the differences between models, Fig. 4 indicates that the observed network consistently performs worse than the other approaches to smoothing the network. The other smoothing mechanisms are generally comparable, with the latent space approach generally performing the best among them. The large scale of the MSE values obscures the size of the differences between the various diffusion approaches. Fig. 5 focuses on the comparison between the latent space model proposed here and the other, alternative approaches, by showing the percentage difference between the MSE values produced by the latent space model, and the MSE values produced by the other approaches.

Figure 5:

Percentage improvement in MSE

Figure 5 is arranged in the same manner as Fig. 4, but shows by what percent the MSE values from a given smoothing approach are greater, or lesser, than the MSE values from the latent space model, giving a direct comparison with the model. Values less than 0 indicate that the comparison model is performing better than the latent space model, and values greater than 0 indicate that the comparison model is performing worse than the latent space model. (The comparison values for the latent space model are 0.) Fig. 5 shows clearly that the observed network predicts future attitude values worse in almost every case. The observed network’s MSE values average around 10% higher, or worse, than the latent space model’s MSE values.

The other smoothing approaches produce results that are more comparable to the latent space model. In the α = 0.5 condition, indicating that social influence gets a weighting of 0.5, the class averaging approach performs about 2 – 3% worse in predicting school adjustment and bonding, 1 – 2% worse at predicting deviance and attitudes towards substance use (with the notable exception of wave 1), and approximately as well as the latent space model at predicting expectations about substance use. The differences between the class average approach and the latent space model increase as the α parameter increase. The class average approach performs approximately 5% worse on school adjustment and bonding when α = 0.7, and approximately 7 – 8% worse on school adjustment and bonding when α = 1. A similar, but smaller, decrease in the relative performance of the class average approach also appears in the attitudes towards substance use and deviance scales, again with the exceptions of the first survey wave. Together, the performance of the class average approach suggests that disregarding the network altogether can lead to some improvement on the predictions generated from the observed network alone, but it is often worse than approaches that consider a smoothed version of the network.

The density smoothing approach generates predictions that are similar to, but rarely better than, the latent space model approach. I tested the density smoothing approach with three parameter values: δ = 0.2, 0.5, and 0.7. This parameter balances the extent to which the network is simply represented by a complete graph with edge weights equal to the density of the network (δ = 1), and the observed network (δ = 0). At lower levels of the self-weighting parameter, α = 0.5, the density smoother’s performance improves monotonically, from worst when it is closest to the observed network ( δ = 0.7), to best when it is closest to the complete graph with density edge weights ( δ = 0.2). At higher levels of α, however, the density smoother’s performance is generally U-shaped, performing best when δ = 0.5 and worst when δ = 0.2 or δ = 0.7. This indicates that, when using the density smoother, there is an optimal level of the parameter δ, particularly when social influence is given a higher weight. However, regardless of the parameter value, the density smoother rarely performs better than the two-dimensional latent space model. At moderate levels of social influence, α = 0.7, the density smoother performs roughly 1 – 2% worse on attitudes towards substance use, roughly the same on expectations about substance use, roughly 2 – 3% worse on school adjustment and bonding, and roughly 2% worse on deviance. The density smoother’s performance is more varied, but often worse overall, when only allowing for social influence by setting the diagonal, α, to 1. The density smoothing approach performs around 2 – 5% worse in predicting school adjustment and bonding, 2 – 3% worse predicting attitudes towards substance use, and 1 – 2% worse predicting expectations about substance use. Taken together, this suggests that much of the improvement in prediction arises from adding noise, but a model that respects the local structure of the network, such as the latent space model, can still perform as well as, and often better, than other, simpler smoothing methods.

Discussion

In this article, I have described a social space diffusion model, which integrates two important aspects of how networks are conceptualized: stable connections through which influence and information travel, and indicators of the relative positions of people. The approach described here integrates those perspectives by estimating the relative positions of people to one another using a latent space model, and then simulating the diffusion of an attitude or a behavior over the latent space. I represented the latent space in two ways: as the predicted probabilities of two people being connected to one another, and as a series of networks randomly drawn from those distances. The two ways refer to a situation where people incorporate information from everyone else in the network, and a situation where people only incorporate information from their immediate network neighbors, but their networks are subject to routine, random churn.

The perspective elaborated here is both more theoretically consistent, and produces better behaved estimates, than using the observed network. Using a latent space model is theoretically more consistent because it represents the measurement error inherent in network observation more accurately. Networks, as we observe them, show continuous, routine, and rapid churn. Under those conditions, if an attitude or belief spreads through the network, the people in the network are likely influenced by all of the people in their social vicinity, or are influenced by the people they happened to talk to that day. This model addresses both of those possibilities.

Furthermore, this approach produces a better behaved estimator of the final consensus that a group would reach over repeated applications of a weighted averaging diffusion process. When only the observed network is used, idiosyncrasies of the ties reported, such as people not receiving any friendship ties, unduly influence the final distribution of attitudes. By contrast, the latent space approach allows random churn in the ties, improving mixing of the people in the model without sacrificing important social distances. Although I focus on the weighted averaging model for simplicity and analytical tractability, this approach could be extended to other diffusion simulation frameworks, such as threshold models and simulation models of culture and structure, in a relatively straightforward manner.

Compared with other options, this model also predicts change in attitudes more accurately. Looking at students in 54 middle and high school settings, I consider how well the social space diffusion model predicts attitudes in the subsequent wave, compared with the observed network, and with several other possible smoothing mechanisms. The social space diffusion model performs approximately 10% better than the observed network across each of the school settings, survey waves, and attitude values, and between 1% and 5% better than two alternative smoothing approaches. These results suggest that better predictions arise when the diffusion model allows students to consider the attitudes of all of the other students in the school in the diffusion process, while still taking into account the importance of socially proximate others. The social space diffusion model effectively balances both of these considerations.

The social space diffusion model presents several advantages that are not elaborated in the results, but which could be developed in future work. First, because the social space diffusion model is a general framework, it could be extended to any situation where a predicted probability of interaction can be estimated. Here, I used estimates from a latent space model to produce predicted probabilities, but, for example, this procedure could be extended to cases where the complete network cannot be enumerated, but where predicted probabilities of interaction can be reasonably inferred, such as from an ERGM fit using a mixing matrix. Second, unlike other diffusion models, the social space diffusion model incorporates uncertainty about whether or not a tie is present – or how meaningful that tie is – into the predicted diffusion estimate. Including this uncertainty bounds our uncertainty about the extent of the diffusion process, and generates predictions that could, potentially, be falsified. Although I primarily focus on the central tendency of the model in the results, the error bounds produced by the model are an important improvement as well, and could be profitably explored in future work.

One potential area of future study, developing this into a regression framework, deserves specific mention. The approach of this study – generating predictions, and then comparing them against future outcomes – is similar to a simple regression approach, where various covariates are used to predict a future outcome. In particular, the approach that I use is closely related to the network autocorrelation model (e.g., Doreian 1980, 1981; Leenders 2002), where the relationships between people are included as a covariate that is measured with error (e.g., Bollen 1989). In spite of the similarity, I did not explore the connection between the model that I propose and the regression framework for two reasons. First, incorporating the uncertainty that the social space diffusion model produces would involve developing a multiple imputation-style approach, where several regressions were fit using different draws from the simulated data, and then averaged together. Second, the network autocorrelation model suffers from a known bias: denser networks produce smaller autocorrelation coefficients (Mizruchi and Neuman 2008; Neuman and Mizruchi 2010). Since the social space diffusion model produces a denser network than the observed network, attempting to compare coefficients from models fit using the social space diffusion approach and the observed network would not yield a valid comparison. Addressing both of these problems is a potentially useful research avenue, but is beyond the scope of this study.

While this model presents a more integrated and theoretically consistent view of network diffusion, it suffers from several limitations. First this model assumes that the observed network is the network that most closely represents the diffusion process. Since the distances in social space are estimated from the observed network, if the observed network does not accurately reflect the diffusion process, then the social space estimated from the observed network will not accurately reflect the diffusion process either. Second, the model assumes that categorical distinctions will be reflected in the observed network proportionally to their salience. If salient categorical distinctions are present, but are not reflected in the network, then the model will not represent in-group biases appropriately. Prior information about the salience of particular categorical distinctions can be incorporated using the prior distributions on model parameters, but I have not attempted that in this study. Third, and finally, the model does not allow the probabilities of interaction to change over time. Instead, changes in the network are seen as different random draws from the same underlying social space, rather than changes in the social space itself. Future work should develop a method that can estimate changes in the social space (e.g., Sewell and Chen 2015), and therefore can estimate how diffusion potential changes over time.

This third limitation highlights the distinction between the social space diffusion model and stochastic actor-based models (Snijders 2017; Snijders et al. 2010), a common framework for modeling the coevolution of networks and beliefs or behaviors. One can imagine that changes in the observed network fall somewhere on a continuum. The social space diffusion model falls on one end of the continuum, assuming that all changes are the result of noisy measurement. SABM’s fall on the other end of this continuum, assuming that all changes are the result of actors making choices about their friends. Reality likely falls somewhere in between: changes in the network are both the result of noisy measurement, and people actually making choices about their friends. However, because SABM’s must simulate people choosing which friends to make from among the other people in the population, they require a considerable amount of data and processing power to estimate. This represents a practical drawback of SABM’s with respect to the social space diffusion model. Further comparison of these two approaches may be a profitable avenue for additional research.

In spite of these limitations, the method proposed in this study represents a significant step forward methodologically. By applying a smoothing function to the observed network, this method also provides an approach to modeling diffusion that is robust to small fluctuations in the observed network, which are a ubiquitous feature of network data collection. Future work may be able to extend this approach to use other models that generate predicted probabilities of network ties, such as the relational events model, to extend the diffusion framework beyond statically observed networks. Networks have long represented two distinct aspects of social structure: the conduits through which information and influence flow, and indicators of positions of positions in social structure, like hierarchy and roles. By constructing a model of diffusion over social space, we can take the first step towards merging these two aspects.

Bio:

Jacob C. Fisher is a research investigator in the Survey Research Center at the University of Michigan’s Institute for Social Research. He obtained his doctorate in sociology and his master’s in statistical science from Duke University. His research focuses on developing and testing better network diffusion models, to understand how ideas, innovations, and information spreading through a group of people help to create and maintain a common culture over time.