A Bayesian hierarchical model for analyzing methylated RNA immunoprecipitation sequencing data

Abstract

Background:

The recently emerged technology of methylated RNA immunoprecipitation sequencing (MeRIP-seq) sheds light on the study of RNA epigenetics. This new bioinformatics question calls for effective and robust peaking calling algorithms to detect mRNA methylation sites from MeRIP-seq data.

Methods:

We propose a Bayesian hierarchical model to detect methylation sites from MeRIP-seq data. Our modeling approach includes several important characteristics. First, it models the zero-inflated and over-dispersed counts by deploying a zero-inflated negative binomial model. Second, it incorporates a hidden Markov model (HMM) to account for the spatial dependency of neighboring read enrichment. Third, our Bayesian inference allows the proposed model to borrow strength in parameter estimation, which greatly improves the model stability when dealing with MeRIP-seq data with a small number of replicates. We use Markov chain Monte Carlo (MCMC) algorithms to simultaneously infer the model parameters in a de novo fashion. The R Shiny demo is available at https://qiwei.shinyapps.io/BaySeqPeak and the R/C ++ code is available at https://github.com/liqiwei2000/BaySeqPeak.

Results:

In simulation studies, the proposed method outperformed the competing methods exomePeak and MeTPeak, especially when an excess of zeros were present in the data. In real MeRIP-seq data analysis, the proposed method identified methylation sites that were more consistent with biological knowledge, and had better spatial resolution compared to the other methods.

Conclusions:

In this study, we develop a Bayesian hierarchical model to identify methylation peaks in MeRIP-seq data. The proposed method has a competitive edge over existing methods in terms of accuracy, robustness and spatial resolution.

INTRODUCTION

Epigenetic modifications of DNAs and histones have demonstrated substantial effects on many biological functions, such as cellular differentiation and development [1,2]. Diverse epigenetic modifications of RNAs are also involved in essential regulatory functions in various biological processes [3]. More than 100 chemical modifications of RNA have been found in eukaryotes and some viruses, among which N⁶-methyladenosine (m⁶A) is the most prevalent in mRNAs and long non-coding RNAs (lncRNAs) [4–6]. Although m⁶A modification was first discovered in the 1970s [7–9], not until recently was it found that m⁶A modification is a dynamic and reversible process in which adenosine methyltransferases (“writers”), demethylases (“erasers”) and m⁶A binding proteins (“readers”) play distinct roles in methylation, demethylation and recognition of m⁶A and conferring downstream effect [10–13]. It has been shown that RNA m⁶A methylation contributes to the regulation of a wide range of fundamental biological processes, such as mRNA maturation and degradation, and RNA-protein interaction [14,15]. However, the mechanism that determines methylation sites and the association between m⁶A modifications and functional consequences are largely unknown.

In 2012, two independent studies [4,5] developed a new approach called methylated RNA immunoprecipitation sequencing (MeRIP-seq) to map the transcriptome-wide landscape of mRNA m⁶A methylome. This technology first fragments total mRNA into short sequences of length approximately 100 nt. Next, the fragmented mRNAs are separated into two parts. One part is used as the control (input) sample, and the other part is subject to immunoprecipitation (IP) by the anti-m⁶A antibody to isolate the methylated sequences. Both the control and IP samples are then submitted for high-throughput sequencing. The IP sample contains enriched methylated RNA fragments because unmethylated fragments are washed off in the immunoprecipitation step, while the control sample includes all RNA fragments and thus can be used to adjust methylated transcript abundance with basal gene expression level. Therefore, MeRIP-seq-based m⁶A detection can be considered as a peak calling problem, since the read counts of those m⁶A sites in the IP samples are enriched compared to those in the control samples. Although the MeRIP-seq experiment measures the transcriptome-wide landscape of mRNA m⁶A methylome, it is usually with few replicates. In addition, similar to RNA-seq, MeRIP-seq data usually involve non-negative counts with drastic variation, resulting from transcriptional expression of different genes and isoforms. Finally, strong spatial dependency exists among the read counts of the neighboring sites along mRNA transcripts. All of these pose challenges to MeRIP-seq data analysis, and need to be carefully considered in order to accurately identify the m⁶A methylation sites.

Currently, several algorithms have been developed to identify the m⁶A sites from MeRIP-seq data. For example, exomePeak [16] models the read counts using a Poisson distribution and conducts a C-test [17] based on the hypothesis that the mean of IP reads at methylated sites is greater than those in the input samples. HEPeak [18] also assumes a Poisson distribution for read count, while introducing a hidden Markov model (HMM) to model the spatial dependency among the reads from neighboring sites. Recently, MeTPeak [19] fits a beta-binomial model to account for highly fluctuating read enrichments across MeRIP-seq replicates. Although each method has its own advantages, the high proportion of zero counts observed in the MeRIP-seq data significantly weakens the stability and performance of the existing methods. In this study, we propose a novel Bayesian method to predict m⁶A sites for the MeRIP-seq data. Our model employs a zero-inflated negative binomial model to capture the zero-inflation and over-dispersion observed in sequencing data. It incorporates the spatial dependency of neighboring read enrichments using an HMM model. Furthermore, the Bayesian inference allows our model to borrow strength in parameter estimation, which greatly improves the model stability when dealing with MeRIP-seq data with a small number of replicates. Markov chain Monte Carlo (MCMC) sampling techniques are used to sample the posterior distributions of the model parameters.

The rest of this paper is arranged as follows. In the Section of Hierarchical Model in Methods, we introduce the Bayesian hierarchical modeling framework. In the Section of Details of the MCMC Algorithm in Methods, we present the MCMC algorithm and discuss the resulting posterior inference. In the Section of Simulation in Results, we assess performance of the proposed model on simulated data and carry out comparisons with exomePeak and MeTPeak (HEPeak is no longer accessible). In the Section of Real MeRIP-seq data in Results, we investigate the results of data analysis from a case study.

METHODS

Hierarchical model

Given a MeRIP-seq dataset observed on a set of n samples, we first divide the concatenated exome of mRNA (i.e., the RefSeq gene) of interest into W mutually adjacent bins. Let Y be an n-by-W matrix of read counts defined on the exons of this particular mRNA, with entry $y_{i,w}\in \mathbb{N},i=1,\dots ,n$, w = 1, …,W indicating the number of reads in bin w for sample i. The MeRIP-seq outputs pairs of IP and control samples. We use a binary vector c = (c₁, …,c_n)^T to allocate the two different groups of samples, with c_i = 1 if sample i is subject to IP, and c_i = 0 otherwise.

Modelling counts by a zero-inflated negative binomial model

As most sequencing data are zero-inflated and over-dispersed, we start by modeling the read counts by a zero-inflated negative binomial (ZINB) model. Specifically, for the number of reads in bin w for sample i, we write a mixture model, where one of the kernels is constrained to be degenerate at zero, thereby allowing for zero-inflation:

$$p\left(y_{i,w}|\pi ,{\lambda }_{i,w},\varphi w\right)=\pi I\left(y_{i,w}=0\right)+(1-\pi )\text{NB}\left(y_{i,w};|{\lambda }_{i,w},\varphi w\right).$$ (1)

In model (1), the weight of extra zero counts, i.e., π, is a positive real number less than 1, and NB(y; λ,ϕ)denotes a negative binomial distribution for the random variable y, with expectation λ and dispersion 1/ϕ. With this parameterization, the variance of the negative binomial distribution can be written as λ + λ²/ϕ, thereby allowing for over-dispersion. Note that increasing ϕ towards infinity leads the negative binomial to a Poisson distribution with both mean and variance equal to λ. Alternatively, we can write model (1) as $p\left(y_{i,w}|{\eta }_{i,w},{\lambda }_{i,w},{\varphi }_w\right)=I{\left(y_{i,w}=0\right)}^{{\eta }_{i,w}}\text{NB}{\left(y_{i,w};{\lambda }_{i,w},{\varphi }_w\right)}^{1-{\eta }_{i,w}}$, by introducing a binary latent variable η_i,w|π ~ Bern(π), such that if η_i,w = 1, then y_i,w = 0, whereas if η_i,w = 0, then y_i,w ~ NB(λ_i,w, ϕ_w). The Bernoulli prior assumption can be further relaxed by formulating a Be(a_π, b_π) hyperprior on π, which leads to a beta-Bernoulli prior for η_i,w with expectation a_π/(a_π + b_π). A vague prior can be elicited by setting a_π = b_π = 1, which leads to a uniform distribution on π. Lastly, we specify the prior distribution for ϕ_w as ϕw ~ Ga(a_ϕ, b_ϕ). One standard way of setting a weakly informative gamma prior is to choose small values for the two hyperparameters, such as a_ϕ = b_ϕ = 0.001 [20].

Modelling negative binomial mean by a random effect model

Sequencing data is also characterized by high variability in the number of reads between different groups, and even across the samples within the same group. To accommodate this setting, we parameterize the mean parameter of the negative binomial distribution as the multiplicative effect of three random effects for the control and IP samples, respectively,

$${\lambda }_{i,w}=\{\begin{array}{ll}{s}_i{g}_w{d}_{0,w}\hfill & \text{ if }{c}_i=0\hfill \\ s_i{g}_w{d}_{1,w}\hfill & \text{ if }{c}_i=1\hfill \end{array}.$$ (2)

We interpret s_i as the size factor for sample i, reflecting the fact that different samples may have been sequenced to different depths, and g_w as the scaling factor for bin w, capturing feature-specific (i.e., bin-specific) levels across all samples. Once the global effects s_i and g_w have been taken into account, the parameters d_0,w and d_1,w are defined as the relative occurrence rate for the counts in bin w in the control and IP samples, respectively. Note that the Poisson and negative binomial versions of model (1) embedded with (2) have been explicitly used to identify differentially expressed genes between different biological conditions for RNA-seq data [21–27].

The parameterization of the negative binomial mean λ_i,w, as shown in (2), results in an identifiability problem among the three random effects. To avoid this issue, we estimate the size factors s_i and the scaling factor g_w by means of plug-in estimators based on the observed data. For example, in the context of RNA-seq data analyses, a number of methods [21,26,28] fix ${\widehat{s}}_i^{\text{total }}=\sum _{j=1}^p{x}_{i,j}/\sum _{i=1}^n\sum _{j=1}^p{x}_{i,j}$, so that $\sum _{i=1}^n{s}_i=1$, where x_i,j is the number of reads mapping to gene j in observation i. Similarly, Anders et al. [23] propose ${\widehat{s}}_i^{\text{median }}=m_i/\sum _{i=1}^n\sum _{j=1}^p{x}_{i,j}$ where $m_i=\text{median}(x_{i,1}/{\left(\prod _{i^{\prime }=1}^n{x}_{i^{\prime },j}I\left(x_{i^{\prime },j}\ne 0\right)\right)}^{1/n},\dots ,x_{i,p}/{\left(\prod _{i^{\prime }=1}^n{x}_{i\prime ,j}I\left(x_{i^{\prime },j}\ne 0\right)\right)}^{1/n})$ is the median of the distribution of the ratios of the counts for observation i to their geometric mean. As a further example, Bullard et al. [22] propose taking ${\widehat{S}}_i^{\text{quantile }}=q_i/\sum _{i=1}^n{q}_i$, with q_i the 75th percentile of the counts (x_i,1, …,x_i,p) for observation i. Many of the examples further fix $g_i=\sum _{i=1}^n{x}_{i,j}$ [26]. Our estimates on s_i and g_w are similar in spirit. Note that s_i should be computed based on the counts of the whole MeRIP-seq dataset, not just from one single RefSeq gene. For g_w, we estimate ${\widehat{g}}_w=\sum _{i=1}^n{y}_{i,w}$.

The use of the plug-in estimates of these two parameters is convenient, but it has noticeable drawbacks, especially for conducting full Bayesian inference. The plug-in estimators can be regarded as maximum likelihood estimators in multiple stage approaches and somewhat akin to empirical Bayes methods, thus relying on implicit assumptions of exchangeability of the observations, which may not be always justified in practice and can introduce bias in the estimation of posterior uncertainties [29,30]. To address the identifiability issue between s_i and g_w, Li et al. [31] developed a novel non-parametric Bayes prior model with soft constraints on their expected values to normalize the size and scaling factors simultaneously. Integrating this prior model with the proposed model in this paper could be one of our future directions.

Modelling relative occurrence rate by a hidden Markov model

IP samples and control samples can have vastly different total numbers of sequence reads. In general, when a bin is methylated, there are more reads in IP samples than in control samples (i.e., d_1,w > d_0,w); otherwise, there are more reads in control samples than in IP samples (i.e., d_0,w > d_1,w). To model this characteristic, we redefine the parameter space (d_0,w, d_1,w, w = 1, …,W) to (d_0,w, δ_w, w = 1, …,W), where δ_w = d_1,w/d_0,w is the fold change in the relative occurrence rate in bin w between the IP and control samples. Thus, given the sample allocation vector c, we rewrite the likelihood for each count as,

$$p\left(y_{i,w}|{\eta }_{i,w},{\varphi }_w,d_{0,w},{\delta }_w\right)=\{\begin{array}{ll}I{\left(y_{i,w}=0\right)}^{{\eta }_{i,w}}\text{NB}{\left(y_{i,w};{\widehat{s}}_i{\widehat{g}}_w\left(d_{0,w}\right),{\varphi }_w\right)}^{1-{\eta }_{i,w}}\hfill & \text{ if }{c}_i=0\hfill \\ I{\left(y_{i,w}=0\right)}^{{\eta }_{i,w}}\text{NB}(y_{i,w};{\widehat{s}}_i{\widehat{g}}_w{\left(d_{0,w}{\delta }_{w)},{\varphi }_w\right)}^{1-{\eta }_{i,w}}\hfill & \text{ if }{c}_i=1\hfill \end{array}.$$ (3)

For each of the non-negative parameters d_0,w, w = 1, …,W, we assume a gamma hyperprior, i.e., d_0,w ~ Ga(a_d, b_d). The choice of a_d = b_d = 0.001 would lead to a non-informative distribution as its variance is 1000.

We use an HMM to model δ_w, w = 1, …,W, which accounts for the variation in the underlying occurrence rate between the methylated and unmethylated bins in the IP samples. The HMM model encourages adjacent bins to be affected by the same process (i.e., methylation/unmethylation). To do this, we first introduce a latent variable z_w to denote the hidden methylation status for bin w, with z_w = 2 indicating bin w is methylated and z_w = 1 otherwise. Conditional on the hidden state z_w, we assume that δ_w is independent and identically normally distributed, defining the emission distribution of the HMM as ${\delta }_w|z_w=q~N\left({\mu }_q,{\sigma }_q^2\right)$, q ∈ {1,2}. The parameters μ_q and ${\sigma }_q^2$ represent the mean and variance of the fold changes in the relative occurrence rates for methylated/unmethylated bins. The spatial dependence between the states at adjacent bins is captured by a first order Markov model, which assumes that the probability of being a particular state at bin w + 1 depends only on the state at its antecedent bin w, i.e., p(z_w|z₁, …,z_W) = p(z_w|z_w−1) = ψ_zw, z_w−1, with ψ = [ψq′, q]_2×2 forming the matrix of transition probabilities with strictly positive elements. Note that in the proposed model, δ_w only switches according to the status of z_w in the IP samples.

As for the prior specification of the HMM, we assume independent Dirichlet priors across the columns of the transition matrix ψ; that is, ψ_·,q ~ Dir(a₁, a₂), q = 1,2. When both α₁ and α₂ are set to 1, the Dirichlet distribution is uniform over all points in its support. For the priors on μ_q, q = 1,2, we follow Guha et al. [32] and assume truncated normal distributions ${\mu }_q~N\left(m_q,s_q^2\right)I({\text{low}}_{u_q}<u_q,\text{ upp }{u}_q),q=1,2$, where low_η1 = 0, upp_η2 = ∞, and upp_η1 = low_η2 = 1. This setting fully accounts for the fact that the read counts of methylated bins in the IP samples are more enriched than those in the control samples, and vice versa for the unmethylated bins. For ${\sigma }_q^2$, q = 1,2 in the emission distribution, we impose inverse-gamma hyperpriors ${\sigma }_q^2~IG\left(a_{\sigma },b_{\sigma }\right)$, q = 1,2. We suggest to set a_σ = 2 and b_σ = 1 so as to obtain a flat inverse-gamma distribution.

Model fitting

Our model space consists of (π, H, f, d₀, δ, z, μ, σ², ψ). The parameters of interest are z = (z₁,…,z_w), which identify the methylated sites. We first design a Markov chain Monte Carlo (MCMC) algorithm based on Gibbs samplers and Metropolis-Hastings algorithms. Then, the resulting posterior inference for z is discussed.

Details of the MCMC algorithm

We start by writing the likelihood of the model (3) for each read count y_i,w given c_i, as,

$$\begin{gathered} p\left(y_{i,w}|c_i,{\eta }_{i,w},{\varphi }_w,d_{0,w},{\delta }_w\right)=I{\left(y_{i,w}=0\right)}^{{\eta }_{i,w}} \\ \cdot \text{NB}{\left(y_{i,w};{\widehat{s}}_i{\widehat{g}}_w\left(d_{0,w}{\delta }_w{}^{c_i}\right),{\varphi }_w\right)}^{1-{\eta }_{i,w}}. \end{gathered}$$

Then, within each iteration, the MCMC updates can be summarized as:

• Update of π: We use a Gibbs sampling step to update π,

  $$\pi |H~\text{Be}\left(a_{\pi }+\sum _{i=1}^n\sum _{w=1}^W{\eta }_{i,w},b_{\pi }+nW-\sum _{i=1}^n\sum _{w=1}^W{\eta }_{i,w}\right)$$
• Update of H: We update each η_i,w, i = 1, …,n, w = 1, …W that corresponds to y_i,w = 0 by sampling from a probability mass distribution, which is proportional to

  $$\begin{gathered} p\left({\eta }_{i,w}|y_{i,w}=0,\pi ,{\varphi }_w,d_{0,w},{\delta }_w\right) \\ \propto p\left(y_{i,w}=0|c_i,{\eta }_{i,w},{\varphi }_w,d_{0,w},{\delta }_w\right)\text{Bern}\left({\eta }_{i,w};\pi \right) \end{gathered}$$
• Update of ϕ: We update each ϕ_w, w = 1, …,W, sequentially by using a random walk Metropolis-Hastings algorithm. We first propose a new ${\varphi }_w^{*}$ from $\text{Ga}({\varphi }_w^2/{\tau }_{\varphi },{\varphi }_w/{\tau }_{\varphi })$ and then accept the proposed value ${\varphi }_w^{*}$ with probability min(1, m_MH), where

  $$\begin{gathered} m_{MH}\text{=} \\ \frac{\prod _{i=1}^{n}p\left(y_{i,w}|c_i,{\eta }_{i,w},{\varphi }_w^{*},d_{0,w},{\delta }_w\right)\text{Ga}\left({\varphi }_w^{*};a_{\varphi },b_{\varphi }\right)J\left({\varphi }_w;{\varphi }_w^{*}\right)}{\prod _{i=1}^{n}p\left(y_{i,w}|c_i,{\eta }_{i,w},{\varphi }_w,d_{0,w},{\delta }_w\right)\text{Ga}\left({\varphi }_w;a_{\varphi },b_{\varphi }\right)J\left({\varphi }_w^{*};{\varphi }_w\right)}. \end{gathered}$$

  Note that the last term, which is the proposal density ratio, equals 1 for this random walk Metropolis update.
• Update of d₀: We update each d_0,w, w = 1, …,W sequentially by using a random walk Metropolis-Hastings algorithm. We first propose a new $d_{0,w}^{*}$ from $\text{Ga}(d_{0,w}^2/{\tau }_{\varphi },d_{0,w}/{\tau }_d)$ and then accept the proposed value $d_{0,w}^{*}$ with probability min(1, m_MH), where

  $$\begin{gathered} m_{MH}\text{=} \\ \frac{\prod _{i=1}^{n}p\left(y_{i,w}|c_i,{\eta }_{i,w},{\varphi }_w,d_{0,w}^{*},{\delta }_w\right)\text{Ga}\left(d_w^{*};a_{\varphi },b_{\varphi }\right)J\left(d_w;d_w^{*}\right)}{\prod _{i=1}^{n}p\left(y_{i,w}|c_i,{\eta }_{i,w},{\varphi }_w,d_{0,w},{\delta }_w\right)\text{Ga}\left(d_w;a_{\varphi },b_{\varphi }\right)J\left(d_w^{*};d_w\right)}. \end{gathered}$$

  Note that the last term, which is the proposal density ratio, equals 1 for this random walk Metropolis update.
• Update of δ: We update each δ_w, w = 1, …,W sequentially by using a random walk Metropolis-Hastings algorithm. We first propose a new ${\delta }_w^{*}$ and from $\text{N}\left({\delta }_w,{\tau }_{\delta }^2\right)$$I\left({\delta }_w^{*}>0\right)$ and then accept the proposed value ${\delta }_w^{*}$ with probability min(1, m_MH), where

  $$m_{MH}=\frac{\prod \left\{i:c_i=1\right\}p\left(y_{i,w}|c_i,{\eta }_{i,w},{\varphi }_w,d_{0,w},{\delta }_w^{*}\right)\text{N}\left({\delta }_w^{*};{\mu }_{Z_w},{\delta }_{Z_w}^2\right)J\left({\delta }_w;{\delta }_w^{*}\right)}{\prod \left\{i:c_i=1\right\}p\left(y_{i,w}|c_i,{\eta }_{i,w},{\varphi }_w,d_{0,w},{\delta }_w\right)\text{N}\left({\delta }_w;{\mu }_{Z_w},{\delta }_{Z_w}^2\right)J\left({\delta }_w^{*};{\delta }_w\right)}.$$

  Note that the last term, which is the proposal density ratio, equals 1 for this random walk Metropolis update.
• Update of z: We update each z_w, w = 1, …,W sequentially by a stochastic version of the forward-backward algorithm. We first generate z_W from $p(z_W=q|{\delta }_W,{\mu }_q,{\sigma }_q^2,\psi )\propto \text{N}\left({\delta }_W,{\mu }_q,{\sigma }_q^2\right)$ at the beginning of the backward step. Then, the backward step is continued to compute and generate a draw for z_w,w = W −1, …,1 from

  $$p\left(z_w=q|{\delta }_w,{\mu }_q,{\sigma }_q^2,\psi \right)\propto \text{N}\left({\delta }_w;{\mu }_q,{\sigma }_q^2\right){\psi }_{Z_{w+1},q}.$$

  This produces a sample from the joint distribution p(z|δ, μ, σ², ψ).
• Update of μ:We update each μ_q, q = 1,2 separately via a Gibbs sampling step,

  $${\mu }_q|\delta ,z,{\sigma }_q^2~\text{N}(\frac{m_q/s_q^2+\sum _{w=1}^W{\delta }_{w}I\left(z_w=q\right)/{\sigma }_q^2}{1/s_q^2+\sum _{w=1}^{W}I\left(z_w=q\right)/{\sigma }_q^2},\frac{1}{1/s_q^2+\sum _{w=1}^{W}I\left(z_w=q\right)/{\sigma }_q^2})I\left({\text{low}}_{{\mu }_q}<{\mu }_q<{\text{upp}}_{{\mu }_q}\right).$$
• Update of σ²: We update each ${\sigma }_q^2$, q = 1,2 separately via a Gibbs sampling step,

  $${\sigma }_q^2|\delta ,z,{\mu }_q~\text{IG}(a_{\sigma }+\sum _{w=1}^{W}I\left(z_w=q\right)/2,b_{\sigma }+\sum _{w=1}^W{\left({\delta }_w-{\mu }_q\right)}^{2}I\left(z_w=q\right)/2).$$
• Update of ψ: We use a Gibbs sampling step to update each column of the matrix ψ_·,q, q = 1,2,

  $${\psi }_{\cdot ,q}~\text{Dir}(a_1+\sum _{w=2}^{W}I\left(z_{w-1}=1,z_w=q\right),a_2+\sum _{w=2}^{W}I\left(z_{w-1}=2,z_w=q\right)).$$

Posterior estimation on the methylation site indicator

For posterior inference, our primary interest lies in the identification of the methylation sites, via the vector z. One way to summarize the posterior distribution of particular parameters is via the maximum-a-posteriori (MAP) estimates obtained as

$${\widehat{z}}^{MAP}={\text{argmax}}_{1⩽b⩽B}\prod _{w=1}^W{\psi }_{z_w^{(b)},z_{w-1}^{(b)}}\text{N}\left({\delta }_w^{(b)};{\mu }_{z_w^{(b)}}^{(b)},{\sigma }_{z_w^{(b)}}^{(b)2}\right),$$

with b = 1, …,B indexing the MCMC iterations, after burn-in. Estimation can also be done by thresholding the estimated marginal posterior probabilities of inclusion (PPI) of single bin, obtained as the proportion of MCMC iterations, after burn-in, in which the corresponding z_w is equal to 2. That is,

$${\text{PPI}}_w^z=\frac{\sum _{b=1}^B\left(z_w^{(b)}=2|\cdot \right)}{B}.$$

In choosing the threshold to obtain ${\widehat{z}}_i^{\text{PPI}}=1+I\left({\text{PPI}}_w^z⩾c\right)$, the value of c = 0.5 results in a median model. Alternatively, we can follow the Ref. [33], which guarantees the expected Bayesian false discovery rate (BFDR) to be smaller than a pre-specified threshold.

RESULTS

Simulation

In this study, simulated data with known ground truth were used to validate the performance of the proposed model. The read counts for the control and IP samples were generated using a strategy similar to the HEPeak model by Cui et al. [18]. We considered multiple scenarios, of which counts were from four different kernels: Poisson, zero-inflated Poisson (ZIP), negative binomial (NB), and zero-inflated negative binomial (ZINB). The percentage of extra zeros, i.e., π, was set to 0.5 for the ZIP and ZINB kernels. Note that for the real data analyzed in the paper, about one-third of counts were zeros. Each scenario included 100 datasets, each of which had 4 control and 4 IP samples, i.e., n = 8, with the number of bins drawn from a uniform distribution, i.e., W ~ Unif(100,500). Reads of each bin in the control samples were allowed to vary according to the corresponding kernel, where we chose the mean parameter ${\lambda }_w^{\text{control }}~\text{Unif}(5,20)$ and assumed it remained constant for both methylated and unmethylated bins. The means of reads of the methylated and unmethylated bins in the IP samples were set to ${\lambda }_w^{\text{IP}}|z_i=2=k{\lambda }_w^{\text{control }}$ and $\left|{\lambda }_w^{\text{IP}}\right|z_i=1~\text{Unif}\left(0,{\lambda }_w^{\text{control}}\right)$, respectively. Here, k can be seen as the fold change in relative occurrence rates in methylated bins between the IP and control samples. The larger the value of k, the more enriched the read counts of methylated bins in the IP samples than in the control samples. Two different settings of k were considered, k = 1.5 and 3. Combined with the four kernels, there were 4 × 2 = 8 scenarios in total. The hidden methylation statuses were generated from HMM models with the transition matrix $\psi =\left(\begin{array}{ll}0.9\hfill & 0.3\hfill \\ 0.1\hfill & 0.7\hfill \end{array}\right)$ at a random initial state. This matrix was based on the estimations using the real data analyzed in Ref. [18].

We implemented our method with different plug-in size factors ${\widehat{s}}_i^{\text{total, }}\text{s}$, ${\widehat{s}}_i^{\text{median, }}\text{s}$, and ${\widehat{s}}_i^{\text{quantile, }}\text{s}$, and called them BaySeqPeak-T, -M, and -Q, respectively. We used the following “non-informative” settings for the priors and hyperpriors. We set the hyperparameters that control the excess of zeros to Be(a_π = 1, b_π = 1). As for the gamma prior on the over-dispersion parameters ϕ_w, w = 1, …,W and the reference relative occurrence rate d_0,w, w = 1, …,W, we set a_ϕ = b_ϕ = a_ϕ = b_d = 0.001, which led to vague gamma priors. For the HMM model, we considered two cases: (i) each column of the transition matrix ψ was independently distributed according to Dir(1,1) and (ii) each column was identical, i.e., a_1q = a_2q, q = 1,2, which corresponds to a special case of a Markov chain, called a Bernoulli scheme. The second case assumes that there was no spatial dependency between adjacent bins and the resulting model was named BaySeqPeak-I, where I stands for independence. Finally, for those reads in the methylated bins, we set ${\mu }_2~N\left(m_2=0,s_2^2=10\right)I\left({\mu }_2>1\right)$ and ${\sigma }_2^2~IG(2,1)$ while for those reads in the unmethylated bins, we set ${\mu }_1~N\left(m_1=0,s_1^2=10\right)I\left(0<{\mu }_1<1\right)$ and ${\sigma }_2^2~IG(2,1)$. For each simulated dataset, we ran four independent MCMC chains with 10W iterations, discarding the first 50% sweeps as burn-in. Results we report below were obtained by pooling together the MCMC outputs from the four chains. All experiments were implemented in R with an Rcpp package to accelerate computation on a Mac PC with 2.60 GHz CPU and 16 GB memory. In our implementation, one MCMC chain ran about 1 second for data with dimensions n = 8 and W = 100.

To quantify the accuracy of the identification of methylation sites (via the parameters z) by the proposed model, we calculated the receiver operating characteristic (ROC) curves, and the areas under the curves (AUCs) as the performance metrics. They consider both the true and false positive rates at various threshold settings. The true positive rate is also known as sensitivity, which is defined as the number of true methylated bins that are correctly estimated. The false positive rate is equal to 1 minus specificity, which is defined as the true unmethylated bins that are correctly estimated. AUC provides a summary of the overall performance across different threshold values. We compared the performance of our proposed method with exomePeak and MeTPeak. Note that they produce threshold P-values to control for the false discovery rate (FDR), while our model-based method controls for FDR by generating marginal posterior probabilities of inclusion.

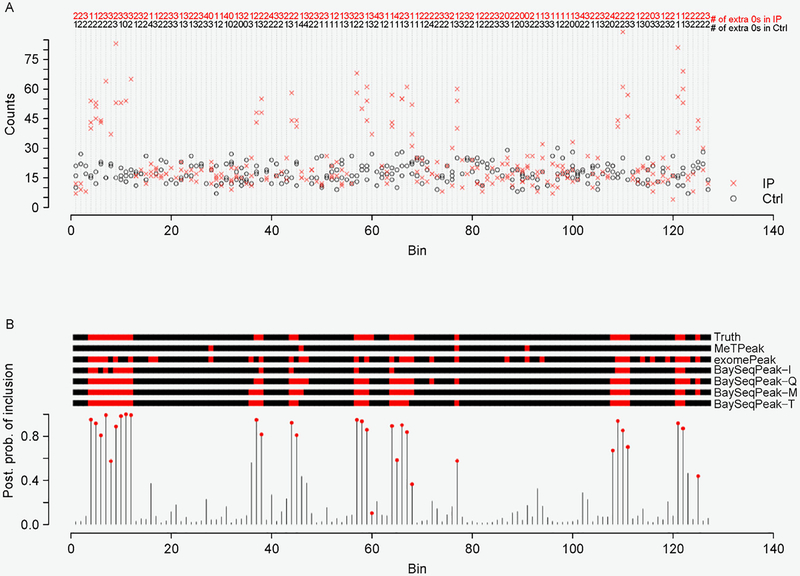
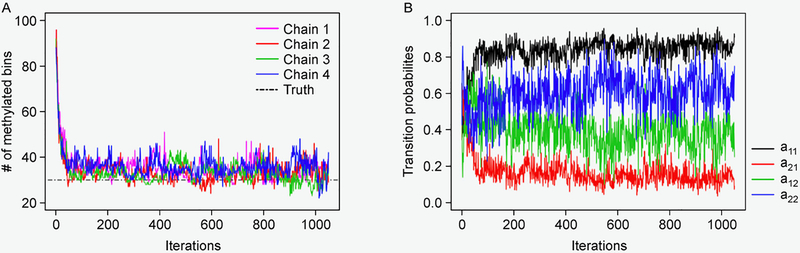
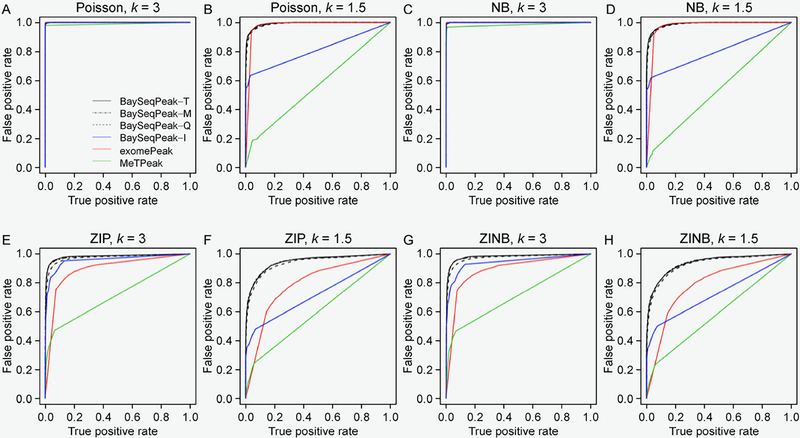
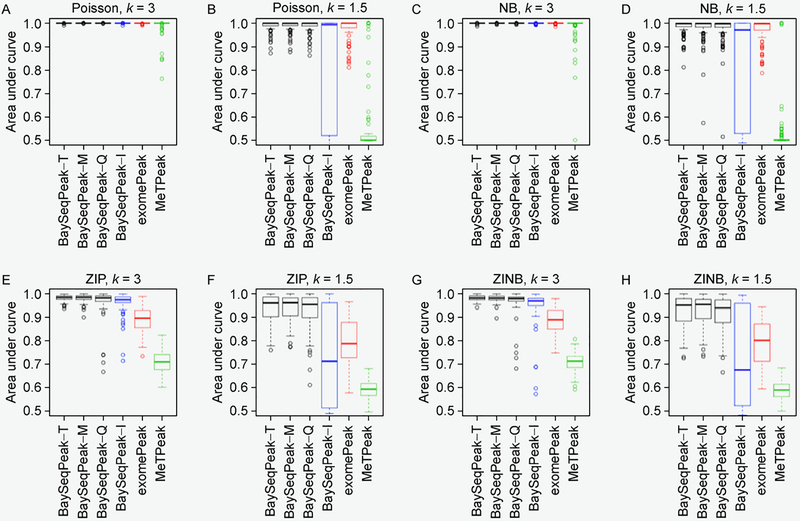
One example of our simulated dataset, which was generated from ZINB kernel and with fold change k = 3, is displayed in Figure 1A. It clearly shows the presence of overdispersion as well as excess zeros. Figure 1B plots the marginal posterior probabilities of inclusion of single bins belonging to methylated regions, inferred by the proposed model with total size factor estimates. The red dots indicate the true methylated bins. A threshold of c = 0.5 results in a median model that included 28 methylated bins, 26 of which were correctly estimated. Our inference only missed four true methylated bins. We also give the true and the estimated methylated bins by exomePeak, MeTPeak, and BaySeqPeak with different settings at the top. As we can see, the proposed model outperformed the competing methods in this example. Unlike other approaches that provide the confidence level via P-values, the posterior distribution of marginal probabilities facilitates the inference and adds a level of interpretation available only through a Bayesian approach. Figure 2A displays the trace plots of the number of methylated bins $\sum _{w=1}^{W}I\left(z_w=2\right)$ of four independent MCMC chains, which clearly shows that each chain converged and stabilized around the true value 30 in a very short run. We also plotted the trace plots of the transition probabilities A for the first chain in Figure 2B. Furthermore, we used Gelman and Rubin’s convergence diagnostics [34] to inspect for signs of convergence of the individual parameters such as A. The statistics were ranging from 1.034 and 1.127, suggesting that the MCMC chains were run for a sufficient number of iterations. We plotted the ROC curves for our method with three different size factor estimates, for different values of the threshold on PPIs, and compared those to the ROC curves obtained with exomePeak and MeTPeak, for different values of the threshold on P-values. The ROC curves, averaged over 100 datasets, are shown in Figure 3. The boxplots of AUCs for the 100 simulated datasets for different methods are summarized in Figure 4. Our observations are four-fold. First, our method that makes use of the dependency of consecutive bins achieved the best accuracy under all scenarios. Second, when the signal strength was strong enough (i.e., less variability and zeros), the statistical performances showed no significant differences from each other. However, the increase of variance and number of zeros led to greater disparity between the competing method and ours. Third, the proposed model was considerably insensitive to the choice of the three size factor estimates. Fourth, if the hidden methylated states followed a Bernoulli scheme, which ignored the dependency of reads, the model performed poorly, especially when the signal strength was weak, e.g., those scenarios with k = 1.5.

Figure 1. Examples of the model input and output.

(A) One simulated data generated from the ZINB kernel and with the fold change k = 3. Non-zero counts in the control samples are marked in black circle (o), while non-zero counts in the IP samples are marked in red cross (x). The number of extra zeros for each bin and each sample group is given at the top. (B) The marginal posterior probabilities of inclusion p(z_w = 2|·) inferred by BaySeqPeak-T with the plug-in size factors ${\widehat{s}}_i^{\text{total, }}\text{s}$. The red dots indicate the true methylated bins. The true and estimated z by MeTPeak, exomePeak (at a 5% significance level cutoff), and BaySeqPeak (with c = 0.5 cutoff) are shown in the top, where the red regions indicate methylated bins.

Figure 2. Examples of the MCMC outputs.

(A) The trace plots of the number of methylated bins $\sum _{w=1}^{W}I\left(z_i=2\right)$ of four independent chains obtained by BaySeqPeak with the plug-in size factors ${\widehat{s}}_i^{\text{total, }}\text{s}$. (B) The trace plots of the transition probabilities a₁₁, a₂₁, a₁₂, and a₂₂ of Chain 1.

Figure 3. ROC curves produced by different methods.

(A–H) The average receiver operating characteristic (ROC) curves for different values of the threshold on PPIs (our method) and on P-values (competing methods) for different scenarios. BaySeqPeak-T, -M, -Q stand for our method with different plug-in size factors ${\widehat{s}}_i^{\text{total, }}\text{s}$, ${\widehat{s}}_i^{\text{median, }}\text{s}$, and ${\widehat{s}}_i^{\text{quantile, }}\text{s}$, respectively. BaySeqPeak-I stands for our method with the plug-in size factors ${\widehat{s}}_i^{\text{total, }}\text{s}$, and the Bernoulli scheme, a special HMM where no spatial dependency is assumed between adjacent bins.

Figure 4. AUCs produced by different methods.

(A–H) The boxplot of areas under the curves (AUCs) over 100 datasets for different scenarios, corresponding to Figure 3 (A–H).

Real MeRIP-seq data

To further evaluate the performance of our method in a real biological scenario, we applied both the proposed algorithm and exomePeak to a MeRIP-seq dataset from a study investigating the role of demethylase obesity-associated protein (FTO) in mouse midbrain [35]. MeRIP-seq data was generated in both wild type (WT) and FTO knock-out (FTO-KO) mice, with each condition having 3 IP replicates and 3 input replicates, respectively. The data was downloaded from the Gene Expression Omnibus (GEO) repository [36] (Accession number: GSE47217) and processed following the protocol by Jia et al. [37]. The mouse transcriptome (UCSC mm10) was scanned using 200 bp window with sliding step 30 bp (default setting of exomePeak), and reads of each sample in each window were counted. For exomePeak, a C test was performed in each window independently to test the significance of enrichment of reads in IP samples versus input samples. Windows with FDR less than 0.05 were reported as methylated bins. For our methods, a Bayesian hierarchical model either with or without HMM integration was fitted for each transcript, respectively, in order to estimate the posterior probability of inclusion (ppi) of each window within each region. Windows with ppi greater than 0.5 were reported as methylated bins. Finally, the adjacent methylated bins were joined to form a methylation site in the transcriptome.

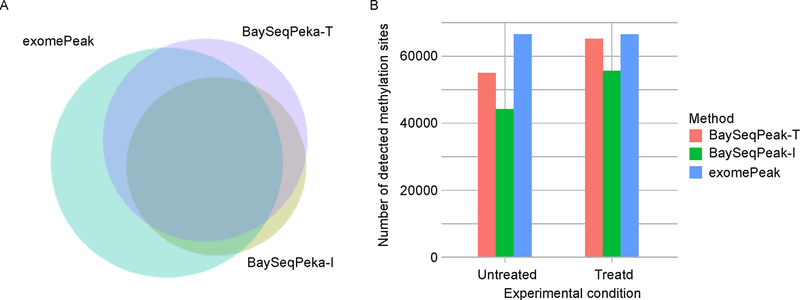
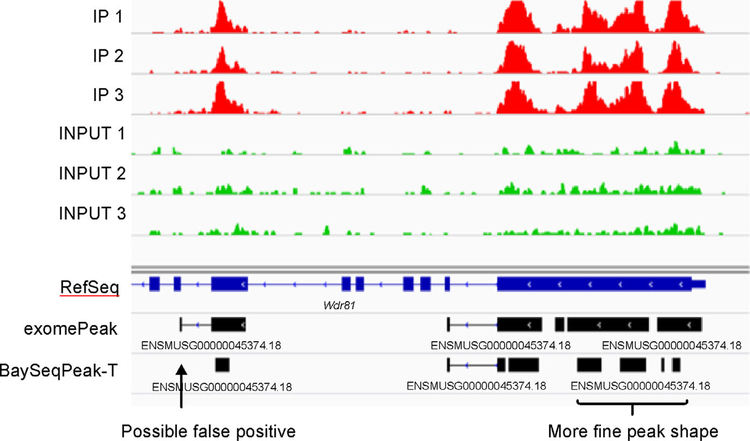
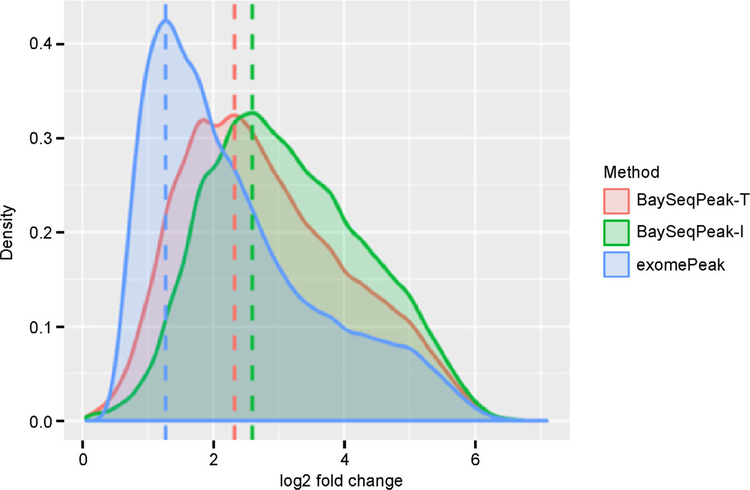
The mouse mm10 reference transcriptome was divided into a total of 2916,847 bins (gene with all 0 counts were filtered out). exomePeak reported 853,151 bins as significant in WT condition datasets, while our BaySeqPeak-T and -I reported 664,513 and 512,754 bins (Figure 5A). The overall agreement between the results of our methods and exomePeak indicates that all methods performed reasonably well. However, BaySeqPeak-T reported a smaller number of significant bins, and BaySeqPeak-I reported even less (also observed in the FTO-KO condition). This may due to the failure to detect methylated bins with weak signals that are adjacent to significant regions when HMM is not applied. This trend is also represented at the transcript level. BaySeqPeak-T and -I identified 55,199 and 44,210 methylation sites in WT condition, and 65,110 and 55,829 methylation sites in FTO-KO condition, while exomePeak identified 66,696 and 66,388 methylation sites in two conditions. More methylation sites being found in FTO-KO condition than WT condition by our methods (Figure 5B) is consistent with the fact that FTO is a demethylase, knocking out of which should increase the m⁶A peaks. However, the result of exomePeak was contradictory. To investigate the reason why our method detected fewer peaks than exomePeak, we visualize the identified peaks in the IGV browser. Figure 6 shows one example of detected methylation sites in Wdr81 gene. The figure indicates that there are 4 peaks by comparing IP samples with input samples, and our method correctly detected all 4 peaks. Though exomePeak also reported the corresponding methylated region, it reported 3 additional peaks, which are likely false positive discoveries from the figure. Furthermore, it only claimed the middle 2 peaks to be a single methylated site, but the detailed peak information was lost, and such case happened often. To get a sense of the overall performance methods, we compared the distribution of log fold change of identified methylation sites (dividing total read counts in IP samples by total read counts in input sample) by each method in Figure 7. The figure shows that the methylation sites identified by BaySeqPeak have larger average fold change than exomePeak, and BaySeqPeak-I has slightly larger average fold change than BaySeqPeak-T, which indicates that the exomePeak may include a lot of false positive discoveries, while BaySeqPeak-I may miss some potential peaks without using spatial information. Overall, our method is more reliable in identifying methylation sites and more capable of detecting peaks in higher resolution, compared with the exomePeak method.

Figure 5. A comparison of the real data results obtained by our method and exomePeak.

(A) Venn diagram of total detected methylated windows by BaySeqPeak-T, -I along with exomePeak in WT datasets. The sizes of the circles are proportional to the number of methylated bins found by each method. (B) Total detected methylation sites (adjacent methylated windows are clustered to one methylated site) in WT and FTO knock out datasets by our methods and exomePeak.

Figure 6. An exemplary methylation region detected by both exomePeak and BaySeqPeak-T shown in the IGV browser.

Figure 7. Distribution of log2 fold change in read counts of detected methylated sites by BaySeqPeak-T, -I and exomePeak.

CONCLLUSION

In this paper, a hierarchical Bayesian model is proposed to detect methylation peaks in MeRIP-seq data. By deploying a zero-inflated negative binomial model, our algorithm tackles the zero-inflated and over-dispersed count problem of MeRIP-seq data, which had not been properly solved before. A hidden Markov model (HMM) is also incorporated to model the nearby methylation status dependency. A Markov chain Monte Carlo (MCMC) method was used to draw samples from the posterior distribution and infer the model parameters. The proposed method outperformed the previous package exomePeak under all simulation settings that suffered a high rate of false discovery. A real case study revealed our method to have enough sensitivity to detect the majority of peaks found by exomePeak along with higher specificity against low count data, and to be able to capture the fine structures of peaks that are spatially approximate to each other. Moreover, the proposed method can be easily extended to accommodate study designs that compare multiple factors under an ANOVA setting.

Author summary:

Methylated RNA immunoprecipatation combined with RNA sequencing (MeRIP-seq), which can be viewed as a marriage of two well-studied techniques: ChIP-seq and RNA-seq, is changing the landscape of RNA epigenomics study at a higher resolution. We propose a Bayesian statistical model to identify the transcriptome methylation sites using MeRIP-seq data. Our approach includes several innovative characteristics by taking into account: (i) the high proportion of zeros in the data due to the insufficient sequencing depth; (ii) the spatial dependence of neighboring read enrichment. Compared to the existing methods, it is shown that our prediction is more consistent with the biological knowledge, and has better accuracy and spatial resolution.