Abstract
Popular models of decision-making propose that noisy sensory evidence accumulates until reaching a bound. Behavioral evidence as well as trial-averaged ramping of neuronal activity in sensorimotor regions of the brain support this idea. However, averaging activity across trials can mask other processes, such as rapid shifts in decision commitment, calling into question the hypothesis that evidence accumulation is encoded by delay period activity of individual neurons. We mined two sets of data from experiments in four monkeys in which we recorded from superior colliculus neurons during two different decision-making tasks and a delayed saccade task. We applied second-order statistical measures and spike train simulations to determine whether spiking statistics were similar or different in the different tasks and monkeys, despite similar trial-averaged activity across tasks and monkeys. During a motion direction discrimination task, single-trial delay period activity behaved statistically consistent with accumulation. During an orientation detection task, the activity behaved superficially like accumulation, but statistically consistent with stepping. Simulations confirmed both findings. Importantly, during a simple saccade task, with similar trial-averaged activity, neither process explained spiking activity, ruling out interpretations based on differences in attention, reward, or motor planning. These results highlight the need for exploring single-trial spiking dynamics to understand cognitive processing and raise the interesting hypothesis that the superior colliculus participates in different aspects of decision-making depending on task differences.
SIGNIFICANCE STATEMENT How are decisions based on sensory information transformed into actions? We report that single-trial neuronal activity dynamics in the superior colliculus of monkeys show differences in decision-making tasks depending on task idiosyncrasies and requirements and despite similar trial-averaged ramping activity. These results highlight the importance of exploring single-trial spiking dynamics to understand cognitive processing and raise the interesting hypothesis that the superior colliculus participates in different aspects of decision-making depending on task requirements.
Keywords: accumulation, decision-making, nonhuman primate, ramping activity, spiking statistics, superior colliclulus
Introduction
Influential models of perceptual decision-making propose that samples of noisy sensory evidence are accumulated over time until a threshold is reached. Once the threshold is crossed, a decision is made (Ratcliff and McKoon, 2008). Behavioral studies support sequential sampling models of decision-making (Ratcliff and Rouder, 1998; Ratcliff et al., 2003), and electrophysiological recordings suggest that the trial-averaged ramping activity of individual neurons in sensorimotor areas reflects the process of evidence accumulation (Roitman and Shadlen, 2002; Mazurek et al., 2003; Hanks et al., 2015; Brody and Hanks, 2016). Indeed, trial-averaged ramping activity of neurons appears in the medial intraparietal area (MIP) and lateral intraparietal area (LIP) of cerebral cortex, areas 8 and 46 of the PFC, caudate nucleus, and the superior colliculus (SC) (Shadlen and Newsome, 1996, 2001; Kim and Shadlen, 1999; Horwitz and Newsome, 2001; Roitman and Shadlen, 2002; Ding and Gold, 2010, 2012; de Lafuente et al., 2015; Ding, 2015; Brody and Hanks, 2016; Yartsev et al., 2018). Whether accumulation is instantiated by single neurons or across populations or whether trial-averaged activity reflects accumulation or other cognitive processes, such as vacillations in decision commitment or the urgency to decide, are ongoing foci of research efforts (e.g., Harvey et al., 2012; Thura et al., 2012; Latimer et al., 2015).
Recordings in monkey area LIP suggest that trial-averaged neuronal activity appears superficially consistent with accumulation but may mask other decision-making processes, such as stepping from uncommitted to committed states (Latimer et al., 2015). SC neurons show similar trial-averaged ramping during decision-making tasks, superficially consistent with accumulation (Horwitz and Newsome, 2001; Ratcliff et al., 2003, 2007; Horwitz et al., 2004), but also in other tasks not requiring accumulation, such as simple saccade tasks (Glimcher and Sparks, 1992; Munoz and Wurtz, 1995). Indeed, ramping activity during saccade preparation gave the motor layer SC neurons their names, buildup or prelude (Glimcher and Sparks, 1992; Munoz and Wurtz, 1995). In light of the LIP results (Latimer et al., 2015) and other models proposing that processes other than accumulation can explain ramping activity, such as urgency (Thura et al., 2012), we hypothesized that averaging SC neuronal activity over trials may mask different processing ongoing during different tasks, despite similar trial-averaged ramping activity. To test the hypothesis that trial-averaged ramping activity in the SC masks varieties of processes, we mined two datasets collected from 4 monkeys, each pair performing a 2-choice random dot motion (RDM) direction discrimination task or a Yes-No detection task using Glass patterns and one pair performing a simple delayed saccade task. We compared second-order statistics of spike trains across tasks for both pairs of monkeys. We calculated the variance of the conditional expectation (VarCE) of SC spike counts, the autocorrelation of conditional expectation (CorCE) (Churchland et al., 2011; de Lafuente et al., 2015), and the streak index (SI) (Horwitz and Newsome, 2001; Bollimunta et al., 2012). Importantly, the measures we used provide information about single-trial processing. We also applied these measures to simulated datasets from accumulation and stepping processes, assessing similarity between simulations and actual data using the R2CorCE and the deviance information criterion (DIC) (Latimer et al., 2015) and the Watanabe Akaike information criterion (WAIC) (Zoltowski et al., 2019).
The analyses of spiking dynamics revealed that the activity of SC neurons of monkeys performing the RDM task was statistically consistent with accumulation rather than stepping. In monkeys performing the Glass pattern detection task, despite similar trial-averaged ramping activity in all 4 monkeys and across both tasks, the spiking dynamics aligned with accumulation, but were statistically consistent with stepping. Neuronal activity was statistically consistent with neither process in the delayed saccade task. The results provide evidence that similar trial-averaged ramping activity in SC may reflect different underlying cognitive processes and raise the interesting hypothesis that the SC participates in different aspects of decision-making depending on task differences.
Materials and Methods
Animals and surgery
Four male rhesus monkeys (Monkeys P, H, S, and B) weighing 9-13 kg were prepared for behavioral training and assessment, electrophysiological recordings, and measurement of eye position. A headpost was implanted to stabilize the head and an MRI-compatible recording chamber (Crist Instruments) was placed to access the SC (AP −3, ML 0, angled posteriorly at 38°). Three monkeys (Monkeys B, H, and S) were implanted with eye loops (Judge et al., 1980) to measure eye position using the magnetic induction technique (Fuchs and Robinson, 1966). For Monkey P, eye position was monitored with an iView camera (Sensomotoric Instruments). All surgical procedures were performed under general anesthesia using aseptic procedures. Anesthesia was induced with ketamine and midazolam (5.0 and 0.2 mg/kg, i.m.), and atropine (0.04 mg/kg, i.m.) was provided to reduce salivation. Monkeys were intubated and maintained under general anesthesia with isoflurane. One hour before the procedure, animals received buprenorphine (0.01 mg/kg, i.m.) and the antibiotic Excede (20 mg/kg, i.m.; 7 d slow release) followed by meloxicam (0.3 mg/kg, i.m.) at the conclusion of the procedure. Meloxicam (0.2 mg/kg, i.m.) and buprenorphine (0.01 mg/kg, i.m.) were administered for 3 d after surgery for analgesia. All experimental protocols were approved by the UCLA Chancellor's animal research committee and complied with and generally exceeded standards set by the Public Health Service policy on the humane care and use of laboratory animals.
Eye movement recording procedures
We used a QNX-based real-time experimental data acquisition system (“Rex”) (Hays et al., 1982) and a Windows-based visual stimulus generation system (“Vex”; Laboratory of Sensorimotor Research, National Eye Institute) to create the behavioral paradigm, display the visual stimulus, and acquire eye position. Voltage signals proportional to horizontal and vertical components of eye position were filtered (8 pole Bessel –3 dB, 180 Hz), digitized at 16-bit resolution, and sampled at 1 kHz (National Instruments; PCI-6036E). Eye-tracking camera-acquired eye position signals were filtered digitally using a built-in bilateral filter. We used an automated procedure to define saccadic eye movements using eye velocity (20°/s) and acceleration criteria (5000°/s2), respectively. The adequacy of the algorithm was verified and adjusted as necessary on a trial × trial basis by the experimenter.
Behavioral tasks
RDM task
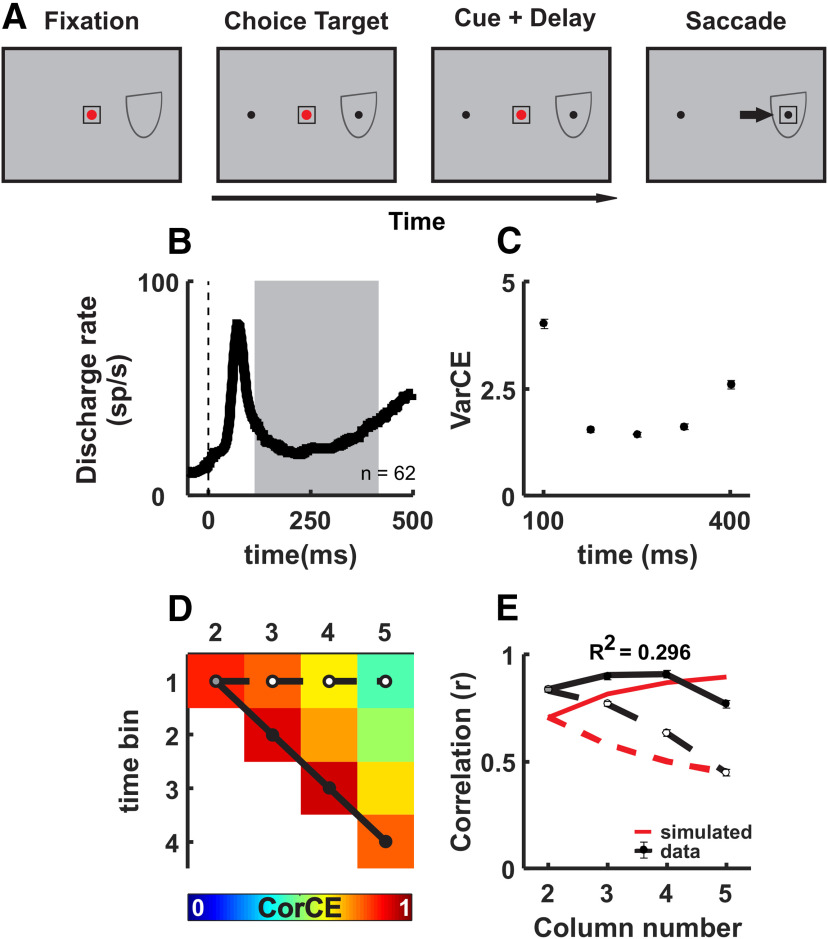
The trial began when Monkeys H and P fixated a red dot at the center of the monitor (see Fig. 1A). Once the monkeys acquired fixation on the centrally located spot, two isoluminant white (13 cd/m2) choice targets appeared. One choice target appeared in the center of the response field (RF), and the other was placed symmetrically in the opposite hemifield; 500 ms after the targets appeared, a random dot moving stimulus (motion speed = 5°/s; dot lifetime = 16 ms; diameter = 3°; luminance = 13 cd/m2; dot size = 0.05°; total density = 50 dots/deg2) appeared at the center of the screen for 200 ms, followed by a delay period in which the cue was absent, of 500-700 ms randomized with a mean of 595 ms (the exact timing was drawn randomly from an exponential distribution to avoid prediction; λ = 0.15). The fixation dot disappeared next, and the monkeys made a saccade to the choice target located in the hemifield corresponding to the direction of motion to report their choice. The direction of motion was randomized on each trial. Monkeys made saccades to the choice target in the right hemifield if they saw rightward motion and made a saccade to the choice target in the left hemifield for leftward motion. If fixation was broken before the fixation spot disappeared, the trial aborted. Eye position was monitored and was required to remain within a 2° × 2° electronic window. We varied the strength of the sensory information for the decision with four randomly interleaved coherences (0%, 6%, 10%, and 20%) for Monkey P and (0%, 10%, 20%, and 50%) for Monkey H. The coherences differed because of Monkey P's exceptional discrimination performance. Monkeys received a sip of juice or water for correct decisions and no fluid and a 2000 ms time-out for incorrect decisions. Since there is no correct decision for the 0% coherence trials in the RDM task, monkeys received reward on 50% of these trials randomly. This condition was randomly interleaved with a second condition in which a sure bet choice was provided and used to assess decision confidence. We only used the data from the first condition without the sure bet choice option for the analysis presented in this manuscript. Confidence data are reported by Odegaard et al. (2018) and Grimaldi et al. (2018).
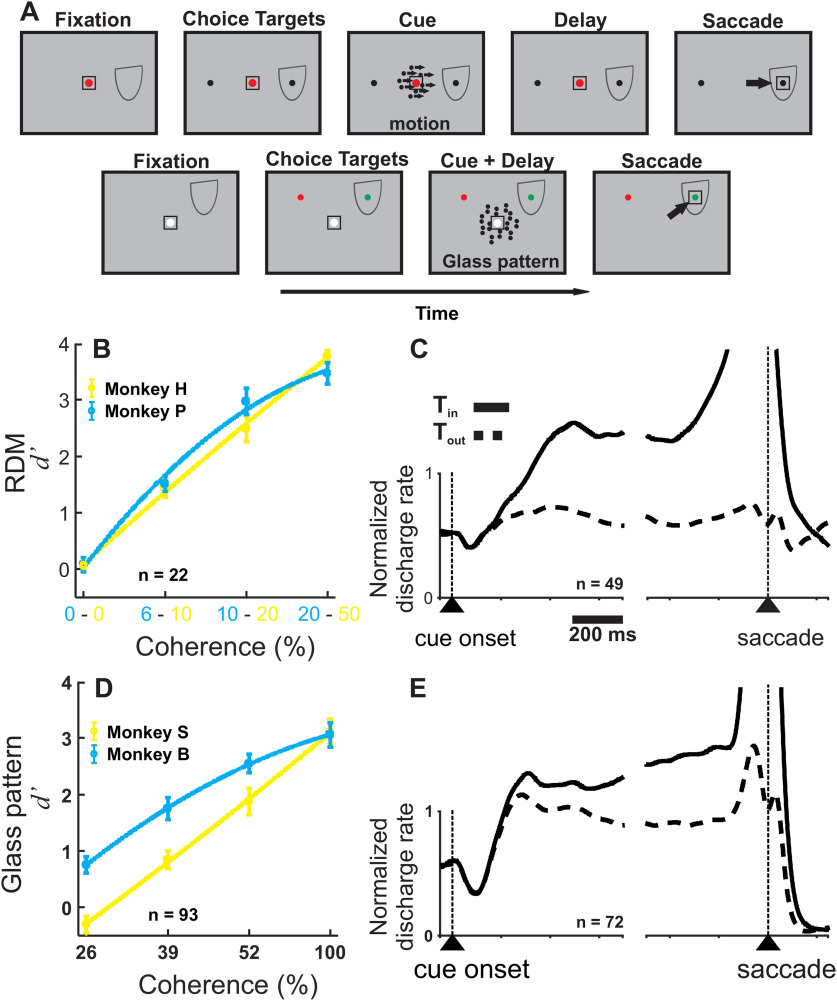
Figure 1.
SC neurons show ramping activity in the RDM and Glass pattern perceptual decision-making tasks. A, Schematic of the spatial and temporal arrangement of both the RDM and Glass pattern tasks. Boxes represent the screen, and the temporal order of the task events is from left to right. Top panels, Red circle represents the fixation spot. Black circles represent the choice targets in the RDM task. Bottom panels, White circle represents the fixation spot. Red and green circles represent the choice targets in the Glass pattern task. Box around the fixation spot and choice target represents the accuracy window for the monkeys' eye position. The motion or Glass pattern cue appeared at the center of the screen overlapping with the fixation spot. Half oval represents a schematic of the RF of a recorded SC neuron. Black arrow indicates the required saccade, in this example, rightward. B, d′ for Monkey P (cyan) and Monkey H (yellow) performing the RDM task plotted against motion coherence (%) (n = 22 sessions). Stimulus strengths across monkeys are not pooled together. C, Normalized discharge rate collapsed over all coherences is plotted against time for n = 49 intermediate layer neurons of the SC recorded in the RDM discrimination task. Solid black lines indicate the averaged SDF (α = 20 ms) for trials in which monkeys reported decisions toward the RF (Tin). Black dashed lines indicate trials in which the monkeys reported decisions away from the RF (Tout). The two sets of traces are aligned on the onset of the motion cue (cue onset) and the choice report (saccade), indicated by the upward arrowhead and dashed vertical lines. D, d′ for Monkey S (yellow) and Monkey B (cyan) performing the Glass pattern task plotted against Glass pattern coherence (%) (n = 93 sessions). Error bars indicate SEM and may be obscured by the symbols. E, Same as in C, but for the 72 neurons recorded in the Glass pattern detection task.
Yes-No Glass pattern task
A trial began when Monkeys S and B looked at a white dot appearing at the center of the monitor (see Fig. 1A, bottom). After a brief delay of ∼500 ms, randomized from the same exponential distribution incorporated in the RDM task to prevent prediction, a red and green isoluminant (13.0 cd/m2) choice target appeared: one was placed in the center of the RF and the other was placed in the opposite hemifield at a 90° angle relative to the fixation point and the RF. Which choice target appeared in the RF (Yes or No) was randomly interleaved on a trial × trial basis to dissociate the choice report from the direction of the eye movement (Ferrera et al., 2009; Bennur and Gold, 2011). After a second randomized delay (600-1050 ms), a dynamic Glass pattern stimulus (Glass, 1969; Nankoo et al., 2012), consisting of vertically oriented dot pairs (diameter = 6°, 26 cd/m2; dot size = 0.10°; dot separation = 0.1820; total density = 5 dots/deg2), appeared at the center of the monitor together with the white fixation point and remained on the screen for a random duration between 800 and 1500 ms (Cue + Delay) at which point it disappeared, instructing the monkeys to report their choice with an eye movement. The Glass pattern stimulus can be thought of as the form equivalent of the RDM stimulus (Smith et al., 2002, 2007). Eye position accuracy was monitored and required to remain within a 2° × 2° electronic window around the fixation point and the correct choice target. On half the trials, the Glass pattern coherence was 0% (No). Of the remaining half, the coherence of the Glass pattern varied randomly on each trial with equal probability from coherences among 26%, 39%, 52%, or 100% (Yes). The monkeys indicated their Yes or No decisions by making a saccade to the green Yes choice target if it perceived orientation in the Glass pattern or the red No target if it did not and the red and green choice target switched between the two locations randomly on each trial. Monkeys remained fixating at the choice target for ∼300 ms to receive a sip of juice as a reward if correct or no reward and a 2400 ms time-out if incorrect. These trials preceded a block of trials in which the presence or absence of an orientation signal appeared was varied probabilistically. Then a third block of trials repeated the first block of trials in which the presence or absence of orientation in the Glass pattern stimulus occurred equally. Only the first block of baseline trials was used for analysis in this report. The data analyzed here come from experiments reported previously (Crapse et al., 2018). The Glass pattern task and the RDM task were similar in that both stimuli produced noisy evidence across frames but that the tasks differed on other points. First, the viewing duration in the RDM task was briefer than in the Glass pattern task. Second, there was no stimulus absent delay period in the Glass task as there was in the RDM task. Third, the choice targets were white or differently colored, and were aligned with the direction of motion in the RDM tasks and were decoupled from the choice in the Glass pattern task. Fourth, the RDM task required motion direction discrimination, whereas the Glass pattern task required orientation detection.
Delayed saccade task
The trial started when a red dot appeared at the center of the monitor. When the monkey fixated the red dot, a single target appeared randomly throughout the visual field for RF mapping, or as part of the comparison with the decision tasks, either in the RF or in the hemifield opposite the RF. Following a 200 ms delay, the red fixation spot disappeared, signaling the monkey to make a saccade to the target. Monkeys received a sip of juice or water if the saccade landed within a 2° × 2° electronic window around the target. The data from the delayed saccade task come from Monkeys H and P, which also performed the RDM task.
Electrophysiological procedures
For the RDM task, we recorded single neurons and multineuron activity throughout the layers of the SC, in 2 monkeys (Monkeys P and H), with a 16-channel platinum/iridium V Probe coated with polyimide (Plexon), with contact impedances of 275 (± 50) kΩ. For the Glass pattern task, we recorded neurons in the intermediate layers of the SC from 2 monkeys (Monkeys S and B), with tungsten electrodes (Frederick Haer, ∼1.3-2 MOhm measured at 1 kHz). All electrodes were inserted through a guide tube positioned by a grid system (Crist et al., 1988) and were moved in-depth by an electronic microdrive system controlled by a graphical user interface on a PC running Windows (Nan Instruments). Action potential waveforms were bandpass filtered (250 Hz to 5 kHz; 4 pole Butterworth; 300 Hz to 5.5 kHz; 6 pole Butterworth), and amplified using the Blackrock NSP hardware system controlled by the Cerebus software suite (Blackrock Microsystems). Neurons were isolated online using time and amplitude windowing criteria, and times of occurrence of action potentials were digitized at 16 bit resolution and sampled at 1 kHz and saved to disk. Neuronal waveform data were digitized at 16 bit resolution and sampled at 30 kHz and saved to disk. Neuronal sorting was performed and/or confirmed with offline waveform inspection and principal component analysis using the Plexon Offline Sorter software x64 version 3.
For both tasks, RFs of SC neurons were mapped online. Mapping was done by moving a spot around the monitor and having monkeys make delayed saccades to the different spots while we listened for maximal discharge rate. We considered the center of the RF of a neuron to be the location at which a saccade was associated with maximal audible discharge. We confirmed the center of the RF by plotting the discharge rate as a heat map in Cartesian coordinates online for visual inspection. Only neurons with RF eccentricities between 7° and 20° were studied in both tasks to ensure no overlap of the RF with the RDM or Glass pattern cue.
Data analysis
All data used for this report were collected as part of other experiments (Crapse et al., 2018; Grimaldi et al., 2018; Odegaard et al., 2018). All statistical analyses were performed using MATLAB (The MathWorks). For both the RDM and the Glass pattern task data, only neurons that exhibited significant task modulation after the cue appeared and during the delay period were used for all analyses. To select neurons in the RDM task, we compared the average activity 200-600 ms after motion onset to a 200 ms epoch of baseline activity beginning 200 ms before motion onset and considered neurons as task-modulated if the activity in these two periods was significantly different (t test, p < 0.05). For the Glass pattern task, we compared the average activity 300-500 ms after Glass pattern onset to a 100 ms baseline epoch before Glass pattern onset and considered neurons as task-modulated if the activity in these two periods was significantly different (t test, p < 0.05). We selected neurons for which we had clearly isolated waveforms. This resulted in 18 neurons from Monkey H and 31 neurons from Monkey P in the RDM task (total n = 49) and 36 neurons from Monkey S and 36 neurons from Monkey B in the Glass pattern task (total n = 72). To display the spike density functions (SDFs), we convolved the times of occurrence of action potentials with a Gaussian (σ) of 20 ms.
Generation of simulated datasets
We simulated idealized spike trains for two models: a model of accumulation and a model of a single rapid state transition within a trial (stepping). The rates were used to calculate a simulated CorCE and ϕ estimate to compare the SC data with rates generated by an accumulating or stepping process. We extracted the model parameters based on the methodology of Latimer et al. (2015) by applying the Markov chain Monte Carlo method to sample the posterior distribution of model parameters, given the observed spike trains (for more details, see Latimer et al., 2015). Parameter estimation was completed separately for each coherence using both Tin and Tout trial conditions. Four sets of parameters were estimated, one for each coherence. Simulations only use the corresponding parameter estimates when making comparisons to empirical data (i.e., 0% coherence RDM empirical data compared with simulations using 0% coherence RDM parameter estimates). Comparisons between simulated (using parameter estimates) and empirical spike trains across different coherences did not occur. The posterior means were used as an estimate of the model parameters. To simulate the Poisson spike trains for an accumulating neuron, we used the following model from Latimer et al. (2015) using parameter estimates:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where x is the drift diffusion process that determines the spike rate for trial j. β is the drift term and ω2 is the diffusion term. γ is the bound height. We only consider trials in which the diffusion particle has reached either decision bound (Tin and Tout correct and error choices). Simulations sampled from β, ω2, γ, and x0 parameter distributions (see Fig. 2B,F). To simulate the Poisson spike trains for a stepping model, we used the following function also from Latimer et al. (2015):
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
where z is the time of the step. Negative binomial distributions were defined using the parameters, r and p; where r is the number of times an outcome occurs given an event and 1 – p is the chance that an outcome occurs given the event, such that the distribution reflects the likelihood of events necessary to obtain r outcomes. d, is the direction of the step. It is possible for the model to assume a step time outside the selected decision epoch. Under these circumstances, trials were categorized as uncommitted and were simulated as having the prestimulus discharge rate through the entire analysis epoch. Simulations sampled from ϕ, α, p, and r parameter distributions (see Fig. 2D,H). Step time distributions used to simulate stepping CorCEs required Equations 7–11; 10,000 trials were simulated, sampling randomly from the negative binomial defined in Equation 7.
Figure 2.
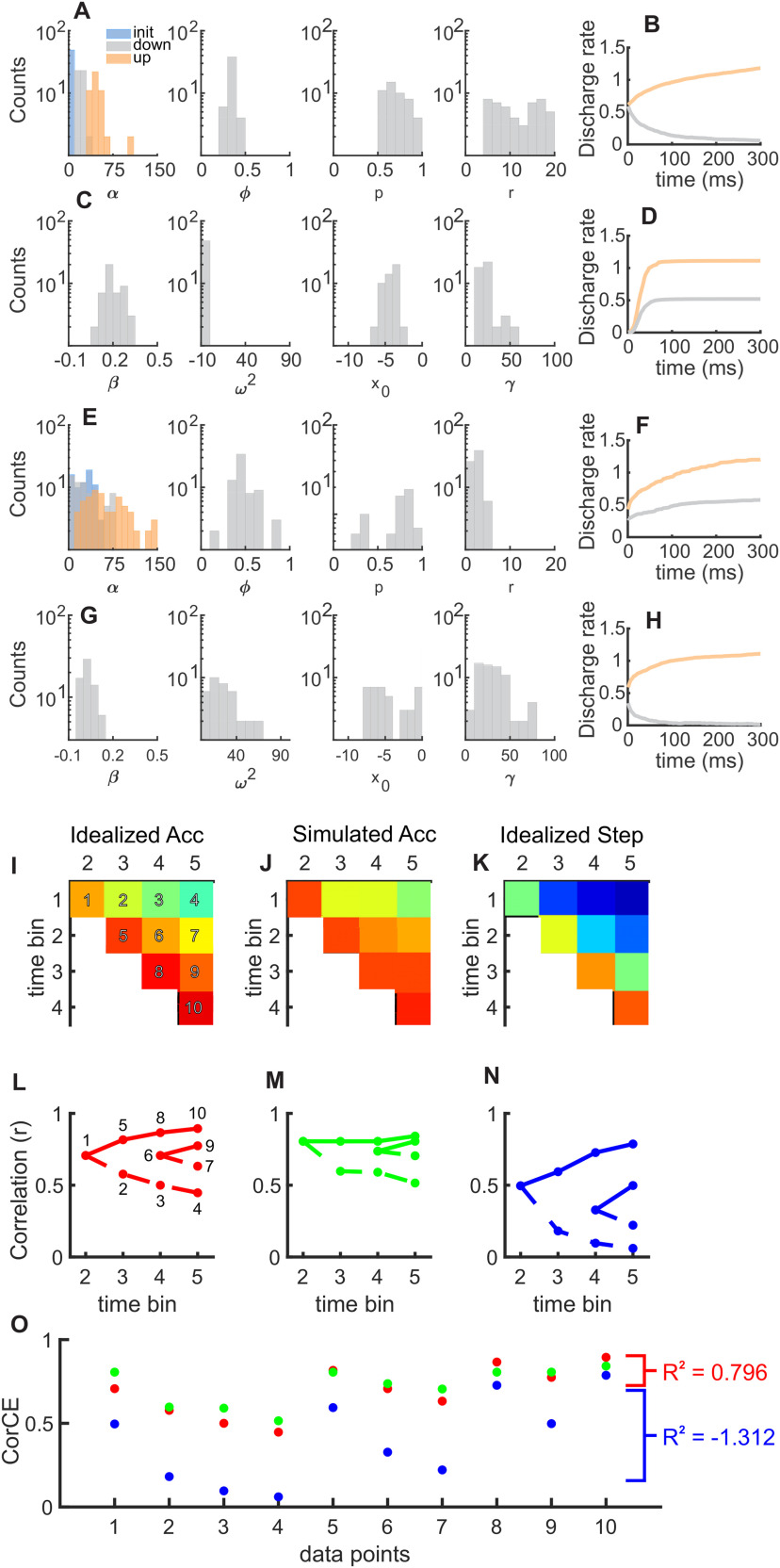
Parameter SDFs and examples of analyses. A, Histograms of the stepping model parameters obtained using the methods from Latimer et al. (2015) from the RDM discrimination task. Plot of α parameters (left-most) as overlain histogram of the rate of the initial state (blue), down state (gray), and up state (orange). Posterior means from single neurons are plotted. B, Simulated SDFs using parameters in A, repeated with 10,000 iterations (trials) for Tin (orange) and Tout (gray) conditions. C, D, Same as in A, B, but for the accumulation model parameters. E–H, Same as in A–D, but for the Glass pattern detection task. Bottom panels, Toy dataset of spike trains from a series of simulated accumulating neurons (n = 49) compared with idealized accumulation and idealized stepping CorCEs used in the RDM task CorCE analyses. I, Idealized accumulation (Acc). Each colored block represents the CorCE value between two time bins and are assigned a data point label (1-10) on the left-most plot. J, Same as in I, but for simulated accumulation. K, Same as in I, but for an idealized stepping process. L, Graphical depiction of the CorCE values for the idealized accumulation (red points and lines), (M) simulated dataset (green points and lines), and (N) idealized stepping (right; blue points and lines). L, Each data point has been labeled with the corresponding number from I. Data points 6, 7, and 9 are excluded from the figures in the main analyses for clarity of visual presentation but are included during all statistical analyses. O, Comparison of the CorCE values for each data point between the simulated dataset and the idealized CorCE values. The R2 values represent the comparison between the simulated dataset and the idealized dataset. The relative similarity between the simulated dataset and the idealized accumulation compared with the similarity to the idealized accumulation is the basis for the intuition captured in the R2 values.
To broaden the scope of models we used for simulated datasets, we also used a dynamical attractor model, selected for its biological plausibility in switching between two different processes within the same circuit (Wong and Wang, 2006; Wong et al., 2007). The model simulates discharge rates resembling an accumulation or stepping process based on the weights of the recurrent input such that the network can be competitive (accumulating) or noncompetitive (stepping). We used the same model parameters as used by Wong and Wang (2006) and Churchland et al. (2011), except for the following: (1) for the accumulation implementation, the NMDA recurrent weights were set to 0.3725 nA; and (2) for the stepping implementation, the NDMA recurrent weights were set to 0.5 nA. We selected a 300 ms epoch in each trial during the transition from the initial to the final discharge rate. The rates were used to calculate a simulated CorCE and subsequent ϕ estimate to compare the SC data with rates generated by an accumulating or stepping process. Although the Wong and Wang (2006) model is compatible with non-reaction time decision tasks, we did not fit the parameters to our behavioral data.
Estimation of the VarCE and CorCE
To compute the VarCE from each trial of each neuron, the spike count was extracted from 60 ms consecutive, nonoverlapping bins of SC data. The mean and variance were calculated across all trials for a given neuron, and the residuals were obtained by taking each time bin and subtracting the mean counts for the same bin for each neuron individually for all trials where a saccade was made to the RF. We then calculated the VarCE of the spike count residuals by subtracting the estimate of the point process variance (using spike counts; Poisson point variance [PPV]) from the total variance (using residuals), as described by Churchland et al. (2011). The PPV was determined by calculating the product of the mean counts with ϕ, an estimate of the contribution of point process noise in the spike counts. The VarCE is approximated by the following equation:
| (12) |
Where Ni is the number of spikes in each epoch, s2Ni is the sample variance of the spike counts within the same epoch and is the sample mean. The z∪ is the union of residuals from all conditions, ni is the number of samples, and n∪ is the total number of samples across all conditions. The CorCE is an extension of the VarCE that estimates the correlation between spike counts at different time bins. It complements the VarCE measure and is given by the following equation:
| (13) |
The indices i and j refer to time bins across the analyzed epoch, and N and λ refer to the spike counts and the rates, respectively. The right term, 〈Cov [Ni,Nj|λI,λj]〉, is akin to the PPV and is 0 by reasonable assumption (see Churchland et al., 2011) when i ≠ j. The left term, Cov [〈Ni|λi 〉,〈 Nj|λj〉], is calculated by dividing each element of the correlation matrix by the term . Solving for the expected values for each paired epoch in the covariance matrix results in the CorCE. To calculate the VarCE, the exact value of ϕ is not necessary to observe changes in VarCE as long as ϕ allows for VarCE > 0. The exact value of ϕ does not change the interpretation of the VarCE so long as ϕ > 0, at which value, there is no PPV and the VarCE is the sample variance of the spike count (Churchland et al., 2011, their Supplemental Fig. 1). We estimated ϕ using a principled approached similar to that used by de Lafuente et al. (2015). The value of ϕ is a free parameter. Therefore, estimating ϕ requires calculating the actual SC data CorCE pattern that best fits the theoretical or modeled CorCE (using estimated parameters; see Table 1) (Latimer et al., 2015). The algorithm calculates a CorCE across all possible ϕ values between 0 and 1, starting at 0.01, before converging on the answer. This requires applying a particle swarm optimization algorithm to identify a ϕ that minimizes the error between the observed CorCE calculated using ϕ and a theoretical CorCE (either accumulation or stepping). Here, the error is an R2CorCE score for goodness of fit. The R2CorCE score is calculated over the aggregated CorCE. The particle swarm optimization algorithm was used to avoid local minima. The ϕ that produces the SC data CorCE most similar (or has smallest error) to the theoretical CorCE was chosen for subsequent analyses (Table 1). To calculate the error, we took an estimate of the VarCE by using the residuals of the spike counts and initial ϕ in the above equation from Churchland et al. (2011). Using the residuals, a 5 × 5 covariance matrix (CovCE) was calculated where the VarCE occupied the diagonal of this matrix. The CovCE was transformed into the CorCE. The CorCE was then Fisher z-transformed for both the observed CorCE and the theoretical CorCE. We then selected the ϕ that provided the smallest sum of squared errors (SSE) between the zobserved – ztheory. The theoretical CorCE was calculated as where i and j are times of the bins and i < j. It is important to note our estimate relies on aggregating all trials together to obtain a single ϕ for the entire sample of neurons.
Table 1.
ϕ estimates used in the VarCE and CorCE analyses
| Fit | ϕ |
|---|---|
| RDM: accumulation | 0.425 |
| RDM: stepping | 3.965e-06 |
| Glass pattern: accumulation | 0.445 |
| Glass pattern: stepping | 0.538 |
| RDM: attractor accumulation | 0.392 |
| RDM: attractor stepping | 4.229e-06 |
| Glass pattern: attractor accumulation | 0.400 |
| Glass pattern: attractor stepping | 8.331e-05 |
| RDM: 0% coherence | 0.426 |
| RDM: 6%-10% coherence | 0.458 |
| RDM: 10%-20% coherence | 0.453 |
| RDM: 20%-50% coherence | 0.429 |
| Glass pattern: 26% coherence | 0.547 |
| Glass pattern: 39% coherence | 0.536 |
| Glass pattern: 52% coherence | 0.439 |
| Glass pattern: 100% coherence | 0.511 |
| RDM: saccade | 0.550 |
| Monkey P: accumulation | 0.353 |
| Monkey H: accumulation | 0.556 |
| Monkey B: accumulation | 0.432 |
| Monkey S: accumulation | 0.418 |
| Monkey P: stepping | 8.043e-06 |
| Monkey H: stepping | 3.565e-06 |
| Monkey B: stepping | 0.457 |
| Monkey S: stepping | 0.527 |
Because estimating ϕ requires comparing the idealized CorCE with the empirical CorCE, the CorCE was calculated over a range of ϕ values and the ϕ value with the smallest SSE was used. When calculating the CorCE from the simulated rates, the rate was integrated to give spike counts. Trials were sampled from each neuron, with replacement, to produce a resampled set of trials. Using this resampled population, we estimated the ϕ using a theoretical accumulation CorCE and simulated stepping CorCE. This produced a CorCE that best fit to the theoretical accumulation CorCE or simulated stepping CorCE from the resampled population. The SSE was then calculated for the resampled CorCE and the idealized CorCE. This process of resampling and calculating the SSE was repeated 1000 times to produce SSE distributions. The SSE provides a measure of the distance between the empirical CorCE and the idealized ramping and stepping CorCEs. We then assessed the null hypothesis that the distributions were the same using the Wilcoxon rank sum test.
Deviation information criterion (DIC)
We compared model fits using the DIC. The DIC implementation taken from Latimer et al. (2015), is defined as follows:
| (14) |
where is the posterior mean of the parameters given the data. M is either the accumulation or stepping model, depending on the parameters given by (for more details, see Latimer et al., 2015, their Supplemental methods).
WAIC
We compared model fits using WAIC. The WAIC implementation was taken from Zoltowski et al. (2019), defined as follows:
| (15) |
Where N is trials, S is posterior samples, and is the posterior mean of the parameters given the data. In the WAIC analyses, we extended both accumulation and stepping models using a history filter to account for spike history effects, such as refractory periods and bursting. This addition to the model accounts for non-Poisson spike history effects that are independent of the spiking driven by the latent variable. In addition, the accumulation model incorporates a non-zero baseline and a SoftPlus nonlinearity between the latent variable and the firing rate. For more details regarding these additions to the model, see Zoltowski et al. (2019, their Methods).
Predictive activity
To calculate predictive activity, normalized discharge rates (stimulus onset to 700 ms for the RDM task and stimulus onset to 900 ms for Glass pattern task) were binned into 100 ms consecutive, nonoverlapping epochs and areas under the receiver operating characteristic (auROC) were calculated between the Tin and Tout trials. To calculate the auROC, an ROC is computed by sweeping a criterion between the Tin and Tout activity distribution and finding the proportion of Tin counts to Tout counts greater than the criterion. We incremented the criterion from the minimum to the maximum discharge rate measured across all trials within the epoch of analysis. The area underneath the ROC is integrated to produce the auROC. Here we refer to the auROCs as the predictive activity as done previously and for comparison with previous reports in SC (Horwitz and Newsome, 2001).
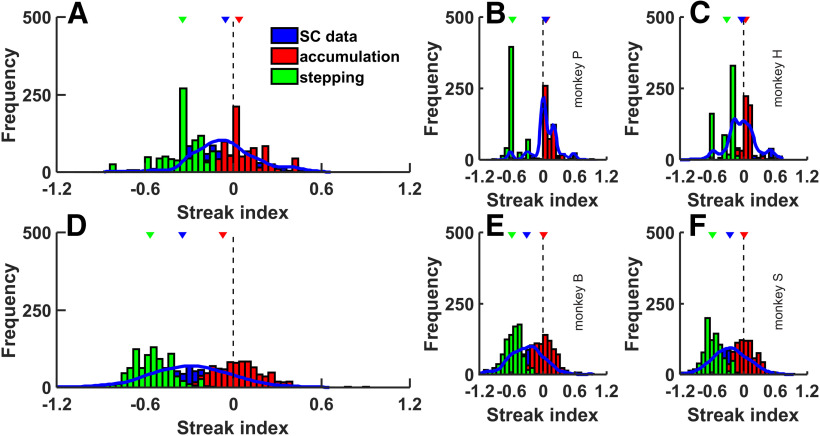
SI analysis
The analysis epoch was divided into consecutive, nonoverlapping, 40 ms bins from 204 to 524 ms for Monkey P and 255 to 675 ms for Monkey H after the onset of the motion and from 209 to 800 ms for Monkey B and 337 to 800 ms after the onset of the Glass pattern for Tin trials, and the median spike count of each bin was calculated per neuron. On a trial × trial basis, the spike count within a bin was compared with the median and if the count was higher than the median, the bin for that trial was assigned a 1. If the spike count was lower than the median, the bin for that trial was assigned a 0. If the spike count within a bin was equivalent to the median, it was randomly assigned either a 1 or a 0. To calculate the SI, the following equation was used:
| (16) |
where N is the number of times the adjacent bins switch from 1 to 0 or from 0 to 1 throughout a trial. The mean of N, μ, is given by the following:
| (17) |
where m is the number of 0s in a trial and n is the number of 1s in a trail. The SD of N, σ, is defined as follows:
| (18) |
If the spike train is generated from the same underlying Poisson process (homogenous or nonhomogenous), then the SI should be 0. However, if a neuron undergoes a change in state, resulting in a jump or step in discharge rate, the μ will be greater than N as the neuron undergoes fewer switches from 0 to 1 or vice versa. In this case, the SI will fall below 0. Therefore, if the underlying rate for a spike train does not change throughout a trial, the likelihood of the spike counts being higher or lower than the median would be random resulting in a mean SI of 0. However, a positive or negative SI indicates a change in underlying rate such that in the next time bin the spike count is less likely or more likely, respectively, to be higher than the median count. A Wilcoxon rank sum test determined differences between the SIs from spike trains of the SC neurons and simulated neurons. These procedures are the same as those used previously for LIP and SC as previously reported (Horwitz and Newsome, 2001; Bollimunta et al., 2012). However, like Bollimunta et al. (2012) and unlike Horwitz and Newsome (2001), our SI analysis took place over single trials. This makes the measure robust to the trial counts, whereas computing the SI over all trials, scales the SI to the total number of trials.
We generated the SI distributions by a resampling procedure in which we first simulated accumulating and stepping spike trains for the same number of SC neurons recorded in the RDM and Glass pattern tasks. We next calculated SIs for each simulated neuron and classified each as showing accumulation if the SI was not significantly different from 0 (p < 0.05) and stepping if the SI was significantly <0 (p< 0.05) using a Wilcoxon rank sum test. Simulated SI distributions results in negative median SI for simulated stepping and a 0 median SI for simulated ramping spike trains for both RDM and Glass pattern tasks. This makes sense if the median spike count represents the drift rate and the actual spike count in a bin represents the drift rate plus some diffusion noise. If this is the case, across time bins, the spike counts would either be randomly higher or lower as the diffusion noise randomly pushes the decision variable up and down. Single-trial SIs would be <0 or >0, but overall have a distribution centered at ∼0. However, in stepping, the SI is likely to be negative. Negative SIs indicate deviations from a constant underlying rate such that given a time bin with a higher than median spike count, the next time bin the spike count is more likely to be higher as well. The occurrence of an instantaneous transition (step) from a lower to higher spike rate within a given bin would produce spike counts higher than the median in the bins after and counts lower than the median in the bin before. This would produce SIs <0 as the spike counts diverge from the median count since the median count resembles a ramp across trials.
Results
Trained monkeys performed either a two choice motion direction discrimination task (RDM; Monkeys H and P) or a Yes-No detection task in which they reported whether or not they detected orientation in a dynamic Glass pattern display (Monkeys B and S). Both tasks included noisy and varying amounts of sensory evidence (see Materials and Methods). We recorded SC neuronal activity while monkeys performed these tasks, and a description of the relationships between neuronal activity and decision performance appears elsewhere (Crapse et al., 2018; Grimaldi et al., 2018; Odegaard et al., 2018). Here, we focus on single-trial neuronal activity dynamics to reveal whether the underlying neuronal processes reflected in SC activity differ in different decision-making tasks, despite similar trial-averaged ramping activity across tasks and monkeys. We report on data from 49 neurons from 2 monkeys performing the RDM task and 72 neurons from 2 monkeys performing the Glass pattern task and 62 neurons from 2 monkeys performing a delayed saccade task (see Materials and Methods).
Figure 1A shows schematics of the RDM and Glass pattern tasks. The temporal arrangement of both was similar, with the exception that the RDM task included a delay time that was randomized between 500 and 700 ms after the motion cue presentation, whereas the Glass pattern task included a delay time randomized between 800 and 1500 ms after the Glass pattern cue onset (Fig. 1; Cue + Delay). In the RDM task, the motion cue disappeared after 200 ms, whereas in the Glass pattern task, the cue remained visible throughout. Both tasks used delays and therefore were not reaction time tasks. In the RDM task, the choice targets appeared at locations in the visual field corresponding to the two possible motion directions (e.g., left motion–left choice target) and in the Glass pattern task, the choice target was determined by color (red for No and green for Yes); and the two positions were randomized between the two locations on every trial, decoupling the choice report from the saccade location. The RDM task required motion direction discrimination, whereas the Glass pattern task required orientation detection.
Figure 1B, D shows that each of our monkeys produced typical psychophysical performance in the RDM and Glass pattern tasks. We manipulated the strength of the sensory evidence in both tasks by varying the coherence of the motion direction in the RDM task and the oriented dot pairs in the Glass pattern task. Figure 1B, D shows that perceptual sensitivity (d′) increases as coherence increases for both monkeys in both tasks. Monkey H saw coherences of 0%, 10%, 20%, and 50%, and Monkey P saw coherences of 0%, 6%, 10%, and 20% (Fig. 1B; Monkey H; d′: 0% = 0.07; 10% = 1.45; 20% = 2.50; 50% = 3.77 and Monkey P; d′: 0% = 0.08; 6% = 1.51; 10% = 2.97; 20% = 3.47), but we grouped the data into four bins according to matched d′, 0%, 6%-10%, 10%-20%, and 20%-50% coherence (n = 22 sessions). For the Glass pattern task, both monkeys experienced 0%, 26%, 39%, 52%, and 100% coherences and showed different sensitivities (Fig. 1D; Monkey B, d′: 26% = 0.75; 39% = 1.74; 52% = 2.55; 100% = 3.06 and for Monkey S, d′: 26% = −0.30; 39% = 0.84; 52% = 1.88; 100% = 3.11; n = 93 sessions). This typical psychophysical performance on the RDM and Glass pattern tasks indicates that the monkeys used the sensory information to inform their decisions; as the strength of the sensory evidence increased, the probability of correctly discriminating the motion direction in the RDM task or reporting Yes in the Glass pattern detection task also increased (see also Crapse et al., 2018; Odegaard et al., 2018; Grimaldi, et al., 2018). Figure 1C, E shows that trial-averaged neuronal activity recorded from the SC of the 4 monkeys behaves similarly, despite the differences in the tasks, and as others have reported, consistent with a process of accumulation (Horwitz and Newsome, 2001; Ratcliff et al., 2003; Kim and Basso, 2008). In both the RDM and Glass pattern tasks, after an initial dip in activity following the motion or Glass pattern cue onset, a sharp increase in the discharge rate follows for trials in which monkeys report their decision correctly by making saccades to the choice target in the RF (Tin), whereas for correct choices made away from the RF (Tout), neuronal activity declines or remains at a relatively reduced level (Fig. 1C,E). Some SC neurons show a weak transient on Tout trials around the time of saccades, which is common and likely a transient visual response (Fig. 1E, dashed line). Trial-averaged ramping activity like this is found in many SC neurons in the motor layers and is associated with many processes, including attention, target selection and evidence accumulation, and even saccade preparation and generation (Glimcher and Sparks, 1992; Munoz and Wurtz, 1995; Horwitz and Newsome, 2001; McPeek and Keller, 2002; Horwitz et al., 2004; Felsen and Mainen, 2008; Kim and Basso, 2008, 2010; Thevarajah et al., 2009; Krauzlis et al., 2013; Basso and May, 2017). The similar trial-averaged ramping behavior of SC neurons, despite differences in tasks and monkeys' histories, justifies the further analysis of the statistics of SC spike trains to determine the relationship of delay period activity to the underlying processes in different types of decision tasks and a simple saccade task.
Spiking dynamics of SC neurons show accumulation and stepping
To ensure our analyses focused on an equivalent epoch of neuronal discharge that likely included the decision time in both tasks, despite the differences between tasks, we used a principled approach to measure an equivalent decision epoch for each. Identifying a likely decision epoch ensures that the spike train epoch used to calculate the DIC, WAIC, VarCE, CorCE, and SI includes the decision process. To determine this epoch, we calculated the auROC for the highest coherence trials (see Materials and Methods; RDM: 20%/50%; Glass pattern: 100%) using a sliding window with 100 ms bins separately for each monkey performing each task. To ensure consistency across monkeys and tasks, we defined the decision epoch as the earliest time bin for which the auROC reached significance (p ≤ 0.05), as determined using a bootstrapping procedure. The auROC reached significance for Monkeys P and H at 204 and 255 ms, respectively, in the RDM task, and for Monkeys B and S at 209 and 337 ms, respectively, in the Glass pattern task. Based on these numbers, we used a 300 ms decision epoch: 204-504 ms for Monkey P, 255-555 ms for Monkey H, 209-509 ms for Monkey B, and 337-637 ms for Monkey S. These decision epochs were used for each monkey for all analyses unless otherwise stated.
We computed five related, but different, measures of neuronal activity variability using the 0% (RDM) or 26% (Glass pattern) coherence trials and all Tin and Tout trials unless otherwise specified. The use of low coherence trials ensured that we assessed the data with the longest possible integration times. Our first measure was the DIC as applied by Latimer et al. (2015), where it was used to compare accumulation and stepping models. DIC uses Bayesian methods to fit model parameters to the spike trains. Parameter distributions are used to calculate the DIC by using the deviance to obtain a goodness-of-fit term in combination with a penalty for the effective number of parameters. Higher ΔDIC values indicate stronger separability between models, with the sign of the ΔDIC indicating the preferred model. Second, we also used the WAIC, which builds on the DIC but is more robust because of its penalty term. The WAIC is generally consistent with leave-one-out cross-validation (Gelman et al., 2014). Third was the VarCE, which assumes that the recorded spike trains originate from a generalized renewal process. Formally, the VarCE is the difference between the total variance of the spike count and the PPV (see Materials and Methods). This measure was introduced by Churchland et al. (2011) and further refined by de Lafuente et al. (2015) as a way to glean information about neuronal processing associated with patterns of variance in spike trains. Calculating the VarCE requires estimating ϕ, a constant that describes the relationship between the PPV and the mean spike count. Subtracting the PPV from the total variance produces the VarCE. If the variance of the measured spike trains is consistent with a diffusion process and reflects the accumulation of noisy sensory samples, we expect the VarCE to show a linear, monotonic rise with time; as the rate increases the longer the decision process has been going on, the more variable the state of the decision process is across trials. The fourth measure examined the autocorrelation between expected counts across time bins, called the CorCE. Particular neuronal processes appear as unique patterns of time-dependent changes in the CorCE, and comparisons of CorCE matrices obtained from spiking data with CorCE matrices obtained from simulated data or theoretical CorCEs allow us to determine the process that best explains the pattern in the spiking data. Here, the simulated stepping CorCE was obtained by simulating the stepping firing rates using a step time distribution. Step times were randomly sampled from a negative binomial distribution, informed by fitted parameters (Fig. 2A,E). We analyzed the results statistically by determining the goodness of fits by comparing the R2CorCE fits between the actual and simulated data. The R2CorCE comparison determines whether the predictions from an accumulation or a stepping model better correlate with the results from SC data, and is a relative comparison rather than an absolute assessment of accumulation or stepping. Figure 2I–O shows a toy example of the CorCE analysis using simulated accumulating spike trains for further clarification of this method. The fifth measure is the SI, which measures the temporal structure of spikes within a single trial relative by counting the number of transitions of the spike counts higher or lower than the median spike count. Therefore, the SI assesses whether spike count fluctuations are random in each trial as a result of the same, nonhomogeneous Poisson process (e.g., continuous ramping), or whether there exists a pattern that might result from different, nonhomogeneous Poisson processes (e.g., stepping). This measure was introduced by Horwitz and Newsome (2001) to assess trial-averaged activity in SC and extended to assess single-trial dynamics in LIP by Bollimunta et al. (2012). It is this latter method that we apply here using only the Tin trials (see Materials and Methods).
To compare between models of accumulation and stepping, we calculated the DIC as described above and also calculated theoretical CorCE matrices for an accumulation process and a simulated CorCE for a stepping process (see Materials and Methods). The accumulation model results in a gradual rise in activity reflecting evidence accumulation and the stepping model results in a categorical, binary change in activity potentially reflecting a change in decision state. Next, we calculated the VarCE using estimated ϕ values (described below) from these idealized CorCEs. Then, we compared idealized CorCE matrices with CorCEs created from the SC data. Finally, we calculated SIs from simulated accumulation and stepping spike trains and the actual SC data. We constrained the simulated datasets by using the same number of trials and the initial and final discharge rates of the decision epoch measured from the actual SC spike trains. The stepping and accumulation models assume that the spike trains result from a nonhomogeneous Poisson process that reflects either a linear increase or a stepped transition.
Using parameters extracted from the observed dataset, we first simulated SDFs for accumulation and stepping processes and compared these with the actual data recorded from monkeys performing the RDM and Glass pattern tasks. This exercise ensured that the simulated data of both models (Fig. 2B,D,F,H) accurately captured the observed trial-averaged data before embarking on an extensive single-trial analysis as described below.
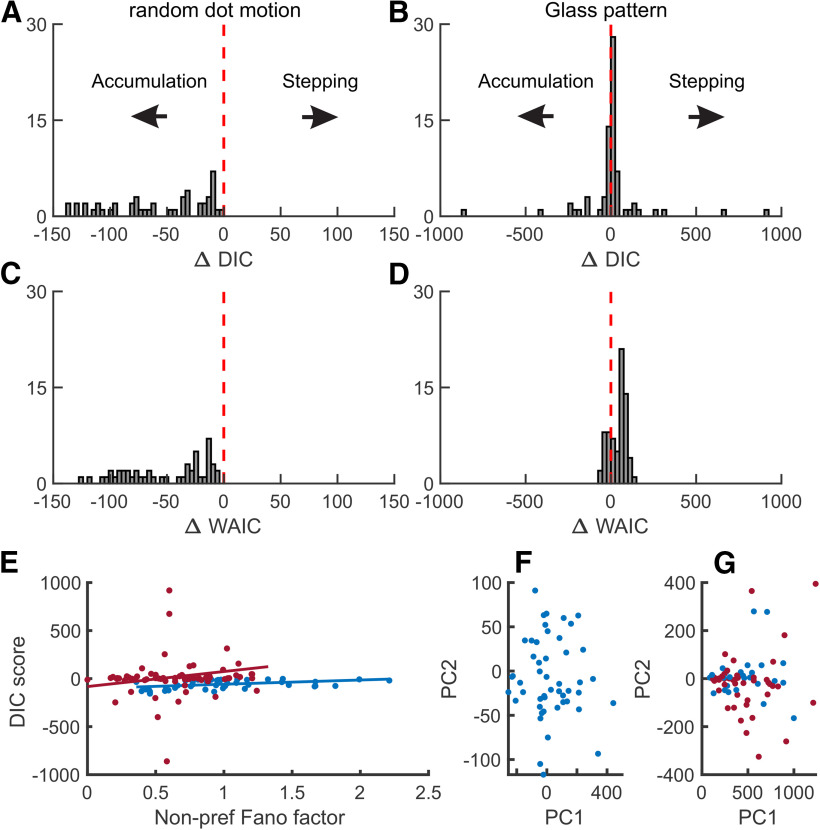
To assess the relationship of SC spiking activity to the processes of stepping and accumulation, we first calculated the DIC (Latimer et al., 2015). For the RDM data, 49 of 49 SC neurons (100%) favored accumulation (ΔDIC < 0) with 44 SC neurons (90%), strongly favoring accumulation (ΔDIC < 10; Fig. 3A). For the Glass pattern task, 45 of 72 SC neurons (62.5%) favored stepping (ΔDIC > 0) with 42 SC neurons (43%) strongly favoring stepping (ΔDIC > 10; Fig. 3B). These results indicate that SC delay period activity in most SC neurons is statistically consistent with accumulation rather than stepping during the RDM task and is statistically consistent with stepping slightly more than accumulation during the Glass pattern task.
Figure 3.
DIC and WAIC analyses distinguish accumulation and stepping. Frequency histogram of ΔDIC and ΔWAIC values obtained for SC neurons in the RDM discrimination task and the Glass pattern detection task. Red vertical dashed line indicates no change in DIC or WAIC. Values to the right of 0 indicate larger support for stepping, and values to the left of 0 indicate larger support for accumulation. Each count shows the result from a single neuron. Note the x axis scale difference between A and B, as some neurons had extreme DIC values in the Glass pattern task. A, RDM task data. B, Glass pattern task data. C, D, Same as in A, B for the ΔWAIC. E, The nonpreferred (Tout) Fano factor plotted as a function of the ΔDIC score for both RDM (blue) and Glass pattern (red) tasks. The nonpreferred Fano factor was calculated from the same 300 ms epoch used for the DIC and VarCE/CorCE analyses. F, The first PC loadings plotted against the second PC loadings for each RDM neuron and (G) Glass pattern neurons. Blue points indicate a negative ΔDIC (accumulating). Red points indicate a positive ΔDIC (stepping). Units on the PC1 and PC2 axes are arbitrary.
We also calculated the WAIC values to assess stepping and accumulation (Zoltowski et al., 2019). For the RDM data, 49 of 49 SC neurons (100%) favored accumulation (ΔWAIC < 0; Fig. 3C). For the Glass pattern task, 52 of 72 SC neurons (72.2%) favored stepping (ΔWAIC > 0; Fig. 3D). Consistent with the ΔDIC, these results indicate that SC delay period activity is statistically consistent with accumulation rather than stepping during the RDM task and with stepping rather than accumulation during the Glass pattern task.
Brittleness describes a general phenomenon where loosely defined mathematical models produce unintended results when minor assumptions are violated. Chandrasekaran et al. (2018) outlined several cases where ΔDIC values are sensitive to data characteristics independent of the underlying decision-making process. We sought to address some of these concerns by replicating some of the analyses reported by Chandrasekaran et al. (2018). One particular challenge suggests that the ΔDIC is sensitive to whether the neuron demonstrates sub- or super-Poisson firing. The Tout Fano factor is a significant predictor of the ΔDIC, such that lower Fano factors indicate a greater likelihood of being labeled as stepping. Like Chandrasekaran et al. (2018), we regressed the ΔDIC for each neuron against the Tout Fano factor over the 300 ms analysis epoch. For the RDM task, the nonpreferred Fano factor is predictive of the ΔDIC (R2 = 0.175, p = 0.002, β = 43.938, t(47) = 3.160, p = 0.002; Fig. 3E, red). The analysis applied to the Glass pattern dataset indicates no predictive relationship between the nonpreferred Fano factor and the ΔDIC (R2 = 2e-4, p = 0.904, β = −8.276, t(70) = −0.121, p = 0. 904; Fig. 3E, blue). Interestingly, although the nonpreferred Fano factors were predictive of the ΔDIC for the RDM activity, none of the neurons was classified as stepping according to their ΔDIC. In addition, all SC neurons of either sub- and super-Poisson dispersion (min Fano factor: 0.35; max Fano factor: 2.12) had ΔDIC that were classified as accumulating; 32 of 49 of the neurons had nonpreferred Fano factors < 1, which are expected to have ΔDIC < 0. Although dispersion is predictive of the ΔDIC, the predictive capacity does not necessarily extend into class labels. Given the above results, we conclude that there lacks a clear relationship between dispersion and the ΔDIC in our SC dataset, making it unlikely that the ΔDIC we calculated is significantly affected by dispersion.
Chandrasekaran et al. (2018) also found that applying principle component analysis (PCA) to spike rates revealed a mixture of monotonic and nonmonotonic PCs. Crucially, the extent of loading on the nonmonotonic PCs was predictive of the ΔDIC, such that greater loading predicted a greater likelihood of being labeled stepping. We replicated the PCA analyses on the rates from our SC neurons. In applying PCA to the RDM task activity, both the first and second PCs displayed monotonic behavior, of which only the first was consistent with an accumulation or stepping process (monotonic rise). The first and the second PC explained 89% and 8% of the total variance, respectively. Since both first and second PCs displayed monotonic-like behavior, a clear relationship between the ΔDIC and nonmonotonicity cannot be made because of the lack of counterfactual evidence. However, for the Glass pattern, both accumulation and stepping DIC labels were available. PCA revealed similar results as the RDM, with a first component capturing 94% of the variance and the second component capturing 4% of the variance. However, the first PC was nonmonotonic, and this nonmonotonicity was present for neurons classified as step or ramp by the DIC analyses. This might explain the majority of neurons being classified as stepping in the Glass pattern dataset. Therefore, we decided to split the dataset into both DIC stepping and accumulating classified datasets and ran PCA on the discharge rates. We found the same results where the first PC contained 94% of the variance. In addition, plotting the PC score comparing PC1 and PC2 (Fig. 3F,G), we found no significant correlation between the DIC classification and the loadings on either PCs for either RDM (R2 = −0.067, p = 0.65) or Glass pattern task data (accumulation: R2 = 0.330, p = 0.09; stepping: R2 = −0.165, p = 0.27). Therefore, the second point by Chandrasekaran et al. (2018) is also unlikely to be a concern for the analysis reported here. Together, our results demonstrate that the ΔDIC from the SC data is unlikely to be susceptible to brittleness.
As the DIC results showed, the VarCE and the CorCE also show that SC activity is more consistent with an accumulation process than a stepping process during the RDM task. SC activity increases linearly as the decision evolves in the RDM task, and the VarCE shows a similar monotonic rise (Fig. 4A–C). We computed the VarCE using ϕ estimates derived from a theoretical accumulation CorCE (Fig. 4B) and a simulated stepping CorCE (Fig. 4C; for the ϕ estimates, see Table 1). Both VarCE measures showed linear increases. The more stringent assessment of whether the underlying neuronal process is consistent with accumulation is the CorCE because this measure is constrained by the two models separately. Figure 4D shows the CorCE of SC spike trains during the decision epoch of the RDM task, using ϕ estimates from a theoretical accumulation CorCE. Figure 4E shows the same using ϕ estimates from a simulated stepping CorCE. Theoretically, the correlation of spike count bins across time should increase and the correlation between spike counts bins separated in time should decrease gradually for an accumulation process. For a stepping processes, the correlation between spike counts across time should decrease abruptly as the width of the step time distributions decreases. We computed the R2 comparing the theoretical accumulation CorCE to the SC data and the simulated stepping CorCE to the SC data (R2CorCE), over the 10 CorCE data points, which yielded an R2CorCE of 0.711 and 0.475, respectively. Bootstrapping the SSEs between the accumulation and stepping CorCEs revealed a significant difference between the two (Fig. 4F,G; p < 0.001). We present only the top row of the CorCE matrix (dashed lines) and the juxtadiagonal (solid lines) in Figure 4F and G for clarity. The red lines indicate theoretical predictions, and the circles and black lines indicate the data points from SC spike trains.
Figure 4.
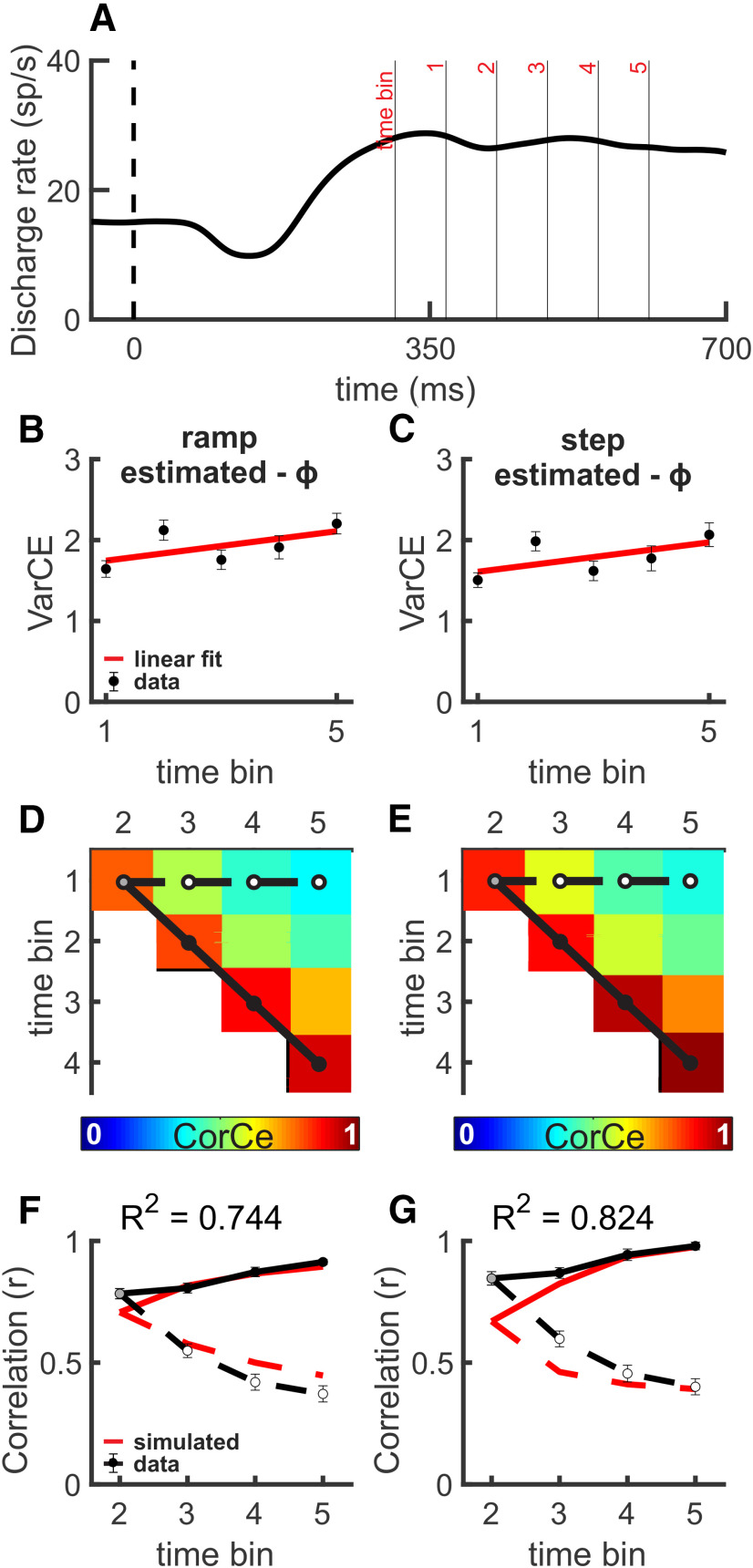
SC spiking during the RDM task is consistent with accumulation. A, Averaged SDF (α = 20 ms) for all choices plotted against time and aligned to the onset of the motion cue (vertical dashed line) for 0% coherence trials. n = 49 neurons. Overlain lines indicate example time bins (1-5) for Monkey P as an example. B, VarCE (filled black circles) and fitted line (red) calculated in 60 ms time bins for 0% coherence plotted against time during the decision epoch using estimates of ϕ derived from best fits to the theoretical accumulation CorCE matrix (see Materials and Methods). Error bars indicate the SD obtained from bootstrapping but are obscured by the symbols. C, Same as in B, but for a stepping process used to estimate ϕ. D, The upper triangle of a symmetric CorCE matrix through time displayed as a heat map. Warmer colors represent higher CorCE. The CorCE analysis used the same 60 ms time bins. E, Same as in D, but for a stepping process used to estimate ϕ. F, Comparisons between the CorCE values from the SC data (black lines) and the theoretical CorCE (red lines) from an accumulation process used to estimate ϕ in B. Only the top row of the CorCE matrix (dashed line in D) and the first juxtadiagonal (solid line in D) are presented. F, Filled circles represent the corresponding filled circles in the CorCE matrix plotted in D. Inset, R2 values were calculated over all 10 r values of the matrices. Error bars indicate the SD obtained from bootstrapping and may be obscured by the symbols in some cases. G, Same as in F, but for a stepping process used to estimate ϕ. The theoretical CorCE shown in G was obtained from simulations using a step time distribution.
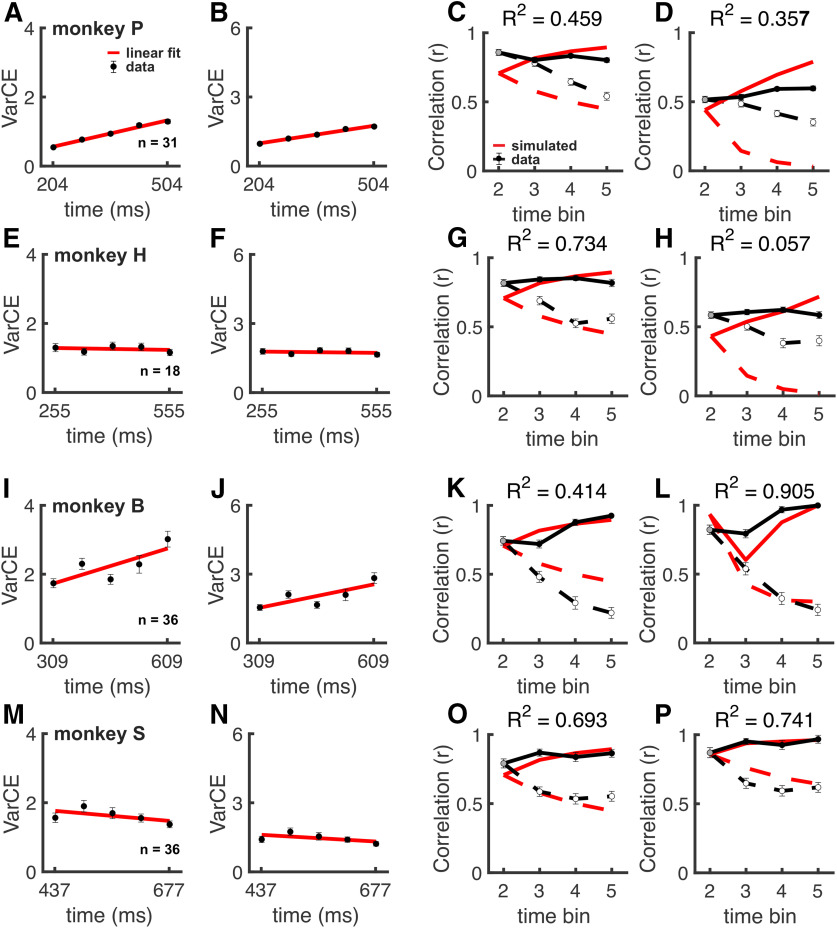
Figure 5 shows spike train dynamics of SC neurons during the Glass pattern detection task. Although the VarCE showed a rise during the decision epoch, it was qualitatively nonmonotonic compared with that seen in the RDM task (Fig. 5A–C). This behavior is inconsistent with a process of accumulation. As we did for the RDM task data, we next computed R2CorCE comparing the theoretical accumulation CorCE to the SC data CorCE and the simulated stepping CorCE to the SC data CorCE to determine the step times as described above. The resulting R2CorCE values were 0.744 and 0.824, respectively (Fig. 5D–G). Bootstrapping the SSEs revealed a significant difference between both pairs of R2CorCE values (Fig. 5D,E; p < 0.001). Thus, the comparatively nonmonotonic rise of the VarCE, and the CorCE analyses of SC spiking data, indicate that decision activity during the Glass pattern detection task is unlikely to reflect an accumulation process (Churchland et al., 2011). Although the R2 values were largely consistent with an accumulation process, the R2 values were larger and significantly different for a stepping process (compare Fig. 5F,G). We performed the same analyses for the RDM and Glass pattern data for individual monkeys and replicated the group results in each monkey, indicating that the results stem from differences in task and not idiosyncrasies of the individual monkeys (Fig. 6). Bootstrapping the individual monkey SSEs revealed a significant difference between the R2CorCE values (p < 0.001).
Figure 5.
SC spiking during the Glass pattern task is consistent with stepping. A, Averaged SDF (α = 20 ms) for all choices plotted against time and aligned to the onset of the Glass pattern cue (vertical dashed line) for the 26% coherence trials. N = 72 neurons. Overlain lines indicate example time bins for Monkey B. B, Plot of VarCE (filled black circles) and fitted line (red) calculated in 60 ms time bins for 26% coherence, all choices plotted against time using estimates of ϕ derived from the best fits to the theoretical accumulation CorCE matrix. Error bars indicate the SD obtained from bootstrapping but are obscured by the symbols. C, Same as in B, but for a stepping process used to estimate ϕ. D, Top triangle of a symmetric CorCE matrix through time displayed as a heat map. Warmer colors represent higher CorCE. The CorCE analysis used the same 60 ms time bins. E, Same as in D, but for a stepping process used to estimate ϕ. F, Comparisons between the CorCE values between the SC data (black lines) and the theoretical CorCE (red lines) from an accumulation process used to estimate ϕ in B. Only the top row of the CorCE matrix (solid line in C) and the first juxtadiagonal (dashed line in C) are presented. Filled circles represent the corresponding filled circles in the CorCE matrix plotted in D. Inset, R2 values were calculated over all 10 r values of the matrices. Error bars indicate the SD obtained from bootstrapping. G, Same as in F, but for a stepping process used to estimate ϕ. The theoretical CorCE was obtained from simulations using a step time distribution.
Figure 6.
Accumulation and stepping depend on the task and not monkey idiosyncrasies. A, VarCE obtained using the same methods as described in Figures 2 and 5, for 0% coherence in Monkey P from the RDM. n = the number of neurons from each monkey. Error bars indicate the SD obtained from bootstrapping and may be obscured by the symbols. B, VarCE obtained using the same methods as described in Figures 2 and 6, for 0% coherence in Monkey P. Error bars indicate the SD obtained from bootstrapping and may be obscured by the symbols. C, Comparisons between the CorCE values between the SC data (circles) and the expected values from the theoretical ramping CorCE for Monkey P. Error bars indicate the SD obtained from bootstrapping. D, Comparisons between the CorCE values between the SC data (circles) and the expected values from the theoretical stepping CorCE for Monkey P. Error bars indicate the SD obtained from bootstrapping. E-H, VarCE and CorCE analyses from A, B, repeated for Monkey H. I-L, VarCE and CorCE analyses from A, B, repeated for Monkey B. M-P, VarCE and CorCE analyses from A, B, repeated for Monkey S. An accumulation process explained the data for Monkeys B and S performing the Glass pattern task well, but not as well as a stepping process.
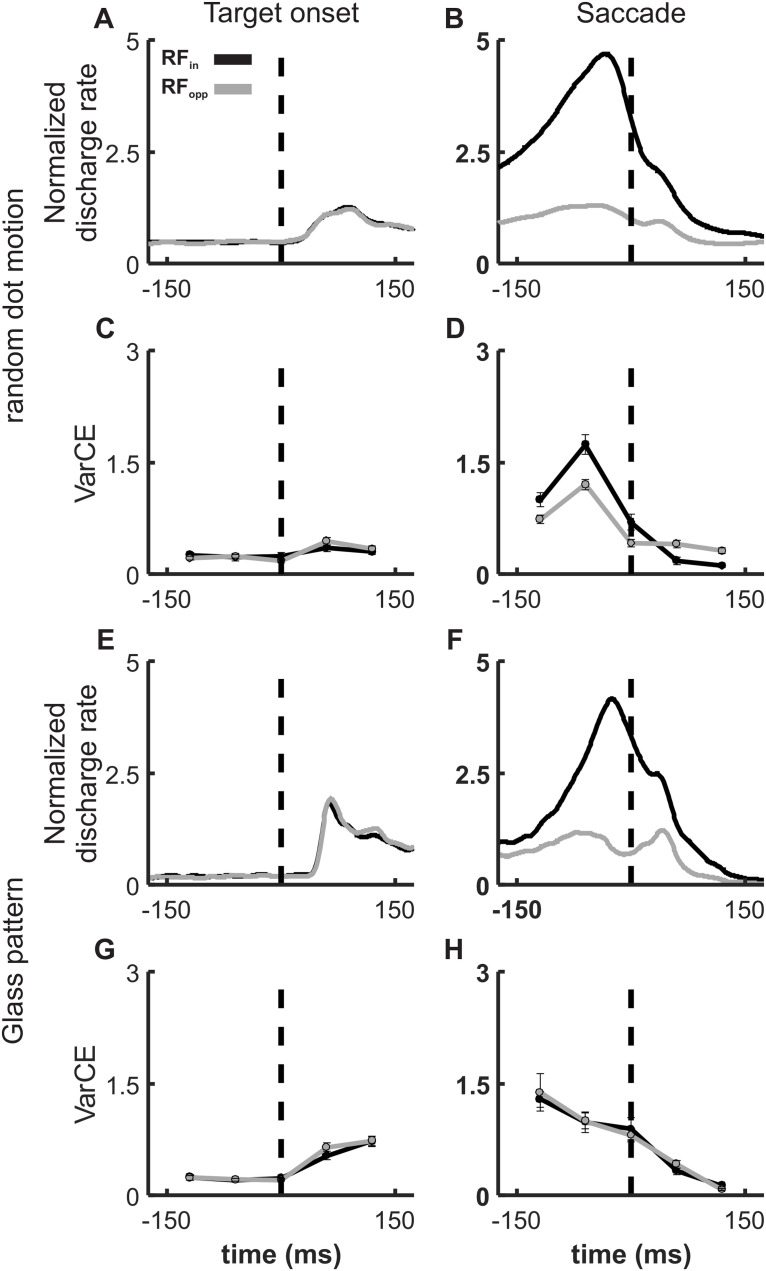
We then calculated the VarCE using a 300 ms epoch around visual target onset for both the RDM and Glass pattern task data, in which a target stimulus appeared in the RF of a recorded neuron leading to a short burst of spikes (Fig. 7A,E). We also calculated the VarCE during the saccade epoch, when the high-frequency motor-related activity of SC neurons occurred (Fig. 7B,F). In doing so, we could address possible concerns that the VarCE was conflated with a disproportionally increasing PPV as spike rate increased. The data showed that the peak VarCE did not coincide with the peak mean rate during the visual target onset (Fig. 7C,G) nor during the saccade. Rather, the VarCE decreased as the mean rate increased (Fig. 7D,H), revealing a decoupling of the spike rate and the VarCE. The exact value of ϕ does not change the interpretation of the VarCE so long as ϕ > 0, at which value, there is no PPV and the VarCE is the sample variance of the spike count (Churchland et al., 2011, their Supplemental Fig. 1).
Figure 7.
The VarCE decreases around the time of saccade onset in decision tasks. Normalized discharge rate collapsed over all coherences is plotted against time for SC neurons recorded in the RDM discrimination task. Solid black lines indicate the averaged SDF (α = 20 ms) for Tin trials. Gray lines indicate Tout trials aligned to the onset of the choice targets (A) and the saccade onset (B), indicated by dashed vertical lines. E, F, Same as in A and B, respectively, for the 72 neurons recorded in the Glass pattern detection task. Because neither a stepping nor an accumulation process describes SC activity at the time of saccade, we used Fano factor-guided estimates of ϕ to calculate the VarCE around the time of the visual target and saccade onsets as did Churchland et al. (2011). This method of using the Fano factor as an estimate of the ϕ ensures that the VarCE remains non-negative throughout the trial. The smallest Fano factor was selected as the upper bound of ϕ. C, The VarCE aligned on the time of the visual target onset (dashed vertical line) from the RDM task and (D) aligned on the time of the saccade onset in which the monkeys made Tin choices (black) and Tout choices (gray). The VarCE is calculated using five consecutive 60 ms bins from 150 ms before the saccade onset to 150 ms after. Error bars indicate the SD obtained from bootstrapping. G, Same as in C (and H, same as D), for the Glass pattern detection task.
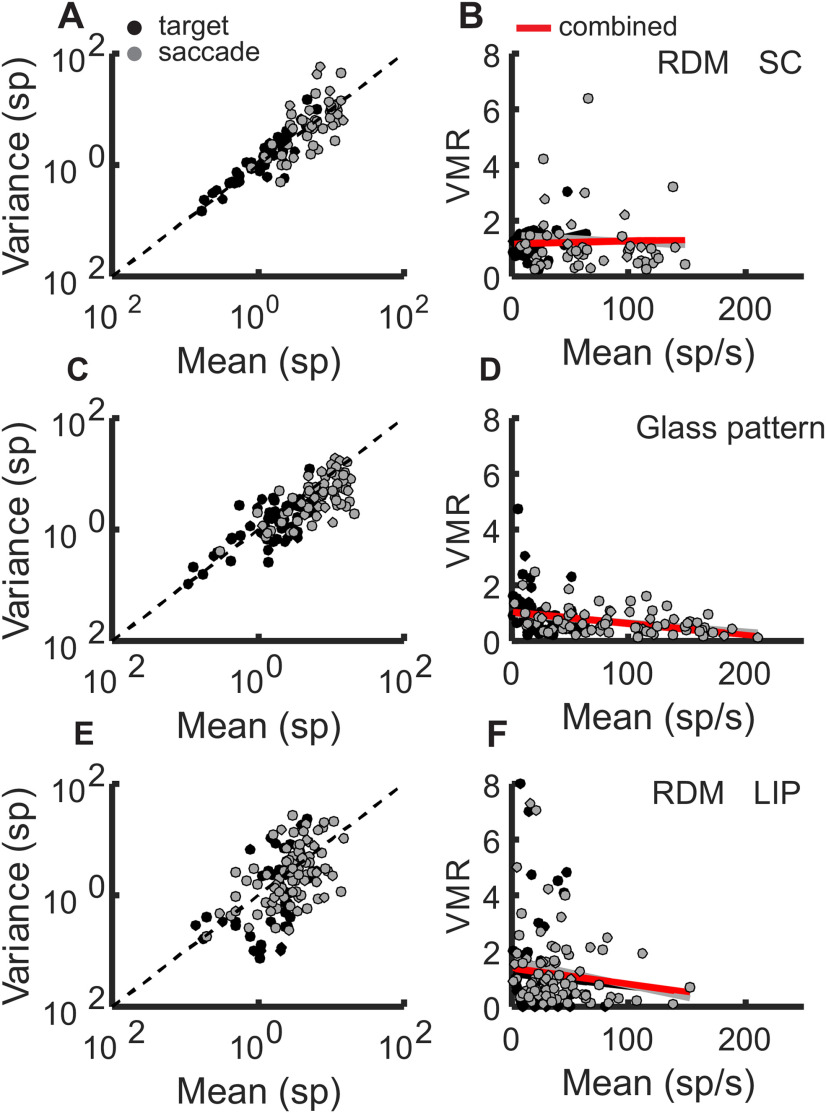
We also assessed the relationship between the spike count variance and the means across spike rate increases to justify our use of a stationary ϕ (Fig. 8). We found that the variance scaled linearly or decreased with the mean during a 100 ms bin around the target onset or saccade for all neurons recorded in both RDM (Fig. 8A,B) and Glass pattern (Fig. 8C,D) tasks. We found the same using LIP data recorded during the RDM task from Roitman and Shadlen, 2002) (Fig. 8E,F). For both target onset and saccade activity, SC neuronal activity increased in mean spike rate, but the variance to mean ratio (VMR) changed little or decreased (Fig. 8B,D,F; compare black and gray circles). If there were a concern about nonlinear increases in PPV, we would expect to see the VMR turn upward with the higher spike rates. Figure 8 shows that, for the data recorded in both the RDM task and the Glass pattern task, the VMR remains stationary or decreases, despite the increases in spike rate. Comparisons of our SC neurons to neurons from area LIP on a similar RDM discrimination task reveal a similarly decreasing VMR with increasing mean rate (Fig. 8E,F). Wilcoxon rank sum over the target onset and saccade VMR revealed no statistically significant differences in the RDM task (p > 0.05) and a statistically significant difference, but decreasing, VMR in the Glass pattern task (p = 0.029).
Figure 8.
The variance to mean relationship is stable over a range of spike rates. A, Spike count variance plotted against the mean spike counts for each neuron in the RDM discrimination task from the SC. n = 49. Black dots indicate the data for the target onset epoch. Gray dots indicate the saccade onset epoch. B, The VMR plotted against the mean rate for each neuron with a line fit to the target onset bins (black), the saccade bins (gray), and a line fit to a dataset consisting of both target onset and saccade (red). Black and gray lines are somewhat obscured by the red line. C, Same as in A, but for the SC neurons from the Glass pattern detection task, n = 72. D, Same as in B, but for the Glass pattern task data. E, F, Same as in A and B, but for a 100 ms time bins around the target onset and the saccade from 809 LIP neurons. LIP data were obtained from Roitman and Shadlen (2002).
As a sanity check, we also jittered spike trains from the original data set to test the hypothesis that a CorCE measured from random spike trains, presumably containing no accumulation or stepping related processes, differ significantly from the CorCEs obtained from the SC data acquired during the RDM and Glass pattern tasks. Spikes trains recorded from the SC were jittered using a 75 ms interval window for the duration of the decision epoch, randomizing the occurrence of the spike within the window (Amarasingham et al., 2012). We then calculated the CorCE for the jittered spike trains using ϕ estimated from theoretical CorCEs. Next, we compared the jittered CorCE to the theoretical CorCE for both accumulation and stepping by calculating the R2 goodness of fit. This process was repeated 1000 times to obtain a distribution of R2 values. The median R2 for the jittered dataset was 0.44, whereas the R2 for the accumulation and stepping processes was 0.711 and 0.798. R2 values from the SC data for both RDM and Glass pattern tasks were greater than all of the jittered R2 values. Therefore, the R2 goodness of fit from the SC data and the jittered data set are significantly different (p < 0.01), indicating that the CorCE using the SC data reveals time varying structure in spike trains that is not present in the jittered spike trains.
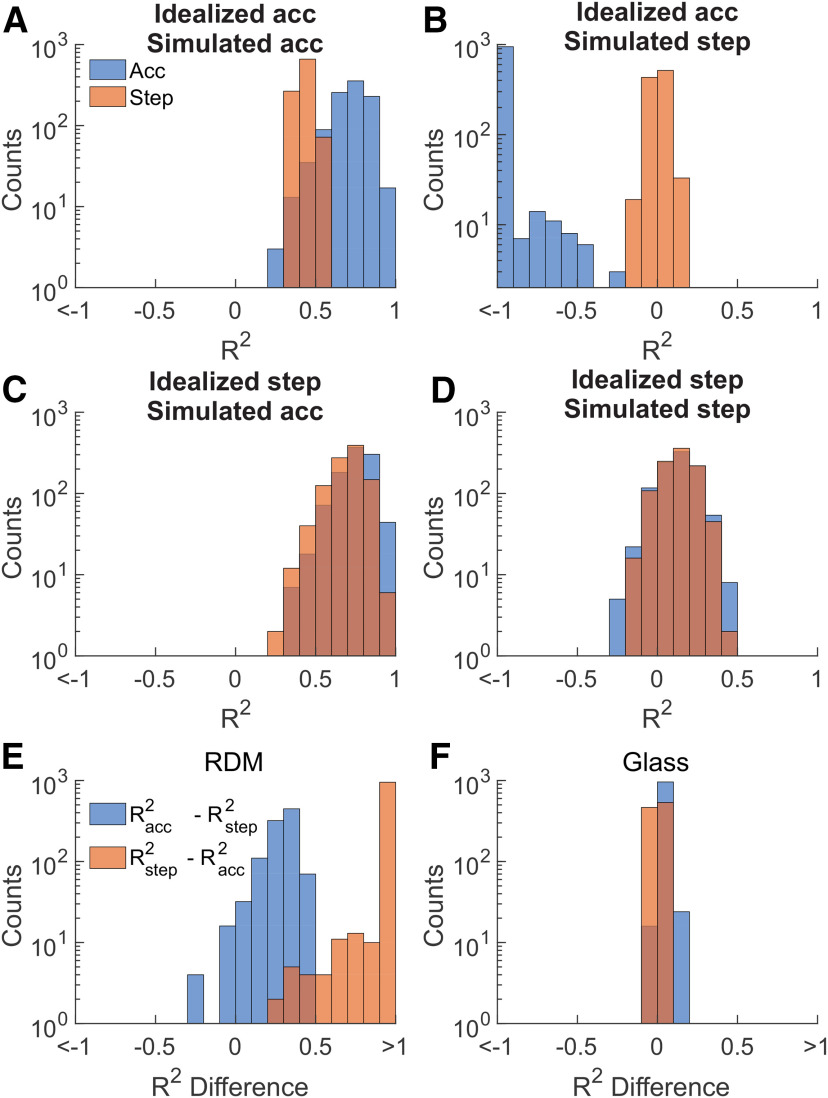
We also performed a series of analyses using simulated spike rates to assess whether comparing the CorCE R2 goodness-of-fit values could reliably select a true underlying model. To do this, we generated an artificial dataset using the same number of neurons, number of trials, and single-trial parameters as in our empirical dataset. Some of the parameters used to generate the rates were preset to create idealized 0% coherence spiking activity (e.g., the starting point set to 0.5 or chance). The remaining parameters were obtained from the parameter fits. Simulated rates were calculated independently for both accumulation and stepping models using RDM or Glass pattern estimated parameters, for a total of four simulated datasets. Each simulated dataset underwent the same procedure used in the analyses shown in Figures 2, 4, and 5, resulting in a pair of R2 distributions for each artificial dataset as the simulated CorCE is fit to either accumulation or stepping (Fig. 9A–D). Statistical testing between each pair of R2 distributions across all four simulated datasets revealed significant differences (idealized accumulation − simulated accumulation: Z = 27.129, p < 0.001; idealized accumulation − simulated stepping: Z = −27.393, p < 0.001; idealized step − simulated accumulation: Z = 27.234, p < 0.001; idealized step − simulated stepping: Z = 2.590, p < 0.010), suggesting that the CorCE is unlikely to misinterpret different models as being the same.
Figure 9.
CorCE classification as applied to simulated rates from accumulation and stepping models using SC parameters determined from empirical data. A, Pairs of R2 distributions obtained by applying the R2 goodness of fit of CorCE analysis on simulated accumulating spikes. Here, the artificial spikes are simulated using parameters estimated from the RDM dataset. The R2 distribution reflects the analysis repeated over 1000 different simulated datasets. The blue distribution was obtained by comparing the simulated data to an idealized accumulation CorCE. The orange distribution is the same using an idealized stepping CorCE. B, Same as in A, but using simulated stepping spikes using parameters from the RDM dataset. C, Same as in A, but using simulated accumulating spikes using parameters from the Glass pattern dataset. D, Same as in A, but using simulated stepping spikes using parameters from the Glass pattern dataset. E, Pairwise differences of R2 vales from the RDM parameterized spikes used in the R2 goodness of fit of CorCE analysis to identify the better fitting model. Blue histogram represents the pairwise R2 differences between the R2 values in A. Orange histogram represents the pairwise R2 differences between the R2 values in B. Difference values >0 indicate that the simulated spikes we correctly categorized as stepping or accumulating. F, Same as in D, but for the Glass pattern parameterized spikes.
A key note, however, is that the comparisons rely on the relative R2 values for the two models. Therefore, we took the pairwise difference between the R2step and R2acc for each simulated dataset to calculate the true positive, true negative, false positive, and false negative rates to then calculate the sensitivity and specificity of the classification processes based on CorCE (Fig. 9E,F). Overall, the sensitivity was 0.757 and specificity was 0.992. However, the RDM dataset had better performance with a sensitivity of 0.979 and specificity of 1.0 compared with the Glass pattern's sensitivity of 0.535 and specificity of 0.983. These values indicate that classification based on relative CorCE R2 goodness-of-fit values is likely to select the true underlying process between the two, under ideal conditions.
In addition to the accumulation and stepping models described above, we performed the same analyses using a recurrent neural network model from the class of dynamical “attractor” models of decision-making developed by Wong et al. (Wong and Wang, 2006; Wong et al., 2007). We selected this model because of its biological plausibility; changes in recurrent weights can shift network activity from accumulation to stepping, and we reasoned this type of mechanism may underlie the differences in the spiking activity of SC neurons in the RDM and Glass pattern tasks. For the accumulation model, we used a lower recurrent weight; and for the stepping model, we used a higher recurrent weight (see Materials and Methods). The VarCE for the RDM task shows a linear rise across both ϕ estimates and regardless of weight (Fig. 10A,B). The SC data CorCE observed for the RDM task revealed higher conformity with the accumulation recurrent weight CorCE (Fig. 10C,D; R2CorCE = 0.848) compared with the stepping recurrent weight CorCE (Fig. 10F,G; R2CorCE = 0.529). Bootstrapping the SSEs revealed a significant difference between the R2CorCE values (Fig. 10C,F; p < 0.001). In the Glass pattern task, the VarCE showed the same transient, early flattening (Fig. 10H,I). And the CorCE conformed less with the accumulation recurrent weight (Fig. 10J,K; R2CorCE = 0.205) than with the stepping recurrent weight (Fig. 10M,N; R2CorCE = 0.696). Bootstrapping the SSEs revealed a significant difference between the R2CorCE values (Fig. 10J,M; p < 0.001).
Figure 10.
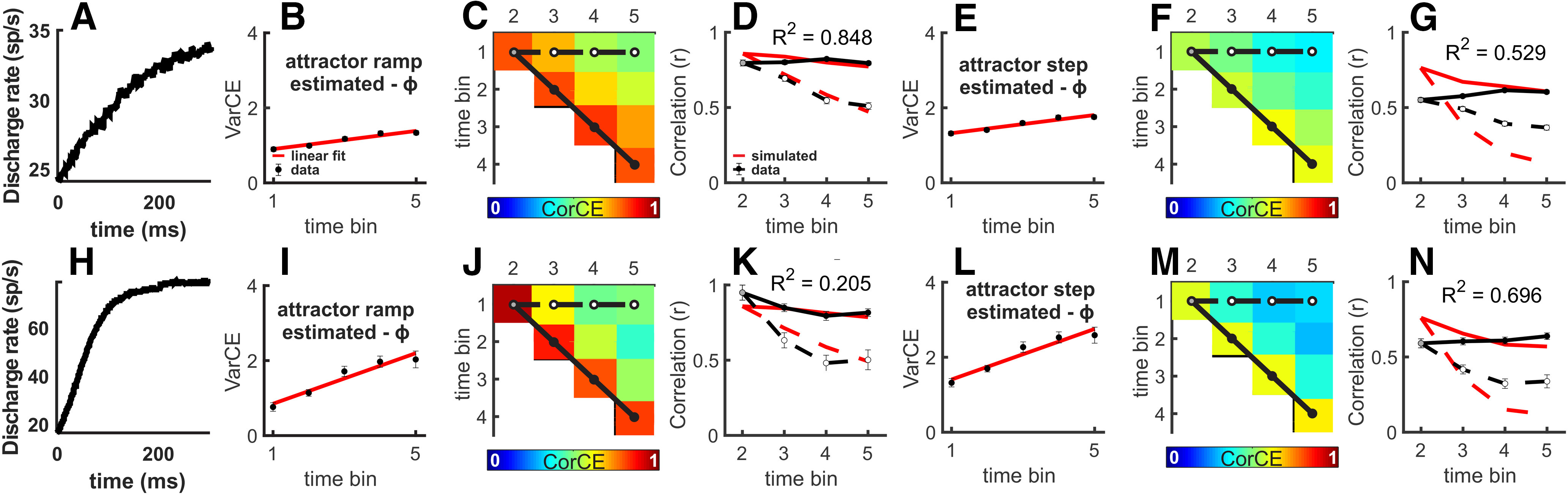
SC spiking during the RDM task is consistent with accumulation and during the Glass pattern task is consistent with stepping using a recurrent neural network model. A, The mean of 10,000 simulated SDFs with recurrent weights produces a ramping process. B-G, Results for the same analyses applied to the RDM task as shown in Figure 5B-G, except for these plots we used the theoretical CorCE from a ramping and stepping attractor process to estimate the ϕ. The R2 values were calculated over all 10 r values. Error bars indicate the SD obtained from bootstrapping. H, Same as in A, except the recurrent weights produce a stepping process. I-N, Results from the same analyses applied to the Glass pattern task as shown in Figure 6B-G, except for these plots we used the theoretical CorCE from a ramping and stepping attractor process to estimate the ϕ. The R2 values were calculated over all 10 r values. Error bars indicate the SD obtained from bootstrapping.
The VarCE and CorCE results using simulated rates from an attractor model (Fig. 10) are consistent with those obtained using predictions from accumulator and stepping models and the DIC and WAIC analyses (Figs. 3–5). Together, these results indicate that the spiking dynamics of SC neurons during the delay period of the RDM discrimination task are more consistent with an accumulation process compared with a stepping process. During the Glass pattern detection task, SC neuronal activity is well explained by an accumulation process but is comparatively more consistent with a stepping process. These differences occurred despite similar trial-averaged ramping activity across tasks and across both monkeys.
Variance measures and the strength of evidence
We used the lowest coherences in the preceding analyses to maximize the length of the decision epoch and therefore the likelihood of observing either an accumulation or stepping process. However, in the presence of stronger sensory evidence, and assuming fixed decision bounds, we expect the decision variable to hit the bound sooner and to remain at the bound for a longer period of time. Therefore, the VarCE might reflect this by decreasing as the strength of the evidence increases. The CorCE should also show decreases with time because the neuronal activity is no longer changing. For a stepping process, the time of the step change from an uncommitted to committed state should occur earlier in time, resulting in a flattening or a decrease of the VarCE with stronger sensory evidence. Also, because the stepping model we implemented estimated step time distributions from parameter fits across coherences (see Materials and Methods) (Latimer et al., 2015), the CorCE fits should be similar across coherences for a stepping process.
We first examined the mean discharge rate in the RDM task plotted over time, and separated for different coherences (Fig. 11A) and the Glass pattern task (Fig. 11F). A curiosity of SC activity that we and others see in some neurons is that the discharge patterns for Tin correct choices associated with different levels of sensory strength show less sensitivity to the strength of sensory evidence than the Tout correct choice discharges (Horwitz and Newsome, 2001; Horwitz et al., 2004; Ratcliff et al., 2007). But because the Tout activity is modulated by sensory evidence, calculating the ROC between the Tin and Tout activities, referred to as the predictive index (Horwitz and Newsome, 2001) (see Materials and Methods), for different coherences shows that the predictive power of the combined activity increases for strong sensory signals and decreases for weaker sensory signals, consistent with signaling the decision (Fig. 11B). LIP often shows similar trial-averaged behavior (Kiani et al., 2008). Figure 11C shows the VarCE sorted by motion coherence during the decision epoch. For all the motion coherences and Tin and Tout choices, with the exception of the 20%/50% coherence Tout choices, the pattern of VarCE is increasing, similar to that seen on average (compare Fig. 11C, solid Tin, dashed Tout and Fig. 4B). The VarCE shows a slow linear rise that decreases in slope with increased coherence, consistent with an accumulation process. Figure 11D shows the peak VarCE, calculated by taking the mean of the VarCE over Tin and Tout choice outcomes for the different coherences, decreases as the strength of the sensory evidence increases (ANOVA F(3,999) = 17,536.56, p < 0.001). The R2CorCE over time also shows a progressive decrease as coherence increases (0%: 0.710; 6%/10%: 0.559; 10%/20%: 0.620; 20%/50%: 0.221; Fig. 11E), consistent with predictions of an accumulation process. At the time of the choice report, when trial-averaged activity is showing large increases in discharge rate associated with the generation of the saccade, the VarCE drops precipitously and equally for Tin and Tout correct choices, a point to which we return in the discussion.
Figure 11.
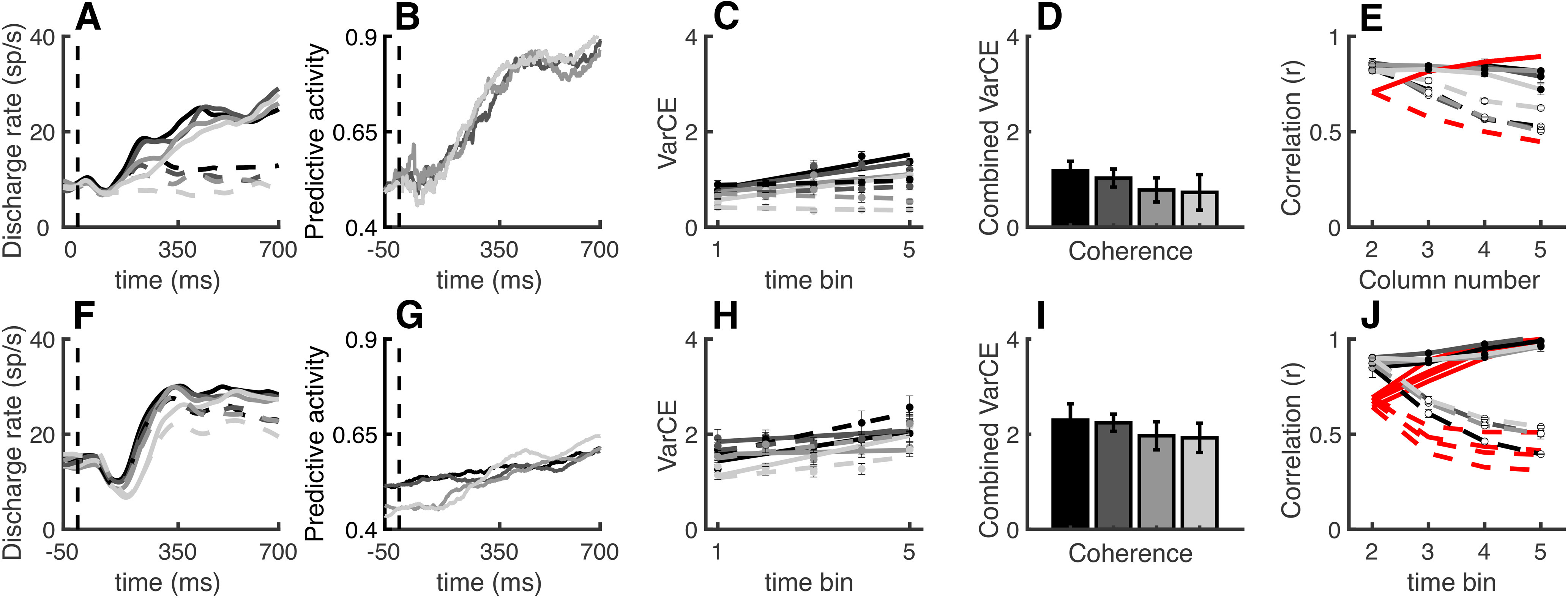
Predictive activity and the VarCE scale with the strength of the sensory evidence. A, The averaged SDF (α = 20 ms) of SC neuronal activity for each coherence is plotted against time and aligned on the onset of the motion cue (vertical dashed line). The strength of the sensory evidence is represented by a grayscale, with lighter gray indicating higher coherence. B, Predictive activity calculated over 100 ms bins, separated by coherence and plotted over time aligned to motion stimulus (vertical dashed line). C, VarCE averaged over 60 ms bins, plotted over time and aligned on the motion cue (vertical dashed line) using ϕ estimates from the best fits to the theoretical accumulation CorCE. In all panels, solid lines indicate Tin trials and dashed lines indicate Tout trials. D, The peak VarCE, calculated by taking the mean of the VarCE over Tin and Tout choices plotted for each coherence. The same grayscale convention is used for the strength of the sensory evidence. Vertical black bars indicate SEM. E, The CorCE of the corresponding VarCE of 0% to 20%-50% coherence trials for the RDM task from A-D. Top row of the CorCE matrix (open circles and fitted lines) and the first juxtadiagonal (filled circles and dashed lines) are shown for the data (black) and theory (red). Error bars indicate SD; some may be obscured by the symbols. F-J, The same results as in A-D, but for the Glass pattern data. G, The VarCE was calculated using the best fit ϕ estimates from the theoretical stepping CorCE.
For most coherences, the predictive index and VarCE calculated across Glass pattern coherences showed a similar trend as seen in the averaged data (compare Fig. 11F,G, solid Tin correct, dashed Tout correct, and Fig. 5B). And the peak VarCE values decreased as the strength of the sensory evidence increased (Fig. 11I; ANOVA F(3,999) = 2194.36, p < 0.001). However, the CorCE remained high for almost all coherences and time points, which is inconsistent with an accumulation process (26%: 0.809; 39%: 0.669; 52%: 0.702; 100%: 0.611; Fig. 11J). Thus, sorting the data by coherences and examining the spike train statistics confirmed the results from the low or no coherence trials; during performance of the Glass pattern task, SC spiking activity is statistically consistent with a stepping process compared with an accumulation process.
SI during decision formation
As an additional test of whether SC activity is better explained by an accumulation or stepping process in the two decision tasks, we also implemented another measure of variability, but one based on within-trial variance rather than across-trial variance. For this, we measured and compared the SI for SC neuronal activity data and for simulated spike trains for accumulation and stepping processes (see Materials and Methods).
Figure 12 shows the distributions of SIs for SC spike trains (blue), simulated accumulation spike trains (red), and simulated stepping spike trains (green). We generated the distributions shown in Figure 12 by a resampling procedure in which we first simulated accumulating and stepping spike trains for the same number of SC neurons recorded in the two tasks. We next calculated SIs for each simulated neuron and classified it as showing accumulation if the SI was not significantly different from 0 (p < 0.05) and stepping if the SI was significantly <0 (p < 0.05). The Poisson process used to generate spike trains from the simulated rates can introduce noise that results in overlapping simulated SI distributions, although the underlying processes differ. To ensure the results were not impacted by this potential noise, the sampling procedure included criteria that resulted in idealized (i.e., nonoverlapping) stepping and accumulating rate distributions. We simulated spike trains using parameters extracted from our empirical SC spike trains. If the neuron passed the criterion, the corresponding empirical SC neuron from which the parameters were sourced was included for analysis. This approach ensured that we would not mistakenly identify simulated spike trains as accumulating when they were indeed stepping, or vice versa. The median SI was calculated from the simulated and subsampled SC neurons, and the process was iterated 1000 times to populate the distributions of SIs shown in Figure 12. This was done because the SI analysis randomly assigns a 0 or 1 to the bin when the spike count of a bin is equivalent to the median. As a result, multiple repetitions of the SI analysis on the same spike train samples result in slight variations in the median SI across repetitions. This method of calculating SIs resulted in variation in the classified samples for each iteration (see Materials and Methods). The median SI for the SC neurons from the RDM task was −0.063, the median SI for simulated stepping was −0.321, and for the simulated accumulation was 0. The median differences (0.063 vs 0.258) were statistically significant (Fig. 12A; Wilcoxon's signed rank, p < 0.001) and indicate that the distribution of SIs for SC spiking data measured during the RDM task is more similar to the distribution of SIs obtained from simulated accumulation than simulated stepping. We observed the opposite pattern for the Glass pattern task. The median SI for the SC data was −0.345, whereas the median of the SI distribution for the simulated accumulation was −0.073 and the simulated stepping was −0.565. The difference in medians between the SC data and the accumulation (0.257) versus the difference in medians between the SC data and the stepping (0.306) was statistically significant (Fig. 12D; Wilcoxon's signed rank, p < 0.001).
Figure 12.
The SI reveals accumulation and stepping in SC neuronal activity. A, Frequency histograms of SIs calculated from SC neuronal spike trains during performance of the RDM task (blue), simulated accumulation spike trains (red), and simulated stepping spike trains (green). Values ∼0 indicate accumulation, and values <0 indicate stepping. Each bar plots the number of neurons, or simulated neurons with a particular SI. Blue line is fit to the SI distribution from the SC spike trains. Data from both monkeys are collapsed. B, C, Same as in A, but separated for individual monkeys: Monkeys P and H. The spikes trains are measured from 204 to 574 ms for Monkey P and 255 to 700 ms for Monkey H after the onset of the motion. D–F, Same as in A-C, but for SC neuronal spike trains during performance of the Glass pattern task (blue), simulated accumulation spike trains (red), and simulated stepping spike trains (green). The spike trains are measured from 209 to 800 for Monkey B and 337 to 800 ms for Monkey S after the onset of the Glass pattern. Values <0 indicate stepping. Downward arrow indicates the median of each distribution color-coded. Vertical dashed line indicates the zero point.
Running the SI analysis for the individual monkeys separately, for both the RDM discrimination task and the Glass pattern detection task, produced the same results as seen in the group data and, notably, were consistent for each monkey in each task (Fig. 12B,C,E,F). Therefore, the differences between the SIs for the RDM and the Glass pattern tasks are unlikely to result from idiosyncratic differences between the monkeys, but rather, reflect real differences in the underlying processes occurring in the two tasks; accumulation for the RDM task and more likely stepping than accumulation in the Glass pattern task.
The underlying process during saccade specification differs from accumulation
It is well known that the SC is involved in saccade generation and is modulated by the likelihood of choosing a particular saccade and that trial-averaged activity shows ramping during simple saccade tasks (Glimcher and Sparks, 1992; Munoz and Wurtz, 1995; Basso and Wurtz, 1998; Dorris and Munoz, 1998; Kim and Basso, 2008). Therefore, it is possible that the changes in spiking variability we measured during these tasks result from processing other than that related to decision-making, such as the saccade specification process, shifts of attention from the fovea to the choice target location, and reward probability. To rule out whether the patterns observed in the VarCE and CorCE arise from decision independent processes, we analyzed the SC spike trains as we did for the decision tasks but for data collected while monkeys performed simple delayed saccades, and in which the saccade target, shift of attention and likelihood of reward were the same as in the decision tasks (Fig. 13A). We used the data recorded from an additional 62 neurons from Monkeys H and P that performed the RDM task. The mean discharge rate of the neurons, aligned to the target onset, showed a sharp increase associated with the onset of the target and then another gradual rise before saccade generation (Fig. 13B). Using a 300 ms epoch 100 ms after target onset, we calculated the VarCE (Fig. 13C) using ϕ estimates derived from a theoretical accumulation CorCE (see Materials and Methods). The VarCE shows an initial dip following target onset, and then remains flat until the onset of the saccade, ∼400 ms after the target onset, at which time it increases. This rise in VarCE occurs because the data are aligned to target onset. When the data are aligned to saccade onset, the VarCE decreases at this time (Fig. 7). We computed R2CorCE comparing the theoretical accumulation CorCE to the SC data over the 10 CorCE data points, which yielded an R2CorCE of 0.296 (Fig. 13D,E). This is consistent with the results from the VarCE and unlike what was found for the RDM discrimination task. Together, the results from the delayed saccade task show that SC neuronal spike train variability during performance of a simple saccade task differs from that measured during performance of a decision task; therefore, the changes measured during the decision tasks likely result from decision-related processes and not saccade preparation, shifts of attention, predictability, or expectation of reward. The results also confirm that trial-averaged ramping activity of SC neurons is insufficient to identify conclusively the underlying processing of neurons and their relationship to behavior and cognition.
Figure 13.
Spiking statistics during simple saccades are not explained by decision processes. A, Schematic of the spatial arrangement of the delayed saccade task in which no evidence accumulation is required. The arrangement is the same as in Figure 1. B, Solid black lines indicate the averaged SDF (α = 20 ms) for SC neuronal activity plotted over time and aligned on the onset of the target (dashed vertical line). n = 62 recorded neurons over 19 sessions from the same 2 monkeys that performed the RDM task. Gray shaded region represents the epoch used for the VarCE and CorCE analyses. Error bars indicate the SD obtained from bootstrapping. C, The VarCE is plotted over time from 100 to 400 ms after target onset using the same data as in B. D, The matrix of CorCE through time displayed as a heat map. Warmer colors represent higher CorCE. The CorCE analysis used the same 60 ms time bins and the same data as in B. E, Comparisons between the CorCE values from the SC data (circles) and the theoretical CorCE (lines) from an accumulation process used to estimate ϕ in D. Top row of the CorCE matrix (filled dots) and the first juxtadiagonal (open dots) are presented. Error bars indicate the SD obtained from bootstrapping and are obscured by the symbols.
Discussion
We described spike train dynamics recorded from SC neurons in monkeys while they performed an RDM direction discrimination task, a Glass pattern orientation detection task, and a simple saccade task. We found that the dynamics of variability in spiking activity of SC neurons during the RDM task show a linear rise and better fits to a theoretical model of accumulation compared with a simulated stepping process. In the Glass pattern detection task, SC spiking activity showed similar rises but also dips or plateaus and better fits to a stepping process than an accumulation process. These differences were consistent across individual monkeys. Finally, although trial-averaged ramping activity showed linear rises, the variance measures of spiking that occurred during the delayed saccade task differed from those measured during either decision task, indicating that the changes in spiking variance during performance of the RDM and Glass pattern tasks is unlikely to reflect attention, saccade specification, or processing related to rewards. These results point out the importance of not relying on trial-averaged activity to infer function. The results further highlight an interesting hypothesis that neurons in the SC play different roles in decision-making depending on the task. For discrimination, SC neurons may play a role in evidence accumulation, whereas for detection, they may play a role in decision commitment (Horwitz and Newsome, 2001; Ratcliff et al., 2003; Crapse et al., 2018). We are currently performing causal experiments to test aspects of this hypothesis.
Relationship to previous findings
Many brain areas are implicated in decision-making, notably the parietal cortex (posterior parietal cortex [PPC] in rodents and LIP/MIP in monkeys) the dorsolateral frontal cortex (FOF in rodents and areas 8 and 46 in monkeys), caudate nucleus (dorsal striatum in rodents), and the SC. Each shows trial-averaged ramping consistent with accumulation culminating in a decision (Schall, 1991; Kim and Shadlen, 1999; Gold and Shadlen, 2000; Horwitz and Newsome, 2001; Roitman and Shadlen, 2002; Ratcliff et al., 2003, 2007; Horwitz et al., 2004; Felsen and Mainen, 2008; Ding, 2015; Hanks et al., 2015; Brody and Hanks, 2016; Yartsev et al., 2018). Although recent work in monkeys and rodents explores single spike trains on decision-making processes (Roitman and Shadlen, 2002; Churchland, et al., 2011; Ding, 2015; de Lafuente et al., 2015; Yartsev et al., 2018), these methods have not been applied to the SC of monkeys as we do here. Evidence for the role of the SC in perceptual decision-making depends on correlations between trial-averaged ramping activity and performance on perceptual decision tasks and comparisons of model generated accumulation profiles with trial-averaged activity ramping profiles of SC neurons (Horwitz and Newsome, 2001; Ratcliff et al., 2003, 2007; Horwitz et al., 2004). However, the assumption that trial-averaged ramping activity reflects a process of evidence accumulation has been called into question (Thura et al., 2012; Latimer et al., 2015), highlighting the need to assess the ramping activity of neurons more rigorously, and importantly, on single trials, as we do here. Comparing spiking data with theoretical predictions and simulated spike trains, we found that SC neurons contain spiking signatures consistent with an accumulation process as well as rapid shifts of decisions, despite similar trial-averaged activity.
The VarCE, CorCE, and SI measures from LIP neurons during RDM performance all show signatures consistent with accumulation. The VarCE in LIP shows a linear rise that plateaus, and at the time of the choice report, declines. Our findings in SC mirror those from area LIP, including the decrease in VarCE around the time of the choice report for Tin trials. In LIP the VarCE for Tin choices drops quickly during the choice report, whereas for Tout choices it drops comparatively slowly and later (Churchland et al., 2011). However, in SC, the VarCE drops precipitously simultaneously for both Tin and Tout choices. Churchland et al. (2011) hypothesized that the Tout decline in LIP neurons reflected accumulation interruption for the losing choice. Our SC results suggest that both processes reach the decision bound synchronously in the SC. From these differences, we speculate that the SC may terminate processing in LIP for Tout choices. In both the caudate and frontal eye field (FEF) of monkeys, the VarCE shows a linear rise and plateau (Ding, 2015). But the rise appears faster and, in the case of the FEF, reaches higher than LIP or the SC early in the decision epoch. Indeed, variance measures from caudate and FEF during the RDM task appear similar to the SC during Glass pattern detection. These differences suggest that the SC is more similar to LIP than the caudate or FEF. This contrasts with rodent findings in which processing in SC appears more related to the FOF (Kopec et al., 2015).
Interestingly, results from the ΔWAIC and ΔDIC scores for SC were consistent, even when including the SoftPlus nonlinearity and history filter described by Zoltowski et al. (2019). That is, none of the ΔDIC labeled stepping SC neurons changed their classification to accumulation based on the ΔWAIC. This result is in marked contrast to reports of LIP neurons, where the WAIC and the DIC result in different classifications for some neurons. Based on these differences between DIC and WAIC in SC and LIP, we hypothesize that the specific implementation of accumulation in SC and LIP may differ. The differences between LIP and SC further motivate the application of these novel methods to other brain regions implicated in decision-making processes.
The measures of variability from SC neurons appear different during the performance of the RDM and Glass pattern tasks, and we interpret this as reflecting different neuronal processing underlying different task requirements. Both the RDM and the Glass pattern tasks are one-interval decision tasks; a single stimulus appears on each trial, and the observer must determine to which of two categories the stimulus belongs. In the RDM task, the observer performs a direction discrimination. In the Glass pattern task, the observer detects whether orientation is present or absent. Because the former task compares between two possibilities, it is referred to as discrimination, whereas the latter compares a stimulus to a null case and is referred to as detection. Whether or not evidence accumulation is required for detection tasks is not well studied, although behavior in such tasks is well explained by a diffusion process. The drift diffusion model of decision-making explains reaction times in a brightness change detection task, and the effects of difficulty that occur from variations in stimulus contrast are well captured by the drift rate parameter of the model, consistent with a type of evidence accumulation at least for the difficult trials (Ratcliff and Van Dongen, 2011). Our results are less consistent with a process of accumulation for the Glass pattern task, at least at the level of the SC. The differences are unlikely to stem from differences in visual stimuli (form vs motion), although motion cues and Glass patterns activate both overlapping and nonoverlapping regions of visual cortex (Krekelberg et al., 2003, 2005; Smith et al., 2007; Lestou et al., 2014). The dynamic Glass patterns contain noisy sensory evidence that varies over time as does the motion cue in the RDM task. Like the motion cue, Glass patterns give rise to global orientation percepts through sparse local cues (Glass, 1969; Smith et al., 2002, 2007), and the difficulty of the orientation detection varies with coherence just as is done for motion in the RDM task. Thus, noisy samples of sensory evidence occur in both tasks. The key difference between the tasks, therefore, is the decision strategy used for discrimination versus detection. Moreover, since the results were the same in the 2 monkeys that performed the Glass pattern task and the 2 monkeys that performed the RDM task, the differences are unlikely to result from monkey idiosyncrasies.
One concern, however, is that the tasks differed in ways other than just discrimination and detection. For example, the cue stimulus presence during the delay period and timings differed between the tasks, which may impact the monkeys' training history and thus strategy for performing the tasks. Moreover, the datasets from the RDM task were collected during performance of a confidence task and the Glass pattern task dataset were part of an experiment that manipulated priors. To mitigate concerns about timing, we used a principled and model-free approach to define a decision epoch used for all analyses, similarly across all monkeys and tasks. Moreover, we used control trials from both tasks mitigating concerns about confidence trials or prior manipulations (Crapse et al., 2018; Grimaldi et al., 2018; Odegaard et al., 2018). Despite all these differences, the trial-averaged activity was remarkably similar, showing ramping activity in both tasks and across both pairs of monkeys and even during a delayed saccade task. Even if differences in the monkeys' strategy occurred because of these other reasons, the differences are not as apparent in the trial-averaged activity than they are in the single-trial spiking dynamics. We think that the similarity in trial-averaged activity is a key reason why the analytical effort we engaged in here is so important. It is possible that the monkeys are not engaged in a process of accumulation, yet the trial-averaged responses look as though they are, even in the delayed saccade task, which is how these neurons received their name (Glimcher and Sparks, 1992; Munoz and Wurtz, 1995).
Placing the SC in decision-making circuits
Although a number of areas in the brain contain accumulation signatures from trial-averaged spike rate measures, their precise role within the decision-making circuit is only recently coming to light. These insights result from the measures described in this report as well as causal manipulations in brain areas implicated in decision-making. Causal manipulations in monkeys and rodents reveal a circuit involved in different aspects of decision-making. Stimulation of the FEF in monkeys during the RDM viewing period results in deviations of electrically evoked saccades depending on the decision report (Gold and Shadlen, 2000). These findings provide evidence for shared circuitry between evidence accumulation and motor preparation. Similar rat experiments have used halorhodopsin to inactivate the FOF during the Poisson clicks task, an auditory discrimination task dependent on an accumulation process (Brunton et al., 2013; Erlich et al., 2015; Hanks et al., 2015). Inactivation of FOF late in the decision epoch biases performance toward decisions to the inactivated hemifield. These results indicate that the FOF of rodents participates at a stage after accumulation, when the sensory evidence is converted into a categorical decision. A role for the FEF in processes occurring after accumulation is consistent with experiments performed in monkey (Ferrera et al., 2009) and may be reflected in the VarCE measures (Ding, 2015).
Area LIP of the monkey and the PPC of rodents show response properties consistent with sensory evidence accumulation. Stimulation of monkey LIP produces more and faster choices to the stimulated hemifield to and fewer and slower choices to the nonstimulated hemifield (Hanks et al., 2006). However, a recent study showed that inactivation of LIP with muscimol fails to alter decision-making performance (Katz et al., 2016; Zhou and Freedman, 2019). In the rodent, activation or inactivation of PPC fails to alter decision-making performance on the auditory Poisson clicks tasks (Erlich et al., 2015; Licata et al., 2017). However, activation of PPC alters decision performance of a visual equivalent, but inconsistently with accumulation (Licata et al., 2017). Whatever the role of LIP, our results provide evidence that SC neurons support accumulation in the RDM discrimination task and stepping in the Glass pattern detection task. These results highlight important caveats in decision-making studies: (1) trial-averaged activity correlations with behavior are insufficient to reveal the role of a brain area; and (2) it is critical to know the monkeys' strategy while performing a given cognitive task, as neurons even in areas just a few synapses from motor neurons, such as the SC, may change their contribution depending on task demands.
Footnotes
This work was supported by National Institutes of Health EY013962 to M.A.B. and Neural Microcircuits Training Program at UCLA postdoctoral fellowship T32NS05820-07 to T.C. We thank Adam Myers for outstanding animal care; Dr. Michael N. Shadlen for providing critical comments and advice on a previous version of the manuscript; Drs. Anne K. Churchland and Kenneth W. Latimer for helpful discussions and sharing MATLAB code; and Dr. Matthew Smith for helpful discussions.
The authors declare no competing financial interests.
References
- Amarasingham A, Harrison MT, Hatsopoulos NG, Geman S (2012) Conditional modeling and the jitter method of spike resampling. J Neurophysiol 107:517–531. 10.1152/jn.00633.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basso MA, Wurtz RH (1998) Modulation of neuronal activity in superior colliculus by changes in target probability. J Neurosci 18:7519–7534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basso MA, May PJ (2017) Circuits for action and cognition: a view from the superior colliculus. Annu Rev Vis Sci 3:197–226. 10.1146/annurev-vision-102016-061234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennur S, Gold JI (2011) Distinct representations of a perceptual decision and the associated oculomotor plan in the monkey lateral intraparietal area. J Neurosci 31:913–921. 10.1523/JNEUROSCI.4417-10.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollimunta A, Totten D, Ditterich J (2012) Neural dynamics of choice: single-trial analysis of decision-related activity in parietal cortex. J Neurosci 32:12684–12701. 10.1523/JNEUROSCI.5752-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brody CD, Hanks TD (2016) Neural underpinnings of the evidence accumulator. Curr Opin Neurobiol 37:149–157. 10.1016/j.conb.2016.01.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunton BW, Botvinick MM, Brody CD (2013) Rats and humans can optimally accumulate evidence for decision-making. Science 340:95–98. 10.1126/science.1233912 [DOI] [PubMed] [Google Scholar]
- Chandrasekaran C, Soldado-Magraner J, Peixoto D, Newsome WT, Shenoy KV, Sahani M (2018) Brittleness in model selection analysis of single neuron firing rates. bioRxiv. doi: 10.1101/430710. [DOI] [Google Scholar]
- Churchland AK, Kiani R, Chaudhuri R, Wang XJ, Pouget A, Shadlen MN (2011) Variance as a signature of neural computations during decision making. Neuron 69:818–831. 10.1016/j.neuron.2010.12.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crapse TB, Lau H, Basso MA (2018) A role for the superior colliculus in decision criteria. Neuron 97:181–194.e6. 10.1016/j.neuron.2017.12.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crist CF, Yamasaki DS, Komatsu H, Wurtz RH (1988) A grid system and a microsyringe for single cell recording. J Neurosci Methods 26:117–122. [DOI] [PubMed] [Google Scholar]
- de Lafuente V, Jazayeri M, Shadlen MN (2015) Representation of accumulating evidence for a decision in two parietal areas. J Neurosci 35:4306–4318. 10.1523/JNEUROSCI.2451-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding L (2015) Distinct dynamics of ramping activity in the frontal cortex and caudate nucleus in monkeys. J Neurophysiol 114:1850–1861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding L, Gold JI (2010) Caudate encodes multiple computations for perceptual decisions. J Neurosci 30:15747–15759. 10.1523/JNEUROSCI.2894-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding L, Gold JI (2012) Separate, causal roles of the caudate in saccadic choice and execution in a perceptual decision task. Neuron 75:865–874. 10.1016/j.neuron.2012.07.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorris MC, Munoz DP (1998) Saccadic probability influences motor preparation signals and time to saccadic initiation. J Neurosci 18:7015–7026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erlich JC, Brunton BW, Duan CA, Hanks TD, Brody CD (2015) Distinct effects of prefrontal and parietal cortex inactivations on an accumulation of evidence task in the rat. Elife 4:e05457. 10.7554/eLife.05457 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsen G, Mainen ZF (2008) Neural substrates of sensory-guided locomotor decisions in the rat superior colliculus. Neuron 60:137–148. 10.1016/j.neuron.2008.09.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrera VP, Yanike M, Cassanello C (2009) Frontal eye field neurons signal changes in decision criteria. Nat Neurosci 12:1458–1462. 10.1038/nn.2434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs AF, Robinson DA (1966) A method for measuring horizontal and vertical eye movement chronically in the monkey. J Appl Physiol 21:1068–1070. 10.1152/jappl.1966.21.3.1068 [DOI] [PubMed] [Google Scholar]
- Glass L (1969) Moiré effect from random dots. Nature 223:578–580. 10.1038/223578a0 [DOI] [PubMed] [Google Scholar]
- Glimcher PW, Sparks DL (1992) Movement selection in advance of action in the superior colliculus. Nature 355:542–545. 10.1038/355542a0 [DOI] [PubMed] [Google Scholar]
- Gelman A, Hwang J, Vehtari A (2014) Understanding prediction information criteria for Bayesian models. Stat Comput 24:997–1916. 10.1007/s11222-013-9416-2 [DOI] [Google Scholar]
- Gold JI, Shadlen MN (2000) Representation of a perceptual decision in developing oculomotor commands. Nature 404:390–394. 10.1038/35006062 [DOI] [PubMed] [Google Scholar]
- Grimaldi P, Cho SH, Lau H, Basso MA (2018) Superior colliculus signals decisions rather than confidence: analysis of single neurons. J Neurophysiol 120:2614–2629. 10.1152/jn.00152.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks TD, Ditterich J, Shadlen MN (2006) Microstimulation of macaque area LIP affects decision-making in a motion discrimination task. Nat Neurosci 9:682–689. 10.1038/nn1683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks TD, Kopec CD, Brunton BW, Duan CA, Erlich JC, Brody CD (2015) Distinct relationships of parietal and prefrontal cortices to evidence accumulation. Nature 520:220–223. 10.1038/nature14066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Coen P, Tank DW (2012) Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484:62–68. 10.1038/nature10918 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hays AV Jr, Richmond BJ, Optican LM (1982) Unix-based multiple-process system, for real-time data acquisition and control. WESCON Conf Proc. 2:1–10. [Google Scholar]
- Horwitz GD, Newsome WT (2001) Target selection for saccadic eye movements: prelude activity in the superior colliculus during a direction-discrimination task. J Neurophysiol 86:2543–2558. 10.1152/jn.2001.86.5.2543 [DOI] [PubMed] [Google Scholar]
- Horwitz GD, Batista AP, Newsome WT (2004) Representation of an abstract perceptual decision in macaque superior colliculus. J Neurophysiol 91:2281–2296. 10.1152/jn.00872.2003 [DOI] [PubMed] [Google Scholar]
- Judge SJ, Richmond BJ, Chu FC (1980) Implantation of magnetic search coils for measurement of eye position: an improved method. Vision Research 20:535–538. [DOI] [PubMed] [Google Scholar]
- Katz LN, Yates JL, Pillow JW, Huk AC (2016) Dissociated functional significance of decision-related activity in the primate dorsal stream. Nature 535:285–288. 10.1038/nature18617 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiani R, Hanks TD, Shadlen MN (2008) Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J Neurosci 28:3017–3029. 10.1523/JNEUROSCI.4761-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim B, Basso MA (2008) Saccade target selection in the superior colliculus: a signal detection theory approach. J Neurosci 28:2991–3007. 10.1523/JNEUROSCI.5424-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim B, Basso MA (2010) A probabilistic strategy for understanding action selection. J Neurosci 30:2340–2355. 10.1523/JNEUROSCI.1730-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim JN, Shadlen MN (1999) Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat Neurosci 2:176–185. 10.1038/5739 [DOI] [PubMed] [Google Scholar]
- Kopec CD, Erlich JC, Brunton BW, Deisseroth K, Brody CD (2015) Cortical and subcortical contributions to short-term memory for orienting movements. Neuron 88:367–377. 10.1016/j.neuron.2015.08.033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krauzlis RJ, Lovejoy LP, Zénon A (2013) Superior colliculus and visual spatial attention. Annu Rev Neurosci 36:165–182. 10.1146/annurev-neuro-062012-170249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krekelberg B, Vatakis A, Kourtzi Z (2005) Implied motion from form in the human visual cortex. J Neurophysiol 94:4373–4386. 10.1152/jn.00690.2005 [DOI] [PubMed] [Google Scholar]
- Krekelberg B, Dannenberg S, Hoffmann KP, Bremmer F, Ross J (2003) Neural correlates of implied motion. Nature 424:674–677. 10.1038/nature01852 [DOI] [PubMed] [Google Scholar]
- Latimer KW, Yates JL, Meister ML, Huk AC, Pillow JW (2015) NEURONAL MODELING: single-trial spike trains in parietal cortex reveal discrete steps during decision-making. Science 349:184–187. 10.1126/science.aaa4056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lestou V, Lam JM, Humphreys K, Kourtzi Z, Humphreys GW (2014) A dorsal visual route necessary for global form perception: evidence from neuropsychological fMRI. J Cogn Neurosci 26:621–634. 10.1162/jocn_a_00489 [DOI] [PubMed] [Google Scholar]
- Licata AM, Kaufman MT, Raposo D, Ryan MB, Sheppard JP, Churchland AK (2017) Posterior parietal cortex guides visual decisions in rats. J Neurosci 37:4954–4966. 10.1523/JNEUROSCI.0105-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazurek ME, Roitman JD, Ditterich J, Shadlen MN (2003) A role for neural integrators in perceptual decision making. Cereb Cortex 13:1257–1269. 10.1093/cercor/bhg097 [DOI] [PubMed] [Google Scholar]
- McPeek RM, Keller EL (2002) Saccade target selection in the superior colliculus during a visual search task. J Neurophysiol 88:2019–2034. 10.1152/jn.2002.88.4.2019 [DOI] [PubMed] [Google Scholar]
- Munoz DP, Wurtz RH (1995) Saccade-related activity in monkey superior colliculus: I. Characteristics of burst and buildup cells. J Neurophysiol 73:2313–2333. 10.1152/jn.1995.73.6.2313 [DOI] [PubMed] [Google Scholar]
- Nankoo JF, Madan CR, Spetch ML, Wylie DR (2012) Perception of dynamic Glass patterns. Vision Res 72:55–62. 10.1016/j.visres.2012.09.008 [DOI] [PubMed] [Google Scholar]
- Odegaard B, Grimaldi P, Cho SH, Peters MA, Lau H, Basso MA (2018) Superior colliculus neuronal ensemble activity signals optimal rather than subjective confidence. Proc Natl Acad Sci USA 115:1588–1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G (2008) The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput 20:873–922. 10.1162/neco.2008.12-06-420 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN (1998) Modeling response times for two-choice decisions. Psychol Sci 9:347–356. 10.1111/1467-9280.00067 [DOI] [Google Scholar]
- Ratcliff R, Cherian A, Segraves M (2003) A comparison of macaque behavior and superior colliculus neuronal activity to predictions from models of two-choice decisions. J Neurophysiol 90:1392–1407. 10.1152/jn.01049.2002 [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Hasegawa YT, Hasegawa RP, Smith PL, Segraves MA (2007) Dual diffusion model for single-cell recording data from the superior colliculus in a brightness-discrimination task. J Neurophysiol 97:1756–1774. 10.1152/jn.00393.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Van Dongen HPA (2011) Diffusion model for one-choice reaction-time tasks and the cognitive effects of sleep deprivation. PNAS 108:11285–11290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roitman JD, Shadlen MN (2002) Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J Neurosci 22:9475–9489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schall JD (1991) Neuronal activity related to visually guided saccades in the frontal eye fields of rhesus monkeys: comparison with supplemental eye fields. J Neurophysiol 66:559–579. 10.1152/jn.1991.66.2.559 [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT (1996) Motion perception:seeing and deciding. PNAS 93:628–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT (2001) Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J Neurophysiol 86:1916–1936. 10.1152/jn.2001.86.4.1916 [DOI] [PubMed] [Google Scholar]
- Smith MA, Bair W, Movshon JA (2002) Signals in macaque striate cortical neurons that support the perception of Glass patterns. J Neurosci 22:8334–8345. 10.1523/JNEUROSCI.22-18-08334.2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Kohn A, Movshon JA (2007) Glass pattern responses in macaque V2 neurons. J Vis 7:5. 10.1167/7.3.5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thevarajah D, Mikulić A, Dorris MC (2009) Role of the superior colliculus in choosing mixed-strategy saccades. J Neurosci 29:1998–2008. 10.1523/JNEUROSCI.4764-08.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thura D, Beauregard-Racine J, Fradet CW, Cisek P (2012) Decision making by urgency gating: theory and experimental support. J Neurophysiol 108:2912–2930. 10.1152/jn.01071.2011 [DOI] [PubMed] [Google Scholar]
- Wong KF, Wang XJ (2006) A recurrent network mechanism of time integration in perceptual decisions. J Neurosci 26:1314–1328. 10.1523/JNEUROSCI.3733-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong KF, Huk AC, Shadlen MN, Wang XJ (2007) Neural circuit dynamics underlying accumulation of time-varying evidence during perceptual decision making. Front Comput Neurosci 1:6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yartsev MM, Hanks TD, Yoon AM, Brody CD (2018) Causal contribution and dynamical encoding in the striatum during evidence accumulation. Elife 7:e34929. 10.7554/eLife.34929 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Y, Freedman DJ (2019) Posterior parietal cortex plays a causal role in perceptual and categorical decisions. Science 365:180–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zoltowski DM, Latimer KW, Yates JL, Huk AC, Pillow JW (2019) Discrete stepping and nonlinear ramping dynamics underlie spiking responses of LIP neurons during decision-making. Neuron 102:1249–1258. 10.1016/j.neuron.2019.04.031 [DOI] [PubMed] [Google Scholar]