Abstract
In recent years, due to the difficulty and inefficiency of experimental methods, numerous computational methods have been introduced for inferring the structure of Gene Regulatory Networks (GRNs). The Path Consistency (PC) algorithm is one of the popular methods to infer the structure of GRNs. However, this group of methods still has limitations and there is a potential for improvements in this field. For example, the PC-based algorithms are still sensitive to the ordering of nodes i.e. different node orders results in different network structures. The second is that the networks inferred by these methods are highly dependent on the threshold used for independence testing. Also, it is still a challenge to select the set of conditional genes in an optimal way, which affects the performance and computation complexity of the PC-based algorithm. We introduce a novel algorithm, namely Order Independent PC-based algorithm using Quantile value (OIPCQ), which improves the accuracy of the learning process of GRNs and solves the order dependency issue. The quantile-based thresholds are considered for different orders of CMI tests. For conditional gene selection, we consider the paths between genes with length equal or greater than 2 while other well-known PC-based methods only consider the paths of length 2. We applied OIPCQ on the various networks of the DREAM3 and DREAM4 in silico challenges. As a real-world case study, we used OIPCQ to reconstruct SOS DNA network obtained from Escherichia coli and GRN for acute myeloid leukemia based on the RNA sequencing data from The Cancer Genome Atlas. The results show that OIPCQ produces the same network structure for all the permutations of the genes and improves the resulted GRN through accurately quantifying the causal regulation strength in comparison with other well-known PC-based methods. According to the GRN constructed by OIPCQ, for acute myeloid leukemia, two regulators BCLAF1 and NRSF reported previously are significantly important. However, the highest degree nodes in this GRN are ZBTB7A and PU1 which play a significant role in cancer, especially in leukemia. OIPCQ is freely accessible at https://github.com/haammim/OIPCQ-and-OIPCQ2.
Subject terms: Gene regulatory networks, Bayesian inference, Regulatory networks
Introduction
Identifying regulations between genes is an important issue for better understanding the biological processes1–4. It provides information on what genes of particular interest are over-expressed or under-expressed by different environmental conditions. Experimental methods for inference of Gene Regulatory Networks (GRN) are expensive, tedious, time-consuming and sometimes not reproducible. Recently, gene expression data is accessible through high-throughput sequencing technologies, which provides an insight on the regulatory mechanism1,3,5–7. In GRN, genes are denoted as nodes while the goal is to detect interactions between them, referred to as edges. Computational methods developed to reconstruct GRNs are generally categorized in either machine-learning-based or model-based methods8–35. In literature, Pearson correlation coefficients36,37 and information theory5,16,19–27,29–32 are widely used to measure the regulation strength between genes. Both information theory and Pearson correlation coefficient can infer large-scale networks, but Mutual Information (MI) has the capability to measure non-linear dependencies which is a suitable measure to distinguish the relation between genes36,38. The Path Consistency (PC) method and its improvements (PC-based methods) are used for inferring the structure of GRN. PC-based methods such as Fast Causal Inference (FCI), Really Fast Causal Inference (RFCI), PC Algorithm based on Conditional Mutual Information (PCA-CMI) and their modifications25,39–46 have two common drawbacks. The first is that these methods are not consistent for different sequential node orders47. The second is that the networks inferred by these methods are highly dependent on the threshold used for independence testing. Consensus Network (CN)16, introduced Sequential ORDERing (SORDER) algorithm to selects a suitable sequential ordering of genes. It also improves the accuracy of the obtained results by taking the consensus of different networks. Zhang et al.19 introduced Conditional Mutual Inclusive Information (CMI2), which improves the GRN skeleton by utilizing interventional probability and Kullback–Leibler (KL) divergence. One of the issues so far unresolved in the literature is the order-dependency restriction of the algorithms, which the current work aims to address. Also, in conditional-independent tests, the proper selection of a collection of nodes which contains the separator sets significantly influences the performance of constraint-based methods. In the proposed method, a strategy for an effective selection of nodes based on existing paths between any pair of genes is devised in order to improve the network results. Also, our method is an order independent algorithm to reconstruct GRNs from gene expression data to overcome restrictions of order-dependent algorithms. The rest of the paper is organized as follows: Section Preliminaries is related to the details of MI, CMI, CMI2, PCA-CMI, and CMI2NI algorithm. In section Results, the results of OIPCQ on the Dialogue for Reverse Engineering Assessments and Methods (DREAM) challenges and the SOS DNA network in Escherichia coli were compared with the results of three state-of-the-art approaches including PCA-CMI, CN and CMI2NI. Finally, a case study was provided to evaluate the performance of OIPCQ for inferring a network of Acute Myeloid Leukemia (AML). The gene expression data is available in The Cancer Genome Atlas (TCGA) website at http://cancergenome.nih.gov/. The discussion and some possible further works are presented in Section Discussion. In section Methods, the drawbacks of PC-based algorithms and the details of OIPCQ Algorithm are presented.
Preliminaries
Mutual information and conditional mutual information
Both MI and CMI are proven to be effective for inferring GRNs due to their capability to measure nonlinear dependencies between variables48. MI and CMI between the variables X and Y, given the vector of variables Z, are defined as follows49,50:
| 1 |
| 2 |
where p is the dimension of vector Z and p(x, y), p(x) and p(y) represent the joint distribution of X and Y, marginal distribution of X, marginal distribution of Y, respectively. , , and indicate joint distribution of X, Y and , the conditional density distribution of X and Y given , the conditional density distribution of X given and the conditional density distribution of Y given , respectively. Under the assumption that gene expression data follows a Gaussian distribution, MI for two continuous variables X and Y can be calculated as:
| 3 |
where , and indicate the variance of X, the variance of Y and the covariance between X and Y, respectively. When X and Y are independent, then . Similarly, is defined as:
| 4 |
where C is the covariance matrix and |.| is the determinant of matrix C. In which C(X,Y) and C(X,Y, Z) denote the covariance matrix of variables X and Y and variables X,Y and Z, respectively. When X and Y are conditionally independent given Z, then .
Conditional mutual inclusive information (CMI2)
The CMI2 uses both KL divergence and interventional and is defined as:
| 5 |
where p(x, y, z) is the joint probability distribution of X, Y and Z, and are the interventional probability distributions of X, Y and Z for removing edges and , respectively. and are KL divergences from P to , and from P to , respectively. Similar to CMI, the order of CMI2 is equal to the size of Z (|Z|).
PC algorithm based on conditional mutual information (PCA-CMI)
In PCA-CMI25, a network is initiated with a completely undirected graph. Then, through an iterative process, the skeleton gets updated as edges are removed based on the results of the independent tests between adjacent nodes. Finally, the algorithm makes the skeleton which is fully undirected.
Let be a skeleton of ith order with i starting from . So, denotes a completely undirected graph from which the algorithm starts. For two adjacent nodes X and Y in , a set is defined where ADJ(X) being a set of adjacent vertices of X in . is calculated for each i-subset of . For calculating MI(X, Y) and , Eqs. (3) and (4) are used respectively. For removing the edge between two adjacent nodes X and Y in , as and as the threshold for independent test are considered. The edges for which are removed from .
CMI2NI: GRN inference method based on CMI2
Given an expression dataset with n genes and m samples, CMI2NI infers its underlying GRN. In CMI2NI, after obtaining MI and CMI2 with Eqs. (3) and (5), the PCA-CMI algorithm was used to remove the (conditional) indirect edges from the complete graph. GRN inference is performed by removing those edges without strong causal regulations recursively until there is no change in the network topology. For more details of the CMI2NI algorithm, see19.
Results
In this section, the performance of OIPCQ and OIPCQ2 are benchmarked against other well-known methods (PCA-CMI, CN and CMINI) using both simulated (DREAM project) and real data (SOS DNA and AML). The DREAM project is an in silico network challenge introduced in 2006. In this work, we used DREAM3 and DREAM4 datasets. DREAM3 contains three sub-challenges of size 10, 50 and 100 genes. Each sub-challenge contains five gold standard networks (Ecoli1, Ecoli2, Yeast1, Yeast2 and Yeast3) and for each, there are three gene expression sets (heterozygous knockdown, null-mutants (steady state) and trajectories (time courses)). Among these sets, Yeast1, which is a steady-state dataset, is used. DREAM4 contains three sub-challenges of size 10, 100 and 100-multifactorial, among which, we have used all five networks of the 100-multifactorial sub-challenge. The five gold standard networks of the 100-multifactorial sub-challenge have 100 genes and they have 176, 249, 195, 211 and 193 gold standard links, respectively. To benchmark the performance of OIPCQ and OIPCQ2 against well-known algorithms, True Positive (TP), False Positive (FP), True Positive Rate (TPR), Positive Predictive Value (PPV), False Positive Rate (FPR), False Discovery Rate (FDR), overall ACCuracy (ACC), F-measure and Matthews Correlation Coefficient (MCC) are calculated. They are defined as follows:
Results for DREAM3
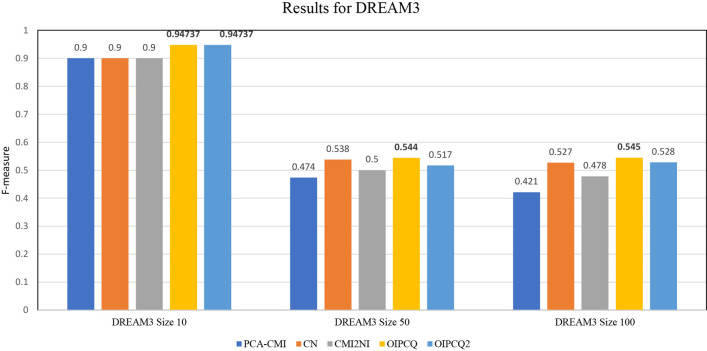
On the DREAM3 datasets, OIPCQ with two thresholds ( for MI and for CMI) were implemented and compared with PCA-CMI, CN and CMI2NI. For OIPCQ and OIPCQ2 the same parameters ( and ) are considered. For PCA-CMI and CMI2NI algorithms one parameter is considered. CN algorithm requires two thresholds, one for producing a consensus network () and interval threshold for independent tests (). The selected thresholds for the mentioned methods are selected based on receiver operating characteristic (ROC) curve. These thresholds are shown in Table 1. The benchmark results for DREAM3 are summarized in Tables 2, S1 and S2 in Supplementary file. The F-measure values for mentioned algorithms are illustrated in Fig. 1. The results show that OIPCQ and OIPCQ2 consistently perform better than all other algorithms in terms of PPV, ACC, MCC and F-measure criteria. OIPCQ and OIPCQ2 algorithms were benchmarked with CMI2NI using DREAM3 datasets with sizes 10, 50 and 100. In all sizes, OIPCQ and OIPCQ2 had better performance compared to CMI2NI in terms of F-measure criteria. For size 10, FP was improved from 1 to 0 with no change in TP. For size 50, FP was decreased from 40 to 30 and TP was increased from 39 to 40. For size 100, FP was changed from 38 to 34 and TP was improved from 64 to 75.
Table 1.
Threshold values for methods used on three sets of DREAM3-Yeast1-null-mutant dataset.
| Algorithm | Dataset | ||
|---|---|---|---|
| 10 genes, 10 edges | 50 genes, 77 edges | 100 genes, 166 edges | |
| PCA-CMI | 0.03 | 0.03 | 0.05 |
| 0.6 | 0.6 | 0.6 | |
| (0.02 , 0.05) | (0.02 , 0.05) | (0.03 , 0.05) | |
| CMI2NI | 0.03 | 0.04 | 0.06 |
| 0.05 | 0.02 | 0.03 | |
| 0.01 | 0.05 | 0.05 | |
Table 2.
Results for DREAM3-size10-Yeast1.
| Algorithm | TP | FP | PPV | TPR | ACC | F-measure | FPR | FDR | MCC |
|---|---|---|---|---|---|---|---|---|---|
| PCA-CMI | 9 | 1 | 0.9 | 0.9 | 0.95556 | 0.9 | 0.02857 | 0.1 | 0.87143 |
| CN | 9 | 1 | 0.9 | 0.9 | 0.95556 | 0.9 | 0.02857 | 0.1 | 0.87143 |
| CMI2NI | 9 | 1 | 0.9 | 0.9 | 0.95556 | 0.9 | 0.02857 | 0.1 | 0.87143 |
| OIPCQ | 9 | 0 | 1 | 0.9 | 0.97778 | 0.94737 | 0 | 0 | 0.93541 |
| OIPCQ2 | 9 | 0 | 1 | 0.9 | 0.97778 | 0.94737 | 0 | 0 | 0.93541 |
Best results are indicated in bold.
Figure 1.
Comparison of F-measure values of OIPCQ and OIPCQ2 algorithms with other methods for learning DREAM3 Challenge with 10 genes, DREAM3 Challenge with 50 gene and DREAM3 Challenge with 100 genes.
We evaluated the performance of OIPCQ and OIPCQ2 algorithms in three orders (order 0, order 1 and order 2). The results suggest that a higher-order network has higher accuracy (ACC) and F-measure with a lower FPR than that of a lower order network. This observation demonstrates that both OIPCQ and OIPCQ2 methods can construct the true network step by step, and are effective and efficient in inferring GRNs in order 2. The results of different orders of OIPCQ and OIPCQ2 algorithms for DREAM3 are shown in Tables 3 and 4, respectively.
Table 3.
Results for different orders of OIPCQ algorithm for DREAM3-Yeast1 of size10, 50 and 100.
| TP | FP | PPV | TPR | ACC | F-measure | FPR | FDR | MCC | |
|---|---|---|---|---|---|---|---|---|---|
| Size10-Order 0 | 9 | 1 | 0.9 | 0.9 | 0.955556 | 0.9 | 0.028571 | 0.1 | 0.871429 |
| Size10-Order 1 | 9 | 0 | 1 | 0.9 | 0.977778 | 0.947368 | 0 | 0 | 0.935414 |
| Size10-Order 1 | 9 | 0 | 1 | 0.9 | 0.977778 | 0.947368 | 0 | 0 | 0.935414 |
| Size50-Order 0 | 57 | 156 | 0.267606 | 0.74026 | 0.856327 | 0.393103 | 0.135889 | 0.732394 | 0.387026 |
| Size50-Order 1 | 43 | 57 | 0.43 | 0.558442 | 0.925714 | 0.485876 | 0.049652 | 0.57 | 0.451002 |
| Size50-Order 2 | 40 | 30 | 0.571429 | 0.519481 | 0.945306 | 0.544218 | 0.026132 | 0.428571 | 0.515858 |
| Size100-Order 0 | 98 | 161 | 0.378378 | 0.590361 | 0.953737 | 0.461176 | 0.033654 | 0.621622 | 0.450085 |
| Size100-Order 1 | 77 | 64 | 0.546099 | 0.463855 | 0.969091 | 0.501629 | 0.013378 | 0.453901 | 0.487513 |
| Size100-Order 2 | 75 | 34 | 0.688073 | 0.451807 | 0.974747 | 0.545455 | 0.007107 | 0.311927 | 0.545552 |
Best results are indicated in bold.
Table 4.
Results for different orders of OIPCQ2 algorithm for DREAM3-Yeast1 of size10, 50 and 100.
| TP | FP | PPV | TPR | ACC | F-measure | FPR | FDR | MCC | |
|---|---|---|---|---|---|---|---|---|---|
| Size10-Order 0 | 9 | 1 | 0.9 | 0.9 | 0.955556 | 0.9 | 0.028571 | 0.1 | 0.871429 |
| Size10-Order 1 | 9 | 0 | 1 | 0.9 | 0.977778 | 0.947368 | 0 | 0 | 0.935414 |
| Size10-Order 2 | 9 | 0 | 1 | 0.9 | 0.977778 | 0.947368 | 0 | 0 | 0.935414 |
| Size50-Order 0 | 57 | 156 | 0.267606 | 0.74026 | 0.856327 | 0.393103 | 0.135889 | 0.732394 | 0.387026 |
| Size50-Order 1 | 40 | 52 | 0.434783 | 0.519481 | 0.927347 | 0.473373 | 0.045296 | 0.565217 | 0.436671 |
| Size50-Order 2 | 39 | 35 | 0.527027 | 0.506494 | 0.940408 | 0.516556 | 0.030488 | 0.472973 | 0.484925 |
| Size100-Order 0 | 99 | 166 | 0.373585 | 0.596386 | 0.952929 | 0.459397 | 0.034699 | 0.626415 | 0.449227 |
| Size100-Order 1 | 80 | 64 | 0.555556 | 0.481928 | 0.969697 | 0.516129 | 0.013378 | 0.444444 | 0.501917 |
| Size100-Order 2 | 75 | 43 | 0.635593 | 0.451807 | 0.972929 | 0.528169 | 0.008988 | 0.364407 | 0.522602 |
Best results are indicated in bold.
Results for DREAM4
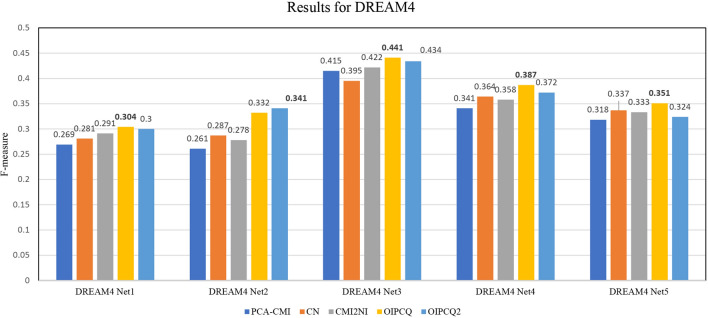
Similar to the DREAM3 case, for DREAM4, OIPCQ and OIPCQ2 with two thresholds ( for MI and for CMI) were implemented and compared with PCA-CMI, CN and CMI2NI. The selected thresholds for the mentioned methods are shown in Table S3 in Supplementary file. The benchmark results for DREAM4 for five networks of the 100-multifactorial sub-challenge are summarized in Tables S4 through S8 and Fig. 2. Similar to DREAM3, the results show that OIPCQ and OIPCQ2 consistently perform better than all other algorithms in terms of PPV, ACC, MCC and F-measure metrics.
Figure 2.
Comparison of F-measure values of OIPCQ and OIPCQ2 algorithms with other methods for learning DREAM4 challenge for five networks of the 100-multifactorial sub-challenge.
Range of the variation of TP and FP values
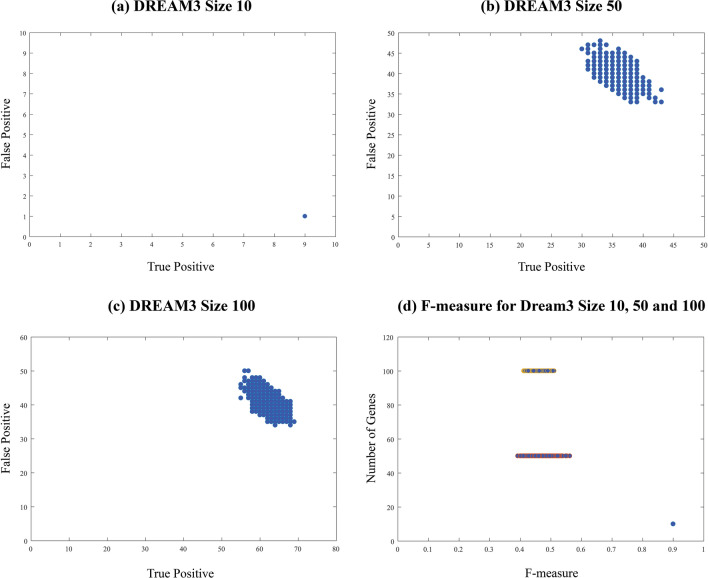
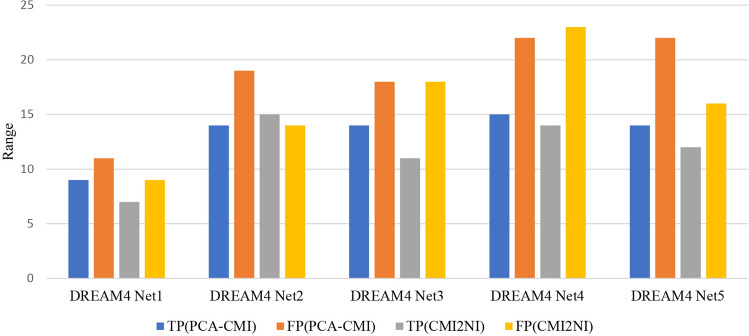
In the Materials and methods section, the order dependency of PC-based Algorithms is discussed. To illustrate the order dependency of PC-based algorithms, we implemented the PCA-CMI on the DREAM3 dataset with 10, 50 and 100 genes. For each of these sets, 1000 different gene order permutations were generated and tested. The threshold was set as for CMI tests. Figure 3 parts (a), (b) and (c) show the TP against FP for each randomly-generated permutation for DREAM3 dataset with 10, 50 and 100 genes, respectively. Figure 3 part (d) shows the F-measure values for these datasets. The study on different sequential node ordering resulted in different TP and FP. It is concluded that, by considering different sequential node ordering, the resulted networks are also different. Figure 3d illustrates that the larger the networks are, the more they are affected by the order of the input genes. The order dependency is less of a concern in networks with fewer variables (networks with less that 10 genes). Also, 1000 random sequences of genes for DREAM4 dataset are generated and the range of the variation of TP and FP are calculated. Figure 4 illustrates the range of values for DREAM4 datasets resulted by PCA-CMI and CMI2NI algorithms. It is concluded that, the range of variation of the values is significant and indicates the importance of using order-independent algorithm or selecting an appropriate order of genes as the algorithm input. The standard deviations for TPs and FPs are approximately equal to 2 and 3, respectively.
Figure 3.
True Positive against False Positive for 1000 randomly-generated permutations for DREAM3 dataset with (a) 10 genes, (b) 50 genes, and (c) 100 genes resulted by PCA-CMI. The F-measure values for DREAM3 dataset with 10, 50 and 100 genes is represented in part (d).
Figure 4.
Range of the variation TP and FP values for 1000 randomly-generated permutation for DREAM3 and DREAM4 datasets resulted by PCA-CMI and CMI2NI algorithms.
Results for SOS-DNA and AML
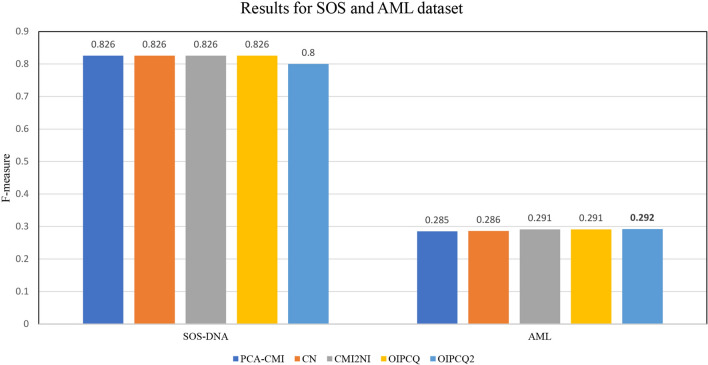
The efficiency of OIPCQ and OIPCQ2 algorithms are also tested on real datasets E. coli(SOS-DNA) and AML. The real network for SOS-DNA consists of a network with 9 genes and 24 edges. Thresholds used for the implemented algorithms are listed in Table S9 in Supplementary file. The benchmark results on the SOS-DNA dataset are presented in Fig. 5 and Table S10 in Supplementary file.
Figure 5.
Comparison of F-measure values of OIPCQ and OIPCQ2 algorithms with other methods for learning SOS-DNA and AML.
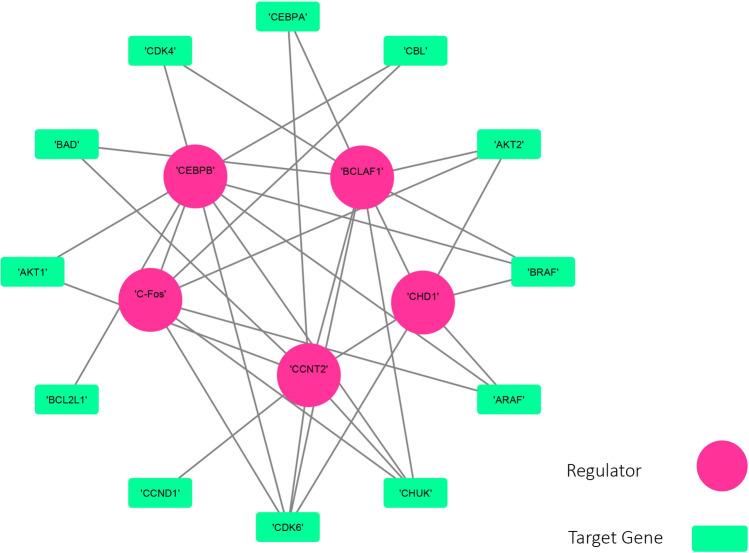
The results show that OIPCQ performs consistent with the benchmark algorithms. The AML network contains 81 genes, of which 65 are target and 16 are regulatory genes. RACER algorithm, presented in51, was developed to infer the GRN in AML dataset and is referred to as a Golden Standard for this dataset. Zhang’s CMI2NI algorithm19 produced a network with 549 edges, of which 113 are common with RACER. In order to compare the networks constructed by OIPCQ and OIPCQ2 with CMI2NI, we have selected thresholds such that the constructed network has equal edges to the CMI2NI’s network. Hence, the produced network contains 549 edges from which 114 are in common with RACER. The results of OIPCQ and OIPCQ2 on AML dataset are summarized in Table S11 in the supplementary file. Figures S1 and Fig S2 generated by Cytoscape52 show the GRN constructed by OIPCQ and OIPCQ2 on AML, respectively. The central nodes in these figures show the 16 regulators. In these networks, the highest degrees belonged to ZBTB7A and PU1 regulators with respective values of 53 and 47 (see Table S12). Figure 6 generated by Cytoscape52 illustrates the resulted subnetwork by OIPCQ algorithm for the first 17 regulators and their targets of the AML dataset.
Figure 6.
Subnetwork of GRN of AML that infer by OIPCQ.
These values are significantly higher compared to that of RACER network with 12 and 9 degrees. Previous studies53,54 have shown that ZBTB7A functions as a transcriptional suppressor. ZBTB7A was also proven to play a critical role in AML as a transcription factor55. AML is also influenced by the slow decline of the transcript factor PU156,57. In addition to the mentioned two regulators, BCLAF1 and NRSF are reported by Zhang et al.19, as significant regulators with significant role in cancer. In both of our networks, BCLAF1 and NRSF (Figs. S1 and Fig S2) had high degrees as well, which is consistent with the results of CMI2NI19 . In order to verify these findings, the pathway enrichment was done separately for each of the four regulators ZBTB7A, PU1, BCLAF1 and NRSF, along with their target genes. The pathway enrichment was done in the cancer annotation system CaGe (http://mgrc.kribb.re.kr/cage/)58–61. The results of the pathway enrichments are presented in Tables S13 to S20, which include significant pathways. In these tables the obtained p-values related to the pathways correspond to each of the four regulators and their target genes in the resulted networks from OIPCQ and OIPCQ2 algorithms are more meaningful than those of CMI2NI. In order to compare the importance of target genes of BCLAF1 and NRSF in OIPCQ and OIPCQ2 with CMI2NI, three most significant pathways were selected and compared (Table 5). The result of Table 5 indicate that the relationship between genes in our networks are more related to LEUKEMIA cancer in comparison with CMI2NI’s network. In summary, based on the results obtained in this study, we can claim that the regulators ZBTB7A and PU1 beside to BCLAF1 and NRSF play a significant role in cancer, and especially in leukemia.
Table 5.
Comparison of CMI2NI, OIPCQ and OIPCQ2 methods based on the three important pathways resulted by KEGG.
| No. | Pathway (number of genes in pathways) | Regulator | Method | Genes overlapped | p value | q-value |
|---|---|---|---|---|---|---|
| 1 | CHRONIC MYELOID LEUKEMIA (73 genes) | BCLAF1 | CMI2NI/OIPCQ/OIPCQ2 | 22/25/25 | 2.90e-35/2.17e−41/2.17e−41 | 2.41e−32/1.80e−38/1.80e−38 |
| 2 | ACUTE MYELOID LEUKEMIA (60 genes) | BCLAF1 | CMI2NI/OIPCQ/OIPCQ2 | 18/20/20 | 1.94e−28/3.03e−32/ 3.03e−32 | 5.38e−26/8.41e−30/ 8.41e−30 |
| 3 | PATHWAYS IN CANCER ( 328 genes) | BCLAF1 | CMI2NI/OIPCQ/OIPCQ2 | 28/31/31 | 5.05e−30/2.41e−34/2.41e−34 | 2.10e−27/1.00e−31/1.00e−31 |
| 1 | CHRONIC MYELOID LEUKEMIA (73 genes) | NRSF | CMI2NI/OIPCQ/OIPCQ2 | 18/26/26 | 2.94e−29/8.90e−44/8.90e−44 | 2.45e−26/7.42e−41/ 7.42e−41 |
| 2 | ACUTE MYELOID LEUKEMIA (60 genes) | NRSF | CMI2NI/OIPCQ/OIPCQ2 | 15/14/14 | 3.32e−24/6.78e−20/6.78e−20 | 1.38e−21/1.88e−17/1.88e−17 |
| 3 | PATHWAYS IN CANCER (328 genes) | NRSF | CMI2NI/OIPCQ/OIPCQ2 | 22/28/28 | 1.02e−23/5.47e−29/ 5.47e−29 | 2.83e−21/2.28e−26/2.28e−26 |
Best results are indicated in bold.
Among the significant pathways, three most significant ones were selected. The pathway enrichment was done separately for each of the four regulators ZBTB7A, PU1, BCLAF1 and NRSF. Column 1 indicates the name of pathways and number of genes in pathways. The name of regulators and algorithms are in columns 2 and 3, respectively. The overlap between resulted sets and genes in pathways are represented in columns 4. The related p values and q-values are collected in columns 5 and 6, respectively.
Summary: all cases
For threshold-dependent methods, TPR and FPR are used to generate the Receiver Operating Characteristic (ROC) curve. The area under the ROC Curve (AUC) is calculated to measure the performance of each method and benchmark them. To make a fair comparison, we referred to the algorithms’ reference articles and used their suggested thresholds that have produced the best results based on F-measure values.
We also ran these algorithms on additional datasets. If a better threshold than what was suggested in the references was found, we included it in our paper for comparison. The rationale was to compare the best outcome of our algorithm with the best outcome of the benchmark algorithms in a fair manner.
To study and illustrate the dependency of the four algorithms (PCA-CMI, CMI2NI, OIPCQ and OIPCQ2) on the threshold for MI and CMI tests, the standard deviation of TP and FP based on different threshold values are calculated and shown in Tables 6 and 7, respectively. Among the four algorithms, the smallest standard deviation values for TP and FP are from OIPCQ and OIPCQ2 algorithms. For the aforementioned algorithms, the 1000 threshold values for MI and CMI tests are selected in the range (0,1) with the incremental step of 0.001. For each data, approximately 1000 different TP and FP are obtained based on different thresholds and standard deviation of them are calculated. To calculate the standard deviation of the results for OIPCQ and OIPCQ2, 1000 different threshold values for CMI(X, Y|Z) and CMI(X, Y|Z, W) are used. The standard deviations are calculated by considering a constant quantile of 70 and a constant value for the MI(X, Y). In addition, for OIPCQ and OIPCQ2, the standard deviation of the TP and FP are also calculated based on different values for quantile CMI(X, Y|Z) and CMI(X, Y|Z, W). For this purpose, the range of a quantile was (0.5, 0.9) with steps of 0.001 (400 steps) and fixed value of 0.05 for MI and CMI tests. The standard deviation of TP and FP based on different values for quantiles are shown in two last columns (OIPCQ and OIPCQ2) of Tables 6 and 7, respectively. In addition, to investigate the dependence of algorithms on sample values and evaluate the stability of the results by removing a percentage of samples, 10% of the samples are removed and new F-measure values are calculated. These steps are repeated 200 times and the standard deviations for resulted F-measure values are shown in Table 8. Results indicate that the algorithms are robust and have a relatively similar performance according to the standard deviation of F-measure values. In summary, by removing a small percentage of the samples, the results do not change significantly.
Table 6.
Standard deviation for true positive based on different thresholds.
| PCA-CMI | CMI2NI | OIPCQ | OIPCQ2 | OIPCQ | OIPCQ2 | |
|---|---|---|---|---|---|---|
| DREAM3-size10 | 3.1476 | 3.3372 | 0 | 0 | 0 | 0 |
| DREAM3-size50 | 9.7928 | 9.8719 | 3.1112 | 1.6733 | 4.5769 | 3.3982 |
| DREAM3-size100 | 20.8978 | 21.6884 | 3.4808 | 0.9072 | 6.1006 | 5.1318 |
| DREAM4-Net1 | 12.9749 | 12.7407 | 0.7739 | 0.8604 | 1.2504 | 1.1699 |
| DREAM4-Net2 | 19.7166 | 20.9606 | 2.0103 | 5.0361 | 3.843 | 6.6629 |
| DREAM4-Net3 | 19.1421 | 19.6161 | 1.7407 | 1.07 | 2.39 | 2.7508 |
| DREAM4-Net4 | 19.7112 | 20.724 | 3.4289 | 2.5650 | 5.16 | 3.0038 |
| DREAM4-Net5 | 21.9107 | 22.6012 | 1.6316 | 1.7157 | 2.4411 | 2.3825 |
| SOS-DNA | 3.881 | 3.927 | 0 | 0.3457 | 0 | 0.8439 |
| AML | 20.6249 | 18.0287 | 4.5840 | 3.9921 | 6.5335 | 6.1059 |
Table 7.
Standard deviation for false positive based on different thresholds.
| PCA-CMI | CMI2NI | OIPCQ | OIPCQ2 | OIPCQ | OIPCQ2 | |
|---|---|---|---|---|---|---|
| DREAM3-size10 | 1.1896 | 1.2965 | 0 | 0 | 0 | 0 |
| DREAM3-size50 | 18.3173 | 24.27 | 9.0795 | 7.5631 | 10.551 | 8.1585 |
| DREAM3-size100 | 44.3284 | 49.291 | 8.6476 | 6.4613 | 9.9375 | 7.8771 |
| DREAM4-Net1 | 86.4018 | 91.0742 | 1.9737 | 1.3515 | 2.3155 | 2.0872 |
| DREAM4-Net2 | 92.1005 | 95.4474 | 16.8821 | 31.3403 | 20.1067 | 33.2911 |
| DREAM4-Net3 | 130.5841 | 140.8131 | 11.6187 | 8.1272 | 13.6606 | 10.914 |
| DREAM4-Net4 | 128.34 | 137.1658 | 15.2308 | 10.1293 | 18.6175 | 13.1936 |
| DREAM4-Net5 | 178.9869 | 189.3208 | 8.7945 | 7.2971 | 10.38 | 9.4407 |
| SOS-DNA | 1.0464 | 1.0947 | 0 | 0 | 0.1581 | 0.3616 |
| AML | 86.1101 | 77.3476 | 18.7795 | 16.3635 | 27.8585 | 25.7403 |
Table 8.
Standard Deviation for F-measure based on removing 10% of the samples.
| PCA-CMI | CN | CMI2NI | OIPCQ | OIPCQ2 | |
|---|---|---|---|---|---|
| DREAM3-size10 | 0.1126 | 0.1072 | 0.1021 | 0.1097 | 0.0943 |
| DREAM3-size50 | 0.0237 | 0.0243 | 0.0237 | 0.0231 | 0.0211 |
| DREAM3-size100 | 0.0184 | 0.0196 | 0.02 | 0.0177 | 0.0182 |
| DREAM4-Net1 | 0.014 | 0.1262 | 0.0122 | 0.0098 | 0.0104 |
| DREAM4-Net2 | 0.0121 | 0.012 | 0.0125 | 0.0111 | 0.0125 |
| DREAM4-Net3 | 0.0156 | 0.0142 | 0.0133 | 0.0132 | 0.013 |
| DREAM4-Net4 | 0.0116 | 0.0109 | 0.0148 | 0.0127 | 0.0099 |
| DREAM4-Net5 | 0.0131 | 0.137 | 0.0142 | 0.0145 | 0.0119 |
| SOS-DNA | 0.0379 | 0.0336 | 0.034 | 0.0363 | 0.0326 |
| AML | 0.0091 | 0.0096 | 0.0111 | 0.0116 | 0.0073 |
Best results are indicated in bold.
Table 9 shows the performance of algorithms on each dataset according to the important measures. For DREAM3-size50-Yeast1 and DREAM4-Net1 datasets CN algorithm superior to OIPCQ based on FP and FDR measures. Based on F-measure, which considers TP, FN and FP together, OIPCQ outperforms other algorithms in learning the GRN structure in all the tested data sets.
Table 9.
Report Best algorithm for each data sets.
| Dataset | FP | F-measure | FDR | MCC |
|---|---|---|---|---|
| DREAM3-size10-Yeast1 | OIPCQ-OIPCQ2 | OIPCQ-OIPCQ2 | OIPCQ-OIPCQ2 | OIPCQ-OIPCQ2 |
| DREAM3-size50-Yeast1 | CN | OIPCQ | CN | OIPCQ |
| DREAM3-size100-Yeast1 | OIPCQ | OIPCQ | OIPCQ | OIPCQ |
| DREAM4-Net1 | CN | OIPCQ | CN | OIPCQ |
| DREAM4-Net2 | OIPCQ | OIPCQ | OIPCQ | OIPCQ |
| DREAM4-Net3 | OIPCQ | OIPCQ | OIPCQ | OIPCQ |
| DREAM4-Net4 | OIPCQ | OIPCQ | OIPCQ | OIPCQ |
| DREAM4-Net5 | OIPCQ | OIPCQ | OIPCQ | OIPCQ |
| SOS-DNA | All algorithms | All algorithms | All algorithms | All algorithms |
| AML | OIPCQ | OIPCQ2 | OIPCQ2 | OIPCQ2 |
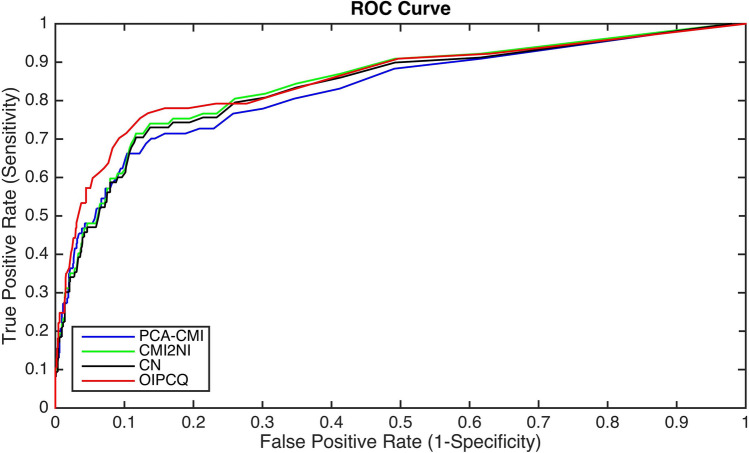
The OIPCQ and OIPCQ2 algorithms have three parameters: (the threshold for MI test); (the threshold for CMI test), and k as kth percentile of all CMI(X,Y|Z) values. In order to benchmark our algorithms against other methods, we set and , and calculate AUC based on the parameter. In our algorithms, by keeping the parameters constant and and equal, the performance of the algorithms declines. Despite the decline, they still outperform the benchmarked algorithms. Since the OIPCQ and OIPCQ2 algorithms are similar, we just report the result of OIPCQ algorithm. Results of AUC for DREAM3 of sizes 10, 50 and 100 are shown in Table 10. As an example, the ROC curves of different methods for the DREAM3 challenge with 50 nodes are shown in Fig. 7 which shows the better performance of the OIPCQ algorithm in comparison with the benchmarked methods (PCA-CMI, CMI2NI and CN).
Table 10.
Comparison of different methods for learning DREAM3.
| Method | PCA-CMI | CN | CMI2NI | OIPCQ |
|---|---|---|---|---|
| AUCD10 | 0.9642 | 0.9734 | 0.956 | 0.9800 |
| AUCD50 | 0.8101 | 0.8315 | 0.834 | 0.8458 |
| AUCD100 | 0.8419 | 0.8558 | 0.855 | 0.8656 |
Best results are indicated in bold.
AUCD10 AUC value for a 10-gene network in DREAM3, AUCD50 AUC value for a 50-gene network in DREAM3, AUCD100 AUC value for a 100-gene network in DREAM3.
Figure 7.
ROC curves of different methods for DREAM3 challenge with 50 nodes. The red line is related to the ROC curve of OIPCQ algorithm with a AUC of 0.8458 value which has a larger value than other methods.
Table 11 shows the results on DREAM4 data sets for different methods. The result of AUC values for OIPCQ algorithm is compared with that of PCA-CMI, CN and three best teams which participated on this challenge in http://wiki.c2b2.columbia.edu/dream/results/DREAM4/. From Table 11, we can find that the proposed method (OIPCQ) performs as good as the best method in DREAM4 challenge. In Networks 1,3 and 4, the results of the OIPCQ algorithm are similar to the best team (TEAM415). In Network 5, our algorithm has the best performance and in Networks 2, the CN algorithm among the challenge participants has the best result.
Table 11.
Comparison of different methods for Learning DREAM4 Challenge.
| Method | Net1 | Net2 | Net3 | Net4 | Net5 |
|---|---|---|---|---|---|
| Team415 | 0.75 | 0.69 | 0.76 | 0.77 | 0.76 |
| Team549 | 0.73 | 0.70 | 0.74 | 0.74 | 0.74 |
| Team395 | 0.69 | 0.64 | 0.72 | 0.72 | 0.71 |
| PCA-CMI | 0.70 | 0.69 | 0.74 | 0.74 | 0.74 |
| CN | 0.75 | 0.73 | 0.76 | 0.70 | 0.76 |
| OIPCQ | 0.75 | 0.71 | 0.76 | 0.77 | 0.77 |
TeamName is the name of the team which registered for this challenge. The best performer for the relative item is noted in bold.
AUC values related to different algorithms for SOS is illustrated in Table 12. According to this table, the AUC values of CMI2NI and OIPCQ algorithms are larger than other those of methods.
Table 12.
Comparison of AUC for real data sets (AUCSOS: AUC values for a SOS network with 9 genes).
| Method | PCA-CMI | CN | CMI2NI | OIPCQ |
|---|---|---|---|---|
| AUCSOS | 0.79 | 0.791 | 0.8 | 0.8 |
Best results are indicated in bold.
According to Tables 10, 11 and 12, the AUC values of all algorithms are almost similar and AUC values of OIPCQ algorithm are larger than those of other methods.
Discussion
Survival of living organisms depends on the interaction between thousands of genes. GRN are schematic representations of interactions among all gene pairs in a given cell. The functions and dynamics of various cells can be figured out through reconstructing the GRNs. In PC-based methods, the maximum of CMI values is used as a threshold for removing the network edges. Considering the distribution of the CMI values, the choice of the maximum value may not always be appropriate. For example, a single large value within a set of CMI values that are significantly lower, may result in high false positives. In our approach, the distribution of the CMI values is taken into account by choosing a certain quantile threshold. This quantile threshold is set based on the training process on DREAM3 dataset. This threshold is also applied to other datasets considered as independent data sets. In fact, this threshold can be adjusted for each dataset differently and better results can be obtained. In order to reduce the parameters and the computation time of the algorithm, this threshold is set based on the training process on DREAM3 dataset. In PC-based methods, the edges are removed in an iterative process until some criteria are met. In OIPCQ on the other hand, the edges are removed at the end of each order of algorithm, a threshold is determined and a number of edges are removed based on the selected threshold (Fig. 9).
Figure 9.
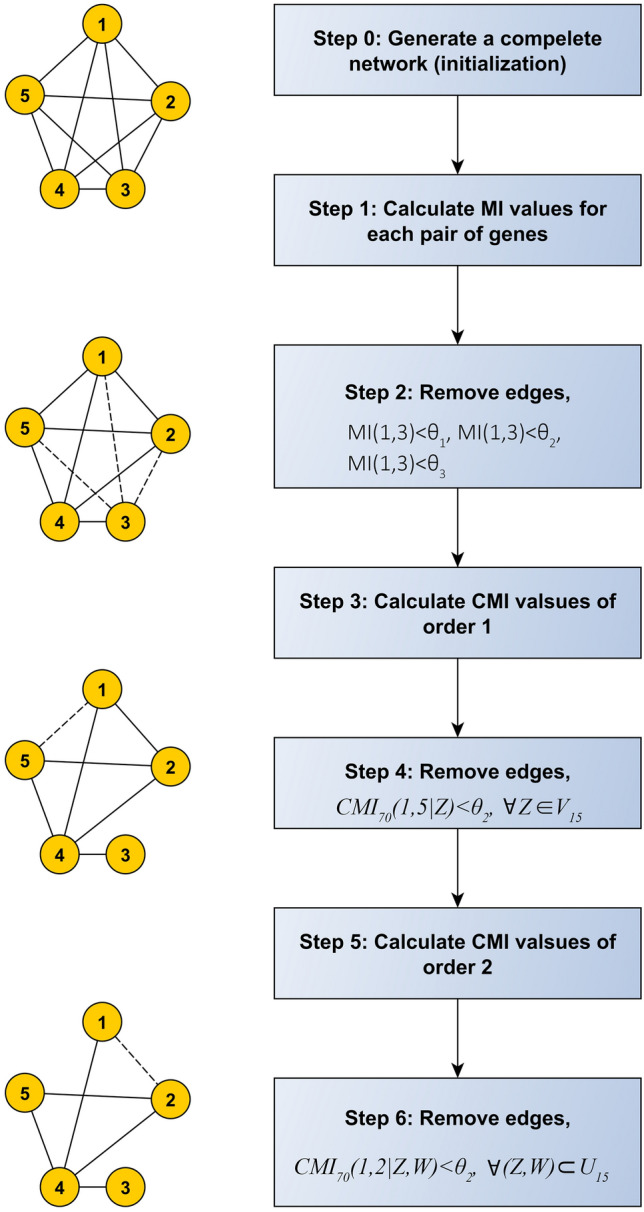
An example of the OIPCQ algorithm. MI and CMI denote the mutual information and conditional mutual information. indicates the 70th percentile of the CMI values. and
The iterative process used in PC-based methods for removing edges from a network has two main drawbacks:
1-In each order of the PC-based algorithm and during each step in the iterative process, if an edge is removed in error, it will cause the error to propagate to the future steps at the same order of algorithm. In OIPCQ, on the other hand, the edges are removed at the end of each order of the algorithm. If an edge is removed in error at the end of each order, it will cause the error to propagate to the future orders of the algorithm and not the subsequent steps in each order of the algorithm. In other word, since in PC-based methods, and are updated in each iterative step (by removing edges in each iterative step, the size of and gets smaller), it is possible that the informative nodes in the separator sets are eliminated incorrectly. Subsequently, the test of independency considers the smallest set of vertices and therefore it is possible that an edge is retained by mistake (increasing FP). In OIPCQ, on the other hand, and are updated at the end of each order of the algorithm which mitigates this source of error.
2-The order of input variables has an impact on the final network constructed. In our simplified version of the algorithm, firstly, in each order set of neighbors of all adjacent nodes are determined. Then, the independence tests are performed and their test statistics are obtained as criteria for removing the edges. Such a process eliminates the chance for removing an edge in error that would cause an incorrect change in the set of neighbors. As a result, any order of inputs will result in the same network construction. The results we obtained on all tested datasets confirm that the number of FP’s are reduced in our approach compared to the iterative approach. The drawback of the OIPCQ algorithm compared to PC-based algorithms is the running time of the algorithm. In fact, by removing edges in each iteration of PC-based methods the size of for the adjacent node X and Y can be decreased. So, the number of calculations for CMI tests is decreased. In the OIPCQ algorithm, first in each order of algorithm (for order 1) and (for orders greater than 1) are calculated and considered constant. As a result, more calculations are needed in the OIPCQ algorithm.
It can concluded that OIPCQ and OIPCQ2 outperform other algorithms on simulated datasets. Also, the OIPCQ and OIPCQ2 results on the AML data shows more similarities with RACER compared to some popular inferring network methods. Similar results are concluded by using OIPCQ and OIPCQ2 algorithms, therefore, applying Eq. (5) instead of 4 for calculating CMI, the constructed GRN do not change the result significantly. Finally, the main advantage of the proposed method is that it is applicable to all PC-based methods.
Methods
In this section, we discuss about drawbacks of PC-based algorithms. Following that, the details of the proposed OIPCQ algorithm for inferring the structure of GRN are introduced.
Drawbacks of PC-based algorithms
The first is that these methods are not robust for different sequential node orders. The second is that the results by these methods are highly dependent on the maximum value of CMI tests used for removing edges in each step of the algorithms. In addition, the proper selection of a collection of nodes which contains the separator sets significantly influences the performance of these methods.
PC-based algorithms are order-dependent
The network topology resulted from PC-based algorithms are dependent on the order of genes taken as input. In each order of PC-based algorithms, the edges are removed based on conditional mutual information tests which explained in section “PC Algorithm based on Conditional Mutual Information (PCA-CMI)”. Therefore, the adjacent of the vertices are updated as a result of sequential removing edges from the network. According to this method, depends on the initial order of the nodes and a different nodes order may eventually result in a different final network.
Construction of separator sets
In PCA-CMI, CMI2NI, and CN algorithms, the separator set is extracted from . So, these algorithms in each order only considers the paths of length 2 and ignores any existing connections with length greater than 2. One way of dealing with this constraint is to use for order greater than one (). For , by using instead of , the decision will be made by more information considering all the paths between X and Y. For example, in Fig. 8 by using only the CMI(X, Y|M, N) for order is calculated and only two paths of length 2, and , between X and Y are considered. By using , we also considered the path of length 3, , for checking the dependency between X and Y. The results show that, by considering more paths, OIPCQ helps to keep more reliable edges compared to other methods.
Figure 8.
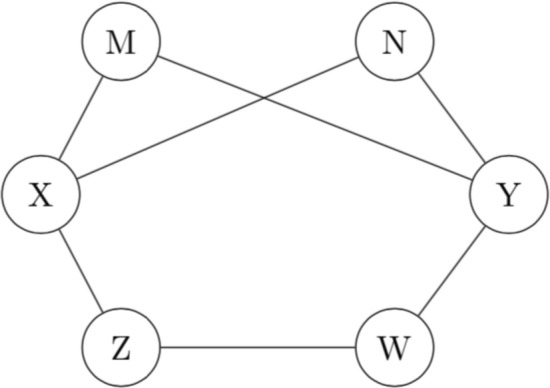
Example of Paths of length 2 and greater than 2 between X and Y.
Removing edges in PC-based algorithms is threshold-dependent
In PC-based algorithms, the decision for removing edges from a network strictly depends on the value of and threshold as the criterion for removing the edges. In fact, the edge XY is removed if for each Z in separator X and Y, . This method results in many FN. On the other hand, if the most CMI(X, Y|Z) are close to zero and only one of them is greater than , PCA-CMI, CN and CMI2NI keep the edge XY in the network. Our investigation show that most of such edges are FP. So, considering the distribution of CMI(X, Y|Z), quantile-based criterion for removing an edge is more effective and yield better results than using constant value as a threshold for removing edge. Our algorithm is trained by 70th percentile of all CMI(X, Y|Z) values in one dataset and this quantile is used for all datasets. In OIPCQ and OIPCQ2 algorithms, user sets the threshold.
The OIPCQ algorithm
The OIPCQ starts from a complete graph and iterates the following process to extract skeleton from .
Step 0: Initialization: Generate a complete network with number of nodes equal to the number of genes.
Step 1: Calculate MI: Compute MI values for each pair of genes.
Step 2: Remove Edges: Eliminate corresponding edges for which MI values are smaller than ( denotes the threshold for MI test). The resulted network in this step is denoted by .
Step 3: Calculate CMI of order 1: If there exists any edges between X and Y in , find all genes Z which are adjacent to both X and Y, and then calculate their CMI(X, Y|Z) for Z belongs to . In this step, the paths of length 2 are considered between X and Y.
Step 4: Remove Edges: Define as all 70th percentile of all CMI(X, Y|Z) values. If is less than ( is the threshold for CMI test), remove the edge between X and Y. The resulted network in this step is denoted by .
Step 5: Calculate CMI of order 2: Do the steps above for X and Y and calculate CMI(X, Y|Z, W), where Z and W belong to . In this step, the paths of length at least 2 are considered between X and Y.
Step 6: Remove Edges: Define as the 70th percentile of all CMI(X, Y|Z, W) values. If is less than , remove the edge between X and Y.
An example of the OIPCQ algorithm is illustrated in Fig. 9 for network with 5 genes. The other version of OIPCQ, named OIPCQ2 was introduced using CMI2 for detecting dependency between genes. In both OIPCQ and OIPCQ2 algorithms, in each order of algorithms for each X and Y, and are defined and fixed. Then, at the end of each order the algorithm decides to remove edges based on threshold and . By using this method and fixing the and in each order of algorithms, the order dependency issue is solved and both OIPCQ and OIPCQ2 algorithms are order independent.
OIPCQ and OIPCQ2 algorithms compute MI(X, Y) in steps 1 and 2, CMI(X, Y|Z) in steps 3 and 4, and CMI(X, Y|Z, W) in steps 5 and 6.
In PCA-CMI, CMI2NI, and CN algorithms, the separator set is extracted from . So, these algorithms in each order only consider the paths of length 2 and ignore any existing connections with lengths of greater than 2. One way of dealing with this constraint is to use for orders greater than one (). For , by using instead of , the decision will be made by more information considering all the paths between X and Y. In general, PC-based algorithms first consider a complete graph, then try to reduce the number of edges in the early steps to reach the desired network. In the early steps, such as CMI(X, Y|Z), the computational time is less than the computational time for CMI(X, Y|Z, W).
If CMI(X, Y|Z, W) has a low value for the 70th percentile of all Z and W, CMI(X, Y|Z) also has a low value. These steps (first order one then second order) are performed to increase the speed of the algorithm and reduce the computational complexity.
Supplementary information
Acknowledgements
Rosa Aghdam is a postdoctoral fellow at Faculty of Mathematical Sciences, Department of Computer Science, the Shahid Beheshti University under support of Iranian National Science Foundation (INSF97009558).
Author contributions
R.A., S.H.M. and C.E. developed the method and performed computational and statistical analysis. R.A., S.H.M. and C.E. design and wrote the paper. R.A. and C.E. contributed in writing and editing the manuscript. All authors read and approved the final manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Rosa Aghdam, Email: rosa.aghdam@ipm.ir.
Changiz Eslahchi, Email: ch-eslahchi@sbu.ac.ir.
Supplementary information
is available for this paper at 10.1038/s41598-021-87074-5.
References
- 1.Marbach D, et al. Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. 2010;107:6286–6291. doi: 10.1073/pnas.0913357107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bansal M, Belcastro V, Ambesi-Impiombato A, Di Bernardo D. How to infer gene networks from expression profiles. Mol. Syst. Biol. 2007;3:78. doi: 10.1038/msb4100120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.De Smet R, Marchal K. Advantages and limitations of current network inference methods. Nat. Rev. Microbiol. 2010;8:717. doi: 10.1038/nrmicro2419. [DOI] [PubMed] [Google Scholar]
- 4.Chai LE, et al. A review on the computational approaches for gene regulatory network construction. Comput. Biol. Med. 2014;48:55–65. doi: 10.1016/j.compbiomed.2014.02.011. [DOI] [PubMed] [Google Scholar]
- 5.Aghdam R, Ganjali M, Eslahchi C. Ipca-cmi: an algorithm for inferring gene regulatory networks based on a combination of pca-cmi and mit score. PLoS ONE. 2014;9:e92600. doi: 10.1371/journal.pone.0092600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hughes TR, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/S0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- 7.Hurley D, et al. Gene network inference and visualization tools for biologists: application to new human transcriptome datasets. Nucleic Acids Res. 2011;40:2377–2398. doi: 10.1093/nar/gkr902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Friedman N, Linial M, Nachman I, Pe’er D. Using Bayesian networks to analyze expression data. J. Comput. Biol. 2000;7:601–620. doi: 10.1089/106652700750050961. [DOI] [PubMed] [Google Scholar]
- 9.Marbach D, et al. Wisdom of crowds for robust gene network inference. Nat. Methods. 2012;9:796. doi: 10.1038/nmeth.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhang X, et al. Narromi: a noise and redundancy reduction technique improves accuracy of gene regulatory network inference. Bioinformatics. 2012;29:106–113. doi: 10.1093/bioinformatics/bts619. [DOI] [PubMed] [Google Scholar]
- 11.Zhu H, Rao RSP, Zeng T, Chen L. Reconstructing dynamic gene regulatory networks from sample-based transcriptional data. Nucleic Acids Res. 2012;40:10657–10667. doi: 10.1093/nar/gks860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Akutsu, T., Miyano, S. & Kuhara, S. Identification of genetic networks from a small number of gene expression patterns under the Boolean network model. In Biocomputing’99, 17–28 (World Scientific, 1999). [DOI] [PubMed]
- 13.Zhu D, Li H. Improved Bayesian network inference using relaxed gene ordering. Int. J. Data Min. Bioinform. 2010;4:44–59. doi: 10.1504/IJDMB.2010.030966. [DOI] [PubMed] [Google Scholar]
- 14.Krämer N, Schäfer J, Boulesteix A-L. Regularized estimation of large-scale gene association networks using graphical Gaussian models. BMC Bioinform. 2009;10:384. doi: 10.1186/1471-2105-10-384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Menéndez P, Kourmpetis YA, ter Braak CJ, van Eeuwijk FA. Gene regulatory networks from multifactorial perturbations using graphical lasso: application to the dream4 challenge. PLoS ONE. 2010;5:e14147. doi: 10.1371/journal.pone.0014147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aghdam R, Ganjali M, Zhang X, Eslahchi C. CN: a consensus algorithm for inferring gene regulatory networks using the Sorder algorithm and conditional mutual information test. Mol. BioSyst. 2015;11:942–949. doi: 10.1039/C4MB00413B. [DOI] [PubMed] [Google Scholar]
- 17.Husmeier D. Sensitivity and specificity of inferring genetic regulatory interactions from microarray experiments with dynamic Bayesian networks. Bioinformatics. 2003;19:2271–2282. doi: 10.1093/bioinformatics/btg313. [DOI] [PubMed] [Google Scholar]
- 18.Nair A, Chetty M, Wangikar PP. Improving gene regulatory network inference using network topology information. Mol. BioSyst. 2015;11:2449–2463. doi: 10.1039/C5MB00122F. [DOI] [PubMed] [Google Scholar]
- 19.Zhang X, Zhao J, Hao J-K, Zhao X-M, Chen L. Conditional mutual inclusive information enables accurate quantification of associations in gene regulatory networks. Nucleic Acids Res. 2015;43:e31–e31. doi: 10.1093/nar/gku1315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chaitankar V, Ghosh P, Perkins EJ, Gong P, Zhang C. Time lagged information theoretic approaches to the reverse engineering of gene regulatory networks. BMC Bioinformatics. 2010;11:S19. doi: 10.1186/1471-2105-11-S6-S19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Faith JJ, et al. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007;5:e8. doi: 10.1371/journal.pbio.0050008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Luo W, Hankenson KD, Woolf PJ. Learning transcriptional regulatory networks from high throughput gene expression data using continuous three-way mutual information. BMC Bioinform. 2008;9:467. doi: 10.1186/1471-2105-9-467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Margolin AA, Nemenman I, Basso K, Wiggins C, Stolovitzky G, Dalla Favera R. Learning transcriptional regulatory networks from high throughput gene expression data using continuous three-way mutual information. BMC Bioinform. 2008;9:467. doi: 10.1186/1471-2105-9-467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang K, et al. Genome-wide identification of post-translational modulators of transcription factor activity in human b cells. Nat. Biotechnol. 2009;27:829. doi: 10.1038/nbt.1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang X, et al. Inferring gene regulatory networks from gene expression data by path consistency algorithm based on conditional mutual information. Bioinformatics. 2011;28:98–104. doi: 10.1093/bioinformatics/btr626. [DOI] [PubMed] [Google Scholar]
- 26.Zhou C, Zhang S-W, Liu F. An ensemble method for reconstructing gene regulatory network with jackknife resampling and arithmetic mean fusion. Int. J. Data Min. Bioinform. 2015;12:328–342. doi: 10.1504/IJDMB.2015.069658. [DOI] [PubMed] [Google Scholar]
- 27.Villaverde A, Ross J, Banga J. Reverse engineering cellular networks with information theoretic methods. Cells. 2013;2:306–329. doi: 10.3390/cells2020306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.López-Kleine L, Leal L, López C. Biostatistical approaches for the reconstruction of gene co-expression networks based on transcriptomic data. Brief. Funct. Genomics. 2013;12:457–467. doi: 10.1093/bfgp/elt003. [DOI] [PubMed] [Google Scholar]
- 29.Basso K, et al. Reverse engineering of regulatory networks in human b cells. Nat. Genet. 2005;37:382. doi: 10.1038/ng1532. [DOI] [PubMed] [Google Scholar]
- 30.Modi SR, Camacho DM, Kohanski MA, Walker GC, Collins JJ. Functional characterization of bacterial srnas using a network biology approach. Proc. Natl. Acad. Sci. 2011;108:15522–15527. doi: 10.1073/pnas.1104318108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang J, et al. Reconstructing regulatory networks from the dynamic plasticity of gene expression by mutual information. Nucleic Acids Res. 2013;41:e97–e97. doi: 10.1093/nar/gkt147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sumazin P, et al. An extensive microrna-mediated network of RNA–RNA interactions regulates established oncogenic pathways in glioblastoma. Cell. 2011;147:370–381. doi: 10.1016/j.cell.2011.09.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Li Z, Li P, Krishnan A, Liu J. Large-scale dynamic gene regulatory network inference combining differential equation models with local dynamic Bayesian network analysis. Bioinformatics. 2011;27:2686–2691. doi: 10.1093/bioinformatics/btr454. [DOI] [PubMed] [Google Scholar]
- 34.Barabási A-L, Gulbahce N, Loscalzo J. Network medicine: a network-based approach to human disease. Nat. Rev. Genet. 2011;12:56. doi: 10.1038/nrg2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rezaei Tabar V, Zareifard H, Salimi S, Plewczynski D. Learning directed acyclic graphs by determination of candidate causes for discrete variables. J. Stat. Comput. Simul. 2011;89:1957–1970. doi: 10.1080/00949655.2019.1604709. [DOI] [Google Scholar]
- 36.De La Fuente A, Bing N, Hoeschele I, Mendes P. Discovery of meaningful associations in genomic data using partial correlation coefficients. Bioinformatics. 2004;20:3565–3574. doi: 10.1093/bioinformatics/bth445. [DOI] [PubMed] [Google Scholar]
- 37.Saito S, Hirokawa T, Horimoto K. Discovery of chemical compound groups with common structures by a network analysis approach (affinity prediction method) J. Chem. Inf. Model. 2010;51:61–68. doi: 10.1021/ci100262s. [DOI] [PubMed] [Google Scholar]
- 38.Meyer PE, Lafitte F, Bontempi G. minet: Ar/bioconductor package for inferring large transcriptional networks using mutual information. BMC Bioinform. 2008;9:461. doi: 10.1186/1471-2105-9-461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Spirtes, P., Meek, C. & Richardson, T. Causal inference in the presence of latent variables and selection bias. In Proceedings of the Eleventh conference on Uncertainty in Artificial Intelligence, 499–506 (Morgan Kaufmann Publishers Inc., 1995).
- 40.Spirtes P, Glymour CN, Scheines R. Causation, Prediction, and Search. Cambridge: MIT Press; 2000. [Google Scholar]
- 41.Spirtes, P. An anytime algorithm for causal inference. In Proceedings of the Eighth International Workshop on Artificial Intelligence and Statistics, 213–221 (Citeseer, 2001).
- 42.Zhang J. On the completeness of orientation rules for causal discovery in the presence of latent confounders and selection bias. Artif. Intell. 2008;172:1873–1896. doi: 10.1016/j.artint.2008.08.001. [DOI] [Google Scholar]
- 43.Colombo D, Maathuis MH, Kalisch M, Richardson TS, et al. Learning high-dimensional directed acyclic graphs with latent and selection variables. Ann. Stat. 2012;40:294–321. doi: 10.1214/11-AOS940. [DOI] [Google Scholar]
- 44.Claassen, T., Mooij, J. & Heskes, T. Learning sparse causal models is not np-hard. arXiv preprint arXiv:1309.6824 (2013).
- 45.Aghdam R, Ganjali M, Niloofar P, Eslahchi C. Inferring gene regulatory networks by an order independent algorithm using incomplete data sets. J. Appl. Stat. 2016;43:893–913. doi: 10.1080/02664763.2015.1079307. [DOI] [Google Scholar]
- 46.Aghdam R, et al. Inferring gene regulatory networks by pca-cmi using hill climbing algorithm based on mit score and Sorder method. Int. J. Biomath. 2016;9:1650040. doi: 10.1142/S1793524516500406. [DOI] [Google Scholar]
- 47.Aghdam R, Rezaei Tabar V, Pezeshk H. Some node ordering methods for the k2 algorithm. Comput. Intell. 2019;35:42–58. doi: 10.1111/coin.12182. [DOI] [Google Scholar]
- 48.Brunel H, et al. Miss: a non-linear methodology based on mutual information for genetic association studies in both population and sib-pairs analysis. Bioinformatics. 2010;26:1811–1818. doi: 10.1093/bioinformatics/btq273. [DOI] [PubMed] [Google Scholar]
- 49.Altay G, Emmert-Streib F. Revealing differences in gene network inference algorithms on the network level by ensemble methods. Bioinformatics. 2010;26:1738–1744. doi: 10.1093/bioinformatics/btq259. [DOI] [PubMed] [Google Scholar]
- 50.Darbellay GA. An estimator of the mutual information based on a criterion for conditional independence. Comput. Stat. Data Anal. 1999;32:1–17. doi: 10.1016/S0167-9473(99)00020-1. [DOI] [Google Scholar]
- 51.Li Y, Liang M, Zhang Z. Regression analysis of combined gene expression regulation in acute myeloid leukemia. PLoS Comput. Biol. 2014;10:e1003908. doi: 10.1371/journal.pcbi.1003908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Shannon P, et al. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13:2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Liu X-S, et al. Zbtb7a acts as a tumor suppressor through the transcriptional repression of glycolysis. Genes Dev. 2014;28:1917–1928. doi: 10.1101/gad.245910.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Liu X, et al. Somatic human zbtb7a zinc finger mutations promote cancer progression. Oncogene. 2016;35:3071. doi: 10.1038/onc.2015.371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hartmann L, et al. Zbtb7a mutations in acute myeloid leukaemia with t (8; 21) translocation. Nat. Commun. 2016;7:11733. doi: 10.1038/ncomms11733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Rosenbauer F, et al. Acute myeloid leukemia induced by graded reduction of a lineage-specific transcription factor, pu. 1. Nat. Genet. 2004;36:624. doi: 10.1038/ng1361. [DOI] [PubMed] [Google Scholar]
- 57.Steidl U, et al. Essential role of jun family transcription factors in pu. 1 knockdown-induced leukemic stem cells. Nat. Genet. 2006;38:1269. doi: 10.1038/ng1898. [DOI] [PubMed] [Google Scholar]
- 58.Park Y-K, et al. Cage: a web-based cancer gene annotation system for cancer genomics. Genomics Inform. 2012;10:33. doi: 10.5808/GI.2012.10.1.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kanehisa M, Goto S. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Kanehisa M. Toward understanding the origin and evolution of cellular organisms. Protein Sci. 2019;28:1947–1951. doi: 10.1002/pro.3715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Kanehisa M, Furumichi M, Sato Y, Ishiguro-Watanabe M, Tanabe M. KEGG: integrating viruses and cellular organisms. Nucleic Acids Res. 2020;49(D1):D545–D551. doi: 10.1093/nar/gkaa970. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.