Small-scale population divergence is driven by local larval environment in a temperate amphibian

Abstract

Genomic variation within and among populations is shaped by the interplay between natural selection and the effects of genetic drift and gene flow. Adaptive divergence can be found in small-scale natural systems even when population sizes are small, and the potential for gene flow is high, suggesting that local environments exert selection pressures strong enough to counteract the opposing effects of drift and gene flow. Here, we investigated genomic differentiation in nine moor frog (Rana arvalis) populations in a small-scale network of local wetlands using 16,707 ddRAD-seq SNPs, relating levels of differentiation with local environments, as well as with properties of the surrounding landscape. We characterized population structure and differentiation, and partitioned the effects of geographic distance, local larval environment, and landscape features on total genomic variation. We also conducted gene–environment association studies using univariate and multivariate approaches. We found small-scale population structure corresponding to 6–8 clusters. Local larval environment was the most influential component explaining 2.3% of the total genetic variation followed by landscape features (1.8%) and geographic distance (0.8%), indicative of isolation-by-environment, -by-landscape, and -by-distance, respectively. We identified 1000 potential candidate SNPs putatively under divergent selection mediated by the local larval environment. The candidate SNPs were involved in, among other biological functions, immune system function and development. Our results suggest that small-scale environmental differences can exert selection pressures strong enough to counteract homogenizing effects of gene flow and drift in this small-scale system, leading to observable population differentiation.

Introduction

As evolution takes place at the population level, understanding local adaptation is central to many aspects of evolutionary, population, and conservation biology (Hoban et al. 2016; Delph 2018). The interplay between spatially varying selection, gene flow, and random genetic drift affects the genetic diversity of organisms and determines the ability of a population to adapt to local environmental conditions. Therefore, quantifying the relative contributions of natural selection, genetic drift, and gene flow to population divergence is crucial for understanding the local adaptation process (Savolainen et al. 2007). The relative strength of these processes is tightly linked with the spatial scale of environmental variation (Kawecki and Ebert 2004; Richardson et al. 2014; Bachmann et al. 2020). According to the more traditional view, gene flow is expected to counteract adaptation, and strong selection is needed to maintain beneficial alleles in a population (Haldane 1930). A more current view, however, suggests that gene flow has a multifaceted role in local adaptation (reviewed in Tigano and Friesen 2016). Depending on the relative strengths of gene flow and selection, gene flow can lead to gene swamping, where less beneficial alleles enter a locally adapted population (Balkau and Feldman 1973; Lenormand 2002), and thus serves as an obstacle for local adaptation. Here the effect size of the alleles involved is important as large-effect alleles are more resistant to gene swamping than small-effect alleles (Yeaman and Otto 2011). However, unless complete swamping occurs, the increase in standing genetic variation through gene flow may result in a larger set of available alleles for selection to work on (Barrett, Schluter 2008), and introgression of directly beneficial alleles into a population may aid adaptation (Hedrick 2013).

Multiple factors acting at various spatial scales affect the spatial distribution of genetic variation and rates of gene flow across landscapes. Geographic separation and environmental heterogeneity are two key factors affecting genetic structure among populations (Shafer, Wolf 2013; Sexton et al. 2014), but landscape resistance, partial barriers to dispersal, and differences in timing of reproduction can play important roles as well (Hendry and Day 2005; Van Strien et al. 2015). Geographic separation is directly related to the interplay of genetic drift and movement. Dispersal is often limited by geographic distance, resulting in higher gene flow between more closely located populations where low levels of migration will increase the influence of genetic drift and reinforce population divergence. This pattern is known as genetic isolation or isolation-by-distance (IBD), and is commonly observed as a correlation between neutral genetic differentiation and geographic distance (Wright 1943; Jenkins et al. 2010).

Adaptive local population divergence is typically mediated by abiotic and/or biotic differences in local environments, a pattern known as isolation-by-environment (IBE, Rundle and Nosil 2005). While the definition of IBE does not make any particular claim about the mechanisms shaping it, allele-frequency shifts correlated with environmental differences are often interpreted as the result of local variation in selection pressures (Kawecki and Ebert 2004; Sexton et al. 2014). Environmental differences can also influence the movements of animals, as well as the behavior of seed and pollen disperses, affecting the genetic structure of organisms (Dyer et al. 2012; Wang and Bradburd 2014). In heterogeneous environments, landscape characteristics, such as rivers, roads, habitat fragmentation, or mountain ridges, may promote or resist individual dispersal, which may lead to a pattern of isolation-by-resistance (IBR, McRae 2006). Habitat features can also result in small-scale shifts in phenology, where populations that occupy the same geographic distribution reproduce at different times, resulting in isolation-by-time (Hendry and Day 2005). Genetic divergence and allochronic reproductive isolation have been described in insects, vertebrates, and plants (Maes et al. 2006; Santos et al. 2007; Ribolli et al. 2017; Ismail and Kokko 2019).

Geography and landscape features are often correlated with local environmental variation, making it difficult to separate the relative effects of IBE from those of the others, and thereby understand their roles in genetic differentiation (Wang and Bradburd 2014). The autocorrelation between climatic and environmental gradients with geography is more evident at large spatial scales, which will confound the detection of IBE, and in particular, complicate any attempt to identify genomic regions involved in adaptive divergence (Vasemägi 2006). At small spatial scales, with a weak correlation between local environments and geographic distances, it would be easier to disentangle the genetic signatures of these different types of evolutionary processes. However, until recently, analyses have often suffered from low power to detect genetic differentiation among populations over small spatial scales. Indeed, in many cases where molecular methods have suggested low divergence, phenotypic methods have indicated considerable adaptive divergence (Leinonen et al. 2013; Savolainen et al. 2013). The study of divergence at small spatial scales has become increasingly feasible with modern genomic techniques, genotyping tens of thousands of single-nucleotide polymorphisms (SNPs), providing the resolution to detect population divergence over short spatial scales (Aguillon et al. 2017), and detecting signatures of selection within the genome (Hemmer-Hansen et al. 2013).

Several studies have aimed to unveil the causes of population differentiation at different environmental and spatial resolutions, such as along latitudinal and altitudinal gradients (e.g., Luquet et al. 2019; Yu et al. 2016; Campbell-Staton et al. 2017; Rödin-Mörch et al. 2019; Montero-Mendieta et al. 2019), as well as across land-, sea-, and riverscapes (e.g., Vincent et al. 2013; Whelan et al. 2019). Amphibians provide excellent systems to study adaptive divergence, where species with a metapopulation structure and a relatively low mobility are exposed to different environments even at small spatial scales. Ecoevolutionary models used to explore the dynamics of adaptation in spatially heterogeneous metapopulations show that depending on gene flow and demographic parameters, adaptation may be local at the network scale, and leads to a mosaic specialization (Hanski et al. 2011; Papaïx et al. 2013). Several studies performed on amphibians have found evidence of adaptive divergence at small spatial scales (Skelly 2004; Lind and Johansson 2007; Hangartner et al. 2012; Richter-Boix et al. 2013; Zellmer 2018). For example, earlier studies in moor frogs (Rana arvalis) in central Sweden identified adaptive phenotypic divergence as well as the transcription factor C/EBP-1 as a candidate gene associated with larval development time, and highlighted the roles of temperature, canopy cover, and breeding time in local adaptation of larval development rate (Richter-Boix et al. 2013, 2015). These studies have demonstrated that amphibian metapopulations are good systems to disentangle the genetic signatures of local natural selection, gene drift, and gene flow. However, studies with a higher density of genetic markers, allowing for detailed analyses of gene flow and adaptation, are lacking at small spatial scales.

In this study, we used double-digest restriction-associated DNA sequencing (ddRAD-seq) to characterize small-scale differentiation among nine R. arvalis populations in a network of wetlands in central Sweden. We investigated the importance of different modes of isolation (geographic distance (IBD), environment (IBE), and landscape resistance (IBR)) in shaping population divergence, and identified candidate loci involved in adaptive divergence. We expected that the influence of geographic distance on population divergence would be minor relative to the influence of landscape features and local larval environment and the latter to shape adaptive divergence in this small-scale system. More specifically, we (1) investigated fine-scale population structure in a landscape with high potential for dispersal and gene flow, (2) partitioned the effects of local larval environment, landscape features, and spatial separation on total genetic variation across the wetland network, conducting model selection to test which scenario fits the data the best, and (3) identified loci under putative divergent selection associated with fine-grained local larval environmental variation.

Methods

Sample collection and characterization of local environments

R. arvalis is a widespread frog occurring from western Europe to western Siberia (Sillero et al. 2014). It is an explosive breeder spawning in permanent and temporary ponds, marshes, and lakes in early spring. In late March–April 2016, we collected eggs from 16 to 20 egg masses (each mass representing a separate family) in each of nine populations in a metapopulation-like network of interconnected wetlands located in Uppland in central Sweden (Fig. 1, Table S1). This system consists of temporary and permanent ponds and marshes in a landscape of agricultural fields and mixed forests (Richter-Boix et al. 2013). The eggs were brought to the laboratory at Uppsala University where they hatched. Tadpoles were raised in a common garden experiment in a separate life-history study (Rödin-Mörch 2019). In short, tadpoles were raised in two different temperature treatments (16 and 19 °C), until they reached metamorphosis (stage 42, Gosner 1960) and were euthanized with an overdose of MS222.

Fig. 1. Map of the sampled population in Uppland (Sweden).

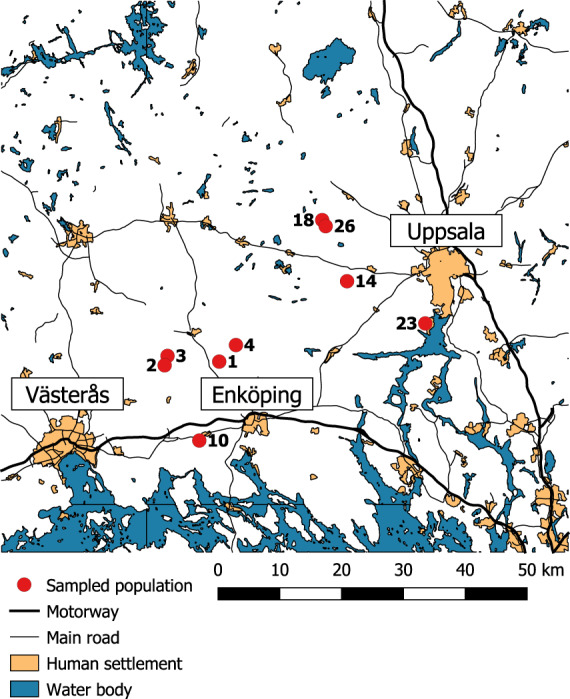
The map shows the population number and the location of those populations relative to urban areas, roads and large bodies of water.

The average distance between the study populations was 24.1 (min 1.1, max 42.6) km. Although the maximum pairwise distance between ponds is higher than the maximum known dispersal distance of the species, this system is characterized by numerous adjacent wetlands to the focal ponds that can facilitate dispersal across the landscape (Richter-Boix et al. 2013). Given these aspects of the current study system in terms of geography and environment, we characterize it as a small-scale system as opposed to microgeographic scales or large environmental gradients. We assessed multiple aspects of the local larval environment (Table S1) in order to analyze IBE. We first measured pH for each wetland at the time of egg laying using a multiparameter device (HANNA instruments). We then measured water temperature for 2 months following egg laying using data loggers (HOBO Water temp Pro v2 Data Logger). The loggers were placed in the immediate vicinity of the area where the eggs were laid and set to record every 15 min. Mean temperature for the entire recording period in each wetland was used in the analyses. In early June, the same person (ARB) measured the percentage of canopy cover in each wetland by visually estimating the amount of nonvisible sky into 10% categories (Korhonen et al. 2006). We estimated the percentage of aquatic vegetation cover along a 15-m transect (Palik et al. 2001) and a predation risk index, the latter being measured by counting macroinvertebrates and newts collected using five standardized dip net sweeps at each of five locations in each wetland (Michel 2011). Finally, we defined breeding time as the number of days from January 1st to the date when the first egg was found in the pond. In R. arvalis, the egg-laying period within a wetland is very short (Richter-Boix et al. 2013), and the date of the first egg is a good proxy of breeding date. In the present study, eggs were laid between 29th of March and 18th of April with a maximum difference of 20 days in breeding time.

To investigate the effect of landscape features on population divergence (IBR), we measured four landscape variables around each of the nine sites by summing the areas of each landscape variable within circular buffer zones at a spatial scale of 2000 m (Table S1), as this is the most common movement distance of amphibians (Smith and Green 2005). The amount of arable land was extracted using topographic vector maps converted to raster format. Mature forest (defined as >200 m³ ha⁻¹) was quantified using k-Nearest-Neighbor-raster (Reese et al. 2003) originally at 25 × 25-m resolution and aggregated to 100 × 100 m by averaging due to low-volume accuracy at the original scale (Gjertsen 2007). The total road length was estimated by summing up the total length of roads within the buffer zone. Additionally, a connectivity index in terms of number and size of nearby wetlands was estimated, using a kernel estimation weighted by distance (smoothing curve of 5 km from each pond) and perimeter of all the surrounding ponds, as vegetated shallow shores are important breeding sites for moor frogs. All landscape variables were processed in ArcMap 10.6 (ArcGIS, ESRI, Redlands, CA, USA).

DNA extraction and ddRAD library prep

To minimize confounding effects of potentially including siblings in the analysis, we used one individual that was picked at random from each egg mass. We extracted DNA from a total of 16–20 individuals from each population (163 individuals in total), from the hind leg or head of metamorphosed individuals using a high salt extraction precipitation protocol with an extra ethanol precipitation step (modified from Paxton et al. 1996). DNA concentration and purity were checked using NanoDrop® 2000 spectrophotometer and Qubit® 3.0 fluorometer Quantitation Kit (Invitrogen™). We prepared a ddRAD-seq library following the protocol by Johansson et al. 2017 (modified from Peterson et al. 2012; Mastretta‐Yanes et al. 2015). DNA was digested for 18 h using the restriction enzyme combination SbfI-HF® and MseI, and digestion was confirmed by gel electrophoresis. We ligated 16 uniquely barcoded (6 bp) P1 adapters and one P2 adapter to the digested DNA. The ligation product was cleaned using AMPure XP beads. For PCR amplification, we used custom Illumina primers containing 12 unique indices, and DNA was amplified using Q5 DNA polymerase (New England Biolabs, Massachusetts, USA). In order to correct for any biased amplification, each individual sample was PCR-amplified in four separate reactions. Samples were then pooled in equimolar concentrations, and amplification success was confirmed using gel electrophoresis. For size selection, we performed agarose gel extraction by cutting out the desired fragments between ~350 and 600 bp, and extracted the product using the QIAquick Minielute Gel Extraction Kit. The final library was then pooled, checked for purity, and the concentration (50.6 ng/μl) was measured using NanoDrop^® 2000 spectrophotometer and the Qubit^®3.0 fluorometer Quantitation Kit (Invitrogen™). The library was sequenced on four lanes of Illumina 2500 (2 × 125 bp) in high-throughput mode by SciLifeLab, Uppsala, Sweden.

ddRAD bioinformatics

Using process_radtags in STACKS v.2.1 (Catchen et al. 2013), we demultiplexed, cleaned, and filtered the raw reads based on quality and base calling. To reconstruct loci and call SNPs, we ran the individual programs included in denovo_map (cstacks, sstacks, tsv2bam, gstacks, and populations) separately for pair-end reads using starting parameter settings similar to the optimal parameter combinations in Rödin-Mörch et al. (2019). We then changed the values of the parameters -M (the number of mismatches allowed between loci when an individual is being processed) and -n (the number of mismatches allowed when constructing the catalog) by increasing or decreasing the parameter value one step. We tried four different parameter combinations (Table S2) and evaluated which of them yielded the maximum number of variant sites, resulting in selection of the combination -M 4 and -n 3. A final filtering step was performed in the program populations, where we filtered SNPs based on a minor allele frequency of 0.02, present in all nine populations and in at least 70% of the individuals. We only retained the first SNP of each RAD locus.

Population structure

We filtered out SNPs suggested to be under putative divergent selection (described below) to obtain a data set evolving under neutral expectations. All the following analyses were conducted in R v.3.5.2 (R Core Team 2019). To analyze and visualize population structure, we first used discriminant analysis of principal components (DAPC) in the adegenet package v.2.1.1 (Jombart 2008; Jombart and Ahmed 2011) and determined the number of PCs to retain by performing stratified cross-validation. We ran cross-validation using the xvalDapc function for 300 repetitions, keeping default settings. Second, we used the spatially informed package tess3r v.1.1.0 (Caye et al. 2018), which estimates ancestry coefficients using geographically constrained nonnegative matrix factorization to characterize population structure, and evaluates the optimal number of clusters fitting the data based on the cross-validation score. Finally, we estimated global and pairwise F_ST (Weir and Cockerham 1984) with 95% confidence intervals for the total data set in assigner v.0.4.1 (Gosselin et al. 2016).

Identifying differentiation outliers

In order to identify differentiation outliers, we used pcadapt v.4.0.3 (Luu et al. 2017), which utilizes principal component analysis to detect SNPs most associated with the axes related to population structure. The method estimates Mahalanobis distances between SNP z scores and the first K principal components (PCs) capturing population structure. We ran the initial analysis for ten PCs and evaluated the optimal K PCs to retain for the final analysis by graphically inspecting the per-PC decrease in variance in a scree plot, and the individual clustering using a score plot (Fig. S1). We retained three PCs in order to calculate the test statistic, transformed per-SNP p values into q values, in order to correct for multiple comparisons using the R package qvalue v.2.4.2 (Storey et al. 2019), and filtered the final list of outliers using a false-discovery rate (FDR) of 0.05 in order to correct for multiple comparions.

Identifying environmentally based differentiation in the landscape

We estimated the influence of geographical distance, local environmental, and landscape variables on total genetic variation using redundancy analysis (RDA) and partial redundancy analysis (pRDA) in the R package vegan v.2.5.3 (Oksanen et al. 2019). As RDA does not allow for missing data, we imputed the 2% missing genotypes found in the data set using Random Forest on-the-fly imputation (Tang and Ishwaran 2017) from the randomForestSRC package v.2.7 (Ishwaran and Kogalur 2018) implemented in the grur package v. 0.0.11 (Gosselin 2018). RDA uses a multivariate linear regression with the genotype matrix as a response variable and environmental variables as predictors; a PCA is then performed on the new matrix of fitted values from the regression in order to construct constrained axes summarizing the variation explained by the predictor variables (Legendre and Legendre 1998).

As compared to RDA, pRDA differs in that it removes the influence of some predictor variable on the response matrix when trying to estimate the influence of the remaining predictors; here we control for spatial influence (IBD) on the response matrix by incorporating geographical coordinates. We present the raw r² values, which for pRDA is referred to as semipartial r² (Legendre et al. 2011), and adjusted r² for the models. As a response matrix, we used a transposed matrix of allele abundance in pcadapt format (encoded as 0/1/2) and the predictors consisted of geographical coordinates, local larval environmental, and landscape variables that were scaled and centered for the analyses. We performed RDA on geographic coordinates and pRDA on local larval environmental and landscape variables after testing the correlation between variables to remove any potential multicollinearity, by removing one of the correlated variables if |r| > 0.7 (Table S3 a–c). We tested the significance of each model with the anova.cca function using 999 permutations.

To complement the RDA, we used Maximum-likelihood population-effect (MLPE) mixed models (Clarke et al. 2002). MLPE models analyze the effect of one or several predictor distance matrices on the response distance matrix. The method accounts for the nonindependence between the pairwise measurements in the distance matrices by including population origin as a random effect. We fitted six different MLPE models in lme4 (Bates et al. 2015) using the Euclidean distance between individuals in the same genotype matrix as used for the RDA as a response variable. We included Euclidean geographic, local larval environmental, and landscape distance matrices as fixed effects, either separately testing for IBD, IBE, and IBR, but also in combination two by two (IBD and IBE, IBD and IBR, and IBE and IBR), testing their individual effects combined with their interaction. We included population as a random effect where individuals were implicitly nested within each population. We ran the models with the setting REML = FALSE, as this yields an unbiased estimate of Akaike’s information criterion (AIC) for model comparison (Clarke et al. 2002). We compared each model testing IBD, IBE, and IBR, as well as the best-ranked models based on AIC with a null model just containing the intercept term and the population-specific random effects using the Anova function in the car package (Fox and Weisberg 2019). We used the function r2 from the performance package (Lüdecke et al. 2020) to estimate the amount of variance explained by the fixed effects only (marginal R²) and the variance explained by the fixed and random effects together (conditional R²).

Gene–environment association (GEA)

We used two different gene–environment association (GEA) approaches to identify candidates for adaptive divergence using the imputed SNP data. First, we used the univariate method latent factor mixed models (LFMM) implemented in the LEA package v.1.99.2 (Frichot et al. 2013; Frichot, François 2015). LFMM identifies associations between individual SNPs and environmental variables that are included as fixed effects, while at the same time modeling any underlying population structure included as a latent or hidden factor to correct for its influence. We ran LFMM assuming six latent factors based on graphically evaluating the cross-entropy scores, as well as the number of clusters identified by tess3r and DAPC, and the number of environmental variables included (see below). The Gibbs sampling algorithm was initialized with a burn-in of 50,000 iterations followed by 200,000 main iterations for each scaled and centered environmental variable for 30 independent runs. We then combined the resulting z scores across runs from which the median was used. The p values were then calibrated using the genomic inflation factor to account for population structure, and corrected for multiple comparisons using an FDR of 0.05 calculated as above. Second, we followed the approach described in Capblancq et al. (2018) to identify SNPs associated with the local larval environment, and that of Forester et al. (2018) for pre- and postprocessing of data. The association method combines RDA and the outlier detection approach implemented in pcadapt described above, and has the ability to detect multilocus selection imposed by the combined effect of multiple environmental gradients. We used the pRDA model described above, where we removed the spatial influence on the genetic response matrix. We then calculated the Mahalanobis distance for the loci loading on the six retained constrained axes, and adjusted the p values using an FDR of 0.05 calculated as above.

SNP annotation

We conducted BLAST searches with the RAD tags containing the SNPs putatively under divergent selection against the nonredundant protein database (blastx) and nucleotide database (dc-megablast). A match was considered and retained if it passed an e-value threshold of <10⁻⁵ (BLASTX) or <10⁻²⁰ (dc-megablast) and had at least ~70% query coverage and similarity. We retrieved gene ontology terms and performed enrichment analysis in BLAST2GO using Fisher’s exact tests and an FDR of 0.05 using BLAST2GO (Conesa et al. 2005).

Results

Sequencing, ddRAD bioinformatics, and population summary statistics

We obtained 746.2 M reads from four lanes of Illumina sequencing. After quality control, running every individual component of the de novo pipeline separately and filtering, we obtained a total of 5,915,415 sites (average: 30,888 RAD tags, mean length: 191.51 bp, average depth of coverage: 34.4×). This resulted in a final data set of 16,707 SNP loci across populations with the number of polymorphic sites within populations ranging from 14,580 to 15,460. Expected heterozygosity (H_E), nucleotide diversity (π), and inbreeding coefficients (F_IS) ranged between 0.277 and 0.289, 0.286 and 0.297, and 0.016 and 0.050, respectively (Table S4).

Population structure

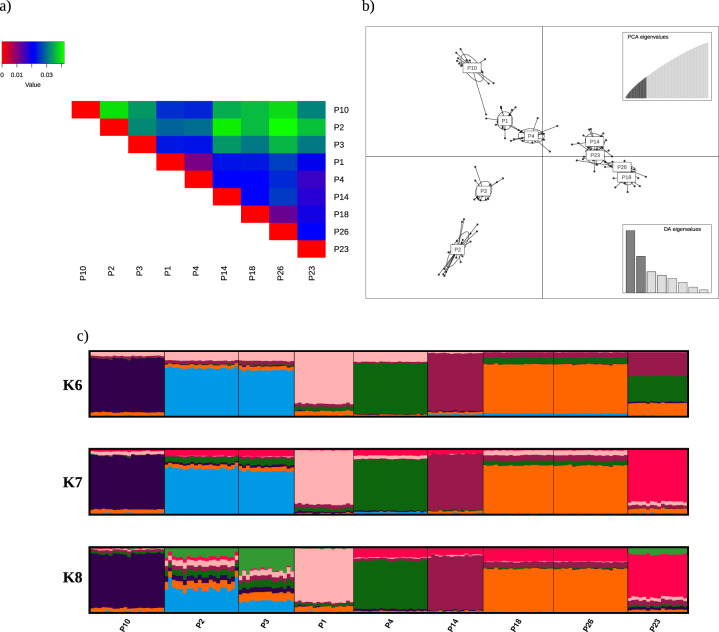
Estimating F_ST revealed overall low levels of genetic differentiation (global F_ST = 0.0277, 95% CI 0.0274–0.0282). Pairwise F_ST ranged between 0.0111 and 0.0417 (mean = 0.02735, Table S5), with a cluster of three populations (P2, P3, and P10) showing elevated pairwise F_ST values compared to the rest of the populations (Fig. 2a). Using only the neutral data, after running cross-validation retaining 40 PCs with the lowest MSE and eight discriminant functions, the DAPC revealed the presence of five to six somewhat discrete clusters (Fig. 2b). The first axis separated P1–P4 and P10 from P14, P18, P23, and P26. The second axis further separated the populations, most notably P2 and P3 from P1, P4, and P10. Using tess3r and neutral SNPs, the cross-validation scores calculated for each K-ancestral populations showed a relatively steep decline with increasing K and a hint of a plateau at around K6–8, signifying the optimal K (Fig. S2). Each wetland represents to a certain extent a discrete cluster with the exception of populations very close to each other (P18–P26: 1.13 km; P2–P3: 1.59 km, but where P2 and P3 start to separate at K7 and K8, Fig. 2c).

Fig. 2. Panel showing estimates of population differentiation and structure.

Panel showing a pairwise F_ST values represented as a triangular heat map. b DAPC ordination showing population structure along the first two axes. c Tess3r ancestry coefficient barplots for the K’s with the lowest cross-validation score.

Identifying environmentally based differentiation in the landscape

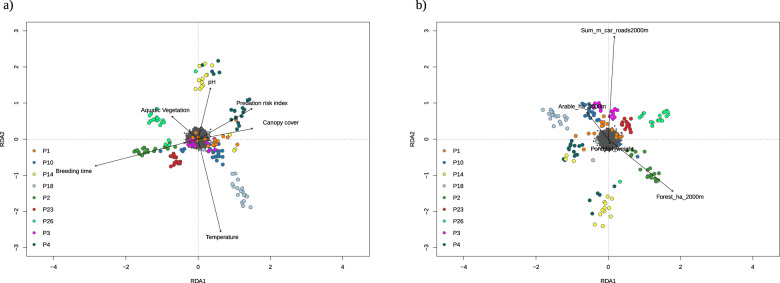
The RDA, including only geographical coordinates, showed a significant effect of spatial separation on total genetic variation, explaining 0.8% of the variation (F_2,158 = 1.664, p < 0.001), indicating IBD. Using MLPE, we found that geographic distance explained less variation than in the RDA, although still a significant proportion (0.2%, χ² = 26.58, Df = 1, p < 0.001). In order to account for the possible confounding effects of spatial autocorrelation when evaluating the effect of the local larval environment, we ran a pRDA controlling for IBD. We found a significant effect of the local larval environment on total genetic variation (2.3% of the variation explained, Table 1), indicating IBE (F_6,152 = 1.624, p < 0.001). This would indicate that the impact of spatial correlation was relatively low relative to the influence of the local larval environment. This was supported by the MLPE models where the local larval environmental distance matrix explained 1.2% of the variation (χ² = 141.98, Df = 1, p < 0.001); this was however less variation explained than by the pRDA. For the pRDA, the two major axes of variation showed clear environmentally based population clustering (variance explained: RDA1 = 25%, RDA2 = 18%, Fig. 3a). The first axis differentiates populations inhabiting ponds with more aquatic vegetation and later breeding time from ponds with higher predation risk and canopy cover. The second axis separates populations from warmer ponds with later breeding from those with higher pH. The pRDA also found a significant effect of landscape features (roads, amount of forest, arable land, and pond connectivity) on total genetic variation (F_4,156 = 1.68, p < 0.001), but this explained slightly less of the total genetic variation (1.8%, Table 1) than the local larval environment. This indicates an additional level of IBE, serving as a coarse estimate of IBR. For the first two axes (33 and 25% of the variance explained), we observed clear landscape-influenced population structure. The first axis differentiates populations from ponds surrounded by the highest amount of roads and arable land from populations surrounded by more forest (Fig. 3b). However unlike the RDA, the results from the MLPE models reveal a larger effect of landscape distance compared to local larval environment distance (2% of the variance explained, χ² = 209.33, Df = 1, p < 0.001). Furthermore, we conducted model selection for the MLPE models and found all three models representing IBD, IBE, and IBR, as well as the more complex models including two fixed effects showing a better fit than the null model (Table 2). Based on the AIC score, we found that the IBR model fits the data slightly better than the strict IBE model. However, two of the three models containing two fixed effects fit the data better than any of the simpler IBD, IBE, and IBR models. The best-fitting model based on AIC included the geographic and local larval environmental distance matrices as well as their interaction (3.6% of the variance explained, IBD: χ² = 0.363, Df = 1, p = 0.55, IBE: χ² = 118.97, Df = 1, p < 0.001, and IBE × IBD: χ² = 304.53, Df = 1, p < 0.001). The second best model included landscape and local larval environmental distance matrices and their interaction (3.5% of the variance explained, IBE: χ² = 2.07, Df = 1, p = 0.15, IBR: χ² = 67.47, Df = 1, p < 0.001, and IBE × IBR: χ² = 205.84, Df = 1, p < 0.001).

Table 1.

Amount of total genetic variance explained in RDA and pRDA models by geographical distance, local larval environment, and landscape features.

RDA	Spatial	Local environment	Landscape
r2	0.026	0.059	0.042
Adjusted r2	0.008	0.023	0.018

Fig. 3. RDA plots showing the influence of the local larval environment and landscape features on population structure.

The length of the vectors denotes their relative importance. a) local larval environment b) landscape features.

Table 2.

Proportion of variance explained estimates from MLPE models testing the effect of geographic, local environmental, and landscape distances as well as their interactions on genetic distance, with the best-fitting model in bold.

	Conditional R2	Marginal R2	Df	AIC
Null	0.096	0	3	63193.7
IBD	0.088	0.002	4	63169.1
IBE	0.074	0.012	4	63054.9
IBR	0.075	0.020	4	62989.0
IBD and IBE	0.080	0.036	6	62757.6
IBD and IBR	0.068	0.025	6	62908.6
IBE and IBR	0.077	0.035	6	62786.7

Conditional R² here refers to the proportion of variance explained by the fixed and random effects together, and marginal R² refers to the variance explained by the fixed effects only.

Identifying differentiation outliers and GEA

We identified 29 differentiation outliers using pcadapt (Fig. S3), the low number of outliers reflecting the overall low level of population differentiation. The univariate GEA with LFMM identified 110 SNPs associated with aquatic vegetation cover (Fig. S4a), 109 with canopy cover (Fig. S4b), 76 with pH (Fig. S4c), 133 with predation risk index (Fig. S4d), 49 with mean temperature (Fig. S4e), and 153 with breeding time (Fig. S4f). Some of the SNPs identified overlapped between environmental variables, LFMM in total identifying 547 candidates. Furthermore, using the pRDA-based GEA approach, we identified in total 576 candidate SNPs associated with the environmental variables. From these, 60 showed the highest correlation with aquatic vegetation cover (|r| = 0.066–0.307), 150 with canopy cover (|r| = 0.056–0.379), 94 with pH at breeding (|r| = 0.080–0.448), 68 with predation risk index (|r| = 0.092–0.376), 127 with mean temperature (|r| = 0.093–0.363), and 77 with breeding time (|r| = 0.075–0.356). The two methods only converged on 123 SNPs, and in total, we identified 1000 candidates putatively under environmentally mediated divergent selection.

SNP annotation

None of the candidates identified by pcadapt could be matched to any known genes or proteins by querying the blastx and megablast databases. For the SNPs associated with local larval environment, the RAD tags containing those SNPs matched 32 genes or genomic regions (Table S6) and 21 proteins, eight of these matching unknown or hypothetical proteins (Table S7). Hits of particular interest for the local larval environment-associated SNPs were the immune genes MHC class 1a, brevinin-2-CE, palustrin-2-CE, TRIM25, and NLRP3, as well as genes potentially related to development and stress, such as ITGB1, Mab21, DAGLB, and TRH, and a protein similar to bifunctional apoptosis regulator. Due to the relatively few hits, no significant GO enrichment could be retrieved.

Discussion

In this study, we attempted to disentangle the relative influence of different layers of the environment on putative adaptive genomic divergence in a system where we have earlier shown strong phenotypic divergence and ample opportunity for dispersal and gene flow across the landscape (Richter-Boix et al. 2013, 2015). Over the past decade, accumulating studies have indicated that geographic distance are geographical barriers that are not the only factors affecting gene flow and thereby population differentiation, and environmental differences may be the key factor underlying effective migration (Shafer, Wolf 2013; Sexton et al. 2014). Using a ddRAD-seq approach, we identified genomic variation that we posit is associated with adaptive divergence in the R. arvalis populations, and detected fine-scale population structure and differentiation. Our results suggest that small-scale adaptive divergence in R. arvalis is mainly driven by the local larval environment, but where the combined effect between local environmental and spatial and landscape features is also very influential. We found that, much like what would be expected (Meirmans 2015), the effect size of local larval environment on total genetic variation was relatively small, which was also true for landscape features and geographic separation. Nevertheless, larval environment explained more total genetic variation than landscape features or geographic distance, the latter explaining the smallest amount of variation. These results suggest that selection is efficient enough to counteract the potential negative effects of gene flow and genetic drift on adaptive divergence in this small-scale system. We identified a number of genes involved in immunity, development, and stress associated with local larval environmental variables, and might thus potentially be involved in adaptive divergence. Our results agree with previous studies that have shown the importance of thermal environment, canopy cover, time constraints, predation, desiccation risk, and pH as important selective agents for larval amphibians (e.g., Skelly 2004; Lind and Johansson 2007; Hangartner et al. 2012; Richter-Boix et al. 2013, 2015; Nunes et al. 2014; Van Buskirk J 2014).

Population structure

In spite of the low levels of population differentiation observed in the landscape, we were able to identify somewhat discrete clusters in the landscape. The tess3r analysis revealed that there are between six and eight population clusters in the landscape. At these levels, most populations represented clusters with various degrees of admixture, lending further support for the occurrence of gene flow. When populations are grouped into an increasing number of clusters, more apparent substructure reveals itself. The DAPC analysis supported five to six somewhat discrete clusters, corresponding to the positions of populations in the landscape. Here, the first axis represented the component explaining a large part of the spatial and landscape variation based on the position of the populations in the landscape, whereas separation along the second axis mainly reflected local variation and smaller-scale dispersal barriers. Taken together, we found evidence of neutral population structure in spite of the assumed high gene flow. However, the absence of very clear population boundaries, and increased admixture among some of the population, could possibly indicate asymmetrical patterns of gene flow in the landscape.

Identifying environmentally based differentiation in the landscape

Over the past few years, numerous studies have presented evidence for small-scale divergence between habitats without physical barriers in organisms from plants and insects to fish and amphibians (Skelly 2004; Leimu and Fischer 2008; Fraser et al. 2011; Watanabe et al. 2014). In the present study, we found that a variety of mechanisms influenced population structure in our study system, identifying three distinct ways. First, as in a previous study using five microsatelite loci involving some of the same populations as the present study (Richter-Boix et al. 2013), we found evidence of differentiation caused by the local larval environment (IBE), detectable as larger allele-frequency differences among populations inhabiting more contrasting environments. The overall F_ST in the network of wetlands was low, as expected, with moderate-to-high levels of gene flow. However, using F_ST as a direct proxy for gene flow without additional information is problematic, giving only indications that gene flow might be occurring (Whitlock and McCauley 1999). In the present system, the level of connectivity with ponds surrounding our focal ponds suggests that low F_ST is the result of high gene flow (Richter-Boix et al. 2013). Local selection would have to be strong to remove migrants to generate divergence between the ponds. Environmentally induced or genotype-dependent dispersal preferences could plausibly generate the observed genetic divergence between different breeding environments. Biased dispersal is an effective cause of reproductive isolation that can reduce migration rates and gene flow over small spatial scales (Bolnick and Otto 2013). Divergent habitat choice has been documented experimentally in sticklebacks (Bolnick et al. 2009), and in amphibians, site fidelity (Semlitsch 2008) as well as breeding pond selection in response to the presence of predators and competitors (Buxton et al. 2017) are well known. The environmental variable contributing most to the IBE pattern on the first two RDA axes was temperature, closely followed by breeding time, predation risk, pH, canopy cover, and aquatic vegetation, differentiating populations into four different clusters along the axis. As opposed to a linear environmental gradient such as temperature, these results highlight the multivariate effect of the local larval environment shaping IBE in this system. The results from the MLPE model selection further corroborate the importance of the local larval environment in shaping divergence in the landscape.

Second, we found that connectivity was affected by landscape complexity, showing a pattern of IBR. Earlier studies demonstrated that natural and anthropogenic landscape features contribute to the population structure in urodeles and anurans (Vos et al. 2001; Lenhardt et al. 2017; Homola et al. 2019). Different urban landscape elements are capable of influencing connectivity in metapopulation-structured species (Graham et al. 2017), and earlier studies on R. arvalis showed that geographical distance and density of roads were best predictors of population structure (Vos et al. 2001; Arens et al. 2007). In our system, the strongest landscape predictors influencing total genetic variation were the total length of roads within 2000 m of the focal pond and the amount of forest surrounding the ponds. Our results are in line with observations that large-scale landscape features can cause population differentiation, depending on the level of human disturbance and its influence on connectivity in the landscape (Storfer et al. 2007; Safner et al. 2011; Youngquist et al. 2017). MLPE results suggested that landscape distance (IBR) fits the data better than local larval environmental distance (IBE), explaining slightly more of genetic variation than what we found in pRDA models. However, R² in MLPE models has a tendency to increase with model complexity (Row et al. 2017), and R² values from the more complex models should therefore perhaps be interpreted with some caution. More specifically, an explanation for the discrepancies between the different types of models could be the relative influence of the random effects on local larval environmental and landscape distance. Indeed, a comparison of the conditional R² accounting for both the fixed and random effects in the IBE and IBR models shows roughly the same variance explained, suggesting that Euclidean local larval environmental distance is more specific to the individual populations than landscape distance. This interpretation is further strengthened by the RDA results: we found a higher proportion of genetic variation explained by the local larval environment than the landscape features when we corrected for the influence of geographical separation, as opposed to population origin in the MLPE models. Furthermore, the best-fitting MLPE model includes both larval environmental and geographic distances as well as their interaction, suggesting that environmental variation and allele frequencies are not distributed homogeneously in the landscape, but are, to a certain extent, spatially structured, which contributes to the divergence.

The third effect we detected was the small influence of geographic distance shaping genetic differentiation. Previous works in the same system found no signature of IBD or IBR, possibly as a result of lower genetic resolution (five microsatellites). Using a larger number of markers, we found that geographical distance explained a small but significant amount of genetic variation, demonstrating that population structure can be more clearly resolved with RAD sequencing than with microsatellites (Rašić et al. 2014; Vendrami et al. 2017), the increased number of markers giving us more power to detect subtle effects of spatial separation. The spatial genetic autocorrelation signature expected under IBD has been observed in other amphibian species at similar spatial scales (Johansson et al. 2005; Zamudio and Wieczorek 2007; Zellmer 2018).

Identifying differentiation outliers and GEA

Given the relatively low levels of population differentiation in the landscape, the low number of differentiation outliers found by pcadapt in comparison to the number of candidate SNPs found associated with the local larval environment was expected. Using the two methods based on associations between SNPs and local larval environmental variation (LFMM and pRDA), we identified a much larger number of candidate SNPs under putative divergent selection. These methods identified a similar number of outlier SNPs, but they only converged on 123 SNPs. This however might be explained by the differences in analytical strength between multivariate and univariate analyses. The highest number of candidates identified by LFMM was for breeding time followed by predation risk index, aquatic vegetation, canopy cover, pH, and mean temperature. The highest numbers of the candidate SNPs obtained by pRDA-based analyses were correlated with canopy cover, followed by mean temperature, pH, breeding time, predation risk index, and aquatic vegetation. The ranking of the relative importance of the environmental variables could also highlight the discrepancy between univariate and multivariate methods used in this study, where associations found at the additional dimensions in the pRDA are potentially lacking in LFMM. Their importance can also be further explained by the relationship between the variables that might more easily be detected with a multivariate approach. Ponds with high forest canopy have more emergent vegetation, lower temperature, and relatively few predators, while open ponds in human landscapes have little canopy cover, few emergent vegetation, higher temperature, and more predators (Richter-Boix et al. 2013). The genome size of R. arvalis is estimated to be ~6 Gb (Vinogradov 1998) and attempts to identify loci under selection in reduced-representation sequencing studies, where the study organism has a large genome, most often suffering from limited power to detect any larger proportion of causal loci. Consequently, our results should be treated with some caution as they likely only represent a relatively smaller part of the whole picture. However, any identified candidate can be compared in studies covering the whole genome as the latter becomes more affordable.

We annotated 4.3% of the SNPs associated with the local larval environment, and none of the differentiation outliers, to known genes and proteins using BLAST. These low numbers reflect the difficulty to obtain functional and biological annotation for nonmodel organisms (Yandell and Ence 2012), and amphibians in particular, given the general scarcity of genomic resources in this group (but see, e.g., Hellsten et al. 2010; Sun et al. 2015; Session et al. 2016; Hammond et al. 2017). Our BLAST hits matched known genes and proteins that had a relatively wide variety of biological functions (Tables S6, S7), suggesting fine-grained and multifaceted selection acting among, as well as within populations. However, there is a potential risk of overinterpreting candidate gene hits from various genome scan methods, in particular in reduced-representation sequencing studies like ours where only a small part of the genome has been covered, and the number of BLAST hits are relatively few. With this in mind, we discuss a few hits below in more detail that align with genes of importance in amphibian development and immune response, as well as hits we have identified to be under putative divergent selection in previous studies.

We obtained two matches with a possible function related to larval development. The first was bifunctional apoptosis regulator most correlated with mean temperature (r = −0.156), which we have previously identified to be under putative divergent selection along a 1700-km latitudinal gradient (Rödin-Mörch et al. 2019). While the exact function of this gene in amphibians is uncertain, the product of this gene suppresses cell death in mammals (Zhang et al. 2000). Common garden studies have revealed large among-population differences in larval life histories (development rate and mass at metamorphosis) in the present system (Richter-Boix et al. 2013, 2015) as well as along the latitudinal gradient (Luquet et al. 2019; Rödin-Mörch 2019). It seems plausible that the regulation of cell death is related to the development rate as amphibian metamorphosis involves large-scale body restructuring, and thyroid hormone-induced cell death plays a major role in this process (Nakajima et al. 2005). We also matched two different RAD tags containing SNPs with thyrotropin-releasing hormone receptor 1 (TRHR1), mostly correlated with breeding time and pH (r = 0.095 and 0.141). Thyrotropin-releasing hormone stimulates the secretion of growth hormone and prolactine (Denver 1997; Galas et al. 2009), which is known to inhibit amphibian metamorphosis by promoting growth (Brown and Frye 1969; Galas et al. 2009).

The second candidate that we also found along a latitudinal gradient was brevinin-2-CE that is part of the innate immune system. This gene codes for an antimicrobial peptide (AMP) secreted in the skin of amphibians, protecting against bacterial, viral, and fungal pathogens (Rollins-Smith 2009). The associated SNP was also most correlated with mean temperature (r = −0.275). We also obtained a match to another AMP gene palustrin-2-CE, which was most correlated to pH (r = 0.067). AMPs protect anurans against pathogens, such as the chytrid fungus Batrachochytridium dendrobatides (Bd) and ranavirus (Rollins-Smith and Conlon 2005; Rollins-Smith 2009). Previous studies have found that Bd prevalence in R. arvalis is moderately high in this area (Meurling et al. 2020), but studies on ranavirus are lacking in Sweden. Furthermore, we identified matches with additional genes related to immune response, such as the major histocompatibility complex class I (MHC class I) correlated with the amount of aquatic vegetation (r = −0.106), MHC class II correlated with predation risk index (r = 0.249), and TRIM25 and NLRP3 (inflammasome) correlated with mean temperature (r = −0.144 and r = 0.252, respectively). Previous studies have revealed complex interactions between local larval environmental characteristics and disease: depending on parasite type, aspects of the local larval environment, such as abundance of predators and canopy cover, can have an effect on disease risk (Holt and Roy 2007; Becker et al. 2012).

Conclusions

In recent years, landscape genomics studies have started to identify the relative effects of the environment, the landscape and distance, in limiting gene flow and shaping genetic differentiation. Here we document modest but significant patterns of IBE, IBR, and IBD between amphibian populations in a small-scale network of breeding ponds. We find that IBE, either alone or in combination with that of the others, is larger than IBR and IBD, supporting the long-standing view of pond-level local adaptation of amphibian populations. We identify outlier SNPs under putative divergent selection associated with specific aspects of the local environment, those SNPs being involved in developmental processes and the immune system. Our analyses show that regardless of ongoing gene flow populations, local adaptation can lead to genomic divergence, and showcase the complexity of different factors acting at different scales in determining these patterns of divergence.

Data availability

Sequencing raw data is accessible at NCBI SRA under BioProject accession number: PRJNA660937. Relevant input and output files and analysis scripts are accessible at Dryad (10.5061/dryad.b5mkkwhbc).

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Supplementary information

The online version of this article (10.1038/s41437-020-00371-z) contains supplementary material, which is available to authorized users.