Abstract
Background: The brain magnetic resonance imaging (MRI) image segmentation method mainly refers to the division of brain tissue, which can be divided into tissue parts such as white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF). The segmentation results can provide a basis for medical image registration, 3D reconstruction, and visualization. Generally, MRI images have defects such as partial volume effects, uneven grayscale, and noise. Therefore, in practical applications, the segmentation of brain MRI images has difficulty obtaining high accuracy.
Materials and Methods: The fuzzy clustering algorithm establishes the expression of the uncertainty of the sample category and can describe the ambiguity brought by the partial volume effect to the brain MRI image, so it is very suitable for brain MRI image segmentation (B-MRI-IS). The classic fuzzy c-means (FCM) algorithm is extremely sensitive to noise and offset fields. If the algorithm is used directly to segment the brain MRI image, the ideal segmentation result cannot be obtained. Accordingly, considering the defects of MRI medical images, this study uses an improved multiview FCM clustering algorithm (IMV-FCM) to improve the algorithm’s segmentation accuracy of brain images. IMV-FCM uses a view weight adaptive learning mechanism so that each view obtains the optimal weight according to its cluster contribution. The final division result is obtained through the view ensemble method. Under the view weight adaptive learning mechanism, the coordination between various views is more flexible, and each view can be adaptively learned to achieve better clustering effects.
Results: The segmentation results of a large number of brain MRI images show that IMV-FCM has better segmentation performance and can accurately segment brain tissue. Compared with several related clustering algorithms, the IMV-FCM algorithm has better adaptability and better clustering performance.
Keywords: brain magnetic resonance imaging, multi-view learning, fuzzy clustering, adaptive learning, image segmentation
Introduction
The brain is the human body’s nerve center, controlling people’s thinking, memory, speech, and movement, and plays a role in regulating human organs. When the brain is healthy, it can work quickly and efficiently. However, when something goes wrong, the result can be devastating. In recent years, the problem of brain diseases has become increasingly prominent due to comprehensive factors such as high pressure in people’s lives, fast-paced activities, extreme tension in thoughts and emotions, frequent accidents, and serious aging in the population, which continue to threaten people’s health. In clinical medicine, doctors usually use MRI technology to diagnose brain diseases. MRI is a very advanced medical imaging technology. It visualizes the structure and function of the human body through radiology and is particularly suitable for brain tissue research. By using this technology, high soft tissue contrast can be obtained, and it has the advantages of noninvasiveness, nonradiation, and high-precision spatial resolution (Ji et al., 2011; Jiang et al., 2012; Thanh and Wu, 2013).
Neuroscience researchers need to segment brain MRI images to quantitatively study brain diseases. B-MRI-IS marks each pixel in the image as the corresponding brain tissue anatomical structure, such as the thalamus, hippocampus, and ventricles. Then, the segmented tissue size, shape, location, and other characteristics are used to evaluate and formulate medical plans. Experiments have shown that the abnormal shape or volume of certain anatomical regions of the brain is related to brain diseases, such as Alzheimer’s disease and Parkinson’s disease. The quality of B-MRI-IS determines the reliability of researchers’ assessment of brain diseases. The segmentation quality is determined by the segmentation method, so the segmentation method is very important in the entire diagnosis process. Usually, accurate segmentation results of brain tissue are obtained by manual segmentation by experienced brain experts. However, when faced with a large number of datasets, manual segmentation methods become quite expensive, time consuming, and impractical. Moreover, due to differences in experience and knowledge among experts, the segmentation results are not uniform. Therefore, the use of more accurate B-MRI-IS algorithms to quantitatively analyze the volume shape of each tissue in brain MRI images has become the focus of medical image research.
Traditional image segmentation methods include threshold-based methods, clustering-based methods, region-based methods, edge-based methods, and graph theory-based methods (Gu et al., 2019; Kumar et al., 2020). Considering the problems in the segmentation process, scholars have proposed their solutions. Among them, fuzzy clustering algorithms are widely used. The literature (Bezdek, 1981) proposed the FCM algorithm for the first time, introducing the concept of ambiguity into the clustering method (Li et al., 2014), and proposed an optimized bias field estimation and tissue segmentation method. Through the simultaneous iteration of bias field estimation and tissue segmentation, the final segmentation accuracy is improved, and the algorithm is very robust to initialization. The literature (Chuang et al., 2006) proposed the FCM algorithm based on spatial relationships. The algorithm integrates the spatial information of the sum of membership degrees of all points in the window into the traditional FCM. Experiments show that the improved algorithm has certain robustness to noise. Noise interference has always been one of the important interference factors in medical image segmentation. Due to the complexity of the human brain tissue structure and the imaging mechanism of MRI technology, MRI images will show phenomena such as strong noise, false images, and weak boundaries. For example, traditional active contour models often only use target edge information, which leads to premature stopping when processing strongly noisy images, and weak boundary leakage occurs when the boundary is blurred. Many studies use grayscale information and spatial information to suppress noise interference. The literature (Ahmed et al., 2002) introduces local spatial terms into the objective function of FCM to make the algorithm perform better. The literature (Chen and Zhang, 2004) replaces the traditional Euclidean distance with the core distance to make the algorithm more robust. The literature (Krinidis and Chatzis, 2010) proposed a new blur factor and introduced the kernel distance, which is more robust to noise. The literature (Gong et al., 2013) proposed a kernel-based adaptive regularization FCM algorithm. This method introduces adaptive parameters and uses mean filtering, median filtering, and custom filtering of images. There is no need to calculate parameters for each iteration, which greatly saves time and cost. Additionally, the robustness of the algorithm to noise is improved. The literature (Elazab et al., 2015) improves the quality and compression rate of the reconstructed image by compressing the image in blocks.
Figure 1 shows the motivation for this research. To reduce the influence of noise in the segmentation process, the accuracy of B-MRI-IS is improved. This article uses an improved multiview FCM algorithm. The work in this paper is summarized as follows:
FIGURE 1.
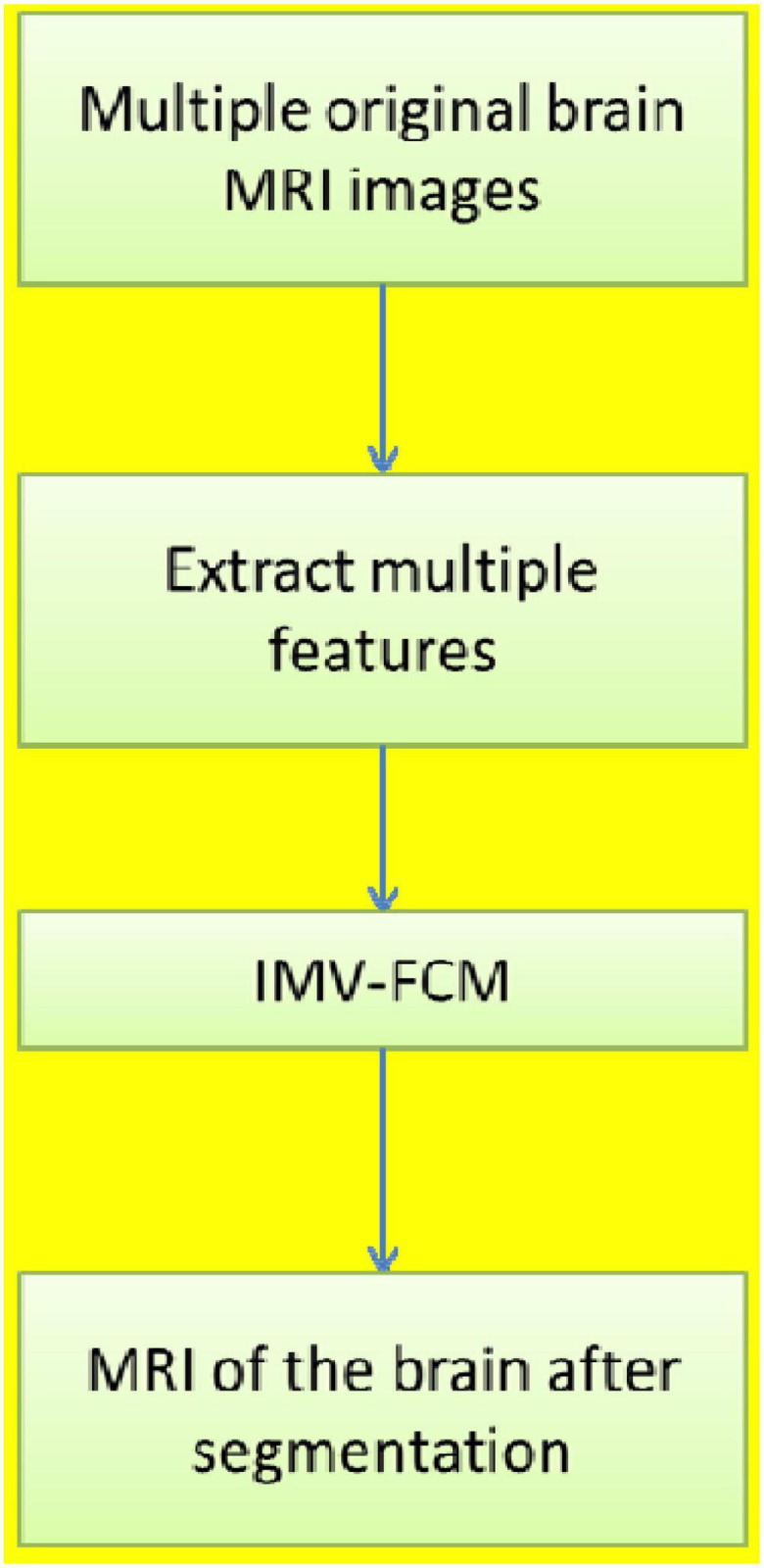
The motivation for this research.
-
1.
The B-MRI-IS process is proposed. First, the original brain MRI image is preprocessed, such as denoising. Second, the histogram of oriented gradient (HOG) feature, entropy feature, gradient feature, and contrast feature of the original image are extracted. Each feature data point is used as view data to construct multiview data (MVD). Third, the constructed MVD is input into the clustering model to obtain the final clustering result. The clustering result is the image segmentation result.
-
2.
Based on multiview FCM, the IMV-FCM algorithm is proposed. IMV-FCM uses a view weight adaptive learning mechanism so that each view obtains the optimal weight according to its cluster contribution. The final division result is obtained through the view ensemble method. Under the view weight adaptive learning mechanism, the coordination between various views is more flexible, and each view can be adaptively learned to achieve better clustering effects.
-
3.
To demonstrate the effectiveness of the clustering model used in this paper, single-view clustering and multiview clustering algorithms are used for experimental comparison. To demonstrate the antinoise of the algorithm, after adding noise to the experimental image, each algorithm is used for clustering comparison. The results show that the algorithm used in this paper is the most robust to noise compared with other comparison algorithms and can accurately segment brain tissue.
Backgrounds
MRI Technology
In medicine, human brain tissue includes the cerebrum, cerebellum, and brainstem, each of which has relatively independent characteristics. At the same time, the skull structure can be divided into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) (Wang et al., 2015). GM contains WM, and CSF fills the crooked groove formed by the GM folds. The brain tissue images show that the gray levels of various brain tissues change slowly and are not constant. Coupled with the influence of various noises, it is easy to cause the gray values to cross and overlap the internal brain tissues. The only correspondence is that one gray value may correspond to several brain internal tissues. In addition, internal brain images with different imaging morphologies also provide different information, and they appear as different gray levels on the images. According to the image gray level, it can be divided into four types, namely, white, off-white, gray, and black. Table 1 shows the characteristics of different gray levels.
TABLE 1.
Image grayscale characteristics of adult brain tissue.
| Organization | T1-weighted image | Pd weighted image | T2 weighted image |
| WM | Off-white | Gray | Black gray |
| GM | Gray | Off-white | Off-white |
| CSF | Black | Gray | White |
The proton density ρ, longitudinal relaxation time T1, and transverse relaxation time T2 of brain tissue constitute the high-dimensional biophysical property space of the brain. The T1 and T2 parameters of normal and pathological tissues in different organs of the human body are fixed, and there are certain differences between them. Additionally, different tissues have different densities, and the differences in these properties between brain tissues are the biological basis of the solvability of brain tissue segmentation. Table 2 shows the relevant attributes of the main brain tissues in MRI images.
TABLE 2.
Related attributes of main brain tissues in MRI images.
| Tissue | T1 (s) | T2 (ms) | ρ (1.5) |
| CSF | 0.8–20 | 110–2,000 | 70–230 |
| WM | 0.76–1.08 | 61–100 | 70–90 |
| GM | 1.09–2.15 | 61–109 | 85–125 |
| Meninges | 0.5–2.2 | 50–165 | 5–44 |
| Muscle | 0.95–1.82 | 20–67 | 45–90 |
| Adipose | 0.2–0.75 | 53–94 | 50–100 |
Clustering Algorithm
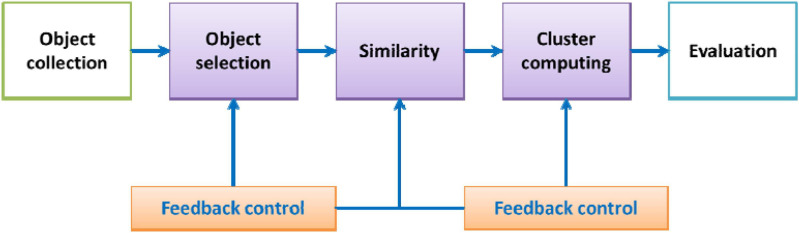
These attributes are determined by factors such as the composition of the brain tissue and the local microstructure. Cluster analysis aims to make reasonable classifications according to the characteristics of the sample and divide the data points with similar characteristics into one category. The idea of the cluster analysis algorithm comes from taxonomy. As MRI images contain increasing information, the requirements for classification are increasing. People have introduced multivariate analysis into taxonomy, forming cluster analysis. The goal of cluster analysis is to collect data to classify when the data points are similar (Bezdek, 1980; Hall et al., 1992; Jiang et al., 2014; Qian et al., 2015, 2016, 2018; Zheng et al., 2015; Jiang et al., 2019; Jiang et al., 2020). Cluster analysis is a technique to study the relationship between sample data points. The clustering results reveal the internal connections and differences between sample data and provide an important basis for data processing. The cluster analysis process is shown in Figure 2.
FIGURE 2.
Cluster analysis flowchart.
The clustering object refers to the grayscale collection of image pixels. The similarity measure is a key step used to measure the similarity between data points. Euclidean distance is often used as the similarity measure. The clustering algorithm uses similarity measures to select data points that are very close to each other and classify them into a cluster. Additionally, the result of clustering will affect the selection of subsequent objects and the similarity measurement, so there is a feedback process. The last step of clustering is to evaluate the clustering results. The importance of evaluating the clustering results will not be lower than the importance of the previous steps. For example, in a cluster analysis method based on a threshold value, it is necessary to judge the classification result to guide the selection of the threshold value. In the cluster analysis method with the function as the criterion, the judgment or evaluation of the classification result can be used to guide the selection of the appropriate criterion function.
Clustering algorithms can be divided into partition-based (Jing et al., 2007; Zhu et al., 2009; Yu et al., 2012; Qian et al., 2017), hierarchy-based (Hall and Goldgof, 2011; Devi and Setty, 2018), density-based (Sunjana and Azizah, 2020; Yin et al., 2020), grid-based (Wang et al., 2019; Zhang et al., 2020), and model-based (Lee et al., 2018; Chrobak et al., 2020) algorithms. Due to the complexity of brain medical images, the boundaries and boundaries of different tissues in the brain are uncertain and unclear. This requires a method for reducing the unclearness. Fuzzy mathematics based on fuzzy sets can solve these uncertain and imprecise problems. The fuzzy clustering algorithm in the clustering algorithm is most suitable for B-MRI-IS. The typical fuzzy clustering algorithm is the FCM algorithm. The principle of image segmentation based on FCM is to use the uncertainty of the classification of image pixels. The degree of membership is used to describe this uncertainty, the distance relationship between pixels is described according to the objective function, and the best cluster center is selected. To describe the clustering algorithm more clearly, Table 3 shows the symbols used in the FCM algorithm.
TABLE 3.
Description of related symbols in FCM.
| Symbols | Description | Symbols | Description |
| X | Dataset | xj | The jth pixel |
| C | Number of clusters | N | Total number of image pixels |
| uij | The membership degree of pixel xi belonging to the jth cluster | zi | The ith cluster center |
| dij | Euclidean distance from sample point xj to cluster centerzi | m | Fuzzy factor |
Assume the image pixel dataset is X = {x1,x2,…,xN}, where xi represents the gray value of the image pixel. FCM’s idea is to transform the image segmentation process into the optimization process of the feature function when the objective function converges to realize the fuzzy classification of pixel data. That is, the image segmentation problem is transformed into a clustering problem of dividing N pixels into C classes, and the cluster center of each class is expressed as Z = {z1,z2,…,zN}. The functional expression of FCM is
| (1) |
| (2) |
The size of m determines the clustering ambiguity. If the value of m is too large, the fuzziness of clustering will increase accordingly, which is not conducive to the defuzzification of the model. In contrast, the smaller the value of m is, the smaller the clustering ambiguity, and the segmentation result is close to hard segmentation. In practical applications, the value of m is usually taken as 2. Equations (3) and (4) give the iterative formula of cluster center zi and membership degree uij.
| (3) |
| (4) |
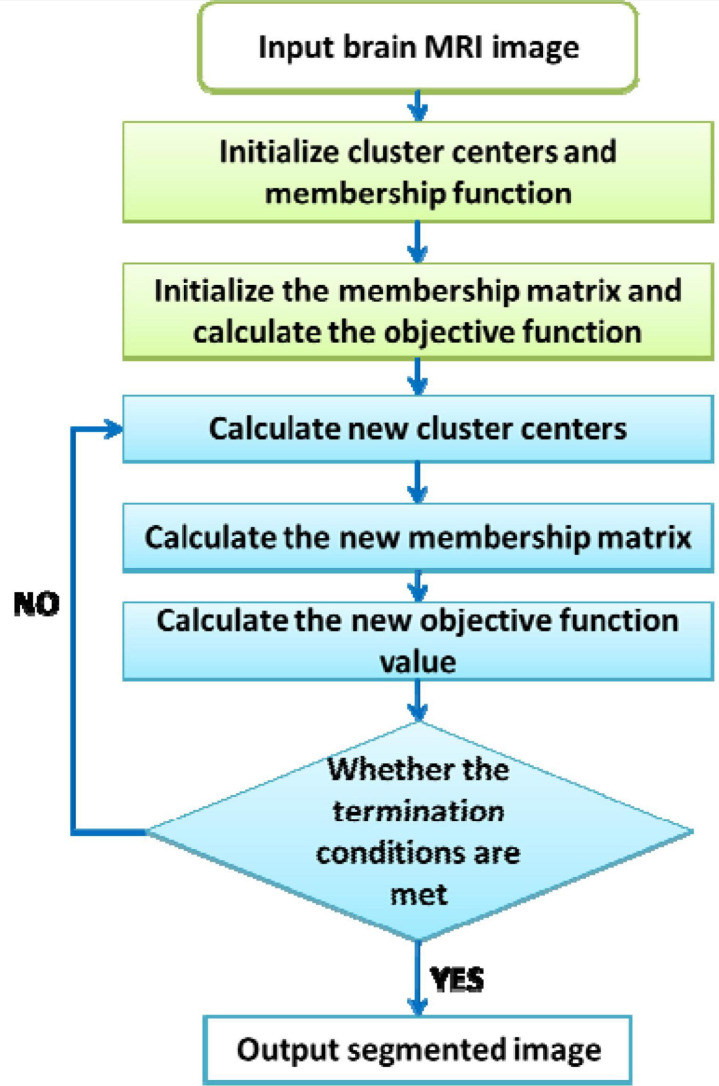
The steps of the FCM-based image segmentation algorithm are as follows: (1) Input the brain MRI image; (2) set the fuzzy factor m = 2, the maximum number of iterations ε (ε > 0), the number of clusters C, and initialize the cluster center and membership matrix randomly; (3) according to Eqs 3 and 4, update the clustering center z and membership degree u; (4) make the objective function converge until the cluster center no longer changes; and (5) output the segmented image. The flow of B-MRI-IS based on FCM is shown in Figure 3.
FIGURE 3.
B-MRI-IS process based on FCM.
Multiview Clustering Algorithm
Traditional fuzzy clustering cannot achieve ideal results when processing multiview data. Based on this requirement, many multiview-related algorithms have been proposed. The existing multiview-related clustering algorithms include coclustering (Gu and Zhou, 2009), collaborative clustering algorithms (Pedrycz, 2002), and multitask clustering algorithms (Chen et al., 2013). There are many multiview clustering algorithms, the most classic of which is CoFKM. Next, we will briefly introduce the principle and implementation steps of the algorithm. Table 4 gives the definition of each symbol of the algorithm.
TABLE 4.
Description of related symbols in the multiview clustering algorithm.
| Symbols | Description | Symbols | Description |
| X = {view1,view2,…,viewV} | Multiview dataset | viewv = [cpsbreak]{x1,v,x2,v,…,xN,v} | vth view data |
| N | Total number of samples | V | Number of views |
| C(2≤C≤N) | Number of clusters | η | Parameters that regulate the importance of each view |
| Zv = [z1,v,z2,v,…,zc,v] | Class center of the vth view | Uv = [uij,v] | Membership of the vth view |
Equation (5) gives the function expression of CoFKM:
| (5) |
| (6) |
| (7) |
where represents the weighted fusion of the membership degree under the current view and the membership degree of the other views. According to Eq. 5, through the Lagrangian extremum solution method, the calculation formulas of the clustering center and membership degree are obtained. Equations (8) and (9) give the calculation formulas of the cluster center and membership matrix of the vth view.
| (8) |
| (9) |
Through Eqs 8 and 9, the division matrix for any view is calculated. The final division result is obtained using the ensemble method of the geometric mean. The expression of the integrated method is
| (10) |
Algorithm Evaluation Index
The goal of segmentation is to divide pixels with certain characteristic properties (such as grayscale and spatial position) in an image into a region. All the pixels in a region have similar properties, and the characteristic properties of pixels in different regions are quite different. The evaluation index of the effectiveness of image segmentation is used to describe the pros and cons of the segmentation results. The commonly used evaluation indicators include segmentation accuracy JS, Dice coefficient (DSC), similarity (KI), segmentation coefficient (Vpc), segmentation entropy (Vpe), and pixel error rate (ME). The specific descriptions of commonly used evaluation indicators are shown in Table 5.
TABLE 5.
Evaluation index descriptions.
| Index | Description |
| S1 represents the segmentation area and S2 represents the ground truth. The larger the JS value, the better the segmentation accuracy of the algorithm and the better the effect. | |
| True positive (TP), false positive (FP), false negative (FN); KI is a value greater than 0 and less than 1. KI = 1 means that the algorithm segmentation result is completely consistent with the standard segmentation. The closer the KI is to 1, the more accurate the segmentation result and the better the algorithm performance. | |
| These two segmentation indexes are related to the degree of membership uij. Generally, a segmentation model with less ambiguity is considered to have better performance. The closer Vpc is to 1, and the closer Vpe is to 0, the higher the segmentation accuracy of the algorithm. | |
| ME(A,B) = | The segmented image is compared with the “gold standard” image, and the ME. SA of the obtained model represents the target area extracted by the segmentation algorithm, and SB represents the “gold standard” target area. The value range of ME is 0 to infinity. The closer ME is to 0, the smaller the mis-segmentation area and the higher the segmentation accuracy. |
Experimental Dataset
Common brain image databases are mainly as follows: Brain Perfusion Database, Allen Brain Atlas, BRATS database, simulated brain MR image data from the Brain Web website, and the Internet Brain Segmentation Repository (IBSR). The description of each database is shown in Table 6.
TABLE 6.
Brain image database.
| Database | Image size | Classification details |
| Brain Perfusion Database (Cleuziou et al., 2009) | 194*237 | Number of clusters: 4, which are WM, GM, CSF, and background |
| Allen Brain Atlas (Okita et al., 2015) | 256*128 | |
| BRATS (Rosati et al., 2018) | 155*240*240 | |
| Brain Web (Weijer and Gevers, 2006) | 181*217*181 | |
| IBSR (Liu et al., 2020) | 256*256 |
“*” Represents multiplication.
Brain MRI Image Segmentation Based on Multiview Fuzzy Clustering
Brain MRI Image Segmentation Process Based on Multiview Clustering
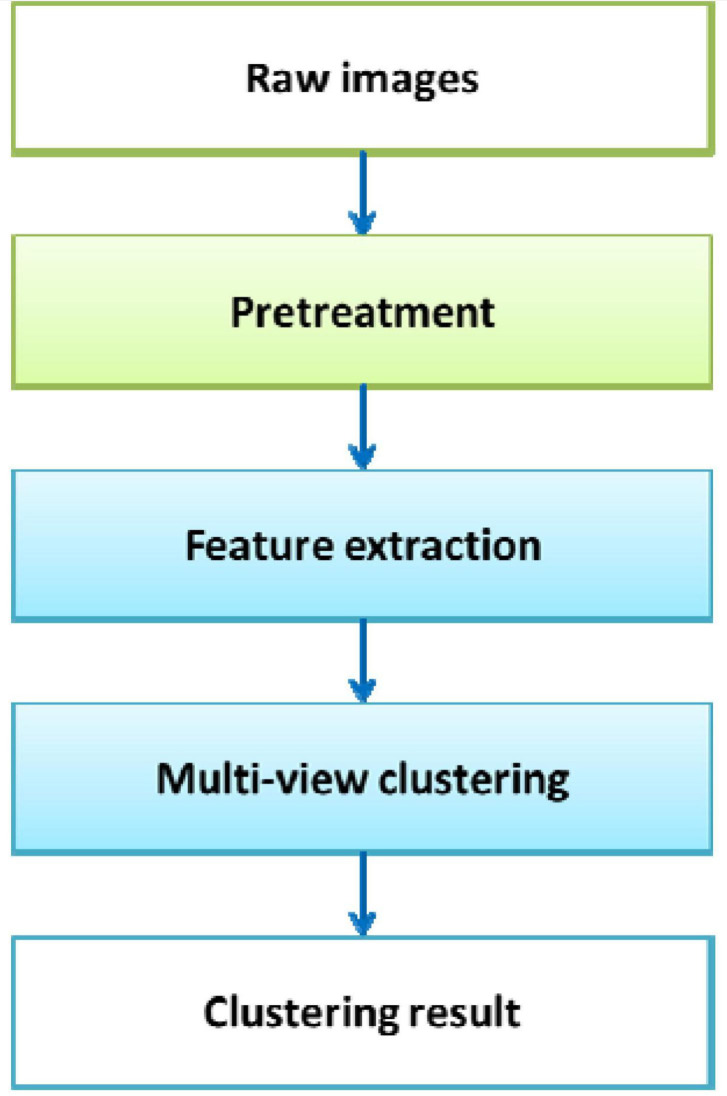
MVD carries more information than single-view data. This MVD feature is beneficial to the improvement of cluster analysis. For clustering analysis of MVD, the traditional single-view clustering algorithm is to first separate each view data from the MVD. Second, the single-view clustering algorithm is used to process the data of each view, and the clustering results of the data of each view are obtained. Finally, a suitable ensemble strategy is used to fuse the clustering results of all views to obtain the final division result. The single-view clustering algorithm for processing MVD has the following shortcomings. When the clustering results of a certain view have obvious deviations or the clustering results between different views are very different, if each view is artificially separated for analysis in this way, the final division result obtained by integrated learning is likely to be poor or the performance of the algorithm is unstable. To make full use of the information carried by MVD and improve the accuracy of clustering, this research introduces multiview technology into the single-view clustering method. The multiview clustering algorithm enables the collaborative learning of various views in the clustering process, makes full use of the data information of each view, and improves the clustering performance and stability of the algorithm. The B-MRI-IS process based on multiview clustering is shown in Figure 4.
FIGURE 4.
B-MRI-IS process based on multiview clustering.
As shown in Figure 4, first, the original brain image is preprocessed, such as denoising. Second, the HOG feature, entropy feature, gradient feature, and contrast feature of the original image are extracted. The feature data serve as view data. Third, all view data are input into the multiview clustering model to obtain the final clustering result. Due to the different amounts of information contained in different features, the contribution of the formed view data to the clustering result is also different. Therefore, how to effectively adjust the weight of each view is very important during the use of the multiview clustering algorithm.
IMV-FCM
The CoFKM introduced in the section “Multiview Clustering Algorithm” assigns the same weight to each view, which shows that the CoFKM believes that the contribution of each view data to the clustering is the same. This is obviously inconsistent with the actual situation. For MVD in real production and living environments, the contribution of each view data to the clustering is necessarily different. If the angle of view data with a high degree of contribution is given a high weight and the angle of view data with a low degree of contribution is given a low weight, the overall clustering performance can be improved. Therefore, a multiview fuzzy clustering method with adaptive viewing angle adjustment capability is used in this study, and its objective function is
| (11) |
where and Uv = [uij,v] is the division matrix corresponding to the ith view. is the division fusion item, which realizes the view fusion of different views in the vth view clustering task. At this time, the importance of each view is reflected by the weight wv,t. wv,t represents the importance of the tth view in the vth view cluster. W is the weight matrix of all views. The Lagrange multiplier method is used to solve the extreme value of Eq. 11, and the expression of each variable is obtained as follows:
| (12) |
| (13) |
| (14) |
The following ensemble method is used to obtain the final partition matrix:
| (15) |
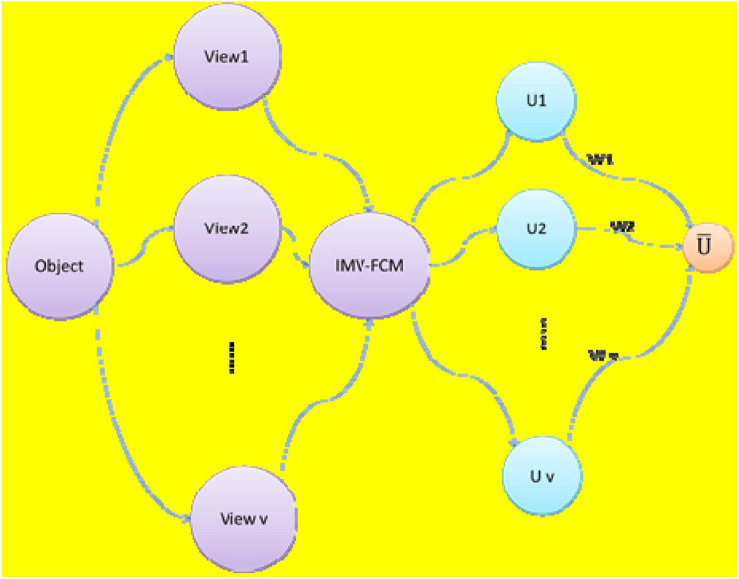
Figure 5 shows the schematic diagram of the IMV-FCM algorithm. As shown in Figure 5, after the multiview data with v views are executed by the IMV-FCM algorithm, v membership matrices are obtained. Each membership matrix is assigned a corresponding weight w, and the final global membership matrix is obtained according to the fusion strategy of Eq. 15.
FIGURE 5.
Schematic diagram of IMV-FCM algorithm.
The specific steps of the IMV-FCM algorithm are in Algorithm 1.
Algorithm 1.
IMV-FCM algorithm.
| Input | Multiview sample set X, number of views V, number of clustering C, iteration threshold ε, fuzzy index m, iteration number l, parameter γ. |
| Output | The final division matrix , the clustering center of each view zi,v, the view fusion weight matrix W = {wv,t}. |
| Step 1 | Randomly generate fuzzy membership matrix uij,t(1≤t≤V) for each view and view fusion weight matrix W = {wv,t} for each view; |
| Step 2 | According to Eq. 12, the cluster center zi,v of each view is updated. |
| Step 3 | According to Eq. 13, the membership degree uij,t of each view is updated. |
| Step 4 | According to Eq. 14, the view fusion weight matrix W = {wv,t} is updated. |
| Step 5 | If ||Jl + 1−Jl|| < ε, the algorithm stops iterating; otherwise, it returns to Step 2. |
| Step 6 | After the algorithm converges, the fuzzy membership of each view is output. |
| Step 7 | According to the fuzzy membership degree of each view obtained in Step 6, Eq. 15 is used to obtain the final division matrix. |
Simulation Experiment Analysis
Experimental Background
The dataset used in this study was the data downloaded from BrainWeb. The 2D images of 89 cross sections (89 CS), 92 cross sections (95 CS), and 95 cross sections (95 CS) in the T1-weighted brain MRI image were selected for segmentation. The comparison algorithms used were FCM, CoFKM (Cai et al., 2019), two-layer automatic weighted clustering algorithm (TW-k-means) (Singh et al., 2020), multitask-based K-means (CombKM) (Chen et al., 2013), and collaborative clustering based on sample and feature space (coclustering) (Gu and Zhou, 2009). In the experiment, the iteration stop threshold ε of each algorithm is set to 0.001, and the maximum number of iterations l was set to 100. The parameter settings of each algorithm are shown in Table 7. The parameter selection methods of each comparison algorithm include the grid search method and clustering index. This article mainly uses the grid search method to confirm the optimal parameters. The reason for choosing the grid search method for parameter selection is that the performance of the model trained based on the parameters selected by this method is the best. The evaluation index adopts JS and DSC. All experiments were based on the MATLAB 2018a programming environment, which was simulated on a Lenovo PC configured with a Windows 10 operating system, 2.60 GHz CPU, and 8G memory Intel(R) Core(TM)i7 processor.
TABLE 7.
Parameter setting of various algorithms based on grid search.
| Algorithm | Parameter setting range |
| FCM | Fuzzy factor m = {1.05,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,2} |
| CoFKM | Fuzzy factor m = {1.05,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,2}, collaborative learning parameters η = [0,(K−1)/K], K is the number of views |
| TW-k-means | Regularization parameters λ = {1,2,…,30} and η = {10,20,…,100} |
| CombKM | None |
| Coclustering | Regularization parameter λ = {1,10,100,300,500,800,1000}, regularization parameter μ = {1,10,100,300,500,800,1000}, feature category number m = ⌊d/2⌋, d is the characteristic number, ⌊⌋ means rounding down. |
| IMV-FCM | Fuzzy factor m = {1.05,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,2} Regularization parameters γ = {2−12,2−11,…,212} |
Experimental Results and Analysis
To verify the superiority of the IMV-FCM algorithm, the experiment section gives a comparison of the effect of each algorithm on image segmentation. In analyzing the antinoise performance of the algorithm, this study adds different proportions of Gaussian noise to the image. The segmentation results of each algorithm are shown in Tables 8, 9. The symbol A represents WM, B represents GM, and C represents CSF.
TABLE 8.
JS indicators of each algorithm (100%).
| Noise | Organization | FCM | CoFKM | TW-k-means | CombKM | Coclustering | IMV-FCM |
| 0% | A | 85.73% | 88.22% | 87.76% | 87.85% | 89.96% | 90.45% |
| B | 74.52% | 77.85% | 76.90% | 77.11% | 79.93% | 79.76% | |
| C | 65.98% | 68.31% | 67.58% | 68.32% | 69.94% | 70.74% | |
| Mean | 75.41% | 78.13% | 77.41% | 77.76% | 79.94% | 80.32% | |
| 3% | A | 84.98% | 87.52% | 88.65% | 87.03% | 87.67% | 89.20% |
| B | 73.87% | 76.48% | 76.77% | 75.96% | 76.35% | 78.16% | |
| C | 64.76% | 66.54% | 67.12% | 65.87% | 66.11% | 67.91% | |
| Mean | 74.54% | 76.85% | 77.51% | 76.29% | 76.71% | 78.42% | |
| 5% | A | 84.17% | 86.11% | 86.59% | 85.90% | 85.97% | 87.79% |
| B | 73.25% | 75.43% | 75.86% | 74.97% | 74.98% | 76.58% | |
| C | 64.88% | 66.35% | 66.36% | 65.89% | 66.99% | 67.02% | |
| Mean | 74.10% | 75.96% | 76.27% | 75.59% | 75.98% | 77.13% | |
| 7% | A | 82.21% | 84.46% | 82.32% | 82.98% | 82.12% | 85.80% |
| B | 72.62% | 74.02% | 73.52% | 73.87% | 73.48% | 75.35% | |
| C | 64.14% | 66.62% | 65.07% | 65.85% | 65.17% | 67.56% | |
| Mean | 72.99% | 75.03% | 73.64% | 74.23% | 73.59% | 76.24% | |
| 9% | A | 76.68% | 82.23% | 80.61% | 81.02% | 81.43% | 83.56% |
| B | 70.25% | 73.18% | 71.17% | 71.65% | 71.98% | 72.20% | |
| C | 62.27% | 65.83% | 64.59% | 64.04% | 64.47% | 71.80% | |
| Mean | 69.73% | 73.75% | 72.12% | 72.24% | 72.63% | 75.85% |
TABLE 9.
DSC indicators of each algorithm (100%).
| Noise | Organization | FCM | CoFKM | TW-k-means | CombKM | Coclustering | IMV-FCM |
| 0% | A | 93.24% | 94.75% | 94.28% | 93.39% | 94.02% | 95.27% |
| B | 86.51% | 87.79% | 87.61% | 86.87% | 87.99% | 88.51% | |
| C | 80.45% | 82.44% | 82.83% | 82.10% | 83.04% | 85.06% | |
| Mean | 86.73% | 88.33% | 88.24% | 87.45% | 88.35% | 89.61% | |
| 3% | A | 92.28% | 93.68% | 93.77% | 93.91% | 94.23% | 95.08% |
| B | 85.30% | 86.84% | 87.04% | 86.89% | 86.57% | 87.62% | |
| C | 79.47% | 82.02% | 83.22% | 82.16% | 83.01% | 84.41% | |
| Mean | 85.68% | 87.51% | 88.01% | 87.65% | 87.94% | 89.04% | |
| 5% | A | 91.36% | 91.03% | 91.14% | 91.09% | 91.74% | 93.86% |
| B | 84.89% | 84.47% | 84.66% | 84.82% | 84.96% | 86.68% | |
| C | 78.55% | 80.10% | 80.23% | 80.34% | 80.08% | 83.71% | |
| Mean | 84.93% | 85.20% | 85.34% | 85.41% | 85.59% | 88.08% | |
| 7% | A | 89.62% | 90.02% | 90.91% | 90.54% | 90.74% | 92.95% |
| B | 84.01% | 83.36% | 83.82% | 83.57% | 84.10% | 85.45% | |
| C | 77.86% | 79.03% | 79.65% | 79.66% | 80.12% | 82.79% | |
| Mean | 83.83% | 84.14% | 84.79% | 84.59% | 84.99% | 87.06% | |
| 9% | A | 85.76% | 88.44% | 88.62% | 88.79% | 89.76% | 91.87% |
| B | 83.79% | 81.45% | 81.89% | 81.63% | 82.30% | 83.67% | |
| C | 77.23% | 77.72% | 77.79% | 77.87% | 78.31% | 81.32% | |
| Mean | 82.26% | 82.54% | 82.77% | 82.76% | 83.46% | 85.62% |
From the experimental data in Tables 8, 9, it can be determined that when processing original brain images, the segmentation performance of the multiview algorithm used in this study is significantly better than FCM. This shows that the introduction of the multiview mechanism can mine information from multiple views, thereby improving the clustering accuracy. Compared with other multiview clustering algorithms, the segmentation effect of the IMV-FCM algorithm in this study is better. This shows that the IMV-FCM algorithm with partition adaptive fusion capability requires the Co-FKM algorithm and CombKM algorithm to manually set the degree of partition fusion. The IMV-FCM algorithm can obtain better view weights during multiview learning and finally obtain better multiview clustering effects.
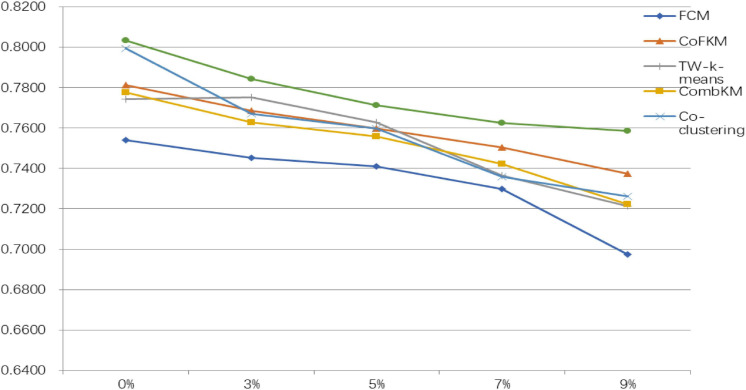
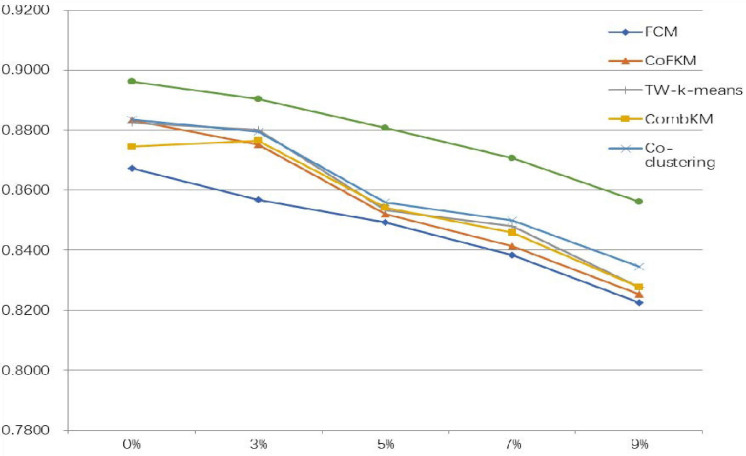
As the image noise increases, the clustering performance of all clustering algorithms begins to decline. However, even if the performance of each algorithm is declining, the performance of the IMV-FCM algorithm is still better than that of the other algorithms. This is manifested in two aspects. First, the clustering performance of IMV-FCM is better than that of the comparison algorithm. The second is that with the increase in image noise, the clustering performance of the IMV-FCM algorithm decreases the most slowly, as shown in Figures 6, 7. This fully shows that IMV-FCM is more robust to noise.
FIGURE 6.
JS indicator drop rate of each algorithm.
FIGURE 7.
DSC index drop rate of each algorithm.
Conclusion
To further improve the performance of B-MRI-IS, the IMV-FCM algorithm is applied in this research. The IMV-FCM algorithm is a multiview fuzzy clustering algorithm with adaptive view weight. Under the adaptive learning of the view fusion weight matrix, the coordination between various views is more flexible. Additionally, each view can be self-adapted to learn and then achieve a better clustering effect. Since the original brain MRI image is not MVD, this study extracts multiple feature data of the original image and uses one feature data as one view data to construct MVD. The experimental results prove that the segmentation method used in this paper optimizes the segmentation effect. With the increase in noise, the clustering effect of IMV-FCM decreases more slowly than the comparison method, which shows that the method used has stronger noise immunity. Although the effectiveness of IMV-FCM was verified, it still faces certain limitations. For example, the proposed method uses the classic FCM algorithm as a framework and uses Euclidean distance, which causes it to suffer from the dimensionality disaster problem when facing high-dimensional multiview clustering tasks. How to solve this problem will be the focus of future research. In addition, similar to most unsupervised learning algorithms, the selection of optimal parameters is an important issue. Different practical applications require different ranges of parameter values. Since the optimal parameters are usually determined by the application, for an exact application, the appropriate parameter range of the algorithm used can be determined through prior knowledge or available valid labeled datasets. The ensemble learning strategy can avoid the selection of optimal parameters to a certain extent, and it is planned to be further studied in follow-up work.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://brainweb.bic.mni.mcgill.ca.
Author Contributions
LH and YG conceived and developed the theoretical framework of the manuscript. YG and XG designed and performed the surgical procedure of the case presentation. LH, JX, and TN performed the data evaluation, analysis, and interpretation, designed the figures, designed and wrote the manuscript in consultation with YG and XG, who took the lead in writing the manuscript. All authors participated in the editing process.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
Funding. This work was supported in part by the National Natural Science Foundation of China under Grants 81701793, 61702225, 61772241, 61873321, and61806026; in part by the Natural Science Foundation of Jiangsu Province under Grant BK20180956; in part by the 2018 Six Talent Peaks Project of Jiangsu Province under Grant XYDXX-127; in part by the Science and Technology Demonstration Project of Social Development of Wuxi under Grant WX18IVJN002; and in part by the Youth Foundation of the Commission of Health and Family Planning of Wuxi under Grant Q201654.
References
- Ahmed M. N., Yamany S. M., Mohamed N., Farag A. A., Moriarty T. (2002). Amodified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data. IEEE Trans. Med. Imaging 21 193–199. 10.1109/42.996338 [DOI] [PubMed] [Google Scholar]
- Bezdek J. C. (1980). A convergence theorem for the fuzzy ISODATA clustering algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2 1–8. 10.1109/TPAMI.1980.4766964 [DOI] [PubMed] [Google Scholar]
- Bezdek J. C. (1981). Pattern Recognition With Fuzzy Objective Function Algorithms. New York, NY: Plenum Press. [Google Scholar]
- Cai T. T., Ma J., Zhang L. (2019). Chime: clustering of high-dimensional Gaussian mixtures with EM algorithm and its optimality. Ann. Stat. 47 1234–1267. 10.1214/18-AOS1711 [DOI] [Google Scholar]
- Chen S., Zhang D. (2004). Robust image segmentation using FCM with spatialconstraints based on new kernel-induced distance measure. IEEE Trans. Syst. Man Cybern. B Cyber. 34 1907–1916. 10.1109/TSMCB.2004.831165 [DOI] [PubMed] [Google Scholar]
- Chen X., Xu X., Huang J. Z., Ye Y. (2013). TW-k-means: automated two-level variable weighting clustering algorithm for multiview data. IEEE Trans. Knowl. Data Eng. 25 932–944. 10.1109/TKDE.2011.262 [DOI] [Google Scholar]
- Chrobak M., Dürr C., Aleksander F., Nilsson B. J. (2020). Online clique clustering. Algorithmica 82 938–965. 10.1007/s00453-019-00625-1 [DOI] [Google Scholar]
- Chuang K. S., Tzeng H. L., Chen S., Wu J., Chen T. J. (2006). Fuzzy c-means clustering with spatial information for image segmentation. Comput. Med. Imaging Graph. Official J. Comput. Med. Imaging Soc. 30 9–15. 10.1016/j.compmedimag.2005.10.001 [DOI] [PubMed] [Google Scholar]
- Cleuziou G., Exbrayat M., Martin L., Sublemontier J. H. (2009). “Co FKM: a centralized method for multiple-view clustering,” in Proceedings of the 9th IEEE Internaional Conference on Data Mining, (Miami FL: IEEE; ), 752–757. 10.1109/ICDM.2009.138 [DOI] [Google Scholar]
- Devi B. R., Setty S. P. (2018). Hybrid clustering algorithm ‘KCu’ for combining the features of K-means and CURE Algorithm for efficient outliers handling. Adv. Model. Anal. B 61 76–79. 10.18280/ama_b.610204 [DOI] [Google Scholar]
- Elazab A., Wang C., Jia F., Wu J., Li G., Hu Q. (2015). Segmentation of brain tissues from magnetic resonance images using adaptively regularized kernel-based fuzzy c-means clustering. Comput. Math. Methods Med. 2015:485495. 10.1155/2015/485495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong M., Liang Y., Shi J., Ma W., Ma J. (2013). Fuzzy c-means clustering with local information and kernel metric for image segmentation. IEEE Trans. Image Process. 22 573–584. 10.1109/TIP.2012.2219547 [DOI] [PubMed] [Google Scholar]
- Gu J., Cheng T., Hua L., Wang J., Zhao J., Cao Y. (2019). Overview of image segmentation and registration for spine biological modeling. J. Syst. Simul. 31 167–173. 10.16182/j.issn1004731x.joss.18-0806 [DOI] [Google Scholar]
- Gu Q., Zhou J. (2009). Learning the shared subspace for multi-task clustering and transductive transfer classification. Proceedings of the 2009 9th IEEE International Conference on Data Mining, (Miami Beach, FL: IEEE; ), 159–168. 10.1109/ICDM.2009.32 [DOI] [Google Scholar]
- Hall L. O., Bensaid A. M., Clarke L. P. (1992). A comparison of neural network and fuzzy clustering techniques in segmenting magnetic resonance images of the brain. IEEE Trans. Neural Netw. 3 672–681. 10.1109/72.159057 [DOI] [PubMed] [Google Scholar]
- Hall L. O., Goldgof D. B. (2011). Convergence of the single-pass and online fuzzy C-means algorithms. IEEE Trans Fuzzy Syst. 19 792–794. 10.1109/TFUZZ.2011.2143418 [DOI] [Google Scholar]
- Ji Z. X., Sun Q. S., Xia D. S. (2011). A modified possibilisticfuzzy c-means clustering algorithm for bias field estimation and segmentation of brain MR image. Comput. Med. Imaging Graph. 35 383–397. 10.1016/j.compmedimag.2010.12.001 [DOI] [PubMed] [Google Scholar]
- Jiang C. F., Chang C. C., Huang S. H. (2012). Regions of interest extraction fromspect images for neural degeneration assessment using multimodality image fusion. Multidimen. Syst. Signal Process. 23 437–449. 10.1007/s11045-011-0162-3 [DOI] [Google Scholar]
- Jiang Y., Bi A., Xia K., Xue J., Qian P. (2020). Exemplar-based data stream clustering toward internet of things. J. Supercomput. 76 2929–2957. 10.1007/s11227-019-03080-5 [DOI] [Google Scholar]
- Jiang Y., Chung F. L., Wang S., Deng Z., Wang J., Qian P. (2014). Collaborative fuzzy clustering from multiple weighted views. IEEE Trans. Cybern. 45 688–701. 10.1109/TCYB.2014.2334595 [DOI] [PubMed] [Google Scholar]
- Jiang Y., Zhao K., Xia K., Xue J., Zhou L., Ding Y., et al. (2019). A novel distributed multitask fuzzy clustering algorithm for automatic MR brain image segmentation. J. Med. Syst. 43:118. 10.1007/s10916-019-1245-1 [DOI] [PubMed] [Google Scholar]
- Jing L. P., Ng M. K., Huang J. Z. (2007). An entropy weighting k-means algorithm for subspace clustering of high-dimensional sparse data. IEEE Trans. Knowl. Data Eng. 19 1026–1041. 10.1109/TKDE.2007.1048 [DOI] [Google Scholar]
- Krinidis S., Chatzis V. (2010). A robust fuzzy local information C-means clustering algorithm. IEEE Trans. Image Process. 19 1328–1337. 10.1109/TIP.2010.2040763 [DOI] [PubMed] [Google Scholar]
- Kumar S. N., Lenin F. A., Sebastin V. P. (2020). An overview of segmentation algorithms for the analysis of anomalies on medical images. J. Intell. Syst. 29 612–625. 10.1515/jisys-2017-0629 [DOI] [Google Scholar]
- Lee K., Moon C., Nam Y. (2018). Diagnosing vocal disorders using cobweb clustering of the jitter, shimmer, and harmonics-to-noise ratio. KSII Trans. Internet Inform. Syst. 12 5541–5554. 10.3837/tiis.2018.11.020 [DOI] [Google Scholar]
- Li C., Gore J. C., Davatzikos C. (2014). Multiplicative intrinsic component optimization(MICO) for MRI bias field estimation and tissue segmentation. Magn. Reson. Imaging 32 413–439. 10.1016/j.mri.2014.03.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu L., Kuang L., Ji Y. (2020). Multimodal MRI brain tumor image segmentation using sparse subspace clustering algorithm. Comput. Math. Methods Med. 2020:8620403. 10.1155/2020/8620403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okita Y., Miyata A. H., Motomura B. N., Takamoto S. (2015). A study of brain protection during total arch replacement comparing antegrade cerebral perfusion versus hypothermic circulatory arrest, with or without retrograde cerebral perfusion: analysis based on the Japan adult cardiovascular surgery database. J. Thorac. Cardiovasc. Surgery 149 65–73. 10.1016/j.jtcvs.2014.08.070 [DOI] [PubMed] [Google Scholar]
- Pedrycz W. (2002). Collaborative fuzzy clustering. Pattern Recogn. Lett. 23 1675–1686. [Google Scholar]
- Qian P., Jiang Y., Deng Z., Hu L., Sun S., Wang S., et al. (2015). Cluster prototypes and fuzzy memberships jointly leveraged cross-domain maximum entropy clustering. IEEE Trans. Cybern. 46 181–193. 10.1109/TCYB.2015.2399351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian P., Jiang Y., Wang S., Su K. H., Wang J., Hu L., et al. (2016). Affinity and penalty jointly constrained spectral clustering with all-compatibility, flexibility, and robustness. IEEE Trans. Neural Netw. Learn. Syst. 28 1123–1138. 10.1109/TNNLS.2015.2511179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian P., Zhao K., Jiang Y., Su K. H., Deng Z., Wang S., et al. (2017). Knowledge-leveraged transfer fuzzy C-Means for texture image segmentation with self-adaptive cluster prototype matching. Knowl. Based Syst. 130 33–50. 10.1016/j.knosys.2017.05.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian P., Zhou J., Jiang Y., Liang F., Muzic R. F., Jr. (2018). Multi-view maximum entropy clustering by jointly leveraging inter-view collaborations and intra-view-weighted attributes. IEEE Access 6 28594–28610. 10.1109/ACCESS.2018.2825352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosati P., Lupascu C. A., Tegolo D. (2018). Analysis of low-correlated spatial gene expression patterns: a clustering approach in the mouse brain data hosted in the Allen Brain Atlas. IET Comput. Vision 12 996–1006. 10.1049/iet-cvi.2018.5217 [DOI] [Google Scholar]
- Singh M., Vishal V., Verma A., Sharma N. (2020). Segmentation of MRI data using multi-objective antlion based improved fuzzy c-means. Biocybern. Biomed. Eng. 40 1250–1266. 10.1016/j.bbe.2020.07.001 [DOI] [Google Scholar]
- Sunjana Azizah Z. (2020). Outlier detection of transaction data using DBSCAN algorithm. Int. J. Psychosoc. Rehabil. 24 3232–3240. 10.37200/IJPR/V24I2/PR200632 [DOI] [Google Scholar]
- Thanh M. N., Wu Q. M. J. (2013). A fuzzy logic model based Markov random field for medical image segmentation. Evolv. Syst. 4 171–181. 10.1007/s12530-012-9066-1 [DOI] [Google Scholar]
- Wang J., Schreiber D. K., Bailey N., Hosemann P., Toloczko M. B. (2019). The application of the OPTICS algorithm to cluster analysis in atom probe tomography data. Microsc. Microanal. 25 338–348. 10.1017/S1431927618015386 [DOI] [PubMed] [Google Scholar]
- Wang X. Y., Zhang D. D., Wei N. (2015). Fractal image coding algorithm using particle swarm optimisation and hybrid quadtree partition scheme. Iet Image Process. 9 153–161. 10.1049/iet-ipr.2014.0001 [DOI] [Google Scholar]
- Weijer J., Gevers T. (2006). Boosting color saliency in image feature. IEEE Trans. Pattern Anal. Mach. Intell. 28 150–156. 10.1109/TPAMI.2006.3 [DOI] [PubMed] [Google Scholar]
- Yin S., Li H., Liu D., Karim S. (2020). Active contour modal based on density-oriented BIRCH clustering method for medical image segmentation. Multimedia Tools Appl. 79 31049–31068. 10.1016/j.ijleo.2018.01.004 [DOI] [Google Scholar]
- Yu S., Tranchevent L., Liu X., Glanzel W., Suykens J. A. K., De Moor B., et al. (2012). Optimized data fusion for kernel k-means clustering. IEEE Trans. Pattern Anal. Mach. Intell. 34 1031–1039. 10.1109/TPAMI.2011.255 [DOI] [PubMed] [Google Scholar]
- Zhang C., Churazov E., Zhuravleva I. (2020). Pairs of giant shock waves (N-waves) in merging galaxy clusters. Monthly Notices R. Astronomic. Soc. 501 1038–1045. [Google Scholar]
- Zheng Y., Byeungwoo J., Xu D., Wu Q. M. J., Hui Z. (2015). Image segmentation by generalized hierarchical fuzzy C- means algorithm. J. Intell. Fuzzy Syst. 28 4024–4028. 10.3233/IFS-141378 [DOI] [Google Scholar]
- Zhu L., Chung F. L., Wang S. T. (2009). Generalized fuzzy k-means clustering algorithm with improved fuzzy partitions. IEEE Trans Syst. Man Cybern. 39 578–591. 10.1109/TSMCB.2008.2004818 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://brainweb.bic.mni.mcgill.ca.