Changes in EEG permutation entropy in the evening and in the transition from wake to sleep

Abstract

Quantifying the complexity of the EEG signal during prolonged wakefulness and during sleep is gaining interest as an additional mean to characterize the mechanisms associated with sleep and wakefulness regulation. Here, we characterized how EEG complexity, as indexed by Multiscale Permutation Entropy (MSPE), changed progressively in the evening prior to light off and during the transition from wakefulness to sleep. We further explored whether MSPE was able to discriminate between wakefulness and sleep around sleep onset and whether MSPE changes were correlated with spectral measures of the EEG related to sleep need during concomitant wakefulness (theta power—P_theta: 4–8 Hz). To address these questions, we took advantage of large datasets of several hundred of ambulatory EEG recordings of individual of both sexes aged 25–101 years. Results show that MSPE significantly decreases before light off (i.e. before sleep time) and in the transition from wakefulness to sleep onset. Furthermore, MSPE allows for an excellent discrimination between pre-sleep wakefulness and early sleep. Finally, we show that MSPE is correlated with concomitant P_theta. Yet, the direction of the latter correlation changed from before light-off to the transition to sleep. Given the association between EEG complexity and consciousness, MSPE may track efficiently putative changes in consciousness preceding sleep onset. An MSPE stands as a comprehensive measure that is not limited to a given frequency band and reflects a progressive change brain state associated with sleep and wakefulness regulation. It may be an effective mean to detect when the brain is in a state close to sleep onset.

Statement of Significance.

Quantifying the complexity of the EEG signal during prolonged wakefulness and sleep is an additional mean to understand the mechanisms associated with sleep and wakefulness regulation. We computed EEG signal complexity, using Multiscale Permutation Entropy (MSPE) analysis, over the 2 h preceding light-off and in the transition to sleep. We find that EEG complexity decreases progressively prior to light-off and during the transition from wakefulness to sleep. Furthermore, EEG signal complexity allows for an excellent discrimination between pre-sleep wakefulness and early sleep. MSPE stands as a comprehensive measure that is not limited to a given frequency band and reflects a progressive change brain state associated with sleep and wakefulness regulation. It may be an effective means to detect when the brain is in a state close to sleep onset.

Introduction

Sleep is determined by the interaction between homeostatic and circadian processes [1]. The neuroanatomy, neurochemistry, and neurophysiology of the changes associated with this interaction have been partly elucidated [2–4]. The aspect that may appear best characterized may be the electrophysiology of sleep–wake regulation and its link with the need for sleep.

Fourier transformations of the electroencephalography (EEG) signal are typically used to characterize sleep–wake regulation. During wakefulness, the build-up of sleep need can be captured in the power of EEG theta rhythm [5], which encompasses EEG components in the frequency range of 4–8 Hz [6–8]. Theta rhythm of EEG is associated with a variety of psychological states including hypnagogic imagery, low levels of alertness, or vigilance and drowsiness [9]. It has, for instance, been widely investigated in drowsy driving detection [10–14].

However, the EEG signal is nonlinear and non-stationary with a high degree of complexity, so that it may not be fully appropriate for Fourier transformation [15]. In recent years, with increased awareness of complexity theories, entropy-based approaches have been used as nonlinear analyses of EEG to provide independent and complementary measures to conventional EEG spectral analysis [16, 17]. Permutation Entropy (PE) has received substantial attention [18]: its low computational cost and robustness to observational noise [19], trends [20] and even common blink and eye-movement artifact in EEG [21], makes it an interesting approach for large datasets that could, otherwise, require long processing, as well as for, potential noisier, ambulatory recordings. PE was found to be useful in detecting epileptic seizure [22–25], assessing the effects of anesthesia [26–28], understanding cognitive brain activity [29, 30] and assessing disorders of consciousness [31, 32] Moreover, PE was found to progressively decrease during slow wave sleep [33, 34]. How PE changes during wakefulness over the few hours preceding sleep and in the transition from wake to sleep is not established. In addition, its ability to discriminate between wakefulness and sleep states around sleep onset has not yet been investigated as well as whether pre-sleep PE is related to typical spectral EEG measures.

As an outcome of the brain with its complex self-regulation and inputs from multiple spatial and temporal scales, EEG activity in a healthy human brain possesses scale-free structure over multiple time scales [35, 36]. Multiscale entropy analysis, proposed by Costa et al. [37, 38], was widely used to quantify the complexity of physiologic time series, such as EEG [39–41] and heart rate [42–44]. The application of multiscale approach could account for the multiple time scales inherent in healthy physiologic dynamics and thus provide a more comprehensive tool to capture the dynamical characteristics of physiological time series than single-scale analysis does. Take PE for example, Li et al. found that measurement of multiscale PE (MSPE) behaves much better than the single-scale PE to track the effect of sevoflurane anesthesia on the central nervous system [45].

Here, we characterized the changes in EEG signal complexity, using MSPE, during the 2 h wakefulness period preceding light-off and in the transition from wake to sleep. We further explored whether MSPE could discriminate wakefulness and sleep around sleep onset and whether pre-sleep MSPE was significantly correlated to simultaneous theta power. We took advantage of large datasets of several hundred of ambulatory EEG recordings to address these questions. We hypothesized that MSPE would decrease in the evening as well as after light-off, during the transition from wake to sleep.

Methods

Datasets

Data analyzed in this study were obtained from two datasets: the PhysioNet and the Sleep Heart Health Study (SHHS) datasets. Subjects and recordings of the PhysioNet dataset were described in reference [46]. Briefly, two polysomnograms (PSGs) of about 20 h each were recorded during two subsequent day–night periods at the subjects’ homes. Subjects were of both sexes and aged between 25 and 101 years and continued their normal activities but wore a modified Walkman-like cassette-tape recorder. Two channel of EEGs, Fpz/Cz and Pz/Oz, sampled at 100 Hz, were included.

The SHHS is a multi-center cohort study that was implemented by the American National Heart, Lung, and Blood Institute to determine cardiovascular and other consequences of sleep-disordered breathing, and its characteristics have been described in detail elsewhere [47, 48]. One overnight PSG was obtained at home using an unattended setting placed by trained and certified technicians in individuals of both sexes aged 39–90 years. Two EEG channels, C3/A2 and C4/A1, were included and sampled at 125 Hz.

In the current study, Pz/Oz and C4/A1 derivations were using in PhysioNet and SHHS datasets, respectively. For both datasets, sleep stages were visually scored per 30-s EEG epoch based on Rechtschaffen and Kales (R&K) rules [49] by trained sleep technologists, including wakefulness, rapid eye movement (REM) sleep and stage 1–4 of non-REM sleep (NREM).

Included subjects

Seventy-eight participants who were free of any sleep-related medication intake were recruited for two consecutive day–night PSGs in the PhysioNet dataset. However, one participant was excluded due to the loss of PSG data in the second night. Therefore, 77 participants were included and their EEG data of the second night were involved in further analysis.

Three hundred and seventy-eight healthy adults from SHHS were considered based on the following inclusion criteria: (1) no benzodiazepines, tricyclic, or non-tricyclic antidepressants intake within 2 weeks of the SHHS visit; (2) no history of stroke; (3) apnea–hypopnea index, representing the number of apnea and hypopnea events with ≥3% oxygen desaturation per hour of sleep, <5; (4) no major trouble falling asleep (the frequency of trouble falling asleep <16 x/month); (5) night time wake up or difficulty resuming sleep <16 x/month; (6) waking up too early or unable to resume sleep <16 x/month; (7) no chronic use of sleeping pills or other medication intake to help sleep (the frequency <16 x/month); (8) entire recording was scored; scoring stared before light-off and ended after light-on; (9) sleep latency (SL), defined as the duration from light-off to sleep-onset, ≥10 min. Each participant in SHHS has one-night PSG recording, leading to 367 EEG recordings for further analysis. A study code varying from outstanding to fair was given to each recording in SHHS based on the quality and duration of EEG, respiratory and oximetry signals [50]. Such a code was used as a measure of signal quality in the statistical analyses of the present study. For the 378 recordings included, 20.4% rated as outstanding, 23.8% as excellent, 24.1% as very good, 23% as good, and 8.73% as fair.

Table 1 illustrated the demographics and sleep structures for the included subjects from both datasets.

Table 1.

Demographics and sleep structures of the included subjects

Dataset	Subjects	Sex male/ female	Age	SL	Stage (%)
					S1	S2	S3	S4	REM	Wakefulness
PhysioNet	77	36/41	57	10	6.1	23	3.2	0.2	8.8	57
			[46,73]	[5,22]	[4.5,9.4]	[19,26]	[0.8,4.8]	[0,2]	[6.4,11]	[54,62]
SHHS	378	130/248	58	21	3	39	12	0	15	28
			[50,66]	[15,33]	[1.9,4.6]	[31,45]	[7.6,17]	[0,0.1]	[11,18]	[21,36]

Values are expressed as median [lower quartile, upper quartile].

Abbreviations: REM, Rapid Eye Movement; S1, stage 1 of NREM sleep; S2, stage 2 of NREM sleep; S3, stage 3 of NREM sleep; S4, stage 4 of NREM sleep; SHHS, the Sleep Heart Health Study; SL, sleep latency.

MSPE algorithm

There are two main steps in the MSPE algorithm, one is a coarse-graining process and the other is the calculation of PE for each coarse-grained time series.

The coarse-graining process

Given a time series with N data points $\{x_1,x_2,\cdots ,x_N\}$, a consecutive coarse-grained time series, {y^(s)}, can be constructed according to the equation (1), where s represents the scale factor.

$${\displaystyle \begin{array}{l}{\displaystyle y_j^{(s)}=\frac{1}{s}{\displaystyle \underset{i=(j-1)s+1}{{\displaystyle \sum ^{js}}}}{x}_i,1\le j\le N/s}\end{array}}$$ (1)

The length of {y^(s)}, denoted as Ns in the following, is equal to the length of the original time series N divided by s. When s equals to 1, the coarse-grained time series {y⁽¹⁾} is exactly the original time series. Figure 1, A illustrated the construction of {y⁽³⁾} of time series $\{x_1,x_2,\cdots ,x_N\}$.

Figure 1.

(Color online) Illustration of the MSPE algorithm. (A) The coarse-graining procedure for scale factor of 3. Each black dot represents a data point in the original time series. (B) The ordinal patterns in MSPE calculation with embedding dimension of 4 and time lag of 1. The circle dots in (B) represent the data points in a time series, and the combination of four numbers under a rectangle or a horizontal line stands for an ordinal pattern of the segment in the rectangle or right above the line. The segments in the rectangles have the same pattern [1–4].

The calculation of PE for each coarse-grained series

According to the algorithm proposed by Bandt and Pompe [19], PE values can be calculated for each coarse-grained time series {y^(s)} with length Ns. {y^(s)} is the first embedded in a m-dimensional space with a lag $\mathrm{\tau }$, leading to $Ns-(m-1)\mathrm{\tau }$ vectors. The construction of the ith vector is shown in equation (2).

$${\displaystyle \begin{array}{l}{\displaystyle Y_i=[y_i^{\left(s\right)},y_{i+\tau }^{\left(s\right)},y_{i+2\tau }^{\left(s\right)},\cdots ,y_{i+(m-1)\tau }^{\left(s\right)}],i=1,2,\dots ,Ns-(m-1)\tau }\end{array}}$$ (2)

Each vector $Y_i$ is then mapped into an ordinal pattern, that is, a permutation, based on the rankings of its elements after sorting them in an ascending order. For example, the vector [7, 8, 12, 15] in a 4-dimensional space can be mapped to the ordinal pattern [1–4]. In the case of two or more equal elements, the equal values will be ordered by their time of appearance within the vector. Therefore, the vector [11, 13, 15] will be mapped to the ordinal pattern [1–4]. Figure 1, B indicates how the mapping is developed, in which Ns, $\mathrm{\tau }$, and m are set as 20, 1, and 4, respectively.

As aforementioned, there will be $Ns-(m-1)\mathrm{\tau }$ vectors after embedding {y^(s)} in a m-dimensional space with lag $\mathrm{\tau }$, and each vector corresponds to an ordinal pattern. For a m-dimensional vector, the number of its possible ordinal patterns equals the factorial of m (denoted as m!). For each ordinal pattern ${\mathrm{\pi }}_i$, we can count its occurrence on all the m-dimensional vectors and then obtain its probability, denoted as $\mathrm{p}({\mathrm{\pi }}_i)$, by calculating the ratio of its occurrence to $Ns-(m-1)\mathrm{\tau }$. Take the time series shown in Figure 1, B as an example, the pattern [1–4] occurs three times in all the 17 vectors, resulting in a probability of 3/17 for this pattern. Therefore, the PE of the coarse-grained time series {y^(s)} in m-dimensional embedding space can be defined as the Shannon entropy associated to the distribution of all possible ordinal patterns and normalized as shown in equation (3).

$${\displaystyle \begin{array}{l}{\displaystyle PE=\frac{-{\displaystyle \sum _{i=1}^{m!}}\mathrm{p}({\mathrm{\pi }}_i)log(\mathrm{p}({\mathrm{\pi }}_i))}{\mathrm{l}\mathrm{o}\mathrm{g}(m!)}}\end{array}}$$ (3)

In simple words, PE estimates the complexity of a time series by taking into account the temporal order of the values. As similar fluctuations can be identified as the same pattern, it is possible to derive information about the dynamics of the underlying system by assessing probabilities of the ordinal patterns embedded in a time series. In order to assess the quantity of information encoded by such distribution, the logarithm is usually in base 2. PE value will be 1 when all patterns have equal probability, that is, when the signal contains a variety of likely pattern. Conversely, PE will be small if the time series is regular, that is, when a single or few pattern have higher probably than most others. Thus, the more regular the time series, the smaller the PE value.

The measurement of MSPE

In this study, the coarse graining process was conducted at 10 scales, that is, scale factor ranging from 1 to 10, with steps of 1. PE for each coarse-grained time series was computed and averaged as the final measurement of the MSPE analysis. In agreement with the R&K rules, MSPE analysis was performed on each 30 s EEG epoch from both datasets.

The calculation of PE of a time series depends on the selection of the data length Ns, embedding dimension m and lag $\mathrm{\tau }$. For the EEG recordings in PhysioNet dataset, the maximal Ns is 3000 (30 s *100 Hz at scale one) and the minimal is 300 (at scale 10). For the EEG recordings in SHHS dataset, the maximal and minimal Ns are 3750 and 375, respectively. As far as the embedding dimension m is considered, Bandt and Pompe [19] recommended $m=3\mathrm{t}\mathrm{o}7$ in practice. Since there is a necessary condition m! < Ns, here we only considered and compared the results obtained with m = 3, 4, or 5. In the literature, τ = 1 was often chosen for EEG signals while other values of τ were suggested to possibly provide additional information related with the intrinsic time scales of the system [18]. Considering that multiscale approach has been adopted, we only considered τ = 1 in the present study.

The computational complexity of MSPE algorithm

Theoretically, the computational complexity of MSPE on a time series with N data point depends on the maximal scale S, the embedding dimension m, and the lag τ. According to Table 2, the time complexity of the MSPE (T_MSPE) can be evaluated as,

Table 2.

A pseudocode of the MSPE algorithm

[Entropy] = MSPE(N, S, m, tau)

% N is the data length of the original signal, S is the maximal scale, m is the embedding dimension, and tau is the lag

Entropy = 0

for (i = 1: S) % treat the ith coarse-grained time series

for (j = 1: (N/i – (m − 1)) * tau)) % process the jth m-dimensional vector

% sort the vector with a lowest computational complexity of O(mlogm)

% increase the count for its corresponding pattern with a computational complexity of O(1)

PE = 0 % the PE value of the ith coarse-grained time series

for (k = 1: m!) % calculate the Shannon_entropy of all the possible patterns

% calculate − p(k) * log(k) and add it to PE with a computational complexity of O(1)

% normalize PE with a computational complexity of O(1)

Entropy = Entropy + PE

Entropy = Entropy / S % multiple-scales average

$${\displaystyle \begin{array}{ll}{\displaystyle T_{MSPE}=}& O\left(1\right)+{\displaystyle \underset{i=1}{{\displaystyle \sum ^S}}}(O(m\ast lo{g}_{2}m)+O\left(1\right))\ast (\frac{N}{i}-(m-1)\ast \tau )\\ & +O(m!)+O\left(1\right)<O(N\ast S\ast m\ast lo{g}_{2}m)+O(m!)\end{array}}$$

Considering the requirements m! < N/S, m << N and S << N in the practice of MSPE algorithm, T_MSPE can be further simplified as O(N), suggesting a superior performance (especially when N is large) than the FFT algorithm as its time complexity is O(Nlog₂N) [51].

Spectral analyses

For each 30 s EEG epoch, theta (4–8 Hz) power, denoted as P_theta in the following, was computed and averaged on successive 5-s bins by using the period-gram procedure method with direct current filtering and Hamming windowing. Theta band definition varies slightly in the literature [52–57] and 4–8 Hz is very common [6–8].

The exclusion of artifacts and outliers

If the MSPE value or P_theta of a 30 s epoch was extremely high, that is, larger than the third quartile (of each included 30 s epochs at each acquisition period) plus 1.5 times of interquartile ranges, or was extremely low, that is, lower than first quartile minus 1.5 times of interquartile ranges, it was considered as an artifact in this study and excluded from the statistical analysis of MSPE or P_theta. If all the epochs in a subject were determined as artifacts, the subject was excluded as outliers.

Framework of the current research

The framework of the current research is illustrated in Figure 2. In all the analyses, sleep-onset was defined as the first presence of two consecutive sleep epochs (i.e. Stage 1/2).

Figure 2.

Schematic diagram of the timeline in the analyses. (A) The timeline for the analysis on PhysioNet dataset. MSPE and P_theta were evaluated in three different periods, that is, 2 h pre-light-off, the sleep transition from light-off to sleep onset, and the first sleep cycle. (B) The timeline for the analysis on SHHS dataset. The included subjects must have a sleep latency more than 10 min. MSPE and P_theta were computed over each 30 s epoch within the 10 min immediately preceding and following sleep onset.

Analysis on the PhysioNet dataset

Including at least 2 h pre-light-off data is the most appealing advantage of the included PhysioNet dataset compared with the SHHS dataset. Thus, EEG recordings obtained from PhysioNet dataset (on Pz/Oz channel) were employed first to assess whether MSPE changed over the 2 h preceding light off and whether this change was correlated to concomitant theta power. Furthermore, we investigated the alteration of MSPE during three different periods, that is, the 2 h preceding light off, the transition of wake to sleep after light-off, and the first sleep cycle (Figure 2, A). For each subject, MSPE and P_theta were calculated on 30 s EEG epochs acquired in those periods.

The definition of sleep cycle used corresponded to Feinberg’s criteria [58], that is: (1) each sleep cycle contains a continuous NREM and a continuous REM period except for the first cycle, in which there is no requirement for the REM sleep; (2) for each NREM period in a sleep cycle, it must start with stage 2 and last no <15 min. If wakefulness interrupts NREM sleep, it should be last <5 min for the cycle not to be interrupted; (3) REM period should last more than 5 min with possible wakefulness interruption(s) ≤1 min.

Analysis on the SHHS dataset

We further tested the hypothesis that MSPE is significantly altered in the transition from wakefulness to sleep with SHHS dataset, because it includes many more subjects than the PhysioNet dataset. For each EEG recording, MSPE was thus computed over each 30 s epoch within the 10 min immediately preceding sleep onset (Figure 2, B). During this period, the participants were still awake and most likely eyes closed. Furthermore, concomitant P_theta was computed and whether pre-sleep MSPE was correlated to pre-sleep theta power on SHHS dataset (C4/A1 channel) was assessed.

Moreover, with the help of the large sample included in SHHS dataset, we estimated the ability of MSPE to discriminate between wakefulness and sleep around sleep onset by using the area under the receiver operating characteristic (ROC) curve (AUC). AUC is an effective way to summarize the overall accuracy of the test with values ranging from 0 to 1. A value of 0 indicates a perfectly inaccurate test and a value of 1 reflects a perfectly accurate test. In general, an AUC of 0.5 suggests no discrimination, 0.7–0.8 is considered acceptable, 0.8–0.9 is considered excellent, and more than 0.9 is considered outstanding [59]. Furthermore, the optimal cutoff value, below which sleep possibly initiates, was calculated at the ROC through Youden index analysis [60]. Here, for each participant included in SHHS dataset, ROC was computed on the MSPE of 20 consecutive 30 s epochs immediately before and after sleep onset, respectively. We also calculated the ROC, AUC, and cutoff values for P_theta in a similar way for comparison.

Statistical analyses

MATLAB (Mathworks Inc., Natick, MA) and SAS® (SAS® Institute Inc., Cary, NC) were used for statistical analyses. Descriptive statistics were reported as number or percentage for categorical data, and for continuous data, presented as median (lower quartile, upper quartile) as the data violates the normality. Generalized linear mixed models (GLMMs) were employed to investigate changes in MSPE over the period of interest and its association with P_theta. GLMMs first included MSPE as dependent variable with lognormal distribution and fixed effects included in the models consisted of acquisition period, sex, age, and recording quality (only in Analysis of SHHS dataset). To assess the link between sleep need marker and MSPE, GLMMs included MSPE, acquisition period, sex, age, and recording quality as fixed effects and P_theta as dependent variable with lognormal distribution. When present as factor, period of acquisition was included as repeated measure in all GLMMs. For completeness, we computed Spearman’s rho between MSPE and P_theta [61], however, only GLMM output was considered for statistical considerations. Moreover, two-tailed Mann–Kendall test [62] was employed to test the null hypothesis of trend absence in the vector of MSPE or P_theta across different acquisition period, that is, 2 h before light-off or 10 min before sleep-onset in the transition from wake to sleep. A one-way analysis of variance (ANOVA) was adopted to evaluate the effect of state (wakefulness during 2 h before light-off, sleep transition in the sleep latency after light-off, and the first sleep cycle) on MSPE or P_theta.

The GLMM evaluation was conducted in SAS while the Spearman correlation analysis and Mann–Kendall test were performed in MATLAB. In all GLMMs, subjects were used as random factors and a p-value <0.05 was considered statistically significant. Moreover, the Kenward and Roger (KR) approach [63] was used to estimate degrees of freedom and to obtain standard errors and associated statistical significance.

Results

For each subject, we calculated MSPE and P_theta on each 30 s epoch during the periods of interest for both datasets (Figure 2). Artifacts and outliers were detected and excluded based on MSPE or P_theta before further analysis. Table 3 summaries the artifacts and outliers excluded.

Table 3.

Artifacts and outliers detected for the periods of interest in both datasets, based on MSPE or P_theta values

Dataset	Period	Artifacts (%)				Outliers
		MSPE			P  theta	MSPE			P  theta
		m = 3	m = 4	m = 5		m = 3	m = 4	m = 5
PhysioNet	2 h pre-light-off	5.67 ± 2.34	4.03 ± 1.77	3.67 ± 1.63	5.30 ± 2.32	0	0	0	0
	Sleep transition	3.37 ± 11.9	3.21 ± 11.5	3.28 ± 11.6	9.22 ± 24.5	0	0	0	3
	The 1st sleep cycle	2.82 ± 8.43	2.58 ± 7.83	2.29 ± 7.03	5.85 ± 16	0	0	0	0
SHHS	10 min before sleep onset	3.88 ± 1.19	4.35 ± 1.00	4.46 ± 1.08	7.99 ± 1.18	2	2	2	5
	10 min after sleep onset	1.27 ± 0.85	1.3 ± 0.94	1.43 ± 0.95	5.11 ± 1.34	0	0	0	5

Analysis on PhysioNet dataset: MSPE gradually decreases and correlates with concomitant theta power toward light off

We first wondered whether MSPE would vary over the 2 h preceding light off and correlate with concomitant P_theta. To address this question, we used PhysioNet dataset as it contains >2 h of data preceding light-off.

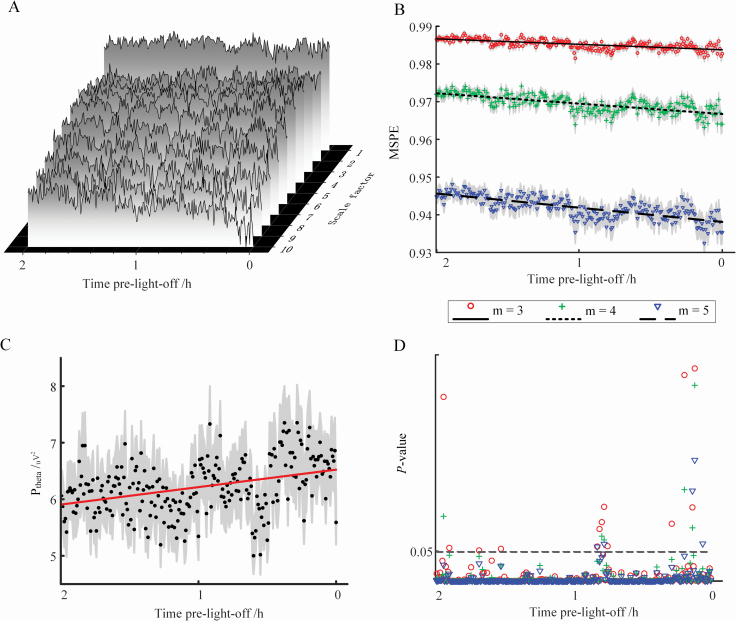
Figure 3, A illustrates the average PE value (for all the participants) of each scale across the acquisition period before light off with embedding dimension m = 3 (the display obtained with m = 4 or 5 is similar; not shown here). Intuitively, the PE values at most of the scales fluctuate with a tendency of decreasing towards light-off. Figure 3, B illustrated the MSPE values (mean ± standard errors) obtained with m = 3, 4, or 5 and the lines were fitted with the averaged MSPE values across the acquisition periods. Progressive decline of MSPE towards light-off can be observed regardless of the value of m (Figure 3, B; Mann–Kendall test, z = −10.9, −11.9, and −12.8 for m = 3, 4, and 5, respectively, with p < 0.0001). GLMMs also show a significant change of MSPE with time (Table 4; main effect of acquisition period, p = 0.0002, 0.002, and 0.022 for m = 3, 4, and 5, respectively). Moreover, at each time bin, MSPE value consistently decreases as m increases from 3 to 5 because the larger the embedding dimension, the more details are obtained from the signal; thus, less random the signal becomes and the smaller its MSPE value [64].

Figure 3.

(color online) Variations in MSPE and P_theta values before light off. (A) Average value of PE for all the participants in PhysioNet datasets using different scale factors. For the calculation of PE, the embedding dimension m was set as 3. (B) Average MSPE at m = 3, 4, or 5 at each time bin; shade areas represent the standard errors of the mean. (C) Average P_theta at each time bin; shade areas represent the standard errors of the mean. (D) p-values of the Spearman correlation between MSPE (with m set as 3, 4, or 5) and concomitant P_theta over each time bin.

Table 4.

Results of GLMM evaluating the association between acquisition periods preceding light off and MSPE or P_theta

Dependent variable	Factors	m = 3			m = 4			m = 5
		Estimate	p	R  2	Estimate	p	R  2	Estimate	p	R  2
MSPE	Period		0.0002	0.019		0.002	0.018		0.022	0.017
	Age	<0.0001	0.343	0.012	<0.0001	0.362	0.011	<0.0001	0.318	0.014
	Sex	−0.004	0.021	0.075	−0.007	0.017	0.081	−0.01	0.016	0.083
P  theta	Period		0.429	0.015		0.642	0.014		0.7	0.014
	MSPE	3.771	<0.0001	0.004	2.55	<0.0001	0.005	2.02	<0.0001	0.005
	Age	−0.008	0.01	0.096	−0.008	0.010	0.094	−0.008	0.01	0.094
	Sex	−0.654	<0.0001	0.313	−0.65	<0.0001	0.316	−0.652	<0.0001	0.312

Similarly, an increase tendency toward light-off was observed in P_theta (Mann–Kendall test, z = 5.88 and p < 0.0001; Figure 3, C). After controlling for all confounding factors in a GLMM, no significant effect of acquisition period on P_theta was found (Table 4; GLMM, main effect of acquisition period, p > 0.05). Moreover, in line with the literature [65], sex and age were significantly associated with P_theta with women showing higher theta power and theta power declining with age (Table 4; GLMM, for sex and age, p < 0.0001 and p = 0.01, respectively, regardless of m). Importantly, Spearman’s correlation analyses over time bins indicate that P_theta shows a significant positive link with MSPE for most time bins within 2 h before light off (occurs at 227, 234, and 235 out 240 time bins for m = 3, 4, and 5, respectively) (Figure 3, D). Such a positive association is surprising given that, overall, both metrics evolve in opposite direction. GLMMs confirm, however, the significant positive association (Table 4; main effect of MSPE, p < 0.0001 regardless of m) after controlling for the effects of age and sex.

Furthermore, for each participant, we computed and compared the median values of MSPE during three periods of interest (Figure 2, A), that is, 2 h before light-off, sleep transition after light-off, and the first sleep cycle. As the results obtained with m = 3, 4, or 5 are similar, only these with m = 3 are displayed in Figure 4 which shows that MSPE gradually decrease from wakefulness to sleep transition and then to the first sleep cycle (Figure 4, A). The results of ANOVA further indicate that period is a main effect of MSPE (F = 332, p < 0.0001) and post hoc analysis suggests there is significant difference between the MSPE values of each two periods. As for the concomitant P_theta, although ANOVA also indicates a significant effect of period (F = 35, p < 0.0001), only significant difference between the pre-light-off state and the sleep state was revealed (Figure 4, B).

Figure 4.

The values of MSPE (A) and P_theta (B) during pre-light-off wakefulness, pre-sleep wakefulness and first sleep NREM-REM cycle. Each dot represents the median value of MSPE or P_theta for a participant during the corresponding period. The box-plots illustrate the distribution of these median values for all the participants in PhysioNet dataset. The symbol ‘*’ represents for a significant difference of median values between groups (post hoc tests of ANOVA, p < 0.05).

Analysis on SHHS dataset: MSPE decreases in wake-to-sleep transition and predicts sleep-onset

We then asked whether MSPE would vary during the transition from wake to sleep preceding sleep-onset (Figure 2, B). To address this question, we switched to SHHS datasets as it includes many more subjects.

Figure 5, A illustrates the average PE value for all the participants (m = 3; the display is similar in the situation of m = 4 and 5; not shown) over each time bin within 10 min immediately before sleep onset. A progressive decline of PE toward sleep can be observed at scale one and two (Figure 5, A). Although Mann–Kendall test only indicates significant decline of MSPE toward sleep in the situation of m = 3 (Figure 5, B; z = −3.34 and p < 0.0001), GLMM analysis (Table 5) shows significant effect of acquisition period on MSPE (p < 0.05) regardless of m used. Likewise, significant decrease of P_theta with time was found (Figure 5, C; Mann–Kendall test, z = −2.11 and p = 0.035; Table 5, GLMM, main effect of acquisition period, p < 0.05, regardless of m). Spearman’s correlation analyses over each time bin indicated significant negative association between P_theta and MSPE for most of the time bins and for all the embedding dimensions considered (Figure 5, D). GLMMs confirmed that P_theta was significantly negatively associated to MSPE (Table 5; main effect of MSPE, p < 0.001, regardless of m) including sex and age as covariates. The negative association comes again as a surprise given that, overall, both metrics evolve in the same direction in the transition to sleep (i.e. they both decrease).

Figure 5.

(Color online) Variations in MSPE and P_theta values within 10 min immediately before sleep-onset. (A) Average value of PE for all the participants in PhysioNet datasets using different scale factors. For the calculation of PE, the embedding dimension m was set as 3. (B) Average MSPE at m = 3, 4, or 5 at each time bin; shade areas represent the standard errors of the mean. (C) Average P_theta at each time bin; shade areas represent the standard errors of the mean. (D) p-Values of the Spearman correlation between MSPE (with m set as 3, 4, or 5) and concomitant P_theta over each time bin.

Table 5.

Results of GLMM evaluating the association between acquisition periods preceding sleep onset and MSPE or P_theta

Dependent variable	Factors	m = 3			m = 4			m = 5
		Estimate	p	R  2	Estimate	p	R  2	Estimate	p	R  2
MSPE	Period		0.0001	0.008		0.016	0.006		0.02	0.005
	Age	<0.0001	0.116	0.007	<0.0001	0.072	0.009	0.0001	0.082	0.009
	Sex	−0.0004	0.598	0.001	−0.0009	0.494	0.001	−0.001	0.453	0.002
	Quality	<0.0001	0.969	<0.0001	−0.0001	0.762	0.003	−0.0004	0.521	0.001
P  theta	Period		0.039	0.005		0.012	0.006		0.007	0.006
	MSPE	−16.50	<0.0001	0.054	−10.76	<0.0001	0.063	−9.08	<0.0001	0.073
	Age	−0.001	0.575	0.001	−0.001	0.602	0.0008	−0.001	0.596	0.001
	Sex	0.05	0.463	0.0014	0.046	0.492	0.001	0.044	0.513	0.001
	Quality	−0.024	0.33	0.003	−0.025	0.302	0.003	−0.026	0.28	0.003

To investigate further the switch in correlation direction from pre-light-off wakefulness to the transition to sleep, we assesses the association between MSPE (m = 3) and the ratio of EEG power in theta band and the fast beta frequency band (beta, 13–30 Hz; theta/beta ratio, TBR). The analyses indicates that both during the 2 h preceding light-off (PhysioNet dataset) and during the transition toward sleep (SHHS dataset), the more theta, relative to faster frequencies, the lower the EEG signal complexity (Figure 6, A and B, significant negative correlation between TBR and MSPE; Table 6, GLMM, main effect of MSPE, p < 0.001).

Figure 6.

(Color online) The Spearman’s rho and its p-value between MSPE and TBR during (A) the 2 h pre-light-off with PhysioNet dataset and (B) the 10 min before sleep-onset with SHHS dataset. Here, m was set as 3 in the calculation of MSPE and TBR represents the ratio of EEG power in theta band and beta band.

Table 6.

Results of GLMM evaluating the association between MSPE (m = 3) and TBR during two periods

Dependent variable	Factors	2 h pre-light-off			10 min before sleep onset
		Estimate	p	R  2	Estimate	p	R  2
TBR	Period		<0.0001	0.022		<0.0001	0.093
	MSPE	−23	<0.0001	0.131	−31.12	<0.0001	0.161
	Age	−0.001	0.685	0.002	0.001	0.578	0.001
	Sex	0.169	0.176	0.025	−0.016	0.743	0.0003
	Quality				0.012	0.467	0.002

TBR, the ratio of EEG power in theta band and beta band.

We finally focused on the ability of PE measures to discriminate between sleep and wakefulness around sleep onset. PE at different scales was found to have different ability to discriminate epochs before or after sleep onset (i.e. wake or sleep stages; Figure 7, A) and excellent AUCs (more than 0.8) can be obtained at scales from 2 to 5 for all the embedding dimensions considered. Moreover, PEs calculated with a parameter m = 3 outperforms those obtained with m = 4 or 5 at all the scales. In the situation of m = 3, PE of the original time series yielded to an acceptable AUC of 0.753, while the highest AUC, 0.870, was achieved at scale 4 (Figure 7, A). We can also conclude from Figure 7, B that MSPE with a parameter m = 3 serves as the most discriminative method while the ROC of P_theta is nearest to the diagonal line. The AUC and cutoff values of the ROCs obtained by MSPE, PE of the original time series and P_theta are further shown in Table 7, which indicates an obvious promotion of discriminative ability with the application of multiscale analysis. In consistence with Figure 7, B, an excellent AUC of 0.856 was achieved by MSPE with m = 3. However, the AUC was 0.730 when P_theta was used (Table 7), even less than those obtained by the PE values of the original time series.

Figure 7.

(Color online) The AUC values to differentiate states before and after sleep-onset. (A) AUC values of PE obtained with different scale factors and different embedding dimensions (3, 4, or 5). AUC values above the dashed line correspond to an excellent ability of the test. (B) ROC curves of P_theta and MSPE obtained with m = 3, 4, or 5.

Table 7.

The AUC and cutoff values of MSPE and original PE obtained with m = 3, 4, or 5 and of P_theta

	MSPE			Original PE			P  theta
	m = 3	m = 4	m = 5	m = 3	m = 4	m = 5
AUC	0.856	0.846	0.84	0.753	0.737	0.736	0.73
Cutoff	0.968	0.947	0.921	0.848	0.780	0.741	18.33/uV2

Discussion

Quantifying the complexity of the EEG signal during prolonged wakefulness and during sleep is gaining interest as an additional mean to characterize the mechanisms associated with sleep and wakefulness regulation.Here, we report significant changes in EEG complexity, as indexed by MSPE, immediately prior to light off and during the transition from wakefulness to sleep. We further report that MSPE can reach excellent (AUC > 0.8) discrimination between wakefulness and sleep around sleep onset and that MSPE changes are correlated with concomitant P_theta spectral measures.

Standard Fast Fourier transformations (FFT) assume that the measured EEG signal consists in a linear combination of fluctuations of different frequencies. Brain oscillations are, however, not a linear combination of frequency components that could be added up. In other words, they are intrinsically nonlinear [17]. Two main types of non-linear methods have been proposed to enrich the characterization of the (sleep) EEG, fractal-based and entropy methods. Here, we used the latter type which measures the uncertainty about the information source and the probability distribution of the samples drawn from it, so that entropy can be an indicator of the complexity of the EEG signal [17]. By utilizing the recurrence of ordinal patterns in the signal, the calculation of PE takes into account time causality between the values of the time series and reflects the time characteristics of the underlying dynamics [19]. A high PE value of scalp EEG signal was reported as a direct reflection of a more active cortex with an EEG output which is less regular and exhibits higher frequency content [33]. Entropy of the sleep EEG has consistently been reported to gradually decrease from wake to sleep stage N1, N2, and N3, indicating that brain activity becomes less complex, more coherent, and periodic, while entropy increases during REM as compare to NREM sleep [17, 64, 66, 67]. Entropy likely decreases during sleep because neurons are more synchronized (i.e. regular interactions within the neuronal network) [68]: frequency content slows down and amplitude increases, generating a less complex signal. The entropy decrease during NREM sleep could also arise from the fact that fewer neurons are involved in information processing. There are indeed several reports that brain signal remains more local during sleep with less interaction between distant brain regions [69, 70], and therefore potentially less neurons contributing to the EEG signal. Here, we report that there is a decrease in MSPE during the 2 h preceding light-off and in the transition from wakefulness to sleep, suggesting that, as for NREM sleep progression from N1 to N3 [71], falling asleep is a gradual process. This is reminiscent of previous intracranial recording in epileptic patients that detected spindles before sleep onset, particularly in the hippocampus [72]. As for sleep, lower MSPE likely arises from a progressively more synchronized neuronal activity. Whether reduced signal propagation also contributes is unclear as previous reports suggest that signal scattering increases in the evening before decreasing during nighttime wakefulness [73–75].

Complexity measures have been used to differentiate conscious from unconscious states by quantifying the information content of the spatiotemporal cortical activity. Compared to wakefulness, reduced complexity was recorded during anesthesia, sleep and disorders of consciousness [31, 76, 77], suggesting that complex brain activity is a prerequisite or a consequence of consciousness. Previous studies also demonstrated PE is maximal during wakefulness while decreases during sleep [64] and tends to be greatest when the subjects are in fully alert states while falling in states with loss of awareness or consciousness [78]. In line with these findings, we find that EEG complexity (or MSPE) can effectively differentiate pre-sleep wakefulness, when computed over the 10 min preceding sleep-onset onset (defined as the first two consecutives epoch of N1 or N2 stages), from early sleep, when computed over the 10 min following sleep onset. It outperforms in fact theta band power in doing so. Furthermore, we show that MSPE decreases over the 2 h preceding light off and over the 10 min preceding sleep (especially when m = 3). Whether these changes reflect a progressive loss of consciousness remains an open question. While one can posit that it is the case over the transition between sleep and wakefulness, it may be more difficult to argue that our sample of healthy participants was progressively less conscious before light-off.

We stress that any settings of MSPE computation could be used to efficiently track pre-sleep signal complexity changes. However, the results obtained from an embedding dimension of 3 and scale factor of 4 appear best for discriminating pre- and after- sleep-onset states. Future research will confirm whether the MSPE parameters (m = 3, τ = 1 and maximal scales = 10) we used to be indeed the most effective to track pre-sleep EEG signal complexity alterations. We further emphasize that MSPE is an efficient method which is, in principle, more efficient than FFT. In computer science, an algorithm with a time complexity of O(N), as MSPE, is considered to be more efficient than that with a time complexity of O(NlogN), such as FFT. In this respect, the MSPE has less computational cost than FFT. In practice, however, especially when N, representing the length of an EEG signal, is small (e.g. <3000), the difference of the running times between both methods should be small.

Our explorations of the link with P_theta show that this well-accepted spectral measure of sleep need is significantly associated with MSPE. Yet, the link is puzzling. While MSPE and P_theta evolve in overall opposite direction over the 2 h preceding light-off, their values are positively associated. In contrast in the transition to sleep, both metrics are globally decreasing and yet they are negatively correlated. Faster frequencies are progressively dominated by slower theta power during pre-light-off wakefulness as a reflection of the increase in sleep need [79]. Our results suggest that during this period, the more theta, relative to faster frequencies, the lower the EEG signal complexity. Following light-off, in the eye-closed transition toward sleep, the EEG further slows downs so that the dominant frequency likely lies in the theta/delta. This likely explains why our results show that during transition to sleep, the link with theta power switches to being negative. From a frequency analysis point of view, MSPE covers the entire spectrum of oscillations included in a time series, so one could consider it as a comprehensive measure that is not limited to a given frequency band and yet reflects a progressive change brain state associated with sleep and wakefulness regulation.

We acknowledge that our study bears some limitations. First, as stated above, recording was ambulatory, thus providing less control over the experimental condition. We do not have information regarding the behavior of the participants, for example, when they went to bed relative to light-off or the type of activities they were engaged in prior to going to bed. It is therefore unclear whether participants’ behavior may underlie part of the evolution of MSPE prior to light-off. This limitation may however constitute a strength: our findings are valid in real life situations. Second, artifacts in the data were not excluded following visual or validated automatic procedures, but were rather considered to be efficiently removed by excluding sudden variations in MSPE or P_theta within each recording. In addition, while the current findings are based on large set of data in individuals devoid of sleep disorders (N = 378), providing relatively high statistical sensitivity, MSPE may come with the cost of reduced sensitivity for some individual differences such as sex and age which are typically associated to EEG spectral analyses. Yet, MSPE significantly varied close to light-off and sleep onset, particularly when setting the embedding dimension to 3. It may therefore constitute an entropy approach more sensitive than others that previously failed to identify significant changes during in-lab sleep deprivation protocols [34, 74].

Modern society lifestyle often leads to sleep loss [80–82] and chronic sleep restriction [83] that cause fatigue and impairment in vigilance, working memory, and cognitive throughput [84] and may lead to accidents [10]. MSPE is a low computation time method that may be an effective mean to detect when the brain is in a state close to sleep onset.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No.61401518) and the Double First‐Class University project of China. GV is supported by Fonds National de la Recherche Scientifique (FNRS-Belgium). GG was supported by Wallonia-Brussels International and University of Liège. The Sleep Heart Health Study was supported by the National Institutes of Health, National Heart Lung and Blood Institute (U01HL53916, U01HL53931, U01HL53934, U01HL53937, U01HL53938, U01HL53940, U01HL53941, U01HL64360). The National Sleep Research Resource was supported by the National Institutes of Health, National Heart Lung and Blood Institute (R24 HL114473, RFP 75N92019R002).

Conflict of interest statement. None declared.

Data Availability

The data underlying this article are available at https://www.physionet.org/content/sleep-edfx/1.0.0/ and https://sleepdata.org/datasets/shhs/files/datasets.