Abstract
Background:
Quantitative susceptibility mapping (QSM) uses prior information to reconstruct maps, but prior information may not show pathology and introduce inconsistencies with susceptibility maps, degrade image quality and inadvertently smoothing image features.
Purpose:
To develop a local field data-driven QSM reconstruction that does not depend on spatial edge prior information.
Study Type:
Retrospective.
Subjects, animal models:
A dataset from 2016 ISMRM QSM Challenge, 11 patients with glioblastoma, a patient with microbleeds and porcine heart.
Sequence/Field Strength:
3D gradient echo sequence on 3T and 7T scanners.
Assessment:
Accuracy was compared to Calculation of Susceptibility through Multiple Orientation Sampling (COSMOS), and several published techniques using region of interest (ROI) measurements, root-mean-squared error (RMSE), structural similarity index metric (SSIM), and high-frequency error norm (HFEN). Numerical ranking and semiquantitative image grading was performed by three expert observers to assess overall image quality (IQ) and image sharpness (IS).
Statistical Tests:
Bland–Altman, Friedman test, and Conover multiple comparisons.
Results:
Loss adaptive dipole inversion (LADI) (β = 0.82, R2 = 0.96), morphology-enabled dipole inversion (MEDI) (β = 0.91, R2 = 0.97), and fast nonlinear susceptibility inversion (FANSI) (β = 0.81, R2 = 0.98) had excellent correlation with COSMOS and no bias was detected (bias = 0.006 ± 0.014, P < 0.05). In glioblastoma patients, LADI showed consistently better performance (IQGrade = 2.6 ± 0.4, ISGrade = 2.6 ± 0.3, IQRank = 3.5 ± 0.4, ISRank = 3.9 ± 0.2) compared with MEDI (IQGrade = 2.1 ± 0.3, ISGrade = 2 ± 0.5, IQRank = 2.4 ± 0.5, ISRank = 2.8 ± 0.2) and FANSI (IQGrade = 2.2 ± 0.5, ISGrade = 2 ± 0.4, IQRank = 2.8 ± 0.3, ISRank = 2.1 ± 0.2). Dark artifact visible near the infarcted region in MEDI (InfMEDI = −0.27 ± 0.06 ppm) was better mitigated by FANSI (InfFANSI-TGV = −0.17 ± 0.05 ppm) and LADI (InfLADI = −0.18 ± 0.05 ppm).
Conclusion:
For neuroimaging applications, LADI preserved image sharpness and fine features in glioblastoma and microbleed patients. LADI performed better at mitigating artifacts in cardiac QSM.
Evidence Level:
4
Technical Efficacy Stage:
1
QUANTITATIVE SUSCEPTIBILITY MAPPING (QSM) is a magnetic resonance imaging (MRI) technique that maps tissue magnetic susceptibility and has been used for noninvasive imaging of pathologic tissue biometals1 and measure blood oxygen saturation.2 Magnetic susceptibility mapping shows distinct patterns of disease compared to conventional MRI contrasts and the method has clinical imaging applications in the fields of stroke,3 impaired tissue oxygen consumption, and neuronal demyelination research.3 The principle of QSM is that an applied magnetic field induces a smaller local field that depends on the tissue magnetic susceptibility and can be detected by the MRI signal phase. Reconstruction of the magnetic susceptibility map from the local field is nevertheless a challenging, ill-posed mathematical inverse problem.4 The local field ϕ and the magnetic susceptibility χ are related by ϕ = d *χ, in which the magnetic susceptibility χ is convolved with the dipole kernel d. The inverse problem deconvolves d and ϕ to determine χ. However, the estimated magnetic susceptibility is not unique, since the Fourier domain representation of d tends to zero over a conical surface and can result in image artifacts. Although there has been significant progress in the development of new inversion techniques, these methods have some outstanding issues. The algorithms are not standardized, and depending on the reconstruction algorithm and error metric used, there are variations in contrast, edge sharpness, and morphological patterns seen in the reconstructed susceptibility maps.4 In addition, these reconstruction techniques may be computationally expensive and time-consuming to execute. There continues to be a need to develop and evaluate fast and accurate algorithms to solve this problem to enable clinical translation.
Thresholded k-space division (TKD)5 is a direct inversion technique that reduces inversion errors by using a truncated approximation of the dipole kernel Fourier domain representation, which reduces artifacts,5 but amplifies image noise and reduces accuracy.6 Several techniques to solve this ill-posed inverse problem were evaluated in the 2016 International Society for Magnetic Resonance in Medicine QSM competition.4 These QSM reconstruction techniques use a compressed sensing (CS) framework7 for removal of artifacts. Most of the popular CS techniques use a combination of least squares fidelity constraint and a data regularization (sparsifying) constraint such as total variation (TV).3,4,8–12 TV-based techniques such as these enforce a piecewise constant/smooth model for artifact removal, but can reduce image contrast, as shown for denoising applications.13 Additionally, regularization may inadvertently reduce spatial resolution, remove anatomical features, and reduce accuracy.4,12
Spatial priors can help preserve image fidelity when regularization is used, but there are some important limitations. A common spatial prior is a T2*-weighted image derived from QSM magnitude data, as used in morphology-enabled dipole inversion (MEDI).12 The prior is used to estimate phase noise nonuniformity and locate anatomical boundaries (edge location) in the susceptibility map. The main limitation of this approach is that anatomical boundaries in the magnitude image may not match those in the susceptibility map. Anatomical boundaries that are not relevant to susceptibility maps may be falsely introduced from the magnitude image or, more interestingly, the susceptibility map may contain regions of varying magnetic susceptibility that are not clearly shown in the magnitude image. In multiple sclerosis, there is pathologic evidence that iron accumulates in macrophages at the boundaries of some white matter lesions.14 In these lesions, the magnetic susceptibility map shows a ring of elevated magnetic susceptibility around the lesion that does not appear on the corresponding T2*-weighted image from which the map was derived.1 In reperfused myocardial infarction, there has also been similar pathologic evidence of iron accumulation at the transition zone between nonviable cardiomyocytes and granulation tissue.15,16
To improve image quality and edge sharpness, a novel data-driven approach was developed17 for ill-posed inverse problems that used a constrained TV formulation and iteratively updated the measured data in the fidelity constraint depending on discrepancy between the measured data and image estimate. The iterative update to improve edge sharpness, called the “adding-noise-back” step,17 has been studied for applications such as image denoising,17 deblurring,18 and reconstruction of undersampled MR images,19,20 although the technique has not been evaluated for QSM applications.
The minimization of CS-based QSM formulation such as MEDI can be relatively slow due to the ill-posed nature of the reconstruction problem. In the field of CS, several popular techniques such as Split Bregman (SB),21 Augmented Lagrangians (AL),22 and the fast iterative shrinkage-thresholding algorithm (FISTA)23 technique have been employed to accelerate convergence of the cost functional. For QSM, techniques based on the application of SB-based variable substitution have been developed8 for rapid minimization of several variants of the MEDI formulation. This technique was based on the application of SB21 -based variable substitution to the data regularization term, and was combined with the use of matrix preconditioners to allow for rapid minimization of the cost functional. In Berkin et al,8 the main aim was to develop rapid QSM reconstruction formulations.
We present an alternative approach that aims to preserve the underlying local field information of the magnetic susceptibility map. The technique, loss adaptive dipole inversion (LADI), is a novel application of the constrained TV formulation to QSM and integrates two unique features in QSM:
We apply Bregman iterations21 to a constrained TV formulation and achieve an update for the measured local field, which is aimed at improving the quality of the reconstructed image. The advantage of this data-driven technique is that it does not require spatial priors to identify anatomical boundaries and prevent blurring. Hence, it is unaffected by errors such as mismatch between the spatial edge prior and susceptibility map. By data-driven QSM, we mean a local field data-based technique that does not require any other additional data.
We developed a rapid minimization technique that does not depend on the use of matrix preconditioners,8 but instead uses a combination of SB-based variable substitution and Nesterovs’ accelerated gradient (NAG)23 descent algorithm. In addition, the matrix preconditioner-based techniques developed previously8 are effective only for specific variants of MEDI (for example, when magnitude spatial priors are not used for data fidelity), while the NAG-based technique developed here provides a more generalized framework for acceleration of CS-based QSM reconstructions.
We sought to compare its performance to CS-based algorithms in neuroimaging (healthy human brain, glioblastoma patients, and a patient with microbleeds) and cardiac applications (pig model of reperfusion injury after hemorrhagic myocardial infarction) using the 2016 ISMRM QSM competition image quality metrics and semiquantitative scoring of images by expert physicians.
Theory
Assuming an isotropic susceptibility model, the forward problem relating the tissue susceptibility to the local field can be expressed as:
| (1) |
where D is the magnetic dipole kernel represented in the frequency domain, χ is the susceptibility distribution, F is the Fourier operator, FH the inverse Fourier operator, ϕ is the local field, and σ is the noise standard deviation. Single-orientation QSM formulations solve the ill-posed problem by combining Eq. 1 with a regularizer in the form of a Lagrangian. The unconstrained formulation8 is of the form:
| (2) |
Thikhonov regularization or TV constraint are often used to enforce spatial smoothness or a piecewise-constant model. These constraints penalize the gradient of the estimated susceptibility maps by using a suitable norm. Two QSM reconstruction models that are used to enforce the Thikhonov constraint and TV constraint, respectively, are:
| (3) |
| (4) |
Here is either the identity matrix I or a binary edge mask8 derived from the magnitude image to prevent smoothing of sharp transitions such as edges in the image, α is a weight that controls the amount of regularization applied, and ▽=[▽x; ▽y; ▽z] is the 3D spatial gradient operator.
Previously,11,12 a spatially varying weight is added to the fidelity term to account for the nonuniform phase noise:
| (5) |
Here, Nmag is the spatially varying weight that is estimated from the magnitude image.
Data-Driven QSM Reconstruction
In distinction to Eqs. 3 and 4, in which the unconstrained formulation was solved, we aimed to solve the constrained formulation:
| (6) |
Here, MBin is a binary mask that has a value of 1 for pixel locations that correspond to the local field and 0 for pixel locations that correspond to the background. Due to the ill-posed nature of the reconstruction formulation and the data being iteratively projected between the Fourier domain and image domain, sometimes susceptibility values are spuriously estimated beyond the region from where the local field has been estimated. The binary mask limits the estimation of the susceptibility map to the spatial region defined by the local field. In Osher et al,17 a method was developed to solve problems such as Eq. 6 by optimizing the Bregman distance.17,21 Using the Bregman iterations technique,17,21 Eq. 6 can be reduced to a combination of an unconstrained minimization problem and an update of the measured local field:
| (7) |
| (8) |
As described in Goldstein and Osher21 (Section 4.2, Eq. (4.5)–(4.7)), minimizing Eq. 7 and performing the update in Eq. 8 solves the constrained formulation in Eq. 6. The iterative update of ϕ in Eq. 6 is described as the “adding noise back” step,18,19,21 although a better description is that it adds the residual back to the measured data in Eq. 8 since the former implies that the technique would degrade the image quality. For applications such as denoising,17 deblurring,17 and reconstruction of undersampled MR images,19,20 the constrained formulation has been shown to produce improved image quality beyond that achieved by an unconstrained TV formulation.
To rapidly solve Eq. 7, we perform Split Bregman-based variable substitution using surrogate variables S = ▽ χ and rewrite Eq. 7 as:
| (9) |
Here, P comes from optimizing the Bregman distance.21 When we minimize Eq. 9 with respect to χ, only the L2 norm terms remain:
| (10) |
Here, we sought to minimize Eq. 10 rapidly using the iterative reweighting used in NAG.23 Defining a sequence of weights:
| (11) |
For two successive iterates χn and χn + 1, the NAG update to accelerate convergence is given by
| (12) |
This NAG update is fed back into the iterative reconstruction algorithm.
When minimizing Eq. 9 with respect to S:
| (13) |
Eq. 13 can be rapidly minimized using soft thresholding/shrinkage.21
The variable P is updated as:
| (14) |
The steps rapidly minimize Eq. 8 and Eq. 9 using a combination of SB variable substitution and NAG, as outlined in Supplementary Fig S1.
The minimization technique developed here for LADI Eqs. 7, (8) is different from the rapid SB-based minimization technique developed previously8 (Eqs. 11, 12). In Berkin et al,8 the SB-based variable substitution is applied to the data regularization term and the convergence was accelerated by using a combination of soft-thresholding and the application of conjugate gradient minimization with the use of a matrix preconditioner. Here we develop a rapid minimization technique that uses a combination of SB-based variable substitution and the iterative reweighting technique used in NAG.
Methods
Data Collection
Imaging data were obtained from the 2016 quantitative susceptibility mapping reconstruction challenge,4 brain MR exams from 11 patients with glioblastoma, a patient with mircobleeds, and an explant whole heart from a pig model of hemorrhagic myocardial infarction. The subject who provided data for the 2016 ISMRM Reconstruction Challenge gave informed consent to participate in a protocol approved by the Massachusetts General Hospital.4 The brain MRI patients gave informed consent to participate under a protocol approved by the Institutional Review Board of the University of Pennsylvania. Institutional Animal Care and Use Committee (IACUC) approval was obtained for collection of ex vivo cardiac data.
2016 ISMRM QSM Challenge
In 2016, the International Society for Magnetic Resonance in Medicine sponsored a quantitative susceptibility mapping reconstruction challenge to develop and compare new algorithms for QSM reconstruction.4 Two reference standards, namely, susceptibility tensor imaging (STI)4 data and multiorientation calculation of susceptibility through multiple orientation sampling (COSMOS),4 were provided as a part of the QSM reconstruction challenge. We used COSMOS as the standard to compare all the reconstructions. The 3D gradient echo (GRE) data were obtained using a wave-CAIPI acquisition on a 3 T scanner (Tim Trio Model; Siemens Healthcare, Erlangen, Germany) equipped with a 32-channel head coil, 1.06 × 1.06 × 1.06 mm3 isotropic resolution, and 15-fold acceleration. Images were acquired in 12 different orientations with respect to B0, aligned using affine registration,4,24 brain anatomy was extracted,4,24 and magnetic susceptibility maps were reconstructed using COSMOS.4,25 The sequence parameters were flip angle = 15, echo time / relaxation time [TE/TR] = 25/35 msec, 240 × 196 × 120 matrix size, and bandwidth = 100 Hz/pixel. As detailed in the challenge,4 QSM images were reconstructed from single orientation gradient echo MRI using the same imaging parameters.
Brain MRI in Glioblastoma
QSM data were obtained from 11 patients with tumor lesions (five males and six females, age = 61.7 ± 11.6 years) on a 3 T scanner (Trio Model; Siemens) equipped with a 12-channel head coil. Single echo gradient echo MRI was obtained in the axial orientation using the following imaging parameters: in-plane spatial resolution = 0.86 × 0.86 mm2, slice thickness = 3 mm, matrix =256 × 256 × 24, flip angle (FA) = 20, TE/TR = 18/55 msec, and bandwidth = 444 Hz/pixel. Additional imaging included postcontrast T1 magnetization-prepared rapid gradient-echo (MPRAGE) (in-plane spatial resolution = 0.977 × 0.977 mm2, slice thickness = 1 mm, matrix =256 × 192 × 192, TE/TR/TI = 3.11/1750/950 msec, FA = 15, and bandwidth = 150 Hz/pixel) and fluid-attenuated inversion recovery imaging (FLAIR) (in-plane spatial resolution = 0.938 × 0.938 mm2, slice thickness = 3 mm, matrix =256 × 192 × 60, TE/TR/TI = 141/9420/2500 msec, FA = 170, and bandwidth = 287 Hz/pixel) after intravenous administration of gadolinium-containing contrast material (MultiHance, Bracco, Princeton, NJ; 0.1 mmol/kg, double dose).
Brain MRI in Patient With Microbleeds
QSM data were acquired from a patient with microbleeds on a 3 T scanner (Skyra model, Siemens) equipped with 12-channel head coil. A single echo gradient echo sequence was used to acquire axial images with matrix size = 320 × 250 × 112, in-plane spatial resolution = 0.72 × 0.72 mm2, slice thickness = 1.5 mm, FA = 15, bandwidth = 120 Hz/pixel, and TE/TR = 20/28 msec.
Hemorrhagic Myocardial Infarction
A pig model of hemorrhagic myocardial infarction was created as previously described.16,26 The heart was excised and subsequently bathed in non-1H magnetic susceptibility-matched fluid (Fomblin, Solvay, Augusta, GA). Multiecho GRE images were obtained on a 7 T Siemens Terra scanner at 0.25 × 0.25 × 0.25 mm3 isotropic resolution with TR = 42 msec, FA = 28, FOV = 13 × 13 cm2, bandwidth = 725 Hz/pixel, and five TEs = 2.81–19.86 with ΔTE = 3.41 msec.
QSM Reconstruction
A brain mask was obtained from the magnitude image using the FSL brain extraction tool.24 Phase unwrapping was performed using Laplacian unwrapping,8 transmit phase was removed by fitting and subtracting a fourth-order 3D polynomial,4 and background field removal was performed using the Laplacian boundary value method.8,27 The same local field was used for all the reconstruction implementations. Regularization weights were empirically tuned to give good image quality. As reported previously,4 choosing regularization weights that gave images with least MSE resulted in blurred images and oversmoothing of edges.
The proposed 1) LADI technique (Eqs. 7, 8) was compared with, 2) Thikhonov regularized linear MEDI formulation (closed form L2, Eq. 3 with W=I),8 3) TV regularized linear MEDI formulation (MEDI, Eq. 5),8,12 4) the nonlinear MEDI formulation that uses total generalized variation (TGV) constraints (FANSI-TGV)9 and, when data were available, 5) COSMOS.9 For clarity, the cost functionals used in reconstruction techniques (1–4) are provided in Supplementary Table S1. The FANSI-TGV formulation uses a rapid Split Bregman21 -based implementation.
Image Analysis and Statistics
Comparison of the mean susceptibility in each region-of-interest (ROI) was performed using Bland–Altman plots and linear regression. Bias was reported as mean bias 2σ. The results of linear regression are reported as slope (β), coefficient of determination (R2), and the level of significance for correlation was determined at P < 0.05. Reconstruction quality was compared using global quality metrics: root-mean-squared error (RMSE),4 structural similarity index metric (SSIM),6 high-frequency error norm (HFEN),4 and mutual information (MI).4 Using a combination of ITK-SNAP28 and FSL,29 anatomical brain regions were manually segmented on the T1-weighted images and computed masks were applied to the reconstructed susceptibility maps after suitable transformation.
The visual image quality of the QSM reconstructions on the hemorrhagic tumor data were assessed by three board-certified neuroradiologists (R.M.K., J.W.S., J.B.W.) for overall image quality (IQ), and image sharpness (IS). Two different types of assessments were performed; namely, 1) numerical grading (scale 1–3, 1 = low, 3 = high) of individual images and 2) numerical ranking of reconstructions (scale 1–4, 4 = best, 1 = worst) by side-by-side comparison for the two variants IQ and IS. From a total of 11 datasets, four datasets were randomly chosen for training the three observers on the scoring criterion and the remaining seven datasets were used to perform numeric grading and ranking. Initial scores provided by a fourth neuroradiologist (S.A.N.) were used as reference to train the three observers. The two assessments were performed as separate sessions on different days.
A description of the scoring criteria used for grading the images appears in Supplementary Table S2. The numerical grades were meant to reflect the ease with which the expert observer could accurately delineate anatomical features, track vessels, and differentiate between tumor vasculature, and intratumoral hemorrhage. Half scores (for example 1.5 or 2.5) were allowed if the observers felt the images were between two categories of scores. The scores were reported as mean and standard deviation (mean ± SD). Higher scores were indicative of better structure visibility and higher image quality. The reconstructed 3D images from the seven datasets and four reconstruction techniques were viewed one at a time. The order in which the 28 reconstructions (seven datasets and four reconstruction techniques for each dataset total) were viewed as randomized, and the observers were blinded to the reconstruction technique. For the numerical ranking of reconstructed images, the images from the four reconstruction techniques were viewed simultaneously so that the ranking reflects the comparative difference in image quality between the techniques. The observers were blinded to the reconstruction type and the order of the four reconstructions were randomly shuffled for each dataset.
We used a Friedman test to verify if there was a significant difference in the median scores between at least two reconstruction methods; the level of significance was determined at P < 0.05. We then performed a post-hoc Conover multiple comparison test with Bonferroni P-value adjustment to adjust for the familywise error rate introduced when doing multiple comparisons.
For the hemorrhagic myocardial infarction data, the reconstructed images were visually inspected for the presence of artifacts and the magnetic susceptibilities were calculated from the hemorrhage (Hem), infarct (Inf), and remote myocardial (Myo) regions.16 The susceptibilities are reported as mean ± SD in ppm.
Results
QSM Reconstruction Challenge
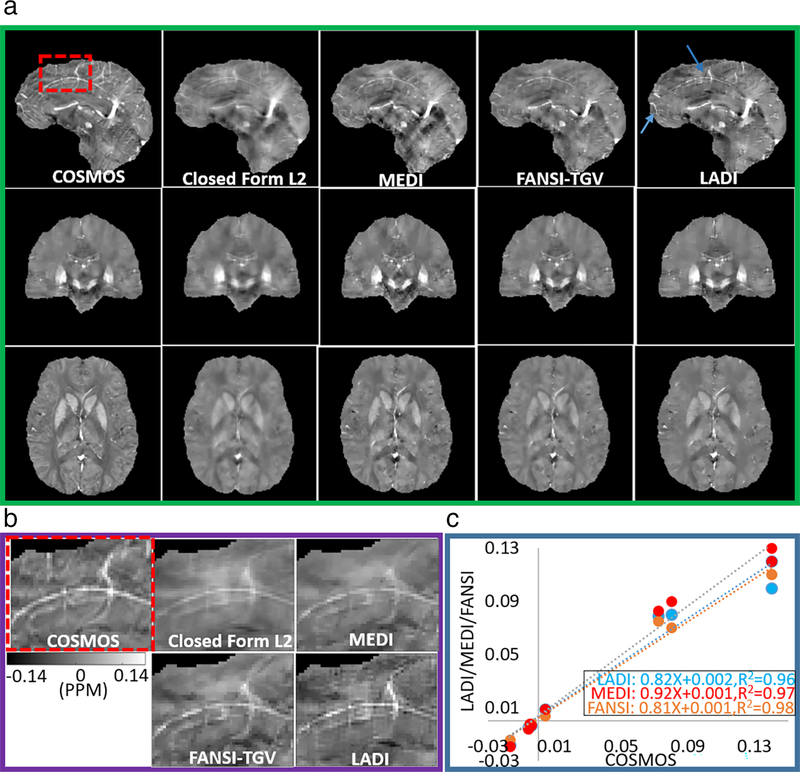
Figure 1 shows a comparison of reconstructions using the different QSM reconstruction formulations. MEDI (β = 0.91, R2 = 0.97, P < 0.05) showed marginally better association with COSMOS than FANSI-TGV (β = 0.81, R2 = 0.98, P < 0.05) and LADI (β = 0.82, R2 = 0.96, P < 0.05), but lower spatial fidelity (RMSEMEDI = 70.1, RMSEFANSI-TGV = 60.6, RMSELADI = 61.1), and (HFENMEDI = 65.9, HFENFANSI-TGV = 58.9, HFENLADI = 57.1). Similar SSIM and MI were observed for MEDI (SSIMMEDI = 0.84, MIMEDI = 0.45), FANSI-TGV (SSIMFANSI-TGV = 0.85, MIFANSI-TGV = 0.45), and LADI (SSIMLADI = 0.85, MIMEDI = 0.46) reconstructions. The global image quality metrics are reported in Table 1 and magnetic susceptibilities from different regions of the brain in Supplementary Table S3. We were not able to detect a bias in the images reconstructed using MEDI (bias = 0.002 ± 0.009), FANSI-TGV (bias = 0.007 ± 0.012), and LADI (bias = 0.006 ± 0.014) techniques. Bland–Altman plots are shown in Supplementary Fig S1. As expected, closed form L2 reconstructions had significant image blur compared to MEDI, FANSI-TGV, and LADI reconstructions. We observed that features such as small vessel detail had improved conspicuity with LADI compared to the other techniques (Fig. 1 B).
FIGURE 1:
(a) Reconstruction of susceptibility maps on the ISMRM QSM reconstruction challenge dataset and comparison with the multiorientation COSMOS. LADI reconstructions exhibiting sharper edges and better vessel delineation is feasible as compared to MEDI and closed form L2 reconstructions and is further emphasized in (b) zoomed-in images (dashed red box). (c) The mean magnetic susceptibilities calculated from LADI, FANSI-TGV, and MEDI exhibit good correlation with the multiorientation COSMOS.
TABLE 1.
Comparison of Global Error Quality Metrics
| LADI | FANSI-TGV | MEDI | |
|---|---|---|---|
| RMSE | 61.1 | 60.6 | 70.1 |
| HFEN | 57.1 | 58.9 | 65.9 |
| SSIM | 0.85 | 0.85 | 0.84 |
| MI | 0.46 | 0.45 | 0.45 |
Mean root mean squared error (RMSE), high frequency error norm (HFEN), structural similarity index (SSIM), and mutual information (MI) are reported for LADI, FANSI-TGV, and MEDI-based reconstructions.
QSM in Glioblastoma Patients
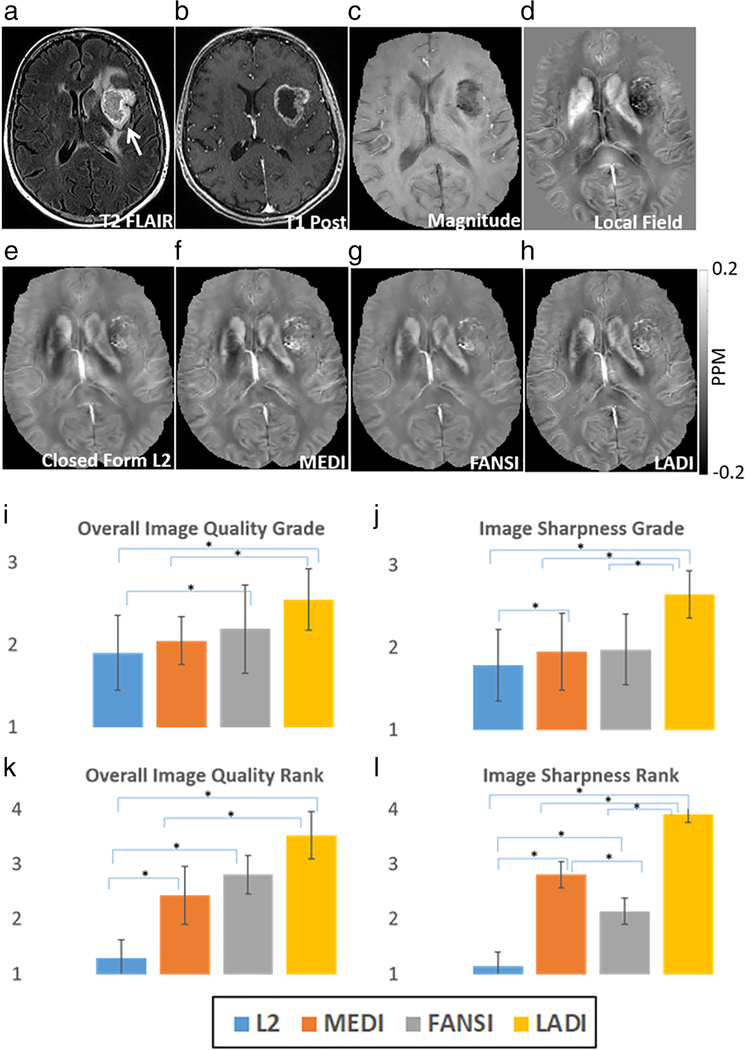
QSM images for a representative patient are shown in Fig. 2. The reconstruction time of the proposed LADI technique was ~54 ± 3 sec, FANSI-TGV was ~136 ± 12 sec, MEDI was ~372 ± 26 sec, and closed form L2 was ~0.14 ± 0.02 sec. The pseudocode of the proposed reconstruction algorithm is shown in Supplementary Fig S2. LADI showed higher image quality and sharper structures (IQGrade = 2.6 ± 0.4, ISGrade = 2.6 ± 0.3) compared to MEDI (IQGrade = 2.1 ± 0.3, ISGrade = 2 ± 0.5) and FANSI-TGV (IQGrade = 2.2 ± 0.5, ISGrade = 2 ± 0.4). Higher image quality enabled better differentiation between intratumoral punctate hemorrhage, and regions with a linear increase in magnetic susceptibility due to vessels. For numerical ranking, LADI (IQRank = 3.5 ± 0.4, ISRank = 3.9 ± 0.2) was consistently ranked higher than MEDI (IQRank = 2.4 ± 0.5, ISRank = 2.8 ± 0.2) and FANSI (IQRank = 2.8 ± 0.4, ISRank = 2.1 ± 0.2). The mean scores are reported in Tables 2 and 3; pairs with a statistically significant difference in medians are shown in Fig. 2 I–L and multiple comparisons testing in Supplementary Table S4 and Supplementary Table S5.
FIGURE 2:
Reconstruction of susceptibility maps from hemorrhagic tumor data. The location of the tumor is indicated by the white arrow in the T2 FLAIR image (a), T1 postcontrast image (b), and the magnitude image (c). (d) Tissue field used to reconstruct the QSM maps. Compared to (e) closed form L2, (f) MEDI and (g) FANSI reconstructions; (h) LADI reconstructions have sharper edges and better tumor vasculature conspicuity. (i–l) The average scores from numerical grading and numerical ranking of images for overall image quality, and image sharpness. Pairs for which a significant (P < 0.05) difference was seen in the median scores are indicated using an asterisk.
TABLE 2.
Comparison of Image Quality: Numerical Grading
| FANSI-TGV | MEDI | L2 | LADI | P | |
|---|---|---|---|---|---|
| Overall image quality (IQ) grade | 2.2 ± 0.5 | 2.1 ± 0.3 | 1.9 ± 0.5 | 2.6 ± 0.4 | P < 0.05 |
| Image sharpness (IS) grade | 2 ± 0.4 | 2 ± 0.5 | 1.8 ± 0.4 | 2.6 ± 0.3 | P < 0.05 |
The images were graded by three neuroradiologists (Scale 1–3; 1 = least, 3 = most) for overall image quality (IQ), image sharpness (IS). Statistical testing performed using Friedman chi-squared test. Test for multiple comparisons using Conover’s test shown in Supplementary Table S4. In all categories, LADI reconstructions were consistently scored the highest when compared to FANSI-TGV and MEDI reconstructions.
TABLE 3.
Comparison of Image Quality: Numerical Ranking
| FANSI-TGV | MEDI | L2 | LADI | P | |
|---|---|---|---|---|---|
| Overall image quality (IQ) rank | 2.8 ± 0.4 | 2.4 ± 0.5 | 1.3 ± 0.3 | 3.5 ± 0.4 | P < 0.05 |
| Image sharpness (IS) rank | 2.1 ± 0.2 | 2.8 ± 0.2 | 1.1 ± 0.3 | 3.9 ± 0.2 | P < 0.05 |
The images were ranked by three neuroradiologists (Scale 1–4; 4 = best, 1 = worst) for overall image quality (IQ), image sharpness (IS). Statistical testing performed using Friedman chi-squared test. Test for multiple comparisons using Conover’s test shown in Supplementary Table S5. In all categories, LADI reconstructions were consistently scored the highest when compared to FANSI-TGV and MEDI reconstructions.
QSM in Patient With Microbleeds
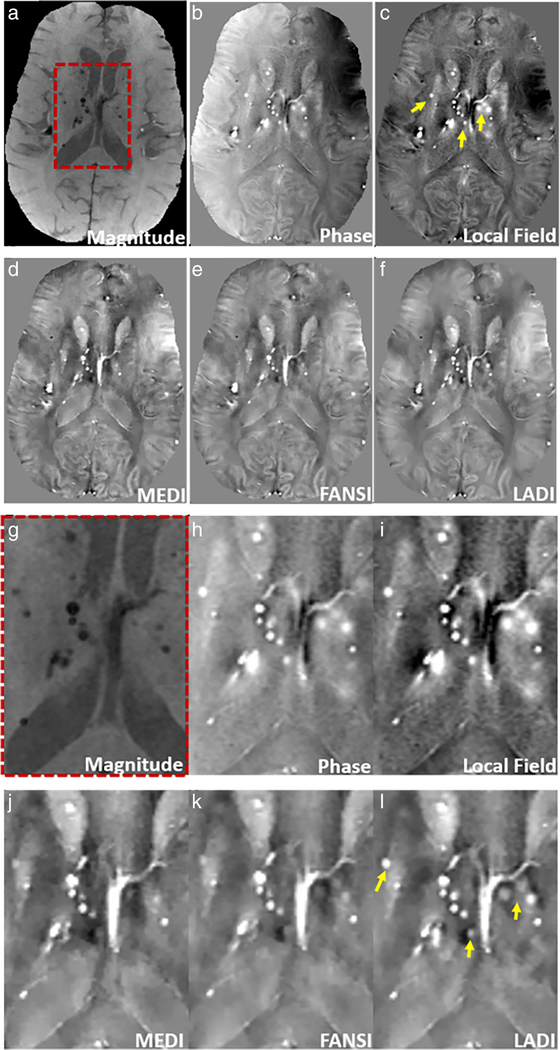
The QSM reconstructions on the patient with microbleeds in shown in Fig. 3. Microbleeds appear to have better conspicuity on the phase image (Fig. 3b) and local field (Fig. 3c) as compared to the magnitude image (Fig. 3a). Locations with microbleeds appear sharper in LADI (Fig. 3f) and are better visualized when compared to MEDI (Fig. 3d) and FANSI (Fig. 3e) (locations shown by arrows on the local field map in Fig. 3c).
FIGURE 3:
Reconstruction of susceptibility maps from a patient with microbleeds. (a) The magnitude image, (b) unwrapped phase image, (c) local field, and reconstructions using (d) MEDI, (e) FANSI, and (f) LADI are shown. Microbleeds have better conspicuity on the phase image (b) and local field (c) image as compared the magnitude image (a). Microbleeds appear sharper and are better visualized on the LADI reconstructions (f) as compared to MEDI (d) and FANSI (e) reconstructions, locations shown by arrows on the local field map (c). (g–l) Zoomed-in image of a small region (indicated by the dashed red box in (a)).
QSM in Reperfused Myocardial Infarction
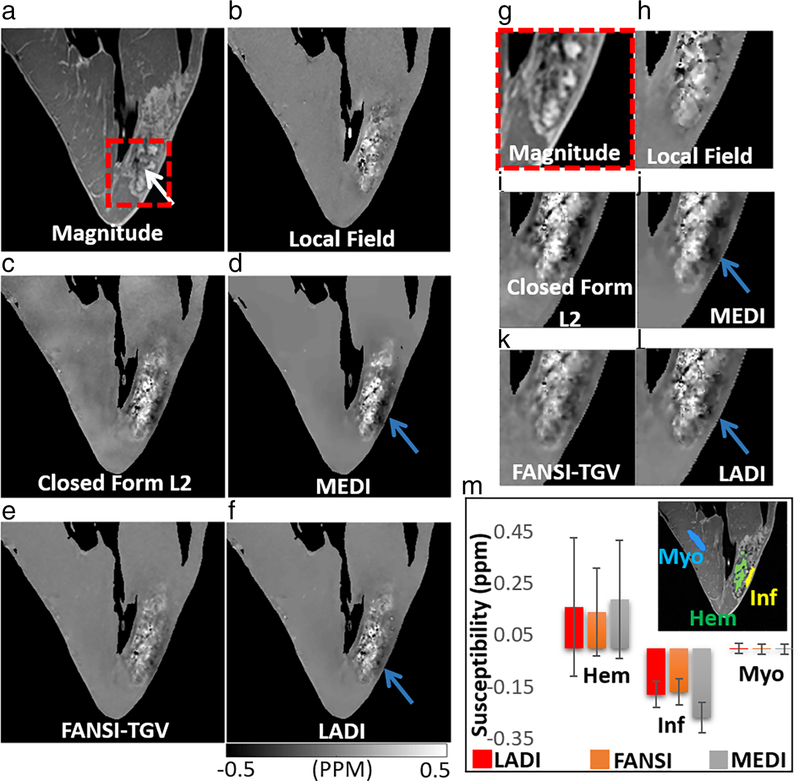
The images of reconstructed hemorrhagic myocardial infarction data are shown in Fig. 4. The location of the hemorrhage is indicated by a white arrow (Fig. 4a). As expected, the images reconstructed using closed form L2 reconstruction appear to have reduced spatial resolution compared to the MEDI, FANSI-TGV, and LADI reconstructions. Similar mean susceptibility values were estimated in the remote myocardial (MyoLADI = −0.0018 ± 0.02 ppm, MyoFANSI-TGV = −0.0028 ± 0.02 ppm, MyoMEDI = −0.0032 ± 0.02 ppm) and hemorrhagic regions (HemLADI = 0.16 ± 0.27 ppm, HemFANSI-TGV = 0.14 ± 0.17 ppm, HemMEDI = 0.19 ± 0.23 ppm) for the three reconstructions. The dark artifact that is visible in the infarcted region (indicated by a blue arrow, close to the bright hemorrhagic region) is reduced by FANSI-TGV (InfFANSI-TGV = −0.17 ± 0.05 ppm) and LADI (InfLADI = −0.18 ± 0.05 ppm) compared to MEDI (InfMEDI = −0.27 ± 0.06 ppm).
FIGURE 4:
Quantitative susceptibility mapping on an ex vivo large animal model of reperfusion injury myocardial infarction. (a) Magnitude image with the location of the hemorrhage indicated by a white arrow, and (b) local field. The dark artifact visible in (c) closed form L2 and (d) MEDI reconstructions is reduced in (e) FANSI-TGV and (f) LADI reconstructions (location indicated by blue arrow). (g–l) Zoomed-in image of a small region indicated by the dashed-red box in (a). (m) Comparison of mean susceptibilities calculated from the hemorrhage (Hem), infarct (Inf), and remote myocardial (Myo) regions.
Discussion
We present a novel application of a data-driven approach for reconstructing high-quality magnetic susceptibility maps utilizing only information contained in the local field. This technique may prove effective in adjacent anatomical regions where there is excellent gradient echo image contrast, but low magnetic susceptibility variation. Alternatively, and more interestingly, it may be effective for showing true variations in tissue magnetic susceptibility for regions that are poorly discriminated in gradient echo images. Regions with low-to-moderate levels of tissue iron in nonhemorrhagic myocardial infarction or glioblastoma may show elevated T2* relaxation times due to inflammation or water content, despite moderately increased iron content.15 The water or inflammation-related increase in T2* may partially reduce the sensitivity of T2* to detect low to moderate levels of iron content.
In the MEDI formulation, a binary edge mask was used to prevent smoothing of edges by ensuring that TV is only applied in uniform or smooth regions in the image. The use of spatially varying weights to improve the performance of TV has been previously studied for applications such as image denoising30 and reconstruction of cardiac MR images.31,32 It should be noted that the spatial edge prior based approaches that have been developed for QSM applications use a binary edge weight to separate smooth regions from edges, while other techniques,30,31 developed for non-QSM applications, used continuously varying edge weights. A recently published technique33 attempted to improve MEDI by using a continuous spatial edge weight, although this technique still depends on the use of the magnitude image to extract edge features.
Anatomical structures in the magnitude image do not always match those in the susceptibility map. This discrepancy can cause spatial smoothing and loss of information in the susceptibility maps.34,35 While inclusion of structural priors have been shown to be useful for simulation,36 they often lead to smoothing and underestimation of subtle susceptibility variations when applied in vivo.34 Since the use of TV can cause smoothing of edges along with removal of noise and artifacts from the estimated image, the adding-noise-back step ensures that by updating the local field (Eq. 8), sharp transitions such as edges that may be lost due to regularization are added back to the reconstruction. While adding-noise-back has been studied for applications such as denoising,17 deblurring,18 and reconstruction of undersampled MR images,19,20 this is the first application of the technique to improve QSM image quality.
In Berkin et al,8 an SB-based technique was developed to rapidly minimize a variant of the MEDI formulation that does not use a magnitude weighting in the data fidelity term. The technique uses a combination of SB-based variable substitutions and preconditioned conjugate-gradient.8 A drawback associated with the use of the magnitude weighting in the data fidelity term is that it makes it a more challenging matrix inversion problem8 and matrix preconditioner-based rapid minimization techniques for regularized QSM become less effective.8 The SB-based variable splitting applied here is the same,8 although instead of using a preconditioned conjugate gradient implementation, we used the iterative reweighting used in the NAG formulation, which is easy to implement, more general, and hence can be easily applied to regularized QSM formulations.
High-quality reconstructions were estimated using the proposed QSM reconstruction formulation and overall image quality matched that achieved by MEDI and FANSI-TGV. Overall, similar error metrics were estimated from the COSMOS challenge images reconstructed using MEDI, FANSI-TGV, and LADI. There was good agreement in the mean susceptibility estimated by MEDI, FANSI-TGV, and MEDI as compared to COSMOS and we were unable to detect a significant bias. LADI and FANSI-TGV performed slightly better when analyzed using image quality metrics like RMSE and HFEN, while MEDI performed slightly better at ROI accuracy. One advantage of LADI was that features such as bright veins that were present in the COSMOS images were better visualized, while some smoothing was visible in reconstructions using MEDI and FANSI-TGV reconstruction. The presence of sharper vessels in the LADI reconstructions could aid in applications such as automated vein segmentation37 or venous oximetry.38
The LADI reconstruction performed on the hemorrhagic tumor data had better image quality compared to MEDI and FANSI-TGV, as reflected in the consistently higher grade and rank in all categories of visual quality assessment. A statistically significant difference was seen in IS between LADI and other reconstruction techniques. QSM images can provide a variety of different information about the tumor microenvironment that is indicative of different aspects of tumor biology, and oversmoothing can prevent extraction of this information. This is secondary to imaging features that contribute to signal on QSM maps in a brain tumor. For example, intratumoral susceptibility signal has shown to be correlated with tumor perfusion in patients with glioma, and this is likely secondary to vascular structures that are bright on QSM maps (venous structures secondary to increased deoxyhemoglobin content).39 In addition, QSM can be applied to differentiate the presence of iron in hemorrhagic regions of the tumor and to track tumor-associated macrophages.40
In the assessment of the patient with microbleeds, we found that LADI reconstructions are sharper when compared to MEDI and FANSI reconstructions, and the microbleeds are better visualized. Blurring of microbleeds was found in some parts of the MEDI and FANSI reconstructions. Some of these microbleeds are not easily identified on the magnitude image, but are visible on the phase image and local field image. An example is shown in Supplementary Fig S3, and the location is indicated by an arrow.
The reconstructions of the hemorrhagic myocardial infarction data showed that LADI and FANSI-TGV mitigated artifacts visible in MEDI reconstructions. The dark artifact appears due to the presence of the bright signal in the hemorrhage causing a dark artifact in neighboring regions due to the difficulty in inverting the QSM problem.
FANSI-TGV uses a nonlinear data fidelity model to reconstruct high-quality and artifact-free images. Minimization of the nonlinear data fidelity formulations is generally slow, and advanced minimization techniques are required for the rapid minimization of the cost functional.9 This entails multiple variable substitutions and therefore the reconstruction technique becomes memory intensive. The proposed LADI formulation uses a combination of a simple linear data fidelity model, a TV constraint, and an iterative update of the local field based on the loss of data fidelity. Based on several metrics discussed previously, we found that this simple formulation performs as well as the nonlinear FANSI-TGV.
Limitations
There were several limitations to the experimental study. Additional experience in a larger number of patients using a prospective experimental design and showing prognosis in neuroradiological and cardiac applications are required to improve the clinical evidence. The study described here could be further improved by increasing the number of datasets. In the absence of a non-MRI-based independent measurement of tissue iron, COSMOS serves as a gold standard and requires several scans at different orientations. COSMOS data was available for the ISMRM reconstruction challenge, but not for our patients or in the swine heart study. Additional experiments are needed to validate the association between magnetic susceptibility and iron; however, there are limited techniques available to noninvasively assess iron in vivo. Validation with histopathology could independently confirm the findings of elevated iron content; however, these data were not available for our patients.
Conclusion
We developed a data-driven approach for high-quality QSM reconstructions by solving the constrained TV reconstruction formulation. In addition, we developed a technique for rapid QSM reconstructions that is based on a combination of SB variable substitution and NAG. The results show that, while the proposed technique performs as well as existing popular QSM techniques when assessed using global quality metrics and ROI measurements, it achieves sharper edges and consistently performs better at preservation of fine features such as vessel and microbleeds.
Supplementary Material
Acknowledgments
Additional supporting information may be found in the online version of this article
References
- 1.Wang Y, Spincemaille P, Liu Z, et al. Clinical quantitative susceptibility mapping (QSM): Biometal imaging and its emerging roles in patient care. J Magn Reson Imaging 2017;46(4):951–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fan AP, Bilgic B, Gagnon L, et al. Quantitative oxygenation venography from MRI phase. Magn Reson Med 2014;72(1):149–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yi W, Tian L. Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker. Magn Reson Med 2015;73(1): 82–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Christian L, Ferdinand S, Karin S, et al. Quantitative susceptibility mapping: Report from the 2016 reconstruction challenge. Magn Reson Med 2018;79(3):1661–1673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sam W, Andreas S, Richard B. Susceptibility mapping in the human brain using threshold-based k-space division. Magn Reson Med 2010; 63(5):1292–1304. [DOI] [PubMed] [Google Scholar]
- 6.Karin S, de Zwart JA, Peter vG, tie-Qiang L, Stephen D, Jeff D Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data. Magn Reson Med 2009;62(6):1510–1522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed sensing MRI. IEEE Signal Process Magz 2008;25(2):72–82. [Google Scholar]
- 8.Berkin B, Audrey F, Jonathan P, et al. Fast quantitative susceptibility mapping with L1-regularization and automatic parameter selection. Magn Reson Med 2014;72(5):1444–1459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Carlos M, Berkin B, Bo Z, Julio A-C, Cristian T. Fast nonlinear susceptibility inversion with variational regularization. Magn Reson Med 2018; 80(2):814–821. [DOI] [PubMed] [Google Scholar]
- 10.Liu J, Liu T, de Rochefort L, et al. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map. Neuroimage 2012;59(3):2560–2568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu T, Xu W, Spincemaille P, Avestimehr AS, Wang Y. Accuracy of the morphology enabled dipole inversion (MEDI) algorithm for quantitative susceptibility mapping in MRI. IEEE Trans Med Imaging 2012;31(3): 816–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tian L, Jing L. Ludovic dR, et al. morphology enabled dipole inversion (MEDI) from a single-angle acquisition: Comparison with COSMOS in human brain imaging. Magn Reson Med 2011;66(3):777–783. [DOI] [PubMed] [Google Scholar]
- 13.Strong D, Chan T. Exact solutions to total variation regularization problems. UCLA CAM Rep. 1996;96–41: 259–268. [Google Scholar]
- 14.Cronin MJ, Wharton S, Al-Radaideh A, et al. A comparison of phase imaging and quantitative susceptibility mapping in the imaging of multiple sclerosis lesions at ultrahigh field. Magn Reson Mater Phys, Biol Med 2016;29(3):543–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Moon B, Iyer SK, Solomon M, et al. Magnetic susceptibility of hemorrhagic myocardial infarction: Correlation with tissue iron and comparison with relaxation time MRI. In: Proc 26th Annual Meeting ISMRM, Paris; 2018. [Google Scholar]
- 16.Moon B, Iyer SK, Josselyn N, et al. Magnetic susceptibility and T2* of myocardial reperfusion injury at 3 and 7 T. In: Proc 27th Annual Meeting ISMRM, Montreal; 2019. [Google Scholar]
- 17.Osher S, Burger M, Goldfarb D, Xu J, Yin W. An iterative regularization method for total variation-based image restoration. Multiscale Model Simul 2005;4(2):460–489. [Google Scholar]
- 18.Dong F, Zhang H, Kong D-X. Nonlocal total variation models for multiplicative noise removal using split Bregman iteration. Math Comput Model 2012;55(3):939–954. [Google Scholar]
- 19.Chartrand R Fast algorithms for nonconvex compressive sensing: MRI reconstruction from very few data. 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro; 2009. p 262–265. [Google Scholar]
- 20.Iyer SK, Tasdizen T, Likhite D, DiBella E. Split Bregman multicoil accelerated reconstruction technique: A new framework for rapid reconstruction of cardiac perfusion MRI. Med Phys 2016;43(4):1969–1981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Goldstein T, Osher S. The Split Bregman method for L1-regularized problems. SIAM J Imaging Sci 2009;2(2):323–343. [Google Scholar]
- 22.Wu C, Tai X-C. Augmented Lagrangian method, dual methods, and Split Bregman iteration for ROF, vectorial TV, and high order models. SIAM J Imaging Sci 2010;3(3):300–339. [Google Scholar]
- 23.Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J Imaging Sci 2009;2(1):183–202. [Google Scholar]
- 24.Smith SM. Fast robust automated brain extraction. Hum Brain Mapp 2002;17(3):143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tian L, Pascal S, Ludovic dR, Bryan K, Yi W Calculation of susceptibility through multiple orientation sampling (COSMOS): A method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn Reson Med 2009;61(1):196–204. [DOI] [PubMed] [Google Scholar]
- 26.Stoffers RH, Madden M, Shahid M, et al. Assessment of myocardial injury after reperfused infarction by T1ρ cardiovascular magnetic resonance. J Cardiovasc Mag Reson 2017;19(1):17–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schweser F, Robinson SD, de Rochefort L, Li W, Bredies K. An illustrated comparison of processing methods for phase MRI and QSM: Removal of background field contributions from sources outside the region of interest. NMR Biomed 2017;30(4):e3604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yushkevich PA, Piven J, Hazlett HC, et al. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage 2006;31(3):1116–1128. [DOI] [PubMed] [Google Scholar]
- 29.Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004;23:S208–S219. [DOI] [PubMed] [Google Scholar]
- 30.Strong D, Chan T. Spatially and scale adaptive total varaiton based regularization and anisotropic diffusion in image processing. UCLA Math dept CAM rep 1996; pp. 94–146. [Google Scholar]
- 31.Iyer SK, DiBella EVR, Tasdizen T. Edge enhanced spatio-temporal constrained reconstruction of undersampled dynamic contrast enhanced radial MRI. 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro; 2010. p 704–707. [Google Scholar]
- 32.Royuela-del-Val J, Cordero-Grande L, Simmross-Wattenberg F, Martín-Fernández M, Alberola-López C. Jacobian weighted temporal total variation for motion compensated compressed sensing reconstruction of dynamic MRI. Magn Reson Med 2017;77(3):1208–1215. [DOI] [PubMed] [Google Scholar]
- 33.Guo L, Mei Y, Guan J, et al. Morphology-adaptive total variation for the reconstruction of quantitative susceptibility map from the magnetic resonance imaging phase. PLoS One 2018;13(5):e0196922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schweser F, Sommer K, Deistung A, Reichenbach JR. Quantitative susceptibility mapping for investigating subtle susceptibility variations in the human brain. Neuroimage 2012;62(3):2083–2100. [DOI] [PubMed] [Google Scholar]
- 35.Liu T, Liu J, de Rochefort L, et al. Morphology enabled dipole inversion (MEDI) from a single-angle acquisition: Comparison with COSMOS in human brain imaging. Magn Reson Med 2011;66(3):777–783. [DOI] [PubMed] [Google Scholar]
- 36.Wang S, Liu T, Chen W, et al. Noise effects in various quantitative susceptibility mapping methods. IEEE Trans Biomed Eng 2013;60(12): 3441–3448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ward PGD, Ferris NJ, Raniga P, et al. Combining images and anatomical knowledge to improve automated vein segmentation in MRI. Neuroimage 2018;165:294–305. [DOI] [PubMed] [Google Scholar]
- 38.Xu B, Liu T, Spincemaille P, Prince M, Wang Y. Flow compensated quantitative susceptibility mapping for venous oxygenation imaging. Magn Reson Med 2014;72(2):438–445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Park MJ, Kim HS, Jahng GH, Ryu CW, Park SM, Kim SY. Semiquantitative assessment of intratumoral susceptibility signals using non-contrast-enhanced high-field high-resolution susceptibility-weighted imaging in patients with gliomas: Comparison with MR perfusion imaging. Am J Neuroradiol 2009;30(7):1402–1408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Iv M, Samghabadi P, Holdsworth S, et al. Quantification of macrophages in high-grade gliomas by using ferumoxytol-enhanced MRI: A pilot study. Radiology 2019;290(1):198–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.