Effects of Aging in a Task-Switch Paradigm with the Diffusion Decision Model

Abstract

We investigated aging effects in a task-switch paradigm with degraded stimuli administered to college students, 61–74 year olds, and 75–89 year olds. We studied switch costs (the performance difference between task-repeat and task-switch trials) in terms of accuracy and mean reaction times (RTs). Previous aging research focused on switch costs in terms of mean RTs (with accuracy at ceiling). Our results emphasize the importance of distinguishing between switch costs indexed by accuracy and by mean RTs because these measures lead to different interpretations. We used the Diffusion Decision Model (DDM; Ratcliff, 1978) to study the cognitive components contributing to switch costs. The DDM decomposed the cognitive process of task switching into multiple components. Two parameters of the model, the quality of evidence on which decisions were based (drift rate) and the duration of processes outside the decision process (nondecision time), indexed different sources of switch costs. We found that older participants had larger switch costs indexed by nondecision time than younger participants. This result suggests age-related deficits in preparatory cognitive processes. We also found group differences in switch costs indexed by drift rate for switch trials with high stimulus interference (stimuli with features relevant for both tasks). This result suggests that older participants have less effective cognitive processes involved in resolving interference. Our findings show that age-related effects in separate components of switch costs can be studied with the DDM. Our results demonstrate the utility of using discrimination tasks with degraded stimuli in conjunction with model-based analyses.

Introduction

Most daily life activities involve switching back and forth between multiple tasks. Research suggests that successfully switching between tasks requires a coordinated interplay between the activation and the inhibition of control processes (Allport, Styles, and Hsich, 1994; Allport and Wylie, 2000; Hasher, Lustig, and Zacks, 2007; Hasher, Zacks, and May, 1999). The efficiency of these control processes is presumed to decline with age (Bäckman et al., 2000; Braver and Bach, 2002; Cepeda, Kramer, and Gonzalez de Sather, 2001; de Bruin and Della Sala, 2018; Dennis and Cabeza, 2008; Zelazo, Craik, and Booth, 2004). For instance, many studies examined control processes in experimental settings using task-switch paradigms and they found that older participants perform worse than younger participants (Gajewski, Ferdinand, Kray, and Falkenstein, 2018; Kray & Lindenberger, 2000; Kray, Lindenberger & Mayr, 2001; Giller, Zhang, Roessner, and Beste, 2018; Madden et al., 2009; Meiran, Gotler, and Perlman, 2001; Tisserand et al., 2002; Verhaeghen and Cerella, 2002; Wasylyshyn, Verhaeghen, & Sliwinski, 2011). However, most of these studies relied on mean RTs when examining group differences in task performance. This measure does not allow for the decomposition of the cognitive process into separate components that are associated with different control processes. In this article, we show how the Diffusion Decision Model (DDM; Ratcliff, 1978) can be used to study age-specific differences in distinct components of task switching.

In the following, we first address classical accounts of performance in task-switch paradigms and how they relate to control processes. Next, we describe the sources of different switch costs and how they are affected by aging. We then introduce the diffusion model and how its parameters can be linked to control processes. Finally, we describe our task-switch paradigm and why it is particularly suitable for the study of age-related switch costs with the diffusion model.

Task Switching

Task-switch paradigms generally involve pure blocks and mixed blocks (see for a review: Vandierendonck, Liefooghe, and Verbruggen, 2010). In the pure blocks, participants repeat the same task throughout the block (i.e., pure trials). In the mixed blocks, participants switch between multiple (usually two) tasks - repeating the same task on some trials (i.e., no-switch trials), while switching to another task on other trials (i.e., switch trials). Experimental evidence has consistently shown that performance is slower and more error-prone in mixed blocks than in pure blocks (e.g. De Jong, 2000; Rubinstein, Meyer, and Evans, 2001; Rogers and Monsell, 1995; Schmitz and Voss, 2012; Wylie and Allport, 2000; Yehene and Meiran, 2007). This performance difference has been referred to as switch cost. Two types of switch costs are distinguished: Global switch costs that refer to the performance difference between pure and no-switch trials; and local switch costs that refer to the performance difference between no-switch and switch trials (Meiran, 1996; Rogers & Monsell, 1995).

To study the sources of switch costs, theories suggested a decomposition of task switching, as a cognitive process, into three phases: 1) preparation for the upcoming task; 2) resolution of any interference from the prior task; and 3) selection of a response (see the review: Schmitz & Voss, 2012; also Gilbert & Shallice, 2002; Koch & Allport, 2006; Mayr & Kliegl, 2003; Meiran, 1996; Meiran, Chorev, & Sapir, 2000; Monsell, 2003; Rubinstein et al., 2001; Ruthruff, Remington, & Johnston, 2001; Sohn & Anderson, 2001; Yeung & Monsell, 2003). Each of these phases is assumed to be governed by a distinct set of control processes (Gopher, Armony, & Greenshpan, 2000; Kray & Lindenberger, 2000; Mayr & Kliegl, 2003; Meyer & Kieras, 1997; Rubinstein et al., 2001; Ruthruff et al., 2001; Schmitz & Voss, 2012). In particular, the “multiple components of task switching” - approach (henceforth, MCT approach) assumes that different control processes affect the process of task switching at different points in time, contributing to different switch costs (Gilbert & Shallice, 2002; Koch & Allport, 2006; Mayr & Kliegl, 2000; Meiran, 1996; Meiran, Chorev, & Sapir, 2000; Monsell, 2003; Rubinstein et al., 2001; Ruthruff et al., 2001; Sohn & Anderson, 2001; Yeung & Monsell, 2003). On one hand, it is assumed that early-stage preparatory control processes are needed to switch between different tasks (by reconfiguring the cognitive system for the new task). Hence, early-stage preparatory control processes are assumed to contribute predominantly to local switch costs (Baddeley, Chincotta, & Adlam, 2001; Miyake, Friedman, Emerson, Witzki, & Howerter, 2000). On the other hand, it is assumed that late-stage control processes are needed to reaffirm processing the current task by resolving or reiterating existing mental representations from the previous task such as prior response selection or prior stimulus-task set associations (Kiesel, Wendt, & Peters, 2005; Koch & Allport, 2006; Waszak & Hommel, 2007). For instance, it is presumed that mental representations need to be updated more often in mixed blocks than in pure blocks (irrespective of whether a task switch occurred). Hence, late-stage control processes are presumed to contribute predominantly to global switch costs (e.g., Druey & Hübner, 2008; Gilbert & Shallice, 2002; Mayr & Bryck, 2005). A more detailed review of sources and components of switch costs can be found in Meiran et al. (2000), and Schmitz and Voss (2012).

Age-Related Switch Costs

Global Switch Costs.

Many studies (Kray & Lindenberger, 2000; Meiran et al., 2001; Verhaeghen & Cerella, 2002; Wasylyshyn, Verhaeghen, & Sliwinski, 2011; Zelazo et al., 2004) found large age-related global switch costs. Some of these studies proposed that age-related increases in global switch costs are due to an age-related decline in working memory (WM) capacities (e.g., Frensch, Lindenberger & Kray, 1999; Lindenberger & Mayr, 2014; Mayr & Kliegl, 1993; 2000a; Mayr, Kliegl, & Krampe, 1996; Kray & Lindenberger, 2000; Zelazo et al., 2004). Specifically, they argued that the mixed blocks generally demand higher WM than the pure blocks because the mixed blocks require the participant to maintain multiple task rules in mind. In contrast, the pure blocks require the participant to maintain only one task rule in mind. Other studies argued that age-related increases in global switch costs are due to an age-related decline in control processes. In particular, they proposed that older participants tend to accommodate a generally slower, more cautious processing mode in task-switch paradigms and that this age-related difference in response strategy is what contributes the most to age-related global switch costs (e.g., Duncan, 1995; Keele & Rafal, 2000; Mayr, 2001; Raz, 2000).

Local Switch Costs.

Many studies have not found age-related local switch costs (Kray & Lindenberger, 2000; Mayr & Kliegl, 2000b; Salthouse, Fristoe, McGuthry, & Hambrick, 1998). These studies proposed that older participants experience a “general” age-related slowdown in cognitive functioning (in line with the explanation for age-related global switch costs). For instance, Mayr (2001) proposed that older participants need to update the task-specific mental representation on switch and no-switch trials, whereas younger participants need to do so only on switch trials. Other studies (Eppinger, Kray, Mecklinger, & John, 2007; Gajewski, et al., 2018; Kray, Eppinger, & Mecklinger, 2005; Mayr & Kliegl, 2003) did find age-related local switch costs. They proposed that older participants show increased local switch costs due to a greater sensitivity to interference between the prior and the current task (Baddeley, 1986; Gajewski et al., 2018; Kray & Lindenberger, 2000; Mayr & Kliegl, 2003; Meyer & Kieras, 1997). Specifically, performing the prior task would produce a task-specific mental representation that decays more slowly in older participants than in younger participants. This representation may interfere with the representation produced by performing the current task, leading to an age-related decline in performance particularly on switch trials.

The Diffusion Decision Model

The Diffusion Decision Model (Ratcliff, 1978) (henceforth, diffusion model) is an attractive tool to study task switching. This is because it decomposes the cognitive process into separable components (in line with the MCT approach previously introduced). A general introduction into the diffusion model, its assumptions and model parameters is presented in the Supplemental Material. We will introduce the main model parameters in the context of task switching shortly. Before doing so, we will summarize the benefits of a diffusion model analysis compared to conventional performance measures.

The diffusion model uses more information than classical analysis methods because its parameters are derived from the simultaneous consideration of accuracy and the entire RT distributions for correct and error responses. There have been a number of successful applications of the diffusion model to the data from a variety of tasks (Ratcliff, 2014; Ratcliff & McKoon 2008; Ratcliff & Rouder, 1998; Ratcliff, Smith, Brown, & McKoon, 2016; Ratcliff, Van Zandt, & McKoon, 1999; Voss, Rothermund, & Voss, 2004). Some of these studies have led to a reinterpretation of experimental results in the aging research domain. For instances, Ratcliff, Thapar, and McKoon (2001; 2004; 2006; 2007; 2010; 2011), and Thapar, Ratcliff, and McKoon (2003) (henceforth, RTM studies), as well as Ratcliff (2008), Ratcliff, Thapar, Gomez, & McKoon (2004), and Voskuilen, Ratcliff, and McKoon (2018) applied the model to a variety of different perceptual and cognitive tasks (outside the domain of task switching). They found that younger and older participants differed in two cognitive components. First, the older participants usually required more information to make a response (higher boundary separation) than the younger participants. Second, the older participants took longer to encode, build a decision-related representation to drive the decision process, and to produce a response (longer nondecision time component) than the younger participants.

The temporal separation of control processes, proposed by the MCT approach, can be used to link diffusion model parameters to the distinct phases of task switching. Based on previous diffusion model applications to task-switch paradigms (e.g., Karayanidis et al., 2009; Klauer, Schmitz & Voss, 2012; Voss, Schmitz, & Teige-Mocigemba, 2007), the diffusion model involves three main parameters presumed to be most informative for the study of task switching. In the following paragraphs, we will introduce these three model parameters (T_er, v, and a) as well as reasons for the proposed associations between model parameters and control processes. In the last subsection, we will also discuss empirical evidence that supports the proposed associations.

Nondecision Time Component.

This parameter represents the latency of processes outside the decision process such as task preparation, time to access working memory, perceptual encoding of cue and/or stimuli, and execution of the response (Ratcliff, Thapar, & McKoon, 2006; Voss et al., 2004). In the context of task switching, processes of basic encoding and response execution contribute to the nondecision time component of all trial types in a task-switch paradigm (i.e., pure, no-switch, and switch trials). Moreover, several studies found that differences in the nondecision time components (between no-switch and switch trials) additionally contributed to the local switch costs (Karayanidis et al., 2009; Klauer et al., 2007; Madden et al., 2009; Schmitz & Voss, 2012). For instance, Karayanidis et al. (2009) paired characters such as letters, digits, and nonalphanumeric symbols (either in gray or in color) for a task-switch paradigm that involved three tasks (classifying the compound stimuli either according to the letter, the digit, or the color) and four cues (i.e., repeat, switch-to, switch-away, and a cue not specifying whether a task-switch would occur). Applying a diffusion model analysis, they found increased nondecision time component on switch trials relative to no-switch trials. Based on these results, Karayanidis et al. (2009) concluded that the nondecision time component could be used to index early-stage control processes associated with the preparation time of task switches. This view is in line with the MCT approach, associating the nondecision time component with the first and the last phase of task switching. Specifically, based on the MCT approach, a longer nondecision time component on switch trials (relative to no-switch trials) is due to the additional preparatory processes that would take place on switch trials (Ruthruff et al., 2001; Schmitz & Voss, 2012).

Drift Rate.

This parameter represents the mean rate of information accumulation during the decision process. Specifically, high drift rates correspond to fast and accurate responses. Drift rates usually vary across experimental conditions as a function of task difficulty (e.g., Ratcliff, 1978; Ratcliff & McKoon, 2008; Voss et al., 2004). For instance, highly discriminable stimuli were associated with high drift rates. Moreover, drift rates have also been found to vary between individuals. For instance, multiple studies found positive associations between drift rate and IQ scores, as well as between drift rate and working memory capacity (e.g., Schmiedek, Oberauer, Wilhelm, Süß, & Wittmann, 2007; Ratcliff, Thapar, & McKoon, 2010). In the context of task switching, Schmitz and Voss (2012) suggested that drift rate can be used to index the efficiency of control processes associated with the activation of stimulus-response mapping rules, the resolution of interference from prior task-set preparation, and other carry-over effects from previous trials (e.g., stimulus-driven effects). This proposal is supported by findings showing that drift rates were decreased on switch trials relative to no-switch trials, contributing to the local switch costs (Karayanidis et al., 2009; Madden et al., 2009; Schmitz & Voss, 2012). For instance, Karayanidis et al. (2009) found decreased drift rate on switch trials relative to no-switch trials. The type of cue did not affect the drift rates on switch trials. Based on these results, Karayanidis et al. (2009) concluded (a similar conclusion as Schmitz and Voss, 2012) that drift rate could be used to index late-stage control processes associated with interference resolution. This view is in line with the MCT approach, associating drift rate with the second phase of task switching.

Boundary Separation.

Multiple studies have shown that this parameter reflects an individual’s response strategy. Specifically, in a variety of different discrimination and memory tasks, participants who preferred a more conservative, cautious response strategy had larger boundary separation, resulting in generally slower, but more accurate responses (e.g., Mulder et al., 2010; Ratcliff, 1985; Ratcliff & McKoon, 2008; Schmitz & Voss, 2012; Starns & Ratcliff, 2010; Voss et al., 2004). Moreover, studies have found that boundary separation is affected by the type of instructions (emphasis of speed vs. accuracy) (e.g., Mulder et al., 2010; Ratcliff & Rouder, 1998), or the introduction of reward for accurate responses (e.g., Voss et al., 2004). In the field of aging research, multiple studies found larger boundary separation for older participants compared to younger participants (Ratcliff, Thapar & McKoon, 2001; Starns & Ratcliff, 2010; 2012). In the context of task switching, Schmitz and Voss (2012) argued that larger boundary separation in mixed blocks relative to pure blocks could be explained by the higher working memory load in mixed blocks relative to pure blocks. This view is based on their study in which they administered a task-switch paradigm¹ to college students and in which they found larger boundary separation for mixed blocks relative to pure blocks.

Previous DDM Applications To Task Switching In Aging Research.

Only a few studies have utilized the diffusion model to analyze performance data from task-switch paradigms (see for an overview Schmitz & Voss, 2012). Even fewer studies have used the diffusion model to examine age-related performance differences in task-switch paradigms (i.e., Karayanidis et al., 2009; Madden et al., 2009; Schuch, 2016). Those studies used simplified versions of the diffusion model and we will review their results in the following paragraphs.

Madden et al. (2009) administered a task-switch paradigm (composed of two tasks) to younger and older participants. In one task, words had to be categorized based on their meanings as either “man-made” or “natural.” In the other task, words had to be categorized based on their referent as either “larger” or “smaller” than a computer monitor. Like in the previously discussed study by Karayanidis et al. (2009), the paradigm involved mixed blocks only. A constrained diffusion model was fit to the data. Specifically, the model allowed for differences only in drift rates and nondecision time components as a function of age group and trial type (no-switch and switch trials). Madden et al. (2009) found that older participants had lower drift rates and longer nondecision time components than younger participants for both trial types. However, the researchers did not find any group differences in switch costs in terms of nondecision time component or drift rate. These results suggest that the early-stage as well as the late-stage control processes of older participants were as good as those of the younger participants.

Schuch (2016) administered a task-switch paradigm (composed of three tasks) to younger and older participants. In their paradigm, photographs of faces had to be categorized based on gender (male vs. female), age (younger vs. old), or emotional expression (happy vs. angry). Schuch (2016) found, among other results, that older participants had larger boundary separation and longer nondecision time component than younger participants. Most importantly, older participants had larger local switch costs in terms of nondecision time component, but not in terms of drift rate, than younger participants. While Schuch (2016) found age-related local switch costs, Madden et al. (2009) did not find age-related local switch costs. Therefore, the extent to which age-related switch costs become apparent seems to depend on the specifics of the task-switch paradigm. Moreover, the studies discussed above only examined local switch costs but not global switch costs. Most probably because accuracy in pure blocks was too high to adequately estimate model parameters. This discussion highlights the importance of re-designing existing experimental paradigms to utilize a computational model’s full potential.

Present Study

Our task-switch paradigm allowed us to address multiple limitations in the domain of task switching and aging:

First, past research mostly studied switch costs in terms of mean RTs because accuracy was almost always at ceiling (accuracy values > 95%) for all participants (e.g., Mayr, 2001; Mayr & Kliegl, 2000a, 2000b; Kray & Lindenberger, 2000; Wasylyshyn, Verhaeghen, & Sliwinski, 2011). However, many hypotheses regarding age-related switch costs (e.g., age-related local switch costs due to older participants being more sensitive to task interference than younger participants) can only be tested in a sufficiently demanding task-switch paradigm in which most conditions have accuracy values that are not at ceiling. Our task-switch paradigm involved degraded target stimuli, producing accuracy values that were off ceiling. This allowed us to study differences between conditions (i.e., between pure and mixed blocks as well as within mixed blocks) as well as to examine switch costs in terms of RTs (as has been the focus of previous aging research) and accuracy. We will show that switch costs indexed by mean RTs and accuracy lead to different conclusions regarding the effects of aging.

Second, our task-switch paradigm involved target stimuli that were bivalent when processing one task (i.e., it was possible to classify the target stimuli according to the task rules of both tasks) but univalent when processing the other task (i.e., it was possible to classify the target stimuli according to the task rule of only one task.) This experimental feature allowed us to examine whether local switch costs are higher for bivalent target stimuli than for univalent target stimuli and whether there are any age-related effects. Previously discussed studies suggested that older participants are more sensitive to interferences caused by bivalent stimuli. Therefore, we expected that older participants, relative to younger participants, would produce larger increases in local switch costs for bivalent target stimuli as compared to univalent target stimuli.

Third, most existing task-switch paradigms required participants to learn and maintain multiple task rules for the mixed blocks (e.g., press the left response button for either odd numbers or consonant letters versus press the right response button for either even numbers or vowel letters). Therefore, these paradigms likely assess age-related differences in “working memory capacities” besides those in “task switching” (see for a review: Cepeda, Kramer, & Gonzalez de Sather, 2001; Hasher et al., 1999; 2007). As previously outlined, some researchers argued that age-related global switch costs are mainly produced by age-related declines in working memory capacity (e.g., Mayr, 2001; Mayr & Kliegl, 2003; Zelazo et al., 2004). Our task-switch paradigm involved predictable task switches and explicitly displayed response alternatives (see Method Section for details). These measures are known to reduce the demand of working memory (e.g., Korteling, 1993; Kray, Li, & Lindenberger, 2002; Kray & Lindenberger, 2000; Rogers & Monsell, 1995; Wasylyshyn et al., 2011).

Method

Participants

The participants in our study were 52 younger participants (18–26 year olds), 38 older participants (61–74 year olds), and 22 older participants (75–89 year olds). The younger participants were students who participated for course credit in an introductory psychology course at The Ohio State University (OSU) or at Bryn Mawr College (BMC). The older participants were healthy, active, community-dwelling individuals who lived in the surrounding area of OSU or BMC. They met the following inclusion criteria to participate in the study: a score of 26 or above on the Mini-Mental State Examination (MMSE; Folstein, Folstein, & McHugh, 1975); and no evidence of disturbances in consciousness, medical or neurological diseases that would cause cognitive impairment, head injury with loss of consciousness, or current psychiatric disorder. All participants completed the Vocabulary and Matrix Reasoning subtests of the Wechsler Adult Intelligence Scale – 3rd Edition (WAIS-III: Wechsler, 1997).

One-way analyses of variance (ANOVAs) suggested no significant group differences on the subtests of the WAIS-III, all F(2, 108) ≤ 1.63, all p > 0.05 (Table 1). There were significant group differences in years of education, F(2, 108) = 11.08, p < 0.05. Subsequent contrast tests confirmed that the 61–74 year olds had significantly more years of education than the college students and the 75–89 year olds, college students vs. 61–74 year olds: t(51.05) = 4.03, p < 0.05; 75–89 year olds vs. 61–74 year olds: t(52.01) = −3.13, p < 0.05. The 75–89 year olds had as many years of education as the college students, t(28.49) = −0.13, p > 0.05. We also found group differences in ratings on the MMSE, F(2, 108) = 4.88, p < 0.05. Subsequent contrast tests confirmed that 61–74 year olds had lower ratings on the MMSE than college students, t(31.85) = −2.79, p < 0.05. The 75–89 year olds had similar ratings on the MMSE compared to college students, t(38.56) = −1.51, p > 0.05. Similarly, the 75–89 year olds had similar ratings on the MMSE compared to the 61–74 year olds, t(74.22) = −1.61, p > 0.05.

Table 1.

Participant background characteristics.

	College students		61–74 year olds		75–89 year olds
Measure	M	SD	M	SD	M	SD
Mean age	20.66	1.76	68.11	3.68	79.28	2.88
Years of education	13.69	1.56	15.88	3.08	13.61	2.46
MMSE	29.06	1.16	28.63	1.30	28.05	1.53
WAIS-III Vocabulary	12.63	2.83	12.79	2.61	11.55	2.60
WAIS-III Matrix	12.06	2.89	12.55	3.06	12.91	3.54

Note. There are three missing values for the college participants, and one missing value for the 75–89 year olds. MMSE = Mini-Mental State Examination; WAIS-III = Wechsler Adult Intelligence Scale – 3^rd Edition (raw scores). The college students included 11 men and 40 women. The 61–74 year olds included 38 women only, whereas the 75–89 year olds included 5 men and 17 women.

Experimental Procedure

This study was approved by the Ohio State University Institutional Review Board (IRB; research ethics committee; protocol: #2003B0201). The task-switch paradigm consisted of 4 pure blocks and 8 mixed blocks in each experimental session. In the pure blocks, participants performed either the letter discrimination task or the brightness discrimination task (2 blocks of each). In the mixed blocks, participants switched between the two discrimination tasks predictably, every third trial. The order of the pure and mixed blocks was randomized across participants. Each block was composed of 144 trials and there were breaks between blocks. Half of the pure and mixed blocks had a response-stimulus interval (RSI) of 260ms, while the other half had a RSI of 750ms (RSI was kept constant within blocks). The order of blocks with short/long RSI was random and differed across participants.

Participants were tested for two to three sessions in order to obtain enough data for modeling. The reason for the difference in the number of sessions completed by individual participants is that some of the older participants could not complete a whole task-switch session in the time allocated. For all participants, at least two sessions of data were used for the analyses.

To construct the stimuli, a 64 × 64 array of pixels was generated with 50% black and 50% white randomly placed. For the letter stimuli, a black or white letter was generated and 10% of the pixels were flipped to the opposite polarity. Then the letter replaced the pixels in the 64 × 64 array. For the brightness stimuli, the same procedure was used except that 30% of the pixels in the letter were flipped. This resulted in a slightly white or dark blob in the center of the pixel array, but it was not possible to determine the identity of the letter. If the letters were made identifiable by reducing the proportion of pixels in the letter that were flipped, then the brightness discrimination task was too easy and accuracy was near ceiling. For both discrimination tasks, there was only one level of difficulty.

For letter discrimination, the same two letters were the response alternatives (i.e., cues) for all of the letter trials of a block. The pairs of letters were designed to be dissimilar from each other (the pairs were: F/Q, B/N, P/L, T/X, W/K, and G/R). They were simultaneously displayed one to the left of the center of the computer screen and one to the right. Participants were instructed to press the / key on the keyboard if the right alternative had been presented and the Z key if the left alternative had been presented. Figure 1 shows an example stimulus for a letter discrimination trial.

Figure 1.

Example of the stimulus for letter discrimination (correct response: T).

For brightness discrimination, a white square and a black square represented the response alternatives (i.e., cues) for all the brightness trials of a block. They were simultaneously displayed one to the left of the center of the computer screen and one to the right. Figure 2 shows an example stimulus for a brightness discrimination trial.

Figure 2.

Example of the stimulus for brightness discrimination (correct response: bright).

The response alternatives remained on screen for pure and no-switch trials, and for both discrimination tasks. For the switch trials, the response alternatives of the prior task disappeared before the response alternatives of the current task were shown. These current response alternatives were displayed for 50ms, following which, the stimulus was displayed at the center of the screen.

Participants were provided feedback: Incorrect responses were followed by a message “ERROR” displayed for 200ms at the center of the screen. Correct responses were followed by a blank screen for 200ms. Responses shorter than 250ms were followed by a “TOO FAST” message displayed for 1,000ms at the center of the screen in order to discourage participants from going too fast (if they were responding quickly to finish the experiment quickly, the 1,000ms delay would slow them more than the fast responding would speed them up). If fast incorrect responses were made, then both messages, “TOO FAST” and “ERROR,” were presented.

It should be stressed that the brightness stimuli were not the same as the stimuli used in other RTM brightness tasks. In this brightness discrimination task, the stimulus was a blob of brighter or darker pixels in the middle of an array of 50/50 black and white pixels, whereas in the RTM studies, the whole pixel array was darker or brighter than 50/50. This means that the brightness stimuli used here are similar to letter stimuli (from which they were derived) as well as the brightness stimuli used in the RTM studies.

Data Analysis Of Conventional Performance Measures

We computed global and local switch costs once in terms of mean RTs and once in terms of accuracy for each participant group. For each type of switch cost (global vs. local), we performed a mixed analysis of variance (ANOVA) to test for significant group differences in switch costs. The three participant groups represented the between-subject factor. The type of switch cost and the two discrimination tasks served as within-subject factors. Mean RTs and accuracy values were similar for the two RSIs and were combined (we present an analysis of the results of RSI on performance measures in the Supplemental Material). Because there were multiple hypothesis tests, Bonferroni corrections were used in the analysis. We then used contrast tests to examine separate group-specific differences in global and local switch costs. Specifically, we performed three pairwise comparisons: 1) college students vs. 61–74 year olds; 2) college students vs. 75–89 year olds; 3) 61–74 year olds vs. 75–89-year olds.

Data Analysis With The Diffusion Model

In the following paragraphs, we introduce the model parametrization, the model fit procedure, and the method of data analysis with the diffusion model. Further results (i.e., analysis of quantile-probability plots, assessment of model fits, correlations between model parameters) can be found in the Supplemental Material.

Model Parametrization.

Our task-switch paradigm was composed of two discrimination tasks, each of which had three types of trials (i.e., pure, no-switch, and switch trials). We introduced a separate value for boundary separation (a) for each discrimination task (keeping boundary separation constant across trial types of a given task). This is one major difference in model parametrization compared to previous studies discussed in the Introduction (Karayanidis et al., 2009; Madden et al., 2009; Schmitz & Voss, 2012; Schuch, 2016). Specifically, prior studies that applied a diffusion model analysis to task-switch paradigms introduced a separate decision criterion for each trial type (pure, no-switch, and switch trials) whereas we assumed one value of boundary separation for all these trial types.

We kept boundary separation constant across all trial types because initial analyses showed that it could be assumed to be constant without making the quality of fits worse. Furthermore, increasing the number of fixed model parameters generally increases the constraints on a model. Creating a highly constrained model is preferred, because such a model can be falsified more easily (Ratcliff, 2002). In this sense, keeping boundary separation fixed across all trial types is a more conservative approach. Moreover, the aging research reviewed above provided evidence that older participants tend to generally accommodate a different response strategy in task-switch paradigms and in line with this research, we used boundary separation as an index to account for the general “more cautious” response strategy in older participants. We provide an analysis of an alternative model in which we varied boundary separation by block type in the Supplemental Material. The main results are similar to those obtained from the model with a fixed boundary across conditions.

The analysis of mean RTs and accuracy on each trial type and for each task did not suggest a bias towards either alternative (i.e., for brightness discrimination: bright vs. dark, and for letter discrimination: letter 1 vs. letter 2). Therefore, we combined correct responses for bright and dark stimuli (and the same for errors) and the same for the two letter types. In the diffusion model, this required that the starting point was set to be halfway between the two response boundaries (i.e., z=a/2) and this reduced the number of free parameters in the model. We provide an overview of this analysis in Supplemental Table S14.

Based on past research discussed in the Introduction section, we expected nondecision time components to increase from pure to no-switch trials and from no-switch to switch trials. Similarly, we expected drift rate to decrease from pure to no-switch trials and from no-switch to switch trials. We further hypothesized that these differences across trial types would be more pronounced for short RSI than for long RSI. Therefore, we introduced separate drift rates and separate nondecision time components for each trial type and for each RSI, resulting in 6 drift rates for each discrimination task. Moreover, we expected larger variability in the nondecision time components for the mixed blocks compared to the pure blocks, because the latency of early-stage control processes is presumed to facilitate task switching on mixed blocks (and is presumed to vary across RSIs). Therefore, we introduced 4 parameters for the variability in nondecision time components (Ratcliff, Gomez, & McKoon, 2004; Ratcliff & Tuerlinckx, 2002), i.e., s_t,1 = RSI short, pure and no-switch trials; s_t,2 = RSI short, switch trials; s_t,3 = RSI long, pure and no-switch trials; s_t,4 = RSI long, switch trials. Across trial SD in drift rate (ƞ) and the range in starting point (s_z) were assumed to be constant across all trial types of a given discrimination task. These hypotheses were consistent with the quantile probability plots in Supplementary Figure S1. These plots show a shift and a spread in the RT distributions as a function of trial types (see analysis in the Supplemental Material).

The assumptions that only drift rates and nondecision time components can change across the three trial types of each discrimination task, and that boundary separation can only change between the two discrimination tasks, yielded a highly constrained model (Ratcliff, 2002).

Model Fit Procedure.

The diffusion model was fit to the data by using a standard method (Ratcliff & Tuerlinckx, 2002) in which the model parameters are adjusted to produce a minimum value of chi-square value. For each of the six experimental conditions (i.e., three trial types × two RSIs), accuracy values as well as five RT quantiles (.1, .3, .5, .7, and .9 quantile RTs) for correct and error responses, were entered into the minimization routine. For each participant, a separate model was fit for the letter and the brightness discrimination tasks. Table A1 in the Appendix present the parameter values averaged over participants for each participant group. Details of RT quantiles as a function of accuracy (i.e., quantile probability plots), which present accuracy and the entire RT distributions for correct and error responses for each participant group are also presented in the Supplemental Material. An assessment of goodness of fit as well as plots of model fits at an individual participant level, which show that the model provided an adequate description of the behavioral data, can be found in Supplemental Table S2. A bootstrapping analysis, which shows the expected range of variability in accuracy and RT quantiles for the comparison between predictions and data, can be found in Supplemental Tables S10 to S13.

Data Analysis.

We conducted three mixed ANOVAs: In the first ANOVA, we tested for group-specific differences in boundary separation for which the three participant groups presented the between-subject factor, and the two tasks presented the within-subject factor. In the second ANOVA, we tested for group-specific differences in global and local switch costs when calculated in terms of nondecision time component. The three participant groups presented the between-subject factor. The two tasks and the two types of switch cost served as within-subject factors. In the third ANOVA, we tested for group-specific differences in global and local switch costs when calculated in terms of drift rate. The three participant groups presented the between-subject factor. The two tasks and the two types of switch cost served as within-subject factors. Since multiple hypothesis tests were conducted on the same data, Bonferroni corrections were used in all the analyses. We then used contrast tests to examine separate group-specific differences in global and local switch costs. Specifically, we performed three pairwise comparisons: 1) college students vs. 61–74 year olds; 2) college students vs. 75–89 year olds; 3) 61–74 year olds vs. 75–89-year olds.

Results

Response times shorter than 350ms for the college students and 500ms for the two older participant groups, as well as response times longer than 5,000ms for all three participant groups, were eliminated from the analysis. This resulted in 1.7% of the data being eliminated for the college students, and 2.1% of the data being eliminated for each of the two older participant groups. Most of the data eliminated were fast responses are likely to be contaminants because they were fast responses that were too fast to have come from the decision process.

The results are presented in two parts. In the first, we present results when switch costs were calculated based on conventional performance measures (i.e., mean RTs, accuracy). In the second, we present results when switch costs were calculated based on the main model parameters (i.e., nondecision time component, drift rate). We provide further analyses in the Supplemental Material (i.e., analysis of effects of RSI on switch costs, correlations between model parameters, and an alternative diffusion model analysis with boundary separation as a function of block type).

Results From Conventional Performance Measures

Figure 3 shows the mean RTs for correct responses and accuracy values across the three trial types (pure, no-switch, and switch trials) for each participant group. The left side of Figure 3 presents data from the letter discrimination task, and the right side those from the brightness discrimination task (Supplemental Table S1 provides values of mean RTs and accuracy). Figure 3 shows that the 61–74 year olds and the 75–89 year olds were slower than the college students on all trial types (pure, no-switch, and switch trials) for both discrimination tasks.

Figure 3.

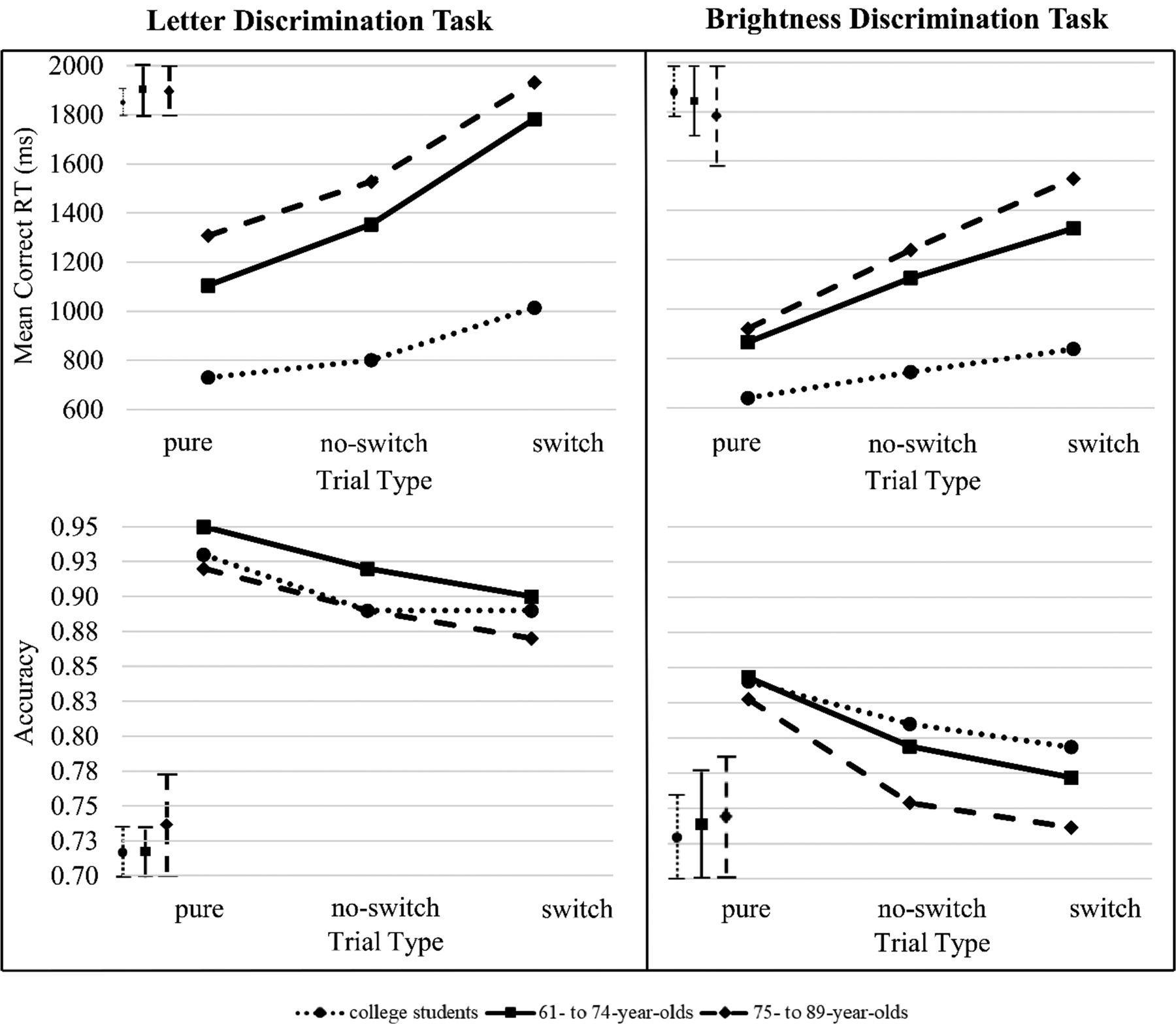
Plots of accuracy and mean correct response time (RT) for the letter discrimination (left panel) and the brightness discrimination task (right panel) and for each trial type, averaged over participants of each group, respectively. The left side presents the data for letter discrimination. The right side presents the data for brightness discrimination. Accuracy and mean correct RTs were averaged over the short and long response-stimulus intervals (RSIs). The bars in the top left (for mean correct RTs), and the bottom left (for accuracy) represent the standard deviations averaged over trial types for each participant group. For a given participant group, the standard deviation of each participant was averaged to obtain the average standard deviation.

Next, we first discuss global switch costs in terms of mean RTs and accuracy, then we discuss local switch costs in terms of mean RTs and accuracy. Table 2 presents the global and local switch costs in terms of mean RTs for each participant group and for each task (including statistics from ANOVAs and contrast tests). Table 3 presents the global and local switch costs in terms of accuracy for each participant group and for each task (including statistics from ANOVAs and contrast tests).

Table 2.

Global and local switch costs in terms of mean RTs for correct responses (in ms) for each participant group and for each discrimination task.

Groups	Global SC			Local SC			ANOVA				Contrast Tests
	M	SE	99% CI	M	SE	99% CI	Effect	F ratio	df	Partial ƞ2	GC	Global SC	Local SC
Letter Discrimination Task
College Students	71	26	[2,140]	215	21	[159,270]	G	719.38**	1	0.87	1	t(50.2) = −5.4**	t(54.6) = −6.1**
61–74 year olds	249	31	[168,330]	429	25	[364,494]	T	24.18**	1	0.18	2	t(22.6) = −2.1*	t(29.7) = −5.1**
75–89 year olds	220	40	[114,326]	405	33	[320,491]	C	19.47**	1	0.15	3	t(29.6) = 0.4	t(50.7) = 0.5
Brightness Discrimination Task
College Students	105	14	[67,142]	93	14	[58,129]	G × T	6.88**	2	0.11	1	t(49.6) = −6.7**	t(52.9) = −6.0**
61–74 year olds	260	17	[216,304]	201	16	[160,242]	G × C	0.08	2	0.00	2	t(26.2) = −7.9**	t(23.2) = −5.7**
75–89 year olds	320	22	[262,377]	289	21	[234,343]	C × T	77.02**	1	0.41	3	t(47.8) = −1.8	t(31.3) = −2.4*
							G × C × T	1.53	2	0.03

Note. SC = Switch Costs; Global SC = performance difference between pure and no-switch trials. Local SC = performance difference between no-switch and switch trials; ANOVA = analysis of variance; G = group; T = task type; C = switch cost type; CI = confidence interval; GC = group comparisons (1 = college students vs. 61–74 year olds; 2 = college students vs. 75–89 year olds; 3 = 61–74 year olds vs. 75–89 year olds).

^*p < .05;

^**p < .01.

Table 3.

Global and local switch costs in terms of accuracy (in %) for each participant group and for each discrimination task.

Groups	Global SC			Local SC			ANOVA				Contrast Tests
	M	SE	99% CI	M	SE	99% CI	Effect	F ratio	df	Partial ƞ2	GC	Global SC	Local SC
Letter Discrimination Task
College Students	4	1	[3,5]	0	0	[0,1]	G	206.12**	1	0.65	1	t(84.1) = −1.8	t(84.0) = 4.2**
61–74 year olds	3	1	[0,3]	2	1	[0,3]	T	17.00**	1	0.14	2	t(25.4) = −0.7	t(35.3) = 3.1**
75–89 year olds	3	1	[1,5]	2	1	[0,3]	C	46.93**	1	0.30	3	t(25.9) = 0.1	t(36.3) = 0.1
Brightness Discrimination Task
College Students	3	1	[0,4]	2	1	[3,5]	G × T	3.84*	2	0.07	1	t(61.2) = 2.5**	t(66.7) = 0.4
61–74 year olds	5	1	[3,7]	2	1	[0,4]	G × C	1.18	2	0.02	2	t(27.4) = 3.5**	t(40.0) = −0.3
75–89 year olds	8	1	[5,10]	1	1	[0,3]	C × T	1.61	1	0.02	3	t(39.2) = 1.5	t(53.7) = −0.7
							G × C × T	11.74**	2	0.18

Note. SC = Switch Costs; Global SC = performance difference between pure and no-switch trials. Local SC = performance difference between no-switch and switch trials; ANOVA = analysis of variance; G = group; T = task type; C = switch cost type; CI = confidence interval; GC = group comparisons (1 = college students vs. 61–74 year olds; 2 = college students vs. 75–89 year olds; 3 = 61–74 year olds vs. 75–89 year olds).

^*p < .05;

^**p < .01.

Age-Related Differences In Global Switch Costs.

Calculating switch costs in terms of mean RTs, the 61–74 year olds and the 75–89 year olds had significantly larger global switch costs than the college students for both discrimination tasks (Table 2). The global switch costs of the 61–74 year olds were similar to those of the 75–89 year olds for both discrimination tasks. Indexing switch costs in terms of accuracy (Table 3), group-specific differences varied as a function of the discrimination task: for the letter discrimination task, the 75–89 year olds and the 61–74 year olds had similar global switch costs to the college students. For the brightness discrimination task, the 75–89 year olds and the 61–74 year olds had significantly larger global switch costs than the college students. The global switch costs of the 75–89 year olds were similar to those of the 61–74 year olds for both discrimination tasks.

Age-Related Differences In Local Switch Costs.

Calculating switch costs in terms of mean RTs, the 61–74 year olds and the 75–89 year olds had significantly larger local switch costs than the college students for both discrimination tasks. The local switch costs of the 61–74 year olds were similar to those of the 75–89 year olds for the letter discrimination task. However, the local switch costs of the 61–74 year olds were significantly smaller than those of the 75–89 year olds for the brightness discrimination. Indexing switch costs in terms of accuracy, group-specific differences in switch costs varied as a function of the discrimination task: for the letter discrimination task, the 75–89 year olds and the 61–74 year olds had significantly larger local switch costs than the college students. For the brightness discrimination task, the 75–89 year olds and the 61–74 year olds had similar local switch costs to the college students. The local switch costs of the 61–74 year olds were similar to those of the 75–89 year for both discrimination tasks.

Interim Summary For Conventional Performance Measures.

The results presented thus far illustrate that it is important to distinguish not only between local and global switch costs, but also between switch costs indexed by mean RTs and accuracy. The underlying components that lead to these effects are examined with the diffusion model analysis in the following subsections.

Results From The Diffusion Model Analysis

Our goal with the diffusion model analysis was to understand the cognitive components involved in task switching and how these components change with age. In particular, the diffusion model can help to identify sources of age-related switch costs (e.g., the relative contributions of early-stage preparatory control processes and late-stage control processes).

In the next subsection, we discuss group-specific differences in boundary separation (Table 4). We then discuss global switch costs in terms of nondecision time component and drift rate, followed by a discussion of local switch costs in terms of nondecision time component and drift rate. Table 5 presents the global and local switch costs in terms of nondecision time component for each participant group and for each task (including statistics from ANOVAs and contrast tests). Table 6 presents the global and local switch costs in terms of drift rate for each participant group and for each task (including statistics from ANOVAs and contrast tests).

Table 4.

Boundary separation for the letter and the brightness discrimination task, averaged over participants of each group.

Groups	Boundary Separation			ANOVA				Contrast Tests
	M	SE	99% CI	Effect	F ratio	df	Partial ƞ2	GC	Test statistic
Letter Discrimination Task
College Students	0.15	0.01	[0.13,0.17]	G	53.8**	2	0.50	1	t(57.1) = −9.0**
61–74 year olds	0.23	0.01	[0.20,0.25]	T	8.762**	1	0.07	2	t(30.6) = −10.1**
75–89 year olds	0.26	0.01	[0.20,0.24]	G × T	0.35	2	0.01	3	t(49.7) = −1.5
Brightness Discrimination Task
College Students	0.14	0.01	[0.12,0.15]					1	t(63.4) = −6.6**
61–74 year olds	0.22	0.01	[0.20,0.24]					2	t(26.5) = −5.8**
75–89 year olds	0.24	0.01	[0.22,0.26]					3	t(35.5) = −1.4

Note. G = group; T = task type; CI = confidence interval; GC = group comparison (1 = college students vs. 61–74 year olds; 2 = college students vs. 75–89 year olds; 3 = 61–74 year olds vs. 75–89 year olds).

^*p < .05;

^**p < .01.

Table 5.

Global and local switch costs in terms of nondecision time component for each participant group and for each discrimination task.

Groups	Global SC			Local SC			ANOVA				Contrast Tests
	M	SE	99% CI	M	SE	99% CI	Effect	F ratio	df	Partial ƞ2	GC	Global SC	Local SC
Letter Discrimination Task
College Students	0.04	0.01	[0.03,0.06]	0.06	0.01	[0.03,0.08]	G	41.70**	2	0.43	1	t(52.9) = 5.0**	t(46.1) = 6.3**
61–74 year olds	0.09	0.01	[0.07,0.10]	0.14	0.01	[0.11,0.17]	T	37.23**	1	0.26	2	t(25.6) = 5.7**	t(22.1) = 5.2**
75–89 year olds	0.11	0.01	[0.09,0.13]	0.19	0.02	[0.15,0.23]	C	128.15**	1	0.54	3	t(41.3) = 1.7	t(30.5) = 1.8
Brightness Discrimination Task
College Students	0.02	0.01	[0.0,0.06]	0.13	0.02	[0.09,0.18]	G × T	9.90**	2	0.15	1	t(47.1) = 4.7**	t(48.8) = 5.7**
61–74 year olds	0.10	0.02	[0.06,0.14]	0.30	0.02	[0.25,0.36]	G × C	6.54**	2	0.11	2	t(22.0) = 1.5	t(25.2) = 3.2**
75–89 year olds	0.08	0.02	[0.02,0.13]	0.25	0.03	[0.18,0.33]	C × T	44.26**	1	0.29	3	t(28.9) = −0.6	t(45.0) = −1.1
							G × C × T	1.53	2	0.03

Note. SC = Switch Costs; Global SC = performance difference between pure and no-switch trials. Local SC = performance difference between no-switch and switch trials; ANOVA = analysis of variance; G = group; T = task type; C = switch cost type; CI = confidence interval; GC = group comparisons (1 = college students vs. 61–74 year olds; 2 = college students vs. 75–89 year olds; 3 = 61–74 year olds vs. 75–89 year olds).

^*p < .05;

^**p < .01.

Table 6.

Global and local switch costs in terms of drift rate for each participant group and for each discrimination task.

Groups	Global SC			Local SC			ANOVA				Contrast Tests
	M	SE	99% CI	M	SE	99% CI	Effect	F ratio	df	Partial ƞ2	GC	Global SC	Local SC
Letter Discrimination Task
College Students	−0.07	0.01	[−0.09, −0.05]	−0.01	0.01	[−0.02, 0.0]	G	7.09**	2	0.00	1	t(64.2) = −1.6	t(80.7) = −2.7**
61–74 year olds	−0.09	0.01	[−0.12, −0.07]	−0.03	0.01	[−0.05, −0.02]	T	22.17**	1	0.17	2	t(31.4) = −1.7	t(42.8) = −2.1*
75–89 year olds	−0.10	0.01	[−0.13, −0.07]	−0.03	0.01	[−0.05, −0.01]	C	69.94**	1	0.39	3	t(45.0) = −0.3	t(46.4) = 0.3
Brightness Discrimination Task
College Students	−0.04	0.01	[−0.05, −0.02]	−0.03	0.01	[−0.04, −0.02]	G × T	2.27	2	0.04	1	t(60.3) = −1.1	t(83.2) = 0.2
61–74 year olds	−0.05	0.01	[−0.07, −0.03]	−0.03	0.01	[−0.04, −0.02]	G × C	0.60	2	0.01	2	t(30.1) = −1.5	t(34.7) = 0.3
75–89 year olds	−0.06	0.01	[−0.08, −0.03]	−0.03	0.01	[−0.05, −0.01]	C × T	24.80**	1	0.19	3	t(45.8) = −0.5	t(36.5) = 0.1
							G × C × T	0.34	2	0.01

Note. SC = Switch Costs; Global SC = performance difference between pure and no-switch trials. Local SC = performance difference between no-switch and switch trials; ANOVA = analysis of variance; G = group; T = task type; C = switch cost type; CI = confidence interval; GC = group comparisons (1 = college students vs. 61–74 year olds; 2 = college students vs. 75–89 year olds; 3 = 61–74 year olds vs. 75–89 year olds).

^*p < .05;

^**p < .01.

Age-Related Differences In Boundary Separation.

Results from the ANOVA suggested group-specific differences in boundary separation (Table 4). Subsequent contrast tests confirmed that boundary separation was significantly larger for the two older participant groups than for college students for both discrimination tasks. The 61–74 year olds had similar boundary separation values compared to those of the 75–89 year olds for both discrimination tasks.

Age-Related Differences In Global Switch Costs.

Calculating switch costs in terms of nondecision time component, the 61–74 year olds and the 75–89 year olds had significantly larger global switch costs than the college students for the letter discrimination task (Table 5). The global switch costs of the 61–74 year olds were similar to those of the 75–89 year olds for the letter discrimination task. For the brightness discrimination task, the 61–74 year olds and the 75–89 year olds had larger global switch costs than the college students. However, only the difference between the 61–74 year olds and the college students was statistically significant. The difference between the 75–89 year olds and the college students did not reach statistical significance. The global switch costs of the 61–74 year olds were similar to those of the 75–89 year olds for the brightness discrimination task. Indexing switch costs in terms of drift rate (Table 6), the three participant groups had similar global switch costs for both discrimination tasks.

Age-Related Differences In Local Switch Costs.

Calculating switch costs in terms of nondecision time component, the 61–74 year olds and the 75–89 year olds had significantly larger local switch costs than the college students for both discrimination tasks (Table 5). The local switch costs of the 61–74 year olds were similar to those of the 75–89 year olds for both discrimination tasks. Indexing switch costs in terms of drift rate (Table 6), group-specific differences varied as a function of the discrimination task: for the letter discrimination task, the 75–89 year olds and the 61–74 year olds had significantly larger local switch costs than the college students. The local switch costs of the 61–74 year olds were similar to those of the 75–89 year olds for the letter discrimination task. For the brightness discrimination task, the 75–89 year olds and the 61–74 year olds had similar local switch costs to the college students.

Interim Summary For Diffusion Model Analysis.

Calculating switch costs in terms of nondecision time components, we found age-related local and global switch costs for both discrimination tasks. Calculating switch costs in terms of drift rate, we found age-related local switch costs only for the letter discrimination task, but not for the brightness discrimination task. These results suggest that relative to the college students, older participants were more sensitive to stimulus interference when the target stimuli were bivalent (as on switch trials in the letter discrimination task) than when target stimuli were univalent (as on switch trials in the brightness discrimination task.)

General Discussion

For univalent target stimuli (brightness discrimination task), older participants had larger global switch costs (both in terms of mean RTs and accuracy) than younger participants. For bivalent target stimuli (letter discrimination task), older participants had larger global switch costs in terms of mean RTs (but not in terms of accuracy) than younger participants. This pattern of results was reversed for local switch costs, namely: For univalent target stimuli, older participants had larger local switch costs in terms of mean RTs (but not in terms of accuracy) than younger participants. For bivalent target stimuli, older participants had larger local switch costs (both in terms of mean RTs and accuracy) than younger participants. These results suggest that switch costs in terms of accuracy and mean RTs most likely reflect age-related differences in distinct components of task switching.

We then showed that the diffusion model parameters separated components of task switching in a principled way, allowing us to identify the sources of age-related switch costs (i.e., early-stage preparatory control processes as indexed by nondecision time component and late-stage control processes as indexed by drift rate.) Figure 4 illustrates global and local switch costs for univalent and bivalent target stimuli, respectively. The diffusion model components that contributed to age-related differences in each of these switch costs are represented by circles. Irrespective of whether target stimuli were univalent or bivalent, age-related global and local switch costs were composed of nondecision time components (T_er). Based on the MCT approach, this result suggests slower early-stage preparatory control processes for older participants than for younger participants. For bivalent target stimuli only, age-related local switch costs additionally had a drift rate (v) component. Based on the MCT approach, this result suggests deficits in late-stage control processes (presumed to resolve stimulus interference) for older participants than for younger participants.

Figure 4.

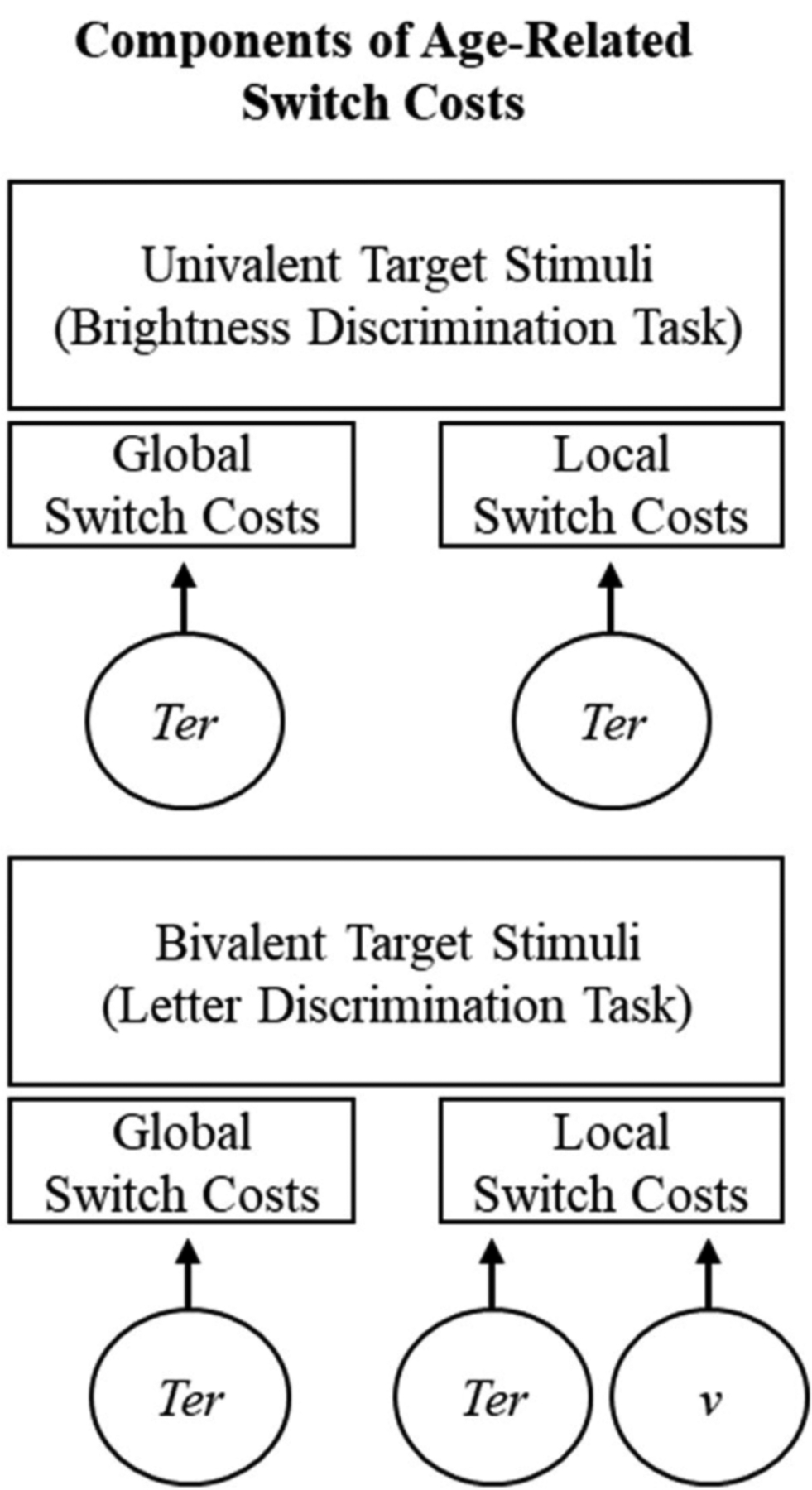
Graphical illustration of age-related switch costs.

Mayr (2001) proposed that a task-switch paradigm with univalent and bivalent stimuli intermixed in a block may allow one to determine how much late-stage control processes (i.e., the ambiguity of the bivalent target stimuli may cause interference that has to be resolved by these processes) and early-stage control processes (i.e., processes that prepare for task switches irrespective of whether the target stimuli is bivalent or univalent) contribute to switch costs. In line with Mayr (2001)’s view, we found that the older participants were more sensitive to interference caused by bivalent stimuli (as suggested by the age-related increase in local switch costs indexed by drift rate for the letter discrimination task). Because this result was specific to switch costs measured by drift rate, it seems that late-stage control processes contribute more to these switch costs than do early-stage control processes. Another way to see that these components represent separate components of processing is to examine correlations between them. Supplemental Table S9 shows that nondecision time component and drift rate were not correlated with each other over participants and this supports the view that they index different processing components.

Some aging studies discussed earlier hypothesized that older participants adopt a generally more conservative response strategy in task-switch paradigms (e.g., Lindenberger and Mayr, 2014; Mayr, 2001). In line with this view, we found that older participants had significantly larger boundary separation than college students for both discrimination tasks. In contrast to the conclusions from previous studies, the general more conservative response strategy did not explain all the effects of age-related switch costs. Specifically, we found age-related differences in global and local switch costs indexed by nondecision time component and drift rate beyond the age-related increase in boundary separation.

Previous aging studies that used task-switch paradigms found that older participants have larger global switch costs (as indexed mostly by mean RTs) than younger participants (Gajewski et al., 2018; Meiran et al., 2001, Verhaeghen & Cerella, 2002; Wasylyshyn et al., 2011; Zelazo et al., 2004). Recent diffusion model applications discussed in the Introduction mostly focused on local switch costs by using paradigms that involved mixed blocks only. To estimate consistent model parameters for pure blocks, a sufficiently high error rate is necessary on those trials. However, accuracy values on pure blocks are often high (i.e., above 95%) (Huizinga & van der Molen, 2007; Salthouse et al., 2000; Schmitz & Voss, 20112; Schuch, 2016; Zelazo et al., 2004). The task-switch paradigm presented here involved two discrimination tasks with degraded stimuli (and predictable task switches). The use of degraded stimuli resulted in a sufficiently high error rate that allowed us to study global and local switch costs. We found that older participants, relative to younger participants, had larger global switch costs when computed in terms of reaction times or in terms of nondecision time components (Gajewski et al., 2018; Meiran et al., 2001, Verhaeghen & Cerella, 2002; Wasylyshyn et al., 2011; Zelazo et al., 2004). Some researchers argued that age-related global switch costs are mainly produced by age-related declines in working memory capacity (e.g., Mayr, 2001; Mayr & Kliegl, 2003; Zelazo et al., 2004). However, importantly, we found age-related global switch costs, despite the fact that we reduced the demand of working memory as much as possible in our task-switch paradigm (see Introduction: Present Study and Method Section: Experimental Procedure).

Previous studies (Karayanidis et al., 2009; Madden et al., 2009; Schmitz & Voss, 2012; Schuch, 2016) suggested that nondecision time component and drift rates might not be able to index global and local switch costs in task-switch paradigms that involved predictable task switches. For instance, Schmitz and Voss (2012) presented stimuli (composed of a letter and a digit) to participants and asked them to categorize stimuli either based on their digits (odd or even) or their letters (consonant or vowel). They found local switch costs in terms of nondecision time component but only when task switches occurred randomly, not when task switches occurred predictably (every third trial). Furthermore, Schmitz and Voss (2012) did not find any global switch costs in terms of nondecision time component. In contrast to these results, we found that younger and older participants exhibited global and local switch costs in terms of nondecision time component and drift rate. The fact that Schmitz and Voss (2012) did not find differences in nondecision time component between no-switch and switch trials when task switches occurred predictably, whereas we did, could be due to their use of clearly identifiable stimuli (unlike the stimuli used here).

For the RSI manipulation, we found that RSI significantly modulated global and local switch costs, and that the older participant groups were more affected by changes in RSI. We discuss these secondary results in the Supplemental Material in more detail. Overall, the results suggested that RSI mainly affected switch costs in terms of nondecision time component. Furthermore, differences between the two older participant groups were more pronounced when RSI was short rather than long. For both discrimination tasks, group differences in global switch costs indexed by nondecision time component were largest when RSI was short, whereas group differences in local switch costs indexed by nondecision time component were largest when RSI was long. Previous results suggested that an increase of RSI decreases switch costs, and that it does more so for older participants (Kiesel et al., 2010; Koch & Allport, 2006; Schmitz & Voss, 2012; Vandierendonck et al., 2010). Our findings put previous results into perspective by suggesting that it depends on the type of task as well as on the type of switch costs whether an increase in RSI decreases switch costs particularly of older participants.

The MCT approach (Gilbert & Shallice, 2002; Koch & Allport, 2006; Mayr & Kliegl, 2003; Meiran, 1996; Meiran et al., 2000; Monsell, 2003; Rubinstein et al., 2001; Ruthruff et al., 2001; Sohn & Anderson, 2001; Yeung & Monsell, 2003) hypothesized that early-stage preparatory control processes and late-stage control processes affect cognitive-processing at different points in time, leading to different types of switch costs. Our results provide evidence for this hypothesis and further suggest that the diffusion model provides the means with which to decompose these control processes. The findings from our study suggest that switch costs indexed by nondecision time component and drift rate represent different cognitive components. Our results illustrate the utility of using a task-switch paradigm with degraded stimuli and in conjunction with model-based analyses.

Appendix

Table A1.

Means and standard deviations in parameter values across participant groups for fits of the diffusion model to the task-switch paradigm (for the model in the main text).

Group	Task	a	ƞ	sz	st1	st2	st3	st4
		Mean
college students	Brightness	0.148	0.135	0.048	0.166	0.354	0.192	0.432
	Letter	0.139	0.113	0.045	0.136	0.231	0.143	0.249
61–74 year olds	Brightness	0.228	0.141	0.042	0.243	0.430	0.251	0.579
	Letter	0.221	0.145	0.046	0.152	0.337	0.140	0.357
75–89 year olds	Brightness	0.256	0.138	0.051	0.298	0.364	0.275	0.563
	Letter	0.239	0.152	0.060	0.154	0.354	0.140	0.400
		Standard deviation
college students	Brightness	0.043	0.038	0.026	0.078	0.157	0.083	0.191
	Letter	0.030	0.033	0.024	0.042	0.094	0.046	0.111
61–74 year olds	Brightness	0.061	0.038	0.042	0.107	0.222	0.173	0.189
	Letter	0.049	0.034	0.034	0.072	0.180	0.075	0.211
75–89 year olds	Brightness	0.079	0.041	0.064	0.168	0.194	0.199	0.227
	Letter	0.042	0.034	0.043	0.094	0.201	0.082	0.232

Note. Model with one boundary separation for pure and mixed blocks. a = boundary separation; ƞ = standard deviation in drift across trials; s_z = range of the distribution of starting point (z); s_t1 = range of the distribution of nondecision time components for pure and no-switch trials with short RSI; s_t2 = range of the distribution of nondecision time components for switch trials with short RSI; s_t3 = range of the distribution of nondecision time components for pure and no-switch trials with long RSI; s_t4 = range of the distribution of nondecision time components for switch trials with long RSI.

Table A2.

Means and standard deviations in nondecision time components across participant groups for fits of the diffusion model to the task-switch paradigm (for the model in the main text).

Group	Task	Ter1	Ter2	Ter3	Ter4	Ter5	Ter6
		Mean
college students	Brightness	0.396	0.412	0.537	0.397	0.425	0.562
	Letter	0.393	0.430	0.488	0.400	0.443	0.499
61–74 year olds	Brightness	0.525	0.628	0.919	0.514	0.605	0.923
	Letter	0.487	0.577	0.705	0.475	0.558	0.701
75–89 year olds	Brightness	0.615	0.702	0.946	0.593	0.657	0.920
	Letter	0.487	0.606	0.803	0.474	0.576	0.756
		Standard deviation
college students	Brightness	0.072	0.058	0.108	0.064	0.061	0.119
	Letter	0.031	0.040	0.054	0.027	0.040	0.055
61–74 year olds	Brightness	0.143	0.129	0.239	0.112	0.111	0.185
	Letter	0.083	0.106	0.116	0.068	0.074	0.112
75–89 year olds	Brightness	0.237	0.208	0.297	0.167	0.184	0.183
	Letter	0.052	0.090	0.175	0.064	0.058	0.135

Note. Model with one boundary separation for pure and mixed blocks. T_er1 = nondecision time component of response time for pure trials with short RSI; T_er2 = nondecision time component of response time for no-switch trials with short RSI; T_er3 = nondecision time component of response time for switch trials with short RSI; T_er4 = nondecision time component of response time for pure trials with long RSI; T_er5 = nondecision time component of response time for no-switch trials with long RSI; T_er6 = nondecision time component of response time for switch trials with long RSI.

Table A3.

Means and standard deviations in drift rates across participant groups for fits of the diffusion model to the task-switch paradigm (for the model in the main text).

Group	Task	v1	v2	v3	v4	v5	v6
		Mean
college students	Brightness	.217	.177	.146	.213	.179	.149
	Letter	.307	.230	.216	.295	.224	.220
61–74 year olds	Brightness	.178	.138	.105	.190	.135	.110
	Letter	.339	.246	.207	.328	.234	.212
75–89 year olds	Brightness	.176	.118	.082	.168	.115	.094
	Letter	.315	.202	.187	.307	.222	.182
		Standard deviation
college students	Brightness	0.070	0.060	0.052	0.081	0.067	0.046
	Letter	0.076	0.053	0.058	0.062	0.057	0.059
61–74 year olds	Brightness	0.084	0.057	0.047	0.078	0.062	0.051
	Letter	0.098	0.068	0.064	0.083	0.061	0.056
75–89 year olds	Brightness	0.071	0.063	0.059	0.073	0.057	0.062
	Letter	0.102	0.085	0.071	0.096	0.071	0.059f

Note. Model with one boundary separation for pure and mixed blocks. v₁ = drift rate for pure trials with short RSI; v₂ = drift rate for no-switch trials with short RSI; v₃ = drift rate for switch trials with short RSI; v₄ = drift rate for pure trials with long RSI; v₅ = drift rate for no-switch trials with long RSI; v₆ = drift rate for switch trials with long RSI.