Abstract
Purpose:
To probe the feasibility of deep learning-based super-resolution (SR) reconstruction applied to nonenhanced magnetic resonance angiography (MRA) of the head and neck.
Methods:
High-resolution 3D thin-slab stack-of-stars quiescent interval slice selective (QISS) MRA of the head and neck was obtained in 8 subjects (7 healthy volunteers, 1 patient) at 3 Tesla. The spatial resolution of high-resolution ground-truth MRA data in the slice-encoding direction was reduced by factors of 2 to 6. Four deep neural network (DNN) SR reconstructions were applied, with two based on U-Net architectures (2D and 3D) and two (2D and 3D) consisting of serial convolutions with a residual connection. SR images were compared to ground-truth high-resolution data using Dice similarity coefficient (DSC), structural similarity index (SSIM), arterial diameter, and arterial sharpness measurements. Image review of the optimal DNN SR reconstruction was done by two experienced neuroradiologists.
Results:
DNN SR of up to 2-fold and 4-fold lower-resolution (LR) input volumes provided images that resembled those of the original high-resolution ground-truth volumes for intracranial and extracranial arterial segments, and improved DSC, SSIM, arterial diameters, and arterial sharpness relative to LR volumes (P<0.001). 3D DNN SR outperformed 2D DNN SR reconstruction. According to two neuroradiologists, 3D DNN SR reconstruction consistently improved image quality with respect to LR input volumes (P<0.001).
Conclusion:
DNN-based SR reconstruction of 3D head and neck QISS MRA offers the potential for up to 4-fold reduction in acquisition time for neck vessels without the need to commensurately sacrifice spatial resolution.
Keywords: Super-resolution, deep learning, MRA, neck, head
INTRODUCTION
Vascular evaluation of the head and neck remains a key component in the diagnostic evaluation of patients presenting with suspected stroke (1). Cross-sectional imaging of the head and neck vessels is typically performed with contrast-enhanced CT angiography (CTA) or magnetic resonance angiography (MRA) (2). As an alternative to contrast-enhanced CTA and MRA, nonenhanced MRA (NEMRA) avoids any risk from contrast agents (3). However, scan times associated with NEMRA are relatively long, typically ~10-15 minutes for evaluation of the entire neck and proximal intracranial arteries using 2D or 3D time-of-flight (TOF) protocols. Recently, 3D thin-slab stack-of-stars quiescent interval slice-selective (QISS) MRA has been shown to provide high spatial resolution of the entire neck and Circle of Willis in ≈7 minutes with better image quality than TOF (4). Nonetheless, further reduction of scan time would be desirable to improve patient comfort, reduce motion artifacts, hasten diagnostic evaluation, and compete with the shorter scan times of contrast-enhanced CTA and MRA (5-7).
3D thin-slab QISS utilizes a stack-of-stars k-space trajectory with radial sampling performed in the transversal axis and phase-encoding performed in the slice direction. This k-space trajectory provides robustness to motion and pulsation artifacts as well as efficient imaging while maintaining spatial resolution and vessel sharpness (8-10,4). As undersampling in the radially sampled transversal axis is already high (≈12-fold with respect to the Nyquist rate), additional scan acceleration can be achieved primarily through undersampling of the slice-encoding direction. Established data acceleration strategies include parallel imaging and compressed sensing (11,12). However, the very thin slabs (≈2 cm thickness) acquired with 3D thin-slab stack-of-stars QISS complicates the application of parallel imaging in the slice-encoding direction due to limitations in receiver coil sensitivity and signal-to-noise ratio (11). On the other hand, compressed sensing entails the use of specialized imaging sequences (for customized undersampling of k-space) and associated iterative image reconstruction routines, which despite growing commercial offerings in recent years, remain unavailable on many installed MR systems. Moreover, even with judiciously tuned image acquisitions and reconstructions, compressed sensing inevitably degrades fine image detail due to deliberate undersampling of high frequency k-space (13-19). Additionally, compressed sensing reconstructions enforce data consistency and image sparsity, and thus are not designed to recover unacquired image details which are largely defined by high frequency k-space.
As potential complementary or alternative methods to standard MRI acceleration strategies, deep neural network (DNN)-based methods have found uses in numerous medical imaging applications, including for image reconstruction and restoration in accelerated MRI (20-23). With the goal improving apparent spatial resolution and reducing acquisition time, DNN methods show particular promise for super-resolution (SR) reconstruction that enables the recovery and restoration of unacquired image details based on prior learning (24-27). In particular, we hypothesized that DNN-based SR reconstruction could be applied to nonenhanced 3D head and neck MRA to allow the acquisition of a reduced number of thicker slices, thereby shortening scan time while preserving spatial resolution. The purpose of this study was to probe the feasibility and extent to which four DNN-based SR approaches could potentially shorten the scan times of nonenhanced 3D thin-slab stack-of-stars QISS MRA by factors of up to 6, while comparing results to high-resolution ground truth data.
METHODS
This research study was approved by our institutional review board and all subjects provided written informed consent. The imaging data used in this study consisted of thin multiple overlapping slab stack-of-stars QISS MRA obtained in eight subjects (7 healthy volunteers, 1 patient with bilateral carotid arterial disease) on a 3 Tesla MRI system (MAGNETOM Skyrafit, Siemens Healthineers, Erlangen, Germany) as previously described (4). A 20-channel head and neck coil received the MRI signal. Acquired spatial resolution was 0.86×0.86×1.30 mm, which was reconstructed to 0.43×0.43×0.65 mm using zero filling interpolation. An axial coverage of 288.6 mm was obtained in 6 minutes 39 seconds. Other imaging parameters were: 300 mm field of view, 352 acquisition matrix (704 reconstruction matrix after zero filling interpolation), fast low-angle shot readout with TR 9.9 ms and TEs of 1.6 ms, 3.7 ms, and 5.7 ms which were combined using a root mean square procedure, QISS TR/QI of 1500/583 ms.
Acquired high-resolution (HR) data sets were considered as ground truth, while the 2-fold, 3-fold, 4-fold, 5-fold, and 6-fold low-resolution (LR) data sets were generated by applying a Fourier transform to the HR data sets along the slice-direction, zeroing the highest 50.0%, 66.6%, 75.0%, 80.0%, and 83.3% acquired spatial frequencies along the slice direction, and inverse Fourier transforming the result back to the image domain. This Fourier-based low-pass filtering process mimics the acquisition of fewer slice-encoding steps as is done during 3D MRI prescribed with reduced spatial resolution in the slice direction.
Deep Learning-Based SR Methods
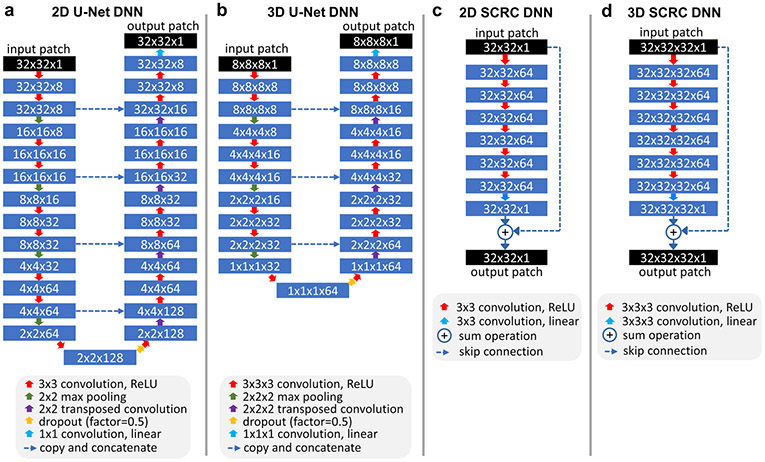
Four deep neural network (DNN) models were tested: 2D U-Net and 3D U-Net (28), and 2D and 3D networks consisting of serial convolutions and a residual connection (SCRC) (24); these DNNs are hereafter referred to as 2D U-Net, 3D U-Net, 2D SCRC, and 3D SCRC, respectively. To avoid needless inclusion of superfluous air regions outside the body due to the large field of view and to better focus DNN training on arterial and adjacent structures, imaging volumes were cropped 50% in the anterior-posterior and left-right directions before DNN training.
U-Net DNNs:
Similar to an implementation reported previously in the field of nonenhanced MRA (29), the 2D U-Net DNN used 4 levels of downsampling, 4 levels of upsampling with concatenation of downsampled features of the same level, and 8 channels (Figure 1a). 2D convolution (of size 3×3) with rectified linear unit activation was used on each level, with maximum pooling for downsampling, and transposed convolution for upsampling. The network took LR 2D image patches (of size 32×32 voxels) as inputs and produced patches of the same size as outputs. Ten thousand training patches from coronal reformatted images were selected (from all unique candidate patches separated by a stride of 16 voxels in each direction) from each subject, with half of the training patches obtained from edge-bearing patches (based on the maximal signal contained in the HR volume after convolving with a 5-tap [−1, 0.5, 1, 0.5, −1] filter along all three orthogonal directions), and with the other half obtained from randomly selected locations within the 3D volume used for training. Output patches were tiled together (with patches overlapped by 16 voxels in both the head-foot and lateral directions) to generate the final reconstructed volume.
Figure 1.
Architectures of the deep neural networks used for super-resolution reconstruction. ReLU = rectified linear unit.
The 3D U-Net DNN (Figure 1b) consisted of 3 levels of downsampling followed by 3 levels of upsampling with concatenation of downsampled features. The network took LR 3D image blocks (of size 8×8×8 voxels) as inputs and produced output blocks of the same size. Image blocks of size 8×8×8 instead of larger block sizes (e.g., of size 32×32×32) were chosen for the 3D U-Net DNN as they provided better reconstruction results. Twenty thousand training blocks (separated by a stride of 4 voxels in each direction) were selected from each subject, with half obtained from edge-bearing blocks (based on the maximum filtered signal in the HR volume as defined previously), and the remaining blocks obtained from randomly selected locations within the 3D volume. Output blocks were stacked together using a 4 voxel overlap in all directions.
SCRC DNNs:
Similar to prior work applying DNN SR reconstruction to knee MRI (24), the 3D SCRC DNN was based on serial 3D convolutions (size 3×3×3) combined with rectified linear unit activation, except for the final layer where only convolution was used (Figure 1d). The network output was then summed with the LR input block to generate the final SR volume. The network took 32×32×32 voxel blocks as inputs and used 7 convolution layers and 64 filters; 7 layers were used as more convolutional layers produced similar results or failed to train. For DNN training, one thousand spatially-registered 3D blocks (from all unique candidate blocks separated by a stride of 16 voxels in each direction) from the LR source and HR target volumes were selected, with half of these blocks chosen on the basis of edge strength in the HR volume, while the remaining half were chosen randomly from the 3D field of view. Output blocks of size 32×32×32 were stacked together with blocks overlapped by 16 voxels in all three directions to produce the final reconstructed volume. The 2D SCRC DNN (Figure 1c) was analogous to the 3D SCRC DNN but was based on 2D convolutions (size 3×3) and took 32×32 image patches as inputs. The training and reconstruction approach for the 2D SCRC DNN was identical to that of the 2D U-Net DNN.
All DNN training was done using leave-one-out cross-validation, an adaptive moment estimation optimizer (learning rate=0.001, β1=0.9, β2=0.999), a mean squared error loss function, validation split of 20%, and early stopping based on validation loss (training was stopped after 3 epochs with no improvement in validation loss). A 50% dropout probability between the central U-Net DNN layers was applied. Training batch sizes for the 2D U-Net, 3D U-Net, 2D SCRC and 3D SCRC DNNs were 400, 80, 400 and 20, respectively, whereas the number of trainable parameters were 540,073, 436,521, 185,857 and 556,801, respectively. Training and execution of the DNNs was done in the Python programming language using open-source packages (Keras v2.2.4, Tensorflow v1.12.0) and a commodity graphics processing unit (GTX 1060, Nvidia Corporation, Santa Clara, CA). Typical training times for the 2D U-Net, 3D U-Net, 2D SCRC and 3D SCRC DNNs were approximately 2 min (9 epochs), 9 min (7 epochs), 5 min (9 epochs) and 60 min (9 epochs), respectively.
Quantitative Image Analysis
Quantitative analysis consisted of measuring the degree of anatomical agreement between HR volumes, LR volumes and the four SR volumes using various quantitative metrics including Dice similarity coefficient (DSC), structural similarity index (SSIM), normalized root mean squared error (NRMSE), arterial sharpness, and arterial diameter measurements.
Overall arterial anatomical congruence between the ground truth, LR and SR reconstructions was evaluated using the DSC (30). In assessing anatomical congruence with the DSC, 3D arterial masks were generated using a bespoke region-growing routine with four extracranial seed points placed manually in the bilateral common carotid arteries and V2 segments of the vertebral arteries (≈2 cm below the carotid bifurcation), as well as with additional seed points placed in the intracranial arteries. The minimum signal intensity allowed in the arterial mask enlarged via region growing was set to 50% (6 of 8 subjects) or 55% (2 of 8 subjects) of the mean signal intensity contained in the four extracranial seed points to avoid unwanted inclusion of venous signal. DSCs were computed over the entire arterial anatomy (including both the extracranial and intracranial vessels), as well as for the extracranial and intracranial vessels separately.
SSIM, NRMSE, arterial sharpness, and arterial diameters were computed for the bilateral M1 segments of the middle cerebral arteries. In calculating SSIM and NRMSE, two square image patches (size ≈100 mm2) were obtained from coronal views of each image set, centered on the bilateral M1 middle cerebral arteries. SSIM and NRMSE calculations were done using the Python “scikit-image” package (version 0.16.1). Arterial diameter and edge sharpness in the slice direction (i.e., the direction of resolution reduction) were calculated in each subject within ImageJ software (version 1.53f, National Institutes of Health, Bethesda, MA), by analyzing one-dimensional ≈10-mm-long intensity profiles along the slice-encoding axis which were bicubically interpolated by a factor of 5. With respect to background signal levels which were defined as the minimum signal levels on both sides of the arterial profile, arterial diameter (in mm units) was computed as the full-width-at-half-maximum (FWHM) of the intensity profile. Using the same signal intensity profiles, arterial sharpness (in mm−1 units) was computed as the inverse of the distance between 20% and 80% of vessel maximum intensity (relative to background signal levels), averaged from both sides of the vessel (31).
SR reconstructions providing median DSC and SSIM values of ≥0.9, as well arterial sharpness and diameter measures not significantly differing from those of the HR ground truth volumes were interpreted to provide sufficiently accurate displays of the arterial anatomy with potential for diagnostic usage.
Qualitative Image Analysis
Coronal maximum intensity projections of the LR volumes and volumes provided by the optimal SR reconstruction approach (as determined by the largest DSC, SSIM and arterial sharpness measures, as well as the smallest arterial diameter measures) were randomized (with the SR reconstruction displayed on either the left or right side) and displayed side-by-side to two neuroradiologists with over 15 years of experience interpreting MRA. Using a two-alternative forced choice paradigm, the neuroradiologists were asked to identify the volume (left or right) which provided the best image quality for diagnostic interpretation.
Statistical Analysis
Differences in quantitative measures were identified using Friedman and post-hoc Wilcoxon signed-rank tests. One-sided binomial tests with a test probability of 0.5 were used to analyze two-alternative forced choice evaluations performed by neuroradiologists. P-values less than 0.05 indicated statistical significance. Bonferroni correction was used for post-hoc Wilcoxon signed-ranked test comparisons of arterial SSIM, NRMSE, diameter and sharpness to avoid type I error. Statistical analyses were done using SciPy (version 1.4.1, https://scipy.org/).
RESULTS
Mean reconstruction times of the 2D U-Net, 3D U-Net, 2D SCRC and 3D SCRC DNN SR methods over the entire field of view (704×704 matrix, 444 axial slices) were 2 min 34 sec, 13 min 9 sec, 3 min 40 sec, and 15 min 51 sec, respectively.
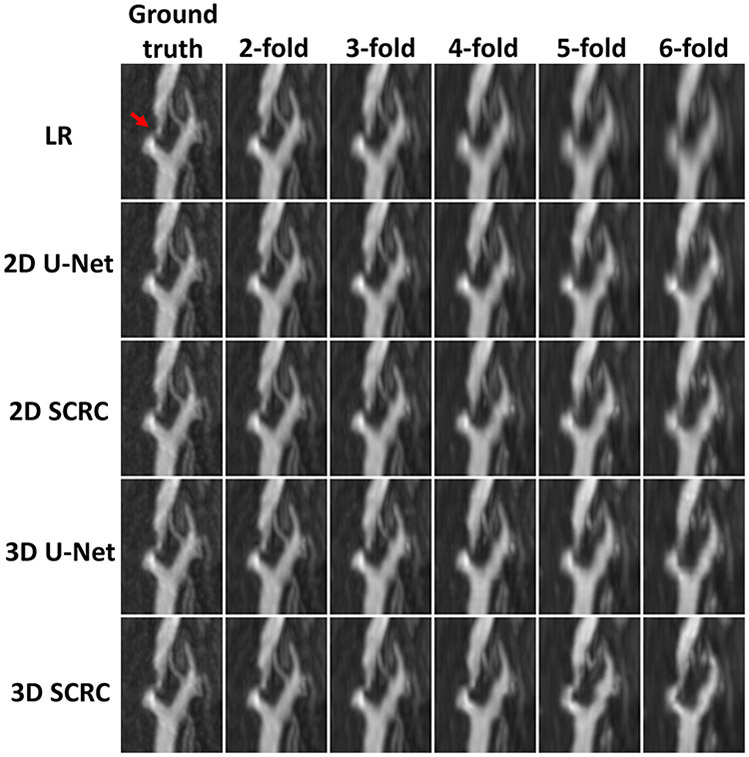
Figure 2 shows the image quality obtained with the 3D SCRC SR technique with respect to the LR input volumes, and the target high resolution output volume. With respect to the LR volume, 3D SCRC SR improved vessel conspicuity and sharpness in the slice-encoding (i.e., axial) direction, which mimicked that of the target volume for all tested resolution reduction factors. Supporting Information Video S1 shows corresponding results obtained with 2D U-Net, 2D SCRC, and 3D U-Net SR reconstructions, where similar improvements in vessel conspicuity with respect to LR data were noted.
Figure 2.
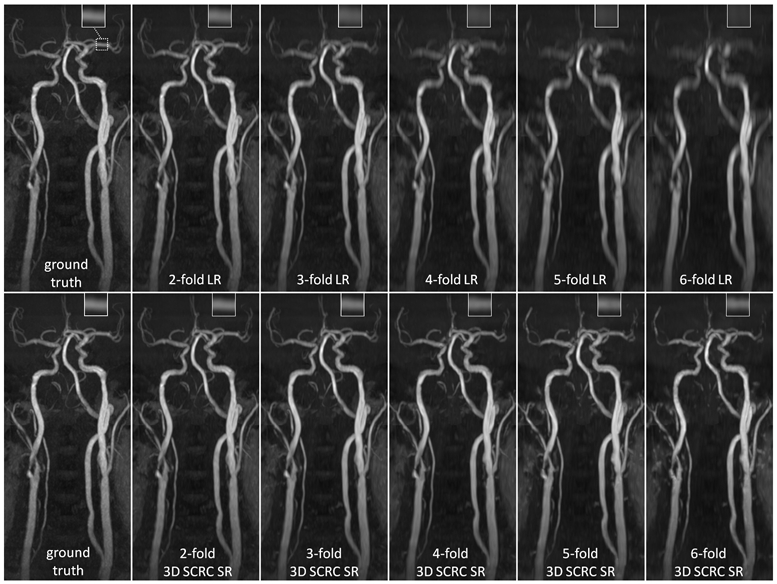
Coronal maximum intensity projection 3D thin-slab stack-of-stars QISS MRA images obtained in a patient with bilateral carotid arterial disease showing the impact of 3D SCRC SR DNN reconstruction on image quality for 2- to 6-fold reduced of axial spatial resolution with respect to ground truth data (left-most column) and input lower resolution (LR) data (right-most upper panels). Insets show magnified views of the left middle cerebral artery (dashed boxed region in ground truth image). Note the improved spatial resolution of the 3D SCRC SR DNN with respect to input LR volumes as well as the improved correlation with respect to ground truth data. LR = low resolution; SCRC = serial convolution residual connection; SR = super-resolution.
Quantitative Analysis
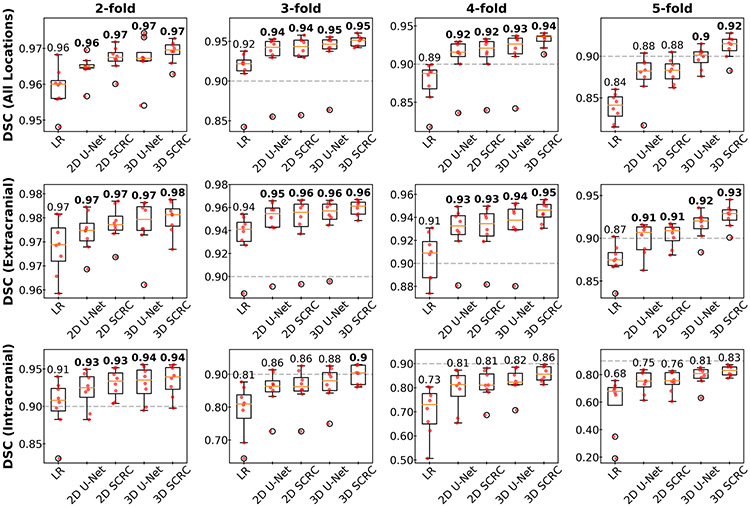
DSC measures of agreement in arterial anatomy portrayed in the SR-reconstructed and the ground truth volumes are shown in Figure 3 and Supporting Information Figure S2. In general, 3D DNN outperformed 2D DNN SR reconstructions, while SCRC DNNs outperformed U-Net DNNs of the same dimensionality. The 3D SCRC DNN method provided the largest overall DSC values. Due to the smaller caliber of the intracranial arteries as well as their greater orthogonality with respect to the slice-encoding direction, DSCs were improved to a greater degree intracranially as opposed to extracranially. For all four tested DNNs, median DSCs of at least 0.9 were maintained for resolution reduction factors of up to 2 and 5 for the intracranial and extracranial vessels, respectively, whereas this threshold was achieved for the 3D SCRC DNN for factors of 3 intracranially and 6 extracranially.
Figure 3.
Boxplots showing DSCs obtained with the SR DNNs for select spatial resolution reduction factors and locations. 3D DNN SR reconstructions provided the largest DSCs, with the 3D SCRC DNN providing the largest DSCs. Numbers are medians; bold numbers indicate DNNs providing DSCs≥0.9. Horizontal dashed lines show the minimum DSC adequacy threshold of 0.9. DSC = Dice similarity coefficient; LR= low resolution; SCRC = serial convolution residual connection.
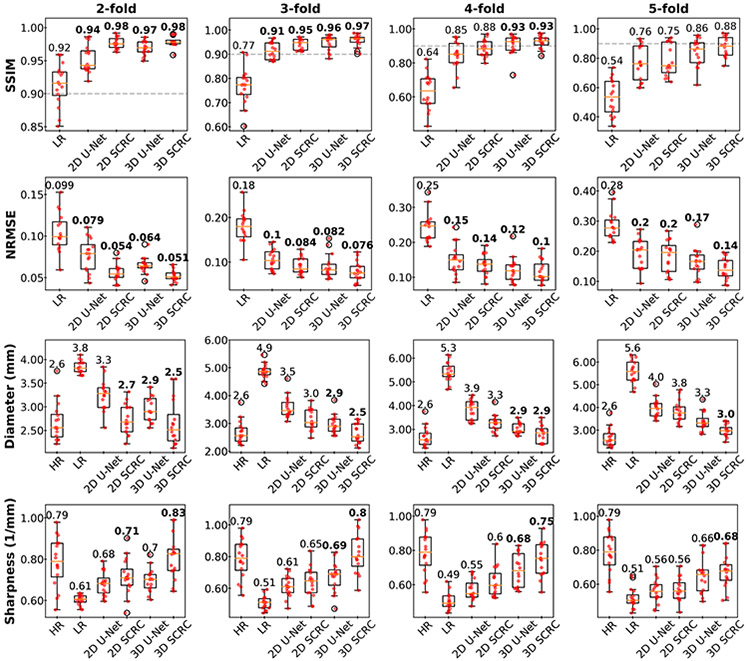
Arterial SSIM, NRMSE, diameter and sharpness metrics are shown in Figure 4 and Supporting Information Figure S3. All four quantitative metrics improved with application of the DNN SR techniques (Friedman, P<0.001), with arterial SSIM and sharpness values increasing, and with arterial NRMSE and diameter values decreasing with respect to values obtained from the LR volumes. In general, progressive improvement in quantitative metrics was observed with the SR DNNs in the following order: 2D U-Net, 2D SCRC, 3D U-Net and 3D SCRC. Of note, the 3D DNNs provided median SSIM values of ≥0.9 and retained the apparent image sharpness of the HR volumes for reduction factors of up to 4.
Figure 4.
Bar plots showing arterial SSIM, NRMSE, diameter and sharpness results obtained with the DNN SR reconstructions for select factors of spatial resolution reduction. Numbers are medians; bold numbers indicate DNNs providing SSIMs≥0.9, NRMSE values significantly differing from those of the LR volumes, and arterial sharpness and diameter measurements not significantly differing from those of the HR volumes. Dashed horizontal lines in SSIM plots indicate the minimum adequacy threshold of 0.9. SSIM = structural similarity index; NRMSE = normalized root mean square error; LR = low resolution; HR = high-resolution ground truth.
Image Appearance and Artifacts
Figure 5 shows magnified views of extracranial and intracranial arteries obtained with all SR reconstruction techniques, where the improved arterial display using SR reconstruction was obtained with respect to the LR volumes. Visually, for modest reduction factors of 2 to 3, all four SR DNNs restored the lost spatial resolution of the LR volumes in the slice-encoding direction. Consistent with the quantitative results, 3D SR DNNs generally outperformed 2D SR DNNs, and SCRC DNNs outperformed U-Net DNNs of the same dimensionality. In general, the 3D SR DNNs restored arterial detail for resolution reduction factors of up to 4.
Figure 5.

Comparison of DNN SR techniques in a healthy volunteer. Coronal maximum intensity projection images showing magnified views of the low resolution and DNN SR reconstructions at the four locations marked in the coronal QISS MRA image. Note the improved correlation with respect to the ground truth images obtained with the 3D DNN SR reconstructions (with respect to 2D DNN reconstructions), and with the SCRC DNNs (with respect to U-Net DNNs). Best agreement with the ground truth data was generally obtained with the 3D SCRC method. ICA = internal carotid artery; MCA = middle cerebral artery; MIP = maximum intensity projection; SCRC = serial convolution residual connection; VA = vertebral artery.
At large resolution reduction factors of ≥5, SR DNN reconstruction artifacts included loss of arterial conspicuity (e.g., in the left M2 segment of the middle cerebral artery), arterial narrowing (e.g., in the left V3 segment of the vertebral artery), distortion of arterial contours (e.g., in the left petrous internal carotid artery), and a beaded vessel appearance (e.g., in the right V4 vertebral artery). The severity of such artifacts depended on the DNN technique and the factor of spatial resolution reduction.
Figure 6 and Supporting Information Figure S4 show the results of the various SR reconstructions on the appearance of two carotid stenoses. The DNN SR reconstructions recovered the original HR display of the carotid bifurcation up to resolution reduction factors of approximately 4.
Figure 6.
15-mm-thick maximum intensity projection 3D QISS MRA images obtained with the SR DNNs showing a severe stenosis of the right internal carotid artery (arrow). Note the preservation of arterial detail with the various SR DNNs for resolution reduction factors of up to ≈4. LR = low resolution; SCRC = serial convolution residual connection.
Qualitative Image Analysis by Neuroradiologists
Qualitative evaluation by two experienced neuroradiologists showed that the best performing 3D SCRC SR DNN produced MR angiograms that were preferred over angiograms obtained from the input LR volumes 100% of the time (40 of 40 comparisons, P=9.09×10−13) for both reviewers.
DISCUSSION
In this study, we probed the capability of four DNN-based SR methods to improve spatial resolution in QISS MRA acquired with 2- to 6-fold degraded spatial resolution in the axial direction. We found that 2D and 3D DNN-based approaches restored image spatial resolution and appearance according to multiple quantitative image metrics including arterial SSIM, NRMSE, sharpness and diameter. Using stack-of-stars QISS data, we found that DNN-based SR reconstruction can improve apparent spatial resolution in the slice direction and holds promise for shortening the acquisition times of nonenhanced QISS MRA by factors of up to 4.
The 3D SCRC SR reconstruction technique used in this work resembles that of Chaudhari and colleagues (24) which was applied to improve the apparent spatial resolution in knee MRI. Using layers of 3D CNNs, both networks generate a difference volume which is then added back to the lower-resolution volume to generate the final resolution-improved volume. Seven convolutional layers were used in the present work as we observed that more convolutional layers (i.e. >7) provided negligible benefit at substantially higher computational expense during training and inference, whereas the use of 20 layers resulted in the SCRC DNN failing to learn. Because the receptive field of the SCRC DNN increases with number of convolutional layers, this observation suggests that high-spatial frequency arterial edge information in neurological MRA is best inferred from image data in the immediate vicinity of the artery.
With respect to prior work in the field of SR-enhanced MRA of the neurovasculature (31,32), our study adds further support to the notion that SR-based methods can provide improvements in apparent spatial resolution. Our work differs from a prior SR study in the field of MRA (31) in that a 3D rather than a 2D MRA acquisition was used, and that DNN-based SR methods (as opposed to more conventional SR methods) were tested. In contrast to this prior study which reported only modest (≈15%) increases in arterial sharpness values with conventional (i.e., non-DNN) Irani-Peleg-based SR reconstruction (33), the 3D DNN SR methods tested here provided much larger increases (≈60% at 3-fold reduced spatial resolution) in arterial sharpness. Moreover, the DNN SR methods markedly reduced the broadening of arterial diameter seen in LR volumes. Of note, we tested conventional Irani-Peleg SR reconstruction on the LR volumes of this study but the approach provided no substantial benefit (due to the lack of distinct overlapping data) and consequently results are not reported.
Using leave-one-out cross-validation, we found that the 2D and 3D DNN SR techniques could be trained using limited training data obtained in only 7 subjects. This finding is notable as it suggests that such DNN networks can be sufficiently trained using a small number of existing data sets. We also found that the various DNNs required substantially different training times and application times despite having nearly the same number of training parameters. Even though the 3D DNNs outperformed the 2D DNNs in terms of quantitative metrics, the latter were faster to train and apply. 2D SR DNNs may therefore be advantageous when faster image reconstruction is preferred at the cost of reconstruction accuracy. Of note, the SR DNNs used in this study were applied to a very large imaging matrix obtained after two-fold interpolation in all three directions. Reconstruction times for all four DNNs can be shortened substantially by disabling interpolation, limiting reconstruction to arterial locations, or using more powerful graphical processing units.
This study has some limitations. First, reconstruction artifacts in the form of vessel blurring and distortion from some of the evaluated DNNs were noted at large resolution reduction factors of ≥4; accordingly, the use of more modest reduction factors of 2–3 is recommended. Second, the approach used to select the training 2D patches and 3D blocks was determined empirically and may not be optimal. Additional improvements in SR performance may be feasible with further DNN hyperparameter optimization and other DNN architectures. Third, with the exception of one patient with bilateral carotid disease, this study was performed in a small cohort of primarily healthy subjects. Fourth, the DNN approaches presented were applied exclusively to magnitude images; further work is needed to evaluate whether the incorporation of phase data (which was not available in this study) would be helpful. Lastly, our study was limited to data in which spatial resolution was reduced retrospectively and ground truth higher-resolution data was available. Future work must validate the presented DNN SR methods on data acquired prospectively with reduced axial spatial resolution.
Interestingly, generalizations and extensions of the described DNN SR methods are anticipated. Due to similarities in image appearance (bright vessels on a dark background) and assuming the use of analogous DNN training methods, we anticipate that the benefits of DNN-based SR reconstruction strategies will extend to other MRA techniques such as 3D time-of-flight MRA and contrast-enhanced MRA, as well as to MRA outside the head and neck. Lastly, since the DNN SR techniques tested here are carried out in the image domain, they can readily complement and be synergistically combined with other MRI acceleration strategies such as parallel imaging and compressed sensing (34,35) to realize very fast 3D neurological MRA protocols.
CONCLUSION
In conclusion, we found that the use of DNN-based SR reconstruction of head and neck MRA is feasible, and potentially enables scan time reductions of up to 4-fold for displaying the extracranial arteries. Further work remains to validate the DNN SR reconstruction approaches in patients with known or suspected cerebrovascular disease.
Supplementary Material
Supporting Information Figure S2. Boxplots with statistical markings showing DSCs obtained with the SR DNNs for all resolution reduction factors and locations. 3D DNN SR reconstructions provided the largest DSCs, with the 3D SCRC DNN providing the largest DSCs. Horizontal gray bars indicate significant differences (P<0.05, Wilcoxon signed-rank tests) between reconstruction techniques. Numbers are medians; bold numbers indicate DNNs providing DSCs≥0.9. Horizontal dashed lines show the minimum DSC adequacy threshold of 0.9. DSC = Dice similarity coefficient; LR= low resolution; SCRC = serial convolution residual connection.
Supporting Information Figure S3. Bar plots with statistical markings showing arterial SSIM, NRMSE, diameter and sharpness results obtained with the DNN SR reconstructions for all resolution reduction factors. Horizontal gray bars indicate significant differences (P<0.05, Bonferroni-corrected Wilcoxon signed-rank tests) between SR reconstruction techniques. Numbers are medians; bold numbers indicate DNNs providing SSIMs≥0.9, NRMSE values significantly differing from those of the LR volumes, and arterial sharpness and diameter measurements not significantly differing from those of the HR volumes. Dashed horizontal lines in SSIM plots indicate the minimum adequacy threshold of 0.9. SSIM = structural similarity index; NRMSE = normalized root mean square error; LR = low resolution; HR = high-resolution ground truth; SCRC = serial convolution residual connection.
Supporting Information Figure S4. 15-mm-thick maximum intensity projection 3D QISS MRA images obtained with the SR DNNs showing a moderate stenosis of the left internal carotid artery (arrow). Note the preservation of arterial detail with the various SR DNNs for resolution reduction factors of up to ≈4. LR = low resolution; SCRC = serial convolution residual connection.
Supporting Information Video S1. Image quality obtained with all the various super resolution reconstruction techniques for 2 to 6-fold reduced axial spatial resolution, corresponding to Figure 2. Note the progressively improved image quality with respect to high-resolution ground truth data provided by the 2D U-Net, 2D SCRC, 3D U-Net and 3D SCRC SR reconstructions. LR = low resolution; SCRC = serial convolution residual connection.
ACKNOWLEDGEMENT
This work was supported in part by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under Award Number R01EB027475. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Data Availability Statement
Python scripts for training and applying the described super-resolution deep neural networks are available at https://github.com/ikoktz/super-mra.
REFERENCES
- 1.Powers WJ, Rabinstein AA, Ackerson T, et al. Guidelines for the Early Management of Patients With Acute Ischemic Stroke: 2019 Update to the 2018 Guidelines for the Early Management of Acute Ischemic Stroke: A Guideline for Healthcare Professionals From the American Heart Association/American Stroke Association. Stroke 2019;50:e344–e418 doi: 10.1161/STR.0000000000000211. [DOI] [PubMed] [Google Scholar]
- 2.Srinivasan A, Goyal M, Azri FA, Lum C. State-of-the-Art Imaging of Acute Stroke. RadioGraphics 2006;26:S75–S95 doi: 10.1148/rg.26si065501. [DOI] [PubMed] [Google Scholar]
- 3.Edelman RR, Koktzoglou I. Noncontrast MR angiography: An update. J. Magn. Reson. Imaging 2019;49:355–373 doi: 10.1002/jmri.26288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Koktzoglou I, Huang R, Ong AL, Aouad PJ, Walker MT, Edelman RR. High spatial resolution whole-neck MR angiography using thin-slab stack-of-stars quiescent interval slice-selective acquisition. Magn. Reson. Med 2020;84:3316–3324 doi: 10.1002/mrm.28339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Saver Jeffrey L Time Is Brain—Quantified. Stroke 2006;37:263–266 doi: 10.1161/01.STR.0000196957.55928.ab. [DOI] [PubMed] [Google Scholar]
- 6.Jahan R, Saver JL, Schwamm LH, et al. Association Between Time to Treatment With Endovascular Reperfusion Therapy and Outcomes in Patients With Acute Ischemic Stroke Treated in Clinical Practice. JAMA 2019;322:252–263 doi: 10.1001/jama.2019.8286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nguyen XV, Oztek MA, Nelakurti DD, et al. Applying Artificial Intelligence to Mitigate Effects of Patient Motion or Other Complicating Factors on Image Quality. Top. Magn. Reson. Imaging 2020;29:175–180 doi: 10.1097/RMR.0000000000000249. [DOI] [PubMed] [Google Scholar]
- 8.Glover GH, Pauly JM. Projection Reconstruction Techniques for Reduction of Motion Effects in MRI. Magn. Reson. Med 1992;28:275–289 doi: 10.1002/mrm.1910280209. [DOI] [PubMed] [Google Scholar]
- 9.Peters DC, Korosec FR, Grist TM, et al. Undersampled projection reconstruction applied to MR angiography. Magn. Reson. Med 2000;43:91–101 doi: . [DOI] [PubMed] [Google Scholar]
- 10.Edelman RR, Aherne E, Leloudas N, Pang J, Koktzoglou I. Near-isotropic noncontrast MRA of the renal and peripheral arteries using a thin-slab stack-of-stars quiescent interval slice-selective acquisition. Magn. Reson. Med 2020;83:1711–1720 doi: 10.1002/mrm.28032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Glockner JF, Hu HH, Stanley DW, Angelos L, King K. Parallel MR Imaging: A User’s Guide. RadioGraphics 2005;25:1279–1297 doi: 10.1148/rg.255045202. [DOI] [PubMed] [Google Scholar]
- 12.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med 2007;58:1182–1195 doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 13.Sharma SD, Fong CL, Tzung BS, Law M, Nayak KS. Clinical image quality assessment of accelerated magnetic resonance neuroimaging using compressed sensing. Invest. Radiol 2013;48:638–645 doi: 10.1097/RLI.0b013e31828a012d. [DOI] [PubMed] [Google Scholar]
- 14.Jaspan ON, Fleysher R, Lipton ML. Compressed sensing MRI: a review of the clinical literature. Br. J. Radiol 2015;88:20150487 doi: 10.1259/bjr.20150487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yang AC, Kretzler M, Sudarski S, Gulani V, Seiberlich N. Sparse Reconstruction Techniques in Magnetic Resonance Imaging: Methods, Applications, and Challenges to Clinical Adoption. Invest. Radiol 2016;51:349–364 doi: 10.1097/RLI.0000000000000274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kayvanrad M, Lin A, Joshi R, Chiu J, Peters T. Diagnostic quality assessment of compressed sensing accelerated magnetic resonance neuroimaging. J. Magn. Reson. Imaging 2016;44:433–444 doi: 10.1002/jmri.25149. [DOI] [PubMed] [Google Scholar]
- 17.Akasaka T, Fujimoto K, Yamamoto T, et al. Optimization of Regularization Parameters in Compressed Sensing of Magnetic Resonance Angiography: Can Statistical Image Metrics Mimic Radiologists’ Perception? PLOS ONE 2016;11:e0146548 doi: 10.1371/journal.pone.0146548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sartoretti T, Reischauer C, Sartoretti E, Binkert C, Najafi A, Sartoretti-Schefer S. Common artefacts encountered on images acquired with combined compressed sensing and SENSE. Insights Imaging 2018;9:1107–1115 doi: 10.1007/s13244-018-0668-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Eun D, Jang R, Ha WS, Lee H, Jung SC, Kim N. Deep-learning-based image quality enhancement of compressed sensing magnetic resonance imaging of vessel wall: comparison of self-supervised and unsupervised approaches. Sci. Rep 2020;10:13950 doi: 10.1038/s41598-020-69932-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yasaka K, Abe O. Deep learning and artificial intelligence in radiology: Current applications and future directions. PLOS Med. 2018;15:e1002707 doi: 10.1371/journal.pmed.1002707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Choy G, Khalilzadeh O, Michalski M, et al. Current Applications and Future Impact of Machine Learning in Radiology. Radiology 2018;288:318–328 doi: 10.1148/radiol.2018171820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lundervold AS, Lundervold A. An overview of deep learning in medical imaging focusing on MRI. Z. Für Med. Phys 2019;29:102–127 doi: 10.1016/j.zemedi.2018.11.002. [DOI] [PubMed] [Google Scholar]
- 23.Mazurowski MA, Buda M, Saha A, Bashir MR. Deep learning in radiology: An overview of the concepts and a survey of the state of the art with focus on MRI. J. Magn. Reson. Imaging 2019;49:939–954 doi: 10.1002/jmri.26534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chaudhari AS, Fang Z, Kogan F, et al. Super-resolution musculoskeletal MRI using deep learning. Magn. Reson. Med 2018;80:2139–2154 doi: 10.1002/mrm.27178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Van Dyck P, Smekens C, Vanhevel F, et al. Super-Resolution Magnetic Resonance Imaging of the Knee Using 2-Dimensional Turbo Spin Echo Imaging. Invest. Radiol 2020;55:481–493 doi: 10.1097/RLI.0000000000000676. [DOI] [PubMed] [Google Scholar]
- 26.Wang Z, Chen J, Hoi SCH. Deep Learning for Image Super-resolution: A Survey. IEEE Trans. Pattern Anal. Mach. Intell 2020:1–1 doi: 10.1109/TPAMI.2020.2982166. [DOI] [PubMed] [Google Scholar]
- 27.Kobayashi H, Nakayama R, Hizukuri A, Ishida M, Kitagawa K, Sakuma H. Improving Image Resolution of Whole-Heart Coronary MRA Using Convolutional Neural Network. J. Digit. Imaging 2020;33:497–503 doi: 10.1007/s10278-019-00264-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. ArXiv150504597 Cs 2015. [Google Scholar]
- 29.Koktzoglou I, Huang R, Ong AL, Aouad PJ, Aherne EA, Edelman RR. Feasibility of a sub-3-minute imaging strategy for ungated quiescent interval slice-selective MRA of the extracranial carotid arteries using radial k-space sampling and deep learning–based image processing. Magn. Reson. Med 2020;84:825–837 doi: 10.1002/mrm.28179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dice LR. Measures of the Amount of Ecologic Association Between Species. Ecology 1945;26:297–302 doi: 10.2307/1932409. [DOI] [Google Scholar]
- 31.Koktzoglou I, Edelman RR. Super-resolution intracranial quiescent interval slice-selective magnetic resonance angiography. Magn. Reson. Med 2018;79:683–691 doi: 10.1002/mrm.26715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Okanovic M, Hillig B, Breuer F, Jakob P, Blaimer M. Time-of-flight MR-angiography with a helical trajectory and slice-super-resolution reconstruction. Magn. Reson. Med 2018;80:1812–1823 doi: 10.1002/mrm.27167. [DOI] [PubMed] [Google Scholar]
- 33.Irani M, Peleg S. Super resolution from image sequences. In: 10th International Conference on Pattern Recognition [1990] Proceedings. Vol. ii. ; 1990. pp. 115–120 vol.2. doi: 10.1109/ICPR.1990.119340. [DOI] [Google Scholar]
- 34.Deshmane A, Gulani V, Griswold MA, Seiberlich N. Parallel MR imaging. J. Magn. Reson. Imaging JMRI 2012;36:55–72 doi: 10.1002/jmri.23639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hollingsworth KG. Reducing acquisition time in clinical MRI by data undersampling and compressed sensing reconstruction. Phys. Med. Biol 2015;60:R297–R322 doi: 10.1088/0031-9155/60/21/R297. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Figure S2. Boxplots with statistical markings showing DSCs obtained with the SR DNNs for all resolution reduction factors and locations. 3D DNN SR reconstructions provided the largest DSCs, with the 3D SCRC DNN providing the largest DSCs. Horizontal gray bars indicate significant differences (P<0.05, Wilcoxon signed-rank tests) between reconstruction techniques. Numbers are medians; bold numbers indicate DNNs providing DSCs≥0.9. Horizontal dashed lines show the minimum DSC adequacy threshold of 0.9. DSC = Dice similarity coefficient; LR= low resolution; SCRC = serial convolution residual connection.
Supporting Information Figure S3. Bar plots with statistical markings showing arterial SSIM, NRMSE, diameter and sharpness results obtained with the DNN SR reconstructions for all resolution reduction factors. Horizontal gray bars indicate significant differences (P<0.05, Bonferroni-corrected Wilcoxon signed-rank tests) between SR reconstruction techniques. Numbers are medians; bold numbers indicate DNNs providing SSIMs≥0.9, NRMSE values significantly differing from those of the LR volumes, and arterial sharpness and diameter measurements not significantly differing from those of the HR volumes. Dashed horizontal lines in SSIM plots indicate the minimum adequacy threshold of 0.9. SSIM = structural similarity index; NRMSE = normalized root mean square error; LR = low resolution; HR = high-resolution ground truth; SCRC = serial convolution residual connection.
Supporting Information Figure S4. 15-mm-thick maximum intensity projection 3D QISS MRA images obtained with the SR DNNs showing a moderate stenosis of the left internal carotid artery (arrow). Note the preservation of arterial detail with the various SR DNNs for resolution reduction factors of up to ≈4. LR = low resolution; SCRC = serial convolution residual connection.
Supporting Information Video S1. Image quality obtained with all the various super resolution reconstruction techniques for 2 to 6-fold reduced axial spatial resolution, corresponding to Figure 2. Note the progressively improved image quality with respect to high-resolution ground truth data provided by the 2D U-Net, 2D SCRC, 3D U-Net and 3D SCRC SR reconstructions. LR = low resolution; SCRC = serial convolution residual connection.
Data Availability Statement
Python scripts for training and applying the described super-resolution deep neural networks are available at https://github.com/ikoktz/super-mra.