Latent Representation Learning for Alzheimer’s Disease Diagnosis with Incomplete Multi-modality Neuroimaging and Genetic Data

Abstract

The fusion of complementary information contained in multi-modality data (e.g., Magnetic Resonance Imaging (MRI), Positron Emission Tomography (PET) and genetic data) has advanced the progress of automated Alzheimer’s disease (AD) diagnosis. However, multi-modality based AD diagnostic models are often hindered by the missing data, i.e., not all the subjects have complete multi-modality data. One simple solution used by many previous studies is to discard samples with missing modalities. However, this significantly reduces the number of training samples, thus leading to a sub-optimal classification model. Furthermore, when building the classification model, most existing methods simply concatenate features from different modalities into a single feature vector without considering their underlying associations. As features from different modalities are often closely related (e.g., MRI and PET features are extracted from the same brain region), utilizing their inter-modality associations may improve the robustness of the diagnostic model. To this end, we propose a novel latent representation learning method for multi-modality based AD diagnosis. Specifically, we use all the available samples (including samples with incomplete modality data) to learn a latent representation space. Within this space, we not only use samples with complete multi-modality data to learn a common latent representation, but also use samples with incomplete multi-modality data to learn independent modality-specific latent representations. We then project the latent representations to the label space for AD diagnosis. We perform experiments using 737 subjects from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database, and the experimental results verify the effectiveness of our proposed method.

I. Introduction

AS one of the most common neurodegenerative diseases, Alzheimer’s disease (AD) often appears in people over 65 years old, and gradually affects their memory and other brain functions. According to a recent research report from the Alzheimer’s Association [1], the total prevalence of AD is expected to reach 60 million worldwide over the next 50 years. Thus, a lot of research efforts have been devoted to understand the underlying biological or physiological mechanisms of AD [2], [3]. Although there is no effective cure for AD, studies have demonstrated that the diagnosis of its early stage (i.e., Mild Cognitive Impairment (MCI)) is highly desirable in clinical practice, so that early treatments could be administered to possibly slow down the disease progression [4], [5].

Advanced multi-modality neuroimaging technology, such as Magnetic Resonance Imaging (MRI) [2], [6]–[10] and Positron Emission Tomography (PET) [11], [12], have provided unprecedented opportunities for the early diagnosis of AD. In particular, the fusion of multi-modality data has advanced the progress of automatic AD diagnosis, thanks to the complementary information contained within them [12]–[16]. In addition, several Genome-Wide Association Studies (GWAS) have identified a series of genetic variations (e.g., Single Nucleotide Polymorphism (SNP)) associated with AD [17], which are likely to increase the risk of developing the disease [18], [19]. Therefore, it is of interest to develop a prediction model that fuses both neuroimaging (e.g., MRI and PET) and genetic data (e.g., SNP) to further improve the performance of AD diagnosis [20].

In automated AD diagnosis studies using multi-modality data, the feature dimension is usually very high (e.g., tens of thousands) while the number of training samples is limited, i.e., it is a typical small-sample-size problem. To address this issue, previous studies have applied various dimension reduction or feature selection techniques [21], [22] on multi-modality data, to find the most informative feature subset for accurate AD diagnosis. For example, Salas-Gonzalez et al. [22] utilize the statistical t-test method to select voxels of interest for AD diagnosis. Sparse learning based feature selection methods have also been widely applied in AD diagnosis [23], [24]. In addition, many classic feature dimensionality reduction algorithms, e.g., Principal Component Analysis (PCA) [25], Linear Discriminant Analysis (LDA) [26], and Laplacian Preserving Projection (LPP) [27], have been applied to AD status prediction.

Although various feature selection and dimension reduction methods have been proposed, there are still two challenges with automatic AD diagnosis systems using multi-modality neuroimaging (i.e., MRI and PET) and genetic data (i.e., SNP). The first challenge is that it is difficult to exploit the inherent association among multi-modality data. To fuse multi-modality data, conventional methods usually first conduct feature selection for each modality separately and then concatenate the selected features for diagnosis or prognosis. However, such approaches ignore the underlying association between different modalities. Although several classic multi-modality fusion approaches (e.g., Multiple Kernel Learning (MKL) [28] and Canonical Correlation Analysis (CCA) [29]) can exploit the relationship between different modalities, they can only be applied to the complete multi-modality data.

As briefly mentioned above, the second challenge in multi-modality based AD diagnosis system is the missing data issue, i.e., not all the samples have complete multi-modality data. Generally, there are two approaches for dealing with this issue, i.e., 1) discarding the samples with missing values, and 2) imputing the missing values. Several current AD diagnostic models follow the first approach, i.e., they simply discard samples with at least one missing modality and perform disease diagnosis using the remaining samples that have complete multi-modality data. However, this simple strategy not only disregards lots of useful information in the discarded samples, it also escalates the small-sample-size issue. The second approach uses various data imputation techniques (e.g., Zero imputation, k-Nearest Neighbor (KNN), expectation maximization, low-rank matrix completion, etc.) to impute the missing data, so that any diagnostic model that works with complete data can be used. However, this strategy could introduce unnecessary noise and thus reduce the classification performance. Several approaches have also been developed to handle incomplete multi-modality data [7], [30], [31]. However, these approaches do not effectively exploit the correlations across multiple modalities. It is expected to boost diagnostic performance by fusing these multi-modality data.

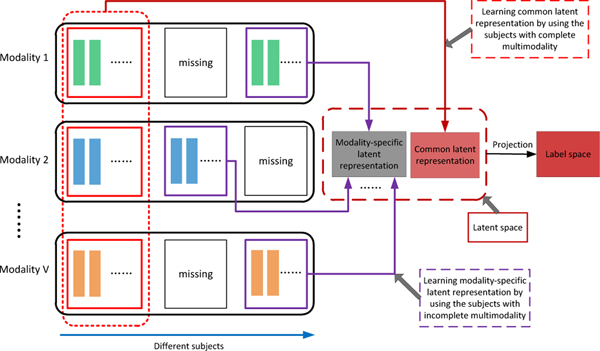
To this end, we propose a novel latent representation learning framework for AD diagnosis (as shown in Fig. 1). Specifically, we assume there exists a latent space for multi-modality data, to which each modality can be projected. The projection from different modalities to this common latent space is expected to model the association among different modalities. That is, we first treat data from each modality (e.g., MRI, PET, and SNP) as explicit features that can reflect different attribute information. For instance, MRI data can provide us with anatomical brain information, while PET and SNP data can provide us with functional brain information and congenital genetic information, respectively. To make full use of all available samples for learning a more reliable prediction model, we utilize samples with complete multi-modality data to learn the common latent feature representation, and utilize samples with incomplete multi-modality data to learn an independent (i.e., modality-specific) latent feature representation for each modality. Furthermore, the learned latent representations are projected to the corresponding label space for AD diagnosis. We evaluate our proposed method on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database, and the experimental results verify its effectiveness.

Fig. 1.

Illustration of our proposed AD diagnosis framework. First, we project original features into a latent representation space. Within this space, we utilize samples with complete multi-modality data to learn a common latent representation, and utilize samples with incomplete multi-modality to learn modality-specific representations. Finally, the latent feature representations are projected to the label space for AD diagnosis.

The key contribution of this paper is three-fold. First, our method performs classification tasks using new feature representations in a latent space, instead of the original features. These new feature representations are expected to be less noisy than the original features, since projecting the original features into the latent space involves sparse feature learning. Second, our method makes use of all the available subjects to train a more reliable model, while the conventional methods usually use only subjects with complete multi-modality data or impute missing values via specific algorithms. Third, we integrate both the latent feature learning and classifier training into a unified framework, while most conventional methods often conduct the two tasks separately.

The rest of this paper is organized as follows. We describe the materials used in this study and present the data preprocessing steps in Section II. Then, we introduce our proposed latent representation learning method in Section III. We further describe experiments in Section IV and provide the related discussion in Section V. Finally, we conclude this paper in Section VI.

II. Materials and Data preprocessing

We used the data from the public ADNI database [32] to evaluate our proposed framework. The ADNI dataset was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and nonprofit organizations with a five-year public-private partnership. The main aim of ADNI is to research the potential of fusing multi-modality data, including neuroimaging, clinical, biological, and genetic biomarkers, to effectively diagnose AD and its early stage.

A. Studied Subjects

In this study, we used 737 subjects from the ADNI-1 database, including 171 AD, 362 MCI, and 204 normal control (NC) subjects. For MCI subjects, we further labeled those who progressed to AD after a certain period of time as progressive MCI (pMCI) subjects, and those who remained stable as stable MCI (sMCI) subjects. In this study, there are 205 sMCI subjects and 157 pMCI subjects. All the studied subjects have baseline MR images acquired at the first screening time (i.e., the baseline time-point). Among them, only 360 subjects have baseline PET data. Table I shows the demographic information of the studied subjects.

TABLE I.

Demographic information of the baseline subjects in this study (MMSE: mini-mental state examination).

	Female/male	Education	Age	MMSE
NC	92 / 112	15.9 ± 3.0	76.1 ± 4.9	29.1 ± 1.0
sMCI	68 / 137	15.8 ± 3.1	75.1 ± 7.6	27.4 ± 1.6
pMCI	62 / 95	16.1 ± 2.5	74.8 ± 7.0	26.9 ± 1.8
AD	77 / 94	14.5 ± 3.7	75.5 ± 7.7	23.7 ± 1.9

B. Data Preprocessing

In this study, we downloaded 1.5T MR images from the ADNI website¹. The MR images were collected using a variety of scanners with protocols customized to each scanner. For quality control, ADNI reviewed the MR images and corrected them for spatial distortion caused by B1 field inhomogeneity and gradient nonlinearity. Following previous studies [33], we further processed these MR images and extracted ROI-based features. Specifically, the MR images were processed under the following steps: 1) anterior commissure-posterior commissure (AC-PC) correction using MIPAV software², 2) intensity inhomogeneity correction using the N3 algorithm [34], 3) brain extraction using a robust skull-stripping algorithm [35], 4) cerebellum removal, 5) tissues segmentation using the FAST algorithm in the FSL package [36] to obtain three main tissues (i.e., white matter (WM), gray matter (GM), and cerebrospinal fluid), 6) registration to a template [37] using the HAMMER algorithm [38], and 7) ROI labels projection from the template image to the subject image. Finally, we computed the GM tissue volume of each ROI in the labeled image, and normalized them with the intracranial volume as the ROI-based feature representation for each subject. Moreover, for each subject, we first aligned PET images to their corresponding T1 MR images using affine registration, and then computed the average PET intensity value of each ROI as a feature representation. Using a template with 93 ROIs [37], we obtained a 93-dimensional ROI-based feature vector from a specific type of neuroimaging data (i.e., MRI or PET) for each subject.

Genetic variations can provide us microscopic information about AD. In this study, the SNP data were genotyped using the Human 610-Quad BeadChip. According to the AlzGene database³, only SNPs belonging to the top AD gene candidates were selected. The selected SNPs were imputed to estimate the missing genotypes, and Illumina annotation information was used to select a subset of SNPs [39].

III. Methodology

In this section, we provide the details of the proposed AD diagnosis framework, and then present the optimization algorithm, as well as the model prediction steps.

A. Formulation

Let $\mathbf{X}\in {ℝ}^{d\times n}$ denote a feature matrix, where d and n indicate the feature dimension and the number of subjects, respectively, and $\mathbf{Y}\in {ℝ}^{l\times n}$ denote the corresponding label matrix, with l being the total number of classes. The least square regression model with multi-class group sparse feature selection method is given as

$$\underset{\mathbf{W}}{\min }\parallel {\mathbf{W}}^{\top }\mathbf{X}-\mathbf{Y}{\parallel }_F^2+\beta \parallel \mathbf{W}{\parallel }_{2,1},$$ (1)

where $\mathbf{W}\in {ℝ}^{d\times l}$ is a regression coefficient matrix, ⊤ denotes the transpose operator, $\parallel \cdot {\parallel }_F$ denotes the Frobenius norm, $\parallel \cdot {\parallel }_{2,1}$ denotes the ℓ_2,1-norm, i.e., $\parallel \mathbf{W}{\parallel }_{2,1}={\sum }_i^d\sqrt{{\sum }_j^l{w}_{ij}^2}$, and β is a trade-off parameter that is used to balance the reconstruction error (the first term) and the regularizer (the second term). The ℓ_2,1-norm regularizer has been widely applied to multi-task feature learning [40]–[42], and is used to penalize the coefficients in each row of W, so that only certain rows in W are non-zeros. In Eq. (1), the optimal solution assigns relatively large weights to informative features while zero or small weights to uninformative or less informative features.

For multi-modality data fusion, as in our case, Eq. (1) can be extended to

$$\underset{{\mathbf{W}}_v}{\min }\sum _{v=1}^V\parallel {\mathbf{W}}_v^{\top }{\mathbf{X}}_v-\mathbf{Y}{\parallel }_F^2+\beta \parallel {\mathbf{W}}_v{\parallel }_{2,1},$$ (2)

where V is the number of modalities, and X_v denotes feature matrix for the v-th modality. In Eq. (2), the original features from different modalities are projected into the label space without considering the correlation among different modalities. However, we know that both neuroimaging and genetic features are related in some ways, as they are directly and indirectly associated with the AD disease label, respectively, thus giving different views for the AD prediction task. Hence, we hypothesize that there exists a common latent feature space for those modalities, which contains information from different perspectives and gives us a more comprehensive view of the AD prediction task. Thus, we extend Eq. (2) into the following formulation as

$$\begin{gathered} \underset{{\mathbf{W}}_v,{\mathbf{E}}_v,\mathbf{H},\mathbf{P}}{\min }\frac{1}{2}\parallel \mathbf{P}\mathbf{H}-\mathbf{Y}{\parallel }_F^2+\gamma \sum _{v=1}^V\Vert {\mathbf{W}}_v^{\top }{\mathbf{X}}_v-\mathbf{H}{\Vert }_F^2 \\ +\beta \sum _{v=1}^V\parallel {\mathbf{W}}_v{\parallel }_{2,1}+\frac{\eta }{2}\parallel \mathbf{P}{\parallel }_F^2. \end{gathered}$$ (3)

Furthermore, to alleviate outlier effect in latent space learning, we adopt the ℓ₁-norm to replace the Frobenius norm. Thus, the objective function in Eq. (3) is transformed to

$$\begin{gathered} \begin{array}{c}\underset{{\mathbf{W}}_v,{\mathbf{E}}_v,\mathbf{H},\mathbf{P}}{\min }\frac{1}{2}\parallel \mathbf{P}\mathbf{H}-\mathbf{Y}{\parallel }_F^2+\beta \sum _v^V\parallel {\mathbf{W}}_v{\parallel }_{2,1}\\ +\gamma \sum _v^V\parallel {\mathbf{E}}_v{\parallel }_1+\frac{\eta }{2}\parallel \mathbf{P}{\parallel }_F^2,\end{array} \\ s.t.{\mathbf{W}}_v^{\top }{\mathbf{X}}_v=\mathbf{H}+{\mathbf{E}}_v,\forall v\in \{1,2,\cdots ,V\}, \end{gathered}$$ (4)

where β, γ and η are the regularization parameters, $\mathbf{H}\in {ℝ}^{h\times n}$ is the common latent feature representation for all modalities, ${\mathbf{W}}_v\in {ℝ}^{d_v\times h}$ is a feature projection matrix for the v-th modality, ${\mathbf{E}}_v\in {ℝ}^{h\times n_v}$ is the sparse error matrix for the v-th modality, and $\mathbf{P}\in {ℝ}^{l\times h}$ is a label projection matrix that projects the common latent feature representation to the label space. Note that the dimensions of the coefficient matrix W_v in Eq. (4) and Eq. (2) are different, where W_v in Eq. (2) maps the v-th feature matrix to the label space directly, while W_v in Eq. (4) maps the v-th feature matrix to a common latent space H, which will be subsequently mapped to the label space via P. The equality constraints in Eq. (4) are used to enforce different modality data of the same subject to have a common feature component (H) and a modality specific discrepancy component (E_v) after they are projected by W_v. Furthermore, assuming that the discrepancy component is sparse, we impose ℓ₁-norm on E_v, while Frobenius norm is imposed on P to limit the magnitudes of its coefficient values.

In addition, to preserve the local structure of the data after the projection (i.e., to preserve the local neighborhood of the samples before and after the projection), we add a Laplacian regularizer in Eq. (4), given as

$$\begin{gathered} \underset{{\mathbf{W}}_v,{\mathbf{E}}_v,\mathbf{H},\mathbf{P}}{\min }\frac{1}{2}\parallel \mathbf{P}\mathbf{H}-\mathbf{Y}{\parallel }_F^2+\lambda \sum _{v=1}^V\text{tr}\left({\mathbf{W}}_v^{\top }{\mathbf{X}}_v{\mathbf{L}}_v{\left({\mathbf{W}}_v^{\top }{\mathbf{X}}_v\right)}^{\top }\right) \\ +\beta \sum _{v=1}^V\parallel {\mathbf{W}}_v{\parallel }_{2,1}+\gamma \sum _{v=1}^V\parallel {\mathbf{E}}_v{\parallel }_1+\frac{\eta }{2}\parallel \mathbf{P}{\parallel }_F^2, \\ s.t.{\mathbf{W}}_v^{\top }{\mathbf{X}}_v=\mathbf{H}+{\mathbf{E}}_v,\forall v\in \{1,2,\cdots ,V\}, \end{gathered}$$ (5)

where the second term is the Laplacian regularization term, which is added to ensure that similar inputs have similar latent feature representations, and λ is its regularization parameter. Specifically, the Laplacian matrix is given as L_v = D_v − S_v, where D_v is a diagonal matrix with its i-th diagonal element denoting the sum of the i-th row in S_v. S_v is a similarity matrix for the v-th modality, whose (i, j)-th element is given as exp($-\parallel {\mathbf{X}}_{v,:i}-{\mathbf{X}}_{v,:j}{\parallel }_2^2/\sigma$), where X_v,:i and X_v,:j denote the i-th column and the j-th column of X_v, respectively, and σ = 1 is empirically set in this study.

So far, the proposed method in Eq. (5) can only be applied to subjects with complete multi-modality data, i.e., each modality has the same number of samples, $n=n_v,\forall v=\{1,2,\cdots ,V\}$. However, using Eq. (5), subjects with incomplete multi-modality data will be discarded. Intuitively, using more samples for model training should result in a more reliable prediction model. To make the joint latent feature learning model in Eq. (5) applicable to incomplete multi-modality data, we have to make some modifications. First, we decompose X_v into two parts, one with complete multi-modality data, and the other with incomplete multi-modality data, i.e., ${\mathbf{X}}_v=\left[{\mathbf{X}}_v^c,{\mathbf{X}}_v^{\overline{c}}\right]\in {ℝ}^{d_v\times \left(n^c+n_v^{\overline{c}}\right)}$, where $n_v=n^c+n_v^{\overline{c}}$ is the total number of samples in v-modality. Note that the number of complete multi-modality data, denoted by n^c, is the same for each X_v. Then, the corresponding label for X_v is given by ${\mathbf{Y}}_v=\left[{\mathbf{Y}}^c,{\mathbf{Y}}_v^{\overline{c}}\right]$. Similarly, the matrix H in the constraint of Eq. (5) is also decomposed into two parts, i.e., ${\mathbf{H}}_v=\left[{\mathbf{H}}^c,{\mathbf{H}}_v^{\overline{c}}\right]\in {ℝ}^{h\times \left(n^c+n_v^{\overline{c}}\right)}$, where H^c denotes the latent feature representation for the complete multi-modality data, and ${\mathbf{H}}_v^{\overline{c}}$ denotes the latent feature representation for the remaning v-th modality data (other than that included in H^c).

Using the notations above, we extend Eq. (5) to

$$\begin{gathered} \underset{{\mathbf{W}}_v,{\mathbf{E}}_v,\mathbf{H},\mathbf{P}}{\min }\frac{1}{2}\parallel \mathbf{P}\left[{\mathbf{H}}^c,{\mathbf{H}}_1^{\overline{c}},\dots ,{\mathbf{H}}_V^{\overline{c}}\right]-\left[{\mathbf{Y}}^c,{\mathbf{Y}}_1^{\overline{c}},\dots ,{\mathbf{Y}}_V^{\overline{c}}\right]{\parallel }_F^2 \\ +\lambda \sum _v^V\text{tr}\left({\mathbf{W}}_v^{\top }\left[{\mathbf{X}}_v^c,{\mathbf{X}}_v^{\overline{c}}\right]{\mathbf{L}}_v{\left({\mathbf{W}}_v^{\top }\left[{\mathbf{X}}_v^c,{\mathbf{X}}_v^{\overline{c}}\right]\right)}^{\top }\right) \\ +\beta \sum _v^V\parallel {\mathbf{W}}_v{\parallel }_{2,1}+\gamma \sum _v^V\parallel {\mathbf{E}}_v{\parallel }_1+\frac{\eta }{2}\parallel \mathbf{P}{\parallel }_F^2, \\ s.t.{\mathbf{W}}_v^{\top }\left[{\mathbf{X}}_v^c,{\mathbf{X}}_v^{\overline{c}}\right]=\left[{\mathbf{H}}^c,{\mathbf{H}}_v^{\overline{c}}\right]+{\mathbf{E}}_v,\forall v\in \{1,2,\cdots ,V\}, \end{gathered}$$ (6)

where $\mathbf{H}=\left[{\mathbf{H}}^c,{\mathbf{H}}_1^{\overline{c}},\dots ,{\mathbf{H}}_V^{\overline{c}}\right]$ is the latent representation matrix for all the samples. Note that the latent representation ${\mathbf{H}}_v^{\overline{c}}$ is specific to the v-th modality, as it is not shared with other modalities like H^c. Thus, we also refer to ${\mathbf{H}}_v^{\overline{c}}$ as the modality-specific latent representation.

Using Eq. (6), we can include all the data from the dataset, regardless of modality completeness when training the model, i.e., to learn W_v and P. All the modalities are projected to a common latent feature space via W_v, and P is the classifier coefficient matrix that predicts disease label from the data point in the latent feature space. For clarity, the notations used in Eq. (6) are summarized in Table. II.

TABLE II.

The main notations used in the proposed formulation in Eq. (6).

otation	Size	Description
${\mathbf{X}}_v^c$	dv × nc	The v-th modality feature matrix for samples with complete multi-modality data
${\mathbf{X}}_v^{\overline{c}}$	$d_v\times n_v^{\overline{c}}$	The v-th modality feature matrix for samples with incomplete multi-modality data
Wv	dv × h	Projection matrix for the v-th modality
Hc	h × nc	Latent feature representation for samples with complete multi-modality data
${\mathbf{H}}_v^{\overline{c}}$	$h\times n_v^{\overline{c}}$	Label matrix for samples with complete multi-modality data
Yc	l × mc	Label matrix for samples with complete multi-modality data
${\mathbf{Y}}_v^{\overline{c}}$	$l\times n_v^{\overline{c}}$	Label matrix for samples with complete multi-modality data Label matrix of the v-th modality for samples with incomplete multi-modality data
P	l × h	Projection matrix from the learned latent feature representation to the label space
dv	–	Feature dimension of the v-th modality
nv	–	Number of samples with the v-th modality
nc	–	Number of samples with complete multi-modality data
$n_v^{\overline{c}}$	–	Number of samples with the v-th modality excluding samples with complete multi-modality data
h	–	Dimension of the latent feature representation
l	–	Number of classes
V	–	Number of multi-modality data
λ, β, γ, η	–	Regularization parameters

B. Optimization and Model Prediction

The objective function in Eq. (6) is not jointly convex with respect to all variables. Therefore, we utilize the Augmented Lagrange Multiplier (ALM) [43] algorithm to solve the problem efficiently and effectively. The detailed optimization steps are provided in the Supplementary Materials of this manuscript. After training our model, we can obtain the feature projection matrix W_v for the v-th modality, and the label projection matrix P. For a given testing sample x^te with Ω available modalities, the latent feature representation is computed by averaging the feature projections from each available modality, i.e., ${\mathbf{h}}^{te}=\frac{1}{|\text{Ω}|}{\sum }_{v\in \text{Ω}}{\mathbf{W}}_v{\mathbf{x}}_v^{te}$, where |Ω| denotes the number of modalities in Ω. Consequently, the final classification label for this test sample is given as y^te = Ph^te.

IV. Experiments

In this section, we first describe the parameter settings of our method and the comparison methods. Then we report the classification performance of all the comparison methods, and show the results using different combinations of modalities. In addition, we show classification results using incomplete multi-modality data with different missing rates.

A. Experimental Setup

We evaluate our method using the ADNI dataset for two multi-class classification tasks, including 1) NC vs. MCI vs. AD (i.e., three-class classification task), and 2) NC vs. sMCI vs. pMCI vs. AD (i.e., four-class classification task). In addition, as it is important to distinguish progressive MCI from stable MCI for early diagnosis, we also evaluated our proposed method for the sMCI vs. pMCI classification task. Using only the complete multi-modality data (i.e., subjects with no missing modality), we first compare the proposed method with several conventional methods, the details of which are briefly introduced below.

• Baseline method. We conduct an experiment using only the original features without performing any feature selection (denoted as “Baseline”).

• Feature reduction (or selection) methods. Three comparison methods are used in this category, namely 1) Principal Component Analysis (PCA) [25], 2) Locality Preserving Projection (LPP) [27], and 3) the ℓ_2,1-norm based feature selection method as described in Eq. (2), which is denoted as “L21”. For PCA and LPP, we determined the optimal dimensionality of the data based on the eigenvalues computed using the generalized eigen-decomposition method described in [44]. For the L21 method, we optimize its sparsity parameter (λ) by cross-validating its value in the range of {10⁻⁴, . . . , 10²}.

• Modality (or feature) fusion methods. Two comparison methods in this category are used, i.e., 1) CCA [45] and 2) MKL [28]. For CCA, we optimize the regularization parameter by cross-validating its value in the range of {10⁻⁴, . . . , 10²}. For MKL, we optimize the normalized weight parameter for each modality by cross-validating its value in the range of {0, . . . , 1}.

• Deep learning based feature representation method. In this category, we compare our method with the Stacked Auto-Encoder (SAE) [46] method. In SAE, the main parameter to be determined is the number of hidden units. Following [46], we build a three-layer network with multi-modality data input using a grid search from [100, 300, 500]-[50, 100]-[10, 20, 30] (bottom-top).

Furthermore, to verify the advantage of our proposed method in handling the missing data issue in the testing phase, we also compare it with the following state-of-the-art methods.

• Data imputation methods. 1) Zero imputation. In this method, the missing values are filled with zeros. Since all the features are z-normalized (i.e., subtract the mean and divide by the standard deviation) before the imputation process, this method is equivalent to filling the missing feature values with the average observed values. 2) k-Nearest Neighbor (KNN) imputation [47]. In this method, the missing values are filled with the weighted mean of the k nearest-neighbor samples. Following [7], the weights are inversely proportional to the Euclidean distances between the neighboring samples. 3) Low-rank Matrix Completion (LRMC) [48], [49] based imputation method. This was proposed to recover missing data from a limited number of samples. After data imputation, we employe a linear SVM to perform disease classification in these three methods.

• Incomplete Multi-Source Feature learning (iMSF) method [30], [31]. This is a multi-task learning method, which first partitions the data into several groups according to the availability of modalities, and treats the learning of a classifier for each group of data as a task. A joint sparse learning model is then employed to select a common set of features among all these tasks. There are two versions of iMSF, which use different loss functions, i.e., the least square loss (denoted as “iMSF-R”) and the logistic loss (denoted as “iMSF-L”). Note that the source code of the iMSF method is designed for binary classification tasks, and here we adopt a one-vs-all strategy for multi-class classification tasks.

• Doubly Aligned Incomplete Multi-view Clustering (DAIMC) method [50]. This is a clustering method that is designed for incomplete multi-modality data using weighted semi-nonnegative matrix factorization [50]. To apply this method for the classification task, we train a SVM classifier using the learned common latent features in DAIMC.

• Matrix Shrinkage and Completion method (MSC) [7]. This method first partitions the combined matrix (e.g., features and targets) into sub-matrices, where each submatrix consists of samples with complete features (corresponding to a certain combination of modalities) and target outputs. Then, a multi-task sparse learning framework is employed to select informative features and samples. Subsequently, the shrunk combined matrix with missing features and unknown target outputs is imputed via low-rank matrix completion using a fixed-point continuation method [51].

We use a ten-fold cross-validation strategy to evaluate all comparison methods. Specifically, we first randomly partition the whole dataset into ten subsets (with each subset having a roughly equal number of samples), and then select one subset for testing and use the remaining nine subsets for training. We repeat the whole process fifty times to avoid possible bias in dataset partitioning during cross-validation. Thus, the final results are computed by averaging the fifty repetition results. In our proposed method, it would take a significant amount of time if we simultaneously tune five hyper-parameters. In this case, we first tune λ and h by fixing other hyper-parameters. Here, we empirically set λ = 0.01 and h = 30, and then apply a five-fold inner cross-validation to tune values of the other three hyper-parameters, i.e., β, γ, η ∈ {10⁻⁴, 10⁻³, . . . , 10⁴}, in Eq. (6). Note that we use the SVM classifier from the LIBSVM toolbox [52] to perform classification for all the comparison methods (except for iMSF and MSC), and determine the margin parameter C in the SVM classifier using a grid search in the range of {10⁻⁵, 10⁻⁴, . . . , 10³}. Moreover, for fair comparison, we also conduct five-fold inner cross-validation to conduct parameter selection for all the comparison methods. We use classification accuracy (ACC) and Area Under Curve (AUC) to evaluate all the comparison methods, and follow the AUC computation method in [53] for multi-class classification tasks.

The SNP data are high-dimensional, but only parts of SNPs are related to AD, as shown by previous studies [20]. Thus, in order to reduce the computational complexity for the AD prediction task [17], we employ sparse learning to select 100 SNPs. Specifically, we first randomly partition the whole dataset into 10 subsets (with each subset having a roughly equal number of samples), and select one subset for testing, while the remaining nine subsets are used for training. We then use a five-fold inner cross-validation on the training set to select SNPs via a sparse learning method [54]. Finally, we select the top 100 most related SNPs.

B. Classification Results using Complete Multi-modality Data

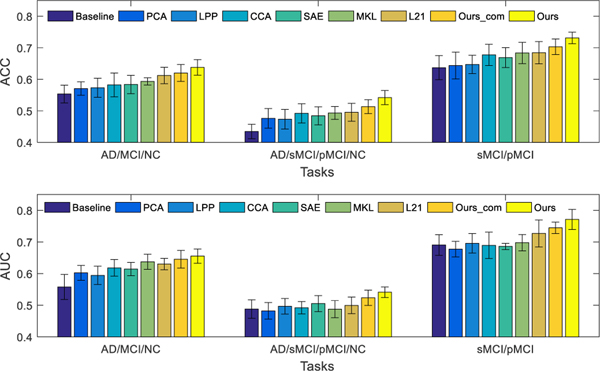
Fig. 2 shows the classification performance of all the competing methods on three classification tasks, using complete multi-modality data (i.e., using only subjects with all three modalities). Here, “Ours_com” denotes our proposed method that uses the samples with only complete multi-modality data to train a model, while “Ours” denotes the proposed method that uses all available samples (including the samples with incomplete multi-modalities). The comparison methods only train models using samples with complete multi-modality data, as they are inapplicable to incomplete dataset.

Fig. 2.

Classification results in terms of ACC (top) and AUC (bottom) achieved by 9 different methods for three classification tasks, i.e., NC vs. MCI vs. AD (left), NC vs. sMCI vs. pMCI/AD (middle), and sMCI vs. pMCI (right), using complete multi-modality data in training and testing (except “Ours”, which denotes our method uses all available samples with incomplete multi-modality data for model training). The error bars denote the standard deviations of the results.

From Fig. 2, we can have following observations. First, our proposed method (i.e., Ours_com) outperforms the three feature selection methods (i.e., PCA, LPP and L21), which implies that the new feature representation learned by our proposed method can help improve the classification performance. It also outperforms modality fusion methods (e.g., CCA and MKL) for all three classification tasks. The comparison results indicate that our method is more effective than both the CCA and MKL methods in exploiting the correlations among different modalities. Additionally, it also outperforms the deep learning based method (i.e., SAE) that learns high-level features for classification. Generally, deep learning based methods can learn “good” features for classification, but the diagnosis performance is likely degraded due to the limited number of samples in this study. Second, the results reported for multi-class classification tasks (i.e., NC vs. MCI vs. AD, NC vs. sMCI vs. pMCI vs. AD) are lower than the performance on the binary classification task (i.e., sMCI vs. pMCI). A possible reason for this is that multi-class classification tasks are much more challenging than binary classification tasks. Also, our proposed method that uses all available data (“Ours”) is better than its degraded version, (“Ours_com”), which only uses complete multi-modality data for training. This shows the advantage of using all available data during the training, rather than discarding samples with incomplete multi-modality data.

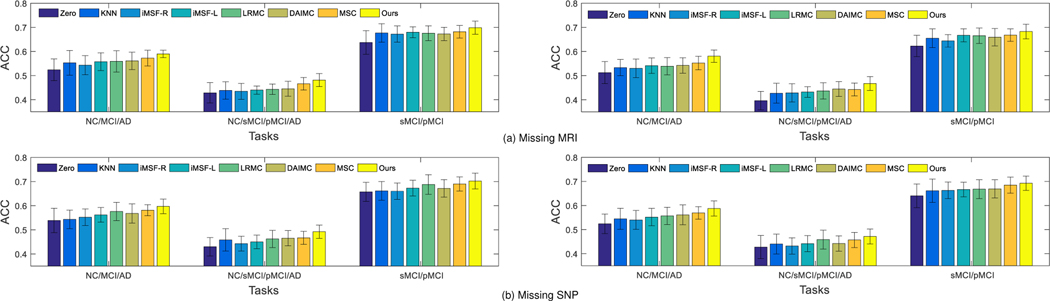
C. Classification Results using Incomplete Multi-modality Data

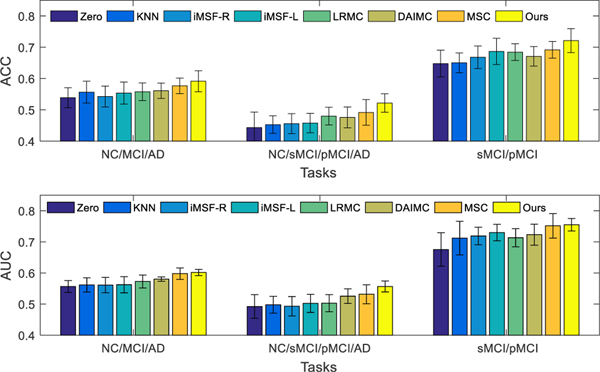
Based on all available subjects with incomplete multi-modality, we perform three classification tasks and report the ACC and AUC results in Fig. 3. The results show that our method outperforms imputation based methods in terms of ACC and AUC. On one hand, this is probably due to the fact that our proposed method does not involve any imputation, and thus avoids imputation errors that may affect the classification model like in the imputation based methods. On the other hand, this may also result from the use of latent feature representations when learning the prediction model, which are less noisy (due to the explicit learning of the error matrix), more discriminative (due to feature selection), and more comprehensive (by considering information from different data views). Thus, introducing the latent feature representation not only solves the missing data problem, but also results in a more accurate prediction model. Our method also performs better than two state-of-the-art methods (i.e., DAIMC and MSC). In addition, we perform the McNemar test between our method and other comparison methods. Specifically, we utilize the “testcholdout” function (Matlab code) to conduct the McNemar test, which returns an h value that indicates whether the two comparison classification models have equal predictive accuracies. That is, h = 0 (accepting the null hypothesis) indicates that the two models have equal predictive accuracies, while h = 1 indicates that the predictive accuracies between the two methods are statistically different. In our experiments, we obtain h = 1 for all the McNemar tests, indicating that the predictions between our method and all comparison methods are significantly different statistically.

Fig. 3.

Classification results in terms of ACC (top) and AUC (bottom) achieved by 8 different methods for three classification tasks, i.e., NC vs. MCI vs. AD (left), NC vs. sMCI vs. pMCI vs. AD (middle), and sMCI vs. pMCI (right), using incomplete multi-modality data in training and testing. The error bars denote the standard deviations of the results.

D. Results Using Different Combinations of Modalities

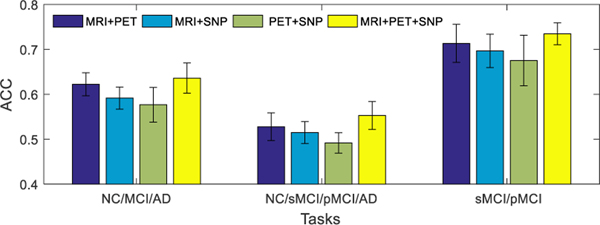
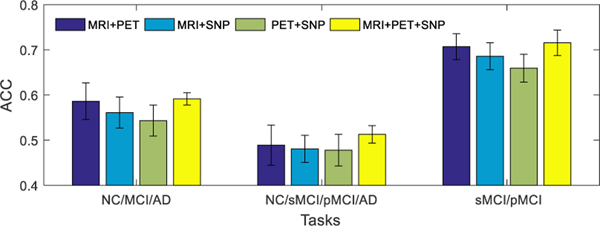
The main aim of this study is to learn the latent feature representations from multiple modalities by exploiting the correlations among them. To further analyze the benefit of fusing multi-modality neuroimaging and genetic data, we show the performance of our proposed method for different combinations of modalities on different classification tasks in Fig. 4 (i.e., results with only complete multi-modality testing data) and Fig. 5 (i.e., results with incomplete multi-modality testing data). From Fig. 4 and Fig. 5, it can be seen that our model using MRI and PET data outperforms the models using other two modality combinations (e.g., MRI and SNP, or PET and SNP). These results show that SNP data is less discriminative in AD status diagnosis. A possible reason could be that the MRI and PET data are the phenotype features that are closely related to diagnostic labels, while the SNP data are genotype features that are relatively less related to diagnostic labels [17], [20]. On the other hand, when all the three modalities are used, our model performs better than the case of using any combination of two modalities.

Fig. 4.

Classification accuracies of the proposed method trained using all available training data (including incomplete multi-modality data), and tested using only complete multi-modality data. Four different combinations of modalities (i.e., MRI+PET, MRI+SNP, PET+SNP, and MRI+PET+SNP) and three different combinations of disease cohorts (or classification tasks) are used in this group of experiments. The error bars denote the standard deviations of results.

Fig. 5.

The classification accuracies of the proposed method, which was trained using all available training data (including incomplete multi-modality data) and tested using all available testing data (including incomplete multi-modality data). Four different combinations of modalities (i.e., MRI+PET, MRI+SNP, PET+SNP, and MRI+PET+SNP) and three different combinations of disease cohorts (or classification tasks) were used in this group of experiments. The error bars denote the standard deviations of results.

E. Study on Different Missing Modalities

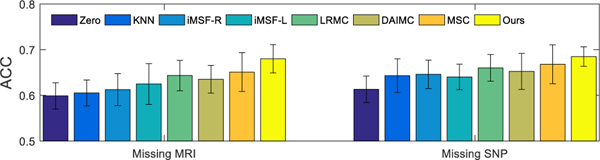
In the aforementioned experiments, we use 737 subjects from the ADNI-1 database, where all subjects have complete MRI scans and only 360 subjects have PET data. To further verify the effectiveness of our method in handling the missing data issue, we randomly discard partial MRI or SNP data. Specifically, we randomly select r% (in this study, we set r = 10, 20) of subjects to discard their MRI or SNP data to simulate the missing data issue for MRI and SNP modalities. Then, we conduct a set of experiments to investigate the performance of different methods in AD diagnosis based on these subjects. The experimental results are shown in Fig. 6. From Fig. 6, it can be seen that our proposed method outperforms all the comparison methods under different missing modalities and different missing rates.

Fig. 6.

Classification accuracy (i.e., ACC) achieved by different methods using data with r% (Left: r = 10; Right: r = 20) subjects associated with missing MRI (top) or SNP (bottom) data. The error bar denotes the standard deviation of the results.

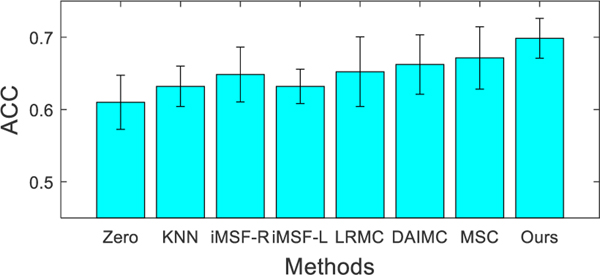
To verify the effectiveness of our proposed method in handling problems with more missing data (e.g., r=50), we include a second set of experiments with 50% MRI or PET data being missing. That is, half of the studied subjects have missing MRI or SNP data. Fig. 7 shows the comparison results obtained by using different methods for sMCI/pMCI classification. From Fig. 7, it can be seen that our proposed method outperforms all the comparison methods.

Fig. 7.

Classification accuracy (i.e., ACC) achieved by different methods when 50% subjects are with missing MRI (left) or SNP (right) in sMCI/pMCI classification.

Further, we also include a set of experiments when 50% of subjects have no both MRI and SNP data (i.e., only the PET data available) for sMCI/pMCI classification task. Among all 362 subjects in sMCI/pMCI classification, only 185 subjects have the PET data. Therefore, we first select 50% of these 185 subjects and discard both their MRI and SNP data (i.e., these subjects now only have PET data). Fig. 8 shows the comparison results, which further verifies the effectiveness of our method in dealing with the cases when more modalities are missing.

Fig. 8.

Classification accuracy (i.e., ACC) achieved by different methods when half of the subjects are missing both MRI and SNP in sMCI/pMCI classification.

V. Discussion

In this section, we first investigate the influences of different parameters and present the most discriminative ROIs and SNPs identified by our proposed method. Then, we compare our method with several state-of-the-art methods, and provide the differences between our method and several related approaches. Finally, we discuss several limitations of our model.

A. Influences of Parameters

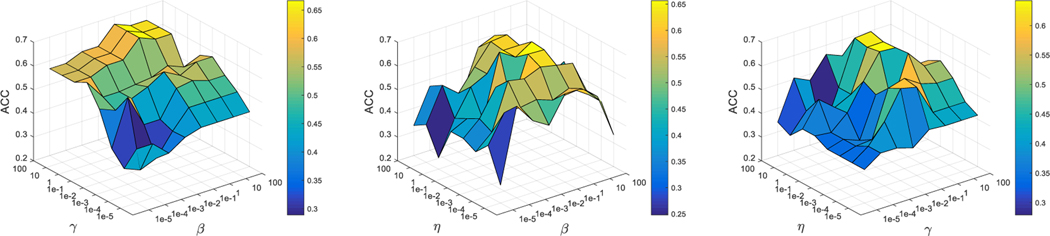
In this section, we study the effects of hyper-parameters (i.e., β, γ, and η). Specifically, we set the values of these parameters in the range of {10⁻⁵, 10⁻⁴, . . . , 10²} for each experiment. We fix the value of one parameter and tune the other two parameters. As an example, Fig. 9 shows the classification accuracy (of the testing samples with complete multi-modality data) achieved by our method for the NC/MCI/AD classification task using different parameter values. From Fig. 9, the experimental results demonstrate that our proposed method obtains better classification results when the values of β, γ, and η fall in [0.1, 10], [1, 10], and [0.1, 10], respectively.

Fig. 9.

Classification accuracies of our proposed method for the NC/MCI/AD classification task using different settings of hyper-parameters, i.e., β, γ, η ∈ {10⁻⁵, . . . , 10²}.

B. Most Related ROIs and SNPs

Based on the formulation in the proposed model (see Eq. (5)), it is expected that when the optimal weight matrices (i.e., W_v) are found, a small or even zero weight will be assigned to uninformative or less informative feature, while a larger weight will be assigned to more informative feature. For example, for the v-th modality, the element in the learned W_v denotes the contribution of the original feature in the latent space. To study which ROIs/SNPs are selected by our proposed method, we rank the absolute values of all the elements in W_v, and then report the top elements (with each element corresponding to a specific ROI/SNP) that are frequently selected across all folds.

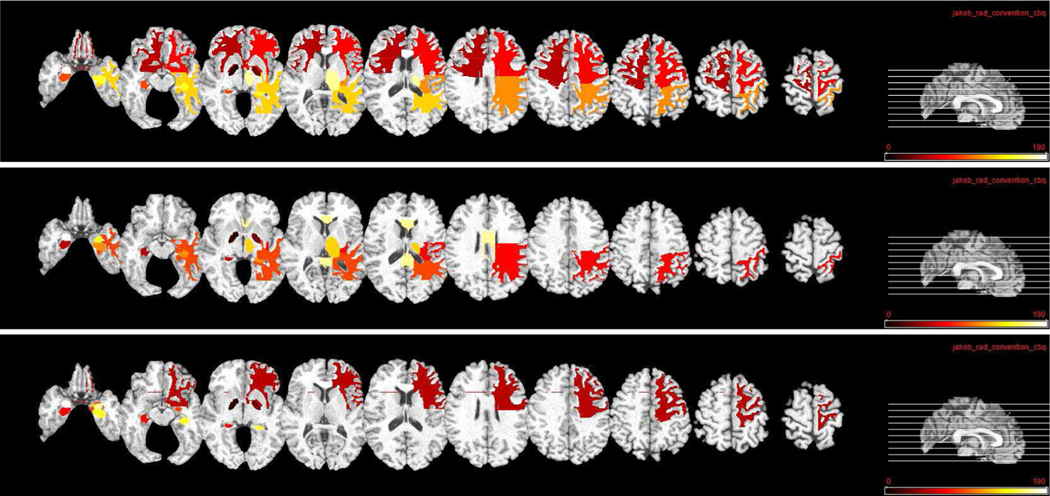
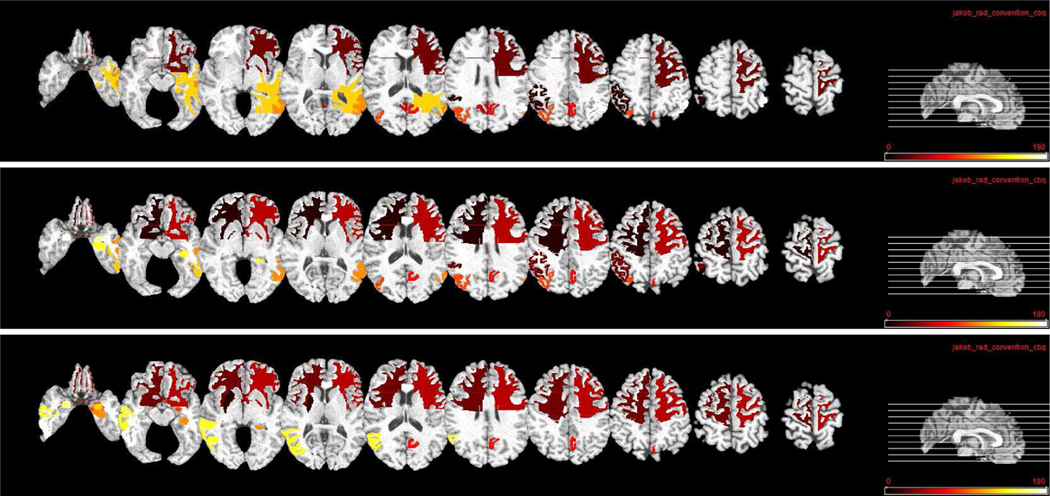
We show the top ten most related ROIs for MRI and PET data in three classification tasks in Fig. 10 and Fig. 11, respectively. Fig. 10 shows that, hippocampal, amygdala, globus, and lobe WM regions are identified as most related ROIs for AD diagnosis for MRI data. This is consistent with several previous studies which also show that these regions are highly related to AD and MCI classification [44], [55], [56]. For PET data, Fig. 11 shows that precuneus, gyrus, and hippocampal regions are identified as discriminative ROIs for AD and early MCI diagnosis. Again, these identified ROIs are consistent with those reported in previous AD-related studies [20], [44], [57].

Fig. 10.

Top ten selected ROIs for MRI data in three classification tasks. From top to bottom: NC/MCI/AD, NC/sMCI/pMCI/AD, and sMCI/pMCI. Here, different colors denote different ROIs.

Fig. 11.

Top ten selected ROIs for PET data in three classification tasks. From top to bottom: NC/MCI/AD, NC/sMCI/pMCI/AD, and sMCI/pMCI. Here, different colors denote different ROIs.

In Table S2 of the Supplementary Materials, we report those most related ROIs that are frequently selected by our method for the three classification tasks. We also include the color bar to visualize the correspondence between the color and the selected ROI in Fig. S1 and Table S2 of the Supplementary Materials. We further report the top five discriminative SNPs that are most frequently identified by our method, which include rs429358, rs10740220, rs2298525, rs7073924, and rs11655156. These genes have been reported to be related to AD in previous studies [17], [58]–[60]. These results suggest that our method is able to identify the most relevant SNPs for AD and early MCI diagnosis. The top 100 selected SNPs can be found in Table S1 of the Supplementary Materials.

C. Comparison With State-of-the-art Methods

We compare the results achieved by our proposed method with those obtained by other state-of-the-art methods that use ADNI subjects. Since very few studies are conducted on multi-class classification tasks, we only report the result of sMCI vs. pMCI classification in Table III. As can be seen, our proposed method generally outperforms other comparison methods [4], [46], [61]–[63] on the sMCI vs. pMCI classification task. The main reason is that our method projects the original features from multi-modality data into a latent space which provides more comprehensive views for improving diagnosis performance.

TABLE III.

Comparison with state-of-the-art methods on sMCI vs. pMCI Classification.

Method	Modality	ACC	AUC
Feature-trans [61]	MRI	0.721	–
Modal-fusion [62]	MRI+CSF	0.685	–
Suk et al. [46]	MRI+PET	0.733	–
Thung et al. [4]	MRI+PET	0.737	–
Liu et al. [63]	MRI+PET	0.733	0.716
Ours	MRI+PET+SNP	0.743	0.755

D. Comparison with Previous Studies

Our proposed method is similar to but different from several previous studies [64]–[66]. First, previous methods [64]–[66] typically conduct the clustering task by first learning common representations and then applying a spectral clustering algorithm on the representation. Different from [64]–[66], our method conducts the latent representation learning and model training in a unified framework, thus seamlessly integrating them together. In this way, a “good” latent representation helps to induce a better classification model, and in return a more accurate prediction model will promote the learning of more discriminative latent representations. However, previous methods [64]–[66] have ignored the underlying relationship between latent representation learning and model training. Second, we utilize the ℓ₁-norm [67]–[71] to alleviate the outlier (e.g., noise) issue in latent space learning, while these methods [64]–[66] do not consider this issue. Intuitively, our method should be more robust to outliers (e.g., noises), resulting in improved classification performance in comparison with previous studies. Third, we adopt the ℓ_2,1 constraint on the projection matrices to ensure that the discriminative features have much larger contributions to the latent learning across different modalities. In contrast, the methods in [64]–[66] do not consider this point. We further compare our method with the Partial Multi-View Clustering (PVC) method [64] on the sMCI vs. pMCI classification task, with the comparison results shown in Fig. S2 of the Supplementary Materials.

E. Limitations

Although our proposed method achieves promising results in AD and early MCI diagnosis, there are several technical issues to be addressed in future work. First, a linear projection is employed in our model, but it may not be effective to model the complex brain patterns. As such, a non-linear projection can be applied to our formulation in the future. Second, we could extend the proposed model for dealing with the problem of incomplete multi-modality data using a deep learning framework to further improve the classification performance, since deep neural network based features are typically more discriminative than hand-crafted features.

VI. Conclusion

In this paper, we propose a novel AD diagnosis framework with latent feature representation learning. Specifically, we first project multi-modality data to a latent feature space, to exploit the underlying association among different modalities. To make use of all available samples to learn an accurate AD prediction model from the incomplete multi-modality dataset, we utilize samples with complete multi-modality data to learn the common latent feature representation, and also utilize samples with the incomplete multi-modality data to learn the modality-specific latent feature representation. Finally, the learned latent feature representations can be linearly projected to the label space for AD diagnosis. Experimental results demonstrate the effectiveness of our proposed method. In future work, our method can be also applied to other diagnosis tasks, such as for schizophrenia [72].