Frustrated folding of guanine quadruplexes in telomeric DNA

Abstract

Human chromosomes terminate in long, single-stranded, DNA overhangs of the repetitive sequence (TTAGGG)n. Sets of four adjacent TTAGGG repeats can fold into guanine quadruplexes (GQ), four-stranded structures that are implicated in telomere maintenance and cell immortalization and are targets in cancer therapy. Isolated GQs have been studied in detail, however much less is known about folding in long repeat sequences. Such chains adopt an enormous number of configurations containing various arrangements of GQs and unfolded gaps, leading to a highly frustrated energy landscape. To better understand this phenomenon, we used mutagenesis, thermal melting, and global analysis to determine stability, kinetic, and cooperativity parameters for GQ folding within chains containing 8–12 TTAGGG repeats. We then used these parameters to simulate the folding of 32-repeat chains, more representative of intact telomeres. We found that a combination of folding frustration and negative cooperativity between adjacent GQs increases TTAGGG unfolding by up to 40-fold, providing an abundance of unfolded gaps that are potential binding sites for telomeric proteins. This effect was most pronounced at the chain termini, which could promote telomere extension by telomerase. We conclude that folding frustration is an important and largely overlooked factor controlling the structure of telomeric DNA.

Graphical Abstract

Graphical Abstract.

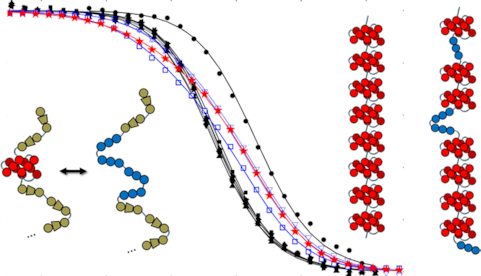
Mutagenesis, thermal melts and computational analyses show that folding frustration is a key determinant of guanine quadruplex folding in long telomeric repeat DNA.

INTRODUCTION

DNA G-quadruplexes (GQs) are structures adopted by deoxyguanine (dG)-rich nucleic acids. They are typically composed of four G-tracts of three or more consecutive dGs connected by loop sequences. The tracts come together to form G-tetrads, planes of four Hoogsteen-hydrogen bonded dGs that are stacked to form the core GQ structure (1–3) (Figure 1A). GQ-forming DNA sequences are found in oncogene promoters where they are involved in the regulation of gene expression (4). They are also abundant in telomeres, DNA/protein structures located at the ends of chromosomes which protect the genetic material (5). The telomeric DNA is shortened after each round of replication, ultimately triggering cell senescence (6). This process is reversed by the enzyme telomerase, which elongates telomeres and thus modulates cell aging. Healthy differentiated cells are characterized by extremely low telomerase activity (7). Conversely, cancer cells usually overexpress telomerase, which is closely linked to their immortalization (8). Human telomerase extends telomeres by adding units of d(TTAGGG) to the 3′ end of the DNA. Telomeric DNA therefore consists of 5–25 kb of this repeated sequence, with a single-stranded overhang of 35–600 nucleotides (9–11). d(TTAGGG)₄ closely matches the GQ consensus motif (12) and it has long been known that telomeric DNA forms GQs in vitro (13) and in vivo (14–16). GQ folding at the 3′ end of the telomere inhibits telomerase activity (17) and may also control binding of helicases and telomerase activity regulators such as POT1 and SSB1 (18). Consequently, telomeric GQs are regarded as potential drug targets (19), and understanding of how GQs fold in the context of the telomeric DNA is of great importance.

Figure 1.

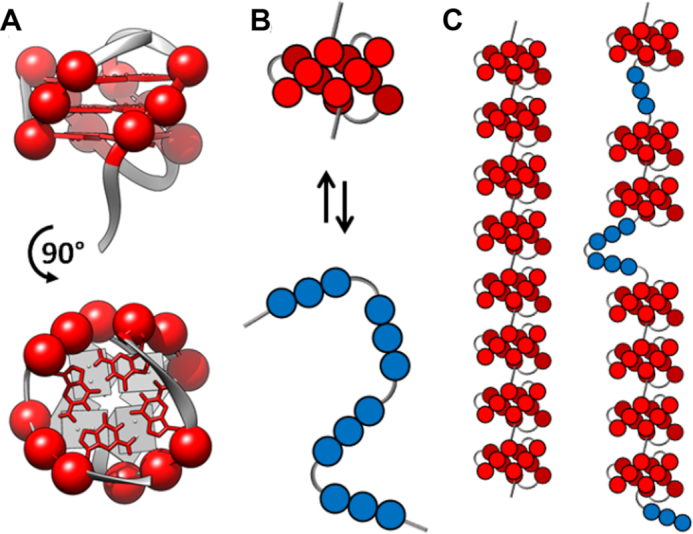
(A) Ribbon representation of a telomeric GQ structure (PDB 2JPZ (20)). Nucleobases and C3′ atoms for guanine residues are shown as red sticks and spheres, respectively. (B) Cartoon representation of the transition between folded (red) and unfolded (blue) states of a GQ. Each G-tract is represented by three consecutive circles. (C) 8-GQ and 7-GQ forms of a 32 telomeric repeat Tel₃₂ DNA sequence.

There have been numerous studies delineating the relationship between nucleotide sequence and solution conditions on GQ stability (21,22), topology (23) and folding pathways for DNA strands containing four G-tracts (24–26). However much less is known about how the highly repetitive nature of telomeric DNA affects GQ folding. In principle, the presence of large numbers of tandem G-tracts significantly complicates the folding landscape. For a DNA strand containing 4 telomeric repeats (Tel₄), folding is well-approximated as a two-state process (Figure 1B) (27,28). Although partly-structured intermediates and alternative folded topologies (29,30) can be populated to some extent, the folding landscape is dominated by the equilibrium between folded and unfolded states. For a longer sequence containing, for example, 32 telomeric repeats (Tel₃₂), the lowest energy conformation under physiological conditions has 8 consecutive folded GQs (Figure 1C). However there exists a great abundance of alternative folding arrangements with only slightly higher energies, potentially leading to a highly frustrated energy landscape (31). To illustrate, reorganization of the 7-GQ folding arrangement in Figure 1C into the 8-GQ ground-state structure requires the unfolding of at least six folded GQs. This effect, which we will refer to as kinetic frustration, could introduce large energy barriers that trap tandem sequences in a variety of misfolded states, strongly hindering the system from reaching equilibrium. Similarly, if the number of misfolded states is sufficiently large, then despite having the lowest energy, the ground state may be only sparsely populated at equilibrium, an effect we refer to as thermodynamic frustration.

In order to better understand how a frustrated energy landscape influences the folding of telomeric DNA, we used a combination of mutagenesis, thermal melt, and hysteresis analyses to dissect the folding pathways of Tel₄, Tel₈ and Tel₁₂ DNA, whose ground states contain one, two and three GQs, respectively. These measurements yielded the thermodynamic stabilities of all fully folded and partly folded states as well as the kinetic rate constants describing their interconversion. This, in turn, gave all the information necessary for quantitative modelling of longer telomeric DNA, using a combination of statistical mechanical theory, discrete time Markov chain, and Monte Carlo simulations. The experimental data for the shorter DNA sequences showed evidence of both kinetic and thermodynamic folding frustration. The models of longer telomeric sequences exhibited much more pronounced effects. Folding frustration significantly interfered with GQ formation. This led to an apparent 9-fold destabilization of G-tracts in long repeats compared to those in individual Tel₄ sequences. Furthermore, a surprising periodic pattern of more and less exposed G-tracts along the DNA chain emerged as an inevitable consequence of frustrated folding in finite chains, with the terminal G-tracts exposed 40-fold more frequently than expected based on the stabilities of individual GQs alone.

MATERIALS AND METHODS

Sample preparation

DNA samples were produced on a Mermade 6 synthesizer (Bioautomation, USA) using reagents from Chemgenes Corporation (USA), then cleaved from the CPG with AMA (1:1 ammonium hydroxide and methylamine). G₃T samples were purified with Glen-Pak columns (Glen Research, USA); Telomeric samples were purified by ion exchange chromatography using an Agilent 1200 Infinity Series HPLC (Agilent Technologies), then desalted with Glen Gel-Pak columns (Glen Research, USA). The purities of all oligonucleotides were verified by LC–ESI-MS on a Bruker Maxis Impact mass spectrometer (Bruker, USA). Samples were redissolved in milliQ water and their concentration measured using a NanoDrop Lite (Thermo Fisher Scientific, USA). Note that all sequences employed here contained a flanking 5′ TTA and 3′ TT, as these were shown to promote two-state folding for a simple four G-tract telomeric sequence (28).

Thermal equilibrium UV–Vis melts

Tel₁₂ and mutants at concentrations of 3 μM DNA in Buffer D (10 mM KH₂PO₄, 10 mM K₂HPO₄ and 110 mM KCl, pH 7.00) were unfolded by incubation at 363 K and then scanned between 363 and 293 K at 1 K/min, or at 0.2 K/min in the case of sequences forming two or three GQs to minimize thermal hysteresis, recording spectroscopic absorbance at 295 nm. Under these conditions, heating and cooling scans were nearly superimposable for all experiments (Supplementary Figure S1). Cooling scans were used for the global analysis. The data analysis is described in the Supplemental Methods. All experiments were performed in duplicate (Supplementary Figure S2)

Thermal hysteresis UV–Vis melts

All UV–Vis experiments were performed on a Cary 100 Bio spectrophotometer (Agilent, USA) at 295 nm. 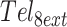and mutants at concentrations of 3 μM DNA in buffer C (5 mM KH₂PO₄, 5 mM K₂HPO₄ and 60 mM KCl, pH 7.00) were scanned at 2.5 and K/min, between 353 and 283 K. (TGGG)₈T and mutants at concentrations of 3 μM DNA in Buffer B (5 mM LiH₂PO₄, 5 mM Li₂HPO₄ and 1 mM KCl, pH 7.00) were scanned at 2 and 3 K/min, between 368 and 293 K. Temperature calibration of the instruments was performed as described previously (32). In all cases, a layer of mineral oil was applied to each sample to minimize evaporation, and when necessary a flow of nitrogen was used to prevent condensation. All experiments were performed in duplicate (Supplementary Figure S3).

Isothermal refolding experiments were performed at four different temperatures (288, 293, 298, 303 K). 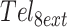at a concentration of 3 μM DNA in buffer C was incubated for 5 min at 363 K for complete unfolding. Temperature was monitored with a Cary Series II (Agilent, USA) probe and then changed to the target value at the fastest rate possible, (≈30 K/min). The absorbance at 295 nm, was monitored as soon as the target temperature was reached. The data analysis is described in the Supplemental Methods. All experiments were performed in duplicate (Supplementary Figure S4).

Circular dichroism spectroscopy

CD experiments were performed using a JASCO J-810 (JASCO, USA) spectropolarimeter with a cell path length of 0.1 cm. Samples were prepared at 10 μM DNA concentration in 10 mM KH₂PO₄, 10 mM K₂HPO₄ and 100 mM KCl, pH 7.00. The samples were first denatured at 373 K for 15 min and then cooled to room temperature over 3 h. The spectra were first collected at the lower temperature (298 K) and then each sample was equilibrated for 15 min before collecting the high temperature spectra (368 K). Each spectrum was scanned three times from 330 to 230 nm for signal averaging. The resulting spectra were baseline corrected using a buffer blank.

Combinatorial calculations

A telomeric repeat sequence with a total of n_tot G-tracts and n_GQ folded GQs contains n_U = n_tot – 4n_GQ unfolded G-tracts. Calculating the number of distinct ways to rearrange the GQs and unfolded G-tracts is an n-choose-k type problem, with the answer given by the binomial coefficient as follows:

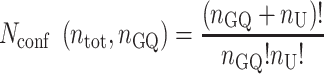(1)

The relative population of the ith rearrangement with n_GQ folded GQs and n_adj interfaces between adjacent GQs, compared to that of the completely unfolded state, is given by

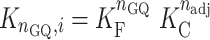(2)

where KF = exp(–ΔH_F/(RT) + ΔS_F/R) and KC = exp(–ΔH_C/(RT) + ΔS_C/R) are the equilibrium constants for folding and cooperativity, respectively, R is the ideal gas constant, and isolated GQs at all positions along the chain are assumed to have the same stability. The total number of conformations is given by

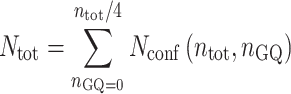(3)

and the folding partition function is given by

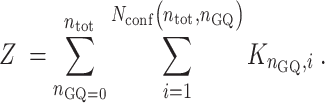(4)

The fractional population of any specific conformation is calculated according to:

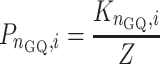(5)

While the probability the chain will have exactly n_GQ folded GQs is

(6)

All calculations were performed using MATLAB software and the built-in function nchoosek() to generate all possible arrangements GQs and unfolded G-tracts for evaluation in Equations (4–6).

Monte Carlo simulations

Simulations were performed according to the Metropolis–Hastings algorithm (33) such that in step i, a set of four contiguous G-tracts were chosen at random from the state in step i – 1 and (a) if the four tracts were unfolded, they were converted to folded and the new conformation was assigned to step i; (b) if the four tracts contained incomplete portions of GQs, the conformation from step i – 1 was assigned to step i; (c) if the four tracts comprised a complete folded GQ it was unfolded on a probabilistic basis: if 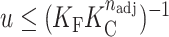, the tracts were converted to unfolded and the new conformation assigned to step i, otherwise the conformation from step i – 1 was assigned to step i, where u is a random number between 0 and 1, K_F is the position-specific folding equilibrium constant, K_C is the cooperativity constant, and n_adj is the number of immediately adjacent GQs, i.e. 0, 1 or 2. The GQs separated from the termini by 0, 1 and >1 G-tracts were assigned K_F = 229, 80 and 59, respectively, and K_C = 0.64, which corresponds to the experimental values (Supplementary Table S1) at 310 K. Simulations were started from the completely unfolded state, and a burn-in period of 30 × 10³ initial steps was discarded before collecting 570 × 10³ productive Monte Carlo steps. For more detailed descriptions of the Metropolis algorithm, please see articles by Janke (34) or Landau and Binder (35), among many other excellent references. Note that each Monte Carlo step does not correspond to the passage of a finite amount of time. Thus, a series of Monte Carlo steps does not necessarily include any dynamic or kinetic information. The output of the calculation is a random sample from the full ensemble of conformations, such that the probability distribution of the Monte Carlo sample approaches that of the full ensemble after a sufficient number of steps. The conformations selected in adjacent steps are related to one another in terms of free energy, but are not necessarily connected by elementary chemical steps.

Discrete time Markov chain simulations

DNA chain conformations were calculated at time intervals of Δt. The probability that any isolated stretch of four G-tracts would fold during a Δt period was given by k_F × Δt, while the probability that any isolated GQ would unfold during the same period was k_U × Δt, where k_F = 4.7 × 10⁻² s⁻¹ and k_U = 3.8 × 10⁻³ s⁻¹ [averages of single-GQ (un)folding rates in Supplementary Table S2 at 310 K]. Based on the cooperativity observed for Tel_8ext, the folding and unfolding rates of a singly-contiguous GQ were 2.10-fold slower and 1.16-fold faster respectively (comparing the rates above with xx||||- - - -xx ↔ xx||||||||xx kinetics). We assumed that the cooperativity is multiplicative, such that folding and unfolding of a doubly-contiguous GQ are related to those of a singly-contiguous one by the same factors. Δt was chosen such that any rate constant multiplied by Δt was less than or equal to 0.01, i.e. there was ≤1% chance of a folding or unfolding event occurring at any given site during any Δt interval.

RESULTS

Tandem GQ folding thermodynamics

We first examined the folding thermodynamics of Tel₁₂, a telomeric sequence containing twelve G-tracts that can fold into a maximum of three sequential GQs. Our goal was to determine how the stability of a GQ depends on its position relative to the 5′ and 3′ termini and to measure how the presence of a folded GQ affects the tendency of nearby G-tracts to fold adjacently. We performed a thermal melt analysis of Tel₁₂, monitoring the spectroscopic absorbance at 295 nm as a probe of folding (36) as the temperature was varied from 373 to 293 K. Spectroscopic absorbance values were used to calculated the fraction of folded molecules as a function of temperature (see Supplemental Methods). As shown in Figure 2A (red stars, and Supplementary Figure S5), we obtained a sigmoidal decrease in folding as the temperature was raised. Although this denaturation curve presents a simple sigmoidal appearance, consideration of the underlying free energy landscape implies that it derives from a complex multi-state folding process. To illustrate, we will employ a nomenclature where each G-tract is represented by ‘|’ in the folded state and ‘-‘ in the unfolded state. For instance, ‘-||||- - - - - - -‘ refers to a DNA sequence with 12 telomeric repeats in which G-tracts 2–5 have folded into a GQ. In principle there are nine ways of forming a single GQ (||||- - - - - - - - -, -||||- - - - - - - etc.), five ways of forming two adjacent GQs (||||||||- - - -, -||||||||- - - etc.), 10 ways of forming two non-adjacent GQs (||||-||||- - -, ||||- -||||- - etc.) and one way of forming three GQs, ||||||||||||, for Tel₁₂. The unfolding curve of Tel₁₂ alone does not provide enough information to unambiguously characterize the populations of all these partly folded intermediates as a function of temperature. Nevertheless, their relative populations are of great interest, as they reveal positional and cooperative effects in GQ folding.

Figure 2.

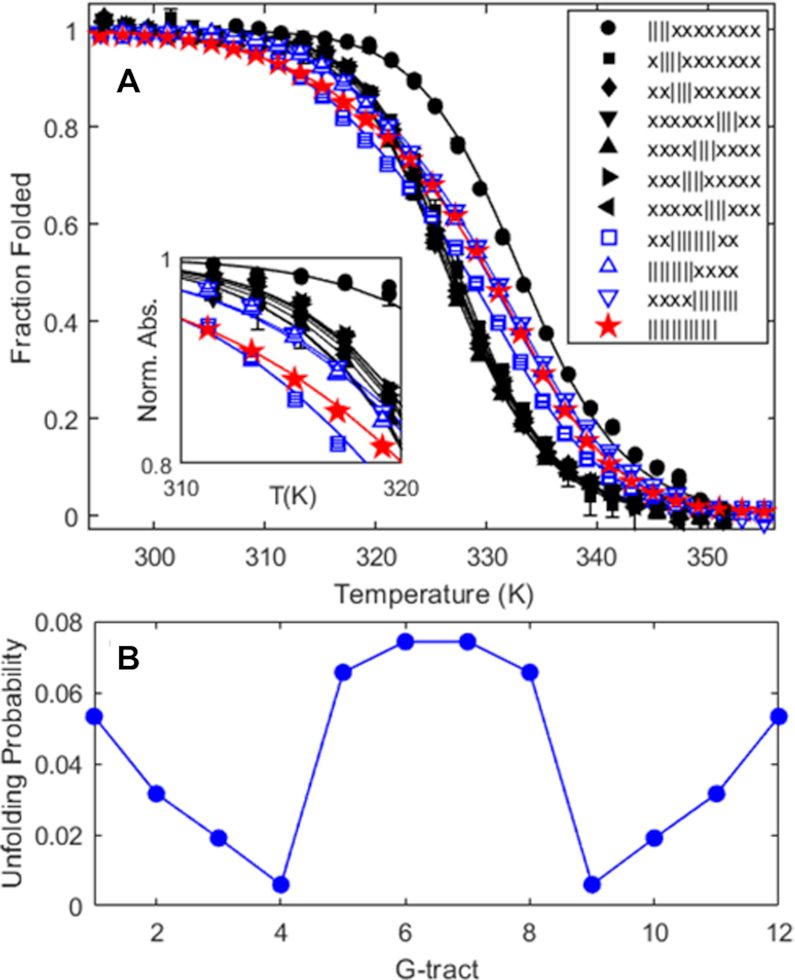
(A) Fraction of potential GQs that are folded as a function of temperature, determined from spectroscopic absorbance measurements at 295 nm, for an oligonucleotide containing 12 telomeric repeats (Tel₁₂, red stars, maximum three GQs), as well as G-tract knockout mutants capable of forming one GQ (filled black symbols) or two adjacent GQs (blue open symbols). In the legend, x and | correspond to G-tracts containing GTG or GGG, as described in the text. Curves represent the best fit of a global thermodynamic folding model. Error bars are often smaller than the symbols used. (B) Unfolding probabilities at 310K for individual G-tracts in a WT Tel₁₂ DNA molecule calculated from the globally fitted thermodynamic parameters, where G-tracts 1, 2, 3, 4, 5, etc. correspond to GGG stretches beginning at nucleotides 4, 10, 16, 22, 28, etc. in the WT sequence.

In order to proceed, we employed a mutational trapping approach our lab previously used to investigate conformational dynamics within individual GQs (32). A set of mutants was used to probe the individual two-state equilibria that comprise the complex multi-state folding landscape of . The mutants were melted individually and the data globally fit, yielding the populations of all Tel₁₂ folding intermediates as a function of temperature. Different sets of 8 of the 12 G-tracts in Tel₁₂ were mutated from GGG to GTG, i.e. folding-incompetent, leaving four contiguous GGG tracts capable of folding into a single GQ in a two-state manner. In our nomenclature, ‘x’ corresponds to a telomeric repeat in which GGG has been replaced with GTG and DNA molecules containing these substitutions will be referred to as ‘G-tract knockout mutants’. The key hypothesis of this approach is that the stability of a G-tract knockout mutant is identical to that of the corresponding wild-type (WT) configuration. This is equivalent to assuming that the stabilities of GQs are then same when they are adjacent to unfolded TTAGGG versus unfolded TTAGTG tracts. Although this assumption is difficult to test directly (since GGG can form GQs while GTG cannot) previous studies have shown that GQ stability is insensitive modest sequence changes in flanking regions (37).To illustrate, we assumed that the folding equilibrium constant for the GQ comprising G-tracts 2–5 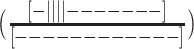is exactly equal to the folding equilibrium constant for the knockout mutant in which G-tracts 1 and 6–12 have been substituted with GTG 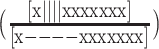, where square brackets indicate concentrations of the folded and unfolded species. We measured the unfolding profiles of seven two-state G-tract knockout mutants, as well as four G-tract knockout mutants that could form two adjacent GQs, as listed in Supplementary Table S4 of the Supporting Information. We used circular dichroism (CD) spectroscopy to check the folding of sequence variants capable of forming one, two, or three GQs (Supplementary Figure S6). At 298 K, the spectrum of the 3-GQ forming Tel₁₂ (||||||||||||) resembled previously published spectra for this molecule, with a maximum at 290 nm, shoulders at 270 and 250 nm, and a small minimum around 238 nm (28). The spectra of the 1-GQ (||||xxxxxxxx) and 2-GQ (||||||||xxxx) trapped mutants were similar to that of Tel₁₂ and lower in magnitude, but not simply scaled versions of the Tel₁₂ spectrum. This was expected, since the unfolded TTAGTG (x) regions also contributed to the spectra. CD data for thermally-denatured molecules at 368 K were very similar for all three sequence variants with minima at about 248 nm, maxima at about 278 nm, and values of zero ([θ] ≈ 0) at about 262 and 300 nm. Taking the thermally denatured spectra as representative of the unfolded (x) signals at 298 K, we would predict that the CD signals at 262 and 300 nm reflect purely GQ content, since [θ] ≈ 0 for the unfolded (x) regions at these wavelengths. The CD data for the variants did indeed scale roughly linearly with the predicted number of quadruplexes 298 K at these wavelengths with [θ] ≈ 2, 4 and 6 × 10⁵ and [θ] ≈ 1.5, 3 and 4.5 × 10⁵ deg dmol⁻¹ cm² for the 1-GQ, 2-GQ and 3-GQ (Tel₁₂) variants at 300 and 262 nm, respectively. Thus, the CD data are consistent with the WT and trapped mutant sequences forming the expected number of telomeric GQs.

The melting curve for each two-state G-tract knockout mutant depends only on the enthalpy (ΔH_F) and entropy (ΔS_F) of folding for that particular GQ (assuming a heat capacity change, 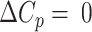), revealing how the stabilities of individual GQs vary as a function of position. Data for chains with two or three adjacent GQs provide information on folding cooperativity. This relationship derives from the fact that free energy is a state function, and the values of state functions are pathway independent. For instance, the total folding free energy of the ||||||||- - - - isomer is equal to the free energy of firstly folding the 5′ GQ plus that of secondly folding the 3′ GQ

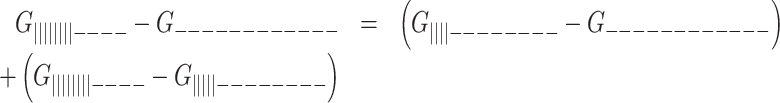(7)

This is equivalent to the free energy of firstly folding the 3′ GQ first plus that of secondly folding the 5′ GQ

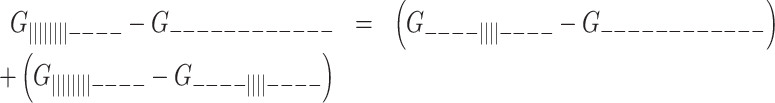(8)

The cooperative interaction energy, ΔG_C, is defined as the difference in stability between folding in the presence versus the absence of an adjacent GQ,

(9)

such that ΔG_C < 0 implies that a GQ stabilizes adjacent GQs and ΔG_C > 0 implies that a GQ destabilizes adjacent GQs. By combining Equations (7–9) we see that the folding free energy of the ||||||||- - - - isomer (ΔG_{||||||||- - - -} = G_{||||||||- - - -} – G_{- - - - - - - - - - - -}) is exactly equal to the folding free energy of the ||||- - - - - - - - isomer (ΔG_{||||- - - - - - - -} = G_{||||- - - - - - - -} – G_{- - - - - - - - - - - -}) plus the folding free energy of the - - - -||||- - - - isomer (ΔG_{- - - -||||- - - -} = G_{- - - -||||- - - -} – G_{- - - - - - - - - - - -}) plus ΔG_C. Our key assumption is that knockout mutants are good thermodynamic mimics of the corresponding WT isomers, i.e. ΔG_{||||||||- - - -} = ΔG_||||||||xxxx, ΔG_{||||- - - - - - - -} = ΔG_||||xxxxxxxx, and ΔG_{- - - -||||- - - -} = ΔG_xxxx||||xxxx, implying that ΔG_||||||||xxxx = ΔG_||||xxxxxxxx + ΔG_xxxx||||xxxx + ΔG_C. Similarly, the folding free energy of |||||||||||| was taken to be equal to the sum of the energies for ||||xxxxxxxx, xxxx||||xxxx, xxxxxxxx|||| plus 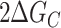. Thus the unfolding traces of all mutants and the WT Tel₁₂ strand depend on the same set of thermodynamic parameters: 7 different ΔH_F and ΔS_F values for the seven different GQ positions tested, and ΔH_C and ΔS_C describing interactions of adjacent GQs. We performed a global analysis of all mutant and WT melting profiles to extract these 16 thermodynamic parameters, which are listed in Supplementary Table S1. Importantly, the global fit gave excellent agreement with all data sets, which validates the two main assumptions of the model: firstly that folding cooperativity is position-independent and additive, and secondly that the G-tract knockout mutations do not affect the folding stability of the remaining GQ, i.e. flanking unfolded TTAGGG and TTAGTG regions are interchangeable. Importantly, violations of these assumptions would be expected to produce sets of mutant and WT data that are mutually inconsistent (32). Furthermore, we wanted to validate the assumption that long loop (3 + 1) GQs can be ignored. Such GQs can fold under physiologically relevant conditions (38), however due to the entropic penalty of closing a long loop, they are significantly less stable than regular telomeric GQs. Supplementary Figure S7 shows the melting profiles of sequences xx||||xx and xx|||x|xx in 100 mM K⁺; The T_m of the latter is about 15°C below the T_m of the regular GQ. This implies that the folding stabilities of 3 + 1 folding isomers are much lower than those of GQs formed from contiguous G-tracts. Longer loop isomers (|||xx|, |||xxx|, etc.) would be expected to be even less stable. While trace quantities of long-loop GQs likely do form in telomeric repeat sequences, their populations would be much lower than those of GQs formed from contiguous G-tracts. Thus the overall behavior of long repeat sequences is dominated by the frustrated folding of contiguous G-tracts and explicitly taking long-loop GQ folding into account would make an already very complex folding landscape intractable. We have therefore ignored folding of long loop GQs in our analysis, which is commonly taken to be a safe assumption in the study of long telomeric repeat sequences (28,39).

Folding of all two-state G-tract knockout mutants was enthalpically driven with ΔH_F values ranging from –196 to –208 kJ mol⁻¹ and entropically unfavorable with ΔS_F values between –599 and –659 J mol⁻¹ K⁻¹. as expected for a disorder-to-order transition. It has been previously reported that the melting temperatures of terminal GQs are higher than those of internal GQs (40,41). This was borne out in our extracted folding parameters. The melting temperature ( 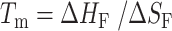) of a terminal GQ was about 6° higher than a GQ one G-tract away from a terminus, and about 7° higher than GQs two or more tracts away from the termini. Although the flanking sequences at the 5′ and 3′ ends of chain are slightly different, 5′-TTA- and -TT-3′, respectively, we found that the melting curves of 5′ and 3′ terminal GQs were superimposable (Supplementary Figure S8). As well, our analysis showed that folded GQs have a weak tendency to destabilize their immediate neighbors at physiological temperatures. We find that at 310 K, ΔG_C = 1.14 kJ mol⁻¹, implying that four contiguous G-tracts are only 64% as likely to fold adjacent to an already folded GQ as they would be in an isolated location.

Interestingly, the sequence variants forming two (||||||||xxxx, x||||||||xxx, xx||||||||xx, xxx||||||||x, and xxxx|||||||||) or three (||||||||||||) consecutive GQs showed distinctly broader melting transitions than did the mutants that can only fold into a single GQ (Figure 2A). This is due to their ability to adopt a variety of partly-folded configurations in addition to their fully-folded forms. For instance, in addition to the two-GQ fully folded state, ||||||||xxxx can adopt several one-GQ partly folded forms, such as ||||- - - -xxxx, -||||- - -xxxx, - -||||- -xxxx, etc. In the case of the WT Tel₁₂ chain, there are 24 different partly-folded forms with one or two folded GQs in addition to the fully folded conformation with three folded GQs. Close inspection of the melting profiles reveals that at physiologically-relevant temperatures near 310 K, the WT Tel₁₂ chain is more unfolded, on average, than any of the single-GQ mutants (5.4% versus 1.7% unfolded), due to the abundance of partly-folded intermediates. This is an example of thermodynamic frustration leading to destabilization of GQs, simply by virtue of their being located in sequences containing multiple telomeric repeats.

Furthermore, these thermodynamic parameters allowed us to calculate separate probabilities of unfolding for each of the 12 G-tracts in Tel₁₂. Surprisingly, the unfolding probabilities of specific G-tracts exhibited a distinctly different and opposing pattern to the positional dependences of GQ stabilities described above (Figure 2B). For example, the terminal G-tracts are about 5.3% unfolded (94.7% folded) while the fourth and ninth G-tracts are only 0.6% unfolded (99.4% folded). In what follows, we prefer to compare the probabilities of unfolding rather than folding, since unfolded G-tracts are implicated in binding shelterin proteins (42,43) and in the initiation of telomere extension by telomerase (17,41), and unfolding probabilities are proportional to the average number of sites accessible to single-stranded binding proteins. The unfolding probability is 9-fold higher at the terminus even though an isolated terminal GQ is about 4-fold more stable than an interior one. The most exposed G-tracts are the middle four, which are about 12-fold less likely to be folded than the 4th and 10th. These pronounced position-specific differences in G-tract folding are due to the interplay between folding frustration and end effects. For example, there are four distinct GQs that incorporate the fourth G-tract (1-4, 2-5, 3-6, and 4-7), while there is only one that incorporates the the first G-tract (1-4). Thus, there exist many more partly-structured states in which the fourth G-tract is folded compared to the first, leading to an overall much lower unfolding probability. This combinatorial effect overwhelms the position-specific differences in the stability of individual GQs.

Tandem GQ folding kinetics

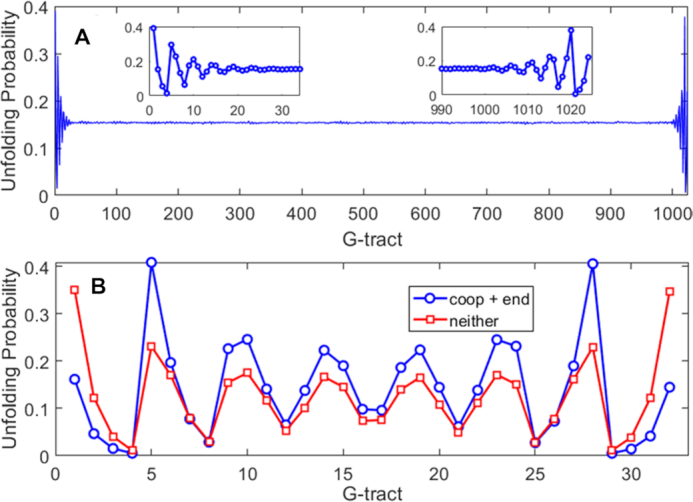
In order to better understand how the folding of one GQ affects the ability of nearby G-tracts to fold, we then analyzed the folding kinetics of a Tel₁₂ variant capable of forming two adjacent interior quadruplexes (xx||||||||xx). In what follows we will refer to this as the extended Tel₈ sequence, Tel_8ext. The folding reaction pathway for Tel_8ext is shown in Figure 3A. There are two on-pathway folding intermediates (xx||||- - - -xx and xx- - - -||||xx) in which either the 5′ or 3′ GQ folds first. Folding of the second GQ converts these on-pathway intermediates directly into the fully folded (2-GQ) state. In addition, there are three off-pathway or misfolded intermediates (xx-||||- - -xx, xx- -||||- -xx and xx- - -||||-xx), in which folding of the first GQ sterically blocks the remaining G-tracts from forming a second GQ. Importantly, misfolded molecules must unfold before they can follow one of the two pathways leading to the fully folded state. Thus, the off-pathway intermediates are potentially deep kinetic traps.

Figure 3.

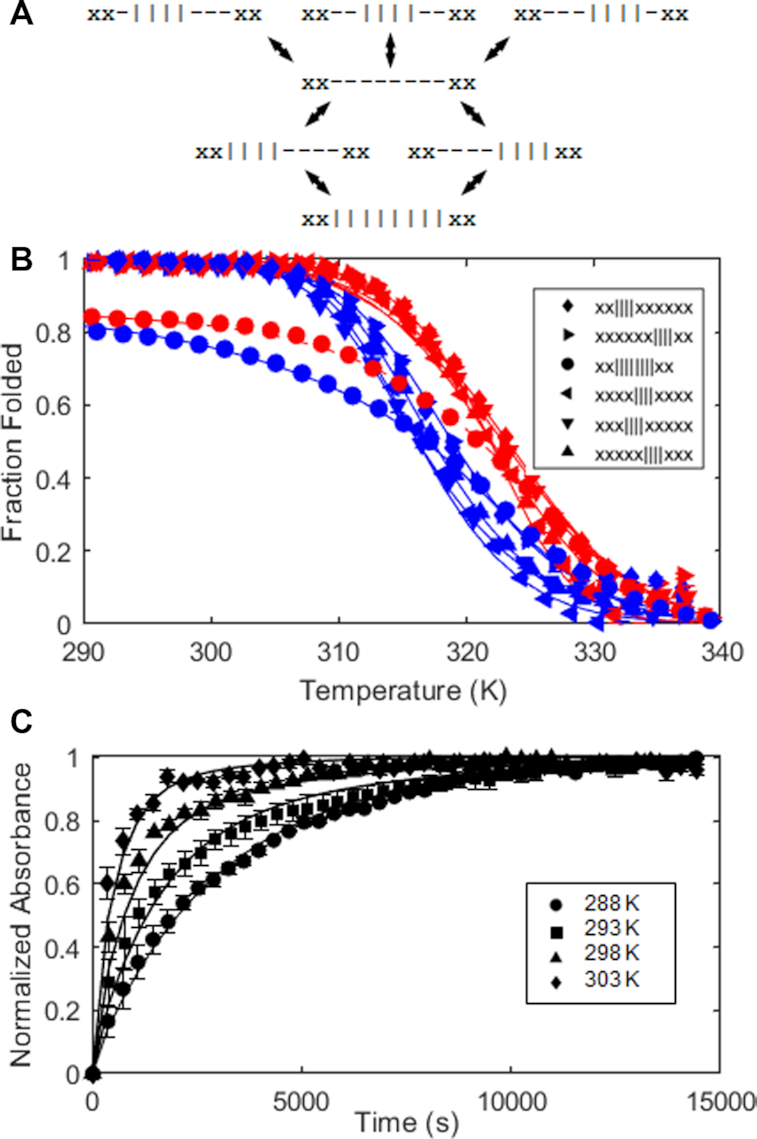
(A) Folding pathway of the Tel_8,ext DNA molecule. The four rows from top to bottom correspond to misfolded, fully unfolded, on-pathway intermediate, and fully folded states. The symbols | and – represent folded and unfolded G-tracts. x's represent G-tracts with GGG to GTG substitutions. (B) Thermal hysteresis folding/unfolding data for Tel_8,ext DNA and variants. Spectroscopic absorbance values obtained at 295 nm with temperature ramp rates of 4° min⁻¹ were converted to the fractions of folded GQs as a function of temperature. Data for G-tract knockout mutants capable of forming a single GQ are shown as triangles and diamonds, while those of the wild-type are shown as circles. Red and blue correspond to heating and cooling scans. Error bars are often smaller than the symbols used. (C) Isothermal refolding data for Tel_8,ext DNA. Tel_8ext refolding experiments. Spectroscopic absorbance at 295 nm for samples rapidly cooled from 373 K to 288, 293, 298 or 303 K, normalized to lie between 0 and 1, are plotted as a function of time and reflect conversion of misfolded 1-GQ states to the fully folded 2-GQ ground state. Curves in (B) and (C) correspond to the best fit to a global kinetic model.

We used thermal hysteresis (TH) UV–Vis denaturation experiments to characterize the folding pathway of the Tel_8ext molecule, monitoring the spectroscopic absorbance at 295 nm as the temperature was varied between 373 and 293 K (Figure 3). In the TH approach, the rates of heating and cooling are chosen to be rapid compared to the rate at which the system relaxes to equilibrium. The balance between folded and unfolded states is therefore pushed slightly out of equilibrium, with the apparent melting temperature (T_m) shifted to higher values on the up-scans and lower values on the down-scans (plotted in red and blue in Figure 3B). The gap between heating and cooling profiles provides quantitative information on folding and unfolding rates. TH has typically been used to measure the kinetics of nucleic acids that fold in a two-state manner, giving the rate constants for folding and unfolding (k_UF and k_FU) as well as the activation enthalpies (E_a,UF and E_a,FU) which describe how k_UF and k_FU vary with temperature (44). We performed the thermal hysteresis experiments under slightly different conditions than the equilibrium folding experiments described above. The equilibrium experiments were performed in the presence of 140 mM K⁺ ions, in line with physiological concentrations. However, under these conditions, the folding/unfolding reactions equilibrated more rapidly than the fastest temperature ramp rates available (≈4° min⁻¹) and there was negligible thermal hysteresis. We therefore performed the experiments in 75 mM K⁺ ions where the GQs are slightly less stable than in the equilibrium experiments, folding and unfolding occur more slowly in the transition region, and considerable hysteresis is evident.

In this study, we have developed an extension of the TH approach for more complex folding equilibria and used it to characterize the seven-state folding pathway of Tel_8ext. We constructed G-tract knockout mutants corresponding to the two on-pathway (xx||||xxxxxx and xxxxxx||||xx) and the three off-pathway (xxx||||xxxxx, xxxx||||xxxx, and xxxxx||||xxx) folding intermediates. Each of these mutants is expected to fold in a two-state manner (eg. xx||||xxxxxx ↔ xx- - - -xxxxxx),(27,28) in principle giving information on five of the seven transitions that define the Tel_8ext folding pathway (Supplementary Scheme S1 and Supplementary Table S5). In order to get information on the remaining two transitions (xx||||- - - -xx ↔ xx||||||||xx and xx- - - -||||xx ↔ xx||||||||xx), we also collected TH data for the WT Tel_8ext molecule and globally fit all six datasets. In performing this analysis, we noticed that WT Tel_8ext folded to only about 80% on the down-scan, while all of single-GQ knockout mutants folded to nearly 100% under the same conditions. The model parameters predict that this is due to about 40% of the molecules becoming trapped in misfolded 1-GQ states during the down-scans. We tested this hypothesis by rapidly cooling Tel_8ext samples from 363 K down to specific temperatures well below the refolding temperature and monitoring the spectroscopic absorbance at 295 nm once the lower temperature was reached. In all cases, we saw gradual increases in absorbance occurring over several hours (∼0.01 a.u.) (Figure 3C), corresponding to refolding of the off-pathway intermediates. This process involves transient unfolding from the misfolded 1-GQ states into the unfolded state, which is populated to ∼1% at equilibrium under these conditions. This is followed either by productive folding to the 2-GQ state or falling back into a misfolded state, as illustrated by the middle two or upper three arrows in Figure 3A, respectively, and defined mathematically in the Supplemental Methods. Note that in Figure 3C, at all temperatures, when t = 0, roughly 40% of the molecules are trapped in the misfolded states xx-||||- - -xx, xx- -||||- -xx, or xx- - -||||-xx, 60% are in the 2-GQ state xx||||||||xx, and the normalized absorbance is equated to zero. At very long times, close to 100% of molecules are in the 2-GQ state and the normalized absorbance is equated to one. The rate of refolding was slower at lower temperatures, as expected, since the endothermic unfolding of the misfolded forms is rate limiting. This tendency of WT Tel_8ext molecules to become trapped in partly folded off-pathway intermediates is an example of kinetic frustration, which opposes GQ folding. The isothermal refolding rates are defined by the same kinetic parameters that describe the TH datasets. We simultaneously fitted the four isothermal refolding traces obtained at 288, 293, 298 and 303 K and all six TH datasets obtained for five knockout mutants and the WT to extract eight unique rate constants and eight unique activation enthalpies, as listed in Supplementary Table S2. The individual folding rates for the various steps are similar at about 2–7 × 10⁻² s⁻¹ while unfolding rates are in the range of 2–6 × 10⁻³ s⁻¹ at 310 K. As seen for the Tel₁₂ sequence, folding of adjacent GQs was negatively cooperative. In this case, four contiguous G-tracts are only 45% as likely to fold adjacent to an already folded GQ as they would be in an isolated location. The good agreement with experimental data we obtained for both TH and isothermal refolding datasets gives us confidence in the fitted parameters. Furthermore, the isothermal refolding rates themselves pertain directly to the kinetics of tandem GQ conformational rearrangement in a frustrated energy landscape, with implications for the folding of longer telomeric repeats, as outlined below.

As a further test of our global TH kinetic analysis, we also measured the folding of a (TGGG)₈T DNA strand, which like 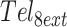, has a 2-GQ fully folded state with two on-pathway and three off-pathway 1-GQ intermediates. Applying the same mutational approach described above, we collected TH data for all five knockout mutants and the WT and fit them globally to extract the rate constants and activation enthalpies listed in Supplementary Table S3. In contrast to the telomeric sequences, folding of consecutive TGGG GQs is highly positively cooperative. The folding rate is ∼4-fold higher and unfolding ∼1200-fold slower when a folded GQ is immediately adjacent, leading to a 4800-fold increase in stability compared to an isolated GQ. As a result, the fully folded 2-GQ state forms early during the TH scans, and the population of misfolded chains is predicted to be ≤5% at the same scan rate that produces ∼40% misfolding for the telomeric sequence. These results are in good agreement with the previously-reported formation of stacked GQs by TGGG repeats, (45) providing validation for our TH folding measurements and highlighting the very different thermodynamic landscapes associated with different GQ-forming sequences.

Thermodynamic frustration in long tandem repeats

In principle, the folding parameters measured for Tel₁₂ and Tel_8ext allow one to quantitatively predict the equilibrium behavior of arbitrarily long telomeric repeats. However, this is not a simple task, since the folding landscapes of longer telomeric repeats are far more complicated than those of shorter sequences. The number of folding isomers increases roughly exponentially with the length of DNA. To illustrate, a typical telomeric single-stranded overhang of ∼200–300 nucleotides contains 32–48 repeats and can form 10⁴ to 10⁶ distinct partly folded structures. A chain with 1024 telomeric repeats can adopt over 10¹⁴³ distinct states. In order to address this challenge, we used a multi-pronged approach. Firstly, we applied statistical mechanical theory developed by McGhee and Hippel (MGVH) (46) to calculate the equilibrium folding behavior of telomeric repeats in the context of infinitely long DNA strands. Secondly, we performed Monte Carlo (MC) simulations of finite DNA chains, benchmarking the results against the predictions of MGVH theory. These simulations allowed us to study how the presence of chain termini affects GQ folding patterns at equilibrium in long (>60 repeat) sequences. Lastly, we completely enumerated all conformations available to a Tel₃₂ sequence, calculating the unfolding probability on a per-G-tract basis, similarly to our treatment of the Tel₁₂ chain described above.

The MGVH model was originally designed to study the cooperative binding of ligands to overlapping sites on a one-dimensional, infinitely long, homogeneous lattice. The problem is formally identically to that of tandem GQ folding; there are an enormous number of ways to arrange the ligands on the lattice and most have short gaps between the occupied sites, just as there are an enormous number of ways to arrange folded GQs along the chain, and most have short gaps of unfolded G-tracts between the folded regions. For a given folding stability (ΔG_F) and cooperativity (ΔG_C), MGVH theory yields the average number of folded GQs per given length of DNA, n_GQ. The theory allows this value to be further separated into the numbers of doubly-contiguous (n_dc), singly-contiguous (n_sc) and isolated (n_isol) GQs, which are immediately adjacent to GQs on both sides, one side, or neither side, respectively. We used the average folding stability of internal GQs (separated from the ends by two or more G-tracts, ΔG_F = –10.51 kJ mol⁻¹) and the slightly unfavourable folding cooperativity, (ΔG_C= 1.14 kJ mol⁻¹) we measured for Tel₁₂ to calculate GQ formation within a stretch of 100 G-tracts embedded in an infinitely long chain at 310 K. MGVH theory predicts that on average this region would contain n_dc= 6.42, n_sc= 10.56 and n_isol = 4.34 doubly-contiguous, singly-contiguous, and isolated GQs, respectively. Thus on average, n_GQ = 21.4 out of a maximum of 25 GQs are formed, implying that the unfolding probability of any given G-tract is about 15%. Interestingly, the unfolding probability of a single GQ with the same ΔG_F is 1.7%. Therefore, G-tracts in the context of long tandem repeats are ∼9-fold more likely to be unfolded than those of isolated GQs.

Some of this destabilization is due to the unfavourable folding cooperativity. The average per-GQ coupling energy in the stretch of 100 G-tracts is given by <ΔG_c> = ΔG_c(n_sc + 2n_dc)/n_GQ = 1.2 kJ mol⁻¹. Even taking into account this cooperative destabilization, the unfolding probability of a single GQ with a stability equal to ΔG_F + <ΔG_c> is only 2.7%. Thus there is a ∼5-fold destabilization of GQs due exclusively to thermodynamic frustration. This makes sense from a statistical mechanical perspective: although the 25-GQ state has the lowest free energy amongst all possible folding isomers of 100 G-tracts, there are about 2 × 10⁴ distinct ways of arranging 24 GQs and four unfolded G-tracts and 8 × 10⁶ ways of arranging 23 GQs and eight unfolded G-tracts, providing a strong entropic drive towards partial unfolding.

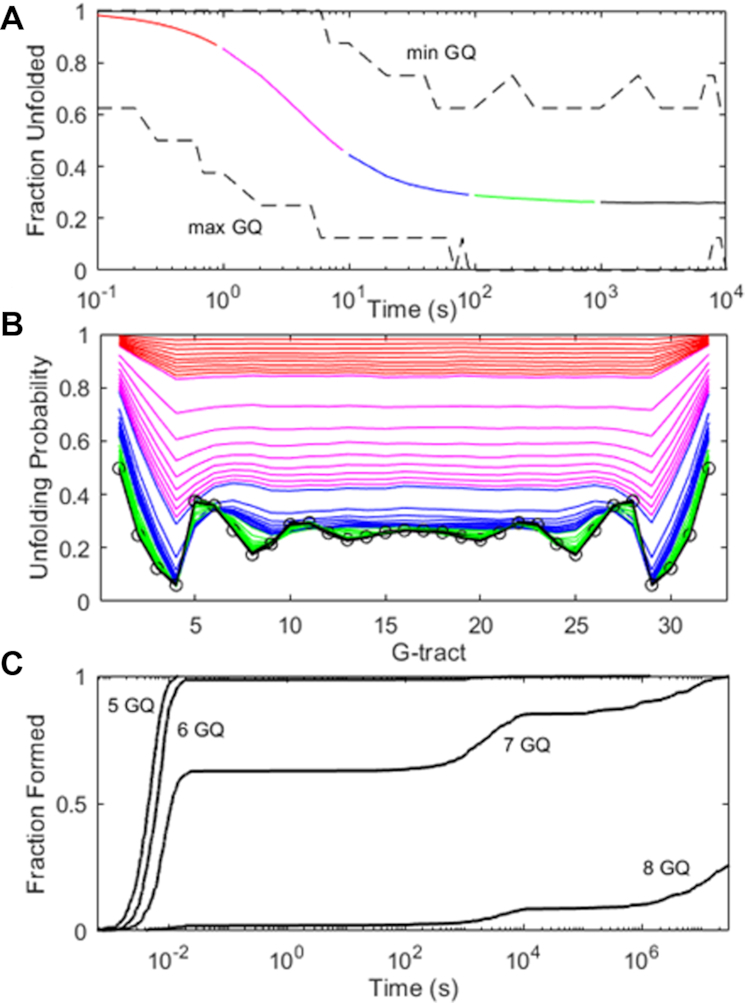
While the MGVH model provides a simple way to account for thermodynamic frustration of GQs folding in the interior of long tandem repeats, it does not apply to GQ folding near the ends of the DNA chain. For the shorter Tel₁₂ sequence, we observed interesting patterns of unfolding at the level of individual G-tracts, which we attributed to proximity to the 5′ and 3′ ends. In order to investigate how these effects might manifest in longer chains, we turned to MC simulations using the Metropolis-Hastings algorithm, applying our experimental stability and cooperativity parameters to a Tel₁₀₂₄ chain. For most G-tracts, the MC calculation predicted a uniform unfolding probability of about 15%, in good agreement with MGVH theory (Figure 5A). A closer inspection of the sampled conformations yielded an average of 6.15, 10.71 and 4.42 doubly-contiguous, singly contiguous, and isolated GQs, respectively, per 100 G-tract region. These numbers are very close to the MGVH values, which gives us confidence in our MC approach. We attribute the small discrepancies to the fact that the system contains an enormous number of states (10¹⁴³), so that any simulated population will necessarily be an approximation. Interestingly, both 5′ and 3′ terminal G-tracts showed oscillating patterns of unfolding probability very similar to those exhibited by the Tel₁₂ sequence. The 1st, 5th, 9th and 13th G-tracts were substantially more likely to be unfolded while the 4th, 8th and 12th were substantially less so, with a symmetrical pattern occurring at the 3′ end (Figure 4A).

Figure 5.

(A) Simulated folding of 10⁴Tel₃₂ DNA molecules using a discrete Markov chain model and experimental rate constants. The average fraction of G-tracts that are unfolded is plotted in solid colors as a function of time, with values for the most and least folded molecules in the ensemble shown with black dashed lines. (B) Unfolding probabilities for individual G-tracts calculated at 1 – 9 × 10^–1 (red), × 10⁰ (magenta), × 10¹ (blue), × 10² (green) and × 10³ (black) seconds. The unfolding probabilities at equilibrium are indicated with open circles. (C) Simulated folding of 500 (TGGG)₃₂T DNA molecules. The fractions of chains with ≥5, 6, 7 and 8 GQs are plotted as a function of time.

Figure 4.

Unfolding probabilities for individual G-tracts calculated for (A) Tel₁₀₂₄ and (B) Tel₃₂ DNA molecules using Monte Carlo calculations or complete enumeration of the folding partition function, respectively, using experimental stability and cooperativity parameters. In (B), blue circles correspond to calculations with position-specific GQ stabilities and cooperativity included, while red squares have position-independent GQ stability and no cooperative effects. G-tract refers to the position along the nucleic acid molecule in terms of TTAGGG repeat.

We then applied the same methodology to a Tel₃₂ DNA sequence more representative of the length of a single-stranded telomeric overhang. We note that in a telomere, the 5′ end would mark the transition from single-stranded to double-stranded DNA, rather than a chain terminus. Nevertheless, G-tracts involved in duplex formation are unavailable for GQ folding and we might expect that a similar sort of end effect could also influence G-tract accessibility. For the sake of simplicity, we considered a single chain containing 32 telomeric repeats. In this case, there are 16 493 distinct conformations, which are small enough in number to allow the folding partition function to be calculated completely (See Methods section). The MC simulations gave identical results to those of the exact calculation, further validating the methods used here. Once again, there were dramatic position-dependent differences in the unfolding probabilities (Figure 4B). The terminal G-tracts at the 5′ and 3′ ends were unfolded 16% of the time, even though a terminal GQ would only be unfolded 0.4% of the time in the absence of frustration. Notably, this corresponds to a 40-fold increase in unfolding at the chain terminus due almost entirely to folding frustration. The 4th and 29th G-tracts were highly protected, unfolding just 0.5% of the time. In contrast, the 5th and 28th were 40% unfolded. Furthermore, the unfolding probabilities showed pronounced oscillations throughout the entire length of the chain. Thus end effects influence the unfolding probabilities of G-tracts even 98 nucleotides away from the termini. Finally, we explored to what extent this patterning was due to position-dependent GQ stability and negatively cooperative folding. We repeated the calculation with ΔG_C = 0 and all ΔG_F = –10.51 kJ mol⁻¹. As expected, the unfolding probabilities were slightly elevated at the termini, since ΔG_F was less favourable at the ends, and depressed in the centre, due to the absence of destabilizing cooperative interactions. However, the oscillating pattern of unfolding probabilities reappeared robustly. Long-range end effects seem to be a consistent feature of this type of frustrated folding landscape.

Kinetic frustration in tandem repeats

Thus far, our analysis of conformational sampling in long tandem sequences has assumed that the probability of adopting a particular structure depends only on its free energy. However, this does not take into account the length of time taken to reach each conformation. For a single chain to explore all conformational possibilities, individual GQs must unfold and refold multiple times, leading to a rugged and kinetically frustrated energy landscape. It has been suggested that this process is so time consuming that the conformational distributions of long telomeric repeats are governed by kinetic trapping rather than by thermodynamics (47). The kinetic parameters we measured for Tel_8ext allow us to compare the relative importance of thermodynamic and kinetic frustration to folding of the longer Tel₃₂. We performed a series of discrete time Markov chain simulations on 10⁴ DNA molecules, starting each one from a completely unfolded state and evaluating how their conformations evolved over time. Figure 5A shows the average fraction of G-tracts that were unfolded in the 10⁴ simulated chains as a function of time, as well as the fractions of unfolded G-tracts in the most- and least-folded members of the ensemble. The bulk of the folding occurred rapidly, within the first 10 s, and was largely complete at 10³ s. The first chain to form eight GQs did so after just 100 s, while the least-folded members of the ensemble had consistently four or five GQs after about the 100 s mark. A more stringent test of reaching equilibrium is how the per-G-tract unfolding probability, calculated across the 10⁴ chains, compares with the equilibrium values. Figure 5B shows the G-tract unfolding probabilities, evaluated at 46 time points between 10⁻¹ and 10⁴ s. Interestingly, the maxima at the termini and minima at the 4th and 29th G-tracts are apparent even at the sub-second time points, becoming pronounced by about 10 s. However, other characteristic features of the oscillating pattern took longer to appear. For instance, the unfolding maxima at the 5th and 28th G-tracts only started to appear in the 50–100 s range. By ∼500 s, the unfolding probabilities were indistinguishable from their equilibrium values and to all intents and purposes the system was equilibrated. Based on the measured Tel_8ext kinetics, folding of a single GQ is 95% complete after about 30 s. On average the Tel₃₂ chains had attained the same level of folding in the same length of time, thus kinetic frustration did not appear to impede greatly the accretion of structure for this system.

Interestingly, although the pattern of G-tract equilibrium unfolding probabilities shown in Figures 4B (folding thermodynamics) and 5B (folding kinetics) are very similar, there are a few distinct differences. In particular, there are seven minima in the unfolding probability versus position plot in Figure 4B, while in Figure 5B, there are only six minima. This is likely because the simulation parameters used in Figure 4 were taken from equilibrium melting experiments performed in 140 mM K⁺ (where GQs are relative more stable) whereas those of Figure 5 were taken from thermal hysteresis measurements performed in 75 mM K⁺ (where GQs are relatively less stable and cooperativity is slightly more negative, as discussed above). We calculated a series of G-tract unfolding profiles for various GQ stabilities (K_F = 10³ – 10¹) and cooperativities (K_C = 2–0.4). The combination of less stable GQs and more negative cooperativity (lower values K_F and K_C) led to 6-minimum profiles whereas higher stability and positive cooperativity (larger K_F and K_C) led to 7-minimum profiles (Supplementary Figure S9). This also begs the question as to whether a system of 32 tandem G-tracts would equilibrate equally rapidly in the presence of 140 mM K⁺ as we have calculated for 75 mM K⁺. Although it is difficult to answer this directly, since the required kinetic parameters are experimentally inaccessible at the higher salt concentration, we can gain insight by simulating a system with identical values of K_F and K_C to those observed in 140 mM K⁺. In a recent GQ kinetic study, we found that increasing the salt concentration led to faster folding and slower unfolding, with the folding/unfolding rates increasing/decreasing by about the same factor (48). We applied this approximate relationship to the Tel_8ext folding parameters, multiplying and dividing the experimental (75 mM K⁺) folding and unfolding rates of an isolated GQ (k₁ and k_–1 in Supplementary Scheme S1) by a factor of 2.3, respectively, and those of a singly-contiguous GQ (k₂ and k_–2) by a factor of 2.7. This exactly reproduced the stability and cooperativity observed at 140 mM K⁺. Unsurprisingly, kinetic simulations run with these modified parameters (Supplementary Figure S10) converged on an equilibrium unfolding probability pattern with seven minima, matching the one in Figure 4. Furthermore, this simulation took ∼3000 s (50 min) to reach the equilibrium number of GQs and unfolding probability pattern, which is about 5-fold longer than the results using the 75 mM K⁺ kinetic parameters but still lies within a biologically-accessible timeframe.

For the sake of comparison, we also simulated the folding of 32 tandem TGGG repeats, where GQ unfolding is about 6 × 10⁴-fold slower than for the telomeric sequence. In this case, kinetic frustration appeared to have a much more dramatic effect. TGGG repeats fold with high positive cooperativity and, at equilibrium, essentially all chains are predicted to have 8 GQs (average number of GQ > 7.9999). We performed folding simulations for 500 chains; almost all of them formed up to six GQs within milliseconds (Figure 5C). The length of time needed to form the seventh GQ varied widely from 10⁻² to over 10⁶ s. Notably, the 8-GQ structure was kinetically inaccessible to the majority of chains. About 10% of simulations had reached this state by 10⁴ s, likely those which had initially folded into structures requiring little remodeling. Only about 25% of chains had attained eight GQs after a year of simulated folding (3.5 × 10⁷ s). Thus slow unfolding rates can make the redistribution of GQs in long sequences an extremely time-consuming process, and can trap chains kinetically, essentially indefinitely.

DISCUSSION

There is growing evidence that the rate of telomere shortening, and thus cell senescence and death, are related to the formation of GQs in the telomeric DNA single-stranded overhang (17,49,50). It is well recognized that GQ folding in the context of a 200–300 nucleotide region may differ fundamentally from the folding of isolated GQs composed of short oligonucleotides (51–53) Consequently there have been considerable efforts made to understand the physical properties of long, tandem GQ-forming DNA sequences. A wide variety of biophysical techniques have been applied to this problem, yet there are some unresolved inconsistencies in the results and some aspects remain controversial. Our hybrid experimental and statistical mechanical approach confirms some previous observations, helps to resolve some apparent contradictions, and offers new and surprising insights into the implications of GQ folding in the context of long repetitive sequences.

For instance, there have been conflicting opinions regarding the nature of GQ/GQ interactions in telomeric repeats. Based on structures of individual telomeric GQs (54) and computer models, (55) it has been proposed that GQs stack one atop the other, producing a rod-like superstructure (53). However, such favorable stacking interactions would be expected to stabilize GQ folding and this has not been observed. In fact, multiple GQs in longer DNA chains have been reported to have similar or slightly lower thermal stabilities than separate GQs in short chains (56). This led to a ‘beads on a string’ model of telomere folding, in which GQs largely do not interact with their neighbors (39). This idea was supported by single molecule pulling experiments, which showed that tandem GQs unfolded in a largely uncorrelated manner (51). Strong GQ/GQ stacking interactions would have been expected to produce an excess of simultaneous unfolding events. Our results move even further in this direction, indicating that GQs destabilize their neighbors. Our thermodynamic and kinetic global fits both showed that the probability of folding immediately adjacent to another folded GQ is only 40% to 64% that of folding at an isolated site. 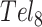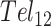Similar weak negative folding cooperativity was previously observed in a differential scanning calorimetric study of and folding (28). Deconvolution of the DSC data revealed two- and three-step folding processes, respectively. In 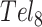, this presumably corresponded to transitions from the fully folded two-GQ form to the manifold of one-GQ partly folded forms to the fully unfolded state. In 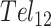this presumably corresponded to transitions from fully folded to the two-GQ manifold to the one-GQ manifold to the fully unfolded state. In both cases, the first unfolding transition from the fully folded state occurred more easily than the other transitions, which was attributed to the presence of one or more adjacent GQs and an unfavorable coupling energy, 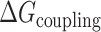. For 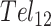, 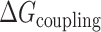was similar (roughly double) the 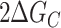value we extrapolated at the same temperature for the microscopic pairwise energy. We believe this level of agreement is quite good, given the differences between the UV–Vis versus DSC methodologies and macroscopic versus microscopic analyses, and provides strong evidence that the folding of adjacent telomeric GQs is, in fact, negatively cooperative.

Another area of uncertainty pertains to the relative numbers of folded GQs and unfolded gaps present in telomeric DNA. The situation is extremely complicated in an intact telomere, due to formation of the t-loop and protein/DNA shelterin complex (57). However, even for naked single-stranded telomeric DNA, the question of how many GQs are formed remains unresolved. This question is of paramount importance to telomere function as many of the shelterin components, including POT1 and SSB1, bind to the single-stranded gaps between GQs (42,43). It has been sometimes assumed that the fully-folded state will dominate, presumably because it is lowest in energy (47). The folded CD signal of telomeric repeats increases roughly linearly with DNA length up to Tel₂₀ (5 GQ), which has been taken as a sign that all possible GQs are indeed formed (52). A study using atomic force microscopy (AFM) and image-averaging analysis supported this idea, reporting that Tel₁₆ DNA consistently formed the maximum number (4) of GQs (53). However, contradictory evidence came from the same technique applied with a statistical analysis of individual images, which suggested that Tel₁₆ DNA generally forms only two GQs, i.e. half the maximum number (58). Our hybrid experimental/statistical mechanical approach provides a new way to estimate the relative numbers of gaps and folded GQs in DNA sequences of arbitrary length. For instance, in the Tel₁₂ chain, we calculate that about 88% of molecules contain 3 GQs, ∼12% contain two GQs, and <<1% contain 1 or 0 GQs. This agrees well with previous analytical ultracentrifugation and CD measurements which suggested that 7–13% of Tel₁₂ chains form 2 GQs and the remainder form 3 (28). In long tandem repeats, we predict that the average G-tract unfolding probability is about 15%, which implies that there are roughly two unfolded G-tracts for every three GQs, providing ample protein binding sites. This level of unfolding is about 9-fold larger than that of a single GQ, thus the abundance of single-stranded binding sites is due to a combination of thermodynamic frustration and negative cooperativity. We find that these destabilizing effects gradually become stronger as the DNA lengthens (Supplementary Figure S11). This means that even though G-tracts in long telomeric repeats are more likely to be unfolded than those in short ones, the number of folded GQs increases roughly linearly with DNA length, in agreement with previous CD studies.

Our results also help to shed light on the question of whether the folding of naked telomeric DNA is under kinetic or thermodynamic control. These two situations are easy to distinguish in simple reactions where kinetically versus thermodynamically favored products can be clearly differentiated (59). In the case of telomeric DNA folding, the reaction involves populating tens of thousands of different conformations and the distinction is less obvious. In simulated folding experiments on Tel₃₂ DNA, we found that the equilibrium number of GQs was reached almost as quickly as for an individual GQ. The equilibrium distribution of GQs was reached more slowly, but nevertheless within under an hour. Therefore, we conclude that telomeric repeat folding is predominantly under thermodynamic control. This finding is seemingly at odds with a recent study that reported that tandem GQ folding was under kinetic control, based on single molecule pulling experiments that showed the chain contained a large number of unfolded G-tracts after 30 s of refolding (47). The authors defined ‘thermodynamic folding’ as a process where the chain adopts only conformations that are on-pathway towards the maximally folded state (i.e. can proceed towards forming the maximum number of GQs without a single unfolding step). All other (off-pathway) conformations were defined as misfolded or kinetically trapped. Their ‘thermodynamic folding’ model over-predicted the number of GQs observed experimentally so it was concluded that folding is kinetically controlled, at least on the timescale of tens of seconds. However, our simulations show that the vast majority of conformations adopted by long telomeric repeats at equilibrium are not on-pathway to maximal folding; they would be categorized as kinetically trapped in the previous study. We prefer to define a system under thermodynamic control as one where the population of each sub-state depends solely on its free energy. According to this definition, folding of naked telomeric DNA is overwhelmingly under thermodynamic control. Interestingly, we observed quite different behavior for the G₃T GQ system, where the equilibrium state does indeed correspond to the maximally folded one and most chains end up becoming kinetically trapped in misfolded states. This is relevant to the design of small molecule ligands that bind to and stabilize telomeric GQs (60). If unfolding is much slower for a GQ bound to a stabilizing ligand, then the system is likely to become kinetically trapped with the initial number of GQs. In other words, it might be difficult for GQ-stabilizing ligands to increase the overall number of GQs formed; this would involve redistributing GQs along the chain by repeated unfolding/refolding events, a process that would be substantially slowed by the ligand itself.

One of the more surprising results in our study is the distinct oscillating pattern of G-tract unfolding probabilities that results from thermodynamic frustration. To our knowledge, this has not been noted previously, but it is an inescapable consequence of conformational averaging near the ends of tandem-GQ forming DNA sequences. This patterning has functional implications, since telomere extension at the 3′ end is strongly related to cell senescence (61). It has been shown that both the telomerase and ALT (alternative lengthening of telomeres) mechanisms require 3′ unfolded regions of 8–12 nucleotides (17). Our measurements, and those of others (17,39,41), have shown that isolated GQ folding at the extreme terminus is more favorable than in the interior. It has been argued that this would tend to sequester the terminal G-tracts in folded GQs and obstruct telomere extension (17,41). However, focusing on the stability of individual GQs ignores the tendency of the frustrated energy landscape to expose terminal G-tracts, even while terminal GQs are more stable than internal ones. In fact, we find the unfolding probabilities of terminal G-tracts are on par with many sites in the interior, which would have the opposite effect of promoting telomere extension. Another interesting aspect of the unfolding pattern is that certain sites in a conformationally equilibrated DNA chain would have higher accessibility to single-stranded DNA binding proteins such as POT1 and SSB1, while other sites would be far more likely to be sequestered in a GQ. Thus the long-range pattern of more and less unfolded G-tracts could be involved in directing the higher order structure of the telomere. Overall, these experiments and calculations have pointed to the emergence of distinctive and unexpected folding patterns for long tandem GQ repeat sequences. Our approach provides a new, comprehensive framework for measuring and understanding the behavior of these important and challenging systems.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Science and Engineering Research Council (NSERC) Discovery Grant [327028-09]. Funding for open access charge: National Science and Engineering Research Council (NSERC) Discovery Grant [327028-09].

Conflict of interest statement. None declared.