Abstract
Our previously developed mbCO2 potential [O. Sode and J. N. Cherry, J. Comput. Chem. 38, 2763 (2017)] is used to describe the vibrational structure of the intermolecular motions of the CO2 trimers: barrel-shaped and cyclic trimers. Anharmonic corrections are accounted for using the vibrational self-consistent field theory, vibrational second-order Møller–Plesset perturbation (VMP2) theory, and vibrational configuration interaction (VCI) methods and compared with experimental observations. For the cyclic structure, we revise the assignments of two previously observed experimental peaks based on our VCI and VMP2 results. We note that the experimental band observed near 13 cm−1 is the out-of-phase out-of-plane degenerate motion with E″ symmetry, while the peak observed at 18 cm−1 likely corresponds to the symmetric out-of-plane torsion A″ vibration. Since the VCI treatment of the vibrational motions accounts for vibrational mixing and delocalization, overtones and combination bands were also observed and quantified in the intermolecular regions of the two trimer isomers.
I. INTRODUCTION
Due to its impact on climate change, the greenhouse gas carbon dioxide and its complexes have been the focus of an extensive amount of recent research. Likewise, the large role that CO2 plays in industrial and environmental applications as an environmentally friendly solvent is of great interest to the general public. Essential to broadening our knowledge of such universal chemical phenomena is an understanding of the interactions that govern the molecule. In particular, the weak intermolecular van der Waals interactions are very sensitive and thus difficult to describe correctly. Fortunately, vibrational spectroscopy represents a precise technique to explore these complicated interactions and provides insight into the true nature of the potential energy surface (PES) and chemistry of carbon dioxide systems.
The vibrational structure of the CO2 monomer and dimer has long been studied by various spectroscopic techniques. The fundamental, overtone, and combination bands, along with the Fermi dyad of the isolated molecule, have been observed with great experimental precision, typically in the infrared spectrum.1–12 Likewise, theoretical studies of the monomer are also numerous, showing agreement with experimental band assignments within only a few wavenumbers.13–19 The weak van der Waals interactions of the carbon dioxide dimer have also become the focal point of recent experimental and theoretical investigations.20–25 In particular, Moazzen-Ahmadi and co-workers26,27 have observed five intermolecular vibrations via infrared combination bands for this species with the help of the accurate ab initio calculations performed by Wang et al.28 The current authors have also contributed to this exploration by investigating the CO2 monomer and dimer and obtaining theoretical vibrational frequencies that closely match the experimental observables.19
Yet, research into the CO2 trimer is sparse. Infrared spectroscopy has identified two structures: a planar cyclic (C3h symmetry) isomer and a non-planar barrel-shaped (C2 symmetry) isomer, both shown in Fig. 1.29–31 These structures, along with a few others, have also been predicted theoretically.32–37 Density functional theory methods and newly developed PESs have been able to distinguish these two structures, usually showing the barrel-shaped isomer as two tenths of a kcal mol−1 more stable than the cyclic isomer. Even less understood is the vibrational structure for the trimer. Deghany et al.26,38 have shown through high-resolution infrared spectroscopy two vibrational band assignments in the cyclic spectrum at 12–13 and 18.5–19.5 cm−1. They originally attributed these peaks to the A″ symmetric out-of-plane torsion and the degenerate E″ asymmetric out-of-plane torsion, respectively. Yet, the theoretical work of Weida et al.30 places the A″ mode at a slightly higher frequency of 22.4 cm−1. To our knowledge, no examination of the intermolecular vibrational frequencies of the barrel-shaped trimer has been previously reported experimentally or theoretically.
FIG. 1.
The two carbon dioxide trimer isomers highlighted in this study are shown, along with their characteristic coordinates.
Recently, one of the current authors developed a flexible-monomer two-body potential energy function (PEF) for the carbon dioxide system.37 This new potential, termed mbCO2, was constructed by fitting permutationally invariant polynomials to the CO2 monomer and dimer configurations calculated at the CCSD(T)-F12b/aug-cc-pVTZ level of electronic structure theory. This procedure is effective at accurately describing the PES for many small molecular systems, including water,39–43 methane,44 and the hydronium ion,45 to name only a few. The accuracy of the mbCO2 PEF was observed at the time on the structural parameters and energetics of flexible dimers and trimers, as well as on the binding energies of larger CO2 clusters, up to the tridecamer. More recently, its accuracy was exhibited in predicting the vibrational structure for the CO2 monomer and dimer, including the combination and overtone band assignments and Fermi resonance.19
The accuracy of the calculated vibrational frequencies is also partially dictated by the chosen coordinate system and the approximations involved in solving the vibrational Schrödinger equation. Vibrational self-consistent field (VSCF), vibrational second-order Møller–Plesset perturbation (VMP2), and vibrational configuration interaction (VCI) methods have been developed to go beyond harmonic approximation and incorporate anharmonic contributions. These vibrational methods are constructed similar to their electronic structure counterparts and represent a hierarchy of increasing accuracy. Additionally, the choice of coordinate space is crucial for an accurate depiction of the vibrational degrees of freedom. Often, Cartesian coordinates are preferred since they reduce the complexity of the kinetic energy operator (KEO) and produce accurate results for rigid motions, typically in the intramolecular region. However, the slow, floppy vibrations in the intermolecular region are best described using curvilinear coordinates.46–50
In this work, we combine internal coordinates with a hierarchy of theoretical vibrational structure techniques to treat the large-amplitude motions of the CO2 trimer isomers. This approach allows for the accurate determination of the intermolecular vibrational frequencies and direct comparison with the experimental results. Using the mbCO2 PEF, we can accurately show the fundamental, overtone, and combination band assignments in this sparsely studied complex.
II. METHODOLOGY
A. Potential energy surface
The PES calculations in this work were performed with our previously developed flexible-monomer two-body potential energy function, mbCO2.37 The fourth-degree polynomial function was used for two-body interactions, instead of the originally constructed fifth-degree function. The contour plots of the trimer PESs are shown in Figs. 2 and 3 along characteristic coordinates for each isomer. The energy minimum for the cyclic trimer is located at RCC = 4.014, ϕ = 0°, and β = 39.1°. The minimum for the barrel-shaped trimer is located at x = 2.151 Å, y = 3.00 Å, z = 2.870 Å, β = 21.0°, and γ = 11°. To obtain these minimum energy structures, the CO2 trimers were optimized using the mbCO2 potential, and the harmonic vibrational frequencies were determined. For both geometry optimizations and vibrational frequency calculations, numerical energy derivatives were performed with the central difference approach and a step size of 5.0 × 10−3 Å.
FIG. 2.
Intermolecular potential energy surface of the cyclic CO2 trimer near the minimum energy structure (−1335 cm−1) with a contour spacing of 20 cm−1. The fourth-degree mbCO2 potential function37 was used. In each plot, all other coordinates, including the intramolecular bond distances, are held fixed.
FIG. 3.
Intermolecular potential energy surface of the barrel-shaped CO2 trimer near the minimum energy structure (−1404 cm−1) with a contour spacing of 20 cm−1. The fourth-degree mbCO2 potential function37 was used. In each plot, all other coordinates, including the intramolecular bond distances, are held fixed.
Additionally, the carbon dioxide trimers were evaluated using ab initio electronic structure calculations at the CCSD(T)-F12b level of theory and aug-cc-pVTZ basis set implemented in the MOLPRO software package.51 Each of the trimers was first optimized, after which the harmonic frequencies were calculated numerically.
For the anharmonic vibrational structure calculations, we expressed the full PES of the CO2 trimers using an n-mode grid expansion with curvilinear normal coordinates, Q, as
| (1) |
where
| (2) |
| (3) |
| (4) |
etc. Each expansion term included 7n potential-optimized discrete variable representation (DVR) basis points, where n is the number of coupled modes. In this work, nine coupled modes were considered for the PES. Even though the total number of basis points is large, the relatively modest amount of grid points along any single coordinate could lead to the slow convergence of the vibrational correlation methods mentioned below. The NITROGEN program52 was used to compile the grid points, and the mbCO2 function was used to evaluate the single point potential energies at each grid point.
We describe the intermolecular modes of the two trimers using curvilinear normal coordinates and a reduced-dimensional treatment of the PES. This approach, which entails ignoring the intramolecular motions of the trimers, is justified due to the small coupling between the intramolecular and intermolecular degrees of freedom. Many previous studies have remarked on this fact, especially in the case of water molecules.46–50,53,54 The truncated treatment helps mitigate the size of the potential term with little loss in accuracy. In addition, it allows for more complete expansions of the potential and kinetic energy terms, as well as more exact solutions of the vibrational Schrödinger equation.
B. Vibrational Schrödinger equation
The PES of the carbon dioxide trimers is included in the following vibrational Hamiltonian with curvilinear coordinates:55,56
| (5) |
where
| (6) |
G is the kinetic energy operator (KEO) G matrix, g−1 is its determinant, and V(Q) is the potential energy term. Applying the chain rule to the KEO [the first term in Eq. (5)] yields a separable version of the operator, which can be evaluated through an n-mode expansion.56,57 These separable components refer to the diagonal (M) and off-diagonal (K) elements of the G matrix terms, the ∇G term, and the pseudo-potential term, commonly denoted as Vg,
| (7) |
The n-mode representation used for the description of the PES is equally applicable and effective at treating the matrix element terms in the KEO. Many-body expansion orders of the Hamiltonian are denoted as , following the notation used by Strobusch and Scheurer.56,57 Throughout this work, the following expansion was used: V(9)/T(9,4,4,4). This specific expansion order was chosen based on how closely the resulting VSCF calculation agreed with the complete expansion, V(9)/T(9,9,9,9), for the intermolecular frequencies of the cyclic and barrel-shaped trimers. Additionally, the truncated expansion significantly reduces the computational cost of the vibrational calculations, especially for correlated methods. We have chosen a high-coupling approach for accuracy, but it should be noted that reasonable results are also obtained with lower level couplings. For example, V(3)/T(3,3,3,3) produces results within 3% of the complete expansion for the considered states from VSCF estimates (see the supplementary material).
Solutions to the vibrational Schrödinger equation are described at length in the literature,58–63 and only a brief refresher is presented here. The solutions can be obtained with a number of vibrational structure approaches, which are formulated much like their electronic structure counterparts. The vibrational self-consistent field approach (VSCF),64–67 which is exact when the Hamiltonian is additively separable, defines the solutions to the Schrödinger equation wavefunctions as products of one-mode functions, given by
| (8) |
where nk represents the quantum number of the kth mode and is the one-mode function with energy . More accurate vibrational correlation methods, including vibrational second-order Møller–Plesset perturbation theory (VMP2)58,61,68 and vibrational configuration interaction (VCI),69–71 improve on the VSCF ansatz by explicitly accounting for the interactions between molecular vibrations (mode–mode coupling).
In this study for VMP2, we used a full Hamiltonian and only computed configurations where the maximum sum of quantum numbers was less than or equal to 6. This choice was justified considering the large energy differences between the excited modes and the fundamentals and the convergence of the VMP2 energies at increasing quantum numbers. However, it is possible that nearly degenerate energies could lead to (artificially) large contributions due to a very small VMP2 energy denominator. VCI results can be obtained in a familiar way to the electronic structure approach, and the procedure is found elsewhere in the literature.58,61,68–71 Similarly, only configurations with sums of quantum numbers less than or equal to 5 were considered in this work (a maximum number of 2002 VCI configurations were considered for each CO2 trimer). Excited state energies and VCI configuration amplitudes can be found in the supplementary material.
III. RESULTS
A. Cyclic
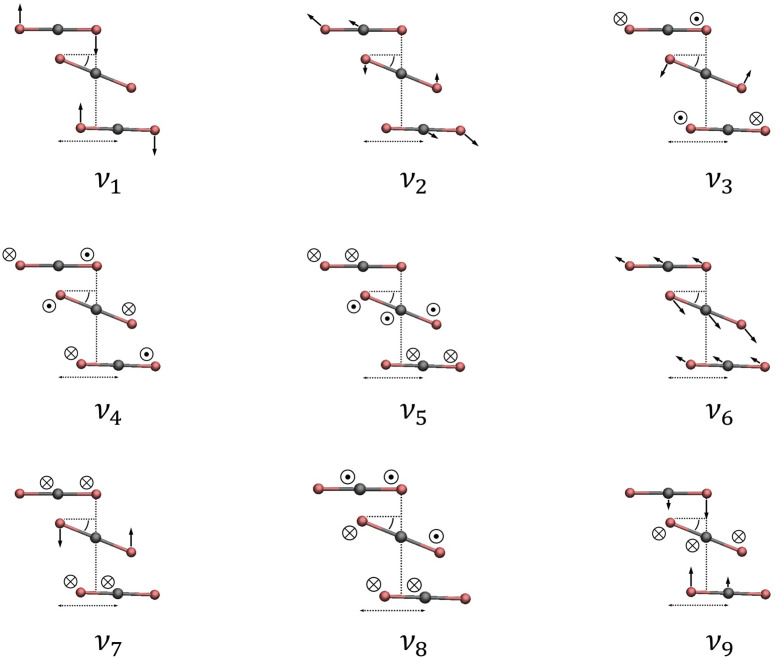
The cyclic C3ν CO2 trimer contains nine intermolecular fundamental vibrational modes, as shown in Fig. 4, ordered by increasing VSCF energy. The remaining 12 high-frequency intramolecular modes are not described in this work. The two vibrations with the lowest frequencies (ν1 and ν2) both have E″ symmetry and are degenerate, representing out-of-plane motions. Next is the out-of-plane symmetric torsion fundamental (ν3), with A″ symmetry. There are four in-plane stretch and bend modes, all with E′ symmetry, which have frequencies according to the VSCF between 49 and 55 cm−1. Finally, the most energetic fundamentals in the intermolecular region are the symmetric in-plane stretch (ν8) and the symmetric in-plane bend (ν9) modes, both having A′ symmetry.
FIG. 4.
The nine intermolecular fundamental vibrational modes of the CO2 trimer are shown, ordered by increasing energy from the VSCF computation. Only the E″ degenerate out-of-plane torsions (ν1 and ν2) and the A″ symmetric out-of-plane torsion (ν3) have been observed experimentally.
Table I shows the energy levels associated with each fundamental vibration in the intermolecular region at different levels of vibrational structure theory. The agreement among the lower energy vibrations at different levels of theory is particularly good. This is the case even when comparing the CCSD(T)-F12/aVDZ/HAR results to those using the mbCO2 potential. However, at this CCSD(T)-F12 level, large symmetry breaking is observed for the E″ modes, as well as to a lesser degree for the E′ modes (ν4 and ν5, and ν6 and ν7). This behavior is strange but is likely attributable to the use of numerical derivatives and an incomplete convergence to the minimum energy structure. A good agreement between the low energy vibrations was also observed for the in-plane bend and the out-of-phase torsion modes of the CO2 dimer.19 There, the fundamental vibrations with energies less than 30 cm−1 exhibited fairly consistent results. The outliers in both the dimer and the cyclic trimer are the mbCO2/HAR results, which are overestimated and underestimated, respectively. The E′ modes, which exhibit frequencies between 40 and 60 cm−1 when evaluated with the mbCO2 potential, are slightly overestimated by the coupled cluster harmonic approximation treatment. Furthermore, VMP2 shows that modes ν4 and ν5 are slightly less energetic compared to the other vibrational structure methods. This is likely due to the more complete treatment of the vibrational frequencies with VMP2 than that with VSCF. In addition, the VCI results may be less accurate than those of VMP2 as well due in part to the smaller number of configurations used and the slow convergence of the approach (see the supplementary material). In addition, the A′ modes are overestimated at the harmonic level compared to the other vibrational structure approaches. This overestimation is mainly due to the one-dimensional anharmonicity (deviations from the harmonic approximation), given that VSCF compares favorably to both VMP2 and VCI results. Again, this result is similar to the most energetic intermolecular fundamental vibration of the CO2 dimer (symmetric in-plane bend).19
TABLE I.
The low-lying intermolecular vibrational energy levels in cm−1 of the CO2 cyclic trimer obtained with the harmonic approximation, as well as VSCF, VMP2, and VCI methods.
| HAR | HAR | VSCF | VMP2 | VCI | |||
|---|---|---|---|---|---|---|---|
| CCSD(T)-F12b/aVDZ | mbCO2 | mbCO2 | mbCO2 | mbCO2 | Experimenta | Theoryb | |
| ν1(E″)c | 16.9 | 11.0 | 15.9 | 12.0 | 13.5 | 12.301 | |
| ν2(E″)c | 10.75 | 11.4 | 16.6 | 12.3 | 15.7 | ||
| ν3(A″) | 25.58 | 19.6 | 24.2 | 21.0 | 22.2 | 18.7 | 22.4 |
| ν4(E′)c | 60.12 | 51.8 | 49.5 | 44.1 | 49.8 | ||
| ν5(E′)c | 58.12 | 52.4 | 49.9 | 43.0 | 49.1 | ||
| ν6(E′)c | 68.82 | 58.2 | 53.9 | 55.4 | 54.6 | ||
| ν7(E′)c | 66.34 | 58.8 | 54.4 | 54.6 | 53.9 | ||
| ν8(A′) | 77.43 | 65.5 | 59.9 | 57.2 | 59.4 | ||
| ν9(A′) | 108.59 | 99.5 | 87.9 | 94.5 | 91.3 |
Furthermore, our results suggest that the previous experimental assignments of the vibrational motions in the intermolecular region are incorrect. Using infrared spectroscopy, Deghany et al. assigned an out-of-plane intermolecular torsion mode to a frequency between 12 and 13 cm−1, yet they indicated difficulty in distinguishing between the E″ and A″ motions.26 Their preferred assignment was 13.0 cm−1 for the A″ symmetric torsion due to the presence of only one unperturbed band, instead of two as expected for the degenerate E″ modes. However, recently in a review, Moazzen-Ahmadi and McKellar indicated that “there is really no clear criterion for the choice.”74 Yet, assuming E″ symmetry of the out-of-plane torsional band yields a frequency of 12.301 cm−1. This result compares favorably with the degenerate E″ modes in this work found at 12.0 and 12.3 cm−1 at the VMP2 level of theory. Conversely, then, the symmetric torsion (A″) can be assumed to have a frequency near 18.7 cm−1 according to the experimental spectrum, which is slightly overestimated with the VMP2 frequency at 21.0 cm−1. Another theoretical investigation has shown this symmetric torsion to have a frequency of 22.4 cm−1, and our previous work on the CO2 dimer gives a similar symmetric out-of-plane torsion a value of 22.6 cm−1. However, the assignment of peaks in this region is difficult due to the abundance of possible combination modes and allowed symmetries. Although our results cannot completely explain the general peculiarity in the experimental combination band region, they do favor a revised assignment of the peaks.
Additional insights into the nature of the overtone and combination bands in the intermolecular region can be gleaned from VCI theory. A complete list of VCI frequencies and wavefunction coefficients is found in the supplementary material. The relatively large amount of mixing in these modes would tend to indicate that the VSCF would perform poorly when compared to the correlated methods. Instead, fortuitous error cancellation is likely a factor. The overwhelming amount of mode–mode coupling in the region underscores the difficulty in interpreting the combination bands in the asymmetric region of the experimental spectrum. Yet, due to the symmetry of the cyclic trimer, there do exist experimental and theoretical points of comparison, unlike for the intermolecular vibrational modes of the barrel-shaped trimer, which have never been investigated at this level of accuracy.
B. Barrel-shaped
The nine fundamental intermolecular vibrational degrees of freedom for the barrel-shaped CO2 trimer are shown in Fig. 5, ordered by increasing VSCF energy. Again, we neglect the treatment of the 12 high-frequency intramolecular modes in this work. The C2 point group symmetry of the isomer allows for only A and B symmetric mode vibrations, listed in Table II—all of which are infrared-active. Although not depicted in Fig. 5, most of the vibrational modes involve combinations of both in-plane (arrows) and out-of-plane (circles) motions; however, for clarity, we only show the predominant motion. The two lowest energy modes contain a C2 rotation axis (A symmetry) and are best characterized by their in-plane (also in-phase due to the C2 rotational symmetry) motions. Mode ν3, also with A symmetry, contains out-of-plane torsions of the CO2 basal dimer pair coupled with an in-plane torsion of the dorsal monomer. The ν4 mode exhibits B symmetry and involves an out-of-phase torsion of the basal monomers about the x axis. Modes ν3, ν7, and ν9 are all symmetric motions that contain combinations of in-plane and out-of-plane vibrations. Modes ν5 and ν8 are asymmetric vibrations, characterized by the out-of-phase motions of all the molecules. Finally, ν6 is the only in-plane vibration that exhibits B symmetry.
FIG. 5.
The nine intermolecular fundamental vibrational modes of the CO2 barrel-shaped trimer are shown, ordered by increasing energy from the VSCF computation.
TABLE II.
The fundamental intermolecular vibrational energy levels in cm−1 of the CO2 barrel-shaped trimer obtained with the harmonic approximation, as well as VSCF, VMP2, and VCI methods.
| HAR | HAR | VSCF | VMP2 | VCI | |
|---|---|---|---|---|---|
| CCSD(T)-F12b/aVDZ | mbCO2 | mbCO2 | mbCO2 | mbCO2 | |
| ν1(A) | 9.69 | 9.3 | 11.6 | 9.7 | 10.5 |
| ν2(A) | 30.38 | 26.7 | 25.6 | 21.4 | 25.7 |
| ν3(A) | 37.68 | 33.2 | 30.6 | 29.0 | 29.3 |
| ν4(B) | 42.85 | 39.9 | 33.7 | 30.9 | 32.2 |
| ν5(A) | 59.51 | 53.6 | 46.6 | 39.4 | 45.5 |
| ν6(B) | 57.62 | 52.5 | 47.6 | 44.6 | 49.2 |
| ν7(A) | 89.38 | 85.0 | 77.1 | 69.5 | 74.9 |
| ν8(B) | 100.22 | 99.5 | 89.9 | 88.1 | 88.8 |
| ν9(A) | 117.22 | 111.7 | 96.8 | 86.6 | 91.6 |
The frequencies associated with these vibrations are detailed in Table II using different PESs and at varying levels of theory. Each theoretical method identifies the symmetric in-plane torsion of the basal dimer pair (ν1) as the lowest energy vibration ranging anywhere from 9 to 12 cm−1. The harmonic approximation frequencies using both CCSD(T) theory and mbCO2 potential show a very close agreement with the VMP2 result, while VSCF and VCI frequencies for this mode are, however, slightly more energetic. The ν2 mode is observed at about 25 cm−1 for all of the mbCO2 computations. The next five mode frequencies (ν3–ν7) are found with excitations as low as 29 cm−1 and as high as 85 cm−1. The two most energetic vibrations for the barrel-shaped trimer are both found near 90 cm−1 at all levels of theory, except the harmonic approximation. Here, both of these modes are found at or above 100 cm−1. This speaks to the apparent one-dimensional anharmonicity of the ν8 and ν9 modes. Notably, VMP2 predicts that the ν8 frequency is slightly (1.5 cm−1) higher than the ν9 frequency. Elsewhere, the VSCF ordering of the intermolecular fundamentals is fairly consistent with other methods. Exceptions also include the ν5 and ν6 pair at both harmonic approximations.
To our knowledge, there are no experimental spectra for the intermolecular frequencies of the CO2 barrel-shaped trimer. Hopefully, this work will serve as a guidepost for future experimental explorations. As is the case for the cyclic trimer, the VCI approach normally provides the most accurate representation of the vibrational structure of molecules. Yet, in this case, since the number of configurations in the VCI approach was limited, there is some concern about its convergence and thus about the accuracy compared to that of VMP2. In any case, the VCI coefficients provide insight into the large amount of mode coupling in the intermolecular region of the barrel-shaped spectrum. Again, fortuitous error cancellation is likely a strong component for the agreement between the VSCF and the correlated approaches. This also more clearly contextualizes the overtones and combination bands. A complete list of the VCI coefficients is found in the supplementary material.
IV. CONCLUSIONS
We have presented the intermolecular vibrational structure of two CO2 trimer isomers evaluated with our mbCO2 PES. Fundamental, overtone, and combination bands are outlined for each structure. For the cyclic trimer, a comparison to the experimental spectra indicates a mischaracterization of the two previously assigned vibrational excited states. In particular, the vibrational excitation at 12 cm−1 is shown to have E″ symmetry, while the frequency found about 7 cm−1 higher is predicted to be the symmetric A″ mode. This agrees with other theoretical work on the cyclic trimer and is supported by frequencies associated with similar vibrational motions for the CO2 dimer. However, there is still the question of the missing combination band peak in this region, which hopefully future investigations can resolve. We also show the first complete description of the intermolecular frequencies for the barrel-shaped trimer. Future endeavors will aim to rigorously address the vibrational spectrum of other molecular systems containing CO2 molecules, including the CO2 tetramer and rare gas carbon dioxide complexes.
SUPPLEMENTARY MATERIAL
See the supplementary material for a complete list of VSCF, VMP2, and VCI vibrational frequencies.
ACKNOWLEDGMENTS
This research was supported by the National Science Foundation through a subaward (Grant No. ACI-1550588), by the American Chemical Society Petroleum Research Fund (Grant No. 58240-UNI6), and by the National Institutes of Health. O.S. was supported by the Florida Education Fund. A.S. was supported by LSAMP-BD, funded by the National Science Foundation (Grant No. HRD-1700556). J.R. was supported by the National Institute of General Medical Sciences of the National Institutes of Health (Grant No. R25GM061331). Computing resources were provided by XSEDE (Grant No. TG-CHE150093) and by the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract No. DE-AC02-06CH11357.
DATA AVAILABILITY
The data that support the findings of this study are available within the article and its supplementary material and are openly available in the GitHub repository (https://github.com/sodelab) at https://doi.org/10.5281/zenodo.4310535.
REFERENCES
- 1.Martin P. E. and Barker E. F., Phys. Rev. 41, 291 (1932). 10.1103/physrev.41.291 [DOI] [Google Scholar]
- 2.Adel A. and Dennison D. M., Phys. Rev. 43, 716 (1933). 10.1103/physrev.43.716 [DOI] [Google Scholar]
- 3.Adel A. and Dennison D. M., Phys. Rev. 44, 99 (1933). 10.1103/physrev.44.99 [DOI] [Google Scholar]
- 4.Chedin A., J. Mol. Spectrosc. 76, 430 (1979). 10.1016/0022-2852(79)90236-4 [DOI] [Google Scholar]
- 5.Baranov Y. I. and Vigasin A. A., J. Mol. Spectrosc. 193, 319 (1999). 10.1006/jmsp.1998.7743 [DOI] [PubMed] [Google Scholar]
- 6.Vigasin A. A., Baranov Y. I., and Chlenova G. V., J. Mol. Spectrosc. 213, 51 (2002). 10.1006/jmsp.2002.8529 [DOI] [Google Scholar]
- 7.Stoicheff B. P., Can. J. Phys. 36, 218 (1958). 10.1139/p58-026 [DOI] [Google Scholar]
- 8.Amat G. and Pimbert M., J. Mol. Spectrosc. 16, 278 (1965). 10.1016/0022-2852(65)90123-2 [DOI] [Google Scholar]
- 9.Andrade e Silva M. H. and Amat G., J. Mol. Spectrosc. 29, 384 (1969). 10.1016/0022-2852(69)90115-5 [DOI] [Google Scholar]
- 10.Howard-Lock H. E. and Stoicheff B. P., J. Mol. Spectrosc. 37, 321 (1971). 10.1016/0022-2852(71)90302-x [DOI] [Google Scholar]
- 11.Bertrán J. F., Spectrochim. Acta, Part A 39, 119 (1983). 10.1016/0584-8539(83)80066-x [DOI] [Google Scholar]
- 12.Montero S., J. Chem. Phys. 79, 4091 (1983). 10.1063/1.446357 [DOI] [Google Scholar]
- 13.Allen W. D., Yamaguchi Y., Császár A. G., D. A. Clabo, Jr., Remington R. B., and Schaefer H. F. III, Chem. Phys. 145, 427 (1990). 10.1016/0301-0104(90)87051-c [DOI] [Google Scholar]
- 14.Maslen P. E., Jayatilaka D., Colwell S. M., Amos R. D., and Handy N. C., J. Chem. Phys. 95, 7409 (1991). 10.1063/1.461367 [DOI] [Google Scholar]
- 15.Martin J. M. L., Taylor P. R., and Lee T. J., Chem. Phys. Lett. 205, 535 (1993). 10.1016/0009-2614(93)80009-e [DOI] [Google Scholar]
- 16.Martins Filho H. P., Spectrochim. Acta, Part A 58, 2621 (2002). 10.1016/s1386-1425(02)00006-9 [DOI] [PubMed] [Google Scholar]
- 17.Czakó G., Furtenbacher T., Császár A. G., and Szalay V., Mol. Phys. 102, 2411 (2004). 10.1080/0026897042000274991 [DOI] [Google Scholar]
- 18.Rodriguez-Garcia V., Hirata S., Yagi K., Hirao K., Taketsugu T., Schweigert I., and Tasumi M., J. Chem. Phys. 126, 124303 (2007). 10.1063/1.2710256 [DOI] [PubMed] [Google Scholar]
- 19.Maystrovsky S., Keçeli M., and Sode O., J. Chem. Phys. 150, 144302 (2019). 10.1063/1.5089460 [DOI] [PubMed] [Google Scholar]
- 20.Miller R. E. and Watts R. O., Chem. Phys. Lett. 105, 409 (1984). 10.1016/0009-2614(84)80051-2 [DOI] [Google Scholar]
- 21.Pubanz G. A., Maroncelli M., and Nibler J. W., Chem. Phys. Lett. 120, 313 (1985). 10.1016/0009-2614(85)87064-0 [DOI] [Google Scholar]
- 22.Jucks K. W., Huang Z. S., Dayton D., Miller R. E., and Lafferty W. J., J. Chem. Phys. 86, 4341 (1987). 10.1063/1.451895 [DOI] [Google Scholar]
- 23.Walsh M. A., England T. H., Dyke T. R., and Howard B. J., Chem. Phys. Lett. 142, 265 (1987). 10.1016/0009-2614(87)80935-1 [DOI] [Google Scholar]
- 24.Pine A. S. and Fraser G. T., J. Chem. Phys. 89, 100 (1988). 10.1063/1.455512 [DOI] [Google Scholar]
- 25.Konno T. and Ozaki Y., Chem. Phys. Lett. 394, 198 (2004). 10.1016/j.cplett.2004.06.133 [DOI] [Google Scholar]
- 26.Dehghany M., Afshari M., Moazzen-Ahmadi N., and McKellar A. R. W., J. Chem. Phys. 128, 064308 (2008). 10.1063/1.2834931 [DOI] [PubMed] [Google Scholar]
- 27.Oliaee J. N., Dehghany M., Rezaei M., McKellar A. R. W., and Moazzen-Ahmadi N., J. Chem. Phys. 145, 174302 (2016). 10.1063/1.4966146 [DOI] [PubMed] [Google Scholar]
- 28.Wang X.-G., T. Carrington, Jr., and Dawes R., J. Mol. Spectrosc. 330, 179 (2016). 10.1016/j.jms.2016.08.006 [DOI] [Google Scholar]
- 29.Fraser G. T., Pine A. S., Lafferty W. J., and Miller R. E., J. Chem. Phys. 87, 1502 (1987). 10.1063/1.453260 [DOI] [Google Scholar]
- 30.Weida M. J., Sperhac J. M., and Nesbitt D. J., J. Chem. Phys. 103, 7685 (1995). 10.1063/1.470291 [DOI] [Google Scholar]
- 31.Weida M. J. and Nesbitt D. J., J. Chem. Phys. 105, 10210 (1996). 10.1063/1.472930 [DOI] [Google Scholar]
- 32.Tsuzuki S., Klopper W., and Lüthi H. P., J. Chem. Phys. 111, 3846 (1999). 10.1063/1.479688 [DOI] [Google Scholar]
- 33.Boychenko I. V. and Huber H., J. Chem. Phys. 124, 014305 (2006). 10.1063/1.2139090 [DOI] [PubMed] [Google Scholar]
- 34.Lemke K. H. and Seward T. M., Chem. Phys. Lett. 573, 19 (2013). 10.1016/j.cplett.2013.04.044 [DOI] [Google Scholar]
- 35.Yeole S. D., Sahu N., and Gadre S. R., Phys. Chem. Chem. Phys. 14, 7718 (2012). 10.1039/c2cp23761j [DOI] [PubMed] [Google Scholar]
- 36.Neogi S. G., Talukder S., and Chaudhury P., Struct. Chem. 25, 909 (2013). 10.1007/s11224-013-0360-8 [DOI] [Google Scholar]
- 37.Sode O. and Cherry J. N., J. Comput. Chem. 38, 2763 (2017). 10.1002/jcc.25053 [DOI] [PubMed] [Google Scholar]
- 38.Dehghany M., McKellar A. R. W., Afshari M., and Moazzen-Ahmadi N., Mol. Phys. 108, 2195 (2010). 10.1080/00268976.2010.496742 [DOI] [Google Scholar]
- 39.Cisneros G. A., Wikfeldt K. T., Ojamäe L., Lu J., Xu Y., Torabifard H., Bartók A. P., Csányi G., Molinero V., and Paesani F., Chem. Rev. 116, 7501 (2016). 10.1021/acs.chemrev.5b00644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Medders G. R., Götz A. W., Morales M. A., Bajaj P., and Paesani F., J. Chem. Phys. 143, 104102 (2015). 10.1063/1.4930194 [DOI] [PubMed] [Google Scholar]
- 41.Babin V., Leforestier C., and Paesani F., J. Chem. Theory Comput. 9, 5395 (2013). 10.1021/ct400863t [DOI] [PubMed] [Google Scholar]
- 42.Medders G. R., Babin V., and Paesani F., J. Chem. Theory Comput. 10, 2906 (2014). 10.1021/ct5004115 [DOI] [PubMed] [Google Scholar]
- 43.Babin V., Medders G. R., and Paesani F., J. Chem. Theory Comput. 10, 1599 (2014). 10.1021/ct500079y [DOI] [PubMed] [Google Scholar]
- 44.Majumder M., Hegger S. E., Dawes R., Manzhos S., Wang X.-G., C. Tucker, Jr., Li J., and Guo H., Mol. Phys. 113, 1823 (2015). 10.1080/00268976.2015.1015642 [DOI] [Google Scholar]
- 45.Xie Z. and Bowman J. M., J. Chem. Theory Comput. 6, 26 (2009). 10.1021/ct9004917 [DOI] [PubMed] [Google Scholar]
- 46.Low G. R. and Kjaergaard H. G., J. Chem. Phys. 110, 9104 (1999). 10.1063/1.478832 [DOI] [Google Scholar]
- 47.Wang Y., Carter S., Braams B. J., and Bowman J. M., J. Chem. Phys. 128, 071101 (2008). 10.1063/1.2839303 [DOI] [PubMed] [Google Scholar]
- 48.Watanabe Y., Maeda S., and Ohno K., J. Chem. Phys. 129, 074315 (2008). 10.1063/1.2973605 [DOI] [PubMed] [Google Scholar]
- 49.Wang Y. and Bowman J. M., Chem. Phys. Lett. 491, 1 (2010). 10.1016/j.cplett.2010.03.025 [DOI] [Google Scholar]
- 50.Yagi K., Keçeli M., and Hirata S., J. Chem. Phys. 137, 204118 (2012). 10.1063/1.4767776 [DOI] [PubMed] [Google Scholar]
- 51.Werner H. J., Knowles P. J., Knizia G., Manby F. R., Schütz M., Celani P., Györffy W., Kats D., Korona T., Lindh R., Mitrushenkov A., Rauhut G., Shamasundar K. R., Adler T. B., Amos R. D., Bernhardsson A., Berning A., Cooper D. L., Deegan M. J. O., Dobbyn A. J., Eckert F., Goll E., Hampel C., Hesselmann A., Hetzer G., Hrenar T., Jansen G., Köppl C., Liu Y., Lloyd A. W., Mata R. A., May A. J., McNicholas S. J., Meyer W., Mura M. E., Nicklass A., O’Neill D. P., Palmieri P., Peng D., Pflüger K., Pitzer R., Reiher M., Shiozaki T., Stoll H., Stone A. J., Tarroni R., Thorsteinsson T., and Wang M., MOLPRO, version 2015.1, a package of ab initio programs (2015), see http:// www.molpro.net.
- 52.Changala P. B., http://www.colorado.edu/nitrogen, 2018.
- 53.Schofield D. P. and Kjaergaard H. G., Phys. Chem. Chem. Phys. 5, 3100 (2003). 10.1039/b304952c [DOI] [Google Scholar]
- 54.Salmi T., Hänninen V., Garden A. L., Kjaergaard H. G., Tennyson J., and Halonen L., J. Phys. Chem. A 112, 6305 (2008). 10.1021/jp800754y [DOI] [PubMed] [Google Scholar]
- 55.Podolsky B., Phys. Rev. 32, 812 (1928). 10.1103/physrev.32.812 [DOI] [Google Scholar]
- 56.Strobusch D. and Scheurer C., J. Chem. Phys. 135, 124102 (2011). 10.1063/1.3637629 [DOI] [PubMed] [Google Scholar]
- 57.Strobusch D. and Scheurer C., J. Chem. Phys. 135, 144101 (2011). 10.1063/1.3646514 [DOI] [PubMed] [Google Scholar]
- 58.Norris L. S., Ratner M. A., Roitberg A. E., and Gerber R. B., J. Chem. Phys. 105, 11261 (1998). 10.1063/1.472922 [DOI] [Google Scholar]
- 59.Chaban G. M., Jung J. O., and Gerber R. B., J. Chem. Phys. 111, 1823 (1999). 10.1063/1.479452 [DOI] [Google Scholar]
- 60.Yagi K., Hirao K., Taketsugu T., Schmidt M. W., and Gordon M. S., J. Chem. Phys. 121, 1383 (2004). 10.1063/1.1764501 [DOI] [PubMed] [Google Scholar]
- 61.Christiansen O., J. Chem. Phys. 119, 5773 (2003). 10.1063/1.1601593 [DOI] [Google Scholar]
- 62.Christiansen O., Phys. Chem. Chem. Phys. 9, 2942 (2007). 10.1039/b618764a [DOI] [PubMed] [Google Scholar]
- 63.Keçeli M., Shiozaki T., Yagi K., and Hirata S., Mol. Phys. 107, 1283 (2009). 10.1080/00268970902889626 [DOI] [Google Scholar]
- 64.Bowman J. M., J. Chem. Phys. 68, 608 (1978). 10.1063/1.435782 [DOI] [Google Scholar]
- 65.Gerber R. B. and Ratner M. A., Chem. Phys. Lett. 68, 195 (1979). 10.1016/0009-2614(79)80099-8 [DOI] [Google Scholar]
- 66.Bowman J. M., Acc. Chem. Res. 19, 202 (1986). 10.1021/ar00127a002 [DOI] [Google Scholar]
- 67.Ratner M. A. and Gerber R. B., J. Phys. Chem. 90, 20 (1986). 10.1021/j100273a008 [DOI] [Google Scholar]
- 68.Yagi K., Hirata S., and Hirao K., Phys. Chem. Chem. Phys. 10, 1781 (2008). 10.1039/b719093j [DOI] [PubMed] [Google Scholar]
- 69.Christoffel K. M. and Bowman J. M., Chem. Phys. Lett. 85, 220 (1982). 10.1016/0009-2614(82)80335-7 [DOI] [Google Scholar]
- 70.Rauhut G., J. Chem. Phys. 127, 184109 (2007). 10.1063/1.2790016 [DOI] [PubMed] [Google Scholar]
- 71.Scribano Y. and Benoit D. M., Chem. Phys. Lett. 458, 384 (2008). 10.1016/j.cplett.2008.05.001 [DOI] [Google Scholar]
- 72.Murthy C. S., Singer K., and McDonald I. R., Mol. Phys. 44, 135 (1981). 10.1080/00268978100102331 [DOI] [Google Scholar]
- 73.Murthy C. S., O’Shea S. F., and McDonald I. R., Mol. Phys. 50, 531 (1983). 10.1080/00268978300102531 [DOI] [Google Scholar]
- 74.Moazzen-Ahmadi N. and McKellar A. R. W., Int. Rev. Phys. Chem. 32, 611 (2013). 10.1080/0144235x.2013.813799 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for a complete list of VSCF, VMP2, and VCI vibrational frequencies.
Data Availability Statement
The data that support the findings of this study are available within the article and its supplementary material and are openly available in the GitHub repository (https://github.com/sodelab) at https://doi.org/10.5281/zenodo.4310535.