SECAT: Quantifying differential protein-protein interaction states by network-centric analysis

Summary

Protein-protein interactions (PPIs) play critical functional and regulatory roles in cellular processes. They are essential for macromolecular complex formation, which in turn constitutes the basis for protein interaction networks that determine the functional state of a cell. We and others have previously shown that chromatographic fractionation of native protein complexes in combination with bottom-up mass spectrometric analysis of consecutive fractions supports the multiplexed characterization and detection of state-specific changes of protein complexes.

In this study, we extend co-fractionation / mass spectrometric data analysis to study PPI network dynamics, thus enabling qualitative and quantitative proteome organization assessment across samples and states. The Size-Exclusion Chromatography Algorithmic Toolkit (SECAT) implements a novel, network-centric computational framework for differential PPI network analysis. Its underlying statistical framework supports elucidation of differential quantitative abundance and stoichiometry protein attributes in a PPI context. Systematic analysis of different datasets shows that SECAT represents a more scalable and effective methodology to assess protein-network state, thus obviating explicit inference of individual protein complexes. Further, by differential analysis of PPI networks of HeLa cells in interphase and mitotic state, respectively, we demonstrate the ability of the algorithm to detect PPI network differences and to thus suggest molecular mechanisms that differentiate cellular states.

Introduction

Living cells depend on many coordinated and concurrent biochemical reactions. Most of these are catalyzed and controlled by macromolecular entities of well-defined subunit composition and 3D structure. This notion inspired the term “modular cell biology” by Hartwell and colleagues (Hartwell et al., 1999), since most biological modules consist of or contain protein complexes. It is thus a basic assumption of the modular cell biology model that alterations in protein complex structure, composition and abundance will alter the biochemical state of cells. Elucidating protein complexes and their organization in extended protein-protein interaction (PPI) networks is, therefore, of paramount importance for both basic and translational research.

Traditionally, composition and structure of protein complexes has been determined by two broad and complementary approaches, structural biology and interaction proteomics. Structural biology encompasses a suite of powerful techniques to characterize individual, purified or reconstituted protein complexes at high, at times, atomic resolution. High resolution structures have provided a wealth of functional and mechanistic insights into biochemical reactions (Campbell, 2002). However, they have been solved for only a few hundred human protein complexes and the number of cases where the structure of protein complexes is assessed across different functional states is even lower. This is contrasted by the observation that, under mild lysis conditions, approximately 60% of proteins and total protein cell mass in protein cell extracts is engaged in protein complexes (Heusel et al., 2019). As a result, methodologies for the rapid elucidation of protein complexes are still critically needed.

Interaction proteomics encompasses multiple methodologies to determine composition and, when possible, subcellular location and abundance of protein complexes, albeit at lower resolution, yet higher throughput, than structural biology techniques. Among these methods, liquid chromatography coupled to tandem mass spectrometry (Aebersold and Mann, 2003, 2016) (LC-MS/MS)—and more specifically affinity purification coupled to LC-MS/MS (AP-MS (Gingras et al., 2007))—has been most widely used. For AP-MS analyses, individual proteins are engineered to display an affinity tag and are expressed as “bait” proteins in cells. The bait and the corresponding “prey” proteins assembled around it are then isolated and qualitatively (Choi et al., 2011; Herzog et al., 2012; Krogan et al., 2006; Sowa et al., 2009) or quantitatively (Bisson et al., 2011; Collins et al., 2013; Keilhauer et al., 2015; Lambert et al., 2013) analyzed by MS. This method has proven robust across laboratories (Varjosalo et al., 2013) and, through process automation and integrative data analysis, efforts to map PPIs across the entire human proteome (Hein et al., 2015; Huttlin et al., 2015) are underway and have so far characterized interactions of more than half of canonical human proteins (Huttlin et al., 2017). This knowledge, further supported by orthogonal experimental data (e.g. yeast two-hybrid screens (Y2H) (Luck et al., 2020)) is embedded in a variety of databases, including BioPlex (Huttlin et al., 2015, 2017), STRING (Szklarczyk et al., 2019), IntAct (Orchard et al., 2014), hu.MAP (Drew et al., 2017), BioGRID (Oughtred et al., 2019) and HuRI (Luck et al., 2020) that present generic (i.e. non-context-specific) human PPI maps. These data were also used to computationally predict PPIs for previously uncharacterized proteins, for instance, via the PrePPI algorithm (Garzón et al., 2016; Zhang et al., 2013b, 2013a). While systematic PPI-mapping projects will likely further increase human interactome coverage in selected contexts (e.g. cell lines) over the next few years (Huttlin et al., 2020), their underlying technology is fundamentally limited in its ability to detect system-wide compositional or abundance changes across multiple cell states.

Protein correlation profiling (PCP) (Foster et al., 2006) and related methods (Havugimana et al., 2012; Heusel et al., 2019; Hu et al., 2019; Kirkwood et al., 2013; Kristensen et al., 2012; Scott et al., 2017; Wan et al., 2015) have been proposed as a means to concurrently analyze multiple complexes from the same sample. PCP proceeds by first separating native protein complexes, e.g. according to their hydrodynamic radius by size-exclusion chromatography (SEC), by collecting 40–80 consecutive fractions and by finally performing bottom-up mass spectrometric analysis of the proteins in each consecutive fraction. The result is a set of quantitative protein abundance profiles across the SEC separation range (Fig. 1a). Under the assumption that protein subunits of the same complex have congruent SEC profiles, the latter can be used to infer protein-protein interactions and protein complex composition. Conditional to availability of quantitative mass spectrometric data, the method further supports comparative analysis across multiple biological conditions, thus revealing condition-specific differences, critically missing from existing PPI databases. PCP datasets have been mostly analyzed using interaction-centric algorithms (Havugimana et al., 2012; Hu et al., 2019; Kristensen et al., 2012; Scott et al., 2015; Stacey et al., 2017; Wan et al., 2013, 2015). These use protein profiles from chromatographic co-elution to identify PPIs, to infer protein complex composition and to conduct qualitative and quantitative comparisons across biological conditions (Heusel et al., 2020; Scott et al., 2017). Interaction-centric algorithms are limited by the inherently low SEC resolution and the high degree of complexity of proteomic samples, thus creating a critical issue in trading off accuracy vs. sensitivity. With hundreds to thousands of proteins per SEC fraction, inferred interaction confidence is reduced, since a large fraction of non-interacting proteins may show indistinguishable elution profiles by chance (Stacey et al., 2017).

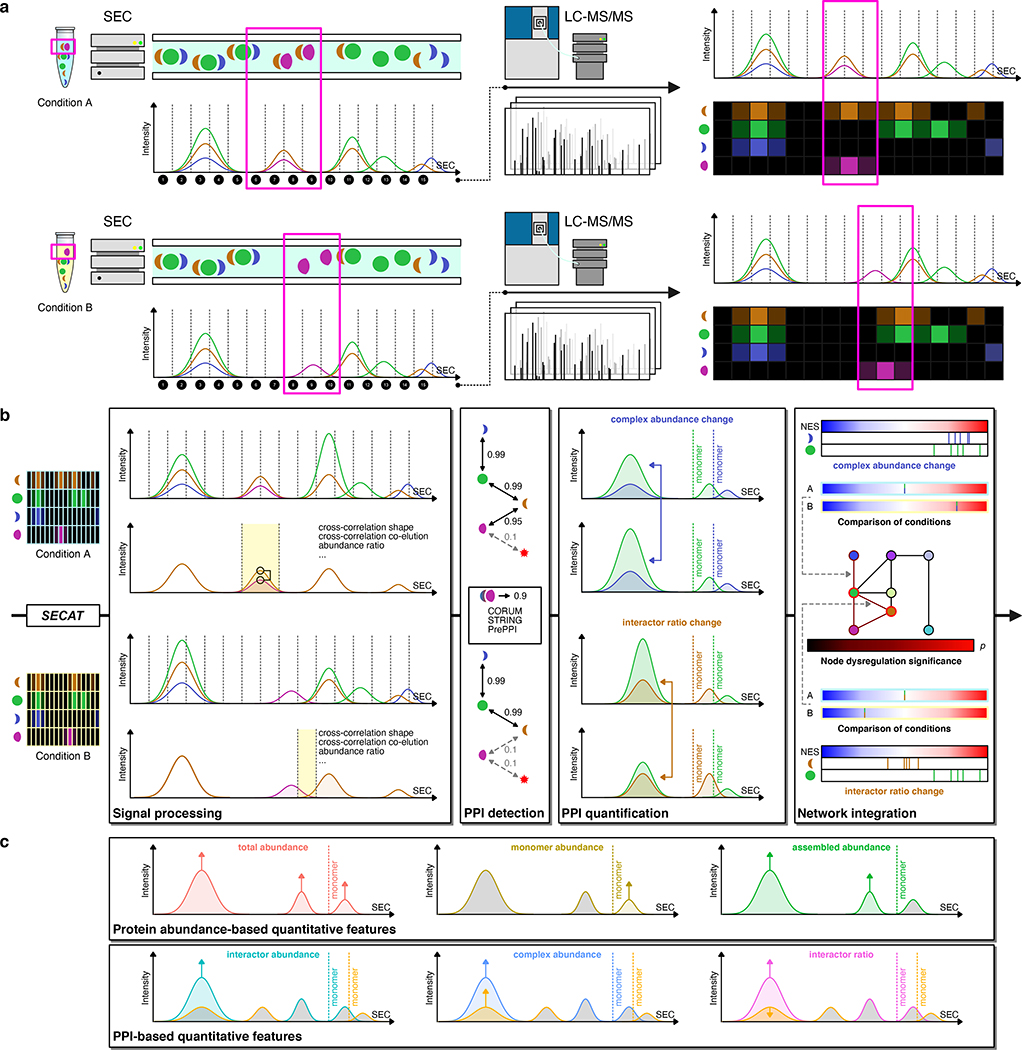
Figure 1.

Methodological overview. Symbol colors, elution profiles and network representations are matched for each protein throughout subfigures (a) and (b). (a) The SEC-SWATH-MS workflow is depicted comparing two different experimental conditions A and B. Native protein extracts are separated by SEC and individual fractions are sampled (1–15). Each fraction is separately measured by LC-MS/MS. Peptide or protein abundance grouped according to SEC fraction can be depicted as profile, whereby co-eluting proteins might be part of the same protein complex. Two experimental conditions can result in similar protein complex profiles but might differ for some proteins (highlighted in pink). (b) The SECAT algorithm uses peptide-level protein complex profiles and reference PPI networks as input. The example from (a) is used, however quantitative changes are introduced. The signal processing module computes a set of scores for the peptide profiles of candidate interactors (highlighted in yellow). Using the set of scores and ground truth positive and negative interactomes, the PPI detection module conducts semi-supervised learning and generates context-specific PPI subnetworks (proteins represented by nodes and PPIs represented by edges). Confident PPIs (solid edges) are quantified to assess complex abundance and interactor ratio changes (indicated by colored arrows) left to the monomer threshold using the PPI quantification module. The proteoVIPER algorithm based on VIPER (Alvarez et al., 2016) is used for quantitative protein inference from peptide-level abundances. Network integration: The normalized enrichment score (NES) is indicated from blue (negative) to red (positive enrichment) for each protein of a binary PPI. A statistical test is conducted to compare the NES between the conditions. Significance of changes between the experimental conditions is then integrated by a network-centric approach on all different levels. (c) SECAT provides quantitative insights on different levels, indicated by different colors. Protein abundance-based quantitative metrics are computed for total abundance, monomer abundance and assembled abundance. PPI-based quantitative metrics are provided separately for each interactor, integrated as positively correlated complex abundance or negatively correlated interactor ratio metric. Colored arrows indicate the quantitative properties used to compute the features. For total, monomer, assembled and interactor abundance, only the abundances of one interactor are used. For complex abundance and interactor ratio, both interactor abundances are used in a positively or negatively correlated setting (STAR Methods).

To address these limitations, we recently developed the algorithm CCprofiler (Heusel et al., 2019), which implements a targeted, complex-centric strategy to query the protein elution profiles generated by high resolution SEC-SWATH-MS (Heusel et al., 2019) to assess presence, composition and abundance of predefined protein complexes. Similar to targeted proteomic approaches (Picotti et al., 2012; Ting et al., 2015), transforming the problem from de novo inference of unknown protein complexes to a posteriori detection of established complexes significantly increases sensitivity. Using prior knowledge from reference databases like CORUM (Giurgiu et al., 2019), BioPlex (Huttlin et al., 2015, 2017) or STRING (Szklarczyk et al., 2019), substantially improved protein complex detection confidence, albeit at the cost of missing potential novel interactions or complexes not included in the query set. Taking advantage of the precise quantitative values generated by SWATH-MS, we have also shown that the CCprofiler strategy is well-suited to detect changes in complex-associated protein abundance across conditions (Heusel et al., 2020).

However, several critical challenges remain, that cannot be addressed by the preexisting interaction- or complex-centric strategies, especially when they are applied to studies where an increasing number of experimental conditions or samples are compared, which are already starting to emerge (Heusel et al., 2020; Scott et al., 2017). The key assumption underlying the above-described approaches is that protein complexes constitute time- and context-independent structures. This is both highly restrictive and biologically unrealistic. In contrast, accurate detection of protein complex composition differences across conditions is increasingly relevant to address key biological questions (De Lichtenberg et al., 2005). For example, the spliceosome—a complex molecular machinery controlling intron removal from pre-mRNA—consists of small nuclear RNAs (snRNA) and more than 100 protein subunits, which are assembled into a variety of submodules—each presenting highly context-specific activity and composition (Hofmann et al., 2010; Will and Luhrmann, 2011). Since only a fraction of these protein subunits is detectable across all conditions in typical bottom-up proteomic experiments, differentiating between biological effects and technical artefacts is challenging. However, if the PPIs underlying a protein complex (e.g. consisting of subunits A, B, C and D) were interpreted as a network rather than disconnected individual relationships, lack of PPI detection in a condition due to technical reasons (e.g. missing a PPI between protein A and B) is less problematic as that interaction may be substituted by another PPI (e.g. PPIs A-C or A-D). In contrast, were PPIs of these proteins with other interaction partners (e.g. PPIs A-X or A-Y) detected in this condition, the data might rather support rearrangement of protein complex composition due to biological effects.

To address these limitations, we introduce the Size-Exclusion Chromatography Algorithmic Toolkit (SECAT), which extends the PCP data analysis from well-defined, yet static complexes to PPI networks underlying potential alternative complex organization across different context and thus obviating explicit inference of protein complexes. For this purpose, SECAT leverages error-rate-controlled PPI networks for each tested condition. But in contrast to existing methods, rather than using the resulting interaction maps to infer protein complexes, SECAT transforms differential protein abundance across fractions into quantitative metrics for each PPI, representing differential complex subunit pair abundance and stoichiometry, which can be further integrated on network-level to derive a differential representation of the protein network state. In analogy to the extension of AP-MS from a qualitative (Choi et al., 2011; Herzog et al., 2012; Krogan et al., 2006; Sowa et al., 2009) to a quantitative (Bisson et al., 2011; Collins et al., 2013; Keilhauer et al., 2015; Lambert et al., 2013) characterization of PPIs, SECAT supports the quantitative characterization of PPI network states, by accounting for the dynamic rather than static nature of protein complexes.

We demonstrate that this novel, network-centric strategy for PPI analysis is robust against technical variability and overcomes key limitations of current protein-complex inference methods, while representing changes in network connectivity in an intuitive and unbiased way. By focusing on quantitative assessment of PPIs and the representation of protein complexes as dynamic rather than static entities, SECAT can identify hundreds of additional proteins associated with context-specific function in comparison to CCprofiler due to technical, conceptual and sensitivity advances. Applying SECAT to conduct differential analysis of PPI networks of HeLa cells in interphase and mitotic state, respectively, we demonstrate the ability of the algorithm to detect PPI network differences and to thus suggest molecular mechanisms that differentiate cellular states.

Results

The Size-Exclusion Chromatography Algorithmic Toolkit

SECAT was designed to systematically quantify differences in complex-bound protein abundance and interaction stoichiometry, across different conditions. It is predicated on the rationale that protein complexes represent dynamic rather than static entities with variable composition of subunits. Therefore, the algorithm makes two fundamental assumptions: First, if a specific PPI is present within different complexes, it must be mediated by the same mode of interaction (i.e. binding interface). Thus, any perturbation of a specific PPI should produce consistent effects across all complexes that include it. Second, the PPI repertoire for any given protein may consist of redundant (i.e. PPIs between a given protein and other subunits of the same complex) and orthogonal (i.e. PPIs between a given protein with subunits in different complexes) interactions.

Consistent with these assumptions, SECAT employs a network-centric strategy: First, using the experimental data, context-specific PPI networks are derived from pre-existing databases and algorithms for each tested condition. This dramatically reduces the PPI search space in comparison to previous approaches (Hu et al., 2019; Stacey et al., 2017; Wan et al., 2013). Second, these networks are used to derive novel quantitative metrics representing changes in abundance and interaction stoichiometry for proteins that are detected in complexed form based on their SEC profiles. Third, the redundant and orthogonal PPIs of the detected proteins are statistically integrated to represent the global PPI network state. In contrast to existing methods, our approach omits the explicit inference of protein complexes and provides representation of the qualitative and quantitative changes of PPI networks between experimental conditions.

The algorithm workflow comprises five steps: i) Data preprocessing, ii) Signal processing, iii) PPI detection, iv) PPI quantification and v) Network integration. The main input data include (i) the peptide-level intensity vs. SEC elution fraction profiles for the tested conditions, as acquired by SEC-SWATH-MS (Heusel et al., 2019, 2020), and (ii) one or more reference PPI networks (Fig. 1b, STAR Methods).

For data preprocessing and PPI detection, SECAT operates on proteotypic peptide-level profiles and uses the inferred proteins from upstream bottom-up proteomic analysis pipelines to assign peptides to proteins and to compute attributes, such as the expected monomeric weight for each protein. For quantitative protein and PPI abundance and interactor ratio inference, SECAT implements a novel methodology termed proteoVIPER (STAR Methods). The output of SECAT is a set of condition-specific PPI networks with metrics summarizing differential protein and PPI properties (Fig. 1c, STAR Methods).

Data preprocessing (Step 1):

As main input, SECAT requires quantitative peptide-level intensity vs. SEC elution fraction profiles, as acquired by SEC-SWATH-MS (Heusel et al., 2019, 2020) across one or more conditions. To account for sample amount differences and batch effects between SEC runs, peptide signal intensities are first normalized within conditions and replicates and then across SEC fractions (STAR Methods). Next, based on the molecular weight calibration curve of the SEC separation (Heusel et al., 2019), the SEC fraction index dividing assembled and monomeric states is determined for each inferred protein (STAR Methods). This “monomer threshold” is defined by the expected molecular weight of the monomeric subunit and is multiplied by a user-defined factor (F = 2 by default) to account for potential homomultimers and deviations of the protein’s chromatographic behavior from the calibration curve. Optionally, peptide-level profiles, grouped by inferred proteins, can be preprocessed by detrending or local-maximum peak-picking (STAR Methods). However, since consistent cross-condition and cross-replicate quantification of peptides, inferred proteins, and PPIs is a crucial requirement for SECAT, only minimal or no preprocessing is necessary.

Signal processing (Step 2):

To assess PPIs, peptide-level profiles from the complex-bound fractions of the corresponding protein pairs are queried and scored. To allow proteins to participate in multiple complexes, SECAT focuses PPI analysis on SEC fractions where both proteins are detectable (STAR Methods). To restrict the query space, candidate interactions are obtained from a comprehensive set of PPI network representations, such as CORUM (Giurgiu et al., 2019), STRING (Szklarczyk et al., 2019) or PrePPI (Garzón et al., 2016). Alternatively, all putative PPI combinations can be assessed. For each candidate PPI, peptide-level elution profiles from each protein are processed to compute chromatographic cross-correlation shape and shift (Reiter et al., 2011; Röst et al., 2014), maximal and total information criterion (Albanese et al., 2013), interactor ratio (normalized stoichiometry between interactors), SEC coverage, and monomeric fraction distance metrics (Fig. 1b, STAR Methods). The result of this step is a table in which each candidate PPI is associated with a score vector representing the properties that can differentiate between true-positive and false-positive interactions.

PPI detection (Step 3):

To generate context-specific interaction networks, partial scores from the second step are used as input to a machine learning (ML) approach based on the PyProphet algorithm (Reiter et al., 2011; Rosenberger et al., 2017; Teleman et al., 2015). This step is designed to discriminate true-positive vs. false-positive interactions and to estimate their confidence. For this purpose, a classifier is trained in a semi-supervised manner using a set of true-negative PPIs as null model and the most confidently detected PPIs (based on high confidence PPI networks, generating perfectly overlapping SEC-SWATH-MS profiles), which are evaluated and selected over multiple iterations, as a true-positive interaction gold standard model (Fig. 1b, STAR Methods). Since queried or tested candidate PPIs may by chance match co-eluting protein profiles that are not representative of true-positive interactions detectable within the experimental context, this semi-supervised learning approach is designed to achieve high sensitivity at high confidence levels (Fig. 1b, STAR Methods).

Classification is performed using an XGBoost-based (Chen and Guestrin, 2016) gradient boosting approach (STAR Methods). The first machine learning iteration is initialized by a single composite score (kickstart score) that selects only the most confident PPIs by maximizing cross-correlation shape and total interactor ratio scores, while minimizing the cross-correlation shift score between interactors (STAR Methods). The partial scores for all tested PPIs are then used to identify a new set of most confident interactions in each subsequent iteration, thus progressively increasing the classifier sensitivity. Cross-validation and “early stopping” are employed to avoid overfitting (STAR Methods). By default, SECAT learns a classifier using high confidence PPI networks (“learning reference network”; e.g. CORUM (Giurgiu et al., 2019)) and then applies it to integrate additional potential interactions from less stringent, optional networks (“query reference network”; e.g. STRING (Szklarczyk et al., 2019) or PrePPI (Garzón et al., 2016)) or all potential interactions, thus maximizing sensitivity and coverage of the assessed interactions. If a query reference network was used to restrict the query space, potentially available confidence metrics for individual interactions can be incorporated as priors by computing a group-based false discovery rate (FDR) metric (STAR Methods). In summary, this step generates a set of confidence metrics for each candidate PPI (posterior error probabilities and q-values), that allow thresholding the list at any user-defined FDR.

PPI quantification (Step 4):

The combined set of PPIs that are confidently detected—q-value < 0.05, across all experimental conditions and replicates—is then used for quantification. Specifically, for each peptide of a protein in a candidate PPI, peptide-level data within the boundaries of the SEC fractions defined in Step 2 are independently summarized. In addition, for each peptide of a protein, three metrics summarizing the total, assembled and monomeric fractions are computed. This provides quantitative metrics that can be used to assess inferred protein or PPI changes across experimental conditions, as described in the following steps (Fig. 1b, STAR Methods).

The VIPER (Alvarez et al., 2016) algorithm infers the activity of a protein from the differential expression of its transcriptional targets using a regulatory network model inferred by the ARACNe algorithm (Lachmann et al., 2016; Margolin et al., 2006). SECAT extends this conceptual strategy to estimate protein- or PPI-level metrics, i.e. abundance or interactor ratio. This is achieved by adapting VIPER to use fractionated peptide abundances instead of gene expression data (STAR Methods). To estimate protein-level metrics from peptide-level data, proteotypic peptide-protein mappings are used from upstream bottom-up proteomic analysis pipelines to compute a normalized enrichment score (NES), assessing the differences of proteins or PPIs within individual replicates and conditions against the reference samples (STAR Methods). While proteoVIPER is also applicable to generic bottom-up proteomic data, more specific metrics can be inferred when selected SEC fractions are used.

When all fractions are considered, a metric for “total” protein abundance can be computed, in analogy to generic bottom-up proteomic experiments. Alternatively, considering the above-defined monomer threshold, metrics for “monomeric” (right side of threshold, i.e. the SEC fraction index dividing assembled and monomeric states) or “assembled” (left side of threshold) states can be estimated (Fig. 1c, STAR Methods), thus providing the basis to quantify differences in PPIs across samples and states. Thus, similar to other quantitative protein inference strategies (Ahrné et al., 2013), protein-level NES represents a protein abundance metric. But in addition, the underlying statistical framework increases quantification robustness with diverse sets of peptides, e.g. when obtained from complex samples, and enables differential assessment with respect to a control state (STAR Methods).

To estimate PPI-level metrics, the peptides of two interactor proteins are quantified using only their overlapping SEC fractions instead of their full elution profiles. For each protein, a separate “interactor abundance” metric can be computed to assess the quantitative changes for the individual protein within the PPI. In addition, complex-related metrics can be derived, where the quantitative relations of the two interactors are represented. First, to measure the closely correlated abundances of subunits within the same protein complex, the peptides of the two interactors are grouped by proteoVIPER and evaluated in a positively correlated setting (STAR Methods), where the resulting metric can be used to assess “complex abundance”. Second, to assess how subunit stoichiometry is altered within a complex, the interactor peptides are evaluated in a negatively correlated setting to derive a metric representing “interactor ratio” (Fig. 1c, STAR Methods). This metric can represent stoichiometric changes between interacting subunits within a complex or alterations in their connectivity if a PPI is abrogated or quantitatively changed in some conditions.

proteoVIPER reports six quantitative metrics. At the protein level, it reports total abundance, assembled abundance, monomer abundance and at the PPI-level it reports interactor abundance, complex abundance and interactor ratio. While these values represent different properties of a protein and its interactions, in some cases they are strongly correlated. For example, proteins present in assembled state only will have strongly correlated total and assembled abundances.

Network integration (Step 5):

This step integrates individual quantitative protein and binary PPI metrics from the previous step into comprehensive PPI network states. In the ensuing representation, nodes represent individual proteins annotated with attributes such as differential protein or complex abundance and interactor ratio across conditions and replicates, whereas edges represent specific binary PPIs and their consensus across conditions and replicates (Fig. 1b, STAR Methods). This transformation can be used to provide a summary overview of the PPI network state differences between two or more conditions.

Using the experimental design, SECAT first compares the quantitative metrics between different conditions to identify condition-dependent PPIs (STAR Methods). However, since our approach is agnostic to protein complexes, the PPIs for a given protein can be both redundant (interactions within the same complex) and orthogonal (interactions within different complexes). For this reason, differential PPI-level (edges) metrics are integrated using the Empirical Brown’s Method (Poole et al., 2016) on a protein-by-protein basis to assess protein abundance or protein-complex-based changes for every protein of interest. This method is specifically designed to account for non-statistically-independent evidence and can integrate both redundant and orthogonal information (STAR Methods).

In conclusion, SECAT leverages large-scale, quantitatively consistent co-fractionation mass spectrometry measurements across multiple replicates and conditions, such as those acquired by SEC-SWATH-MS, to assemble context-specific PPI networks, as well as to measure total and complex-bound protein abundance and other PPI-related metrics. Taken together, these metrics provide a comprehensive characterization of condition-specific proteome abundance and PPI network structure in a single operation.

Parameter selection and validation of signal processing and PPI detection modules

In different fields of computational proteomics, the quantification of analytes, i.e. peptides or proteins (Domon and Aebersold, 2010), or their interactions, i.e. protein-protein interactions (Bisson et al., 2011; Collins et al., 2013; Keilhauer et al., 2015; Lambert et al., 2013) or cross-linked peptides (Walzthoeni et al., 2015), have relied on their prior identification at high confidence. Therefore, by analogy, the consistent identification/detection of PPIs across multiple samples with accurate confidence estimation is also a critical property for quantitative PCP-based PPI studies.

Due to SEC’s limited resolution and the large PPI query space, previous approaches have either used ad hoc thresholds to filter out unlikely interactions (e.g. by requiring a minimum correlation of 0.5 for two candidate interactors (Hu et al., 2019)) or have reduced background noise by peak-picking (Heusel et al., 2019; Stacey et al., 2017), under the assumption of Gaussian elution peaks in the SEC dimension. SECAT, in contrast, maintains quantitative consistency between conditions and replicates by applying an optimized semi-supervised learning strategy that requires only minimal signal preprocessing and obviates the need for prefiltering.

To show that SECAT does not require extensive data preprocessing, we compared the effects of different preprocessing methods on a publicly available SEC-SWATH-MS dataset (Heusel et al., 2020) of HeLa CCL2 cells in both interphase and mitotic cell state, in triplicate (HeLa-CC dataset, STAR Methods). We then assessed the method’s robustness based on its ability to infer bona fide PPIs using reference networks with an increasing ratio of positive vs. negative PPIs.

Defining reference sets of positive and negative PPIs is a non-trivial problem. For this benchmark, we adapted a previously applied strategy used by the PrInCE algorithm (Stacey et al., 2017) (STAR Methods). It leverages CORUM (Giurgiu et al., 2019) PPIs as positive PPI gold standard and all other interactions of CORUM proteins that are not included in the database (CORUM-inverted set) as negative PPI gold standard (STAR Methods). For the purpose of the benchmark we further excluded any known or predicted interactions from the CORUM-inverted set and split the combined positive/negative reference set into equally sized training/validation and hold-out subsets (STAR Methods).

Signal preprocessing has minimal effect on PPI detection:

To better assess the effects of different preprocessing strategies on PPI detection consistency, we compared the default, minimal preprocessing approach of SECAT (none) to two different peak-picking strategies, termed “detrend”—base line removal with (detrend zero) or without (detrend drop) missing values—and “localmax” —local maximum peak-picking (STAR Methods).

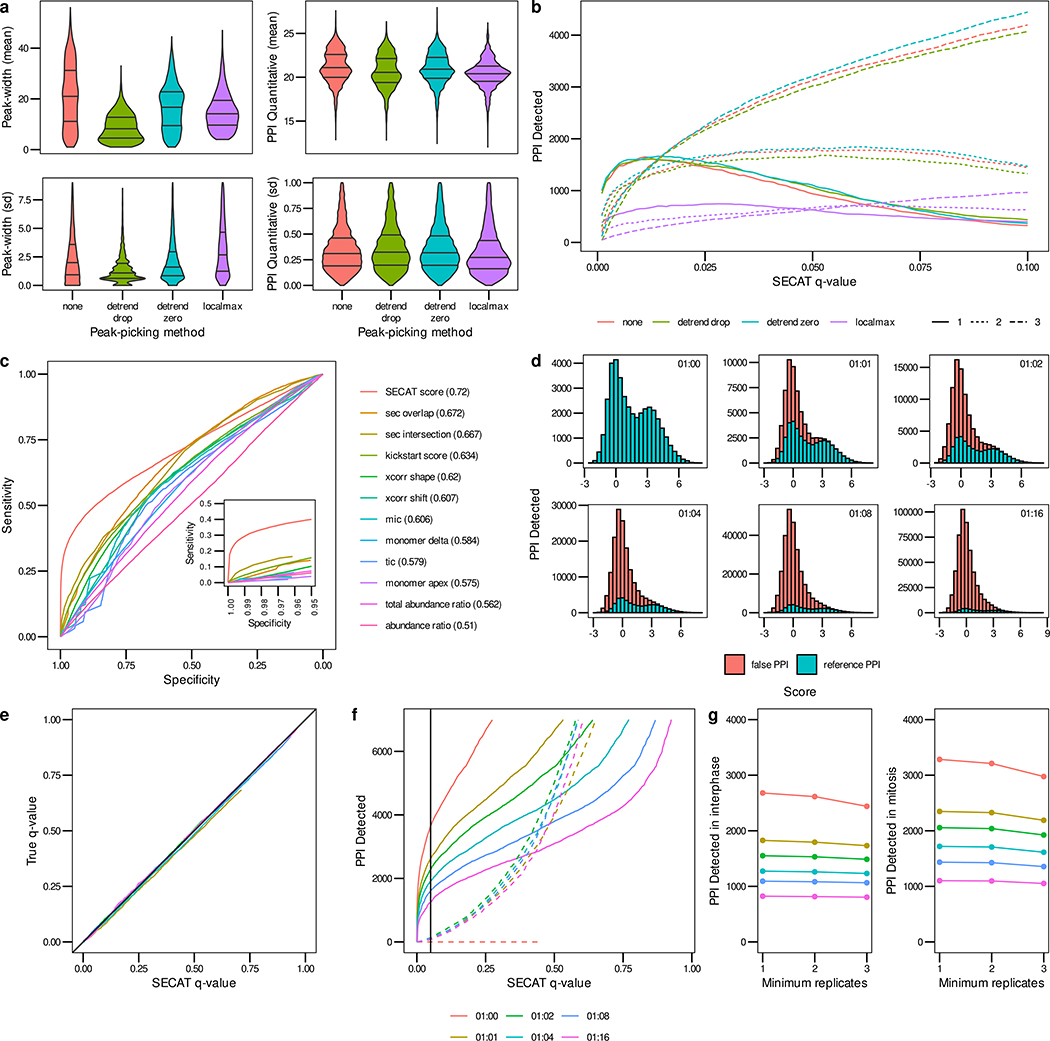
Analysis of three replicates from each HeLa-CC condition with the different peak-picking options (Fig. 2a) shows that detrending or peak-picking based noise removal results in tighter, i.e., less variable mean peak width detections across conditions and replicates. When comparing peak-width standard deviation across the three replicates, the “localmax” method produced slightly higher variability (Fig. 2a). In contrast, integrated peak area-based metrics and standard deviation, in particular, were highly consistent across all three options (Fig. 2a), suggesting that the three peak-picking methods perform roughly equivalently. However, considerable differences were found when comparing detection consistency (Fig. 2b). Indeed, decomposing the total number of detected PPIs for detectability across experimental replicates revealed that the fractions of PPIs consistently detected across replicates was substantially higher if no preprocessing or detrending was used, thus supporting the omission of peak-picking in SECAT.

Figure 2.

Signal processing and PPI detection performance evaluated using the HeLa-CC (Heusel et al., 2020) dataset. (a) The effect of different peak-picking methods for signal processing on peak-width and PPI quantification within replicates of the same experimental condition is depicted in violin plots (lines representing 25, 50 and 75% quantiles respectively, STAR Methods). (b) Sensitivity of PPI detection vs. SECAT q-value for peak-picking options. The PPI were filtered to a global context q-value<0.05. Colors indicate different peak-picking options; line types indicate number of detections with the three replicates per condition. (c) The receiver-operating characteristic (ROC) illustrates the sensitivity vs. specificity of the different SECAT partial scores, the kickstart score and the integrated SECAT score. Numbers in brackets indicate ROC area under the curve values for each partial or combined score. (d) The SECAT score histograms depict the dilution of the reference PPI network (true: CORUM) with negative PPIs (false: CORUM-inverted) for the benchmark (STAR Methods). (e) The SECAT estimated q-value is accurate as evaluated against the ground truth for all levels of reference PPI network accuracy. For the dilution 1:0, no a priori negative PPI are tested, thus the true FDR equals to 0. (f) The sensitivity of PPI detection in dependency of SECAT q-value for different levels of reference PPI network accuracy is depicted. Solid lines represent the positive, whereas dashed lines represent the negative PPIs. (g) Consistency of PPI detection between replicates of the same conditions.

SECAT is robust to false-positive interactions in the gold standard:

To optimally separate true-positive vs. false-positive candidate PPIs, SECAT integrates 11 partial scores into a composite score (Fig. 2c), using a semi-supervised learning strategy initialized by a high confidence PPI score (kickstart score, STAR Methods). Consistent with other evidence integration approaches, the final integrative score (SECAT score) is more discriminative than the initial or partial scores (Fig. 2c). To assess error-rate estimation accuracy and algorithm sensitivity, we performed cross-validation analysis by applying the classifier to the hold-out subset when including increasing fractions (1:0 –1:16) of negative reference interactions (STAR Methods, Fig. 2d). PPI detection accuracy was then assessed by comparing the q-value estimates with the ground truth estimated FDR (Fig. 2e). Our results show that q-value estimates for the hold-out dataset were accurate within the assessed range. This shows that the SECAT PPI detection module is robust against a variable fraction of negative or undetectable PPIs in reference databases, especially in the more relevant high-confidence region (q-value < 0.1).

In contrast, assessing all potential PPI combinations, rather than only those in reference PPI networks substantially reduces sensitivity due to measurement noise and multiple hypotheses testing correction (Sham and Purcell, 2014), both cumulatively across all conditions and replicates and separately for each replicate and condition (Fig. 2f–g). At the same high confidence level (q-value < 0.05), the reference-network-based approach, detected 3,630 PPIs, whereas a reference-network-free approach, represented by using 16 times as many negative reference interactions as positive interactions, only detected 1,244 bona fide PPIs, suggesting loss of accuracy when low-quality PPIs are included and even greater loss when no prior PPI network is used and PPI interactions must be discovered de novo. Indeed, the substantially higher PPI recovery rate at the same confidence threshold level, illustrates the benefit of using a high-quality reference PPI network, rather than comparing all potential PPI interactions using the proposed scoring approach.

Compatibility with different data modalities and comparison of SECAT with established algorithms:

To assess whether SECAT is also compatible with other data modalities, we applied it to a label-based PCP-MS study (Scott et al., 2017), where the results indicate similar performance characteristics in terms of signal processing and error-rate control robustness in comparison to the HeLa-CC dataset, although with lower sensitivity and detection consistency across the replicates (Supplemental Figure 1, Supplemental Note 1).

To our knowledge, no other algorithms have been published to quantitatively assess differential PPI network states using PCP datasets. This constitutes a key element of the proposed algorithm’s novelty, which makes direct comparative benchmarking challenging. However, several algorithms have been developed for the interaction- and complex-centric analysis of proteomic co-fractionation profiles. They share with SECAT the requirement to accurately estimate the confidence of identified or detect PPIs. For the purpose of this benchmark, we thus compared the PPI identification or detection modules of three representative algorithms, EPIC (Hu et al., 2019) (interaction-centric), CCprofiler (Heusel et al., 2019) (complex-centric) and SECAT (network-centric) using a manually curated reference dataset (Heusel et al., 2019). The results show that SECAT achieves the best classification performance with an area under the receiver operating characteristic (AUROC) of 0.856, with CCprofiler reporting a slightly lower performance of 0.805, whereas the AUROC of EPIC was substantially lower at 0.690 (Supplemental Figure 2, Supplemental Note 2).

In summary, SECAT’s novel approach for accurate estimation of PPI detection confidence combines reference-network-based assessment of PPIs with a semi-supervised machine learning strategy. While the semi-supervised learning component provides selectivity by exclusion of spontaneously co-eluting PPIs present in the ground truth dataset during the first learning iteration, the restriction of the PPI query space using reference networks dramatically increases sensitivity, thus enabling an optimal tradeoff between the two metrics. In turn, these improvements allow SECAT to operate with minimal data preprocessing, ensuring reproducible detection of PPIs across replicates and conditions, a crucial requirement for their quantification.

Validation of PPI quantification & network integration modules

Building on SECAT’s benchmarked ability to detect true PPIs from PCP datasets, we next validated its PPI quantification and network integration modules. For these analyses, we used the previously described HeLa-CC dataset (Heusel et al., 2020). We performed independent analyses, either assessing all potential PPI combinations or by using a restricted query space based on CORUM (Giurgiu et al., 2019), STRING (Szklarczyk et al., 2019) or PrePPI (Garzón et al., 2016) as reference PPI networks. The classifiers were trained on the full CORUM positive/negative reference network.

PPI detection with different reference networks:

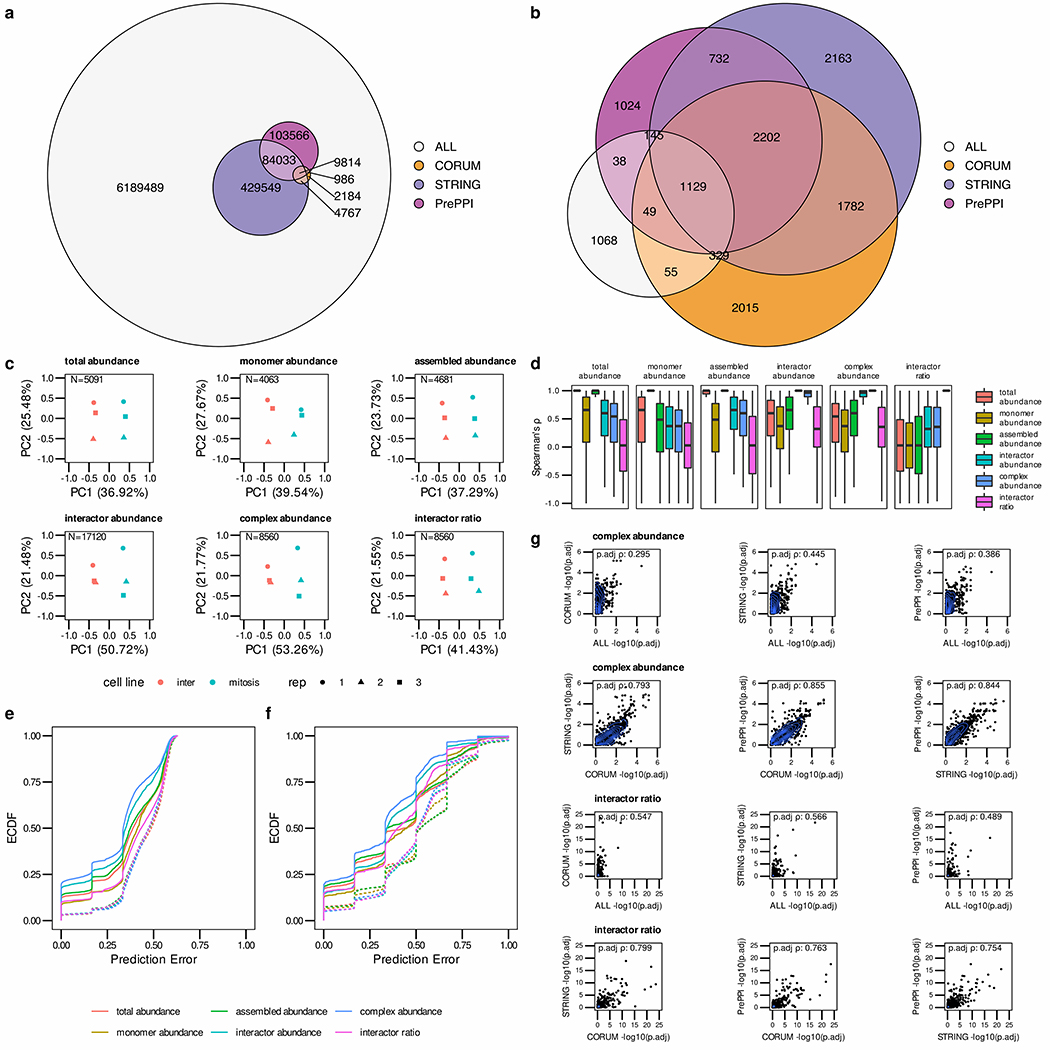
For the analyses involving the three reference PPI networks or all combinations, the total respective query space ranged from 17,751 (CORUM), 198,399 (PrePPI) to 528,163 (STRING) and 6,824,388 (all combinations) PPIs (Fig. 3a). Of these, between 2,891 (all combinations), 5,656 (PrePPI), 7,898 (CORUM) and 8,560 (STRING) high-confidence PPIs (q-value < 0.05) were detected, with a core set of 1,129 common PPIs (Fig. 3b). Notably, the full intersection of detected true PPIs might be larger, but two factors conspire to make objective comparison more complex. First, different confidence scores provided by each database are used as priors in our analyses. Second, the largely variable number of PPIs represented in each database needs to be accounted for during multiple testing correction (STAR Methods). As expected, not constraining the PPI query space resulted in the lowest number of detected PPIs (N = 2,891). While this mode still discovered 1,068 unique PPIs not detected using the other PPI networks, the sensitivity was dramatically lower for the same specificity threshold, a considerable drawback for quantitative applications. To further assess the effects of reference networks based on different measurement technologies on SECAT PPI detection performance, e.g. yeast-two-hybrid screens (Y2H) or integrative approaches, we investigated the query spaces (Supplemental Fig. 3a) and detection rates (Supplemental Fig. 3b) when using BioPlex (Huttlin et al., 2015, 2017), IntAct (Orchard et al., 2014), hu.MAP (Drew et al., 2017) and HuRI (Luck et al., 2020) (STAR Methods). Whereas SECAT analyses using reference networks derived from protein-complex-based datasets, i.e. hu.MAP (co-fractionation profiling) and BioPlex (AP-MS), resulted in similar PPI detection metrics as CORUM, the analysis of reference networks built on Y2H-based data, i.e. the HuRI network, provided substantially lower coverage of the query space (1,306 proteins, 2,511 PPIs) and thus detected PPIs (394 PPIs). To some extent, this might be attributed to limited sensitivity and potential context-specificity of PPIs in Y2H screens (Luck et al., 2020). Consequently, we settled on using STRING as prior network for further analyses.

Figure 3.

PPI quantification and Network integration assessment using the HeLa-CC (Heusel et al., 2020) dataset. (a) The Euler diagram indicates the overlap of STRING, PrePPI and CORUM reference PPI networks resulting in at least a partial overlap of the interactors in any of the replicates. (b) Overlap of confident (q-value < 0.05) PPI detections after SECAT analysis with different reference PPI networks. (c) Quantitative SECAT metrics can be used to separate experimental conditions and replicates. (d) The distributions of Spearman’s rank correlation coefficient (Spearman’s ρ) of the metrics (PPI: summarized by averaging) in reference to the other levels are depicted in individual boxplots (lower and upper hinges represent the first and third quartiles; the bar represents the median; lower and upper whisker extend to 1.5 * IQR from the hinge). (e) Predictive error quantified by the empirical cumulative distribution function (ECDF) for leave-one-out cross-validated logistic regression classification of replicates to biological conditions. (f) Predictive error for group-wise leave-one-out cross-validated logistic regression classification of replicates to biological conditions. Groups represent several metrics connected to a core metric based on the PPI network. (g) Correlation of node-level integrated adjusted p-values estimated using different reference PPI networks.

PPI quantification and relation of metric classes:

SECAT’s quantification module computes two main quantitative property categories from SEC-SWATH-MS data: one indicating protein abundance, the other representing PPIs. Some of these metrics are expected to be related. For example, if a protein is only present in an “assembled” conformation, the “total abundance” and “assembled abundance” values will be highly correlated. To assess the relation and redundancy within metric classes, we conducted dimensionality reduction using principal component analysis (PCA), separating replicates and conditions (Fig. 3c). The data show that the first two principal components of the “total abundance”, “monomer abundance” and “assembled abundance” metrics explain 62.40–67.21% of the variance between them, while the first two principal components for the “interactor abundance”, “complex abundance” and “interactor ratio” metrics explain 62.98–75.03% of the variance. The small difference in variance between protein abundance- and PPI-based metrics might potentially arise from metrics quantifying redundant interactions between same-complex proteins.

To assess the relationship between metric classes, we further computed the distribution of Spearman’s rank correlation coefficient (Spearman’s ρ) of metrics aggregated over conditions, replicates and proteins to the other metrics in a pairwise fashion (Fig. 3d). As expected, the “assembled abundance” metrics which cover most SEC fractions have the strongest correlation to “total abundance”, followed by “monomer abundance”, “interactor abundance” and “complex abundance” metrics. Considering the set of PPI-based SECAT metrics, “interactor abundance” and “complex abundance” are expectedly in closest relation, whereas “monomer abundance” is less correlated. Notably, since the “interactor ratio” metrics summarize relative changes between the interactors, they are substantially less correlated to any of the other metrics.

Assessment of predictive power of quantitative metrics:

To assess the predictive power of the different metric classes for classifying the six samples to one of the two represented mitotic states, we estimated the prediction error using leave-one-out cross-validation using a logistic regression classifier applied to each metric separately (Fig. 3e). The empirical cumulative distribution function (ECDF) in dependency of the prediction error indicates that the “complex abundance” metrics are most informative, followed by “interactor abundance” and the other metrics, to separate the two mitotic states. While these metrics are computed for single proteins or PPIs, network-centric data integration might further boost the predictive power of the respective values.

To assess this effect, we combined individual PPI metrics based on the SECAT PPI networks by extending the score vector for the classifier from single metrics to all PPI scores connected to a specific protein (Fig. 3f). The results show that the “complex abundance”-based metrics performed best and the “assembled abundance” metrics performed second best, indicating that the fractions covering assembled protein states have a higher information content than those covering monomeric subunits and that the connectivity information calculated by SECAT has higher information content than the protein abundance.

Redundancy of network integration:

In higher order complexes composed of three or more subunits, PPI information is expected to be partly redundant, with each subunit relating to at least two other co-complex members. Thus, a change in one subunit might be apparent in other PPIs as well. This PPI redundancy between subunits of a multiprotein complex is critically relevant to any strategy attempting to integrate individual protein or PPI properties at the network level. Consistent with this observation, SECAT assumes that changes in the individual subunits of a protein complex can be measured redundantly by assessing its interactions with all proteins in the complex. Different reference PPI networks are thus expected to provide comparable quantitative metrics if they partially overlap. To test this assumption, we compared the differential integrated metrics on “complex abundance” and “interactor ratio” levels using different reference PPI networks. The results indicate a high degree of correlation among the “complex abundance” (Spearman’s ρ: 0.793–0.855) and “interactor ratio” levels (Spearman’s ρ: 0.754–0.799) (Fig. 3g), confirming robustness to PPI network choice. Notably, the comparison with the reference-network-free mode indicates much lower correlation. This can be explained by differences in the topologies of the generated PPI networks. Although the node degree distributions of both reference-network-free and reference-network-based PPI networks approximate a power-law (Barabási and Oltvai, 2004), substantially more high degree nodes (k>60) could be detected when using reference networks (Supplemental Fig. 3c).

In summary, SECAT’s PPI quantification and network integration modules generate instances of PPI networks for each sample or phenotypic state. To achieve this, the signal processing and PPI detection modules first transform SEC fraction peptide abundance values to a set of protein abundance or complex-associated metrics. The presented validation results show that PPI-level quantitative metrics have higher predictive power to separate sample groups than the underlying total protein abundances. In a second step, redundant and orthogonal PPI-level metrics (edges) are integrated to protein-level (nodes). With different empirical or predicted reference PPI networks, this transformation achieves similar results attesting to the robustness of results despite different background PPI networks.

Comparison of complex- and network-centric analysis strategies

To demonstrate SECAT’s ability to identify molecular mechanisms that differ between experimental conditions or phenotypes, we further investigated the results obtained from the HeLa-CC dataset (Heusel et al., 2020). This study was designed to compare differences at the level of protein complexes between cell cycle states of a HeLa CCL2 cell line. The HeLa cell states were induced by thymidine blocking which arrested cells in interphase and by a subsequent release in nocodazole which arrested cells in mitosis (Heusel et al., 2020). For each experimental condition, three full-process replicates were generated, and 65 SEC fractions per condition and replicates were measured by SEC-SWATH-MS. Cumulatively, 70,445 peptides associated with 5,514 proteins were quantified across the full dataset. We conducted the SECAT analysis of this quantitative matrix with the goal to identify phenotype-associated molecular mechanisms (STAR Methods). Since the cell cycle and its checkpoints are controlled by clearly defined events involving selected checkpoint proteins, the literature provides a reference and validation framework for the interpretation of the results.

With STRING as reference PPI network and after network-centric data integration, SECAT identified 25 differentially abundant proteins (“total abundance”-level) across the two cell states, 44 alterations affecting “assembled abundance”, no alterations regarding “monomer abundance”, 117 alterations affecting “interactor abundance”, 129 alterations in “complex abundance”, and 141 alterations in “interactor ratio” (adj. p-value < 0.01; |log₂(fold-change)| > 1) (Supplemental Data 2–3).

These sets of differentially abundant proteins obtained by SECAT vary substantially from those previously identified with CCprofiler (Heusel et al., 2020). In comparison, the overlap of the SECAT results with the CCprofiler top 250 ranking proteins ranges from 28.4% (interactor ratio) to 52.0% (total abundance), illustrating the differences between the algorithms, particularly when protein complex composition is affected. Because the algorithms apply different analysis concepts (complex- vs. network-centric), a direct comparison of the results is difficult to achieve (Supplemental Note 2). Nevertheless, we conducted a comparative analysis of functionally relevant proteins identified by the two approaches. Using Gene Set Enrichment Analysis (GSEA) (Subramanian et al., 2005) and the Reactome (Jassal et al., 2020) database, which provides a hierarchical representation of (sub-)pathways and the involved proteins, our goal was to assess how CCprofiler and SECAT identify differentially abundant or connected protein complexes or network components.

GSEA is based on the idea that functionally or otherwise related co-regulated genes can identify shared pathways or modules (Subramanian et al., 2005). For this analysis, we extended the concept from gene co-regulation to the CCprofiler and SECAT scores, where our assumption was that proteins, similarly affected by protein complex abundance or stoichiometry changes might identify shared subpathways. The analysis was conducted for each CCprofiler and SECAT score separately using the full Reactome pathway set and a cell-cycle-associated subset in parallel (STAR Methods). The CCprofiler and SECAT scores can further be grouped into two categories to facilitate the comparison: First, the two CCprofiler scores based on “protein complex feature” and “total” protein abundance (referred to here as “interactor” and “total” abundances, respectively), as well as the SECAT protein-level scores (“monomer”, “assembled” and “total” abundances) represent summarized abundances over (selected) SEC fractions. Second, the SECAT PPI scores (“interactor”, “complex” abundances and “interactor ratio”) are generated by our network-centric approach and represent protein complex abundance and stoichiometry-based metrics.

The GSEA results based on the cell-cyle-associated pathway subset (Fig. 4a) and the full Reactome database (Supplemental Fig. 4) illustrate the similarities and differences of results generated by the algorithms (Supplemental Data 4). Of the 22 cell-cycle-associated Reactome subpathways with at least one significant detection in any of the scores, CCprofiler identified 11 as significant (adj. p-value < 0.01), whereas the protein-level SECAT scores identified 15, with an overlap of 10 subpathways (Fig. 4a). This suggests that for protein quantification without PPI information, the algorithms produce similar high-level results, even though they use different methods. As expected, the differences in results obtained are more pronounced when PPI-based SECAT scores are compared with the protein-abundance-based scores, where 14 cell-cycle-associated subpathways were identified with the STRING network, resulting in a smaller overlap with CCprofiler of 6 subpathways. These PPI-based analyses were also performed with other reference networks as background. They resulted in the detection of similar enriched subpathways, however, the lower PPI coverage of these networks compared to STRING produced fewer significant results (Supplemental Fig. 4). For this reason, we continued all further analyses using the STRING reference network.

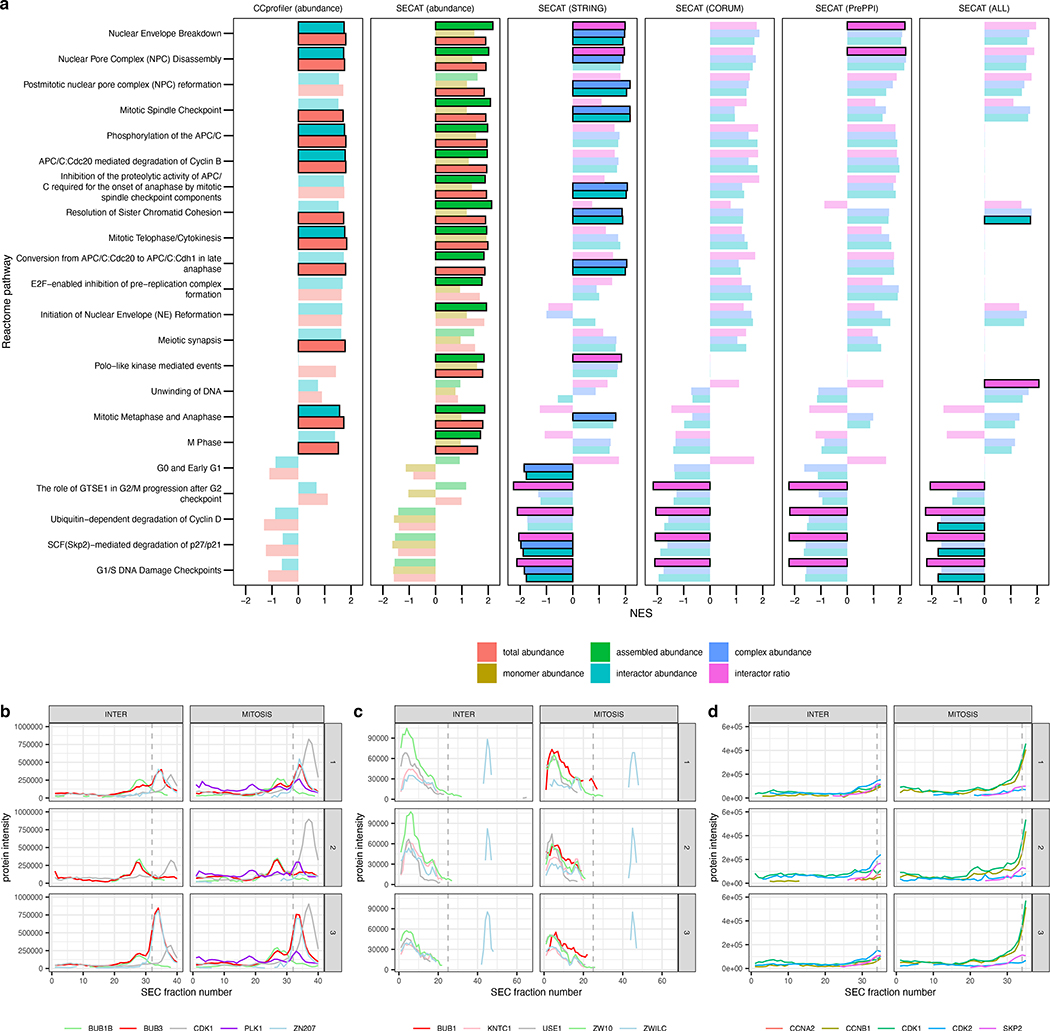
Figure 4.

Comparison of CCprofiler and SECAT scores for elucidation of cell-cycle-associated molecular mechanisms. (a) Gene set enrichment analysis was conducted using the cell-cycle-associated Reactome subpathways (STAR Methods). Opaque bars with black borders indicate significant enrichment (adj. p-value < 0.01) (STAR Methods). Subpathways are only depicted if the significance threshold is reached in at least one subscore. (b-d) Protein-level SEC-SWATH-MS profiles of HeLa cell cycle states visualized separately for conditions (columns) and replicates (rows). Lines indicate different protein subunits, whereas the dashed line indicates the highest monomer threshold per group. (b) Complexes involving BUB3 result in heterogeneous elution profiles within replicates of the same conditions. (c) The activity of the Rod (KNTC1)-ZW10-Zwilch (RZZ) complex is dependent on localization by BUB1. (d) SECAT can also detect and quantify transient interactions of CDK2.

The enrichment signal of a gene set is frequently dominated by a subset of genes or proteins which result in similar observed characteristics, referred to as “leading edge” genes or proteins (Subramanian et al., 2005). We thus compared the “leading edge” proteins unique to the SECAT PPI scores with the goal to investigate potential limitations of the CCprofiler scores, that might have resulted in missed associations. For example, these proteins might have been missed by CCprofiler due to technical or conceptual differences, because “total abundance” was unchanged or “interactor abundance” could not be accurately assessed (Supplemental Data 4). For the cell-cycle-associated subpathways, SECAT identified 21 additional proteins with high confidence in comparison to CCprofiler (SECAT adj. p-value < 0.05; GSEA adj. p-value < 0.01), including well-known cell-cycle-associated proteins such as cyclin-dependent kinases. Considering the full set of Reactome pathways, SECAT identified 205 additional proteins with high confidence in comparison to CCprofiler (SECAT adj. p-value < 0.05; GSEA adj. p-value < 0.01). To illustrate the technical and conceptual differences between the algorithms, we selected three out of the 21 cell-cycle-associated proteins, which were found to be involved in resolution of sister chromatid cohesion, a well characterized biological process part of the cell cycle (Fig. 4b–d).

A major technical challenge for peak-picking based algorithms such as CCprofiler is the processing of heterogeneous non-Gaussian elution peaks to detect protein complexes. This is exemplified by the mitotic checkpoint protein BUB3. In complex with BUB1, BUB3 mediates inhibition of the anaphase-promoting complex or cyclosome (APC/C) (Overlack et al., 2017). Although BUB3 is a protein with known interactors, the elution profiles of the respective complex components are heterogeneous, even within replicates of the same condition (Fig. 4b). Whereas this technical challenge resulted in limited quantification accuracy for CCprofiler (Supplemental Data 4), SECAT could confidently assess and quantify the (partial) interactions with interactors BUB1B, ZN207, CDK1 and PLK1 and detect significant changes affecting interactor and complex abundance across mitotic states, as indicated by the co-elution profiles (Fig. 4b) and PPI confidence scores (Supplemental Data 3).

The Rod (KNTC1)-ZW10-Zwilch (RZZ) complex illustrates conceptual limitations of complex-centric analyses. The complex composition is well characterized and its function as co-factor involved in kinetochore localization of the Mad1-Mad2 complex, an important component of the spindle assembly checkpoint (SAC), has been investigated in detail (Zhang et al., 2015). The RZZ complex is also represented in CORUM (Giurgiu et al., 2019). Both complex-centric analysis by CCprofiler, and the protein abundance scores of SECAT did not suggest strong quantitative alterations of individual subunits or the complex between the mitotic states. However, the PPI scores of SECAT detected complex-related differences of ZW10 between the two conditions. Inspection of the four confidently detected PPIs of ZW10 (with Rod, Zwilch, USE1 and BUB1), identified BUB1 as mitosis-exclusive interactor of RZZ (Fig. 4c). Indeed, it was recently found that BUB1 is a condition-specific localizer of RZZ to kinetochores, representing a functionally essential component for checkpoint signaling (Zhang et al., 2015). The unchanged RZZ complex abundance between the conditions tested might indicate that BUB1-dependent cellular localization represents a crucial property for complex activity. This example illustrates the importance of assessing protein complexes as dynamic rather than static entities.

In contrast to CCprofiler, SECAT is also capable to assess interactions between subunits that do not form typical protein complexes resulting in Gaussian elution profiles. This is illustrated by the cyclin-dependent kinase 2 (CDK2), a protein involved in the cell cycle through a variety of different mechanisms (Wood and Endicott, 2018). While the protein-complex bound fraction of the protein is not significantly different between the two conditions, the SECAT interactor ratio score was able to detect alterations of interactions with CDK1, CCNB1 and SKP2 and complex abundance alterations affecting the interactions with CCNA2 (Fig. 4d). Although the protein co-elution profiles of CDK2 and its interactors, e.g. SKP2, do not form Gaussian-like elution peaks within the intersection, the SECAT PPI detection scores for the interphase replicates indicate high cross-correlation shape scores (0.95–0.98), low cross-correlation shift scores (0.0) and matching abundance ratios of the peptide elution profiles (0.60–0.65), resulting in confident detection of the CDK2-SKP2 PPI (q-value: 0.0003 – 0.002) within this condition. In turn the quantitative difference of this PPI between the conditions supports cell-cycle associated gene sets “G0 and Early G1”, “SCF(Skp2)-mediated degradation of p27/p21” and “G1/S” DNA Damage Checkpoints” to be enriched for the SECAT PPI scores indicating the ability of the algorithm to detect state-specific, non-typical interactions (Supplemental Data 4).

Conversely, the set of proteins associated with cell cycle processes using the CCprofiler scores but not the SECAT scores illustrates the limitations of the network-centric approach. For 13 out of 19 proteins detect by the CCprofiler “interactor abundance” score (all CCprofiler results; GSEA adj. p-value < 0.01), SECAT could not detect any PPIs with confidence (Supplemental Fig. 5a–m). Because SECAT’s peptide-level scoring module benefits from multiple peptides per protein, coverage by only few peptides (<3) might have lowered the scores below the threshold of significance in at least five of those case (Supplemental Fig. 5a–e). For proteins where PPIs could be detected, large variability between replicates of the same conditions likely reduced statistical significance in four out of six cases (Supplemental Fig. 5n–q). For the 26S proteasome non-ATPase regulatory subunits 4 and 6, many interactions were detected and quantified, but only a small change was detected by SECAT (Supplemental Fig. 5r).

In summary, the comparison of the performance of CCprofiler and SECAT demonstrates that the results reported by the two algorithms on protein-abundance-level are similar, although obtained by different methodologies. In contrast, the SECAT PPI-based scores can be used to overcome some of the technical and conceptual challenges of complex-centric scoring and thus provide insights into phenotype-associated molecular mechanisms that require protein complexes to be assessed as dynamic rather than static entities.

Molecular mechanisms differentiating HeLa cell cycle states

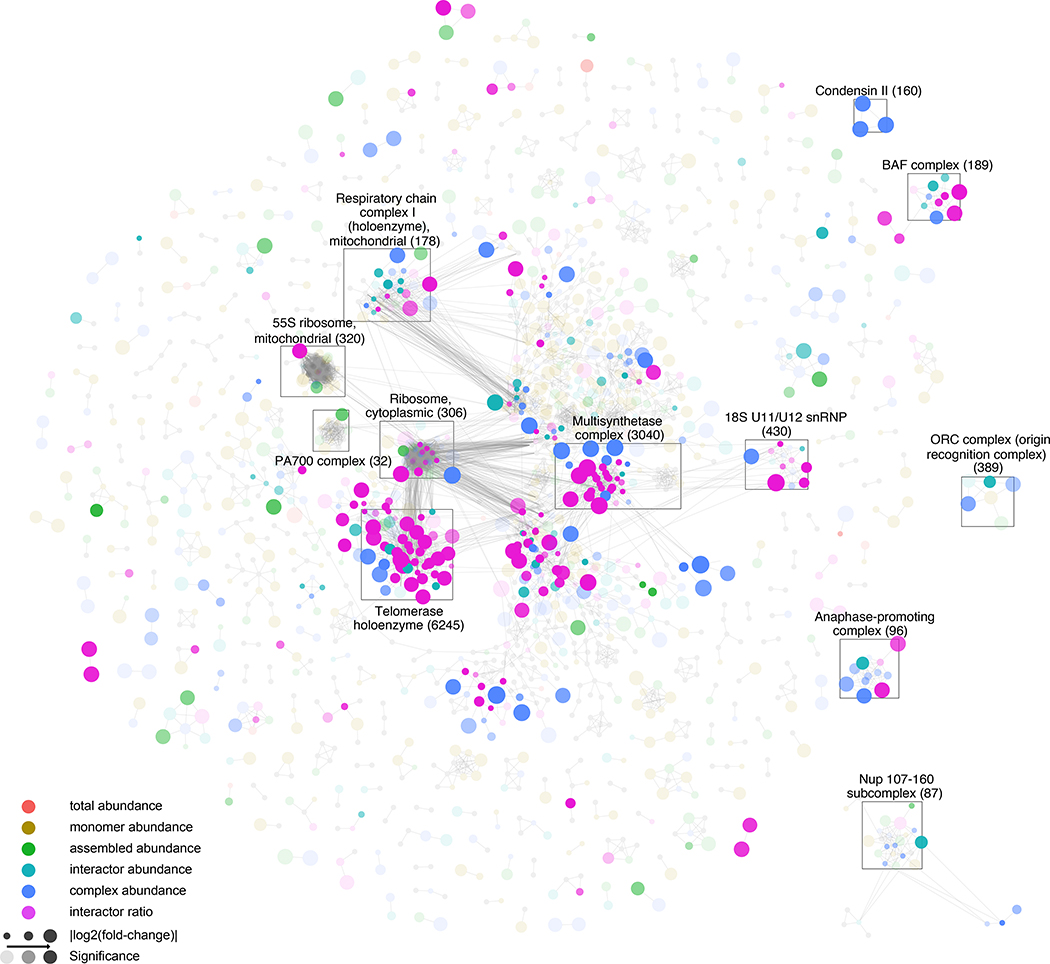
A primary goal of SECAT is to enable a systematic investigation of phenotype-associated molecular mechanisms. For this purpose, we evaluated different representations of the SECAT results to guide analysis and more detailed investigations. Protein subunits within complexes can be differentially abundant and altered in their stoichiometry at the same time. To visualize the data SECAT implements a simplistic aggregation to the most significant level per protein that provides a reduced overview. This can be further augmented by integrating the context-specific PPI network with CORUM (Fig. 5, Supplemental Fig. 6) or Reactome (Jassal et al., 2020) (Supplemental Fig. 7), visualizing changes affecting protein complexes or modules, respectively (STAR Methods). Importantly, modules and complexes can represent the same entities, e.g. the anaphase-promoting complex (APC), which constitutes a well-defined complex in both complex or module representations (Supplemental Fig. 6–7), or their modularization cannot be attributed to specific complexes, e.g. the proteins part of the rRNA processing module (Supplemental Fig. 7).

Figure 5.

Complex-level molecular mechanisms differentiating HeLa cell cycle states. The integrated STRING-based PPI network of the HeLa cell cycle dataset (Heusel et al., 2020) is depicted with proteins (nodes) and binary PPIs (edges) clustered against CORUM complexes (identifiers in brackets; STAR Methods). Different colors indicate the most significant metric-level (legend, STAR Methods). Node-size indicates effect-size and opacity indicates significance. The most prominent clusters highlight essential macromolecular assemblies. Interactive results (Cytoscape) and visualizations of separate levels are provided as Supplemental Data 1.

The data show that a few primary clusters representing large protein complexes and their interactors dominate the modules covered by the network of detected PPIs. These include the cytoplasmic ribosome (80 proteins; peptide chain elongation module), the mitochondrial 55S ribosome (72 proteins; mitochondrial translation termination module), the multisynthetase complex (44 proteins; selenoamino acid metabolism module), the telomerase holoenzyme (41 proteins; rRNA modification in the nucleus and cytosol module) and the mitochondrial respiratory chain complex I (holoenzyme) (32 proteins; respiratory electron chain transport module). These structures have in common that they consist of numerous subunits with many intra-complex PPIs. For the ribosomal complexes and the respiratory chain complex, many PPIs could be detected and quantified, but most PPIs and complex subunits did not change between conditions. In contrast, for the telomerase holoenzyme and the multisynthetase complexes, a larger number of subunits were significantly altered between the conditions (Fig. 5, Supplemental Fig. 6) indicating that these structures changed composition between mitotic states. Specifically, the subunits of the multisynthetase complex form a single complex in interphase (Fig. 6a), whereas two subunits of the telomerase holoenzyme, DKC1 and NHP2, and their interaction, are only detectable in mitosis suggesting a significant quantitative difference of the two proteins between mitotic states (Fig. 6b). These results indicate SECAT’s ability to quantify different types of alterations of large molecular modules between cellular states.

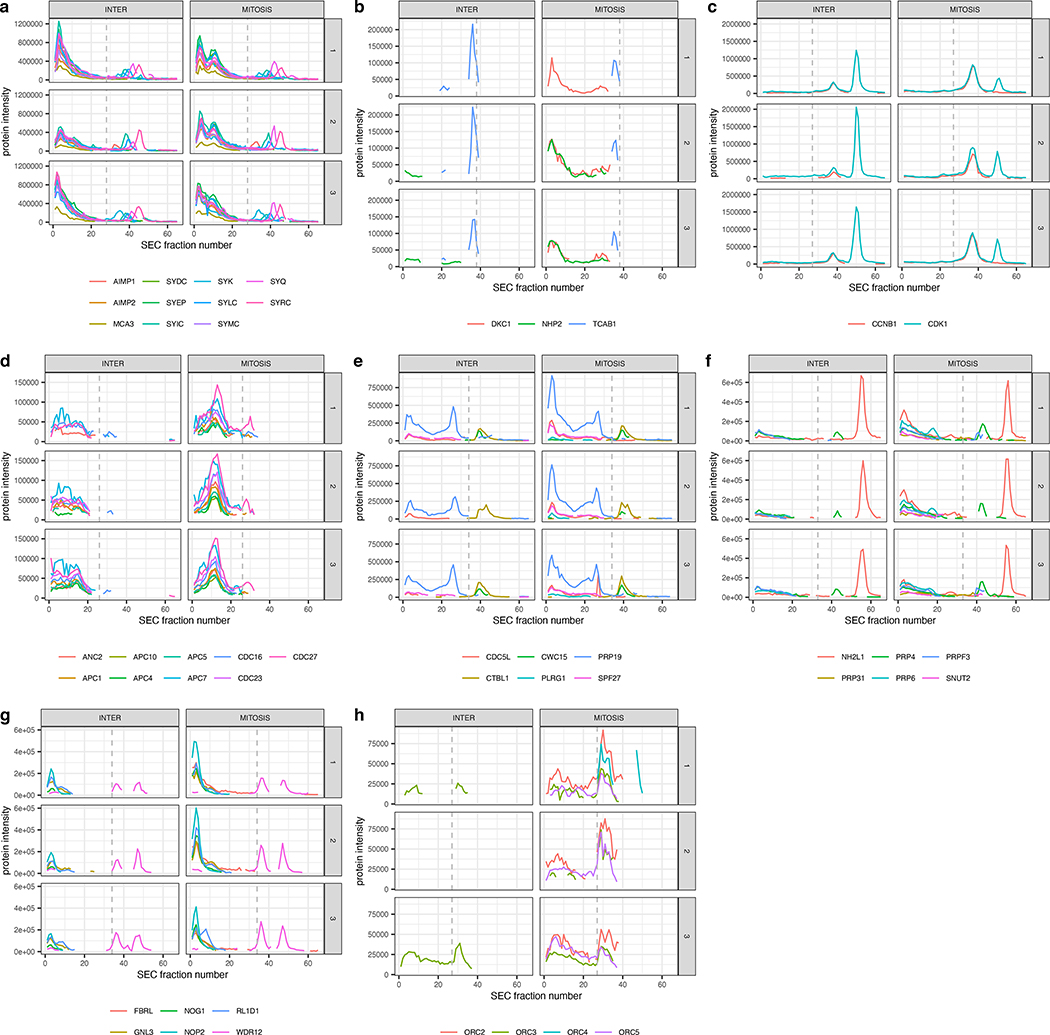
Figure 6.

Protein-level SEC-SWATH-MS profiles of HeLa cell cycle states visualized separately for conditions (columns) and replicates (rows). Lines indicate different protein subunits, whereas the dashed line indicates the highest monomer threshold per group. (a) Multisynthetase complex. (b) Telomerase holoenzyme. (c) Cyclin B1-Cdk1 complex. (d) Subunits of the anaphase-promoting complex (APC). (e) Subunits of the NineTeen Complex (NTC). (f) Associated U4/U6.U5 tri-snRNP subcomplex proteins. (g) The most abundant ribosome biogenesis-associated proteins. (h) Subunits of the origin recognition complex (ORC).

Numerous changes were also detected for smaller modules and their interactions. Cyclin B1 bound to Cyclin-dependent kinase 1 (Cdk1) is a major catalytic factor promoting mitosis (Gavet and Pines, 2010). Counteracting Cyclin B1-Cdk1 mediated activation, sequential degradation of cell cycle regulating proteins via the ubiquitin pathway is important to progress through mitosis (Castro et al., 2005). SECAT recalled these well-known biochemical events from the SEC-SWATH-MS data. Specifically, it detected different levels of Cdk1 “complex abundance” and “interactor ratio” as a principal factor differentiating the two cell cycle states (Fig. 6c). Further, SECAT identified several subunits of the anaphase-promoting complex (APC) to be significantly more abundant during mitosis (Fig. 6d). The network visualization further illustrates the high connectivity between the individual subunits, resulting in a distinctive complex module within the graph, primarily affected by differential protein abundance between the mitosis states (Fig. 5). This is consistent with the role of the APC as a ubiquitin ligase mediating this particular step (Castro et al., 2005).

Between transcription and translation, pre-mRNA is processed to remove introns and splice exons to produce mature mRNA molecules for translation. This process is catalyzed by the spliceosome, a multi-megadalton ribonucleoprotein complex, which highly dynamically adapts to context-dependent functions (Will and Luhrmann, 2011). Spliceosome assembly and function typically involve several intermediate complexes, requiring the integrity of the nuclear compartment (Hofmann et al., 2010). With the disassembly of the nucleus and associated nuclear pore complex (NPC) proteins during mitosis, the rate of transcription is reduced and it is currently believed that spliceosome subunits are distributed across the mitotic cytoplasm awaiting re-activation upon nuclear reassembly (Hofmann et al., 2010). However, systematic screens identified spliceosome subcomplexes, including the NineTeen Complex (NTC) with five out of seven of its core proteins (PRPF19 (PRP19), CDC5L, SPF27, PLRG1 and CTNNBL1 (CTBL1)) as essential components for mitosis (Neumann et al., 2010). Correspondingly, in our analyses PRPF19 and CDC5L were identified as differentially abundant between interphase and mitosis on the “complex abundance” level. In addition, they display changes on the “interactor ratio” level. Specifically, the NTC subunits form a more distinctive SEC elution peak during mitosis (Fig. 6e). Similarly, NHP2-like protein 1 (NH2L1), a component of the U4/U6.U5 tri-snRNP subcomplex, has been found to be required during mitosis (Neumann et al., 2010). Our analysis further supports the importance of NH2L1 during mitosis, as it is among the most significantly changed proteins in terms of “interactor ratio” but not “total abundance”. SECAT further found the linked U4/U6.U5 tri-snRNP subcomplex proteins such as the tri-snRNP-associated protein 2 (SNUT2), the pre-mRNA-processing factors 3, 4, 6 and 31 (PRP3,4,6,31) to be of similar differential “interactor ratio” significance, suggesting subcomplex activity during the cell cycle (Fig. 6f).

The Ribosomal RNA Processing complex represents one of the larger and most densely connected submodules of the dataset. SECAT found several proteins known to belong to this group to be differentially abundant (Fig. 6g). Of those, the majority is associated with ribosome biogenesis, a process located in both cytoplasm and nucleolus. Similar to the origin recognition complex (ORC, Fig. 6h), which is only active in the nucleus, this difference in abundance might be explained by the experimental design, because under the conditions used for cell lysis, proteins of the nucleus are less accessible during interphase than mitosis, a cell cycle state where the NPC is disassembled. The proteins, complexes and modules involved in rRNA processing illustrate a further important asset of network-centric analysis: Reactome modularization in Supplemental Fig. 7 shows that although the proteins involved in the associated rRNA processing and modification processes cannot always be attributed to specific complexes, their functional association can provide clues about differential mechanisms, either by visualization or pathways analysis. Further examples illustrating the SEC profiles of the protein complexes covered by Fig. 5 are visualized in Supplemental Fig. 8.

In summary, SECAT provides context-specific networks and protein-level metrics that can be visualized as intuitive maps (Fig. 5), facilitating the interpretation of observed molecular differences between cell states at different levels including protein abundance, PPIs, protein complexes and PPI network modules, concurrently, from the same dataset. This representation allows to analyze changes on different levels, from larger network modules to complexes and specific PPIs, thus providing an interpretable and scalable resource from overview representations to zoomed-in molecular mechanisms for expert analysis or multi-omic data integration.

Discussion

Protein-protein interactions are a principal characteristic of proteome organization and are significantly affected by or determine the biochemical state of the cell. Most biochemical functions are catalyzed and controlled by multiprotein complexes which, in turn, are organized in extensive interaction networks, exemplified by PPI interaction resources such as STRING (Szklarczyk et al., 2019). The ability to accurately compare PPI networks of different cellular states and to deduce from the detected differences altered biochemical functions and mechanisms is therefore of fundamental importance for molecular biology. To address this need under the term “interaction proteomics” several powerful methods have been developed, including AP-MS that investigates the interactions of specific proteins at relatively high throughput. The cumulative results of thousands of AP-MS measurements constitute PPI network maps for investigated organisms (Huttlin et al., 2015, 2017). However, the extension of the AP-MS approach to compare PPI networks at different states is intrinsically limited because it would require the comparative analysis of the results of a high number of AP-MS measurements in the different states.

For this reason, PCP-based methods, such as SEC-SWATH-MS, have emerged as complementary approaches. They can measure protein profiles across the chromatographic size separation range quickly and reproducibly for thousands of proteins, thus indicating their abundance and association with complexes. They achieve, however, lower proteome coverage than typical bottom-up proteomic measurements and are limited to medium to high affinity-binding protein complexes that are soluble and remain intact under the extraction conditions used. Previous studies have already demonstrated the application of PCP to qualitatively characterize metazoan macromolecular complexes (Wan et al., 2015). With increasing throughput and further methodological improvements, it can be expected that these developments enable the qualitative and quantitative comparison of dozen to hundreds of samples in single studies.

However, the relatively low peak capacity of SEC imposes major limitations for PPI identification, i.e. the number of proteins identified by far exceeds the number of separable peaks and thus fractions collected. In previous studies this limitation was addressed by sequentially applying orthogonal biochemical fractionation methods (Havugimana et al., 2012) or by focusing on protein complex detection using predetermined subunits (Heusel et al., 2019). This requires either more complex and costly experimental designs or focus on well characterized protein complexes, limiting the scalability and generic applicability of protein complex profiling studies.

With SECAT, we introduce an alternative analysis strategy which makes use of the high consistency of peptide-level quantification of SWATH-MS and prior knowledge from PPI reference databases. We demonstrate that SECAT applied to data with these qualities provides accurate estimation of PPI detection confidence while substantially increasing the coverage of binary interactions. The robustness of the scoring and semi-supervised learning strategy further permits omission of preprocessing steps such as peak-picking and obviates the need for scoring thresholds, making the algorithm robust against context-specific deviations related to SEC peak shape or different calibration of SEC fractions.

Because SEC separates stable native protein complexes, the inference of their composition from binary interactions is a key component of most previous data analysis strategies. This provides the opportunity to identify previously unknown associations in a global fashion, however, the underlying challenges of annotating and comparing context-specific related subcomplexes will become more severe with increasing number of conditions tested in a study. We show that the proposed protein abundance-level and PPI-based metrics are comparable across different PPI reference networks and thus their implementation in SECAT provides a scalable alternative to protein complex inference that makes use of redundant information to increase the consistency of quantitative comparisons. In turn, these improvements allow quantitative comparisons of the PPI network state, which can further be grouped to protein complexes or functional modules, where concurrent changes highlight differential molecular mechanisms between the investigated conditions.

Our application of SECAT to the HeLa-CC dataset (Heusel et al., 2020) illustrates that different network states can efficiently be visualized in a network-centric representation to highlight the complex relations of different qualities. This provides a bird’s-eye view of alterations in PPI networks that can be used intuitively to guide follow-up investigations. SECAT is available for all platforms as open source software implemented in Python and is compatible with different LC-MS/MS profile and reference PPI database formats. We expect that our toolkit and the underlying concepts will be particularly useful for future PCP datasets, guiding the qualitative and quantitative comparison of multiple conditions, where protein complexes represent dynamic rather than static modules.

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources should be directed and will be fulfilled by the Lead Contact, Andrea Califano (ac2248@cumc.columbia.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

SECAT is available as platform-independent open source software under the Modified BSD License and distributed as part of the SECAT (https://pypi.org/project/secat/) and PyProphet (https://pypi.org/project/pyprophet/) Python PyPI packages. SECAT further depends on the R/Bioconductor package “viper”, which is distributed under a non-commercial usage license. Further documentation and instructions for usage can be found on the SECAT source code repository (https://github.com/grosenberger/secat). A preconfigured Docker container is available from Dockerhub (https://hub.docker.com/r/grosenberger/secat).

All analysis results are available on Zenodo (https://zenodo.org) with the dataset identifier 10.5281/zenodo.3982049.

METHOD DETAILS

The Size-Exclusion Chromatography Algorithmic Toolkit

Input data

The primary input data for SECAT are quantitative, proteotypic/unique peptide-level profiles, e.g. acquired by SEC-SWATH-MS (Heusel et al., 2019, 2020). The input can be supplied either as matrix (protein, peptide and run-wise peptide intensity columns) or as transposed long list. Protein identifiers need to be provided in UniProtKB/Swiss-Prot format. The column names can be freely specified, and example files are provided and referred to in the online documentation.

The second required input file represents the experimental design and molecular weight calibration of the experiment (Heusel et al., 2019, 2020). The primary column is the run identifier (matching the quantitative profiles above), with additional columns for SEC fraction identifier (integer value), SEC molecular weight (float value, as specified previously (Heusel et al., 2019, 2020)), a group condition identifier (freetext value) and a replicate identifier (freetext value). The column names can be freely specified, and example files are provided and referred to in the online documentation.

The third required file covers matching UniProtKB/Swiss-Prot meta data in XML format and can be obtained from UniProt (https://www.uniprot.org/downloads).

Reference PPI networks can be specified to support semi-supervised learning and to restrict the peptide query space. SECAT can accept three files: A positive and a negative reference network for the learning step and a separate reference network to restrict the query space. SECAT natively supports HUPO-PSI MITAB (2.5–2.7), STRING-DB, BioPlex and PrePPI formats and provides filtering options to optionally exclude lower confidence PPIs. Example files for CORUM (version 3.0), PrePPI (version 2016) and STRING (version 11.0) are provided and referred to in the online documentation.

Data preprocessing

By default, SECAT first normalizes the quantitative profiles on peptide-level. To reduce local fluctuations in total protein abundance between individual samples, but to still conserve the global distribution of the SEC-fraction-dependent protein abundances, SECAT implements a sliding window-based approach: Cyclic lowess (Ballman et al., 2004; Bolstad et al., 2003) (span=0.7, iterations=3) is applied group-wise to all conditions and replicates by a sliding window (default: N = 5) and a step-size (default: N = 1) over the SEC fraction indices and the average intensity is computed for each peptide in each SEC fraction. The sliding windows are by default “padded”, meaning that the average of the first and last window frames is computed over the restricted set of covered fractions only. Supplemental Fig. 9–12 illustrate the effects of the normalization on the total protein abundance profiles.

Using the user-provided molecular weight calibration of the experiment (Heusel et al., 2019, 2020), the apparent molecular weights of the SEC fractions are matched with the reference molecular weights for each monomeric subunit to identify the closest SEC fraction index, representing a protein-specific “monomer threshold”. In this process, a user-defined factor (default: F = 2) can be specified that is used to multiply the reference molecular weights prior to matching to account for potential homomultimers.

By default, SECAT does not conduct strict prefiltering or peak-picking of the SEC elution profiles. Optionally, peptide-level detrending including or excluding zero values can be conducted, where the quantitative matrix I_s, represents sample s. I_s consists of peptide intensities i_s with rows, representing peptides of the complete set P with index p and columns, representing runs of the complete set R with index r. I_s can be transformed to I_{s,detrendzero} or I_{s,detrenddrop}:

$$i_{s,p,r,detren{d}_{zero}}=\left\{i_{s,p,r}|i_{s,p,r}-\frac{{\sum }_{r=1}^R{i}_{s,p,r}}{R}>0\right\}$$

$$s_{s,p,r}=\left\{\begin{array}{c}0,if{i}_{s,p,r}=0\\ 1,if{i}_{s,p,r}>0\end{array}\right.$$

$$i_{s,p,r,detren{d}_{drop}}=\left\{i_{s,p,r}|i_{s,p,r}-\frac{{\sum }_{r=1}^R{i}_{s,p,r}}{{\sum }_{r=1}^R{s}_{s,p,r}}>0\right\}$$

As alternative option, a local maximum (“local-max”) peak-picking algorithm can be applied on protein-level, either individually per sample or averaged over the replicates of the same conditions under the same assumptions as stated above. First, the quantitative matrix is extended to protein-level J_s for sample s or averaged over all replicates of condition $c,\stackrel{-}{J_c}$, with rows, representing proteins of the complete set O with index o and o_p indicating the set of peptides p mapping to the protein with a minimum (default: N = 1) and maximum (default: N = 3) peptides, sorted according to decreasing total intensity over the full SEC gradient.

$$j_{s,o,r}=\frac{{\sum }_{p=1}^{p=o_p}{i}_{s,p,r}}{o_p}$$

$$\stackrel{-}{j_{c,o,r}}=\frac{{\sum }_{p=1}^{p=o_p}\stackrel{-}{i_{c,p,r}}}{o_p}$$

Protein level arrays are then used as input for the SciPy (Virtanen et al., 2020) local maxima peak-picking function “scipy.signal.find_peaks” (minimum width=3, relative height=0.9), which returns a binary vector k_s,o(r) for each protein indicating the peak boundaries. Using this vector, the peptide-level matrix is transformed: Peptide intensities i_s,p,r are set to zero if the binary vector k_s,o(r) of mapping protein o at run index r is zero, indicating outside-peak boundaries:

$$i_{s,p,r,localma{x}_{replicates}}=\left\{i_{s,p,r}|k_{s,o}\left(p,r\right)>0\right\}$$

$$i_{s,p,r,localma{x}_{conditions}}=\left\{i_{s,p,r}|\stackrel{-}{k_{c,o}\left(p,r\right)}>0\right\}$$

Signal processing

Candidate PPIs, either defined by the reference PPI networks or by computing all pairwise combinations, are evaluated in the signal processing module. First, a minimum (default: N = 1) and maximum (default: N = 3) number of peptides are selected according to total intensity computed over the full SEC profile and all samples. If there are at least 3 consecutive non-zero values on protein-level, a vector of 11 scores is computed within the assembled fractions of each candidate PPI, where the input data are the preprocessed SEC profile intensities of the peptides corresponding to the two interactor proteins. The peptide p_A,j denotes the j-th ranking peptide with the complete set J of protein A, whereas i_A,j,r denotes the peptide intensity of that peptide in run r of the complete set R.

Cross-correlation-based scores:

Inspired by the chromatographic cross-correlation-based scores of mQuest/mProphet (Reiter et al., 2011), two scores are computed by comparing the peptides of protein A with the peptides of protein B.

First, peptides intensities are normalized over all runs:

$$i_{A,j,r,norm}=\frac{i_{A,j,r}-\stackrel{-}{i_{A,j}}}{{\sigma }_{i_{A,j}}}$$

Second, the cross-correlation function between each combination of peptides of protein A and B is computed using the NumPy function “numpy.correlate”:

$$\left(i_{A,j,norm}\star i_{B,k,norm}\right)\left(\tau \right)\triangleq {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\stackrel{-}{l_{A,j,norm}\left(r\right)}{i}_{B,k,norm}(r+\tau )dr$$

Based on this function, two scores are derived. xcorr_shape describes the average of all normalized peptide pair convolution products retrieved at full signal overlap. xcorr_shift describes the maximum difference between the intersection and protein A or B in xcorr_apex, which represents the average delay τ at which the cross-correlation is maximal:

$$xcor{r}_{shape}=\frac{{\sum }_{j=1}^{j=J}{\sum }_{k=1}^{k=K}ma{x}_{overlap}\left(\left(i_{A,j,norm}\star i_{B,k,norm}\right)\left(\tau \right)\right)}{J\mathrm{*}K}$$

$$xcor{r}_{apex,A\cap B}=\frac{{\sum }_{j=1}^{j=J}{\sum }_{k=1}^{k=K}argmax\left(\left(i_{A,j,norm}\star i_{B,k,norm}\right)\left(\tau \right)\right)}{J\mathrm{*}K}$$

$$xcor{r}_{apex,A}=\frac{{\sum }_{j=1}^{j=J}{\sum }_{k=1}^{k=J}argmax\left(\left(i_{A,j,norm}\star i_{A,k,norm}\right)\left(\tau \right)\right)}{J\mathrm{*}J}$$

$$xcor{r}_{apex,B}=\frac{{\sum }_{j=1}^{j=K}{\sum }_{k=1}^{k=K}argmax\left(\left(i_{B,j,norm}\star i_{B,k,norm}\right)\left(\tau \right)\right)}{K\mathrm{*}K}$$

$$xcor{r}_{shift}=\mathrm{m}\mathrm{a}\mathrm{x}(\left|xcor{r}_{apex,A\cap B}-xcor{r}_{apex,A}\right|,\left|xcor{r}_{apex,A\cap B}-xcor{r}_{apex,B}\right|)$$

Monomer-based scores:

Two scores are computed to measure the distance in SEC fractions between monomers of proteins A and B and their PPIs. m_A denotes the monomer threshold computed for protein A:

$$delt{a}_{monomer}=\left|m_A-m_B\right|$$

$$ape{x}_{monomer}=\mathrm{m}\mathrm{i}\mathrm{n}(m_A-xcor{r}_{apex,A\cap B},m_B-xcor{r}_{apex,A\cap B})$$

Maximal and total information coefficient-based scores (MIC/TIC):

Mean equicharacteristic mic and tic scores are computed for all peptide combinations between proteins A and B using the minepy package (Albanese et al., 2013):

$$mic=\frac{{\sum }_{j=1}^{j=J}{\sum }_{k=1}^{k=K}mi{c}_e(i_{A,j}\left(r\right),i_{B,k}\left(r\right))}{J\mathrm{*}K}$$

$$tic=\frac{{\sum }_{j=1}^{j=J}{\sum }_{k=1}^{k=K}ti{c}_e(i_{A,j}\left(r\right),i_{B,k}\left(r\right))}{J\mathrm{*}K}$$

SEC profile intersection-based scores:

Two scores are computed to describe the intersection of the protein profiles. The intersection of proteins A and B over the SEC profile is defined as true at index r, if any peptide of protein A and any peptide of protein B have non-zero intensities:

$${is}_{A\cap B,r}=\left\{i_{A,j\in J,r}>0\wedge i_{B,k\in K,r}>0\right\}$$

The union of protein A and B over the SEC profile is defined as true at index r, if any peptide of protein A or B has non-zero intensities:

$$u_{A\cup B,r}=\left\{i_{A,j\in J,r}>0\vee i_{B,k\in K,r}>0\right\}$$

The score sec_intersection describes the maximum stretch of consecutive intersecting fractions:

$${\mathrm{s}\mathrm{e}\mathrm{c}}_{intersection}={\mathrm{m}\mathrm{a}\mathrm{x}}_{consecutive}\left({is}_{A\cap B}\right(r\left)\right)$$

The score sec_overlap represents the Jaccard Index and describes the total intersection divided by the total overlap.

$${\mathrm{s}\mathrm{e}\mathrm{c}}_{overlap}=\frac{{\sum }_{r=1}^{r=R}{is}_{A\cap B,r}}{{\sum }_{r=1}^{r=R}{u}_{A\cup B,r}}$$

Protein-abundance-based scores:

Two scores are derived to describe the relative ratio of proteins A and B. First, the peptide intensities are summarized over the intersection or the full SEC profile:

$$i_{A\cap B,j}={\sum }_{r=1}^{r=R}\left\{i_{A,j,r}|i_{A,j\in J,r}>0\wedge i_{B,k\in K,r}>0\right\}$$

$$i_{A,j,total}={\sum }_{r=1}^{r=R}{i}_{A,j,r}$$

Second, for each protein an abundance metric is computed by averaging the peptide intensities:

$$O_{A\cap B}=\frac{{\sum }_{j=1}^{j=J}{i}_{A\cap B,j}}{J}$$

$$O_{A,total}=\frac{{\sum }_{j=1}^{j=J}{i}_{A,j,total}}{J}$$

The score abundance_ratio defines the relative abundance ratio between the intersection of proteins A and B. The score total_abundance_ratio defines the abundance ratio between the full SEC profiles of proteins A and B. If the values are larger than 1, the inverse values are computed:

$$abundanc{e}_{ratio}=\left(\frac{O_{A\cap B}}{O_{B\cap A}}<1\to \frac{O_{A\cap B}}{O_{B\cap A}}\right)\wedge \left(\neg \frac{O_{A\cap B}}{O_{B\cap A}}<1\to \frac{O_{B\cap A}}{O_{A\cap B}}\right)$$

$$total\_abundanc{e}_{ratio}=\left(\frac{O_{A,total}}{O_{B,total}}<1\to \frac{O_{A,total}}{O_{B,total}}\right)\wedge \left(\neg \frac{O_{A,total}}{O_{B,total}}<1\to \frac{O_{B,total}}{O_{A,total}}\right)$$

Kickstart score:

To initialize semi-supervised learning, a kickstart score is computed to select PPIs that co-elute, have similar shape, and similar interactor mass, where values range between 0 and 1 with higher values indicating better signals:

$$kickstart=\frac{xcor{r}_{shape}\mathrm{*}total\_abundanc{e}_{ratio}}{xcor{r}_{shift}+1}$$

PPI detection

Spontaneous co-elution of protein subunits in PCP datasets represents a considerable challenge to identify or detect PPIs. While partial scores can describe properties to discriminate true-positive from false-positive candidate PPIs, several properties need to be combined to achieve sensitivity and selectivity. For this reason, supervised learning of classifiers for PPI identification using a ground truth dataset was a critical component of all previous approaches (Havugimana et al., 2012; Heusel et al., 2019; Hu et al., 2019; Kristensen et al., 2012; Scott et al., 2015; Stacey et al., 2017; Wan et al., 2013, 2015).

The CORUM (Giurgiu et al., 2019) protein complex reference database has been used previously for this purpose. For the application in SECAT, the complexes were transformed to PPIs, representing the positive ground truth dataset. For the negative ground truth dataset, we adapted the approach proposed by the PrInCE algorithm (Stacey et al., 2017). It leverages CORUM PPIs as positive and all other interactions of CORUM proteins that are not included in the database (CORUM-inverted) as negative PPIs. Since proteins in CORUM complexes are well characterized and, for the most part, supported by 3D structure data, this strategy assumes that any true interactions within that set of proteins should be known already. As such, identified or detected interactions that are not reported are likely false-positives (Stacey et al., 2017). For the purpose of the benchmark we further excluded any known or predicted interactions from CORUM-inverted and split the combined positive/negative reference set into equally sized training/validation and hold-out subsets.

However, since SECAT does by default not conduct strict prefiltering and uses considerably more candidate PPIs for machine learning and scoring, spontaneous co-elution events of (partially) overlapping interactors within the positive ground truth dataset would lead to an accumulation of false positives. For this reason, a semi-supervised learning approach, inspired by the solutions developed as part of Percolator (Käll et al., 2007), mProphet (Reiter et al., 2011) and PyProphet (Rosenberger et al., 2017; Teleman et al., 2015) for related challenges within computational proteomics was implemented, where the true-positive ground truth set is learned over several iterations, ensuring both selective and sensitive scoring of candidate signals.

The input for the semi-supervised learning step are the partial score vectors for the positive and negative ground truth dataset. Optionally, two filters can be applied to remove the most unlikely candidate PPIs. The minimum abundance ratio filter (default: F = 0.1) ensures that only PPIs within a maximum 10-fold difference of protein abundance ratios are considered. The maximum SEC fraction shift filter (default: F = 10) ensures that only PPIs with maximum elution peaks within 10 SEC fractions are considered. The PyProphet learning module is then applied to the ground truth dataset.

Semi-supervised learning:

This step is conducted essentially as described before (Reiter et al., 2011) with modifications:

1. Cross-validation is conducted with a randomly sampled fraction f of the data (default: f = 0.8) and repeated r (default: r = 10) times.

   1. Initialization of semi-supervised learning:

      1. All negative ground truth PPIs of the cross-validation fold are used. The kickstart score is used to select the initial positive ground truth PPI subset at a defined q-value threshold (default: q = 0.1).
      2. As part of the initialization step, all partial scores, except the kickstart score are then used to train an XGBoost (Chen and Guestrin, 2016)-based classifier. Hyperparameters can optionally be tuned as described below, but a default set (num_boost_round=100, early_stopping_rounds=10, test_size=0.33, eta=1.0, gamma=0, max_depth=6, min_child_weight=1, subsample=1, colsample_bytree=1, colsample_bylevel=1, colsample_bynode=1, lambda=1, alpha=0, scale_pos_weight=1, silent=1, objective=binary:logitraw, nthread=1, eval_metric=auc) is provided.
      3. Based on this classification, the positive ground truth dataset is re-scored for the next iteration.
   2. Iterate i (default: i = 3) times:

      1. All negative ground truth PPIs of the cross-validation fold are used. The previous classifier is applied to the ground truth dataset to select the iteration positive ground truth PPI subset at a defined q-value threshold (default: q = 0.05).
      2. Classification of the new dataset is conducted as described above in the initialization step.
      3. Based on this classification, the positive ground truth dataset is re-scored for the next iteration.
   3. The classifier discriminant scores are normalized relative to the negative ground truth data points by subtracting the mean and dividing by the standard deviation of the negative ground truth data points as described previously (Reiter et al., 2011).

2. Classifier discriminant scores are averaged over all cross-validation folds. In combination with the negative ground truth dataset, this score is used to select the final positive ground truth PPI subset at a defined q-value threshold (default: q = 0.05). A final classifier is trained and stored, which will later be used and applied to the full dataset for classification. Optionally, hyperparameters can be tuned at this stage using the hyperopt framework (Bergstra et al., 2013) in a hierarchical fashion within 10 rounds optimizing the evaluation metric “auc”: 1) Complexity hyperparameters: max_depth=(2,8) and min_child_weight=(1,5), 2) Gamma hyperparameter: gamma=(0.0,0.5), 3) Subsampling hyperparameters: subsample=(0.5,1.0), colsample_bytree=(1.0), colsample_bylevel=(1.0), colsample_bynode=(1.0), 4) Regularization hyperparameters: lambda=(0.0,1.0), alpha=(0.0,1.0), 5) Learning rate: eta=(0.5,1.0). Integer ranges are sampled by a quantized uniform distribution, floating number ranges are sampled by a uniform distribution. In our applications, we found that the default hyperparameter set described above was applicable to all tested datasets and we thus omitted autotuning in further iterations.

Statistical validation:

The Storey-Tibshirani q-value framework (Storey and Tibshirani, 2003) is used to assess false-discovery rates. First, empirical p-values are estimated for the positive ground truth dataset using the negative ground truth dataset as null model (Storey and Tibshirani, 2003). Q-values are then estimated as described previously (Storey and Tibshirani, 2003) with the following parameters in all iterations: pi0_lambda=(min=0.01,max=0.5,step=0.01), pi0_method=bootstrap.

Incorporation of prior information from reference PPI networks:

If a reference PPI network was used to restrict the query space, the optionally provided confidence scores can be incorporated during statistical validation. Because these scores often only to some extent represent the PPIs measurable by PCP datasets and can be differently calibrated across databases, SECAT uses them to compute a grouped FDR. Queried PPIs are grouped according to their prior score in N predefined confidence bins (default: N = 100) and q-value estimation is conducted for each bin separately. This enables multiple hypothesis testing correction to account for different prior probabilities of false detection of interactions and is generically applicable to confidence scores with different statistical properties.

Integration across multiple replicates:

If multiple replicates of the same biological condition are scored together, a global q-value is computed for each PPI by prior computing of the average of the classifier scores over all replicates.

PPI quantification

SEC peptide profiles can be partitioned into components to represent quantitative information on different levels. Based on the peptide-level SEC profiles, SECAT computes four quantitative metrics for selected peptides of a protein (default: minimum N = 1; maximum N = 3 peptides per protein, ranked according to total protein abundance):

Total intensity:

The sum of the full elution profile corresponds to the total peptide abundance, which to some degree represents protein abundances measured by conventional, non-fractionated LC-MS/MS.

Assembled intensity:

Based on the protein-specific monomer threshold defined in the preprocessing step, the peptide signals of all assembled fractions (left hand-side of monomer threshold) are summarized.

Monomer intensity:

Based on the protein-specific monomer threshold defined in the preprocessing step, the peptide signals of all monomer fractions (right hand-side of monomer threshold) are summarized.

Interactor intensity:

To compute the PPI-level quantities, for each PPI below a specified confidence threshold (default: integrated q-value < 0.05 in any of the compared conditions), the intersecting fractions of the two interactor protein profiles are analogously extracted on peptide level.

These summarized peptide-level quantities are then log₂-transformed and the log₂-fold-change between groups is computed. The intensities are further used by the proteoVIPER module for differential quantitative protein and PPI assessment. proteoVIPER is based on the VIPER algorithm (Alvarez et al., 2016), which was originally developed to assess protein activity from transcriptomic profiles using gene regulatory networks. Using the peptide-protein relationships, proteoVIPER computes three differential protein-level metrics, total, assembled and monomer abundance to describe changes between the groups. In addition, proteoVIPER computes three differential PPI-level metrics based on the peptide interactor intensities of the two proteins within a PPI: interactor and complex abundance and interactor ratio.

The main component of VIPER and thus proteoVIPER is the analytic rank-based enrichment analysis (aREA) module, which tests for a global shift in the position of the peptides mapping to the same protein or PPI when projected on the rank-sorted peptide intensities of a run on separate levels (Alvarez et al., 2016). The description of the algorithm below is adapted from the original publication (Alvarez et al., 2016):

1. To compute total, assembled and monomer abundances, the peptides mapping to the protein-of-interest are used. To compute the interactor abundance, for each PPI, the peptides of each interactor are separately assessed with a positively correlated mode of interaction. To compute complex abundance, the peptides of proteins A and B are used with the same, positively correlated mode of interaction. To compute interactor ratio, the peptides of proteins A and B are used with negatively correlated mode of interaction.

2. The means of the quantile-transformed rank positions are used as test statistic (enrichment score), which is computed twice:

   1. First, a one-tail approach is used based on the absolute value of the peptide intensities, which rank-sorts proteins from the less invariant between groups to the most differentially abundant.
   2. Second, a two-tail approach is used, where the positions of the peptides of one interactor is inverted (negatively correlated mode of interaction) within the peptide intensity signature to compute the interactor ratio enrichment score.

3. The one-tail and two-tail enrichment scores are then integrated exactly as described previously (Alvarez et al., 2016), but with equal confidence for each peptide. The scores are normalized and calibrated against the reference exactly as described previously (Alvarez et al., 2016).

The quantitative metrics reported by proteoVIPER have several advantages: First, quantitative changes of proteins between different samples can also be assessed by only partially overlapping sets of peptides. Second, complex abundance changes can be estimated by contributions of the peptides of both interactor proteins. Third, by assessing the interactor proteins in a negatively correlated mode of interaction, a differential metric for changes affecting the ratio of the interactors can be derived, which to some extent represents a metric describing changes in complex stoichiometry. proteoVIPER reports six quantitative matrices, representing protein or PPI metrics on each level that can be used for differential comparisons between the samples and conditions. Experimental conditions can then be statistically compared by independent t-tests (Alvarez et al., 2016) on each level.

Network inference

Using the PPI-level quantitative metrics from above, SECAT conducts network-centric data integration. For each protein, the test statistics and proteoVIPER normalized enrichment scores of its PPIs are integrated using Empirical Brown’s Method (Poole et al., 2016). The evidence of multiple measured PPI is thus summarized to protein complex metrics summarizing changes in protein complex abundance or interactor ratio for each protein. Notably, highly correlated PPI (e.g. from the same protein complex) are integrated in a dependent fashion, whereas independent PPI (e.g. from different protein complexes) combine and increase the significance of the protein complex engagement metric.

In a network context, this helps to identify the most perturbed or dysregulated proteins based on changes of their protein complexes. Instead of clustering or inferring protein complexes, which are difficult to define in presence of subcomplexes across multiple experimental conditions, SECAT’s metrics can be more robustly characterized from a partial subset of their interactions.

Integrated p-values are adjusted for multiple testing using the Benjamini-Hochberg (Benjamini and Hochberg, 1995) approach, as suggested in the original publication (Poole et al., 2016).

Primary data analysis

Processed mass spectrometry datasets have been obtained from the repositories linked by the original publications or the authors of the corresponding publications.

SECAT data analysis

SECAT (version 1.0.5), PyProphet (version 2.1.4) and VIPER (version 1.20) were used for all data analyses with CORUM (Giurgiu et al., 2019) (version 3.0), PrePPI (Garzón et al., 2016) (version 2016) and STRING (Szklarczyk et al., 2019) (version 11.0) and default parameters if not otherwise specified. SECAT (version 1.0.8), PyProphet (version 2.1.5) and VIPER (version 1.22.0) were used for all data analyses with BioPlex (version 3.0 (293T) and version 1.0 (HCT116)) (Huttlin et al., 2015, 2017), IntAct-micluster (version 20200729) (Orchard et al., 2014), hu.MAP (version 20200729) (Drew et al., 2017) and HuRI (version 20200721) (Luck et al., 2020) and default parameters if not otherwise specified.

Semi-supervised learning was conducted using CORUM as positive network and CORUM-inverted as negative network. The inverted CORUM reference PPI network was generated by using the inverted set of PPIs (i.e. all possible PPIs that are not covered by CORUM) and removing all PPI in this set covered by STRING (version 11.0), IID (Kotlyar et al., 2019) (version 2018–11), PrePPI (version 2016) or BioPlex (Huttlin et al., 2017) (version 2.0).

All input and output data and used parameters are provided on the Zenodo repository to reproduce all analysis steps.

QUANTIFICATION AND STATISTICAL ANALYSIS

Parameter selection and validation of signal processing and PPI detection modules

The SECAT PPI detection benchmark was conducted by using 50% of the CORUM reference PPI network for learning and the other fraction for evaluation. For all assessments, this random selection was conducted on PPI-level, except for the algorithm comparison, where the selection was conducted on complex-level. Reference negative PPIs from CORUM-inverted were randomly selected in predefined ratios (1:0 – 1:16) and added to the target set for evaluation but not learning.

Fig. 2a and Supplemental Fig. 1a depict violin plots with the following parameters: Lower and upper hinges represent the first and third quartiles; the bar represents the median. This represents the default parameters of the function “geom_violin” of ggplot2.

Fig. 2b and Supplemental Fig. 1b were generated by assessing the PPIs with a global-context q-value < 0.05 and decomposing the number of PPIs for detection amongst replicates at different confidence thresholds.

Fig. 2e and Supplemental Fig. 1e were generated by using the ground truth CORUM and CORUM-inverted reference values. Because the estimated q-values are dependent on the combined reference sets with unknown ratios of true-positive and false-positive PPIs, the “true q-values” were corrected by a factor, which accounts for the PyProphet estimated proportion of false targets in the 1:0 dilution step.

For Supplemental Fig. 2, the CORUM reference PPI network was similarly used as described above to generate a pseudo-ground truth dataset for classifier training. However, for the validation subset, an excess of 10 times as many negative interactions as targets prior to analysis was added and subsets were generated by randomly selecting protein complexes instead of PPIs. For the downstream analysis, the CORUM targets only were reduced to the intersection with a previously published (Heusel et al., 2019), manually curated annotation of the dataset.

The CCprofiler (Heusel et al., 2019) analysis (git revision: 39650f2) was conducted as suggested by the software documentation. All input data and parameters are provided on the Zenodo repository.

The EPIC (Hu et al., 2019) analysis (git revision: b6432b9) was conducted as suggested by the software documentation with the provided Docker container. The input data was first aggregated from peptide-level to protein-level using the top3 method implemented in aLFQ (Rosenberger et al., 2014) (version 1.3.5). All input data and parameters are provided on the Zenodo repository.

Validation of PPI quantification & network integration modules

The data was analyzed as described above with the full CORUM, PrePPI and STRING reference networks and a network encompassing all potential PPIs. Fig. 3c–f were generated using the STRING-based analysis. Fig. 3d depicts boxplots with the following parameters: Lower and upper hinges represent the first and third quartiles; the bar represents the median. Lower and upper whisker extend to 1.5 * IQR from the hinge. This represents the default parameters of the function “geom_boxplot” of ggplot2.

Supplemental Fig. 3a–b were generated using the” UpSetR” R-package (Conway et al., 2017) (version 1.4.0). Supplemental Fig. 3c was generated by computing the node degrees with the “NetworkAnalyzer” module of Cytoscape (Shannon et al., 2003) (version 3.7.2) and visualization of the density distributions of each network using the function density compare from the R-package “sm” (version 2.2–5.6) with default parameters.

Comparison of complex- and network-centric analysis strategies

CCprofiler results on “protein complex feature” and “total” protein abundance level were obtained from the original study (Heusel et al., 2020) and filtered for the best feature per protein. The score “median.Log2FC” was used for both feature and total protein levels, because in comparison to other metrics or combinations thereof, GSEA resulted in most significantly enriched subpathways.

SECAT results were transformed to an integrated score by sign(log2FC) * (-log10(adj. p-value)) for total, assembled, monomer, interactor and complex abundances. For “interactor ratio”, the score was computed by sign(log2FC) * (-log10(adj. p-value)) * abundance_ratio.

GSEA (Subramanian et al., 2005) was conducted using the “fgsea” (Sergushichev, 2016) R-package (version 1.14.0) and the full set of Reactome (version 73) subpathways or a version reduced to include only subpathways of the cell cycle (R-HSA-1640170). Each score was separately assessed by fgsea with 10,000 permutations and a minimum gene set size of 5, reducing pathways to primary subsets.

Fig. 4a and Supplemental Fig. 4 were generated using the function “geom_bar” from ggplot2; opaque bars with black borders indicate significance (adj. p-value < 0.01). Bars are ordered by descending mean of normalized enrichment scores (NES) across all scores for visualization.

The “leading edge” (Subramanian et al., 2005) proteins were selected to compare CCprofiler and SECAT results. For the SECAT unique proteins set, the significant results (adj. p-value < 0.01) not present in the set of CCprofiler leading edge proteins were further investigated. For the CCprofiler unique proteins set, all results were investigated.

Visualization of protein-level SEC-SWATH-MS profiles in Fig. 4b–d and Supplemental Fig. 5 were conducted using the R-package “ggplot2” by averaging the three most intense peptide precursors per protein.

Molecular mechanisms differentiating HeLa cell cycle states

To annotate and visualize differential proteins in Fig. 5 and Supplemental Fig. 6–7 between the HeLa cell cycle states identified by SECAT, we used Cytoscape (Shannon et al., 2003) (version 3.7.2). CORUM (version 3.0) or Reactome (Jassal et al., 2020) (version 71) was used to cluster PPI using the Cytoscape App AutoAnnotate (Kucera et al., 2016) (version 1.3.2) with default parameters and a maximum cluster size (“Max words per label”) of 1. For this purpose, CORUM complexes and Reactome pathways were transformed to a list, where for each protein identifier, the set of complex or pathway identifiers in the reference database was appended. This set was then used as input for AutoAnnotate. Clusters were arranged according to the CoSE layout.

Visualization of protein-level SEC-SWATH-MS profiles in Fig. 6 and Supplemental Fig. 8 was conducted using the R-package “ggplot2” by averaging the three most intense peptide precursors per protein.

Supplementary Material

sFig 2

Supplemental Figure 2. Receiver operating characteristic for the comparison of SECAT with EPIC and CCprofiler using the HEK293-EG (Heusel et al., 2019) dataset. Because the sets of identified or detected PPIs vary substantially (EPIC: 4,592 PPIs, CORUM: 4,955 PPIs, SECAT: 31,932 PPIs), the full intersection of all three algorithms (a), as well as all pairwise comparisons (b-d) were computed (Supplemental Note 2).

sFig 3

Supplemental Figure 3. (a) UpSet visualization of PPI query space using different reference PPI networks and the HeLa-CC (Heusel et al., 2020) dataset. (b) Overlap of confident (q-value < 0.05) PPI detections after SECAT analysis with different reference PPI networks. (c) Comparison of node degree densities between different reference PPI networks and the network covering all possible PPI combinations.

sFig 1

Supplemental Figure 1. Signal processing and PPI detection performance evaluated using the Jurkat-Fas (Scott et al., 2017) dataset. (a) The effect of different peak-picking methods for signal processing on peak-width and PPI quantification within replicates of the same experimental condition is depicted in violin plots (lines representing 25, 50 and 75% quantiles respectively, STAR Methods). (b) Sensitivity of PPI detection vs. SECAT q-value for peak-picking options. The PPI were filtered to a global context q-value<0.05. Colors indicate different peak-picking options; line types indicate number of detections with the three replicates per condition. (c) The receiver-operating characteristic (ROC) illustrates the sensitivity vs. specificity of the different SECAT partial scores, the kickstart score and the integrated SECAT score. Numbers in brackets indicate ROC area under the curve values for each partial or combined score. (d) The SECAT score histograms depict the dilution of the reference PPI network (true: CORUM) with negative PPIs (false: CORUM-inverted) for the benchmark (STAR Methods). (e) The SECAT estimated q-value is accurate as evaluated against the ground truth for all levels of reference PPI network accuracy. For the dilution 1:0, no a priori false PPIs are tested, thus the true FDR equals to 0. (f) The sensitivity of PPI detection in dependency of SECAT q-value for different levels of reference PPI network accuracy is depicted. Solid lines represent the true, whereas dashed lines represent the false PPIs. (g) Consistency of PPI detection between replicates of the same conditions.

sFig 4

Supplemental Figure 4. Gene set enrichment analysis was conducted using all Reactome subpathways for CCprofiler and SECAT scores generated by different reference PPI networks. Opaque bars with black borders indicate significant enrichment (adj. p-value < 0.01) (STAR Methods). Subpathways are only depicted if the significance threshold is reached in at least one subscore.

sFig 5

Supplemental Figure 5. CCprofiler exclusive leading edge proteins are not detected by SECAT due to different reasons. (a-m) No confidently detected PPIs, potentially due to low number of peptides (a-e). (n-q) Although some PPIs could be detected, large variability between replicates might have lowered statistical significance.

sFig 6

Supplemental Figure 6. Extended complex-level molecular mechanisms differentiating HeLa cell cycle states. The integrated STRING-based PPI network of the HeLa cell cycle dataset (Heusel et al., 2020) is depicted with proteins (nodes) and binary PPIs (edges) clustered against CORUM complexes (identifiers in brackets; STAR Methods). Different colors indicate the most significant metric-level (legend, STAR Methods). Node-size indicates effect-size and opacity indicates significance. The most prominent clusters highlight essential macromolecular assemblies. Interactive results (Cytoscape) are provided as Supplemental Data 1.

sFig 7

Supplemental Figure 7. Pathway-level molecular mechanisms differentiating HeLa cell cycle states. The integrated STRING-based PPI network of the HeLa cell cycle dataset (Heusel et al., 2020) is depicted with proteins (nodes) and binary PPI (edges) clustered against Reactome pathways (identifiers in brackets; STAR Methods). Different colors indicate the most significant metric-level (legend, STAR Methods). Node-size indicates effect-size and opacity indicates significance. The most prominent clusters highlight essential macromolecular assemblies. Interactive results (Cytoscape) are provided as Supplemental Data 1.

sFig 8

Supplemental Figure 8. Extended protein-level SEC-SWATH-MS profiles of HeLa cell cycle states. Lines indicate different protein subunits, whereas the dashed line indicates the highest monomer threshold per group. (a) BAF complex. (b) 18S U11/U12 snRNP. (c) Condensin II. (d) Nup 107-160 subcomplex.

sFig 9

Supplemental Figure 9. Summarized raw peptide precursor intensities over the SEC profile for the HeLa-CC (Heusel et al., 2020) dataset.

sFig 11

Supplemental Figure 11. Summarized raw peptide precursor intensities over the SEC profile for the Jurkat-Fas (Scott et al., 2017) dataset.

sFig 10

Supplemental Figure 10. Summarized normalized peptide precursor intensities over the SEC profile for the HeLa-CC (Heusel et al., 2020) dataset.

sFig 12

Supplemental Figure 12. Summarized normalized peptide precursor intensities over the SEC profile for the Jurkat-Fas (Scott et al., 2017) dataset.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
CORUM (version 3.0)	(Giurgiu et al., 2019)	https://mips.helmholtz-muenchen.de/corum/
PrePPI (version 2016)	(Garzón et al., 2016)	https://honiglab.c2b2.columbia.edu/PrePPI/
STRING (version 11.0)	(Szklarczyk et al., 2019)	https://string-db.org/
IID (version 2018–11)	(Kotlyar et al., 2019)	http://iid.ophid.utoronto.ca/
BioPlex (version 2.0)	(Huttlin et al., 2017)	https://bioplex.hms.harvard.edu/
BioPlex (version 3.0)	(Huttlin et al., 2017)	https://bioplex.hms.harvard.edu/
IntAct (version 20200729)	(Orchard et al., 2014)	https://www.ebi.ac.uk/intact/
hu.MAP (version 20200729)	(Drew et al., 2017)	http://proteincomplexes.org/
HuRI (version 20200721)	(Luck et al., 2020)	http://www.interactome-atlas.org/
HeLa-CC SEC-SWATH-MS dataset	(Heusel et al., 2020)	https://doi.org/10.1016/j.cels.2020.01.001
HEK293-EG SEC-SWATH-MS dataset	(Heusel et al., 2019)	https://doi.org/10.15252/msb.20188438
Jurkat-Fas PCP dataset	(Scott et al., 2017)	Leonard Foster, PhD foster@msl.ubc.ca
Reactome (version 71)	(Jassal et al., 2020)	https://reactome.org/
Reactome (version 73)	(Jassal et al., 2020)	https://reactome.org/
UniProtKB XML reference file (version 20190402)	UniProt Consortium	https://www.uniprot.org/
Preprocessed SECAT input/output files	This Paper	https://doi.org/10.5281/zenodo.3982049
Software and Algorithms
SECAT (version 1.0.5)	This Paper	https://github.com/grosenberger/secat
SECAT (version 1.0.8)	This Paper	https://github.com/grosenberger/secat
PyProphet (version 2.1.4)	This Paper	https://github.com/PyProphet/pyprophet
PyProphet (version 2.1.5)	This Paper	https://github.com/PyProphet/pyprophet
VIPER (version 1.20)	(Alvarez et al., 2016)	https://dx.doi.org/10.18129/B9.bioc.viper
VIPER (version 1.22.0)	(Alvarez et al., 2016)	https://dx.doi.org/10.18129/B9.bioc.viper
CCprofiler (version 39650f2)	(Heusel et al., 2019)	https://github.com/CCprofiler/CCprofiler
EPIC (version b6432b9)	(Hu et al., 2019)	https://github.com/BaderLab/EPIC
aLFQ (version 1.3.5)	(Rosenberger et al., 2014)	https://cran.r-project.org/web/packages/aLFQ/index.html
Cytoscape (version 3.7.2)	(Shannon et al., 2003)	https://cytoscape.org/
AutoAnnotate (version 1.3.2)	(Kucera et al., 2016)	http://apps.cytoscape.org/apps/autoannotate
R (version 3.6.1)	The R Foundation	https://www.r-project.org/