Abstract
Temperature-dependent interaction parameters of Redlich-Kister (R–K) polynomials for Li–Mg alloy in liquid phase have been optimized using experimental data in the framework of linear and exponential models. These parameters have then been used to compute the thermodynamic properties (excess Gibbs free energy of mixing, enthalpy of mixing and activity) and structural property (concentration fluctuations in the long-wavelength limit) of the alloy at temperatures 1000 K, 1300 K, 1600 K, 1900 K, and 2200 K. The negative values of excess Gibbs free energy of mixing computed using linear T-dependent parameters increases with the rise in the temperature of the system beyond 1000 K while the same physical quantity computed using the exponential T-dependent interaction parameters decreases with the rise in temperatures and does not show any unusual trends up to 2200 K. Similar behavior has been found in the case of other thermodynamic and structural functions. The unusual behavior that appears in the thermodynamic and structural functions computed using linear T-dependent parameters can be eliminated if these functions are computed using exponential T-dependent parameters.
Keywords: Li-Mg alloy, R–K polynomial, Exponential parameters, Miscibility gap, High temperature
Li-Mg alloy; R–K polynomial; Exponential parameters; Miscibility gap; High temperature
1. Introduction
The coexistence of two distinct liquid phases causes miscibility gaps in the liquid phase of alloys [1, 2]. The miscibility gaps which appear in phase diagrams and thermodynamic functions are termed thermodynamic artifacts. Several researchers [3, 4, 5, 6, 7, 8, 9, 10, 11, 12] have revealed the existence of artificial inverted miscibility gaps in different alloy systems. Kevorkov et al. [3] analyzed published parameters of Feufel [13] and Yan et al. [14] for Mg–Si system and studied the presence of artificial inverted miscibility gaps in the liquid phase at higher temperatures. They then remodeled the system using the data of Yan et al. [14] and computed the phase diagram without the inverted miscibility gaps up to 4273 K. Kaptay [4] explained that the artifacts appear in some alloy systems at high temperature when the coefficients of Redlich-Kister (R–K) polynomials are considered to be linear temperature (T) dependent. The linear T-dependence of interaction parameters are expressed in the form where is the enthalpy term in unit J mol−1 and is the entropy term in J mol−1 K−1. Following Kaptay, if and , then the existence of artifacts is observed. To overcome this, he proposed a model in which the interaction parameters depend exponentially on T called the exponential model. Later Schmidt-Fetzer et al. [7] detected the presence of low-temperature artifact in the phase diagram of Mg–Si system using two exponentially optimized parameters. With this regard, Liang et al. [11] employed the combined linear-exponential T- dependent (LET) interaction parameter in order to remove both high and low T-artifacts of the system. Contrary to Schmidt-Fetzer et al., Kaptay removed both high and low-T artifacts of fifteen different systems by considering four exponential interaction parameters [12]. Furthermore, Kaptay suggested the utility of LET interaction parameters for those systems in which the excess Gibbs free energy changes sign with the temperature. In the present work, we have observed the presence of high T-artifacts in Li–Mg system in the temperature range 1000–2200 K while assuming the interaction parameters to be linear T-dependent.
Lithium–Magnesium based alloys are metallic materials having low densities which are mostly used in aerospace, automotive, portable electronics, etc. [15], among which Li–Mg alloys have extremely lightweight, high mechanical strength, and high stiffness. As a result, they have been assessed by several researchers [16, 17, 18, 19] in the field of metallurgical science. Gasior et al. [16] have optimized coefficients of R–K polynomials for Gibbs energy of mixing for the system using data obtained by electromotive force (emf) method and other experimental techniques. Jha et al. [18] studied the same system employing a regular associated solution model assuming the favorable complex Li2Mg and concluded it to be moderately interacting. The phase diagram of Li–Mg alloy shows that there exist three stable liquid phases namely bcc-A2, fcc-A3, and one metastable phase fcc-Al in a liquid solution and two metastable compounds Al12Mg17 and AlLi [20]. Braga et al. [17] computed the phase diagram using the reoptimized parameters for the system using the data of Cost 507 [20]. It was found that the computed phase diagram agrees well with the experimental in the composition range Later, Wang et al. [19] found that there appeared inverse miscibility gap while considering the reassessed parameters of Brag et al. above 973 K. Therefore, they reassessed the system by taking account of experimental data and eliminated inverse miscibility gap and artificial phase relations in Li-rich region which had been appeared in the calculations using parameters from [16, 17] near to its melting temperature. However, it is found that the negative values of excess Gibbs free energy of mixing of the system calculated using parameters of Wang et al. increases with rise in temperature indicating the increase in mixing tendency of the liquid alloy. But the liquid alloys should show ideal mixing behavior at elevated temperatures [21, 22, 23, 24].
In the present work, both the linear and exponential T- dependent interaction parameters have been optimized for the Li–Mg system using experimental data [25]. The excess Gibbs free energy, enthalpy of mixing, activity, and concentration fluctuations in the long-wavelength limit (Scc(0)) have been computed using the optimized parameters in the framework of R–K polynomials at different temperatures. Additionally, the presence of artifacts in the thermodynamic as well as structural functions of the system has been detected using the linear T-dependent interaction parameters. These artifacts have been removed by assuming the exponential T-dependent interaction parameters.
2. Formalism
2.1. Thermodynamic properties
Thermodynamic properties like excess Gibbs free energy of mixing (), heat of mixing () and excess entropy of mixing () can be expressed in terms of Redlich-Kister (R–K) polynomials. These three thermodynamic functions can be related in standard form as
| (1) |
The excess entropy of mixing ( ) in terms can be given as
| (2) |
In the frame work of R–K polynomials, the excess thermodynamic functions () for the binary liquid alloys of the type A-B can be expressed in the form [26].
| (3) |
where and are the concentrations of components A and B of the alloy and Li are the coefficients of R–K polynomials. stands for , and . For linear T-dependent parameters Li be expressed as [7, 11, 12].
| (4) |
where ai and bi are the parameters associated with the heat of mixing and excess entropy of mixing respectively. Using Eq. (4) in Eq. (3), we get
| (5) |
Now, using Eq. (5) in Eq. (2) and then in Eq. (1), one can obtain the relations for and as
| (6) |
and
| (7) |
Following, Kaptay [4], Li in terms of exponential T-dependent interaction parameters can be given as
| (8) |
where hi and τi are exponential parameters which are to be optimized. Similarly, using Eqs. (5), (6), (7) and (8) can be transformed as
| (9) |
| (10) |
and
| (11) |
Activity is an important thermodynamic property of the liquid alloy which are directly computed from the experimental measurements. It provides an immediate insight of the mixing tendency of the system. The activity of components A and B of the liquid alloy can be related to as
| (12) |
where = 1, 2 for components A and B and are partial excess Gibbs free energy of components A and B of the alloy which can further be expressed as [27].
| (13) |
2.2. Structural properties
It is well known fact that the liquid alloys are disorder systems having no long-range interactions. Therefore, the knowledge of the local arrangements of the atoms of the liquid mixture is mandatory to understand the energetic of the initial melt. The extent of local ordering of the atoms can be studied and explained in terms of concentration fluctuations in long-wavelength limit (). The standard relation for in terms of excess free energy of mixing can be given as [28].
| (14) |
Using Eq. (3) in Eq. (13), we get
| (15) |
and ideal value of concentration fluctuations in long-wavelength limit is
The experimental values of Scc(0) can also be calculated using activity of components of binary liquid alloy [22, 29] as
| (16) |
Here liquid A-B alloy stands for liquid Li–Mg alloy.
3. Results and discussion
The experimental data of enthalpy of mixing and excess entropy of mixing for liquid Li–Mg alloy [25] were used to optimize the linear T-dependent interaction parameters of R–K polynomials for excess Gibbs free energy of mixing using Eqs. (5), (6), and (7). The optimized linear parameters were then used to obtain exponential T-dependent interaction parameters using Eqs. (8), (9), (10), and (11). The optimized linear and exponential interaction parameters are presented in Table 1.
Table 1.
Optimized parameters for liquid Li–Mg alloy.
| Linear | Exponential | |
|---|---|---|
| -21318 + 2.9 T | -31362 exp (-1.46 × 10−4 T) | |
| 7930 - 15.1T | 1154251 exp (-1.60 × 10−2 T) | |
| 10668–8.9 T | 12138 exp (-1.34 × 10−3 T) | |
| -7765 + 7.4 T | -9382 exp (-1.67 × 10−3 T) |
The excess Gibbs free energy of mixing () of the liquid alloy has been computed at temperatures 1000 K, 1300 K, 1600 K, 1900 K and 2200 K using Eqs. (5) and (9) with the help of the optimized parameters and listed in Table 2. The values so obtained have been compared with the available literature and experimental data (Figure 1(a–e)). The values of computed using the linear parameters of this work are in excellent agreement with the experimental results. But the values so obtained using exponential parameters slightly deviate from experimental results [25] and its variation is similar to the work of Wang et al. [19]. The computed values of using parameters of Cost 507 [20] are much less than the experimental and the present work results (Figure 1(a)). The values of obtained using linear parameter of this work decrease rapidly with the rise in temperature of the system in Mg-rich region (Figure 1(c), (d)) showing the presence of inverse miscibility gap at higher temperatures while the values computed using the exponential parameter changes smoothly at all concentrations. The negative values of excess Gibbs free energy of mixing using parameters of Wang et al. [19] increases with the rise in the temperature of the system beyond 1000 K (Figure 1(a)–(e)). This result contradicts with the predictions of other researchers that the liquid alloys must show ideal behavior with respect to mixing tendency at elevated temperatures [9, 10, 11]. When the same physical quantity is computed using the exponential T-dependent interaction parameters, it decreases with the rise in temperatures and does not show any unusual trends or so-called artifacts up to 2200 K.
Table 2.
Excess Gibbs free energy of mixing () of liquid Li–Mg alloy at temperatures 1000 K, 1300 K, 1600 K, 1900 K and 2200 K.
| XMg | Excess Gibbs free energy of mixing () in (J/mol) |
|||||||
|---|---|---|---|---|---|---|---|---|
| T = 1000K |
T = 1300 K |
|||||||
| Linear fit | Expon. fit | Experimental [25] | Wang et al. [19] | Cost 507 [20] | Linear fit | Expon. fit | Wang et al. [19] | |
| 0.1 | -2095.23 | -1557.95 | -2085.82 | -1369.21 | -466.40 | -2336.12 | -1515.10 | -1426.77 |
| 0.2 | -3562.91 | -2828.97 | -3540.46 | -2573.13 | -801.39 | -3797.62 | -2738.52 | -2701.48 |
| 0.3 | -4434.11 | -3790.56 | -4405.72 | -3517.11 | -1018.03 | -4533.01 | -3649.81 | -3719.74 |
| 0.4 | -4756.84 | -4400.12 | -4740.12 | -4130.82 | -1127.89 | -4682.10 | -4218.27 | -4401.44 |
| 0.5 | -4596.06 | -4611.78 | -4598.00 | -4368.23 | -1141.00 | -4376.03 | -4413.21 | -4690.79 |
| 0.6 | -4033.70 | -4393.37 | -4050.42 | -4207.57 | -1065.87 | -3737.25 | -4214.18 | -4556.28 |
| 0.7 | -3168.61 | -3743.26 | -3193.52 | -3651.43 | -909.50 | -2879.53 | -3621.17 | -3990.71 |
| 0.8 | -2116.63 | -2707.32 | -2135.98 | -2726.63 | -677.35 | -1907.93 | -2664.87 | -3011.16 |
| 0.9 | -1010.52 | -1395.74 | -1019.92 | -1484.34 | -373.38 | -918.85 | -1416.90 | -1659.03 |
| XMg | Excess Gibbs free energy of mixing () in (J/mol) |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| T = 1600 K |
T = 1900 K |
T = 2200 K |
|||||||
| Linear fit | Expon. fit | Wang et al. [19] | Linear fit | Expon. fit | Wang et al. [19] | Linear fit | Expon. fit | Wang et al. [19] | |
| 0.1 | -2577.0 | -1467.9 | -1484.3 | -2817.9 | -1417.9 | -1541.9 | -3058.8 | -1366.3 | -1599.4 |
| 0.2 | -4032.3 | -2643.0 | -2829.8 | -4267.0 | -2545.0 | -2958.2 | -4501.8 | -2446.5 | -3086.5 |
| 0.3 | -4631.9 | -3508.2 | -3922.4 | -4730.8 | -3367.9 | -4125.0 | -4829.7 | -3230.3 | -4327.6 |
| 0.4 | -4607.4 | -4041.8 | -4672.1 | -4532.6 | -3871.3 | -4942.7 | -4457.9 | -3707.0 | -5213.3 |
| 0.5 | -4156.0 | -4223.2 | -5013.4 | -3936.0 | -4041.3 | -5335.9 | -3715.9 | -3867.3 | -5658.5 |
| 0.6 | -3440.8 | -4039.3 | -4905.0 | -3144.4 | -3869.8 | -5253.7 | -2847.9 | -3706.1 | -5602.4 |
| 0.7 | -2590.4 | -3490.9 | -4330.0 | -2301.3 | -3357.4 | -4669.3 | -2012.3 | -3223.9 | -5008.6 |
| 0.8 | -1699.2 | -2598.4 | -3295.7 | -1490.5 | -2518.0 | -3580.2 | -1281.8 | -2430.1 | -3864.8 |
| 0.9 | -827.2 | -1408.5 | -1833.7 | -735.5 | -1381.9 | -2008.4 | -643.8 | -1344.5 | -2183.1 |
Figure 1.
The compositional dependence of the excess Gibbs free energy of mixing () of the liquid Li–Mg alloy at temperatures (a) 1000 K, (b) 1300 K, (c) 1600 K, (d) 1900 K and (e) 2200 K.
The enthalpy of mixing () of the liquid Li–Mg alloy has been computed at 1000 K using Eqs. (7) and (11) with the aid of the exponential T-dependent parameters and listed in Table 3. The theoretical and experimental values as the function of concentration are in considerable agreement (Figure 2(a)). But computed using the parameters of Wang et al. [19], differ significantly with the results of the present work as well as experimental values (Figure 2(a)). Further, the enthalpy of mixing () of the liquid Li–Mg alloy has also been computed at temperatures 1300 K, 1600 K, 1900 K and 2200 K following a similar procedure as above. The computed negative values of gradually decreases with the increase in the temperature of the system beyond 1000 K (Figure 2(b)). The present theoretical investigations thus predict that the compound forming tendency of the considered system gradually decreases with the rise in its temperatures. These findings further support the results predicted by the excess free energy of mixing in the previous section of the work and are in accordance with other researchers [21, 22, 23, 24] too. These results correspond to the reliability and fruitfulness of exponential T-dependent optimized parameters of this work.
Table 3.
Enthalpy of mixing (HM) of liquid Li–Mg alloy 1000 K, 1300 K, 1600 K, 1900 K and 2200 K.
| XMg | Enthalpy of mixing (HM) in (J/mol) |
|||||||
|---|---|---|---|---|---|---|---|---|
| T = 1000 K |
Expon. fit |
|||||||
| Linear fit | Expon. fit | Experimental [25] | Wang et al. [19] | T = 1300K | T = 1600K | T = 1900K | T = 2200K | |
| 0.1 | -1091.0 | -1424.2 | -1091.0 | -1177.4 | -1318.8 | -1207.4 | -1095.0 | -985.3 |
| 0.2 | -2303.5 | -2539.8 | -2340.8 | -2145.3 | -2333.3 | -2124.8 | -1920.9 | -1725.9 |
| 0.3 | -3556.6 | -3326.0 | -3582.3 | -2841.7 | -3036.2 | -2754.9 | -2486.5 | -2233.3 |
| 0.4 | -4648.2 | -3786.0 | -4648.2 | -3228.8 | -3441.4 | -3116.2 | -2810.8 | -2525.1 |
| 0.5 | -5329.5 | -3935.2 | -5362.9 | -3293.0 | -3571.5 | -3231.9 | -2914.9 | -2619.1 |
| 0.6 | -5379.7 | -3790.3 | -5379.7 | -3045.2 | -3446.2 | -3120.3 | -2814.0 | -2527.5 |
| 0.7 | -4680.1 | -3357.5 | -4606.4 | -2520.5 | -3069.9 | -2784.0 | -2509.4 | -2250.3 |
| 0.8 | -3289.4 | -2621.3 | -3201.9 | -1778.2 | -2419.9 | -2199.6 | -1979.8 | -1769.7 |
| 0.9 | -1517.3 | -1533.2 | -1517.3 | -902.0 | -1434.3 | -1307.1 | -1173.4 | -1043.7 |
Figure 2.
The compositional dependence of the enthalpy of mixing () of liquid the Li–Mg alloy at (a) 1000 K and (b) 1300 K–2200 K.
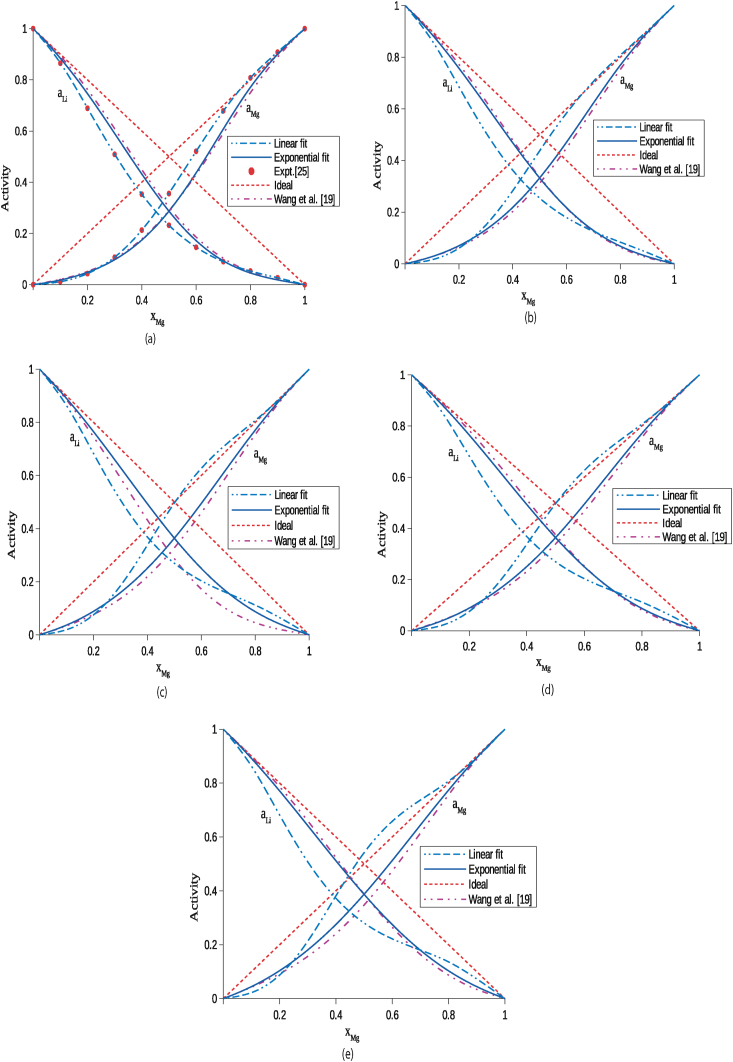
Activities of the components Li and Mg of the system have been computed using optimized parameters in Eq. (12) and listed in Table 4 in the above-mentioned temperature range. The values so computed using the exponential parameters of this work and parameters of Wang et al. are in a good agreement and show negative deviations from ideal values (Raoult's law) at 1000 K (Figure 3 (a)). Moreover, both the experimental values and values calculated using exponential parameters are in well harmonic. When the temperature of the liquid alloy is gradually increased, the activities calculated using exponential parameters gradually move toward ideal value revealing the decrease in the mixing tendency (Figure 3(a)–(e)). These predictions further support the results of excess free energy of mixing and enthalpy of mixing presented in the earlier sections of the work. The activity of Mg calculated using linear T-dependent parameters exceeds the ideal value at higher temperatures beyond 1000 K indicating the presence of unusual trend (Figure 4(b)–(e)). These unusual trends, however, have been removed considering the exponential T-dependent parameters. Hence, it can be stated that at higher temperatures, the thermodynamic functions depend exponentially on temperature rather than linear.
Table 4.
Activities of components of liquid Li–Mg alloy at temperatures 1000 K, 1300 K, 1600 K, 1900 K and 2200 K.
| XMg | Activities |
|||||||
|---|---|---|---|---|---|---|---|---|
| T = 1000 K | ||||||||
| Linear fit |
Expon. fit |
Experimental [25] |
Wang et al. [19] |
|||||
| aLi | aMg | aLi | aMg | aLi | aMg | aLi | aMg | |
| 0.1 | 0.866 | 0.012 | 0.885 | 0.018 | 0.865 | 0.012 | 0.893 | 0.021 |
| 0.2 | 0.690 | 0.043 | 0.746 | 0.048 | 0.689 | 0.043 | 0.763 | 0.052 |
| 0.3 | 0.510 | 0.107 | 0.591 | 0.097 | 0.509 | 0.107 | 0.609 | 0.101 |
| 0.4 | 0.353 | 0.213 | 0.432 | 0.174 | 0.353 | 0.213 | 0.449 | 0.178 |
| 0.5 | 0.232 | 0.357 | 0.287 | 0.287 | 0.232 | 0.356 | 0.303 | 0.289 |
| 0.6 | 0.146 | 0.521 | 0.172 | 0.437 | 0.146 | 0.521 | 0.186 | 0.430 |
| 0.7 | 0.090 | 0.678 | 0.093 | 0.608 | 0.090 | 0.679 | 0.103 | 0.591 |
| 0.8 | 0.053 | 0.808 | 0.046 | 0.771 | 0.053 | 0.808 | 0.050 | 0.750 |
| 0.9 | 0.027 | 0.909 | 0.019 | 0.900 | 0.027 | 0.908 | 0.019 | 0.889 |
| Activities | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T = 1300 K |
T = 1600 K |
||||||||||
| Linear fit |
Expon. fit |
Wang et al. [19] |
Linear fit |
Expon. fit |
Wang et al. [19] |
||||||
| aLi | aMg | aLi | aMg | aLi | aMg | aLi | aMg | aLi | aMg | aLi | aMg |
| 0.864 | 0.016 | 0.888 | 0.028 | 0.895 | 0.028 | 0.863 | 0.019 | 0.890 | 0.037 | 0.897 | 0.034 |
| 0.686 | 0.061 | 0.757 | 0.070 | 0.773 | 0.066 | 0.683 | 0.075 | 0.765 | 0.089 | 0.779 | 0.077 |
| 0.509 | 0.150 | 0.614 | 0.132 | 0.630 | 0.122 | 0.508 | 0.185 | 0.630 | 0.159 | 0.643 | 0.137 |
| 0.362 | 0.283 | 0.469 | 0.218 | 0.479 | 0.202 | 0.368 | 0.338 | 0.493 | 0.251 | 0.499 | 0.219 |
| 0.254 | 0.437 | 0.332 | 0.332 | 0.336 | 0.312 | 0.270 | 0.496 | 0.364 | 0.364 | 0.359 | 0.328 |
| 0.179 | 0.584 | 0.217 | 0.471 | 0.216 | 0.448 | 0.203 | 0.627 | 0.250 | 0.495 | 0.237 | 0.460 |
| 0.126 | 0.706 | 0.129 | 0.622 | 0.125 | 0.600 | 0.156 | 0.724 | 0.157 | 0.634 | 0.142 | 0.607 |
| 0.084 | 0.808 | 0.068 | 0.769 | 0.063 | 0.752 | 0.112 | 0.807 | 0.087 | 0.771 | 0.073 | 0.754 |
| 0.044 | 0.902 | 0.028 | 0.895 | 0.024 | 0.888 | 0.059 | 0.898 | 0.037 | 0.894 | 0.028 | 0.888 |
| T = 1900 K |
T = 2200 K |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Linear fit |
Expon. fit |
Wang et al. [19] |
Linear fit |
Expon. fit |
Wang et al. [19] |
||||||
| aLi | aMg | aLi | aMg | aLi | aMg | aLi | aMg | aLi | aMg | aLi | aMg |
| 0.863 | 0.022 | 0.892 | 0.044 | 0.898 | 0.039 | 0.862 | 0.024 | 0.893 | 0.051 | 0.898 | 0.042 |
| 0.681 | 0.087 | 0.771 | 0.104 | 0.783 | 0.085 | 0.680 | 0.097 | 0.775 | 0.116 | 0.786 | 0.092 |
| 0.507 | 0.213 | 0.642 | 0.180 | 0.653 | 0.148 | 0.507 | 0.237 | 0.651 | 0.197 | 0.660 | 0.157 |
| 0.372 | 0.381 | 0.512 | 0.275 | 0.513 | 0.232 | 0.375 | 0.417 | 0.525 | 0.294 | 0.523 | 0.241 |
| 0.281 | 0.541 | 0.387 | 0.387 | 0.375 | 0.339 | 0.289 | 0.577 | 0.405 | 0.405 | 0.388 | 0.347 |
| 0.222 | 0.658 | 0.275 | 0.512 | 0.253 | 0.468 | 0.236 | 0.682 | 0.294 | 0.526 | 0.265 | 0.474 |
| 0.180 | 0.737 | 0.179 | 0.644 | 0.154 | 0.611 | 0.200 | 0.746 | 0.197 | 0.652 | 0.164 | 0.614 |
| 0.136 | 0.807 | 0.103 | 0.774 | 0.081 | 0.755 | 0.157 | 0.807 | 0.116 | 0.777 | 0.087 | 0.756 |
| 0.073 | 0.895 | 0.044 | 0.894 | 0.032 | 0.888 | 0.085 | 0.893 | 0.051 | 0.894 | 0.034 | 0.888 |
Figure 3.
Activities of components Li and Mg of the liquid Li–Mg alloy at temperatures (a) 1000 K, (b) 1300 K, (c) 1600 K, (d) 1900 K and (e) 2200 K.
Figure 4.
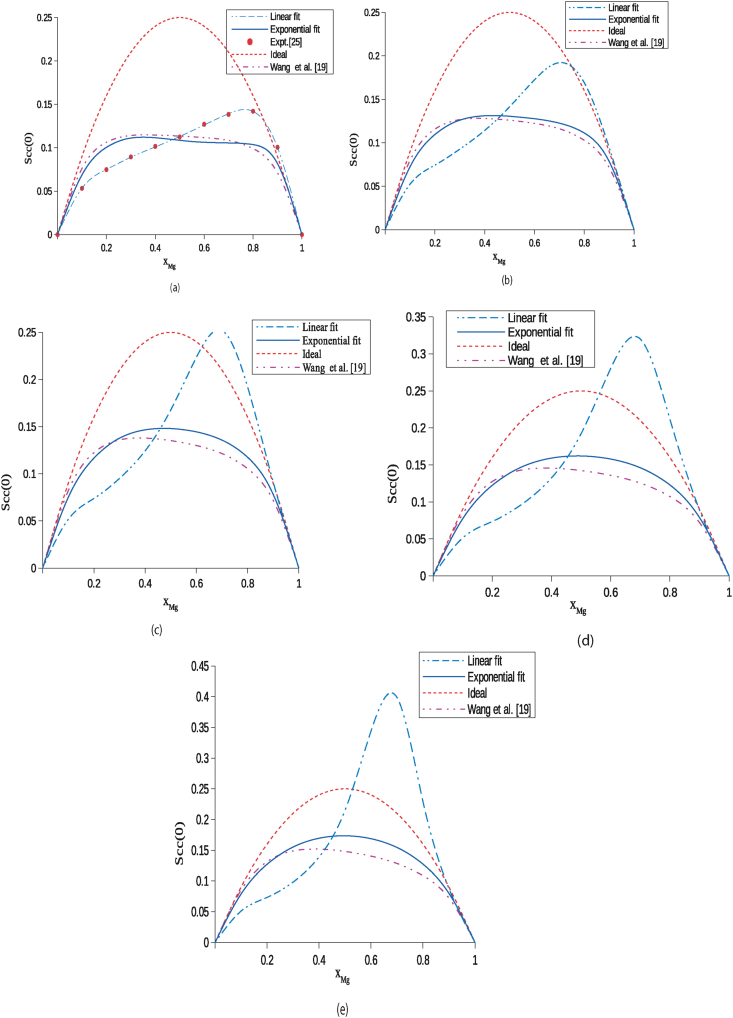
Concentration fluctuations in long-wavelength limit () of the liquid Li–Mg alloy at temperatures (a) 1000 K, (b) 1300 K, (c) 1600 K, (d) 1900 K and (e) 2200 K.
In structural properties, concentration fluctuations in long-wavelength limit (Scc(0)) has been established as an important tool to study and explain the hetero or homo-coordinating nature of the liquid alloys. At a given concentration and temperature, if , then it indicates the hetero-coordinating or ordering nature and if , then it corresponds to the homo-coordinating or segregating nature of the liquid system. The theoretical, ideal and observed values of at 1000 K have been computed using optimized parameters in Eqs. (14), (15) and (16) and depicted in Table 5. Both the computed values of using the exponential T-dependent parameters are in reasonable agreement and less than the ideal value indicating the ordering nature of the system at 1000 K (Figure 4(a)). But the values computed using linear T-dependent parameters exceeds ideal values in the concentration range indicating the segregating tendency of the alloy (Figure 4(a)) and can be termed as unusual trend. Likewise, Singh et al. [30] had revealed the appearance of the narrow miscibility gap in the liquid phase of Li–Mg alloy in region of 18–30 at % of Li at 830 K. They had further calculated Scc(0) from data of neutron diffraction measurement at 695 K, 830 K and 887 K by using quasi-chemical expression (exponential parameters) in which no miscibility gap was found to appear which supports the findings of this work.
Table 5.
Concentration fluctuations in long-wavelength limit (Scc(0)) of liquid Li–Mg alloy at temperatures 1000 K, 1300 K, 1600 K, 1900 K and 2200 K.
| XMg | Concentration fluctuations in long-wavelength limit (Scc(0)) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T = 1000 K |
T = 1300 K |
T = 1600 K |
||||||||
| Linear fit | Expon. fit | Experimental [25] | Wang et al. [19] | Linear fit | Expon. fit | Wang et al. [19] | Linear fit | Expon. fit | Wang et al. [19] | |
| 0.1 | 0.0535 | 0.0688 | 0.0533 | 0.0762 | 0.0524 | 0.0725 | 0.0798 | 0.0517 | 0.0752 | 0.0822 |
| 0.2 | 0.0751 | 0.1005 | 0.0749 | 0.1064 | 0.0743 | 0.1095 | 0.1157 | 0.0738 | 0.1166 | 0.1224 |
| 0.3 | 0.0891 | 0.1112 | 0.0894 | 0.1142 | 0.0927 | 0.1260 | 0.1267 | 0.0951 | 0.1378 | 0.1360 |
| 0.4 | 0.1010 | 0.1115 | 0.1016 | 0.1147 | 0.1142 | 0.1311 | 0.1279 | 0.1244 | 0.1466 | 0.1379 |
| 0.5 | 0.1130 | 0.1087 | 0.1124 | 0.1135 | 0.1414 | 0.1305 | 0.1259 | 0.1677 | 0.1481 | 0.1352 |
| 0.6 | 0.1262 | 0.1063 | 0.1271 | 0.1118 | 0.1724 | 0.1276 | 0.1223 | 0.2235 | 0.1445 | 0.1300 |
| 0.7 | 0.1393 | 0.1056 | 0.1385 | 0.1085 | 0.1922 | 0.1226 | 0.1161 | 0.2520 | 0.1358 | 0.1215 |
| 0.8 | 0.1420 | 0.1037 | 0.1421 | 0.0991 | 0.1692 | 0.1113 | 0.1029 | 0.1923 | 0.1176 | 0.1055 |
| 0.9 | 0.1005 | 0.0818 | 0.1006 | 0.0712 | 0.0947 | 0.0786 | 0.0716 | 0.0913 | 0.0783 | 0.0718 |
| Concentration fluctuations in long-wavelength limit (Scc(0)) | |||||
|---|---|---|---|---|---|
| T = 1900 K |
T = 2200 K |
||||
| Linear fit | Expon. fit | Wang et al. [19] | Linear fit | Expon. fit | Wang et al. [19] |
| 0.0513 | 0.0772 | 0.0839 | 0.0510 | 0.0789 | 0.0852 |
| 0.0735 | 0.1223 | 0.1275 | 0.0733 | 0.1271 | 0.1315 |
| 0.0969 | 0.1474 | 0.1432 | 0.0982 | 0.1552 | 0.1489 |
| 0.1324 | 0.1592 | 0.1456 | 0.1390 | 0.1696 | 0.1518 |
| 0.1922 | 0.1621 | 0.1424 | 0.2150 | 0.1736 | 0.1481 |
| 0.2803 | 0.1580 | 0.1359 | 0.3440 | 0.1688 | 0.1405 |
| 0.3202 | 0.1462 | 0.1255 | 0.3987 | 0.1545 | 0.1285 |
| 0.2120 | 0.1229 | 0.1073 | 0.2291 | 0.1274 | 0.1087 |
| 0.0892 | 0.0789 | 0.0720 | 0.0877 | 0.0790 | 0.0721 |
The theoretical values of have been computed at higher temperatures in the range 1300–2200 K employing the similar procedure as discussed above (Figure 4(b)–(e)). At higher temperatures, the values computed using linear parameters exceed ideal value but those computed using exponential parameters are found to be less than ideal values at all concentrations. These findings further correspond that the thermodynamic functions depend exponentially on temperature at higher temperatures. Additionally, the computed values of using the exponential parameters gradually move towards ideal values with an increase in temperature of the alloy supporting the results predicted by thermodynamic functions.
4. Conclusions
The theoretical investigation predicts the appearance of artifacts in the thermodynamic and structural properties of liquid Li–Mg alloy at higher temperatures when the parameters are assumed to be linear T-dependent. When the same thermodynamic and structural properties are calculated using exponential T-dependent parameters, the above discrepancies have been removed. Therefore, it can be concluded that at higher temperatures, the interaction parameters depend exponentially on temperature for liquid alloys. Moreover, the thermodynamic and structural properties of the preferred liquid alloy show ideal mixing tendency at higher temperatures.
Declarations
Author contribution statement
R. K. Gohivar: Conceived and designed the experiments; Performed the experiments; Wrote the paper.
S. K. Yadav, R. P. Koirala: Analyzed and interpreted the data; Wrote the paper.
D. Adhikari: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.
Funding statement
R K Gohivar was supported by RMC, MMAMC, TU (2020).
Data availability statement
Data included in article/supp. material/referenced in article.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Derimow N., Abbaschian R. Liquid phase separation in high-entropy alloys-a review. Entropy. 2018;20:11. doi: 10.3390/e20110890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bo L., Li S., Wang L., Wu D., Zuo M., Zhao D. Liquid-liquid phase separation and solidification behavior of Al55Bi36Cu9 monotectic alloy with different cooling rates. Results Phys. 2018;8:1086–1091. [Google Scholar]
- 3.Kevorkov D., Schmid-Fetzer R., Zhang F. Phase equilibria and thermodynamics of the Mg-Si-Li system and remodeling of the Mg-Si system. J. Phase Equilibria Diffus. 2004;25:140–151. [Google Scholar]
- 4.Kaptay G. A new equation for the temperature dependence of the excess Gibbs energy of solution phases. Calphad Comput. Coupling Phase Diagrams Thermochem. 2004;28:115. [Google Scholar]
- 5.Schmid-Fetzer R., Janz A., Gröbner J., Ohno M. Aspects of quality assurance in a thermodynamic Mg alloy database. Adv. Eng. Mater. 2005;7:1142–1149. [Google Scholar]
- 6.Nakano J., Malakhov D.V., Yamaguchi S., Purdy G.R. A full thermodynamic optimization of the Zn-Fe-Al system within the 420-500 °C temperature range, Calphad Comput. Coupling Phase Diagrams Thermochem. 2007;31:125–140. [Google Scholar]
- 7.Schmid-Fetzer R., Andersson D., Chevalier P.Y., Elenod L., Fabrichnaya O., Kattner U.R., Sundman B., Wang C., Watson A., Zabdyr L., Zinkevich M. Assessment techniques , database design and software facilities for thermodynamics and diffusion. Calphad Comput. Coupling Phase Diagrams Thermochem. 2007;31:38. [Google Scholar]
- 8.Yuan X., Sun W., Du Y., Zhao D., Yang H. Thermodynamic modeling of the Mg-Si system with the Kaptay equation for the excess Gibbs energy of the liquid phase. CALPHAD Comput. Coupling Phase Diagrams Thermochem. 2009;33:673. [Google Scholar]
- 9.Tang Y., Yuan X., Du Y., Xiong W. Thermodynamic modeling of the Fe − Zn system using exponential temperature dependence for the excess Gibbs energy. J. Min. Met. Sect. B-Metall. 2011;47:1. [Google Scholar]
- 10.Tang Y., Du Y., Zhang L., Yuan X., Kaptay G. Thermodynamic description of the Al-Mg-Si system using a new formulation for the temperature dependence of the excess Gibbs energy. Thermochim. Acta. 2012;527:131. [Google Scholar]
- 11.Liang S., Wang P., Schmid-Fetzer R. Inherently consistent temperature function for interaction parameters demonstrated for the Mg – Si assessment, CALPHAD Comput. Coupling Phase Diagrams Thermochem. 2016;54:82. [Google Scholar]
- 12.Kaptay G. The exponential excess Gibbs energy model revisited. Calphad Comput. Coupling Phase Diagrams Thermochem. 2017;56:169. [Google Scholar]
- 13.Feufel H., Godecke T., Lukas H., Sommer F. Investigation of the Al-Mg-Si system by experiments and thermodynamic calculations. J. Alloys Compd. 1997;247:31–42. [Google Scholar]
- 14.Yan X., Zhang F., Chang Y.A. A thermodynamic analysis of the Mg-Si system. Basic Appl. Res. 2000;21:379–384. [Google Scholar]
- 15.Wu1 R., Yan Y., Wang G., Murr L.E., Han W., Zhang Z., Zhang M. Recent progress in magnesium-lithium alloys. Int. Mater. Rev. 2015;60:65. [Google Scholar]
- 16.Gasior W., Moser Z., Zakulski W., Schwitzgebel G. Thermodynamic studies and the phase diagram of the Li-Mg system. Metall. Mater. Trans. A. 1996;27A:2419. [Google Scholar]
- 17.Braga M.H., Malheiros L.F., Hämäläinen M. The Cu-Li-Mg system at room temperature. Thermochim. Act. 2000;344:47. [Google Scholar]
- 18.Jha I.S., Adhikari D., Kumar J., Singh B.P. Anomaly in mixing properties of lithium-magnesium liquid alloy. Phase Transitions. 2011;84:1075. [Google Scholar]
- 19.Wang P., Du Y., Liu S. Thermodynamic optimization of the Li-Mg and Al-Li-Mg systems, Calphad Comput. Coupling Phase Diagrams Thermochem. 2011;35:523. [Google Scholar]
- 20.Ansara I., Dinsdale A.T., Rand M.H. Thermochemical database for light metal alloys. Cost. 1998;507:2. [Google Scholar]
- 21.Kaptay G. The exponential excess Gibbs energy model revisited. Calphad Comput. Coupling Phase Diagrams Thermochem. 2017;56:169. [Google Scholar]
- 22.Yadav S.K., Jha L.N., Jha I.S., Singh B.P., Koirala R.P., Adhikari D. Prediction of thermodynamic and surface properties of Pb-Hg liquid alloys at different temperatures. Philos. Mag. 2016;96:1909–1925. [Google Scholar]
- 23.Yadav S.K., Jha L.N., Adhikari D. Modeling equations to predict the mixing behaviours of Al-Fe liquid alloy at different temperatures. Bibechana. 2018;15:60–69. [Google Scholar]
- 24.Yadav S.K., Mehta U., Gohivar R.K., Dhungana A., Koirala R.P., Adhikari D. Reassessments of thermo-physical properties of Si-Ti melt at different temperatures. Bibechana. 2020;17:146–155. [Google Scholar]
- 25.Hultgren K.K., Desai R., Hawkins P.D., Gleiser D.T., Kelley M. Met. Park. Ohio ASM.; 1973. Selected Values of Thermodynamic Properties of Binary Alloy. [Google Scholar]
- 26.Redlich O., Kister A.T. Algebraic representation of thermodynamic properties and the classification. Ind. Eng. Chem. 1948;40:345. [Google Scholar]
- 27.Ding X., Fan P., Wang W. Thermodynamic calculation for alloy systems. Metall. Mater. Trans. B. 1999;30:7–8. [Google Scholar]
- 28.Bhatia A.B., Thornton D.E. Structural aspects of the electrical resistivity of binary alloys. Phys. Rev. B. 1970;2(8):3004–3012. [Google Scholar]
- 29.Singh R.N., Pandey D.K., Sinha S., Mitra N.R., Srivastava P.L. Thermodynamic properties of molten Li-Mg alloy. Physica. 1987;145B:358. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supp. material/referenced in article.