Abstract
This paper offers a summary of the latest studies on healthcare scheduling problems including patients’ admission scheduling problem, nurse scheduling problem, operation room scheduling problem, surgery scheduling problem and other healthcare scheduling problems. The paper provides a comprehensive survey on healthcare scheduling focuses on the recent literature. The development of healthcare scheduling research plays a critical role in optimizing costs and improving the patient flow, providing prompt administration of treatment, and the optimal use of the resources provided and accessible in the hospitals. In the last decades, the healthcare scheduling methods that aim to automate the search for optimal resource management in hospitals by using metaheuristics methods have proliferated. However, the reported results are disintegrated since they solved every specific problem independently, given that there are many versions of problem definition and various data sets available for each of these problems. Therefore, this paper integrates the existing results by performing a comprehensive review and analyzing 190 articles based on four essential components in solving optimization problems: problem definition, formulations, data sets, and methods. This paper summarizes the latest healthcare scheduling problems focusing on patients’ admission scheduling problems, nurse scheduling problems, and operation room scheduling problems considering these are the most common issues found in the literature. Furthermore, this review aims to help researchers to highlight some development from the most recent papers and grasp the new trends for future directions.
Keywords: Heurstic, Metaheurstic, Meta-heurstics, Nurse scheduling, Patient admission scheduling, Patient to bed assignment, Operating room scheduling, Operating theater, Surgery scheduling, Surgical scheduling, Physician scheduling, Healthcare scheduling
Introduction
Nowadays, healthcare optimization problems have received significant attention in order to provide more appropriate services at a lower cost [1, 2]. Moreover, it is imperative and attracts many researchers’ attention due to the high cost and limitation of resources (e.g. medical supplies, equipment, doctors, and staff) in the hospital. Without a doubt, healthcare scheduling is a challenge due to high constraints and preferences, such as personnel requirements, resources limitation. Unlike any other institution, healthcare sectors are working around the clock. However, the lack of staffing and irregular working shifts leads to job dissatisfaction and might influence patient satisfaction. Moreover, increasing population longevity will lead to a rising in demand for medical services [2, 3]. However, increasing in demand for medical care, and the absence or shortage of it may cause patients threatened lives, overworking manpower, patients infection rates, and patients flow overcrowding [4].
A scheduling system could decrease patients waiting time, ease access to medical services and impact the quality of healthcare operations [1, 5]. In order to get feasible scheduling for any healthcare system, the hard and soft constraints have to be determined. Hard constraints could not be violated whilst, the soft constraints integrated as a part of the cost function and should be minimized.
Hence, enhancing, planning and scheduling procedures of hospital resources play a vital role in the improvement of the hospital’s benefit and service quality delivered to patients. An improved scheduling system is essential because it is a crucial role in reducing costs revenue, and for enhanced accessibility to the healthcare system as well [6].
In recent years, many reviews have been conducted in healthcare scheduling considering the different scopes. for instance, healthcare scheduling based data mining is discussed in [7]. The author provides a systematic review of the literature that reflects an industrial engineering approach to healthcare scheduling with an emphasis on the behaviour of the patients’ role in scheduling. An integrated hospital scheduling issue has been reviewed in [8]. The review has been done based on collects scientific papers related to integrated hospital scheduling problems published between 1995 and 2016. In addition, operational research applicable to healthcare was surveyed in [2]. One of the major contributions of this work is to cover recent improvement issues in this area. In addition, there are several review papers dealing with healthcare scheduling that include part of scheduling issues such as [9], resource scheduling, operating room scheduling [10, 11], and outpatient appointment scheduling [12].
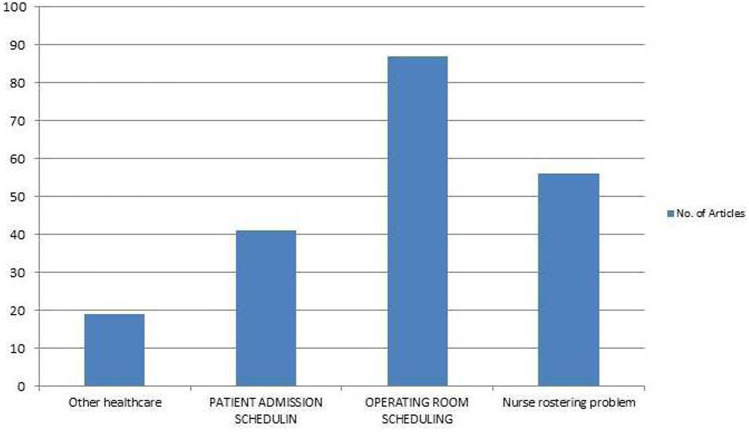
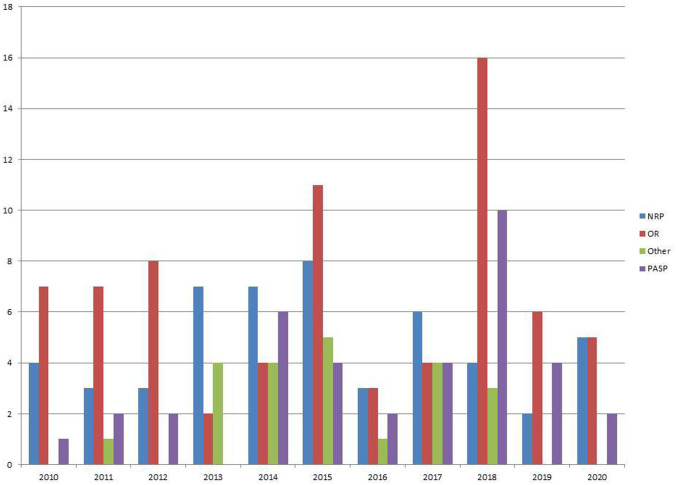
Our contribution in this review paper is to compare and analyze all scientific work between 2010 -2020 in optimization-based healthcare scheduling, focusing on metaheuristic approaches. We investigate several versions of problem definitions in the research of patient admission scheduling. Furthermore, we also review the works available in solving other healthcare scheduling, including nurse scheduling problems and operating room scheduling/surgical scheduling. Our review work centered around patient admission scheduling research, nurse scheduling problems, and operating room scheduling/surgical scheduling, considering these problems are the most studied healthcare scheduling problems as described in Fig. 1 and 2.
Fig. 1.
Number of covered article
Fig. 2.
Healthcare scheduling papers between 2010-2020
We cover several articles written in English and published in peer reviewed journals, searched the databases covering several disciplines such as, Scopus, Google scholar for relevant papers using combinations of relevant keywords such as “nurse scheduling”, “nurse rostering”, “patient admission scheduling”, “patient to bed assignment”, “operating room scheduling”, “operating theater”, “surgery scheduling”, “surgical scheduling”, “physician scheduling”, and healthcare scheduling with “heurstic” or “metaheurstics” “meta-heurstics”. For each article found, we performed a forward and backward search to find additional manuscripts. We limited the review to papers that are written in English and are published from 2010 to 2020 (see Fig. 1). The search procedure resulted in a set of 190 articles (see Fig.2), we included papers that described the scheduling technique in healthcare, an overview of healthcare scheduling process which covers in this survey. We also included all papers that described the effects of metaheuristics in scheduling healthcare decision-making in an optimization context.
The organization of this survey is based on recent research papers which provide optimization-based for the most common healthcare scheduling problems including definition and formulations, data sets, methods. The major part of the paper discussed the patient admission scheduling, considering the recent problem found in the literature. We also reviewed the problems in allocating nurse to shift; and scheduling of operating room and surgery.
The importance and growth in using these optimization methods revealed very effective results when used for healthcare scheduling problem. However, it is still possible to improve the outcomes generated by present studies. Thus the research trends can be directed to investigate the applicability of other optimization methods for healthcare scheduling problems. This review has been analyzed based on optimization technique which especially based on heuristics, metaheuristic, hybrid metaheuristic to address any healthcare scheduling problem such as patient admission, nurse scheduling/rostering, operating room scheduling/surgery scheduling, etc (see Table 1).
Table 1.
Other healthcare problem in optimization context
| Healthcare problems | Scopus | Google scholar |
|---|---|---|
| Physician scheduling problem | 14 | 6 |
| Home healthcare problem | 20 | 21 |
| Telemedicine | 6 | 3 |
Thereby, we achieve a better understanding of this spectrum, point out some development from the most recent papers, summarise some of the existing methods and grasp the new trends for future directions in this field. The organization of the paper is as the following. Section 2 discusses patient admission scheduling problems, definition, versions, formulation, and data sets. Then, it is followed by Section 3, which describes the nurse rostering problem. Section 4 presents an operating room scheduling problem, and Section 5 briefly discusses other different healthcare optimization problems and solutions. Finally, Section 6 comprises the the conclusion and future work directions.
Patient admission scheduling problem (PASP)
The Patient Admission Scheduling (PASP) is referred to assign patients to room in the hospital over a time horizons [13]. Patient admission scheduling is combinatorial optimisation problem that is gaining a researchers concern in the healthcare career. PASP support a decision makers at various level such as long term (strategic level), med-term (tactical level), and short-term (operational level) in the healthcare institutes [14], which determine whether the hospital’s resources is ready for accepting patients through satisfactory services.
Definition of patient admission scheduling problem (PASP)
The Patient Admission Scheduling (PASP) is a problem of scheduling patients within certain time slots in the hospital to maximize both management competency, and patient comfort and safety, in addition to enhancing medical care in the hospital. Patient admission scheduling problem is a complex combinatorial problem [15]. Since the problem is first formulated in [16], its solution enables the scheduling of patients allocated to specific beds in particular relevant departments, fulfilling in an optimal way to the needs of the patients and ensures all the required medical restrictions. Usually, the assignment of patients to beds is executed by a centralized admission office, by contacting the departments several days prior for efficient patient admission. Some hospitals control the admission of their patients without a central admission office, leaving the admission responsibility to the various respective departments. As in the second case, an absence of the overall knowledge and information of the departments may cause in not being occupied optimally. There could be shortage of beds available for patients in some departments, but extra beds in other departments.
PASP Formulation
First, the Patient Admission Scheduling version (1) also called (original problem) has been introduced by [17], which entails the supposition that the dates for admission and discharge are prior knowledge. In addition, each patient should occupy at least one bed for a certain duration of time. The basic terminology of the problem can be described in the following:
Nigh: The variables representing time horizon for individual patient located in the hospital
Admitted patients are patients that are effectively admitted to the hospital and are assigned to a room and a bed.
Patient: A person requiring healthcare in a hospital and must be allocated a bedroom with a determined date of admission and discharge.
Room: Every department possesses its specific room, where each room possesses its specific capacity dependent upon the number of beds in it, which may be in the form of single/twin/ward beds.
Specialism: Every individual department in the hospital is determined by a single or additional treatment. Furthermore, individual rooms belonging to a specific department possesses its own specific level of treatment ranging from (1-3) dependent upon specific patient case.
Transfer: Moving admitted patient from room to another during her/his stay.
The problems faced in the original version of PASP are the adherence to some of the constraints, which is to break them up into hard and soft constraints categories, depending on the level of impact on the patients. The patient admission scheduling problem constraints (original PASP) is as follwing:
HC1: The availability of the room ().
HC2: Admission, discharge date , and time horizon for the elective patient should be fixed, and unchangeable.
HC3: Time horizon should be continuous.
HC4: Two patients () cannot be allocated in the same bed at the same time horizons.
HC5: Gender schema should be carried out.
HC6: The patient should be allocated to a department which is is acceptable to his/her age.
HC7: Mandatory room properties should be available in the assignment rooms.
HC8: Quarantine policy for some patients who need to be isolated, according to their illness requirement.
Furthermore, the soft constraints for this problem could be summarized as follow:
SC1:Room preference, which indicates the patient preference regarding room capacity such as(single, double, ward, etc). These constraints might be considered, otherwise they should be penalized (Table 3) for the weight penalty.
SC2: Preferred room properties, which represented some medical equipment in the department, and staff such as nurses.
SC3: Degree of specialism, in some cases, patients preferred to get medical treatment in departments that have highest degree of specialism.
SC4: Needed properties, some patients should assigned to a room with special equipment’s. This constraints is related to HC7.
SC5: Transfer, the unplanned transfers should be minimised.
All soft constraints should be satisfied as much as possible, and sometimes impossible to satisfy all the soft constraints. Otherwise, could be penalized the solution, the weight for each those constraints is as the following Table 2.
Table 3.
Default values of the weights of the cost components [18]
| Cost component | Accounting | Value |
|---|---|---|
| Missing room equipment (PRC1) | per day, per patient | 20 |
| Unsatisfied room preference (PRC2) | per day, per patient | 10 |
| Partial specialty level (PRC3) | per day, per patient | 20 |
| Unsatisfied gender policy (PRC4) | per day, per patient | 10 |
| Transfer (Tr) | per patient | 100 |
| Delay (De) | per day, per patient, per priority | 5 |
| Overcrowd Risk (Ri) | per patient | 1 |
| Idle Operating Room Slots (IOS) | per minute | 10 |
| Idle Room Capacity (IR) | per day, per bed | 20 |
| Overtime (ORO and ORTO) | per minute | 3 |
Table 2.
Soft constraints weight [17]
| Constraints | Corresponding weight |
|---|---|
| Mandatory room properties | 5.0 |
| Patient age should obey the maximum or minimum age of the department | 10 |
| Preferred room properties | 2.0 |
| Preferred room category | 0.8 |
| Department specialism | 1.0 |
| Transfer rate | 11 |
The objective function of Patient Admission Scheduling (PASP) is to minimize all soft constraints, while satisfying the patients preferences, and respecting all the hard constraints to the problem, in order to obtain feasible solutions.
Patient admission scheduling problem under uncertainty (PASU) version 2
The PASU version involve in allocating room for each patient upon a number of days equal to her/his stay period, starting in a day, not before the planned admission. The extended version from PASP was proposed and formulated by [13], However, it included several real-world features, such as the presence of emergency patients, uncertainty in stay lengths; and the possibility of delaying admissions. The problem formulation considered many attributes in order to develop medical service in the hospital. It takes into consideration the possibility that a patient’s stay can be extended. The patient’s extended stay might affect the room scheduling, and this may lead to overcrowding. The PASU problem have several basic concepts [13]:
Day (planning horizon) : This entails the measurement of time and is to denote the duration of the determined stay of individual patient in the hospital; the set of sequential days taken into account in the problem is termed as the planning horizon.
Patient: A patient is the person who needs specific treatments in the hospital and is required to stay in the hospital, the duration of the stay should be continuous. In addition, two kinds of patients have been used in this version, inpatients who are already admitted to the hospital, and a new patients, new patient refers to a patient who will be admitted.
Room/Department: Each room in the hospital belongs to specific department depending on the patient’s needs. Every room in the hospital can be a single, twin room, or a ward. The capacity of a room depends on the number of beds available. A patient may want to occupy a specific room capacity, but might need to pay extra.
Specialism: Every patient in the hospital needs a specific treatment. Thus, the management office in the hospital should distribute the patients according to their diseases. However, a specific departments may be considered as fully, partially qualified, or not qualified for the patients. It is considered as unreasonable to schedule a patient to a non-qualified department for the treatment of the patient’s disease; whereas, allocating a patient to a partially qualified department is acceptable. However this might maximize the cost function.
Room Feature: The quality in the room is depends on its feature. Some of room have additional features such as oxygen, telemetry, nitrogen, and television. Some patients need/prefer certain specific features which are case-dependent. Assigning a patient to a room without considering the needs is deemed to be an unfeasible solution, whereas missing the desired features will maximize the objective function depending on the weight value of this element.
Room Gender Policy: Every individual room has a gender policy. There are four policies (SG, Fe, Ma, All). Fe: is for female patients only; Ma: is for male patients only; SG: both genders can be accepted. But in the same day should be from the same gender. All: the same gender can be accepted at the same time, for example (intensive care).
- Age Policy: Certain departments have age limits. For example; the pediatrics department accepts patients ranging from 0 to 12. PASU involved hard and soft constraints and have to be met. In this problem Department Specialism (DS), Room Features (RF), they are hard for the missing qualification, or needed features, but soft for partial qualification and the desired feature. The hard constraints are:
- HC1: Room capacity (RC), allocating two patients at the same bed simultaneously make the solution infeasible.
- HC2: Patient Age (PA), patients should be assigned to a department that accept his/her age.
- SC1: Room Gender (RG), gender policy room should be fulfilled.
- SC2: Room Preference (RP), patient prefer to be allocated room with special preference.
- SC3: Transfer (Tr), transfer inpatient from room to another during her stay is undesirable.
- Delay (De): delay patients admission.
- Overcrowd Risk (OR): calculated a number of patients who have been allocated for each room and take the certain, potential attend overstay length of some patients, and capacity of the room.
PASU formulation in mathematics
The mathematical formulation for PASU is described and formulated by [13], and for self- integration for this paper, we introduce the mathematical formulation here.
P: is a set of all patients.
is a set of female. is a set of male patients. Where P.
is a set of in-patients and is the room occupied by in-patient where
D: is a set of days.
R: the set of rooms and is the capacity of room .
: the subset of rooms with policy SG. Additionally we have
: is a set of days in which a patient is present in the hospital.
: is a set of patients present in day d (i.e., set of patients p such that ). The main decision variables are the following:
: 1 if patient p is assigned to room r, And 0 if not. The constraints on the x variables are:
| 1 |
| 2 |
| 3 |
The equations describes how the constraints are defined in PASU, equation (1) explains how the patient is assigned to the specified room, while equation (2) ensure the capacity of the room does not exceed the limits (RC). Finally, equation (3) provides against infeasible assignments for patient-room unsuitability (PRS). The variable x represents the search space of the problem. There are other variables to describe the components of the objective function F. The variables for the Room Preference (RP) management component is shown in the mathematical expression below:
,:1 if there is one female at least (resp.male) patient in room r in day d,0 otherwise.
:1 if there is both male and female patients in room r in day d,0 otherwise. These new variables are related to the x and to each other by the following constraints:
| 4 |
| 5 |
| 6 |
As well as the equation (4), and (5) establishing relation between the auxiliary variables f and m to x, stating that when there is a female (resp.male) patient in room, then all the f (resp.male) variables corresponding to the days must be set to 1, whereas, constraints (d) relate both m and f to b, in the way that if m and f are then b must be 1. For the constraint (OR) overcrowd risk components the modeling is as follow:
:1 if room r risks to be overcrowded in day d, 0 otherwise. So as to define the constraints that have relating y variables to x, the following definition will complete the mathematical expression. : is a set of patients that are possible to attend to hospital in day d, which are the patients that existing in day d plus those present in day with the risk of overstay. :the cardinally of a set Z. and :the complement of variable z. The constraints relating y to x are the following:
| 7 |
It’s worth noting when the variables can be any value. On the contrary, when then at least of the x include should take the value 0. Additionally the objective function can computed as follow:
| 8 |
The components of the objective function PRC,RG,and OR is defined as follow:
| 9 |
| 10 |
| 11 |
The equation (9) calculates the cost for patient-room assignment, while equation (10) calculates the number of rooms occupied by both male and female patients. The last equation (11) assesses the overcrowd risk. The PASU problem is modeled as Integer Linear Programming (ILP). In addition, it can be implemented in any general purpose Integer Programming IP solver. In general the problem is modeled as three dimensional matrix of decision variables z, if and only if patient p is in room r in day d. It is worth mentioning that the in the matrix z are consecutive, and its equal to patients stay length.
Dynamic patient admission scheduling with operating room constraints, flexible horizons, and patient delay (version 3)
This version of patient admission scheduling problem engaged with operating room scheduling [18], it is presented into two phases, patients admission constraints phase, and operating room constraints phase.
The basic concept of the first phase is as following [18]:
Patients: Is the main component in this problem, and the patient should have an admission and discharge date, the duration between the admission and discharge date is termed as the length of stay (LoS). Some patients may need to extend their stay in the hospital, because of their situation, and these extension is termed as overstay risk.
Day: A day is a unit specifying the time spent by the patients in the hospital, where each patient should spent a few continuous days. These days are termed as a planning horizon.
Room: A room belongs to a department, the quantity of beds that can occupy a room is termed as capacity (typically one, two, four rooms, or a ward). The room may have properties such as oxygen, nitrogen, telemetry, and TV). These properties may become preferences or patients’ requirements.
- Specialty/Specialism: Ordinarily, patients usually need to get one type of treatment, whereas there are some patients who might need more than one treatment and those with special cases. In fact, each department in the hospital is responsible for treating a specific disease that needs different types of specialization but at diverse levels of expertise. Three levels of specialists sets in the department, complete treatment (no penalty), partial treatment with a penalty, last level none, which mean that the patient can not be treated in this department. Beside the features mentioned above, there are two polices, age and gender, some departments which specialized in treatment for one type of patients such as pediatrics and geriatrics, only host patients from a certain range of age, with minimum and maximum age terms and conditions. While (Gender policy), refer to four types of rooms in the hospital which are: D,F,M, and N. The room from type D can accept patients from both genders, but in the same day the patient should be from the same gender. Type F only accepts female patients, whereas type M only accepts male patients. Finally, room type N, accepts both genders, for instance, recovery rooms and the intensive care rooms. Dynamic Patient Admission Scheduling with Operating Room Constraints, Flexible Horizon, and Patient delays are to assign a patient to a room in a department, and the patient is currently present at the hospital, making the admission realistic, and the discharge of a patient from a room could be done later, depending on the patient’s situation. The solution to this problem should satisfy all of the hard constraints and categorized in this problem as:
- HC1: Room capacity (RC), each room has a limited number of beds, thus, the number of patients cannot exceed the number of the rooms.
- HC2: Patient-Room Suitability (PRS), the assignment of individual patient to a room must be a match and appropriate to the patient’s needs and condition.
Hence, the cost function could be calculated based on the violation of the following four soft constraints related to the patient’s admission problem. Patient-room cost (PRC), [18] generated a matrix that consists of an integer value termed as Patient-Room Matrix. It explains the penalty of patient-to-room allocations. If the value in the matrix is 1, that signifies that the room is not suitable for the patient. Meanwhile, if it has a positive value, it means that the room accepts the patient with penalty. Additionally, if it is 0, that signifies that it is matches the requirements, and it is a suitable fit. The second constraints is Room gender (RG), based on the room types mentioned above, the room type N is the result of no cost, whilst the room type D denotes that it can be occupied by both genders concurrently. However, there is a penalty imposed that is proportionate to the size of the smaller of the two patients. The cost for rooms of type F and M are inclusive in the patients room matrix. The third constraints is Delay (De), the delay results with cost incurred depending on the length of the delay. The delay is usually undesirable if the admission date is nearer, then the delay expense is multiplied by priority that is reciprocally proportionate to the nearness of the admission day. Finally, Overcrowding risk (Ri), additional penalty added for the cost function, if the patient is to be discharged and needs to stay, and his/her room is fully occupied.
The basic concept of the second phase (operating room notions) is as follow:
Operating room scheduling is assigned specialities to the Master Surgical Schedule (MSS). Master surgical schedule regularly repeated schedule [19], in which assigning one specialist for the operating room for the duration of time (typically each week). Patient admission scheduling problem (version 3) has been bounded with operating room scheduling, and the basic notation for operating in this problem is as follow:
Operating Room Slot: It is the smallest amount of time, in which the operating room could be reserved for one specialty in that day. In any day in the scheduling planning for Master Surgical Schedule(MSS) an integer number of operating room slots will be assigned a specialty. In the same day/the operating room could be occupied by different surgeon in the same specialty.
Surgery Treatment: Each patient in the hospital is subject to a special treatment. Some of them need to get surgery of corresponding specialty. In this situation the day of the surgery (may be in the same day of admission or the next day after admission), so the expected length of the surgery should be fixed with the specialty. The assignment is as long as subject to all the constraints that are presented previously (RC,PRS,PRC,RG,De,Ri) and for the operating room there are additional constraints: Operating Room Utilization(ORU): In each day and specialty, there is a limited time specified by the (MSS), where the total length for each surgery belonging to the specialty should not exceed the limit. This condition is considered as a hard constraint, and its effect on the search space of the problem. Meanwhile, [18] is only covered the admission day of a patient; the problem of sequencing operating room slots in diverse operating rooms and surgeries within each OR slot is not included in this problem. In addition, the length of emergencies for patient is not take in consideration in the computation of the utilization for the ORU constraint. Further more the total occupation should be lower than the capacity. So there is another constraint, should take in consideration that deals specifically with this issue, which is Operating Room Total Utilization (ORTU): In each day the total length of all surgeries including urgent cases and belong to the same specialty should not exceed the capacity of the operating rooms. The ORU and ORTU constraints cover only the total length of slots. In reality, this length is divided into normal time and overtime. Normal time can be used freely, whilst overtime is allowed but should be minimized. To model this situation, the problem includes a cost component soft for the overtime work. Operating Room Overtime (ORO): for each day and specialty, the total length of surgeries with the same specialty must not exceed the limitation of normal time that giving to it. In some cases specialty goes overtime, this will lead to cost related to dedicated personnel, but not for all staff in the operating room. In contrast, other specialty may not use the operating room full time, so this will balance the occupancy. Also the total overtime of the rooms could be calculated by adding the next component called an operating room total overtime in order to count the costs. Operating Room Total Overtime (ORTO): For any day, the cost for the overall length surgeries in all specialties including (urgent cases) should not exceed the total normal time of the operating rooms.
Dynamic patient admission scheduling with operating room constraints, flexible horizons, and patient delay (version 3) formulation in mathematics
Mathematical formulation for this problem is extension for (PASU) problem version 2. However, The cost function for this problem could be calculated according to various weight based on the importance of the constraint for the patients. Tables 3 and 4 reports the weight of the cost components.
Table 4.
Data set 1
| Instances | Bed | Room | Patients | Planning horizons |
|---|---|---|---|---|
| 1 | 286 | 98 | 693 | 14 |
| 2 | 465 | 151 | 778 | 14 |
| 3 | 395 | 131 | 757 | 14 |
| 4 | 471 | 155 | 782 | 14 |
| 5 | 325 | 102 | 631 | 14 |
| 6 | 313 | 104 | 726 | 14 |
| 7 | 472 | 162 | 770 | 14 |
| 8 | 441 | 148 | 895 | 21 |
| 9 | 310 | 105 | 1400 | 28 |
| 10 | 308 | 104 | 1575 | 56 |
| 11 | 318 | 107 | 2514 | 91 |
| 12 | 310 | 105 | 2750 | 84 |
| 13 multi specialism | 368 | 125 | 907 | 28 |
PASP Data sets versions
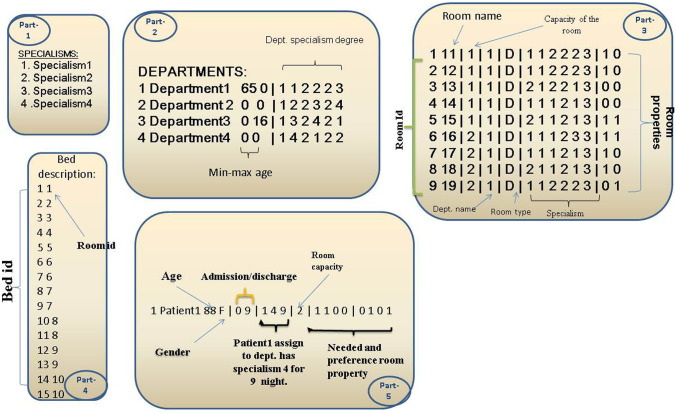
The original data set which belong to the first version of the problem1 is firstly reported by [17]. The data set consists of 13 instances as shown in Table 3. The instances 1 to 6 have equal time slots of 14 days. While, the instances 7 to 12 have the time slots between 14 to 91 days. All the patients in these instances are in need of only one specific treatment, but in instance 13, the patients need multiple treatments during the patients’ stay. This signifies that the instance 13 is more complex than others. In addition, this data set which reported by [15, 17] describes the original data set features including all present patients, even those whose admission and discharge dates are the same day. Figure 3 give an example description of the data set. The data set involved two-stage, first stage describes the rooms in the hospital, including room name, capacity, type (mean type of patients gender, which occupied the room), specialist for each room, finally the room properties. Second stage represented the patients needed/preference feature. Starting with patient id, age, gender, duration of stay. Then the department and specialist need for each patient, room capacity preferred by the patient, finally the needed and preferred properties.
Fig. 3.
Example for PASP original version data set
The second data set type is generated by [13], the author created and designed a data generator that is able to generate realistic data for a huge set of varying sizes. The generator accepts parameters such as: the number of patients, departments, days, rooms, and features. Randomized instances generated according to preset dissemination related to varying features like the duration of the stay, the room capacity, the number of specialism, and others. Meanwhile, the generator is not designed for single-day-cases to give opportunity for a complex to be solved. The data set consists of 9 families of 50 instances each. The data set entities is divided into three varying sizes in terms of the number of patients and the planning horizons. By observing this data set, on the doubling of number of days, the number of patients is equally doubled in order to keep the average occupancy balanced. Tables 5 and 6 reports the data set features.
Table 5.
Data set 2 [13]
| Family | Depts | Rooms | Features | Patients | Specialism | Days |
|---|---|---|---|---|---|---|
| Small Short | 4 | 8 | 4 | 50 | 3 | 14 |
| Small Mid | 4 | 8 | 4 | 100 | 3 | 28 |
| Small Long | 4 | 8 | 4 | 200 | 3 | 56 |
| Med Short | 6 | 40 | 5 | 250 | 10 | 14 |
| Med Mid | 6 | 40 | 5 | 500 | 10 | 28 |
| Med Long | 6 | 40 | 5 | 1000 | 10 | 56 |
| Large Short | 8 | 160 | 6 | 1000 | 15 | 14 |
| Large Mid | 8 | 160 | 6 | 2000 | 15 | 28 |
| Large Long | 8 | 160 | 6 | 4000 | 15 | 56 |
Table 6.
Data set 3
| Family | Rooms | Depts | OR | Specs | Treats | Patients | Days |
|---|---|---|---|---|---|---|---|
| Short1 | 25 | 2 | 2 | 9 | 15 | 391−439 | 14 |
| Short2 | 50 | 4 | 4 | 18 | 25 | 574−644 | 14 |
| Short3 | 75 | 6 | 5 | 23 | 35 | 821−925 | 14 |
| Long1 | 25 | 2 | 2 | 9 | 15 | 693−762 | 28 |
| Long2 | 50 | 4 | 4 | 18 | 25 | 1089−1169 | 28 |
| Long3 | 75 | 6 | 5 | 23 | 35 | 1488−602 | 28 |
PASP-based optimization methods
The ways that are presented by the researchers to optimize the patient admission scheduling can be classified into two types of search methodologies and solution technique. There are many scheduling techniques available for solving patient admission scheduling problem (PASP). The work done by [17], local search called tabu search hybrid engaged with token ring and a variable neighborhood descent approach, has been applied to assign a patient to bed in the hospital. Randomly generated data set have been used to evaluate the proposed method. The method needs more be investigated due to the complexity of this problem and could also be expanded further in terms of considered emergency admissions, and intensive care department. Moreover, another local search have been applied by [20] to tackle PASP, simulated annealing hybrid with local search and get the best known results. The method was tested on data set 1; the author excluded one constraint, which is transfer patients form one room to another.
A hyper heuristic approach has been used to tackle two combinatorial optimization problem, the patient admission scheduling problem and the nurse rostering problem [15]. Applying hyper heuristic is not appropriate, if the occupancy bed rate is increased in the hospital, which is due to the fix admission date. Moreover, the method has not considered the intensive care patients, patients who need isolation, patients on waiting lists. On another hand, theses two problems could be integrated together and come up with new version of PASP. The method was tested on a new benchmark data set introduced by the author.
Two Integer linear programming models (ILP) has been developed for tackling a day- to- day planning process for (PASP) problem [21]. This work is an extension of the work done by [20], and similar to [13]. The main contribution is by adding random registration date and predicted leaving date. The first model calculate for determining the optimal assignment for patients who have just arrived, while the second model calculate for forthcoming, but planned, arrivals. Hence, the performances of these models are compared with each other. The result shows that the second model is superior to the first in all conditions. In this method the over-crowed risk and the delayed in admission are not considered.
In addition, [22] introduced meta-heuristics algorithm for tackling appointment scheduling problem in an imaging clinic. A discrete-event simulation model bound with an optimization technique in order to minimize the patients’ waiting time. To evaluated this approach data is collected from 966 medical test for specific duration (4 month). This method has been focused on one aspect of the patient’s admission, which is imagine clinic.
Certain methods were developed using various types of metaheurstics such as in [23] the author introduced a Biogeography (BBO) algorithm which is population based meta-heuristic to address PASP problem. The proposed method evaluated its performance through the utilization instances from dataset 1. The result of BBO needs to be investigated further because it has reached a stagnation state earlier and could utilize all instances instead of only (1-6). In addition, an exact method was used by [24], the proposed method utilized column generation based heurstic incorporated with dynamic constraint aggregation, and new mathematical formulation for PASP problem was introduced. In this method, six instances were used from data set 1 to evaluate the method. The proposed method obtained good result in term of accuracy for small instances (1-5 instances). An exact method could be used to solve small instances, for large instances, the approach needs further investigation. Another metaheurstic was proposed by [25] known as an adaptive non-linear deluge algorithm to address patient admission scheduling PASP. The result of this approach was compared with other algorithms in literature, and was found to obtain superior results through the utilization of the six instances out of 13 from data set 1.
Furthermore, [14] proposed a metaheurstic approach using large neighborhood search by utilizing simulated annealing for solving dynamic patient admission scheduling problem. This method is based on [13], and tested using 450 instances from data set 2. The result demonstrated an improvement for the small and medium instances and much faster than the work done by [13], while for large instances there is a need for further improvement.
In similar context, [26] studied a dynamic patient-to-room assignment planning by expanded the PASP proposed by [17]. In this method, two outline Integer linear programming ILP models for solving this problem. The developed method engaged in certain testing using benchmark data set with some extension on its parameters, such as registration date and expected departure and also explicit the emergency patients. The result of these two models showed a more superior performance by the second model under all circumstances. Two methods known as Fix-and-Relax (FR) and Fix- and-Optimize (FO) has been conducted by [27] to solve (PASP). These two methods are based on heurstic using mixed integer programming. The problem is divided into two sub-problem based on time frame, and then the sub-problem are optimized. It entails the decomposition with the consideration of LoS, preference. The solution that was generated by the first method (FR) was used as input to the second method (FO). The proposed method that used (12) instances out of (13) from the data set 1 obtained promising feasible result at a faster rate of less than 3 minutes comparable with the state-of-arts. Recently [28] introduced an offline patient admissions scheduling problem under uncertainty with new suggestion on how to set the weight for the constraints. The method was tested on small short families from data set. This method was developed based on previous work of the same author [29] which proposed three optimization models based matheuristic called (FiNeMat) for solving patient to bed assignment which considered it as a sub-task from PASP [17]. In this work the author gives a guideline on how to set up the penalty values for the soft constraints. Moreover, [30] presented a newly metaheurstic approach known as Late Acceptance Hill Climbing Algorithm (LAHC) to address PASP problem. LAHC type of meta-heurstic and considered as a one-point solution technique. The proposed method involves two steps: the first step includes the generation of the initial feasible solution utilizing the room oriented-based approach whilst, the second step entailed the embedment of three neighbourhood structures inside the LAHC-based PASP component for the extended enhancement of the initial resolution generated at the beginning step. The suggested algorithm was assessed utilising the dataset 1. The result showed that the technique outperformed numerous other existing techniques from the literature using 1-6 instances out of 13. The main purpose behind the scheduling method is in the reduction of the patient waiting time, and in the hospital resource utilization enhancement. Moreover, [31] tackled PASP using a population-based metaheurstic called harmony search algorithm. The method has been tested on 6 instances of data set 1 and compare with other metaheurstic approaches. The proposed method needs more enhancement and should be tested on the rest of the data set.
In the work done by [32] the author proposed an exact method to address PASP. A new mathematical formulation bulit up, and mixed integer programming has been utilized with parameter free, and without pre- processing phase. The proposed approach tested on (1-13) instances from data set 1, and proof an optimal results for 2 of the instances and 9 new best result have been reported. Recently [33] revisited and extend biogeography-based optimization algorithm (BBO) to tackle PASP. The author introduced a selection technique called guided bed selection to enhance the ability of BBO and increased the diversity. Modified BBO yield better results than simple BBO using 6 instances from the original data set. On the other hand, [34] have studied the effect of compatible between short term and long term (strategic) in context dynamic patient admission scheduling problem which proposed by [18]. The results of this method using Dantzig-Wolfe decomposition and column generation get better results for 26 instances out of 30.
Discussion
The problem of optimizing patients admission scheduling has received attention recently. Patients scheduling in optimization can be considered from different side of aspects, (short,med,long) term scheduling, patients group, and methods which can be used to tackle such problem. Patient admission scheduling problem has been aroused at all levels of hospital planning and scheduling. Generally, most studies have focused on the operational level more than the tactical and strategical level. The operational level is also called the decision support level by assigning one task to resources in the hospital. There is fewer scheduling system that uses multiple level of decisions. The compatibility between all decision level very challenging problem and the studies on it is not rather vast and need to be further investigation.
Moreover, the patients have been classified into groups, elective patients and non-elective patients, elective patients have been widely studied in the literature which used a historical data from the hospital and scheduling the patients according to fixed data (statically). Non-elective patients refer to the patients whose the admission and discharge dates are unknown, such as emergency patients or uncertainty patients (dynamically). However, scheduling uncertainty is a complex task and there are few studies on scheduling the uncertainty patients. It should be noted that most studies on elective patients and neglect the problems arose in non-elective patients. Static PASP optimality are open challenges and still most of the researchers focusing on the short data set (1-6), due to the complexity of the rest. However, instance 13 only addressed in three articles because the patients need to be treated in multi departments. Dynamic version of this problem get less attention, and also many researchers focused on the small families and medium data sets. Patient admission scheduling problem integrated with other healthcare resources such as nurse, physician, and operating room could be improved the services in the hospital for future challenge work.
From an algorithmic point of view, patient admission scheduling problem versions were handled using different heuristics, metaheuristic, or exact method. The researchers have to develop new algorithms for handling this problem. The Table 7 summarizes the patient admission scheduling problem versions, approaches, and data sets.
Table 7.
Summaries of PASP versions, methods, patients, and data sets
| Name of method | PASP versions | Category | Data set | References |
|---|---|---|---|---|
| Tabu search | version 1 | Metaheurstics | Randomly generated | [17] |
| One hyper-heuristic | version 1 | Heuristic | Newly generated data set | [15] |
| Late accepting hill climbing | version 1 | Metaheurstics | Data set 1 | [30] |
| Local search | version 1 | Metaheuristic | Data set 1 | [20] |
| Simulated annealing with neighborhood structure | version 2 | Metaheuristic | Data set 2 | [13] |
| Local search | version 3 | Metaheuristic | Data set 3 | [18] |
| Tabu search | version 1 | Metaheuristic | Data set 1 | [17] |
| Markov decision process and dynamic programming | version 2 | Heuristics | Data set 2 | [35] |
| FiNeMath | version 1 | Metaheuristic | Data set 1 | [29] |
| Biogeography based optimization | version 1 | Metaheuristic | Data set 1 | [23] |
| None linear great deluge | version 1 | Metaheuristic1 | Data set 1 | [25] |
| Large neighborhood search | version 2 | Metaheuristic | Version 1 | [14] |
| Column generation approach | version 1 | Heuristic | Data set1 | [24] |
| Mixed integer programming | version 1 | Exact | Data set1 | [27] |
| Mixed integer programming | version 1 | Exactc | Data set 1 | [32] |
| Column generation | version 2 | Heurstics | Data set 3 | [36] |
Nurse rostering problem
Nurse rostering problem is a type of staff scheduling issues [37]. It is defined as a procedure to organize a time table that satisfies the demand of each person without conflict [37]. Nurse rostering have adjudged to be particularly complex and difficult optimization problem. Many researchers attempt to solve this problem using a different optimization model. Nurse rostering is N/P hard problem which involves two steps; the first step is to determine the number of staff to be scheduled, and second step is to allocate them in the time horizon for the schedule. The following section will give further details about this particular problem including its definition, mathematical formulation, versions, and finally the data set types for each version.
Nurse scheduling problem definition
The problem in nurse scheduling is so entrenched in the healthcare system, which is considered as under resource scheduling in healthcare, entailing the scheduling of a personnel [38] or staff in the hospital, by balancing the workload and preferences. The nurse scheduling problem entails NP hard optimization problem which is set through the allocation of a group of differing skilled nurses to various kinds of shifts as shown in Table 8, over a predefined scheduling time [39]. To obtain the feasible scheduling, the hard constraint should be achieved, while the soft constraints are allowed, however will be penalized. Nurse scheduling preference should be maximized, and the overall cost should be minimized.
Table 8.
Nurse scheduling type shifts [40]
| Shift type | Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|---|
| Morning | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Afternoon | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Night | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
Nurse rostering problem versions
Nurse rostering problem has been widely studied in the last decades. The first version has been run in 2002, and then in 2007 an extension model was developed in order to provide the researchers with various models and increase the real world constraints. Recently in 2010, (INRC-I) has been expanded and later (INRC-II). The next section will illustrated (INRC-I) and (INRC-II) in details.
NRP version1 (INRC-I)
The first international competition (INRC-I) [41] was established in 2010, based on two influential competition ITC2002, ITC2007 [42]. The generic model in this problem is how to allocate a nurse in a shift subject to several numbers of constraints. The objective function of this problem is to minimize all the soft constraints and this will lead to reduced penalties. The NRP description is [41]:
Roster: List which is made for several days for each ward in the healthcare institution.
Shift/rotation types: Appointed a nurse with specific skill based on period of time.
The number of nurses required for each day and for each type of shift is provided.
A series of arrangements reflecting the nurses ’ work regulation. Every nurse performs precisely according to a contract. A contract should provide a rules of the work as shown in Table 9:
Table 9.
Nurse regulation
| Regulation | Description |
|---|---|
| Maximum number of assignments | Total number of shifts the nurse can be given |
| Minimum number of assignments | Minimum number of rotation for each nurse |
| Maximum number of consecutive working days | Total number of consecutive working days for each nurse |
| Maximum number of consecutive free days | Total number of consecutive free days for each nurse |
| Minimum number of consecutive free days | Minimum consecutive free days for each nurse |
| Maximum number of consecutive working weekends | Total number of consecutive working weekend days for each nurse |
| Maximum number of working weekends in four weeks | Total number of consecutive working weekend days for each nurse per month |
| The number of days off after a series of night shifts complete weekends | Set it “true” if a nurse has to work on all days in a working weekends |
| Identical shift types during the weekend | Set it “true” if a nurse is assigned to task at the same rotation on all days of a working weekend |
| unwanted shift patterns | For example, if the nurse preferred morning shifts |
NRP Datasets versions
There are several data set type publicly available for NRP. However, most of them are real world data, first of them KAHO data sets https://people.cs.kuleuven.be/pieter.smet/nursero, represented instances of six wards in two different Belgian hospitals. These wards include three different scenario’s: normal, overload and absence. The first scenario represents a usual working case with average working conditions. The second scenario offers unexpected condition, for example when there is a disaster or an unexpected absence case. On the other hand, the second data set type belongs to the First International Nurse Rostering Competition (INRC-2010) prepared by the research group at the University of Udine in Italy and the Second International Nurse Rostering Competition (INRC-II), all instances and data set could be find https://mobiz.vives.be/inrc2/?paged=20. NSPLib http://www.projectmanagement.ugent.be/research/data/realdata is another data but it is not derived from real data,but its constructed with that problem generator. Nottingham datasets [43] which has been provided by Nottingham university which, established a website consist of a wide range of data sets from world wide hospitals. Additionally, the UK data set [43] which is the earlier one that is obtained from the UK hospital and consists of 411 preprocessed valid shift patterns.
NRP-based Optimization Methods
NRP typically considers staff scheduling problem [44] Numerous researchers give special attention to nurse scheduling and attempts to optimize it in order to achieve a workable roster that has positive scheduling quality. Recently, [45] proposed directed Bee Colony algorithm which is used to address NRP. The researchers utilized a multi-objective mathematical programming model and adapted a Multi-Objective Directed Bee Colony Optimization (MODBCO). The performance of this algorithm is evaluated using INRC2010. A set of 69 different cases of various sized data sets are chosen, and 34 out of 69 instances obtained the best results. Furthermore, [46] proposed a hybrid harmony search algorithm with hill climbing as a resolution in addressing the greatly limited nurse rostering problem (NRP). This method utilizes hill climbing to empower its exploitation in the search space. Moreover, the harmony memory consideration in the harmony search algorithm is through replacement by random selection scheme along side the global best concept of particle swarm optimization, in order to accelerate the convergence rate. The result of this technique demonstrated that the proposed method obtained five new best outcomes in relations to the quality of the solution, and time necessities. In addition, [39] offered another method to address NRP. The author introduced harmony search algorithm with a modification in its operators, replacing random selection with the global-best selection of Particle Swarm Optimization in memory consideration operator to enhance convergence speed. In order to develop a local utilization in this method, multi-pitch adjustment procedures were added. The result of this method proved that harmony search algorithm have the ability to solve the NRP using INRC2010 data set. Furthermore [47] proposed hybrid Artificial Bee Colony algorithm to address NRP. The author replaced the bee phase by hill climbing method in order to rise up the exploitation. The performance of this algorithm is evaluated using INRC-I. For two instances the proposed method has had good results.
In the work done by [48], the author proposed an integer programming techniques to solve NRP. On the other hand, [49] solved a dynamic version of NRP which was formulated for the second nurse rostering competition (INRC-II). In this proposed method two solvers were created, which were dependent on Mixed Integer Linear Programming (MILP) and Simulated Annealing respectively. The first solver was based on the exact method using the MILP solver CPLEX (v. 12.5), Meanwhile the second solver was implemented using EasyLocal++ (v.3). In addition [50] had also solved the dynamic version for NRP. The researchers have added a new expansion to the problem in the version of additional constraints to address incomplete data, and have used an integer programming model to solve the problem. The experimental result using this approach had shown an improvement on the basic model outcome, and had attained competitive outcome in comparison to the contest finalists competition. The work done by [51], branch-and-price procedure engaged with large-neighborhood-search framework has been used to solve INRC-II. The results in large instances has been achieved. In addition, [52] tackled NRP by utilized local search method (SA) based on a large neighborhood. The proposed method tested on INRC-II and getting better results in small instances (4-8) weeks whilst, for large instance are worst in comparing with [51]. Moreover, [53] developing two heuristic algorithms to solve NRP in a radio logical technologist rosters in the research hospital. Decision tree method and greedy search algorithm has been integrated with bat algorithm and particle swarm in order to generate a feasible solution. This method has a limitation in considering a scheduling for long period. Fix-and-Relax (F and R) and Fix-and-Optimize based simulated annealing, are two methods has been utilized by [54] to tackle NRP. The method has been tested on 24 available data set, and has been reported seven new best-known results. In Table 10 summaries of NRP and various version with its method, datasets, and categories
Table 10.
Summaries of NRP versions, methods,categories, and data sets
| Method | NRP verssion | Category | Dataset | Reference |
|---|---|---|---|---|
| Local search | weekly shift patterns | Metaheurstics | ORTEC01 | [55] |
| local search/large neighbourhood | INRC-II (static) | Metaheurstics | INRC-II competition datasets (hidden instances) | [52] |
| Column generation | Shift Scheduling | Heurstics | standard benchmark data sets | [56] |
| Harmony search/Great deluge | UKMMC (real world) | Metaheurstics | Malaysia Medical Center data | [57] |
| bat algorithm/particle swarm optimization | radio-logical technologists’ shifts | Heuristics | [53] | |
| Simulated Annealing/MIP | - | Metaheurstic | New generated dataset | [54] |
| Tabu Search | Specific scheduling/ hospital in Canada | Metaheurstics | 5real datasets | [58] |
| Evolutionary algorithm and ABC | Chinese NRP | Metaheurstic | N/A | [59] |
| Great deluge | INRC-I | Metaheurstic | INRC-2010 | [60] |
| Harmony Search Algorithm/Hill climbing | Medical Center of Universiti Kebangsaan | Metaheurstics | real-world NRP | [61] |
| Ant colony/ hill climbing | Malaysian hospital | Metaheurstic | Real data | [62] |
| Harmony search/greedy local search | ORTEC NRP | Metaheurstics | 12 real-world | [63] |
| Haramony search | INRC-I | Metaheurstics | INRC2010 | [64] |
| Greedy algorithm/Simulated Annealin | Malaysia Medical Cente | Heurstics | Real data from UKM medical center | [65] |
| Cyber swarm algorithm | Multi-Objective NRP | Metaheurstic | ZDT | [66] |
| Hyper heurstic | INRC-I | aheurstics | INRC-2010 | [67] |
| Ant colony | weekly schedules in a large U.K. hospita | Metaheurstic | nchmark i | [68] |
| Bee Colony | INRC-I | Metaheurstic | INRC2010 | [45] |
| Harmony search/artificial immune systems t | Metaheurstic | INRC2010 ANROM/INRC-2010 | [69] | |
| Mixed Integer LinearProgramming/Simulated Annealing, | INRC-II(dynamic) | Metaheurstic | N/A | [49] |
Discussion
The problem of optimization Nurse rostering (NRP) has become a major topic for scholar among the personnel scheduling problems. It become an attractive problem for many optimization researchers. Nursing shortages are a significant and multifaceted problem in healthcare systems and in optimization field is crucial. Many researchers have tackled the problems with different techniques such as exact methods, heuristic procedures and metaheuristics. Nurse rostering problem is an open research challenge in operational level using various metaheuristics approaches. Hybridization of metaheuristics with local search show the ability to solve NRP [47], Due to the ability to balance the exploration and exploitation.
Nurse rostering problem has been studied with a different type of constraints, features and evaluated in various countries [43] using different real hospital data sets. Most studies have focused on the data sets (INRC-I), and INRC2010. There is a limitation of creating real data sets from hospitals from different countries, this belongs to the privacy for the hospitals. INRC-II dynamic version has limited studies due to its complexity and the multi-stage scenario. Most studies for INRC-II focused on the small instances (4-8) weeks for this problem. Nurse scheduling problem could be developed further by taking in consideration, each country conditions. Integrating between nurse scheduling and other healthcare problem such as patients scheduling, physician scheduling could enhance the performance of the medical institution.
Operating room scheduling
Operating room theatre plays a significant part in the health care sector, because of its major impact on hospital performance. Operating room requires a special combination of personnel and equipment. In addition, each surgery requires preparation, before and after the surgery. So, the operating room theatre consists of two parts, namely the preoperative and the postoperative [70]. Managing/scheduling the operating room theatre is extremely difficult due to its constraints, and the preferences of the stakeholders. Moreover, the resources limitations, and the increase in demand for surgical services have to lead to improved approaches to room scheduling, by applying different approaches to manage the operating room theatre. The next sections will explicate the operating room scheduling extensively.
Operating room scheduling problem definition
The operating theatre scheduling also called surgery scheduling consists of two parts; the operating room and the recovery room [71]. The Operating Theater (OT) involves the required resources for surgeries. These include personnel such as nurses, surgeons, anaesthetists and others, meanwhile, others involve facilities such as equipment, pre-operative holding units, multiple ORs, post-anaesthesia care units, and intensive care. There are varying operating room scheduling definitions, [72] has been described the operating room scheduling as “sequence of job/activities to allocate in the operating room”. The operating room is the ultimate important part of the hospital; it represents the source of income and expense for hospitals. The operating room has an immense significance with other hospital resources, and represent approximately from the hospital income [73]. “The OR schedule is a patient flow management tool, and it assists the flow of other hospital resources, such as equipment, instrumentation, and ancillary hospital staffing resources” [74]. In addition [74] defined the operating room scheduling as a central system where the operating room is run by operation room leadership team, functioning as an efficient instrument, for the transmission of real-time patients flow and resources data of all departments, including the care of surgical patients. Hence operating room scheduling allows the coordination of resources in the hospital such as surgeons, anesthesiologists, nurses, technicians, and ancillary staff to be allocated in the appropriate technicians, and ancillary staff to be allocated in the appropriate way. On the other hand [75] defined the Operating Room Surgical Schedule in his article as the assignment of a surgical operation to an operating room, according to a different type of factors such as room availability, weekly working hours, doctor’s preferences, and operating room capabilities.
The main goal for each hospital is the high-quality service deliverance for patients, therefore there is an essential requirement for the boosting of operating room/department achievement through optimal resources usage. The operating room surgery scheduling is to distribute the operation start time and allocate the resources for scheduled surgeries, taking into consideration the multiple constraints in order to obtain the entire surgery flow, the existence and accessibility of resources, and the specializations and credentials of the staff [76].
Operating room theatre could be classified into different levels, according to patients type (elective, emergency), upon decision level such as (short, mid, long) term, or according to management procedures (block scheduling, open scheduling, or modified block scheduling) [77]. In this study, the primary emphasis is on the short term of the operating room scheduling which is split up to advance scheduling and allocation scheduling.
Operating room scheduling versions
Operating room scheduling at operational decision level is called surgical case scheduling problem (SCSP). There are mainly two scheduling versions of Operating Room Scheduling, namely: Advanced scheduling and Allocation scheduling. Advance scheduling is the procedure of establishing a patient’s (elective) surgery date and aim to get patients satisfaction (minimize patients waiting time), while allocation scheduling involves the setting of the operating room and the process initiation time on the particular surgery day. This literature focused on the operating room planning, in which the scheduling of the patients needs two essential procedures to be carried out; firstly, the assignment of patients to the operation room as (advanced scheduling), and secondly, the determination of the sequence of surgeries in each operating room block by the allocation schedule. Generally, each hospital has determined one of the following strategies which have been classified by Fei et al to establish a surgery scheduling procedure. The first group of strategy encompasses an open scheduling strategy, block scheduling strategy, and modified block scheduling strategy [1].
Open scheduling strategy
or “any workday” model of scheduling on OR scheduling entails no reservation in the time slot for a specific surgeon, and any workday option for surgeons. Additionally, this model is constraint-free [78]and follow the prioritization of chronology sequencing, starting from the earliest patient time-in strategy.
Block scheduling strategy
surgeons or the appointment of a collective of surgeons assigned to a grouped time blocks, where the organization of surgical patients (usually half-day or full-day length) are made. Block scheduling is a particular open scheduling matter.
Modified block scheduling strategy
This model is modified to obtain two types of scheduling: Firstly, by reserving some operating rooms opening hours while others are left open, and secondly, by freeing unused time blocks determined previously.
Practically the block scheduling and modified block scheduling has been widely applied in hospitals [1]. Moreover, this model is more flexible and provides an opportunity to re-use free time slots of operating room scheduling [78].
OR Advanced scheduling (version 1)
Advanced scheduling entails the surgery date establishment process for scheduling elective patients, which implicates a future event occurrence [79]. Advanced scheduling also has been diverse to dynamic and static scheduling based on the surgery settings [80]. However, the dynamic type refers to the patients who given a surgery date at consultation time. Whereas, the static type based on the patients waiting list. Advanced scheduling of the operating room is segregated into two categories, dependent on the type of constraints. The first constraints which are the total available operating room, while the rest of the constraints are determined by the available resources such as staff, and equipment.
Allocation scheduling (version 2)
Allocation scheduling also has other name called intervention scheduling, and surgical case scheduling. Allocation scheduling is to set the starting time of the operation and the resources are required for utilization. Allocation scheduling generates feasible scheduling for the operating room for each surgery per day with the assumption is that all patients in the hospital and ready for surgery [79].
Operating room scheduling mathematical formulation
The mathematical formulation of operating room planing and scheduling are presented in the huge majority of papers presented by [1, 81, 82]. This review will consider the mathematical formulation as it is modelled by [82] as advanced scheduling formulation. Lets (R) is the operating rooms, and . Q be a set of patients, (), and patients are scheduled in a set of time blocks,, in a set of days, in a set of weeks, . The patients possess a priority coefficient utilized in the determination of the sum of weighted waiting times, and delays over all patients. The coefficient is utilized to distinguish between inpatient and emergency patients. The coefficient is used to distinctive between inpatient and emergency patients.
Let be the release time for the surgery of each patient. Let due time for the surgery of each patient. - be the clinical case for individual patient that will decrease if the patient does not receive his/her surgical services. Conversely, when compared with the elective patients, the emergency patients delays will result in a higher penalty on the objective function. Thus,the advance emergency patients arrival predication be ,
Notations
The operating room planning and scheduling notations are presented by [82] as the following: P is the elective patients index, P is represent the number of the elective patients. i represented the non-elective patients where I is elective patients number. q indicate to the elective and non elective patients where is the total number of patients. r refers to operating rooms , R R is the operating rooms number. b indicates the blocks ,B is the total operating rooms blocks. s surgeon indicator , and S is the number of surgeons. e refer to expertise,.E is the number of expertise d denotes the number of days in a week , D is the number of days. w number of weeks , W denotes the number of weeks.
Parameter
block (b) capacity in day (d) in a week (w). parameter occupation of block (b). surgery duration expectation for the patient q. releasing time for the patientq surgery. a sufficient time for patient q surgery. clinical priority factor of patient. in the objective function the weight term j . a number of blocks that are assigned to expertise e in day d in week w. expertise which patient q needs . is a group of blocks that are assigned to room r in day d in a week w. denotes the surgeon assigned to operate patient p . is set of blocks that the patient undergo surgery in day d in week w. overtime permitted by each block. overtime permitted by each operating room. The total number of surgeries allowed in that day by a surgeon. is calculated by ,total number of waiting days by patient during the planning horizon. Decision variables: if the patient q is scheduled undergo surgery in block b in day d in week w;0 otherwise. is the amount of overtime of block b in day d in week w. if the surgeon s is scheduled for surgery in day d in week w;0 otherwise. The mathematical formulation for operating room scheduling using deterministic approaches is generated according to the mean value of surgery duration as follow:
| 12 |
| 13 |
Subject to:
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
| 20 |
| 21 |
| 22 |
| 23 |
| 24 |
Operating room scheduling data sets
Operating room scheduling problems have been studied by various researchers and tested based on different data sets up on their countries hospital. To the best of our knowledge, no commonly utilized test sets were identified for other healthcare scheduling issues, such as the issue of surgical scheduling. In this review, we have presented a data set which has been introduced by [83], which involved (20,880) instances with small family subset instances which involved (146) instances. This data set was generated based on real life data from Dutch hospitals (11 surgical specialties), the experimental design for real-life instance generation shown in Table 11. Whilst, Table 12 presents the statics outcomes, and the experiment design for the generation of theoretical instances shown in Table13https://www.utwente.nl/en/choir/research/BenchmarkORScheduling/introduction.
Table 11.
Experimental design for real-life instance generation [83]
| Problem parameter | Values considered | Number of values |
|---|---|---|
| Specialty (p) | CHI, ORT, ENT, GYN, PLA, URO, EYE, THO, ONC, NEU, MIX | |
| Number of ORs(j) | 5, 10, 15, 20, 25, 30, 35, 40 | |
| Load | 0.80,0.85,...,1.2 | |
| Total instance= | 880 |
Table 12.
Statistics of the outcome
| Specialty short name | Specialty full name | Surgery types | Surgery realizations |
|---|---|---|---|
| CHI | General surgery | 149 | 931 |
| ENT | Otolaryngology | 146 | 11,986 |
| EYE | Ophthalmic surgery | 91 | 7953 |
| GYN | Obstetric and gynecologic surgery | 60 | 4116 |
| MIX | Remaining specialties, such as colorectalsurgery, pediatric surgery, traumasurgery, vascular surgery, etc. | 173 | 46,938 |
| NEU | Neurological surgery | 47 | 2832 |
| ONC | Surgical oncology | 43 | 6466 |
| ORT | Orthopedic surgery | 133 | 7618 |
| PLA | Plastic surgery | 73 | 3022 |
| THO | Thoracic surgery | 28 | 224 |
| URO | Thoracic surgery | ||
| Total | 1018 | 108,11 |
Table 13.
Shows the experiment design for the generation of theoretical instances [83]
| Problem parameter | Values considered | Number of values |
|---|---|---|
| Case mix profile (p) | 0,1,..,16 | |
| Number of | 5, 10, 15, 20, 25, 30, 35, 40 | |
| Load | 0.80,0.85,..,1.20 | |
| Total instance parameters | 1360 |
Operating room scheduling in optimization
The literature in scheduling operating room has a wide range of methodologies that fit with optimization domain. Various heurstics and metaheurtics has been applied to tackle operating room scheduling problem. In this context, constructed a weekly operating theater surgery scheduling using open scheduling strategy has been proposed by [1]. The objectives of this work is in the maximization of the operating rooms usage, and the minimization of the operating theatre overtime expenditure, in addition to the minimization of the unanticipated idle time among surgical patients. The solution procedure in this work is distinguished into two phases, the first phase involves the assignment of a specific date for surgeon to each patient, and that the surgeons are free to assign his case in the time block. Next, the daily scheduling is determined in order to fix the operation sequence and takes into consideration the recovery beds that are available. The proposed method is characterized by a set-partitioning integer-programming model, and where the solution is arrived through a column-generation-based heuristic process. The second phase which entails the daily scheduling problem is outlined as a two-staged hybrid flow-shop model, that is resolved by a hybrid genetic algorithm, utilizing a Tabu search procedure for executing local search. A evaluation of the proposed method has been done with different actual surgery schedules based on Belgian university hospital data. The results showed lesser idle time between the surgical cases as derived from the surgery schedules, in addition to the greater operating rooms usage, with minimal overtime. Furthermore [84] proposed a novel two-stage stochastic mixed-integer programming model to solve surgery schedules across multiple operating room under uncertainty has been developed by [84]. The main idea in this paper observes the enablement of numerous operations to be completed simultaneously, because of the availed presence of various operating room, aid and support from other surgeons, especially from the principal staff surgeon. It described the benefit behind the sharing of resources among the surgeons. The summaries of all optimization algorithm and data sets with categorize is illustrated in (Table 14)
Table 14.
Summaries of OR method,version,data sets,categories
| Method | Version | Data set | Categories | Ref. |
|---|---|---|---|---|
| Local search | Integrated with PASP | [18] | ||
| Genetic Algorithm/ILP | Operating room+anesthesia recovery bed | Randomly generated | Metaheurstic/exact | [85] |
| Monte Carlo/greedy local search | Advanced scheduling OR | 10 generated instances | heuristic | [86] |
| Mixed integer programming | Uncertainty OR scheduling | real data | stochastic/Heuristic | [87] |
| Ant Colony Optimization | Multi-objective OR | data from Cancer Center | metaheuristic | [88] |
| Genetic algorithm is | Allocation scheduling | N/A | Metaheurstics | [89] |
| Genetic Algorithm/Particle swarm | Multi constraints OR | real data from public hospital | Metaheurstic | [90] |
| Column generation | Integrated OR model | Real data | Heuristic | [91] |
| Grey Wolf/VNS O | Integrating 3 stage OR | data base 2017 | Meta heuristic | [36] |
| Simulated Annealing/Tabu search | Operating Theater Room | Three real datasets/Scottish hospital | Heuristic/metaheuristics. | [92] |
| Column Generation/Local Branching | Surgical Case re-Planning and Scheduling problem | Real data | Heuristics | [93] |
| Mixed-integer linear programming | OR/elective surgery | Real data/Iraq | Heurstics | [94] |
| Scheduling surgery in OR/Advanced scheduling | Real data | Heurstic, | [95] | |
| Hybrid genetic algorithm/local search | OR surgery scheduling | real data/hospitalin China | Metaheurstics | [96] |
| Ant colony | Surgery scheduling/Open scheduling | Generated five test cases | Metaheurstics | [76] |
| Genetic Algorithm | OR | N/A | Metaheuristic | [97] |
| Uncertain single OR | Random generated dataset | heuristic | [98] | |
| Genetic Algorithm/local search | Surgeries assignment problems | 20 instances randomly generated | Metaheurtstic | [99] |
| Genetic algorithm | OR scheduling | Randomly generated | Metaheurstic | [100] |
| OR/Advanced scheduling | Real data/San Martino University Hospita | Metaheurstic | [101] | |
| Bees Algorithm/Simulated anealing | Master Surgery Scheduling Problem/ Surgical Case Assignment Problem | Real data/San Martino University Hospital | Metaheurstic | [102] |
| Local search | Surgical case assignment | real instances/Portuguese | Heuristics | [103] |
Surgery scheduling problem in optimization
Surgical scheduling problem was resolved using different optimization method. Some of those researchers used deterministic models, whereas others used stochastic method. In the optimization field, there are several researchers who applied different techniques to solve this problem. In recent years [104] solved the surgical scheduling procedures by applying a discrete event simulation model in the first stage, that evaluated the 12 varying sequencing and patient appointment time-setting, including expected patient waiting time, in addition to the expected surgical suite overtime as per day. In the second stage, a bi-criteria genetic algorithm (GA) was utilized to evaluate whether there are more superior solutions can be obtained for the single-day scheduling problem. Moreover, the efficiency of the bi-criteria genetic algorithm in the event of a the surgery date change was investigated. In addition, [105] considered the application of operational surgery scheduling problems at a medium sized Norwegian hospital. In the study, the execution of the scheduling planning for day scheduling, with the weekly scheduling and admission planning was discussed. The proposed method used a generalized model for surgery scheduling problems. The equalization of computational loads between a construction and an enhancement method was achieved through the implementation of a parented model solution using an on-line learning. The result of this algorithm showed an excellent performance traversing various problem categories. In the same context, [85] has been proposed two exact and metaheurstic method to scheduling surgery in operating room integrated with post-anesthesia recovery beds. Table 3 presents the surgery scheduling problem and the respective methods employed and patients categories.
Discussion
Operating rooms are an important and expensive sector in the most hospitals [70]. Thus, various studies have been conducted on scheduling and planning of the operating room under operational, tactical [119], strategic levels, which concerned as a decision level for operating rooms.
Various solution procedures have been utilized to tackle this problem, heuristic and metaheuristic methods have been intensified in the literature in the context of optimization. Due to the high constraints problem could not be solved using the exact method. The uncertainty in scheduling techniques are the most difficult task, and they are more concrete, since, the uncertainty in time frame is the most interesting topic. Operating room scheduling integrated with other healthcare services such as patient [13] scheduling, nurse [120] is limited. However, the integration between an operating room with other systems in the hospital will enhance the hospital performance and will lead to improving the hospitalization services (Table 14) summaries recent methods, versions and categories. Moreover, most studies have pay particular attention to elective patients than on, non-elective patients. Urgent patients and emergency patients get less attention (Table 15). Furthermore, surgery scheduling problem involved three forms of scheduling [121], first the surgeon is assigned by hospital administration, then the surgeon is assigned to time block, and finally the last minute adjustment (if required). Surgery scheduling problem has been addressed by various approaches and considered elective/uncertain patients. Tackling elective and emergency patients in surgery scheduling is limited. Several articles consider the problem separately, while others have used integrated models [122]. Most studies have focused on surgery scheduling integrated with other healthcare scheduling such as with operating room [108], patient scheduling [116], physician scheduling [77]. The integrating between surgery scheduling with different healthcare problem could provide high-quality services, and minimizing overtime cost. Developing multi decision healthcare scheduling system which combines between surgery scheduling, operating room planning, and physician scheduling is better to address a real-life situation and balancing hospital resource utilization.
Table 15.
SSP
| References | method | Uncertain/Elective |
|---|---|---|
| [106] | Stochastic programming | Uncertainty |
| [107] | Integer programs | − |
| [108] | stochastic linear program | Uncertainty |
| [109] | branch-and-price exact solution algorithm | |
| [110] | branch-and-bound algorithm | − |
| [111] | heuristics and local search | elective |
| [112] | stochastic dynamic programming | elective |
| [113] | mixed integer linear formulation and light robustness approach | elective |
| [114] | integer linear programming model | elective |
| [115] | stochastic dynamic programming model | elective |
| [104] | heuristics- discrete event simulation model- bi-criteria GA | elective |
| [116] | local search,integer programming,binary programming | elective/emergency |
| [117] | discrete-event model | uncertain |
| [118] | Discrete Event Dynamic System | elective |
Other healthcare scheduling and planning problems
In healthcare scheduling problems many problems receive less attention by researchers, in this section will surveyed and give an overview of other healthcare scheduling such as scheduling physicians [123–125], home healthcare [126–128], telemedicine scheduling [129]. Physician scheduling is a real-world problem which arises in hospitals, physician scheduling is a type of staff schedules with more complex regulation. Physician scheduling is defined as assigning a physician to duty such as surgeries, clinics, scopes, calls, administration and others over time slots /shifts according to planning horizons with different types of preferences and constraints [125]. Physician scheduling problem have two roster planning cyclic/ad-hoc which refer to planning period must be reconstructed because physicians may have different work rosters each week. Where as cyclic planning refer to set models for doctors, with or without weekly rotation. Planning and scheduling in physician problem has been arouse in a three decision level (strategic, tactical and operational planning). However, physician scheduling is represented by day-to-day scheduling, in which the physician is given various duties [77]. Scheduling physician problems have been studied by different researchers such as [125] who proposed a mathematical programming models to solve a master physician scheduling problem. In addition [123] and [130] had proposed a mix integer linear programming for solving this problem. In addition [131] studied the scheduling of physicians in the pediatric intensive care unit (PICU) too. On the other hand [77] integrated physicians and surgery scheduling for the purpose of solving operating room scheduling problems by using mix integer linear programming. Furthermore, [132] had described physician problems in a case study, in Swedish public hospitals. Moreover [133] had presented the problem from the perspectives of US hospitals. The author have studied different types of physician scheduling using different priorities. Besides that, [134] had studied the problem by using a case hospital from the King Khalid University a Hospital in the Kingdom of Saudi Arabia. Home healthcare scheduling another healthcare complex optimization problem which has been grown in various decision levels, such as assigning staff or scheduling shifts [135]. For instance, various sets of nurses could be allocated to different clients which are located in diverse areas. Therefore, various constraints, requirements, and preference should be considered, such as nurse expertise, clients requirements, and nurse working time. However, balancing the expertise of nurses and customers is a standard function of home healthcare scheduling optimization and the selection of skills considered varies based on the needs of the client and the particular regulatory environment. The major solution method of home healthcare scheduling has been done using metaheurstic algorithm [136, 137]. Recently the field of telemedicine has attracted a multitude of researchers because it provides a new platform for patients to access the healthcare services. It provides medical care for patients in distant remote areas such as villages that need outreach services.
Conclusion and future work
In this survey paper, we address healthcare scheduling problem as an optimization problem. Scheduling in healthcare is segregated into two types; personnel and resources. This review on healthcare scheduling has identified the areas of healthcare scheduling such as patient admission scheduling, nurse rostering problem, operating room scheduling problem and other healthcare scheduling problem. The objective of all scheduling systems in optimization aspect is to reduce the cost and patient’s waiting time and maximize the resources efficiency. The quality of the solution is dependent upon the cost function which is involved in the summation of the soft constraints. In addition, this review summarized all scheduling systems on healthcare, and are supported by most successful algorithms, which have used a diverse spectrum of search methodologies. We noticed that several latest sophisticated systems obtained significant results. Furthermore, the metaheuristics algorithms involved in the local search methods and population-based method, have been highlighted in this paper. However, the major successful algorithms are from nature-inspired algorithms, which proved their ability to solve N/P hard problem. This is due to their ability to explore the search space, especially swarm-based algorithms. The challenges for future research direction are to:
Utilized other metaheuristic algorithms such as a swarm-based algorithm for solving healthcare scheduling problems in order to obtain better results.
Study and analysed the robustness of each algorithm that has been applied to each problem.
Build a scheduling system for the hospital, which covers the entire hospital dynamically.
Focusing on particular real-world problems on healthcare such as telemedicine which will help during a disaster such as COVID 19 pandemic.
We can also be adapting big data analytic methods in order to get real data sets for different scheduling systems, by focusing on the most complex situations such as COVID 19 pandemic and get historical data for a number of patients and nurse shift as well as physician scheduling, to come up with new data sets regarding those problems.
Most studies focus on the elective patients more than other patients type, further research direction could be on scheduling triage, emergency, urgent patients could be an interesting topic if it is integrated with other scheduling techniques problems such as physician scheduling and nurse scheduling.
Integrated scheduling system which involved patients, nurse, physician, and operating rooms could improve the service quality for the medical system.
Declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Footnotes
Contributor Information
Zahraa A. Abdalkareem, Email: zahraa20102015@gmail.com, Email: zahraaadnan@studentmail.unimap.edu.my
Mohammed Azmi Al-Betar, Email: mohbetar@bau.edu.jo.
Abdelaziz I. Hammouri, Email: Aziz@bau.edu.jo
References
- 1.Fei H, Meskens N, Chu C. A planning and scheduling problem for an operating theatre using an open scheduling strategy. Comp Industrial Eng. 2010;58(2):221–230. doi: 10.1016/j.cie.2009.02.012. [DOI] [Google Scholar]
- 2.Rais A, Viana A. Operations research in healthcare: a survey. Int Trans Operation Res. 2011;18(1):1–31. doi: 10.1111/j.1475-3995.2010.00767.x. [DOI] [Google Scholar]
- 3.Batun S, Begen MA. Optimization in healthcare delivery modeling: Methods and applications. In Handbook of Healthcare Operations Management, pages 75–119. Springer, 2013.
- 4.Oueida S. Modeling a New Computer Framework for Managing Healthcare Organizations: Balancing and Optimizing Patient Satisfaction, Owner Satisfaction, and Medical Resources. CRC Press; 2020.
- 5.Hall RW, et al. Handbook of healthcare system scheduling. Springer; 2012.
- 6.Gupta D, Denton B. Appointment scheduling in health care: Challenges and opportunities. IIE transactions. 2008;40(9):800–819. doi: 10.1080/07408170802165880. [DOI] [Google Scholar]
- 7.Rinder MM, Weckman G, Schwerha D, Snow A, Dreher PA, Park N, Paschold H, and Young W. Healthcare scheduling by data mining: Literature review and future directions. J Healthcare Eng, 3, 2012.
- 8.Marynissen J, Demeulemeester E. Literature review on integrated hospital scheduling problems. KU Leuven, Faculty of Economics and Business, KBI_1627, 2016.
- 9.Van den Bergh J, Beliën J, De Bruecker P, Demeulemeester E, De Boeck L. Personnel scheduling: A literature review. Euro J Oper Res. 2013;226(3):367–385. doi: 10.1016/j.ejor.2012.11.029. [DOI] [Google Scholar]
- 10.Rahimi I, and Gandomi AH. A comprehensive review and analysis of operating room and surgery scheduling. Arch Comp Methods in Eng. 2020.
- 11.Zhu S, Fan W, Yang S, Pei J, Pardalos PM. Operating room planning and surgical case scheduling: a review of literature. J Combi Opt. 2019;37(3):757–805. doi: 10.1007/s10878-018-0322-6. [DOI] [Google Scholar]
- 12.Ahmadi-Javid A, Jalali Z, Klassen KJ. Outpatient appointment systems in healthcare: A review of optimization studies. Euro J Oper Res. 2017;258(1):3–34. doi: 10.1016/j.ejor.2016.06.064. [DOI] [Google Scholar]
- 13.Ceschia S, Schaerf A. Modeling and solving the dynamic patient admission scheduling problem under uncertainty. Artif Intell Med. 2012;56(3):199–205. doi: 10.1016/j.artmed.2012.09.001. [DOI] [PubMed] [Google Scholar]
- 14.Lusby RM, Schwierz M, Range TM, Larsen J. An adaptive large neighborhood search procedure applied to the dynamic patient admission scheduling problem. Artif Intell Med. 2016;74:21–31. doi: 10.1016/j.artmed.2016.10.002. [DOI] [PubMed] [Google Scholar]
- 15.Bilgin B, Demeester P, Misir M, Vancroonenburg W, Berghe GV. One hyper-heuristic approach to two timetabling problems in health care. J Heuristics. 2012;18(3):401–434. doi: 10.1007/s10732-011-9192-0. [DOI] [Google Scholar]
- 16.Demeester P, de Causmaecker P, and Vanden Berghe G. Applying a local search algorithm to automatically assign patients to beds. In Proceedings of the 22nd conference on quantitative methods for decision making (Orbel 22), pages 35–36, 2008.
- 17.Demeester P, Souffriau W, De Causmaecker P, Berghe GV. A hybrid tabu search algorithm for automatically assigning patients to beds. Artif Intell Med. 2010;48(1):61–70. doi: 10.1016/j.artmed.2009.09.001. [DOI] [PubMed] [Google Scholar]
- 18.Ceschia S, Schaerf A. Dynamic patient admission scheduling with operating room constraints, flexible horizons, and patient delays. J Sched. 2016;19(4):377–389. doi: 10.1007/s10951-014-0407-8. [DOI] [Google Scholar]
- 19.Sigurpalsson AO, Runarsson TP, and Saemundsson RJ. Stochastic master surgical scheduling under ward uncertainty. In International Conference on Human-Centred Software Engineering, pages 163–176. Springer, 2019.
- 20.Ceschia S, Schaerf A. Local search and lower bounds for the patient admission scheduling problem. Comp Operations Res. 2011;38(10):1452–1463. doi: 10.1016/j.cor.2011.01.007. [DOI] [Google Scholar]
- 21.Vancroonenburg W, de Causmaecker P, and Vanden Berghe G. Patient-to-room assignment planning in a dynamic context. In Proceedings of the 9th International Conference on the Practice and Theory of Automated Timetabling (PATAT-2012), pages 193–208. Citeseer, 2012.
- 22.Granja C, Almada-Lobo B, Janela F, Seabra J, Mendes A. An optimization based on simulation approach to the patient admission scheduling problem using a linear programing algorithm. J Biomed info. 2014;52:427–437. doi: 10.1016/j.jbi.2014.08.007. [DOI] [PubMed] [Google Scholar]
- 23.Hammouri AI, and Alrifai B. Investigating biogeography-based optimisation for patient admission scheduling problems. J Theo Appl Info Tech. 70(3), 2014.
- 24.Range TM, Lusby RM, Larsen J. A column generation approach for solving the patient admission scheduling problem. Euro J Oper Res. 2014;235(1):252–264. doi: 10.1016/j.ejor.2013.10.050. [DOI] [Google Scholar]
- 25.Kifah S, Abdullah S. An adaptive non-linear great deluge algorithm for the patient-admission problem. Info Sci. 2015;295:573–585. doi: 10.1016/j.ins.2014.10.004. [DOI] [Google Scholar]
- 26.Vancroonenburg W, De Causmaecker P, Berghe GV. A study of decision support models for online patient-to-room assignment planning. Ann Oper Res. 2016;239(1):253–271. doi: 10.1007/s10479-013-1478-1. [DOI] [Google Scholar]
- 27.Turhan AM, Bilgen B. Mixed integer programming based heuristics for the patient admission scheduling problem. Comp Oper Res. 2017;80:38–49. doi: 10.1016/j.cor.2016.11.016. [DOI] [Google Scholar]
- 28.Guido R, Solina V, Mirabelli G, and Conforti D. Offline patient admission, room and surgery scheduling problems. In New Trends in Emerging Complex Real Life Problems, pages 275–283. Springer, 2018.
- 29.Guido R, Groccia MC, Conforti D. An efficient matheuristic for offline patient-to-bed assignment problems. Euro J Oper Res. 2018.
- 30.Bolaji AL, Bamigbola AF, Shola PB. Late acceptance hill climbing algorithm for solving patient admission scheduling problem. Knowledge-Based Systems. 2018;145:197–206. doi: 10.1016/j.knosys.2018.01.017. [DOI] [Google Scholar]
- 31.Doush IA, Al-Betar MA, Awadallah MA, Hammouri AI, Raed M, ElMustafa S, and ALkhraisat H. Harmony search algorithm for patient admission scheduling problem. J Intel Sys, 2018;29(1):540–553.
- 32.Bastos LS, Marchesi JF, Hamacher S, Fleck JL. A mixed integer programming approach to the patient admission scheduling problem. Euro J Operational Res. 2019;273(3):831–840. doi: 10.1016/j.ejor.2018.09.003. [DOI] [Google Scholar]
- 33.Hammouri AI. A modified biogeography-based optimization algorithm with guided bed selection mechanism for patient admission scheduling problems. J King Saud Univ-Comp Info Sci, 2020.
- 34.Zhu YH, Toffolo TA, Vancroonenburg W, Berghe GV. Compatibility of short and long term objectives for dynamic patient admission scheduling. Comp Operations Res. 2019;104:98–112. doi: 10.1016/j.cor.2018.12.001. [DOI] [Google Scholar]
- 35.Diamant A, Milner J, Quereshy F. Dynamic patient scheduling for multi-appointment health care programs. Prod Operations Manage. 2018;27(1):58–79. doi: 10.1111/poms.12783. [DOI] [Google Scholar]
- 36.Zhu S, Fan W, Liu T, Yang S, Pardalos PM. Dynamic three-stage operating room scheduling considering patient waiting time and surgical overtime costs. J Combinatorial Opt. 2020;39(1):185–215. doi: 10.1007/s10878-019-00463-5. [DOI] [Google Scholar]
- 37.Ernst AT, Jiang H, Krishnamoorthy M, Sier D. Staff scheduling and rostering: A review of applications, methods and models. Euro J Operational Res. 2004;153(1):3–27. doi: 10.1016/S0377-2217(03)00095-X. [DOI] [Google Scholar]
- 38.Burke EK, De Causmaecker P, Berghe GV, Van Landeghem H. The state of the art of nurse rostering. J Sched. 2004;7(6):441–499. doi: 10.1023/B:JOSH.0000046076.75950.0b. [DOI] [Google Scholar]
- 39.Awadallah MA, Khader AT, Al-Betar MA, Bolaji AL. Global best harmony search with a new pitch adjustment designed for nurse rostering. J King Saud Univ Comp Info Sci. 2013;25(2):145–162. [Google Scholar]
- 40.F. Della Croce and F. Salassa. A variable neighborhood search based matheuristic for nurse rostering problems. Ann Oper Res. 218(1):185–199, 2014.
- 41.Haspeslagh S, De Causmaecker P, Schaerf A, Stølevik M. The first international nurse rostering competition 2010. Ann Oper Res. 2014;218(1):221–236. doi: 10.1007/s10479-012-1062-0. [DOI] [Google Scholar]
- 42.McCollum B, Schaerf A, Paechter B, McMullan P, Lewis R, Parkes AJ, Gaspero LD, Qu R, Burke EK. Setting the research agenda in automated timetabling: The second international timetabling competition. Info J Comp. 2010;22(1):120–130. doi: 10.1287/ijoc.1090.0320. [DOI] [Google Scholar]
- 43.Pillay N, and Qu R. Nurse rostering problems. In Hyper-Heuristics: Theory and Applications, 2018;61–66. Springer.
- 44.Smet P. Nurse rostering: models and algorithms for theory, practice and integration with other problems. 2015.
- 45.Rajeswari M, Amudhavel J, Pothula S, Dhavachelvan P. Directed bee colony optimization algorithm to solve the nurse rostering problem. Comp Intell Neurosci. 2017;2017: [DOI] [PMC free article] [PubMed]
- 46.Awadallah MA, Al-Betar MA, Khader AT, Bolaji AL, Alkoffash M. Hybridization of harmony search with hill climbing for highly constrained nurse rostering problem. Neural Comp Appl. 2017;28(3):463–482. doi: 10.1007/s00521-015-2076-8. [DOI] [Google Scholar]
- 47.Awadallah MA, Bolaji AL, Al-Betar MA. A hybrid artificial bee colony for a nurse rostering problem. Appl Soft Comp. 2015;35:726–739. doi: 10.1016/j.asoc.2015.07.004. [DOI] [Google Scholar]
- 48.Santos HG, Toffolo TA, Gomes RA, Ribas S. Integer programming techniques for the nurse rostering problem. Ann Oper Res. 2016;239(1):225–251. doi: 10.1007/s10479-014-1594-6. [DOI] [Google Scholar]
- 49.Dang NTT, Ceschia S, Schaerf A, de Causmaecker P, and Haspeslagh S. Solving the multi-stage nurse rostering problem. In Proceedings of the 11th international conference of the practice and theory of automated timetabling. 2016;473–475.
- 50.Mischek F, and Musliu N. Integer programming model extensions for a multi-stage nurse rostering problem. Ann Oper Res. 2017;1–21. [DOI] [PMC free article] [PubMed]
- 51.Legrain A, Omer J, and Rosat S. A rotation-based branch-and-price approach for the nurse scheduling problem. Math Prog Comp. 2019;1–34.
- 52.Ceschia S, Guido R, and Schaerf A. Solving the static inrc-ii nurse rostering problem by simulated annealing based on large neighborhoods. Ann Oper Res. 2020;1–19.
- 53.Chen PS, and Zeng ZY. Developing two heuristic algorithms with metaheuristic algorithms to improve solutions of optimization problems with soft and hard constraints: An application to nurse rostering problems. Appl Soft Comp. 2020;106336.
- 54.Turhan AM, and Bilgen B. A hybrid fix-and-optimize and simulated annealing approaches for nurse rostering problem. Comp Industrial Eng. 2020;106531.
- 55.Yabing N, Bing W, and Xingbao H. An adaptive method with local search for nurse rostering problem. In 2015 34th Chinese Control Conference (CCC). 2015;2726–2731. IEEE.
- 56.Strandmark P, Qu Y, and Curtois T. First-order linear programming in a column generation based heuristic approach to the nurse rostering problem. Comp Opera Res. 2020;104945.
- 57.Hadwan M, Ayob M, Rassam MA, and Hezam EA. Deluge harmony search algorithm for nurse rostering problems. In 2019 First International Conference of Intell Comp Eng (ICOICE). 2019;1–5. IEEE.
- 58.Vu SN, Nguyen MHN, Duc LM, Baril C, Gascon V, Dinh TB. Iterated local search in nurse rostering problem. In Proceedings of the Fourth Symposium on Info Com Tech. 2013;71–80.
- 59.Zhuo X, Huang H, Cai Z, and Hu H. An hybrid evolutionary algorithm with scout bee global search strategy for chinese nurse rostering problems. In 2015 IEEE Congress on Evolutionary Computation (CEC). 2015;769–775. IEEE.
- 60.Arajy YZ, Abdullah S, Kifah S. Non-liner great deluge algorithm for handling nurse rostering problem. Int J Appl Eng Res. 2017;12(15):4959–4966. [Google Scholar]
- 61.Hadwan M, Ayob M, Al-Hagery M, and Al-Tamimi BN. Climbing harmony search algorithm for nurse rostering problems. In International Conference of Reliable Information and Communication Technology. 2018;74–83. Springer.
- 62.Ramli R, Abd Rahman R, Rohim N. A hybrid ant colony optimization algorithm for solving a highly constrained nurse rostering problem. J Info Comm Tech. 2019;18(3):305–326.
- 63.Nie T, Wang B, and Zhang X. Hybrid harmony search algorithm for nurse rostering problem. In Harmony Search Algorithm. 2016;109–120. Springer.
- 64.Awadallah MA, Khader AT, Al-Betar MA, and Bolaji AL. Hybrid harmony search for nurse rostering problems. In 2013 IEEE Symposium on Computational Intelligence in Scheduling (CISched), 2013;60–67. IEEE.
- 65.Abobaker RA, Ayob M, and Hadwan M. Greedy constructive heuristic and local search algorithm for solving nurse rostering problems. In 2011 3rd Conference on Data Mining and Optimization (DMO). 2011;194–198. IEEE.
- 66.Yin PY, Chiang YT. Cyber swarm algorithms for multi-objective nurse rostering problem. Int J Innovative Comp, Info Control. 2013;9(5):2043–2063. [Google Scholar]
- 67.Rae C, and Pillay N. Investigation into an evolutionary algorithm hyperheuristic for the nurse rostering problem. In Proceedings of the 10th International Conference on the Practice and Theory of Automated, PATAT, pages 527–532, 2014.
- 68.Wu JJ, Lin Y, Zhan ZH, Chen WN, Lin TB, and Chen JY. An ant colony optimization approach for nurse rostering problem. In 2013 IEEE International Conference on Systems, Man, and Cybernetics, pages 1672–1676. IEEE, 2013.
- 69.Jin SH, Yun HY, Jeong SJ, Kim KS. Hybrid and cooperative strategies using harmony search and artificial immune systems for solving the nurse rostering problem. Sustainability. 2017;9(7):1090. doi: 10.3390/su9071090. [DOI] [Google Scholar]
- 70.Pariente JMM. Operating theatre planning and scheduling in real-life settings: Problem analysis, models, and solution procedures. PhD thesis, Universidad de Sevilla, 2016.
- 71.Guerriero F, Guido R. Operational research in the management of the operating theatre: a survey. Health care management science. 2011;14(1):89–114. doi: 10.1007/s10729-010-9143-6. [DOI] [PubMed] [Google Scholar]
- 72.Cardoen B, Demeulemeester E, Beliën J. Operating room planning and scheduling: A literature review. Euro J Oper Res. 2010;201(3):921–932. doi: 10.1016/j.ejor.2009.04.011. [DOI] [Google Scholar]
- 73.Denton B, Viapiano J, Vogl A. Optimization of surgery sequencing and scheduling decisions under uncertainty. Health care management science. 2007;10(1):13–24. doi: 10.1007/s10729-006-9005-4. [DOI] [PubMed] [Google Scholar]
- 74.Levine WC, Dunn PF. Optimizing operating room scheduling. Anesthesiology clinics. 2015;33(4):697–711. doi: 10.1016/j.anclin.2015.07.006. [DOI] [PubMed] [Google Scholar]
- 75.Romanyuk A, Silva A. Optimization of an operating room surgical schedule. Louis: Ese. wustl. edu. Washingon University in St; 2012. [Google Scholar]
- 76.Xiang W, Yin J, Lim G. An ant colony optimization approach for solving an operating room surgery scheduling problem. Comp Industrial Eng. 2015;85:335–345. doi: 10.1016/j.cie.2015.04.010. [DOI] [Google Scholar]
- 77.Van Huele C, Vanhoucke M. Analysis of the integration of the physician rostering problem and the surgery scheduling problem. J Med Sys. 2014;38(6):43. doi: 10.1007/s10916-014-0043-z. [DOI] [PubMed] [Google Scholar]
- 78.Roland B, Di Martinelly C, Riane F, Pochet Y. Scheduling an operating theatre under human resource constraints. Comp Industrial Eng. 2010;58(2):212–220. doi: 10.1016/j.cie.2009.01.005. [DOI] [Google Scholar]
- 79.Magerlein JM, Martin JB. Surgical demand scheduling: a review. Health services research. 1978;13(4):418. [PMC free article] [PubMed] [Google Scholar]
- 80.Samudra M, Van Riet C, Demeulemeester E, Cardoen B, Vansteenkiste N, Rademakers FE. Scheduling operating rooms: achievements, challenges and pitfalls. J Sched. 2016;19(5):493–525. doi: 10.1007/s10951-016-0489-6. [DOI] [Google Scholar]
- 81.Addis B, Carello G, Grosso A, Tànfani E. Operating room scheduling and rescheduling: a rolling horizon approach. Flexible Services and Manufacturing Journal. 2016;28(1–2):206–232. doi: 10.1007/s10696-015-9213-7. [DOI] [Google Scholar]
- 82.Kamran MA, Karimi B, Dellaert N. Uncertainty in advance scheduling problem in operating room planning. Comp Industrial Eng. 2018;126:252–268. doi: 10.1016/j.cie.2018.09.030. [DOI] [Google Scholar]
- 83.Leeftink G, Hans EW. Case mix classification and a benchmark set for surgery scheduling. J Sched. 2018;21(1):17–33. doi: 10.1007/s10951-017-0539-8. [DOI] [Google Scholar]
- 84.Batun S, Denton BT, Huschka TR, Schaefer AJ. Operating room pooling and parallel surgery processing under uncertainty. Info J Comp. 2011;23(2):220–237. doi: 10.1287/ijoc.1100.0396. [DOI] [Google Scholar]
- 85.Latorre-Núñez G, Lüer-Villagra A, Marianov V, Obreque C, Ramis F, Neriz L. Scheduling operating rooms with consideration of all resources, post anesthesia beds and emergency surgeries. Comp Industrial Eng. 2016;97:248–257. doi: 10.1016/j.cie.2016.05.016. [DOI] [Google Scholar]
- 86.Molina-Pariente JM, Hans EW, Framinan JM. A stochastic approach for solving the operating room scheduling problem. Flex Serv Manu J. 2018;30(1–2):224–251. doi: 10.1007/s10696-016-9250-x. [DOI] [Google Scholar]
- 87.Kroer LR, Foverskov K, Vilhelmsen C, Hansen AS, Larsen J. Planning and scheduling operating rooms for elective and emergency surgeries with uncertain duration. Oper Res Healthcare. 2018;19:107–119. [Google Scholar]
- 88.Xiang W. A multi-objective aco for operating room scheduling optimization. Nat Comp. 2017;16(4):607–617. doi: 10.1007/s11047-016-9607-9. [DOI] [Google Scholar]
- 89.Lee S, and Yih Y. Surgery scheduling of multiple operating rooms under uncertainty and resource constraints of post-anesthesia care units. In IIE Annual Conference. Proceedings, page 1. Institute of Industrial and Systems Engineers (IISE), 2012.
- 90.Ansarifar J, Tavakkoli-Moghaddam R, Akhavizadegan F, and Amin SH. Multi-objective integrated planning and scheduling model for operating rooms under uncertainty. Proceedings of the Institution of Mechanical Engineers, Part H: J Eng Med, 232(9):930–948, 2018. [DOI] [PubMed]
- 91.Akbarzadeh B, Moslehi G, Reisi-Nafchi M, Maenhout B. A diving heuristic for planning and scheduling surgical cases in the operating room department with nurse re-rostering. J Sched, pages 1–24, 2020.
- 92.Varmazyar M, Akhavan-Tabatabaei R, Salmasi N, Modarres M. Operating room scheduling problem under uncertainty: Application of continuous phase-type distributions. IISE Transactions. 2020;52(2):216–235. doi: 10.1080/24725854.2019.1628372. [DOI] [Google Scholar]
- 93.Akbarzadeh B, Moslehi G, Reisi-Nafchi M, Maenhout B. The re-planning and scheduling of surgical cases in the operating room department after block release time with resource rescheduling. Euro J Oper Res. 2019;278(2):596–614. doi: 10.1016/j.ejor.2019.04.037. [DOI] [Google Scholar]
- 94.Ali HH, Lamsali H, Othman SN. Operating rooms scheduling for elective surgeries in a hospital affected by war-related incidents. J Med Sys. 2019;43(5):139. doi: 10.1007/s10916-019-1263-z. [DOI] [PubMed] [Google Scholar]
- 95.D. Clavel, D. Botez, C. Mahulea, and J. Albareda. Software tool for operating room scheduling in a spanish hospital department. In 2018 22nd International Conference on System Theory, Control and Computing (ICSTCC), pages 413–420. IEEE, 2018.
- 96.Belkhamsa M, Jarboui B, Masmoudi M. Two metaheuristics for solving no-wait operating room surgery scheduling problem under various resource constraints. Comp Ind Eng. 2018;126:494–506. doi: 10.1016/j.cie.2018.10.017. [DOI] [Google Scholar]
- 97.Timuçin T, and Biroğul S. Effect the number of reservations on implementation of operating room scheduling with genetic algorithm. In The International Conference on Artificial Intelligence and Applied Mathematics in Engineering. 2019;252–265. Springer.
- 98.Khaniyev T, Kayiş E, Güllü R. Next-day operating room scheduling with uncertain surgery durations: Exact analysis and heuristics. Euro J Oper Res. 2020.
- 99.Lin TK, and Chou YY. A hybrid genetic algorithm for operating room scheduling. Health Care Management Science, pages 1–15, 2019. [DOI] [PubMed]
- 100.Timucin T, and Birogul S. Implementation of operating room scheduling with genetic algorithm and the importance of repair operator. In 2018 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), pages 1–6. IEEE, 2018.
- 101.Aringhieri R, Landa P, Soriano P, Tànfani E, Testi A. A two level metaheuristic for the operating room scheduling and assignment problem. Comp Oper Res. 2015;54:21–34. doi: 10.1016/j.cor.2014.08.014. [DOI] [Google Scholar]
- 102.L. I. Almaneea and M. I. Hosny. A two level hybrid bees algorithm for operating room scheduling problem. In Science and Information Conference, pages 272–290. Springer, 2018.
- 103.Mateus C, Marques I, Captivo ME. Local search heuristics for a surgical case assignment problem. Oper Res Healthcare. 2018;17:71–81. [Google Scholar]
- 104.Gul S, Denton BT, Fowler JW, Huschka T. Bi-criteria scheduling of surgical services for an outpatient procedure center. Prod Oper Manage. 2011;20(3):406–417. doi: 10.1111/j.1937-5956.2011.01232.x. [DOI] [Google Scholar]
- 105.Riise A, Mannino C, Burke EK. Modelling and solving generalised operational surgery scheduling problems. Comp Oper Res. 2016;66:1–11. doi: 10.1016/j.cor.2015.07.003. [DOI] [Google Scholar]
- 106.Bruni M, Beraldi P, Conforti D. A stochastic programming approach for operating theatre scheduling under uncertainty. IMA J Manage Math. 2015;26(1):99–119. doi: 10.1093/imaman/dpt027. [DOI] [Google Scholar]
- 107.Chaabane S, Meskens N, Guinet A, Laurent M. Comparison of two methods of operating theatre planning: application in belgian hospital. J Sys Sci Sys Eng. 2008;17(2):171–186. doi: 10.1007/s11518-008-5074-x. [DOI] [Google Scholar]
- 108.Denton BT, Miller AJ, Balasubramanian HJ, and Huschka TR. Optimal allocation of surgery blocks to operating rooms under uncertainty. Oper Res. 58(4-part-1):802–816, 2010.
- 109.Fei H, Chu C, Meskens N, Artiba A. Solving surgical cases assignment problem by a branch-and-price approach. Int J Prod Eco. 2008;112(1):96–108. doi: 10.1016/j.ijpe.2006.08.030. [DOI] [Google Scholar]
- 110.Fügener A, Hans EW, Kolisch R, Kortbeek N, Vanberkel PT. Master surgery scheduling with consideration of multiple downstream units. Euro J Oper Res. 2014;239(1):227–236. doi: 10.1016/j.ejor.2014.05.009. [DOI] [Google Scholar]
- 111.Hans E, Wullink G, Van Houdenhoven M, Kazemier G. Robust surgery loading. Euro J Oper Res. 2008;185(3):1038–1050. doi: 10.1016/j.ejor.2006.08.022. [DOI] [Google Scholar]
- 112.Herring WL, Herrmann JW. The single-day surgery scheduling problem: sequential decision-making and threshold-based heuristics. OR spectrum. 2012;34(2):429–459. doi: 10.1007/s00291-011-0270-3. [DOI] [Google Scholar]
- 113.Mannino C, Nilssen EJ, Nordlander TE. A pattern based, robust approach to cyclic master surgery scheduling. J Sched. 2012;15(5):553–563. doi: 10.1007/s10951-012-0275-z. [DOI] [Google Scholar]
- 114.Marques I, Captivo ME, Pato MV. An integer programming approach to elective surgery scheduling. OR spectrum. 2012;34(2):407–427. doi: 10.1007/s00291-011-0279-7. [DOI] [Google Scholar]
- 115.Min D, Yih Y. An elective surgery scheduling problem considering patient priority. Comp Oper Res. 2010;37(6):1091–1099. doi: 10.1016/j.cor.2009.09.016. [DOI] [Google Scholar]
- 116.Saremi A, Jula P, ElMekkawy T, Wang GG. Appointment scheduling of outpatient surgical services in a multistage operating room department. Int J Prod Eco. 2013;141(2):646–658. doi: 10.1016/j.ijpe.2012.10.004. [DOI] [Google Scholar]
- 117.Zhang Z, Xie X. Simulation-based optimization for surgery appointment scheduling of multiple operating rooms. IIE Transactions. 2015;47(9):998–1012. doi: 10.1080/0740817X.2014.999900. [DOI] [Google Scholar]
- 118.Bai M, Storer RH, Tonkay GL. A sample gradient-based algorithm for a multiple-or and pacu surgery scheduling problem. IISE Transactions. 2017;49(4):367–380. doi: 10.1080/0740817X.2016.1237061. [DOI] [Google Scholar]
- 119.Siqueira CL, Arruda EF, Bahiense L, Bahr GL, Motta GR. Long-term integrated surgery room optimization and recovery ward planning, with a case study in the brazilian national institute of traumatology and orthopedics (into) Euro J Oper Res. 2018;264(3):870–883. doi: 10.1016/j.ejor.2016.09.021. [DOI] [Google Scholar]
- 120.Di Martinelly C, Baptiste P, Maknoon M. An assessment of the integration of nurse timetable changes with operating room planning and scheduling. Int J Prod Res. 2014;52(24):7239–7250. doi: 10.1080/00207543.2014.916827. [DOI] [Google Scholar]
- 121.May JH, Spangler WE, Strum DP, Vargas LG. The surgical scheduling problem: Current research and future opportunities. Prod Oper Manage. 2011;20(3):392–405. doi: 10.1111/j.1937-5956.2011.01221.x. [DOI] [Google Scholar]
- 122.Molina-Pariente JM, Fernandez-Viagas V, Framinan JM. Integrated operating room planning and scheduling problem with assistant surgeon dependent surgery durations. Comp Industrial Eng. 2015;82:8–20. doi: 10.1016/j.cie.2015.01.006. [DOI] [Google Scholar]
- 123.Bruni R, Detti P. A flexible discrete optimization approach to the physician scheduling problem. Oper Res Healthcare. 2014;3(4):191–199. [Google Scholar]
- 124.M. Gendreau, J. Ferland, B. Gendron, N. Hail, B. Jaumard, S. Lapierre, G. Pesant, and P. Soriano. Physician scheduling in emergency rooms. In International Conference on the Practice and Theory of Automated Timetabling, pages 53–66. Springer, 2006.
- 125.Gunawan A, Lau HC. Master physician scheduling problem. J Oper Res Soc. 2013;64(3):410–425. doi: 10.1057/jors.2012.48. [DOI] [Google Scholar]
- 126.Demirbilek M, Branke J, Strauss A. Dynamically accepting and scheduling patients for home healthcare. Health care management science. 2019;22(1):140–155. doi: 10.1007/s10729-017-9428-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Demirbilek M, Branke J, and Strauss AK. Home healthcare routing and scheduling of multiple nurses in a dynamic environment. Flex Services Manu J. 2019;1–28.
- 128.Restrepo MI, Rousseau LM, and Vallée J. Home healthcare integrated staffing and scheduling. Omega. 2019;102057.
- 129.Erdogan SA, Krupski TL, Lobo JM. Optimization of telemedicine appointments in rural areas. Service Science. 2018;10(3):261–276. doi: 10.1287/serv.2018.0222. [DOI] [Google Scholar]
- 130.Gross CN, Fügener A, and Brunner JO. Online rescheduling of physicians in hospitals. Flex Services Manu J. 2017;1–33.
- 131.Smalley HK, Keskinocak P, Vats A. Physician scheduling for continuity: an application in pediatric intensive care. Interfaces. 2015;45(2):133–148. doi: 10.1287/inte.2014.0774. [DOI] [Google Scholar]
- 132.António Ferreira Rodrigues Nogueira dos Santos M, and Kurt Olof Eriksson H. Insights into physician scheduling: a case study of public hospital departments in sweden. International journal of health care quality assurance. 2014;27(2):76–90. [DOI] [PubMed]
- 133.Damcı-Kurt P, Zhang M, Marentay B, Govind N. Improving physician schedules by leveraging equalization: Cases from hospitals in us. Omega. 2018.
- 134.Gharbi A, Louly M, and Azaiez M. Physician scheduling using goal programming-an application to a large hospital in saudi arabia. In Control, Decision and Information Technologies (CoDIT), 2017 4th International Conference on. 2017;0922–0925. IEEE.
- 135.Fikar C, Hirsch P. Home health care routing and scheduling: A review. Comp Oper Res. 2017;77:86–95. doi: 10.1016/j.cor.2016.07.019. [DOI] [Google Scholar]
- 136.Allaoua H, Borne S, Létocart L, Calvo RW. A matheuristic approach for solving a home health care problem. Electronic Notes in Discrete Mathematics. 2013;41:471–478. doi: 10.1016/j.endm.2013.05.127. [DOI] [Google Scholar]
- 137.Bennett AR, Erera AL. Dynamic periodic fixed appointment scheduling for home health. IIE Trans Healthcare Sys Eng. 2011;1(1):6–19. doi: 10.1080/19488300.2010.549818. [DOI] [Google Scholar]