Abstract.
Purpose: Sharing medical images between institutions, or even inside the same institution, is restricted by various laws and regulations; research projects requiring large datasets may suffer as a result. These limitations might be addressed by an abundant supply of synthetic data that (1) are representative (i.e., the synthetic data could produce comparable research results as the original data) and (2) do not closely resemble the original images (i.e., patient privacy is protected). We introduce a framework that generates data with these requirements leveraging generative adversarial network (GAN) ensembles in a controlled fashion.
Approach: To this end, an adaptive ensemble scaling strategy with the objective of representativeness is defined. A sampled Fréchet distance-based constraint was then created to eliminate poorly converged candidates. Finally, a mutual information-based validation metric was embedded into the framework to confirm there are visual differences between the original and the generated synthetic images.
Results: The applicability of the solution is demonstrated with a case study for generating three-dimensional brain metastasis (BM) from T1-weighted contrast-enhanced MRI studies. A previously published BM detection system was reported to produce 9.12 false-positives at 90% detection sensitivity based on the original data. By using the synthetic data generated with the proposed framework, the system produced 9.53 false-positives at the same sensitivity level.
Conclusions: Achieving comparable algorithm performance relying solely on synthetic data unveils a significant potential to eliminate/reduce patient privacy concerns when sharing data in medical imaging.
Keywords: synthetic data generators, sharable medical imaging data, ensemble learning, generative adversarial networks
1. Introduction
Neural networks with deeper (i.e., with higher numbers of layers) and progressively more sophisticated architectures revolutionized the field of computer vision over the last decade.1 These mathematical models, also referred to as deep neural networks (DNNs), were utilized for various medical imaging applications including segmentation/extraction of regions of interests, object/lesion detection, and classification tasks.2,3 As DNNs are highly parametric (i.e., requiring a vast amount of parameters to be optimized), the accuracy and generalizability of the developed models heavily depend on the scale of the dataset.4 However, sharing medical data is difficult due to several laws and regulations designed to protect patient privacy.5 While there are multiple successful initiatives for aggregating multi-institutional datasets,6–8 public availability of large-scale datasets focused on specific modalities and medical conditions is limited.9
One way to partially address the data deficiency problem is to augment the available data with synthetic ones based on originals. Generative adversarial networks (GANs),10 which exploit adversarial loss functions to generate realistic synthetic data,11 have been utilized for the augmentation purposes in medical imaging.12–16 However, as reported by Bowles et al.,13 GAN-generated data are commonly not representative enough to replace the original data; thus, they were used as a complementary tool to maximize the gain from the original data by smoothing the information domain with more samples. Furthermore, GANs have the potential to generate synthetic images that are identical with or closely resemble the original images,17,18 potentially resulting in patient privacy concerns.
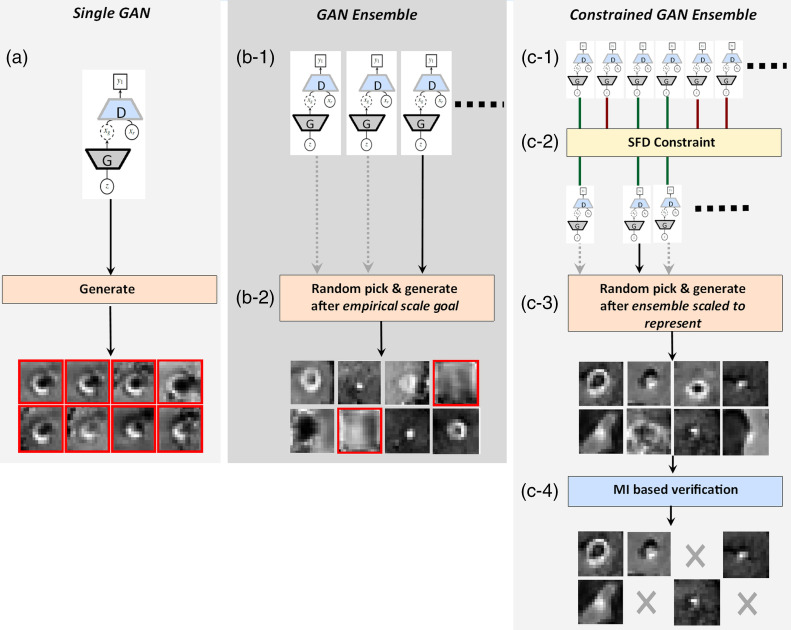
The goal of this paper is to introduce a framework to generate synthetic data that are (1) representative (the synthetic data could produce comparable research results as the original data) and (2) do not closely resemble the original images; thus, sharable. Accordingly, the ensemble of GANs approach,19 having the premise of improving the generalizability of GANs, is further advanced with the aforementioned aspects. To this end, an adaptive ensemble scaling strategy is first defined with the goal of ensuring representativeness of the synthetic images. The appropriate growth of an ensemble depends on its member-performances; hence, a sampled Fréchet distance (SFD) metric is introduced to eliminate poorly converged candidates during the ensemble growth-process. Finally, a mutual information (MI)-based verification stage is embedded into the framework to ensure the generated data do not include samples that are either identical to or closely resembling the originals. In an ideal deployment scenario, multiple institutions would generate synthetic datasets with the presented approach then share it with other institutions; this would enable research projects to be performed with vast synthetic datasets vetted to represent their originals. The applications of GAN, GAN ensemble, and the introduced constrained GAN ensemble in medical image synthesis are shown in Fig. 1.
Fig. 1.
(a) GAN, (b) GAN ensemble, and (c) constrained GAN ensemble for medical image synthesis.
This report first describes the framework for forming a constrained GAN ensemble. Then, it represents the applicability of the proposed methodology via a case study: synthesizing 3D brain metastatic region data for T1-weighted contrast-enhanced MRI studies. In the given application, 3D regions of interest containing cerebral metastases were generated using the introduced constrained GAN ensemble framework. Then, the generated synthetic data were used for training a previously published brain metastasis (BM) detection system.20 Section 3.3 compares the accuracies of the system trained with the synthetic and original data. The report concludes with a discussion of the results, system limitations, and future work considerations.
2. Material and Methods
2.1. Standard GAN and the GAN Ensemble
The GAN is a generative machine learning model used in various applications of computer vision including image synthesis.21 A typical GAN is formulated with two neural networks (i.e., generator and discriminator) that are optimized in tandem for a minimax problem:
| (1) |
where (1) and are the discriminator and synthetic data generation models, (2) is the unknown probability distribution function (PDF) for the real data, and (3) is the PDF for the generator’s noise type input (typically uniform or Gaussian). Over the recent years, various GAN formulations modifying the network architectures and/or loss functions were proposed,22 whereas depending on the target data type and problem domain, some formulations were shown to be more applicable than the others.23
One of the most common problems in GANs is the limited generalizability of their solutions, emerging from the limited representation of information. State-of-the-art GAN formulations such as those in Refs. 24–26, and multiple hypothesis-based techniques (utilizing parts or all of GAN architecture) including the ensembles,19,27 generator-mixture,28 and multiagents,29 were proposed to tackle/reduce the problem. While our solution is agnostic and leaves the selection of the GAN type as a design choice of the researcher, it introduces an ensemble growth strategy to provide representative synthetic datasets.
The ensemble of GANs is an algorithm, where multiple GAN models (regardless of the GAN formulation) are trained using a single training dataset, then the synthetic data are generated via a randomly picked ensemble member for each synthetic data request.19,30 It was shown that the ensemble of GANs outperforms a single GAN with respect to the information coverage, computed using Wilcoxon signed-rank test,31 and a manifold projection distance metric.19 The results outline the common traits of ensembles; (1) the avoidance of overfitting due to multiple hypotheses covered by its components, (2) reduced chance of stagnating at local optima as each component runs its optimization process individually, and (3) improved representation of the optimal hypothesis since the combination of different models commonly expands the solution search space.32,33 The approach was further customized by (1) integrating ensemble members with similar network initializations to speed up the training process (self-ensemble of GANs) and (2) using discriminator feedbacks to detect/improve GANs with limited information coverage (cascade of GANs).19
2.2. Technical Contributions: Objective Oriented Ensemble Formulation
2.2.1. Ensemble growth strategy
The commonly used optimization goals for the generative algorithms, such as (1) minimizing information divergence from the original data34 (e.g., computed via Jensen–Shannon, Kullback–Leibler), (2) generating subjectively highly realistic outputs (e.g., visual Turing test35), or (3) information coverage optimization (e.g., Wilcoxon signed-rank test), do not necessarily lead to the generation of researchwise representative data:13 The representativeness in this context is the ability to produce comparable research results using the synthetic data as with the original data. The complex metric of representativeness would require the execution of a complete validation study with an external algorithm for a new set of data at each optimization step; thus, it is not part of any generative approach, including the ensemble of GANs. In this study, we propose an adaptive growth strategy for GAN ensembles to address this objective by introducing an additional computational overhead as:
– The baseline performance using an algorithm executed on the original data is defined as
| (2) |
where (1) is the algorithm, referred to as the validation model (e.g., cardiac segmentation, liver tumor detection, etc.), (2) is the original data set, (3) is the evaluation methodology [e.g., -fold cross-validation (CV), bootstrapping, etc.], and (4) is the baseline performance value (e.g., Dice score, the area under the receiver operating characteristic curve, etc.).
– Temporary ensemble performance is described as
| (3) |
| (4) |
where (1) is the temporary ensemble performance, (2) is the data set generated by the ensemble’s ’th iteration with the same size as the original data, and (3) each data in is generated by a random member of called ; receiving noise type input .
– The growth of the ensemble can be halted when the ensemble performance becomes comparable with the baseline performance; , where gives the acceptable performance gap threshold. Divergence of the performance with the growth of the ensemble might indicate (1) improper GAN formulation selection or its parametrization and/or (2) inadequate original training data; therefore, they need to be reconsidered.
2.2.2. Ensemble member constraint
While the proposed ensemble growth strategy is intuitive, it causes a significant computational overhead due to the iterative calculation of the temporary ensemble performance. The issue could be partially addressed by computing the performance metric periodically (e.g., after every 10 additional GAN members) instead of each iteration. However, the number of iterations could still be high, depending on the individual performances of ensemble members:33 Diverged or mode-collapsed members would fail to produce plausible synthetic samples making the ensemble overgrown and inefficient.
The Fréchet inception distance (FID)36 was introduced for evaluating a GAN performance; the Fréchet distance between the original and synthetic data’s lower-dimensional manifold representations extracted from the Inception model37 is used for model assessment. The FID allows the robust detection of mode-collapsed and diverged GAN models.38 However, as the Inception network is trained for two-dimensional (2D) color images of random scenes in ImageNet,39 the metric cannot be used for the evaluation of models that produce any-dimensional (e.g., 3D, 3D+T, etc.) medical imaging data. Accordingly, we propose an SFD that is mostly identical with the FID whereas differing with respect to its inputs as
| (5) |
where (1) and give original and generated data’s sampled mean and covariance tuples, respectively, and (2) Re gives the real components of its input. Unlike the FID (which uses lower-dimensional representation extracted from a pretrained Inception model), the metric uses the flattened vector representations for the downsampled original and synthetic data with the assumption of these having multivariate Gaussian distributions. Hence, it can be used for evaluating any generative model by verifying , with giving the maximum allowed SFD between synthetic and original samples.
2.2.3. Visual resemblance test
The shared synthetic data are strictly forbidden to be identical with the original data for protecting the patients’ privacy. Therefore, each synthetic data sample needs to be compared with the original data set. While voxelwise image comparison (e.g., mean square difference, etc.) might be adequate to eliminate synthetic samples having high visual similarity with the originals, it would not necessarily detect statistically dependent samples (e.g., intensity inversed version of an image, etc.). Thus, we propose a MI-based metric defined for each synthetic sample as:
| (6) |
where (1) is the number of original training samples (i.e., ), (2) is the synthetic sample, (3) is the ’th original sample, (4) is the geometrically transformed synthetic sample (i.e., translation, rotation), (4) is the Shannon entropy of the synthetic sample, and (5) is the conditional entropy. Accordingly, gives the maximum MI between the synthetic sample and all real samples, and is the maximum acceptable MI; a synthetic sample with is not shared due to its high similarity with an original sample(s). This stage may also be described as finding an optimal (i.e., based on MI) rigid transformation between the synthetic sample and all real samples, then eliminating the synthetic one if it returns a high MI.
2.2.4. Framework
The described ensemble growth strategy, member constrain, and visual resemblance test can be integrated into a framework for the synthetic data generation:
-
1.
The baseline performance () is computed using a validation model () on the original data set ().
-
2.
A proper GAN formulation is chosen for the target data type. The ensemble is grown with the selected type of GANs to produce synthetic samples having SFD with the originals less than a threshold ().
-
3.
Step 2 is repeated iteratively until the baseline performance metric is achieved with an acceptable performance gap () using the ensemble generated data. If the temporary performance diverges, then the GAN type and are reconsidered.
-
4.
The matured ensemble’s output is validated using the visual resemblance test; the synthetic samples having low MI () with the original data set are shared.
3. Case Study: 3D Brain Metastasis Data Generation
3.1. Problem Definition
The BMs are the most common form of brain cancer, where 20% to 40% of cancer cases have this complication. The metastatic lesions can vary significantly in size and appearance; early forms of the disease present as punctate foci measuring as small as 1 mm in diameter. In Ref. 20, the authors have proposed an approach for the detection of particularly small BMs, with diameters of , for the gadolinium-enhanced T1-weighted 3D MRI. Briefly, the method first determines all BM candidates using an information-theory-based algorithm. Next, the candidates are processed using a parametrized deep-neural-network formulation (CropNet) to give the final BM detections; the CropNet learns the statistical representation of a BM from isometric metastatic region volumes with 16-mm edge length and differentiates it from any other similar size volumetric region extracted from the brain image. The approach was validated using fivefold-CV on 217 datasets acquired from 158 patients including 932 BMs in total. It was reported to produce 9.12 average number of false-positive BMs for 90% detection sensitivity. An interested reader is referred to Ref. 20 for detailed information on (1) the algorithm, (2) data collection and scanner parameters, and (3) dimensional histograms of BMs used in that study.
In the detection study, while negative samples were abundant (random volumetric extractions from brain images), BM regions were limited (932 3D volumes with 16 mm edges). Accordingly, the purpose of this case study is to generate synthetic BM regions using the constrained GAN ensemble framework. The ensemble growth objective is set as the detection system trained with the synthetic samples produces a comparable number of false-positives for the given sensitivity level using the same dataset used in Ref. 20:
| (7) |
3.2. Framework Setup and Parameters
3.2.1. GAN setup
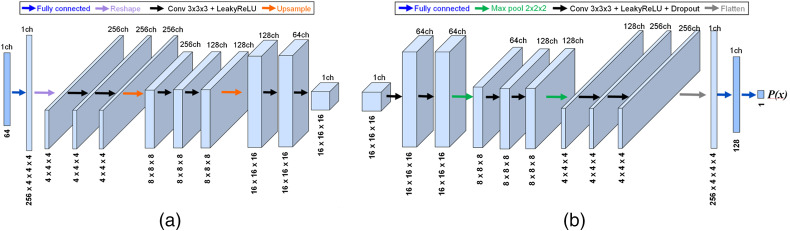
In this case study, deep convolutional GANs (DCGANs)40 were utilized as the ensemble members for generating 3D brain metastatic regions segmented from T1-weighted contrast-enhanced MRI. The formulation was chosen as it has been successfully deployed for medical image synthesis in numerous previous studies.12,15,41,42 The DCGAN was originally designed for 2D images; hence, we adapted it for 3D by (1) modifying the generator to produce volumes that represent cropped BM regions, and (2) modifying the discriminator to classify volumetric input type. The implemented DCGAN architecture is shown in Fig. 2, and some examples for the real and DCGAN generated synthetic BM samples are shown in Fig. 3. All ensemble members are proposed to have the same network architecture.
Fig. 2.
(a) The generator and (b) discriminator networks of the used 3D DCGAN.
Fig. 3.
Mosaic of mid-axial slices of (a) real and (b) DCGAN generated synthetic BM region volumes.
3.2.2. Data preprocessing
All datasets were resampled to have isotropic () voxels. The voxel values were normalized to [0, 1] range, where the maximum and minimum intensity voxels for each dataset had the normalized values of 1 and 0, respectively.
3.2.3. Parameters
The DCGAN type ensemble member candidates were trained where (1) binary-cross entropy type loss was used for the discriminator and generator networks (as in Ref. 40), (2) Adam algorithm43 was used for the network optimization, (3) learning rates for the discriminator and generator networks were set as 0.00005 and 0.0003, respectively, (4) the dropout rate of the discriminator network was 0.15, (5) leaky ReLU units’ alpha values were 0.1 for both of the networks, and (6) 1500 training epochs were executed with batches each consisting of eight pairs of positive and negative samples.
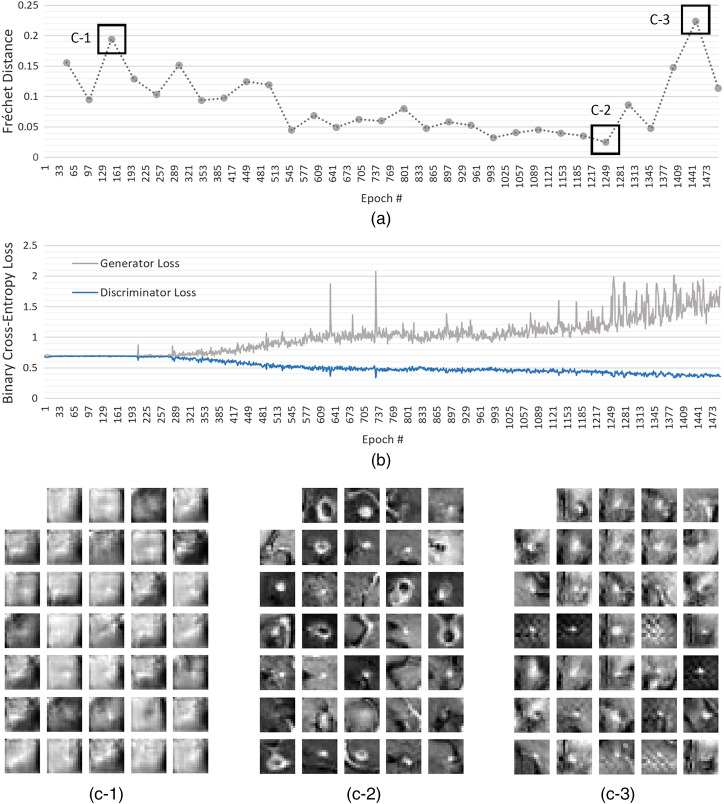
For a given member candidate, to compute the mean and covariance estimates of its synthetic data , 2000 synthetic samples were generated by its generator in every 50 epochs of the training, whereas the real data statistics were computed using the original data prior to the training. The member candidates that generated synthetic data having SFD of less than were added into the ensemble (see Fig. 4).
Fig. 4.
SFD for the DCGAN validation.
The acceptable performance criteria for the BM detection algorithm, trained using the synthetic data generated by the ensemble, was set as 10.12 false positives at 90% BM-detection sensitivity: acceptable performance gap () was an additional false-positive with respect to the baseline performance .
Identification of a patient based on a BM region volume is not likely as the area spans a very limited area. However, to have a glance of the visual resemblance test, the generated sharable samples were allowed to have MI with the original data less than , where the transformation domain kept empty due to the simplicity of the target data.
3.3. Results
3.3.1. Validation study
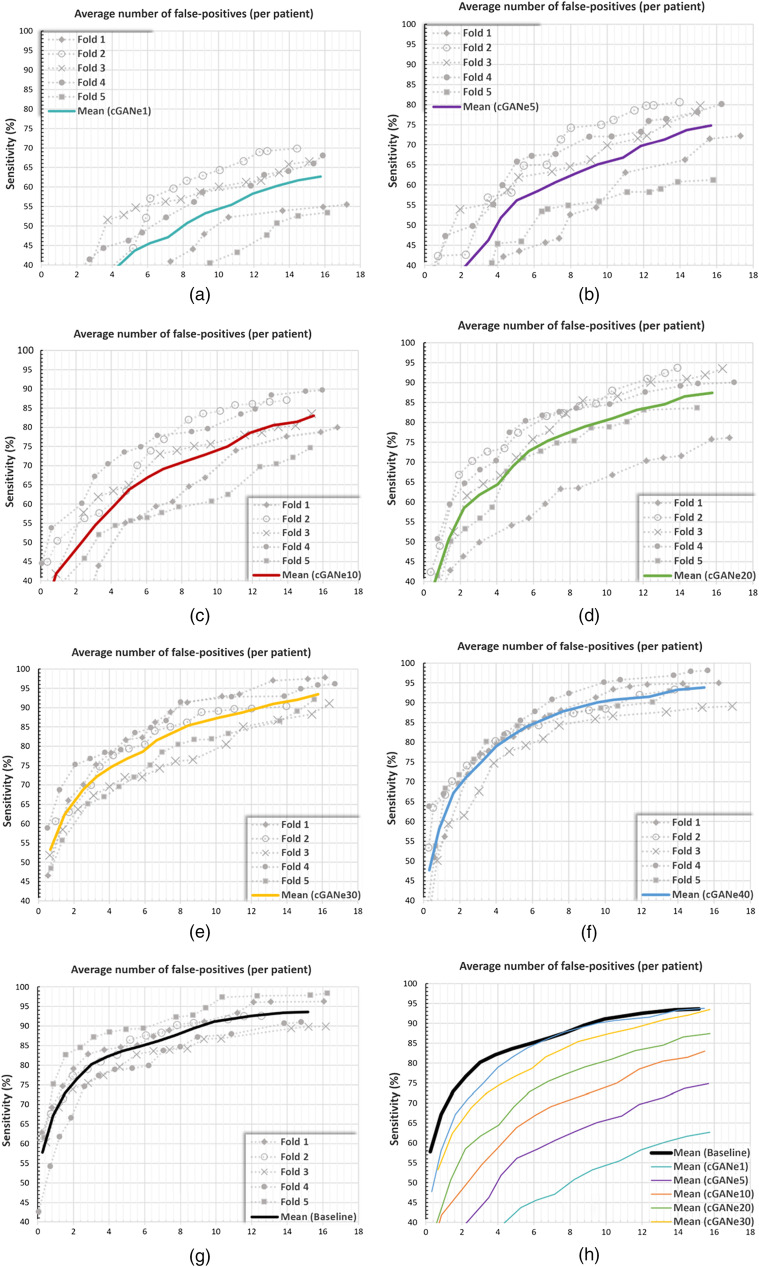
The performance of the BM detection algorithm using the synthetic data, generated by the proposed framework, was validated using a fivefold CV: 217 datasets acquired from 158 patients were patientwise divided into fivefolds of 31, 31, 32, 32, and 32 patients, respectively. For each fold, (1) the other four folds were used for generating the constrained GAN ensemble (cGANe), (2) synthetic data produced by the ensemble was used for training the BM detection algorithm, and (3) and the original data in the selected fold were used for the testing. The average number of false positives (AFP) with respect to the system’s detection sensitivity is represented for the ensembles containing 1, 5, 10, 20, 30, and 40 DCGAN models (i.e., cGANe1, cGANe5, cGANe10, cGANe20, cGANe30, and cGANe40) in Fig. 5. The information is summarized for the 75%, 80%, 85%, and 90% detection sensitivities in Table 1.
Fig. 5.
AFP in relation to the detection sensitivity for the (a) cGANe1, (b) cGANe5, (c) cGANe10, (d) cGANe20, (e) cGANe30, (f) cGANe40, and (g) baseline. (h) The average curves for the baseline and cGANe setups.
Table 1.
AFP versus sensitivity.
| Sensitivity (%) | Baseline | cGANe1 | cGANe5 | cGANe10 | cGANe20 | cGANe30 | cGANe40 |
|---|---|---|---|---|---|---|---|
| 75 | 1.90 | — | 16.02 | 10.60 | 6.62 | 4.26 | 3.19 |
| 80 | 2.96 | — | — | 12.82 | 9.56 | 6.24 | 4.32 |
| 85 | 5.85 | — | — | — | 13.42 | 8.26 | 6.22 |
| 90 | 9.12 | — | — | — | — | 12.47 | 9.53 |
The visual resemblance test eliminated 5.7% of the 2000 synthetic samples. In Fig. 6, some examples for these eliminated synthetic images and the corresponding original images are shown.
Fig. 6.
(a) Mid-axial slices of some originals and synthetic samples that were eliminated due to high resemblance to those (b).
The proposed solution was implemented using the Python programming language (v3.6.8). The neural network implementations were performed using Keras library (v2.1.6-tf) with TensorFlow (v1.12.0) backend. The training of each DCGAN was done in , where a DCGAN satisfying the SFD constraint was generated in on average. Thus, growing a given cGANe with 10 additional DCGANs took on average. The training of the validation model for each fold took . The network training was performed using four parallel processing NVIDIA 1080ti graphics cards, having 11 GB RAM each.
3.3.2. Ablation study: unconstrained ensembles
To quantify the impact SFD-based ensemble growth constraint, we performed the validation study for ensembles that grew without it (GANe); each newly trained DCGAN was added into the ensemble without verifying their output’s statistical distribution via SFD. The summary for the results of this experiment is provided in Table 2.
Table 2.
AFP versus sensitivity for unconstrained ensembles.
| Sensitivity (%) | Baseline | GANe1 | GANe5 | GANe10 | GANe20 | GANe30 | GANe40 |
|---|---|---|---|---|---|---|---|
| 75 | 1.90 | — | — | — | 14.16 | 8.97 | 8.04 |
| 80 | 2.96 | — | — | — | — | 10.22 | 9.45 |
| 85 | 5.85 | — | — | — | — | 13.81 | 11.66 |
| 90 | 9.12 | — | — | — | — | — | 16.03 |
3.3.3. Visualizing the ensemble information coverage
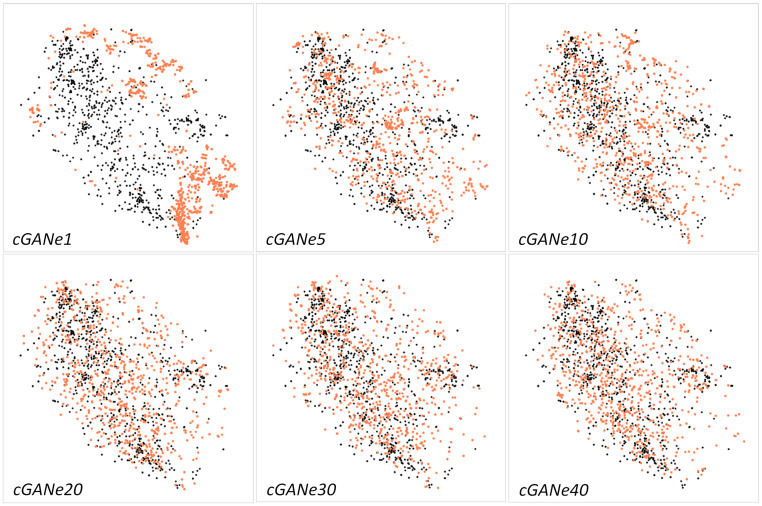
As described previously, a potential problem with the usage of a single GAN is the partial representation of the real data PDF. The issue and the validity of our solution was further illustrated by performing a low dimensional data embedding analysis (see Fig. 7). The real data (i.e., all 932 BMs) and the matching number of cGANe generated synthetic samples were visualized via 2D embeddings, generated by (1) reducing the flattened 4096-dimensional volumetric data into 80-dimensional data using principal component analysis,44 explaining of the data variance, and (2) embedding these 80-dimensional representations into 2D using -distributed stochastic neighbor embedding (t-SNE).45 (The mapping of very high dimensional data into highly representative lower-dimensional data prior to t-SNE was suggested in Ref. 45.) As shown in the cGANe1 plot, the usage of a single constrained DCGAN caused the lower-dimensional mappings to accumulate in regions that do not align well with the original data. As DCGANs (among various other GAN formulations) are susceptible to full or partial mode-collapse,46 this was an expected outcome. The misrepresentation declined with the cGANe scale, where the cGAN () plots have better real and synthetic data mixtures; explaining the improved validation model performances of cGANe settings with higher numbers of components.
Fig. 7.
t-SNE representations for real (black) and cGANe generated (orange) data samples.
3.3.4. Data scale and computational cost relationship
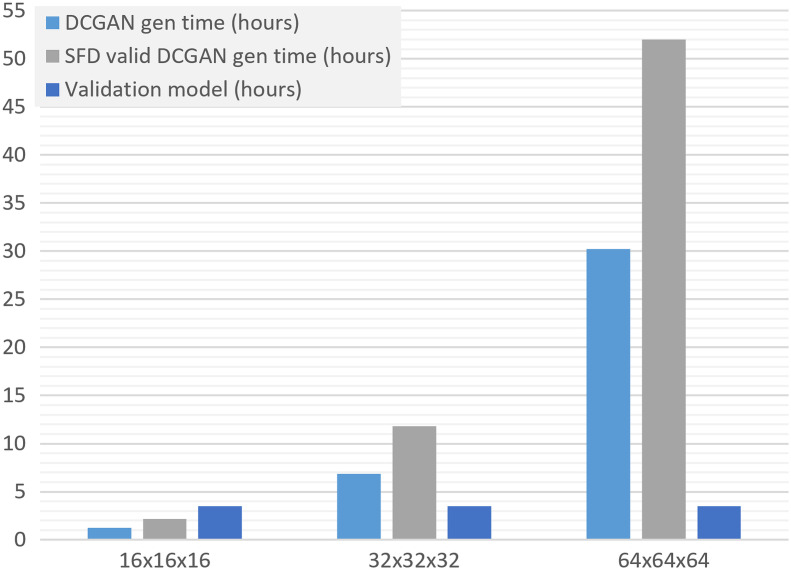
The computational cost of the introduced framework depends on various factors, including the GAN type, validation model, and convergence of an ensemble. We performed a hypothetical study to estimate the relationship between the target image resolution and the cGANe computation time: (1) DCGAN training times for and volumes were computed by upscaling the network shown in Fig. 2 with the same contraction/expansion strategy and using the upscaled version of the original data, and (2) SFD constraint satisfaction rate and validation model computation times were assumed to be constant values inferred from the original study (see Fig. 8). Based on these, we expect that the training time for a cGANe ensemble with 10 members is for volumes, and it is for volumes, respectively (using the same hardware specified in the Sec. 3.3.1). Note that for these higher image resolutions, DCGAN might lead to imaging artifacts and lower sample variety47 (causing larger-scale ensembles); hence, a different GAN formulation might be preferable.
Fig. 8.
Estimated DCGAN, SFD valid DCGAN, and validation model generation times for different resolutions.
4. Discussion and Conclusion
The validation study showed that the synthetic data generated by a constrained ensemble of 40 DCGANs (cGANe40) can be used for training a BM-detection model successfully. The model trained using the dataset generated by cGANe40 produced 9.53 false-positives for 90% detection sensitivity. The result is comparable with the 9.12 false-positives for the same sensitivity level produced using the original data for the model training (see Fig. 5 and Table 1). Accordingly, the ensemble can be utilized for producing positive synthetic data samples for client sites intending to (1) reproduce the results with the same BM-detection model or (2) use it for performing another research with this specific data type (i.e., volumetric BM region data for T1-weighted contrast-enhanced MRI examinations).
The ablation study was performed to present the impact of SFD-based ensemble member constraint on final performance. As shown in Table 2, the elimination of this constraint led to a BM-detection performance that is significantly worse than the original performance; using the data produced by an unconstrained ensemble with 40 members (GANe40) caused false-positives for 90% detection sensitivity.
The visual resemblance test was shown to eliminate synthetic samples (see Fig. 6) that closely resemble the originals. However, the technique needs to be further validated in a future study for modalities in which the patient could be identified from the medical images (i.e., full head CT). This might also require the geometric transformation component of Eq. (6) (i.e., ) to be adapted for nonrigid transformations. The visual resemblance test may also be reformulated to utilize (1) image feature-based comparisons (i.e., computed via volumetric interest point detectors48) or (2) a dedicated image similarity detection DNN such as Siamese networks.49 A future study may investigate the integration of these alternative approaches into the given framework and provide comparative analyses.
The visualization of the low dimensional data embeddings provided a glimpse of enhanced information mode coverage with the ensemble scaling, whereas the study primarily focused on the representativeness of the synthetic data concerning the reproduction of research results. The representativeness is correlated with the coverage of parts of the information domain in this context [e.g., synthetic data for BM should contain visually correct tumor(s), while the visual correctness of surroundings may be less critical for a validation model to perform]. We aim to analytically quantify the relationship between representatives and information-coverage in a future study: various GAN formulations with the objective of information coverage (such as Refs. 24 and 26) could be introduced into the framework, then the convergence rate for different parametrizations could be visualized for a selected medical imaging study.
The framework currently holds various parameters (e.g., the GAN type, acceptable performance gap, visual resemblance test threshold, etc.), which were set empirically for the given case study. Future studies might benefit from the provided values as a starting point; yet, they need to be determined for each synthetic data generation application.
As mentioned previously, GANs were used for data augmentation purposes in various medical imaging applications.12–16 The introduced approach may also be suitable for the data augmentation tasks since it produces synthetic samples that are validated for their representativeness. As an application example, the BM detection framework could be reformulated to use cGANe produced-samples in addition to original data during its training stage; hence, replacing its original data augmentation pipeline (consisting of random elastic deformation, gamma correction, flip and rotation operations20) with the cGANe. Accordingly, we aim to investigate the data augmentation aspects of cGANe approach in a future study.
The major limitation of the introduced framework is its computational efficiency. For the given case study, a constrained ensemble grew with 10 additional members in ; hence, the cGANe40 computation took (for a single fold). After the completion of the constrained ensemble, the synthetic data then can be generated in magnitudes of thousands in a few seconds (i.e., 2000 synthetic volumes are generated in ). We also performed a hypothetical study to estimate the computation times for higher scale models (Sec. 3.3.4). Different framework setups (i.e., with different GAN formulation, validation model, etc.) are associated with very different computational timeframes and needs.
The study introduced the constrained ensemble of GANs, formulated to generate synthetic datasets that are research worthy and do not contain samples closely resembling the original data, aiming to make them sharable. The solution provided technical novelties including the (1) objective oriented ensemble growth strategy, (2) SFD constraint for ensemble members, and (3) visual resemblance metric. The case study presented the applicability of the proposed solution by generating BM region volumes, where replacing the original data with the synthetic ones during the model training led to acceptable performance during the model testing.
Medical image processing has evolved over the last decade in the direction of being heavily data-driven.3 Accordingly, the amount of data utilized during the development is a determining factor for the performances of deployed models. However, the sharing of medical data between the institutions, and even between the departments of the same institution, is limited due to regulations and laws. The paper presented a framework to address this issue via synthetic medical data, vetted to enable reproducible research results and ensure patient privacy. A redundant supply of such synthetic medical datasets, produced for a variety of modalities and medical conditions, could potentially foster more collaboration among organizations and expedite scientific discoveries in this field.
Biographies
Engin Dikici is a research scientist in the Laboratory for Augmented Intelligence in Imaging of the Department of Radiology in the Ohio State University (OSU) College of Medicine. He received his MSc degree from the Computer and Information Science Department at the University of Pennsylvania in 2006 and his PhD in biomedical engineering from the College of Medicine of Norwegian University of Science and Technology in 2012. His research interests include segmentation, registration, real-time tracking, and synthesis of medical images.
Matthew Bigelow is a data analytics consultant for the Department of Radiology in the OSU College of Medicine. He received his BS and MBA degrees from OSU in 2012 and 2019, respectively. He has clinical background as an imaging technologist in nuclear medicine, computed tomography, and imaging informatics. He currently runs business intelligence operations for the department and is the data curator for the AI Lab.
Richard D. White is medical director for the Program for Augmented Intelligence in Imaging at Mayo Clinic–Florida from 2020 to present. He previously held radiology chairmanships at OSU (from 2010 to 2020) and University of Florida–Jacksonville (from 2006 to 2010); these followed Cleveland Clinic cardiovascular-imaging leadership from 1989 to 2006. He received his MD in 1981 and held a Sarnoff Foundation fellowship at Duke University from 1981 to 1982. At the University of California, San Francisco, he completed his residency with ABR-certification, 1982 to 1986, and cardiovascular-imaging fellowship, 1985 to 1987. Post-training, he had cardiovascular-imaging leaderships at Georgetown University from 1987 to 1988 and Case Western Reserve University from 1988 to 1989. He recently refocused toward imaging informatics with an MS in Health Informatics from Northwestern University, 2016 to 2018.
Barbaros S. Erdal is the technical director of Center for Augmented Intelligence in Imaging, Mayo Clinic, Florida. He received his PhD in electrical and computer engineering from Ohio State University in 2012. He then joined the OSU College of Medicine, Department of Radiology (associate professor), where he also served as the assistant chief, Division of Medical Imaging Informatics, and the director for Scholarly Activities from 2012 to 2020. He joined the Mayo Clinic in June 2020.
Luciano M. Prevedello, MD, MPH (associate professor of radiology) is vice-chair for Medical Informatics and Augmented Intelligence in Imaging at the Ohio State University. He is board certified in radiology, neuroradiology, and clinical informatics. He is a member of the Machine Learning Steering Committee at the Radiological Society of North America and is an associate editor of the journal Radiology: Artificial Intelligence.
Disclosures
No conflicts of interests, financial or otherwise, are declared by the authors.
Contributor Information
Engin Dikici, Email: engin.dikici@osumc.edu.
Matthew Bigelow, Email: matthew.bigelow@osumc.edu.
Richard D. White, Email: white.richard1@mayo.edu.
Barbaros S. Erdal, Email: erdal.barbaros@mayo.edu.
Luciano M. Prevedello, Email: luciano.prevedello@osumc.edu.
References
- 1.Liu W., et al. , “A survey of deep neural network architectures and their applications,” Neurocomputing 234, 11–26 (2017). 10.1016/j.neucom.2016.12.038 [DOI] [Google Scholar]
- 2.Litjens G., et al. , “A survey on deep learning in medical image analysis,” Med. Image Anal. 42, 60–88 (2017). 10.1016/j.media.2017.07.005 [DOI] [PubMed] [Google Scholar]
- 3.Shen D., Wu G., Suk H.-I., “Deep learning in medical image analysis,” Annu. Rev. Biomed. Eng. 19, 221–248 (2017). 10.1146/annurev-bioeng-071516-044442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sze V., et al. , “Efficient processing of deep neural networks: a tutorial and survey,” Proc. IEEE 105(12), 2295–2329 (2017). 10.1109/JPROC.2017.2761740 [DOI] [Google Scholar]
- 5.Nass S., Levit L., Gostin L., Beyond the HIPAA Privacy Rule: Enhancing Privacy, Improving Health Through Research, The National Academies Press, Washington, DC: (2009). [PubMed] [Google Scholar]
- 6.Petersen R. C., et al. , “Alzheimer’s disease neuroimaging initiative (ADNI): clinical characterization,” Neurology 74(3), 201–209 (2010). 10.1212/WNL.0b013e3181cb3e25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Oakden-Rayner L., “Exploring large-scale public medical image datasets,” Acad. Radiol. 27(1), 106–112 (2019). 10.1016/j.acra.2019.10.006 [DOI] [PubMed] [Google Scholar]
- 8.Clark K., et al. , “The Cancer Imaging Archive (TCIA): maintaining and operating a public information repository,” J. Digital Imaging 26(6), 1045–1057 (2013). 10.1007/s10278-013-9622-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dluhos P., et al. , “Multi-center machine learning in imaging psychiatry: a meta-model approach,” Neuroimage 155, 10–24 (2017). 10.1016/j.neuroimage.2017.03.027 [DOI] [PubMed] [Google Scholar]
- 10.Goodfellow I., et al. , “Generative adversarial networks,” in Adv. Neural Inf. Process. Syst., Vol. 3 (2014). [Google Scholar]
- 11.Tzeng E., et al. , “Adversarial discriminative domain adaptation,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 7167–7176 (2017). 10.1109/CVPR.2017.316 [DOI] [Google Scholar]
- 12.Frid-Adar M., et al. , “GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification,” Neurocomputing 321, 321–331 (2018). 10.1016/j.neucom.2018.09.013 [DOI] [Google Scholar]
- 13.Bowles C., et al. , “GAN augmentation: augmenting training data using generative adversarial networks,” arXiv:1810.10863 (2018).
- 14.Han C., et al. , “Combining noise-to-image and image-to-image GANs: brain MR image augmentation for tumor detection,” IEEE Access 7, 1 (2019). [Google Scholar]
- 15.Madani A., et al. , “Semi-supervised learning with generative adversarial networks for chest x-ray classification with ability of data domain adaptation,” in IEEE 15th Int. Symp. Biomed. Imaging, pp. 1038–1042 (2018). 10.1109/ISBI.2018.8363749 [DOI] [Google Scholar]
- 16.Salehinejad H., et al. , “Generalization of deep neural networks for chest pathology classification in x-rays using generative adversarial networks,” in IEEE Int. Conf. Acoust. Speech and Signal Process. (IEEE ICASSP) (2018). 10.1109/ICASSP.2018.8461430 [DOI] [Google Scholar]
- 17.Arandjelović R., Zisserman A., “Object discovery with a copy-pasting GAN,” arXiv1905.11369 (2019).
- 18.Lee D., et al. , “Context-aware synthesis and placement of object instances,” in Proc. 32nd Int. Conf. Neural Inf. Process. Syst., Curran Associates Inc., Red Hook, New York, pp. 10414–10424 (2018). [Google Scholar]
- 19.Wang Y., Zhang L., Van De Weijer J., “Ensembles of generative adversarial networks,” arXiv1612.00991 (2016).
- 20.Dikici E., et al. , “Automated brain metastases detection framework for T1-weighted contrast-enhanced 3D MRI,” IEEE J. Biomed. Heal. Inf. 24, 1 (2020). [DOI] [PubMed] [Google Scholar]
- 21.Wu X., Xu K., Hall P., “A survey of image synthesis and editing with generative adversarial networks,” Tsinghua Sci. Technol. 22(6), 660–674 (2017). 10.23919/TST.2017.8195348 [DOI] [Google Scholar]
- 22.Pan Z., et al. , “Recent progress on generative adversarial networks (GANs): a survey,” IEEE Access 7, 1 (2019). [Google Scholar]
- 23.Yi X., Walia E., Babyn P., “Generative adversarial network in medical imaging: a review,” Med. Image Anal. 58, 101552 (2019). 10.1016/j.media.2019.101552 [DOI] [PubMed] [Google Scholar]
- 24.Mao Q., et al. , “Mode seeking generative adversarial networks for diverse image synthesis,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 1429–1437 (2019). [Google Scholar]
- 25.Lin Z., et al. , “PacGAN: the power of two samples in generative adversarial networks,” IEEE J. Sel. Areas Inf. Theory 1(1), 324–335 (2020). 10.1109/JSAIT.2020.2983071 [DOI] [Google Scholar]
- 26.Park S.-W., Huh J.-H., Kim J.-C., “BEGAN v3: avoiding mode collapse in GANs using variational inference,” Electronics 9(4), 688 (2020). 10.3390/electronics9040688 [DOI] [Google Scholar]
- 27.Adlam B., et al. , “Learning GANs and ensembles using discrepancy,” in Adv. Neural Inf. Process. Syst., pp. 5796–5807 (2019). [Google Scholar]
- 28.Zhong P., et al. , “Rethinking generative mode coverage: a pointwise guaranteed approach,” in Adv. Neural Inf. Process. Syst., pp. 2088–2099 (2019). [Google Scholar]
- 29.Ghosh A., et al. , “Multi-agent diverse generative adversarial networks,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 8513–8521 (2018). 10.1109/CVPR.2018.00888 [DOI] [Google Scholar]
- 30.Wang X., Gupta A., “Unsupervised learning of visual representations using videos,” in IEEE Int. Conf. Comput. Vision (ICCV), pp. 2794–2802 (2015). 10.1109/ICCV.2015.320 [DOI] [Google Scholar]
- 31.Woolson R. F., “Wilcoxon signed-rank test,” in Wiley Encyclopedia of Clinical Trials, D’Agostino R. B., Sullivan L., Massaro J., Eds., pp. 1–3, American Cancer Society; (2008). [Google Scholar]
- 32.Polikar R., “Ensemble based systems in decision making,” IEEE Circuits Syst. Mag. 6(3), 21–45 (2006). 10.1109/MCAS.2006.1688199 [DOI] [Google Scholar]
- 33.Sagi O., Rokach L., “Ensemble learning: a survey,” Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 8(4), e1249 (2018). 10.1002/widm.1249 [DOI] [Google Scholar]
- 34.Theis L., van den Oord A., Bethge M., “A note on the evaluation of generative models,” in Int. Conf. Learn. Represent. (2016). [Google Scholar]
- 35.Geman D., et al. , “Visual Turing test for computer vision systems,” Proc. Natl. Acad. Sci. U. S. A. 112, 3618–3623 (2015). 10.1073/pnas.1422953112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Heusel M., et al. , “GANs trained by a two time-scale update rule converge to a local Nash equilibrium,” in Adv. Neural Inf. Process. Syst., pp. 6627–6638 (2017). [Google Scholar]
- 37.Szegedy C., et al. , “Going deeper with convolutions,” in IEEE Conf. Comput. Vision and Pattern Recognit. (CVPR), pp. 1–9 (2015). 10.1109/CVPR.2015.7298594 [DOI] [Google Scholar]
- 38.Shmelkov K., Schmid C., Alahari K., “How good is my GAN?” in Eur. Conf. Comput. Vision (ECCV) (2018). [Google Scholar]
- 39.Deng J., et al. , “ImageNet: a large-scale hierarchical image database,” in IEEE Conf. Comput. Vision and Pattern Recognit., pp. 248–255 (2009). 10.1109/CVPR.2009.5206848 [DOI] [Google Scholar]
- 40.Radford A., Metz L., Chintala S., “Unsupervised representation learning with deep convolutional generative adversarial networks,” arXiv1511.06434 (2015).
- 41.Chuquicusma M. J. M., et al. , “How to fool radiologists with generative adversarial networks? A visual Turing test for lung cancer diagnosis,” in IEEE 15th Int. Symp. Biomed. Imaging (ISBI 2018), pp. 240–244 (2018). 10.1109/ISBI.2018.8363564 [DOI] [Google Scholar]
- 42.Plassard A., et al. , “Learning implicit brain MRI manifolds with deep learning,” Proc. SPIE 10574, 105741L (2018). 10.1117/12.2293515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kingma D., Ba J., “Adam: a method for stochastic optimization,” in Int. Conf. Learn. Represent. (2014). [Google Scholar]
- 44.Hastie T., Tibshirani R., Friedman J., Eds., “Linear methods for regression,” in The Elements of Statistical Learning: Data Mining, Inference, and Prediction, pp. 43–94, Springer; (2009). [Google Scholar]
- 45.van der Maaten L., Hinton G., “Visualizing data using t-SNE,” J. Mach. Learn. Res. 9, 2579–2605 (2008). [Google Scholar]
- 46.Richardson E., Weiss Y., “On GANS and GMMS,” Adv. Neural Inf. Process. Syst. 31, 5847–5858 (2018). [Google Scholar]
- 47.Baur C., Albarqouni S., Navab N., “MelanoGANs: high resolution skin lesion synthesis with GANs,” arXiv1804.04338 (2018).
- 48.Yu T.-H., Woodford O., Cipolla R., “A performance evaluation of volumetric 3D interest point detectors,” Int. J. Comput. Vis. 102, 180–197 (2013). 10.1007/s11263-012-0563-2 [DOI] [Google Scholar]
- 49.Melekhov I., Kannala J., Rahtu E., “Siamese network features for image matching,” in 23rd Int. Conf. Pattern Recognit. (ICPR), pp. 378–383 (2016). [Google Scholar]