Adaptive empirical pattern transformation (ADEPT) with application to walking stride segmentation

Summary

Quantifying gait parameters and ambulatory monitoring of changes in these parameters have become increasingly important in epidemiological and clinical studies. Using high-density accelerometry measurements, we propose adaptive empirical pattern transformation (ADEPT), a fast, scalable, and accurate method for segmentation of individual walking strides. ADEPT computes the covariance between a scaled and translated pattern function and the data, an idea similar to the continuous wavelet transform. The difference is that ADEPT uses a data-based pattern function, allows multiple pattern functions, can use other distances instead of the covariance, and the pattern function is not required to satisfy the wavelet admissibility condition. Compared to many existing approaches, ADEPT is designed to work with data collected at various body locations and is invariant to the direction of accelerometer axes relative to body orientation. The method is applied to and validated on accelerometry data collected during a 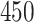-m outdoor walk of 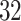study participants wearing accelerometers on the wrist, hip, and both ankles. Additionally, all scripts and data needed to reproduce presented results are included in supplementary material available at Biostatistics online.

1. Introduction

The purpose of this article is to introduce and evaluate a new class of methods for automatic pattern segmentation from sub-second accelerometry data recordings. The problem was motivated by individual walking stride segmentation from continuous walking in large observational studies as well as in clinical trial settings. Obtaining individual strides from such data are important in scientific studies, because it can provide a detailed estimation of walking characteristics including a number of steps, cadence, acceleration, pattern, as well as the variability of these characteristics within- and between-days. Such measurements have the potential to better characterize large populations (Studenski and others, 2011; Urbanek and others, 2017), identify the disease onset and describe the pathophysiological cascade of a particular disease or patterns of recovery after treatment. However, manual segmentation of individual strides from very large accelerometry data is difficult, can only be applied in short time windows and is not scalable. Therefore, fast, automated, and reliable procedures for automatic detection of strides are needed.

1.1. Accelerometry data in physical activity monitoring

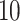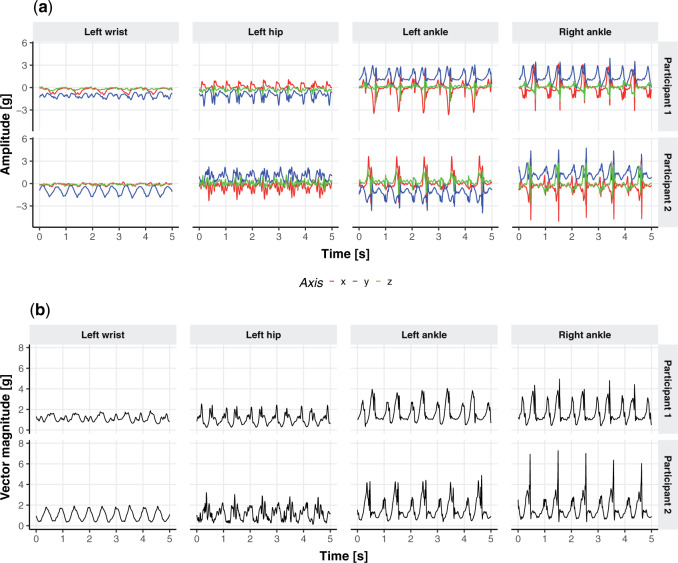
Technological advances led to an explosion in the popularity of wearable sensors in health research (Matthews and others, 2008; Healy and others, 2011; Schrack and others, 2014; Xiao and others, 2015; Karas and others, 2019). Modern wearable accelerometers typically collect – 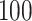observations per second along each of three orthogonal axes. To better understand the data, Figure 1a displays the three-dimensional time series of raw acceleration values collected from 5 s of walking for two different persons by sensors located at the four body locations (left wrist, left hip, left ankle, and right ankle). Each row of Figure 1a corresponds to one of two individuals, while each column corresponds to a body location: left wrist, left hip, left ankle, and right ankle, respectively. In the online version of the article, a different color (red, blue, and green) corresponds to one of the three orthogonal axes of the device: up/down, left/right, forward/backward in the device’s frame of reference. Figure 1b provides the acceleration vector magnitude (VM), computed as the square root of the sum of squares of the three acceleration values at each time point. The panels in Figure 1b correspond directly to the panels in Figure 1a. While the original data is three-dimensional, we will work with the one-dimensional VM time series, which is easier to handle and is sufficient for stride segmentation.

Fig. 1.

(a) Three-dimensional acceleration time series from 5 s of walking for two different study participants (separate row panels) at four body locations: wrist, hip, left, and right ankle (separate column panels). In the online version of the article, a different color (red, blue, and green) corresponds to one of the three orthogonal axes of the device. (b) Same as the (a) panels but showing the vector magnitude, a one-dimensional summary of the three-dimensional time series.

1.2. Challenges in stride identification from accelerometry data

Figure 1a and b display clear repetitive patterns characterized by high amplitude peaks in the data. While these patterns are relatively clear to a human observer, identifying them algorithmically is, however, more complicated. There are many reasons why this problem is challenging. First, there is variation in the duration and shape of the repetitive patterns with substantial differences both within and between subjects. Second, there are multiple local maxima and exact identification of the start and end of a stride may depend on the position of the device. Third, the device can move, which further affects the time-series characteristics. Fourth, the shape, duration, and intensity of the signal can change with the time of day and energy level of the movement. Thus, any method that is designed to work well and reproducibly will need to account for these challenges and provide evidence that it can work for different subjects in complex environments. Below we describe the intuition and the main components of our idea.

1.3. Pattern definition and recognition

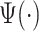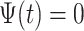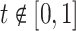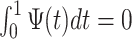That brings us to the question: “what is a pattern and what does it mean to find patterns in the data?” We propose that a pattern is a function, , with mean zero, variance one and compact support in the same domain as the data. For example, in our case, because we are working with univariate time series, if , , and 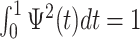. The requirements that the mean of the function is zero and variance is one is not necessary, but keeps pattern functions comparable. We also propose that finding a pattern is maximizing a distance (e.g., covariance) between this function, translated and scaled, and the original signal. More precisely, if the univariate VM time-series is denoted by 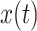then we are interested in the following covariance function

(1.1)

This is a simple formula, but it packs a powerful methodological punch that is worth watching again in slow motion. Note that the 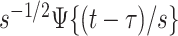is the function 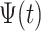translated by 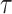and scaled by 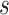, and its domain is 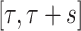. Moreover, the function 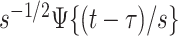continues to have mean zero and variance one. Of course, we can use the correlation between the original signal and the translated and scaled patterns, which can be done by dividing by the standard deviation of the time-series 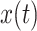in the interval 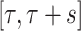. We could use other distance measures including 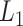, 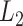or any other distance between two vectors of the same length.

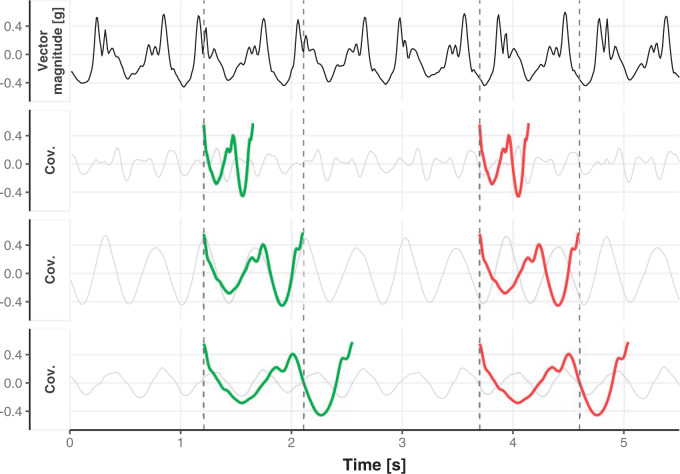
To visualize the translation and scaling operations on the data, Figure 2 displays four panels. The first panel displays 6 s of VM accelerometry data during walking for one person. Panels 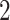, , 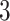and 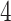display the covariance between a pattern, scaled by a particular scale parameter 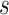, and subsequent windows of VM. The reason the covariance function is continuous is that the translation of the pattern is continuous in the translation parameter 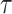. For each scale parameter 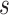, we display two instances of the translated scaled pattern; in the online version of the article, one appears in green and one in red. As one compares the scaled patterns across scaling parameters (panels 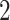, , 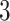and 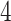), it should become clear what the effect of scaling will be.

Fig. 2.

First horizontal panel: vector magnitude signal derived from accelerometry data of continuous walking. Three following horizontal panels: covariance (y-axis) between a stride pattern rescaled according to one of three scale parameters, respectively, and a VM signal window that corresponds to particular translation parameter (x-asis) of a pattern. Within each of three covariance horizontal panels, in the online version of the article, red and green colors denote a pattern of the same scale but different translation (location) parameter values.

1.4. Related literature

The transformation we have discussed above is widely used in the continuous wavelet transform (CWT) (Grossmann and Morlet, 1984), where the pattern 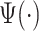is called the mother wavelet. In CWT, the pattern or mother wavelet function is fixed, with popular choices including the Haar (Haar, 1910), Daubechies (Daubechies, 1988), and Biorthogonal (Cohen and others, 1992) mother wavelets. In statistics, discrete wavelet transform (DWT) is typically more well known and allows only discrete scaling of the mother movelet, 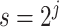, where 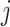is in the set of integers, 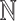. DWT and CWT have been successfully used in a variety of scientific studies that involve digital signal processing including respiratory patterns (Dupuis and Eugene, 2000), cardiac rhythms (Madeiro and others, 2012), electromyography (Phinyomark and others, 2011), electroencephalography (EEG) (Gadhoumi and others, 2012), blood pressure measurements (Li and others, 2013), DNA sequences (Jia and others, 2015), and electrocardiography (ECG) signals (Yochum and others, 2016).

Our proposal is related to the large literature on estimation of activity type in health studies using accelerometers. Bai and others (2012) defined movelets, a family of subsecond-level accelerometry data patterns representing different types of physical activities and used them for activity classification. This approach has been further expanded by He and others (2014) and Xiao and others (2016). Another part of the literature has focused on activity type classification using minute level accelerometry data (Pober and others, 2006; Staudenmayer and others, 2009; Attal and others, 2015). These approaches use a number of accelerometry data features combined with supervised classification algorithms. There are many published algorithms for the quantification of cumulative walking time and quality using sub-second accelerometry data. The most basic ones are based on thresholding the signal amplitude (Dijkstra and others, 2008; Weiss and others, 2013), zero-crossing analysis (Jayalath and Abhayasinghe, 2013), local periodicity estimators (Kavanagh and Menz, 2008), and wavelet analysis (Nyan and others, 2006). More recent approaches have focused on template matching (Soaz and Diepold, 2016) and Fourier transformations (Dirican and Aksoy, 2017; Kang and others, 2018; Urbanek and others, 2018).

Walking strides are often segmented based on landmark events within a stride (e.g., heel-strike, push-off, or swing) (Willemsen and others, 1990; Selles and others, 2005; McCamley and others, 2012; Wang and others, 2012; Godfrey and others, 2015). These approaches rely heavily on the location of the device relative to the body, device orientation, and the assumption that the device is not moving during a task. Therefore, they are not robust to observed changes in signals during quasi free-living environments and are less likely to be extended to true free-living environment. Soaz and Diepold (2016) used template matching and clustering for step detection from data collected from a waist-worn accelerometer. Ying and others (2007) described an algorithm which uses a stride template derived dynamically from the data and proposed to use the auto-correlation of data segments for stride segmentation. Müller (2007) proposed dynamic time warping (DTW), where both the pattern and the signal are transformed non-linearly to obtain an optimal match in a pre-defined family of warping functions. Barth and others (2015) used multi-subsequence DTW to combine information from the different axes of the accelerometer and gyroscope. While we thought that approaches by Ying and others (2007) and Barth and others (2015) can potentially be robust to sensor location and orientation, we were unable to obtain the associated software from the authors to compare our proposal with these approaches.

Here, we propose adaptive empirical pattern transformation (ADEPT), a fast, scalable, and accurate method for segmentation of individual walking strides. ADEPT computes the covariance between a scaled and translated pattern function and the data, an idea similar to the CWT. The difference is that ADEPT uses a data-based pattern function, allows multiple pattern functions, can use other distances instead of the covariance, and the pattern function is not required to satisfy the wavelet admissibility condition. For completeness of the presentation, a function 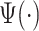satisfies the admissibility condition if 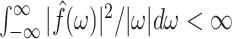, where 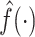denotes Fourier transform of the function 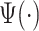. A square integrable function that satisfies the admissibility condition can be used to recover the original signal without loss of information (Sheng, 2000). Our approach does not require the complete recovery of the original signal, which allows us to use a broader class of functions for 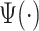. Compared to many existing approaches, ADEPT is designed to work with data collected at various body locations and is invariant to the direction of accelerometer axes relative to body orientation. We also provide open source software that implements ADEPT method, and make available both the data set and reproducible analysis code used in the application example. Those resources are referenced in supplementary material available at Biostatistics online.

The manuscript is organized as follows. Section 2 describes a continuous walking experiment conducted and introduces the notation and definitions. Sections 3 and 4 describe the two components of ADEPT. Section 5 presents the results of automatic segmentation of individual strides from accelerometry data collected from the experiment. Section 6 provides validation of the approach, and Section 7 contains the discussion.

2. Data, notation and definitions

2.1. Participants and data collection

Data were collected as a part of the study on identification of walking, stair climbing, and driving using wearable accelerometers, sponsored by the Indiana University CTSI grant and conducted at the Department of Biostatistics, Fairbanks School of Public Health at Indiana University. The study was led by Dr Jaroslaw Harezlak, assisted by Dr William Fadel and Dr Jacek Urbanek (coauthors on this article) and enrolled 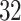healthy participants between 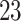and 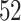years of age. In this article, we focus exclusively on the task of self-paced, undisturbed, outdoor walking on the sidewalk, even though the experiment contained additional tasks. During this task, participants were asked to walk outside on the pathway designed for the purpose of the study (indicated as a blue line on the map in Figure 8 in Appendix A of the supplementary material available at Biostatistics online). Each participant walked unaccompanied to maintain their own pace, while the supervising person recorded the starting and stopping time of the task. The length of the walking pathway was approximately 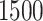feet and the duration of this task ranged between 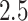and 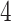min, depending on the pace of each participant. The pathway consists of smooth changes in elevation and has no sharp turns, turnarounds, or physical obstacles. Each participant was equipped with four 3-axial ActiGraph GT3X+ (ActiGraph LLC, Pensacola, FL, USA) accelerometers located on the left wrist, left hip, and both ankles. Accelerometers collected the data along three orthogonal axes with a sampling frequency of 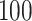Hz. Periods of walking were manually marked in the resulting dataset based on time markers generated during clapping. The study was approved by the IRB of Indiana University; all participants provided written informed consent.

2.2. Notation and definitions

We denote by 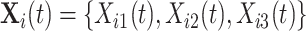the three-dimensional acceleration time-series for subject 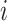at time 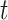corresponding to the three accelerometer device axes. For every time point, we define the VM 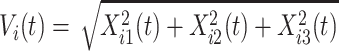. Figure 1b provides an example of how the one-dimensional VM data are obtained from the three-dimensional accelerometry data displayed in Figure 1a. We propose to use the high-resolution one-dimensional VM data to conduct segmentation of individual strides. A stride is defined as a combination of two subsequent steps. We focus on strides as the information collected by an accelerometer about subsequent steps may be asymmetric due to device placement; for example, an accelerometer placed on the right hip will tend to record lower amplitude signals during a step with the left leg.

We denote by 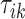, , 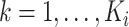the time when 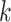-th stride of 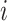-th subject is initiated, where 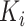is the total number of strides for subject 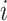. We further define 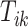, , 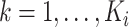to be the time duration for the 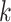-th stride of subject 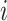. For simplicity, we will express 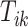in seconds. The 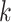-th stride of 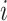-th subject is defined as 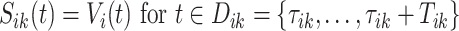, where 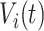is the VM function and 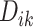is a discrete equally-spaced grid of time points at which the measurements were collected. The parameters 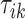, , 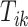and 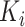are a priori unknown. For continuous walking, the beginning of the next stride is the end of the current stride, that is, 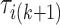is the end of the 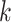-th stride and the beginning of the 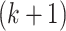-th stride. The duration of a stride is hence given by 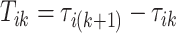and the remaining unknown parameters are 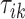’s, the times when strides are initiated. The notation provides the conceptual framework for partitioning the walking VM accelerometry data into adjacent strides. We also introduce the cadence of walking, which is number of steps per second. Cadence is related to the duration of the stride expressed in second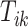s, , as .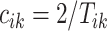

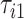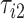Figure 9 in Appendix A of the supplementary material available at Biostatistics online displays acceleration time series for two subsequent strides, where the beginning of a stride is marked by and , respectively. The duration of the first stride, expressed in seconds, is 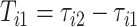. The beginning of the second stride is 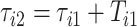. In the figure, the first stride is initiated at 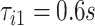and the second stride is initiated at 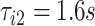, yielding a duration of the first stride of 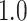s and a cadence estimate equal to 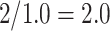steps per second for this segment of walking.

3. Empirical pattern estimation

As we described in Equation 1.1 of Section 1, we need to identify the pattern, 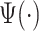. Since we estimate the pattern from the data, we refer to the estimated 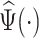as an empirical pattern. For simplicity, we drop the hat notation and continue to denote the empirical pattern as 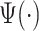. The estimating process is relatively simple but requires some manual segmentation of patterns, which could be tedious. Figure 10a in Appendix A of the supplementary material available at Biostatistics online displays manually segmented strides; these strides represent a random subset from the 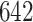strides we obtained from 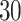individuals, for an average of 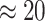strides per person. Figure 10a in Appendix A of the supplementary material available at Biostatistics online shows quite a bit of variation in the length of the stride, with some strides taking as little as 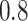s and some strides taking s or more. Some landmarks are de-synchronized across individuals; note, for example, the peak acceleration in the middle of the strides, which corresponds to the heel strike. To construct the empirical pattern we did something simple: (i) take every stride and stretch it or compress it to the interval 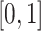; (ii) interpolate every stride on an equally-spaced grid; (iii) standardize every stride to have mean zero and variance one; (iv) average the standardized stride patterns; and (v) standardize resulted average to have mean zero and variance one. Figure 10b in Appendix A of the supplementary material available at Biostatistics online displays the 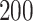stretched, centered, and normalized strides (black lines) and the normalized mean of all 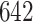such functions (red line). The red line represents the empirical pattern obtained from the data.

If one empirical pattern is insufficient to capture the types of observed stride patterns, we propose to incorporate additional empirical patterns. Figure 11a in Appendix A of the supplementary material available at Biostatistics online displays the normalized strides, as described in Figure 10b in Appendix A of the supplementary material available at Biostatistics online, but clustered into two groups using the correlation similarity. Interestingly, the main difference between the two groups is the location of the peak acceleration in the middle of the stride (heel strike). The first group of strides (top panel) corresponds to a heel strike around 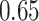, while the second group corresponds to a heel strike around 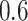. Taking the averages of these two groups leads to two empirical patterns, 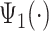and 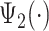(shown as red lines.) Note that these two empirical patterns are correlated but also subtly different. Such differences would be hard to estimate by simply stretching the patterns, as the scaling of the empirical patterns does. We further pushed the envelope on extracting three distinct groups of strides and results are shown in Figure 11b in Appendix A of the supplementary material available at Biostatistics online. Results seem to be a further refinement of the two-group clustering, but it seems that we have hit a point of diminishing returns. In practice one may need to do this especially in cases when there are clearly defined subgroups (e.g., individuals who suffered a stroke).

4. The maximization-tunning procedure for ADEPT

Once the empirical pattern is estimated, we propose a two-step procedure to segment strides. The first step consists of maximization of the covariance between the rescaled empirical pattern and the VM signal in various time windows. This provides a good idea about where the stride is localized, but it can miss the exact location by fractions of a second. The second step is designed to tune the stride segmentation to better match the beginning and end of a stride.

4.1. Vector magnitude smoothing

In the maximization-tuning procedure, the raw VM signal is smoothed using an unweighted moving window average. To understand the window size effect on smoothing, Figure 12 in Appendix A of the supplementary material available at Biostatistics online displays three horizontal panels. The first horizontal panel shows the VM data collected from the left wrist, left hip, and both ankles during 3 s of walking for one person. Panels 2 and 3 display the smoothed version of the VM signal using a moving window of length 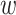equal to 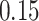(an example of moderate smoothing) and 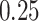s (an example of aggressive smoothing), respectively. The blue vertical lines indicate the local maxima of the VM smoothed signal with a window size of 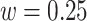s. For the first algorithm step (covariance maximization), we recommend moderate smoothing which preserves the major features of the original signal. However, moderate smoothing may leave the multiple local maxima present at the beginning and end of a stride (note the wiggles in the proximity of the dominant peaks in the second row of panels). If this occurs, to avoid ambiguity in determining which data peak corresponds to stride beginning/end, we recommend applying aggressive smoothing for the second step (tuning) to smooth over neighboring local maxima. The aggressive smoothing used in the tuning step may aid strides segmentation from wrist data in particular, where the stride beginning and end are less well-defined compared to data from the hip and ankle.

4.2. Distance matrix computation

The first step of the procedure starts by calculating the covariance function, 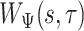, which was described in equation (1.1). This function depends on two parameters, the scale 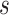and the location 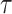and will be calculated on a two-dimensional grid and stored as a matrix. Note that if 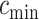and 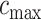denote the minimum and maximum walking cadence, respectively, the duration of strides is between 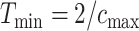and 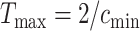. Therefore, we considering a grid of scaling factors, 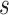, such that the rescaled versions of the pattern function 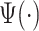cover densely the interval 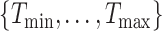. Once the pattern is scaled we use linear interpolation to match the sampling points with those of the observed data. The location of stride patterns can be estimated by identifying the parameters 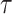and scale 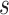that maximize the covariance matrix.

Figure 13 in Appendix A of the supplementary material available at Biostatistics online provides the visualization of the ADEPT covariance matrix for a 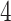s walking period for one individual; data are from the left ankle monitor. The x-axis corresponds to time (the 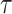location parameter), while the y-axis corresponds to the stride duration (the 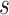scaling parameter.) The black dot indicates the point of the largest sample covariance, which is equal 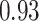. This value is attained for an empirical pattern 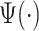rescaled to have a duration of 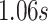that starts at time 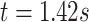from the beginning of the recording. A quick visual inspection indicates that there are four different strides in this particular segment. So far, we have discussed the case when only one empirical pattern is available. When there are multiple empirical patterns 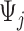, , 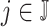we first compute the sample covariance matrix 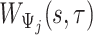for each of them separately and then calculate 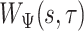as the entry-wise maximum across the pattern-specific covariance matrices. Matrix 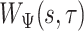is then used throughout the segmentation procedure.

4.3. Tuning procedure

The maximization of the covariance function provides an initial estimator of the stride location, but the estimation can be off by fractions of a second. This is due to the large fluctuations of the VM signal toward the beginning and end of the stride. Therefore, the exact location of the stride may be missed. Recall that the covariance maximization procedure identifies a start point, 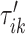, and the scaling parameter, 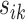. The scaling parameter corresponds to a specific length, 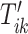, of a stride, 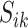. Thus, the stride is estimated to be 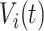for 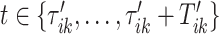. Once this is obtained we are interested in tuning both 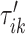and .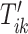

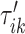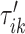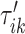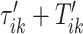To do this we focus on estimating the largest local maximum in a neighborhood of . In general, the covariance maximization procedure does not ensure that is a local maximum and the closest local maximum may not be the largest local maximum in the signal. We start by building two neighborhoods of a fixed length, centered at and , respectively. The tuning procedure is simple: identify the local maximum of (possibly smoothed) VM signal in each of these neighborhoods. This procedure is applied after each 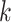-th stride location and duration is estimated using the covariance matrix.

The left panel in Figure 14 in Appendix A of the supplementary material available at Biostatistics online displays a small part of the raw VM signal collected from the left ankle (black line). The blue vertical lines indicate 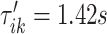and 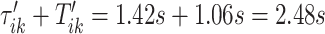, which were identified in the covariance maximization step; refer to Figure 13 in Appendix A of the supplementary material available at Biostatistics online. 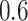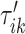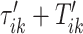The blue shaded areas denote the symmetric neighborhoods of length s around and , respectively. The right panel in Figure 14 in Appendix A of the supplementary material available at Biostatistics online displays the same raw (black line) and smooth (red line) VM signal with a moving average window of 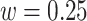s. The red vertical lines mark local maxima of the smoothed VM signal, which are at 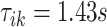and 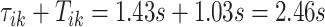. These values are only slightly different from the original ones, but it provides more reproducible estimates of the beginning and end of a stride. The maximization tuning algorithm proceeds until all strides within the VM signal are identified.

5. Strides segmentation from raw accelerometry data

ADEPT was applied to automatically segment strides from accelerometry data collected from all the 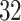study participants in the study. We focused on continuous walking periods and used all four sensor locations: left wrist, left hip, and both ankles. The procedure was applied separately to every sensor location; the algorithm smoothing and fine-tuning parameters were kept the same across sensor locations.

5.1. Estimation of the empirical patterns of strides

The procedure started with the manual segmentation of 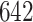strides from all 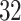individuals ( 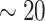strides per individual) conducted by a specialist in accelerometer signal processing (Dr Urbanek, a coauthor on this article). Strides were defined as segments of the data between one heel-strike peak and the subsequent heel-strike of the same leg. For manual segmentation, data from all body-locations were synchronized manually to ensure that heel-strike peaks occur at the same time-points in all four time-series. This substantially reduced manual segmentation time but introduced some small errors which are likely due to the clock drift across devices (Karas and others, 2019). Next, five 5-s data segments were chosen randomly for each individual and a time-index for the beginning and the end of each stride was manually marked using base function in statistical software. This was an extremely laborious process that took approximately 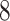h and covered about 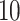% of the walking data. Thus, manual segmentation is impractical even in small studies and impossible in moderately large studies. Moreover, manual segmentation has its own imperfections, which we address using ADEPT.

For each sensor location, we estimated two empirical patterns based on the 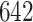manually segmented strides; the sets of estimated patterns are showed in Figure 15 in Appendix A of the supplementary material available at Biostatistics online, where each location corresponds to a panel column and a color. The left wrist and left ankle, the empirical patterns are clearly distinct; note the middle of the stride differences in the pattern shape for the left wrist (first panel column) and size of the local maximum for left ankle (third panel column). The empirical patterns for the right ankle (fourth panel column) differ in terms of the timing of the heel strike (local maximum in the middle of the stride) and intensity. These differences are most likely due to differences between individuals. The empirical patterns for the left hip (second panel column) are slightly different, especially at the beginning and end of the stride. They appear to be the same, but phase-shifted, which is most likely due to manual segmentation artifacts.

5.2. Stride segmentation

Once the empirical patterns were obtained, we estimated the location of strides by maximization of covariance function (1.1) and fine-tuned the location estimation. For the scale parameter, we used a 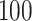-dimensional grid to ensure that the stride pattern function, 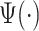, covers densely the interval 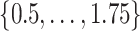expressed in seconds. We used a smoothing window of length 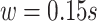in the covariance maximization step, 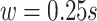in the fine-tuning step, and a window of length 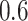s length to search for the local maximum.

Table 1 in Appendix B of the supplementary material available at Biostatistics online summarizes the number of segmented strides per person grouped by sensor location. On average, we identified 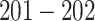strides per person from data collected at each location; the minimum, maximum and three quartiles for the number of strides are close, but not identical, across sensor locations. Table 2 in Appendix B of the supplementary material available at Biostatistics online displays summaries of the estimated stride duration time (in seconds) grouped by sensor location; on average, an estimated stride duration time was between 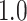and 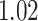s, with slight variations across sensor locations.

5.3. Cadence estimation

Once every individual stride is estimated, the walking cadence (number of steps per second) can be estimated as a function of time. More precisely, for a stride estimated to occur between 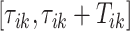the cadence is estimated as 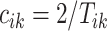. Figure 16 in Appendix A of the supplementary material available at Biostatistics online provides these cadence estimates for the left ankle data. Each row (y-axis) corresponds to one person, and each column (x-axis) corresponds to a 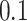second window of walking. More intense blue corresponds to lower cadence and more intense red corresponds to higher cadence. Rows are ordered according to the median cadence, with lower median cadence displayed higher. The median cadence was correlated (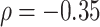) with the average walking duration, with height (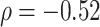), and weight ().

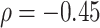6. Segmentation validation

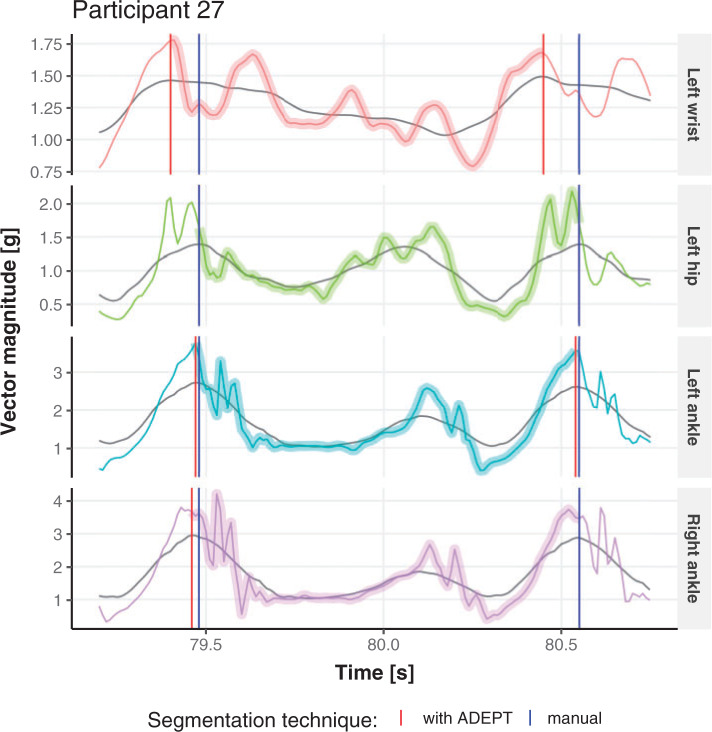
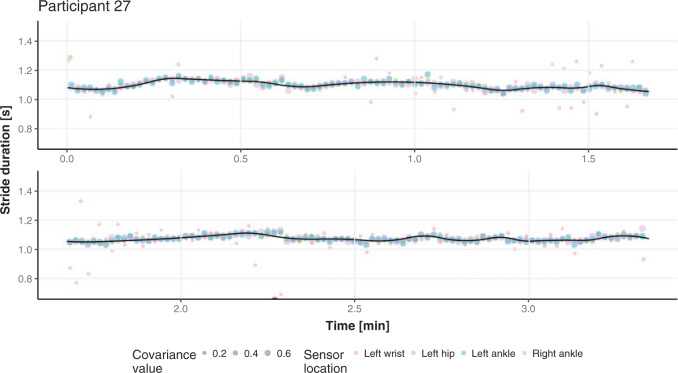
We do not have a true, “gold standard” segmentation of strides, which raises important challenges when it comes to validation. A good first step is to visually inspect the results and ensure that stride estimates are not completely misaligned with the data. We have conducted this visual inspection and we could not find any substantial discrepancies. This process is hard to illustrate in a article, though Figure 4 provides a short snapshot of the process. A second visualization step is to compare the stride estimators obtained from different sensor locations. If strides are consistently estimated across body locations, at least the procedure is consistently right or wrong. For one person, Figure 3 provides the estimated stride duration (y-axis) as a function of the estimated start point of the stride for all four locations (shown as different color bubbles in the online version of the article). In the online version of the article, the color of points corresponds to different sensor location: left wrist (red), left hip (green), left ankle (blue), and right ankle (purple). The size of the point corresponds to the covariance between the VM signal and the empirical pattern (see Section 4.2); the covariance values should be used to only compare estimates within the same sensor location. The black solid line is a nonparametric smoother for the dots across all four body locations. Figure 3 indicates that the stride duration and the beginning of the stride estimates are consistent across the four sensors for most of the walking experiment time; note that most dots are, in fact, overlapping. There are a few discrepancies, and they all correspond to the left wrist. This is important, as many current studies suggest using the non-dominant wrist location for accelerometers.

Fig. 4.

Short segments of the vector magnitude and its smoothed version (gray line) for Participant 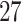. Comparing stride segmentation using the manual (blue vertical lines) and ADEPT (red vertical lines) approaches for four different body locations. The color version of the plot is available in the online version of the article.

Fig. 3.

Estimated start point (x-axis) and duration time (y-axis) of all estimated strides for one study participant across four sensor locations. Each point represents a one estimated stride from particular sensor location. The size of a point corresponds to covariance value between VM signal and empirical pattern that yielded the stride estimate and, in the online version of the article, the color of a point denotes sensor location. Black line represents a nonparametric regression fit curve.

6.1. Segmentation results consistency across sensor locations

Here, we formalize the idea suggested by Figure 3. The solid line provides a consensus estimator of the stride duration across body locations. Denote by 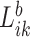the estimated length of the 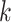-th stride for subject 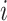using the location 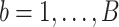(here 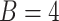because there are four body locations). Also denote by the consensus estimator for the stride length; this was obtained by smoothing the data 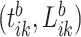, where is the estimated time when stride 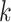was initiated for subject 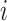according to location 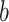. This is done for a fixed 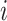and by combining points over locations, 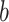. We define the percent absolute deviation for stride 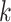as 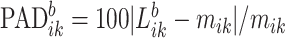, which provides a measure of the error, 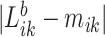, relative to the signal, 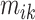. It could be viewed as a noise to signal ratio or an estimator of the coefficient of variation. By averaging these values over 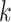we obtain an individual percent absolute deviation for each body location 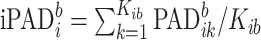, where 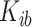is the estimated number of strides for subject 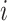at location .

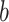For subject 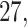the iPAD for the left wrist, left hip, left ankle, and right ankle stride estimates were 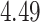%, %, 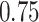%, 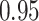and %, respectively. The average iPAD across study participants was 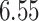%, %, 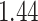%, 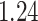and 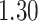%, respectively. All subject-specific iPAD values are showed in Table 3 in Appendix B of the supplementary material available at Biostatistics online. Results indicate that the errors are small relative to the signal for all body locations, though the left wrist has an error that is roughly three to four times larger than for the other locations.

6.2. Consistency between ADEPT and manual segmentation

Manual segmentations were used primarily to estimate location-specific empirical patterns. Once empirical patterns are estimated we can re-estimate these strides using ADEPT. Thus, we can compare the results of the manual and ADEPT segmentations on all the 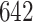manually segmented strides. To do this, we split randomly the 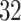study participants into four equally sized groups, eight participants in each. In each group, we used ADEPT to segment strides from data of the eight members of that group, using stride patterns estimated from manually segmented strides of the remaining 24 participants. We repeated the procedure for each four participant groups. For each manually-segmented stride, we identified the closest ADEPT-segmented pattern by minimizing the start point distance. For each matched pair, we computed the differences between the estimated start and end times, respectively.

For example, for Participant 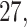the average estimated stride duration was 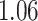s. The stride start difference values has a mean (standard deviation) summaries equal: 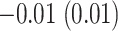, , 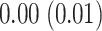and 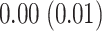(in seconds) for left hip, left ankle, and right ankle, respectively. For the left wrist, the mean of difference was 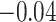s, while the standard deviation was 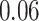s. Thus, the differences are roughly of the order of 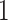–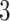% of the length of the stride. A similar result can be observed across subjects. The empirical density distributions of these differences for all subjects combined are shown in Figure 17 in Appendix A of the supplementary material available at Biostatistics online. They indicate excellent agreement for all body locations, with slightly worse performance for the left wrist. The differences for all subjects combined are summarized in Table 4 in Appendix B of the supplementary material available at Biostatistics online. For comparison, in Table 5 in Appendix B of the supplementary material available at Biostatistics online, we included the summary of differences obtained when ADEPT uses stride patterns derived from data of all 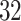study participants. Results are almost identical with the results obtained using the partition into four subgroups.

The differences between manual and ADEPT segmentations should not automatically be interpreted in favor of the manual segmentation. For example, Figure 4 compares four strides of Participant 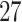, using the manual (blue lines) and ADEPT (red lines) segmentation results using the validation procedure described above (the color version of the plot is available in the online version of the article). Each horizontal plot panel corresponds to a different accelerometry sensor location. Colored lines are the original VM signal, and the gray lines are the smoothed VM signals. The largest observed discrepancy between ADEPT and manual segmentation is for the left wrist, indicating a difference of 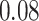and 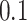s between the estimated stride start and end points, respectively. However, visual inspection seems to indicate that ADEPT estimates the strides more accurately than the manual approach. For the other locations, the differences between manual and ADEPT segmentations are visually indistinguishable.

6.3. Visualization of the estimated stride patterns

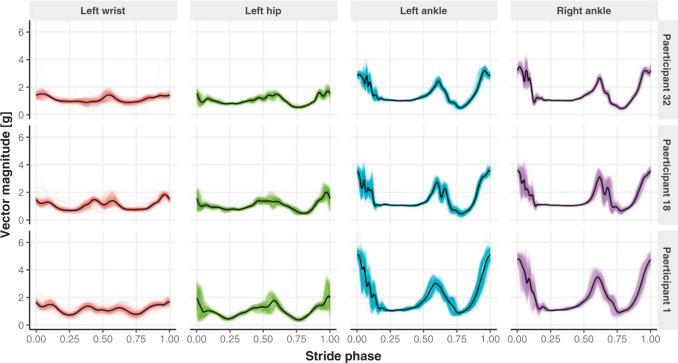
Visually inspecting results could be very difficult and subject to substantial observer bias and measurement error. Instead, we propose to conduct a parallel visualization of the time series, by jointly plotting the segmented strides. More precisely, for each study participant and location we registered the ADEPT segmented stride to the 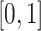interval using linear interpolation. Figure 5 displays these registered ADEPT segmented strides for each location and three study participants. The color version of the plot is available in the online version of the article. Each stride is displayed as a line colored according to the location, while the solid black lines indicate the average of these strides. Participants 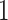and 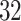were selected because they had the highest and the lowest median walking cadence among the 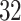study participants, respectively. Participant 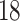was selected because he had the longest execution time of the walking component of the study. Study participant 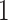performed the walking exercise in the shortest time. Visual inspection of these results does not trigger any particular red flag in terms of segmentation, though we could envision further quantifying the location- and subject-specific variability or outlier detection methods for identifying incorrect stride segmentations. Moreover, even though we started with population-specific patterns of walking, after applying ADEPT we end up with subject-specific strides. These strides can be used to extract subject-specific patterns, which could be used for further refinement of ADEPT at the subject level.

Fig. 5.

Individual strides segmented with the proposed automatic approach (thin colored lines) together with the derived subject- and location-specific stride pattern (black line) for three study participants, across four sensor locations. The color version of the plot is available in the online version of the article.

7. Discussion

We proposed ADEPT for precise identification of individual walking strides from high-resolution raw accelerometry data. Our automated approach reduces strides segmentation time substantially, making the approach feasible for moderate and large studies. ADEPT yields results visually indistinguishable from manual segmentation for most locations, with some larger discrepancies for the non-dominant wrist. ADEPT identifies maxima of the covariance (or other distances) between the scaled and translated stride pattern and a data signal, a concept that has common characteristics with CWT. Unlike CWT, ADEPT uses a data-based pattern function, allows multiple pattern functions, can use other distances instead of the covariance, and the pattern function is not required to satisfy the wavelet admissibility condition. ADEPT also contains a novel fine-tuning procedure. Compared to many existing approaches, ADEPT is designed to work with data collected at various body locations and is invariant to the direction of accelerometer axes relative to body orientation.

ADEPT can be used in various studies that require segmentation of strides from subsecond accelerometry data collected during standardized walking tests (e.g., 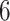-min walk test (Salbach and others, 2015)). The segmented strides can be used to estimate interval-specific walking cadence, derive subject- and population-specific stride patterns, and stride-to-stride amplitude and phase deviation (Urbanek and others, 2017). However, we expect that ADEPT approach will work well in a range of applications including detection of other types of movements or even different biosignals, such as ECG and EEG. A particularly challenging area is walking identification in the free-living environment. The current ADEPT approach has several potential limitations. For example, the study participants consisted of healthy individuals, with age ranging between 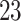and 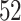years. Whether ADEPT applies to older study participants or individuals with impaired walking remains an open problem. Moreover, we only investigated data collected during continuous outdoor walking on a flat surface, which may not directly generalize to walking in heterogeneous and complex environments.

Funding

Research was partially supported by the NIMH grant R01MH108467.