Summary
We propose a computationally and statistically efficient divide-and-conquer (DAC) algorithm to fit sparse Cox regression to massive datasets where the sample size 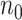 is exceedingly large and the covariate dimension
is exceedingly large and the covariate dimension 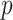 is not small but
is not small but 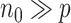 . The proposed algorithm achieves computational efficiency through a one-step linear approximation followed by a least square approximation to the partial likelihood (PL). These sequences of linearization enable us to maximize the PL with only a small subset and perform penalized estimation via a fast approximation to the PL. The algorithm is applicable for the analysis of both time-independent and time-dependent survival data. Simulations suggest that the proposed DAC algorithm substantially outperforms the full sample-based estimators and the existing DAC algorithm with respect to the computational speed, while it achieves similar statistical efficiency as the full sample-based estimators. The proposed algorithm was applied to extraordinarily large survival datasets for the prediction of heart failure-specific readmission within 30 days among Medicare heart failure patients.
. The proposed algorithm achieves computational efficiency through a one-step linear approximation followed by a least square approximation to the partial likelihood (PL). These sequences of linearization enable us to maximize the PL with only a small subset and perform penalized estimation via a fast approximation to the PL. The algorithm is applicable for the analysis of both time-independent and time-dependent survival data. Simulations suggest that the proposed DAC algorithm substantially outperforms the full sample-based estimators and the existing DAC algorithm with respect to the computational speed, while it achieves similar statistical efficiency as the full sample-based estimators. The proposed algorithm was applied to extraordinarily large survival datasets for the prediction of heart failure-specific readmission within 30 days among Medicare heart failure patients.
Keywords: Cox proportional hazards model, Distributed learning, Divide-and-conquer, Least square approximation, Shrinkage estimation, Variable selection
1. Introduction
Large datasets derived from health insurance claims and electronic health records are increasingly available for healthcare and medical research. These datasets are valuable sources for the development of risk prediction models, which are the key components of precision medicine. Fitting risk prediction models to a dataset with a massive sample size (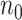 ), however, is computationally challenging, especially when the number of candidate predictors (
), however, is computationally challenging, especially when the number of candidate predictors (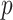 ) is also large and yet only a small subset of the predictors is informative. While it is statistically feasible to fit a full model with all
) is also large and yet only a small subset of the predictors is informative. While it is statistically feasible to fit a full model with all 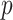 variables, deriving parsimonious risk prediction models has the advantage of being more clinically interpretable and easier to implement in practice. In such a setting, it is highly desirable to fit a sparse regression model to simultaneously remove non-informative predictors and estimate the effects of the informative predictors. When the outcome of interest is time-to-event and is subject to censoring, one may obtain a sparse risk prediction model by fitting a regularized Cox proportional hazards model (Cox, 1972) with penalty functions such as the adaptive least absolute shrinkage and selection operator (LASSO) penalty (Zhang and Lu, 2007).
variables, deriving parsimonious risk prediction models has the advantage of being more clinically interpretable and easier to implement in practice. In such a setting, it is highly desirable to fit a sparse regression model to simultaneously remove non-informative predictors and estimate the effects of the informative predictors. When the outcome of interest is time-to-event and is subject to censoring, one may obtain a sparse risk prediction model by fitting a regularized Cox proportional hazards model (Cox, 1972) with penalty functions such as the adaptive least absolute shrinkage and selection operator (LASSO) penalty (Zhang and Lu, 2007).
When 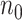 is extraordinarily large, directly fitting an adaptive LASSO (aLASSO) penalized Cox model to such a dataset is not computationally feasible. To overcome the computational difficulty, one may employ the divide-and-conquer (DAC) strategy, which typically divides the full sample into
is extraordinarily large, directly fitting an adaptive LASSO (aLASSO) penalized Cox model to such a dataset is not computationally feasible. To overcome the computational difficulty, one may employ the divide-and-conquer (DAC) strategy, which typically divides the full sample into 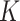 subsets, solves the optimization problem using each subset, and combines the subset-specific estimates into a combined estimate. Various DAC algorithms have been proposed to fit penalized regression models. For example, Chen and Xie (2014) proposed a DAC algorithm to fit penalized generalized linear models (GLMs). The algorithm obtains a sparse GLM estimate for each subset and then combine subset-specific estimates by majority voting and averaging. Tang and others (2016) proposed an alternative DAC algorithm to fit GLM with an extremely large
subsets, solves the optimization problem using each subset, and combines the subset-specific estimates into a combined estimate. Various DAC algorithms have been proposed to fit penalized regression models. For example, Chen and Xie (2014) proposed a DAC algorithm to fit penalized generalized linear models (GLMs). The algorithm obtains a sparse GLM estimate for each subset and then combine subset-specific estimates by majority voting and averaging. Tang and others (2016) proposed an alternative DAC algorithm to fit GLM with an extremely large 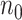 and a large
and a large 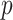 by combining de-biased LASSO estimates from each subset. While both algorithms are effective in reducing the computation burden compared to fitting a penalized regression model to the full data, they remain computationally intensive as
by combining de-biased LASSO estimates from each subset. While both algorithms are effective in reducing the computation burden compared to fitting a penalized regression model to the full data, they remain computationally intensive as 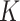 penalized estimation procedures will be required. In addition, the DAC strategy has not been extended to the survival data analysis.
penalized estimation procedures will be required. In addition, the DAC strategy has not been extended to the survival data analysis.
In this article, we propose a novel DAC algorithm using a sequence of linearizations, denoted by 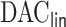 , to fit aLASSO penalized Cox proportional hazards models, which can further reduce the computation burden compared to the existing DAC algorithms.
, to fit aLASSO penalized Cox proportional hazards models, which can further reduce the computation burden compared to the existing DAC algorithms. 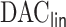 starts with obtaining an estimator that maximizes the partial likelihood (PL) of a subset of the full data, which is then updated using all subsets via one-step approximations. The updated estimator serves as a
starts with obtaining an estimator that maximizes the partial likelihood (PL) of a subset of the full data, which is then updated using all subsets via one-step approximations. The updated estimator serves as a 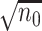 -consistent initial estimator for the aLASSO problem and approximates the full sample-based maximum PL estimator. Subsequently, we obtain the final aLASSO estimator based on an objective function applying the least square approximation (LSA) to the PL as in Wang and Leng (2007). The LSA allows us to fit the aLASSO using a pseudo-likelihood based on a sample of size
-consistent initial estimator for the aLASSO problem and approximates the full sample-based maximum PL estimator. Subsequently, we obtain the final aLASSO estimator based on an objective function applying the least square approximation (LSA) to the PL as in Wang and Leng (2007). The LSA allows us to fit the aLASSO using a pseudo-likelihood based on a sample of size 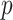 . The penalized regression is only fit once to a
. The penalized regression is only fit once to a 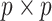 dimensional psuedo data in the proposed
dimensional psuedo data in the proposed 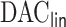 algorithm and the improvement in computation cost is substantial if
algorithm and the improvement in computation cost is substantial if 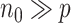 . Our proposed
. Our proposed 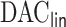 algorithm can also accommodate time-dependent covariates.
algorithm can also accommodate time-dependent covariates.
The rest of the article is organized as follows. We detail the 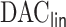 algorithm in Section 2. In Section 3, we present simulation results demonstrating the superiority of
algorithm in Section 2. In Section 3, we present simulation results demonstrating the superiority of 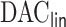 compared to the existing methods when covariates are time-independent and when some covariates are time-dependent. In Section 4, we employ the
compared to the existing methods when covariates are time-independent and when some covariates are time-dependent. In Section 4, we employ the 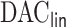 algorithm to develop risk prediction models for 30-day readmission after an index heart failure hospitalization with data from over 10 million Medicare patients by fitting regularized Cox models with (i)
algorithm to develop risk prediction models for 30-day readmission after an index heart failure hospitalization with data from over 10 million Medicare patients by fitting regularized Cox models with (i) 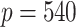 time-independent covariates and (ii)
time-independent covariates and (ii)  time-independent covariates and
time-independent covariates and 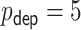 time-dependent environmental covariates. We conclude with some discussions in Section 5.
time-dependent environmental covariates. We conclude with some discussions in Section 5.
2. Methods
2.1. Notation and settings
Let 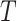 denote the survival time and
denote the survival time and 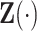 denote the
denote the  vector of bounded and potentially time-dependent covariates. Due to censoring, for
vector of bounded and potentially time-dependent covariates. Due to censoring, for 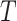 , we only observe
, we only observe 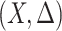 , where
, where 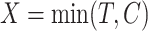 ,
, 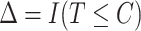 , and
, and 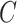 is the censoring time assumed to be independent of
is the censoring time assumed to be independent of  given
given 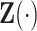 . Suppose the data for analysis consist of
. Suppose the data for analysis consist of 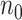 subjects with independent realizations of
subjects with independent realizations of 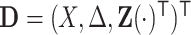 , denoted by
, denoted by 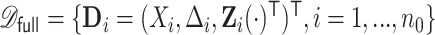 , where we assume that
, where we assume that 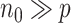 .
.
We denote the index set for the full data by 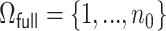 . For all DAC algorithms discussed in this article, we randomly partition
. For all DAC algorithms discussed in this article, we randomly partition 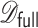 into
into 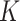 subsets with the
subsets with the 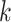 -th subset denoted by
-th subset denoted by 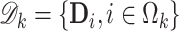 . Without loss of generality, we assume that
. Without loss of generality, we assume that  is an integer and that the index set for the subset
is an integer and that the index set for the subset  is
is 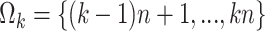 . For any index set
. For any index set 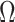 , we denote the size of
, we denote the size of 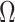 by
by 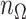 with
with 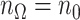 if
if 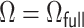 and
and  if
if 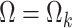 . Throughout we assume that
. Throughout we assume that 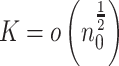 such that
such that 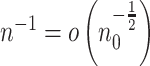 and
and 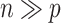 .
.
We aim to predict 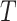 based on
based on 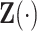 via a Cox model with conditional hazard function
via a Cox model with conditional hazard function
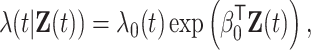 |
(2.1) |
where 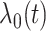 is the baseline hazard function. Our goal is to develop a computationally and statistically efficient procedure to estimate
is the baseline hazard function. Our goal is to develop a computationally and statistically efficient procedure to estimate 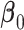 using
using 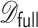 under the assumption that
under the assumption that  is sparse with the size of the active set
is sparse with the size of the active set 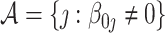 much smaller than
much smaller than 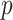 . When
. When 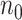 is not extraordinarily large, we may obtain an efficient estimate, denoted by
is not extraordinarily large, we may obtain an efficient estimate, denoted by 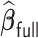 , based on the aLASSO penalized PL likelihood estimator as proposed in Zhang and Lu (2007). Specifically,
, based on the aLASSO penalized PL likelihood estimator as proposed in Zhang and Lu (2007). Specifically,
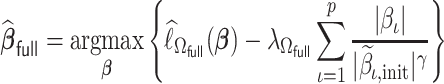 |
(2.2) |
where for any index set 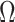 ,
,
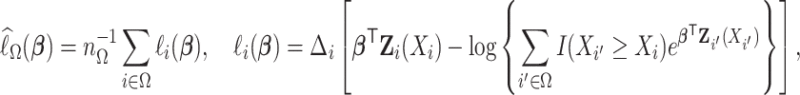 |
(2.3) |
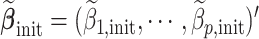 is an initial
is an initial 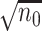 -consistent estimator of model (2.1),
-consistent estimator of model (2.1), 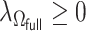 is a tuning parameter, and
is a tuning parameter, and 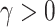 . A simple choice of
. A simple choice of 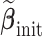 is
is 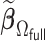 , where for any set
, where for any set  ,
,
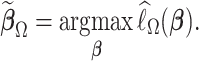 |
Following the arguments given in Zhang and Lu (2007), when 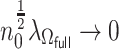 and
and 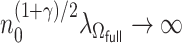 , we can show that
, we can show that  achieves the variable selection consistency, i.e. the estimated active set
achieves the variable selection consistency, i.e. the estimated active set  satisfies
satisfies  and that the oracle property holds, i.e.
and that the oracle property holds, i.e.
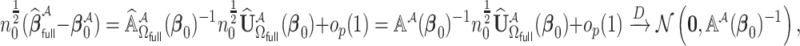 |
where  if
if  is a vector and
is a vector and  if
if  is a matrix,
is a matrix,
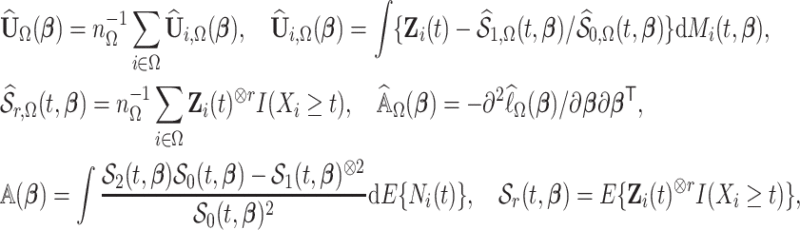 |
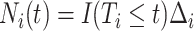 ,
, 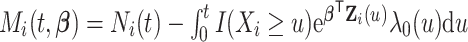 , and for any vector
, and for any vector  ,
, 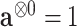 ,
, 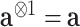 ,
, 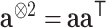 .
.
When 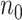 is not too large, multiple algorithms are available to solve (2.2) with time-independent covariates, including a coordinate gradient descent algorithm (Simon and others, 2011), a least angle regression-like algorithm (Park and Hastie, 2007), a combination of gradient descent-Newton Raphson method (Goeman, 2010), and a modified shooting algorithm (Zhang and Lu, 2007). Unfortunately, when
is not too large, multiple algorithms are available to solve (2.2) with time-independent covariates, including a coordinate gradient descent algorithm (Simon and others, 2011), a least angle regression-like algorithm (Park and Hastie, 2007), a combination of gradient descent-Newton Raphson method (Goeman, 2010), and a modified shooting algorithm (Zhang and Lu, 2007). Unfortunately, when 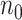 is extraordinarily large, existing algorithms for fitting (2.2) are highly computationally intensive and subject to memory constraints. These algorithms may even be infeasible to compute in the presence of time-dependent covariates as each subject contribute multiple observations in the fitting.
is extraordinarily large, existing algorithms for fitting (2.2) are highly computationally intensive and subject to memory constraints. These algorithms may even be infeasible to compute in the presence of time-dependent covariates as each subject contribute multiple observations in the fitting.
2.2. The 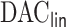 algorithm
algorithm
The goal of this article is to develop an estimator that achieves the same asymptotic efficiency as  but can be computed very efficiently.
but can be computed very efficiently.
Our proposed algorithm, 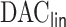 , for attaining such a property is motivated by the LSA proposed in Wang and Leng (2007), with the LSA applied to the full sample-based PL. Specifically, it is not difficult to show that
, for attaining such a property is motivated by the LSA proposed in Wang and Leng (2007), with the LSA applied to the full sample-based PL. Specifically, it is not difficult to show that 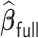 is asymptotically equivalent to
is asymptotically equivalent to 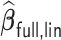 , where
, where
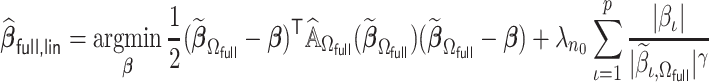 |
That is, 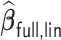 will also achieve the variable selection consistency as
will also achieve the variable selection consistency as 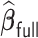 and
and  has the same limiting distribution as that of
has the same limiting distribution as that of 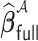 . This suggests that an estimator can recover the distribution of
. This suggests that an estimator can recover the distribution of 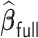 if we can construct accurate DAC approximations to
if we can construct accurate DAC approximations to  and
and 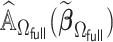 . To this end, we propose a linearization-based DAC estimator, denoted by
. To this end, we propose a linearization-based DAC estimator, denoted by  , which requires three main steps: (i) obtaining an estimator for the unpenalized problem
, which requires three main steps: (i) obtaining an estimator for the unpenalized problem  based on a subset, say
based on a subset, say 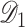 ; (ii) obtaining updated estimators for the unpenalized problem through one-step approximations using all
; (ii) obtaining updated estimators for the unpenalized problem through one-step approximations using all  subsets; and (iii) constructing an aLASSO penalized estimator based on LSA. The procedure also brings a
subsets; and (iii) constructing an aLASSO penalized estimator based on LSA. The procedure also brings a 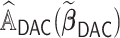 that well approximates
that well approximates  .
.
Specifically, in step (i), we use subset 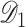 to obtain a standard maximum PL estimator,
to obtain a standard maximum PL estimator,
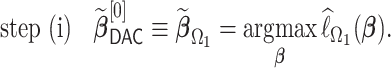 |
In step (ii), we obtain a DAC one-step approximation to 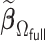 ,
,
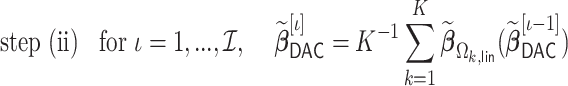 |
where
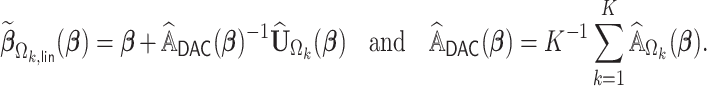 |
(2.4) |
Let 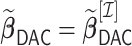 be our DAC approximation to
be our DAC approximation to 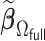 . In practice, we find that it suffices to let
. In practice, we find that it suffices to let 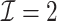 . Finally, we apply the LSA to the PL and approximate
. Finally, we apply the LSA to the PL and approximate 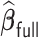 using
using 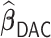 , where
, where
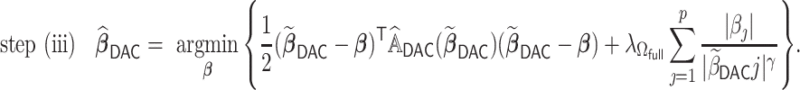 |
The optimization problem in step (iii) is equivalent to
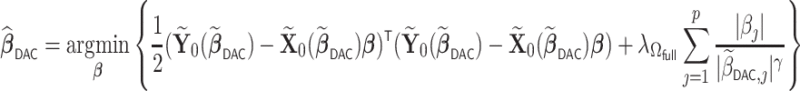 |
(2.5) |
where 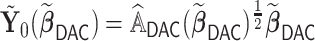 is a
is a  vector and
vector and 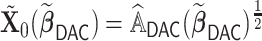 is a
is a  matrix. The linearization in step (iii) is exactly the same as that in Zhang and Lu (2007), which allows us to solve the penalized regression step using a pseudo likelihood based on a sample of size
matrix. The linearization in step (iii) is exactly the same as that in Zhang and Lu (2007), which allows us to solve the penalized regression step using a pseudo likelihood based on a sample of size 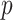 . The computation cost of this step compared to solving (2.2) reduces substantially when
. The computation cost of this step compared to solving (2.2) reduces substantially when 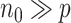 . In the Appendix of the supplementary material available at Biostatistics online, we show that
. In the Appendix of the supplementary material available at Biostatistics online, we show that 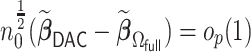 . It then follows from the similar arguments given in Wang and Leng (2007) that if
. It then follows from the similar arguments given in Wang and Leng (2007) that if 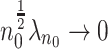 ,
, 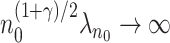 , the estimated active set using
, the estimated active set using 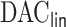
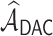 achieves the variable selection consistency, i.e.
achieves the variable selection consistency, i.e. 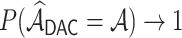 and the oracle property holds, i.e.
and the oracle property holds, i.e. 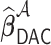 and
and 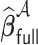 have the same limiting distribution.
have the same limiting distribution.
2.3. Tuning and standard error calculation
The tuning parameter 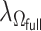 is chosen by minimizing the Bayesian information criteria (BIC) of the fitted model. Volinsky and Raftery (2000) showed that the exact Bayes factor can be better approximated for the Cox model if the number of uncensored cases,
is chosen by minimizing the Bayesian information criteria (BIC) of the fitted model. Volinsky and Raftery (2000) showed that the exact Bayes factor can be better approximated for the Cox model if the number of uncensored cases, 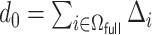 , is used to penalize the degrees of freedom in the BIC. Specifically, for any given tuning parameter
, is used to penalize the degrees of freedom in the BIC. Specifically, for any given tuning parameter 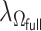 with its corresponding estimate of
with its corresponding estimate of 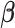 ,
, 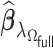 , the BIC suggested by Volinsky and Raftery (2000) is defined as
, the BIC suggested by Volinsky and Raftery (2000) is defined as
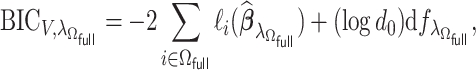 |
(2.6) |
where 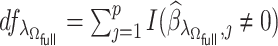 . With the LSA, we may further approximate
. With the LSA, we may further approximate 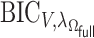 by
by
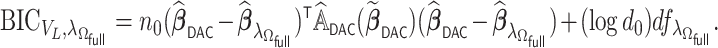 |
(2.7) |
For the estimation of 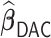 , we chose a
, we chose a 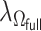 such that
such that 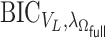 is minimized. The oracle property is expected to hold in the setting where
is minimized. The oracle property is expected to hold in the setting where 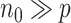 and
and 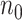 is extraordinarily large. We may thus estimate the variance-covariance matrix for
is extraordinarily large. We may thus estimate the variance-covariance matrix for 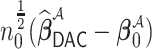 using
using  . For
. For 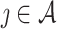 , a
, a  confidence interval for
confidence interval for 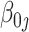 can be calculated accordingly.
can be calculated accordingly.
3. Simulations
3.1. Simulation settings
We performed two sets of simulations to evaluate the performance of 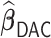 for the fitting of sparse Cox models, one with only time-independent covariates and the other with time-dependent covariates. For both scenarios, we focused primarily on
for the fitting of sparse Cox models, one with only time-independent covariates and the other with time-dependent covariates. For both scenarios, we focused primarily on 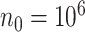 and
and 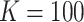 . We consider the number of iterations
. We consider the number of iterations 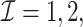 and
and 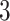 to examine the impact of
to examine the impact of 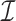 on the proposed estimator.
on the proposed estimator.
3.1.1. Time-independent covariates
We conducted extensive simulations to evaluate the performance of the proposed estimator 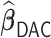 relative to (a) the performance of the full sample-based aLASSO estimator for the Cox model
relative to (a) the performance of the full sample-based aLASSO estimator for the Cox model  and (b) a majority voting-based DAC method for the Cox model, denoted by
and (b) a majority voting-based DAC method for the Cox model, denoted by  also with
also with 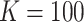 , penalized by a minimax concave penalty (MCP), which extends the majority voting-based DAC scheme for GLM proposed by Chen and Xie (2014). The reason of choosing
, penalized by a minimax concave penalty (MCP), which extends the majority voting-based DAC scheme for GLM proposed by Chen and Xie (2014). The reason of choosing 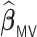 as a comparison is that there is no other DAC method available for the Cox model and only Chen and Xie (2014) considered a similar majority voting-based DAC method for the penalized GLM with non-adaptive penalties. We set a priori that
as a comparison is that there is no other DAC method available for the Cox model and only Chen and Xie (2014) considered a similar majority voting-based DAC method for the penalized GLM with non-adaptive penalties. We set a priori that 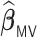 sets the estimate of a coefficient at zero, if at least 50% of the subset-specific estimates have a zero estimate for that coefficient. In addition, we compared the performance of the DAC estimator
sets the estimate of a coefficient at zero, if at least 50% of the subset-specific estimates have a zero estimate for that coefficient. In addition, we compared the performance of the DAC estimator 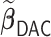 relative to the full sample maximum PL estimator
relative to the full sample maximum PL estimator 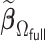 .
.
For the penalized procedures, we selected the tuning parameter based on the BIC discussed in Section 2.3. The aLASSO procedures were fit using the 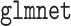 function in R package
function in R package 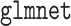 (Friedman and others, 2010; Simon and others, 2011; R Core Team, 2017) with
(Friedman and others, 2010; Simon and others, 2011; R Core Team, 2017) with 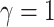 ; the MCP procedures were fit using the
; the MCP procedures were fit using the  function in R package
function in R package  (Breheny and Huang, 2011; R Core Team, 2017). When there are ties among failure times, we used the Efron’s method within each data subset (Efron, 1977).
(Breheny and Huang, 2011; R Core Team, 2017). When there are ties among failure times, we used the Efron’s method within each data subset (Efron, 1977).
For the covariates, we considered 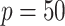 and
and 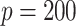 . We generated
. We generated 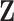 from a multivariate normal distribution with mean
from a multivariate normal distribution with mean 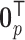 and variance-covariance matrix
and variance-covariance matrix 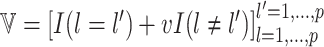 , where
, where 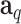 denotes a
denotes a 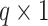 vector with all elements being
vector with all elements being 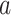 and we considered
and we considered  ,
, 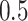 , and
, and  to represent weak, moderate, and strong correlations among the covariates. For a given
to represent weak, moderate, and strong correlations among the covariates. For a given 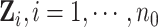 , we generated
, we generated 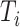 from a Weibull distribution with a shape parameter of 2 and a scale parameter of
from a Weibull distribution with a shape parameter of 2 and a scale parameter of 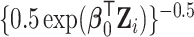 , where we considered three choices of
, where we considered three choices of 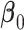 to reflect different degrees of sparsity and signal strength:
to reflect different degrees of sparsity and signal strength:
 |
For censoring, we generated 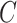 from an exponential distribution with a rate parameter of
from an exponential distribution with a rate parameter of 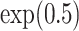 , resulting in
, resulting in 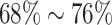 of censoring across different configurations.
of censoring across different configurations.
We additionally considered 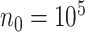 ,
,  ,
, 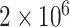 and
and 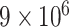 to evaluate how different choices of
to evaluate how different choices of 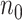 impact the relative performance of different procedures.
impact the relative performance of different procedures.
3.1.2. Time-dependent covariates
We also conducted simulations for the settings where time-dependent covariates are present to evaluate the performance of 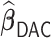 . Since neither
. Since neither 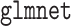 nor
nor 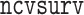 allows time-dependent survival data, we used
allows time-dependent survival data, we used 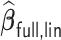 as a benchmark to compare
as a benchmark to compare 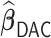 with. In addition, we compared the performance of
with. In addition, we compared the performance of 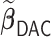 relative to
relative to 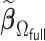 .
.
We considered 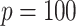 consisting of
consisting of  time-independent covariates and
time-independent covariates and 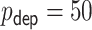 time-dependent covariates. The simulation of the survival data with time-dependent covariates extended the simulation scheme of Austin (2012) from dichotomous time-dependent covariates to continuous time-dependent covariates. We considered four time intervals
time-dependent covariates. The simulation of the survival data with time-dependent covariates extended the simulation scheme of Austin (2012) from dichotomous time-dependent covariates to continuous time-dependent covariates. We considered four time intervals 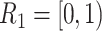 ,
, 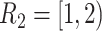 ,
, 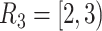 , and
, and 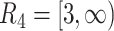 , where the time-dependent covariates are constant within each interval but can vary between intervals. We generated
, where the time-dependent covariates are constant within each interval but can vary between intervals. We generated 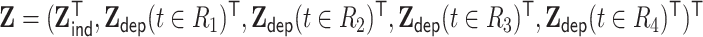 from a multivariate normal distribution with mean
from a multivariate normal distribution with mean 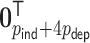 and variance-covariance matrix
and variance-covariance matrix 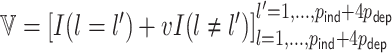 , where
, where  are the time-independent covariates and
are the time-independent covariates and 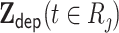 are the time-dependent for
are the time-dependent for 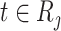 . We similarly considered
. We similarly considered 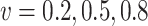 to represent weak, moderate, and strong correlations.
to represent weak, moderate, and strong correlations.
We generated 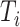 from a Weibull distribution with a shape parameter of 2 and a scale parameter of
from a Weibull distribution with a shape parameter of 2 and a scale parameter of 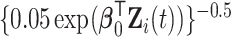 , where
, where 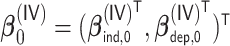 ,
,
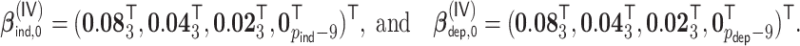 |
We considered an administrative censoring with 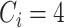 , leading to
, leading to 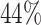 censoring under the three scenarios represented by weak, moderate, and strong correlations of the design matrix.
censoring under the three scenarios represented by weak, moderate, and strong correlations of the design matrix.
3.1.3. Measures of performance
For any 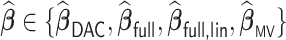 , we report (i) the average computation time for
, we report (i) the average computation time for 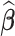 ; (ii) the global mean squared error (GMSE), defined as
; (ii) the global mean squared error (GMSE), defined as 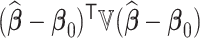 ; (iii) empirical probability of
; (iii) empirical probability of 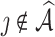 ; (iv) the bias of each individual coefficient; and (v) mean squared error (MSE) of each individual coefficient. For
; (iv) the bias of each individual coefficient; and (v) mean squared error (MSE) of each individual coefficient. For  and
and  , we also report the empirical coverage level of the 95% normal confidence interval with standard error estimated as described in Section 2.3. For any
, we also report the empirical coverage level of the 95% normal confidence interval with standard error estimated as described in Section 2.3. For any 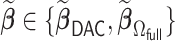 , we report (i) the average computation time for
, we report (i) the average computation time for 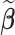 ; (ii) the global mean squared error (GMSE), defined as
; (ii) the global mean squared error (GMSE), defined as 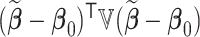 .
.
When only computing time is of interest, we calculate the average computation time for each configuration by averaging over 10 simulated datasets performed on Intel® Xeon® CPU E5-2697 v3 @ 2.60GHz. The average computation time for each configuration in the time-dependent settings is based on simulations using 50 simulated datasets performed on Intel® Xeon® E5-2620 v3 @2.40GHz. The statistical performance is evaluated based on 1000 simulated datasets for each configuration. Although the DAC algorithms can be more efficiently implemented via parallel computing, we report the computational time for DAC algorithms carried out without parallelization for fair comparisons to other algorithms, and for each simulation, we run a single-core job including all the methods under comparison.
3.2. Simulation results
We first show in Table 1, the average computation time and GMSE of unpenalized estimators 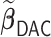 and
and 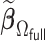 . The results suggest that
. The results suggest that 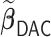 with two iterations (
with two iterations (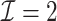 ) attains a GMSE comparable to the full sample-based estimator
) attains a GMSE comparable to the full sample-based estimator 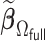 and reduced the computation time by more than 50%. The DAC estimator
and reduced the computation time by more than 50%. The DAC estimator 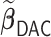 with two iterations (
with two iterations (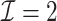 ) has a similar GMSE to
) has a similar GMSE to 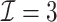 . Across all settings, the results of
. Across all settings, the results of  are nearly identical with
are nearly identical with 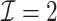 or
or 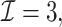 and hence we summarize below the results for
and hence we summarize below the results for 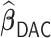 only for
only for 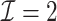 unless noted otherwise.
unless noted otherwise.
Table 1.
Comparisons of 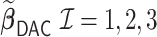 and
and 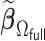 with respect to average computation time in seconds and global mean squared error (GMSE
with respect to average computation time in seconds and global mean squared error (GMSE  ) for the estimation of
) for the estimation of 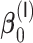 ,
,  ,
, 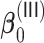 , and
, and 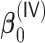
| (a) Time-independent | ||||||||
|---|---|---|---|---|---|---|---|---|
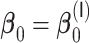
|
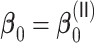
|
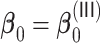
|
||||||

|
Estimator | Time | GMSE | Time | GMSE | Time | GMSE | |
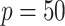
|
||||||||
| 0.20 |

|
5.2 | 19.3 | 4.5 | 21.1 | 4.3 | 21.2 | |

|

|
10.1 | 19.3 | 8.7 | 21.1 | 8.4 | 21.2 | |
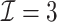
|
15.1 | 19.3 | 12.9 | 21.1 | 12.4 | 21.2 | ||

|
26.1 | 19.2 | 24.0 | 21.0 | 24.2 | 21.1 | ||
| 0.50 |
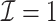
|
6.3 | 18.1 | 5.8 | 19.5 | 5.5 | 20.4 | |
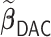
|
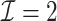
|
10.3 | 18.1 | 9.8 | 19.5 | 9.3 | 20.4 | |
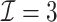
|
14.3 | 18.1 | 13.7 | 19.5 | 13.2 | 20.4 | ||
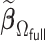
|
32.9 | 18.0 | 31.3 | 19.4 | 30.3 | 20.4 | ||
| 0.80 |
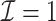
|
5.3 | 17.9 | 5.2 | 18.7 | 5.1 | 19.7 | |
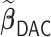
|
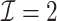
|
9.2 | 17.8 | 9.0 | 18.7 | 8.9 | 19.7 | |

|
13.1 | 17.8 | 12.9 | 18.7 | 12.8 | 19.7 | ||
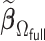
|
30.3 | 17.7 | 29.6 | 18.6 | 29.2 | 19.7 | ||

|
||||||||
| 0.20 |
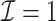
|
10.2 | 74.9 | 13.9 | 83.8 | 17.1 | 85.0 | |
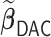
|
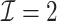
|
19.0 | 74.5 | 26.4 | 83.4 | 32.7 | 84.6 | |
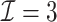
|
27.8 | 74.5 | 38.8 | 83.4 | 48.2 | 84.6 | ||
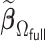
|
62.0 | 74.3 | 83.1 | 83.2 | 102 | 84.4 | ||
| 0.50 |

|
20.5 | 69.0 | 22.8 | 76.5 | 24.7 | 80.6 | |
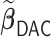
|
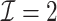
|
39.3 | 68.3 | 43.9 | 76.1 | 47.7 | 80.3 | |

|
58.0 | 68.3 | 64.8 | 76.1 | 70.5 | 80.3 | ||

|
126 | 68.1 | 142 | 75.9 | 151 | 80.1 | ||
| 0.80 |
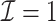
|
26.9 | 66.0 | 28.6 | 72.0 | 30.0 | 77.3 | |
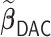
|

|
51.9 | 65.0 | 55.2 | 71.5 | 57.9 | 76.9 | |
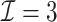
|
76.8 | 65.0 | 81.7 | 71.5 | 85.7 | 76.9 | ||
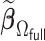
|
169 | 64.9 | 180 | 71.3 | 190 | 76.7 | ||
| (b) Time-dependent | ||||
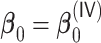
|
||||
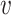
|
Estimator | Time | GMSE | |
| 0.2 |
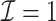
|
62.0 | 17.9 | |
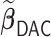
|
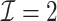
|
121 | 17.9 | |
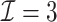
|
179 | 17.9 | ||

|
262 | 18.0 | ||
| 0.5 |
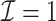
|
58.0 | 17.9 | |
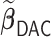
|
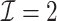
|
112 | 17.9 | |

|
166 | 17.9 | ||
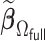
|
263 | 17.9 | ||
| 0.8 |
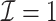
|
58.3 | 18.0 | |
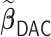
|
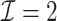
|
114 | 18.0 | |
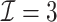
|
169 | 18.0 | ||
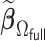
|
254 | 17.9 | ||
3.2.1. Computation time
The computation time is summarized in Tables 2 and 3 for 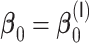 and
and 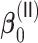 , and Tables S1 and S2 of supplementary material available at Biostatistics online for
, and Tables S1 and S2 of supplementary material available at Biostatistics online for 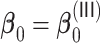 for time-independent survival data. There are substantial differences in computation time across methods. Across different settings, the average computation time of
for time-independent survival data. There are substantial differences in computation time across methods. Across different settings, the average computation time of 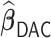 ranges from
ranges from 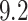 to
to  s for
s for  and from
and from 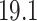 to
to 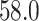 s for
s for 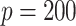 , with virtually all time spent on the computation of the unpenalized estimator
, with virtually all time spent on the computation of the unpenalized estimator 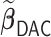 . On the contrary,
. On the contrary, 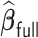 requires a substantially longer computation time with average time ranging from
requires a substantially longer computation time with average time ranging from 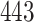 to
to 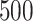 s for
s for 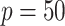 and from
and from 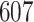 to
to 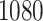 s for
s for 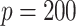 . This suggests that the computation time of
. This suggests that the computation time of  is about
is about 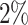 of the full sample estimator when
of the full sample estimator when 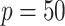 and about
and about 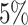 when
when  . On the other hand,
. On the other hand, 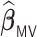 has a substantially longer average computation time than
has a substantially longer average computation time than  . This is because the MCP procedure, requiring more computational time than the aLASSO, needs to be fitted
. This is because the MCP procedure, requiring more computational time than the aLASSO, needs to be fitted  times. As shown in Table S3 of supplementary material available at Biostatistics online, when the sample size varies from
times. As shown in Table S3 of supplementary material available at Biostatistics online, when the sample size varies from 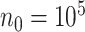 to
to 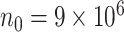 , the computation time increases for all methods but the increase is more drastic for
, the computation time increases for all methods but the increase is more drastic for 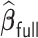 and
and 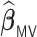 . The full sample estimator
. The full sample estimator 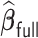 can only be calculated when requesting a very large memory (150GB) when
can only be calculated when requesting a very large memory (150GB) when 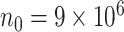 while
while  can be computed with a much smaller memory.
can be computed with a much smaller memory.
Table 2.
Comparisons of  ,
, 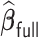 , and
, and 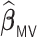 for estimating
for estimating 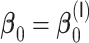 with respect to average computation time in seconds, GMSE (
with respect to average computation time in seconds, GMSE (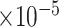 ), coefficient-specific empirical probability (%) of
), coefficient-specific empirical probability (%) of 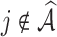 , bias (
, bias (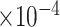 ), MSE (
), MSE (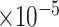 ), and empirical coverage probability (%) of the confidence intervals
), and empirical coverage probability (%) of the confidence intervals
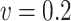
|
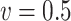
|

|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

|
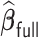
|
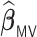
|
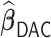
|
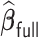
|

|

|
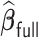
|
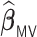
|
||||||||
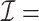
|
|
|
|
|
|

|

|
|
|
|||||||
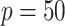
|
||||||||||||||||
| TIME | 5.20 | 10.2 | 15.1 | 443 | 1451 | 6.30 | 10.3 | 14.3 | 499 | 1642 | 5.30 | 9.20 | 13.1 | 500 | 1652 | |
| GMSE | 4.32 | 4.27 | 4.27 | 4.24 | 5.61 | 4.53 | 4.42 | 4.42 | 4.41 | 7.40 | 5.17 | 5.01 | 5.01 | 4.97 | 9.91 | |
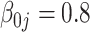
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –0.74 | 0.49 | 0.49 | 0.63 | 12.9 | –1.64 | –0.24 | –0.24 | –0.19 | 12.3 | –0.27 | 1.16 | 1.16 | 1.16 | 14.7 | |
| MSE | 0.55 | 0.55 | 0.55 | 0.55 | 0.72 | 0.70 | 0.70 | 0.70 | 0.70 | 0.86 | 1.50 | 1.50 | 1.50 | 1.50 | 1.76 | |
| CovP | 94.4 | 94.7 | 94.7 | — | — | 94.4 | 94.7 | 94.7 | — | — | 94.6 | 94.7 | 94.7 | — | — | |
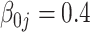
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –1.47 | –0.85 | –0.85 | –0.72 | 5.61 | –0.63 | 0.07 | 0.07 | 0.03 | 6.55 | –0.02 | 0.72 | 0.72 | 0.73 | 8.81 | |
| MSE | 0.49 | 0.48 | 0.48 | 0.48 | 0.52 | 0.55 | 0.55 | 0.55 | 0.55 | 0.60 | 1.48 | 1.48 | 1.48 | 1.46 | 1.60 | |
| CovP | 93.0 | 93.3 | 93.3 | — | — | 94.9 | 95.1 | 95.1 | — | — | 95.0 | 95.1 | 95.1 | — | — | |
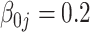
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –1.39 | –1.09 | –1.09 | –1.18 | 2.75 | –0.82 | –0.49 | –0.49 | –0.44 | 3.88 | –3.37 | –3.02 | –3.02 | –2.87 | –3.18 | |
| MSE | 0.44 | 0.44 | 0.44 | 0.44 | 0.46 | 0.63 | 0.63 | 0.63 | 0.63 | 0.67 | 1.49 | 1.48 | 1.48 | 1.48 | 1.76 | |
| CovP | 94.5 | 94.4 | 94.4 | — | — | 94.4 | 94.3 | 94.3 | — | — | 94.4 | 94.4 | 94.4 | — | — | |
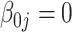
|
%zero | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Bias | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| MSE | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
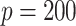
|
||||||||||||||||
| TIME | 10.2 | 19.1 | 27.8 | 607 | 2246 | 20.6 | 39.4 | 58.1 | 859 | 3316 | 27.0 | 52.0 | 76.9 | 1016 | 3641 | |
| GMSE | 4.62 | 4.10 | 4.10 | 4.08 | 5.50 | 5.83 | 4.61 | 4.61 | 4.61 | 9.50 | 6.91 | 5.05 | 5.05 | 5.06 | 17.0 | |
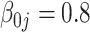
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –5.46 | 0.31 | 0.31 | 0.27 | 13.2 | –6.75 | 0.25 | 0.25 | 0.33 | 16.0 | –6.38 | 0.94 | 0.94 | 0.84 | 20.7 | |
| MSE | 0.58 | 0.53 | 0.53 | 0.53 | 0.71 | 0.77 | 0.70 | 0.70 | 0.70 | 0.97 | 1.49 | 1.45 | 1.45 | 1.45 | 1.96 | |
| CovP | 94.4 | 94.7 | 94.7 | — | — | 94.2 | 94.7 | 94.7 | — | — | 94.3 | 94.8 | 94.8 | — | — | |
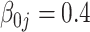
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –2.09 | 0.80 | 0.80 | 0.81 | 7.88 | –3.11 | 0.29 | 0.29 | 0.43 | 8.89 | –3.47 | 0.24 | 0.24 | 0.57 | 11.4 | |
| MSE | 0.45 | 0.44 | 0.44 | 0.44 | 0.51 | 0.68 | 0.66 | 0.66 | 0.66 | 0.76 | 1.42 | 1.42 | 1.42 | 1.42 | 1.62 | |
| CovP | 94.9 | 95.0 | 95.0 | — | — | 94.7 | 94.8 | 94.8 | — | — | 94.8 | 94.9 | 94.9 | — | — | |
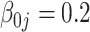
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –4.15 | –2.68 | –2.68 | –2.69 | 0.40 | –4.15 | –2.44 | –2.44 | –2.52 | 3.63 | –2.02 | –0.15 | –0.15 | –0.09 | 1.09 | |
| MSE | 0.44 | 0.43 | 0.43 | 0.43 | 0.45 | 0.61 | 0.60 | 0.60 | 0.60 | 0.61 | 1.34 | 1.33 | 1.33 | 1.33 | 1.62 | |
| CovP | 94.5 | 94.6 | 94.6 | — | — | 94.5 | 94.6 | 94.6 | — | — | 94.7 | 94.9 | 94.9 | — | — | |
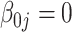
|
%zero | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Bias | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| MSE | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Table 3.
Comparisons of 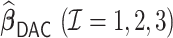 ,
, 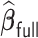 , and
, and 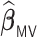 for estimating
for estimating 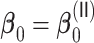 with respect to average computation time in seconds, GMSE (
with respect to average computation time in seconds, GMSE (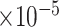 ), coefficient-specific empirical probability (%) of
), coefficient-specific empirical probability (%) of 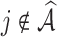 , bias (
, bias (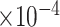 ), MSE (
), MSE (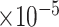 ), and empirical coverage probability (%) of the confidence intervals
), and empirical coverage probability (%) of the confidence intervals
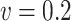
|
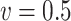
|
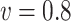
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
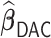
|
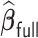
|
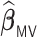
|
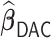
|
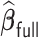
|
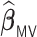
|
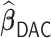
|
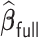
|
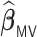
|
||||||||

|
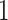
|
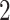
|
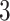
|

|
|

|
|
|
|
|||||||
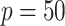
|
||||||||||||||||
| TIME | 4.5 | 8.7 | 12.9 | 461 | 1554 | 5.9 | 9.8 | 13.7 | 497 | 1628 | 5.2 | 9.1 | 12.9 | 499 | 1657 | |
| GMSE | 7.27 | 7.24 | 7.24 | 7.22 | 870 | 6.92 | 6.86 | 6.86 | 6.84 | 1176 | 7.21 | 7.12 | 7.12 | 7.17 | 4452 | |
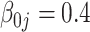
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | 1.14 | 1.59 | 1.59 | 1.60 | 97.8 | 1.47 | 2.07 | 2.07 | 2.11 | 110 | 4.82 | 5.45 | 5.45 | 1.39 | 219 | |
| MSE | 0.53 | 0.53 | 0.53 | 0.53 | 10.1 | 0.71 | 0.71 | 0.71 | 0.71 | 12.8 | 1.70 | 1.70 | 1.70 | 1.68 | 49.6 | |
| CovP | 94.4 | 94.8 | 94.8 | — | — | 94.5 | 94.9 | 94.9 | — | — | 94.5 | 94.8 | 94.8 | — | — | |
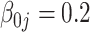
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | 0.72 | 0.94 | 0.94 | 1.14 | 98.3 | 1.61 | 1.90 | 1.90 | 2.02 | 108 | 3.63 | 3.95 | 3.95 | 1.06 | 206 | |
| MSE | 0.50 | 0.50 | 0.50 | 0.50 | 10.2 | 0.76 | 0.76 | 0.76 | 0.75 | 12.4 | 1.65 | 1.65 | 1.65 | 1.66 | 44.2 | |
| CovP | 95.0 | 95.1 | 95.1 | — | — | 95.0 | 95.1 | 95.1 | — | — | 95.0 | 95.1 | 95.1 | — | — | |
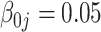
|
%zero | 0 | 0 | 0 | 0 | 61.6 | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 |
| Bias | –4.21 | –4.16 | –4.16 | –4.21 |
 407 407 |
–5.65 | –5.55 | –5.55 | –5.52 |
 500 500 |
–11.4 | –11.3 | –11.3 | –7.22 |
 500 500 |
|
| MSE | 0.50 | 0.50 | 0.50 | 0.49 | 180 | 0.71 | 0.71 | 0.71 | 0.70 | 250 | 2.08 | 2.07 | 2.07 | 2.05 | 250 | |
| CovP | 95.2 | 95.2 | 95.2 | — | — | 94.8 | 94.9 | 94.9 | — | — | 91.5 | 91.7 | 91.7 | — | — | |
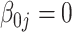
|
%zero | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 99.9 | 100 | 100 | 100 | 100 |
| Bias | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.09 | 0 | 0 | 0 | 0 | |
| MSE | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.01 | 0 | 0 | 0 | 0 | |
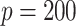
|
||||||||||||||||
| TIME | 14.0 | 26.5 | 38.9 | 696 | 2755 | 22.9 | 43.9 | 64.9 | 920 | 3465 | 28.7 | 55.3 | 81.8 | 1051 | 3764 | |
| GMSE | 7.53 | 7.29 | 7.29 | 7.28 | 1496 | 7.58 | 7.05 | 7.05 | 7.03 | 1300 | 8.38 | 7.46 | 7.46 | 7.67 | 12696 | |
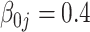
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –0.02 | 2.00 | 2.00 | 2.07 | 139 | 0.84 | 3.59 | 3.59 | 3.58 | 125.2 | 5.70 | 8.81 | 8.81 | 0.58 | 172 | |
| MSE | 0.54 | 0.54 | 0.54 | 0.54 | 19.8 | 0.80 | 0.79 | 0.79 | 0.79 | 16.5 | 1.62 | 1.67 | 1.67 | 1.62 | 31.2 | |
| CovP | 95.4 | 94.9 | 94.9 | — | — | 94.8 | 94.9 | 94.9 | — | — | 96.3 | 96.2 | 96.2 | — | — | |

|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –0.02 | 0.99 | 0.99 | 1.08 | 142 | 0.15 | 1.59 | 1.59 | 1.77 | 122 | 3.94 | 5.37 | 5.37 | 5.56 | 151 | |
| MSE | 0.49 | 0.49 | 0.49 | 0.49 | 20.8 | 0.75 | 0.75 | 0.75 | 0.74 | 15.8 | 1.72 | 1.73 | 1.73 | 1.79 | 25.1 | |
| CovP | 96.4 | 96.4 | 96.4 | — | — | 95.4 | 95.2 | 95.2 | — | — | 95.1 | 95.3 | 95.3 | — | — | |

|
%zero | 0 | 0 | 0 | 0 | 99.1 | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 100 |
| Bias | –6.39 | –6.07 | –6.07 | –6.08 |
 498 498 |
–8.32 | –7.92 | –7.92 | –7.83 |
 500 500 |
–18.5 | –18.1 | –18.1 | –15.4 |
 500 500 |
|
| MSE | 0.59 | 0.57 | 0.57 | 0.57 | 249 | 0.84 | 0.82 | 0.82 | 0.82 | 250 | 2.38 | 2.38 | 2.38 | 2.43 | 250 | |
| CovP | 93.6 | 93.2 | 93.2 | — | — | 93.1 | 93.5 | 93.5 | — | — | 90.5 | 91.0 | 91.0 | — | — | |
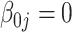
|
%zero | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Bias | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| MSE | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
In the presence of time-dependent covariates, Table 4 shows that 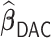 has an average computation time of 112–121 s for
has an average computation time of 112–121 s for 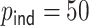 and
and  ;
; 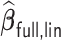 has an average computation time of 254–264 s. Virtually all computation time for
has an average computation time of 254–264 s. Virtually all computation time for 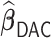 and
and 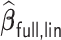 is spent on the computation of the unpenalized initial estimator
is spent on the computation of the unpenalized initial estimator 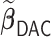 , which has more observations and requires substantially more computation time compared to the setting with time-independent covariates given the same
, which has more observations and requires substantially more computation time compared to the setting with time-independent covariates given the same 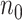 and
and  .
.
Table 4.
Performance of 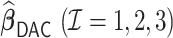 and
and 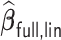 for estimating
for estimating 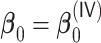 with respect to average computation time in seconds, GMSE (
with respect to average computation time in seconds, GMSE (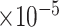 ), coefficient-specific empirical probability (%) of
), coefficient-specific empirical probability (%) of 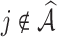 , bias (
, bias (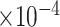 ), MSE (
), MSE (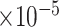 ), and empirical coverage probability (%) of the confidence intervals
), and empirical coverage probability (%) of the confidence intervals
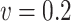
|
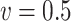
|
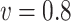
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

|
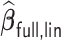
|
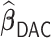
|

|
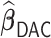
|
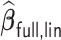
|
||||||||
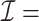
|
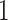
|
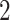
|
|
|
|
|
|
|
|
||||
| Time | 62.0 | 121 | 179 | 262 | 58.0 | 112 | 166 | 264 | 58.3 | 114 | 169 | 254 | |
| GMSE | 3.55 | 3.55 | 3.55 | 3.55 | 3.68 | 3.68 | 3.68 | 3.69 | 4.44 | 4.44 | 4.44 | 4.44 | |
| Time-independent covariates | |||||||||||||
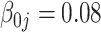
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | 1.45 | 1.46 | 1.46 | 1.46 | 4.62 | 4.63 | 4.63 | 4.65 | 11.9 | 11.9 | 11.9 | 12.0 | |
| MSE | 0.22 | 0.22 | 0.22 | 0.22 | 0.36 | 0.36 | 0.36 | 0.36 | 1.02 | 1.02 | 1.02 | 1.03 | |
| CovP | 95.7 | 95.7 | 95.7 | 95.8 | 94.6 | 94.6 | 94.6 | 94.7 | 93.9 | 93.9 | 93.9 | 93.5 | |
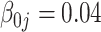
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –0.19 | –0.19 | –0.19 | –0.14 | 0.53 | 0.54 | 0.54 | 0.61 | 3.45 | 3.47 | 3.47 | 3.45 | |
| MSE | 0.22 | 0.22 | 0.22 | 0.22 | 0.33 | 0.33 | 0.33 | 0.33 | 0.93 | 0.93 | 0.93 | 0.93 | |
| CovP | 95.4 | 95.5 | 95.5 | 95.5 | 96.0 | 96.1 | 96.1 | 96.0 | 93.7 | 93.8 | 93.8 | 93.7 | |
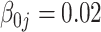
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –4.55 | –4.56 | –4.56 | –4.58 | –6.79 | –6.78 | –6.78 | –6.89 | –17.4 | –17.4 | –17.4 | –17.2 | |
| MSE | 0.25 | 0.25 | 0.25 | 0.25 | 0.45 | 0.45 | 0.45 | 0.45 | 1.59 | 1.59 | 1.59 | 1.57 | |
| CovP | 94.1 | 94.1 | 94.1 | 94.4 | 90.5 | 90.8 | 90.8 | 90.8 | 86.8 | 86.7 | 86.7 | 86.8 | |
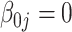
|
%zero | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Bias | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| MSE | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Time-independent covariates | |||||||||||||
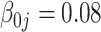
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | 1.01 | 1.01 | 1.01 | 1.04 | 2.65 | 2.65 | 2.65 | 2.61 | 9.72 | 9.74 | 9.74 | 9.74 | |
| MSE | 0.21 | 0.21 | 0.21 | 0.21 | 0.37 | 0.37 | 0.37 | 0.38 | 0.93 | 0.93 | 0.93 | 0.95 | |
| CovP | 96.3 | 96.3 | 96.3 | 96.3 | 94.6 | 94.6 | 94.6 | 94.4 | 95.6 | 95.5 | 95.5 | 95.4 | |
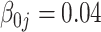
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –1.01 | –1.01 | –1.01 | –1.01 | 1.11 | 1.11 | 1.11 | 1.15 | 3.26 | 3.26 | 3.26 | 3.19 | |
| MSE | 0.21 | 0.21 | 0.21 | 0.21 | 0.33 | 0.33 | 0.33 | 0.33 | 0.93 | 0.93 | 0.93 | 0.94 | |
| CovP | 95.8 | 95.9 | 95.9 | 96.0 | 95.2 | 95.2 | 95.2 | 95.3 | 94.9 | 94.8 | 94.8 | 95.0 | |
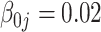
|
%zero | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bias | –3.81 | –3.81 | –3.81 | –3.81 | –6.28 | –6.26 | –6.26 | –6.30 | –16.5 | –16.5 | –16.5 | –16.6 | |
| MSE | 0.26 | 0.26 | 0.26 | 0.25 | 0.45 | 0.45 | 0.45 | 0.45 | 1.49 | 1.48 | 1.48 | 1.49 | |
| CovP | 93.8 | 93.8 | 93.8 | 93.5 | 91.2 | 91.1 | 91.1 | 91.4 | 86.2 | 86.1 | 86.1 | 86.0 | |
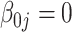
|
%zero | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Bias | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| MSE | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
3.2.2. Statistical performance
The results for the simulation scenarios with only time-independent covariates are summarized in Tables 2 and 3 for 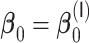 and
and 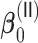 , and Tables S1 and S2 of supplementary material available at Biostatistics online for
, and Tables S1 and S2 of supplementary material available at Biostatistics online for 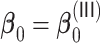 . In general,
. In general, 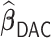 is able to achieve a statistical performance comparable to
is able to achieve a statistical performance comparable to 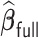 , while
, while 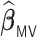 generally has a worse performance, with respect to the GMSE and variable selection, bias, and MSE of individual coefficient. For example, as shown in Table 2, the GMSEs (
generally has a worse performance, with respect to the GMSE and variable selection, bias, and MSE of individual coefficient. For example, as shown in Table 2, the GMSEs (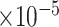 ) for
) for 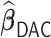 ,
, 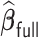 , and
, and 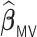 are respectively
are respectively 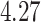 ,
, 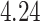 , and
, and 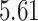 when
when 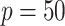 and
and 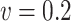 ;
; 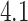 ,
, 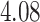 ,
, 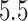 when
when  and
and 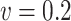 . The relative performance of different procedures has similar patterns across different levels of correlation
. The relative performance of different procedures has similar patterns across different levels of correlation 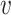 among the covariates. When the signals are relatively strong and sparse as for
among the covariates. When the signals are relatively strong and sparse as for 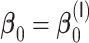 or
or 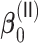 ,
, 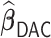 and
and 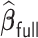 have small biases and achieved perfect variable selection, while
have small biases and achieved perfect variable selection, while 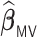 substantially excludes the
substantially excludes the 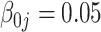 signal when
signal when 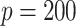 . For the more challenging case of
. For the more challenging case of 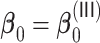 where some of the signals are weak, the variable selection of
where some of the signals are weak, the variable selection of 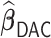 and
and 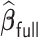 is also near perfect. Both penalized estimators for the weakest signal (0.035) exhibit a small amount of bias when
is also near perfect. Both penalized estimators for the weakest signal (0.035) exhibit a small amount of bias when  and
and 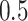 and an increased bias when
and an increased bias when 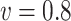 . Such biases in the weak signals are expected for shrinkage estimators (Menelaos and others, 2016), especially in the presence of high correlation among covariates. However, it is important to note that
. Such biases in the weak signals are expected for shrinkage estimators (Menelaos and others, 2016), especially in the presence of high correlation among covariates. However, it is important to note that 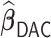 and
and 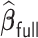 perform nearly identically, suggesting that our
perform nearly identically, suggesting that our 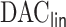 procedure incurs negligible additional approximation errors. On the other hand,
procedure incurs negligible additional approximation errors. On the other hand, 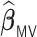 has difficulty in detecting the 0.05 and 0.035 signals and tends to produce substantially higher MSE than
has difficulty in detecting the 0.05 and 0.035 signals and tends to produce substantially higher MSE than 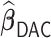 .
.
The empirical coverage levels for the confidence intervals are close to the nominal level across all settings except for the very challenging setting with very weak signals when the correlation is 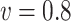 . This again is due to the bias inherent in shrinkage estimators. The relative performance of
. This again is due to the bias inherent in shrinkage estimators. The relative performance of 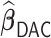 ,
,  and
and 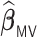 remains similar across different sample sizes. When
remains similar across different sample sizes. When 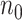 varies from
varies from 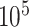 to
to 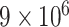 ,
,  remains the best performing estimator with precision comparable to
remains the best performing estimator with precision comparable to 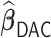 while maintaining substantial advantage with respect to computational efficiency.
while maintaining substantial advantage with respect to computational efficiency.
The results for the time-dependent survival are summarized in Table 4. We find that 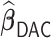 also generally has a good performance in estimating
also generally has a good performance in estimating 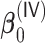 for both time-independent and time-dependent covariates. The variable selection consistency holds perfectly for all parameters of interest. The coverage of the confidence intervals also has similar patterns as the case with time-independent covariates.
for both time-independent and time-dependent covariates. The variable selection consistency holds perfectly for all parameters of interest. The coverage of the confidence intervals also has similar patterns as the case with time-independent covariates.
The proposed DAC approach was implemented as an R software package divideconquer, which is available at https://github.com/michaelyanwang/divideconquer.
4. Application of the DAC procedure to Medicare data
We applied the proposed 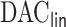 algorithm to develop risk prediction models for heart failure-specific readmission or death within 30 days of discharge among Medicare patients who were admitted due to heart failure. The Medicare inpatient claims were assembled for all Medicare fee-for-service beneficiaries during
algorithm to develop risk prediction models for heart failure-specific readmission or death within 30 days of discharge among Medicare patients who were admitted due to heart failure. The Medicare inpatient claims were assembled for all Medicare fee-for-service beneficiaries during 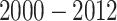 to identify the eligible study population. The index date was defined as the discharge date of the first heart failure admission of each patient. We restricted the study population to patients who were discharged alive from the first heart failure admission. The outcome of interest was time to heart failure-specific readmission or death after the first heart failure admission. Because readmission rates within 30 days were used to assess the quality of care at hospitals by the Centers for Medicare and Medicaid Services (CMS) (CMS, 2016), we censored the time to readmission at 30 days. For a patient who was readmitted or died on the same day as discharge (whose claim did not indicate discharge dead), the time-to-event was set at 0.5 days. Due to the large number of ICD-9 codes, we classified each discharge ICD-9 code into disease phenotypes indexed by phenotype codes according to Denny and others (2013). A heart failure admission or readmission was identified if the claim for that admission or readmission had a heart failure phenotype code at discharge.
to identify the eligible study population. The index date was defined as the discharge date of the first heart failure admission of each patient. We restricted the study population to patients who were discharged alive from the first heart failure admission. The outcome of interest was time to heart failure-specific readmission or death after the first heart failure admission. Because readmission rates within 30 days were used to assess the quality of care at hospitals by the Centers for Medicare and Medicaid Services (CMS) (CMS, 2016), we censored the time to readmission at 30 days. For a patient who was readmitted or died on the same day as discharge (whose claim did not indicate discharge dead), the time-to-event was set at 0.5 days. Due to the large number of ICD-9 codes, we classified each discharge ICD-9 code into disease phenotypes indexed by phenotype codes according to Denny and others (2013). A heart failure admission or readmission was identified if the claim for that admission or readmission had a heart failure phenotype code at discharge.
We considered two sets of covariates: (i) time-independent covariates including baseline individual-level covariates collected at time of discharge from the index heart failure hospitalization, baseline area-level covariates at the residential ZIP code of each patient, and indicators for time trend including dummy variables for each year and dummy variables for each months, and (ii) time-dependent predictors that vary day-by-day. Baseline individual-level covariates included age, sex, race (white, black, others), calendar year, and month of the discharge, Charlson comorbidity index (CCI) (Quan and others, 2005) which described the degree of illness of a patient, and indicators for nonrare comorbidities (defined as prevalence 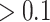 among the study population). Baseline area-level covariates included socioeconomic status variables (percent black residents [ranging from 0 to 1], percent Hispanic residents [ranging from 0 to 1], median household income [per 10 000 increase], median home value [per 10 000 increase], percent below poverty [ranging from 0 to 1], percent below high school [ranging from 0 to 1], percent owned houses [ranging from 0 to 1]), population density (1000 per squared kilometer), and health status variables (percent taking hemoglobin A1C test [ranging from 0 to 1], average BMI, percent ambulance use [ranging from 0 to 1], percent having low-density lipoprotein test [ranging from 0 to 1], and smoke rate [ranging from 0 to 1]). The time-dependent covariates included daily fine particulate matter (PM
among the study population). Baseline area-level covariates included socioeconomic status variables (percent black residents [ranging from 0 to 1], percent Hispanic residents [ranging from 0 to 1], median household income [per 10 000 increase], median home value [per 10 000 increase], percent below poverty [ranging from 0 to 1], percent below high school [ranging from 0 to 1], percent owned houses [ranging from 0 to 1]), population density (1000 per squared kilometer), and health status variables (percent taking hemoglobin A1C test [ranging from 0 to 1], average BMI, percent ambulance use [ranging from 0 to 1], percent having low-density lipoprotein test [ranging from 0 to 1], and smoke rate [ranging from 0 to 1]). The time-dependent covariates included daily fine particulate matter (PM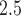 ) predicted using a neural network algorithm (Di and others, 2016), daily temperature with its quadratic form, and daily dew point temperature with its quadratic form. There were 574 time-independent covariates and five time-dependent covariates.
) predicted using a neural network algorithm (Di and others, 2016), daily temperature with its quadratic form, and daily dew point temperature with its quadratic form. There were 574 time-independent covariates and five time-dependent covariates.
There were 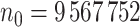 eligible patients with a total of
eligible patients with a total of  heart failure readmissions or deaths, among which
heart failure readmissions or deaths, among which 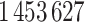 were readmissions and
were readmissions and 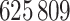 were deaths. After expanding the dataset by accounting for time-dependent variables which vary day-by-day, the time-dependent dataset contained
were deaths. After expanding the dataset by accounting for time-dependent variables which vary day-by-day, the time-dependent dataset contained  rows of records.
rows of records.
We fitted cause-specific Cox models for readmission due to heart failure or deaths as a composite outcome, considering two separate models: (i) a model containing only time-independent covariates and (ii) a model incorporating time-dependent covariates. In both cases, the datasets were too large for 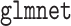 package to analyze as a whole, demonstrating the need for
package to analyze as a whole, demonstrating the need for 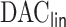 .
.
4.1. Time-independent covariates only
We applied  with
with 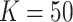 and paralleled
and paralleled 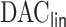 on 25 Authentic AMD Little Endian @2.30GHz CPUs. Computing
on 25 Authentic AMD Little Endian @2.30GHz CPUs. Computing 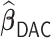 with
with 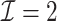 took 1.1 h, including the time of reading datasets from hard drives during each iteration of the update of the one-step estimator. Figure 1a shows the hazard ratio of each covariate based on
took 1.1 h, including the time of reading datasets from hard drives during each iteration of the update of the one-step estimator. Figure 1a shows the hazard ratio of each covariate based on 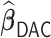 with
with 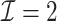 predicting heart failure-specific readmission and death within 30 days.
predicting heart failure-specific readmission and death within 30 days.
Fig. 1.
Hazard ratios of each covariate in estimating hazard of heart failure readmissions or death within 30 days after the first admission using 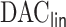 . (a) time-independent variables, (a) time-independent variables (continue), (b) time-dependent variables, and (b) time-dependent variables (continue).
. (a) time-independent variables, (a) time-independent variables (continue), (b) time-dependent variables, and (b) time-dependent variables (continue).
Fig. 1.
Continued. a(3) and a(4) time-independent variables.
Fig. 1.
Continued. b(3) and b(4) time-dependent variables.
Multiple comorbidities are associated with an increased risk of 30-day readmission or death with the leading factors including renal failures, cancers, malnutrition, subdural or intracerebral hemorrhage, myocardial infarction, endocarditis, respiratory failure, and cardiac arrest. CCI is also associated with an increased hazard of the outcome. These findings are generally consistent with those reported in the literature. For example, Philbin and DiSalvo (1999) reported that ischemic heart disease, diabetes, renal diseases, and idiopathic cardiomyopathy were associated with an increased risk of heart failure-specific readmission within a year. Leading factors negatively associated with readmissions include virus infections, asthma, and chronic kidney disease in earlier stages. These negative association findings are reflective of both clinical practice patterns and the biological effects, as most of the negative predictors are generally less severe than the positive predictors.
Some socioeconomic status predictors are relatively less important in predicting the outcome after accounting for the phenotypes, where percentage of black people, median household income, and percent below poverty are dropped and dual eligibility, median home value, percent below high school has a small hazard ratio. By comparison, Philbin and others (2001) reported a decrease in readmission as neighborhood income increased. Foraker and others (2011) reported that given comorbidity measured by CCI, the readmission or death hazard was higher for low socioeconomic status patients. The present article considered more detailed phenotypes in addition to CCI suggesting a relatively smaller impact of socioeconomic status. The difference in results is possibly because comorbidity may be on the causal pathway between socioeconomic status and readmission or death. Adjusting for a detailed set of co-morbidities partially blocks the effect of socioeconomic status. Percent Hispanic residents is negatively associated with readmission or death. Percent occupied houses increase the risk of readmission or death, which is consistent with the strong positive prediction by population density. Most ecological health variables showed a small hazard ratio.
Black and other race groups have a lower hazard than white. Females have a lower hazard than males, which is consistent with Roger and others (2004) that females had a higher survival rate than males after heart failure. Age is associated with an increased hazard of readmission or death, as expected.
The coefficient by month suggests a higher risk of readmission or death in cold seasons than warm seasons, with a larger negative hazard ratio for summer indicators. The short-term readmission or death rate is decreasing over time, which is suggested by the negative hazard ratio of later years. The later calendar year being negatively associated with readmission risk may be an indication of improved follow-up care for patients discharged from heart failure. Consistently, (Roger and others, 2004) also suggested an improved heart failure survival rate over time.
4.2. Incorporating time-dependent covariates
The analysis in Section 4.2 has two goals. First, the covariates serve as the risk predictors of the hazard of heart failure-specific readmission. Second, all covariates other than PM serve as the potential confounders of the association between PM
serve as the potential confounders of the association between PM and readmission, particularly time trend and area-level covariates. The
and readmission, particularly time trend and area-level covariates. The 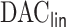 procedure is a variable selection technique to drop non-informative confounders given the high dimensionality of confounders. This goal aligns with Belloni and others (2014), which constructs separate penalized regressions for the propensity score model and outcome regression model to identify confounders. We, herein, focused on building a penalized regression for the outcome regression model.
procedure is a variable selection technique to drop non-informative confounders given the high dimensionality of confounders. This goal aligns with Belloni and others (2014), which constructs separate penalized regressions for the propensity score model and outcome regression model to identify confounders. We, herein, focused on building a penalized regression for the outcome regression model.
We applied 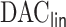 algorithm with
algorithm with 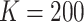 to this time-dependent survival dataset. The procedure was paralleled on 10 Authentic AMD Little Endian @2.30GHz CPUs. The estimation of
to this time-dependent survival dataset. The procedure was paralleled on 10 Authentic AMD Little Endian @2.30GHz CPUs. The estimation of 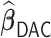 with
with 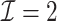 took 36.5 h, including the time of loading the datasets into memory. The result suggests each 10
took 36.5 h, including the time of loading the datasets into memory. The result suggests each 10 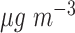 increase in daily PM
increase in daily PM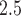 was associated with
was associated with 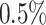 increase of risk (95% confidence interval: 0.3–0.7) adjusting for individual-level, area-level covariates, and temperature. Because there is rare evidence on whether air pollution is associated with heart failure-specific readmission or death among heart failure patients and it is rare to estimate the health effect of daily air pollution using a time-dependent Cox model, this model provides a novel approach to address a new research question. While evidence is rare on the association between daily PM
increase of risk (95% confidence interval: 0.3–0.7) adjusting for individual-level, area-level covariates, and temperature. Because there is rare evidence on whether air pollution is associated with heart failure-specific readmission or death among heart failure patients and it is rare to estimate the health effect of daily air pollution using a time-dependent Cox model, this model provides a novel approach to address a new research question. While evidence is rare on the association between daily PM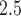 and heart failure-specific readmission, some studies used case-crossover design to estimate the effect of short-term PM
and heart failure-specific readmission, some studies used case-crossover design to estimate the effect of short-term PM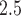 on the incidence of heart failure admissions. Pope and others (2008) found that a 10
on the incidence of heart failure admissions. Pope and others (2008) found that a 10 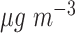 increase in 14-day moving average PM
increase in 14-day moving average PM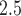 was associated with a 13.1 (1.3–26.2) increase in the incidence of heart failure admissions among elderly patients; Zanobetti and others (2009) reported that each 10
was associated with a 13.1 (1.3–26.2) increase in the incidence of heart failure admissions among elderly patients; Zanobetti and others (2009) reported that each 10 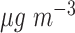 increase in 2-day averaged PM
increase in 2-day averaged PM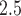 was associated with a 1.85 (1.19–2.51) increase in the incidence of congestive heart failure admission. There is also a large body of literature suggesting that short-term exposure to PM
was associated with a 1.85 (1.19–2.51) increase in the incidence of congestive heart failure admission. There is also a large body of literature suggesting that short-term exposure to PM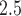 is associated with an increased risk of death. For example, Di and others (2017) shows among the Medicare population during 2000–2012 that each 10
is associated with an increased risk of death. For example, Di and others (2017) shows among the Medicare population during 2000–2012 that each 10 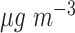 increase in PM
increase in PM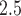 was associated with an 1.05% (0.95–1.15) increase in mortality risk. In addition, Figure 1b shows the covariate-specific estimates of the hazard ratio for all the covariates, with the estimates consistent with the analysis of time-independent dataset.
was associated with an 1.05% (0.95–1.15) increase in mortality risk. In addition, Figure 1b shows the covariate-specific estimates of the hazard ratio for all the covariates, with the estimates consistent with the analysis of time-independent dataset.
Fig. 1.
Continued. b(1) and b(2) time-dependent variables.
5. Discussion
The proposed 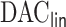 procedure for fitting aLASSO penalized Cox model reduces the computation cost, while it maintains the precision of estimation and accuracy in variable selection with an extraordinarily large
procedure for fitting aLASSO penalized Cox model reduces the computation cost, while it maintains the precision of estimation and accuracy in variable selection with an extraordinarily large 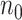 and a numerically large
and a numerically large 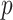 . The use of
. The use of 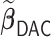 makes it feasible to obtain the
makes it feasible to obtain the 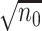 -consistent estimator required by the penalized step (e.g. when there is a constraint in RAM) and shortens the computation time of the initial estimator by
-consistent estimator required by the penalized step (e.g. when there is a constraint in RAM) and shortens the computation time of the initial estimator by 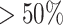 . The improvement in the computation time was substantial in the regularized regression step. The LSA converted the fitting of regularized regression from using a dataset of size
. The improvement in the computation time was substantial in the regularized regression step. The LSA converted the fitting of regularized regression from using a dataset of size  to a dataset of size
to a dataset of size 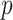 .
.
The majority voting-based method  with MCP (Chen and Xie, 2014) had a substantially longer computation time than
with MCP (Chen and Xie, 2014) had a substantially longer computation time than 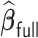 . The difference primarily comes from (i) the fact that the Cox model with MCP is fitted
. The difference primarily comes from (i) the fact that the Cox model with MCP is fitted 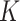 times and (ii) the computational efficiency between
times and (ii) the computational efficiency between 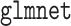 algorithm which is more efficient than the MCP algorithm in
algorithm which is more efficient than the MCP algorithm in 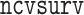 (Breheny and Huang, 2011).
(Breheny and Huang, 2011).
The difference in variable selection between 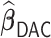 and
and 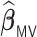 (Chen and Xie, 2014) is primarily due to the majority voting. The simulations in Chen and Xie (2014) have shown that an increase in the percentage for the majority voting decreased the sensitivity and increased the specificity of variable selection. Similarly in the simulations of the present study with a
(Chen and Xie, 2014) is primarily due to the majority voting. The simulations in Chen and Xie (2014) have shown that an increase in the percentage for the majority voting decreased the sensitivity and increased the specificity of variable selection. Similarly in the simulations of the present study with a 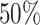 of the majority vote, Chen and Xie’s procedure showed a high specificity but the sensitivity was low for weaker signals as demonstrated in the simulation studies.
of the majority vote, Chen and Xie’s procedure showed a high specificity but the sensitivity was low for weaker signals as demonstrated in the simulation studies.
For non-weak signals, the oracle property appears to hold well as evidenced by the simulation results for 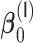 and
and 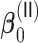 shown in Tables 2 and 3. For weak signals such as 0.035 in
shown in Tables 2 and 3. For weak signals such as 0.035 in 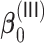 , the oracle property does not appear to hold even with
, the oracle property does not appear to hold even with 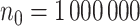 and the bias in the shrinkage estimators results in confidence intervals with low coverage. This is consistent with the impossibility result shown in Potscher and Schneider (2009), which suggests difficulty in deriving precise interval estimators when aLASSO penalty is employed.
and the bias in the shrinkage estimators results in confidence intervals with low coverage. This is consistent with the impossibility result shown in Potscher and Schneider (2009), which suggests difficulty in deriving precise interval estimators when aLASSO penalty is employed.
When parallel computing is available, a larger 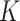 may be preferable for our algorithm as it can reduce the overall computational time provided that
may be preferable for our algorithm as it can reduce the overall computational time provided that 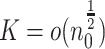 . When
. When 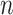 is not large relative to
is not large relative to  , we may increase the stability of the algorithm by replacing
, we may increase the stability of the algorithm by replacing  with
with  for some
for some 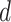 such that
such that 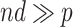 . Potential approaches to further reduce the computation burden for large
. Potential approaches to further reduce the computation burden for large 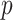 settings include employing a screening step or employing DAC in the second step of the algorithm. However, deriving the statistical properties of DAC algorithms in the large
settings include employing a screening step or employing DAC in the second step of the algorithm. However, deriving the statistical properties of DAC algorithms in the large  setting can be more involved and warrants further research.
setting can be more involved and warrants further research.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
USEPA (RD-83587201), an National Institutes of Health (U54 HG007963), and National Institute of Environmental Health Sciences (R01 ES024332 and P30 ES000002). Its contents are solely the responsibility of the grantee and do not necessarily represent the official views of the USEPA. Further, USEPA does not endorse the purchase of any commercial products or services mentioned in the publication. The analysis of the Medicare data was performed on the secured clusters of Research Computing, Faculty of Arts and Sciences at Harvard University.
References
- Austin, P. C. (2012). Generating survival times to simulate Cox proportional hazards models with time-varying covariates. Statistics in Medicine 31, 3946–3958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belloni, A., Chernozhukov, V. and Hansen, C. (2014). Inference on treatment effects after selection among high-dimensional controls. The Review of Economic Studies 81, 608–650. [Google Scholar]
- Breheny, P. and Huang, J. (2011). Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Annals of Applied Statistics 5, 232–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, X. and Xie, M.-G. (2014). A split-and-conquer approach for analysis of extraordinarily large data. Statistica Sinica 24, 1655–1684. [Google Scholar]
- CMS. (2016). Readmissions Reduction Program https://www.cms.gov/medicare/medicare-fee-for-service-payment/acuteinpatientpps/readmissions-reduction-program.html (accessed November2, 2017). [Google Scholar]
- Cox, D. R. (1972). Regression models and life-tables. Journal of the Royal Statistical Society Series B (Methodological) 34, 87–22. [Google Scholar]
- Denny, J. C., Bastarache, L., Ritchie, M. D., Carroll, R. J., Zink, R., Mosley, J. D., Field, J. R., Pulley, J. M., Ramirez, A. H., Bowton, E.. and others. (2013). Systematic comparison of phenome-wide association study of electronic medical record data and genome-wide association study data. Nature Biotechnology 31, 1102–1110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di, Q., Dai, L., Wang, Y., Zanobetti, A., Choirat, C., Schwartz, J. D., Dominici, F.. and others (2017). Association of short-term exposure to air pollution with mortality in older adults. Journal of the American Medical Association 318, 2446–2456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di, Q., Kloog, I., Koutrakis, P., Lyapustin, A., Wang, Y. and Schwartz, J. (2016). Assessing PM2.5 exposures with high spatiotemporal resolution across the continental United States. Environmental Science Technology 50, 4712–4721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron, B. (1977). The efficiency of Cox’s likelihood function for censored data. Journal of the American Statistical Association 72, 557–565. [Google Scholar]
- Foraker, R. E., Rose, K. M., Suchindran, C. M., Chang, P. P., McNeill, A. M. and Rosamond, W. D. (2011). Socioeconomic status, Medicaid coverage, clinical comorbidity, and rehospitalization or death after an incident heart failure hospitalization. Circulation Heart Failure 4, 308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman, J., Hastie, T. and Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33, 1. [PMC free article] [PubMed] [Google Scholar]
- Goeman, J. J. (2010). L1 penalized estimation in the Cox proportional hazards model. Biometrical Journal 52, 70–84. [DOI] [PubMed] [Google Scholar]
- Pavlou, M., Ambler, G., Seaman, S., De Iorio, M. and Omar, R. Z. (2016). Review and evaluation of penalised regression methods for risk prediction in low-dimensional data with few events. Statistics in Medicine 35, 1159–1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park, M. Y. and Hastie, T. (2007). L1-regularization path algorithm for generalized linear models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 69, 659–677. [Google Scholar]
- Philbin, E. F., Dec, G. W., Jenkins, P. L. and DiSalvo, T. G. (2001). Socioeconomic status as an independent risk factor for hospital readmission for heart failure. The American Journal of Cardiology 87, 1367–1371. [DOI] [PubMed] [Google Scholar]
- Philbin, E. F. and DiSalvo, T. G. (1999). Prediction of hospital readmission for heart failure: development of a simple risk score based on administrative data. Journal of the American College of Cardiology 33, 1560–1566. [DOI] [PubMed] [Google Scholar]
- Pope, C. A., Renlund, D. G., Kfoury, A. G., May, H. T. and Horne, B. D. (2008). Relation of heart failure hospitalization to exposure to fine particulate air pollution. The American Journal of Cardiology 102, 1230–1234. [DOI] [PubMed] [Google Scholar]
- Potscher, B. M. and Schneider, U. (2009). On the distribution of the adaptive LASSO estimator. Journal of Statistical Planning and Inference 139, 2775–2790. [Google Scholar]
- Quan, H., Sundararajan, V., Halfon, P., Fong, A., Burnand, B., Luthi, J.-C., Saunders, L. D., Beck, C. A., Feasby, T. E. and Ghali, W. A. (2005). Coding algorithms for defining comorbidities in ICD-9-CM and ICD-10 administrative data. Medical Care 43, 1130–1139. [DOI] [PubMed] [Google Scholar]
- R Core Team. (2017). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Roger, V. L., Weston, S. A., Redfield, M. M., Hellermann-Homan, J. P., Killian, J., Yawn, B. P., Jacobsen, S. J.. and others (2004). Trends in heart failure incidence and survival in a community-based population. Journal of the American Medical Association 292, 344–350. [DOI] [PubMed] [Google Scholar]
- Simon, N., Friedman, J., Hastie, T. and Tibshirani, R. (2011). Regularization paths for Cox’s proportional hazards model via coordinate descent. Journal of Statistical Software 39, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang, L., Zhou, L. and Song, P. X.-K. (2016). Method of divide-and-combine in regularised generalised linear models for big data. arXiv preprint arXiv:1611.06208. [Google Scholar]
- Volinsky, C. T. and Raftery, A. E. (2000). Bayesian information criterion for censored survival models. Biometrics 56, 256–262. [DOI] [PubMed] [Google Scholar]
- Wang, H. and Leng, C. (2007). Unified LASSO estimation by least squares approximation. Journal of the American Statistical Association 102, 1039–1048. [Google Scholar]
- Zanobetti, A., Franklin, M., Koutrakis, P. and Schwartz, J. (2009). Fine particulate air pollution and its components in association with cause-specific emergency admissions. Environmental Health 8, 58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, H. H. and Lu, W. (2007). Adaptive LASSO for Cox’s proportional hazards model. Biometrika 94, 691–703. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.






