Abstract
A key question in biology is the predictability of the evolutionary process. If we can correctly predict the outcome of evolution, we may be better equipped to anticipate and manage species’ adaptation to climate change, habitat loss, invasive species, or emerging infectious diseases, as well as improve our basic understanding of the history of life on Earth. In the present article, we ask the questions when, why, and if the outcome of future evolution is predictable. We first define predictable and then discuss two conflicting views: that evolution is inherently unpredictable and that evolution is predictable given the ability to collect the right data. We identify factors that generate unpredictability, the data that might be required to make predictions at some level of precision or at a specific timescale, and the intellectual and translational value of understanding when prediction is or is not possible.
Keywords: evolution, predictability, quantitative genetics, adaptive evolution, population genetics, reintegrating biology
A s a fundamental unifying theory of biology, evolution integrates all the disparate disciplines present in the modern biological sciences. Evolutionary biology provides a crucial toolkit to explain how life came to be as we see it today, with both spectacular adaptations and vulnerabilities. It can clarify why individuals differ from each other within populations, the raison d’être for personalized medicine. It reveals why genetic and physiological features are shared across the tree of life, justifying the use of nonhuman organisms as models for studying our own biology. Much of the value of evolutionary biology is it provides critical insight into the history of life on Earth. But by knowing the core mechanisms of evolution we can also look forward and ask what's next. Although it is certain that evolution will occur and that populations will adapt, we have a harder time predicting whether specific species will adapt fast enough to changing climates to avoid extinction. From a more applied perspective, can we anticipate whether an emerging infectious disease will evolve to be more or less virulent? Or can we know in advance which molecular pathways an evolving tumor will exploit to metastasize? Can we know the adaptations a crop pest or pathogen might evolve to bypass our current control measures? Predicting future evolution offers the enticing prospect of anticipating and therefore managing evolutionary outcomes of populations we value, and those we wish to suppress. However, biologists continue to disagree about how effectively we might predict future evolution. Is evolution fundamentally too stochastic to predict (Orr 2005, Stern and Orgogozo 2009, Agrawal 2017, Bolnick et al. 2018)? Or can we make effective predictions (with some sufficient level of precision to address practical questions), if we just have the right kind of data and models? In the present article, we discuss each side of this debate and propose means to forge a path forward.
Support for the predictability of evolution is found in both empirical and theoretical studies. For example, there is evidence of predictable changes of genes under similar selective pressures within populations at relatively short timescales (Monroe et al. 2016, Ramiro et al. 2016, Hawkins et al. 2019). Renaut and colleagues (2014) found that two pairs of sunflower species undergoing similar selective pressures and distributed along similar latitudinal gradients adapted through changes in the same genomic regions, with similar phenotypic effects. These results are supported by theoretical studies showing evolution of the same traits, genes or even alleles (different gene versions) in closely related replicate lineages (Orr 2005, Renaut et al. 2014, Seehausen et al. 2014, Irwin et al. 2016, Ravinet et al. 2017). For instance, replicated invasion of marine threespine stickleback (Gasterosteus aculeatus) into many independent freshwater habitats reliably leads to evolutionary loss of bony armor via changing allele frequencies at a gene called EDA (Colosimo et al. 2005). The extensive literature on parallel and convergent evolution points to a rather widespread tendency for evolution to repeat itself under similar selective pressures, implying predictability.
In contrast, there are studies that support the unpredictability or limited predictability of evolution (Takahashi et al. 2007, Tegze et al. 2012, Fitzpatrick et al. 2014, Sailer and Harms 2017, Bolnick et al. 2018, Langerhans 2018). Langerhans (2018) found limited predictability of phenotypic evolution in Bahama mosquito fish inhabiting blue-hole pools with or without predators: Differences in predation pressure between the pools predicted less than half the morphological variation among populations. There may be many equally functional solutions to a given adaptive challenge (many-to-one mapping), either for protein structure (Sailer and Harms 2017) or for morphological structures (Alfaro et al. 2004). Therefore, knowing that selection favors a particular function might not allow one to predict what genetic or morphological traits should evolve (Alfaro et al. 2004). Compounding this unpredictability, much of evolutionary change is inherently stochastic (random), relying on the input of randomly generated new mutations and of random fluctuations in allele frequency due to finite population size (i.e., genetic drift). The combination of stochasticity and many-to-one mapping suggest that even if we can predict future natural selection, the genotypes and phenotypes that respond to that selection may be fundamentally unpredictable.
Almost surely, the truth lies somewhere between these extreme stances that evolution is predictable or not. Our ability to make predictions depends on the biological level at which we seek to predict. For example, we can reliably predict that birds living at high altitudes evolve increased oxygen carrying capacity in response to lower oxygen partial pressure and that this arises via changes in hemoglobin (Natarajan et al. 2016). This level of prediction is desirable to understand the potential for organisms to diversify to specific niches over time. However, the specific nucleotides or amino acid changes that enable that adaptation are unpredictable in this system (Natarajan et al. 2016). Therefore, at the molecular level, even within a subset of organisms, the specific genes or combinations of genes needed or which mutations are important remains unknown. We argue that this would be a desirable level of prediction for evolutionary biology. In this article, we begin by articulating why evolutionary prediction is a desirable goal and what we mean by prediction, considering various possible levels of biological organization and different timescales. We then summarize the arguments both for unpredictability and predictability and enumerate the many layers of information we need for successful prediction at chosen levels of biological precision and timescales. The approach of understanding evolutionary prediction as a probabilistic continuum can increase our chance of success by integrating information and tools from the fields of molecular biology, genetics, developmental biology, cell biology, evolutionary theory, ecology, phylogeny, paleontology, and biomathematics. Although there is no question that evolution will occur, what we want to understand is our current ability to predict the outcomes of this process, its speed, and its underlying mechanisms. To invert a famous quote from a great evolutionary biologist of the mid-twentieth century, Theodosius Dobzhansky, we argue that nothing in evolution is predictable except in light of the rest of biology.
Why do we wish to predict evolution?
Given accelerated change in global environmental drivers such as climate change, land use changes, introduced species, and emerging infectious diseases this is a critical time to address whether we can make predictions about evolution (Pau et al. 2011, Lassig et al. 2017). From a conservation standpoint, we might wish to predict specific populations or species that are likely to be at risk for extinction. Or we might wish to predict (or create) the specific genotypes and phenotypes that will allow a species or population to adapt and resist extinction in the face of global climate change. A farmer might need to predict the rate and timing of resistance to a pesticide or herbicide or the response of an agricultural system to an introduced pest or disease. Evolutionary prediction also applies to human health. Modern medicine is facing a crisis associated with the evolution of multispectrum antibiotic resistance in human pathogens. Evolutionary prediction could allow the development of novel treatment regimes that might prevent the evolution of drug resistance in pathogens. Similarly, in the Sars-Cov-2 pandemic causing COVID-19, there is extensive interest in predicting the virus's evolutionary trajectory (e.g., Kober et al. 2020, Rehman et al. 2020). Specifically, will the virus evolve to be more or less virulent? How will various social distancing policies alter this evolutionary trajectory? Viral evolution forecasts are especially crucial in designing vaccines, to ensure the vaccines (and the immunity they produce) have a long-lasting effect.
However, the complex organization of biological systems and process of evolution means that prediction needs to be approached and understood on multiple levels. For example, we know that rising temperatures and ocean acidification present significant challenges to coral species throughout the globe. Do we need to predict the likelihood of extinction for a given population or species of coral? Do we need to predict the specific biochemical pathways or processes and underlying genes that will respond to selection under these conditions so we can identify (or create) appropriate genotypes to facilitate adaptation and prevent extinctions? A similar example in human health might be the evolution of human macrophage attack in Escherichia coli. Experimental evolution in pathogenic E. coli has shown these bacteria can evolve resistance to the human immune system (Ramiro et al. 2016). These experiments demonstrated that the biochemical pathway in which adaptation occurred (the electron transport associated with energy producing catabolism) could be reliably predicted, but that the specific genes and mutations that conferred resistance could not be predicted (Ramiro et al. 2016). This result illustrates the point that our ability to predict varies with the level of biological organization being studied. In a similar vein, cancer evolution during growth and metastasis within patients is often highly idiosyncratic, varying from patient to patient, making it difficult to develop broadly effective, anticipatory therapies that head off tumor evolution. Prediction, in this case, would improve our ability to generate patient specific treatment regimes, but the scale and scope of the goal are quite different from either of the other examples above.
Evolutionary prediction: “I do not think it means what you think it means”
When discussing evolutionary prediction, we must first settle on a shared vision of what it means to predict. Biologists often use the term predict rather loosely, conflating a variety of related but distinct ideas. The word derives from the Latin verb praedicere, which itself merges prae (prior or in advance), and dicere (to say). The Merriam-Webster dictionary defines predict as “to declare or indicate in advance.” This is most often used in terms of making statements about future events. But it is important to recognize that scientists can also make predictions about the as-yet-unmeasured outcome of a historical event (sometimes called retrodiction). For instance, knowing the rules of molecular evolution, we can use the DNA sequences for a set of related species to make a probabilistic prediction about the homologous DNA sequence in an as-yet-unsequenced related species. Or, knowing the genetic basis of evolutionary loss of armor in freshwater stickleback in many watersheds, we can predict with confidence that a particular sequence of the gene EDA will occur in a previously unstudied lake population of this fish.
For this article, we are specifically interested in the narrower use of prediction in terms of statements of future evolutionary events. Therefore, we will not be discussing the very large and well-established literature building and documenting biology's understanding of evolutionary history, except where it provides tools or data that illuminate future evolution. With this emphasis on predicting evolutionary future, it is helpful to briefly consider the discipline of future studies (Poli 2017). Researchers in this field distinguish between the terms forecast versus prediction. Forecasts are typically precise and quantitative and are often based on a theoretical model or perhaps time series analysis of historical data that can be projected into the future with quantitative estimates of confidence or error. Prediction, in contrast, is often used to describe qualitative and subjective statements, sometimes based on informed intuition. In keeping with common usage within evolutionary biology, we stick with the term prediction for most of this article as the overarching concept, of which forecasting is a quantitative subset.
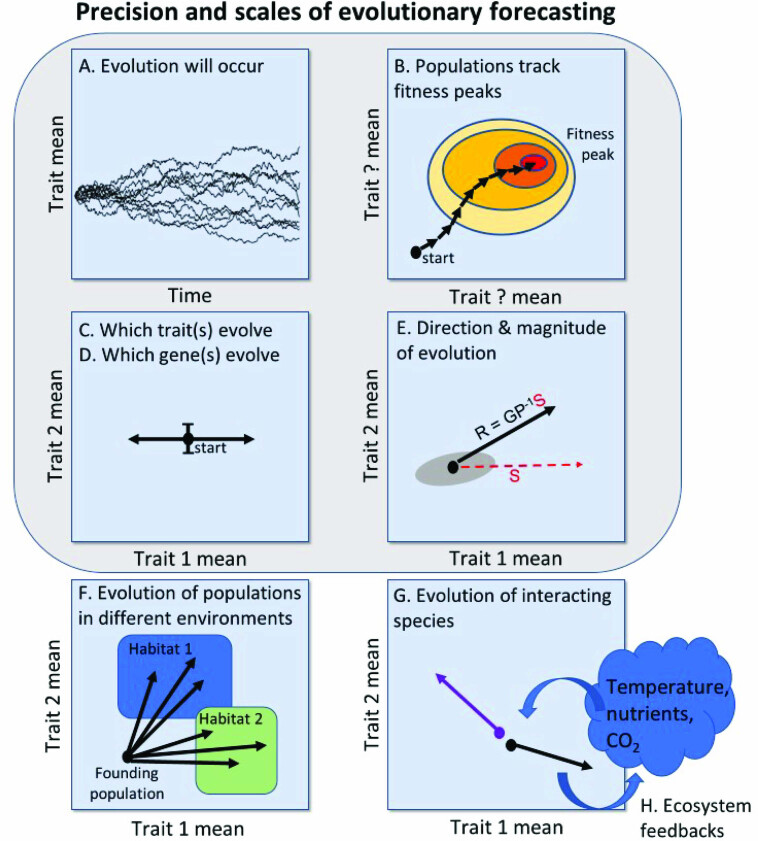
One can make useful predictions at many different biological levels of organization and timescales, as well as with various degrees of precision. At the simplest level, we can confidently state that evolution (genetic change) will take place, whether because of natural selection or genetic drift (figure 1a). Meta-analyses have confirmed that evolutionary forces are pervasive in natural populations, including natural selection (Caruso et al. 2017), sexual selection (Kingsolver et al. 2010), gene flow (Frankham 2015), nonrandom mating (Jiang et al. 2013), and genetic drift (Leinonen et al. 2007). Because evolution is ubiquitous, predicting its existence is trivial and does not provide actionable information.
Figure 1.
Precision and scales of evolutionary forecasting. As was described in the text, there are varying degrees of precision and scale at which evolution may be forecast. (a) Nearly all traits and genes are subject to evolutionary change, making this the most reliable but least precise prediction. (b) In a constant environment, populations with sufficient genetic variation will evolve toward fitness peaks that increase mean fitness (Fisher's fundamental theorem of natural selection). We can therefore forecast that adaptation will occur even if we are uncertain of the specific traits or genes driving this adaptation. A more precise prediction would specify the traits (c) or genes (d) that will drive evolutionary change. (e) Even greater precision comes from forecasting the magnitude and direction of trait evolution (the black line) using quantitative methods such as the breeder's equation, which requires information on genetic and phenotypic covariances (G, P, represented by the grey oval) and selection strength (red dashed line). (f) Forecasting requires information on environmental settings, which may allow us to make predictions for numerous populations spanning a range of environmental settings: To what extent will these evolve in parallel or diverge? (g) Interacting species (species 1 blue and species 2 black lines, respectively) can drive each other's evolution through ecological interactions, such as character displacement between competitors, which requires community-level forecasting. (h) We may seek to forecast how evolutionary change by species within a community alter ecosystem properties, which can feed back to change interactions among and selection on those communities. The gray box that encompasses the top four panels is the focus of this article, the lower two panels (f) and (g) are not specifically addressed in the present article. Abbreviations: GP–1, heritability; R, response to selection; S, strength of selection.
A slightly more useful statement would be that, in a given constant environment, a population's mean fitness should increase over time, as is laid out in Fisher's fundamental theorem of natural selection (Fisher 1930, Shaw 2019). Furthermore, this model predicts that the rate of increase in mean fitness will be proportional to the genetic variance in fitness traits. In other words, populations that have greater genetic variation in traits associated with fitness reach mean fitness more rapidly by natural selection. The necessary assumptions are nontrivial. First, there must be genetic variation for traits affecting fitness (and therefore genetic variation in fitness). Second, selection must be strong enough to overwhelm genetic drift (equivalently, population sizes must be large enough that genetic drift is weak). Third, environmental change and density-dependent competition can both reduce mean fitness faster than adaptation can occur, by changing the phenotypic optimum of the fitness landscape faster than the population can approach (McGill and Brown 2007). Predicting that adaptation will occur is preferable to the generic statement that evolution will take place, because it specifies a metric (mean fitness), direction (increasing mean fitness to an adaptive landscape peak), and a rate (figure 1b). However, it lacks mechanistic detail and so has relatively little utility for applied problems. Note also that mean fitness can increase through nonevolutionary means, via adaptive phenotypic plasticity, matching habitat choice, or niche construction (Edelaar and Bolnick 2019), or by environmental change that increases reproductive success for all individuals (e.g., increased resource availability).
A more useful and interesting goal is to predict which of the vast array of traits are likely to evolve in response to a particular selective challenge (e.g., an environmental change; figure 1c). Not all traits will evolve: Many may be at equilibria (e.g., subject to stabilizing selection), lack genetic variation, or are neutral so their evolution is too slow to be relevant to the timescale in question (Kumar and Subramanian 2002). But, typically, at least some genes and traits are likely to be evolving at any point in time; the question is merely which ones (figure 1d). Typically, evolutionary biologists first seek to specify which phenotypic traits are evolving (and how they affect fitness), then turn to the question of which genes underlie this trait, a topic to which we will return later.
If we can identify traits that will evolve over the relevant timescale, we might then aspire to an even greater degree of predictive power: in what direction the traits will change (figure 1e). Predicting directionality should generally be within our reach because it simply requires knowledge of the sign of the slope of the selection gradients acting on the population means of the relevant traits, but see below for issues associated with predicting multivariate phenotypes. Better still, can we make a quantitative forecast? By what amount (e.g., fold change, standard deviations, proportion) will the evolving traits change over a specified unit of time? What is our uncertainty around this forecast? Such quantitative forecasting is an achievable end goal for quantitative geneticists, given information about heritability and selection acting on one or more traits over a short timescale, which may be plugged into the multivariate breeder's equation (see the glossary in box 1). A related goal is forecasting changes in the full trait distribution (e.g., variance, kurtosis, covariance), but this is a harder problem. There is no simple equation, akin to the breeder's equation, for forecasting the evolution of genetic covariances and higher moments. Phenotypic plasticity poses a substantial challenge for quantitative forecasts of trait change. Plasticity is the ability of a given genotype to produce multiple alternative phenotypes, depending on the environment. As a result, phenotypic distributions can therefore change without any evolution, or plasticity can amplify or obscure heritable changes in traits. We lack methods to forecast plastic trait changes in as-yet-unobserved environmental conditions.
Box 1. Glossary.
Adaptive evolution. In the present article, we use adaptive evolution as a subset of evolutionary outcomes that are driven by natural selection (as opposed to random evolutionary change e.g., genetic drift), which leads to increased mean fitness through time.
Allelic segregation. Segregation of alleles occurs during gamete formation because of meiotic cell division. This and Mendel's principle of independent assortment explain why each gamete produced by a diploid organism is unique in terms of its genetic complement.
Breeder's equation. The breeder's equation R = S × h2 describes the response to selection (R) as a function of the strength of selection (S) and the heritability of a phenotypic trait (h2). It is used to forecast the evolutionary response of complex multigenic traits to either natural or artificial selection. Multivariate approaches incorporate the response of multiple traits that are genetically correlated.
Density dependence. The population ecology processes in which a population's growth rates are regulated by its density. For example, as a population gets larger, resource limitations result in slower population growth or even decline.
Coevolution. The process by which reciprocal selection drives evolutionary change in two or more partner species. A common example of this would be arms-race coevolution in which defensive adaptations, such as increased toxicity drive, increased toxin resistance in a predator. In some cases, this is also used to describe cospeciation in which pairs or groups of lineages diverge together—for example, feather mites and birds.
EDA. The EDA gene encodes a transmembrane signaling protein, Ectodysplasin, involved in early development. This gene is present throughout animal lineages and regulates the interaction between ectoderm and mesoderm.
Effective population size (Ne). A measure of the potential for genetic drift to change allele frequencies due to unbalanced (not 50:50) sex ratios, temporal variation in population size, overlapping generations, and other real-world properties of populations.
Epigenetic. Epigenetic effects are changes in gene function that can be inherited but are not caused by changes in DNA sequence (i.e., mutations). Instead these typically come from modification of maternal or paternal DNA molecules such as DNA methylation that change gene expression.
Epistatic interactions. Epistatic interactions describe phenotypic effects that result from nonadditive interactions between alleles at different loci or between mutations within a single gene. Nonadditive effects imply that the phenotypic effects of alleles at one gene are changed by the genotype at another gene or between different alleles in a single gene. These interactions can generate genetically based phenotypic variation that is not passed from one generation to another because alleles at different loci segregate independently, disrupting epistatic interactions.
Gene flow. Gene flow describes the movement of alleles between populations of a species. In cases in which populations are fully reproductively isolated from each other gene flow is zero, and any gene flow via hybridization is called introgression. Gene flow tends to homogenize otherwise diverging populations, although it may also provide genetic variation on which selection can act.
Genetic architecture. The term genetic architecture describes the underlying genetic basis of traits (number of loci, their effect sizes, recombination rates, epistasis, dominance), as well as the variation within or among populations.
Genetic covariances. In evolutionary quantitative genetics, the genetic covariance is a measurable summary statistic, capturing the effects of pleiotropy and link disequilibrium in generating correlated values of two or more inherited traits. The strength of the covariances determine the extent to which selection on one trait drives evolutionary change in another trait (from Agrawal and Stinchcombe 2009)
Genetic drift. Genetic drift describes an evolutionary process in which sampling error generates changes in allele frequencies across generations. Unlike changes in allele frequencies associated with natural selection changes in allele frequencies associated with genetic drift are random.
Genotype. The genetic makeup of an organism or individual.
Genotype–environment (G×E) interactions. The differential response to environmental variation by different genotypes. These interactions can reflect that fitness of a particular genotype is dependent on its environment and that the relative fitness of two or more genotypes can change depending on the environment.
Heritability. Heritability describes the proportion of phenotypic variation in a character or trait that results from genetic variation. In its broadest sense it can be characterized by the slope of the line that describes the relationship between mean parental trait values and mean offspring trait values.
Homologous. In the present article, we use the term homologous to describe genes that share functional and structural similarities because of common ancestry. A homologous protein is one that is structurally and functionally similar in different lineages because of common ancestry.
Indel. An indel is an insertion or deletion mutation in a region of DNA. This can consist of single nucleotide insertions or deletions or the insertion (or deletion) of multiple nucleotides.
Link disequilibrium. Nonrandom association of alleles at different genes within a population because of reduced recombination generated by physical proximity on a chromosome.
Mean fitness. Mean fitness describes the average fitness of all individuals in a population. In the present article, we use individual fitness in its classic Darwinian definition; for example, an individual's (or a genotype's) fitness is directly proportional to its reproductive contribution to breeding individuals of the next generation.
Metapopulations. An ecological concept that incorporates real world spatial and temporal structures of species and populations. The concept predicts that most species consist of subpopulations in which individuals can freely interbreed connected into larger metapopulations in which movement of individuals (and alleles) is possibly but more limited. The metapopulation model also explicitly incorporates spatial and temporal environmental variation to understand the ecological and evolutionary trajectories of species.
Multivariate phenotypes. A multivariate phenotype approach (as opposed to univariate phenotype) incorporates more than one trait in analyses that assess the genetic basis of complex characters (such as disease or pathogen susceptibility). This approach incorporates multiple individual characters to enhance the power of the analysis.
Parallel evolution. The tendency for two or more replicate populations to evolve similar adaptive solutions (e.g., same gene, or morphology) to a shared environmental challenge. Parallel evolution is widely considered to be diagnostic evidence that evolution can be predictable.
Paralogs. Two or more similar genes, coexisting within the same species's genome, that are the result of gene duplication events
Phenotype. The phenotype of an organism or individual describes the sum total of all observable traits or characteristics. It can include (but is not limited to), morphology, physiology, and behavioral characteristics.
Pleiotropy. When polymorphism at a single gene gives rise to correlated variation in two or more distinct phenotypic traits
Population genetics. A field of genetics that deals with mathematical description of the change in allele frequencies within and between populations.
Price equation. In the present article, we use the Price equation in its original form to represent the change in a trait or allele frequencies across two generations. The Price equation (Price 1972) incorporates the covariance between fitness and traits (or allele) to provide a quantitative description of the change in trait values across a single generation.
Quantitative genetics. A field of genetics that deals with the evolution of complex traits that typically result from the interaction of multiple genes and the environment. This approach allows the quantification, measurement, and prediction of the change in trait means of populations, even when the specific genetic basis of those traits is unknown.
Recombination. During recombination alleles from maternal and paternal chromosomes are swapped resulting in novel combinations of alleles in offspring chromosomes. This process does not generate new mutations but generates novel genotypes in the offspring generation.
Selection differentials and selection gradients. Selection gradients and selection differentials both provide estimates of a trait's relationship with fitness. However, they are quantitatively different. Selection gradients are univariate estimates produced by linear regression (i.e., the slope of the line describing the relationship between trait values and fitness), whereas selection differentials are multivariate and represent the partial regression coefficients of the slope describing the relationship of a trait's contribution to fitness.
SNP. A single nucleotide polymorphism or a mutation of a single position in a DNA molecule that is variable within or among populations.
SPL transcription factors. Squamosa promoter binding-like (SPL) proteins are plant specific transcription factors with a regulatory function in multiple biological processes. Transcription factors are important in regulating the rate of gene expression.
Stabilizing selection. Stabilizing selection is a form of natural selection in which phenotypic extremes are selected against and phenotypes closer to the mean in a population have higher fitness. In theory, this form of selection should reduce the variance for a trait in a population without shifting the mean of the trait. A classic example of this is birth weight for human children in which low birth weight reduces the survival rate of the child and high birth weight reduces the survival of the mother.
Standing genetic variation. The standing genetic variation describes the current sum total of genetic variation within and among populations.
Transitions and transversions. These terms differentiate between types of mutations in DNA molecules. Transitions are DNA substitutions in which a purine base (A or G) or a pyrimidine base (C or T) is exchanged (e.g., G replaces A or C replaces T) in a DNA molecule. Transversions are the replacement of a purine (or pyrimidine) base with its “opposite.” For example, replacement of A with T or G with C.
The quantitative genetic approach often treats genetic, molecular, cellular, and developmental mechanisms as a black box, focusing on emergent and readily observable traits (e.g., size, shape, or behavior). A more complex goal is to predict evolution and action of finer-scale mechanistic traits (which we might call upstream traits) that ultimately generate the traits of interest at the organismal level. Examples might include timing and levels of gene expression, pathway activity, enzymatic activity or concentrations, developmental patterning, and so on. We could also study these upstream traits to attempt to predict which ones will evolve, in what direction, and by how much (figure 1c and 1e, respectively). This approach lets us predict not just evolution of the obvious traits, but could also provide a mechanistic explanation of how these trait changes are actuated by changes in gene expression, development, environment, and so on. Ultimately, all the phenotypic traits we might choose to study arise from changes in the expression of genes (where, when, how much), their translation (speed, timing, splicing), and subsequent protein function (folding, active site properties, dynamics, transport, degradation, interactions). These all have their roots in the sequence, packaging, and epigenetic modification of DNA. Therefore, many biologists feel that the ultimate question of evolutionary prediction is to anticipate the precise genetic changes underlying evolution. We can define distinct levels of predictive precision within this ultimate question of genetic forecasting (box 2).
Box 2. Distinct levels of predictive precision in molecular evolution.
Evolution will occur in a particular group of genes (e.g., gene ontology category, pathway, family of paralogs).
Evolution will occur in a particular gene.
Evolution of that gene will entail changes in particular motifs or properties of a protein (e.g., a shift in polarity or shape, or within a particular active site).
Evolution will entail changes in frequency of particular genetic variants (e.g., single nucleotide polymorphisms [SNPs], indels, gene copy number, chromosomal rearrangements). Precise evolutionary forecasting might go so far as to predict the direction, magnitude, and speed of allele frequency change, ideally with appropriate confidence intervals.
Predicting evolution of single gene is insufficient because evolution is rarely a single gene process. For instance, initial adaptive changes might impose costs that require compensatory mutations after. Therefore, for true predictive power, we should aspire to scale up the goals in figure 1 a– 1 e to multiple genes, how they interact, and—ultimately—the whole genomic shebang (many genes, architecture, and epigenetics).
The preceding kinds of evolutionary predictions are all concerned with evolution that is occurring within a particular focal population (changes in trait distributions and genotype frequencies in a defined group of individuals; figure 1a–1d). However, evolution is more complex in that it occurs among populations connected through networks of gene flow and spatial variability (e.g., metapopulations). Prediction at the level of the species range might include the specific traits that will evolve in individual populations, leading to population divergence, and the role of gene flow among populations in constraining this divergence (figure 1f). From an ecological standpoint, this level of prediction would also include the establishment or extinction probability of individual populations.
Although the preceding points concern evolution within a focal species, ecological interactions between species (e.g., competition, predation, parasitism, mutualism) can drive simultaneous coevolution in two or more species (Thompson 1989). Each species is subject to selection to increase the benefits, or mitigate costs, of their interaction (figure 1g, species 1 and 2 as blue and black lines, respectively). The resulting evolution within each species changes the nature of their interspecific interactions, which, in turn, changes the selection that their partners or antagonists experience (so-called eco–evo feedback loops, Genung et al. 2011, Post and Palkovacs 2009). Therefore, evolutionary forecasts may need to account for coevolutionary dynamics and therefore consider multiple species concurrently.
Moving to a still larger scale, we could instead focus on predictions about emergent community and ecosystem properties rather than a particular species. For example, we can confidently predict that in any biological community, given enough time there will emerge guilds of primary producers, consumers, and predators. There will be communities evolving to certain kinds of body size distributions, rates of energy conversion, and abundance distributions. These higher-level predictions are easiest to make over very long timescales when environments remain stable. Our goal in the present article is to focus on the precision and scales of evolutionary forecasting that encompass the points made in figure 1a–1e and not to address prediction at the level of figure 1f and 1g.
To summarize, we frequently use predict evolution as a shorthand that encompasses a wide range of goals with varying degrees of precision, qualitative or quantitative, applied to various scales of organization (e.g., genes, genomes, phenotypes, performance or fitness, species, communities) because of a range of mechanisms (e.g., selection, genetic drift, gene flow, genetic architecture, species interactions). Beyond defining what we mean by prediction, it is equally crucial that we clearly specify the timescale over which our prediction applies. Predictions for some of these combinations seem well within our reach at present, others seem like moonshots that may require a heroic effort employing all our current theory and technologies, or some may be fundamentally impossible.
Although evolutionary history is well understood, and evolutionary theory provides a powerful and well-validated means of understanding that history, our ability to make long-term quantitative forecasts of future evolution remains beyond our reach. Is that simply because we lack sufficient information at present? We believe it is important that we distinguish between two distinct views: H1 is that evolution is fundamentally unpredictable, not because we lack sufficient knowledge but because it is truly too stochastic for forecasts at any useful degree of precision. H2 is that evolution is predictable, if we simply had the right models and sufficient data to make effective forecasts.
H1. Evolution is not predictable, no matter how much we measure
Stephen Jay Gould famously argued in Wonderful Life: The Burgess Shale and the Nature of History (1989) that evolution would not repeat itself; if we rewound the tape of life and replayed it from the Cambrian, we would be unlikely to end up with anything like humans. In this spirit (and on a shorter time span), we posit that evolution is inherently unpredictable at the molecular and population level. This is because of the unpredictability of many factors scaling from molecular to environmental mechanisms.
Ultimately, evolution is dependent on the random process of genetic mutation. Although probabilistic aspects of mutation are quantifiable and therefore somewhat predictable (e.g., rates, variation in transitions versus transversion, mutational hotspots within the genome), in the near term, we cannot predict exactly which mutations will occur, where, or when. Even if we know the genes and genetic pathways that should be important under a specific selective pressure, reliance on de novo genetic mutation (e.g., mutation-limited evolution) makes it difficult to forecast the specific genetic changes enabling future adaptation. The counterargument (detailed later in this article) is that in large populations all possible mutations will occur with some regularity.
Conversely, selection on standing genetic variation may be easier to forecast. During meiosis in sexual organisms, recombination adds an additional element of stochastic genetic variation, creating new combinations of linked alleles, as well as mutations and chromosomal rearrangements on which selection can act. As with mutation, recombination hotspots and cold spots mean that crossing over events are not equally probable across the genome.
Genetic drift then adds an element of random changes in the frequency of existing alleles. Which adults succeed in reproducing and the number of surviving offspring are somewhat random. Even an individual carrying a beneficial mutation that confers higher expected fitness may fail to find a suitable habitat, or may be killed by a pathogen or predator, leading to the loss of their beneficial mutation. For individuals who do succeed in reproducing, allelic segregation during meiosis means that the resulting offspring will carry a random sample of their parents’ alleles, changing allele frequencies in finite populations. The net effect of these stochastic processes is a modest random change in allele frequencies.
Population genetics has a robust set of model-based descriptions of these stochastic processes. Given data on the distribution of mutation rates, recombination rates, and effective population size, we can forecast a probability distribution of rates and magnitudes of allele frequency change over a specified time. These forecasts can account for mutational and recombination hotspots, across the genome. But the realization of this probabilistic process (e.g., the particular mutations) is fundamentally unpredictable in the immediate future. Over the longer term, there are enough opportunities for new mutations and drift so that, through the law of large numbers, the probabilistic predictions become more useful. This is an important example of how the particulars of evolution may be in a sense more predictable in the longer term, contrary to the usual assumption that short-term evolution is easier to forecast.
The inherent stochasticity of mutation and genetic drift is compounded by epistatic interactions within and among genes. The phenotypic and fitness effect of a given mutation depends on the carrier's genotype at other loci. Therefore, the order in which substitutions occur has a dramatic impact on both the magnitude and sign of their phenotypic and fitness effects and probability of fixation (Costanzo et al. 2010). The inherent randomness of the outcomes of the mutational process means that unpredictable early substitutions impede our ability to predict the fitness effects of later substitutions. This mutation-order effect changes the fitness effects of substitutions, so it may prove inherently impossible (as opposed to impractical) to precisely forecast long-term evolution of epistatic gene networks (Sailer and Harms 2017).
There are also barriers to effective evolutionary prediction that arise from a fundamentally indeterministic aspect of biology, rather than stochasticity. Many-to-one mapping describes the idea that there are many solutions (genotypes, phenotypes) that yield equivalent functional outcomes. Consequently, natural selection could favor any of a number of solutions to a particular adaptive challenge. For many phenotypic traits, there exist numerous combinations of morphological structures that can yield identical functional effects (Wainwright et al. 2005). For example, the four-bar linkage lever system of labrid fishes’ jaws serves to translate force into motion, generating a lever mechanical advantage determining the capacity to produce forceful (crushing) bites versus fast movement useful for evasive prey. Because of the structural complexity of the four-bar lever system, there exist many morphological solutions (head shapes) with identical functional effects (e.g., precisely the same mechanical advantage coefficient). Assuming selection acts on function (e.g., the ability to generate forceful or fast jaw opening), then the evolution of underlying skeletal morphology is unpredictable in the sense that many skeletal shapes yield identical function (any one of which might evolve), although still other skeletal shapes are selected against (Alfaro et al. 2004).
The environments in which some organisms or populations exist may prove so variable or unstable that a consistent model (or prediction) of environment and genotype by environment (G×E) interactions may not be possible as timescales increase. For instance, chaotic dynamics in ecological communities suggest that there are fundamentally unpredictable changes in conditions (as opposed to our theories being incomplete; Hastings et al. 1993). However, timescale matters. Over short to medium timescales (years to decades), chaotic dynamics mean that we have no capacity to predict future environmental conditions that could impose selection on our focal organisms (dependent on population dynamics). Over very long timescales (centuries to millennia), chaotic systems can remain within stable attractors (lacking global catastrophic events), defining a field within which conditions are bounded. Likewise, stochastic processes such as weather might be unpredictable over short timescales (days to weeks) but follow predictable long-term trends (e.g., global warming over the coming centuries, or even cyclic dynamics such as Milankovitch cycles). Considering these timescales and relaxing the need to know the exact species, and given predictable long-term trends and the conserved structure of ecological guilds, we should be able to make some predictions (e.g., at a minimum, we could predict there will be herbivores, carnivores, dominant strategies). However, these predictions will not help us resolve many of the questions and applications of forecasting evolution we highlighted earlier.
H2. Evolution is predictable; we just don't know how yet (models and data)
Our poor performance at correctly forecasting evolutionary outcomes (spanning molecular through organismal to ecosystem levels) may result from incomplete models of evolutionary and biological processes, or insufficient data to parameterize such models. Note that there already exists a large literature of evolutionary theory that provides key building blocks of such a model, drawing on both population genetics and quantitative genetics (e.g., the breeder's equation; Walsh and Lynch 2018). This literature has led to useful computational tools such as SLiM (Haller and Messer 2019), that can carry out whole-genome forward-in-time, spatially explicit population genetic simulations with many of the evolutionary processes we might wish to incorporate: recombination, mutation, selection, and migration. However, even this powerful new tool excludes other processes that we know shape the direction of evolution, including epistasis, genotype-to-phenotype mapping, plasticity, species interactions, population dynamics, and others detailed below. Then, when we have a satisfactory evolutionary forecast model in hand, to apply this model to any real biological system would require extensive, perhaps prohibitive empirical data to parameterize the model and generate the desired forecasts. Therefore, to forecast evolution as defined earlier (figure 1 and box 2), we need both conceptual progress and data, which we detail below.
H2. Genotype to phenotype prediction
To develop predictions from the genotype to phenotype, we argue that we may first need a better understanding of the process of mutation (Kumar and Subramanian 2002). This includes variation in mutation rates for different kinds of molecular changes, at different places within the genome (mutational hot or cold spots). Limited data on mutation rates exist for a few species (e.g., Ellegren 2003, Smeds et al. 2016), but their precision can be improved and we need to determine whether the data can be generalized among species, among individuals or genotypes within species, and within genomes. For short-term evolutionary prediction, de novo mutation has negligible effect on evolution simply for lack of generational time (with some possible exceptions; e.g., Pigliucci and Müller 2010, Hawkins et al. 2019). Because the outcomes of mutation are fundamentally random, we will generally not be able to predict when (or whether) a specific mutation at a specific locus will occur. But over long timescales or in large populations, the law of large numbers provides aggregate statistical predictive power. In very large populations with large per-base mutation rates (e.g., HIV within a patient; Cuevas et al. 2015), one can reliably predict that every feasible mutation will occur within a short time span, so the random nature of individual mutations ceases to matter. Even in humans, we can expect a new mutation at every nucleotide in the genome every year: 140 million humans are born per year globally, each with about 40 de novo point mutations (Donald et al. 2011), introducing more new mutations per year (5.6 billion) than there are nucleotides in the human genome (3.2 billion).
Next, we require the ability to forecast how a given genetic change (e.g., SNP, indel) will produce a change in phenotype and function. This problem encompasses almost the entirety of biology, from genetics to development, physiology, immunology, cell biology, biomechanics, and others, requiring understanding of protein function, gene networks, patterning, and so on. Detailed evolutionary forecasting may be dependent on making significant progress in multiple disciplines of biology. Researchers are currently getting around this difficulty by reverse engineering this process. For instance, genomic methods are being employed that target genes of potential large effect for selection experiments by either losing or suppressing these genes (Monroe et al. 2016, Wang et al. 2018). We can observe physiological, developmental, or protein structural changes for many model organisms in controlled experiments that manipulate genes of large effect (e.g., losing or suppressing genes by knockout or knock down genomic methods). From these inferences, researchers have made progress toward describing mutations that could, individually or collectively, achieve protein or expression changes (e.g., Xu et al. 2016, Younis et al. 2018). We can now do a better job of predicting evolution through studying function to genotype mapping, instead of genotype to function mapping. This approach is especially valuable in applied practice. If we seek to predict how a specific organism will evolve in response to a particular environmental change, this strategy narrows the scope of problems to consider. For instance, in Arabidopsis, Chao and colleagues (2017) examined the importance of SPL transcription factors in thermotolerance by manipulating heat conditions for genetically modified and wild-type plants and measuring differences in expression level in downstream genes activated in an abiotic stress tolerance pathway. Equivalently, if we think of selection imposed by a novel pathogen, we might immediately narrow our focus onto immune genes, and in particular the most relevant of those genes (e.g., pattern recognition genes such as the major histocompatibility complex; Radwan et al. 2020). But by narrowing our focus on specific genes, we might miss other adaptive pathways that respond to the same selective pressure (e.g., glucose aversion versus insecticide resistance in cockroaches; Wada-Katsumata et al. 2011). Encouragingly, theoretical models combined with bioinformatic data seem to predict accurately the evolved distribution of biophysical properties of proteomes (the collection of all the proteins in a species; Zeldovich et al. 2007, Zou et al. 2014). Therefore, there is hope.
Taking a broader view, the mapping of genotype to phenotype (described above) is contingent on many factors including the environment that modifies trait expression (with possible G×E interactions). Also, because of epistasis, genetic variation at one gene can modify the phenotypic effect of alleles at other genes. Therefore, predicting phenotypic effects of mutations must consider genome wide allele frequency data, and the phenotypic effects of possible epistatic interactions (Huang et al. 2012, Csilléry et al. 2018). Three-way gene interactions and higher order epistasis are computationally challenging to model, but are exponentially more abundant (although weaker) than pairwise interactions (Kuzmin 2018). In practice, therefore, evolutionary forecasting requires an understanding of G×E interactions and epistatic modifications of the genotype to phenotype mapping, which requires knowing genome-wide allele frequencies (for epistasis) and the range of environmental conditions experienced at multiple levels of organization. This appears to be a potentially insurmountable task without model simplification given the high dimensionality of the data required.
Overall, we need a better understanding of the impact of genomic (genetic) architecture on the response of individual genes to selection. Studying organisms from across the tree of life, researchers found genomic regions with clusters of loci of high adaptive value, and these clusters were in parallel within lineages and identified for multiple taxa (Yeaman 2013, Holliday et al. 2016, Raeymaekers et al. 2017). Chromosome inversions tend to suppress recombination in heterozygotes and may act as reservoirs of standing genetic variation (Morales et al. 2019). Conversely, inversions mean that different genes tend to be inherited together, so opposing selection on different genes within an inversion can lead to an evolutionary conflict that slows or prevents adaptation. Therefore, to fully understand how chromosome inversions limit adaptation, we need an empirical description of how architecture varies within a focal population (e.g., inversion polymorphisms, and their effects on key genetic properties such as recombination and mutation rates). In other cases, strong selection pressure with a high fitness cost may result in rapid adaptation within a species that is similar in phenotype across populations but varies in the genetic architecture or genomic regions (e.g., the genetic architecture for female choosiness against interspecific mating between species of Aedes; Burford Reiskind et al. 2018). In these cases, we need to know what combinations of genes are contributing to the genetic architecture of the phenotype of interest (e.g., Lehner 2013, Forsberg et al. 2017). Given improvements in the conceptual process and quality and quantity of data, we can address the question of forecasting evolution.
Selection forecast
To forecast evolution, we need to go a step further and link phenotypes to fitness. At the coarsest level this could entail statistical description of covariation between phenotype and fitness (e.g., for the Price equation; Price 1972, Queller 2017), or between genotype and fitness. Currently, we have the statistical tools for this approach. Although this might suffice for making predictions over very short timescales, a lack of mechanistic understanding in this approach limits future projections in changing environmental contexts. Projecting into the future requires a functional understanding of how traits affect fitness, drawing on biomechanics, behavior, ecology, and so on. We lack the capacity, at present, to model how present-day traits, let al.one traits that do not yet exist, generate variation in fitness in as-yet-unobserved environments. However, with improved conceptual models and quality data we can begin to tackle these questions.
As we gain better understanding of genetic process, and selection, we can use existing tools of quantitative or population genetics to forecast the course of evolution. This genetic knowledge can in some instances be simplified by omitting mechanistic detail and taking a quantitative genetic approach (e.g., the breeder's equation), or population genetics for the rare case of simple single-gene traits (Walsh and Lynch 2018). This is an established approach that works well over short timescales, but will break down over longer timescales because we are still refining our mechanistic models of how genetic variance–covariance matrices themselves evolve (we know that they do evolve; Roff 2000), and how selective pressures will change. Therefore, the more mechanistic approach outlined in the above genotype to phenotype predictions provides a potentially robust framework, but one that is harder to parameterize (if possible at all). Whether one takes a mechanistic, quantitative, or population genetics approach, the key is incorporating knowledge about the available genetic variation, how this affects fitness, and how response to the resulting selection is constrained.
Forecasting evolutionary responses to known selective pressures works well when the present-day environment can be safely trusted to remain constant. However, selection on focal species depends on abiotic conditions, and biotic interactions, both of which change through time and we must forecast for evolutionary prediction. To do so, we will need to draw on fields ranging from meteorology (climate change being a major driver of evolution during the Anthropocene), to toxicology (from human pollution), to epidemiology and ecology more generally. We therefore need detailed data on the present-day state of multivariate environmental and ecological factors (e.g., species densities of predators, parasites, prey, competitors, mutualists), and the rules of how these change through time (e.g., how species interact to drive each other's changing population densities).
With models of changing environmental conditions in hand (e.g., the Earth system models used by the IPCC for environmental changes; IPCC 2014), we need to draw inferences about changing selection pressures. To do so, we need to revisit the phenotype to function to fitness mapping by describing how this mapping (particularly function to fitness) changes depending on the future environments (including possible future communities and interactions). This will allow us to forecast how the fitness landscape will shift through time to favor different trait values, trait combinations, and genotypes at various points in the future.
Finally, the selective pressures acting on a focal species may depend on the genotypes of other species, not just their presence, absence, or abundance. Therefore, evolution by other species may modify the direction of evolution of our focal species (i.e., Darwin's tangled bank). Conversely, evolution by our focal species can have reciprocal effects on the abundance, genotypes, phenotypes, and fitness of all the other species with which it interacts directly (or perhaps indirectly; Whitham et al. 2003, Johnson and Stinchcombe 2007). Therefore, effective evolutionary forecasts might also need to consider entire multispecies communities simultaneously in these ecoevolutionary feedback loops.
The above information we need to know to forecast evolution is sobering. And it is likely we will never know enough to effectively forecast evolution with high levels of precision and mechanism over long timescales and in natural environments. This reflects both constraints on our input data, and fundamental stochasticity of biological processes at all levels of organization. However, in many cases we don't need to have absolute precision for practical predictive outcomes. Returning to the subject of what we seek to predict, it may be sufficient to predict that adaptation will occur (Fisher's fundamental theorem), or that a given trait will increase or decrease. For example, predictive evolutionary models are used to determine influenza strain vaccines annually. Although there is limitation in the accuracy of the current models used and evolution of the virus is not entirely predictable, the partial level of accuracy still provides an effective annual vaccine (Agor and Ozaltin 2018). Likewise, in conservation efforts we can predict that in cases of genetic rescue, if we introduce new alleles to a very small, endangered population, issues involving inbreeding depression can be improved. This may be all the information needed for a critically endangered population, but more advanced knowledge about population level adaptations in gene pools across a species's range will help improve models to predict potential outbreeding depression consequences if deleterious alleles are introduced into an already threatened population (Frankham et al. 2011) or help conservation biologist weigh the relative risks of inbreeding or outbreeding depression in a given threatened organism (Edmands 2007). Although precise prediction of evolution is an important goal of evolution biology, our current state of evolutionary prediction still enables many important practical outcomes.
Conclusions
In the present article, we have asked the fundamental question, is evolution predictable at all, and, if so, under which circumstances? Clearly, forecasting would help us address many applied questions needing biological solutions, such as forecasting the rapid evolution of infectious disease or preventing extinction. Forecasting also has value in many applied questions needing biological solutions including tumor growth, rapid evolution of infectious diseases such as HIV and the flu, resistance to control approaches in pathogens and pests, and changing ecosystem services. To the extent evolution is deterministic and predictable, what information and modeling capacity do we need? Will we ever have sufficient data and models? Or is evolution too fundamentally stochastic for comprehensive prediction at all levels of organization? We argue that although any inherent unpredictability is more of an issue for the precision of quantitative or molecular evolutionary processes, less precise predictions are easier. We also argue our ability to forecast precisely will always be timescale dependent. We highlight in the present article that there are many cases in which evolution does converge on the same outcome repeatedly. In situations when evolution is clearly predictable, the questions are when does this happen and why and what can we learn from these situations. We argue that distinguishing between H1 and H2 is useful to address this question and more. Furthermore, research and data generated testing H2 will provide important knowledge about the evolutionary process in general and help us improve forecasting models with greater levels of precision than we currently have. Technological and computational advances in the Biological Sciences, particularly at the genomic level, offer hope that increasing precision and accuracy will be possible moving forward. Ultimately, to apply evolutionary forecasts, we will need an integrated approach encompassing spatiotemporal dynamics and tools generated across multiple fields of biology.
Acknowledgments
This article is part of the National Science Foundation Reintegrating Biology Jumpstart workshop. The project was supported by National Science Foundation Grant no. 1940791. We would like to thank Michael H. Reiskind and Shana L. Geffeney for feedback on an earlier version of the manuscript.
Author Biographical
Martha O. Burford Reiskind (mbreiski@ncsu.edu) is an assistant professor of evolutionary biology and conservation science in the Department of Biological Sciences and the director of the Genetic and Genomic Scholars graduate program at North Carolina State University, in Raleigh, North Carolina, in the United States. Michael L. Moody is an associate professor of ecology and evolutionary biology in the Department of Biological Sciences and director of Herbarium UTEP at the University of Texas at El Paso, in El Paso, Texas, in the United States. Daniel I. Bolnick is a professor of evolutionary biology at the University of Connecticut, in Mansfield, Connecticut, in the United States, and editor-in-chief of The American Naturalist, in Chicago, Illinois, in the United States. Charles T. Hanifin is an associate professor of biology at Utah State University, in Logan, Utah, in the United States. Caroline E. Farrior is an assistant professor in integrative biology at the University of Texas at Austin, in Austin, Texas, in the United States. The author order was determined by a random number generator.
Contributor Information
Martha O Burford Reiskind, Department of Biological Sciences and the director of the Genetic and Genomic Scholars graduate program, North Carolina State University, Raleigh, North Carolina, United States.
Michael L Moody, Department of Biological Sciences and director of Herbarium UTEP, University of Texas, El Paso, El Paso, Texas, United States.
Daniel I Bolnick, University of Connecticut, Mansfield, Connecticut, United States, and editor-in-chief of The American Naturalist, Chicago, Illinois, United States.
Charles T Hanifin, Utah State University, Logan, Utah, United States.
Caroline E Farrior, University of Texas at Austin, Austin, Texas, United States, The author order was determined by a random number generator.
References
- Agor J, Ozaltin O. 2018. Models for predicting the evolution of influenza to inform vaccine strain selection. Human Vaccines and Immunotherapeutics 14: 678–683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agrawal AA. 2017. Toward a predictive framework for convergent evolution: Integrating natural history, genetic mechanisms, and consequences for the diversity of life. American Naturalist 190: S1–S12. [DOI] [PubMed] [Google Scholar]
- Agrawal AF, Stinchcombe JR. 2009. How much do genetic covariances alter the rate of adaptation? Proceedings of the Royal Society B 276: 1183–1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alfaro MA, Bolnick DI, Wainwright PC. 2004. The evolutionary dynamics of complex biomechanical systems: An example using the four-bar mechanism. Evolution 58: 495–503. [PubMed] [Google Scholar]
- Bolnick DI, Barrett RDH, Oke KB, Rennison DJ, Stuart YE. 2018. (Non)parallel evolution. Annual Review of Ecology Evolution and Systematics 49: 303–330. [Google Scholar]
- Burford Reiskind MO, Labadie P, Bargielowski I, Lounibos LP, Reiskind MH. 2018. Rapid evolution and the genomic consequences of selection against interspecific mating. Molecular Ecology 27: 3641–3654. [DOI] [PubMed] [Google Scholar]
- Caruso CM, Martin RA, Sletvold N, Morrissey MB, Wade MJ, Augustine KE, Carlson SM, MacColl ADC, Siepielski AM, Kingsolver JG. 2017. What are the environmental determinants of phenotypic selection? A meta-analysis of experimental studies. American Naturalist 190: 363–376. [DOI] [PubMed] [Google Scholar]
- Chao LM, Liu YQ, Chen DY, Xue XY, Mao TB, Chen XY. 2017. Arabidopsis transcription factors SPL1 and SPL12 confer plant thermotolerance at reproductive stage. Molecular Plant 10: 735–748. [DOI] [PubMed] [Google Scholar]
- Colosimo PF, Hosemann KE, Balabhadra S, Villarreal Jr G, Dickson M, Grimwood J, Schmutz J, Myers RM, Schluter D, Kingsley DM. 2005. Widespread parallel evolution in sticklebacks by repeated fixation of Ectodysplasin alleles. Science 307: 1928–1933. [DOI] [PubMed] [Google Scholar]
- Costanzo M, et al. 2010. The genetic landscape of the cell. Science 327: 425–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csilléry K, Rodríguez-Verdugo A, Rellstab C, Guillaume F. 2018. Detecting the genomic signal of polygenic adaptation and the role of epistasis in evolution. Molecular Ecology 27: 606–612. [DOI] [PubMed] [Google Scholar]
- Cuevas JM, Geller R, Garijo R, Lopez-Aldeguer J, Sanjuan R. 2015. Extremely high mutation rate of HIV-1 in vivo. PLOS Biology 13: e1002251. doi:10.1371/journal.pbio.1002251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [The 1000 Genomes Project], Conrad D, Keebler Jet al. 2011. Variation in genome-wide mutation rates within and between human families. Nature Genetics 43: 712–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelaar P, Bolnick DI. 2019. Appreciating the multiple processes increasing individual or population fitness. Trends in Ecology and Evolution 24: 435–446. [DOI] [PubMed] [Google Scholar]
- Edmands S. 2007. Between a rock and a hard place: Evaluating the relative risks of inbreeding and outbreeding for conservation and management. Molecular Ecology 16: 463–475. [DOI] [PubMed] [Google Scholar]
- Ellegren H, Smith NGC, Webster MT. 2003. Mutation rate variation in the mammalian genome. Current Opinion in Genetics and Development 13: 562–568. [DOI] [PubMed] [Google Scholar]
- Fisher RA. 1930. The Genetical Theory of Natural Selection. Clarendon Press. [Google Scholar]
- Fitzpatrick SW, Torres-Dowdall J, Reznick DN, Ghalambor CK, Funk WC. 2014. Parallelism isn't perfect: Could disease and flooding drive a life-history anomaly in Trinidadian guppies? American Naturalist 183: 290–300. [DOI] [PubMed] [Google Scholar]
- Forsberg SK, Bloom JS, Jadhu MH, Kruglyak L, Carlborg Ö. 2017. Accounting for genetic interactions improves modeling of individual quantitative trait phenotypes in yeast. Nature Genetics 49: 497–503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frankham R. 2015. Genetic rescue of small inbred populations: Meta-analysis reveals large and consistent benefits of gene flow. Molecular Ecology 24: 2610–2618. [DOI] [PubMed] [Google Scholar]
- Frankham R, Ballou JD, Eldrige MDB, Lacy RC, Ralls K, Dudash MR, Fenster CB. 2011. Predicting the probability of outbreeding depression. Conservation Biology 25: 465–475. [DOI] [PubMed] [Google Scholar]
- Genung MA, Schweitzer JA, Ubeda F, Fitzpatrick MB, Pregitzer CC, Felker-Quinn E, Bailey JK. 2011. Genetic variation and community change: Selection, evolution, and feedbacks. Functional Ecology 25: 408–419. [Google Scholar]
- Gould SJ. 1989. Wonderful Life: The Burgess Shale and the Nature of History. Norton. [Google Scholar]
- Haller BC, Messer PW. 2019. SLiM 3: Forward genetic simulations beyond the Wright–Fisher model. Molecular Biology and Evolution 36: 632–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins NJ, Bass C, Dixon A, Neve P. 2019. The evolutionary origins of pesticide resistance. Biological Reviews 94: 135–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastings A, Hom CL, Ellner S, Turchin P, Godfray HCJ. 1993. Chaos in ecology: Is Mother Nature a strange attractor? Annual Review of Ecological Systems 24: 1–33. [Google Scholar]
- Holliday JA, Zhou L, Bawa R, Zhang M, Oubida RW. 2016. Evidence for extensive parallelism but divergent genomic architecture of adaptation along altitudinal and latitudinal gradients in Populus trichocarpa. New Phytologist 209: 1240–1251. [DOI] [PubMed] [Google Scholar]
- Huang W, et al. 2012. Epistasis dominates the genetic architecture of Drosophila quantitative traits. Proceedings of the National Academy of Sciences 109: 15553–15559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [IPCC] Intergovernmental Panel on Climate Change . 2014. Climate Change 2014: Synthesis Report. IPCC. [Google Scholar]
- Irwin DE, Alcaide M, Delmore KE, Irwin JH, Owens GL. 2016. Recurrent selection explains parallel evolution of genomic regions of high relative but low absolute differentiation in a ring species. Molecular Ecology 25: 4488–4507. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Bolnick DI, Kirkpatrick M. 2013. Assortative mating in animals. American Naturalist 181: E125–E138. [DOI] [PubMed] [Google Scholar]
- Johnson MT, Stinchcombe JR. 2007. An emerging synthesis between community ecology and evolutionary biology. Trends in Ecology and Evolution 22: 250–257. [DOI] [PubMed] [Google Scholar]
- Kingsolver JG, Hoekstra HE, Berrigan D, Vignieri SN, Hill CE, Hoang A, Gibert P, Beerli P. 2010. The strength of phenotypic selection in natural populations. American Naturalist 157: 245–261. [DOI] [PubMed] [Google Scholar]
- Kober B, et al. 2020. Spike mutation pipeline reveals the emergence of a more transmissible form of SARS-CoV-2. Cell 182: P812–P827. [Google Scholar]
- Kumar S, Subramanian S. 2002. Mutation rates in mammalian genes .Proceedings of the National Academy of Sciences 99: 803–808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzmin E, et al. 2018. Systematic analysis of complex genetic interactions. Science 360: 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langerhans RB. 2018. Prediction and parallelism of multitrait evolution. Journal of Heredity 1: 59–70. [DOI] [PubMed] [Google Scholar]
- Lassig M, Mustonen V, Walczak A. 2017. Predicting evolution. Nature Ecology and Evolution 1: 0077. [DOI] [PubMed] [Google Scholar]
- Lehner B. 2013. Genotype to phenotype: Lessons from model organisms for human genetics. Nature Reviews Genetics 14: 168–178. [DOI] [PubMed] [Google Scholar]
- Leinonen T, O'Hara RB, Cano JM, Merilä J. 2007. Comparative studies of quantitative trait and neutral marker divergence: A meta-analysis. Journal of Evolutionary Biology 21: 1–17. [DOI] [PubMed] [Google Scholar]
- McGill BJ, Brown JS. 2007. Evolutionary game theory and adaptive dynamics of continuous traits. Annual Review of Ecology, Evolution, and Systematics 38: 403–435. [Google Scholar]
- Monroe JG., McGovern C, Lasky JR, Grogan K, Beck J, McKay JK. 2016. Adaptation to warmer climates by parallel functional evolution of CBF genes in Arabidopsis thaliana. Molecular Ecology 25: 3632–3644. [DOI] [PubMed] [Google Scholar]
- Morales HE, Faria R, Johannesson K, Larsson T, Panova M, Westram AM, Butlin RK. 2019. Genomic architecture of parallel ecological divergence: Beyond a single environmental contrast. Science Advances 5: eaav9963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natarajan C, Hoffmann FG, Weber RE, Fago A, Witt CC, Storz JF. 2016. Predictable convergence in hemoglobin function has unpredictable molecular underpinnings. Science 354: 336–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr HA. 2005. The probability of parallel evolution. Evolution 58: 216–220. [PubMed] [Google Scholar]
- Pau S, Wolkovich EM, Cook BI, Davies J, Kraft NJB, Bolmgren K, Betancourt JL, Cleland EE. 2011. Predicting phenology by integrating ecology, evolution, and climate science. Global Change Biology 17: 3633–3643. [Google Scholar]
- Poli R. 2017. Introduction to Anticipation Studies. Springer. [Google Scholar]
- Post DM, Palkovacs EP. 2009. Eco-evolutionary feedbacks in community and ecosystem ecology: Interactions between the ecological theatre and the evolutionary play. Philosophical Transactions of the Royal Society B 364: 1629–1640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pigliucci M, Müller GD, eds. 2010. Evolution: The Extended Synthesis. MIT Press. [Google Scholar]
- Price GR. 1972. Fisher's “fundamental theorem” made clear. Annals of Human Genetics 36: 129–140. [DOI] [PubMed] [Google Scholar]
- Queller DC. 2017. Fundamental theorems of evolution. American Naturalist 189: 345–353. [DOI] [PubMed] [Google Scholar]
- Raeymaekers JA, et al. 2017. Adaptive and non-adaptive divergence in a common landscape. Nature Communications 8: 267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radwan J, Babik W, Kaufman J, Lenz TL, Winternitz J. 2020. Advances in the evolutionary understanding of MHC polymorphism. Trends in Genetics 36: 298–311. [DOI] [PubMed] [Google Scholar]
- Ramiro RS, Costa H, Gordo I. 2016. Macrophage adaptation leads to parallel evolution of genetically diverse Escherichia coli small-colony variants with increased fitness in vivo and antibiotic collateral sensitivity. Evolutionary Applications 9: 994–1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravinet M, Faria R, Butlin RK, Galindo J, Bierne N, Rafajlović M, Noor MAF, Mehlig B, Westram AM. . 2017. Interpreting the genomic landscape of speciation: A road map for finding barriers to gene flow. Journal of Evolutionary Biology 30: 1450–1477. [DOI] [PubMed] [Google Scholar]
- Rehman SU, Shafique L, Ihsan A, Liu Q. 2020. Evolutionary trajectory for the emergence of novel Coronavirus SARS-Co V-2. Pathogens 9: doi:10.3390/pathogens9030240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renaut S, Owens GL, Rieseberg LH. 2014. Shared selective pressure and local genomic landscape lead to repeatable patterns of genomic divergence in sunflowers. Molecular Ecology 23: 311–324. [DOI] [PubMed] [Google Scholar]
- Roff D. 2000. The evolution of the G matrix: Selection or drift? Heredity 84: 135–142. [DOI] [PubMed] [Google Scholar]
- Sailer ZR, Harms MJ. 2017. Molecular ensembles make evolution unpredictable. Proceedings of the National Academy of Sciences 114: 11938–11943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw RG. 2019. From the past to the future: Considering the value and limits of evolutionary prediction. The American Naturalist 193: 1–10. [DOI] [PubMed] [Google Scholar]
- Seehausen O, et al. 2014. Genomics and the origin of species. Nature Reviews Genetics 15: 176–192. [DOI] [PubMed] [Google Scholar]
- Smeds L, Qvarnstrom A, Ellegren H. 2016. Direct estimate of the rate of germline mutation in a bird. Genome Research 26: 1211–1218. doi:10.1101/gr.204669.116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern DL, Orgogozo V. 2009. Is genetic evolution predictable? Science 323: 746–751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi K, et al. 2007. Clonal and parallel evolution of primary lung cancers and their metastases revealed by molecular dissection of cancer cells. Human Cancer Biology 13: 111–120. [DOI] [PubMed] [Google Scholar]
- Tegze B, et al. 2012. Parallel evolution under chemotherapy pressure in 29 breast cancer cell lines results in dissimilar mechanisms of resistance. PLOS ONE 7: e30804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson JN. 1989. Concepts of coevolution. Trends in Ecology and Evolution 4: 179–183. [DOI] [PubMed] [Google Scholar]
- Wada-Katsumata A, Silverman J, Schal C. 2011. Differential inputs from chemosensory appendages mediate feeding responses to glucose in wild-type and glucose-averse German cockroaches, Blattella germanica. Chemical Senses 36: 589–600. [DOI] [PubMed] [Google Scholar]
- Walsh B, Lynch M. 2018. Evolution and Selection of Quantitative Traits. Oxford University Press. [Google Scholar]
- Wainwright PC, Alfaro ME, Bolnick DI, Hulsey CD. 2005. Many-to-one mapping of form to function: A general principle of organismal design? Integrative and Comparative Biology 45: 256–262. [DOI] [PubMed] [Google Scholar]
- Wang J, et al. 2018. A major locus controls local adaptation and adaptive life history variation in a perennial plant. Genome Biology 19: 72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitham TG, et al. 2003. Community and ecosystem genetics: A consequence of the extended phenotype. Ecology 84: 559–573. [Google Scholar]
- Xu M, Hu T, Zhao J, Park MY, Earley KW, Wu G, Yang L, Poethig RS. 2016. Developmental functions of miR156-regulated Squamosa promoter binding protein-like (SPL) genes in Arabidopsis thaliana. PLOS Genetics 12: e 1006263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeaman S. 2013. Genomic rearrangements and the evolution of clusters of locally adaptive loci. Proceedings of the National Academy of Sciences 110: E1743–E1751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Younis S, et al. 2018. The ZBED6–IGF2 axis has a major effect on growth of skeletal muscle and internal organs in placental mammals .Proceedings of the National Academy of Sciences 115: E2048–E2057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeldovich KB, Chen P, Shakhnovich EI. 2007. Protein stability imposes limits on organism complexity and speed of molecular evolution. Proceedings of the National Academy of Sciences 104: 16152–16157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou T, Williams N, Ozkan SB, Ghosh K. 2014. Proteome folding kinetics is limited by protein halflife. PLOS ONE 9: e112701. [DOI] [PMC free article] [PubMed] [Google Scholar]