Eye movements reflect adaptive predictions and predictive precision

Abstract

Successful decision making depends on the ability to form predictions about uncertain future events. Existing evidence suggests predictive representations are not limited to point estimates, but also include information about the associated level of predictive uncertainty. Estimates of predictive uncertainty have an important role in governing the rate at which beliefs are updated in response to new observations. It is not yet known, however, whether the same form of uncertainty-modulated learning occurs naturally and spontaneously when there is no task requirement to express predictions explicitly. Here we used a gaze-based predictive inference paradigm to show that (1) predictive inference manifested in spontaneous gaze dynamics; (2) feedback-driven updating of spontaneous gaze-based predictions reflected adaptation to environmental statistics; and (3) anticipatory gaze variability tracked predictive uncertainty in an event-by-event manner. Our results demonstrate that sophisticated predictive inference can occur spontaneously, and oculomotor behavior can provide a multidimensional readout of internal predictive beliefs.

INTRODUCTION

Good decision making relies on the ability to make accurate predictions about future events. For instance, your choice of which bus to catch to make an early morning meeting will be guided by a prediction of the time you expect the bus to arrive. Your choice should depend not only on a point prediction (the average or most likely outcome) but also on the associated precision. If the bus’s timing is highly variable, you might want to take an earlier bus.

Existing evidence supports the idea that decision makers cognitively represent information about the width, not merely the central tendency, of the probability distribution that describes an uncertain future event. Bayesian theories of perception, cognition, and action are premised on the idea that the brain encodes probability distributions to quantify the uncertainty in sensory, cognitive, and motor parameters (Griffiths & Tenenbaum, 2006; Knill & Pouget, 2004; Kording & Wolpert, 2004; Stocker & Simoncelli, 2006). Maintaining internal probability distributions at intermediate stages of processing can support the adaptive integration of multiple sources of information.

Signatures of distributional knowledge are apparent in behavior even when internal beliefs must ultimately be collapsed to a point estimate to select an action or express an overt prediction. In tasks that require explicit predictive estimates, variability across repeated responses is suggestive of a process of sampling from an internal distribution (Bonawitz, Denison, Griffiths, & Gopnik, 2014; Vul, Goodman, Griffiths, & Tenenbaum, 2014; Vul & Pashler, 2008). In tasks that involve sequences of predictions or decisions interleaved with feedback, it has been shown that predictions are adaptively modulated by subjective uncertainty, environmental volatility, and the unexpectedness and predictive validity of new observations (Behrens, Woolrich, Walton, & Rushworth, 2007; McGuire, Nassar, Gold, & Kable, 2014; Nassar, Wilson, Heasly, & Gold, 2010; Nassar, Rumsey, Wilson, Parikh Heasly, & Gold, 2012; O’Reilly, Schuffelgen, Cuell, Behrens, Mars, & Rushworth, 2013; Ossmy, Moran, Pfeffer, Tsetsos, Usher, & Donner, 2013; Payzan-LeNestour & Bossaerts, 2011; Payzan-LeNestour, Dunne, Bossaerts, & O’Doherty, 2013; Yu & Dayan, 2005). Internal representations of uncertainty have an important theoretical role in governing belief updating in environments in which observations are noisy and the ground truth is volatile.

For instance, a theoretical delta-rule model developed by Nassar and colleagues (2010; 2012; 2016; 2019; McGuire et al., 2014) identifies multiple specific factors via which uncertainty can influence belief updating. One factor in the model (“change-point probability”) accounts for people’s tendency to adopt a higher learning rate if the previous outcome was extreme relative to their predictive uncertainty. Outcomes outside the predicted range can signal an elevated probability that a change point has occurred in the outcome-generating process and imply that beliefs should be substantially revised. A second factor in the model (“relative uncertainty”) accounts for people’s tendency to adopt higher learning rates at times when their internal beliefs were more uncertain (relative to their total predictive uncertainty). Incoming evidence is therefore weighted more heavily to refine imprecise beliefs. The model can be extended to account for additional factors that should not normatively influence adaptive learning. For example, empirical data show that learning rates can be elevated by incidental reward (Lee, Gold, & Kable, 2020; McGuire et al., 2014) and arousal (Nassar et al., 2012), even in contexts in which reward and arousal carry no predictively relevant information. It is not yet clear whether these incidental effects are mediated by representations of uncertainty or other pathways.

A key open question is whether uncertainty-modulated predictive inference occurs spontaneously or only in response to specific task demands. The experiments discussed above relied on tasks in which participants were instructed to make overt predictions or choices. In a number of the studies (e.g. McGuire et al. 2014) the instructions and training included an explicit description of the structure of the outcome-generating process. It is unknown whether people would spontaneously engage in dynamic tracking of predictive uncertainty on the basis of task structure inferred through direct experience. If so, it would imply predictive inference has a highly general role in cognition, consistent with proposals that the brain naturally functions as a predictive engine (Clark, 2013; Summerfield & De Lange, 2014) and infers statistical regularities from ongoing experience (Griffiths & Tenenbaum, 2006; Turk-Browne, Scholl, Johnson, & Chun, 2010).

A related methodological question is whether there exists a directly measurable behavioral manifestation of predictive uncertainty. Existing task paradigms have exposed the dynamics of predictive inference by behaviorally eliciting a scalar prediction on each trial (Nassar et al., 2010). These paradigms furnish empirical, event-by-event point estimates of a participant’s prediction, the prediction error associated with the subsequent outcome, and the learning rate that guides the ensuing belief update. However, such tasks still require that the width of participants’ internal predictive distribution be computationally inferred on the basis of a theoretical model. It is unknown whether the event-specific degree of predictive uncertainty can be measured directly and unobtrusively from behavior.

Eye tracking potentially provides a means to address both of the above questions. It is well established that gaze is predictive (Henderson, 2017). For example, eye movements can anticipate the trajectory of a bouncing ball in a manner that evinces a sophisticated predictive model (Diaz, Cooper, & Hayhoe, 2013; Hayhoe, Mckinney, Chajka, & Pelz, 2012; Land & McLeod, 2000). Even more broadly, oculomotor behavior is associated with many latent cognitive variables. For instance, microsaccades – saccades with amplitudes less than 0.5–1° (Poletti & Rucci, 2016) – are biased toward the direction of covert spatial attention (Hafed, Lovejoy, & Krauzlis, 2011; Yuval-Greenberg, Merriam, & Heeger, 2014), and tend to predict choice (Yu et al., 2016). Gaze behavior has been used extensively to diagnose internal dynamics of decision processes (Cavanagh, Wiecki, Kochar, & Frank, 2014; Hayhoe & Ballard, 2005; Konovalov & Krajbich, 2016; Krajbich, Armel, & Rangel, 2010; Manohar, Finzi, Drew, & Husain, 2017; Shimojo, Simion, Shimojo, & Scheier, 2003).

We created an eye-tracking task that implicitly incentivized participants to anticipate the spatial locations of visual targets. Participants were not instructed as to the sequential statistical structure of the task, the optimal strategy, or the behaviors of interest. We designed the experiment to test whether uninstructed, spontaneous predictions would show the same adaptive dynamics that have previously been observed during instructed, overtly expressed predictions, and whether different aspects of oculomotor behavior would reflect the central tendency versus the width of the internal predictive distribution.

We hypothesized that gaze position just prior to stimulus onset would be predictive of the upcoming stimulus position, reflecting the central tendency of an internal predictive distribution. To foreshadow our results, this was indeed the case, and such predictions showed evidence for an adaptive learning rate across environments with different generative parameters. We next focused on gaze variability during a pre-stimulus interval, which we hypothesized would be associated with the precision of the predictive distribution. We found that a per-trial measure of pre-stimulus gaze variability was correlated with theoretical levels of uncertainty, both across trials and across environments. Contrary to our expectations, a manipulation of incidental reward had little effect on learning rate or oculomotor dynamics.

Our results suggest that (1) predictive inference manifested in spontaneous gaze dynamics; (2) the updating of gaze-based predictions reflected adaptation to environmental structure; and (3) anticipatory gaze variability carried information about predictive uncertainty. Oculomotor behavior thus appeared to provide a multidimensional readout of internal beliefs, demonstrating the flexibility and generality with which the brain encodes and uses information about predictive uncertainty.

METHODS

Participants

The study was preregistered with the Open Science Framework (https://osf.io/sh76b; Bakst & McGuire, 2019). All procedures were approved by the Boston University Institutional Review Board, and informed consent was obtained for all participants. Participants were recruited from the Boston University community (N=56, 42 female, Age: mean = 20.4, SD=2.0, range 18–27). To determine the appropriate sample size, we performed a power analysis with a significance level of 0.05, power of 0.8, and an effect size of d = 0.4. The sample size required was 51, which we rounded to the next-higher multiple of 8 based on our counterbalancing scheme (see below). Predicted effects and effect sizes were informed by independent pilot data. All participants had normal or corrected-to-normal vision. One additional participant was excluded based on the preregistered criterion of missing eye-tracking data for more than 100 trials in a given condition (see below). No participants were excluded based on the other preregistered criteria (all completed the full session and had >60% task accuracy). A second additional participant was excluded for a reason not anticipated in the preregistration: highly variable eye position in the vertical dimension (standard deviation >3.5°), which was suggestive of poor calibration or other oculomotor issues like nystagmus, given that task stimuli only varied horizontally.

Task

Participants performed an implicit spatial prediction task programmed in Python using PsychoPy (v1.85.1, Peirce, 2007). The nominal task was to report whether briefly presented digits were even or odd in order to earn reward. The horizontal position of the digit on the screen varied across trials.

The digit on each trial appeared with two flanking Xs for 150 ms (Figure 1) before being backward-masked by another X, and the participant had unlimited time to respond by pressing “1” with their left hand for “Odd” or “0” with their right hand for “Even.” Accuracy feedback (a filled or empty circle) was then displayed for 500 ms at the same location as the digit, followed by a 750-ms blank inter-trial interval (ITI). The task was designed to create an implicit incentive for participants to anticipate the location of the next digit during the ITI so they could use central vision to make the odd/even judgment.

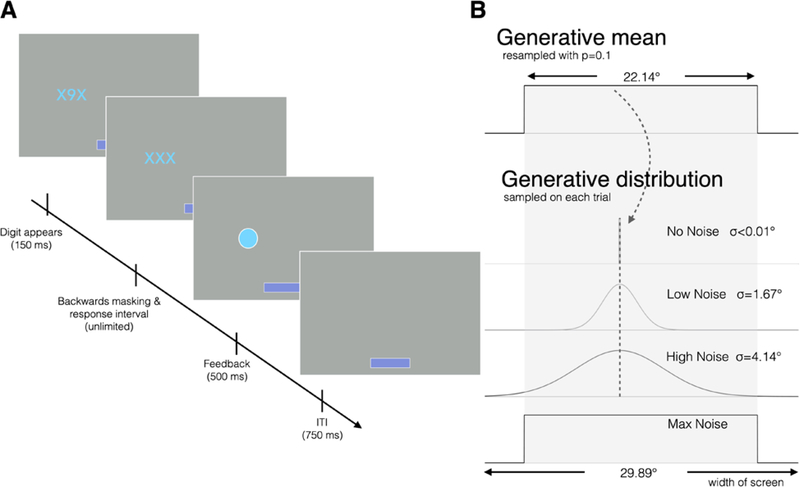
Figure 1.

Gaze-based spatial prediction task. (A) A digit was displayed between flanking Xs for 150 ms, before being masked with a third X. The participant had unlimited time to indicate with a key press whether the digit was even or odd. Feedback then appeared for 500 ms: a filled circle indicated a correct response and an unfilled circle indicated incorrect. The ITI was 750 ms. Total reward for each block of 40 trials was represented by the width of the bar at the bottom of the screen. (B) The generative mean was selected from a uniform distribution 22.14° wide. Gaussian generative distributions in the No, Low, and High Noise conditions had widths of σ<0.01°, σ=1.67°, and σ=4.14° respectively. Digit locations were selected from these distributions, and the mean was resampled with a probability of 0.1. In the Max Noise condition, digit locations were selected from the uniform distribution on every trial.

The stimuli on each trial (digit, Xs, and feedback) were presented in either yellow or blue (randomly, with equal probability). One color (counterbalanced across participants) indicated that a correct response would earn one unit of reward ($0.04), whereas the other color indicated no reward was available. Reward availability was not associated with an outcome’s informativeness about future digit locations. Trials were presented in blocks of 40, and a horizontal bar at the bottom of the screen increased in length proportional to the cumulative reward earned in the current block.

There were four types of blocks: No, Low, High, and Max Noise. In the Max Noise condition, each digit’s horizontal location was drawn independently from a uniform distribution spanning 22.14° of visual angle (42% of the width of the display). For the No, Low, and High Noise conditions, each digit’s horizontal location was drawn from a Gaussian distribution with a condition-specific standard deviation and a mean that was resampled from the uniform distribution at occasional unsignaled change points (cf. Nassar et al., 2010). The generative mean was not resampled during a two-trial refractory period after each change point, and was resampled with a probability of 0.125 thereafter, leading to an overall average change-point probability of approximately 0.1. In the No Noise condition, the standard deviation was essentially zero (σ < 0.01°). In the Low and High Noise conditions, σ=1.67° and 4.14°, respectively. All stimuli were centered vertically. The condition assigned to the first block of the experiment was systematically counterbalanced across participants; otherwise, the four conditions were sampled in random order without replacement in each set of 4 consecutive blocks.

Preliminary training consisted of four 10-trial practice blocks, one of each condition, in order of increasing noise. Participants then completed twenty 40-trial blocks for a total of 800 trials (200 per condition). Participants received no explicit instructions about the different conditions, nor were they told that pre-stimulus gaze position was of interest.

Eye tracking acquisition and preprocessing

Gaze data were collected monocularly at 1000 Hz with an EyeLink 1000+ desk-mounted video eye tracker (SR Research Ltd., Osgoode, Canada). Participants used a chin rest positioned 57 cm from the display monitor (BENQ XL2430 with a resolution of 1920×1080). Gaze position data were decomposed into saccades, fixations, and blinks using the built-in EyeLink algorithm. The algorithm identified saccades based on the conjunction of three thresholds: position (change > 0.15°), velocity (> 22°/s), and acceleration (>4000°/s²). Data from blink periods were excluded from analysis.

Spatial prediction from eye position

Our analyses focused on two summary measures extracted from each trial’s gaze time course: (1) predictive gaze position and (2) gaze variability. Predictive gaze position was the horizontal gaze position at the time of digit onset. Because the feedback and ITI had a fixed duration, we hypothesized that gaze position at digit onset would correspond to a prediction of the digit’s location. Gaze variability was the amount of eye movement during the 750 ms blank ITI that preceded each trial, which we hypothesized would reflect the degree of uncertainty associated with the upcoming prediction. We originally planned to quantify gaze variability in terms of the per-trial standard deviation of horizontal gaze position across samples. In a deviation from the preregistered plan, we subsequently developed a measure of per-trial gaze variability that factored out the net change in gaze position between the start and end of the ITI in order to avoid a confound between gaze variability and predictive gaze position. The analyses reported below quantify each trial’s gaze variability in terms of the total absolute sample-to-sample movement during the ITI minus the absolute value of the net position change (each restricted to the horizontal dimension). Using the originally planned standard deviation metric yielded similar results.

Trials with missing data at the time of digit onset were excluded from analyses of predictive gaze position (0–68 trials per participant, mean=6.3, median=0.5). Trials with missing data for more than half of the ITI were excluded from gaze variability analyses (0–83 trials, mean=10.9, median=3.0). The first trial of each block was also excluded, as participants had no basis for a spatial prediction.

Comparisons across conditions

We used the following general strategy to test for monotonic trends across conditions (in task accuracy, response time, predictive accuracy, gaze variability, saccade and microsaccade amplitude and frequency). Linear mixed-effect models were fit to the per-subject, per-condition averages. The models included fixed-effect terms for the intercept and slope (as a function of condition, coded 1 through 4 in order of increasing noise), and random-effect terms for per-subject intercepts and slopes. Coefficients and 95% confidence intervals were estimated using the fitlme function in Matlab. We additionally report Wilcoxon signed-rank tests for each pair of adjacent noise levels, Bonferroni corrected for three comparisons.

Theoretical delta-rule model

Previous research has shown that a reduced Bayesian model implemented as a delta rule captures key features of dynamic predictive inference (Nassar et al. 2010; 2012; 2019). In brief, the model generates each prediction based on its previous prediction, the prediction error associated with the previous observation, and a dynamically adapted learning rate. The learning rate is itself dependent on estimates of the trial-wise change point probability (CPP) and relative uncertainty (RU). CPP is the probability that the mean of the Gaussian distribution has been resampled, and RU is the fraction of total predictive uncertainty that is due to imprecise knowledge about the location of the generative mean. Higher values of CPP and RU are associated with higher trial-specific learning rates. (For details of the model see Nassar, McGuire, Ritz, & Kable, 2019).

We estimated per-trial values of CPP and RU from the theoretical model on the basis of the sequence of stimulus locations. We then tested the influence of model-derived factors (per-trial CPP and RU) as well as model-unrelated factors (per-trial reward availability and a condition-specific fixed learning rate) on both belief updating and gaze variability, using a linear regression framework described previously (McGuire et al., 2014). For analyses of belief updating, the dependent variable was the trial-to-trial change in predictive gaze position, and each explanatory factor was tested in terms of its multiplicative interaction with the previous prediction error. The estimated regression coefficients therefore represented associations between the explanatory factors and learning rate. For analyses of gaze variability, coefficients represented the direct association of each explanatory factor with the empirically observed per-trial gaze variability. Regression models were fit for each participant separately using only data from the Low and High Noise blocks, with coefficients then tested against zero at the group level using Wilcoxon signed rank tests. The belief updating regression model included nuisance terms to account for left-right bias (mean = 0.003, p = 0.074) and edge avoidance (mean = 0.011, p < 0.001).

We performed further model robustness checks as exploratory analyses. We first estimated the model-derived CPP and RU values and performed the associated regressions on gaze-based update for each of the four conditions separately (with σ set to 0.003°, 1.67°, 4.14°, 6.92° for No, Low, High, and Max Noise conditions, respectively).

We also used a more agnostic approach (Lee et al. 2020) to assess whether larger prediction errors were associated with disproportionately larger (or smaller) updates to gaze-based predictions. We first performed a basic regression for each participant using only an intercept, and a fixed learning rate as regressors for each condition separately. We then combined the residuals across participants and plotted them as a function of prediction error to identify any nonlinear relationships that might be present. We then performed a second regression using an intercept, fixed learning rate, and a nonlinear signed squared prediction error term and overlaid the fit.

To simulate the effect of measurement noise on the parameter estimates, we next performed our original regression with the model-derived update (rather than the empirically measured gaze-based update) as the dependent variable. We added varying levels of Gaussian noise (𝜎=0 to 5°) to the model-derived update, and evaluated its effect on the estimated coefficients.

We also tested the model using only a global fixed learning rate term (instead of condition-specific terms), as well as including a term representing the per-trial total predictive variance (in standard deviation) derived from the model.

RESULTS

We used a gaze-based spatial prediction task to test whether spontaneous eye movements carried information about the central tendency and width of internal predictive probability distributions. Participants (N=56) made even/odd judgments for briefly presented digits (Figure 1A–B). The horizontal position of the digit was selected from a Gaussian distribution on each trial. The mean of the Gaussian distribution was resampled at occasional unsignaled change points, whereas the standard deviation (noise) varied across 40-trial blocks. Three levels of noise were used for the Gaussian distribution, resulting in block types that ranged from No Noise (and minimal uncertainty) to High Noise (and high uncertainty). In a fourth condition, Max Noise, digit locations were drawn from a uniform distribution on each trial, to create a maximally unpredictable context. Greater noise theoretically increased the width of the internal predictive distribution by reducing the precision with which the upcoming event could be estimated on the basis of previous observations.

The overall proportion of correct responses ranged from 0.72 to 0.94 (mean 0.84). Participants tended to respond more accurately and faster when digit locations were highly predictable, and worse, though still above chance, when there was no predictability (Figure 2A). Accuracy depended on the distance between digit and gaze position similarly in all conditions (Figure 2B).

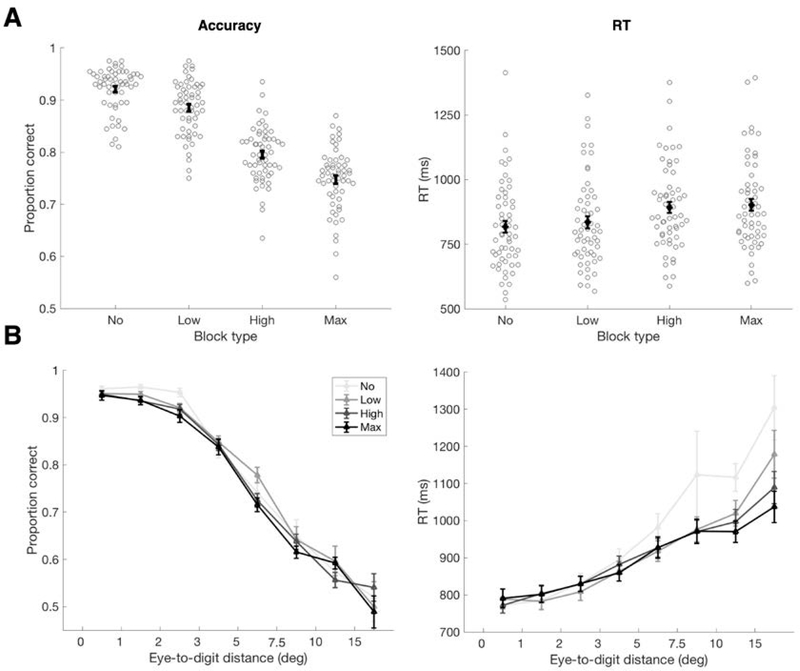
Figure 2.

Behavioral performance. (A) Left: Proportion of correct trials for each participant by block type (grey circles, N=56). Group mean (±SEM) shown in black. Accuracy decreased with increasing noise level (fixed effect of block type 𝛽=−0.06, CI = −0.066 to −0.056, t(55)=−25.39, p<0.001); all block types were significantly different in pairwise comparisons (all p <= 0.001, Wilcoxon signed rank test, Bonferroni corrected for multiple comparisons). Right: Response time (RT) increased with noise level. Within-subject means shown in grey circles, group mean (±SEM) shown in black. There was a significant linear trend (fixed effect of block type 𝛽=30.92, CI = 21.278 to 40.562, t(55)=6.43, p<0.001), though only the Low and High Noise conditions were significantly different using pairwise comparisons with Bonferroni corrections (p < 0.001; No-versus-Low and High-versus-Max comparisons p >= 0.085). (B) Performance as a function of distance between predictive gaze position and the digit. Left shows decreasing accuracy with increasing eye-to-digit distance; right shows increasing RT with increasing eye-to-digit distance. Bins used for eye-to-digit distance were: 0–1°, 1–2°, 2–3°, 3–5°, 5–7.5°, 7.5–10°, 10–15°, 15°+.

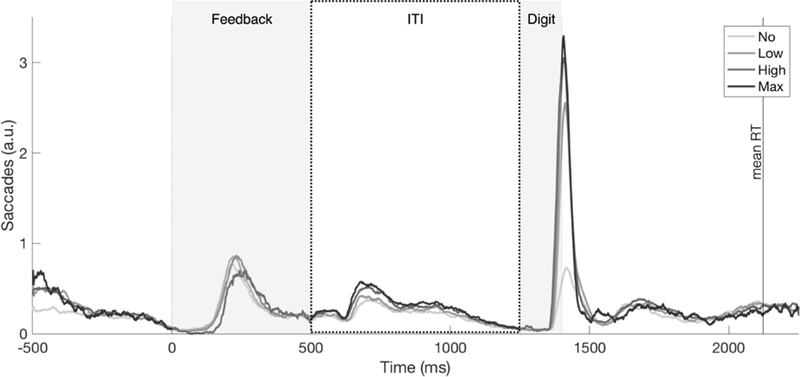
Saccade timing suggested participants learned the task’s temporal structure (Figure 3). In addition to the saccades evoked by visual stimulus onsets (digit and feedback), saccade frequency increased about 150–200 ms after the beginning of the ITI (highest for Max Noise and lowest for No Noise), and then steadily decreased for the remainder of the ITI until digit onset, consistent with anticipatory stabilization of gaze.

Figure 3.

Saccades were tallied throughout the trial for each participant, aligned on keypress response time (feedback onset). The saccade histogram was then averaged across the group and smoothed using a 25-ms moving average. The tallies were performed separately for each block type. Analyses of predictive gaze position used gaze at digit onset (1250 ms). Gaze variability analyses used the ITI (500 to 1250 ms). Mean RT (873 ms) over all participants and block types is shown.

Anticipatory gaze position corresponded to a point prediction

Because digits were presented briefly with crowding and backward masking, the task created an implicit incentive to predict the spatial location of each upcoming digit. Gaze position at the time of digit onset appeared to correspond to a point prediction (Figure 4A). We refer to the horizontal difference between predictive gaze position and the subsequent actual digit location as the “prediction error,” and we refer to the difference between predictive gaze position and the true generative mean as “belief error.”

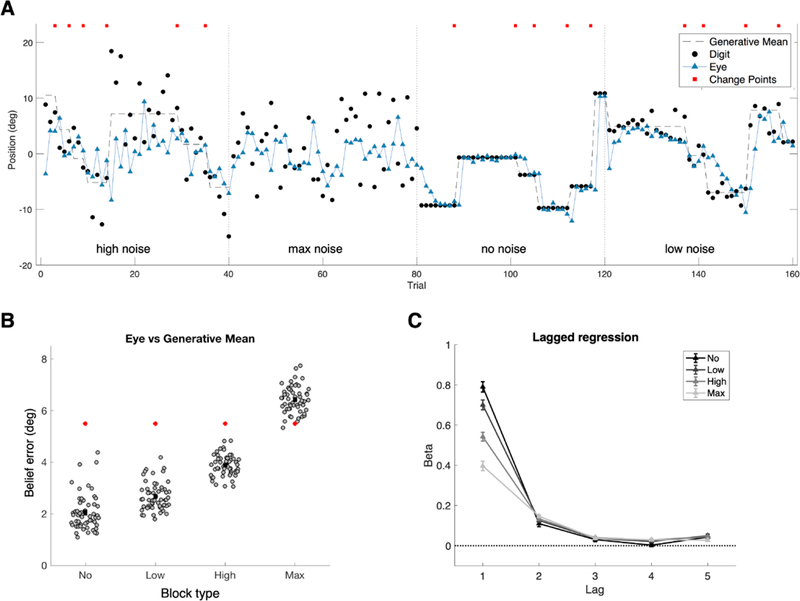
Figure 4.

Predictive gaze position. (A) Predictive gaze position was defined as the horizontal gaze position at the time of digit appearance. Example data are shown for each block type from a representative participant. Dashed line shows the mean of the generative distribution. Black points show actual digit locations. Blue triangles show predictive gaze position. Red squares indicate change points (changes in the generative mean). (B) Belief error by block type. Grey points indicate the mean difference between the eye and generative mean for each participant. For the Max Noise condition, belief error was equivalent to prediction error (the difference between eye and digit). Group means ± SEM are shown in black. Error increased with noise level (fixed effect of block type 𝛽=1.43, CI = 1.347 to 1.522, t(55)=32.43, p<0.001; all pairwise comparisons significantly different p < 0.001, Wilcoxon signed rank test with Bonferroni correction for multiple comparisons). Red points show the mean expected belief error if the gaze were directed at the screen center. (C) Lagged regression to assess the influence of prior digit locations on the current prediction for each participant. Mean coefficients ± SEM are shown for five previous trials separated by block type (indicated by hue). All were significantly greater than zero at the group level (all p <= 0.004, Wilcoxon signed rank test), except No Noise at lag 4 (p = 0.062).

We evaluated the mean belief error in each condition against a hypothetical experience-independent strategy of always directing gaze to the center of the screen (Figure 4B). Participants consistently outperformed the experience-independent strategy in the No, Low, and High Noise conditions, implying predictive gaze position was dynamically updated on the basis of recent observations. Participants underperformed the experience-independent strategy in Max Noise blocks, consistent with having dynamically updated their predictions even when it was not optimal to do so.

Predictive gaze position showed evidence of adaptive learning

We next tested whether participants showed evidence of adaptive learning, as distinct from a simple, non-adaptive strategy such as merely leaving their eyes at the location of the previous digit. The time scale of feedback-driven learning can be assessed by testing the relative influence of multiple previous observations on the current prediction (e.g. Corrado, Sugrue, Seung, & Newsome, 2005). We hypothesized that noisier conditions would favor a prediction that integrated a larger number of observations (Behrens et al., 2007). A lagged regression of predictive gaze position on the five previous observations, pooled across conditions, showed that the greatest weight was given to the most recent digit location but that all five previous trials had decreasing, significantly non-zero weights (all p < 0.001, Wilcoxon signed rank test).

Condition-specific lagged regression analyses showed that participants differentially weighted previous observations depending on the block type, indicative of adaptive learning (Figure 4C). The most recent observation had lower weight in higher-noise conditions than in lower-noise conditions, indicated by significant effects of lag, condition, and their interaction (repeated measures ANOVA, all F(1,55) >= 179.830, all p < 0.001). Examining each lag separately, significant effects of condition were seen at lags 1 and 4 (both F(1,55) >= 8.810, both p <= 0.020 with Bonferroni correction for multiple comparisons), but not at lags 2, 3 and 5 (all F(1,55)<= 5.371, all p >= 0.120 with Bonferroni correction). This suggests predictive gaze position reflected an adaptively weighted integration of multiple previous observations.

Our next set of analyses examined single-trial learning rates, quantifying the degree to which predictive gaze position was updated relative to the previous prediction error. These analyses focused on the High Noise and Low Noise conditions, which included both random noise and true change-point structure, similar to environments tested in previous studies of overt predictions (McGuire et al., 2014; Nassar et al., 2010). In an initial exploratory analysis, we quantified the condition-specific average learning rate in terms of the slope of belief update (current minus previous prediction) as a function of prediction error. There were substantial individual differences in learning rate (Figure 5A–B), but learning rates were systematically higher in the Low Noise condition (p < 0.001, Wilcoxon signed rank test) in addition to being positively correlated between the two conditions across individuals (Spearman ρ = 0.677, p < 0.001). This result was indicative of block-level adaptation of belief updating, consistent with the results of the lagged regression analysis described above.

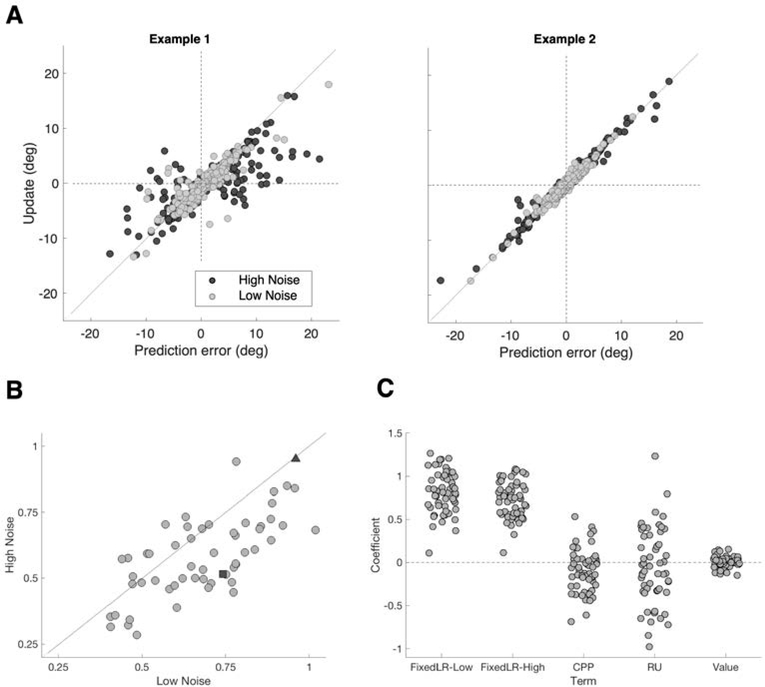
Figure 5.

Blockwise and trialwise adaptive learning. (A) Association between prediction error and update (learning rate) in two example participants, for High Noise blocks (dark grey) and Low Noise blocks (light grey). Learning rate could show evidence of adaptation between the High and Low Noise conditions (Example 1) or could be highly linear and non-adaptive (Example 2). Lines were fit separately for the High and Low Noise condition for each participant. Slopes are plotted in (B), with the two examples from Panel A shown in dark grey (Example 1: square, Example 2: triangle). Low Noise slopes were systematically greater than High Noise slopes (p < 0.001, Wilcoxon signed rank test), and there was a significant positive correlation between the two conditions (Spearman ρ = 0.677, p < 0.001). (C) Coefficients from theoretical model-based regression. Fixed learning rate represents a linear relationship between prediction error and update for Low and High Noise conditions separately. CPP (change point probability) and RU (relative uncertainty) calculated from the delta-rule model (see Methods). Value represents whether or not reward was available on the prior trial. The fixed-learning-rate coefficients differed from zero (both p < 0.001, Wilcoxon signed rank test), and from each other (Low mean = 0.81, High mean = 0.72; p < 0.001). CPP was slightly negative and significantly different from zero (p = 0.004), whereas RU and reward were not (both p >= 0.392).

To assess trial-by-trial adaptive learning, we applied a theoretical delta-rule model of dynamic predictive inference (Nassar et al. 2010; 2012; 2016; 2019). The model generates a prediction on each trial by integrating the probability that a change point just occurred (change point probability, CPP) with the fraction of total predictive uncertainty due to imprecise knowledge about the location of the generative mean (relative uncertainty, RU) to identify a trial-specific learning rate. The model provides trial-wise normative estimates of CPP and RU on the basis of the sequence of previously observed digit locations, independent of participant behavior. We used a previously developed regression-based approach (McGuire et al., 2014) to estimate the influence of CPP and RU on empirically observed trial-specific belief updating. The regression model also estimated terms for a fixed learning rate for High and Low Noise conditions separately, and the effect of reward availability (Figure 5C).

The results yielded evidence for block-level but not trial-level adaptation of learning rates. At the group level, the fixed-learning-rate coefficients for the High Noise and Low Noise conditions significantly differed from zero and from one another (High Noise mean=0.72, Low Noise mean=0.81, p < 0.001, Wilcoxon signed rank test). Coefficients for CPP were slightly negative on average (and significantly different from zero, p = 0.004), whereas coefficients for RU and reward did not differ from zero (both p >= 0.392).

Reward availability has previously been found to influence not only learning rate (Lee et al., 2020; McGuire et al., 2014) but also saccade latency and velocity (Manohar et al., 2017). Here, however, a trial’s reward availability did not influence the velocity or latency of the first saccade within 300 ms after digit onset, nor did it influence the duration or dynamics of the subsequent fixation (Supplemental Figure 1). We observed a non-hypothesized effect of block type such that the post-stimulus saccade tended to be faster (shorter latency and higher velocity) in higher-noise conditions (Supplemental Figure 1).

Gaze variability reflected uncertainty at the block and trial level

We next examined whether gaze variability carried information about the precision of the subjective predictive distribution. We hypothesized that gaze variability during the 750-ms blank ITI prior to each digit’s appearance would be elevated (1) in higher-noise blocks relative to lower-noise blocks; and (2) in trials immediately following change points, when participants had the fewest samples of the current generative mean. Gaze variability was quantified in terms of the total horizontal distance traveled from sample to sample, minus the absolute value of the net distance traveled between the start and end of the ITI.

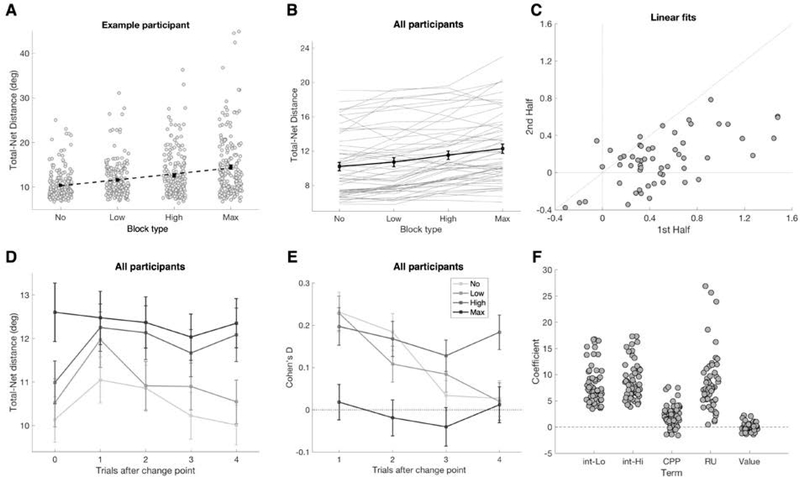
Gaze variability was greater during higher-noise blocks (Figure 6A–B). The linear trend and all pairwise differences between conditions were significant at the group level (fixed effect of block type 𝛽=0.703, CI = 0.581 to 0.824, t(55)=11.6, p<0.001; all pairwise p <= 0.002, Wilcoxon signed rank test with Bonferroni correction for multiple comparisons). The same finding held if gaze variability was alternatively quantified in terms of the standard deviation of sample-to-sample gaze position within the ITI (p < 0.003 for all pairwise comparisons, Wilcoxon signed rank test with Bonferroni correction).

Figure 6.

Gaze variability as a readout of predictive precision. (A) Example data from one participant. Grey circles represent trialwise gaze variability during the ITI. Means ± SEM are in black. Dashed line is linear fit. (B) Gaze variability for all participants. Individual data shown in grey, group mean ± SEM in black. Gaze variability increased with noise level (fixed effect of block type 𝛽=0.703, CI 0.581 to 0.824, t(55)=11.6, p<0.001; all pairwise comparisons significantly different p <= 0.002, Wilcoxon signed rank test with Bonferroni correction). (C) Linear slopes fit to each participant’s gaze variability across the four conditions, for each half of the ITI separately. The slope from the first half of the ITI was significantly greater than from the second (p < 0.001, Wilcoxon signed rank test). (D-E) Gaze variability aligned on change points. (D) Gaze variability ± SEM separated by noise level (indicated by the hue), aligned on change points. Gaze variability on trial zero was calculated before the digit appeared in the resampled location. Max Noise blocks lacked true change point structure; data are shown aligned to arbitrarily designated change point trials for comparison. (E) Effect size for each post-change-point trial relative to trial zero. Cohen’s D was calculated for each participant for each noise level, and the mean ± SEM is shown. For the No, Low, and High Noise levels, all effect sizes were significantly different from zero for the first two trials (all p <= 0.014, Wilcoxon signed rank test). (F) Coefficients from theoretical model-based regression with gaze variability as dependent variable. The coefficients for both intercepts, RU, and CPP were significantly different from zero (all p < 0.001, Wilcoxon signed rank test). The intercept terms differed between the Low-Noise and High-Noise conditions (Low mean = 8.21, High mean = 8.78, p < 0.001, Wilcoxon signed rank test).

The effect of condition was largely driven by gaze variability during the first half of the ITI, consistent with the higher frequency of saccades in that period (Figure 3). To assess this, we calculated gaze variability separately for each half of the ITI (1–375 ms and 376–750 ms). In the first half of the ITI, gaze variability increased across conditions (fixed effect of block type 𝛽=0.494, CI = 0.388 to 0.600, t(55)=9.36, p<0.001; p <= 0.002 for all pairwise comparisons, Wilcoxon signed rank test with Bonferroni correction), whereas the effect was weaker in the second half of the ITI (fixed effect of block type 𝛽=0.139, CI = 0.067 to 0.211, t(55)=3.87, p<0.001; all pairwise comparisons p >= 0.627, with Bonferroni correction for multiple comparison; Supplemental Figure 2). The linear slope across conditions (e.g. Figure 6A) was significantly greater for the first versus second half of the ITI (Figure 6C; p < 0.001, Wilcoxon signed rank test).

We decomposed gaze variability into four potential contributors—saccade frequency, median saccade amplitude, median microsaccade amplitude, and fixational variability—and found that the first three saccade-related measures increased with noise level across conditions (Supplemental Figure 3), whereas fixational variability did not (Supplemental Figure 4).

Gaze variability also transiently increased after change points in the generative mean. Gaze variability increased on the first post-change-point trial in the No, Low, and High Noise conditions, followed by a slow return to baseline over the following trials (Figure 6D). We calculated the Cohen’s D effect size for each post-change-point trial for each participant, using the last pre-change-point trial (trial 0) as a baseline (Figure 6E). For the No, Low, and High Noise levels, all mean effect sizes for the first two trials were significantly different from zero (all p <= 0.014, Wilcoxon signed rank test). Post-change-point increases in gaze variability were more strongly apparent in the first half than the second half of the ITI (Supplemental Figure 2).

We conducted an exploratory analysis using the regression framework introduced above to test trial-by-trial associations between gaze variability and theoretical model-derived factors in the High Noise and Low Noise conditions. The analysis showed significant effects of RU and CPP (Figure 6F, both p < 0.001, Wilcoxon signed rank test), consistent with the post-change-point increase in gaze variability identified above. We found a marginal effect of the prior trial’s reward (mean=0.17, p = 0.035). The Low Noise and High Noise conditions had significantly different intercept coefficients (Low Mean = 8.21, High Mean = 8.78, p < 0.001).

Model robustness checks

The observed trial-level modulation of gaze variability is seemingly at odds with the lack of evidence for trial-level adaptation in the rate of belief updating. We conducted a series of exploratory analyses and robustness checks to probe the pattern of results further. First, we performed a regression analysis of predictive gaze for each of the four conditions individually (Figure 7A). Results differed systematically across conditions. The No Noise condition showed significant positive load on CPP as well as on the fixed learning rate component (p < 0.001, Wilcoxon signed rank test), implying participants adaptively modulated their learning rate at the trial level in that condition. The Low and High Noise conditions both showed stronger weight on the fixed LR component compared to No Noise (p <= 0.005), and a slightly negative weight on CPP (p <= 0.019). In contrast, the Max Noise condition had a larger negative weight on CPP (p < 0.001). This suggests that when participants observed particularly large prediction errors in higher-noise conditions, they updated their prediction using a lower learning rate, treating extreme events as if they represented noise instead of meaningful change.

Figure 7.

Model robustness checks. (A) The analysis of belief updating was performed for each participant separated by condition. Mean coefficient across subjects and standard error are shown. Fixed-learning-rate coefficients (fixed LR) were significantly different between the No, Low, and High noise conditions (p <= 0.038, Wilcoxon signed rank test). CPP was significantly greater than zero only for the No Noise condition (p < 0.001), and significantly less than zero in the other conditions (p <= 0.019). Only the Low Noise condition showed a significant (albeit negative) effect of RU (p = 0.004; all other p >= 0.231). No condition showed any significant load on reward value (p >= 0.105). (B) To visualize a possible nonlinear relationship between prediction error and update, an initial regression was performed with an intercept and fixed LR as regressors for each subject, separated by condition. The residuals from that regression were combined across subjects and plotted against their associated prediction errors. A second regression was then performed with a fixed LR term and a nonlinear term (the signed squared prediction error), and its fit was overlaid (thick black line). (C) A regression was performed on the theoretical model-generated update combined with various levels of Gaussian noise (𝜎=0 to 5°), using the same explanatory variables as the original regression. (D) Regression using one global fixed LR regressor instead of condition-specific regressors. Fixed LR was significantly greater than zero (mean = 0.74, p < 0.001, Wilcoxon signed rank test). CPP was slightly negative on average (−0.07, p = 0.022). Both RU and reward were not significantly different from zero (p >= 0.344). (E) Total predictive variance was added as a regressor with update as the outcome variable. Both condition-specific fixed LR terms were significantly greater than zero (p < 0.001). CPP was slightly less than zero (p = 0.006), while RU was negative on average but statistically indistinguishable from zero (p = 0.081). Neither reward nor total predictive variance (“totVar”) was significantly different from zero (p >= 0.091). (F) Total predictive variance was also added as a regressor with gaze variability as the outcome variable. Coefficients for CPP, RU and total variance were significantly greater than zero (all p <= 0.011). Reward had a very small positive effect (p = 0.031).

To probe the relationship between prediction error and update in a model-agnostic manner, we used an approach from Lee, Gold & Kable (2020). We first performed a basic regression for each participant using only an intercept and a fixed learning rate as regressors for each condition separately. We then combined the residuals across participants and plotted them against the prior prediction error to highlight any nonlinear effects that had not been regressed out (Figure 7B). We then performed a second regression using an intercept, prediction error, and a nonlinear signed squared prediction error term, and overlaid the fit. The more agnostic approach confirmed that the No Noise condition showed nonlinear effects consistent with adopting a higher learning rate for extreme events, whereas the other three conditions show varying levels of nonlinear effects in the opposite direction, consistent with adopting a lower learning rate for extreme events.

We next sought to verify that the lack of expected trial-level effects in learning rate adaptation in the Low and High Noise conditions was not due to the particularities of our model. We implemented an additional three versions of the model (Figure 7C–F): (1) a regression using the normative model output; (2) global fixed learning rate; (3) total predictive variance.

To evaluate the potential effects of measurement noise on the estimated coefficients, we performed the same regression using the theoretical model-derived update as the dependent variable (Figure 7C). Even with Gaussian noise (𝜎 ranged from 0° to 5°) added to the update, the load on the fixed-learning-rate terms for both Low and High noise did not approach levels observed in the empirical data, and the analysis recovered strongly positive coefficients for CPP and RU. This result demonstrates that effects of CPP and RU could theoretically have been detected using our analyses methods.

Next we examined whether condition-specific learning rate terms in the original analysis might have captured variance attributable to CPP or RU (Figure 7D). In a variant of the regression analysis that included only one fixed learning rate parameter, there remained a significant load on the fixed learning rate (p < 0.001, Wilcoxon signed rank test), no significant effect of RU (p = 0.344), and a slightly negative effect of CPP (p = 0.022), suggesting the condition-specific terms had not obscured trial-level effects.

Finally, we implemented a model that included a term for per-trial estimates of total predictive variance derived from the theoretical delta-rule model (Figure 7E). Though total predictive variance is related to RU, the predictor matrix was full-rank indicating that the two were not linearly dependent. The coefficients associated with total predictive variance were not significantly different from zero (p >= 0.071), although the term did tend to improve the fit of the model as a whole: Z-transformed F statistics were computed for the nested model comparison within each individual, and were significantly greater than zero at the group level (p < 0.001, Wilcoxon signed rank test).

In a similar way, we tested the effect of model-derived total predictive variance on gaze variability (Figure 7F). Given that we had already observed a relationship between gaze variability and components of predictive uncertainty (Figure 6), we expected we might identify an effect of total predictive variance as well. The results showed that total predictive variance, CPP, and RU all had significantly positive coefficients (all p <= 0.011), implying all three factors were associated with unique variance in per-trial anticipatory gaze variability. This finding suggests total predictive variance may be a cognitively meaningful factor notwithstanding its lack of any systematic effect on belief updating (Figure 7E).

Optimality and strategy differences across individuals

Previous studies have observed large individual differences in participants’ tendency to adopt successful strategies for adaptive learning (McGuire et al., 2014; Nassar et al., 2010; 2012; 2016). We tested whether the optimality of participants’ belief-updating strategies was related to three indices of gaze variability: (1) average overall gaze variability; (2) gaze variability slope across block types (e.g. Figure 6A); and (3) Cohen’s D effect size for the first post-change-point trial versus baseline in the Low Noise condition (e.g. Figure 6E).

We originally hypothesized that the three indices of gaze variability would be associated with two indices of the optimality of gaze-based predictions. The first optimality index was overall learning rate, calculated as the slope of update as a function of prediction error across all trials (e.g. Figure 5A); based on previous work, we predicted that lower learning rates would track better performance (McGuire et al., 2014; Nassar et al., 2010). In fact, however, the relationship between average learning rate and predictive accuracy in our data set was less straightforward, and accordingly the average learning rate showed no significant associations with gaze variability indices (all p >= 0.151). The second planned optimality index was the sum of the CPP and RU coefficients from the theoretical model-based regression analysis of belief updating (Figure 5C). Consistent with the null effects of trial-level factors on learning rate, that index also showed no associations with gaze variability (all p >= 0.176).

We performed an exploratory analysis in which we compared mean absolute prediction error, an inverse measure of the optimality of gaze-based predictions, with the three gaze variability indices (Figure 8). We observed positive correlations with overall variability and post-change-point effects (all R² >= 0.090, all p <= 0.025), whereas the slope of gaze variability across conditions was positive but not significant (R² = 0.039, p = 0.143). This pattern implies, contrary to our original hypothesis, that larger uncertainty-related changes in gaze variability were associated with less successful performance.

Figure 8.

Individual differences in optimality. The mean absolute prediction error for each participant was compared to three indices of gaze variability: (1) Left: Mean overall gaze variability within the ITI (R² = 0.124, p = 0.008), (2) Center: Slope of a line fit to gaze variability across conditions (R² = 0.039, p = 0.143), (3) Right: Cohen’s D effect size for the first trial after the change point in the Low Noise condition (R² = 0.090, p = 0.025).

DISCUSSION

The present study investigated whether spontaneous, gaze-based predictions would show the same adaptive learning dynamics that have previously been observed for explicit predictions (McGuire et al., 2014; Nassar et al., 2010, 2012, 2016, 2019; O’Reilly et al., 2013). We found evidence that anticipatory gaze position corresponded to the central tendency of participants’ predictive beliefs, whereas gaze variability during the pre-stimulus interval corresponded to belief precision. We found evidence that participants adapted their learning rate across blocks, but we did not observe the trial-level adaptation seen in previous studies involving explicitly elicited predictions. Gaze variability showed evidence of both block-level and trial-level adaptation.

Point predictions

Gaze position at the time of digit onset appeared to reflect the central tendency of participants’ internal predictive probability distribution. The prediction showed evidence of learning (Figure 4B), and integrated multiple previous observations using an adaptive learning rate across conditions (Figure 4C). Gaze-based predictions did not show evidence of the expected trial-level adaptation of learning rate, which differed from previous results in the context of explicit prediction (McGuire et al., 2014). Overall, this set of findings suggests people spontaneously track predictive uncertainty, and supports a highly general role for predictive inference in cognition.

One potential explanation for the absence of trial-level adaptation is that participants may have spontaneously reached a partially inaccurate inference about the task’s generative structure. In reality, the sequence of outcomes was governed by a combination of Gaussian observation noise (a source of expected uncertainty) and occasional, uniformly distributed instances of volatility in the generative mean (a source of unexpected uncertainty). Previous studies that elicited overt predictions in similarly structured environments – and explicitly described the generative structure to participants – have shown evidence that people adaptively used a higher learning rate when outcomes were more surprising or when their beliefs were less precise (e.g. Nassar et al., 2016). However, studies that provided training with other types of generative structure have observed different behavior. Participants correctly adopted a fixed learning rate when volatility in the generative mean was governed by smooth drift (Lee et al., 2020), and downregulated their learning rate for extreme events when such events were uninformative outliers rather than true change points (D’Acremont & Bossaerts, 2016; Nassar, Bruckner, & Frank, 2019; O’Reilly et al., 2013).

A possibility, therefore, is that participants in the present study did not spontaneously tend to infer change-point-like structure from ambiguous sequences of experiences. Participants did show some evidence of having adapted their learning rate in the expected manner in the No Noise condition, where change points were the most obvious (Figure 7A), but in the other conditions they might instead have inferred a generative mechanism characterized by continuous drift or uninformative outliers. An incorrect structural inference could explain why participants might have registered trial-by-trial variability in predictive uncertainty (as suggested by our gaze variability analyses) without translating it into the expected trial-by-trial adaptive learning rate.

Future studies should further examine factors that influence feedback-driven inferences about generative structure in the absence of explicit description. For example, the present task used relatively short 40-trial blocks, and included one condition (Max Noise) that lacked change point structure. It is possible more sustained experience with stable generative statistics would cause different learning rate dynamics to emerge. In addition, future work should investigate dynamic predictive inference in the context of qualitatively different forms of generative structure. For instance, a direct comparison between change-point-like structure and continuous drift with uninformative outliers would help determine whether participants tend to make inaccurate inferences about particular task structures, or if there is a limit to their learning and accuracy in spontaneous predictive inference more generally. This kind of experiment will be critical for determining what structural models participants adopt spontaneously, and how structural assumptions interact with feedback-driven learning.

Gaze variability

Gaze variability during the pre-stimulus interval was inversely related to predictability at the scale of both blocks (Figure 6B) and trials (Figure 6D). A potential interpretation is that oculomotor behavior carries information about the width of the underlying internal predictive distribution. The result raises several questions worth investigating in future research.

First, what is the mechanistic link between gaze variability and predictive uncertainty? Recent work on the link between attention and the variability of neuronal activity suggests one potential explanation. Attention tends to decrease the variability of activity in single neurons (Luo & Maunsell, 2018; Nandy, Nassi, & Reynolds, 2017; von Trapp, Buran, Sen, Semple, & Sanes, 2016). In our task, participants directed overt attention to the predicted location of the next digit, and may have allocated covert attention to a range of locations proportional to the uncertainty in the prediction. A wider attentional window could be associated with greater variability in neural activity, which could propagate to the generated oculomotor commands and result in a more variable eye position.

Increased gaze variability could also be a strategy in its own right. It could represent a process of sampling before converging on a single location to fixate. If the system initially sampled a region proportional to the amount of uncertainty, gaze variability would be expected to increase with uncertainty, especially at early time points. Accordingly, we found that the correspondence between gaze variability and uncertainty was observed primarily in the first half of the ITI (Figure 6C).

A second question has to do with which specific cognitive factor is most strongly reflected in gaze variability. Gaze variability appeared to decouple from learning rate, and tracked trial-by-trial changes in uncertainty that were not reliably reflected in learning dynamics. High gaze variability in the Max Noise condition suggests gaze variability indexed uncertainty either in the current estimate of the generative mean or in the predicted location of the upcoming target. A potentially incongruous observation is that gaze variability increased after change points in the No Noise condition when beliefs and predictions should have been relatively precise. The fact that the post-change-point increase in gaze variability was smallest in the No Noise condition suggests gaze variability was not merely related to the size of the previous prediction error. An increase in uncertainty on those trials could have come about if participants inferred an imprecise model of the task structure.

A third question relates to the extent to which oculomotor behavior in some way represents the full shape of the internal belief distribution. Future work using additional classes of distributions (e.g. skewed, multimodal, etc.) will be essential in answering this question. It remains to be determined whether gaze variability represents a scalar factor like predictive uncertainty or, alternatively, carries additional information about the shape of the subjective probability distribution akin to a sampling process.

Individual differences

Previous work has shown that individuals vary in the extent to which they exhibit optimally adaptive learning (McGuire et al., 2014; Nassar et al., 2010, 2012). Contrary to our expectations, more optimal behavior in our task was generally associated with weaker oculomotor effects (Figure 7). Because the four conditions differed considerably in their governing statistics, participants might have optimized their behavior for only a subset of the conditions they experienced, making it challenging to identify and detect overall signatures of optimal behavior. For example, although participants adapted their learning rates between the High Noise and Low Noise conditions, learning rates in the two conditions also showed substantial shared variance (Figure 5B).

Reward processing

We hypothesized that the availability or receipt of reward would incidentally increase learning rate, in keeping with previous results from explicit prediction (Lee et al., 2020; McGuire et al., 2014). That previous research showed that learning rate was elevated following rewarded trials despite the fact that the reward did not provide additional information. However, we did not find the same to be true in our experiment.

We also hypothesized that reward would alter oculomotor dynamics. Higher-value stimuli tend to elicit saccades with higher peak velocity (Manohar et al., 2017; Takikawa, Kawagoe, Itoh, Nakahara, & Hikosaka, 2002) and shorter latency (Takikawa et al., 2002). However, none of our selected oculomotor features (saccade latency, peak velocity, fixation duration, and fixation gaze variability) showed effects of reward availability. It could be that the fast-paced timing of our task (approximately 2 s per trial) caused participants to ignore reward information in favor of consistent performance across trials. Future work will need to determine whether these differences represent meaningful distinctions between instructed and uninstructed contexts or instead reflect other task features such as timing.

Irrespective of reward, we observed non-hypothesized patterns of decreasing saccade latency and increasing peak velocity in higher-noise conditions. Greater peak velocity could relate to larger prediction errors (and therefore larger saccades) in higher-noise blocks, but this does not explain the finding of shortening latencies. The finding suggests that although participants could not plan the saccade trajectory prior to stimulus appearance, they exhibited some ability to prepare for the saccade execution.

Conclusions

We found that oculomotor behavior carried information about both the central tendency and precision of internal predictive distributions during an uninstructed, gaze-based spatial prediction task. Predictions were updated using a learning rate that was adapted to environmental statistics across task blocks, but did not show the expected fine-scale trial-level adaptation previously reported for overt predictions. Gaze variability during the pre-stimulus interval was associated with the theoretical level of predictive precision.

Our results support a view that dynamic predictive inference is a general aspect of cognition, not merely an esoteric pattern that emerges in response to specific experimental instructions. Our findings on gaze variability suggest predictive representations carry information about the width of predictive probability distributions even at the single-event scale, and that distributional information is not driven solely by inter-event or inter-individual variance. The manifestation of predictive uncertainty in gaze variability might reflect either a high-level strategy of sampling the subjective belief distribution or a low-level side-effect of broadening the covert attentional field. The lack of evidence for trial-level learning rate modulation suggests a scenario in which belief uncertainty interacts with structural inferences about the environment to modulate learning. Investigating how people infer an environment’s generative structure from sequences of experiences, and how structural inferences guide the interpretation of subsequent feedback, is a critical avenue for future work.

Context of the Research

This research began with the observation that the visual system has been a useful testbed for many theories of cognition, including decision making. We broadly hypothesized that since gaze is often predictive, it might be possible to emulate prior research on explicit predictive inference in a more naturalistic manner using spatial prediction and eye tracking. The results suggest that using spatial prediction and the visual system to answer fundamental questions about internal representations of uncertainty is a fruitful avenue for future behavioral, computational, and human neuroscience studies. Exploring biases and flexibility in spontaneous belief updating will be important future directions, as will investigations of the underlying mechanisms.