Abstract
Photoacoustic (PA) imaging can be used to monitor flowing blood inside the microvascular and capillary bed. Ultrasound speckle decorrelation based velocimetry imaging was previously shown to accurately estimate blood flow velocity in mouse brain (micro-)vasculature. Translating this method to photoacoustic imaging will allow simultaneous imaging of flow velocity and extracting functional parameters like blood oxygenation. In this study, we use a pulsed laser diode and a quantitative method based on normalized first order field autocorrelation function of PA field fluctuations to estimate flow velocities in an ink tube phantom and in the microvasculature of the chorioallantoic membrane of a chicken embryo. We demonstrate how the decorrelation time of signals acquired over frames are related to the flow speed and show that the PA flow analysis based on this approach is an angle independent flow velocity imaging method.
Keywords: Speckle dynamics, Photoacoustic flow velocity imaging, Functional imaging, Pulsed Diode Laser
1. Introduction
Flow imaging is an important method for extracting functional information about physiological response to stimuli or pathological changes in tissue. Established technologies like ultrasound and optical coherence tomography (OCT) offer flow imaging capabilities, often based on Doppler or variance analysis [1], [2]. Such flow imaging techniques have yielded valuable information in selected applications, for instance in diagnoses of retinal disorders using OCT angiography (OCTA) [3], [4], [5] and of cardiac valve insufficiency using Color Doppler echocardiography [6], [7]. Recent years have seen an intensive research effort directed at microvascular brain imaging using Power Doppler ultrasound, which allows non- or mildly invasive assessment of functional neurological response from rodents to humans [8], [9], [10], [11].
Scattering-based imaging modalities such as ultrasound and OCT are widely deployed and can be powerful in selected applications but also have limitations, such as low contrast to (mammal) red blood cells (RBCs) in ultrasound, and imaging depth in OCT. Doppler methods are intrinsically angle-dependent, while variance-based flow techniques cannot quantify velocity. Photoacoustic flow imaging has intrinsic contrast to hemoglobin, and can assess oxygen saturation by multispectral imaging. It offers a useful trade-off between spatial resolution and imaging depth, making it a suitable platform for quantitative imaging of microvascular flow.
Recent studies on PA flow imaging are based on Doppler shift [12], [13], density tracking based on cross-correlation in the time [14], [15] or spatial domain [16], [17], transit time of single [18] or particle ensembles [19], [20], and amplitude encoding [21]. As laser technology evolves, more high pulse repetition frequency (PRF) lasers are utilized in PA flow imaging. Liu et al. [22] imaged the blood flow of a mouse ear utilizing a functional optical resolution photoacoustic microscopy system and analyzing based on changes in the Grüneisen relaxation effect [23], [24] caused by blood flow. All these methods share the requirement for many PA acquisitions to characterize flow. Among all these flow imaging approaches, quantitative imaging of vector flow (direction and magnitude) has remained elusive.
Ultrasound speckle decorrelation based velocimetry and imaging was recently shown to accurately estimate blood flow velocity in controlled flow phantoms, and in the mouse brain [25]. Similar analyses have been used in OCTA [26]. In this study, we translate this method to photoacoustic velocity imaging. It allows simultaneous imaging of flow velocities and blood oxygenation.
Randomly distributed absorbing particles within the irradiated region generate an initial positive pressure rise. The propagating acoustic wavelets interfere with each other, creating a random signal that fluctuates subject to the flow in the channel. By retaining the phase of the field and examining the decorrelation time due to motion in the two directions of the image plane, an ascending or descending velocity vector can be extracted.
To determine the blood flow speed using PA signals, we characterize the fluctuation of the beam-formed PA RF signal of the moving particles. We quantitatively analyzed the normalized first-order complex field auto-correlation function of flow-induced fluctuations in the beam-formed images for velocity imaging [25], [26]. In this study, we used a fast pulsed laser diode illuminator (PLDI) enabling kHz frame rates to sample the rapid decorrelation. We validated the analysis in a phantom with known flow speeds. We also imaged microvascular flow in vivo and showed that the obtained results are in agreement with ultrasound velocimetry.
2. Materials and methods
2.1. Theory of normalized first order temporal autocorrelation function
The complex two-dimensional point spread function (PSF) of a photoacoustic imaging system may be approximated by a Gaussian envelope modulating the complex exponential that describes the spatially varying phase of the PSF, denoted as [25]:
| (1) |
where is the (lateral, axial) position of a pixel in the image, parametrize the width of the Gaussian profile in the two directions, is the wave number at the center frequency of the transducer, assuming a broadband signal from the PA source. This function describes the response of the beam-formed radiofrequency (RF) data, by a one-dimensional array along the direction at . The phase term accounts for one-way acoustic propagation. The Gaussian approximation in (1) in assumes that the ultrasound detection array is large in the direction and its response is apodized according to a Gaussian function, for instance by the finite width angular response of the elements. The response is usually governed by the frequency response of the transducer, which can often be approximated by a Gaussian function. We further assume that that .
The induced photoacoustic source pressure by a moving particle can be formulated as [27], [23]
| (2) |
where is the Grüneisen parameter describing the conversion from absorbed optical energy to thermoelastic expansion, is the optical fluence, and is the optical absorption coefficient at the illumination wavelength, assumed to be identical for all particles. The particle is modeled as a point source, located at an instantaneous position . is the slow time, between different PA frames in an acquisition. Note that we disregard spatial variations in and .
The time varying PA signal detected from a measurement pixel at time is computed as the convolution of the source pressure, produced by randomly positioned point sources in the field of view, with the PSF:
| (3) |
Adopting the shorthand , and assuming the particles are moving with a velocity , the PA signal at time lag would become:
| (4) |
In images containing many unresolved PA sources, such as RBCs in a blood vessel, limited sampling of the extensive spectrum of the PA signal introduces the familiar edge, or boundary build-up, artefacts [28], [29], [30]. This dominant stationary component in the image drowns out the fluctuating signal due to flow or particle motion. Applying a spatiotemporal singular value decomposition (SVD) filter [31] to the acquired data will remove the boundary signals. The movement of particles will cause the SVD filtered PA signal to fluctuate at a rate that is proportional to the flow speed. Thus, particle motion can be quantified based on by analyzing the decay of the normalized first-order field autocorrelation function , computed from the beam-formed RF PA image. We consider only relatively large vessels, such that the spatial variation in occurs on length scales smaller than , so the PSF of each measurement pixel samples a uniform velocity. We follow ref. [26] and the derivations therein:
| (5) |
E[] indicates the average over random initial positions; … represents an ensemble temporal average; and * denotes the complex conjugate.
Using Eqs. (3), (4), (5), the normalized first order field autocorrelation function of moving particles can be written as:
| (6) |
The decorrelation of the signal at each location in the image is thus governed by the particle velocities in and , with higher and leading to faster decorrelation. Fitting the complex autocorrelation function of the PA signal from an object with flow thus allows us to extract the ascending or descending vector velocity on a per pixel basis from a series of images. The retention of the phase factor in (6) introduces directionality, as the sign of determines the rotation direction in the complex plane. Analogous to ultrasound velocimetry imaging, which has been called vUS, we propose to name this approach vPA, for photoacoustic velocimetry imaging.
Consequently, for PA flow velocity imaging, we will calculate the based on Eq. (5) and will estimate the values of from Eq. (6) and allocate to each pixel its velocity value. By moving the reference frame, we will be able to do time-resolved velocimetry imaging.
2.2. Experimental setup
In a water tank, a tube made of low-density polyethylene (LDPE) with a inner diameter of 750 was filled with an Indian ink solution, diluted 1:50 v/v in water. Flow ranging from 1.9 mm/s to 19 mm/s was induced using a controllable syringe pump (PERFUSOR secura FT).
A PLDI of wavelength nm with a pulse duration of ns (QD-Q1R10-ILO, Quantel Laser, France) and 1.18 mJ pulse energy, capable of a maximum PRF of 6 kHz, was coupled to a 2 mm core diameter step-index optical fiber. The fiber delivered the pulsed excitation light to the imaging setup.
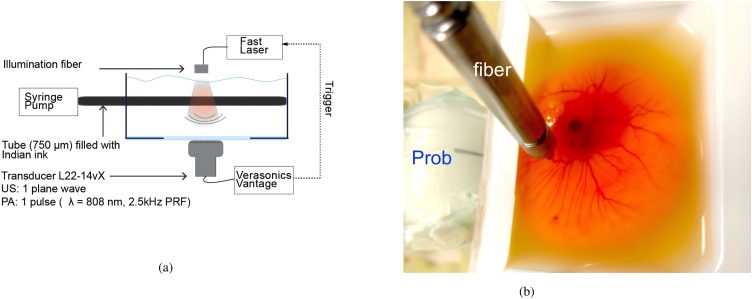
PA signal acquisition, as well as US pulse echo imaging (1 plane wave per frame, ), was performed with a commercial research ultrasound imaging system (Vantage 256, Verasonics Inc. Kirkland, WA, USA) and a linear array ultrasonic probe (L22-14vX, Verasonics Inc. Kirkland, WA, USA). The transducer had 128 elements with a pitch of 0.1 mm and a center frequency of 19 MHz with a bandwidth of 11.5 MHz (60%, 6 dB). It has an elevation focus at mm, and an US imaging resolution of (lateral) and (axial). See Fig. 1a for a schematic.
Fig. 1.
(a) Top view of the acquisition setup, (b) Chicken Embryo setup.
The probe was positioned in front of the tube such that the black Indian ink flowed along the lateral direction of the ultrasound imaging plane. The distance between the probe and the tube was between 10 and 17 mm. We examined two geometries, one in which the tube is oriented along the direction, and one with a angle with the -axis. The optical fiber was positioned over the tube, perpendicular with respect to the imaging plane.
2.3. Photoacoustic flow velocimetry imaging in vivo
We used the chicken embryo model to test our quantitative method in vivo. All animal experiments were conducted in accordance with the Netherlands Experiments on Animals Act and in accordance with the European Council (2010/63/EU) on the protection of animal use for scientific purposes. Fertilized chicken eggs were incubated in a C incubator at 60–65% humidity for 6 days. Immediately prior to imaging, the egg content was removed form the shell by creating an opening over the air sack using tweezers as described in detail by Meijlink et al. [32]. The content was placed in a plastic holder ( mm VWR, the Netherlands) customized with an acoustical window on one side (Fig. 1b). A heater was used to maintain the temperature at C throughout the experiment. The optical fiber was positioned to irradiate the vasculature of the chorioallantoic membrane (CAM). The ultrasound transducer was positioned such that the vascular plexus in the CAM was in the image plane. Ultrasound and photoacoustic signals were recorded for 1 s at a PRF of 2.5 kHz.
2.4. Spatiotemporal resolution
In Eq. (2), we have assumed that the PA sources can be modeled as point particles. In the experiments presented in this study, we have used India ink, in which small suspended carbon particles of a size 0.1–1 [33] are the absorbers. Avian RBCs, which generated the signal in our chicken embryo experiments, are ellipses with a long diameter of approximately 12 [34], which, although large compared to mammal erythrocytes, is still about an order of magnitude smaller than the ultrasound wavelengths we detect.
The usual assumption of stress confinement in PA generation, which justifies Eq. (2) through the separation of the deposited heat and , merits closer inspection. With ns, the stress confinement criterion is satisfied for sources larger than , such as the phantom channel and some of the allantois vessels investigated in this study. The fluctuating PA signal is generated from collections of randomly positioned small particles inside the vessel. In this case, with thermal but not stress confinement, we need to convolve the instantaneous with the temporal characteristic of the laser pulse The laser pulse is nearly Gaussian, so the generated PA spectrum also has a Gaussian envelope with an upper band limit at approximately . Thus; the frequency components that are present in the PA signal are limited to approximately 17 MHz, reducing the effective signal bandwidth [35].
Ordinarily the resolution of raw PA images should be better than that of US images acquired with the same bandwidth, as the band limitation applies only in receive and the frequency spectrum of the source is assumed to be broad. That latter assumption is not true in our experiments, which impacts the spatial resolution in the image, and, equivalently, increases the correlation length in . Instead of the for the transducer, we measured the PSF width in the PA images and found and which we used in the analysis of the signal decorrelation.
2.5. Image acquisition and processing scheme
To accurately sample the fluctuation of the PA speckle dynamics of fast flows, a high-PRF light sources are a critical component. To optimize the data acquisition for the purpose of photoacoustic velocimetry imaging (vPA), we chose to limit US imaging to a single plane wave transmission. After the transmit and receive events of the US image, the ultrasound system was switched to a second receive profile defined for PA acquisition and generated an output trigger signal for the PLDI. There is a fixed 170 ns delay between the laser input trigger and laser firing. With this approach, we were able to acquire the US/PA signals at 2.5 kHz PRF for imaging depth of 20 mm. In addition, the total data acquisition time for each US/PA frames was selected to be 1 s (corresponding to 2500 frames).
We applied SVD filtering to the acquired PA and US data, and removed components with the five highest singular values from the signal in the phantom data to remove stationary components (including the boundary buildup). When imaging the chick embryo, cardiac motion can affect the temporal characteristics of the US/PA signals in an acquisition, and thus the decay of . Therefore, a proper background and bulk motion rejection of the acquired signals is required. To remove stationary signals and bulk motion from the in vivo data, we used a combination of SVD and high pass filtering [31]. The components with the 30 highest singular values were removed form the signal, followed by a tenth order Butterworth high pass filtering with a cutoff frequency of 5 Hz.
vPA images were computed using the algorithm described in Section 2.1. In the in vivo experiments, we also computed flow velocities based on the acquired US images. The analysis of ref. [26] was applied, which describes the two-way acoustic delay in :
| (7) |
3. Results
3.1. Photoacoustic flow velocimetry imaging of the phantom study
Fig. 2 shows the beam-formed ultrasound (gray scale) and photoacoustic (red) image of the diluted India blank ink flowing through the tube. Individual ink particles could not be resolved due to the high particle density; the expected “boundary buildup” is clearly visible, which is removed by SVD filtering before processing for velocimetry.
Fig. 2.
The beam-formed ultrasound (gray scale) and photoacoustic (red) image of the blank ink flowing through the tube, the scale bar is 1 mm.
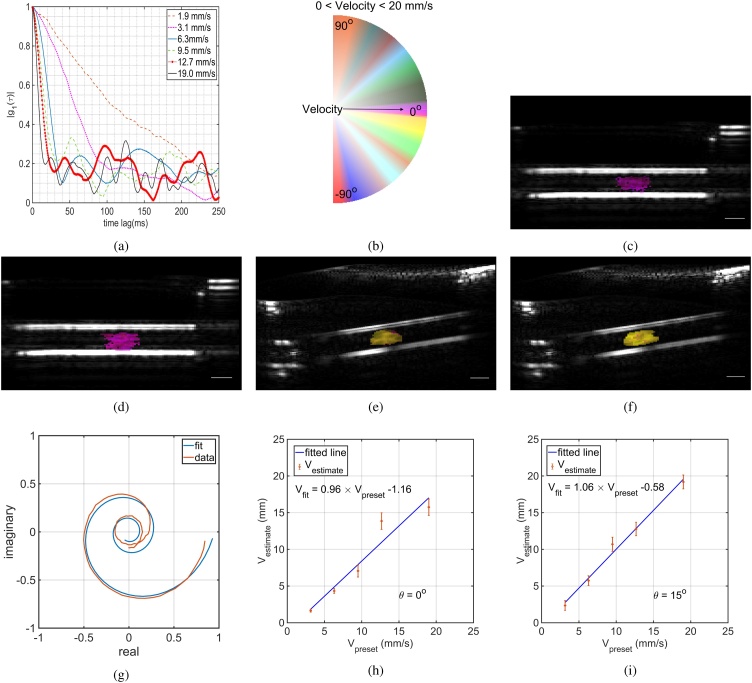
We acquired US/PA data sets for the pre-set velocities induced by the syringe pump and calculated the normalized first order autocorrelation function of based on Eq. (6). Fig. 3a depicts the calculated speckle dynamics up to 250 ms time lag for different preset velocities. It also shows that the correlation drops quicker for the faster flows. By using Eqs. (5) and (6) we can estimate the flow velocity of each pixel. Fig. 3c and 3 d show the photoacoustic velocimetry image of the preset flow speed with 12.7 mm/s and 19.0 mm/s where the tube has no angle with respect to the probe and is compared with the same preset flow speed for the tube (Fig. 3f and 3 e). Fig. 3b is the colormap used to visualize the results where zero velocities are fully transparent represented at the middle and of the color wheel and it becomes more opaque as the flow speed increases. Based on Eq. (6), the component for the ascending flow is negative making the angle between the and to be negative.
Fig. 3.
(a) calculated of the phantom study with pre-set velocities of = 1.9, 3.1, 6.3, 9.5, 12.7, and 19.0 mm/s, (b) is the colormap used for presenting the data vPA and vUS, (c, d) the photoacoustic velocimetry (vPA) image of the pre-set flow speed with 12.7 and 19.0 mm/s, (e, f) depict the vPA of the same pre-set flow speed while the tube has an angle of 15 degree with respect to the probe. The scale bar is 1 mm. (g) The calculated from the experiment and the corresponding fitting curve. The accuracy of the fitting algorithm for (h), and (i).
Fig. 3g shows the calculated based on the flow phantom experiment with preset velocity of 12.7 mm/s and the fitted curve in the complex plane based on Eq. (6). Fig. 3h and 3 i show the high correlation between the preset velocities and the vPA calculated velocities for transverse flows () and angled flows (). The red lines are linear fits to the mean velocities, showing good agreement with errors . The error bars in the figures are the standard deviations of the calculated vPA over different pixels.
3.2. Photoacoustic flow velocimetry imaging in vivo
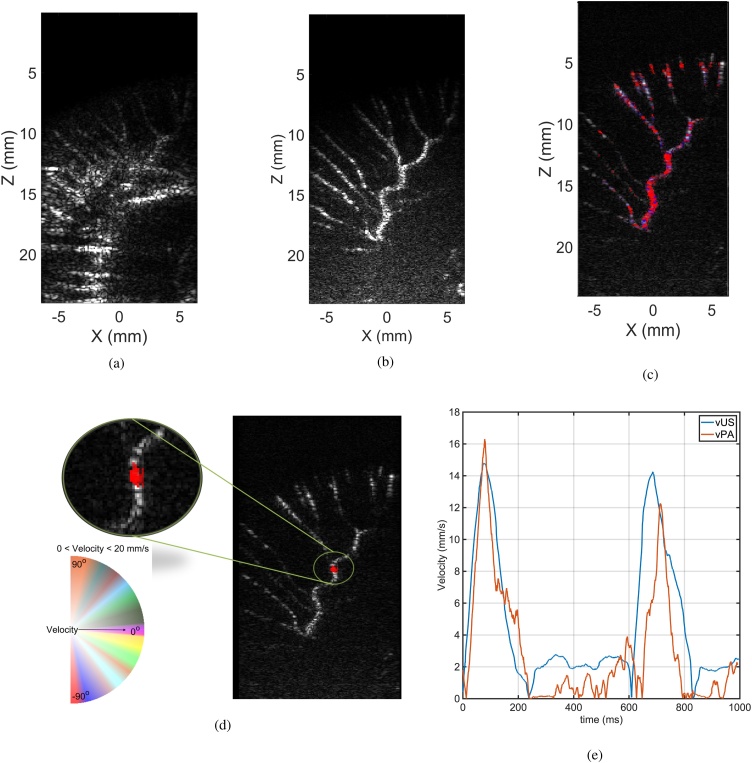
We used a six day-old chicken embryo for the in vivo experiment to image the vasculature of the CAM. Fig. 4a shows the beam-formed ultrasound image of the CAM without filtering. The microvasculature network of the CAM is not clear in this image. After applying SVD filtering, the microvasculature network can be easily distinguished and the stationary clutter was rejected without losing the small vessels. Similarly, bulk motion associated with the cardiac cycle was successfully removed in this manner. We applied this method to all acquired frames and then used the proposed method to estimate the velocity.
Fig. 4.
(a) shows the acquired ultrasound image from the chorioallantoic membrane of the chicken embryo, (b) depicts the spatiotemporally SVD filtered ultrasound image, showing the microvasculature; (c) velocimetry imaging of the CAM using ultrasound, and (d) photoacoustic imaging (The vPA and vUS colormap is based on Fig. 2b). (e) Comparison of the vPA and vUS in the region where PA signals were recorded, showing pulsatile flow.
Fig. 4c and 4 d show the ultrasound velocimetry and photoacoustic velocimetry images of the CAM with the same colormap of the Fig. 3b overlaid on the ultrasound image of the corresponding frame, respectively. The vUS shows that blood flow in the allantois vessels has a maximum flow speed of 16 mm/s. At side branches, the velocity decreases as the vessels get narrower. Furthermore, vPA was compared with vUS in the region where the PA signals were recorded, and resulted in the same maximum flow velocity. Fig. 4e shows the averaged estimated velocity over the pixels in that region. We identified a periodic variation in the flow speed, visible in both the vPA and vUS data. These short bursts of increased blood flow velocity at 150 ms and 700 ms are consistent with arterial flow peaks following cardiac systole.
4. Discussion and conclusion
This study demonstrates that the velocity of a random distribution of micron-scale absorbers can be accurately estimated from the PA speckle dynamics in a series of high frame rate images, quantified using the normalized first order field autocorrelation function. In the phantom study, it has been shown that directional velocimetry imaging up to 20 mm/s can be measured with the proposed system and method. The upper limit of velocimetry imaging flow estimation is a function of the PRF of the PLDI and acquisition system.
The particles in the flow phantom were small and had no ultrasound contrast, yet vPA accurately measured the flow speed. Pixel variation in the measured velocities in the phantom may reflect the (parabolic) flow profile with high central velocity and lower values at the borders. Verification of this hypothesis requires the analysis to be robust in the presence of velocity gradients within the pixel, a situation our algorithm does not handle.
In our experiment, the optical fiber was positioned perpendicular with respect to the imaging plane (see Fig. 1b). The yolk highly attenuates the light at 808 nm and the light cannot penetrate into deep tissues, which necessitates this arrangement. Since the wavelength is longer (808 nm) and not focused onto a sample, thus the theoretic imaging depth is rather higher than the conventional OR-PAM. Addition of an extra (acoustically homogeneous) tissue layer would assist in diffusing the excitation light to a larger area.
We successfully applied vPA to imaging of flow speed in the CAM of a 6-day old chicken embryo. As avian RBCs have good ultrasound contrast due to their size and nucleation [36], [37], vUS measurements validated the measurements. We could visualize the flow in the network. Time resolved vPA and vUS revealed pulsatile flow in the arterial layer of the CAM. Future experiments will be designed to extract blood oxygenation simultaneously using multi-wavelength illumination.
The analysis in its current form still has some details that may be optimized: the approximation of the PSF in the direction may not be valid in the present geometry, and a function may in fact produce more accurate fits of the complex . Furthermore, as in many PA experiments, sensitivity is a limitation. The short-time decorrelation () shows an abrupt drop to , which can be attributed to uncorrelated noise in the data. Inclusion of such a noise term may improve the quantitative performance of the algorithm. Improved sensitivity would also enable a larger field of view in the PA images, as the fiber-coupled PLDI pulse energy was too low to generate a signal from a large area, precluding the investigation of more complex anatomic flow models. Similarly, small vessels were not visible in PA imaging. Moreover, it is possible to extract vector information and bring the vector flow imaging to the vPA. This method can distinguish the flow directionality in but not in due to the square term of in the Eq. (5).
In conclusion, we introduced vPA: quantitative imaging of directional flow using high frame rate PA imaging combined with an analysis of the complex field autocorrelation function. Speed estimation was shown to be numerically accurate on flow speeds up to 20 mm/s. In vivo imaging of flow in the CAM of a chicken embryo revealed pulsatile flow in an artery, in agreement with vUS.
CRediT authorship contribution statement
Reza Pakdaman Zangabad: Developed the data processing method, constructed the experimental setup, carried out the experiments, analyzed the results and wrote the manuscript. Sophinese Iskander-Rizk: Assisted in developing the data acquisition and constructing the experimental setup. Pim van der Meulen: Assisted in developing the data processing method. Bram Meijlink: Prepared the in vivo experiment. Klazina Kooiman: Supervised the in vivo experiment preparation. Tianshi Wang: Assisted in the data processing method.Antonius F.W. van der Steen: Supervised this study. Gijs van Soest: Conceptualized and supervised this study. All authors discussed the results and contributed to the final version of the manuscript.
Conflict of interest
None.
Declaration of Competing Interest
The authors report no declarations of interest.
Acknowledgment
This work is part of the Vici grant 16131 which is financed by the Dutch Research Council (NWO).
Biographies

Reza Pakdaman Zangabad received his B.Sc. degree in Electrical and Computer Engineering/Electronics from University of Tabriz in 2010 and M.Sc. degree in Electronics Engineering from Sabanci University, Istanbul, Turkey in 2014 where he performed research on CMUT based ultrasound imaging system and heat energy harvesting using thermoelectric and thermophotovoltaic cells in collaboration with Lockheed Martin. He joined biomedical engineering group at Erasmus MC university medical center Rotterdam, The Netherlands in 2015 as a PhD candidate and is currently a postdoctoral researcher in the same group. His research interests include CMUT based ultrasound system, transducer and probe development, Photoacoustics, and ultrasound system development/engineering.

Sophinese Iskander-Rizk is an assistant professor at the department of Precision and Microsystems Engineering department at Delft University of Technology. She initially was trained as an electronics engineer (American University in Cairo, 2011) before pursuing a master's degree in biomedical engineering (Delft University of Technology, 2013). She investigated photoacoustic imaging solutions for cardiovascular applications and obtained a doctoral degree at the Biomedical Engineering, Cardiology Department, Erasmus MC, in 2019. Her research interests are in harnessing optical and acoustical solutions to solve current biomedical imaging challenges for diagnostics, treatment and procedural guidance.

Pim van der Meulen received the M.Sc. degree (cum laude) in electrical engineering from Delft University of Technology in 2016. Since then, he has been a Ph.D. candidate at Delft University of Technology, in collaboration with Erasmus Medical Center. His research includes compressive ultrasound imaging, and computational model-based imaging techniques. He is currently researching statistical signal processing methods for imaging through aberrating layers with ultrasound, and is collaborating with the CUBE – Centre of Ultrasound Brain imaging on functional ultrasound imaging for understanding the brain.

Bram Meijlink received his B.Sc. and M.Sc. degrees in Biomedical Sciences with a specialization in Regenerative Medicine and Technology from Utrecht University, Utrecht, The Netherlands in cooperation with Eindhoven Technical University, Eindhoven, The Netherlands, in 2016 and 2019 respectively. He is currently pursuing a Ph.D. degree with the Department of Biomedical Engineering, Erasmus Medical Center, Rotterdam, The Netherlands. His thesis focuses on obtaining more insight into the interaction between vibrating microbubbles, the vessel wall, and drugs in 3D in vitro and in vivo models in order to improve microbubble-mediated drug delivery for cardiovascular diseases and cancer.

Klazina Kooiman (SM’18) received the M.Sc. degree (cum laude) in biopharmaceutical sciences specializing in pharmaceutical technology from Leiden University, Leiden, The Netherlands, and the Ph.D. degree in ultrasound contrast agents for therapy from the Department of Biomedical Engineering, Thoraxcenter, Erasmus MC University Medical Center Rotterdam, The Netherlands, in 2011. In 2018, she acquired the prestigious ERC starting grant from the European Research Council, and in 2019 the prestigious Vidi Grant from the Netherlands Organization for Scientific Research, domain Applied and Engineering Sciences. She is currently an Associate Professor and the Head of the Therapeutic Ultrasound Contrast Agent Group, Department of Biomedical Engineering, Thoraxcenter, Erasmus MC University Medical Center, focusing on using ultrasound contrast agents for drug delivery and molecular imaging. Dr. Kooiman was a recipient of the EFUSMB 2011 Young Investigator Award, Vienna, Austria. She is the co-director of the Annual European Symposium on Ultrasound Contrast Imaging, Rotterdam, which is attended by approximately 180 scientists from universities and industries all over the world.

Tianshi Wang is an Assistant Professor at Department of Cardiology, Erasmus MC. Dr. Wang's research interests are focused on the development of innovative optical coherence imaging technologies to improve the diagnoses in coronary artery, lung and esophagus. His specialties are superfast intravascular Optical Coherence Tomography (OCT) imaging, and phase sensitive OCT imaging, such as Heartbeat OCT, Megahertz Doppler OCT, Thermoelastic-OCT and OCT-based elastography.

Prof. dr. ir. Ton van der Steen (M – 95, SM – 03, fellow – 12) is the head of Biomedical Engineering at the Thorax Centre at Erasmus MC. He is an expert in Ultrasound, Cardiovascular imaging and Cardiovascular Biomechanics. He holds a Master in Applied Physics and a PhD in Medical Sciences. He has a career at the cross roads of Engineering, Health Care and Industry. He is the recipient of the Simon Stevin Master award, and the NWO PIONIER award in Technical Sciences. He is a fellow of IEEE and the European Society of Cardiology. He is member of the Netherlands Academy of Technology (AcTI) and board member of the Royal Netherlands Academy of Sciences (KNAW). Ton has experience in running large consortia as the co-founder and former chairman of the Medical Delta, which comprises of over 280 scientists working on technical solutions for sustainable health. He was also co-PI of ParisK, one of the large CTMM projects (16 MEuro). Ton's international profile is high, with more than 200 invited lectures all over the world, guest professorship/guest researcher in Canada, Japan and China.

Gijs van Soest is a Professor in the Dept. of Cardiology at Erasmus MC, and leads the research group, part of the Biomedical Engineering lab, that specializes in the development of catheter-based and endoscopic imaging technologies based on light, ultrasound, and combinations thereof. Trained as an experimental physicist (MSc University of Groningen 1997, PhD University of Amsterdam 2001), he worked on atmospheric remote sensing before dedicating himself to interventional imaging in cardiology. He is a founder of Kaminari Medical, a company developing intravascular photoacoustic imaging. He is also a scientific director and founder of the biannual Optics in Cardiology conference.
References
- 1.Wang T., Pfeiffer T., Daemen J., Mastik F., Wieser W., van der Steen A.F.W., Huber R., Soest van G. Simultaneous morphological and flow imaging enabled by megahertz intravascular Doppler optical coherence tomography. IEEE Trans. Med. Imaging. 2019;39(5):1535–1544. doi: 10.1109/tmi.2019.2948258. [DOI] [PubMed] [Google Scholar]
- 2.Uribe-Patarroyo N., Villiger M., Bouma B.E. Quantitative technique for robust and noise-tolerant speed measurements based on speckle decorrelation in optical coherence tomography. Opt. Express. 2014;22(20):24411–24429. doi: 10.1364/oe.22.024411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kashani A.H., Chen C.-L., Gahm J.K., Zheng F., Richter G.M., Rosenfeld P.J., Shi Y., Wang R.K. Optical coherence tomography angiography: a comprehensive review of current methods and clinical applications. Prog. Retinal Eye Res. 2017;60:66–100. doi: 10.1016/j.preteyeres.2017.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chen C.-L., Wang R.K. Optical coherence tomography based angiography. Biomed. Opt. Express. 2017;8(2):1056–1082. doi: 10.1364/BOE.8.001056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.De Carlo T.E., Romano A., Waheed N.K., Duker J.S. A review of optical coherence tomography angiography (OCTA) Int. J. Retina Vitreous. 2015;1(1):5. doi: 10.1186/s40942-015-0005-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.de Isla L.P., Zamorano J., Fernandez-Golfin C., Ciocarelli S., Corros C., Sanchez T., Ferreirós J., Marcos-Alberca P., Almeria C., Rodrigo J.L. 3D color-doppler echocardiography and chronic aortic regurgitation: a novel approach for severity assessment. Int. J. Cardiol. 2013;166(3):640–645. doi: 10.1016/j.ijcard.2011.11.094. [DOI] [PubMed] [Google Scholar]
- 7.Deffieux T., Demene C., Pernot M., Tanter M. Functional ultrasound neuroimaging: a review of the preclinical and clinical state of the art. Curr. Opin. Neurobiol. 2018;50:128–135. doi: 10.1016/j.conb.2018.02.001. [DOI] [PubMed] [Google Scholar]
- 8.Dizeux A., Gesnik M., Ahnine H., Blaize K., Arcizet F., Picaud S., Sahel J.-A., Deffieux T., Pouget P., Tanter M. Functional ultrasound imaging of the brain reveals propagation of task-related brain activity in behaving primates. Nat. Commun. 2019;10(1):1–9. doi: 10.1038/s41467-019-09349-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rau R., Kruizinga P., Mastik F., Belau M., de Jong N., Bosch J.G., Scheffer W., Maret G. 3D functional ultrasound imaging of pigeons. NeuroImage. 2018;183:469–477. doi: 10.1101/302323. [DOI] [PubMed] [Google Scholar]
- 10.Soloukey S., Vincent A.J.P.E., Satoer D.D., Mastik F., Smits M., Dirven C.M.F., Strydis C., Bosch J.G., van der Steen A.F.W., De Zeeuw C.I. Functional ultrasound (FUS) during awake brain surgery: the clinical potential of intra-operative functional and vascular brain mapping. Frontier Neurosci. 2020;13:1384. doi: 10.3389/fnins.2019.01384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.He Y., Shi J., Maslov K.I., Cao R., Wang L.V. Wave of single-impulse-stimulated fast initial dip in single vessels of mouse brains imaged by high-speed functional photoacoustic microscopy. J. Biomed. Opt. 2020;25(6):066501. doi: 10.1117/1.JBO.25.6.066501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fang H., Maslov K., Wang L.V. Photoacoustic Doppler effect from flowing small light-absorbing particles. Phys. Rev. Lett. 2007;99(18):184501. doi: 10.1103/physrevlett.99.184501. [DOI] [PubMed] [Google Scholar]
- 13.Brunker J., Beard P. Pulsed photoacoustic doppler flowmetry using time-domain cross-correlation: accuracy, resolution and scalability. J. Acoust. Soc. Am. 2012;132(3):1780–1791. doi: 10.1121/1.4739458. [DOI] [PubMed] [Google Scholar]
- 14.Walker W.F., Trahey G.E. A fundamental limit on delay estimation using partially correlated speckle signals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1995;42(2):301–308. doi: 10.1109/58.365243. [DOI] [Google Scholar]
- 15.Yao J., Maslov K.I., Wang L.V. In vivo photoacoustic tomography of total blood flow and potential imaging of cancer angiogenesis and hypermetabolism. Technol. Cancer Res. Treat. 2012;11(4):301–307. doi: 10.7785/tcrt.2012.500278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liang J., Zhou Y., Maslov K.I., Wang L.V. Cross-correlation-based transverse flow measurements using optical resolution photoacoustic microscopy with a digital micromirror device. J. Biomed. Opt. 2013;18(9):096004. doi: 10.1117/1.jbo.18.9.096004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yao J., Wang L., Yang J.-M., Maslov K.I., Wong T.T.W., Li L., Huang C.-H., Zou J., Wang L.V. High-speed label-free functional photoacoustic microscopy of mouse brain in action. Nat. Methods. 2015;12(5):407–410. doi: 10.1038/nmeth.3336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sarimollaoglu M., Nedosekin D.A., Simanovsky Y., Galanzha E.I., Zharov V.P. In vivo photoacoustic time-of-flight velocity measurement of single cells and nanoparticles. Opt. Lett. 2011;36(20):4086–4088. doi: 10.1364/ol.36.004086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen S.-L., Xie Z., Carson P.L., Wang X., Guo L.J. In vivo flow speed measurement of capillaries by photoacoustic correlation spectroscopy. Opt. Lett. 2011;36(20):4017–4019. doi: 10.1364/ol.36.004017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yao J., Maslov K.I., Shi Y., Taber L.A., Wang L.V. In vivo photoacoustic imaging of transverse blood flow by using Doppler broadening of bandwidth. Opt. Lett. 2010;35(9):1419–1421. doi: 10.1364/ol.35.001419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wei C.-W., Huang S.-W., Wang C.-R.C., Li P.-C. Photoacoustic flow measurements based on wash-in analysis of gold nanorods. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007;54(6):1131–1141. doi: 10.1109/tuffc.2007.367. [DOI] [PubMed] [Google Scholar]
- 22.Liu C., Liang Y., Wang L. Single-shot photoacoustic microscopy of hemoglobin concentration, oxygen saturation, and blood flow in sub-microseconds. Photoacoustics. 2020;17:100156. doi: 10.1016/j.pacs.2019.100156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang L., Zhang C., Wang L.V. Grueneisen relaxation photoacoustic microscopy. Phys. Rev. Lett. 2014;113(17):174301. doi: 10.1103/physrevlett.113.174301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liu W., Lan B., Hu L., Chen R., Zhou Q., Yao J. Photoacoustic thermal flowmetry with a single light source. J. Biomed. Opt. 2017;22(9):096001. doi: 10.1117/1.jbo.22.9.096001. [DOI] [PubMed] [Google Scholar]
- 25.Tang J., Postnov D.D., Kilic K., Erdener S.E., Lee B., Giblin J.T., Szabo T.L., Boas D.A. Functional ultrasound speckle decorrelation-based velocimetry of the brain. Adv. Sci. 2020;7(18):2001044. doi: 10.1002/advs.202001044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tang J., Erdener S.E., Sunil S., Boas D.A. Normalized field autocorrelation function-based optical coherence tomography three-dimensional angiography. J. Biomed. Opt. 2019;24(3):036005. doi: 10.1117/1.jbo.24.3.036005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Xu M., Wang L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006;77(4):041101. doi: 10.1063/1.2195024. [DOI] [Google Scholar]
- 28.Kolkman R.G.M., Hondebrink E., Steenbergen W., van Leeuwen T.G., de Mul F.F.M. Photoacoustic imaging of blood vessels with a double-ring sensor featuring a narrow angular aperture. J. Biomed. Opt. 2004;9(6):1327–1335. doi: 10.1117/1.1805556. ISSN: 1083-3668. [DOI] [PubMed] [Google Scholar]
- 29.Guo Z., Li L., Wang L.V. On the speckle-free nature of photoacoustic tomography. Med. Phys. 2009;36(9 (Pt 1)):4084–4088. doi: 10.1118/1.3187231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kruizinga P., Mastik F., Koeze D., de Jong N., van der Steen A.F.W., van Soest G. Ultrasound-guided photoacoustic image reconstruction: image completion and boundary suppression. J. Biomed. Opt. 2013;18(9):096017. doi: 10.1117/1.jbo.18.9.096017. ISSN: 1083-3668. [DOI] [Google Scholar]
- 31.Demené C., Deffieux T., Pernot M., Osmanski B.-F., Biran V., Gennisson J.-L., Sieu L.-A., Bergel A., Franqui S., Correas J.-M. Spatiotemporal clutter filtering of ultrafast ultrasound data highly increases doppler and ultrasound sensitivity. IEEE Trans. Med. Imaging. 2015;34(11):2271–2285. doi: 10.1109/tmi.2015.2428634. [DOI] [PubMed] [Google Scholar]
- 32.Meijlink B., Skachkov I., van der Steen A.F.W., de Jong N., Kooiman K. The preparation of chicken ex ovo embryos and chorioallantoic membrane vessels as in vivo model for contrast-enhanced ultrasound imaging and microbubble-mediated drug delivery studies. JoVE. 2021;168:e62076. doi: 10.3791/62076. URL https://www.jove.com/t/62076. [DOI] [PubMed] [Google Scholar]
- 33.Madsen S.J., Patterson M.S., Wilson B.C. The use of India ink as an optical absorber in tissue-simulating phantoms. Phys. Med. Biol. 1992;37(4 (April)):985–993. doi: 10.1088/0031-9155/37/4/012. [DOI] [PubMed] [Google Scholar]
- 34.T.R. Gregory, Bird Cell Sizes, 2003. http://www.genomesize.com/cellsize/birds.htm (accessed 25.03.20).
- 35.Cox B.T., Beard P.C. Fast calculation of pulsed photoacoustic fields in fluids using k-space methods. J. Acoust. Soc. Am. 2005;117(6 (June)):3616–3627. doi: 10.1121/1.1920227. ISSN: 0001-4966. [DOI] [PubMed] [Google Scholar]
- 36.McQuinn T.C., Bratoeva M., DeAlmeida A., Remond M., Thompson R.P., Sedmera D. High-frequency ultrasonographic imaging of avian cardiovascular development. Dev. Dyn. 2007;236(12):3503–3513. doi: 10.1002/dvdy.21357. [DOI] [PubMed] [Google Scholar]
- 37.Foster F.S., Hossack J., Adamson S.L. Micro-ultrasound for preclinical imaging. Interface Focus. 2011;1(4):576–601. doi: 10.1098/rsfs.2011.0037. [DOI] [PMC free article] [PubMed] [Google Scholar]