Significance
The adaptive immune system relies on many types of B and T cells, whose functions are reflected in the distinct molecular features of their receptor sequences. Here, we introduce an inference framework, soNNia, which integrates interpretable knowledge-based models of immune receptor generation with flexible and powerful deep learning approaches to characterize sequence determinants of receptor function. Using soNNia, we characterize sequence-specific selection associated with receptors harvested from different cell types and tissues. We quantify synergetic interactions between the molecular features of the paired chains making up the receptor. Lastly, we develop a selection-based classifier to identify T cells specific to distinct pathogenic epitopes. Our approach provides a molecular understanding for how sequence determines the specific functionality of immune receptors.
Keywords: adaptive immune repertoires, thymic selection, central tolerance, deep neural networks, statistical inference
Abstract
Subclasses of lymphocytes carry different functional roles to work together and produce an immune response and lasting immunity. Additionally to these functional roles, T and B cell lymphocytes rely on the diversity of their receptor chains to recognize different pathogens. The lymphocyte subclasses emerge from common ancestors generated with the same diversity of receptors during selection processes. Here, we leverage biophysical models of receptor generation with machine learning models of selection to identify specific sequence features characteristic of functional lymphocyte repertoires and subrepertoires. Specifically, using only repertoire-level sequence information, we classify CD4+ and CD8+ T cells, find correlations between receptor chains arising during selection, and identify T cell subsets that are targets of pathogenic epitopes. We also show examples of when simple linear classifiers do as well as more complex machine learning methods.
The adaptive immune system in vertebrates consists of highly diverse B and T cells whose unique receptors mount specific responses against a multitude of pathogens. These diverse receptors are generated through genomic rearrangement of V-, D-, and J-genes, and sequence insertions and deletions at the junctions, a process known as V(D)J recombination (1, 2). Recognition of a pathogen by a T cell receptor (TCR) or B cell receptor (BCR) is mediated through molecular interactions between an immune receptor protein and a pathogenic epitope. TCRs interact with short protein fragments (peptide antigens) from the pathogen that are presented by specialized pathogen-presenting major histocompatibility complexes (MHCs) on cell surface. BCRs interact directly with epitopes on pathogenic surfaces. Upon an infection, cells carrying those specific receptors that recognize the infecting pathogen become activated and proliferate to control and neutralize the infection. A fraction of these selected responding cells later contributes to the memory repertoire that reacts more readily in future encounters. Unsorted immune receptors sampled from an individual reflect both the history of infections and the ongoing responses to infecting pathogens.
Before entering the periphery where their role is to recognize foreign antigens, the generated receptors undergo a twofold selection process based on their potential to bind to the organism’s own self-proteins. On one hand, they are tested to not be strongly self-reactive (Fig. 1A). On the other hand, they must be able to bind to some of the presented molecules to assure minimal binding capabilities. This pathogen-unspecific selection, known as thymic selection for T cells (6) and the process of central tolerance in B cells (7), can prohibit over 90% of generated receptors from entering the periphery (6, 8, 9).
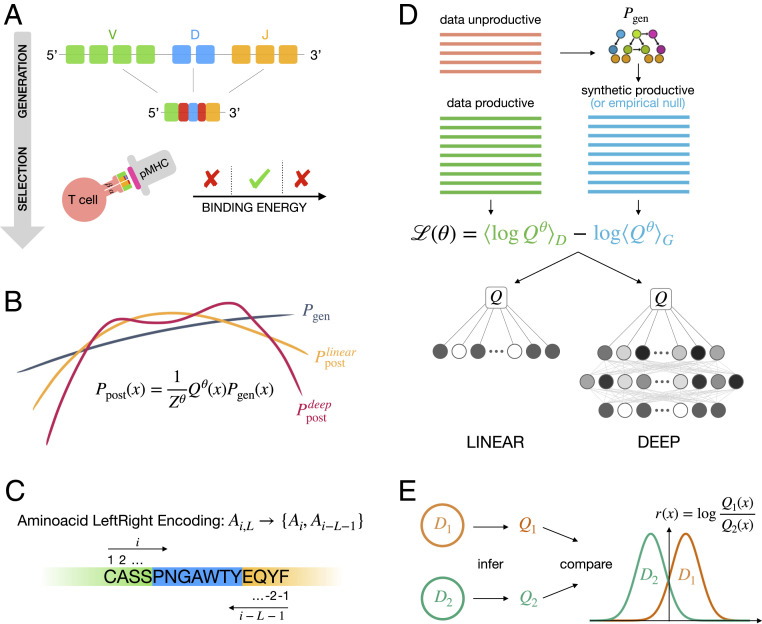
Fig. 1.
Inference of functional selection models for immune receptor repertoires. (A) TCR and chains are stochastically rearranged through a process called V(D)J recombination. Successfully rearranged receptors undergo selection for binding to self-pMHCs (self peptides loaded onto major histocompatibility complexes). Receptors that bind too weakly or too strongly are rejected, while intermediately binding ones exit the thymus and enter peripheral circulation. Development of BCRs follows similar stages of stochastic recombination and selection. (B) We model these two processes independently. The statistics of the V(D)J recombination process described by the probability of generating a given receptor sequence , , are inferred using the IGoR software (3). acts as a baseline for the selection model. We then infer selection factors , which act as weights that modulate the initial distribution . We infer two types of selection weights: linear in log space [using the SONIA software (4)] and nonlinear weights using a DNN, in the soNNia software presented here. Nonlinear selection weights are more flexible than linear ones. (C) Pipeline of the algorithm: is inferred from unproductive sequences using IGoR. Selection factors for both the linear and nonlinear models are inferred from productive sequences by maximizing their log-likelihood , which involves a normalization term calculated by sampling unselected sequences generated by the OLGA software (5). (D) In both selection models, the amino acid composition of the CDR3 is encoded by its relative distance from the left and right borders (left–right encoding). (E) After inferring repertoire-specific selection factors, repertoires are compared by computing, for example, log-likelihood ratios .
Additionally to receptor diversity, T and B cell subtypes are specialized to perform different functions. B and T cells in the adaptive immune system are differentiated from a common cell type, known as lymphoid progenitor. T cells differentiate into cell subtypes identified by their surface markers, including helper T cells (CD4+), killer T cells (CD8+) (6), and regulatory T cells (Tregs; CD4+ FOXP3+) (10), each of which can be found in the nonantigen primed naive or memory compartment. The memory compartment can be further divided into subtypes, such as effector, central, or stem cell-like memory cells, characterized by different lifetimes and roles. B cells develop into, among other subtypes, plasmablasts and plasma cells, which are antibody factories, and memory cells that can be used against future infections. These cell subtypes perform distinct functions, react with different targets, and hence, experience different selection pressures. Here, we ask whether these different functions and selection pressures are reflected in their receptors’ sequence compositions.
Recent progress in high-throughput immune repertoire sequencing both for single-chain (11–14) and paired-chain (15–17) BCRs and TCRs has brought significant insight into the composition of immune repertoires. Based on such data, statistical inference techniques have been developed to infer biophysically informed sequence-based models for the underlying processes involved in generation and selection of immune receptors (3–5, 18). Machine learning techniques have also been used to infer deep generative models to characterize the T cell repertoire composition as a whole (21), as well as discriminate between public and private B cell clones based on complementarity-determining region 3 (CDR3) sequence (22, 23). While biophysically informed models can still match and even outperform machine learning techniques (24), deep learning models can be extremely powerful in describing functional subsets of immune repertoires, for which we lack a full biophysical understanding of the selection process.
Here, we introduce a framework that uses the strengths of both biophysical models and machine learning approaches to characterize signatures of differential selection acting on receptor sequences from subsets associated with specific function. Specifically, we leverage biophysical tools to model what we know (e.g., receptor generation) and exploit the powerful machinery of deep neural networks (DNNs) to model what we do not know (e.g., functional selection). Using the nonlinear and flexible structure of the DNNs, we characterize the sequence properties that encode selection of the specificity of the combined chains during receptor maturation in and chains in T cells and heavy and light ( and ) chains in B cells. We identify informative sequence features that differentiate CD4+ helper T cells, CD8+ killer T cells, and regulatory T cells. Finally, we demonstrate that biophysical selection models can be used as simple classifiers to successfully identify T cells specific to distinct targets of pathogenic epitopes—a problem that is of significant interest for clinical applications (25–29).
Results
Neural Network Models of TCR and BCR Selection.
Previous work has inferred biophysically informed models of V(D)J recombination underlying the generation of TCRs and BCRs (3, 30). In brief, these models are parametrized according to the probabilities by which different V, D, J genes are used and base pairs are inserted in or deleted from the CDR3 junctions to generate a receptor sequence. We infer the parameters of these models using the IGoR software (3) from unproductive receptor sequences, which are generated but due to a frameshift or insertion of stop codons, are not expressed and hence, are not subject to functional selection. The inferred models are used to characterize the generation probability of a receptor sequence and to synthetically generate an ensemble of preselection receptors (5). These generated receptors define a baseline for statistics of repertoires prior to any functional selection.
The amino acid sequence of an immune receptor protein determines its function. To identify sequence properties that are linked to function, we compare the statistics of sequence features (e.g., V-, J-gene usage and CDR3 amino acid composition) present in a given B or T cell functional repertoire with the expected baseline of receptor generation (Fig. 1C). To do so, we encode a receptor sequence as a binary vector whose elements specify whether the feature is present in a sequence . The probability for a given receptor to belong to a functional repertoire is described by modulating the receptor’s generation probability by a selection factor ,
| [1] |
where denotes the parameters of the selection model and ensures normalization of . Previous work (4, 31, 32) inferred selection models for functional repertoires by assuming a multiplicative form of selection , where feature-specific factors contribute independently to selection. We refer to these models as linear SONIA (Fig. 1B). Selection can in general be a highly complex and nonlinear function of the underlying sequence features. Here, we introduce soNNia, a method to infer generic nonlinear selection functions, using DNNs. To infer a selection model that best describes sequence determinants of function in a data sample , soNNia maximizes the mean log likelihood of the data , where the probability is defined by Eq. 1 and denotes expectation over the set of sequences . This likelihood can be rewritten as (SI Appendix)
| [2] |
where is the expectation over the ensemble of sequences that reflect the baseline. This baseline set is often generated by sampling from a previously inferred generation model , using the IGoR software (3). Note that this expression becomes exact as the number of generated sequences approaches infinity.
In soNNia, we divide the sequence features into three categories: 1) (V, J) usage; 2) CDR3 length; and 3) CDR3 amino acid composition encoded by a binary matrix that specifies the identity of an amino acid and its relative position within a 25-amino acid range from both the 5′ and 3′ ends of the CDR3, equivalent to the left–right encoding of the SONIA model (4) (Fig. 1D). Inputs from each of the three categories are first propagated through their own network. Outputs from these three networks are then combined and transformed through a dense layer. This choice of architecture reduces the number of parameters in the DNN and makes the contributions of the three categories (which have different dimensions) comparable; SI Appendix, SI Text and Figs. S1, S3, and S4 have details on the architecture of the DNN.
The baseline ensemble , which we have described as being generated from the model (Fig. 1C), can in principle be replaced by any dataset, including empirical ones, at no additional computational cost, for selection inference with soNNia. This is especially useful when the goal is to only compare the selection models associated with different subrepertoires with distinct functions. We will use this feature of soNNia to learn selection coefficients of subsets relative to an empirically constructed generic functional repertoire. In that case, the inferred selection factors only reflect differential selection relative to the generic baseline. Importantly, this approach enables us to infer differential selection without having to infer a common underlying generation model for the subrepertoires. After two soNNia models have been learned from two distinct datasets, their statistics may be compared by computing a sequence-dependence log-likelihood ratio predicting the preference of a sequence for a subset over the other. This log-likelihood ratio can be used as a functional classifier for receptor repertoires (Fig. 1E).
Deep Nonlinear Selection Model Best Describes Functional TCR Repertoire.
First, we systematically compare the accuracy of the (nonlinear) soNNia model with linear SONIA (4) (Fig. 1B) by inferring selection on TCR repertoires from a large cohort of 743 individuals from ref. 33. Our goal is to characterize selection on functional receptors irrespective of their phenotype. To avoid biases caused by expansions of particular receptors in different individuals, we pool the unique nucleotide sequences of receptors from all individuals and construct a universal donor. Multiplicity of an amino acid sequence in this universal donor indicates the number of independent recombination events that have led to that receptor (in different individuals or in the same individual by convergent recombination).
We randomly split the pooled dataset into a training and a test set of equal sizes and trained both a SONIA and a soNNia selection model on the training set (Methods and Fig. 1C). Our inference is highly stable, and the selection models are reproducible when trained on subsets of the training data (SI Appendix, SI Text and Fig. S2).
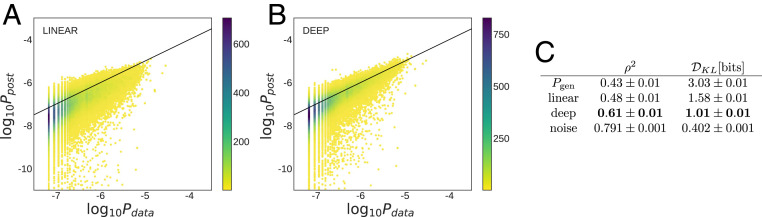
To assess the performance of our selection models, we compared their inferred probabilities with the observed frequencies of the receptor sequences in the test set (Fig. 2 A and B). Prediction accuracy can be quantified through the Pearson correlation between the two log frequencies or through their Kullback–Leibler divergence (Methods and Fig. 2C). A smaller Kullback–Leibler divergence indicates a higher accuracy of the inferred model in predicting the data. The estimated accuracy of an inferred model is limited by the correlation between the test and the training set, which provides a lower bound on the Kullback–Leibler divergence bits and an upper bound on the Pearson correlation .
Fig. 2.
Performance of selection models on TCR repertoires. Scatterplot of observed frequency, , vs. predicted probability for (A) linear SONIA and (B) DNN soNNia models trained on the TCR repertoires of 743 individuals from ref. 33. The baseline is formed by sampling sequences from the model, learned from the nonproductive sequences of the same dataset (SI Appendix). Color indicates number of sequences. (C) The soNNia model performs significantly better, as quantified by both the Kullback–Leibler divergence (Methods) and the Pearson correlation coefficient , without overfitting (SI Appendix, Fig. S2).
We observe a substantial improvement of selection inference for the generalized selection model soNNia with bits (and Pearson correlation ) compared with the linear SONIA model with bits (and Pearson correlation ) (Fig. 2). Both models show a strong effect of selection, reducing the from bits (and increasing the correlation from ) for the comparison of data with the model alone (Fig. 2). This result highlights the role of complex nonlinear selection factors acting on receptor features that shape a functional T cell repertoire. The features that are still inaccessible to the soNNia selection factors are likely due to the sampling of rare features, individual history of pathogenic exposures, or differences in human leukocyte antigen (HLA) complexes among individuals.
Intra- and Interchain Interactions in TCRs and BCRs.
TCRs are disulfide-linked membrane-bound proteins made of variable and chains and expressed as part of a complex that interact with pathogens. Similarly, BCRs and antibodies are made up of a heavy and two major groups ( and ) of light chains. Previous work has identified low but consistent correlations between features of -chain pairs in TCRs, with the largest contributions between and (34–38). In B cells, preferences for receptor features within immunoglobulin heavy (IgH) and light ( or ) chains have been studied separately (39, 40), but interchain correlations have not been systematically investigated.
We first aimed to quantify dependencies between chains by reanalyzing recently published single-cell datasets: TCR pairs of unfractionated repertoires from ref. 37 and BCR of naive cells from ref. 41 (Methods). The blue bars of Fig. 3 show the mutual information between the V and J choices and CDR3 length of each chain, for TCR (Fig. 3A), IgH (Fig. 3B), and IgH (Fig. 3C) repertoires. Mutual information is a nonparametric measure of correlation between pairs of variables (SI Appendix).
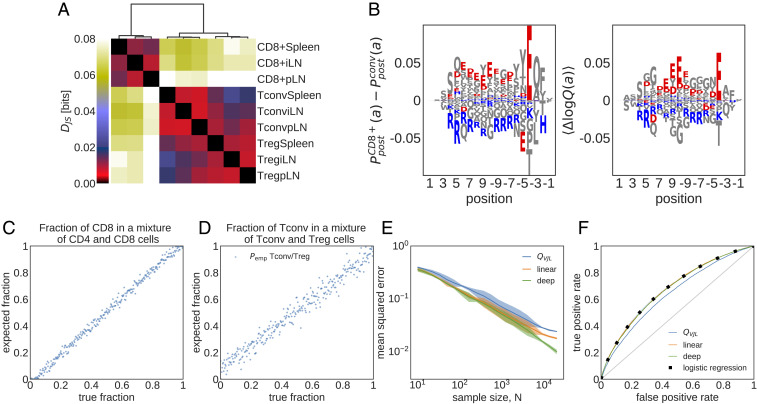
Fig. 3.
Inference of selection on intra- and interchain receptor features. Mutual information between pairs of major intra- and interchain features ( and gene choice and CDR3 length for each chain) for (A) TCR, (B) IgH, and (C) IgH paired chains are shown. Mutual information is estimated directly from data (blue) and from receptors generated based on inferred models: generative baseline (green), linear SONIA (pink), deep-indep (red), and deep joint (yellow). For both TCRs and BCRs, only the deep-joint model (yellow), which correlates the features of both chains through a DNN, is able to recover interchain correlations. Mutual information is corrected for finite-size bias, and error bars are obtained by subsampling (SI Appendix). The diversity of the paired-chain B and T cell repertoires and the contributions of different features to this diversity are reported in SI Appendix, Table S1.
Both TCRs and BCRs have intra- and interchain correlations of sequence features, with stronger empirical mutual dependencies present within chains (Fig. 3).
To account for these dependencies between chains, we generalize the selection model of Eq. 1 to pairs, , where in TCRs or or in BCRs:
| [3] |
where we have dropped the dependence on parameters for ease of notation.
Analogously to single chains, we first define a linear selection model specified by , where the sum now runs over features of both chains and . Because of its multiplicative form, selection can then be decomposed as the product of selection factors for each chain: , where and are linear models. We also define a deep independent model (deep-indep), which has the multiplicative form but where and are each described by DNNs that can account for complex correlations between features of the same chain, similar to the single-chain case (SI Appendix, Fig. S3). The resulting postselection distributions for both the linear and the deep-indep model factorize, , making the two chains independent. Thus, by construction neither the linear nor the deep-indep model can account for correlations between chains. Finally, we define a full soNNia model (deep joint) where is a neural network combining and correlating the features of both chains (SI Appendix, Fig. S4).
We trained these three classes of models on each of the TCR and BCR H and H paired repertoire data described earlier. We then used these models to generate synthetic data with a depth similar to the real data and calculated mutual information between pairs of features (Fig. 3). The preselection generation model [; green bars] explains part but not all of the intrachain feature dependencies, for both T and B cells, while the linear (purple), deep-indep (red), and deep-joint (yellow) models explain them very well (Fig. 3). By construction, the generation, linear, and deep-indep models do not allow for interchain correlations. Only the deep-joint model (yellow) is able to recover part of the interchain dependencies observed in the data. It even overestimates some correlations in BCRs, specifically between the CDR3 length distributions of the two chains and between the heavy-chain and the light-chain CDR3 length. Thus, the deep structure of soNNia recapitulates both intrachain and interchain dependencies of feature-forming immune receptors.
The inferred selection on correlated interchain receptor features is consistent with previous analyses in TCRs (34–38) and is likely due to the synergy of the two chains interacting with self-antigens presented during thymic development for TCRs and preperipheral selection (including central tolerance) for BCRs or later when recognizing antigens in the periphery. Notably, the largest interchain dependencies and synergistic selection are associated with the V-gene usages of the two chains (Fig. 3), which encode a significant portion of antigen-engaging regions in both TCRs and BCRs.
Our results show that the process of selection in BCRs is restrictive, in agreement with previous findings (7), significantly increasing interchain feature correlations. Notably, the increase in correlations (difference between green and other bars) due to selection is larger in naive B cells than in unsorted (memory and naive) T cells. However, the selection strengths inferred by our models should not be directly compared with estimates of the percentage of cells passing preperipheral selection: for B cells vs. for T cells (6). Our models identify features under selection without making reference to the number of cells carrying these features. Since the T cell pool in our analysis is a mixture of naive and memory cells, we can expect stronger selection pressures in the T cell data than in the purely naive T cells. However, previous work analyzing naive and memory TCRs separately using linear selection models did not report substantial differences between the two subsets (31).
Lastly, to quantify the diversity of immune receptor repertoires, we compared the entropy of unpaired- and paired-chain repertoires in SI Appendix, Table S1 (SI Appendix, SI Text). These entropy measures suggest a repertoire size (i.e., a typical number of amino acid sequences) of about receptors for TCR (consistent with ref. 4), receptors for TCR, receptors for BCR heavy-chain, and receptors for BCR light-chain sequences. The paired-chain entropy measures suggest repertoire sizes of for TCR and BCR IgH and IgH receptors, which are compatible with the small correlations observed between heavy and light chains in Fig. 3 and previously reported in refs. 34–38.
Cell Type- and Tissue-Specific Selection on T Cells.
During maturation in the thymus, T cells differentiate into two major cell types: cytotoxic (CD8+) and helper (CD4+) T cells. CD8+ cells bind peptides presented on MHC class I molecules that are expressed by all cells, whereas CD4+ cells bind peptides presented on MHC class II molecules, which are only expressed on specialized antigen presenting cells. Differences in sequence features of CD8+ and CD4+ T cells should reflect the distinct recognition targets of these receptors. Although these differences have already been investigated in refs. 36 and 42, we still lack an understanding as how selection contributes to the differences between CD8+ and CD4+ TCRs. In addition to functional differentiation at the cell-type level, T cells also migrate and reside in different tissues, where they encounter different environments and are prone to infections by different pathogens. As a result, we expect to detect tissue-specific TCR preferences that reflect tissue-specific T cell signatures.
To characterize differential sequence features of TCRs between cell types in different tissues, we pool unique TCRs from nine individuals (from ref. 42) sorted into three cell types (CD4+ conventional T cells [Tconvs], CD4+ Tregs, and CD8+ T cells) and harvested from three tissues (pancreatic draining lymph nodes [pLNs], “irrelevant” nonpancreatic draining lymph nodes [iLNs], and spleen).
Training a nonlinear soNNia model (Fig. 1C) for each subset leads to overfitting issues due to limited data. To solve this problem, we train the model in two steps. First, we use the unfractionated data from ref. 43 to construct a shared baseline for all repertoire subsets. We then learn independent linear SONIA models for each repertoire subset so that the inferred factors only reflect selection relative to the baseline. We approach this problem in two ways. 1) We infer an SONIA model atop an empirical baseline set constructed from the unfractionated repertoire, and 2) we use the technique of transfer learning, which consists of learning a shared nonlinear soNNia model for the unfractionated repertoire and then adding an additional linear layer (similar to standard SONIA) for each subrepertoire (SI Appendix, SI Text and Fig. S5). The subrepertoire selection factors inferred by these two approaches are very similar (SI Appendix, Fig. S5), but the former method is simpler, and we use it for our main analysis in Fig. 4. For comparison, we also used the generation model (trained earlier for Fig. 2) as a baseline, in which case the selection factors include selection effects that are shared among the subrepertoires. Distributions of selection factors obtained by both approaches are shown in SI Appendix, Fig. S6.
Fig. 4.
Cell type- and tissue-specific selection on TCRs. (A) Jensen–Shannon divergences () (Eq. 8) computed from models trained on different subrepertoires are shown. (B) Difference in the marginal probability for amino acid composition along the CDR3, , between CD8+ and CD4+ Tconv (Left) and the mean difference in the corresponding log-selection factors for amino acid usage (Right) are shown (the mean is taken over the distribution ). The negatively charged amino acids (Aspartate, D, and Glutamate, E) and the positively charged amino acids (Lysine, K, and Arginine, R) are indicated in red and blue, respectively. Other amino acids are shown in gray. (C) Maximum likelihood inference of the fraction of CD8+ TCRs in mixed repertoires of conventional CD4+ T cells (Tconvs) and CD8+ cells from spleen (Eq. 4) is shown. Each repertoire comprises unique TCRs. (D) Same as C but for a mixture of Tconv and Treg TCRs. (E) Mean squared error of the inferred sample fraction from C as a function of sample size , averaged over all fractions, using models of increasing complexity: “” is a linear model with only features for CDR3 length and VJ usage, “linear” is linear SONIA model, and “deep” is the full soNNia model (Fig. 1C). (F) ROC for classifying individual sequences coming from CD8+ cells or from CD4+ Tconvs from spleen, using the log-likelihood ratios. Curves are generated by varying the threshold in Eq. 5. The accuracy of the classifier is compared with a traditional logistic classifier inferred on the same set of features as our selection models. The training set for the logistic classifier has Tconv CD4+ and CD8+ TCRs, and the test set has CD4+ and CD8+ TCR sequences.
To quantify differential selection on subrepertoires, we use Jensen–Shannon divergence between the distributions of receptors and for pairs of subrepertoires () (Methods). Clustering of cell types based on Jensen–Shannon divergence shows strong differential selection preferences between the CD4+ and CD8+ receptors, with an average bits across respective tissues and subrepertoires (Fig. 4A; SI Appendix, Fig. S7A has similar results where is used as baseline). We identify differential selection between Tconv and Treg receptors within CD4+ cells with . We also detect moderate tissue specificity for CD8+ and Treg receptors, but no such signal can be detected for CD4+ Tconv cells across different tissues.
Examining the linear selection factors of the SONIA model trained atop as a baseline reveals the VJ (SI Appendix, Fig. S8) and amino acid usage features (Fig. 4C) that are differentially selected in the Tconv CD4+ and CD8+ subsets (in spleen). Linear selection models are organized according to a hierarchy from the least to the most constrained model. As one adds selection factors for each feature, the Kullback–Leibler divergence between the repertoire and the baseline increases (SI Appendix). Decomposing in this way the divergence between CD4+ Tconv and CD8+ repertoires, we find that contributions to the total divergence are evenly split between amino acid features and VJ gene usage, with only a minor contribution from CDR3 length (SI Appendix, Fig. S9). It should be noted that the baseline models for these subrepertoires, inferred from their unproductive receptors, are similar (SI Appendix, Fig. S10) and do not contribute to these differential preferences.
One key difference between CD4+ and CD8+ TCRs amino acid composition is their CDR3 charge preferences. We observe an overrepresentation of positively charged (Lysine, K, and Arginine, R) and suppression of negatively charged (Aspartate, D, and Glutamate, E) amino acids in CD4+ TCRs compared with CD8+ TCRs (Fig. 4B), consistent with previous observations (44). These charge preferences arise due to differential selection on the two subtypes (Fig. 4B), indicating broad differences between amino acid features of peptide–MHC-I and peptide–MHC-II complexes, which respectively interact with CD8+ and CD4+ TCRs. For example, a statistical survey of peptides presented by different MHC classes shows that MHC-I molecules tend to present more positively charged peptides compared with MHC-II molecules—a bias that is complementary to the charge preferences of the respective TCR subtypes (45).
Decomposing Unsorted Repertoires Using Selection Models.
Knowing models specific to subrepertoires enables us to infer the fraction of each class in unsorted data. Estimating the relative fraction of CD4+ and CD8+ subtypes in a repertoire can be informative for clinical purposes (e.g., as a probe for tumor-infiltrating lymphocytes), where overabundance of CD8+ cells in the sample has been associated with positive prognosis in ovarian cancer (46). Given a repertoire composed of the mixture of two subrepertoires and in unknown proportions, we maximize the log-likelihood function based on our selection models to find the fraction of a subrepertoire within the mixture:
| [4] |
where is the empirical mean over sequences in the mixture.
Previous work has used differential V- and J-gene usage and CDR3 length to characterize the relative fraction of CD4+ and CD8+ cells in an unfractionated repertoire (47). The log-likelihood function in Eq. 4 provides a principled approach for inferring cell-type composition using selection factors that capture the differential receptor features of each subrepertoire, including but not limited to their V and J usage and CDR3 length and amino acid preferences.
To test the accuracy of our method, we formed a synthetic mixture of previously sorted CD4+ [Tconv from spleen (42)] and CD8+ [from spleen (42)] receptors with different proportions and show that our selection-based inference can accurately recover the relative fraction of CD8+ in the mix (Fig 4C). Our method can also infer the proportion of Treg cells in a mixture of Tconv and Treg CD4+ cells from spleen (Fig. 4D), which is a much harder task since these subsets are very similar (Fig. 4A). The accuracy of the inference depends on the size of the unfractionated data, with a mean expected error that falls below 1% for datasets with size or larger for the CD8+/CD4+ mixture (red and orange lines in Fig. 4E).
Our method uses a theoretically grounded maximum likelihood approach, which includes all of the features captured by the soNNia model. Nonetheless, a simple linear selection model with only V- and J-gene usage and CDR3 length information (blue line in Fig. 4E), analogous to the method used in ref. 47, reliably infers the composition of the mixture repertoire. Additional information about amino acid usage in the linear SONIA model results in moderate but significant improvement (orange line in Fig. 4E). The accuracy of the inference is insensitive to the choice of the baseline model for receptor repertoires: Using the empirical baseline from ref. 43 (Fig. 4E) or (SI Appendix, Fig. S7D) does not substantially change the results.
The method can be extended to the decomposition of three or more subrepertoires. To illustrate this, we inferred the fractions of Tconv, Treg, and CD8+ cells in synthetic unfractionated repertoires from spleen, showing an accuracy of in reconstructing all three fractions (SI Appendix, Fig. S11) in a mixture of size .
Computational Sorting of CD4+ and CD8+ TCRs.
Selection models are powerful in characterizing the broad statistical differences between distinct functional subsets of immune receptors, including the CD4+ and CD8+ TCRs (Fig. 4A). A more difficult task, which we call computational sorting, is to classify individual receptors into functional classes based on their sequence features. In other words, how accurately can one classify a given receptor as a member of a functional subset (e.g., CD4+ or CD8+ TCRs)?
We use selection models inferred for distinct subrepertoires and to estimate a log-likelihood ratio for a given receptor to belong to either of the subrepertoires,
| [5] |
A larger log-likelihood ratio indicates that the receptor is more likely to be associated with the subrepertoire than . We set a threshold , to assign a receptor to if and to otherwise. The sensitivity and specificity of this classification depend on the threshold value. We evaluate the accuracy of our log-likelihood classifier between sets of CD8+ and Tconv CD4+ receptors harvested from spleen (42). The receiver operating characteristic (ROC) curve in Fig. 4F shows that our selection-based method can classify receptors as CD8+ or CD4+ cells, with an area under the curve (AUC) = 0.68. Performance does not depend on the choice of the baseline model ( in Fig. 4F and in SI Appendix, Fig. S7E). Applying this classification method to all of the possible pairs of subrepertoires in Fig. 4A, we find that CD4+ vs. CD8+ discrimination generally achieves AUC , while discriminating subrepertoires within the CD4+ or CD8+ classes yields much poorer performance (SI Appendix, Fig. S12).
For comparison, we also used a common approach for categorical classification and optimized a linear logistic classifier that takes receptor features (similar to the selection model) as input and classifies receptors into CD8+ or CD4+ cells. The model predicts the probability that sequence belongs to subrepertoire (rather than ) as , with and . We learn the model parameters and by maximizing the log likelihood of the training set:
| [6] |
where labels each TCR by the subrepertoire (e.g., for CD8+ and for CD4+). Note that when selection models are linear, the log-likelihood ratio (Eq. 5) also reduces to a linear form—the only difference being how the linear coefficients are learned. This optimized logistic classifier (Eq. 6) performs equally well compared with the selection-based classifier, with the same AUC = 0.68 (points in Fig. 4F). These AUCs are comparable with those found in ref. 36, which has addressed the same issue using black box machine learning approaches.
It should be emphasized that despite comparable performances, our fully linear selection-based method provides a biologically interpretable basis for subtype classification, in contrast to black box approaches (36). For example, the relative importance of different sequence features (i.e., CDR3 length, V/J gene identity, and amino acid composition) for CD4+ vs. CD8+ classification is shown in SI Appendix, Fig. S9.
Classification of TCRs Targeting Distinct Antigenic Epitopes.
Recognition of a pathogenic epitope by a TCR is mediated through molecular interactions between the two proteins. The strength of this interaction depends on the complementarity of a TCR against an antigen presented by an MHC molecule on the T cell surface. Recent growth of data on paired TCRs and their target epitopes (26, 48) has led to the development of machine learning methods for TCR–epitope mapping (25–29). A TCR–epitope map is a classification problem that determines whether a TCR binds to a specific epitope. We use our selection-based classifier (Eq. 5) to address this problem. We determine the target ensemble from the training set of TCRs associated with a given epitope (positive data) and the alternative ensemble from a set of generic unfractionated TCRs (negative data). For comparison, we also perform the classification task using the linear logistic regression approach (Eq. 6) and the state-of-the-art TCRex algorithm (28), which uses a random forest model for classification.
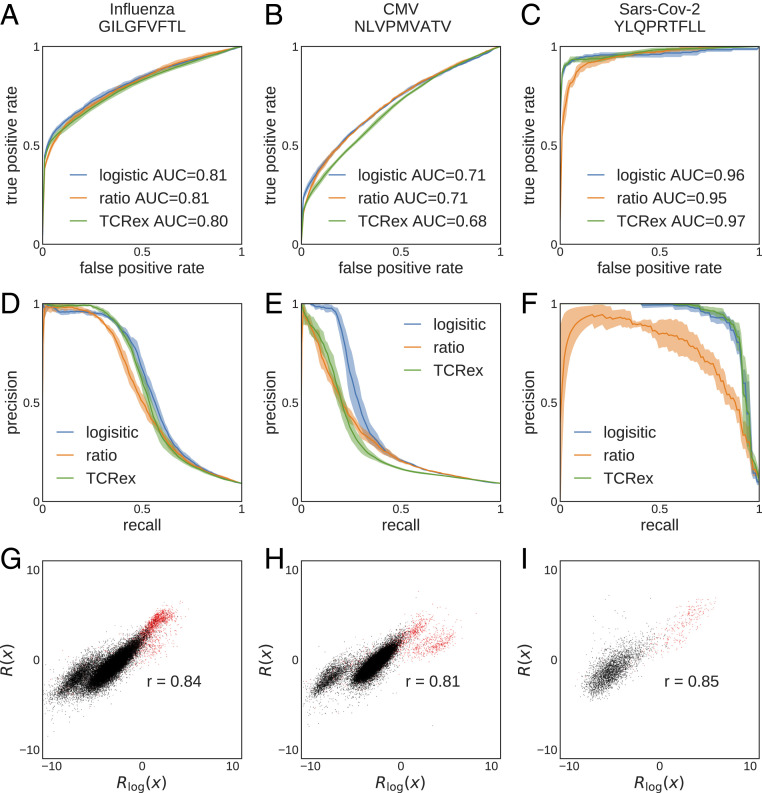
We performed classification for the following CD8+-specific epitopes, presented on HLA-A*02 molecules: 1) the influenza GILGFVFTL epitope (with associated TCRs), 2) the cytomegalovirus (CMV) NLVPMVATV epitope (), and 3) the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) YLQPRTFLL epitope (). The first two epitopes have the most abundant associated TCR sets in VDJdb (26, 48), and the latter is relevant for the ongoing COVID-19 pandemic. For consistency with TCRex (28), we used the pooled data from ref. 43 as the negative set and used 10 times more negative data than positive data for training. To quantify performance of each classifier, we performed a fivefold cross-validation procedure. Due to the scarcity of data, we limit our selection inference to the linear SONIA model (Fig. 1C). The ROC curves show comparable performances for the three classification methods on the three epitope-specific TCR sets (Fig. 5 A–C).
Fig. 5.
Selection-based prediction of epitope specificity for TCR. TCRs are classified based on their reactivity to three pathogenic epitopes (columns), using three classification methods: TCRex, log-likelihood ratio (Eq. 5), and linear logistic regression (Eq. 6). (A–C) ROC curves and (D–F) precision-recall curves for (A and D) influenza epitope GILGFVFTL ( TCR), (B and E) CMV epitope NLVPMVATV (), and (C and F) SARS-CoV-2 epitope YLQPRTFLL () are shown. (G–I) Comparison between log-likelihood scores and logistic regression scores for the three epitopes. Red points are TCRs that bind the specific epitope (positive set), and black points are TCRs from bulk sequencing (negative set). is Pearson’s correlation. For all panels, we used pooled data from ref. 43 as the negative set. We used 10 times more negative data than positive data for training. Performance was quantified using fivefold cross-validation.
The TCR–epitope mapping is a highly unbalanced classification problem, where reactive receptors against a specific epitope comprise a very small fraction of the repertoire [less than (6)]. Precision-recall curves are best suited to evaluate the performance of classification for imbalanced problems. In this case, a classifier should show a large precision (fraction of true predicted positives among all predicted positives) for a broad range of recall or sensitivity (fraction of true predicted positives among positives = true positives + false negatives). The precision-recall curves in Fig. 5 D–F show that TCRex and the logistic classifier can equally well classify the data and moderately outperform the selection-based classifier. While both the logistic classifier and TCRex are optimized for classification tasks, the selection-based classifier is a generative model trained to infer the receptor distribution of interest (positive set) and identify its distinguishing features from the baseline (negative set). As a result, selection-based classification underperforms in the low-data regime, for which fitting a reliable distribution is difficult (e.g., for the SARS-CoV-2 epitope model, with only positive examples). By contrast, the logistic classifier finds a hyperplane that best separates the two sets and therefore, is better suited for classification tasks, and it may be trained on smaller datasets. Nonetheless, we see a strong correlation between the selection-based log-likelihood ratio (Eq. 5) and the estimator of the logistic classifier (Eq. 6), shown for positive set (red points) and the negative set (black points) in Fig. 5 G–I for the three epitopes. This result indicates that the separation hyperplane identified by the logistic classifier aligns well along the effective coordinates of selection that represent sequence features relevant for function in each epitope class.
Discussion
Previous work has developed linear selection models to characterize the distribution of productive TCRs (4). Here, we generalized on these methods by using DNNs implemented in the soNNia algorithm to account for nonlinearities in feature space and have improved the statistical characterization of TCR repertoires in a large cohort of individuals (33).
Using this method, we modeled the selective pressure on paired chains of T and BCRs and found that the observed cross-chain correlations, even if limited, could be partially reproduced with our model (Fig. 3). These observed interchain correlations are likely due to the synergy of the two chains interacting with self- and nonself-antigens, which determine the selection pressure that shapes the functional TCR and BCR repertoires.
We systematically compared T cell subsets and showed that our method identifies differential selection on CD8+ T cells, CD4+ conventional T cells, and CD4+ regulatory T cells. TCRs belonging to families with more closely related developmental paths (i.e., CD4+ regulatory or conventional cells) have more similar selection features, which differentiate them from cells that diverged earlier (CD8+). Cells with similar functions in different tissues are in general similar, with the exception of spleen CD8+ that stands out from lymph node CD8+. These differences capture broad differential preferences of CD8+ and CD4+ TCRs, which can arise from their distinct structural features complementary to their different targets (i.e., peptide–HLAI and peptide–HLAII complexes). A next step would be to uncover more fine-grained differential features, associated with the distinct pathogenic history or HLA composition of different individuals.
One application of the soNNia method is to utilize our selection models to infer ratios of cell subsets in unsorted mixtures, following the proposal of Emerson et al. (47). Consistently with previous results, we find that the estimated ratio of CD4+/CD8+ cells in unsorted mixtures achieves precision of the order of with as few as unique receptors. Emerson et al. (47) validated their computational sorting based on sequence identity on data from in vitro assays and flow cytometry, which gives us confidence that our results would also pass an experimental validation procedure.
As a harder task, we were also able to decompose the fraction of regulatory vs. conventional CD4+ T cells, showing that receptor composition encodes not just signatures of shared developmental history—receptors of these two CD4+ subtypes are still much more similar to each other than to CD8+ receptors—but also, function: Tregs down-regulate effector T cells and curb an immune response, creating tolerance to self-antigens and preventing autoimmune diseases (10), whereas Tconvs assist other lymphocytes, including activation of differentiation of B cells. Since our analysis is performed on fully differentiated peripheral cells, we cannot say at what point in their development these CD4+ T cells are differentially selected. Data from regulatory and conventional T cells at different stages of thymic development could identify how their receptor composition is shaped over time.
During thymic selection, cells first rearrange a receptor, and then, an receptor is added concurrently with positive selection. Negative selection follows positive selection and overlaps with CD4/CD8 differentiation. We found that the Jensen–Shannon divergence between CD8+ and CD4+ cells to be very small (0.1 bit) compared with the divergence between functional and generated repertoires (ranging from 0.8 to 0.9 bits). This result suggests that the selection factors captured by our model mainly act during positive selection, which is partly shared between CD4+ and CD8+ cells, rather than during cell-type differentiation and negative selection, which is distinct for each type. Additionally to showing statistical differences in subrepertoires, we classified cells into CD4+ and CD8+ subclasses with likelihood ratios of selection models and recovered similar results achieved using pure machine learning approaches (36) but in a fully linear and interpretable setting.
In recent years, multiple machine learning methods have been proposed in order to predict antigen specificity of TCRs: TCRex (28, 49), DeepTCR (50), netTCR (51), ERGO (52), TCRGP (27) and TcellMatch (53). All these methods have explored the question in slightly different ways and made comparisons with each other. However, with the sole exception of TcellMatch (53), none of the above methods compared their performance with a simple linear classifier. TcellMatch (53) does not explicitly compare with other existing methods but implicitly compares various neural network architectures. We thus directly compared a representative of the above group of machine learning models, TCRex, with a linear logistic classifier and with the log-likelihood ratio obtained by training two SONIA models on the same set of features. We found that the three models performed similarly (Fig. 5), consistent with the view that amino acids from the CDR3 loop interact with the antigenic peptide in an additive way. This result complements similar results in ref. 53, where a linear classifier gave comparable results to DNN architectures.
The linear classifier based on likelihood ratios achieves state-of-the-art performance both in discriminating CD4+ from CD8+ cells (Fig. 4F) and in predicting epitope specificity (Fig. 5). However, unlike other classifiers, its engine can be used to generate positive and negative samples. Thus, characterizing the distributions of positive and negative examples is more data demanding than mere classification. For this reason, pure classifiers are generally expected to perform better but lack the ability to sample new data. Our analysis complements the collection of proposed classifiers by adding a generative alternative that is grounded on the biophysical process of T cell generation and selection. This model is simple and interpretable and performs well with large amounts of data.
The epitope discrimination task discussed here and in previous work focuses on predicting TCR specificity to one specific epitope. A long-term goal would be to predict the affinity of any TCR–epitope pair. However, currently available databases (26, 48) do not contain sufficiently diverse epitopes to train models that would generalize to unseen epitopes (53). A further complication is that multiple TCR specificity motifs may coexist even for a single epitope (29, 54), which cannot be captured by linear models (55). Progress will be made possible by a combination of high-throughput experiments assaying many TCR–epitope pairs (56) and machine learning-based techniques such as soNNia.
In summary, we show that nonlinear features captured by soNNia capture more information about the initial and peripheral selection processes than linear models. However, DNN methods such as soNNia suffer from the drawback of being data hungry and show their limitations in practical applications where data are scarce. Nonetheless, with the rapid growth of functionally annotated datasets, we expect soNNia to be more readily used for inference of nonlinear selection on immune receptor sequences. Such nonlinearity is expected as it would reflect the ubiquitous epistatic interactions between residues of a receptor protein that encode for a specific function. In a more general context, soNNia is a way to integrate more basic but interpretable knowledge-based models and more flexible but less interpretable deep learning approaches within the same framework.
Methods
Data Description.
In this work, we used different datasets to evaluate selection on TCR and BCR features.
-
1)
To quantify the accuracy of the soNNia model (Fig. 2), we used the TCR repertoires from a large cohort of 743 individuals from ref. 33. We pool the unique nucleotide sequences of receptors from all individuals and construct a universal donor totaling sequences. We randomly split the pooled dataset into a training set and a test set of equal sizes. We then subsampled the training set to to reduce the computational cost of inference.
-
2)
To characterize selection on paired-chain receptors (Fig. 3), we analyzed TCR pairs of unfractionated repertoires from ref. 37 (totaling receptors) and BCR of naive cells from ref. 41 (totaling and receptors for the H and H repertoires, respectively).
-
3)
To characterize differential sequence features of TCRs between cell types in different tissues (Fig. 4), we pooled unique TCRs from nine healthy individuals from ref. 42, sorted into CD4+ Tconvs, CD4+ Tregs, and CD8+ T cells, harvested from three tissues: pLNs ( Tconvs, Tregs, CD8s), iLNs ( Tconvs, Tregs, CD8s), and spleen ( Tconvs, Tregs, CD8s). We used the unfractionated data from ref. 43, composed of receptor sequences, to construct a baseline model for this analysis.
Quantifying Accuracy of Selection Models.
To assess the performance of our selection models, we compare their inferred probabilities with the observed frequencies of the receptor sequences in the test set. Prediction accuracy can be quantified through the Pearson correlation between the two log frequencies or the Kullback–Leibler divergence between the data and the distribution predicted by the selection model :
| [7] |
A smaller Kullback–Leibler divergence indicates a higher accuracy of the inferred model in predicting the data. In Fig. 2, we estimate the Kullback–Leibler divergence using receptors in the test set with multiplicity larger than two.
Comparing Selection on Different Subrepertoires.
To characterize differences in subrepertoires due to selection, we evaluate the Jensen–Shannon divergence between the distribution of pairs of subrepertoires and ,
| [8] |
where denotes averages over (SI Appendix has evaluation details). This divergence is symmetric and only depends on the relative differences of selection factors between functional subrepertoires, and not on the baseline model.
Supplementary Material
Acknowledgments
We thank Phil Bradley for helpful discussions about differential charge preferences of CD4+ and CD8+ TCRs. This work was supported by Deutsche Forschungsgemeinschaft Grant SFB1310 for Predictability in Evolution (G.I., A.M.W., and A.N.), Max Planck Research Group funding through the Max Planck Society (G.I. and A.N.), the Royalty Research Fund from the University of Washington (A.N.), European Research Council Consolidator Grant 724208 (G.I., A.M.W., and T.M.), and Agence Nationale de la Recherche Grant ANR-19-CE45-0018 (G.I., A.M.W., and T.M.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. A.L.F. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2023141118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix.
References
- 1.Tonegawa S., Somatic generation of antibody diversity. Nature 302, 575–581 (1983). [DOI] [PubMed] [Google Scholar]
- 2.Davis M. M., Bjorkman P. J., T-cell antigen receptor genes and T-cell recognition. Nature 334, 395–402 (1988). [DOI] [PubMed] [Google Scholar]
- 3.Marcou Q., Mora T., Walczak A. M., High-throughput immune repertoire analysis with IGoR. Nat. Commun. 9, 561 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sethna Z., et al. , Population variability in the generation and selection of T-cell repertoires. PLoS Comput. Biol. 16, e1008394 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sethna Z., Elhanati Y., Callan C. G., Walczak A. M., Mora T., Olga: Fast computation of generation probabilities of B- and T-cell receptor amino acid sequences and motifs. Bioinformatics 35, 2974–2981 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yates A. J., Theories and quantification of thymic selection. Front. Immunol. 5, 13 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nemazee D., Mechanisms of central tolerance for B cells. Nat. Rev. Immunol. 17, 281–294 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Murphy K., et al. , Janeway’s Immunobiology (Garland Science, 2008). [Google Scholar]
- 9.Klein L., Kyewski B., Allen P. M., Hogquist K. A., Positive and negative selection of the T cell repertoire: What thymocytes see (and don’t see). Nat. Rev. Immunol. 14, 377–391 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wing K., Sakaguchi S., Regulatory T cells exert checks and balances on self tolerance and autoimmunity. Nat. Immunol. 11, 7–13 (2010). [DOI] [PubMed] [Google Scholar]
- 11.Hou X. L., Wang L., Ding Y. L., Xie Q., Diao H. Y., Current status and recent advances of next generation sequencing techniques in immunological repertoire. Gene Immun. 17, 153–164 (2016). [DOI] [PubMed] [Google Scholar]
- 12.Georgiou G., et al. , The promise and challenge of high-throughput sequencing of the antibody repertoire. Nat. Biotechnol. 32, 158–68 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bolotin D. A., et al. , MiXCR: Software for comprehensive adaptive immunity profiling. Nat. Methods 12, 380–381 (2015). [DOI] [PubMed] [Google Scholar]
- 14.Mcdaniel J. R., DeKosky B. J., Tanno H., Ellington A. D., Georgiou G., Ultra-high-throughput sequencing of the immune receptor repertoire from millions of lymphocytes. Nat. Protoc. 11, 429–442 (2016). [DOI] [PubMed] [Google Scholar]
- 15.DeKosky B. J., et al. , High-throughput sequencing of the paired human immunoglobulin heavy and light chain repertoire. Nat. Biotechnol. 31, 166–9 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Turchaninova M., et al. , Pairing of T-cell receptor chains via emulsion PCR. Eur. J. Immunol. 43, 2507–2515 (2013). [DOI] [PubMed] [Google Scholar]
- 17.Dekosky B. J., et al. , In-depth determination and analysis of the human paired heavy- and light-chain antibody repertoire. Nat. Med. 21, 86–91 (2014). [DOI] [PubMed] [Google Scholar]
- 18.Ndifon W., et al. , Chromatin conformation governs T-cell receptor J gene segment usage. Proc. Natl. Acad. Sci. U.S.A. 109, 15865–15870 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ralph D. K., Matsen F. A., Consistency of VDJ rearrangement and substitution parameters enables accurate B cell receptor sequence annotation. PLoS Comput. Biol. 12, 1–25 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Munshaw S., Kepler T. B., SoDA2: A hidden Markov model approach for identification of immunoglobulin rearrangements. Bioinformatics 26, 867–72 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Davidsen K., et al. , Deep generative models for T cell receptor protein sequences. eLife 8, e46935 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Greiff V., et al. , Learning the high-dimensional immunogenomic features that predict public and private antibody repertoires. J. Immun. 199, 2985–2997 (2017). [DOI] [PubMed] [Google Scholar]
- 23.Miho E., Roškar R., Greiff V., Reddy S. T., Large-scale network analysis reveals the sequence space architecture of antibody repertoires. Nat. Commun. 10, 1321 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Isacchini G., et al. , Generative models of T-cell receptor sequences. Phys. Rev. E 101, 062414 (2020). [DOI] [PubMed] [Google Scholar]
- 25.Glanville J., et al. , Identifying specificity groups in the T cell receptor repertoire. Nature 547, 94–98 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shugay M., et al. , VDJdb: A curated database of T-cell receptor sequences with known antigen specificity. Nucleic Acids Res.. 46, D419–D427 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jokinen E., Huuhtanen J., Mustjoki S., Heinonen M., Lähdesmäki H., Determining epitope specificity of T cell receptors with TCRGP. BioRxiv [Preprint] (2019). 10.1101/542332 (Accessed 26 March 2021). [DOI] [Google Scholar]
- 28.Gielis S., et al. , Detection of enriched T cell epitope specificity in full T cell receptor sequence repertoires. Front. Immunol. 10, 2820 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dash P., et al. , Quantifiable predictive features define epitope-specific T cell receptor repertoires. Nature 547, 89–93 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Murugan A., Mora T., Walczak A. M., Callan C. G., Statistical inference of the generation probability of T-cell receptors from sequence repertoires. Proc. Natl. Acad. Sci. U.S.A. 109, 16161–16166 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Elhanati Y., Murugan A., Callan C. G., Mora T., Walczak A. M., Quantifying selection in immune receptor repertoires. Proc. Natl. Acad. Sci. U.S.A. 111, 9875–9880 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Elhanati Y., et al. , Inferring processes underlying B-cell repertoire diversity. Philos. Trans. R. Soc. Lond. B Biol. Sci. 370, 20140243 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Emerson R. O., et al. , Immunosequencing identifies signatures of cytomegalovirus exposure history and HLA-mediated effects on the T cell repertoire. Nat. Genet. 49, 659–665 (2017). [DOI] [PubMed] [Google Scholar]
- 34.Grigaityte K., et al. , Single-cell sequencing reveals chain pairing shapes the T cell repertoire. BioRxiv [Preprint] (2017). 10.1101/213462 (Accessed 26 March 2021). [DOI]
- 35.Dupic T., Marcou Q., Walczak A. M., Mora T., Genesis of the T-cell receptor. PLoS Comput. Biol. 15, 1–19 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Carter J. A., et al. , Single T cell sequencing demonstrates the functional role of TCR pairing in cell lineage and antigen specificity. Front. Immunol. 10, 1516 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tanno H., et al. , Determinants governing T cell receptor -chain pairing in repertoire formation of identical twins. Proc. Natl. Acad. Sci. U.S.A. 117, 532–540 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shcherbinin D. S., Belousov V. A., Shugay M., Comprehensive analysis of structural and sequencing data reveals almost unconstrained chain pairing in TCR complex. PLoS Comput. Biol. 16, 1–17 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Larimore K., McCormick M. W., Robins H. S., Greenberg P. D., Shaping of human germline IgH repertoires revealed by deep sequencing. J. Immunol. 189, 3221–30 (2012). [DOI] [PubMed] [Google Scholar]
- 40.Glanville J., et al. , Precise determination of the diversity of a combinatorial antibody library gives insight into the human immunoglobulin repertoire. Proc. Natl. Acad. Sci. U.S.A. 106, 20216–20221 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.DeKosky B. J., et al. , Large-scale sequence and structural comparisons of human naive and antigen-experienced antibody repertoires. Proc. Natl. Acad. Sci. U.S.A. 113, E2636–E2645 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Seay H. R., et al. , Tissue distribution and clonal diversity of the T and B cell repertoire in type 1 diabetes. JCI Insight 1, 1–19 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dean J., et al. , Annotation of pseudogenic gene segments by massively parallel sequencing of rearranged lymphocyte receptor loci. Genome Med. 7, 123 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Li H. M., et al. , TCR repertoire of CD4+ and CD8+ T cells is distinct in richness, distribution, and CDR3 amino acid composition. J. Leukoc. Biol. 99, 505–513 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rapin N., Hoof I., Lund O., Nielsen M., The MHC motif viewer: A visualization tool for MHC binding motifs. Curr. Protoc. Im. 88, 18.17.1–18.17.13 (2010). [DOI] [PubMed] [Google Scholar]
- 46.Sato E., et al. , Intraepithelial CD8+ tumor-infiltrating lymphocytes and a high CD8+/regulatory T cell ratio are associated with favorable prognosis in ovarian cancer. Proc. Natl. Acad. Sci. U.S.A. 102, 18538–18543 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Emerson R., et al. , Estimating the ratio of CD4+ to CD8+ T cells using high-throughput sequence data. J. Immunol. Methods 391, 14–21 (2013). [DOI] [PubMed] [Google Scholar]
- 48.Bagaev D. V., et al. , VDJdb in 2019: Database extension, new analysis infrastructure and a T-cell receptor motif compendium. Nucleic Acids Res. 8, D1057–D1062 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.De Neuter N., et al. , On the feasibility of mining CD8+ T cell receptor patterns underlying immunogenic peptide recognition. Immunogenetics 70, 159–168 (2018). [DOI] [PubMed] [Google Scholar]
- 50.Sidhom J.-W., et al. , DeepTCR: A deep learning framework for understanding T-cell receptor sequence signatures within complex T-cell repertoires. BioRxiv [Preprint] (2019). 10.1101/464107 (Accessed 26 March 2021). [DOI]
- 51.Jurtz V. I., et al. , NetTCR: Sequence-based prediction of TCR binding to peptide-MHC complexes using convolutional neural networks. BioRxiv [Preprint] (2018). 10.1101/433706 (Accessed 26 March 2021). [DOI]
- 52.Springer I., Besser H., Tickotsky-Moskovitz N., Dvorkin S., Louzoun Y., Prediction of specific TCR-peptide binding from large dictionaries of TCR-peptide pairs. Front. Immunol. 11, 1803 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fischer D. S., Wu Y., Schubert B., Theis F. J., Predicting antigen specificity of single T cells based on TCR CDR3 regions. Mol. Syst. Biol. 16, e9416 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Minervina A. A., et al. , Primary and secondary anti-viral response captured by the dynamics and phenotype of individual T cell clones. eLife 9, e53704 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bravi B., et al. , Probing T-cell response by sequence-based probabilistic modeling. bioRxiv [Preprint] (2020). 10.1101/2020.12.17.423283 (Accessed 26 March 2021). [DOI] [PMC free article] [PubMed]
- 56.Klinger M., et al. , Multiplex identification of antigen-specific T cell receptors using a combination of immune assays and immune receptor sequencing. PloS One 10, e0141561 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix.