Vapor condensation with daytime radiative cooling

Significance

Traditionally, the cooling for passive vapor condensation is mainly provided by convection and conduction. However, these mechanisms do not work when the vapor temperature is near the ambient air temperature. At such temperatures, radiative condensation remains effective. However, existing radiative vapor condensers must operate during the nighttime. Here, a novel radiative-cooling technique is applied to extend radiative condensation to both daytime and nighttime. The technique uses engineered thermal radiators that do not require lithography or other costly fabrication techniques and can be manufactured to cover large areas. When combined with traditional convective and conductive condensers, this passive technology can potentially double the water production rate for passive water technologies.

Abstract

A radiative vapor condenser sheds heat in the form of infrared radiation and cools itself to below the ambient air temperature to produce liquid water from vapor. This effect has been known for centuries, and is exploited by some insects to survive in dry deserts. Humans have also been using radiative condensation for dew collection. However, all existing radiative vapor condensers must operate during the nighttime. Here, we develop daytime radiative condensers that continue to operate 24 h a day. These daytime radiative condensers can produce water from vapor under direct sunlight, without active consumption of energy. Combined with traditional passive cooling via convection and conduction, radiative cooling can substantially increase the performance of passive vapor condensation, which can be used for passive water extraction and purification technologies.

Energy and clean water are global challenges that are intertwined in an unfavorable way: even in areas where water is abundant, energy may not be available to purify it for human use (1, 2). There has been strong interest in developing passive technologies to purify or harvest water without using fuel or electricity. In this context, passive vapor condensation becomes particularly important because many passive water technologies go through the vapor phase of water in their harvesting or purification processes.

Traditional vapor condensation technique is based on convective and conductive heat exchange with ambient environments. This technique is widely used in systems with hot vapors (3–6). However, with ever-increasing emphasis on passive systems, there are many situations in which warm- or even room-temperature vapor needs to be effectively condensed, such as extracting water from atmosphere (7–9) and warm vapor generated from high-efficiency solar evaporation (10). For vapor at such temperatures, most traditional condensers fail. For this reason, there is a clear need for a condensation technique to complement traditional condensers.

A different technique is based on radiative vapor condensation. Darkling beetles in the Namib desert (11) use this technique to collect water. Their bodies function as a cooling surface by shedding thermal energy through midinfrared (mid-IR) radiation toward a clear nighttime sky, generating dew from humid air. This mechanism is also used by commercial radiative dew condensers (7–9). However, neither Namib beetle nor existing dew condensers can operate in the daytime (7). Those nighttime radiative condensers are incompatible with many emerging water technologies that require 24 h operation or direct access to sunlight.

Recently, Fan et al. showed that passive radiative cooling to subambient temperatures can be realized even during the daytime, by integrating a high-efficiency solar reflector with a high-emissivity thermal emitter in the mid-IR atmospheric transparency window (12). Using this work as a basis, here we demonstrate a daytime radiative condenser. Compared to existing radiative vapor condensers (7–9), our condenser can function even in the presence of sunlight, which is essential for integration into passive water-harvesting systems that mainly operate during daytime.

Results

Water vapor condenses when its temperature drops below the dew point. When the dew point is below the ambient air temperature (13), only thermal radiation can continue to cool a condenser, because conduction and convection push the condenser temperature toward the ambient air temperature. In the case of Namib beetles, their black bodies emit infrared radiation around the atmospheric transparency window in the wavelength range from 8 to 13 μm (11). There is little radiation coming back from the atmosphere to the beetle within this transparency window. Consequently, the Namib beetle can create net heat loss and passively cool itself to below the dew point (11).

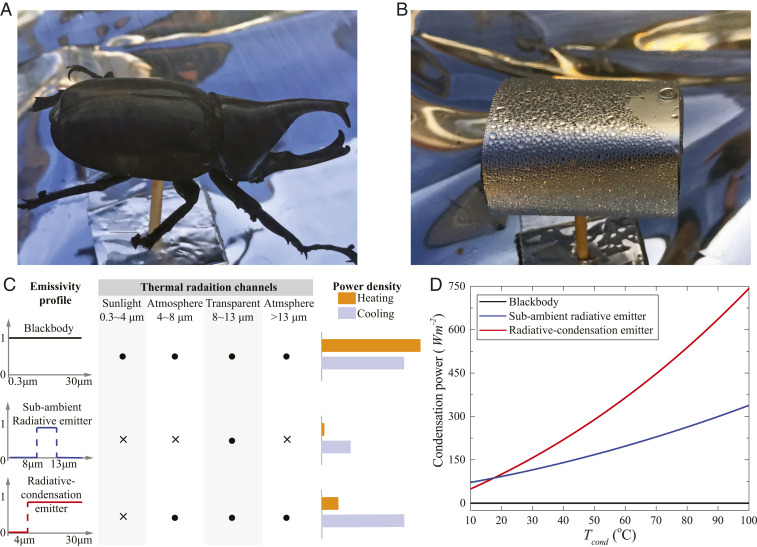
However, this radiative vapor condensation only works before the sun rises. With sunlight, the heat absorbed by the condenser can reach up to 1,000 W · m⁻² (14), which is much more than the radiative cooling power density of a blackbody at $T_{BB}=20\hspace{0.17em}°\mathrm{C}$, which is $\sigma T_{BB}^4\approx 420\hspace{0.17em}\mathrm{W}\hspace{0.17em}{\mathrm{m}}^{-2}$, in which $\sigma$ is the Stefan–Boltzmann constant. As a result, no condensation can be achieved at daytime. To achieve passive condensation in sunlight, here we spectrally engineer the absorptivity of the condenser such that the absorption of sunlight in the visible and near-infrared regions is minimized (7, 12) while maintaining most of its thermal radiation that is largely concentrated in the mid-IR region. Fig. 1 A and B shows a black beetle and our device under direct sunlight. The black beetle absorbs most of the sunlight, suppressing condensation, while our device (Fig. 1B) condenses a considerable amount of water on its surface.

Fig. 1.

Daytime radiative condenser and its design principle. Photos of (A) a dead black beetle and (B) our daytime-condensing device, both placed under sunlight on the roof of a parking ramp at UW-Madison. We introduce humid airflow across both the beetle and our condenser, with 90% to 95% humidity. The experiment was performed on April 26, 2018. Unlike the black beetle, our device reflects most of the sunlight, and thus condenses water vapor during daytime. (C) Thermal radiation channels and emissivity spectra of a blackbody (black), the subambient radiative emitter (blue) from ref. 23, and our radiative condensation emitter (red). The spectrum of the radiation is divided into four channels: the solar channel (0.3 to ∼$4\hspace{0.17em}\mu \text{m}$), the atmospheric–transparency channel (8 to ∼$13\hspace{0.17em}\mu \text{m}$), and the two atmospheric channels (4 to ∼$8\hspace{0.17em}\mu \text{m}$ and $>13\hspace{0.17em}\mu \text{m}$). The dot (cross) indicates that the emitter has the corresponding channel open (closed) for radiative exchange. The radiative heat received and radiated by the emitters at 100 $°\mathrm{C}$ are plotted as orange and blue bars, respectively. (D) Calculated radiative condensation power of the emitters in direct sunlight, operating at different temperatures. The ambient temperature is fixed at 20 °C. We also assume the operation temperature of the condenser varies from 10 °C for dry air to 100 °C for hot steam. The blackbody (black) has zero condensation power. The radiative condensation emitter (red) has much more condensation power than the subambient radiative emitter (blue).

Now we explain the design principle of daytime radiative condensation. The key is to spectrally engineer the radiative surface to enable or disable specific heat-exchange channels with the environment. The spectrum of the radiation can be roughly divided into four segments under a clear sky during the daytime, as shown in Fig. 1C. In the wavelength range of 0.3 to 4 μm, the incoming radiation is dominated by solar radiation. Beyond $4\hspace{0.17em}\mu \text{m}$, the incoming radiation is dominated by the thermal radiation from the atmosphere. From 4 to $8\hspace{0.17em}\mu \text{m}$, the atmospheric radiation is strong. From 8 to $13\hspace{0.17em}\mu \text{m}$, the atmospheric radiation is weak. Beyond $13\hspace{0.17em}\mu \text{m}$, the atmospheric radiation becomes strong again.

By enabling or disabling specific heat-exchange channels, one can maximize the radiative condensation capability of the condenser, which can be quantified by a power density as

$$q_{cond}=q_{rad}-q_{solar}-q_{atm}.$$ [1]

Here, $q_{rad}=\int d\text{Ω}\cos \theta \underset{0}{\overset{\infty }{\int }}d\lambda {ϵ}_{cond}\left(\lambda ,\hspace{0.17em}\theta \right)I_{BB}\left(T_{cond},\hspace{0.17em}\lambda \right)$ is the power density radiated by the condenser, in which ${\mathit{ϵ}}_{cond}\left(\lambda ,\hspace{0.17em}\theta \right)$ and $I_{BB}\left(T,\hspace{0.17em}\lambda \right)$ are the angle-dependent absorptivity/emissivity of the condenser and the spectral irradiance of a blackbody at temperature $T$, respectively. $q_{solar}$ is the absorbed power density due to incident solar radiation and is given by $q_{solar}={\displaystyle \underset{0}{\overset{\infty }{\int }}d\lambda {\mathit{ϵ}}_{cond}\left(\lambda ,\hspace{0.17em}{\theta }_{sun}\right)I_{AM1.5}\left(\lambda \right)}$, in which $I_{AM1.5}\left(\lambda \right)$ is the AM1.5 solar spectral irradiance. Here, we assume the condenser is facing the sun at fixed angle ${\theta }_{sun}$. $q_{atm}$ is the absorbed power density due to incident atmospheric radiation and is given by $q_{atm}=\int d\text{Ω}\cos \theta \underset{0}{\overset{\infty }{\int }}d\lambda {ϵ}_{cond}\left(\lambda ,\hspace{0.17em}\theta \right){ϵ}_{atm}\left(\lambda ,\hspace{0.17em}\theta \right)I_{BB}\left(T_{amb},\hspace{0.17em}\lambda \right)$, in which ${\mathit{ϵ}}_{atm}\left(\lambda ,\hspace{0.17em}\theta \right)=1-t{\left(\lambda \right)}^{1/\cos \theta }$ is the angle-dependent emissivity of the atmosphere (15), in which $t\left(\lambda \right)$ is the atmospheric transmittance in the zenith direction (16). Here, we assume $T_{amb}=20$ °C throughout our calculations (17). We also assume the atmosphere is at the ambient air temperature (i.e., $T_{atm}=T_{amb}$). Note that the atmospheric transmittance also depends on the humidity level of the atmosphere, which can be quantified using the precipitable water vapor (PWV), which is the depth of water in a column of the atmosphere if all the water vapor was precipitated as rain. We provide detailed analysis of the performance of radiative condensation as a function of PWV in SI Appendix, section 5. In the calculations below, we assume humid atmosphere with a PWV of 20 mm, a typical value found in warm and humid regions such as Japan (18).

A blackbody has all four channels open for radiative exchange, as shown in Fig. 1C. Thus, the heat radiated by the blackbody reaches 1,100 W · m⁻² at 100 °C. However, the blackbody also receives all the heating power in all four channels, which reaches 1,230 W · m⁻² because of the absorption of solar radiation (1,000 W · m⁻²) and atmospheric radiation. Thus, a blackbody has no daytime condensation power (Fig. 1D). At the other extreme, Fan et al. designed radiative emitters that close all channels except the atmospheric transparency channel (17). The radiative heat received by these radiative emitters is reduced to almost zero, allowing cooling to well below the ambient air temperature (12, 19). However, because the daytime subambient radiative emitter only emits in the spectral region from 8 to $13\hspace{0.17em}\mu \text{m}$, its cooling power is also substantially reduced compared to that of a blackbody, leading to limited condensation power (Fig. 1D). This design is suboptimal for radiative condensation, in which the figure of merit is maximum condensation power rather than minimum achievable temperature. In contrast, our radiative condensation emitters close the solar channel and leave the atmospheric channels completely open (Fig. 1C). Though this design is not ideal for subambient cooling (20), it is the most efficient for condensation because the vapor created in most passive water-harvesting systems is at or above the ambient air temperature. As shown in Fig. 1D, radiative condensation emitters (red line) have more than double the cooling power when compared to subambient radiative emitters (blue line) at most vapor temperatures of practical relevance. The details of the calculation of the condensation rate are described in SI Appendix, section 6.

Next, we discuss the application of our daytime radiative condensation emitters for condensation of vapor at various temperatures. The steady-state condensation rates are obtained from our model, which is available in SI Appendix, section 1. Here, we assume 100% relative humidity throughout our calculations. Under such an assumption, the calculated condensation rate represents the theoretical upper bound for given ambient air temperature, vapor temperature, and atmospheric humidity level.

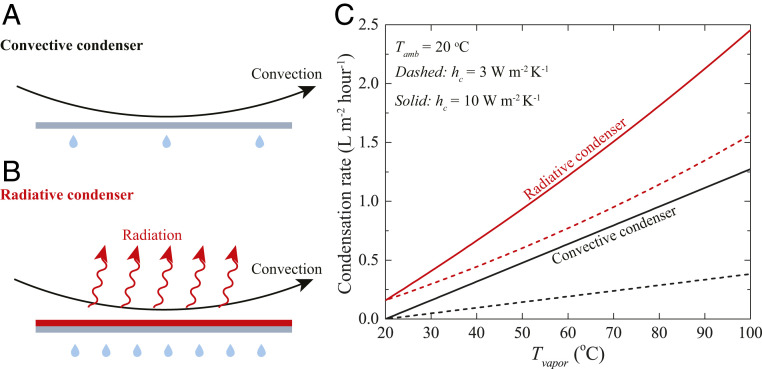
For reference and comparison, we first calculate water vapor condensation rate through natural convection (Fig. 2A) when the vapor temperature $T_{vapor}$ is above the ambient air temperature $T_{amb}$. The convective cooling power density can be calculated as $P_{conv}\cong h_c\left(T_{vapor}-T_{amb}\right)$, in which $h_c$ is the convective heat transfer coefficient. $h_c$ depends on the wind speed at the surface of the condenser (21) and usually ranges from $3$ to $10\hspace{0.17em}{\text{W}\hspace{0.17em}\text{m}}^{-2}\hspace{0.17em}{\text{K}}^{-1}$ for wind speed from $0$ to $10\text{\hspace{1em}mph}$. The condensation rate $W_{water}$ can be calculated from the cooling power as $W_{water}=P_{conv}/{\mathrm{\Delta }}_{vapor}$, in which ${\mathrm{\Delta }}_{vapor}$ is the latent heat of vaporization (22). In most practical situations, the vapor temperature is well below 100 °C. For instance, the temperature of water vapor in the solar water-harvesting system in ref. 23 is only 40 °C, which was shown to have the highest solar-to-thermal efficiency at the time of publication. To illustrate the need for a condenser in these emerging applications, we note that at such temperatures, the upper bound of condensation rate of a convective condenser is less than $0.1\hspace{0.17em}{\text{L}\hspace{0.17em}\text{m}}^{-2}{\hspace{0.17em}\text{hour}}^{-1}$ (black dashed curve in Fig. 2B) when there is no wind $\left(h_c=3\hspace{0.17em}{\text{W}\hspace{0.17em}\text{m}}^{-2}\hspace{0.17em}{\text{K}}^{-1}\right)$, which is way below the limit of the one-sun vapor generation rate of $1.6\hspace{0.17em}{\text{L}\hspace{0.17em}\text{m}}^{-2}{\hspace{0.17em}\text{hour}}^{-1}$ (14). This imbalance of evaporation and condensation becomes the bottleneck of water production in solar water-harvesting systems (24). Even at the most favorable condition for traditional convective condenser (e.g., with vapor at 100 °C and a wind speed of 10 mph $\left(h_c=10\hspace{0.17em}{\text{W}\hspace{0.17em}\text{m}}^{-2}\hspace{0.17em}{\text{K}}^{-1}\right)$), the upper bound of condensation rate is only 1.3 L m⁻² · hour⁻¹ (black solid curve in Fig. 2B).

Fig. 2.

Performances of convective condenser and radiative condenser. (A and B) Schematic of a convective condenser (A) and our radiative condenser (B). The convective condenser dissipates heat through only convection, while the radiative condenser dissipates heat through both convection and radiation. (C) Theoretically calculated condensation rates of the convective (black) and radiative condenser (red), assuming an ambient temperature of 20 °C. To analyze the theoretical upper bound of condensation rate, we assume a relative humidity of 100% throughout our calculation.

Conversely, our daytime radiative condenser utilizes both convection and radiation for cooling and thus can substantially improve the condensation rate. Compared to convective condensers at low vapor temperatures and without wind (black dashed line in Fig. 2B) (e.g., $T_{vapor}=40\hspace{1em}\mathit{℃}$ and $h_c=3\hspace{0.17em}{\text{W}\hspace{0.17em}\text{m}}^{-2}\hspace{0.17em}{\text{K}}^{-1}$), the upper bound of condensation rate is enhanced by more than four times to $0.44\hspace{0.17em}{\text{L}\hspace{0.17em}\text{m}}^{-2}{\hspace{0.17em}\text{hour}}^{-1}$ (red dashed line in Fig. 2B). At the most favorable condition for the convective condenser (black solid line in Fig. 2B) (i.e., $T_{vapor}=100\hspace{1em}\mathit{℃}$ and $h_c=10\hspace{0.17em}{\text{W}\hspace{0.17em}\text{m}}^{-2}\hspace{0.17em}{\text{K}}^{-1}$), the condensation rate of the radiative condenser almost doubles that of the convective condenser, reaching $2.5\hspace{0.17em}\text{L}\hspace{0.17em}{\text{m}}^{-2}\hspace{0.17em}{\text{hour}}^{-1}$ (red solid curve in Fig. 2B), well above the theoretical limit of the one-sun evaporation rate. Such a high condensation rate will also increase the vapor-pressure gradient inside a water-harvesting system, further facilitating the water-production cycle.

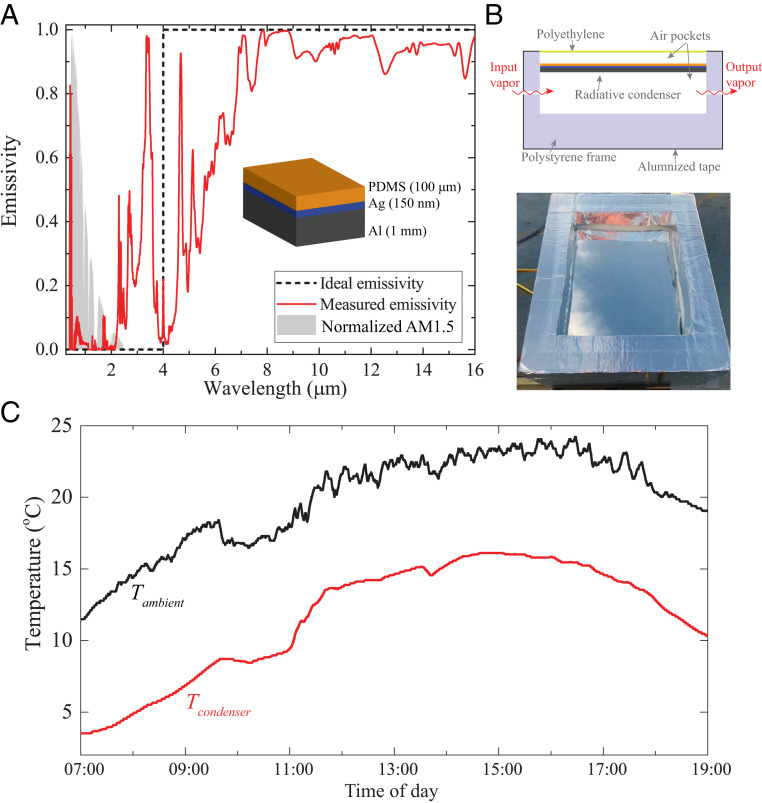
We now describe our experimental realization of daytime radiative condensers. Fig. 3A shows the schematic of a large-area passive condenser designed to approach the near-ideal condenser absorptivity/emissivity spectrum (black dashed line). The condenser is placed on top of a condensation chamber (Fig. 3B), and the condensation is designed to take place at the back surface of the condenser. The structure consists of layers of polydimethylsiloxane (PDMS) and silver (Ag) on an aluminum (Al) substrate, with thickness of $100\hspace{0.17em}\mu \text{m}$, 150 nm, and 1 mm, respectively. The thermal radiation is primarily emitted by the PDMS layer, which has a near-unity emissivity for wavelengths longer than $4.5\hspace{0.17em}\mu \text{m}$ due to Si–O and Si–C bond vibrations, given sufficient film thickness $\left(\hspace{0.17em}\text{>}100\hspace{0.17em}\mu \text{m}\right)$ (25). Simultaneously, PDMS is transparent to sunlight, which is efficiently reflected by the Ag layer to prevent solar heating inside the condensation chamber (Fig. 3B). The Al substrate is chosen because of its high thermal conductivity and low price. In our experiment, the width and length of the condensation region are 25 cm and 20 cm, respectively. The spectral emissivity of the structure is characterized using Fourier transform infrared spectroscopy (26), shown in Fig. 3A. Our daytime radiative condenser reflects ∼93% of the solar radiation (0.3 to ∼$4\hspace{0.17em}\mu \text{m}$) and emits efficiently in mid-IR region $\left(\text{>}4\text{\hspace{1em}μm}\right)$. We placed the radiator inside an insulating box made from polystyrene, as shown in Fig. 3B. The external surface of the insulating box is covered with aluminum tape to limit solar heating. A low-density polyethylene film covers the opening of the insulating box to avoid condensation on the top surface of the condenser.

Fig. 3.

Experimental realization of our daytime radiative condenser. (A) Schematic of the daytime radiative emitter and the measured normal-incidence emissivity spectrum. The emitter consists of a 100-$\mu \text{m}$ layer of PDMS, a 150-nm layer of silver, and a 1-mm-thick aluminum plate. (B) Experimental setup. The emitter is placed inside an insulating polystyrene box. The opening of the insulating box is covered by a thin polyethylene film, and the external surface of the box is covered by aluminized-foil tape. (C) Measured temperature under direct sunlight, which is about 8 °C lower than the ambient temperature throughout the day. The measurement was performed on the roof of the Space Science and Engineering Building at UW–Madison on September 29th, 2017.

To characterize the cooling effect of our radiative condenser under direct sunlight, we placed it on a roof facing the sky. The temperature of the condenser is measured by attaching a thermocouple at the center of the backside of the condenser with conductive tape. The temperature of the ambient air is measured by placing a thermocouple inside a weather shield to avoid sunlight and wind. The measurement was performed on a sunny day with clear sky from 07:00 to 19:00. Fig. 3C shows the temperature of the condenser (red curve) and the ambient air (black curve). Our condenser achieves a temperature reduction (i.e., the difference between the temperatures of the condenser and the ambient air) of about 8 °C throughout the day, which is slightly lower than that of existing subambient radiative emitters (27).

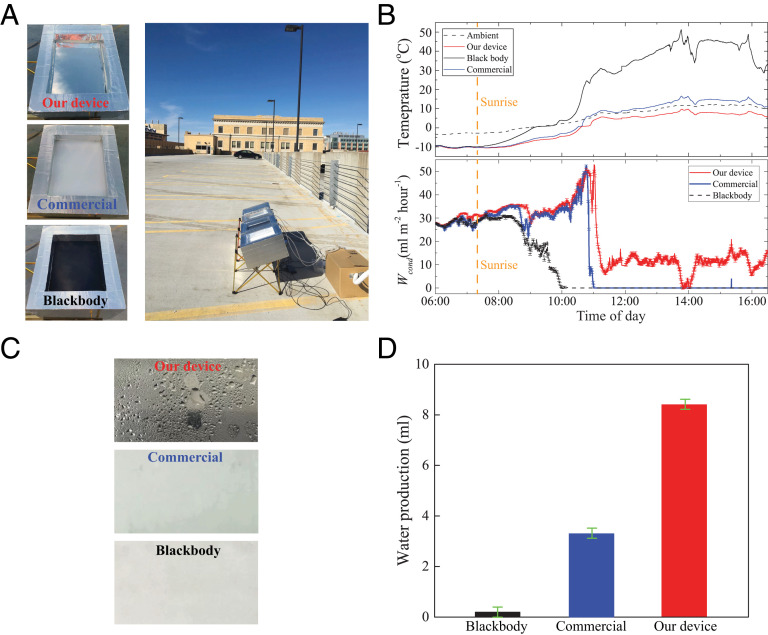
Next, we experimentally demonstrate condensation of vapor at ambient air temperature. To clearly demonstrate the importance of the specifically engineered spectral emissivity of our daytime radiative condenser, three additional condensers were used for comparison: a convective condenser, a blackbody, and a commercial radiative dew condenser (28), as shown in Fig. 4A. The convective condenser consists of a plain Al plate. The blackbody is made by painting a thick layer of graphite-based carbon ink on top of an unpolished Al plate, which has the same dimension as our radiative condenser. The commercial condenser is based on model CRSQ-0.25 from the International Organization for Dew Utilization (OPUR). It is a standard material for nighttime radiative dew condensation and is known as OPUR foil (29, 30). The OPUR foil is a white low-density polyethylene foil, with 5% volume of TiO₂ nanoparticles (diameter $\text{0}.19\hspace{0.17em}\mu \text{m}$) and 5% volume of BaSO₄ nanoparticles (diameter $\text{0}.8\hspace{0.17em}\mu \text{m}$). Compared to our daytime radiative condenser, the OPUR foil also has high emissivity in the mid-IR region but absorbs more than 15% of incident solar radiation (7). Besides the spectral emissivity, condensation is also affected by the surface hydrophilicity/hydrophobicity. To ensure all condensing surfaces have the same surface hydrophilicity/hydrophobicity, we also attached the OPUR foil to an Al plate with the same dimensions as our radiative condenser. These condensers are placed inside insulating boxes with the same dimensions as our radiative condenser. For the convective condenser, the insulating box is completely covered by aluminum foil tape to block all radiative heat–exchange channels.

Fig. 4.

Experimental demonstration of daytime radiative condensation. (A, Left) Front-side photographs of condensers used in our measurements. A blackbody and a commercial radiative dew condenser (OPUR foil) are used for comparison. (A, Right) Outdoor experimental setup. The condensers are placed on the roof of a parking ramp at UW–Madison, under direct sunlight. (B, Top) Real-time temperatures of our daytime radiative condenser (red line), the commercial radiative condenser (blue line), and a blackbody (black line). The black dashed line represents the ambient temperature. (B, Bottom) Real-time condensation rates of our daytime radiative condenser (red line), the commercial radiative condenser (blue line), and a blackbody (black line). The condensation rates are measured relative to the convective condenser. The error of our temperature measurements is $\pm 0.05$ °C, and the error of our relative humidity measurements is $\pm 0.1\%$. The error bars were calculated based on the measurement errors. The measurement was performed on March 11th, 2018. The temperature of the blackbody was higher than the ambient temperature due to absorption of sunlight, and thus, the blackbody had zero condensation rate. The temperature of the commercial condenser initially was below ambient temperature in the morning but increased to above ambient temperature around 11:00. Consequently, the condensation rate of the commercial condenser dropped to zero around 11:00. Conversely, our daytime condenser remained at a temperature lower than the ambient temperature and provided condensation throughout the day. (C) Photos of the condensing surface for each condenser taken around 17:00 on March 11th. (D) Daily water production from dawn to sunset. The water condensed by the blackbody before sunrise was not completely evaporated during daytime, leaving a small amount of water in the condensing chamber.

All condensers were placed on a roof facing the sky, and the polyethylene covers of all condensers were exposed to sunlight. Humified air at ambient air temperature and with a relative humidity of 90% to ∼95% was pumped into all condensers at a constant rate of $V_{in}=0.9\hspace{0.17em}{\text{m}}^3{\text{\hspace{1em}hour}}^{-1}$. The vapor was filtered through a water trap to ensure no water droplets were contained in the vapor entering the cooling chamber. We performed sunset-to-sunset measurements from March 10th to 11th, 2018. The temperature $T_{out}$ and relative humidity $H_{out}$ of the output airflow were measured by directly attaching temperature and relative-humidity probes at the outlet. The moisture content in the output airflow then can be determined. Here, we characterize the radiative condensation performance by using the convective condenser as the control device. Transient condensation rates of the blackbody, the commercial condenser, and our radiative condenser are obtained by comparing the difference between the moisture content in the output airflow with that from the convective condenser (Materials and Methods). Due to the small area of our condensers (0.05 m²), we did not extract the water that was produced. Instead, we obtained the overall production after 24 h by measuring the weight change of the whole device including the insulating box. We validated our measurement method by measuring the weight change of the convective condenser (the control device), as it cannot condense vapor at ambient air temperature. As expected, no observable weight change was observed for the control device during our experiment.

Fig. 4B shows a typical measurement during daytime. The sun’s peak elevation was around 43° above the horizon during the period of measurement. The maximum solar irradiance during the day was $\sim 800\hspace{0.17em}\text{W}/{\text{m}}^2$. The ambient temperature during measurements was below 10 °C. The theoretical maximum condensation rate with 100% solar reflectance at such a low temperature is 0.08 L m⁻² · hour⁻¹. Due to the relatively low solar reflectance of our condenser (∼93%), all the devices were tilted ∼15° toward the west to reduce absorption of solar radiation.

The blackbody absorbed almost all the sunlight and always had a temperature above the ambient air temperature and thus could not condense vapor at ambient air temperature. The commercial condenser absorbed less sunlight and had a temperature lower than the ambient temperature in the morning under relatively weak sunlight. As a result, the commercial condenser was able to condense vapor in the morning. Around 11:00 AM, the temperature of the commercial condenser increased to above the ambient temperature and its condensation rate dropped to zero. In contrast, our daytime condenser remained at a temperature lower than the ambient temperature and continued to condense vapor throughout the day. As shown in Fig. 4D, the daily water production of our daytime radiative condenser was almost twice that of the commercial condenser.

Discussion

In the above theoretical analysis and experiments, we considered vapor at the ambient air temperature. For vapor above the ambient air temperature, such as vapor evaporated by solar radiation, our radiative condenser can potentially provide 100% more condensation rates compared to convective condensers and commercial radiative dew condensers. An experimental demonstration is given in SI Appendix, section 2.

On the other hand, the performance of convective and conductive cooling can be greatly enhanced by using fins (31, 32), flowing water through the condenser (33), or utilizing coldness generated by nighttime radiative cooling (34). Radiative cooling is not meant to replace these cooling mechanisms but rather complement them. When the temperature of cooling surfaces is above the ambient air temperature, radiative cooling can provide sizeable enhancement of condensation, especially when the vapor temperature is around or at the ambient temperature when radiative cooling becomes the dominant cooling mechanism. A theoretical analysis of the benefits of radiative cooling in addition to convective cooling enhanced by fin structures is given in SI Appendix, section 4.

At last, we discuss potential applications of our daytime radiative condenser. The first example is water purification by sunlight (23, 35–42). The system usually comprises a solar absorber and a condenser. The solar absorber evaporates surface water (e.g., seawater) or water vapor adsorbed in a porous metal–organic framework (43) and then generates vapor at temperatures above the ambient air temperature, which then condenses on the condenser, which dissipates heat into the surrounding environment. In SI Appendix, section 3, we used a conventional single-slope solar still as a specific example and theoretically showed that radiative cooling can increase the water production by up to 40%. In this specific case, the radiative condenser can be made on a transparent substrate instead of aluminum to allow sunlight to go into the chamber to evaporate water (SI Appendix, section 10). When integrating a radiative cooling condenser with other solar-water purification systems, the system needs to be carefully designed such that solar evaporated vapor can be efficiently transferred to and condensed at the condenser.

A second application is dew condensation of atmospheric vapor. Atmospheric vapor can often have a low relative humidity such as 30%, especially in the daytime. Direct condensation of vapor at such condition with radiative condenser is possible because the operating temperature of the condenser can reach well below the dew point. However, we could not expect a high rate for water production. A recent work by Kim et al. showed an alternative approach in which atmospheric vapor is first adsorbed by metal–organic frameworks and then converted to hot saturated vapor through solar evaporation (43). By combining this approach with daytime radiative condensation, the rate of water production can be significantly enhanced. Elevating the temperature of vapor also helps to reduce the requirement of high solar reflectance. A theoretical analysis of the condensation rates of radiative condensers with different solar reflectance is provided in SI Appendix, section 8. On the other hand, recent demonstrations of highly solar reflective material exhibit near-unity solar reflectance (44). Such high solar reflectance can further increase the condensation rate for both ambient-temperature vapor and elevated-temperature vapor.

Finally, we discuss the cost and reliability of the radiative cooling material. In the case of PDMS, the cost is typically ∼$150 per kilogram (e.g., Dow Corning), which can cover an area of ∼10 m² when the thickness of the cooling layer is $100\hspace{0.17em}\mu \text{m}$. The PDMS coating also can be fabricated at large scale and low cost (45). On the other hand, the reliability of the radiative cooling material is an important factor over a long lifetime (e.g., one decade). The degradation of the cooling material (e.g., the PDMS layer in our structure) can result in more solar absorption, which is detrimental for both evaporation and condensation when integrated with solar water-harvesting systems. Potential solutions include using thicker cooling material or using other materials as barriers to prevent degradation (46).

In conclusion, we demonstrate a passive device—a daytime radiative condenser—that can significantly accelerate the condensation of water vapor. We experimentally demonstrated water condensation of vapor at ambient air temperature under direct sunlight, which cannot be realized by either conventional radiative dew condensers or convective condensers. Daytime radiative condensers can be applied to vapor generated by solar evaporation, significantly increasing total water production. Such technology is critically needed in areas where the sun is plentiful but clean drinking water is scarce.

Materials and Methods

Outdoor Experimental Conditions.

For the temperature measurement in Fig. 3C, the devices were tested on the roof of the Space Science and Engineering Building at the University of Wisconsin–Madison (UW–Madison) on September 29, 2017. The sun’s peak elevation was around 44° above the horizon during the period of measurement, whereas all the devices were tilted ∼15° toward the North. The typical maximum solar irradiance during the day is $\sim 800\hspace{1em}\hspace{0.17em}\text{W}/{\text{m}}^2$, which is obtained from the Space Science and Engineering Center at UW–Madison. The dew point of ambient air was ∼5 °C during the period of measurement.

For the condensation measurement in Fig. 4B, the devices were tested on the roof of a parking ramp at UW–Madison from March 10th to 11th, 2018. The sun’s peak elevation was around 43° above the horizon during the period of measurement. The maximum solar irradiance during the day is $\sim 800\hspace{0.17em}\text{W}/{\text{m}}^2$, which is also obtained from the Space Science & Engineering Center at UW–Madison. The dew point of ambient air was around −7.5 °C during the period of measurement. All the devices were tiled ∼15° toward the West to reduce absorption of solar radiation.

Measurement of the Transient Condensation Rate.

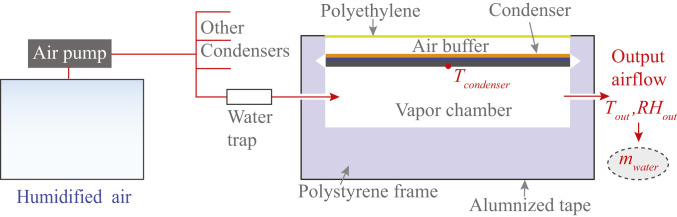
Fig. 5 shows the schematic of the experimental setup for the condensation measurement. Humidified air in a box is constantly pumped into all condensers (the convective, the blackbody, the commercial, and the radiative condensers) at the same rate of $V_{in}=0.9\hspace{0.17em}{\text{m}}^3{\hspace{0.17em}\text{hour}}^{-1}$. The input airflow to each condenser is filtered by a water trap to remove possible water droplets in the airflow. The humidified air then passes through the condensation chamber and then exists the chamber through an outlet. The temperature $T_{out}$ and relative humidity $R{H}_{out}$ of the output airflow are measured. The error of the temperature measurement is ±0.05 °C, and the error of the relative humidity measurement is $\pm 0.1\%$. The moisture content in the airflow then is obtained as

$$m_{water}=\frac{R{H}_{out}P\left(T_{out}\right)V_{in}{M}_{water}}{R},$$ [2]

Fig. 5.

Schematic of the outdoor experimental setup for condensation. Humidified air was pumped into all condensers (the convective, blackbody, commercial, and radiative condensers) at the same rate. All airflow into the condensers were filtered by a water trap to remove water droplets. The humidified air then passed through the condensing chamber and then exited the chamber through an outlet. The temperature $T_{out}$ and relative humidity $R{H}_{out}$ of the output airflow then were measured to determine the moisture contained in the airflow $m_{water}$.

where $P\left(T\right)$ is the vapor pressure at temperature $T$, $R$ is the ideal gas constant, and $M_{water}$ is the molar mass of water.

Here, we focus on the condensation resulting from radiative cooling and thus use the convective condenser as the control device. The condensation rates of the blackbody, the commercial, and the radiative condenser are obtained relative to the convective condenser as

$$W_{cond}^{sample}=\frac{m_{water}^{control}-m_{water}^{sample}}{A_{cond}},$$ [3]

where $m_{water}^{control}$ is the moisture content in the output airflow of the control device (i.e., the convective condenser).

Data Availability

All study data are included in the article and/or SI Appendix.