Why and how the brain weights contributions from a mixture of experts

Abstract

It has long been suggested that human behavior reflects the contributions of multiple systems that cooperate or compete for behavioral control. Here we propose that the brain acts as a “Mixture of Experts” in which different expert systems propose strategies for action. It will be argued that the brain determines which experts should control behavior at any one moment in time by keeping track of the reliability of the predictions within each system, and by allocating control over behavior in a manner that depends on the relative reliabilities across experts. fMRI and neurostimulation studies suggest a specific contribution of the anterior prefrontal cortex in this process. Further, such a mechanism also takes into consideration the complexity of the expert, favoring simpler over more cognitively complex experts. Results from the study of different expert systems in both experiential and social learning domains hint at the possibility that this reliability-based control mechanism is domain general, exerting control over many different expert systems simultaneously in order to produce sophisticated behavior.

Introduction

For decades if not centuries, researchers in psychology and neuroscience across many different domains from cognitive and social psychology, to animal-learning and behavioral and decision neuroscience have proposed the existence of multiple systems in the brain that co-operate or compete to control behavior (Damasio, 1994; Daw et al., 2005; Dickinson, 1985; Figner and Weber, 2011; Kahneman, 2011; Laibson, 1997; Norman and Shallice, 1986; Shiffrin and Schneider, 1977). Typically, a theoretical claim is made for the existence of a dichotomy (in some instances a trichotomy)– such that the interactions between the competing systems can produce nuanced effects on behavior that would not be predicted by the effects of only one system alone. For instance, in a number of theoretical frameworks for value-based decision-making, an impulsive system that wants immediate gratification competes for control over behavior with a more patient reflexive system that is focused on fulfilling longer term goals (Laibson, 1997; McClure et al., 2004). In a framework derived from animal-learning, a goal-directed system that accesses the current incentive value of outcomes as well as the causal relationship between actions and outcomes, competes for control against a habit system that selects actions based on previously reinforced stimulus-response relationships (Dickinson, 1985). In the computational reinforcement-learning literature, a model-based (MB) system that actively plans actions based on a cognitive map competes against a model-free (MF) system that performs actions based on previously learned value predictions (Daw et al., 2005). Such multi-system theories are so ubiquitous, that there is hardly an area of study in the psychology of the mind that does not feature such a theory in some or other form.

We contend that the proliferation of such multiple systems theories is not merely a curiosity in the sociology of the science of the mind. Instead, we believe they reflect a recognition of the fundamental importance of a multiple systems architecture for understanding the brain, because from an evolutionary and individual stand-point, the existence of multiple systems or strategies for solving a cognitive problem is highly advantageous for an organism. One crucial reason boils down to the meaning behind the folk expression that “two heads are better than one”, or to the notion that the crowd can express wisdom not found in a single individual (Surowiecki, 2005). Simply put, just as when polling the ideas of two executives with different backgrounds and expertise might yield better decisions for a company than if only one of those actors had taken a decision, our brain can poll the opinions of different systems, each of which either has access to different forms of information and/or operates on the information differently. Therefore, each system has the potential to reach different conclusions about the state of the world, and/or which policy might be best.

Here, we argue that a useful framework with which to consider how the brain “polls” different systems, is the “mixture of experts” framework adapted loosely from machine-learning (Jacobs et al., 1991). According to the mixture of experts idea, different computational strategies operate on a computational problem, and these experts can each come up with different evaluations/beliefs and/or proposals for action. In some instances, the experts might operate on completely distinct sub-problems, and even operate on different data partitions. For instance, two different experts might be focused on decoding sounds from low and high frequency domains. In other circumstances the experts might work on overlapping sub-problems and even use the same input data, but the experts use different algorithms or strategies to solve the sub-problem. In general we suggest that different experts can be distinguished from each other based on any one of three criteria: (a) the experts operate on different partitions of the state-space, whether input (different sensory input) or output (different motor actions), (b) the experts use qualitatively different algorithms to make predictions, or (c) unique experts might also be identified from studies of neural implementation if distinct experts are mapped to dissociable neural circuits.

Machine learning researchers have considered several strategies for how to produce an overall decision based on integrating across different modules that have distinct expertise either by having access to different partitions of the input data and/or by performing different operations on the input data (Jacobs et al., 1991; Titsias and Likas, 2002; Yuksel et al., 2012). In essence, the goal of training a Mixture of Expert (MoE) system in machine-learning is to train each of the individual experts on the most relevant parts of the problem to which they can contribute, and also to train the “manager” in how to allocate task responsibilities over these experts such that their collective expertise is efficiently utilized to solve the overall problem (Jacobs et al., 1991). That is, the system should assign weights to the individual experts depending on the specific relevance of their expertise for solving a particular problem. One doesn’t want to have an electrician work on one’s kitchen sink, or a plumber work on one’s lighting.

Because the “manager” adapts a behavioral policy that arises from an integration of the opinions of the individual experts, weighted by its relative confidence in their predictions, all possible opinions on the subject by individual experts will have been taken into account in an optimal manner, provided the evaluation of the degree of confidence that one should have in each expert is veridical.

Confidence in an expert can be inferred from the degree of reliability of the expert’s predictions

How can the meta-decision agent determine how confident it should be in an expert’s opinions? We propose that the simplest way to do so is to poll how well the expert is doing in making its own predictions (see Daw et al., (2005) for the original application of this idea to a dual system framework), which we call prediction reliability. Prediction reliability is the converse of prediction uncertainty which has been well studied in the theoretical neuroscience literature, in turn often fractionated into a number of distinct components such as expected uncertainty, unexpected uncertainty and estimation uncertainty (Payzan-LeNestour and Bossaerts, 2011; Yu and Dayan, 2005). Here for the purpose of the MoE framework, there is no need to distinguish between different forms of prediction reliability (or uncertainty). Instead what the manger is interested in is the overall recent performance of the expert – how often it makes a good prediction and how often it makes a poor prediction. Those experts that make good predictions about the world (or which action to select in it) should be deemed more reliable and should be allocated more confidence by the manager. Thus, the simplest mechanism for attributing confidence to an expert’s predictions involves reading out a single reliability signal about that expert’s predictions in a manner that pools over (or is indifferent to) the source of the variance that led to that reliability estimate (i.e. whether it comes from estimation, expected or unexpected uncertainty). This single reliability signal could be used to allocate a relative weight that (when compared to the current level of uncertainties present in the other experts) is used to determine that experts influence over behavior.

But how might such reliability signals be computed in the first place? A computationally cheap way to learn about reliabilities within individual experts is to keep track of the prediction errors produced by a given expert, i.e. comparing its predictions to actual outcomes. We have found evidence for this in the domain of model-based and model-free reinforcement-learning (Lee et al., 2014). The expert can thus build an approximate estimate of the degree of reliability in its predictions by taking the absolute amount of surprise it is experiencing (the absolute value of the prediction error signals), and using this as an update signal for the average reliability of its predictions (Box 1). Although very much an open empirical question, we suggest that given the ubiquity of prediction errors in the brain (Schultz and Dickinson, 2000), a similar mechanism for keeping track of the absolute value of the prediction errors to generate a proxy estimate of prediction reliability could be deployed very universally within the brain, for each of its constituent experts. The average of the absolute prediction error is simply quantifying the deviation of the expert from a perfect prediction (by tracking deviations in the expert’s prediction errors from zero, where zero prediction error implies the expert has made a perfect prediction). Intuitively, it is easiest to understand this averaged unsigned prediction error as simply a measure of the expert’s recent average performance in making predictions: if the expert has made a lot of recent errors in its predictions (whether over or underestimating the consequences of its actions), then it is less reliable than an expert that has made smaller or fewer errors in its predictions.

BOX 1:

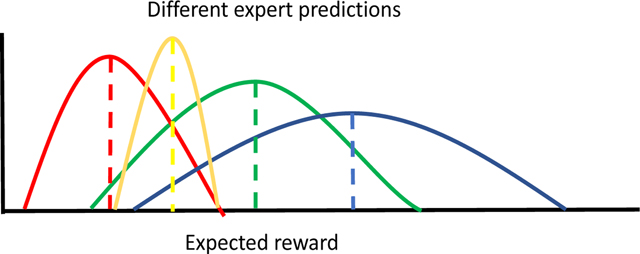
In the illustration above, different experts (colored in red, yellow, green and blue) make different predictions about the expected future reward that will follow for a particular action or set of actions. Each expert has a different mean prediction (dotted lines), but also has an uncertainty about its prediction (depicted by the width of each of the curves). A manager of these experts can elect to compute a more accurate estimate of the expected reward by averaging over the predictions of each expert, weighted by the amount of uncertainty inherent in the predictions of each expert^*. One frugal and efficient way to approximate the uncertainty that each expert has in its predictions, is to see how well the expert has done in successfully predicting actual reward outcomes. A measure of this is the reliability or inverse of the average unsigned prediction error for each expert. The unsigned prediction error for each expert is simply the unsigned difference between its predictions and actual outcomes, and a recency weighted average over that signal corresponds to a measure of current reliability. The averaged unsigned prediction error can also be viewed as a yielding an approximate yet computationally tractable estimate of different forms of uncertainty, thereby linking to theoretical perspectives on distinct forms of prediction uncertainty alluded to in the main text. Expected uncertainty can be approximated by integrating over a longer time window of prediction errors generated in the past, while unexpected uncertainty can be approximated by sampling prediction errors that have occurred in the recent past (see Iigaya, 2016). However, because the MoE does not care about the source of uncertainty, just how well an expert is doing in its predictions overall, those different time-scales of prediction error are pooled over in this case.

Prediction reliability is necessary and sufficient to allocate control weights over experts

An important feature of a number of theories of cognitive control is that the controller takes into account considerations about the cognitive costs and the expected increase in rewards incurred by engaging a particular sub-system. For instance, expected value of control theories propose that the expected gain from engaging a particular cognitive strategy is traded off against the expected cost in terms of the cognitive effort involved in doing so (Shenhav et al., 2013). Various arbitration schemes between model-based and model-free RL also consider the tradeoff between the additional cost of computation for model-based RL vs the decreased accuracy of model-free RL (Dromnelle et al., 2020; Kool et al., 2017; Pezzulo et al., 2013). It is clear that by manipulating task complexity (one way to modulate cognitive cost), it is possible to influence the balance of control between different constituent experts (e.g. see Kim et al., 2019). However, we suggest that it is possible to accomplish this cost benefit tradeoff implicitly without necessitating explicit computations of cognitive cost. The MoE system will indeed be sensitive to the overall expected value of pursuing a particular strategy as well as to the complexity of the model utilized by a particular expert, which should scale with the cognitive cost. However, this comes for free in the MoE framework because it is baked into the prediction uncertainty measure, as follows: Firstly, an expert that has lower prediction uncertainty than another will, all else being equal, perform better in terms of the cumulative gains that would pertain if the agent implements a behavioral policy recommended by that expert. Thus, implicitly minimizing the agent’s overall prediction uncertainty by selecting experts that make better (more precise) predictions will also ensure that the agent will perform more successfully overall in terms of the cumulative rewards obtained. Secondly, selecting experts based on prediction reliability also implicitly favors experts with less complex models. The reason is because of the bias/variance trade-off (Geman et al., 1992; Luxburg and Schölkopf, 2011). Simply put, a more complex model may well explain a particular portion of the input data well, but such a model will often perform much worse when generalizing to new data samples because of the increased risk of overfitting. In the MoE scheme, this would mean that an agent with a more complex model would often fail to make good predictions when faced with new input data, resulting in increased errors and hence increased prediction uncertainty. Relatedly, a model that is too simple, would also end up being biased in its prediction and result in increased errors. Thus, the expert with a sufficient but moderate degree of complexity to solve the task at hand will end up with the lowest degree of prediction uncertainty, being favored for the control of behavior over experts utilizing models that are either too simple to be fit for purpose, or too complex.

Beyond the bias/variance trade-off that will operate in this situation, another important system constraint that will also naturally impose a tendency not to rely on an overly cognitively demanding model is simply that cognitive capacity constraints in the system, such as limitations in working memory, will naturally constrain the cognitive complexity of the experts that can make good predictions. If a highly demanding cognitive strategy is utilized, then this strategy will likely end up making poor predictions if working memory or other cognitive capacities are over-taxed, resulting in an increase in prediction uncertainty. Thus, prediction uncertainty is we argue, sufficient to enable the selection of experts that are complex enough to solve the task, while not being too cognitively complex so as to incur overfitting or to come up against cognitive constraints that limit its performance. In sum, utilizing prediction uncertainty learned through tracking prediction errors generated by each expert, may be both necessary and sufficient to accommodate a mixture of experts architecture that favors better performing and less cognitively demanding experts over experts that are either less well performing and/or more cognitively demanding. We do not doubt that the expected cost of taking particular actions enters into decision values, which could include the expected time taken to solve a particular problem.

It is an open empirical question whether cost is entered as a meta-decision variable determining allocation of behavioral control by the MoE manager. However, we would suggest that it is imperative to first rule out the parsimonious explanation that explicit considerations of cost do not need to be explicitly entered into the MoE scheme, because such considerations are already catered for implicitly via prediction reliability and cognitive constraints.

What experts contribute to the mixture?

Within this framework, the next obvious question arises as to what precisely are the experts that contribute to the mixture? At this point in our understanding of the building blocks of cognition, there are numerous different conceptualizations that can be drawn upon to identify putative “experts”. As alluded to earlier, psychologists and behavioral economists have postulated the existence of various dual or tri-process theories to account for human behavior. A key difference of the proposed MoE framework over existing multiple systems theories in psychology and neuroscience, is that here we are not pre-committing to a specific number of individual experts, such as two or three. Instead, the framework can include many possible experts. Clearly though it does not make sense to presume that there are an infinite or even a very large number of experts, given the brain occupies finite neural real estate. Instead, it is reasonable to assume there is a finite and relatively small number of experts. We speculate that many existing multiple systems theories and the empirical assays that derive from them are simply using different semantic labels and distinct experimental paradigms to describe and characterize the same underlying systems of experts, although little empirical work has yet been conducted to establish the nature of the overlap between constructs in order to determine whether this is indeed the case. The literature on possible expert systems is so fractionated, we think a critical direction for future research on this question will be to gather the various dual and tri-system theories of cognition and the behavioral tasks that are proposed to reveal their operation, and systematically attempt to delineate what is common and what is distinct across all of these different theories, as they are measured through the behavioral tasks and also in terms of the neural circuits on which they depend. A fundamental question is whether there exists a core set of experts that can explain all of the variance in behavior proposed in all of these disparate frameworks. In other words, it should be possible to perform some form of dimensionality reduction or factor analysis to reveal the underlying cognitive ontology (Poldrack and Yarkoni, 2016).

In the following section, we will focus on candidate experts that have been widely considered in the decision neuroscience field. We do this not because we wish to argue that what follows is the only possible set of experts or that they necessarily represent the only meaningful way to carve up the cognitive architecture, but because on a prosaic level these experts happens to be the focus of our own research, and also because they have provided the initial empirical evidence to support our more general claims about the MoE framework. We also do not consider complications to the framework that have yet to be understood, such as how the brain deploys strategies to solve the exploration/exploitation dilemma in the context of multiple experts (Cohen et al., 2007).

We and others suggest the existence of multiple systems or experts for controlling behavior in humans and other animals (Balleine et al., 2009; Balleine and O’Doherty, 2010; Daw et al., 2005; Dickinson, 1985; Lee and Seymour, 2019). These include, a goal-directed system, which as alluded to earlier, involves selecting actions in a manner that is sensitive to the current incentive value of the goal, and a habitual system in which instrumental actions are selected by antecedent stimuli (mediated by stimulus-response associations) without reference to the current incentive value of a goal. At the algorithmic level, it has been suggested these two systems can be accounted for in terms of model-based and model-free reinforcement-learning respectively, although establishing the precise overlap between these sets of constructs and the neural circuits involved is still a focus of on-going research and debate (Dickinson, 1985). Another class of candidate expert systems are ones that mediate Pavlovian behavior in which innate reflexes that have been acquired over an evolutionary timescale, are elicited by stimuli that predict behaviorally significant outcomes (Dayan and Berridge, 2014). Recent evidence suggests that a reliability-based arbitration scheme might also mediate the interactions between Pavlovian and instrumental experts (Dorfman and Gershman, 2019). Notably, there is strong evidence for the existence of multiple forms of Pavlovian prediction, therefore suggesting the existence of multiple forms of Pavlovian experts (Dayan and Long, 1998; Holland and Straub, 1979; Pool et al., 2019). This indicates there is likely to be a rich interplay between multiple Pavlovian experts and other experts, which could be perhaps become a focus of study within the broader canvas of the MoE framework.

In addition to those experts in the domain of experiential learning, we suggest the existence of additional expert systems to mediate learning from observing others. These include, the capacity to learn from the rewards experienced by others – so-called vicarious reinforcement-learning, the capacity to learn to imitate others’ actions – imitation-learning, and the capacity to learn from inferring the goals and/or intentions of others: emulation learning (Charpentier et al., 2020; Heyes and Saggerson, 2002). These three forms of observational learning rely either on distinct algorithms for their implementation compared to MB vs MF, and/or operate on different partitions of the state space thereby meeting the criteria of being classed as distinct experts. For instance, emulation learning is (unlike MB-RL) concerned with inferring the hidden state of the world through observing another’s actions, for instance by trying to work out what goal the observed agent is currently working toward. Imitation learning is concerned with learning to predict which actions an agent will choose next based on the actions it chose in the past. Vicarious RL on the other hand is argued to use the same algorithm as model-free RL, but instead, the reward function that is input into the algorithm is the reward function of the other agent (the rewards received by that other agent) as opposed to the rewards experienced by the observer (Cooper et al., 2011).

An implication of the MoE framework, is that each of these systems will be available to control behavior at each moment in time, and that their contribution to behavior will be weighted by the “confidence” that the manager has in the likely success of a given expert for solving a given problem. In practice, if the manager has little confidence in a given expert’s contribution to a given situation, then the weight assigned to this expert will be effectively zero, so that it will not actively contribute to behavior.

To understand better the implications of the MoE framework for characterizing the nature of the interactions between the systems, let’s consider the interaction between just two experts: the goal-directed and habitual system. Empirically, evidence has accumulated to support the existence of training duration effects on the trade-off between these two systems, such that the goal-directed system dominates behavior early on in the development of instrumental action learning, while the habitual system gradually begins to increase its influence over behavior as action-learning continues, eventually becoming dominant over the goal-directed system in its control of behavior (Adams, 1982). It is also often presumed that the habit or model-free system, necessarily produces noisier and more approximate estimates of the true distribution of rewards associated with particular actions than the goal-directed system (Daw et al., 2005). Thus, the trade-off between the two systems is suggested to be one between a necessarily more accurate model-based system and a less accurate but cognitively cheaper model-free system. However, we would argue that the model-free system may not necessarily always have the less accurate predictions, but in fact that the predictions of the model-free system can be more robust and generalizable and hence more accurate than the model-based system under some conditions. This would happen under situations where the model-based system ends up relying on an overfit and hence brittle cognitive model of the decision problem. In other words, we suggest that it is better not to think about the competition between multiple systems solely as being akin to the trade-off between the cost of taking on a smart and competent professional contractor to work on your house that nevertheless is very expensive, compared to a crude and blundering amateur that often gets the job done but never perfectly, yet is cheap to hire. Instead, we think it may be more useful to think about the trade-offs between systems as being about different systems having different advice and expertise, and that which expert actually has the more accurate predictions at any one moment will depend to a considerable degree on the local properties of the learning environment and the nature of the problem at hand.

There are two important implications of this last point: firstly, which system might end up being dominant in the control of behavior in particular experimental contexts can be expected to be highly situationally specific, albeit not inscrutable. This is because the MoE framework can make specific predictions about when one system might be expected to be favored over the other depending on the nature of the environmental variability. Secondly, the MoE framework also suggests that it is useful and indeed beneficial for both systems to jointly continue to actively make predictions across a wide variety of environmental situations because of their different forms of expertise, so long they continue to be useful to rely on. In other words, it does not necessarily make sense for the model-based system to switch off and yield control over behavior entirely to the model-free or habit system even after a long training duration, even though the habit system is less cognitively expensive. Instead, to maximize accuracy in predictions, under many regimes both systems might continue to provide useful input that the MoE system continues to poll (in proportion to the relative uncertainty in those predictions), even if the relative balance between the experts does shift as a function of environmental experience. We do suspect, however, that if an expert has little in the way of reliable advice to contribute to a particular situation such that its reliability falls below a certain threshold, it would make sense for that expert to no longer be polled at all, and indeed it would be efficient for that expert to no longer make active predictions in that situation, thereby no longer drawing on cognitive resources.

Prefrontal cortex plays a role as a “manager” over the experts.

It could be questioned whether or not the mixture of experts framework we have outlined necessarily requires a “manager” at all. For instance, an alternative implementation could be that the experts would mutually inhibit each other, sharing control proportionately without any top down mechanism or meta-controller: in essence a form of competitive anarchy. However, what we know about the architecture of the brain strongly argues against this type of anarchical system. Decades of work in neuropsychology, electrophysiology and neuroimaging strongly supports the suggestion that the prefrontal cortex plays a major role in cognitive control and in the co-ordination of neural structures elsewhere in the brain for the purpose of guiding behavior (Burgess and Shallice, 1996; Miller and Cohen, 2001). The prefrontal cortex therefore is a natural candidate for the location of a “manager” which exerts control over subsidiary experts. This proposal resonates with a number of longstanding proposals about the prefrontal cortex, in which this region has been proposed to act as a “central executive”, (Baddeley, 1996) or as a conductor of goal-directed control (Miller and Cohen, 2001; Norman and Shallice, 1986).

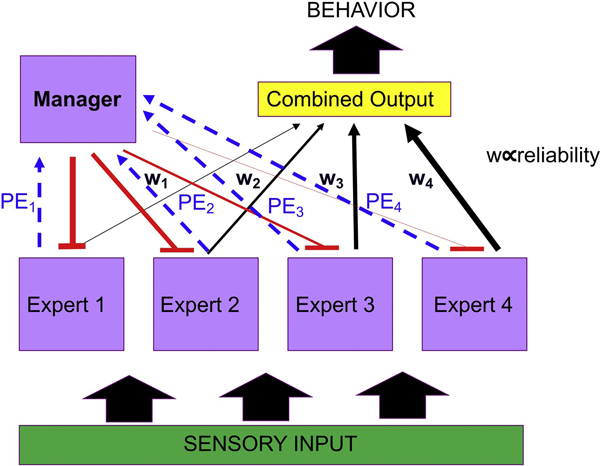
The MoE framework provides for specific predictions about the neural computations that might be expected of the MoE manager. Specifically, one prediction is that the manager will have access to neural signatures of the uncertainty in the predictions of the various expert systems, or even more usefully, the “precision” in the predictions of the various expert systems (the inverse or negative of the uncertainty). These precision signals would subsequently be utilized by the manager to allocate responsibility over behavior. In order to accomplish this, the manager would need to normalize across the relative precisions of each expert in order to assign relative weights for behavioral control. Another feature of the MoE framework is that somewhere in the brain there should be an output channel that encodes the combined recommendations of the various systems about the behavioral policy. In essence, the output channel combines across the predictions of each of the experts weighted by their relative precisions, and this output channel is utilized directly to control behavior. How might the output system be influenced by the manager? One way this could be done is via a gating mechanism – in which the manager gates the contribution of each of the individual experts to the overall recommendation, by for instance, either inhibiting the contributions from the experts that have high prediction uncertainty (or low precision), and/or by actively amplifying the contributions from the experts with low prediction uncertainty (or high precision). A possible architecture for the manager of the mixture of experts is illustrated in Figure 1. In the following section we review neuroscience evidence for the existence of a MoE framework in the brain, highlighting in particular the role of prefrontal cortex as a manager over the experts, further specifically localizing this manager to specific sub-regions of the prefrontal cortex.

Figure 1: Schematic of a putative mixture of experts system for the brain.

Each individual expert receives sensory input and makes its own predictions about the expected value of taking different actions. The predictions of each expert can then be compared with reality, when the organism takes an action and experiences an outcome. The difference between predicted and actual outcomes are then compared to yield a prediction error. The prediction errors for each system are then reported to a “manager” which uses them to compute a reliability signal (blue line), corresponding to a recency-weighted cumulative averaged prediction error for that controller. The manager uses these reliability signals to compute weights over the experts, proportional to their relative reliabilities. These weights are used by the manager to implement a gating of the outputs of each expert (red line), modulating the degree to which each expert contributes its “advice” toward the overall control of behavior (black line). The overall behavioral policy of the organism then corresponds to a combination of the advice of each expert, weighted by its overall reliability. The present schematic is agnostic as to the nature of the experts or their number. Four generic experts are depicted here. For a related mixture of experts implementation in computational reinforcement-learning see Hamrick et al., (2017).

Empirical evidence

The MoE framework makes the following specific predictions: (1) That each expert should compute its own predictions and that these predictions should be measurable in the brain for each putative expert system. (2) That the reliability of the predictions of each expert should be represented somewhere in the brain ideally within the same prefrontal cortex manager, so that they can be flexibly used to assign weights to each expert. (3) That this influence will be exerted possibly due to an inhibitory mechanism operating on the constituent experts (or potentially via both an excitatory and inhibitory mechanism). (4) That the reliability estimates are predicted to enable an overall output to be computed that reflects an integrated policy recommendation and that this output signal will be represented in the brain so that it can be used to guide the agent’s overall choice behavior at the time of decision-making.

In the following section we briefly review evidence in support of these findings from ourselves and others. The evidence we present is inherently limited in scope because to date we and others have focused mostly on only a small number of putative experts, predominantly model-based and model-free RL, and also more recently emulation and imitation in the domain of observational learning.

1. ) Separable value predictions for different experts

We (Lee et al., 2014), studied the interaction and arbitration between model-based and model-free RL using fMRI. We found evidence for a representation of separate value predictions for the two systems in multiple areas of the brain including medial prefrontal cortex (for model-based control) and posterior putamen for model-free control. A number of other studies have also found similar findings (Doll et al., 2015; Horga et al., 2015; Huang et al., 2020; Kim et al., 2019).

2. ) Reliability signals for different experts

In that same Lee et al. study we tested for brain regions involved in representing the reliability of the predictions of both systems. We found evidence for overlapping reliability signals for both MB and MF RL in the ventrolateral prefrontal cortex in particular, as well as in the rostral prefrontal cortex (Figure 2A). The presence of both of these reliability signals in the anterior prefrontal cortex led us to hypothesize a role for this region as mediating the arbitration process between MB and MF RL. In the language of the broader MoE framework this region can be implicated as the “manager” of the MoE. Moreover, Kim et al., (2019) replicated the reliability signal findings in vlPFC in another variant of the multi-step MDP used by Lee et al. (2014). Another study by Korn and Bach (2018), provides evidence of a role for vlPFC in tracking reliability. In that study two different foraging strategies were examined during a sequential decision task in which participants could either deploy an optimal strategy or a simpler heuristic strategy (which may be loosely analogous to a model-based and model-free strategy respectively). Although not the main focus of these authors’ conclusions, they reported a negative correlation with uncertainty in the choice for both the optimal and heuristic strategies in ventrolateral prefrontal cortex. The negative of uncertainty is reliability. Thus, we interpret those findings as likely reflecting a similar signal to that reported by Lee et al. (2014).

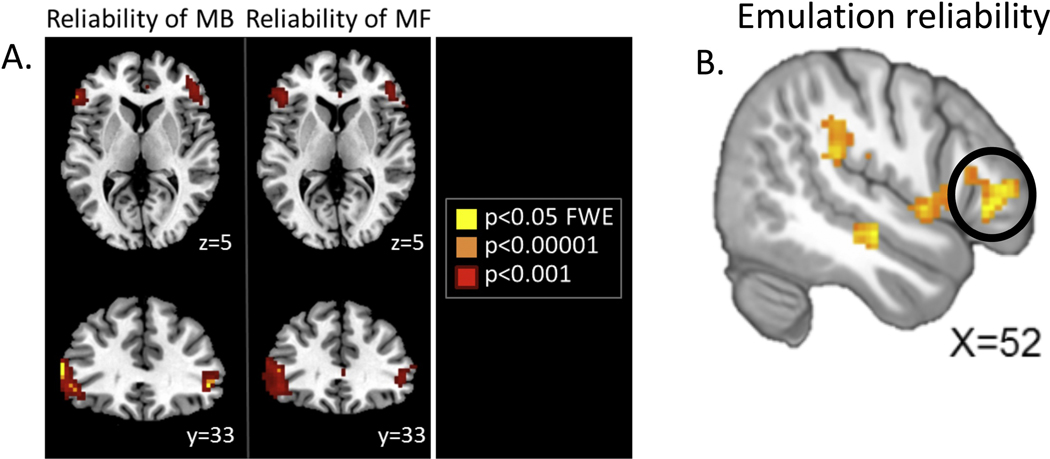
Figure 2. Evidence for the role of anterior prefrontal cortex in encoding the reliability of different “expert” strategies in the human brain.

This signal that could be used by a prefrontal-based manager of the mixture of experts. A. Shows regions of ventrolateral prefrontal cortex bilaterally in which activity (measured with fMRI) correlates with the reliability of both model-based and model-free reinforcement learning systems during performance of a multi-step MDP. From Lee et al., (2014).

(b) A region of ventrolateral prefrontal cortex (on the right) was found to correlate with the reliability of a strategy for “emulation” in which participants infer the goals of another agent while observing them perform a simple decision-making task. This finding supports a wider contribution of ventrolateral prefrontal cortex to the process of representing reliability of different strategies, supporting a more general contribution of anterior prefrontal cortex as the manager over multiple experts. From Charpentier et al., (2020).

Evidence that the contributions of vlPFC might also generalize to managing other experts beyond model-free and model-based RL in the experiential domain, arose from a recent study of observational learning (Charpentier et al., 2020). In this study, we examined the process of arbitration between two of the strategies for guiding observational learning alluded to earlier: emulation and imitation. Using a task that differentially induced variance in the predictions of the two strategies, we found that the control over behavior of the two systems was moderated by the reliability (or precision) of the predictions, especially that of the emulation system. In the brain we found evidence once again of a role for the ventrolateral prefrontal cortex (alongside rostral cingulate cortex and temporoparietal junction) in tracking the reliability or precision of the predictions, particularly of the emulation system (Figure 2B).

When taken together, these results implicate the anterior prefrontal cortex as contributing to the MoE manager.

3. ) The role of prefrontal cortex in setting the weights over the experts.

Furthermore, in the Lee et al. study of model-based and model-free RL arbitration, we also found that functional connectivity between the ventrolateral prefrontal cortex and regions involved in encoding model-free predictions changed as a function of a change in the degree predicted by the reliability-based arbitration system as to which behavior should be under model-based or model-free control. When behavior was predicted to be more model-based, there was an increase in connectivity between these two regions, while conversely when behavior was predicted to be model-free, there was reduced connectivity between these two regions. This finding led us to speculate that one additional contribution of vlPFC is to act as a gate on the degree to which the model-based and model-free systems exert control over behavior. One way this could be accomplished is via an active inhibition of the system involved in model-free control, which would be applied when behavior is predicted to be more model-based, thereby ceding control to the model-based system.

Causal evidence supporting this putative inhibitory mechanism arose from a transcranial direct current stimulation study (tDCS; Weissengruber et al., 2019). In that study, anodal tDCS stimulation was applied over the vlPFC while participants performed the model-based vs model-free arbitration task. We expected that anodal stimulation over this region would produce an increase in activity in vlPFC, thereby producing an increase in the inhibitory action of this region on the model-free areas. This was in turn predicted to cause an increase in model-based control. Consistent with this prediction, we found that when participants were exposed to the anodal stimulation over this region, the degree to which they manifested model-based control was (in one of the key task conditions) increased. In addition to the anodal stimulation we also produced cathodal stimulation over the same region. Because cathodal stimulation is known to decrease or inhibit activity in a given region, we expected that cathodal stimulation would reduce the inhibitory action over the vlPFC which consequently would result in an increase in model-free behavior. Once again, our predictions were supported. These results suggest that one way in which the vlPFC gates the control of the model-based and model-free systems over behavior is via an inhibitory action on striatal areas involved in model-free control. In these findings also lies a clue about the possible gating mechanism for a more generalized MoE framework. Specifically, the prefrontal MoE manager might influence the output of individual experts via an inhibitory effect on those experts as a function of the relative precision in their predictions. Crucially, the inhibition may not impact on the ability of those systems to make predictions in the first place, but only gate the extent to which that individual expert exerts influence on the output channel. A study by Bogdanov et al., (2018) also provided direct evidence that neuromodulation of vlPFC impacts the relative control of different expert systems. In that study, theta-burst TMS was used to inhibit activity in vlPFC while participants performed a slips-of-action task aimed at pitting goal-directed and habitual strategies. In that task, participants learn multiple action-outcome relationships, and then some of the outcomes are devalued, requiring participants to selectively stop responding to those actions, setting up a conflict between goal-directed and habitual performance. Inhibition of ventrolateral prefrontal cortex was found to reduce participant’s capacity to flexibly adjust their behavior in a goal-directed fashion, consistent with an increased engagement of the habitual system. The specific contribution identified here of a causal role for vlPFC in mediating the balance of control between MB and MF systems, is also consistent with a broader literature implicating the vlPFC in inhibitory control more generally, specifically in the capacity for inhibiting motor responses that are no longer relevant (Aron et al., 2014).

Another feature of the findings by Lee et al. (2014) in their connectivity analysis was that the manager putatively located in anterior prefrontal cortex in that study selectively showed changes in functional connectivity with regions involved in model-free control as a function of the arbitration (reliability-based) weights, but did not show any evidence of connectivity-based modulation on regions involved in model-based control. This raises the possibility that one possible way in which the MoE framework might operate is by inhibiting the simpler or default strategy when necessary (in this case model-free control), as opposed to directly modulating brain regions involved in implementing the more complex strategy. However, we should note, that it remains possible that the manager of the MoE could also exert an excitatory influence on experts that are deemed to have higher precision in their predictions. Although we are not aware of any evidence to support this latter possibility, it should not be ruled out at this juncture.

4. ) Candidate neural substrates for the output channel

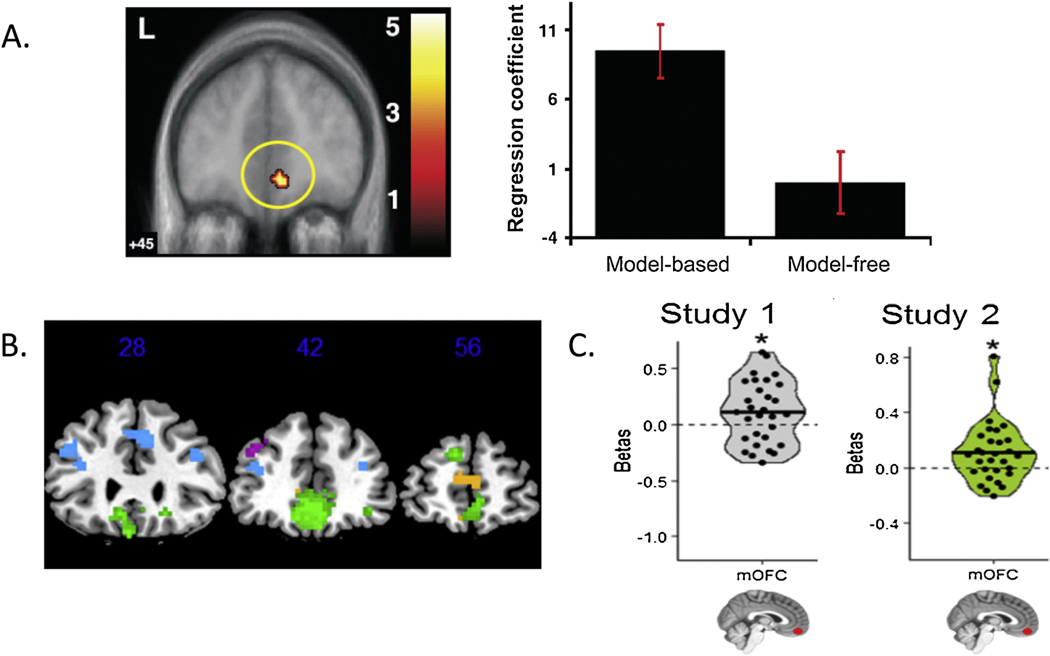
There is evidence to suggest that the ventromedial prefrontal cortex (vmPFC) acts as an output channel of the MoE system. The output channel involves the representation of an integrated prediction, that corresponds to the average across the predictions of the individual experts, weighted by the relative reliabilities of the predictions of each expert. This signal is the one that can be used as an input to the overall decision process, in order to settle on the actual behavioral policy that should be taken on a given trial. The first evidence to implicate the vmPFC in this function arose from a study by Hampton et al. ( 2006), in which two different computational strategies were investigated for their role in accounting for behavior and neural effects during performance of a stimulus-reward reversal learning paradigm. In that study, participants selected one of two stimuli that delivered different amounts of monetary gains and losses. One of the stimuli gave more gains than losses, and hence should be favored, while the other stimulus gave more losses than gains, and hence should be avoided. However, after a period of time the reward contingencies accorded to the two stimuli was reversed, so that participants should then switch their choice of stimulus. The performance of two computational strategies in capturing participants’ behavioral and neural activity on the task was compared. One strategy incorporated knowledge of the task rules and reversals, while another just learned from reward feedback without incorporating any structural knowledge. These two strategies can be seen to map onto a model-based vs model-free framework. Participants appeared to deploy the more model-based strategy, suggesting they were using knowledge of the task to guide their behavior. In the brain within vmPFC, BOLD activity was found to be correlated with both strategies, albeit more strongly with the model-based strategy than the model-free (Figure 3A). This finding could be interpreted in the context of a mixture of experts framework that in fact the recommendations of both strategies are actively represented in the vmPFC, albeit with a stronger weighting toward the “model-based” strategy in this particular instance. Wunderlich et al. (2012), also found evidence to support the existence of an integrated strategy in the ventromedial prefrontal cortex. These authors compared two different strategies for learning values and guiding behavior, a model-based strategy that used planning to guide behavior, and a model-free strategy that emerged with extensive training. They found that while each of the two strategies was encoded in unique brain structures in the striatum (anterior caudate for the planning strategy and posterior putamen for the model-free strategy), an integrated value signal that combined the predictions of both strategies was found in the vmPFC. Once again, these findings support the notion that vmPFC integrates over the predictions of these multiple systems, providing an overall recommendation (in the form of a value signal), that can be used to guide behavior (see also Beierholm et al., 2011). Lee et al., also examined the representation of value signals from both model-based and model-free strategies. They found that similar to Wunderlich et al., while the model-based and model-free strategies were represented in a number of distinct brain structures including posterior putamen for model-free values, and medial prefrontal cortex for model-based values, an integrated value signal which correlated with the value predictions of the two systems weighted by their relative contribution to behavior estimated by the arbitration system, was found to be present in the vmPFC (Figure 3B). Finally, in the recent study by Charpentier et al. on arbitration over observational learning strategies, the vmPFC was found once again to encode an integrated value signal at the time when participants needed to use information they had gleaned through observational learning to make their own decisions, the integrated value signal reflected a combination of the value predictions of the imitation and emulation systems weighted by their relative contributions to behavior as estimated by the arbitration system (Figure 3C). When taking all of these findings together, the evidence points to a role for the vmPFC as integrating across predictions of multiple systems in a manner proportional to the relative reliabilities of the predictions as computed by the arbitrator. In other words, we suggest that the vmPFC acts as an output channel of the MoE system. Value signals computed with vmPFC that reflect the integrated predictions of the MoE system can then be fed into decision-making comparators so as to derive choices over actions, that take into account the different predictions (or advice) of the various constituent experts for each action or object in the choice set.

Figure 3: Evidence of a role for vmPFC in representing combined predictions from multiple controllers.

This is consistent with a role for vmPFC (comprising medial orbital and adjacent medial prefrontal cortex) as the output of the mixture of experts, where predictions are assembled that are used to guide the overall behavior of the organism. A. Region of mPFC showing activity correlating with both model-based and model-free value predictions during performance of probabilistic reversal learning task in humans. From Hampton et al., (2006). B. Region of ventromedial prefrontal cortex (colored in green) correlating with the combined weighted predictions of model-based and model-free RL, in which the weights are set by an arbitration scheme (in essence a reduced form of the proposed mixture of experts mechanism). From Lee et al. (2014). C. Plot of regression coefficients from a functionally defined region of interest defined in the medial orbitofrontal cortex. Average activity in this ROI was found to reflect the combined value predictions of emulation and imitation strategies for observational learning weighted by their relative reliability as determined by an arbitration scheme. The plots show separate results from two independent fMRI studies. From Charpentier et al., (2020).

Hierarchical mixture of experts

So far, we have considered an MoE architecture that is relatively flat in that we have envisaged the existence of multiple experts at the same level of seniority, alongside a manager which reads out the relative reliabilities of the experts’ predictions and combines those together to generate an output signal weighted by their relative precision. However, we think it is likely the case that the MoE architecture is substantially richer. Rather than being flat, we suspect that the MoE architecture is in fact hierarchical, in the sense that each constituent expert likely depends on the nested contributions of sub-experts. In turn, sub-experts produce predictions that are integrated at the level of the individual expert in order to be passed on to the higher-up manager. Such a hierarchical organization would imply that each expert acts as its own manager for its own set of individual sub-experts, gating their contributions to the overall recommendation of each expert. What would the sub-experts be concerned with? We suggest that the sub-experts might be usefully focused on computing recommendations arising from different interpretations of the state-space and/or task structure. It is probably most useful to illustrate this idea by reference to a specific class of experts. For this we will return to the model-based vs model-free distinction, though we emphasize that this idea should not be considered limited to the model-based vs model-free distinction and that in fact a similar principle should apply across a whole host of experts. Let’s take a model-based agent first. When behaving in model-based manner, it is essential for the agent to encode a cognitive map or model of the world, so that when using that cognitive map, it is possible for the agent to engage in planning in order to compute model-based values that in turn can be used to guide behavior. However, in an uncertain and noisy environment, there is no guarantee that (except in a very stereotyped environment such as might happen in a laboratory experiment) the agent has converged on the correct cognitive model. In fact, there may be multiple possible cognitive models of the world that have non-zero probabilities from the organism’s perspective. One way this could be resolved would be by having multiple model-based sub-experts make different predictions on the basis of differing possible hypotheses about the nature of the model of the state-space. So for instance, if computing which model-based policy to pursue to gain access to your office building after office hours, you might compute two model-based policies, one based on the possibility that the main entrance will have a security guard posted and thus be open, and another based on the possibility that the rear entrance will be open instead. At the level of the model-based expert, two possible strategies might therefore be available as recommended policies, with an overall uncertainty over them depending on how likely each of these hypotheses over the state-space are likely to be true. The strategy of considering multiple hypotheses about the nature of the state-space simultaneously, such as by entertaining the possibility that both the front and back doors are open, could help ensure that the brain is maximally sensitive to varying possibilities about the state of the word. It would also likely improve its capacity to flexibly adapt to new situations, because new situations can as a first pass be approached using a weighted combination of existing beliefs about the world.

A recent study by de Silva and Hare (Feher da Silva and Hare, 2020) supports this possibility. In this paper, the authors found evidence to suggest the possibility that participants might actually compute multiple model-based strategies to solve a standard two-step task, based on wildly different beliefs about the nature of the task-structure (and hence leading to very distinct cognitive models). Similarly, for a model-free agent, beliefs over very different state-space structures could give rise to very distinct model-free predictions. For instance, in the typical two-step task, one model-free strategy would be to rely on a state-space structure in which each trial (two-steps) in the MDP is treated as being independent from each other trial, and thus the agent learns about the cached values of each of the states within a trial only. Alternatively, a much richer state-space is possible, in which the outcomes received on the preceding trial become states that are used in the subsequent trial to compute values. Thus, it is easy to imagine that depending on how the state-space is carved up, that a model-free agent can produce very distinct (and sometimes very rich predictions that can appear model-based). Thus, it is possible to envisage that each constituent expert in fact relies on multiple sub-experts which make predictions as a function of differing hypotheses or beliefs about the nature of the state-space and transition probabilities that make up the causal structure of the world. As alluded to earlier, multiple sub-experts have also been suggested to contribute to predictions in the Pavlovian system (Dayan and Long, 1998).

Naturally, a pernicious scaling problem emerges with having multiple sub-experts each trying to provide (sometimes) competing advice: one could quickly end up with an exponentially large number of sub-experts across all the experts each competing to make predictions that would quickly run into limits of cognitive capacity. For this reason, we suspect that the bias/variance tradeoff would quickly result in sub-experts being favored that are likely to have more plausible hypotheses about the state-of-the-world, as well as hypotheses that are parsimonious and not too complex. It is likely that sub-experts with prediction reliabilities that are in fact very low, would end up being discounted completely and not actively polled for their advice. This would imply that once a sub-expert has very poor reliability it will quickly be discounted, ignored and no longer required to actively provide advice.

Relationship between MoE and other frameworks of hierarchical control

The MoE framework we have just outlined might raise the question about how similar it is to other existing frameworks of hierarchical control. One such framework is hierarchical reinforcement-learning (HRL; Botvinick et al., 2009). According to HRL, when solving a decision problem, a given task is typically broken down into sub-tasks. Each sub-task concerns itself with a particular partition of the state-space, which can exist at different levels of the hierarchy. For instance, the sub-task “open the red door”, has to be implemented by performing a number of discrete actions, including walking to the door, putting one’s hand on the handle, turning the handle, and pulling on the door etc. In HRL terms, groups of actions are clustered together to form “options”, which can facilitate easier learning of an overall policy, than if each individual action has to be independently learned about. We suspect that HRL can be viewed as a special case of the MoE framework, where a particular expert is concerned with solving different sub-tasks or problems that exist at different levels of a hierarchy over state-space features. In current implementations of HRL as applied to neurobiology, each of the sub-tasks are solved by the same expert. That is the same algorithm is used to solve problems at each level of the hierarchy, for instance, a model-free RL agent. In the MoE framework, we consider the possibility that the same sub-problem can be focused on by a range of different experts. For instance, when working out how to open the red door, both model-based and model-free experts might contribute to working out how to solve this problem, and indeed multiple model-based and model-free strategies might be deployed depending on how much uncertainty exists about the nature of the state-space and/or transition model within that space. Thus, the MoE framework can accommodate HRL in the sense that unlike a single system HRL framework, the hierarchical decomposition occurs not only at the level of tasks and sub-tasks, but also at the level of which set of experts is utilized to solve a given task and sub-task. The hierarchical MoE framework also bears some relationship to broader theories of cognitive function such as the free energy principle and predictive coding models more generally (Friston, 2010; Mumford, 1992; Rao and Ballard, 1999; Srinivasan et al., 1982). In the free energy theory (Friston, 2010) the agent acts to minimize its own prediction errors, either actively or passively. This theory also envisages a hierarchical organization of brain function, in which each level of the hierarchy computes prediction errors that are passed to the next level of the hierarchy. These prediction errors are minimized throughout the system by adjusting predictions to better account for sensory data, as well as by adjusting behavior to actively minimize uncertainty. In this sense, it is possible to envisage that an MoE architecture would emerge in the context of a system that is designed to minimize prediction errors. Indeed, in the MoE framework, the experts that are nominated to provide the most control over behavior are those that by definition generate the smallest prediction errors, and hence have the highest reliability or precision. The MoE framework as envisaged here has more in common with traditional reinforcement-learning in the sense that it envisages the ultimate goal of the organism is to maximize expected future reward by selecting from those experts best equipped to deliver on that promise as opposed to minimizing surprise per se. However, both frameworks predict an important role for prediction uncertainty and/or precision, as well as making predictions that prediction errors should be prevalent as a means of updating and learning predictions as well in learning about the precision of those predictions within each constituent expert throughout the brain.

Summary and conclusion

Here we outline a framework for conceptualizing the contribution of multiple systems to behavioral control in the human brain. Our main argument is that the brain utilizes a framework loosely analogous to the mixture of experts in machine learning, in which a prefrontal-based manager, reads out the reliability of the predictions by each of the constituent experts, and uses these predictions to allocate control over behavior to the experts in a manner that is proportional to the relative precision or uncertainties in their predictions. This reliability-based framework is suggested to be mediated via prediction errors, which are likely to be present in each expert system provided the system generates a unique prediction. At the level of neural implementation, we propose that the ventrolateral prefrontal cortex and anterior frontal pole encode reliabilities for multiple expert strategies and that connectivity between the anterior frontal cortex and other brain regions is involved in the allocation of control of different systems over behavior. By contrast, the ventromedial prefrontal cortex represents an integrated policy that takes into account the predictions of the different expert systems weighted by their relative reliabilities. We suggest that this reliability-based arbitration process between experts is both necessary and sufficient for the efficient allocation of control between systems, as this approach takes into account not only the accuracy and hence the average expected value of the actions nominated by each expert, but also implicitly takes into account the cognitive costs and cognitive constraints. The interaction between systems that makes up the experts is we suggest, better conceived of as one of polling the advice from different systems that each have different relevant expertise that can and should be respected owing to differences in the nature of the information that is being processed, and in the algorithmic transformations that are performed on that information. These experts should be listened to as a collective, because they provide the right mixture of opinions needed to act in the world effectively.

Highlights.

• The brain can be thought of as a “Mixture of Experts” in which different expert systems propose strategies for action.

• This is accomplished by keeping track of the precision of the predictions within each system, and by allocating control over behavior in a manner that depends on the relative reliability of those predictions.

• This reliability-based control mechanism is domain general, exerting control over many different expert systems simultaneously in order to produce sophisticated behavior.