Machine Learning–Based Prediction of Small Intracranial Aneurysm Rupture Status Using CTA-Derived Hemodynamics: A Multicenter Study

Abstract

BACKGROUND AND PURPOSE:

Small intracranial aneurysms are being increasingly detected while the rupture risk is not well-understood. We aimed to develop rupture-risk models of small aneurysms by combining clinical, morphologic, and hemodynamic information based on machine learning techniques and to test the models in external validation datasets.

MATERIALS AND METHODS:

From January 2010 to December 2016, five hundred four consecutive patients with only small aneurysms (<5 mm) detected by CTA and invasive cerebral angiography (or surgery) were retrospectively enrolled and randomly split into training (81%) and internal validation (19%) sets to derive and validate the proposed machine learning models (support vector machine, random forest, logistic regression, and multilayer perceptron). Hemodynamic parameters were obtained using computational fluid dynamics simulation. External validation was performed in other hospitals to test the models.

RESULTS:

The support vector machine performed the best with areas under the curve of 0.88 (95% CI, 0.85–0.92) and 0.91 (95% CI, 0.74–0.98) in the training and internal validation datasets, respectively. Feature ranks suggested hemodynamic parameters, including stable flow pattern, concentrated inflow streams, and a small (<50%) flow-impingement zone, and the oscillatory shear index coefficient of variation, were the best predictors of aneurysm rupture. The support vector machine showed an area under the curve of 0.82 (95% CI, 0.69–0.94) in the external validation dataset, and no significant difference was found for the areas under the curve between internal and external validation datasets (P = .21).

CONCLUSIONS:

This study revealed that machine learning had a good performance in predicting the rupture status of small aneurysms in both internal and external datasets. Aneurysm hemodynamic parameters were regarded as the most important predictors.

Unruptured intracranial aneurysms are common, with an overall prevalence of 3.2% in adults worldwide.¹ In the past decades, increasing unruptured aneurysms have been detected because of wide application of CTA and MRA. Notably, large numbers of incidentally detected aneurysms (≤87.6%) have small sizes (<3–4 mm) and are usually asymptomatic.² To date, small aneurysms account for 35%–47% of ruptured aneurysms and may impose a great burden on intracranial vessel diseases.^3,4

Treatment of patients with unruptured small aneurysms remains controversial. Some researchers recommend no preventive treatment or imaging follow-up for patients with aneurysms of <3 mm based on the evidence of low annual growth and rupture rates of small aneurysms.^5,6 Current guidelines from the American Heart Association and American Stroke Association have no consensus opinion regarding the management of unruptured aneurysms with small (3–5 mm) and extra-small (≤3 mm) sizes.⁷ Thus, it is imperative to evaluate the rupture risk of small aneurysms to derive optimal clinical decision-making for further treatment and follow-up.

Various rupture risk factors and constructed scoring systems have been advocated by researchers.^8,9 The correlation of risk factors (such as clinical, morphologic, and hemodynamic parameters) makes the prediction of aneurysm rupture complicated, leading to the unreliability of conventional methods such as logistic regression. Current scoring systems are not robust, especially for small aneurysms, which have to be modelled specifically due to their unique histologic characteristics.^10-12 Therefore, novel methodologies are required to construct rupture-risk models for small aneurysms to facilitate clinical decisions.^13,14 Aneurysms were often treated only if any change in size or morphology of the aneurysm was detected during follow-up, which would result in a serious bias in the longitudinal study.¹³ It is feasible to perform a cross-sectional study to discriminate the ruptured aneurysms and, further, to apply the model in predicting rupture risk of unruptured aneurysms.

Machine learning (ML) techniques have attracted attention for their ability to identify patterns from a large sample dataset with multiple variables, using a highly effective method that facilitates the model construction for data-driven prediction or classification.^15-17 Evidence has suggested that ML algorithms are superior to traditional counterparts in contexts in which data input is abundant and have potential for complex interactions.^17,18 ML has also been used in the classification of aneurysm rupture status with relatively high accuracy.^19,20 However, to the best of our knowledge, no report to date has developed ML methods for small aneurysm rupture prediction with routine clinical and morphologic features combined with hemodynamic variables.

The aim of this study was to characterize patients who have a higher risk of aneurysm rupture through developing and validating ML models using routinely collected clinical, morphologic, and hemodynamic variables in an internal cohort and to further test the indicated models in external datasets from other hospitals.

MATERIALS AND METHODS

Study Population

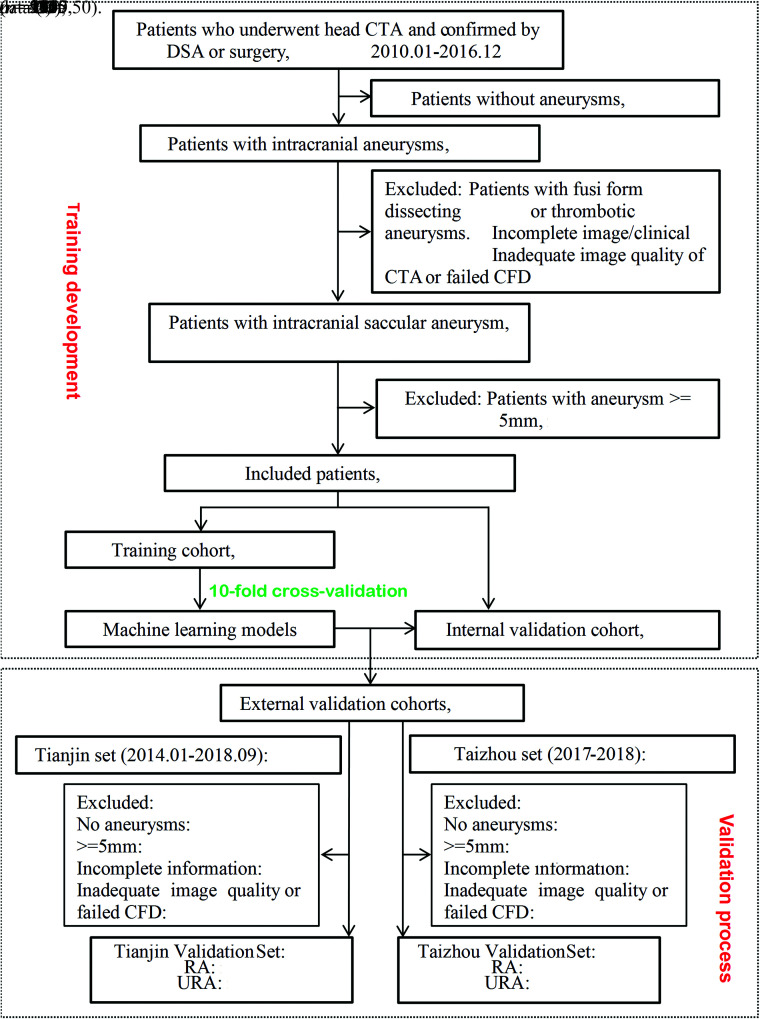
Between January 2010 and December 2016, one thousand five hundred seventy consecutive patients with suspected aneurysms or other cerebral vascular diseases who underwent cerebral CTA in Jinling Hospital verified by DSA or surgery were collected with the interval of no more than 3 months. The inclusion criterion was patients with small aneurysms (<5 mm).¹⁴ Exclusion criteria were as follows: 1) no aneurysms (n = 395); 2) patients with fusiform, dissecting, and thrombotic aneurysms (n = 51); 3) incomplete image/clinical data (n = 50); 4) inadequate CTA image quality or failed computational fluid dynamics (CFD) simulation (n = 67); and 5) patients with aneurysms of ≥ 5 mm (n = 503). Finally, 504 small aneurysms (395 ruptured aneurysms and 109 unruptured aneurysms) were included and were randomly separated into training (410, 81%) and internal validation cohorts (94, 19%).

External validation cohorts enrolled patients who underwent cerebral CTA examinations from the other 2 medical centers (Tianjin First Central Hospital, Tianjin; and Taizhou People’s Hospital, Taizhou, Jiangsu). Two neuroradiologists (G.Z.C. and Z.S. with 7 and 3 years’ experiences in neuroradiology) identified the location of aneurysms. In the case of disagreement between the 2 observers, consensus was reached after a joint reading with a senior neuroradiologist (C.S.Z. with 17 years of neuroimaging experience). The study flow chart is shown in Fig 1. Cerebral CTA protocols in the 3 medical centers are shown in the Online Supplemental Data. Ethics approval was obtained by the institutional review board of Jinling Hospital, Medical School of Nanjing University, Nanjing, China.

FIG 1.

Flow chart of this study. RA indicates ruptured aneurysm; URA, Unruptured aneurysms; CFD, computational fluid dynamics.

Patient and Aneurysm Characteristics

Clinical characteristics included age, sex, family history of aneurysmal SAH; comorbidities such as hypertension, diabetes mellitus, ischemic stroke, and coronary artery diseases; alcohol intake; and smoking status collected in the in-hospital medical record. Aneurysm characteristics included the multiplicity, size, shape, daughter sac, and location. Locations were divided into anterior communicating artery, ICA, MCA, posterior communicating artery, and others. Size was defined as the largest diameter measured on CTA with a volume-rendering algorithm. Specifically, the assessment of rupture status of an aneurysm was established as follows: For patients with SAH, when only 1 aneurysm adjacent to the cisternal clots was identified with CTA, the aneurysm was judged to be ruptured; when 1 aneurysm not adjacent to the cisternal clots was identified, its rupture status was judged intraoperatively; and when ≥2 aneurysms were identified, the rupture status of aneurysm was confirmed intraoperatively.¹⁹ Aneurysms with neither SAH nor symptoms were judged to be unruptured. We analyzed rupture risk on a per-patient basis for the analysis. When a patient had multiple aneurysms, the largest one served to categorize the patient.

Computational Fluid Dynamics–Derived Parameters

The computational model was constructed from CTA. CFD analysis was performed under pulsatile-flow conditions, and the procedure has been described in a previous study.²¹ The Online Supplemental Data shows the procedure of the development of the patient-specific CFD model reconstruction. Eleven quantitative hemodynamic parameters were used to describe and analyze the sophisticated blood flow conditions,^21,22 including pressure, wall shear stress (WSS), averaged WSS-absolute (AWSS-ABSOLUTE), averaged WSS-mean (AWSS-MEAN), WSS gradient, AWSS gradient, oscillatory shear index (OSI), relative residence time, aneurysm formation index, gradient oscillatory number, and spatial WSS gradient (Online Supplemental Data). The coefficient of variation (CV) was used to describe the dispersion degree of data to demonstrate the hemodynamics of the aneurysm sac. Qualitative hemodynamic parameters included flow complexity, impingement zone, stability, and inflow concentration (Online Supplemental Data).²³ Two hundred aneurysms were randomly selected and evaluated independently by 2 observers trained for this task (G.Z.C. and Z.S.), who were blinded to the clinical history and rupture status. After validating good interreader agreement, 1 observer (G.Z.C.) performed the qualitative hemodynamic assessment of the remaining aneurysms.

Construction of Machine Learning Models

All features were preprocessed before model building. The quantitative features were normalized by z scores, while the qualitative features were encoded by one-hot encoder. ML methods were applied in the DeepWise Medical Research platform (https://keyan.deepwise.com). Supervised ML algorithms with binary classification (ruptured and unruptured aneurysm) were used to build predictive models, including logistic regression (LR), random forest, support vector machine with linear kernel (SVM), and multilayer perceptron (MLP). For implementing the procedure, the feature-selection method was used to reduce the overfitting problem. The best hyperparameters of the feature-selection method and models and regularization parameters of each model would be searched automatically on the basis of 10-fold cross-validation. After the optimal hyperparameters and regularization parameters were chosen, the entire training cohort was used to train the model and the performance was evaluated on the internal and external validation cohorts. A brief overview of the models and the description of the feature-selection method are shown in the Online Supplemental Data.

Assessment of Model Performances

For the LR and MLP models, the predicted probability of rupture was estimated by the models directly. For the SVM model, the predicted probability was the normalized distance of the test sample to the separating hyperplane. For the random forest model, the predicted probability was computed as the mean predicted probabilities of the trees in the forest. The performances of the models were represented as the receiver operating characteristic (ROC) curve, the area under curve (AUC), and 95% confidence interval (CI). The sensitivity and specificity were determined by the Youden index. The calibration of the 4 ML models was assessed using the calibration curves in the internal validation dataset with Locally Weighted Scatterplot Smoothing.²⁴ The DeLong test and Bonferroni correction were applied to compare the AUCs of these models. Feature importance was ranked according to the coefficient of each parameter provided by the corresponding ML algorithms. Specifically, the feature importance of the random forest model refers to the Gini importance.

Statistical Analysis

Quantitative variables were expressed as mean ± [SD] if normally distributed, while median and interquartile range were used for non-normally distributed data. Categoric variables (such as sex, the presence of hypertension, qualitative hemodynamic parameters) were expressed as frequencies or percentages; the difference in categoric variables was analyzed using the Pearson χ² test or Fisher exact test when appropriate. For normally distributed data (such as age, OSI_CV), an independent-samples t test was used; otherwise, a Mann-Whitney U test was applied. The independent-samples nonparametric test was used to analyze non-normally distributed data. The interreader agreement of the qualitative hemodynamic assessment was evaluated by the Cohen κ. The CI of the AUC was calculated by the method of Hanley and McNeil.²⁵ Statistical analyses were performed using SPSS statistical and computing software (Version 22.0.0; IBM), Medcalc for Windows (Version 18.2; MedCalc Software), R (Version 3.5.2; http://www.r-project.org/), and the Scikit-learn package²⁶ in Python (https://scikit-learn.org/stable/). A 2-sided P value < .05 was used to represent statistical significance.

RESULTS

Patient and Aneurysm Characteristics

In this retrospective study, most patients with ruptured small aneurysms were women. These patients were younger and had a higher proportion of hypertension and a lower proportion of ischemic stroke and coronary artery disease compared with those with unruptured aneurysms (all, P < .05). In addition, more small aneurysms with irregular shapes were found in the ruptured group. The anterior communicating artery and MCA tended to have more ruptured aneurysms (all, P < .05), while the ICA and other intracranial arteries had fewer ruptured aneurysms (all, P < .05). For hemodynamic parameters, the ruptured group was more likely to have complex flow patterns (52.9% versus 33.0%, P < .001), concentrated inflow streams (61.5% versus 18.3%, P < .001), a small flow-impingement zone (73.4% versus 28.4%, P < .001), and unstable flow patterns (57.0% versus 29.4%, P < .001), as well as a smaller PressureCV gradient oscillatory number, and OSI_CV and higher AWSS-MEAN_CV, WSS_CV, AWSS-ABSOLUTE_CV, WSS gradient, and aneurysm formation index (all, P < .05) (Online Supplemental Data). The interobserver agreement for the qualitative hemodynamic assessment of aneurysms ranged from good to excellent, with κ values from 0.646 to 0.827.

The internal training cohort had 410 cases (320 ruptured aneurysms), and the internal validation cohort had 94 cases (75 ruptured aneurysms). There were no significant differences for the clinical, morphologic, and hemodynamic parameters between the 2 cohorts (all, P > .10) (Online Supplemental Data). In the external cohorts, 177 patients with cerebral CTA (131 patients from the Tianjin center and 46 patients from the Taizhou center) were screened, and 52 patients with small aneurysms (19 unruptured and 11 ruptured aneurysms in the Tianjin center, 11 unruptured and 11 ruptured aneurysms in the Taizhou center) were included (Fig 1). There was a lower incidence of ruptured aneurysms in the Taizhou and Tianjin datasets (P = .002 and <.001, respectively). Because of the small sample size of both external datasets, we merged all the cases into 1 external dataset to validate the performance of ML models (Online Supplemental Data).

Performances of ML Models

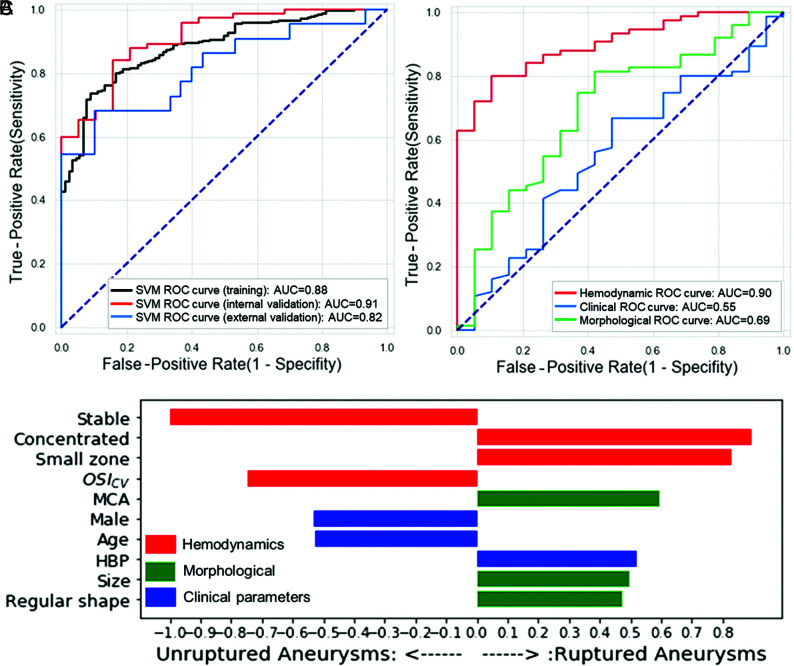
The 4 ML models derived from the training dataset performed equally in all datasets (all, P > .05, DeLong test). The calibration curves are shown in the Online Supplemental Data. Among them, the SVM was well-calibrated with the highest AUC in the internal validation dataset (Table and Fig 2A). The performances of the other 3 models are shown in the Online Supplemental Data. The AUCs of the SVM model were 0.88 (95% CI, 0.85–0.92), 0.91 (95% CI, 0.74–0.98), and 0.82 (95% CI, 0.69–0.94) in the training, internal, and external validation datasets, respectively. The Delong test showed that the AUC had no significant difference between internal validation dataset and the external validation dataset (P = .21).

Performance of SVM to predict rupture status of small aneurysms in the training, internal validation, and external validation datasets

	Training Set (n = 410)		Internal Validation Set (n = 94)		External Validation Set (n = 52)		Tianjin Set (n = 30)		Taizhou Set (n = 22)
AUC	0.88		0.91		0.82		0.71		0.90
95% CI	0.85–0.92		0.74–0.98		0.69–0.94		0.52–0.86		0.70–0.99
Sensitivity	73.4%		77.3%		68.2%		54.5%		81.8%
Specificity	91.1%		84.2%		76.7%		73.7%		81.8%
Delong test	–		–		.21a		–		.15b

Note:—CI indicates confidence interval; LR, logistic regression; SVM, support vector machine; RF, random forest; ROC, receiver operation characteristic; RF, random forest; -, NA.

^aP < . 05 means a significant difference exists in AUCs of SVM in the internal and external validation datasets.

^bP < . 05 means a significant difference exists in AUCs of SVM in Taizhou and Tianjin sets.

FIG 2.

Performance of the SVM algorithm, the derived top 10 variables, and the performances of feature—dependent models in the internal validation dataset. A, ROC curves and AUCs for training and internal and external validation sets. B, The top 10 features of the variables derived from the SVM algorithm. C, ROCs of the SVM based on the features belonging to the 3 categories separately in the internal validation dataset.

We further investigated the application of models in the Tianjin and Taizhou sets (Table and Online Supplemental Data). The SVM had a slightly higher AUC in the Taizhou set (AUC = 0.90; 95% CI, 0.70–0.99) than that in the Tianjin set (AUC = 0.71; 95% CI, 0.52–0.86), without a significant difference (P = .15).

Feature Ranks

Selected features used for model fitting are seen in the Online Supplemental Data.

The feature rank of the corresponding top 10 variants derived by the SVM algorithm is shown in Fig 2B. Hemodynamics-related parameters were the leading predictors contributing to the risk model. Stable flow stream, higher OSI_CV, male sex, and older age were protective variables, while concentrated inflow streams, a small (<50%) flow-impingement zone, MCA, hypertension, larger size, and irregular shape increased the risk of aneurysm rupture.

We also developed models based on sole clinical, morphologic, or hemodynamic features, respectively, and validated the models in the internal validation dataset for further evaluation. Figure 2C demonstrates that the hemodynamic feature–dependent model had a higher AUC (AUC = 0.90; 95% CI, 0.84–0.96) than morphologic features (AUC = 0.69; 95% CI, 0.5–0.83; P = .01) and clinical features (AUC = 0.55; 95% CI, 0.4–0.70; P < .001).

DISCUSSION

In this study, we derived and validated ML-based prediction models for rupture status of small aneurysms, depending on clinical, morphologic, and hemodynamic characteristics in the internal and external datasets. Our study highlighted the role of hemodynamic parameters in predicting small aneurysm rupture status. We found that the ML models, especially the SVM, had good performance in the internal and external datasets, indicating the robustness and generalizability of ML models. Thus, the ML models provided in this study can be regarded as decision-support tools of unruptured small aneurysms, while further validation is required.

Traditional statistical methods, such as multivariable LR, have explored the association between specific features and the ruptured/unruptured end point. However, determination of rupture risk of aneurysms remains challenging, particularly when the exact underlying etiology is unclear.²⁷ In addition, multivariable LR has several limitations, primarily resting on assumptions of the existence of the linear relationship between the log-odd of the predicted probability and the variables. ML has shown the potential to improve diagnostic accuracy and prognostic outcomes compared with conventional statistical methods.^17,20 Our study used 4 representative branches of ML, including the subtypes of logistic regression, ensemble model, SVM, and neural network. The 4 models had good performance in the internal and external cohorts. A previous study had compared the logistic regression probability model with ML classifiers and found that the performance of the logistic regression probability model was comparable, but the study did not specifically focus on small aneurysms.²⁸

A convolutional neural network based on images of 3D-DSA for detecting the rupture status of aneurysms of <7 mm had also been explored.²⁰ And in the presented study, we compared 4 ML methods combined with CTA-derived hemodynamics and found that the SVM and MLP had slightly higher AUCs in predicting small-aneurysm rupture status. The SVM performed better when applied in the 2 external datasets in terms of generalizability. Another interesting finding was that SVM, random forest, and MLP seemed to have less overfitting than LR when applied to the external validation dataset; among these, SVM had the lowest overfitting. Considering the higher AUC and the lowest overfitting of the SVM, it is reasonable for us to regard SVM as the most valuable ML method in this context. The models did not seem well-calibrated, probably due to the small size of the dataset.

Most important, our findings highlighted the role of hemodynamics in the prediction of rupture status of small aneurysms, which had not been quantitatively identified. The process of rupture of an aneurysm is complex because of the intertwining relationship between the blood flow and pathologic responses in the endothelial cells and remodeling of vessel wall.^29,30 Blood flow hemodynamics emerged as an important role that can uncover the underlying mechanism through hemodynamic-biologic pathways.¹¹ Higher WSS_CV and lower OSI_CV were further identified in our study as the paramount rupture risk factors by the ML algorithms. CV is a standardized measure of dispersion of a probability distribution or frequency distribution, and the smaller CV was, the smaller the extent of variation was. That feature means that the ruptured small aneurysms had higher WSS variation in the sac, while OSI had less variation. A similar result had been previously reported in a case-control study that showed a narrow cumulative WSS distribution characterizing a hemodynamic prone-to-rupture range for small-sized aneurysms.³¹ The spatial minimum, maximum, average WSS, normalized WSS, spatial WSS gradient, and OSI had been studied before, and low WSS and high OSI were known to upregulate endothelial surface adhesion molecules, causing dysfunction of flow-induced nitrous oxide, increasing endothelial permeability, thus, promoting inflammatory cell infiltration.^31-35 Our study offered a novel insight into the role of hemodynamics in rupture-risk prediction of unruptured small aneurysms and can be used as a supplement to the existing research. For example, the WSS in ruptured small aneurysms could be lower in minimum/maximum/mean value and more variated than in unruptured aneurysms, and OSI could be higher with less variation.

Our study also found that qualitative hemodynamic parameters had an important role in predicting the rupture status of small aneurysms. The study showed that complex flow patterns, concentrated inflow concentration, unstable flow, and a smaller flow impingement zone played a critical role in the prediction of rupture risk of aneurysms. These findings have been supported by previous studies that showed ruptured aneurysms were more likely to be associated with flow types with changing direction of the blood inflow jet, which will create a single vortex.³⁶ It appears very instructive to add the qualitative hemodynamic parameters in predicting rupture status of small aneurysms.

Specifically, we analyzed the distinctive performances of the 4 models in the 2 external datasets separately, among which random forest and MLP exhibited significant differences (both P = .03). The reasons can be attributed to the baseline characteristic differences, in which 9 variables in the Taizhou set and 12 in the Tianjin set were significantly different, and most of the variables are hemodynamics. Given the different scanner manufacturers in the Tianjin and Jinling sets (Revolution CT, GE Healthcare, versus Somatom Definition, Siemens), the hemodynamic differences may arise from them; this issue requires further investigation. Although the proportion of ruptured aneurysms was lower in the Taizhou set (50% versus 78.4% for the Taizhou and Jinling datasets), the performance of the models was encouraging. These results highlight the influence of manufacturers on CFD simulation.

We acknowledged that our study had some limitations. First, this retrospective study aimed to identify the characteristics of ruptured aneurysms, and the model predicted only the current rupture status rather than future aneurysm risk. Whether the model can be used in the rupture-risk prediction of small aneurysms requires further longitudinal studies. Our model is reliable due to being derived from a large-scale internal cohort of small aneurysms demonstrated by DSA/surgery and validated in independent external validation datasets. Second, the morphologic changes of aneurysms after rupture were not considered in this study. Third, the external validation datasets from the other 2 medical centers had small sample sizes and were not verified by DSA or an operation. Fourth, features of the wall of the vessel and aneurysm have been investigated for precise evaluations using high-resolution MR imaging and optical coherence tomography, while the elements are not included in the study. Fifth, CFD itself has some limitations, such as a huge number of different parameters, the lack of consistency, and being time-consuming, resulting in difficulties in clinical use with CFD.³⁷ Sixth, the assessment of the qualitative hemodynamic parameters was based on the 2 observers, which was subjective and caused intra- and interobserver variations. Other metrics for automated flow-complexity assessment like the “inflow concentration index” and “vortex core line length” may help in this context. Thus, a large, prospective, multicenter study is needed to further demonstrate our findings.

CONCLUSIONS

Our study provided impressive ML models for predicting rupture status of small aneurysms by combining clinical, morphologic, and hemodynamic features. ML methods, especially SVM, had a good performance in internal and external validation datasets and highlighted the role of hemodynamics. Our model has the potential for identifying high-risk aneurysms and facilitating proper clinical management of incidentally found small aneurysms.

ABBREVIATIONS:

AUC

area under the curve

AWSS

averaged WSS

CFD

computational fluid dynamics

CV

coefficient of variation

LR

logistic regression

ML

machine learning

MLP

multilayer perceptron

OSI

oscillatory shear index

ROC

receiver operating characteristic

SVM

support vector machine

WSS

wall shear stress