Quantitative Methods for Metabolomic Analyses Evaluated in the Children’s Health Exposure Analysis Resource (CHEAR)

Abstract

With advances in technologies that facilitate metabolome-wide analyses, the incorporation of metabolomics in the pursuit of biomarkers of exposure and effect is rapidly evolving in population health studies. However, many analytic approaches are limited in their capacity to address high-dimensional metabolomics data within an epidemiologic framework, including the highly collinear nature of the metabolites and consideration of confounding variables. In this Children’s Health Exposure Analysis Resource (CHEAR) network study, we showcase various analytic approaches that are established as well as novel in the field of metabolomics, including univariate single metabolite models, least absolute shrinkage and selection operator (LASSO), random forest, weighted quantile sum (WQS_RS) regression, exploratory factor analysis (EFA) and latent class analysis (LCA). Here, in a Bangladeshi birth cohort (n=199), we illustrate research questions that can be addressed by each analytic method in the assessment of associations between cord blood metabolites (¹H NMR measurements) and birth anthropometric measurements (birth weight and head circumference).

Introduction:

Technological advancements have made ‘omics scale assessments of molecular markers, including DNA variants and modifications, gene transcripts, proteins and metabolites, feasible in human population studies. Profiling the metabolome is of particular interest in environmental epidemiology, as it provides a functional readout of a collection of small molecules produced by the cell, in addition to internalized environmental exposures and the bioeffective dose of those exposures [1]. As this readout reflects an integration of genetic and environmental cues, metabolomic assessments offer more proximal insights into perturbed physiologic processes compared to other commonly surveyed ‘omics approaches [2]. Additionally, with the recognition that adverse metabolic health outcomes across the lifespan may have origins early in life, metabolomic profiling is emerging as a particularly pertinent tool in epidemiologic studies aiming to identify markers reflecting the developmental origins of disease.

While standardized analytic strategies exist to address epidemiologic questions using certain ‘omics scale assessments, including genomic [3,4] and methylomic data [5], mature methodologic pipelines to incorporate metabolome-wide data within an epidemiologic framework are not yet established. For example, greater attention is required to address the control of covariates, a concern that is particularly relevant given the observational nature common to epidemiologic studies. In addition to framing analyses within an epidemiologic framework, additional considerations pertinent to multi-dimensional datasets are also relevant to metabolomics analyses. For instance, co-metabolites may be collinear, complicating the ability to disentangle the effect of a specific metabolite. Co-metabolites may act in synergistic or antagonistic ways, such that an adverse effect is elicited in combination even when no adverse effect is observable due to individual metabolites. Furthermore, the complex relationship among metabolites may translate into nonlinear, non-additive associations with outcomes of interest.

Existing statistical approaches to evaluate metabolomics range from traditional univariate analyses [6] to more complex multivariate methods that consider multiple analytes simultaneously (Table 1, adapted from [7]). These approaches are unambiguously useful in a variety of contexts, but are each constrained in their utility in observational epidemiological studies. Standard regression approaches to high-dimensional data can highlight individual analytes of interest, for example, but typically require adjustments for multiple comparisons, e.g. false discovery rate (FDR), which penalize model sensitivity. Further, this reductionist approach misses the important aforementioned contextual information by failing to take into account the composite presence of co-analytes. Alternative dimensionality-reduction approaches, e.g. exploratory factor analysis (EFA) or partial least squares (PLS), can alleviate the multiple testing burden of traditional univariate approaches but are limited in their capacity to adjust for relevant covariates, which in the context of population-wide studies may introduce confounding or require unwanted stratification. Identifying relevant metabolites among collinear metabolites is facilitated by features selection methods, such as least absolute shrinkage and selection operator (LASSO), while mixture modeling methods, such as weighted quantile sum (WQS) regression analysis, can reveal combinatorial mixture effects. Both are easily implemented in a regression-based framework, facilitating interpretation, however, neither is well suited to model complex nonlinear, non-additive relationships. Other machine learning methods, including Random Forest and Bayesian Kernel Machine Regression (BKMR), can more flexible model associations with outcomes of interest but may not be as easily interpretable. Finally, rather than modeling the analytes, latent class analysis (LCA) and related methods focus on distinguishing subgroups of individuals based on the analyte data. The relationship of these classes to outcomes of interest can then provide insight into at-risk analyte profiles. Given these varying properties across methods, the selection of an analytic strategy should be motivated by the research question of interest.

Table 1.

Analytic Strategies for Evaluating Metabolomics Data in Epidemiologic Studies^*

Question	Methods	Challenges
Which analytes are best for development of biomarkers of effect or exposure?	Shrinkage methods (e.g., LASSO, elastic net) Semi-Bayesian shrinkage methods [32] Tree-based methods (e.g., Random Forest) Environment-wide association study (EWAS) [33]	Ability to address confounding among co-analytes. Discerning individual effects among highly collinear analytes Detection of relevant analytes given stringent multiple comparison adjustments [EWAS]
What are the interactions between analytes?	Generalized linear models (GLMs)with product interaction terms	Sufficient statistical power to detect interaction Interpretability of effect size estimates Degree of interaction to estimate (i.e., 2-way or higher order) [GLMs]
Is there a mixture effect (i.e., a cumulative pattern of association)?	Toxic equivalency (TEQ) summary measures [34] Weighted quantile sum (WQS) regression [17]	Verifying assumption of additivity between individual components [WQS/TEQ] Availability of information of toxicity to create biologically weighted summary measures [TEQ]
Can the metabolome be summarized via dimensionality-reduction techniques?	Exploratory Factor Analysis (EFA) Principal components Analysis (PCA) Partial least squares discriminant analysis (PLS-DA)	Interpretation of factors/components from variable loadings complicated as dimensionality of datasets increase Consideration of covariates in extraction of factors/components/phenotypes
Are there susceptible subgroups within the population?	Latent Class/Profile Analyses (LCA/LPA)	Consideration of covariates in extraction of profiles
Does the metabolome predict disease status or health phenotype?	Artificial Neural Networks / Deep Learning Machine Learning (e.g., LASSO, support vector machine (SVM), Random Forest, gradient boosting)	Inference with respect to individual metabolites given “black box” nature of machine/deep learning methods
What metabolic pathways are affected in the observed association?	Pathway Enrichment Analysis following network based (WGCNA) or clustering-based (k-means clustering) summaries of metabolomics data	Existing experimental data that inform curated datasets (e.g., KEGG) used to infer functional pathways may be incomplete representation of biologic pathways Potential biased representation in the annotation of pathways

^*adapted from [7]

The recognition for the need to develop methods that incorporate ‘omics-scale analyses in epidemiologic studies is underscored by recent initiatives, including the Children’s Health Exposure Analysis Resource (CHEAR) established by the National Institute of Environmental Health Sciences (NIEHS), which provides standardized laboratory protocols and analytic strategies to conduct exposomic assessments in relation to children’s environmental health [8].

Herein, we leverage CHEAR to evaluate methodologies assessing associations between metabolic profiles ascertained in cord blood serum samples using a targeted NMR-based approach and two continuous anthropometric measures assessed at birth, birthweight and head circumference, in a population-wide study. Our approach included applications of standard and novel methods in order to demonstrate analytical services provided through CHEAR and highlight novel approaches that may be advantageous in modeling metabolomics data in environmental epidemiological contexts.

Methods:

Study Population.

(n=199). Women residing in the Sirajdikhan and Pabna Upazilas in Bangladesh were recruited during pregnancy, as previously described [9]. All recruited participants provided written informed consent. The study was approved by the Human Research Committees at the Harvard School of Public Health (HSPH) and Dhaka Community Hospital (DCH). The study population is a representative subset of the total cohort (n=1089) that was selected based on the availability of environmental data ascertained in cord blood samples.

Sample Collection.

Umbilical cord blood was collected at the time of delivery using EDTA-coated vacutainer tubes (B.D. Scientific, Franklin Lakes, NJ, USA). The samples remained at room temperature for 20–30 minutes, centrifuged at 1200 RPM for 12 minutes, and serum was dispensed into 5mL cryogenic vials. Serum samples were transferred on ice to a −80C freezer at DCH. Serum samples were shipped to HSPH on dry ice and stored at −80°C. For the current NMR analysis, serum samples were shipped from HSPH to RTI International on dry ice.

¹H-Nuclear Magnetic Resonance (¹H NMR).

Cord blood serum sample preparation, data acquisition, and concentration determination of metabolites were conducted at RTI International and followed procedures previously described[10]. Briefly, samples were thawed on ice and 150 μL were transferred to labeled tubes where they were mixed with 100 μL of NMR 0.9% saline solution containing 2.5 mM formate. Sample tubes were vortexed for 4 min and centrifuged at 16,000 rcf for 4 min. A volume of 225 μL was taken from each sample supernatant and transferred into 3mm NMR tubes.

In addition to acquiring data for the individual study samples, quality control pools (QC pools) were created. Study samples were randomly assigned to one of two pools - Pool 1 or Pool 2. An aliquot of 15 μL of each study sample was added to create their corresponding pool. A 150 μL aliquot was taken from each pool to make a total of 20 QC pools. In addition, nine pools were created from the CHEAR reference material samples, and were aliquoted and processed along with the study samples and QC pools. QC and CHEAR pool aliquots were processed identically to the study samples, as described above.

¹H NMR spectra of study samples and QC pools were acquired on a Bruker Avance III 600 MHz NMR spectrometer (located at David H Murdock Research Institute, Kannapolis, NC, USA) using a 5 mm cryogenically cooled ATMA inverse probe and ambient temperature of 25°C. A 1D CPMG presaturation pulse sequence (cpmgpr1d) was used for data acquisition. For each sample 128 transients were collected into 64k data points using a spectral width of 12.0 ppm, 2s relaxation delay, and an acquisition time of 4.5 s per FID. The water resonance was suppressed using resonance irradiation during the relaxation delay. NMR spectra were processed using TopSpin 3.5 software (Bruker-Biospin, Germany). Spectra were zero filled, and Fourier transformed after exponential multiplication with line broadening factor of 0.5. Phase and baseline of the spectra were manually corrected for each spectrum. Spectra were referenced internally to the formate signal (8.45 ppm). The quality of each NMR spectrum was assessed for the level of noise and alignment of identified markers. Spectra were assessed for missing data and underwent quality checks.

Unsupervised multivariate statistics (PCA) was used to demonstrate that the QC Pools were tightly clustered and in the center of the samples from which they were derived (Supplementary Figure 1). The Chenomx NMR Suite 8.1 Professional (Chenomx, Edmonton, Alberta, Canada) software was utilize to match NMR signals to metabolites (https://www.chenomx.com/wp-content/uploads/2016/01/Compound-listing.pdf) and to determine the relative concentrations of metabolites relative to 1 mM formate. NMR data are hosted at the CHEAR Data Center Repository (https://cheardatacenter.mssm.edu/).

Statistical Analysis.

Data pre-processing:

The NMR data were restricted to metabolites annotated in the Reference Sequence database [11] (n=50) with detectable levels in more than 50% samples, leaving a total of 39 metabolites in the analysis. Four samples were considered outliers and removed based on Hotelling’s T-squared statistics (p<10⁻⁵). An additional sample with incomplete covariate information was removed, leaving a sample size of 194 subjects. The data was log₂ transformed, centered and scaled.

Single Metabolite models:

Simple linear models, following the equation $y= {\beta }_0+ {\beta }_1{X}_1\dots + {\beta }_z{X}_z$, were initially used to test for associations between individual metabolites and health outcomes, where y was a given anthropometry measure, β_o was the model intercept, β₁X₁ corresponds to a given metabolite’s parameter estimate and concentration, and β_zX _z corresponds to covariates and associated parameter estimates. P-values for metabolite parameters were adjusted for false-discovery rates (FDR) to correct for multiple comparisons.

LASSO.

We reduced the multiple comparisons issue of the single metabolite models and enhanced the model interpretability with a bootstrap least absolute shrinkage and selection operator (LASSO) approach [12–14]. This approach, as in the single metabolite analysis, assumes linearity between each metabolite and the outcome, but also assumes additivity among metabolites. This approach complemented the results from the single metabolite models, showing the significant metabolites after adjusting for all others. We extracted the residuals from linear regression models of each response variable (birthweight/head-circumference) against all considered epidemiological covariates. Covariate-adjusted outcome variables were computed, adding the mean of each outcome variable to the residuals of the corresponding regression. Finally we implemented LASSO using the R-package HCDI, specifying the covariate-adjusted outcomes as dependent variables and all metabolites as predictors in the LASSO models. This approach selected a small subset of metabolites that exhibited an effect on each outcome (birth weight/head circumference), taking into account of the complex correlation structure of metabolites. We finally enhanced the consistency of the results, computing 95% confidence intervals (95% CI) for each estimate with 1,000 bootstraps. The tuning LASSO parameter, controlling for the amount of regularization applied to the estimate, was selected by 5-fold Cross Validation on the LASSO procedure. We validated the robustness of this approach with changes of seed specification.

Random Forest.

To explore non-linear relationships between the metabolites and the outcome, we used the random forest (RF) algorithm, which is an ensemble learning technique that combines random decision trees with bootstrap aggregating for classification and regression (Breiman 2001). We used the R package randomForest [15] to implement the RF algorithm for covariate-adjusted outcome variables (birth weight: 1,000 trees, 3 variables sampled at each split, 55% of sample drawn, and maximum terminal node size of 7; head circumference: 1,000 trees, 6 variables sampled at each split, 80% of sample drawn, and maximum terminal node size of 7). RF parameters were selected based on the lowest out-of-bag root mean square error (OOB-RMSE) from RFs grown from a range of values for mtry (number of variables sampled at each split: 3, 4, 5, and 6), nodesize (maximum size of terminal nodes: 3, 5, 7, and 9), and sampsize (size of samples to draw: 55%, 63.2%, 70%, and 80% of sample). We determined feature significance using the Altmann algorithm with the R package vita, which calculates feature p-values by comparing the original variable importance measures (VIMs) against VIMs obtained from RFs grown with random permutations of the outcome variables (500 permutations) [16].

Weighted Quantile Sum (WQS_RS) Regression.

Weighted Quantile Sum (WQS) regression [17], generally, is a modeling strategy for “mixtures analyses”, wherein high-dimensional predictor sets are accommodated in a traditional regression framework through the construction of an empirically-estimated weighted index. The variant of WQS applied here, WQS_RS[18], utilizes a random subset ensemble strategy during the estimation of variable weights used to construct the WQS index. In contrast to other implementations of WQS[19–21], which rely on a bootstrap ensemble method, the use of a random subset ensemble in WQS_RS was recently shown[18] to be both sensitive and specific to the detection of metabolite-specific effects in the context of high-dimensional datasets, particularly metabolomic data, and for that reason WQS_RS was used in this study. In the implementation of this method, predictors (i.e., analyte concentrations) are scored into quantiles (e.g., quartiles) to diminish the impact of influential observations, and associated parameters are estimated using ensemble techniques associated with bootstrap or random variable subsets. The WQS index is then constructed by averaging the weight parameters estimated for each variable across the ensemble procedure with the quantiled abundance for each subject, such that $WQS=\sum _{j=1}^c{\overline{w}}_j{q}_j$. The high-dimensional matrix of predictors associated with each subject is thus reduced to a single index value (per subject), which can be tested in a traditional generalized linear framework, using the link function g(.), given by

$$g(\mu )={\beta }_0+{\beta }_{1}WQS+{\mathbf{\text{z}}}^{\prime }\mathbf{\text{φ}}$$ (1)

The significance of the WQS term thus provides an overall test for the significance of the analyte set as it relates to the health outcome, and the per-variable weights estimated in the ensemble steps provides a direct measure of analyte importance. In the current analysis, predictors were deciled then randomly divided into training and validation sets, with 40% of data (N=88) used for training and 60% (N=108) used for validation. During the ensemble random subset procedure used for parameter estimation, 1000 random sets comprised of size 6 randomly-selected metabolites were used in each subset, as per Curtin et al [18]. Each of 39 metabolites was included in an average of 154 analyses (SD=11, min=133, max=180).

Exploratory Factor Analysis (EFA).

Exploratory Factor Analysis facilitates reduction of a large set of predictors into a smaller set of summary variables[22]. EFA was conducted using the minimum residual method and oblimin factor rotation implemented by the psych R package [23]. The number of factors to retain in the analysis (n=5) was determined based on evaluating eigenvalues against successive number of components in the observed data compared to a random matrix of the same size. Factor scores were estimated based on the tenBerge method[24]. Covariate-adjusted generalized linear models were run to assess the association between each of the 5 factors and each response variable (birthweight/head circumference).

Latent Class Analysis (LCA):

Latent class analysis (LCA) was used to identify metabolic profiles, and assign each subject to a given profile type. This method, implemented in PROC LCA (SAS v9.4), calculates class membership probabilities to characterize each subjects’ likelihood of belong to a pre-specified class, and provides item-response probabilities, to describe the likelihood of each class responding at a given item. In the context of this study, item responses consisted of the ranked (quintile) concentration for each metabolite; thus, each class is characterized according to its relative abundance for each metabolite to create an overall profile. Class membership was then used as a predictor of anthropometry measures to determine if metabolic profiles relate to infant growth.

All models assessing associations with outcomes of interest considered maternal body mass index (BMI), gestational age at birth, maternal education, maternal age, infant gender and parity as confounding variables. Specifically for the EFA and LCA models, factors were extracted agnostic to any covariates (unsupervised), followed by inclusion of selected confounding variables in regression models testing the association between the extracted factors and the outcome of interest. For the LASSO and Random Forest models, selected confounding variables were regressed out of the data to generate a residual matrix that served as the input for the respective models. Gestational age demonstrated a nonlinear association with the outcome of interest and, to allow this flexible non-linear association with outcome, it was subsequently modeled using cubic splines with the spline R package. Univariate, WQS and LCA analyses were conducted using SAS (v9.4). Random Forest, LASSO and EFA were conducted using R version 3.4.1. Code used in the implementation of these models is available at https://github.com/CHEAR-Metabolomics/Christiani_NMR_Analysis.

Results

Demographic characteristics of the study population are shown in Table 2. Average maternal BMI and maternal age tended to be lower than typically reported in Western populations [25] but in range for demographic characteristics reported in comparable cohorts in Bangladesh [26].The distributions of detected metabolite levels, ranging from lactic acid (mean = 1100.9 umol/L) to isopropyl alcohol (mean=7.7 umol/L), are shown in Figure 1. Extensive correlations were observed across the analyzed metabolites, particularly among metabolites involved in common molecular pathways (Supplementary Figure 2). For example, glucose was inversely correlated with its metabolite, pyruvic acid. Similarly, the branched chain amino acids, leucine, isoleucine and valine, were highly correlated, as were the organic acids, lactic acid, acetic acid and succinic acid.

Table 2.

Demographic characteristics of the study population (n=199)

Variables	Mean (min,max)
Birth weight (z-score)	2.9 (1.7, 3.5)
Birth length	45.7 (33.0, 64.0)
Head circumference	32.5 (28.0, 36.0)
Gestational age (weeks)	38.3 (33.0, 41.0)
Maternal age (years)	23.1 (18.0, 35.0)
Maternal BMI (kg/m2)	20.5 (15.0, 33.3)
	N (%)
Infant Gender
Female (1)	92 (46.2)
Male (0)	107 (53.8)
Maternal Education
0	38 (19.0)
1	60 (30.2)
2	101 (50.8)
Parity
0	88 (44.3)
1	111 (55.7)

Figure 1. Distribution of metabolite levels (umol/L).

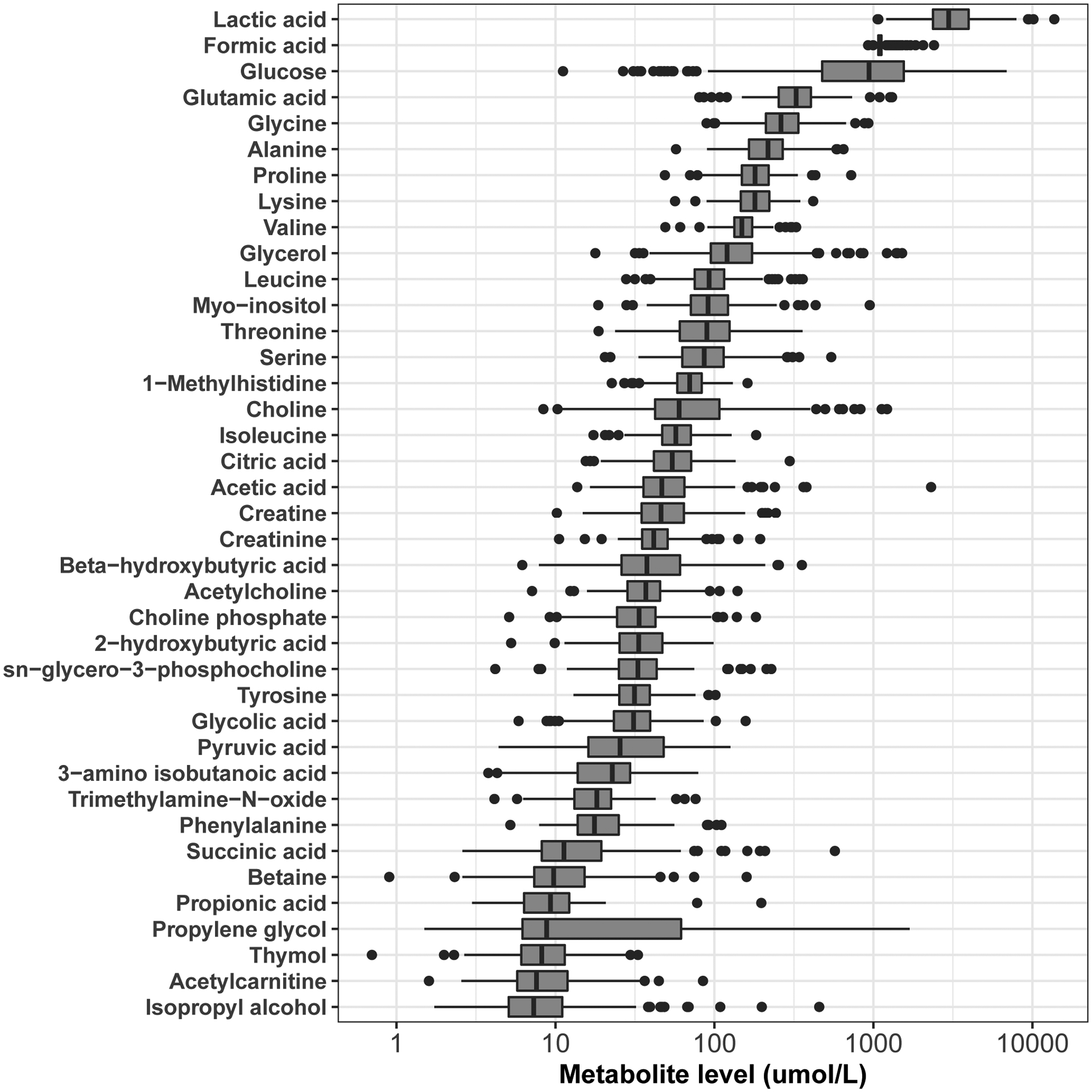
Lactic acid and Isopropyl alcohol were among the most and least abundant metabolites detected, respectively.

Single-metabolite models:

We tested for covariate-adjusted associations between single metabolites and birth outcomes in univariate models. In exploratory analyses conducted without adjustment for multiple comparisons, we found significant negative associations between birthweight and sn-glycero-3-phosphocholine, glycerol, citric acid, leucine, and glycine; however, following adjustment by false-discovery rate (FDR), these associations were no longer statistically significant (Supplementary Table 1). Similar patterns were apparent in our analysis of head circumference with a number of negatively-associated metabolites, including pyruvic acid, trimethylamine-N-oxide, acetylcholine, threonine, alanine, and citric acid. Although these associations did not survive adjustment for multiple comparisons, pyruvic acid and trimethylamine-N-oxide might be considered a noteworthy trend, with FDR-adjusted p-values of 0.08 (Supplementary Table 2).

LASSO:

We identified two metabolites negatively associated with covariate-adjusted birthweight, glycine (β= −0.01 (−0.03, −0.01)) and sn-glycero-3-phosphocholine (β =−0.02 (−0.04, −0.01)), Figure 2A). We additionally identified that covariate-adjusted head-circumference was negatively associated with pyruvic acid (β =−0.1 (−0.22, −0.04)) and threonine (β =0.08 (−0.16, −0.05)) and trimethylamine-N-oxide(β =−0.08 (−0.18, −0.02)) and positively associated with acetylcholine (β =0.05 (0.05,0.12)) (Figure 2B). All results were robust to changes in seed specification.

Figure 2. LASSO-derived associations for (A) birth weight and (B) head circumference.

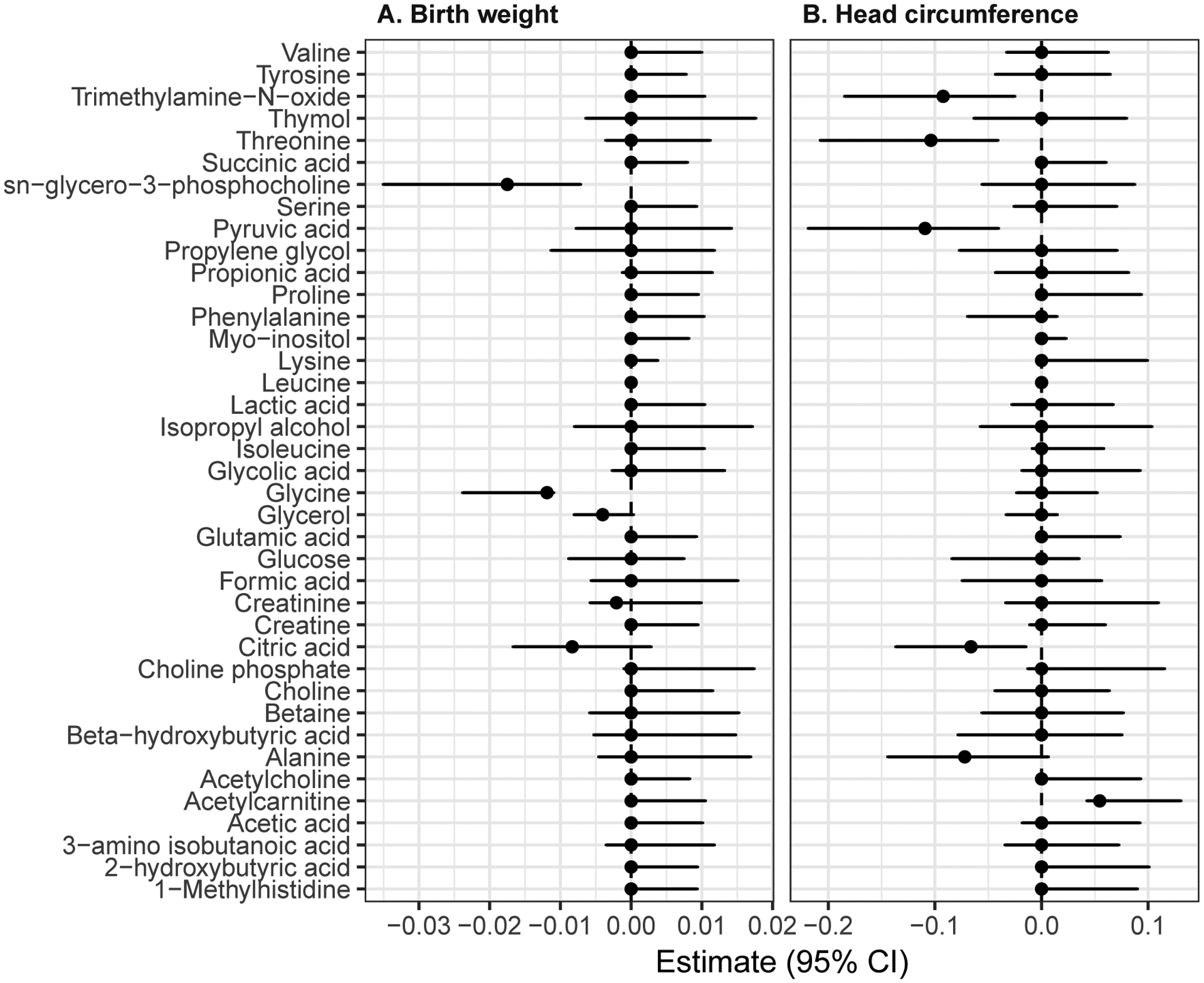
Estimated association and 95% Confidence Interval (95% CI) (X-axis) between 1-Standard Deviation (SD) change of each metabolite (Y-axis) with birthweight (panel A) and head circumference (panel B).

Random Forest:

The Altmann algorithm selected sn-glycero-3-phosphocholine (p=0.04) as a significant predictor of birthweight (Figure 3), which was negatively associated with birthweight in single-metabolite models. We also identified several significant predictors of head circumference with negative associations, including alanine (p=0.04) and trimethylamine-N-oxide (p=0.04) (Figure 3).

Figure 3. Random forest variable importance plots for (A) birth weight and (B) head circumference datasets.

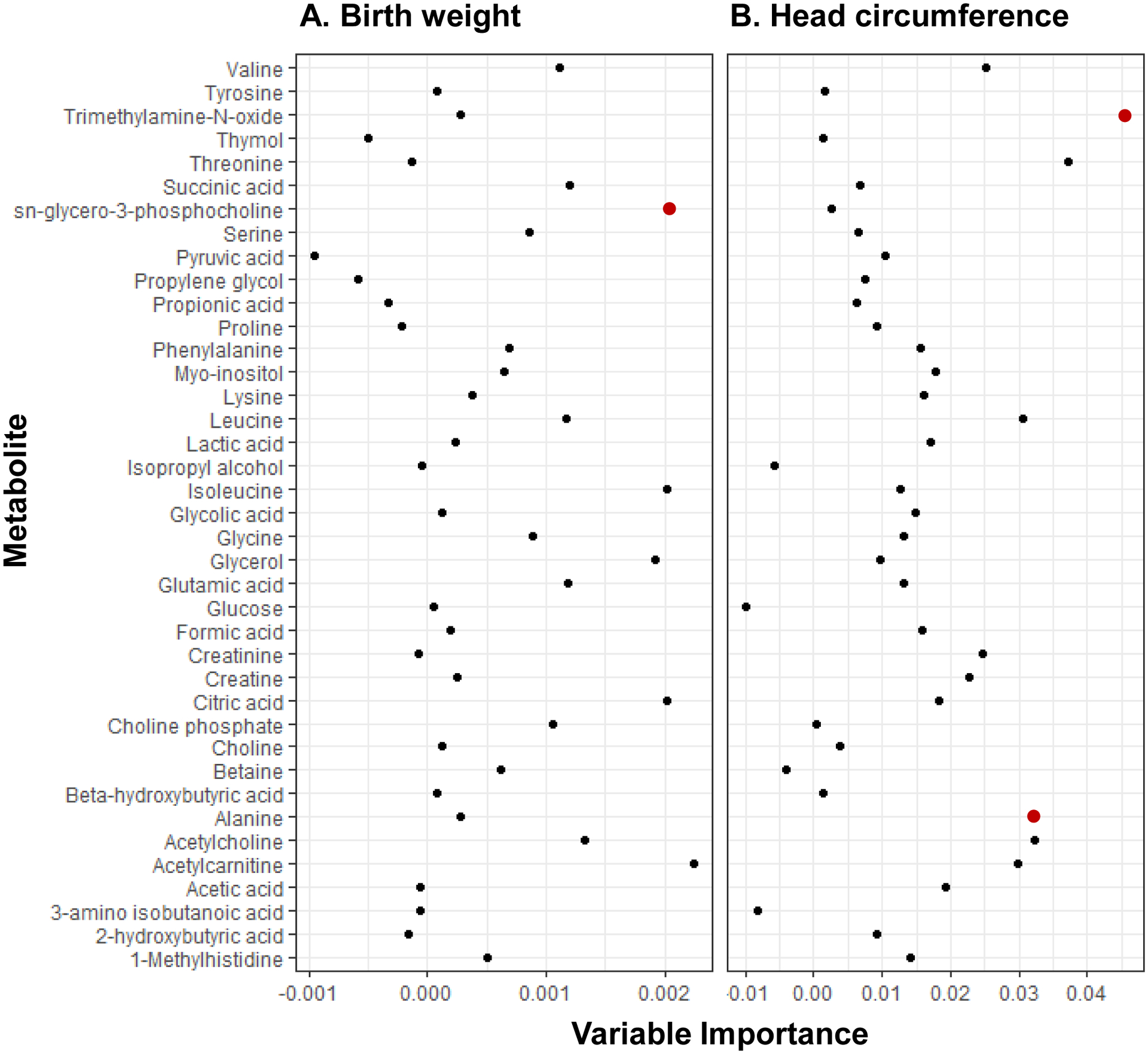
Points in blue and red represent metabolites associated with birth outcomes at p<0.10 and p<0.05 thresholds, respectively.

WQS:

The LOESS (locally estimated scatterplot smoothing) associations between anthropomorphic outcomes and the WQS indices in both training and validation datasets are shown in Figure 4. Significant negative associations were observed in validation datasets between WQS indices and birthweight (p=0.03) and head circumference analyses (p=0.01). Main contributors (>5%) to the birthweight WQS index include citric acid, formic acid, acetic acid, and leucine (Supplementary Table 3). Main contributors to the head circumference WQS index include pyruvic acid, phenylalanine, threonine, acetylcholine, alanine, acetic acid and formic acid (Supplementary Table 4).

Figure 4.

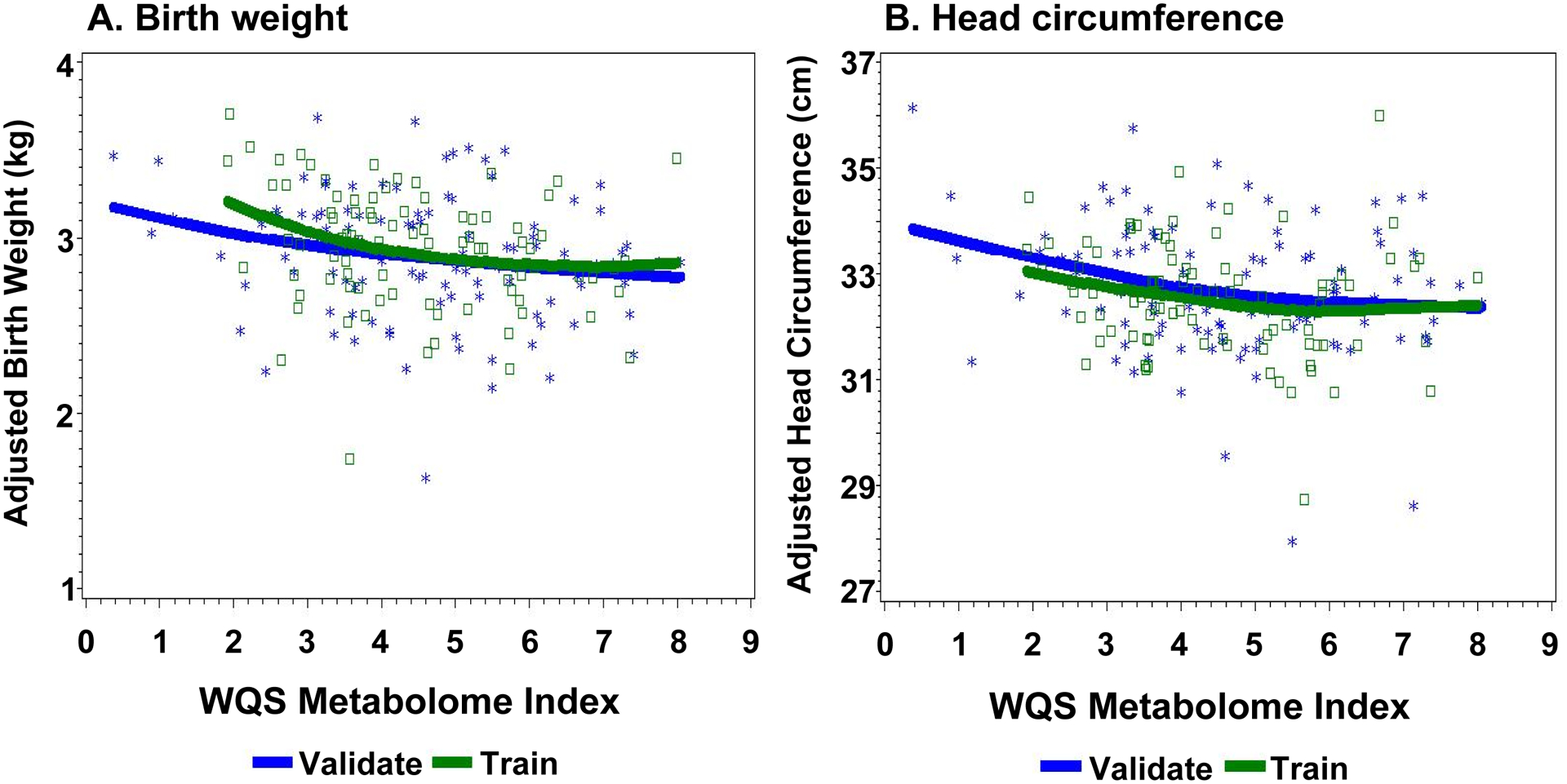
LOESS of association between WQS (training and validation) across (A) birth weight (p=0.018) and (B) head circumference.

EFA:

The loadings of the identified factors (Supplementary Figure 3) largely align with the correlation patterns observed in the data. Two metabolites, betahydroxybutyric acid and 3-amino isobutanoic acid, did not meaningfully contribute to any of the extracted factors (factor loadings <0.2). A negative association (p=0.03) was observed between EFA factor 1 (succinic acid, glycerol, choline, myoinositol, acetic acid, acetylcarnitine, creatine, citric acid, lactic acid, betaine, phenylalanine, serine and sn-glycero-3-phosphocholine) and birthweight in the covariate-adjusted model (Figure 5A). A borderline negative association (p=0.05) was also observed between EFA factor 4 (formic acid, trimethylamine-N-oxide and choline phosphate) and head circumference (Figure 5B).

Figure 5.

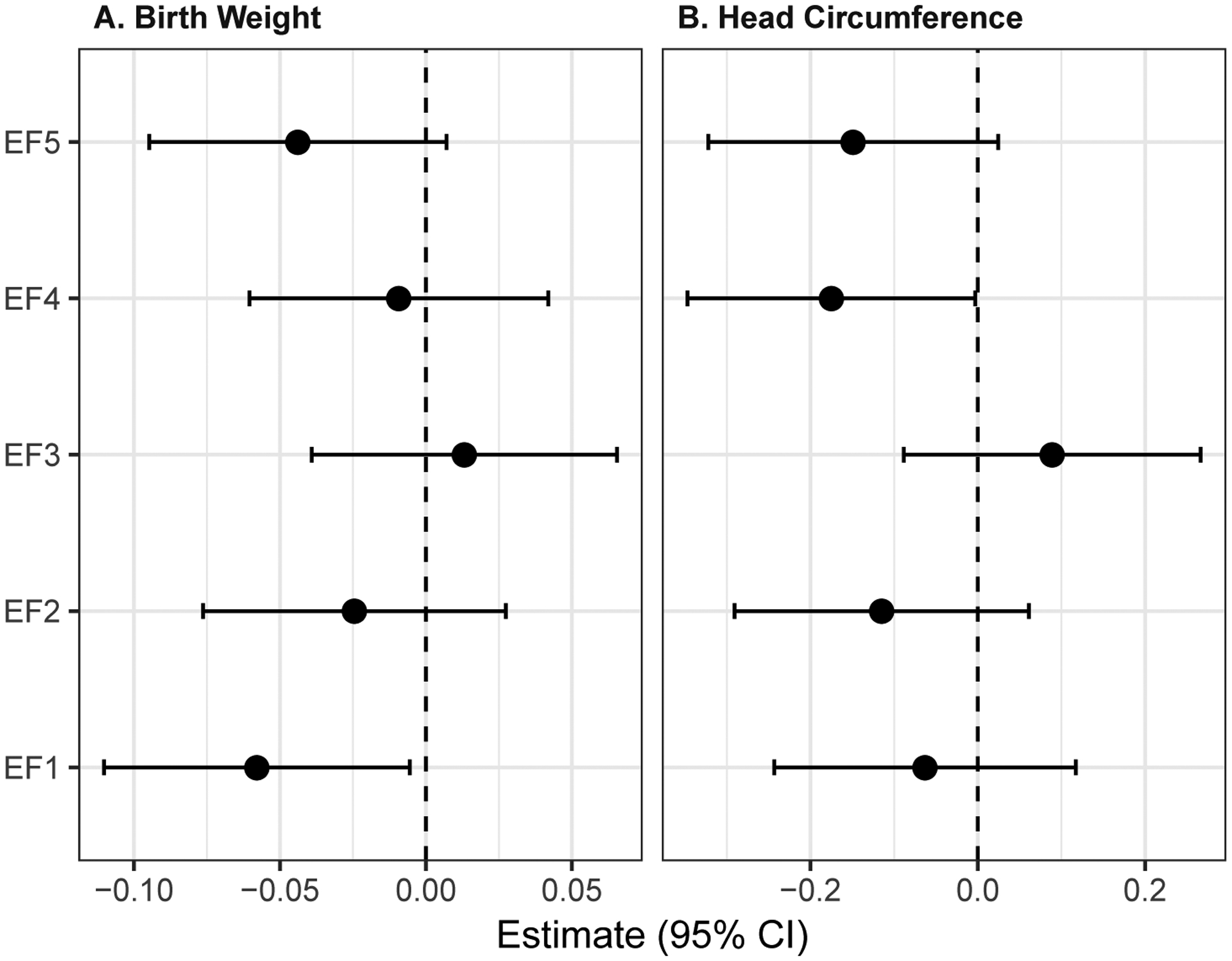
Generalized Linear Models associations between EFA-derived metabolite factors and (A) birth weight and (B) head circumference.

Latent Class Analysis:

Model fit indices indicated a three-class model provided the best fit to these data. Item response profiles, shown in Figure 6, indicate these profiles roughly corresponded to a general profile of low, intermediate, and high exposures. The top panel of Figure 6, showing the likelihood of class members having a per-metabolite exposure in the first quantile, indicates one group (green line) substantially more likely to exhibit low metabolite concentrations. Similarly, the bottom panel of Figure 6, showing likelihood of group members to exhibit per-metabolite concentrations in the highest quintile, indicates another group (red line) is most likely to be represented. The middle panel of Figure 6 shows the third group (blue line) is most likely to be represented with exposures in the third concentration quantile, i.e. a “median abundance” group. These response profiles thus generally discriminate between groupings roughly corresponding to metabolite abundance, but some noticeable exceptions were observed. The “low abundance” group (Figure 6, green line), for example, tended to conversely exhibit high abundance of formic acid and glucose; the “high exposure” group, in contrast, had low abundance of these features.

Figure 6. Item response likelihood for latent metabolomics classes.

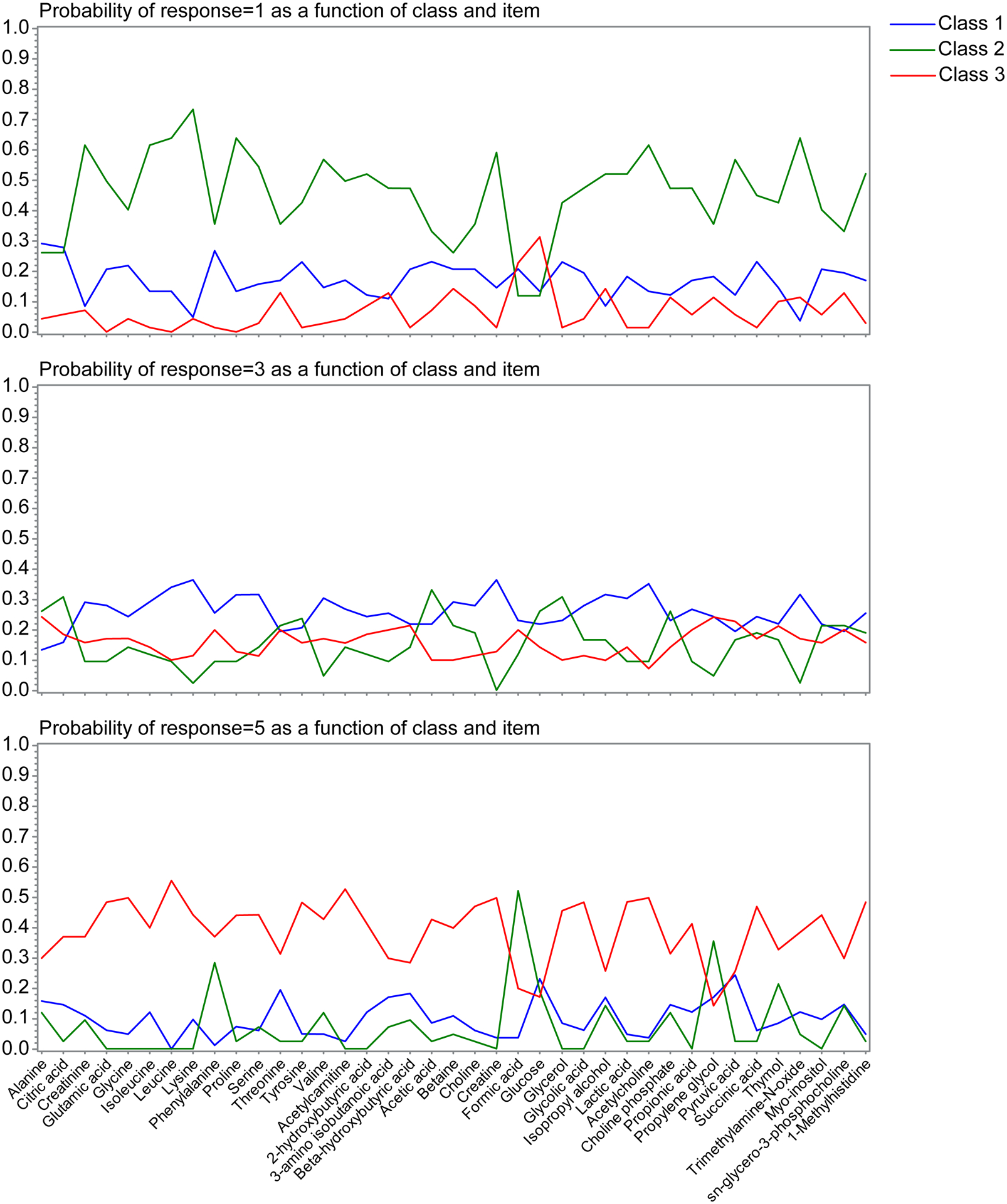
Plots show the likelihood that subjects assigned to varying latent classes (blue, green, red lines) would exhibit concentrations of a given metabolite in the lowest quintile (top plot), third quintile (middle plot), or highest quintile (bottom plot).

To determine the relevance of these profiles to measures of birth anthropometry, we included group membership in an adjusted linear model. We found significant differences in birth weight across metabolomics profiles, with the mid-abundance (p=0.02) and low-abundance (p=0.06) groups exhibiting higher birthweights than the high-abundance groups. Supplementary Table 5 provides full details on parameter estimates in the associated model. Similar models found no significant differences between head circumference and between LCA-derived metabolomics class assignment.

Discussion:

In this study, we applied multiple analytic strategies to identify cord blood serum metabolites associated with birth weight and head circumference using a targeted metabolomics platform. The implemented methods showcase strategies that can be implemented to take the multidimensional nature of metabolomics datasets into account within an epidemiologic framework, each providing context-specific insights.

Environment-wide association studies, which test the associations between individual analytes and outcomes of interest, employ an analytic framework that is widely implemented across ‘omics studies (e.g., genome-wide association studies (GWAS)) and provides outputs that are readily interpretable and easily developed into clinically-relevant biomarkers. However, these studies test the independent effect of individual metabolites without taking into account the presence of co-analytes. Associations with the outcome of interest may vary depending on this metabolomic context, informed by the interrelationships across the metabolites. Co-analytes, particularly those arising from a common metabolic pathway, are also often collinear. Additionally, the detection of relevant metabolites is hampered by the heavy burden of surviving multiple testing adjustments, as highlighted by our single metabolite analysis where no associations surpassed FDR correction.

Tree-based methods, such as Random Forest and LASSO, facilitate identifying relevant features in the presence of collinear analytes. While Random Forest more flexibly allows for nonlinear relationships, LASSO is implemented within a linear model framework, allowing confidence interval estimation. Feature selection is also more easily realized through LASSO. This is a particularly attractive feature in the development of diagnostic/prognostic biomarkers from ‘omics scale data, as this facilitates the identification of a small set of predictive markers that can be screened in a population-based setting. Both methods identified sn-glycero-3-phosphocholine and trimethylamine-N-oxide as relevant metabolites in relation to birth weight and head circumference, respectively. Additional metabolites identified in relation to the assessed outcomes using Random Forest may suggest potential nonlinear relationships that were not captured through the LASSO implementation.

Similar to LASSO, WQS enables simultaneous modeling of all co-analytes within a regression framework. However, unlike feature selection methods, in WQS, the weighted analytes are combined into a unified index that provides additional insight into mixed composition effects on outcomes of interest. Additionally, in contrast to LASSO and Random Forest, in instances where multiple correlated features are associated with an outcome, the ensembling procedure implemented in WQS facilitates retaining information on these correlated metabolites in informing the generated WQS index. Hence, while some major contributors to the WQS indices were also identified in the other evaluated methods (e.g., glycerol (birth weight), glycine (birth weight), pyruvic acid (head circumference), threonine (head circumference) and acetylcholine (head circumference)), other identified major contributors were unique to the WQS index (e.g., leucine (birth weight) and acetic acid (head circumference)). Differences in scaling across methods may also contribute to differences in findings. In binning metabolites into quantiles, WQS is less sensitive to the influence of extreme observations. However, if associations with an outcome are driven by variability within upper quantiles, the averaging effect of quantiling may lead to a loss in resolution to detect such associations.

In contrast to the aforementioned methods implemented in the current study, EFA is an unsupervised method that attempts to resolve the underlying structure within the dataset. Here it is assumed that unobserved latent factors drive the variability among the measured set of metabolites. The uncovered factors are, therefore, summary variables representative of the larger set of measured features. In our study, for example, the 39 analyzed metabolites were captured by 5 underlying factors. In addition to dimension reduction, feature loadings within factors can reveal synergistic relationships. Accordingly, the birth weight-associated EFA factor included sn-glycero-3-phosphocholine, a metabolite that was also identified by a number of other methods evaluated in this study. Additional correlated metabolites (e.g., glycerol and citric acid) also loaded onto this factor, potentially providing additional insight to the involvement of a specific metabolic pathway. However, in instances where a large number of metabolites load onto factors, as in the birth weight-associated factor identified in the current study, there is insufficient resolution to tease out which among the correlated metabolites may be driving the observed association.

The latent class analysis (LCA) applied in this study was generally intended to differentiate between metabolomics profiles rather than the abundance of individual features; in doing so, we differentiated three general classes of response profiles and found these were associated with birthweight. These findings were nonetheless informative toward differentiating relevant metabolites, as two metabolites we found key to differentiating response profiles, glucose and formic acid, are each critical to healthy metabolic function. More generally, this approach may prove a relevant tool in using metabolomics data to classify subject/patient “types” according to their metabolic profiles.

Notable limitations in our study warrant caution in the interpretation of the reported findings. Given the cross-sectional study design, we are unable to resolve the directionality of the observed associations. While on par with other cord blood metabolomics studies [29–31], the limited sample size of our study likely impacts the generalizability of our findings. The analysis implemented in the current study were based on concentrations derived from a targeted panel of metabolites. This interrogated set of metabolites likely captures markers of an internal biologic response to environmental exposures as opposed to direct markers of exogenous sources of exposures that are additionally captured in untargeted metabolomics analyses. In addition, the number of assayed features in the current study entails a smaller scale of features compared to data generated by untargeted platforms. However, despite the differences in dimension, the pitfalls raised in the current study are still relevant and applicable to studies capturing a broader spectrum of the exposome. The current study addresses strategies and considerations, notably dimension reduction, the presence of collinearity and consideration of confounding variables, through the application of both known and novel methods to delineate metabolomic features that distinguish health outcomes in a population health setting.