Economic Aspects of Disease Monitoring with Special Reference to Bovine Paratuberculosis

Abstract

Monte Carlo simulation models were used to evaluate the feasibility and potential results of a proposed national survey of the prevalence of bovine paratuberculosis (PTB) in dairy herds in Norway. The expected herd prevalence was assumed to be 0.2% in the simulations. Infected herds were classified as detected if 1 animal was sero-positive. With a sample size of 6000 herds at least 1 truly infected herd was detected in 99% of the iterations. The low sensitivity of the ELISA test, the assumed low herd prevalence, the typical low within-herd prevalence of PTB and the small herd sizes in Norway all present problems in detection of the disease. The results showed that the ratio between false-positive herds and true positive herds detected had a median of 70:1. At the assumed herd prevalence of 0.2% and a cost/test of 70 NOK the median cost of detecting 1 infected herd was approximately 900,000 NOK. If 2 positive reactors were needed to classify a herd "infected" the median cost of detecting 1 infected herd was 5,055,000 NOK. Our results suggest that a randomized national prevalence survey would not be feasible, due to the low probability of detecting infected herds and because of the high number of false-positive reactions that would be expected.

Introduction

For many years, the Norwegian cattle population was apparently free of paratuberculosis (PTB). PTB was not diagnosed in Norway during the period 1979 through 1996. Because of import restrictions, no cattle were imported between 1987 and 1990. From 1991 through 1997, approximately 1200 predominately beef cattle were imported. In order to prevent the introduction of PTB, all imported cattle were subjected to a 6-month quarantine and required to be negative for PTB on complement-fixation tests and fecal cultures. In 1997, sera from 708 of the surviving imported cattle were tested with a commercial enzyme-linked immunosorbant assay (ELISA) (IDEXX Laboratories, Inc. Westbrook, ME) for antibodies against PTB with 22 sero-positive results. All reacting animals were slaughtered and 6 were confirmed to be infected by culturing Mycobacterium paratuberculosis from organs or feces. Subsequently, the herds with confirmed PTB infections were slaughtered.

At the request of the Norwegian Animal Health Authorities, a series of Monte Carlo simulation models were developed to evaluate the proposed methods and probable outcomes for detecting and eradicating PTB from the imported cattle and any native cattle that might have been infected by the imports. A further objective was to evaluate the feasibility of a national survey to estimate the herd prevalence of PTB in the dairy-cattle population.

This report will describe the models and simulated results for the proposed national dairy survey.

Materials and methods

Herds surveyed

Because there was political pressure to do so and to maintain its PTB-free status, a national survey for PTB in Norway in the dairy cow population had been proposed. Thus, the herds chosen for the simulation were dairy herds. A search of the national data base containing records of all dairy herds that receive state subsidies resulted in 24,218 dairy herds. Herds would be randomly selected from this population for inclusion in the survey.

Herd size

Data from the national register of dairy herds that received subsidies was used to construct a frequency distribution of the herd sizes of the dairy population. Only cows 2 or more years of age were included. A cumulative probability distribution function for the sizes the herds was constructed [20] (Figure 1). The distribution had a range between 1 and 136 cows. The distribution contained 21 classes. Twenty of the classes were of equal size with a difference of 2 between the fewest and most animals in the class. The within-class herd sizes in the these classes were modeled as discrete probability distributions with each herd size within each class having an equal probability (33.34%) of being sampled. These 20 classes (herd sizes 1–60 cows) represented more 99.99% of the herds. The last class consisted of a discrete distribution of 19 herds containing 61–136 animals each. In each iteration of the model, herd sizes (HS) based on these distributions were generated by Latin Hypercube sampling from the herd-size distributions. If more than one infected herd was selected in the model, the size for each herd was generated independently. The individual herd size was used to calculate the number of infected animals in tested herds. All animals greater than 2 years of age in the herds would be tested.

Figure 1.

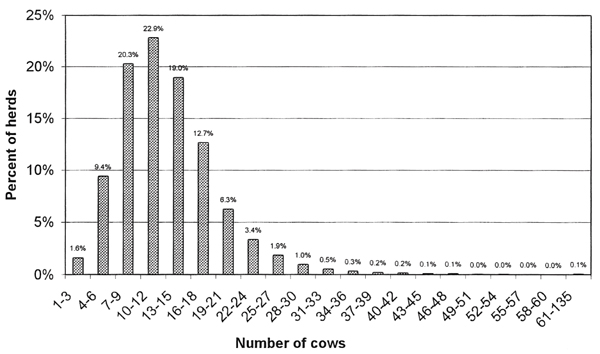
The figure shows the distribution of the number of cows greater than 2 years of age in Norwegian dairy herds.

Number of herds tested (NHT)

The number of herds that were tested in the model was 6000. This number was chosen after trial runs with fewer herds showed that an infected herd would be detected in less than 99% of the iterations.

Herd-level prevalence

A fixed herd-level prevalence (HP) of 0.2% was used in all simulations. This prevalence was chosen because if a country can document that the prevalence of a disease <0.2% with a confidence level of 99%, it can be considered free of that disease [1]. If the Norwegian dairy cattle population is not free of PTB, the prevalence must be very low because no clinical or laboratory diagnoses have been reported in two decades.

Number of infected herds in the population

A binomial distribution will calculate the number of infected herds in n herds based on the probability p that any herd is infected [20]. The number of infected herds in the population (IH) was calculated with a binomial (N, HP) probability distribution function, where N was the 24,218 herds in the dairy population and HP was the herd-level prevalence (0.2%).

Within-herd prevalence

The BetaPERT distribution is a re-scaled version of the Beta distribution that allows the parameters to be estimated from minimum, maximum and most likely values. It is considered the most appropriate distribution for modeling a continuous variable based on expert opinion [20]. The within-herd prevalence (WHP) was modeled as a BetaPERT distribution function with a minimum of 1%, a maximum of 50% and a most likely prevalence of 10%. This distribution was chosen based on the reported within-herd prevalence in several studies [6, 7, 12, 16]. By default, all infected herds had at least 1 infected animal.

ELISA characteristics

[12] emphasized that published estimates of test sensitivity and specificity should be regarded as approximate because they are derived from cattle that may differ from the population of interest. The sensitivity of the ELISA is affected by the stage of the disease (being highest in animals showing clinical signs and shedding the organism). [19] reported a range in sensitivity (SE) of 15% to 87% with an average of 45%. In this study, the sensitivity of the ELISA was modeled with a BetaPERT distribution with a minimum of 15%, a most likely value of 45%, and a maximum of 87%. The specificity (SP) of the ELISA is considered high in comparison to some other diagnostic tests, but it might be of concern if large scale testing is contemplated [12]. The specificity was modeled with a uniform 99.0% to 99.9% distribution.

Number of infected herds tested

The number of infected herds tested (IHT) was calculated with a hypergeometric (NHT, IH, N) distribution function where the number of herds tested (NHT) was 6000. IH was the number of infected herds in the population and N was 24,218 [20].

Number of infected herds detected

The distribution of the number of infected herds detected (NID) was calculated as follows. The size of each infected herd tested was generated, individually, by Latin Hypercube sampling from the herd size distribution. The number of infected animals in each infected herd tested (NIT) was individually calculated with a binomial (HS, WHP). The number of infected animals in each herd that were detected was generated with a binomial (NIT, SE) distribution function where NIT was the number of infected animals tested and SE was the ELISA sensitivity. By default, all infected herds tested had at least 1 infected animal tested. If the number of infected animals detected was greater than 0 then a 1 was generated. The total number of times 1 was generated in each iteration was the total number of infected herds detected. The probability of detecting an infected herd was equal to the percentage of iterations when 1 or more infected herds were detected. Infected herds were classified as detected if 1 or more infected animals were detected by the test in one simulation or if 2 or more infected animals were detected by the test in another simulation. The sensitivity of the ELISA test on a herd basis (HSE) was estimated by dividing the number of infected herds detected in each iteration by the number of infected herds tested in that iteration.

Number of false positive reactions

The distribution of the number of false positive reactions was simulated separately. The number of false positive reactions on a herd basis was calculated with a binomial (HS, 1-SP) distribution function where HS was the number of animals tested. The herd size was generated by Latin Hypercube sampling from the herd size distribution and SP was the ELISA specificity for that iteration. If the number of positive reactions generated was greater than 0 the herd was classified as a false positive herd and a 1 was generated. The percentage of 10,000 iterations when a 1 was generated was the herd false-positive percentage (HFPP). The herd level specificity (HSP) was calculated as 1-HFPP.

Predictive value of the ELISA results

The predictive value of a positive test (PV+) is defined as the proportion of diseased animals among those that test positive [14]. In this model the distribution of the predictive value of a positive herd test (HPV+) was calculated with the formula:

HPV+ = HP*HSE/HP*HSE + 1-HP*1-HSP

where HP was the herd-level prevalence (0.2%), HSE was the distribution of the herd-level sensitivity and HSP was the distribution of herd-level specificity.

The predictive value of a negative test (PV-) is the proportion of non-diseased animals among those that test negative. The distribution of the predictive value of a negative herd test (HPV-) was calculated with the formula:

HPV- = 1-HP*HSP/1-HP*HSP + HP*1-HSE

where HP was the herd-level prevalence (0.2%), HSP was the distribution of herd-level specificity and HSE was the distribution of herd-level sensitivity.

The cost of testing

The cost of testing each sample was set at 70 NOK (1$ = 7.9 NOK). The initial cost (IC) of testing was estimated by:

IC = 6000*12*70

where 6000 was the number of herds tested, 12 was the median herd size and 70 NOK was the cost of each ELISA test. It was assumed that all test positive herds would be re-tested so there would be an additional cost (AC) that was calculated by:

AC = TPH*12*70

where TPH was the number of test positive herds, 12 was the median herd size and 70 was the cost of each ELISA test.

The total cost of testing (TC) was IC+ AC. The distribution of the cost per true positive herd detected (CTP) was calculated by:

CTP = TC/number of infected herds detected.

If no infected herds were detected then CTP = TC.

The simulations

To simulate the sampling and testing for PTB, @Risk software (Version 3.5e, Palisade Corporation, Newfield, NY, USA); a risk-analysis add-in to the Excel spreadsheet of the Microsoft Corporation, Redmond, WA, USA) was used. Preliminary runs of the simulation showed that the outputs changed by <0.5% after approximately 7500 iterations. However, greater precision the simulations were run with 10,000 iterations. The sampling method was Latin Hypercube and Monte Carlo recalculations were used. A list of variables, the distributions and fixed values used in the model are in Table 1.

Table 1.

Description and distribution of input variables for the Paratuberculosis (PTB) survey models.

Variable	Description	Distribution
N	Number of herds	Fixed; 24,218
HP	Prevalence of PTB	Fixed; 0.2%
IH	Number of infected herds	Binomial (N, HP)
NHT	Number of herds tested	Fixed; 6000
IHT	Infected herds tested	Hypergeometric (NHT, IH, N)
HS	Herd size	Cumulative (1, 136)
WHP	Within-herd prevalence	BetaPERT (0.01, 0.10, 0.50)
NIT	Number of infected cows tested	Binomial (HS, WHP); Minimum = 1
SE	Test sensitivity	BetaPERT (0.15, 0.45, 0.87)
NID	Number of infected detected	Binomial(NIT, SE)
HSE	Herd test sensitivity	NID/NIT
SP	Test specificity	Uniform (0.99, 0.999)
HSP	Herd test specificity	1-herd false positive percentage
NIHT	Non-infected herds tested	NHT-IHT
NICT	Non-infected cows tested	NIHT * 12
FP	Number of false positive herd tests	Binomial (NIHT, 1-HSP)
FP:TP	False positive: true positive ratio	ΣNID/FP

Results

Table 2 shows the results when 6000 herds were tested. The results were generated as probability distributions. With an estimated herd prevalence of 0.2%, one would expect to have a minimum of 20, a median of 48 and a maximum of 75 infected herds in the tested model population. The median number of infected herds tested was 12. When testing 12 infected herds, one would expect to detect infection in approximately 6. There was a 99.2% probability that at least 1 infected herd would be detected. Approximately, 72,000 non-infected animals would be tested resulting in a median number of 413 false-positive herd reactions. A median of 70 false-positive reactions for every truly infected herd detected would be expected. The median predictive value of a positive herd test was 0.51% while the median predictive value of a negative herd test was 99.8%. The median cost per infected herd detected was more than 5,05 million NOK.

Table 2.

Outputs of the simulations (10,000 iterations) of the Paratuberculosis survey model with 6000 of 24,218 dairy herds tested.

	Percentiles
Variable	Minimum	5th	50th	95th	Maximum
Number of infected herds in population	20	37	48	60	75
Number of infected herds tested	2	7	12	18	26
Number of animals tested/herd	1	5	12	24	135
Number of infected animals/herd tested	1	1	1	2	10
Number of infected animals/herd detected	0	0	1	1	8
Number of infected herds detected	0	2	6	11	21
Herd sensitivity (1 positive)	0%	18%	50.5%	83%	100%
Herd specificity (1 positive)	91.8%	92.4%	93.0%	93.5%	94.2%
Number of non-infected herds tested	5974	5982	5988	5993	5998
Number of non-infected animals tested	71688	71784	71856	71916	71976
Number of false positive herds	339	381	413	445	486
False positive:true positive ratio	18	36	70	215	486
Predictive value of positive herd test	0.03%	0.14%	0.51%	4.04%	99.5%
Predictive value of negative herd test	99.2%	99.7%	99.8%	99.9%	99.99%
Cost/infected herd detected (NOK)	256,240	488,822	899,791	2,710,965	5,448,500

Discussion

After many years during which the Norwegian cattle population was apparently free of PTB, in 1997 22 of 708 imported animals were sero-positive when tested with an ELISA. All sero-positive animals were slaughtered and 6 animals in 3 herds were confirmed to be infected by culturing organ and/or fecal samples. All confirmed infected animals were imports except 1 offspring of an imported cow. Sero-positive animals were also found in herds with direct or indirect contact with the infected herds [9]. The only evidence of PTB in Norway was confined to beef cattle. However, there had never been a survey determine the prevalence of PTB in the dairy population. Because the severe movement and trade restrictions only affected the beef cattle industry, there was political pressure to determine whether the disease also was present in the native dairy population. Therefore a national survey to confirm the absence of or herd prevalence of PTB in the dairy population was proposed.

Monte Carlo simulation modeling was used to assess the feasibility of the proposed survey. Simulation modeling is an effective tool for evaluating potential programs before committing resources that may be better used elsewhere or in a more effective way.

Herd level and within-herd prevalence greatly influence the outcome of serological surveys. Considering the absence of clinical or laboratory diagnoses, other than in the imported cattle, the prevalence of PTB infected dairy herds in Norway must be very low if not 0%. A herd prevalence of 0.2% was used in the model because to declare a country free of a disease, a survey that will detect 1 or more infected herds at that prevalence with 99% confidence must be done [1]. For this reason, the number of herds tested must be in excess of 4,500 to ensure that infected herds are included in the sample [2]. All animals over 2 years of age in a herd would be tested. However, because of the small herd sizes (model median = 12 cows), the ELISA characteristics and low within-herd prevalence, it is impossible to classify an individual herd as uninfected with an acceptable level of confidence [2, 3]. In the present simulations, in 50% of the iterations the median number of infected animals tested was 1, and 95% of the time the number of infected animals tested was less than or equal to 2. The median number of infected animals detected was 1. From this, one can see that the herd level sensitivity [15, 4] would not be much different from the individual test sensitivity.

One could argue that detecting only about 50% of the potentially infected herds tested is better than detecting none. However, in Norway herds that are diagnosed as PTB infected are placed under severe restrictions regarding animal movements, sales, shared pastures, etc. The potential for false positive reactions due to less than 100% specificity of the ELISA could potentially cause extreme hardship to many dairy farmers. In the simulations the specificity of the ELISA was assumed to follow a uniform distribution with a minimum of 99.0% and a maximum of 99.9%. The mean of this distribution is 99.5%. This might have been an optimistic estimate, because [12] used an array of 95%, 96%, 97%, 98% and 99% to model the ELISA specificity under Australian conditions. If the true herd prevalence of PTB in Norway is about 0.2% and if 6000 herds were tested approximately 5950 of the tested herds would be uninfected. The median herd size in these simulations was 12 animals. Thus, about 71,000 uninfected animals would be tested resulting in a median of 413 false-positive reactions. There would be between 381 and 445 false-positive reactions 95% of the time. The possibility that clustering of false positive reactors might occur was not addressed in this model. The herds with positive reactors (infected or not) would be placed under movement and trade restrictions until the diagnosis could be confirmed or rejected. Confirmation would have to be by some other method (for example, another ELISA, fecal culture, culture of necropsy tissues, or other immunological test) [17–19, 8]. All of these methods have problems with lack of sensitivity, specificity or both and could also result in inconclusive results. Thus, confirming a diagnosis can be very difficult and time consuming.

A common method to compensate for less than 100% specificity is to require more than 1 animal in a herd to test positive before a herd is classified as infected[11, 10, 12, 13]. Requiring more than 1 positive reaction in order to classify a herd as infected in order to reduce the number of false-positive reactors [10, 13] is not a feasible option for Norway. In these simulations, 95% of the time there were fewer than 2 infected animals per herd tested. In 95% of the iterations the number of infected animals per herd that were detected was 1. This would result in a herd-level sensitivity of approximately 5%. However, the herd-level specificity would be approximately 99.7%

Another way to decrease the expected number of false positive reactors would be to decrease the number of herds tested and thus the number of uninfected animals tested. This would also decrease the probability of detecting any truly infected herd. A median of 12.6% of infected herds was detected when 6000 herds were tested, but only 1.8 % if 500 herds were tested. The main reason that the probability of detecting an infected herd is so low is that the median percentage of the total number of infected herds tested would be 4–25% depending on the sample sizes used.

The costs associated with the proposed survey were also analyzed. At 70 NOK per test, the initial cost of testing would be approximately 5 million NOK. In addition, it was assumed that any herds that were classified as sero-positive would be re-tested. If a herd was classified as infected if 1 or more sero-positive animals were found, the median cost of detecting a truly infected herd was approximately 900,000 NOK. If it required 2 or more sero-positive animals to classify a herd as infected, the median cost to detect a truly infected herd was 5.06 million NOK. The costs would be less if the herd prevalence were higher than the 0.2% used in the simulations.

There are good reasons why Norway would like to determine the prevalence of or absence of PTB in the national cattle population. These include the desire to maintain the high health standards in the national herd, the identification of infected herds so that PTB eradication or control could be accomplished, and concerns about a possible relationship between Mycobacterium paratuberculosis and Crohn's disease in humans [5]. However, the results of these simulations suggest that with the available diagnostic methods a national survey to estimate the prevalence of PTB in the national dairy population is not feasible. The results confirm the conclusion of [12] that aggregate (herd) testing is best suited for circumstances where the within herd prevalence is high, where herd size is not a constraint in obtaining adequate sample size, and where the diagnostic test has both high sensitivity and specificity. None of these conditions applies to the conditions for a national prevalence survey for PTB in dairy cattle in Norway.