Abstract
With the expansion of the global novel coronavirus disease (COVID-19) pandemic, unprecedented interventions have been widely implemented in many countries, including China. In view of this scenario, this research aims to explore the effectiveness of population mobility restriction in alleviating epidemic transmission during different stages of the outbreak. Taking Shenzhen, a city with a large immigrant population in China, as a case study, the real-time reproduction number of COVID-19 is estimated by statistical methods to represent the dynamic spatiotemporal transmission pattern of COVID-19. Furthermore, migration data between Shenzhen and other provinces are collected to investigate the impact of nationwide population flow on near-real-time dynamic reproductive numbers. The results show that traffic flow control between populated cities has an inhibitory effect on urban transmission, but this effect is not significant in the late stage of the epidemic spread in China. This finding implies that the government should limit international and domestic population movement starting from the very early stage of the outbreak. This work confirms the effectiveness of travel restriction measures in the face of COVID-19 in China and provides new insight for densely populated cities in imposing intervention measures at various stages of the transmission cycle.
Keywords: Real-time reproduction number, COVID-19, Population mobility, Correlation analysis, Shenzhen
Introduction
Novel coronavirus disease (COVID-19) was first reported in Wuhan, Hubei Province, in December 2019 and then spread rapidly to other parts of China (Chen et al., 2020). COVID-19 is different from previous severe acute respiratory syndrome (SARS) and Middle East respiratory syndrome (MERS), although the three coronavirus infections are usually characterized by fever and cough (Li et al., 2020b). Compared to that of the latter two, the overall case fatality rate of COVID-19 is lower, but the total number of deaths is higher due to the larger number of cases. Because of the high infectivity of COVID-19, the World Health Organization (WHO) defined COVID-19 as a global pandemic on 11 March 2020. With continuously rising numbers of confirmed cases, COVID-19 has become a global health threat (Lau et al., 2020).
As a responsible nation and one of the earliest outbreak areas in the world, China has quickly taken several unprecedented prevention and control measures in response to the spread of this highly infectious disease. Most of China's regions, especially Beijing, Shanghai, Guangdong, Hubei and other provinces with large population mobility, were subject to strict traffic control. With the restrictions of population mobility and other social distancing policies enacted across the country, the number of confirmed cases has shown a decreasing trend, which may indicate that these combined measures have curbed the rapid spread of the epidemic to a certain extent. By 21 June 2020, China had 84,997 confirmed cases and 4646 deaths from COVID-19, making China the country with the lowest infection rate and mortality rate worldwide (WHO, 2020). However, with COVID-19 spreading worldwide, new imported cases or local transmission cases are still reported sporadically.
Population mobility has been found by many recent studies to have significant effects on disease spread (Kraemer et al., 2020; Li et al., 2020a). Rapid urbanization process and the large-scale movement of the population into cities lead to changes in environmental factors, such as climate change, that exacerbate the incidence and mortality of large-scale infectious diseases in cities (Ye et al., 2021). During the rapid spread of the epidemic, the pathogen travelled like a blind passenger (Kuebart & Stabler, 2020). Several works have taken population mobility into consideration to model the spread of the virus (Balcan et al., 2009); for example, human transportation data were integrated by Chinazzi et al. (2020) into epidemiological data using the global epidemic and mobility model (GLEAM). Their work also proposed the relative risk of case importation to other countries given the flow strength and disease dynamics of a certain city in mainland China. Qiu et al. (2020) considered the within-city and between-city flow as factors influencing the daily new case number in a certain city, and flow from the outbreak source region posed a higher risk to destination regions than did other factors. Additionally, the risk of transportation of infectious cases from Wuhan to other cities was estimated by Du et al. (2020) using population mobility.
The apparent effect of population mobility restrictions on alleviating the epidemic could be explained by the properties of infectious viruses based on historical studies. Merler and Ajelli (2010) found that the spread of a virus affects the fluidity of the pathogen and the characteristics of the host. Epidemics spread to a certain level because of long-distance migration, such as the Europeans bringing the smallpox virus to America (Patterson & Runge, 2002), or short-term migration, such as the outbreak of SARS in 2003 (Ruan et al., 2005). Camitz and Liljeros (2006) found that a > 50 km travel ban would drastically reduce the spread of SARS outbreaks. Studies have shown that travel restrictions can be useful in the early stages of an outbreak (Kraemer et al., 2020). The blockade of Wuhan City, Hubei Province, and the travel restrictions on quarantine across the country on 23 January 2020 have effectively delayed the general epidemic both nationally and internationally (Chinazzi et al., 2020). Many other works have focused on the early stage of the outbreak; for example, Du et al. (2020) conducted research on data before the Wuhan travel ban, Fang et al. (2020) adopted data after the Wuhan lockdown, and Qiu et al. (2020) focused on the early stage and outbreak of the epidemic in mainland China. Nevertheless, travel bans and restrictions on movement impact the economy and geopolitics (Grydehøj et al., 2020).
In addition, the spread of the virus and the relationship between the status of the epidemic and population mobility must be measured in an appropriate manner. In terms of the metrics of epidemic transmission, most previous studies applied the cumulative number of infective cases or daily new cases (Fang et al., 2020; Qiu et al., 2020) as a measurement for the spread of the virus, while Kraemer et al. (2020) employed the cumulative case rank. Instead of directly using case number-related metrics, the reproduction number of the infectious disease, defined as the average number of new cases generated by each case, has been applied in many studies to measure the severity of the epidemic (Bandyopadhyay, 2020; Zhang et al. 2020). A tendency towards a reduction in basic reproduction number was found to be associated with travel restrictions (Bandyopadhyay, 2020), indicating the capability of the reproduction number to represent the spread of COVID-19 in relation to human travel volume. While the basic reproduction number represents the transmission of a disease at a certain stage of an epidemic (Chen et al., 2016; Wu & Riley, 2016), the real-time reproduction number represents the time-dependent transmission of a disease over time (Cori et al., 2013; Zhang et al., 2020). To measure the relationship between population mobility and disease outbreak, Kraemer et al. (2020) investigated the contribution of Wuhan mobility to other provinces in China, finding a linear correlation between the cumulative case rank and the mobility rank from Wuhan in each province at the early stage of the epidemic: the growth rates of different provinces showed a positive correlation with migration strength from Wuhan before the Wuhan travel ban and a negative correlation afterwards. Cross-city and within-city population mobility after the Wuhan lockdown was modelled simultaneously by Fang et al. (2020), and the correlations of the number of daily new cases in cities outside Hubei and inflows from all Hubei cities were obtained by regression analysis.
To examine the importance of travel restrictions during epidemics, the aim of this research is to verify the effectiveness of China's national control measures to suppress COVID-19 from the perspective of population mobility. This research has innovations mainly in two aspects. First, instead of analysing mobility data from a certain city, this research considers province-level migration from multiple provinces into Shenzhen. In terms of the metrics for the spread of COVID-19 in Shenzhen, this research employs the best fitted estimation for the real-time reproduction number and assesses the correlation between migration and the dynamics of the epidemic. Second, to provide a reference for decision making related to work and travel migration policy, this research explores the long-term epidemic, starting from the outbreak to the end period in China, with data from March and April. The results provide important information about the efficiency of the travel ban in China and can be used to improve policy guidance for the gradual return to work in mainland China. In addition to emphasizing the necessity of continuing prevention and control policies in the future, this research proposes ways to flexibly use prevention and control policies at different stages throughout the epidemic to provide ideas for containment of the global epidemic.
Methodology
Study area
The Guangdong-Hong Kong-Macao Greater Bay Area (GBA), as a world-class example of urban agglomeration, has the highest degree of openness in China, and Shenzhen is the core engine of the GBA. The frequent passenger flow and interflow of goods and materials make this city one of the most important global trading ports. Travel restrictions and distancing policies are necessary for areas with complex population structures and large population mobilities. In terms of population density, the effect of spatial heterogeneity means that the virus will reach urban areas earlier than rural areas (Merler & Ajelli, 2010). However, most studies have focused on disease transmission in Hubei or the impact of the lockdown of Wuhan (Chinazzi et al., 2020; Du et al., 2020; Kraemer et al., 2020) rather than cities at potential risk of the epidemic caused by population mobility. As a first-tier city with a high population concentration and high mobility in Guangdong Province, it is of great realistic meaning to probe the relationship between interprovincial population flow and transmissibility in Shenzhen to provide a deeper understanding of epidemic transmission patterns and contribute to formulating targeted measures.
Data collection
This research used daily cumulative confirmed, cured and dead case data in Shenzhen from 13th January to 3rd May with data preprocessing and daily migration data during the same period. All the available daily cumulative confirmed, cured, dead case data in Shenzhen before 3rd May 2020 were collected from the open platform of the Shenzhen Municipal Health Commission (SMHC, 2020). The daily cumulative confirmed data indicate unreported and unidentified infected cases in the early stage of the outbreak of COVID-19, especially before 24th January. Considering that confirmed cases from 24th January to 30th January follow an exponential growth model, this research estimates the exponential growth rate using the data during this period and redistributes the daily number of confirmed cases from 13th January to 24th January using exponential growth methods (Zhao et al., 2020).
| 1 |
| 2 |
where is the cumulative number of confirmed cases and is the intrinsic exponential growth rate.
Therefore, the daily data from 13th January to 3rd May were used to estimate the dynamic change in reproductive number. Table 2 in "Appendix" lists the summary statistics of the daily data. The serial interval, denoted as , is well described by a gamma distribution with shape parameter and scale parameter , with values corresponding to a mean serial interval of 8.4 days and a standard deviation of 3.8 days, according to Wallinga and Teunis (2004). The interprovincial migration indicators are constructed based on near real-time people movement statistics from Baidu from 13th January to 3rd May (Baidu Migration, 2020). Based on GPS tracking, the data allow quantification of the population of interprovincial migration. Since the data obtained are the logarithm of the population migrant amounts from all other provinces to Shenzhen, they are multiplied by the moving-in migration ratio of each province to obtain the interprovincial migration index for each province.
Table 2.
Summary statistics of , , , and estimated infected cases
| Variables | _EG | _MLE | _SB | _TD | _Epi | ||||
|---|---|---|---|---|---|---|---|---|---|
| Minimum | 5.00 | 3.00 | 0.00 | 0.00 | 3.63 | 3.70 | 3.69 | 3.63 | 3.63 |
| Maximum | 462.00 | 325.00 | 456.00 | 3.00 | 426.88 | 447.18 | 375.80 | 352.94 | 443.65 |
| Mean | 377.10 | 89.31 | 285.66 | 2.13 | 105.28 | 112.31 | 102.52 | 98.68 | 110.22 |
| Q3(.75) | 462.00 | 320.00 | 455.00 | 3.00 | 415.47 | 437.93 | 370.43 | 346.79 | 431.79 |
| Q1(.25) | 5.00 | 3.00 | 0.00 | 0.00 | 3.63 | 3.70 | 3.69 | 3.63 | 3.63 |
| Median | 420.00 | 30.50 | 393.50 | 3.00 | 32.52 | 33.36 | 32.84 | 32.52 | 32.52 |
| Stdev | 133.28 | 103.44 | 171.97 | 1.33 | 124.81 | 134.26 | 117.94 | 111.51 | 131.76 |
| Kurtosis | 2.53 | 0.02 | − 1.21 | − 1.03 | 0.44 | 0.40 | 0.02 | − 0.07 | 0.46 |
| Skewness | − 1.98 | 1.24 | − 0.71 | − 0.96 | 1.34 | 1.34 | 1.24 | 1.20 | 1.36 |
The definitions of , , , and are shown in Table 1, and _EG, _MLE, _SB, _TD, and _Epi represent the number of existing infected cases on day estimated by the EG, MLE, SB, TD and Epi methods, respectively.
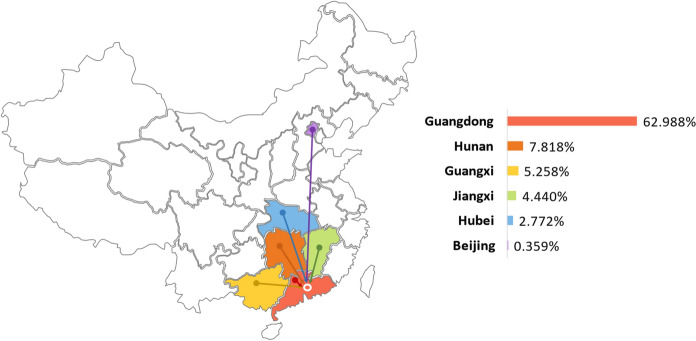
This work takes into account not only the national population but also the inflow from several important provinces. In addition to the most severe epidemic area, Hubei, this work considers Beijing, where approximately 1000 accumulated confirmed cases were reported. The four cities with the largest population mobility in China are Shanghai, Guangzhou, Shenzhen and Beijing. Because Beijing is the capital city with a complex population structure, ignoring Beijing would make the results of this study incomplete. Shanghai, which is located in the Yangtze River Delta urban agglomeration area with the largest economic volume in China, has a strong economic foundation. Considering that the frequency and quantity of the local permanent resident population flowing to other provinces are limited and most of the population migration is into other cities in the Yangtze River Delta, Shanghai is not taken as the study area in this research. In addition, four regions with the highest index since January 2020, namely Guangdong, Hunan, Guangxi and Jiangxi, are selected for the correlation calculation. Figure 1 shows the proportion of these five regions and total areas moving into the Shenzhen Index from 13th January to 3rd May. According to the similarity of the correlation change trend, relevant analysis is conducted for four regions: (1) Guangdong, (2) Hunan, Jiangxi and Guangxi, (3) Hubei and (4) Beijing. Table 4 in "Appendix" lists the summary statistics of the interprovincial migration index into Shenzhen from the above regions and total areas.
Fig. 1.
Proportion map of the migration index of five regions and total areas into Shenzhen
Table 4.
Summary statistics of the interprovincial migration index into Shenzhen
| Variables | SZ_total | Hubei_SZ | Beijing_SZ | Hunan_SZ | Guangd_SZ | Guangx_SZ | Jiangxi_SZ |
|---|---|---|---|---|---|---|---|
| Minimum | 1.96 | 0.29 | 0.39 | 7.03 | 107.38 | 2.91 | 3.79 |
| Maximum | 10.47 | 69.68 | 7.91 | 121.45 | 782.33 | 84.99 | 62.09 |
| Mean | 5.03 | 14.21 | 1.26 | 39.17 | 321.33 | 27.50 | 22.23 |
| Q3(.75) | 9.03 | 67.85 | 7.09 | 96.13 | 654.69 | 75.18 | 47.55 |
| Q1(.25) | 1.96 | 0.29 | 0.39 | 7.03 | 107.38 | 2.91 | 3.79 |
| Median | 4.99 | 5.79 | 0.89 | 29.30 | 308.62 | 21.06 | 17.36 |
| Stdev | 1.43 | 19.33 | 1.39 | 23.76 | 129.85 | 18.60 | 13.17 |
| Kurtosis | 2.09 | 1.91 | 13.16 | 0.84 | 1.42 | 1.54 | − 0.31 |
| Skewness | 0.60 | 1.75 | 3.65 | 1.23 | 0.84 | 1.43 | 0.89 |
SZ_total, Hubei_SZ, Beijing_SZ, Hunan_SZ, Guangd_SZ, Guangx_SZ and Jiangxi_SZ refer to interprovincial migration index into Shenzhen for Total areas, Hubei, Beijing, Hunan, Guangdong, Guangxi and Jiangxi, respectively
Five methods to estimate the reproduction number of COVID-19
The real-time reproduction number of COVID-19 quantitatively reflects the spread of the virus. To determine the relationship between the migration and spread of COVID-19 over time in Shenzhen, this research collected the migration index of moving into Shenzhen from other Chinese provinces applied the best-fitted method to estimate the real-time reproduction number and finally computed the correlation between these values.
The real-time reproduction number can be estimated via diverse methods. A generic Bayesian-based generation time-weighted tool was developed to estimate time-varying reproduction numbers during five historical epidemics (Cori et al., 2013). The Bayesian method was used to estimate the effective reproduction number for pandemic influenza A H1N1 in Guangdong Province, China (Yang et al., 2013). You et al. (2020) adopted the Poisson likelihood (ML) method to estimate the time-varying controlled reproduction number of COVID-19 in China. A method based on the maximum likelihood was proposed by Chintalapudi et al. (2020). Akhmetzhanov et al. (2019) applied the maximum likelihood estimation (MLE)-based extrapolation approach for Ebola in the Democratic Republic of the Congo (DRC).
This research compares the five most popular estimates of , including the exponential growth (EG) method (Zhao et al., 2020), MLE (White & Pagano, 2008), sequential Bayesian (SB) method (Bettencourt & Ribeiro, 2008), time-dependent reproduction numbers (TD) (Wallinga & Teunis, 2004), and the EpiEstim R package (Cori et al., 2013). To estimate daily in the EG method, we set a fixed length period as the time window, and the dynamic change in reproduction number was estimated by the following equations:
| 3 |
| 4 |
where is the cumulative confirmed cases on day ; is the intrinsic exponential growth rate during the last 7 days on day ; and and are the shape parameter and scale parameter of the SI distribution, respectively.
The MLE method also sets 7 days as a time window, and the calculation formula of is described below.
| 5 |
where identifies the number of new infected cases on day and the parameter comes from the probability distribution function of the serial interval, which follows a gamma distribution.
The SB, TD and EpiEstim R package methods provide direct estimates of the real-time . In the SB method, Bayesian estimation of (Bettencourt & Ribeiro, 2008) is based on the equation:
| 6 |
where denotes the number of infected people on day which is approximately Poisson distributed with mean , is the average duration of the infectious period and denotes a discrete probability distribution with mean .
The TD method calculates the likelihood that case was infected by case , denoted as , which can be expressed as Eq. (7).
| 7 |
where is the generation interval time from case onset to case onset. is the probability density function for the generation interval .
The formula of is expressed below:
| 8 |
where indicates the effective reproduction number of an ongoing epidemic for case j and is the number of all reported infected confirmed people on day t.
This research also provides the 95% confidence interval for the estimation of .
Comparison of estimation methods
Two metrics are adopted to select the best estimator, directly compare the width of the confidence interval of and estimate the daily number of new cases from . To estimate the daily number of new cases (Marquetoux et al., 2012):
| 9 |
| 10 |
where is the duration of the infectious period, is the transmission rate on day , , is the number susceptible to infection on day , is the number of infected cases on day , and is the number of new cases on day .
Therefore, an estimate of the daily number of new cases can be obtained by the following formula:
| 11 |
Assuming that all people except cured, dead and confirmed cases are susceptible to COVID-19, equals the population in Shenzhen minus the daily cumulative confirmed cases plus daily cumulative cured cases.
Correlation analysis and hypothesis test
To study the impact of population mobility on the spread of the epidemic, correlation analysis is conducted between and population mobility to indicate the effectiveness of travel restrictions and other social distancing methods. Only the moving-in data are used considering that the moving-out part of the population may not influence the epidemic intercity or interprovince. The biweekly rolling Pearson correlation coefficients between and interprovincial migration index data represent the relationship between virus transmission and population mobility (Ainslie et al., 2020).
Furthermore, the correlation differences in different provinces or cities are studied to determine if information on several provinces or cities can be obtained. Considering that the hypothesis test is based on two dependent and overlapping groups using the same variable , Williams’s test is used to conduct the hypothesis test on correlation differences in different provinces or cities (Lauer et al., 2020; Steiger, 1980). Then, hypothesis tests can be conducted to determine whether the correlations in different cities or provinces are different:
| 12 |
The above methods are used to estimate the daily real-time reproduction number and the 95% confidence interval for each method. To compare and measure the effect of the estimation, this research first compares the fitness of every based on the confidence intervals, calculates the number of daily existing infections using the output daily and compares the results with the actual daily data. The best-fitted estimation of is adopted to estimate the daily reproduction number in Shenzhen from 19th January to 3rd May and to analyse the relationship between the reproduction number and the migration trend from other provinces.
Results
Estimation results of the COVID-19 reproduction number
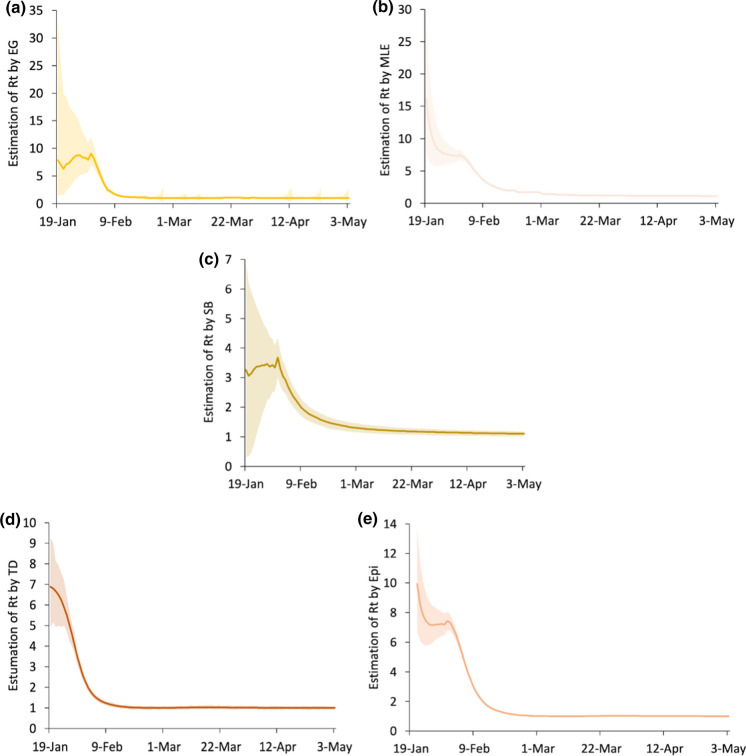
The daily real-time reproduction number and the associated 95% confidence interval are estimated by five methods. Specifically, this research uses the est.R0.EG, est.R0.ML, est.R0.SB and est.R0.TD in the Ro package (Fraser, 2007; Obadia, et al., 2012) and estimate_R in the EpiEstim package (Cori et al., 2013). Table 3 in "Appendix" lists the summary statistics of the values estimated by the five methods and the width of the associated 95% confidence interval. The results of the 5 methods are shown in Fig. 2.
Table 3.
Summary statistics of estimated by five methods and the width of the 95% confidence intervals
| Variables | EG_ | MLE_ | SB_ | TD_ | Epi_ | EG_CI_W | MLE_CI_W | SB_CI_W | TD_CI_W | Epi_CI_W |
|---|---|---|---|---|---|---|---|---|---|---|
| Minimum | 1.00 | 1.11 | 1.09 | 1.00 | 1.00 | 0.00 | 0.03 | 0.17 | 0.14 | 0.00 |
| Maximum | 9.07 | 16.13 | 3.68 | 6.89 | 9.93 | 31.98 | 21.96 | 6.56 | 4.60 | 6.97 |
| Mean | 2.13 | 2.81 | 1.62 | 1.57 | 2.14 | 2.12 | 0.94 | 0.71 | 0.40 | 0.43 |
| Q3(.75) | 8.72 | 10.41 | 3.43 | 6.67 | 7.83 | 18.14 | 10.43 | 5.40 | 3.32 | 4.21 |
| Q1(.25) | 1.00 | 1.11 | 1.09 | 1.00 | 1.00 | 0.00 | 0.03 | 0.17 | 0.14 | 0.00 |
| Median | 1.01 | 1.72 | 1.22 | 1.00 | 1.00 | 0.39 | 0.11 | 0.26 | 0.18 | 0.07 |
| Stdev | 2.44 | 2.77 | 0.78 | 1.46 | 2.29 | 5.11 | 2.93 | 1.23 | 0.72 | 1.07 |
| Kurtosis | 2.13 | 5.83 | 0.87 | 6.23 | 2.09 | 14.88 | 29.86 | 10.22 | 16.88 | 18.04 |
| Skewness | 1.96 | 2.33 | 1.56 | 2.73 | 1.90 | 3.65 | 5.10 | 3.23 | 4.02 | 4.03 |
EG_, MLE_, SB_, TD_, and Epi_ refer to estimated by the EG, MLE, SB, TD and Epi methods, respectively. EG_CI_W, MLE_CI_W, SB_CI_W, TD_CI_W, and Epi_CI_W represent the widths of their respective 95% confidence intervals.
Fig. 2.
Estimation of and 95% confidence intervals by five methods: a exponential growth method (EG); b maximum likelihood estimation (MLE); c sequential Bayesian method (SB); d time-dependent reproduction numbers (TD); e EpiEstim R package (Epi)
The values obtained by these methods show a general downward trend along with the narrowing of the confidence interval. The overall trends of the MLE, TD and EpiEstim R packages are very similar, showing a relatively large decline in the initial stage and then a slower decline towards a stable level. After the end of January, they continued to decline significantly and eventually tended to 1, which may have resulted from the issuance of the travel restriction and social distancing policy. The intrinsic exponential growth rate decreases rapidly, which shows the turning point at the end of January in the curve of the EG method.
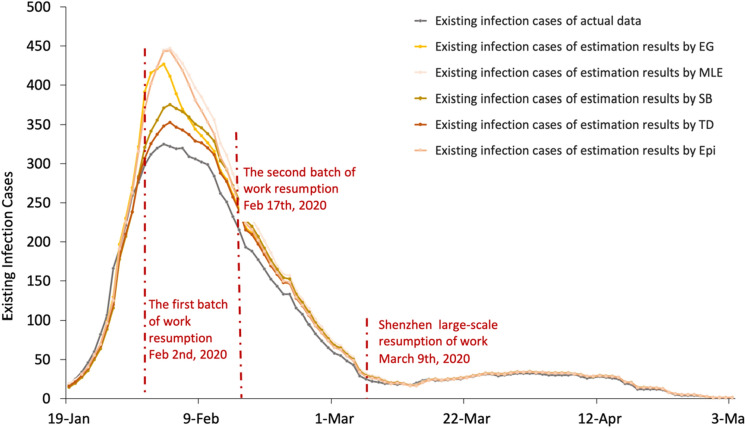
After estimating by these 5 methods, the daily number of new cases is estimated. This research uses the cumulative number of infections per day minus the cumulative number of deaths and the cumulative number of cures to obtain the daily number of infections and then subtracts the cumulative number of diagnoses per day from the total population to obtain the number of susceptible persons per day . Take 12.75 as T and 5 days as the length of the incubation period (Health People, 2020). , , , T and are substituted into Eq. 11 to obtain the daily new cases on day t + 5, denoted by . The number of new infections every day is added to the actual cumulative number of infections of the previous day to obtain the cumulative number of infections for that day, which is . Because the actual cumulative number of infected people on the previous day is substituted during this process, the comparison effect of various methods is not strong. Therefore, the estimated daily existing infections, which are calculated by using the estimated cumulative number of infections minus the actual cumulative number of deaths and the actual cumulative number of cured, are chosen as a comparison indicator. Table 2 in "Appendix" lists the summary statistics of the estimated daily existing infections. A comparison figure of the results is shown in Fig. 3.
Fig. 3.
Existing infection cases for the actual data and estimated results based on . a The estimation period of EG starts on 19th January; b the estimation period of MLE starts on 19th January; c the estimation period of SB starts on 14th January; d the estimation period of TD starts on 13th January; e the estimation period of Epi starts on 21st January. Note that this figure presents data from 19th January to 3rd May
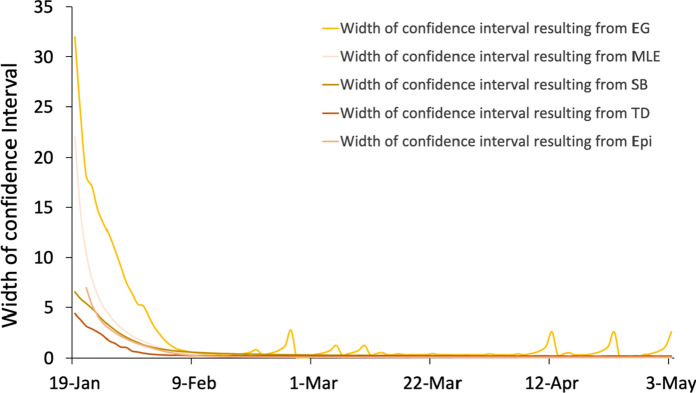
Figure 3 shows that the TD method has the best fitting effect. It also reflects the changing trend of existing infections, which gradually increased from the starting point until reaching the maximum on 4th February and then gradually declining. The magnitude of the error is judged by comparing the width of the confidence intervals, as shown in Fig. 4. Additionally, the ranking of the methods in terms of accuracy was obtained. The results of TD have the narrowest confidence interval, followed by SB, EpiEstim, MLE and EG. However, all confidence intervals begin to decline towards 0 on 6th February. The width of the confidence interval of TD appears abnormal on 8th March, but this issue can be ignored in this research. On the basis of these two aspects, the TD method has the highest accuracy and the closest matching relationship with the actual infective data, and the number of infected people estimated by obtained by TD is closest to the actual data. Therefore, the TD method is adopted for estimating and is applied to the correlation analysis.
Fig. 4.
Width of confidence intervals resulting from the five methods
Correlation analysis between and the interprovincial migration index
Considering that the scale of interprovincial migration after unblocking would take a quantum leap once people from all over the country, even the whole world, were back to work, it is of crucial importance to assess the effectiveness of the early travel restriction measures in moderating the epidemic’s transmission. The results of the correlation analysis cover the main period of transmission of COVID-19 in China. Table 5 in "Appendix" lists summary statistics of the correlation between and the interprovincial migration index in Shenzhen from different regions.
Table 5.
Summary statistics of the correlation between and the interprovincial migration index in Shenzhen from different regions
| Regions | Total areas | Guangdong | Hunan | Guangxi | Jiangxi | Hubei | Beijing |
|---|---|---|---|---|---|---|---|
| Mean | − 0.09 | − 0.03 | − 0.13 | − 0.19 | − 0.12 | 0.28 | 0.22 |
| Median | − 0.05 | − 0.04 | − 0.25 | − 0.26 | − 0.25 | 0.53 | 0.26 |
| Stdev | 0.41 | 0.37 | 0.59 | 0.60 | 0.61 | 0.61 | 0.48 |
| Kurtosis | − 0.86 | − 0.30 | − 1.49 | − 1.17 | − 1.50 | − 1.42 | − 1.03 |
| Skewness | − 0.12 | − 0.15 | 0.26 | 0.43 | 0.17 | − 0.42 | − 0.15 |
| Minimum | − 0.84 | − 0.79 | − 0.89 | − 0.94 | − 0.93 | − 0.85 | − 0.71 |
| Maximum | 0.85 | 0.86 | 0.83 | 0.93 | 0.87 | 0.98 | 0.97 |
| Q3(.75) | 0.53 | 0.61 | 0.82 | 0.90 | 0.83 | 0.98 | 0.95 |
| Q1(.25) | − 0.84 | − 0.79 | − 0.89 | − 0.94 | − 0.93 | − 0.85 | − 0.71 |
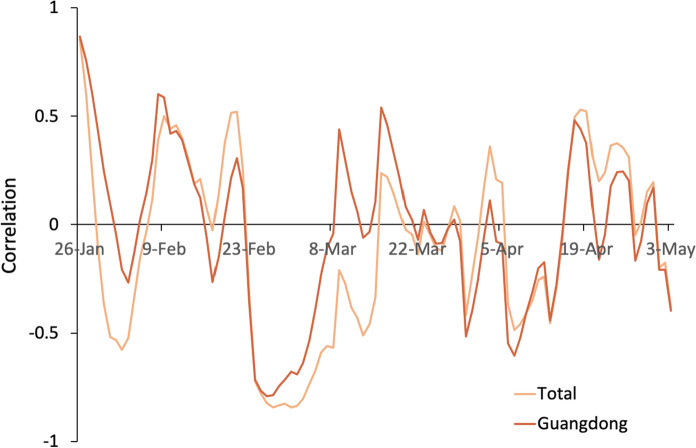
Correlation curve of total areas and Guangdong
According to the proportion map of the migration index into Shenzhen (Fig. 1), Guangdong accounts for the largest proportion of migration to Shenzhen. This can explain why the trend of total migration into Shenzhen is basically consistent with the correlation influence of Guangdong on Shenzhen's migration. The general trend of is declining in Fig. 2, which is believed to be the result of China's efforts to fight the epidemic starting from the end of January. At the end of January, there appears to be an initial negative correlation, possibly because of the home segregation policy. Despite the increase in the migration index, maintains a large decline, so it shows a negative correlation. From 8th February, some enterprises resumed work. During this period, is positively correlated with population movement, indicating that in approximately 2 weeks, population movement aggravated the epidemic to some extent. Starting on 20th February, Shenzhen adopted the green code as a passable health certificate and set up multiple epidemic prevention checkpoints. Because of strict inspection measures for migration into Shenzhen, coupled with a policy of isolation for 14 days, despite the large inflow caused by the reinstatement of labour, maintains a downward trend, showing an overall negative correlation (Fig. 5).
Fig. 5.
Correlation between and the migration index for total areas and Guangdong
With the continuous spread of overseas epidemics in late March, overseas imports gradually had a greater impact on the epidemic in China, especially in Guangdong and Beijing. Therefore, there is a positive correlation between population mobility and . However, as the government and community responded to overseas imports in a timely manner, the correlation again became negative in April. The negative correlation may be due to the strict prevention and control and medical measures to suppress the impact of population inflow on . In this process, epidemic prevention inspections, green codes and home isolation measures have a considerable effect. However, the correlation trend shows that prevention and control are still required in the future, with necessary attention given to the impact of liquidity on the epidemic (Fig. 5).
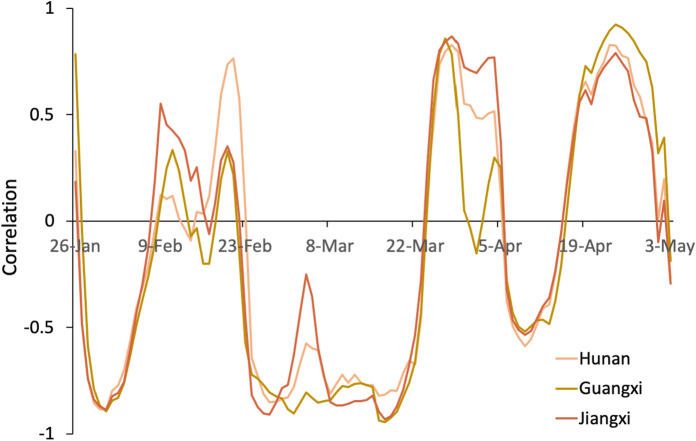
Correlation curve of Hunan, Guangxi and Jiangxi
Since the three provinces of Hunan, Jiangxi and Guangxi border Guangdong, their correlation changes are very similar to those of Guangdong. The two negative correlations before April also illustrate the effect of home isolation and other measures on the epidemic. Notably, since Jiangxi, Hunan and Guangxi are geographically in the middle of Hubei and Guangdong, the resumption of work in Hubei also impacted the correlation of these three provinces. At the end of March, due to the impact of the resumption of labour and the fact that Hubei, except Wuhan, was unsealed, population movement is positively correlated with . After the unblocking of Wuhan on 8th April, negative correlations are again observed in the three regions. This phenomenon may be the result of Wuhan’s counterwork and strengthening prevention and control. The range of population mobility continues to increase, and the positive correlation is more obvious, indicating that attention still needs to be paid to interprovincial population mobility (Fig. 6).
Fig. 6.
Correlation between Rt and the migration index for Hunan, Guangxi and Jiangxi
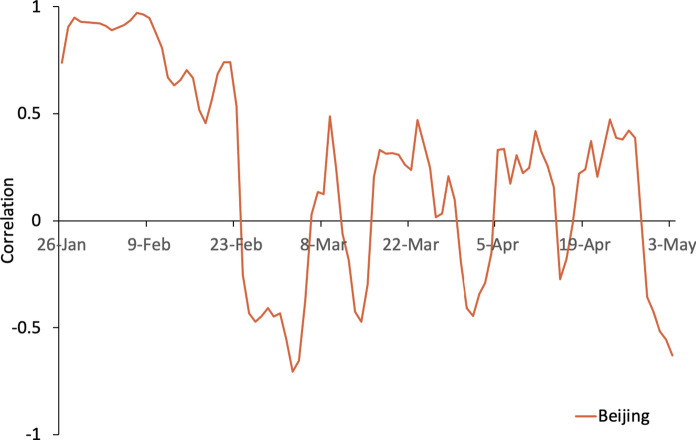
Correlation curve of Beijing
Although the index of Beijing’s migration to Shenzhen since late January is very small, the overall trend of the correlation is positive before late February, similar to the overall situation. The correlation between and the Beijing moving-in index changes from positive to negative on 24th February. The Beijing moving-in index continued to decline before 24th February and beginning to increase after 24th February. The negative correlation at the end of February is likely the result of the green code and other measures that have had a substantial effect on the epidemic, coupled with the remote location of Beijing. The correlation fluctuated around 0 after early March, which indicates the initial success of controlling the epidemic transmissibility from population mobility between Shenzhen and Beijing. However, the correlation remains positive. Considering the impact of overseas imports, the migration from Beijing to Shenzhen requires special focus (Fig. 7).
Fig. 7.
Correlation between Rt and the migration index for Beijing
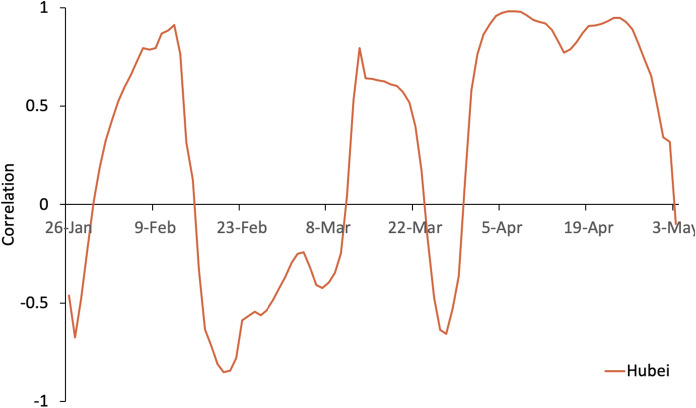
Correlation curve of Hubei
After the closure of Hubei, population inflows plummeted, and the migration index remained low. From mid-February to mid-March, even with a small population inflow from Hubei, continues to decrease, showing a negative correlation. After March, the range of population mobility increased, and the positive correlation is more obvious. From April, the correlation shows a clear positive trend, indicating that attention should be paid to population mobility from the areas hardest hit by the epidemic (Fig. 8).
Fig. 8.
Correlation between Rt and the migration index for Hubei
In general, the correlation between and migration into Shenzhen is low in late February, which illustrates the initial success of the social distancing policy. When domestic interprovincial flows increased in early March because of work resumption, and the migration index become positively correlated, which shows that the movement of people between regions impacts the epidemic. The continuous spread of overseas epidemics in late March increased overseas imports into China, which had a greater impact on the epidemic in Guangdong and Beijing. During this period, the correlation between population mobility and presents an obvious positive trend and quickly decreases as the government and community responded to overseas imports in a timely manner. From April, the correlation shows a clear positive trend, indicating that attention still needs to be paid to population mobility. To conclude, the two measures of home isolation and strict inspection during population migration have effectively suppressed the impact of population mobility on the epidemic. However, the correlation increases at the beginning of April, showing that the spread of the epidemic increased when people from all around the Chinese mainland started returning to work in batches from province to province and city to city.
Hypothesis test on correlation differences in different provinces or cities
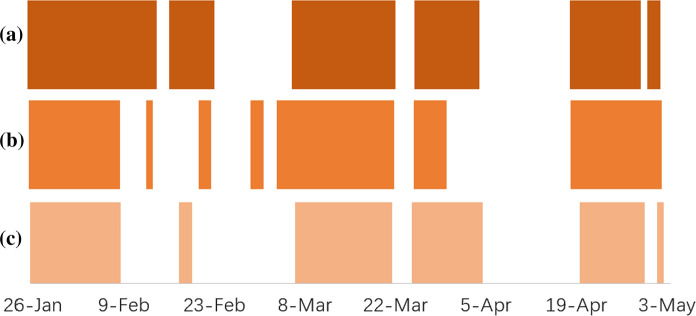
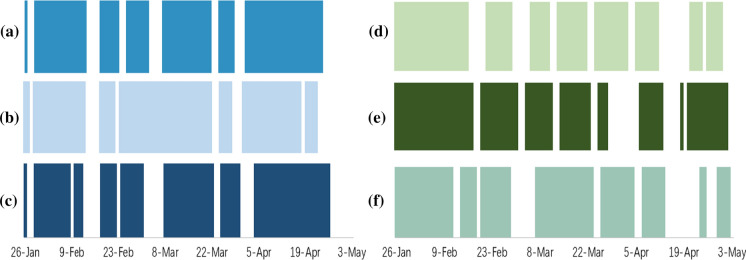
The significance level was set to , and coloured blocks and blanks in the figures denote similar correlations (reject ) and different correlations (fail to reject ) in different provinces or cities, respectively. Figures 9 and 10 show the results between the neighbouring provinces of Shenzhen and the correlation difference in Beijing or Hubei and the neighbouring provinces.
Fig. 9.
Hypothesis test on correlation differences between neighbouring provinces: a Guangdong and Hunan; b Guangdong and Guangxi; c Guangdong and Jiangxi
Fig. 10.
Hypothesis test on correlation differences in Beijing or Hubei and the neighbouring provinces: a Hubei and Hunan; b Hubei and Guangxi; c Hubei and Jiangxi; d Beijing and Hunan; e Beijing and Guangxi; f Beijing and Jiangxi
There were periods in which the correlations between Guangdong and other neighbouring provinces (Guangxi, Hunan and Jiangxi) were similar, especially during mid-February to early March and the first half of April (Fig. 9). Similar correlations may indicate a similar influence of the moving-in index of these three neighbouring provinces and Guangdong, which may be due to the migration of neighbouring provinces into Shenzhen through Guangdong.
Clearly, the correlations are different in Beijing or Hubei and neighbouring provinces, and the correlation between the Beijing or Hubei moving-in index and could hardly be obtained by observing the correlation between the neighbouring provinces’ moving-in index and (Fig. 10). The geographical distance of Beijing from the neighbouring provinces and the epidemic control measures in Hubei may contribute to this phenomenon. For the correlation differences in the other provinces or cities, similar and different correlations alternately appear throughout the entire period, as shown in "Appendix", which provides a few useful observations. In general, the correlations in different cities or provinces are different. Although several periods may show similar correlations, it is difficult to obtain the correlations in one province or city directly through the correlations in another province or city. Therefore, correlation analysis should be conducted in different provinces or cities individually rather than observing one case to replace the other.
Conclusions and policy implications
This paper examines the impact of population mobility on the transmission dynamics of COVID-19 in China, considering between-province transmissions into Shenzhen, Guangdong. Based on the migration data over a long period from 19th January to 3rd May, this research covers different stages from the initial outbreak stage, peak stage, containment stage and end period in Shenzhen, China, to provide a comprehensive perspective of the whole epidemic. As Shenzhen is a typical city with high population mobility, this study also provides insight into the policy of population mobility control during the epidemic period nationwide. Five different methods are employed, and the TD method is chosen to estimate the real-time reproduction number, which represents the time-dependent spreading of the pandemic. Correlation analysis is conducted by calculating and comparing the correlation between and the migration index of five regions and the total areas. With consideration of government policy, community prevention and medical control measures in Shenzhen and five regions, recommendations are made for population mobility restriction policies in different types of areas.
Three major conclusions are as follows: (1) at the initial outbreak stage, the correlation of population mobility from different regions into Shenzhen and the spread of COVID-19 presents a positive trend; (2) during the outbreak and peak periods, China’s national travel ban policy achieved unprecedented effectiveness, and the correlation shows a significant decrease tendency; (3) in the containment period, the correlation no longer shows a clear positive trend, the national restrictions can be appropriately liberalized and appropriate economic recovery policies can be adopted properly, but attention still needs to be paid to large-scale mobility domestically and especially internationally in the long run, especially for high-risk areas.
National restriction of population mobility is an abnormal tool for epidemic prevention that has rarely been implemented during previous infectious disease control but achieved unprecedented results during the epidemic period of COVID-19. Considering the importance of resuming work and production in Shenzhen, restriction adjustment should be performed in different stages of the epidemic. During the initial outbreak stage, strict travel restrictions should be considered and implemented rapidly. In this process, the isolation measures adopted by the government and the high protection awareness of society can effectively weaken this relation and result in negative correlations. In this stage, given the characteristics of infectious diseases, such as acute onset, rapid spread, untraceable sources of infection and serious consequences, stricter control policies for population mobility can achieve better results. In the peak period, population mobility restrictions, including travel restrictions and social distancing measures, should be implemented continuously, and people in the same region should be classified and isolated. In the containment period, for cities with a large migrant population, such as Shenzhen, an appropriate restriction adjustment tool should be applied to account for economic recovery and people’s livelihood demands. Restriction policies or measures should be flexible for people from different areas with different epidemic risk levels; for example, health code measures of the health commission could be widely used.
At present, the epidemic is still in the developing stage in many countries, so it is necessary to impose restrictions on both international and domestic mobility, especially for high-risk countries. Protective measures such as controlling the occupancy rate of vehicles for domestic travel, prohibiting mass socially aggregative activities and keeping quarantined for at least 14 days are still necessary. More research could be conducted on international mobility around the world, and similar results will hopefully show the influence of population mobility on the spread of the epidemic. Countries currently under the very difficult time of COVID-19 should learn from the experiences of other countries that controlled social distance and implemented travel bans. Additionally, for future infectious diseases, lockdown decisions should be made more quickly to control transmission, and international, domestic, intercity and intracity population mobility should all be restricted in the face of the outbreak of a disease. Even when COVID-19 is effectively controlled globally in the future, there is still a long way to go in learning from the epidemic and preparing for the next potential pandemic.
This paper focuses on migration to one city from several provinces in China and does not consider population outflow. Additional studies could be conducted on larger-scale regions domestically in China or even globally in terms of mobility between different counties, with other factors contributing to the spread of the epidemic in addition to the inclusion of the migration index.
Acknowledgements
This work is supported by the MOE (Ministry of Education in China) Project of Humanities and Social Science (No. 19YJC630095).
Appendix
Table 1.
Definitions of all variables and abbreviations
| Variable | Definition | Unit of measurement |
|---|---|---|
| Real-time production number | ||
| EG | The exponential growth method | |
| MLE | The maximum likelihood estimation | |
| SB | The sequential Bayesian method | |
| TD | The time-dependent reproduction numbers | |
| Epi | EpiEstim R package method | |
| Cumulative confirmed cases | People/day | |
| The number of existing infected cases on day | People/day | |
| The number of recovered cases on day | People/day | |
| The number of dead cases on day | People/day | |
| The number of susceptible to the infection on day | People/day | |
| The intrinsic growth rate of the exponential growth | ||
| The average duration of the infectious period | Day | |
| The serial interval | ||
| The shape parameter of SI distribution | ||
| The scale parameter of SI distribution | ||
| A discrete probability distribution with mean | ||
| The likelihood that case was infected by case | ||
| The probability density function for the generation interval | ||
| The duration of the infectious period | Day |
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Honglu Ji and Huan Tong have contributed equally to this work.
References
- Ainslie, K. E. C., Walters, C. E., Fu, H., et al. (2020). Evidence of initial success for China exiting COVID-19 social distancing policy after achieving containment. Wellcome Open Research, 5, 81. [DOI] [PMC free article] [PubMed]
- Akhmetzhanov AR, Lee H, Jung S, et al. Analyzing and forecasting the Ebola incidence in North Kivu, the Democratic Republic of the Congo from 2018–19 in real time. Epidemics. 2019;27:123–131. doi: 10.1016/j.epidem.2019.05.002. [DOI] [PubMed] [Google Scholar]
- Baidu Migration. (2020). https://qianxi.baidu.com/.
- Balcan D, Colizza V, Gonçalves B, et al. Multiscale mobility networks and the spatial spreading of infectious diseases. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:21484–21489. doi: 10.1073/pnas.0906910106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandyopadhyay S. Coronavirus Disease 2019 (COVID-19): We shall overcome. Clean Technologies and Environmental Policy. 2020;22:545–546. doi: 10.1007/s10098-020-01843-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bettencourt LM, Ribeiro RM. Real time Bayesian estimation of the epidemic potential of emerging infectious diseases. PLoS ONE. 2008;3(5):e2185. doi: 10.1371/journal.pone.0002185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camitz M, Liljeros F. The effect of travel restrictions on the spread of a moderately contagious disease. BMC Medicine. 2006;4:32. doi: 10.1186/1741-7015-4-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S, Yang J, Yang W, et al. COVID-19 control in China during mass population movements at new year. The Lancet. 2020;395(10226):764–766. doi: 10.1016/S0140-6736(20)30421-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen T, Chen T, Liu R, et al. Transmissibility of the influenza virus during influenza outbreaks and related asymptomatic infection in Mainland China, 2005–2013. PLoS ONE. 2016;11:e0166180. doi: 10.1371/journal.pone.0166180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chinazzi M, Davis JT, Ajelli M, et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020;368:395–400. doi: 10.1126/science.aba9757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chintalapudi N, Battineni G, Sagaro GG, et al. COVID-19 outbreak reproduction number estimations and forecasting in Marche, Italy. International Journal of Infectious Diseases. 2020;96:327–333. doi: 10.1016/j.ijid.2020.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cori A, Ferguson NM, Fraser C, et al. A new framework and software to estimate time-varying reproduction numbers during epidemics. American Journal of Epidemiology. 2013;178(9):1505–1512. doi: 10.1093/aje/kwt133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Z, Wang L, Cauchemez S, et al. Risk for transportation of coronavirus disease from Wuhan to other cities in China. Emerging Infectious Diseases. 2020;26(5):1049–1052. doi: 10.3201/eid2605.200146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang, H., Wang, L., Yang, Y. (2020). Human mobility restrictions and the spread of the Novel Coronavirus (2019-nCoV) in China. Journal of Public Economics, 191, 104272. [DOI] [PMC free article] [PubMed]
- Fraser C. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS ONE. 2007;2(1):e758. doi: 10.1371/journal.pone.0000758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grydehøj A, Kelman I, Su P. Island geographies of separation and cohesion: The coronavirus (COVID-19) pandemic and the geopolitics of Kalaallit Nunaat (Greenland) Tijdschrift voor economische en sociale geografie. 2020;111:288–301. doi: 10.1111/tesg.12423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Health People. (2020). National Health Commission of the People’s Republic of China: The average hospitalization of discharged patients nationwide is over 9 days, and that in Hubei is 20 days. [DB/OL]. 2020-02-04/2020-04-22. http://health.people.com.cn/n1/2020/0204/c14739-31570937.html.
- Kraemer MUG, Yang CH, Gutierrez B, et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science. 2020;368(6490):493–497. doi: 10.1126/science.abb4218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuebart A, Stabler M. Infectious diseases as socio-spatial processes: The COVID-19 outbreak in Germany. Tijdschrift voor economische en sociale geografie. 2020;111:482–496. doi: 10.1111/tesg.12429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau H, Khosrawipour V, Kocbach P, et al. The positive impact of lockdown in Wuhan on containing the COVID-19 outbreak in China. Journal of Travel Medicine. 2020;27(3):taaa037. doi: 10.1093/jtm/taaa037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer SA, Grantz KH, Bi Q, et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Annals of Internal Medicine. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Pei S, Chen B, et al. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2) Science. 2020;368:489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z, Chen Q, Feng L, et al. Active case finding with case management: The key to tackling the COVID-19 pandemic. The Lancet. 2020;396:63–70. doi: 10.1016/S0140-6736(20)31278-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marquetoux N, Paul M, Wongnarkpet S, et al. Estimating spatial and temporal variations of the reproduction number for highly pathogenic avian influenza H5N1 epidemic in Thailand. Preventive Veterinary Medicine. 2012;106:143–151. doi: 10.1016/j.prevetmed.2012.01.021. [DOI] [PubMed] [Google Scholar]
- Merler S, Ajelli M. The role of population heterogeneity and human mobility in the spread of pandemic influenza. Proceedings Biological Sciences. 2010;277(1681):557–565. doi: 10.1098/rspb.2009.1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obadia T, Haneef R, Boëlle P. The R0 package: A toolbox to estimate reproduction numbers for epidemic outbreaks. BMC Medical Informatics and Decision Making. 2012;12:147. doi: 10.1186/1472-6947-12-147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson KB, Runge T. Smallpox and the native American. The American Journal of the Medical Sciences. 2002;323(4):216–222. doi: 10.1097/00000441-200204000-00009. [DOI] [PubMed] [Google Scholar]
- Qiu Y, Chen X, Shi W. Impacts of social and economic factors on the transmission of coronavirus disease 2019 (COVID-19) in China. Journal of Population Economics. 2020;33:1127–1172. doi: 10.1007/s00148-020-00778-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruan S, Wang W, Levin SA. The effect of global travel on the spread of sars. Mathematical Biosciences and Engineering. 2005;3:205–218. doi: 10.3934/mbe.2006.3.205. [DOI] [PubMed] [Google Scholar]
- Shenzhen Municipal Health Commission. (2020). Daily confirmed cases statistics of COVID-19 in Shenzhen. https://opendata.sz.gov.cn/data/dataSet/toDataDetails/29-200_01503670.
- Steiger JH. Tests for comparing elements of a correlation matrix. Psychological Bulletin. 1980;87:245–251. doi: 10.1037/0033-2909.87.2.245. [DOI] [Google Scholar]
- Wallinga J, Teunis P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. American Journal of Epidemiology. 2004;160(6):509–516. doi: 10.1093/aje/kwh255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White F, Pagano M. A likelihood-based method for real-time estimation of the serial interval and reproductive number of an epidemic. Statistics in Medical Journals. 2008;27(16):2999–3016. doi: 10.1002/sim.3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization. (2020). WHO Director-General’s opening remarks at the media briefing on COVID-19. Retrieved 26 May, 2020, from https://www.who.int/dg/speeches/detail/who-director-general-sopening-remarks-at-the-media-briefing-on-covid-19---11-march-2020.
- Wu KM, Riley S. Estimation of the basic reproductive number and mean serial interval of a novel pathogen in a small, well observed discrete population. PLoS ONE. 2016;11(2):e0148061. doi: 10.1371/journal.pone.0148061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang F, Yuan L, Tan X, et al. Bayesian estimation of the effective reproduction number for pandemic influenza A H1N1 in Guangdong Province, China. Annals of Epidemiology. 2013;23:301–306. doi: 10.1016/j.annepidem.2013.04.005. [DOI] [PubMed] [Google Scholar]
- Ye B, Jiang J, Liu J, et al. Research on quantitative assessment of climate change risk at an urban scale: Review of recent progress and outlook of future direction. Renewable and Sustainable Energy Reviews. 2021;135:110415. doi: 10.1016/j.rser.2020.110415. [DOI] [Google Scholar]
- You C, Deng Y, Hu W, et al. Estimation of the time-varying reproduction number of COVID-19 outbreak in China. International Journal of Hygiene and Environmental Health. 2020;228:1135. doi: 10.1016/j.ijheh.2020.113555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, Diao MY, Duan L, et al. The novel coronavirus (SARS-CoV-2) infections in China: Prevention, control and challenges. Intensive Care Medicine. 2020;46:591–593. doi: 10.1007/s00134-020-05977-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S, Musa SS, Lin Q, et al. Estimating the unreported number of novel coronavirus (2019-nCoV) cases in China in the first half of January 2020: A data-driven modelling analysis of the early outbreak. Journal of Clinical Medicine. 2020;9:388. doi: 10.3390/jcm9020388. [DOI] [PMC free article] [PubMed] [Google Scholar]