Meta-Analysis of Rare Adverse Events in Randomized Clinical Trials: Bayesian and Frequentist Methods

Abstract

Background/Aims:

Regulatory approval of a drug or device involves an assessment of not only the benefits but also the risks of adverse events associated with the therapeutic agent. Although randomized controlled trials (RCTs) are the gold standard for evaluating effectiveness, the number of treated patients in a single RCT may not be enough to detect a rare but serious side effect of the treatment. Meta-analysis plays an important role in the evaluation of the safety of medical products and has advantage over analyzing a single RCT when estimating the rate of adverse events.

Methods:

In this paper, we compare 15 widely-used meta-analysis models under both Bayesian and frequentist frameworks when outcomes are extremely infrequent or rare. We present extensive simulation study results and then apply these methods to a real meta-analysis that considers RCTs investigating the effect of rosiglitazone on the risks of myocardial infarction and of death from cardiovascular causes.

Results:

Our simulation studies suggest that the beta hyperprior method modeling treatment group-specific parameters and accounting for heterogeneity performs the best. Most models ignoring between-study heterogeneity give poor coverage probability when such heterogeneity exists. In the data analysis, different methods provide a wide range of log odds ratio estimates between rosiglitazone and control treatments with a mixed conclusion on their statistical significance based on 95% confidence (or credible) intervals.

Conclusions:

In the rare event setting, treatment effect estimates obtained from traditional meta-analytic methods may be biased and provide poor coverage probability. This trend worsens when the data have large between-study heterogeneity. In general, we recommend methods that first estimate summaries of treatment-specific risks across studies and then relative treatment effects based on the summaries when appropriate. Furthermore, we recommend fitting various methods, comparing the results and model performance, and investigating any significant discrepancies among them.

Introduction

Regulatory approval of a drug or device involves an assessment of not only the benefits but also the risks of adverse events associated with the therapeutic agent. Although we design randomized controlled trials (RCTs), the gold standard for evaluating effectiveness, to be large enough to detect a benefit of clinical importance, the number of treated patients may not be enough to detect infrequent adverse events. The rarer the adverse event, the less likely one or even two randomized clinical trials will provide enough of a signal, which could be problematic if a side effect of a treatment is rare but serious. The Council for International Organizations of Medical Sciences defined adverse drug reactions to be uncommon (or infrequent) with a frequency from 0.1% to 1%, rare with a frequency from 0.01% to 0.1%, and very rare with a frequency smaller than 0.01%¹.

Meta-analysis plays a role in the evaluation of the safety of medical products, whether drugs or medical devices. A single clinical trial may individually not provide sufficient information to make statements on the differential rate of occurrence of adverse events. Meta-analysis pools information on events over trials conducted prior to regulatory approval or surveillance studies after the marketing of a product to increase the number of treated patients and thereby increases the chance of seeing rare and unintended effects of the treatment².

Although meta-analysis has advantages over analyzing a single clinical trial when estimating the rate of adverse events, there are some discussions that traditional meta-analysis methods may be ill-defined or have poor performance properties with rare events^3,4,6–9,35. The main issues include (1) sparsity of data with many trials having no events (so called zero-event trials), (2) insufficient statistical power to infer the effect heterogeneity across studies, and (3) the impact of trials with large sample sizes relative to smaller ones.

It is not hard to find published investigations of the performance of many different meta-analysis methods via extensive simulation studies under the rare-event settings^6,9–11. One common limitation of most simulation studies is that the simulated data sets were generated assuming no heterogeneity in treatment effects across trials. Most studies listed above focused mainly on traditional frequentist meta-analytic methods (such as Peto, Mantel-Haenszel, and inverse variance estimators). Bayesian models for meta-analysis are gaining popularity^12,13 and they are suitable to deal with rare events, because they can handle trials with zero events more naturally than frequentist methods. In addition, Bayesian methods provide model flexibility and many choices of prior specifications based on different model assumptions¹⁴. There are, however, few publications investigating the performance of different Bayesian meta-analytic methods in the setting of rare events. Alternative meta-analysis methods for rare events have been proposed: likelihood-based Poisson random-effects models¹⁵, combining confidence intervals¹⁶, and using an arcsine difference ¹⁷.

The objective of this paper is to provide a comprehensive comparison of widely-used meta-analysis methods under both frequentist and Bayesian frameworks and then to understand the current state of meta-analytic methods for rare events. The remainder of this paper is structured as follows. The methods section provides details of different meta-analysis methods. The simulation study section reports the settings and results of our extensive simulations studies. Then we apply all these methods to a real data example and the rosiglitazone data analysis section presents the results. Finally, the discussion section discusses our work and unmet methodological challenges.

Methods

In this section, we present models estimating the log odds ratio (LOR). Relative risk and risk difference scales could be used for rare events⁶ and the related models and results are presented in Supplementary Material. We summarize the results in the Discussion section.

Models may assume treatment effects to be either constant across studies or heterogeneous; we denote the former assumption as “Common Treatment Effect (CTE)” and the latter as “Heterogeneous Treatment Effect (HTE).” We include moment-based estimators for frequentist meta-analysis methods and likelihood-based approaches for Bayesian meta-analysis methods under both common and heterogeneous treatment effect assumptions. Table 1 summarizes all models we consider.

Table 1:

Model specifications

	Assumption	Model name	Model description
Frequentist approaches
1	CTE	Naïve	Naïvely pooling estimator
2		Peto	Peto estimator
3		MH	MH estimator
4		MH(DM)1	MH estimator with data modification
5		CTE-IV(DM)1	Inverse variance estimator ignoring effect heterogeneity
6		SGS-Unwgt	Unweighted Shuster, Guo, and Skyler (SGS) estimator
7		SGS-Wgt	Weighted Shuster, Guo, and Skyler (SGS) estimator
8	HTE	HTE-DL(DM)1	DerSimonia-Laird inverse variance estimator accounting for effect heterogeneity
9		SA(DM)2	Simple average estimator
Bayesian approaches
10	CTE	CTE-Logit	Logistic model ignoring effect heterogeneity
11		CTE-Beta	Using Beta hyperprior ignoring effect heterogeneity
12	HTE	HTE-Logit	Logistic model accounting for effect heterogeneity
13		HTE-LogitSh	HTE-Logit with shrinkage prior on the effect of control group
14		AB-Logit	Arm-based logistic model
15		HTE-Beta	Using Beta hyperprior accounting for effect heterogeneity

¹Data modification to studies with zero events

²Data modification to all studies

With binary data, each study in a meta-analysis forms a 2×2 table as in Table 2. Here, i indexes study (i = 1, …, M, where M is the number of studies), and k indexes treatment with k = 1 for control and k = 2 for the treated group. We assume that the outcomes follow a binomial distribution

$$y_{ik}\sim \mathit{Bin}\left(n_{ik},p_{ik}\right),$$ (1)

where for the k^th treatment in the i^th study, y_ik is the number of events, n_ik is the number of subjects receiving treatment k, and p_ik is the probability of having an event.

Table 2:

Data structure for study i

	No. of events	No. of nonevents	Total
Active treatment	yi2	ni2 − yi2	ni2
Control treatment	yi1	ni1 − yi1	ni1
Total	yi·	ni· − yi·	ni·

Frequentist meta-analysis models

Naïve estimator.

We first consider an estimator that naïvely pools multiple contingency tables, without accounting for effect heterogeneity across studies (denoted by “Naïve”). The naïve log odds ratio estimator is written as

$${\widehat{LOR}}_{naive}=\log \frac{{\widehat{p}}_2\left(1-{\widehat{p}}_1\right)}{{\widehat{p}}_1\left(1-{\widehat{p}}_2\right)},$$ (2)

where ${\widehat{p}}_1=\frac{{\sum }_i{y}_{i1}}{{\sum }_i{n}_{i1}}$ and ${\widehat{p}}_2=\frac{{\sum }_i{y}_{i2}}{{\sum }_i{n}_{i2}}$. The standard error of ${\widehat{LOR}}_{naive}$ is calculated as $\sqrt{\frac{1}{{\sum }_i{y}_{i1}}+\frac{1}{{\sum }_i\left(n_{i1}-y_{i1}\right)}+\frac{1}{{\sum }_i{y}_{i2}}+\frac{1}{{\sum }_i\left(n_{i2}-y_{i2}\right)}}$.

Peto and Mantel-Haenszel estimators.

Peto¹⁸ and Mantel-Haenszel¹⁹ estimators assume common treatment effect across studies (denoted by “Peto” and “MH” respectively). The Peto estimator and its variance are

$${\widehat{LOR}}_{Peto}=\frac{{\sum }_i{O}_i-{\sum }_i{E}_i}{{\sum }_i{V}_i}\text{and}$$

$$\widehat{Var}({\widehat{LOR}}_{Peto})=1/\sum _i{V}_i,$$

where $O_i=y_{i2},E_i=\frac{y_{i\cdot }{n}_{i2}}{n_{i.}},V_i=\frac{y_{i\cdot }{n}_{i1}{n}_{i2}\left(n_{i\cdot }-y_{i\cdot }\right)}{n_{i.}^2\left(n_{i\cdot }-1\right)},n_{i\cdot }=n_{i1}+n_{i2}$, and y_i· = y_i1 + y_i2.

The Mantel-Haenszel estimator and its approximate variance proposed by Robins et al.²⁰ can be written as

$${\widehat{LOR}}_{MH}=\log \left[\frac{{\sum }_i\frac{y_{i2}\left(n_{i1}-y_{i1}\right)}{n_{i\cdot }}}{{\sum }_i\frac{y_{i1}\left(n_{i2}-y_{i2}\right)}{n_{i\cdot }}}\right]\text{and}$$

$$\widehat{Var}({\widehat{LOR}}_{MH})=\left[\frac{{\sum }_i{P}_i{R}_i}{2{\left({\sum }_i{R}_i\right)}^2}+\frac{{\sum }_i\left(P_i{S}_i+Q_i{R}_i\right)}{2\left({\sum }_i{R}_i\right)\left({\sum }_i{S}_i\right)}+\frac{{\sum }_i{Q}_i{S}_i}{2{\left({\sum }_i{S}_i\right)}^2}\right],$$

where $R_i=\frac{y_{i2}\left(n_{i1}-y_{i1}\right)}{n_i.}$, $S_i=\frac{y_{i1}\left(n_{i2}-y_{i2}\right)}{n_{i\cdot }}$, $P_i=\frac{y_{i2}+n_{i1}-y_{i1}}{n_{i\cdot }}$, and $Q_i=\frac{y_{i1}+n_{i2}-y_{i2}}{n_{i\cdot }}$.

Studies with zero cells are not a problem for the Peto and Mantel-Haenszel estimators because they do not calculate the observed log odds ratios of the individual studies. Nevertheless, a data modification that adds a constant 0.5 to all cells of the 2 × 2 table for a trial with zero events in either group as in Table 3 is often considered with the Mantel-Haenszel estimator. We denote the Mantel-Haenszel estimator with data modification by “MH(DM).” A few alternative data modification approaches have been proposed by Sweeting et al.⁹.

Table 3:

Data modification for study i with zero events (i.e., either y_i1 or y_i2 is zero) using a constant 0.5

	No. of events	No. of nonevents	Total
Control group	yi1 + 0.5	ni1 − yi1 + 0.5	ni1 + 1
Treated group	yi2 + 0.5	ni2 − yi2 + 0.5	ni2 + 1
Total	yi· + 1	ni· − yi· + 1	ni· + 2

Inverse variance estimators.

The inverse variance method²¹ is commonly used in meta-analysis. This method can assume either common or heterogeneous treatment effect. When heterogeneous treatment effect is assumed, we follow DerSimonian and Laird (DL)²¹ to estimate effect heterogeneity, ${\tau }_{DL}^2$ (i.e., between-study variances of log odds ratio). First, we need to calculate a study-specific weight $w_i^{*}$ as a combination of within-study and between-study variances. Suppose ${\widehat{LOR}}_i=\log \left(\frac{y_{i2}\left(n_{i1}-y_{i1}\right)}{y_{i1}\left(n_{i2}-y_{i2}\right)}\right)$ then

$$w_i^{*}=\frac{1}{v_i^{*}}=\frac{1}{\frac{1}{w_i}+{\tau }^2},$$ (3)

where 1/w_i is the within-study variance (i.e., the variance of ${\widehat{LOR}}_i$) and τ² is the between-study variance. We estimate τ² using ${\tau }_{DL}^2$ as follows

$${\widehat{\tau }}_{DL}^2=\{\begin{array}{ll}\frac{Q-df}{C},\hfill & \text{if}Q>df\hfill \\ 0,\hfill & \text{if}Q\le df,\hfill \end{array}$$ (4)

where df is the number of studies minus 1, $Q={\sum }_i{w}_i{({\widehat{LOR}}_i-\widehat{LOR})}^2,\widehat{LOR}=\frac{{\sum }_i{w}_i{\widehat{LOR}}_i}{{\sum }_i{w}_i}$, and $C={\sum }_i{w}_i-\frac{{\sum }_i{w}_i^2}{{\sum }_i{w}_i}$. As a result, the inverse variance estimator and its variance are written as

$${\widehat{LOR}}_{IV}=\frac{{\sum }_i{w}_i^{*}{\widehat{LOR}}_i}{{\sum }_i{w}_i^{*}}\text{and}$$

$$\widehat{Var}({\widehat{LOR}}_{IV})=1/\sum _i{w}_i^{*}.$$

We apply the data modification approach introduced in the previous section to the inverse variance method to handle zero events. Under the common treatment effect assumption, we force τ² in (3) to be zero and denote this estimator by “CTE-IV(DM).” We denote the estimator that uses ${\widehat{\tau }}_{DL}^2$ to account for heterogeneous treatment effect as “HTE-DL(DM).” Other estimators. Shuster, Guo, and Skyler (SGS)¹¹ proposed estimators that are functions of risk estimates in each group. These estimators are nonparametric and assume independence between studies, an assumption called studies at random. They proposed unweighted and weighted estimators, denoted by “SGS-Unwgt” and “SGS-Wgt,” respectively, for odds ratio, risk ratio, and risk difference scales.

For these estimators, one first estimates study-specific risks as ${\widehat{p}}_{ik}=y_{ik}/n_{ik}$ and then calculates summary estimates of group-specific risks as ${\widehat{\pi }}_k={\sum }_i{\widehat{p}}_{ik}/M$, where M is the number of studies. The unweighted log odds ratio estimator is given by $\log \left(\frac{{\widehat{\pi }}_2\left(1-{\widehat{\pi }}_1\right)}{{\widehat{\pi }}_1\left(1-{\widehat{\pi }}_2\right)}\right)$. The weighted log odds ratio estimator applies study-specific weights, u_i = (n_i1 + n_i2)/2, to the study-specific risk estimates for group k, ${\widehat{p}}_{ik}$. One then calculates the estimator from the weighted study-group-specific estimates as with the unweighted estimator. They provided formulas for standard errors of the unweighted and weighted estimators¹¹. We note that their unweighted estimator weights all studies equally, regardless of study sizes, while their weighted estimator weights each study by the study’s total sample size.

Bhaumik et al.¹⁰ proposed a simple average estimator. It is calculated as an average of study-specific log odds ratios after adding 0.5 to all cells in Table 2 for all trials. That is, the study-specific log odds ratio is

$${\widehat{LOR}}_{i,1/2}=\log \left(\frac{y_{i2}+0.5}{n_{i2}-y_{i2}+0.5}\right)-\log \left(\frac{y_{i1}+0.5}{n_{i1}-y_{i1}+0.5}\right).$$

Then, the simple average estimator and its variance are defined as

$${\widehat{LOR}}_{SA}=\frac{{\sum }_i{\widehat{LOR}}_{i,1/2}}{M}\text{and}\widehat{Var}({\widehat{LOR}}_{SA})=\frac{{\sum }_i{\widehat{\sigma }}_i^2({\widehat{\tau }}^2)}{M^2},$$ (5)

where M is the number of studies, ${\widehat{\sigma }}_i^2\left({\widehat{\tau }}^2\right)={\left[n_{i1}{\widehat{p}}_{i1}\left(1-{\widehat{p}}_{i1}\right)\right]}^{-1}+{\left[n_{i2}{\widehat{p}}_{i2}\left(1-{\widehat{p}}_{i2}\right)\right]}^{-1}+{\widehat{\tau }}^2$, and ${\widehat{p}}_{ik}=\frac{y_{ik}+0.5}{n_{ik}+1}$ for k = 1 and 2. We use ${\widehat{\tau }}_{DL}^2$ in (4) in the variance estimator (5). Note that this estimator uses a data modification that is different from the one used with the Mantel-Haenszel and inverse variance estimators. We denote the simple average estimator by “SA(DM).”

Bayesian meta-analysis models

Logistic regression.

Using the likelihood (1), we model the unknown parameter p_ik as follows:

$$\text{CTE-Logit}:logit\left(p_{ik}\right)={\mu }_i+dI(k=2)$$ (6)

$$\text{HTE-Logit}:logit\left(p_{ik}\right)={\mu }_i+{\delta }_{i}I(k=2),$$ (7)

where μ_i is the study-specific baseline effect (i.e., log odds of control group) and I(·) is the indicator function. Under the common treatment effect assumption in (6), d is the assumed common log odds ratio between the two k groups (control and treated) across studies. We assign vague N(0,10²) priors to μ_i and d and denote this model by “CTE-Logit.”

Under the heterogeneous treatment effect assumption in (7), δ_i is the study-specific log odds ratio. We assume δ_i∼N(d, τ²) a priori, where τ quantifies between-study effect heterogeneity, and d has a vague N(0, 10²) prior. We assume a Uniform(0,2) prior distribution for τ, where the range of this uniform prior makes it considerably vague, relative to the scale of the log odds ratio. We consider two priors for μ_i: vague and shrinkage priors (denoted by “HTE-Logit,” and “HTE-LogitSh,” respectively). The HTE-Logit model assigns a vague N(0, 10²) prior to μ_i. The HTE-LogitSh sets ${\mu }_i\sim N\left(m,{\tau }_{\mu }^2\right)$, where m is the overall mean log odds of the event in the control group, and τ_μ is the heterogeneity of the log odds across the studies’ control groups. We set m∼N(0, 10²) and τ_μ∼Uniform(0, 2), so that the shrinkage prior allows study-specific baseline effects (μ_i) and log odds ratios (δ_i) to vary across studies. Arm-based model. Recently, Hong et al.²² proposed an arm-based parameterization in network meta-analysis, an extension of meta-analysis to compare more than two treatments simultaneously. We simplify this model to fit an arm-based meta-analysis. This model estimates the treatment-specific risks and allows heterogeneity across studies. The model can be written as

$$logit\left(p_{ik}\right)={\theta }_k+{\eta }_{ik},$$ (8)

where θ_k is the log odds of treatment k and the η_ik are random effects allowing heterogeneity of the log odds. We assume that ${\left({\eta }_{i1},{\eta }_{i2}\right)}^T\sim BVN({(0,0)}^T,\mathrm{\Sigma })$ where BV N stands for bivariate normal distribution. We use priors θ_k∼N(0, 10²) and Σ⁻¹∼Wishart(Ω, 2), where Ω is a 2 × 2 matrix resulting in a vague prior for Σ⁻¹. Note that the choice of Ω depends on data, outcomes, and scales of parameters of interest. We used a diagonal matrix with diagonal elements equal to 0.02 for simulated data and 0.25 for data analysis. One can obtain log odds ratio from θ₂ − θ₁. We call this model “AB-Logit.”

Beta hyperprior distribution.

We also consider pooling studies’ arm-specific risks using beta hyperprior distributions. First, we assume that the probability of having an event with treatment k is constant across studies. For the likelihood, we replace p_i1 and p_i2 in (1) with p₁ and p₂, such as

$$y_{ik}\sim Bin\left(n_{ik},p_k\right).$$

Then, we assign prior distributions p_k∼Beta(α_k, β_k), where α_k and β_k are pre-specified. We employ common α and β values instead of α_k and β_k for simplicity, given that we use Beta(1,1) priors. We call this model “CTE-Beta.”

We also assume heterogeneity across studies, i.e., the p_ik vary across studies. We define a hierarchical prior distribution for the p_ik, namely,

$$p_{ik}\sim Beta\left(U_k{V}_k,\left(1-U_k\right)V_k\right).$$ (9)

With this notation, E(p_ik |U_k, V_k) = U_k and $Var\left(p_{ik}|U_k,V_k\right)=\frac{U_k\left(1-U_k\right)}{V_k+1}$. In terms of the more common Beta(a_k, b_k) parameterization, $U_k=\frac{a_k}{a_k+b_k}$ and V_k = a_k + b_k. We use this parameterization because we want to assign a prior distribution directly to the mean of p_iks, which is U_k. Study heterogeneity in the probability scale is measured by $\frac{U_k\left(1-U_k\right)}{V_k+1}$. We assign V_k a vague prior, namely Inverse-Gamma(1, 0.01). U_k has a Beta(1, 1) prior distribution. We call this model “HTE-Beta.”

Bayesian model comparison.

We compare the performance of fitted Bayesian models in our data example using the Watanabe-Akaike or widely applicable information criterion²³. This criterion evaluates predictive accuracy for a fitted model and then adjusts for overfitting based on the effective number of parameters. In addition, it provides more stable estimates than the deviance information criterion. One prefers models that have smaller values of Watanabe-Akaike information criterion²⁴.

Computation

Simulation studies and data analyses were conducted in R²⁵. We fit the Peto, Mantel-Haenszel, and inverse variance estimators using the R package metafor²⁶; we used user-written functions to compute the remaining frequentist estimators. Bayesian models were fitted using the R package R2jags²⁷ for simulations and rstan²⁸ for the data analysis, as rstan provided reliable Watanabe-Akaike information criterion values. For Bayesian models, a total of 10,000 posterior samples were used after a 10,000 burn-in from a single Markov chain for our simulation studies, while our data analyses used two Markov chains, with each chain having a total of 30,000 posterior samples after a 20,000 burnin. We checked trace plots and scatter plots of pairs of parameters to ensure convergence; they converged well. The R code and the associated Bayesian model files are available at https://github.com/HwanheeHong/MetaAnalysis_RareEvents.

Simulation study

Settings

In this simulation study, we compare the performance of fifteen meta-analysis methods (9 frequentist and 6 Bayesian), summarized in Table 1. The results compare bias, mean squared error, and coverage probability of 95% intervals for each method’s log odds ratio estimate. The simulation settings and results with relative risk and risk difference scales are presented in Supplementary Material.

Our simulation setup is built upon that used in Shuster et al. (2012)¹¹. We generated 10,000 simulated meta-analysis datasets, each consisting of thirty studies comparing a treatment of interest to a control. The control group’s sample size in study i, n_i1, is sampled from a Uniform(50,1000) distribution. We set the size of the corresponding treated group, n_i2, to be equal to n_i1 to avoid an unrealistic study design that has extremely unbalanced sample sizes. We sampled probabilities for having an event (i.e., risks) for the two groups in study i as follows: p_ik∼Uniform(p_k(1−0.5D), p_k(1+0.5D)). p_k is the true risk for group k = 1 or 2, and D controls between-study heterogeneity of the risks. Table 4 shows the six pairs of true underlying risks that we consider in our six different simulation scenarios. We vary p_k to consider three null cases, namely, (p₁, p₂) = (0.002, 0.002), (0.005, 0.005) and (0.05, 0.05), and three alternative cases, (p₁, p₂) = (0.002, 0.004), (0.005, 0.01), and (0.05, 0.1). The true log odds ratios are 0 and around 0.7 in the null and alternative cases, respectively. As the true risks decrease, the number of studies with zero events increases. For example, the average numbers of studies with zero events in either group over 10,000 iterations were 18, 8, and less than 1 for the three null cases. In addition, we varied the degree of between-study heterogeneity of risks by setting D to 0, 1, or 2, where D = 0 means no heterogeneity in risks. As a result, there are 6 × 3 = 18 different settings. Given p_ik and n_ik samples, we generated the binary events as y_ik∼Binomial(n_ik, p_ik).

Table 4:

True risk parameters, p_k, and the associated odds ratio (OR) and log odds ratio (LOR) values used in the simulation study

Null				Alternative
p1	p2	OR	LOR	p1	p2	OR	LOR
0.002	0.002	1	0	0.002	0.004	2.00	0.70
0.005	0.005	1	0	0.005	0.01	2.01	0.70
0.05	0.05	1	0	0.05	0.1	2.11	0.74

Results

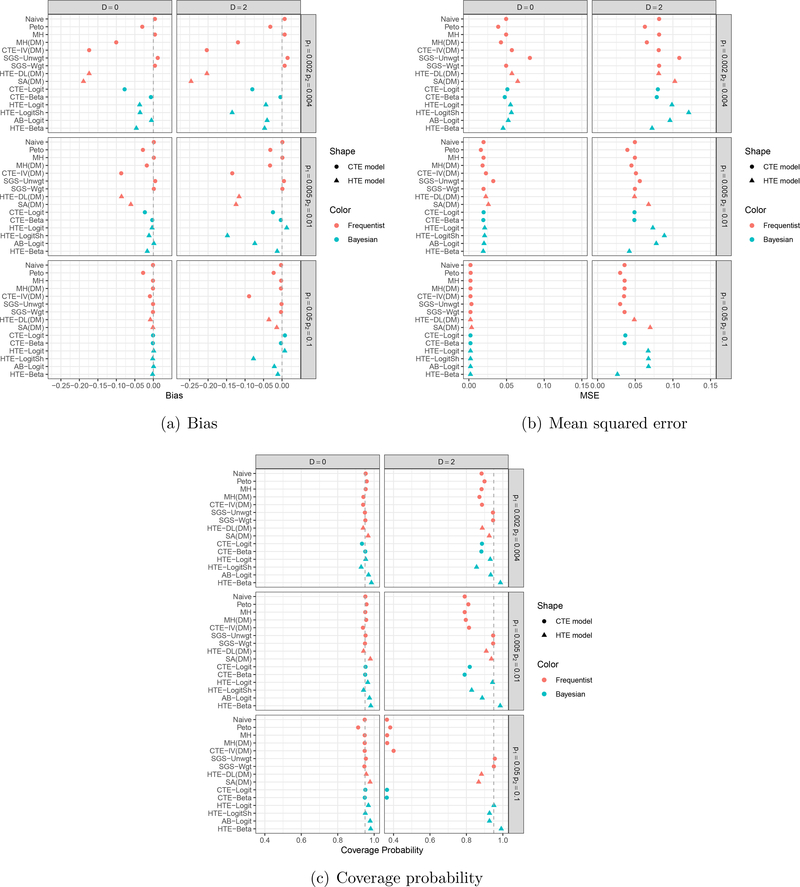
Figures 1 and 2 exhibit bias, mean squared error, and coverage probability of log odds ratio estimates for three null and three alternative cases, respectively. Frequentist and Bayesian models are plotted in red and blue, and common and heterogeneous treatment effect models are plotted using circle and triangle characters, respectively. We present results under D = 0 and 2; the results when D = 1 are presented in Supplementary Material, as they showed similar patterns to those under D = 2 with less extreme quantities.

Figure 1:

Simulation results in the null case: (a) Bias, (b) Mean squared error, and (c) Coverage probability. Frequentist and Bayesian models are plotted in red and blue, respectively; common and heterogeneous treatment effect models are plotted using circles and triangles, respectively.

Figure 2:

Simulation results in the presence of a treatment effect (i.e., the alternative case): (a) Bias, (b) Mean squared error, and (c) Coverage probability. Frequentist and Bayesian models are plotted in red and blue, respectively; common and heterogeneous treatment effect models are plotted using circles and triangles, respectively.

Under the null cases in Figure 1, all frequentist estimators, which are moment-based estimators, showed little or no bias, as did the three Bayesian methods that model treatment-specific risks, namely CTE-Beta, AB-Logit, and HTE-Beta. CTE-Logit, HTE-Logit, and HTE-LogitSh, however, showed relatively large biases, and the true risks were small. The bias may arise because these three methods rely on a logistic regression model. We generated each meta-analysis dataset from a binomial distribution after we sampled treatment-specific risks, p_ik, not treatment effects (i.e., log odds ratios), δ_i in (7). When the risks are small, studies will have zero cells, making study-specific estimation of the log odds ratio mathematically unwieldy. The estimates across studies become roughly bimodal, with some study estimates around 0 and some approaching infinity. CTE-Logit, HTE-Logit, and HTE-LogitSh model log odds ratio directly under the normality assumption of the δ_i, while CTE-Beta, AB-Logit, and HTE-Beta model treatment-specific parameters, such as the log odds of an event. THE-LogitSh had the largest bias when D = 2, suggesting that a shrinkage normal prior on log odds of an event in the control group may not be appropriate in the presence of large heterogeneity.

Mean squared error decreased as true risks increased (i.e., fewer rare events). When D = 2, MH(DM), CTE-IV(DM), HTE-DL(DM), SA(DM), and HTE-Beta tended to give small mean squared errors, while SGS-Unwgt, HTE-Logit, HTE-LogitSh, and AB-Logit gave large mean squared errors. In terms of coverage probability, SGS-Unwgt, SGS-Wgt, and HTE-Beta provided close to or slightly larger than the nominal level 0.95 across all scenarios. All common treatment effect models, except SGS-Unwgt and SGS-Wgt, had poor coverage in the presence of large between-study heterogeneity (D = 2), and it got worse as the true risks grew larger. This seemed counterintuitive, since all common treatment effect models showed little or no bias in Panel (a). We found that the estimated standard errors of these estimates were so small that their 95% confidence or credible intervals were very narrow, except SGS-Unwgt and SGS-Wgt; the widths of their 95% confidence intervals were sufficiently wider than estimators from the other common treatment effect models that their coverage probabilities were close to the nominal level 0.95.

Figure 2 shows the results for the three alternative cases. The Naïve, Mantel-Haenszel, SGS-Unwgt, SGS-Wgt, CTE-Beta, AB-Logit, and HTE-Beta methods had smaller biases when D = 0 and 2. CTE-IV(DM), HTE-DL(DM), and SA(DM) showed large biases when the true risks were small under both D = 0 and 2. Again, HTE-LogitSh gave large biases only when D = 2. In terms of mean squared error, four heterogeneous treatment effect models, SA(DM), HTE-Logit, HTE-LogitSh, and AB-Logit, gave large mean squared error when D = 2, while HTE-Beta and HTE-DL(DM) gave small mean squared error. SGS-Unwgt and SA(DM) had larger mean squared errors in the lowest risk scenario than any other frequentist methods. We see similar results to the null cases in terms of coverage probability.

In the alternative cases, we note two interesting findings that were not observed under the null cases. First, applying the data modification to Mantel-Haenszel resulted in large bias when the true risks were small. That is, adding 0.5 to the contingency table of studies with zero events may bias estimation, especially when a large number of studies report zero events and there is a treatment effect. Second, SGS-Unwgt, SGS-Wgt and SA(DM) provided very different point estimates, with SA(DM) exhibiting large biases. This discrepancy between the methods may relate to the simulated data generating mechanism being aligned with the SGS-Unwgt and SGS-Wgt estimators’ structure but not that of SA(DM). The target of the SGS-Unwgt and SGS-Wgt estimators is estimation of treatment-specific risks. These estimators calculate log odds ratio or other treatment effects based on estimates (weighted or unweighted) of treatment-specific risks, ${\widehat{p}}_k$. The target parameter of SA(DM), on the other hand, is the relative treatment effect, log odds ratio, and it is estimated as an average of study-specific LOR_i after applying the data modification to each study’s table.

Rosiglitazone data analysis

The rosiglitazone dataset²⁹ is a popular example with which to study different meta-analysis models with rare events. Many researchers have re-analyzed these data using various methods^8,30–32. The authors have updated the data by adding a few more relevant trials³³, and we use these updated data as our real data example. They collected and analyzed these data to investigate the effect of rosiglitazone on the risks of myocardial infarction and of death from cardiovascular causes. There are 56 trials, of which 15 did not report any myocardial infarction, and 29 trials did not report any cardiovascular death in either group.

We apply all models in Table 1 to the rosiglitazone data. For the Bayesian methods, we calculate the Watanabe-Akaike information criterion to compare fitted models. We conducted meta-analyses under four different data settings: (1) include all 56 studies; (2) exclude the RECORD trial, considered as large following Nissen and Wolski³³ (55 studies included); (3) select studies comparing rosiglitazone + X to X alone, where X can be either placebo or an active treatment (42 studies included); and (4) select studies strictly comparing rosiglitazone to placebo (13 studies included). In the 56 studies, the total number of subjects in the rosiglitazone group is 19509 with 159 (pooled risk=0.00815) and 105 (0.00538) myocardial infarction and cardiovascular death events, respectively; the total number of subjects in the control group is 16022, with 136 (0.00848) and 100 (0.00624) myocardial infarction and cardiovascular death events, respectively. We note that the correlation between sample size and observed log odds ratio in each data setting vary from −0.32 to 0.37.

Figure 3 shows the estimated log odds ratios for the 4 different data settings. log odds ratios less than zero favor rosiglitazone, i.e., lower odds of having an myocardial infarction or cardiovascular death event than the control group. For the myocardial infarction outcome, the Peto, Mantel-Haenszel, and SGS-Wgt methods yielded 95% confidence intervals that excluded 0 when all studies were included. The estimated between-study variability in log odds ratio estimates, $\widehat{\tau }$, were 0, 0.28, and 0.26 with HTE-DL(DM), HTE-Logit, and HTE-LogitSh, respectively. Note that it is known that frequentist heterogeneous treatment effect models underestimate effect heterogeneity compared to their Bayesian counterparts³⁴. Excluding the RECORD trial did not change the point estimates or conclusions much, although the 95% intervals became slightly wider.

Figure 3:

Results of the rosiglitazone data analyses: (a) Myocardial infarction (b) Death from cardiovascular causes (CV death). Log odds ratios less than zero favor rosiglitazone with lower odds of having an event than control. ^∗ The HTE-Beta model converged poorly for the fourth data setting.

When we considered the trials comparing rosiglitazone + X to treatment X alone, the estimated log odds ratios became larger (i.e., stronger effect of rosiglitazone on the odds of having an myocardial infarction event) than those from the other data settings. The Peto, Mantel-Haenszel, SGS-Unwgt, SGS-Wgt, and CTE-Logit methods’ 95% intervals excluded zero. When we included only the 13 studies that compared rosiglitazone to placebo, the associated 95% intervals were wide, because of the small number of events: 25 and 14 events out of 7449 and 4860 subjects in the rosiglitazone and placebo groups, respectively. As a result, the HTE-Beta model did not converge and a more informative prior of V_k would improve model convergence.

For cardiovascular death, all methods except SGS-Unwgt provided point estimates close to zero and 95% intervals that included zero in the 56-study data set. The $\widehat{\tau }$ were 0, 0.41, and 0.34 with HTE-DL(DM), HTE-Logit, and HTE-LogitSh, respectively. Excluding the RECORD trial or comparing rosiglitazone + X to treatment X alone resulted in log odds ratio estimates unfavorable to rosiglitazone, although most 95% intervals included zero; the exceptions were the SGS-Unwgt and SGS-Wgt estimators. When analyzing only the 13 placebo-controlled trials, all frequentist methods provided similar point estimates to the third data setting, except SGS-Unwgt. Again, all methods provided wider 95% intervals and the HTE-Beta model did not converge in this sparse data setting: eleven trials of the thirteen trials had one or zero cardiovascular death and four out of the eleven trials had no events.

Table 5 displays Watanabe-Akaike information criterion values obtained from the 6 fitted Bayesian models for all outcomes and data settings. For the myocardial infarction outcome, HTE-LogitSh was the best model by the Watanabe-Akaike information criterion for the first three data settings. Although HTE-Beta provided the smallest Watanabe-Akaike information criterion in the fourth setting, when single-agent placebo was the control, the model did not converge. AB-Logit was second place in terms of the Watanabe-Akaike information criterion in each of the data settings. For the cardiovascular death outcome, HTE-Logit (under the first two data settings), HTE-LogitSh (third data setting), and HTE-Beta (fourth data setting) provided the smallest Watanabe-Akaike information criterion values. Again, note that HTE-Beta did not converge in the fourth data setting and AB-Logit provided the second smallest Watanabe-Akaike information criterion value. Across all outcomes and data settings, CTE-Beta provided largest or second largest Watanabe-Akaike information criterion values, indicating a poor fit to the rosiglitazone data.

Table 5:

Watanabe-Akaike information criterion (WAIC) values for 6 Bayesian models fit to the rosiglitazone data. The smallest Watanabe-Akaike information criterion value among the 6 models for an outcome and a data setting is in bold. The predictive accuracy is estimated by the expected log predictive density for a new data point (elpd) and is corrected by the effective number of parameters (p).

	Myocardial Infarction			Cardiovascular Death
Model	elpd	p	WAIC	elpd	p	WAIC
All studies (56 studies)
CTE-Logit	−140.1	35.7	280.2	−90.4	24	180.8
CTE-Beta	−277.9	31.2	555.8	−299.2	59.2	598.3
HTE-Logit	−140.5	36.2	281	−89.7	23.8	179.4
HTE-LogitSh	−129.6	19.4	259.2	−90.4	16.5	180.8
AB-Logit	−132.7	25.2	265.5	−91.8	20	183.7
HTE-Beta	−136.9	31.3	273.8	−96.2	25.5	192.3
All studies except RECORD trial (55 studies)
CTE-Logit	−132.9	35.1	265.9	−80.5	21.7	161.1
CTE-Beta	−187.7	14.1	375.4	−109.6	3.7	219.2
HTE-Logit	−133.2	35.5	266.4	−81.2	22.5	162.4
HTE-LogitSh	−122.8	18.6	245.6	−82.1	14.8	164.1
AB-Logit	−125.6	24.3	251.1	−85.1	19.3	170.3
HTE-Beta	−130.7	29.9	261.4	−92.7	26.1	185.4
Trials comparing rosiglitazone + X vs. X alone (42 studies)
CTE-Logit	−103.9	29.4	207.9	−66	19.4	132.1
CTE-Beta	−104.5	2.7	209	−88.1	4.14	176.2
HTE-Logit	−104.2	30.1	208.3	−65.9	19.7	131.9
HTE-LogitSh	−95.2	15.7	190.4	−65.1	12.7	130.2
AB-Logit	−95.2	19.9	190.4	−66.3	16.06	132.6
HTE-Beta	−99.3	22.8	198.7	−70.1	20.6	140.3
Trials comparing rosiglitazone vs. placebo (13 studies)
CTE-Logit	−35.4	9.7	70.9	−28.6	8.9	57.3
CTE-Beta	−35.1	3.0	70.2	−29.2	3.4	58.4
HTE-Logit	−35.2	10.1	70.3	−28.3	9.2	56.7
HTE-LogitSh	−32.5	5.5	64.9	−25.6	5	51.2
AB-Logit	−32.1	6.9	64.1	−24.7	5.8	49.4
HTE-Beta*	−32.0	7.7	64.0	−24.6	6.9	49.3

^*The HTE-Beta model converged poorly for the fourth data setting.

Discussion

We considered many different meta-analytic models when the outcome event is rare. We assessed and compared the performance of frequentist and Bayesian approaches via an extensive simulation study under various data generating settings. The simulations considered really low frequency to somewhat rare event risks and examined no between-study heterogeneity to large heterogeneity. We also fitted all models to the rosiglitazone data and compared the Bayesian models using the Watanabe-Akaike information criterion.

Our simulation results suggest that we should interpret results of meta-analyses carefully in very low frequency settings. Overall, HTE-Beta seemed to perform among the best. AB-Logit also performed consistently well across all settings, except for mean squared error when between-study heterogeneity in risks existed. Among moment-based frequentist estimators, the SGS-Unwgt and SGS-Wgt estimators performed well, although the SGS-Unwgt estimator gave relatively large mean squared error under the low-risk settings. The Mantel-Haenszel estimator without a data modification provided no or little bias but had somewhat large mean squared error and under-coverage. Peto performed similarly to Mantel-Haenszel but was slightly more biased than Mantel-Haenszel in the alternative case. All frequentist and Bayesian common treatment effect models, except the SGS-Unwgt and SGS-Wgt estimators, tended to provide poor coverage probabilities when between-study heterogeneity existed.

In our data analyses, log odds ratio estimates and their 95% intervals differed by method. We would not expect all of the methods to be quantitatively the same, but most should be qualitatively similar. If there is great discrepancy across methods, then it may be because of a high degree of study-to-study heterogeneity or correlation between study design and risks^11,35. One should investigate the source of such discrepancies, particularly in terms of model goodness of fit. Any method that assumes a common effect across studies may be wrong if there is evidence of a large degree of heterogeneity across studies as, for example, if the studies incorporate different controls.

We noticed a few interesting results in the rosiglitazone data analysis. First, the Naïve and CTE-Beta methods provided similar results, because the closed form of the posterior mean of risks for the CTE-Beta model is equivalent to the Naïve pooled risks. Second, CTE-IV(DM) and HTE-DL(DM) provided exactly the same results, because the estimated between-study heterogeneity ${\widehat{\tau }}_{DL}=0$ with HTE-DL(DM). Third, SGS-Unwgt point and interval estimates were very different from those of SGS-Wgt and gave a totally different conclusion under certain data settings. In the 56-study data set, SGS-Unwgt indicated an increased risk of cardiovascular death for rosiglitazone with the associated 95% interval that excluded zero, while the SGS-Wgt estimate was close to zero and the associated 95% interval included zero. In addition, these two estimators tended to provide largely different point estimates even with the 13 placebo-controlled trials. Finally, SGS-Unwgt and SA(DM) occasionally provided very different point estimates. The SA(DM) estimator gave estimates close to the null across all data settings with both outcomes, while SGS-Unwgt, with narrow 95% intervals, provided strong evidence of greater risk of an event with rosiglitazone. We observed similar trends in our simulation study, again because the target parameters of these two estimators differ.

Furthermore, the rosiglitazone data analysis showed some findings that differed from what we observed in the simulation study. Simulation study results are valid and applicable to a real data analysis only when the simulation data generating mechanism agrees with the true data generating mechanism of the real data. It is untestable, however, whether the rosiglitazone data follow the same data generating mechanism that we used in our simulation study. Instead, we investigated key empirical features (such as correlation between sample size and risks) in the rosiglitazone data and assessed difference between simulated and real data. First, Although our simulation studies suggested that HTE-Beta, AB-Logit, and SGS-Wgt are the generally favored models and HTE-LogitSh may be one of the least favorite models, the Bayesian model comparison using the Watanabe-Akaike information criterion in our rosiglitazone data analysis suggested that HTE-LogitSh was the best fitting model. Second, SGS-Wgt always provided much narrower 95% confidence intervals than SGS-Unwgt. This trend was not observed in our simulations, though. The difference may be because of a non-zero correlation between study design and observed log odds ratio in the rosiglitazone data, whereas the simulations did not include such correlation. Shuster et al. (2012)¹¹ pointed out that SGS-Wgt could be more influenced by large trials than SGS-Unwgt. One advantage of SGS-Wgt, however, is that it tends to have narrower confidence limits as the number of studies increases.

Shuster and Walker³⁵ stated two points that need to be considered in meta-analysis methods. One may need to properly handle an interaction between sample size and treatment effect with meta-analysis methods that use weights based on sample sizes, and one may also need to consider the weights as random variables. They argued that most widely-used meta-analysis methods with binary outcomes do not consider these two issues. Instead, these methods assume independence of within-study effects and design, called effects at random, and could provide biased estimates. Our simulation study did not address these issues specifically, and further studies are needed.

The rosiglitazone data have flaws that limit the ability to assess if rosiglitazone increases the risks of myocardial infarction and cardiovascular death. A major concern is that it is unclear what the control group is. The data set includes some studies with active treatments as the control groups and some with placebo controls. Some trials compared rosiglitazone to placebo while a few trials compared rosiglitazone to glyburide. It is questionable whether we can consider placebo and glyburide as comparable control groups. Similarly, it is questionable whether the log odds ratio of rosiglitazone compared to placebo can be combined with log odds ratio of rosiglitazone + X compared to X alone. Nissen and Wolski³³ tackled this issue by providing results from several meta-analyses that included studies having the same comparator (insulin, metformin, sulfonylurea, or placebo). For these specific data, a network meta-analysis may be a more reasonable approach, because the data have non-comparable treated and control groups across the trials²².

Although our findings and discussion were mainly based on the log odds ratio scale, it is important to consider other scales, such as the log relative risk and risk difference, and check the consistency of findings³⁶. Our simulation and data analysis results with the log relative risk scale were very similar to those for the log odds ratio scale. This is expected as the odds ratio and relative risk are similar numerically for rare events. In our simulations with the risk difference scale, all methods provided very small biases and mean squared errors, but some methods showed poor coverage when outcomes were frequent and heterogeneity was large (see Section 2 in Supplementary Material). In the data analysis, the conclusions about treatment effect with risk difference and log odds ratio estimates were the same as those with log odds ratio. Note that reporting both absolute measures (e.g., risk difference) and relative measures (e.g., log odds ratio and log relative risk) might be useful in a meta-analysis that concerns rare events. Absolute measures usually provide a more clinically straightforward interpretation than relative measures, while relative measures tend to have less statistical heterogeneity than absolute measures³⁶. However, Efthimiou (2018) warns against use of risk differences when faced with rare events³⁷. Bayesian methods are advantageous and flexible when estimating different effect scales and interpreting them based on posterior probabilities.

In summary, when a rare binary event is the outcome of interest, treatment effect estimates obtained from traditional meta-analytic methods may be biased and provide poor coverage probability. This trend worsens when there is large between-study heterogeneity. Effect estimates vary when applying different models and are likely to depend on the characteristics of the data (e.g., level of between-study heterogeneity, rarity of outcomes, correlation between sample size and effect size, and so on). As such, inferences should be drawn cautiously. In general, we recommend methods that focus on first estimating treatment-specific risks and then estimating treatment differences based on summaries of the risks across the studies. Of course, this approach makes most sense when the studies in the meta-analysis share the same treatment and control arms. To avoid making a wrong decision, we recommend fitting various methods, comparing the results and model fit (for Bayesian approaches), and investigating any significant discrepancies across them.